| Issue |
A&A
Volume 512, March-April 2010
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200913303 | |
| Published online | 17 March 2010 | |
On the power spectrum of solar surface flows
M. Rieutord1 - T. Roudier1 - F. Rincon1 - J.-M. Malherbe2 - N. Meunier3 - T. Berger4 - Z. Frank4
1 - Laboratoire d'Astrophysique de Toulouse-Tarbes,
Université de Toulouse, CNRS, 14 avenue E. Belin, 31400 Toulouse, France
2 - LESIA, Observatoire de Paris, Section de Meudon, 92195 Meudon, France
3 - LAOG, Université Joseph Fourier, CNRS, BP 43, 38041 Grenoble Cedex, France
4 - Lockheed Martin Advance Technology Center, Palo Alto, CA, USA
Received 16 September 2009 / Accepted 20 November 2009
Abstract
Context. The surface of the Sun provides us with a unique
and very detailed view of turbulent stellar convection. Studying its
dynamics can therefore help us make significant progress in stellar
convection modelling. Many features of solar surface turbulence like
the supergranulation are still poorly understood.
Aims. The aim of this work is to give new observational
constraints on these flows by determining the horizontal scale
dependence of the velocity and intensity fields, as represented by
their power spectra, and to offer some theoretical guidelines to
interpret these spectra.
Methods. We use long time-series of images taken by the Solar
Optical Telescope (SOT) on board the Hinode satellite; we reconstruct
both horizontal (by granule tracking) and vertical (by Doppler effect)
velocity fields in a field-of-view of
![]() Mm2.
The dynamics in the subgranulation range can be investigated with
unprecedented precision thanks to the absence of seeing effects and the
use of the modulation transfer function of SOT for correcting the
spectra.
Mm2.
The dynamics in the subgranulation range can be investigated with
unprecedented precision thanks to the absence of seeing effects and the
use of the modulation transfer function of SOT for correcting the
spectra.
Results. At small subgranulation scales down to 0.4 Mm the
spectral density of kinetic energy associated with vertical motions
exhibits a k-10/3-like power law, while the intensity fluctuation spectrum follows either a k-17/3 or a k-3-like
power law at the two continuum levels investigated (525 and 450 nm
respectively). We discuss the possible physical origin of these
scalings and interpret the combined presence of k-17/3 and k-10/3
power laws for the intensity and vertical velocity as a signature of
buoyancy-driven turbulent dynamics in a strongly thermally diffusive
regime. In the mesogranulation range and up to a scale of 25 Mm,
we find that the amplitude of the vertical velocity field decreases
like
![]() with the horizontal scale
with the horizontal scale ![]() .
This behaviour corresponds to a k2
spectral power law. Still in the 2.5-10 Mm mesoscale range, we
find that intensity fluctuations in the blue continuum also follow a k2
power law. In passing we show that granule tracking cannot sample
scales below 2.5 Mm. We finally further confirm the presence of a
significant supergranulation energy peak at 30 Mm in the
horizontal velocity power spectrum and show that the emergence of a
pore erases this spectral peak. We tentatively estimate the scale
height of the vertical velocity field in the supergranulation range and
find 1 Mm; this value suggests that supergranulation flows are
shallow.
.
This behaviour corresponds to a k2
spectral power law. Still in the 2.5-10 Mm mesoscale range, we
find that intensity fluctuations in the blue continuum also follow a k2
power law. In passing we show that granule tracking cannot sample
scales below 2.5 Mm. We finally further confirm the presence of a
significant supergranulation energy peak at 30 Mm in the
horizontal velocity power spectrum and show that the emergence of a
pore erases this spectral peak. We tentatively estimate the scale
height of the vertical velocity field in the supergranulation range and
find 1 Mm; this value suggests that supergranulation flows are
shallow.
Key words: convection - turbulence - sun: photosphere
1 Introduction
A complete understanding of thermal convection in stars remains one of the main challenges of present day astrophysics. The Sun offers an unsurpassed detailed view to address this question. Solar convection is highly non-linear - typical Reynolds numbers are over 1010 - making fully detailed direct numerical simulations down to the viscous dissipation scales unaffordable. In spite of this difficulty, some observed features of solar convection like for instance granulation are rather well understood (e.g. Stein & Nordlund 2000). Dynamical features at larger scales like the supergranulation pattern are much less understood. Supergranulation is characterised by a horizontal velocity field spanning scales from 15 Mm to 75 Mm according to the recent work of Rieutord et al. (2008). Despite several attempts, supergranulation has not been identified in large-eddy or direct numerical simulations (e.g. Rieutord et al. 2002; Stein et al. 2009; Rincon et al. 2005). Its origin remains unknown, although some scenarios have been proposed. The classical picture (Simon & Leighton 1964) is a linear thermal convection scenario which associates supergranulation cells with the second ionisation of helium. Other scenarios put forward the idea that supergranulation is a surface phenomenon, as actually indicated by the recent results of local helioseismology (Gizon & Birch 2005). Rieutord et al. (2000) suggested that it could be the result of a large-scale instability of surface granular convection. Rincon & Rieutord (2003) proposed that some fixed flux boundary condition is imposed by the granulation to the layers just below: with these boundary conditions, the buoyancy destabilises the largest available scales. The associated convective motions have a fairly low intensity contrast (van der Borght 1974), very much like supergranulation cells (Meunier et al. 2007). Rincon & Rieutord (2003) further showed that an effective finite but large horizontal convection scale can be obtained in this framework by considering the dynamical effects of a mean magnetic field on the flow. Collective plume interactions (Rast 2003; Crouch et al. 2007) and travelling-wave sheared (Green & Kosovichev 2006) convection or magnetoconvection (Green & Kosovichev 2007) have also been suggested as a possible origin of supergranulation.
Table 1: The position and amplitude of the supergranulation peak for various data sets.
Overall the constraints on the large-scale dynamics of solar convection imposed by models and theories are still very loose. Guidance from observations is thus much desired. Particularly if a dynamical connection exists between granulation and supergranulation, some hints of such a scale interaction should be found in the dynamics of intermediate horizontal scales. Flows in the 3-10 Mm range are little known. This range of scales is traditionally referred to as the mesogranulation range after the work of November et al. (1981), but the very existence of genuine enhanced convective motions at these scales has been much debated (Rieutord et al. 2000; Shine et al. 2000; Straus & Bonaccini 1997; Straus et al. 1992). As pointed out in Rieutord et al. (2000), the main problem with mesogranulation was its way of detection, namely through the measurement of the horizontal divergence of the flows, which is highly sensitive to the way data are reduced. The very nature of the flows at these scales is nonetheless important to answer the question of the origin of supergranulation.
In order to make progress, it is clear that the large-scale side of the granulation spectral peak should be investigated in more detail. Simple models like the mixing-length theory or plume dynamics (Rieutord & Zahn 1997) do not predict any special spectral feature when the scale (horizontal or vertical) grows. Hydrodynamic numerical simulations like the recent ones of Stein et al. (2009) seem to go in the same direction and do not exhibit any spectral feature reminiscent of supergranulation (see also Nordlund et al. 2009). However, kinetic energy spectra derived from the radial velocity measured by SOHO/MDI (i.e. from dopplergrams) do show a rise of the spectral kinetic energy density at a scale of 11 Mm and a peak at 36 Mm (Hathaway et al. 2000). These results are clearly confirmed by the recent measurement of the horizontal surface flows at disc centre with the wide-field high resolution camera CALAS at Pic-du-Midi (Rieutord et al. 2008). These observations are therefore clearly at odds with the most advanced numerical models of solar surface convection.
In this paper we wish to provide accurate observational facts to guide modelling efforts and impose more constraints for theories. For this purpose we use new data sets collected by the Hinode mission and especially by the SOT instrument. Because of their high spatial resolution and their very low noise, these data are appropriate to either refine previous measurements or investigate new properties of the flows. In particular the subgranulation range can now be investigated as never before. We shall focus our attention on the power spectra of the flows because the information that can be obtained from such representations is usually the most robust aspect of these highly turbulent flows.
The paper is organised as follows: after a brief presentation of the data and the techniques to process them (Sect. 2), we detail the spectral properties of the measured velocity fields (Sect. 3) and the intensity field (Sect. 4). A discussion and physical interpretation of the results follows (Sect. 5). The main results and conclusions are summarised at the end of the paper (Sect. 6).
2 The data and the reduction procedure
We used multi-wavelength data sets of the Solar Optical Telescope (SOT)
on board the HINODE![]() mission (e.g. Suematsu et al. 2008; Ichimoto et al. 2004).
The SOT has a 50 cm primary mirror with a spatial resolution about
0.2
mission (e.g. Suematsu et al. 2008; Ichimoto et al. 2004).
The SOT has a 50 cm primary mirror with a spatial resolution about
0.2
![]() at 550 nm.
at 550 nm.
2.1 Horizontal velocities
A first set of images taken at disc centre was recorded continuously
from 29 August 10:17 UT until 31 August 10:19 UT 2007, except for an
interruption of seven minutes on 30 August at 10:43 UT. We used the set taken with the
broadband filter imager (BFI) with a spectral width of 0.22 nm
(Wedemeyer-Böhm & Rouppe van der Voort 2009) in the blue continuum at 450.45 nm. The mean time step
between two successive frames is 50.1 sec. The field-of-view with BFI
is
![]() with a pixel of 0
with a pixel of 0
![]() 109 (
109 (
![]() ). After alignment,
the useful field-of-view was reduced to
). After alignment,
the useful field-of-view was reduced to
![]() or
or
![]() Mm2 during 33 h. The data were also
Mm2 during 33 h. The data were also ![]() filtered with a phase velocity threshold of 6 km s-1 to keep only
convective motions.
filtered with a phase velocity threshold of 6 km s-1 to keep only
convective motions.
We determined the horizontal velocity field for various time averages from this set of data, using our algorithm of granule tracking CST (Rieutord et al. 2007). We recall that because of the nature of granules their motion is representative of the large-scale plasma flow only for length scales larger than 2.5 Mm and time scales longer than 30 min. These limits have been derived from numerical simulations by Rieutord et al. (2001) and are confirmed by these data (see below).
Other data sets were processed in the same way to compare several flow characteristics (see Table 1).
2.2 Vertical velocities
To determine the vertical component of the velocity we used a second data
set from SOT/Hinode, also taken at disc centre
and recorded on 4 September 2009 21:08 UT to 22:25 UT. These data were
taken with the narrowband filter imager (NFI) with a spectral width of
9 pm, near the FeI line at
![]() nm, sampling nine wavelengths
in the line profile. This regular sampling allowed us to accurately measure
the Doppler shift of the line every 28.5 s. The field-of-view
of this series is
nm, sampling nine wavelengths
in the line profile. This regular sampling allowed us to accurately measure
the Doppler shift of the line every 28.5 s. The field-of-view
of this series is
![]() ,
which
represents
,
which
represents
![]() Mm2. The pixel size is
Mm2. The pixel size is
![]() .
.
These data are completed by a third data set from SOT/Hinode, taken at
disc centre and recorded on 4 September 2009 7:35 UT to 10:17 UT with
a regular cadence of one image every 57.5 s. These data were also obtained
with the NFI but around the FeI line at 525.0208 nm. However, in that case
the line profile was sampled only at two wavelengths,
namely
![]() pm and
pm and
![]() pm, which did not
allow us to determine the Doppler shift of the line in the same way
as with the second data set. The radial velocity was instead estimated
through the simple relationship
v=kI_b-I_rI_b+I_r + v_0,
calib_eq
where v0 and k are constants and Ir and Ib are the intensities
in red and blue positions of the filter (+10.8 pm and -1.8 pm)
respectively. The actual relationship between the radial velocity and the
intensity difference for this particular line and positions of the filter
is shown in Fig. 1. Note that an unavoidable pitfall with NFI is
that the red and blue positions of the filter are in general asymmetric
with respect to
pm, which did not
allow us to determine the Doppler shift of the line in the same way
as with the second data set. The radial velocity was instead estimated
through the simple relationship
v=kI_b-I_rI_b+I_r + v_0,
calib_eq
where v0 and k are constants and Ir and Ib are the intensities
in red and blue positions of the filter (+10.8 pm and -1.8 pm)
respectively. The actual relationship between the radial velocity and the
intensity difference for this particular line and positions of the filter
is shown in Fig. 1. Note that an unavoidable pitfall with NFI is
that the red and blue positions of the filter are in general asymmetric
with respect to ![]() .
From the previous plot we see that this
implies that large velocities cannot be measured correctly on one side
of the line for these data (here on the blue side). The field-of-view of
this series is
.
From the previous plot we see that this
implies that large velocities cannot be measured correctly on one side
of the line for these data (here on the blue side). The field-of-view of
this series is
![]() with a pixel of
with a pixel of
![]() ,
corresponding to a physical field of
,
corresponding to a physical field of
![]() Mm2.
Mm2.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13303f5.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg41.png)
|
Figure 1: Relationship between radial velocities and relative intensity fluctuations, using the two wavelengths at -1.8 pm and +10.8 pm aside the FeI line at 525 nm. Positive velocities are towards the observer. |
| Open with DEXTER | |
The Doppler fields were then ![]() filtered to remove fast horizontal
motions of the patterns with a threshold of 6 km s-1.
filtered to remove fast horizontal
motions of the patterns with a threshold of 6 km s-1.
Unfortunately no flat-field image was available for the data sets
taken at
![]() nm. We tried to circumvent this problem
by creating a flat-field image for each image. For this purpose
we averaged 50 images around the desired one and smoothed the result
with a window of
nm. We tried to circumvent this problem
by creating a flat-field image for each image. For this purpose
we averaged 50 images around the desired one and smoothed the result
with a window of
![]() .
The operation possibly
altered the signal at scales larger than 12 Mm. Note finally that unlike
the
.
The operation possibly
altered the signal at scales larger than 12 Mm. Note finally that unlike
the
![]() nm data sets, we were able to correct the data
set taken around
nm data sets, we were able to correct the data
set taken around
![]() nm with a genuine flat-field image.
nm with a genuine flat-field image.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13303f1.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg44.png)
|
Figure 2: Velocity field derived from the motion of granules during a 45 min window, interpolated by a Daubechies wavelet of 4*953 km. Contours mark the horizontal divergence of the velocity. |
| Open with DEXTER | |
Finally, following Danilovic et al. (2008) we computed the PSF and MTF of SOT to deconvolve all the images including those used to derive the Doppler shift from the instrument effects (central obscuration, spider and ccd). This correction turned out to be crucial for the investigation of subgranulation-scale turbulence, which is one of the novelties brought by the Hinode mission.
3 Velocity fields
3.1 Horizontal velocity fields
We give in Fig. 2 a typical view of the velocity field using a time average of 45 min, on which the supergranulation pattern is clearly visible. As is customary with any turbulent flow, it is crucial to investigate the spectral signature of these flows. The high quality of the data enables us to use the highest spatial and temporal resolutions available to granule tracking. Using the CST algorithm, as in Rieutord et al. (2008), we computed the kinetic energy spectrum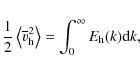
where
For comparisons with other data sets, we plotted the dimensional values (in km3/s2) of the kinetic energy spectral densities in all the figures. Since this value depends on the normalisation of the Fourier transform, we give the details of the expressions used in the paper in Appendix A. In order to give a better spectral resolution, all spectra were computed using zero-padding. Thus, we give the size of the data (Nx,Ny) and the size of the padding area Np for each spectrum.
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{13303f2.eps}\vspace*{-1mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg49.png)
|
Figure 3:
Mean spectra and fluctuations: eleven independent
horizontal kinetic energy spectra (dotted lines) computed with a
three-hours time window, along with their average (thick solid line)
are represented.
Note that the fluctuations may reach an amplitude of 40% compared to
the mean value. The straight line on the right indicates the power law
|
| Open with DEXTER | |
These spectra are interesting for various reasons. First, we notice
in Fig. 3 the prominent supergranulation peak centred
at 30 Mm. This length scale is slightly shorter than the one measured
by Rieutord et al. (2008), who found the maximum at 36.4 Mm. This change in the
peak wavelength does not seem to be an artefact of the smaller field.
Indeed, reducing the field on the data of Rieutord et al. (2008)
to a size comparable to that of the present data, one still obtains a value of
36.4 Mm. The difference seems to result from an intrinsic variability. To
verify this point, we analysed other data from various sources (other
Hinode fields, some data from the TRACE satellite). The results,
together with those obtained from SOHO/MDI data by
Hathaway et al. (2000)![]() are summarised in Table 1. These data indeed show some
variability both in the location of the peak and its amplitude.
The fact that the small fields-of-view tend to give smaller values of
the supergranulation scale may not be statistically significant.
are summarised in Table 1. These data indeed show some
variability both in the location of the peak and its amplitude.
The fact that the small fields-of-view tend to give smaller values of
the supergranulation scale may not be statistically significant.
Figure 3 also displays a plot of the individual spectra together with their average. These spectra provide further evidence of the strong variability of the horizontal velocity field even at the supergranulation scale. They are constructed from three-hours-averaged velocity fields. We note that they do not show any energy excess within the mesogranulation range, i.e. between 3 and 10 Mm. The absence of any specific spectral feature in this range is confirmed when other time windows are used (Fig. 4).
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{13303f3.eps}\hspace*{1.5mm}
\includegraphics[width=8cm,clip]{13303f4.eps}
\vspace{4mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg50.png)
|
Figure 4: Left: kinetic energy spectra of the horizontal velocity field for various time windows. The vertical line marks the 2.3 Mm scale below which noise dominates. The black dots mark the scale at which the spectrum of a given time average disconnects from the 30-min one. Right: relationship between the length scale and the correlation time scale for the horizontal velocity field. Here Nx=Ny=80 and Np=256. |
| Open with DEXTER | |
In Fig. 4 (left) we plot the mean spectra obtained with
time windows ranging from 0.5 to 24 h. Each spectrum is an
average of all the independent spectra that could be extracted from the
whole series. For instance the 0.5 h time window allowed us to extract 66
independent spectra from the 33 hrs of data. Note that all spectra show a
distinct rise at scales below 2.3 Mm (
![]() Mm-1). This
rise follows a linear law (
Mm-1). This
rise follows a linear law (
![]() )
as expected from a
two-dimensional uncorrelated noise. Hence we clearly find the spatial
resolution limit imposed by granule tracking. This confirms the analysis
performed on the numerical simulations by Rieutord et al. (2001), which suggested
that granule tracking could not be used at scales smaller than 2.5 Mm.
)
as expected from a
two-dimensional uncorrelated noise. Hence we clearly find the spatial
resolution limit imposed by granule tracking. This confirms the analysis
performed on the numerical simulations by Rieutord et al. (2001), which suggested
that granule tracking could not be used at scales smaller than 2.5 Mm.
The 30-min spectrum is the closest to an instantaneous one. This spectrum
displays three features: (i) the supergranulation peak, (ii) a minimum
in the kinetic energy density at 10 Mm and (iii) a slow monotonic increase
towards the small scales.
Feature (ii) was also found by
Hathaway et al. (2000) in the Doppler measurements from SOHO/MDI; their
spherical harmonic spectrum shows a minimum near ![]() which
corresponds to
which
corresponds to
![]() Mm, quite close to our value.
Mm, quite close to our value.
We note that the spectra obtained with time windows ranging from 30 min to
24 h almost superpose at large scales. However, shifting the attention
to smaller scales, one finds the existence of a scale ![]() where
the spectrum disconnects from the 30 min one (marked with black dots in
Fig. 4). The time average acts as a low-pass filter which
removes (or simply weakens) the flows on shorter time scales. The size
of the time window can hence be used as a proxy of the correlation time
of the flow at the scale marked by the dot. Figure 4 (right) shows
the scale
where
the spectrum disconnects from the 30 min one (marked with black dots in
Fig. 4). The time average acts as a low-pass filter which
removes (or simply weakens) the flows on shorter time scales. The size
of the time window can hence be used as a proxy of the correlation time
of the flow at the scale marked by the dot. Figure 4 (right) shows
the scale ![]() as a function of the time average associated with
the time window. We find that the relationship between this length scale
and the window size is close to a power law
as a function of the time average associated with
the time window. We find that the relationship between this length scale
and the window size is close to a power law
![]() .
As the correlation time is
.
As the correlation time is
![]() ,
we can relate
,
we can relate ![]() and
and ![]() and find
and find
![]() .
This translates into a power law spectrum
.
This translates into a power law spectrum
![]() for the kinetic energy. This exponent is typical of the range
7-25 Mm.
for the kinetic energy. This exponent is typical of the range
7-25 Mm.
Finally, while processing other data sets to better evaluate the variability of the supergranulation peak, we came across the data recorded in the G-band by Hinode/SOT on 8 March 2007. Two series of images taken at [2:55, 5:45] UT and [6:00, 9:52] UT drew our attention. As shown in Fig. 5, the supergranulation peak has disappeared if we consider the shortest time sampling. In this figure we distinguished the two series because one pore is emerging at the end of the first series (around 4:40 UT) and the second pore emerges in the second series (around 6:18 UT). We note that the kinetic energy density in the supergranulation range has weakened at scales shorter than 33 Mm in the second series when the pair of pores has reached its steady state. We also observe that the TRACE data taken in April 2000 during the solar maximum also show a weaker supergranulation peak compared to the analogous data of 2007 taken at the solar minimum. Hence we note a trend that magnetic fields seem to markedly affect the amplitude of the supergranulation flows. This is likely connected with the anti-correlation between the size of the supergranules and the strength of the magnetic field observed by Meunier et al. (2008,2007).
3.2 Vertical velocity fields
Let us now focus on the vertical velocity fields vz(x,y). As mentioned
above, these are obtained from the Doppler effect and thus each pixel of
the image gives a measure of this component of the velocity field. We now
compute the horizontal spectral density of the vertical velocity, namely
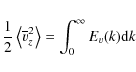
for various time averages.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13303f6.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg62.png)
|
Figure 5: Kinetic energy spectra of the horizontal velocity field during the emergence of two pores in the field-of-view. The solid line corresponds to the first series, at the end of which one pore has emerged. The dotted one corresponds to the second series, during which the second pore emerges. For each series, two time windows were used. The vertical dotted lines mark the 12.5-75 Mm range where the supergranulation peak is found (cf. Fig. 4). Here Nx=81, Ny=82 and Np=1024. |
| Open with DEXTER | |
Figure 6 shows the spectra of the Doppler radial velocity obtained with the bisector method after reconstruction of the line profile at 557.6 nm. We extracted velocities at two different altitudes. A line chord of 16 pm was used to sample a layer around an altitude of 80 km (Berrilli et al. 2002; Altrock et al. 1975) and a second chord of 8 pm, deeper in the line, was used to sample the atmosphere around 190 km. In order to detect potential spurious effects associated with the artificial flat-fielding operation, an additional set of spectra was computed from images not flat-fielded (Fig. 7).
First these spectra seem to follow
![]() in the 2.5-7 Mm range. If the flat-fielding operation
is correct, this power law may extend up to 30 Mm. Note that this
slope is reminiscent of the power law found from the relationship between
correlation time and the scale of horizontal velocities (see the
previous section and Fig. 4-right). In terms of velocity, the
k2 power law for the spectral density implies
in the 2.5-7 Mm range. If the flat-fielding operation
is correct, this power law may extend up to 30 Mm. Note that this
slope is reminiscent of the power law found from the relationship between
correlation time and the scale of horizontal velocities (see the
previous section and Fig. 4-right). In terms of velocity, the
k2 power law for the spectral density implies
![]() .
.
As noted above, the quality of the data allowed us to investigate the subgranulation dynamics accurately for the first time. The absence of Earth atmospheric turbulence and the deconvolution of the images by the instrumental transfer function leads to high quality horizontal spectra of the vertical velocity. As shown by Fig. 6, we observe in this range of scales a decrease of the spectral density closely following a k-10/3 power law. When the signal is slightly averaged over a 4-min interval, the cut-off is steeper and the exponent close to -4.
Concerning the granulation peak, the spectra show that the privileged
scale is 1.7 Mm. The spectral kinetic energy density is around
100 km3/s2 at a mean altitude of ![]() 80 km. At an altitude around
190 km, the same spectra show an amplitude of 50 km3/s2. This
reduction of the spectral kinetic energy density is likely associated with
the braking of upward motions which hit the stably stratified atmosphere.
80 km. At an altitude around
190 km, the same spectra show an amplitude of 50 km3/s2. This
reduction of the spectral kinetic energy density is likely associated with
the braking of upward motions which hit the stably stratified atmosphere.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{13303f7.eps}\hspace*{1.5mm}
\includegraphics[width=8.2cm,clip]{13303f8.eps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg66.png)
|
Figure 6:
Kinetic energy spectra of the vertical velocity field for
various time windows. The vertical dotted line marks the maximum
of the spectrum at
|
| Open with DEXTER | |
To confirm these results with independent data, we used the third set presented in Sect. 2.2 taken with NFI around the FeI line at 525.0 nm. Unlike the previous data at 557.6 nm we only had access to two wavelengths around the FeI line and had to derive the Doppler shift by the poor man's method, following Eq. (1). The results, shown in Fig. 8, are still interesting. With this method a k2 power law is also obtained at large scales both on the 557.6 nm and 525.0 nm data. The latter data, which benefit from a good flat-field image, also indicate that the k2 power law extends up to 30 Mm.
However, we find that the cut-off is sharper on the subgranulation side, not far from a k-17/3 power law. This is presumably a residual of the small-scale cut-off of the intensity power spectrum, which follows the same power law (see below). This result suggests that the poor man's method is probably not appropriate for the computation of the small-scale radial velocity field.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13303f9.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg67.png)
|
Figure 7: Same as in Fig. 6- left, but with data not flat-fielded. |
| Open with DEXTER | |
4 Intensity spectra
With the data sets presented in Sect. 2.1 and 2.2 we
finally investigated the power spectrum of the horizontal intensity
fluctuations defined according to

The spectra obtained from the blue continuum images at
At scales smaller than a maximum located around the scale of 1.5 Mm, the power spectrum decreases steeply. In the subgranulation range, the spectral density almost follows a power law in k-3. We note that these results agree with those of Wedemeyer-Böhm & Rouppe van der Voort (2009) as derived from their Fig. 9. Our longer time series provides a better statistic, which probably improves the determination of the large-scale side of the spectra.
We then used the images taken at 525.0316 nm with the NFI, whose width is 9 pm. It turned out that this light comes from the continuum just besides the FeI line at 525.0208 nm (Uitenbroek, private comm.). As shown in Fig. 9 (right), the intensity spectra show a steeper cut-off in the subgranulation range than for the previous data, close to a k-17/3 law. We note that the granulation scale peak is at 2 Mm for this wavelength.
Finally, the images taken at the blue side of the 525.0 nm FeI line are in fact very close to the line core, namely at 525.019 nm. Atmospheric models of Uitenbroek (private comm.) suggest that this intensity emerges at an altitude of 200 km above the continuum. The spectra shown in Fig. 10 show a clear shift of the granulation peak towards larger scales, namely 2.5 Mm. No power law arises in the meso-scales, while the subgranulation range shows a roundish cut-off with no clear power law.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13303f10.eps}\hspace*{1.5mm}
\includegraphics[width=8cm,clip]{13303f11.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg70.png)
|
Figure 8:
Left: same as in Fig. 7, but with Doppler velocities
computed with just two wavelengths in the line.
Right: same as left but for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13303f12.eps}\hspace*{1.5mm}
\includegraphics[width=8cm,clip]{13303f13.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg71.png)
|
Figure 9: Spectral energy density of the intensity field. Left: data from the BFI at 450.4 nm (spectral width of 0.22 nm sampling the blue continuum) for various time windows (data set of 29-31/8/2007). The spectra are normalised so that the amplitude of the granulation peak is unity. The vertical dotted line marks the position of the granulation peak determined with instantaneous spectra. Here Nx=941, Ny=934and Np=1024. Right: data from the NFI at 525.0208+0.0108 nm (spectral width of 9 pm sampling the continuum on the red side of the line); here Nx=Ny=704 and Np=1024. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13303f14.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg72.png)
|
Figure 10:
Same as Fig. 9-right, but with the NFI almost
centred on the line core at
|
| Open with DEXTER | |
5 Discussion and physical interpretation
5.1 Large scales
The foregoing results first confirm that the power spectra of horizontal
flows at the Sun's surface are dominated by two scales corresponding
to granulation at ![]() 1.7 Mm and supergranulation at
1.7 Mm and supergranulation at ![]() 30 Mm. This result
confirms the one of Hathaway et al. (2000), who used only one velocity component
(the radial velocity) of the flow field. As far as the vertical velocity is
concerned, the granulation scale clearly emerges at 1.7 Mm. On the large-scale
side of granulation, we found that the vertical velocity field decreases like
30 Mm. This result
confirms the one of Hathaway et al. (2000), who used only one velocity component
(the radial velocity) of the flow field. As far as the vertical velocity is
concerned, the granulation scale clearly emerges at 1.7 Mm. On the large-scale
side of granulation, we found that the vertical velocity field decreases like
![]() with the horizontal length scale
with the horizontal length scale ![]() ,
corresponding to
a k2-law for the associated kinetic energy spectral density. This law seems
to be valid up to the supergranulation scale since its prediction of a
supergranule vertical velocity corresponds to the value of 30 m s-1
found by Hathaway et al. (2002) with MDI/SOHO data. Note that this conclusion holds
only if the flat-field operations on the images did not damage the data.
,
corresponding to
a k2-law for the associated kinetic energy spectral density. This law seems
to be valid up to the supergranulation scale since its prediction of a
supergranule vertical velocity corresponds to the value of 30 m s-1
found by Hathaway et al. (2002) with MDI/SOHO data. Note that this conclusion holds
only if the flat-field operations on the images did not damage the data.
The k2-scaling law of vertical kinetic energy can be related to
the scaling law of the horizontal kinetic energy spectral density using
physical arguments. Indeed, mass conservation (see below Eq. (2))
implies that
![]() ,
where H is the vertical scale
height. If H is independent of
,
where H is the vertical scale
height. If H is independent of ![]() ,
and since
,
and since
![]() ,
then
,
then
![]() ,
meaning that
,
meaning that
![]() const. This law is approximately consistent with the
horizontal flow data: as shown by the 30-min spectrum in Fig. 4,
the spectral density
const. This law is approximately consistent with the
horizontal flow data: as shown by the 30-min spectrum in Fig. 4,
the spectral density
![]() does not vary very much in the
2.5-20 Mm range, where it stays between 190 and 260 km3/s2.
does not vary very much in the
2.5-20 Mm range, where it stays between 190 and 260 km3/s2.
To conclude on the k2 power law, we note that it also appears in the intensity fluctuation spectrum obtained with the broadband filter in the blue continuum. This looks like a strong correlation between buoyancy fluctuations traced by intensity fluctuations and vertical velocities. However, we observe that this scaling is not as conspicuous at another wavelength with a narrower filter, which likely samples different layers (see discussion below).
The derived horizontal flows may also be used to obtain some information
on the scale height of the variations of the vertical velocity at the
scale of supergranulation. Assuming that the anelastic approximation
can be used at these scales (it means that acoustic waves are filtered out),
we can write the mass conservation as
_zv_z = -v_z_z-New A_h_h,
mc
where
![]() is the horizontal velocity field and
is the horizontal velocity field and ![]() is the
background density. Using the simple model of Simon et al. (1991) for
a horizontal divergent source, namely
is the
background density. Using the simple model of Simon et al. (1991) for
a horizontal divergent source, namely
![]() ,
we
could estimate for a well-formed supergranule that the divergence is
approximately 10-4 s-1. From Stein & Nordlund (1998),
,
we
could estimate for a well-formed supergranule that the divergence is
approximately 10-4 s-1. From Stein & Nordlund (1998),
![]() Mm-1 near the surface. Then, using the estimate of 30 m s-1
for the vertical velocity at this scale, we find that the vertical scale
height is
Mm-1 near the surface. Then, using the estimate of 30 m s-1
for the vertical velocity at this scale, we find that the vertical scale
height is ![]() Mm, which indicates that the supergranulation flow is
likely shallow. This qualitative estimate agrees with recent
local helioseismic inferences based on Hinode data (Sekii et al. 2007),
which indicate that the imprint of supergranulation flows disappears
around 3 Mm below the surface. Note that the foregoing exercise has
been done using typical values of all quantities and just gives a first
impression. To go further and get a more reliable view, this calculation
should be applied to a large sample of supergranules.
Mm, which indicates that the supergranulation flow is
likely shallow. This qualitative estimate agrees with recent
local helioseismic inferences based on Hinode data (Sekii et al. 2007),
which indicate that the imprint of supergranulation flows disappears
around 3 Mm below the surface. Note that the foregoing exercise has
been done using typical values of all quantities and just gives a first
impression. To go further and get a more reliable view, this calculation
should be applied to a large sample of supergranules.
5.2 Sub-granulation scales: an injection-diffusive range ?
On the other side of the granulation peak, in the subgranulation range, the power spectrum of vertical velocity closely follows a k-10/3 law, which steepens to k-4 with time averaging, while the intensity variance spectrum seems to follow either a k-3 law or a k-17/3law depending on the data set used. These results are summarised in Fig. 11.
| Figure 11: Schematic view of the results. We indicate the layers where power laws are perceptible in the subgranulation range. |
|
| Open with DEXTER | |
A natural question to ask is what these scaling laws tell us about the physics of the solar surface. It is indeed well established that a variety of characteristic power law regimes can be derived for all kinds of turbulent complex flows depending on the detailed physical processes at work in the flow (e.g. shear turbulence (Lumley 1967; Lohse & Müller-Groeling 1996), stably and unstably stratified turbulence (Bolgiano 1962,1959; Obukhov 1959; L'vov 1991), MHD turbulence (Schekochihin et al. 2008, and references therein)) and on the relevant range of scales (e.g. injection, inertial or dissipation range) for each physical field in the problem. In the paragraphs below, we therefore attempt to determine if the observed subgranulation scaling exponents betray a particular flow regime.
First of all, considering the many differences between homogeneous, isotropic, incompressible turbulence and solar surface turbulence at observable scales (Nordlund et al. 1997; Rincon 2007; Petrovay 2001), there is no real reason to expect that the Kolmogorov phenomenology of turbulence (which predicts a k-5/3 power law for the velocity field in the inertial range) applies in the vicinity of the granulation scale.
A possible interpretation for the joint observation of the -10/3and
-17/3 exponents is in terms of buoyant dynamics in the injection
range of solar surface turbulence (i.e. not in the inertial range).
Let us assume that (i) buoyancy fluctuations are directly proportional
to temperature fluctuations (i.e. pressure fluctuations are not
influential) and that (ii) the dynamic is dominated by a balance
between
inertial terms (or acceleration) and buoyancy forcing in the momentum
equation. Further assuming that velocity and temperature perturbations
have the following horizontal scale ![]() dependence
dependence

and that vertical variations are controlled by the typical pressure or density scale height H independent of

hence
Still, this is only one half of the story, since the argument does not
predict the -17/3 slope for the intensity spectrum (it uses it as an input).
This is because two dominant balances are required to determine scaling laws
consistently in active scalar turbulence. In the context of thermal convection,
the second balance is obtained by isolating the dominant physical effects
in the temperature equation or, to be more precise, in the Yaglom equation
(Rincon 2006), which is the analog of the von Kármán-Howarth
equation for the statistics of scalars. In the Boussinesq approximation
(which is not suitable for the problem of solar convection), a k-17/3spectrum for temperature fluctuations can only be obtained if (i) the
following low Péclet number dominant balance![]()
is assumed in the temperature equation (where
Another interesting result regarding the sub-granulation range dynamics is that the intensity fluctuations taken with the BFI in the ``blue continuum" at 450 nm have a much weaker spectral cut-off close to a k-3 power law (k-4 if slightly averaged) than those taken in the continuum near the FeI line at 525 nm. This is quite surprising, because the fluid layer contributing most to the blue continuum should be quite similar to the one contributing to the 525 nm continuum from which the k-17/3 spectrum was derived. Beside the simple wavelength difference, which indicates a slighly lower contributing layer for the 450 nm radiation, the most obvious difference between the two signals comes from the spectral width of the filters. The width of the NFI of 9 pm is such that the continuum near 525 nm is ``pure", while the width of the BFI at 450.45 nm is 220 pm and includes a few absorption lines. For this reason, the layers contributing to the light collected in the two wavebands could be somewhat different. At the moment we have no obvious explanation of these two different cut-offs for the intensity spectrum in the continuum. Of course we cannot totally exclude some unexpected bias in the data processing, but if the result is confirmed by independent approaches, detailed numerical simulations of the dynamics are likely the only way to elucidate this puzzle.
For the sake of completeness, we mention that a k-3 spectrum could
be a simple signature of a physically smooth temperature field, which can
be expanded in Taylor series. Indeed, if
![]() then
then
![]() ,
or equivalently
,
or equivalently
![]() .
But, similarly to the
argument presented previously, we underline that this scaling is not fully
consistent with a k-10/3 scaling for the velocity field if a dominant
balance between inertia and buoyancy is assumed in the momentum equation.
.
But, similarly to the
argument presented previously, we underline that this scaling is not fully
consistent with a k-10/3 scaling for the velocity field if a dominant
balance between inertia and buoyancy is assumed in the momentum equation.
The previous theoretical arguments should of course not be taken at face value. They simply suggest that it might be possible to construct some sort of ``injection-diffusive" turbulent regime characteristic of the sub-granulation range, and serve to illustrate that the standard framework of incompressible homogeneous isotropic turbulence is probably too restrictive to theoretically explain the observations of the thermal boundary layer at the solar surface.
These new observational measurements for the subgranulation range
definitely call for a deeper investigation. A detailed theoretical
understanding of the solar power spectrum at the beginning of the
subgranulation range 0.1-1 Mm might be obtained by re-analysing existing
numerical simulations of solar granulation (Stein & Nordlund 1998), looking for
the dominant terms in the temperature (or energy) equation![]() . Another possibility would be to perform
idealised high-resolution numerical simulations of thermal turbulence
done in the low-Péclet approximation (Lignières 1999; Thual 1992)
to better understand this complex and fairly unusual turbulence
regime from the theoretical point of view.
. Another possibility would be to perform
idealised high-resolution numerical simulations of thermal turbulence
done in the low-Péclet approximation (Lignières 1999; Thual 1992)
to better understand this complex and fairly unusual turbulence
regime from the theoretical point of view.
6 Conclusions
The power spectrum of surface flows at the Sun's surface has been investigated using mainly image series from the Hinode/SOT instrument. The results may be summarised as follows.
- 1.
- The smallest scales, i.e. the subgranulation range, can be
investigated for the first time without a seeing effect and using
corrections of the MTF of the instrument. On the one hand, the
spectral cut-off of intensity fluctuations is similar to a k-17/3power law for images taken with a narrow filter (width
 9 pm) in
the continuum on the red side of the 525 nm FeI line and to k-3for images taken with the broadband filter (width
9 pm) in
the continuum on the red side of the 525 nm FeI line and to k-3for images taken with the broadband filter (width  220 pm) around
450.45 nm. On the other hand, the vertical velocity horizontal spectrum
measured 80 km or 190 km above the continuum at 557.6 nm shows a steep
cut-off in k-10/3, which can be related to the k-17/3 power
law by invoking a balance between buoyancy and inertia. The values of
the two scaling exponents suggest that the temperature fluctuations
impact the dynamics at a scale well below the one determined by the unit
Péclet number. Finally, we also note the decrease of the granulation
peak amplitude with altitude, possibly betraying the deceleration of
the upflows.
220 pm) around
450.45 nm. On the other hand, the vertical velocity horizontal spectrum
measured 80 km or 190 km above the continuum at 557.6 nm shows a steep
cut-off in k-10/3, which can be related to the k-17/3 power
law by invoking a balance between buoyancy and inertia. The values of
the two scaling exponents suggest that the temperature fluctuations
impact the dynamics at a scale well below the one determined by the unit
Péclet number. Finally, we also note the decrease of the granulation
peak amplitude with altitude, possibly betraying the deceleration of
the upflows.
- 2.
- The granulation spectral peak at 1.7 Mm is conspicuous in the vertical velocity spectrum. The location of the intensity spectrum peak depends on the wavelength: it is close to 1.5 Mm in the blue continuum at 450 nm, 2 Mm in the continuum near 525 nm, and to 2.5 Mm in the core of the FeI line at 525.0 nm, which probes the dynamics in a layer 200 km above the continuum.
- 3.
- Moving to the large scales, we note that the spectral density
of vertical kinetic energy decreases as k2 with decreasing k(equivalently, the amplitude of vz decreases as
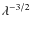 with the horizontal scale
with the horizontal scale  ). This k2 power law also emerges
from the relationship between the scale and the correlation time of the
horizontal flows. Furthermore we note that
the spectral density of intensity fluctuations in the blue continuum
also scales like k2 in the 2.5-10 Mm range.
). This k2 power law also emerges
from the relationship between the scale and the correlation time of the
horizontal flows. Furthermore we note that
the spectral density of intensity fluctuations in the blue continuum
also scales like k2 in the 2.5-10 Mm range.
- 4.
- The power spectrum of horizontal flows has been explored in
the 2.5-40 Mm range. It clearly reveals the supergranulation peak
as well as the large-scale side of the granulation peak.
These observations confirm in passing the result of the numerical simulations of
Rieutord et al. (2001) that granule tracking cannot determine plasma flows at
scales below
 2.5 Mm. The energy density minimum is found
at a scale of 12 Mm. These results confirm with a completely different
technique the spherical harmonics spectra obtained by Hathaway et al. (2000)
from dopplergrams. Focusing on the supergranulation peak, we could
estimate its amplitude to be in the range of 200-700 km3/s2 and show
its strong variability. From Figs. 4 and 5 we may add
that the visible part of the granulation peak points to an amplitude in the
range of 200-400 km3/s2. Interestingly enough, we discovered that
the emergence of a pair of pores is able to erase the supergranulation
peak completely, which points out the sensitivity of the supergranulation
amplitude flow to the ambient magnetic field. Finally, combining all the
data, we tentatively estimated the scale-height of the vertical velocity
field at the supergranulation horizontal scale. We found a scale height
of approximately 1 Mm, indicating that supergranules are likely surface
flows. However, this estimate should be verified for a number
of supergranules to obtain a statistically robust value.
2.5 Mm. The energy density minimum is found
at a scale of 12 Mm. These results confirm with a completely different
technique the spherical harmonics spectra obtained by Hathaway et al. (2000)
from dopplergrams. Focusing on the supergranulation peak, we could
estimate its amplitude to be in the range of 200-700 km3/s2 and show
its strong variability. From Figs. 4 and 5 we may add
that the visible part of the granulation peak points to an amplitude in the
range of 200-400 km3/s2. Interestingly enough, we discovered that
the emergence of a pair of pores is able to erase the supergranulation
peak completely, which points out the sensitivity of the supergranulation
amplitude flow to the ambient magnetic field. Finally, combining all the
data, we tentatively estimated the scale-height of the vertical velocity
field at the supergranulation horizontal scale. We found a scale height
of approximately 1 Mm, indicating that supergranules are likely surface
flows. However, this estimate should be verified for a number
of supergranules to obtain a statistically robust value.
We are grateful to the Hinode team for the possibility to use their data. Hinode is a Japanese mission developed and launched by ISAS/JAXA, collaborating with NAOJ as a domestic partner, NASA and STFC (UK) as international partners. Scientific operation of the Hinode mission is conducted by the Hinode science team organised at ISAS/JAXA. This team mainly consists of scientists from institutes in the partner countries. Support for the post-launch operation is provided by JAXA and NAOJ (Japan), STFC (U.K.), NASA, ESA, and NSC (Norway). This work was (partly) carried out at the NAOJ Hinode Science Center, which is supported by the Grant-in-Aid for Creative Scientific Research ``The Basic Study of Space Weather Prediction" from MEXT, Japan (Head Investigator: K. Shibata), generous donations from Sun Microsystems, and NAOJ internal funding.We thank François Lignières for several interesting comments and remarks on the manuscript. We are also very grateful to Han Uitenbroek who provided us with simulations results of line formation in the Sun's atmosphere. This work was supported by the Centre National de la Recherche Scientifique (C.N.R.S., UMR 5572), through the Programme National Soleil Terre (P.N.S.T.).
Appendix A: Absolute spectra
In this paper, we give the kinetic energy density spectra with their
absolute values in km3/s2. To facilitate future comparisons, we
document the way these spectral densities are computed in detail. We
recall that the kinetic energy spectrum E(k) is defined as

|
(A.1) |
It is related to the Fourier transform of the velocity components by

|
(A.2) |
where

|
(A.3) |
where

|
(A.4) |
which means that the Dirac distribution in a discrete way reads
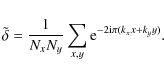
|
(A.5) |
Now, spectral quantities in turbulence theory usually use

|
(A.6) |
as the definition of the 2D-Fourier transform. Setting

|
(A.7) |
the correspondence is accordingly
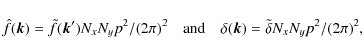
|
(A.8) |
where Nx and Ny are the size of the data. p is the linear size of the pixel. We wish to derive the correct normalisation of E(k)which is that of
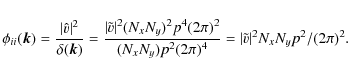
|
(A.9) |
If we restrict our case to a square data set (Nx=Ny=N), then

where we noticed that the dimensional wavenumber k and the non-dimensional one are related by a factor
![\begin{displaymath}E(k) = \demi\frac{N p}{(2\pi)}\sum_{\forall
k'\in[k,k+{\rm d}k]/2\pi}\vert\tilde{v}_x(k')\vert^2+\vert\tilde{v}_y(k')\vert^2,
\end{displaymath}](/articles/aa/full_html/2010/04/aa13303-09/img124.png)
|
(A.10) |
where
![\begin{displaymath}P(k)=\sqrt{\frac{1}{2}\sum_{\forall
k'\in[k,k+{\rm d}k]/2\pi}k'\vert\tilde{v}\vert^2}.
\end{displaymath}](/articles/aa/full_html/2010/04/aa13303-09/img130.png)
|
(A.11) |
Effect of zero padding: the Fourier transforms are done on a square of size
![\begin{displaymath}E(k) = \frac{N^3 p}{4\pi N_xN_y}\sum_{\forall
k'\in[k,k+{\rm d}k]/2\pi}\vert\tilde{v}\vert^2~ ,\end{displaymath}](/articles/aa/full_html/2010/04/aa13303-09/img134.png)
|
(A.12) |
Effect of the normalisation of the Fourier Transform: if the Fourier Transform is multiplied by a factor A, then E(k) is multiplied by A and P(k) is multiplied by a factor
References
- Altrock, R. C., November, L. J., Simon, G. W., Milkey, R. W., & Worden, S. P. 1975, Sol Phys., 43, 33 [Google Scholar]
- Berrilli, F., Consolini, G., Pietropaolo, E., et al. 2002, A&A, 381, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolgiano, R. 1959, J. Geophys. Res., 64, 2226 [NASA ADS] [CrossRef] [Google Scholar]
- Bolgiano, R. 1962, J. Geophys. Res., 67, 3015 [NASA ADS] [CrossRef] [Google Scholar]
- Crouch, A. D., Charbonneau, P., & Thibault, K. 2007, ApJ, 662, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Danilovic, S., Gandorfer, A., Lagg, A., et al. 2008, A&A, 484, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gizon, L., & Birch, A. C. 2005, Liv. Rev. Sol. Phys., 2, 6 [Google Scholar]
- Green, C. A., & Kosovichev, A. G. 2006, ApJ, 641, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Green, C. A., & Kosovichev, A. G. 2007, ApJ, 665, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Hathaway, D., Beck, J., Bogart, R., et al. 2000, Sol. Phys., 193, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Hathaway, D. H., Beck, J. G., Han, S., & Raymond, J. 2002, Sol. Phys., 205, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Ichimoto, K., Tsuneta, S., Suematsu, Y., et al. 2004, in Optical, Infrared, and Millimeter Space Telescopes, ed. J. C. Mather, SPIE Conf., 5487, 1142 [Google Scholar]
- Lesieur, M. 1990, Turbulence in fluids (Kluwer) [Google Scholar]
- Lignières, F. 1999, A&A, 348, 933 [NASA ADS] [Google Scholar]
- Lohse, D., & Müller-Groeling, A. 1996, Phys. Rev. D, 54, 395 [Google Scholar]
- Lumley, J. L. 1967, Phys. Fluids, 10, 855 [NASA ADS] [CrossRef] [Google Scholar]
- L'vov, V. S. 1991, Phys. Rev. Lett., 67, 687 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Meunier, N., Roudier, T., & Tkaczuk, R. 2007, A&A, 466, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N., Roudier, T., & Rieutord, M. 2008, A&A, 488, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordlund, A., Spruit, H., Ludwig, H.-C., & Trampedach, R. 1997, A&A, 328, 229 [NASA ADS] [Google Scholar]
- Nordlund, Å., Stein, R. F., & Asplund, M. 2009, Liv. Rev. Sol. Phys. 6, 1 [Google Scholar]
- November, L. J., Toomre, J., Gebbie, K., & Simon, G. W. 1981, ApJ, 245, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Obukhov, A. 1959, Dokl. Akad. Nauk. SSR, 125 [Google Scholar]
- Petrovay, K. 2001, Space Sci. Rev., 95, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Rast, M. P. 2003, ApJ, 597, 1200 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M., & Zahn, J.-P. 1997, ApJ, 474, 760 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M., Roudier, T., Malherbe, J. M., & Rincon, F. 2000, A&A, 357, 1063 [NASA ADS] [Google Scholar]
- Rieutord, M., Roudier, T., Ludwig, H.-G., Nordlund, Å., & Stein, R. 2001, A&A, 377, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieutord, M., Ludwig, H.-G., Roudier, T., Nordlund, A., & Stein, R. 2002, Nuov. Cim. C - Geophys. Space Phys., 25, 523 [Google Scholar]
- Rieutord, M., Roudier, T., Roques, S., & Ducottet, C. 2007, A&A, 471, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieutord, M., Meunier, N., Roudier, T., et al. 2008, A&A, 479, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rincon, F. 2006, J. Fluid Mech., 563, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Rincon, F. 2007, in Proc. IAU Symp. 239, ed. F. Kupka, I. W. Roxburgh, & K. L. Chan, 58 [Google Scholar]
- Rincon, F., Lignières, F., & Rieutord, M. 2005, A&A, 430, L57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rincon, F., & Rieutord, M. 2003, in SF2A-2003: Semaine de l'Astrophysique Française, ed. F. Combes, D. Barret, T. Contini, & L. Pagani, 103 [Google Scholar]
- Schekochihin, A. A., Cowley, S. C., & Yousef, T. A. 2008, in IUTAM Symposium on Computational Physics and New Perspectives in Turbulence, ed. Y. Kaneda (Netherlands: Springer), 4, 347 [Google Scholar]
- Sekii, T., Kosovichev, A. G., Zhao, J., et al. 2007, Pub. Astron. Soc. Jap., 59, 637 [Google Scholar]
- Shine, R., Simon, G., & Hurlburt, N. 2000, Sol. Phys., 193, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, G., & Leighton, R. 1964, ApJ, 140, 1120 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, G., Title, A., & Weiss, N. 1991, ApJ, 375, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, R. F., & Nordlund, Å. 1998, ApJ, 499, 914 [Google Scholar]
- Stein, R., & Nordlund, A. 2000, Sol. Phys., 192, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, R. F., Georgobiani, D., Schafenberger, W., Nordlund, Å., & Benson, D. 2009, in AIP Conf. Ser. 1094, ed. E. Stempels, 764 [Google Scholar]
- Straus, T., & Bonaccini, D. 1997, A&A, 324, 704 [NASA ADS] [Google Scholar]
- Straus, T., Deubner, F.-L., & Fleck, B. 1992, A&A, 256, 652 [NASA ADS] [Google Scholar]
- Suematsu, Y., Tsuneta, S., Ichimoto, K., et al. 2008, Sol. Phys., 249, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Thual, O. 1992, J. Fluid Mech., 240, 229 [NASA ADS] [CrossRef] [Google Scholar]
- van der Borght, R. 1974, Aust. J. Phys., 27, 481 [NASA ADS] [Google Scholar]
- Wedemeyer-Böhm, S., & Rouppe van der Voort, L. 2009, A&A, 503, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Footnotes
- ... HINODE
![[*]](/icons/foot_motif.png)
- The Hinode spacecraft launched in 2006 was designed and is now operated by JAXA (Japanese Space Authorities) in cooperation with NASA (National Aeronautics and Space Administration) and ESA (European Space Agency).
- ...Hathaway et al. (2000)
![[*]](/icons/foot_motif.png)
- The amplitude of the peak for these data, given in between parenthesis, is an estimate resulting from a crude conversion of Doppler signal to horizontal velocities.
- ... observed
![[*]](/icons/foot_motif.png)
- Assuming isotropy, the dynamical
balance would instead read
 ,
leading to
,
leading to
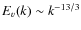 for
for  .This
argument can be
formalised using a generalised exact von Kármán-Howarth-Kolmogorov
equation for thermal convection (Rincon
2006).
.This
argument can be
formalised using a generalised exact von Kármán-Howarth-Kolmogorov
equation for thermal convection (Rincon
2006).
- ... balance
![[*]](/icons/foot_motif.png)
- The Péclet number of a thermal eddy is the ratio between its thermal diffusion time and its typical turnover time. It is effectively of the order of one or smaller in the sub-granulation range.
- ... equation
![[*]](/icons/foot_motif.png)
- It is remarkable that some of the early numerical simulations by Nordlund et al. (1997) seemed to produce a k-17/3 scaling for intensity fluctuations.
All Tables
Table 1: The position and amplitude of the supergranulation peak for various data sets.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13303f5.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg41.png)
|
Figure 1: Relationship between radial velocities and relative intensity fluctuations, using the two wavelengths at -1.8 pm and +10.8 pm aside the FeI line at 525 nm. Positive velocities are towards the observer. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13303f1.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg44.png)
|
Figure 2: Velocity field derived from the motion of granules during a 45 min window, interpolated by a Daubechies wavelet of 4*953 km. Contours mark the horizontal divergence of the velocity. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{13303f2.eps}\vspace*{-1mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg49.png)
|
Figure 3:
Mean spectra and fluctuations: eleven independent
horizontal kinetic energy spectra (dotted lines) computed with a
three-hours time window, along with their average (thick solid line)
are represented.
Note that the fluctuations may reach an amplitude of 40% compared to
the mean value. The straight line on the right indicates the power law
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{13303f3.eps}\hspace*{1.5mm}
\includegraphics[width=8cm,clip]{13303f4.eps}
\vspace{4mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg50.png)
|
Figure 4: Left: kinetic energy spectra of the horizontal velocity field for various time windows. The vertical line marks the 2.3 Mm scale below which noise dominates. The black dots mark the scale at which the spectrum of a given time average disconnects from the 30-min one. Right: relationship between the length scale and the correlation time scale for the horizontal velocity field. Here Nx=Ny=80 and Np=256. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13303f6.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg62.png)
|
Figure 5: Kinetic energy spectra of the horizontal velocity field during the emergence of two pores in the field-of-view. The solid line corresponds to the first series, at the end of which one pore has emerged. The dotted one corresponds to the second series, during which the second pore emerges. For each series, two time windows were used. The vertical dotted lines mark the 12.5-75 Mm range where the supergranulation peak is found (cf. Fig. 4). Here Nx=81, Ny=82 and Np=1024. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{13303f7.eps}\hspace*{1.5mm}
\includegraphics[width=8.2cm,clip]{13303f8.eps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg66.png)
|
Figure 6:
Kinetic energy spectra of the vertical velocity field for
various time windows. The vertical dotted line marks the maximum
of the spectrum at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13303f9.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg67.png)
|
Figure 7: Same as in Fig. 6- left, but with data not flat-fielded. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13303f10.eps}\hspace*{1.5mm}
\includegraphics[width=8cm,clip]{13303f11.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg70.png)
|
Figure 8:
Left: same as in Fig. 7, but with Doppler velocities
computed with just two wavelengths in the line.
Right: same as left but for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13303f12.eps}\hspace*{1.5mm}
\includegraphics[width=8cm,clip]{13303f13.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg71.png)
|
Figure 9: Spectral energy density of the intensity field. Left: data from the BFI at 450.4 nm (spectral width of 0.22 nm sampling the blue continuum) for various time windows (data set of 29-31/8/2007). The spectra are normalised so that the amplitude of the granulation peak is unity. The vertical dotted line marks the position of the granulation peak determined with instantaneous spectra. Here Nx=941, Ny=934and Np=1024. Right: data from the NFI at 525.0208+0.0108 nm (spectral width of 9 pm sampling the continuum on the red side of the line); here Nx=Ny=704 and Np=1024. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13303f14.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13303-09/Timg72.png)
|
Figure 10:
Same as Fig. 9-right, but with the NFI almost
centred on the line core at
|
| Open with DEXTER | |
| In the text | |
| |
Figure 11: Schematic view of the results. We indicate the layers where power laws are perceptible in the subgranulation range. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


