EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 512 (March-April 2010) A&A, 512 (2010) A42 Full HTML
Free Access
Issue
A&A
Volume 512, March-April 2010
Article Number A42
Number of page(s) 5
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/200913013
Published online 26 March 2010
A&A 512, A42 (2010)

Spectroscopic search for g-mode pulsations in 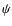$\psi$ Centauri

L. Mantegazza - M. Rainer - E. Antonello

INAF-Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807 Merate (LC), Italy

Received 29 July 2009 / Accepted 15 December 2009

Abstract
Context. Prior analysis of the light curve of the eclipsing binary $\psi $ Cen has shown the possible presence of g-mode pulsations.
Aims. We will try to confirm this claim by means of the analysis of high-resolution and high signal-to-noise echelle spectrograms.
Methods. We studied both the radial velocity curve and the line profile variations of $\psi $ Cen.
Results. We obtained accurate measurements of the masses and radii of the two components. Regarding the study of pulsations, the orbital motion of the stars can explain all the observed variations in the spectrograms.
Conclusions. There is no evidence of g-mode pulsations in $\psi $ Cen in the spectroscopic data.

Key words: binaries: eclipsing - stars: oscillations - stars: fundamental parameters - line: profiles - technique: spectroscopic

1 Introduction

The light curve of the eclipsing binary $\psi$ Centauri has been carefully studied by Bruntt et al. (2006) by means of high precision observations supplied by the WIRE satellite (Schember et al. 1996). They inferred the physical parameters of the system and suggested that according to the WIRE light curve there was evidence of g-mode pulsations in the primary star. They found two periods, 1.996 c/d and 5.127 c/d, with amplitudes of about 0.2 mmag from the Fourier analysis of the light curve.

The low frequencies of the periods found by Bruntt et al. (2006) could be explained by g-modes, which could be present also in late B-type stars (Aerts & Kolenberg 2005; Miglio 2007). Bruntt et al. (2006) estimated the effective temperatures of both components, $10450 \pm 300$ K and $8800 \pm 450$ K. Thus the spectral type of the primary component is consistent with the star possibly being a slowly-pulsating B-star (SPB).

These findings prompted us to include this star in our observational program aimed to find non radial modes in early A-type stars (Antonello et al. 2006). The observations were made with the FEROS spectrograph at ESO-La Silla in July 2006, when the two components had the maximum radial velocity separation. We hoped in this way to have a better chance of detecting line profile variations induced by pulsations in the primary star (Mantegazza 2000; Aerts et al. 2000).

2 Observations and data reduction

In principle, the presence of g-modes can be detected by analysing the line profile variations, since their effects are mainly localized in the wings of the lines. In g-mode pulsations, horizontal velocity components are dominant with respect to the vertical ones (see for instance Kaye et al. 1999; Uytterhoeven et al. 2008).

To this end 16 high-resolution ( R = 48 000) echelle spectrograms were taken with the FEROS spectrograph (Stahl et al. 1999) attached to the 2.2m reflector of ESO-La Silla Observatory during three consecutive nights (28-30 June 2006). The reduction was performed with the semi-automatic approach developed by Rainer (2003). We extracted an average line profile from each spectrum (hereafter LSD profile) using the Least Squares Deconvolution software developed by Donati et al. (1997) in the wavelength regions 4150-4290, 4380-4800 and 4930-5860 $\AA$ (avoiding the regions with the H$\beta$ and H$\gamma$ lines, whose shapes are not dominated by the rotational broadening). The LSD method extracts a mean line profile from the several hundreds of spectral lines in the selected wavelength ranges by deconvolving the spectra with a synthetic line mask. We used a line list from the VALD database (Piskunov et al. 1995; Kupka et al. 1999). The profiles obtained in this way have a signal-to-noise ratio ranging from 1500 to 3000, with an average value of 2200.

Unfortunately, because of the quite large $v \sin i$ (about 124 km s-1 for both components, see Royer et al. 2002) even at the maximum radial velocity separation (30 June-1 July) the two components are never completely separated.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13013fg1.ps} \vspace*{4mm} \end{figure} Figure 1:

Left: LSD profiles of the 16 spectra observed between 28 June and 1 July 2006. Right: the wavelength region centered on the Ti II 4501.273 $\AA$ and Fe II 4508.288 $\AA$ profiles for the same spectra. The spectra are offset for clarity. The higher S/N of the LSD profiles allows a much better detection of line profile variations.

Open with DEXTER

Figure 1 shows the LSD profiles of all the 16 spectra compared with an extracted region of the spectra. It is possible to see in the LSD profiles the entanglement of the binary components and the presence of line profile variations.

Since these variations were explained essentially by the orbital motion, we decided to increase our sample to verify the possible presence of pulsations. We recovered from the ESO archive 35 more spectrograms taken with same instrumentation in the period of 8 April to 27 September 2006, which fully covered an orbital period of 38.8 days, to confirm the previous result.

Table 1:   The S/N, HJD at mid-exposure and phase of the orbit of the 51 spectra used in our analysis.

In Table 1 we report for each spectrum its S/N along with the much higher S/N of its LSD profile, the HJD time at mid-exposure and the phase of the orbit, where the zero phase corresponds to the photometric primary minimum T0 = 2 443 183.04931 HJD. We computed the LSD profiles with the same approach adopted in the previous case for all the 51 spectra of our new sample.

3 Orbital and physical parameters of 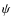${\sf\psi }$ Cen

We used the code FDBinary (Ilijic 2003) to disentangle the profiles of the two components. This code disentangles the spectra of the two components of a spectroscopic binary by means of a non linear least-squares fit in Fourier space. It fits the observed composite spectra with a set of Keplerian radial velocities with an orbit described by five parameters: the two radial velocity semiamplitudes, the eccentricity, an overall phase shift and the periastron longitude. A recent example of the application of this code can be found in Pavloski & Southworth (2009).

We weighted the LSD profiles according to their S/N. One of the spectrograms was excluded since it was taken during a partial eclipse (phase = 0.816). A first solution was computed taking into account the period supplied by the photometry and keeping all the other parameters free (the semi-amplitudes K1 and K2, the mean anomaly at epoch zero $\mu_0$, the longitude of periastron of the primary star at epoch zero $\omega_0$, the eccentricity e). The results are shown in the second column of Table 2.

The two orbital parameters e and $\omega_0$ can be derived independently from both photometry and spectroscopy and the values that we found were not significantly different from those supplied by Bruntt et al. (2006). Since the longer photometric baseline assures more accurate values, we recomputed the spectroscopic solution by adopting the photometric values and their errors for e and $\omega_0$ from Bruntt et al. (2006). We considered this our final solution and the results are shown in the fourth column of Table 2.

The errors on the free parameters were estimated with a MonteCarlo approach for both the solutions: we computed 100 FDBinary solutions changing randomly the weights of the input spectra in the interval covered by the weights derived from the S/N of the LSD profiles. The standard deviations of the parameters of this set of solutions were assumed as estimates of the uncertainties on these parameters. In order to improve the estimate of the errors of the final solution taking into account the photometric errors of e and $\omega_0$ (Bruntt et al. 2006), we computed 10 000 FDBinary solutions: for each of those we changed e and $\omega_0$, assigning to each of them a Gaussian distribution around the photometric value with the standard deviation corresponding to the photometric error. The errors on K1, K2 and $\mu_0$ found in this way were then added in quadrature to those derived for the final solution with the previous MonteCarlo approach.

The results are shown in Table 2 for both solutions: the second and third columns list the values and errors of the first solution (the values were found using FDBinary on the LSD profiles keeping all the parameters free and the errors were computed with a MonteCarlo approach) while the fourth and fifth columns list the final values and errors. The former were found using FDBinary keeping e and $\omega_0$ fixed and equal to the photometric values (Bruntt et al. 2006) and the latter were estimated taking into account also the photometric errors on e and $\omega_0$.

Table 2:   The orbital parameters of $\psi $ Cen found with the first (Cols. 2 and 3) and the final solution (Cols. 4 and 5).

\begin{figure} \par\includegraphics[width=9cm,clip]{13013fg2.ps} \vspace*{5mm} \end{figure} Figure 2:

The radial velocity curve of $\psi $ Cen using the Keplerian velocity obtained from FDBinary. Black dots: primary star. Red circles: secondary star.

Open with DEXTER

After disentangling successfully the components, we were able to compute the radial velocity curve of the system, shown in Fig. 2. The zero phase corresponds to the photometric primary minimum ( T0 = 2 443 183.04931  HJD, see Bruntt et al. 2006).

\begin{figure} \par\includegraphics[width=9cm,clip]{13013fg3.ps} \vspace*{5mm} \end{figure} Figure 3:

The mean line profiles of the system as obtained from FDBinary normalized to the continuum. Black line: primary star. Red line: secondary star.

Open with DEXTER

Using as a starting point the value of the luminosity ratio between the two stars of 6.12 at about 6000 $\AA$ derived from the photometry (Bruntt et al. 2006), we applied the method described by Ilijic et al. (2004) to normalize the disentangled spectra. We iterated the procedure to obtain the best normalization for a luminosity ratio between the two stars at 5000 Å (which is the approximate wavelength of the LSD profiles) of about $7\pm0.5$ (see Fig. 3). The value of the luminosity ratio is only indicative: it was the result of our normalization procedure, but it was not instrumental in our work. Finally we got the physical parameters (reported in Table 3) by combining the parameters derived from the light curve (Bruntt et al. 2006) with those derived from the radial velocity curve, using both the first and the final solution for the orbital parameters (see Table 2).

Table 3:   The physical parameters of $\psi $ Cen obtained using either the first or the final solution for the orbital parameters.

The small final errors stated in Table 3 are based on the very accurate photometric values given by Bruntt et al. (2006) and the very high S/N LSD profiles. To get more realistic uncertainties would require a full simulation of the input spectra, and this is beyond the scope of this work.

We estimated the projected rotational velocities of the two components from the position of the first three zeros of the Fourier transform of their average LSD profiles (Reiners et al. 2002). The results are 123.7 and 126.9 km s-1 respectively. The three different estimates for each profile allow us to estimate their uncertainty, which is about 2.5 km s-1 for the primary star. The errors found depend strongly on the symmetry of the profiles: for this reason the more symmetric line of the secondary component gives a more precise $v \sin i$ value despite the faintness of the star. However, to be conservative we consider the larger error for both components.

Given the orbital inclination ( $i=88.955^\circ \pm 0.012$) derived by Bruntt et al. (2006), the $v \sin i$ values are very close to the equatorial rotational velocities.

4 Search for the evidence of g-modes

We searched for the presence of effects not due to the orbital motion in the spectroscopic variations of $\psi$ Centauri by computing a synthetic mean profile for each observed spectrum. The synthetic profiles were obtained by shifting the disentagled average profiles of the two components as obtained from FDBinary (Fig. 3) according to the derived orbital radial velocities (Fig. 2) and adding their fluxes. These synthetic profiles show only variations due to the orbital motion, because they are built with always the same constant line profiles.

\begin{figure} \par\includegraphics[width=9cm,clip]{13013fg4.ps} \vspace*{5mm} \end{figure} Figure 4:

The LSD profiles are shown in solid black. The synthetic profiles are shown in dashed red and were constructed from the constant line profiles of the two components computed by FDBinary and shifted according to the derived orbital radial velocities. The binary motion is easily visible.

Open with DEXTER

\begin{figure} \par\includegraphics[width=9cm,clip]{13013fg5.ps} \vspace*{5mm} \end{figure} Figure 5:

Upper panel: average LSD profile (black) and synthetic average mean profile (red). Middle panel: standard deviation of both the LSD line profiles (black) and the synthetic ones (red). The difference between the two is shown by the green line. Lower panel: differences between each LSD profile and the corresponding synthetic one, built using the constant line profiles of the two components computed by FDBinary shifted according to the derived orbital radial velocities.

Open with DEXTER

The comparison between the synthetic profiles and the LSD ones is shown in Fig. 4: the two sets agree well. The average of these synthetic profiles and its standard deviation were compared with those of the observed spectra. Figure 5 shows the average LSD profile (black) and the synthetic one (red) in the first panel. The second panel shows the standard deviation of the average LSD profile (black) and of the synthetic average mean line profile (red) with respect to the individual LSD profiles. The green line shows the difference between observed and synthetic standard deviations. This difference is nearly constant across the whole profile with a dispersion comparable to the noise of the observed mean profiles. The third panel shows the differences between each LSD profile and the corresponding synthetic one. No significant deviations are visible in these differences. It seems therefore that the orbital motion fully explains the observed variations in the spectrograms.

Another check was performed. We subtracted from each LSD profile the corresponding synthetic one and then shifted these residual LSD profiles to correct for the radial velocity of the primary component. Figure 6 shows in the upper part the average of the residuals (first panel) and its standard deviation (second panel). The broken lines indicate the position of the borders of the line of the primary component. No significant variations are visible within these borders. The same test was performed by correcting for the secondary component motion. In this case the profile also does not show any detectable variation (see the lower panel of Fig. 6).

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13013fg6.ps} % \end{figure} Figure 6:

First panel: average of the residuals obtained subtracting the synthetic line profiles from the LSD ones and then correcting for the radial velocity of the primary (upper panel) and the secondary component (lower panel). Second panel: standard deviation of these residuals. The broken lines indicate the borders of the line of the primary (upper panel) and the secondary component (lower panel).

Open with DEXTER

We conclude that the spectrograms do not support the hypothesis of variations other than those induced by the orbital motion, and there is no spectroscopic evidence of g-mode pulsations.

In addition to this, there is new evidence that the claim by Bruntt et al. (2006) of the detection of g-mode pulsation in $\psi $ Cen might instead be due to instrumental effects in the WIRE data. Stello et al. (2008) published amplitude spectra of 11 K  giants observed with WIRE, and about half of those targets have a peak at ${\simeq}5.1$ c/day with an amplitude of ${\simeq} 0.2$ mmag (identical to $\psi $ Cen). The frequency is exactly one third of the WIRE orbital frequency. The ${\simeq}2$ c/day peak observed by Bruntt et al. (2006) was not reported by Stello et al. (2008). However, it could potentially be due to changing amounts of scattered light from the illuminated face of the Earth as suggested by the referee.

Acknowledgements

Based on observations made with the European Southern Observatory telescopes at the La Silla Observatory as part of the program 077.D-0164 (PI: L. Mantegazza) and on data obtained from the ESO Science Archive Facility under request number LMANTXXBGE107617. This work was supported by the contract ASI/INAFI/015/07/0. We thank the referee, Dr. H. Bruntt, for the great improvements of this paper due to his suggestions.

References

  1. Aerts, C., & Eyer, L. 2000, ASP Conf. Ser., 210, 113 [Google Scholar]
  2. Aerts, C., & Kolenberg, K. 2005, A&A, 431, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Antonello, E., Mantegazza, L., Rainer, M., & Miglio, A. 2006, A&A, 445, 15 [Google Scholar]
  4. Bruntt, H., Southworth, J., Torres, G., et al. 2006, A&A, 456, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Donati, J. F., Semel, M., Carter, B. D., Rees, D. E., & Cameron, A. C. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  6. Ilijic, S. 2003, Master Thesis, University of Zagreb [Google Scholar]
  7. Ilijic, S., Hensberge, H., Pavlovski, K., & Freyhammer, L. M. 2004, ASP Conf. Ser., 318, 111 [NASA ADS] [Google Scholar]
  8. Kaye, A. B., Henry, G. W., Fekel, F. C., & Hall, D. S. 1999, MNRAS, 308, 1081 [NASA ADS] [CrossRef] [Google Scholar]
  9. Kupka, F., Piskunov, N. E., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
  10. Mantegazza, L. 2000, ASP Conf. Ser. 203, 463 [Google Scholar]
  11. Miglio, A. 2007, PhD Thesis, Université de Liège [Google Scholar]
  12. Pavloski, K., & Southworth, J. 2009 MNRAS, 394, 1519 [Google Scholar]
  13. Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [Google Scholar]
  14. Rainer, M. 2003, Laurea Thesis, Università degli Studi di Milano [Google Scholar]
  15. Reiners, A., & Schmidtt, J. H. M. M. 2002, A&A, 384, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Royer, F., Grenier, S., Baylac, M.-O., Gomez, A. E., & Zorec, J. 2002, A&A, 393, 897 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Schember, H. R., Kemp, J. C. Ames, H. O., et al. 1996, SPIE, 2744, 751 [NASA ADS] [CrossRef] [Google Scholar]
  18. Stahl, O., Kaufer, A., & Tubbesing, S. 1999, ASP Conf. Ser., 188, 331 [NASA ADS] [Google Scholar]
  19. Stello, D., Bruntt, H., Preston, H., & Buzasi, D. 2008, ApJ, 674, 53 [Google Scholar]
  20. Uytterhoeven, K., Mathias, P., Poretti, E., et al. 2008, A&A, 489, 1213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1:   The S/N, HJD at mid-exposure and phase of the orbit of the 51 spectra used in our analysis.

Table 2:   The orbital parameters of $\psi $ Cen found with the first (Cols. 2 and 3) and the final solution (Cols. 4 and 5).

Table 3:   The physical parameters of $\psi $ Cen obtained using either the first or the final solution for the orbital parameters.

All Figures

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13013fg1.ps} \vspace*{4mm} \end{figure} Figure 1:

Left: LSD profiles of the 16 spectra observed between 28 June and 1 July 2006. Right: the wavelength region centered on the Ti II 4501.273 $\AA$ and Fe II 4508.288 $\AA$ profiles for the same spectra. The spectra are offset for clarity. The higher S/N of the LSD profiles allows a much better detection of line profile variations.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13013fg2.ps} \vspace*{5mm} \end{figure} Figure 2:

The radial velocity curve of $\psi $ Cen using the Keplerian velocity obtained from FDBinary. Black dots: primary star. Red circles: secondary star.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13013fg3.ps} \vspace*{5mm} \end{figure} Figure 3:

The mean line profiles of the system as obtained from FDBinary normalized to the continuum. Black line: primary star. Red line: secondary star.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13013fg4.ps} \vspace*{5mm} \end{figure} Figure 4:

The LSD profiles are shown in solid black. The synthetic profiles are shown in dashed red and were constructed from the constant line profiles of the two components computed by FDBinary and shifted according to the derived orbital radial velocities. The binary motion is easily visible.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13013fg5.ps} \vspace*{5mm} \end{figure} Figure 5:

Upper panel: average LSD profile (black) and synthetic average mean profile (red). Middle panel: standard deviation of both the LSD line profiles (black) and the synthetic ones (red). The difference between the two is shown by the green line. Lower panel: differences between each LSD profile and the corresponding synthetic one, built using the constant line profiles of the two components computed by FDBinary shifted according to the derived orbital radial velocities.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13013fg6.ps} % \end{figure} Figure 6:

First panel: average of the residuals obtained subtracting the synthetic line profiles from the LSD ones and then correcting for the radial velocity of the primary (upper panel) and the secondary component (lower panel). Second panel: standard deviation of these residuals. The broken lines indicate the borders of the line of the primary (upper panel) and the secondary component (lower panel).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.