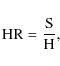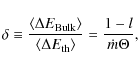EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 512 (March-April 2010) A&A, 512 (2010) A57 Full HTML
Free Access
Issue
A&A
Volume 512, March-April 2010
Article Number A57
Number of page(s) 11
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/200912921
Published online 01 April 2010
A&A 512, A57 (2010)

Spectral evolution of bright NS LMXBs with INTEGRAL: an application of the thermal plus bulk Comptonization model

L. I. Mainardi1 - A. Paizis1 - R. Farinelli2 - E. Kuulkers3 - J. Rodriguez4 - D. Hannikainen5 - P. Savolainen5 - S. Piraino6,7 - A. Bazzano8 - A. Santangelo7

1 - INAF-IASF, Sezione di Milano, via Bassini 15, 20133 Milano, Italy
2 - Dipartimento di Fisica, Università di Ferrara, via Saragat 1, 44100 Ferrara, Italy
3 - ESAC, ISOC, Villañueva de la Cañada, Madrid, Spain
4 - CNRS, FRE 2591, CE Saclay DSM/DAPNIA/SAp, 91191 Gif sur Yvette Cedex, France
5 - Metsähovi Radio Observatory, TKK, Metsähovintite 114, 02540 Kylmälä, Finland
6 - INAF-IASF, Sezione di Palermo, via Ugo La Malfa 153, 90146 Palermo, Italy
7 - IAAT, University of Tübingen, Sand 1, 72076 Tübingen, Germany
8 - INAF-IASF, Sezione di Roma, via del Fosso del Cavaliere 100, 00133 Roma, Italy

Received 17 July 2009 / Accepted 9 December 2009

Abstract
Aims. The aim of this work is to investigate in a physical and quantitative way the spectral evolution of bright neutron star low-mass X-ray binaries (NS LMXBs) with special regard to the transient hard X-ray tails.
Methods. We analyzed INTEGRAL data for five sources (GX 5-1, GX 349+2, GX 13+1, GX 3+1, GX 9+1) and built broad-band X-ray spectra from JEM-X1 and IBIS/ISGRI data. For each source, X-ray spectra from different states were fitted with the recently proposed model  $\mathsf{compTB}$.
Results. The spectra have been fit with a two- $\mathsf{compTB}$ model. In all cases the first  $\mathsf{compTB}$describes the dominant part of the spectrum that we interpret as thermal Comptonization of soft seed photons (<1 keV), likely from the accretion disk, by a 3-5 keV corona. In all cases, this component does not evolve much in terms of Comptonization efficiency, with the system converging to thermal equilibrium for an increasing accretion rate. The second  $\mathsf{compTB}$varies more dramatically, spanning from bulk plus thermal Comptonization of blackbody seed photons to the blackbody emission alone. These seed photons (R < 12 km, $kT_{\rm s}$ > 1 keV), likely from the neutron star and the innermost part of the system, the transition layer, are Comptonized by matter in a converging flow. The presence and nature of this second  $\mathsf{compTB}$component (whether a pure blackbody or Comptonized) are related to the inner local accretion rate which can influence the transient behavior of the hard tail: high values of accretion rates correspond to an efficient bulk Comptonization process (bulk parameter $\delta\neq0$), while even higher values of accretion rates suppress the Comptonization, resulting in simple blackbody emission ($\delta=0$).
Conclusions. The spectral evolution of the sources has been successfully studied in terms of thermal and bulk Comptonization efficiency in relation to the physical conditions in the transition layer.

Key words: stars: general - X-rays: binaries - binaries: close - stars: neutron - accretion, accretion disks

1 Introduction

Low-mass X-ray binaries (LMXBs) are systems where a compact object, either a neutron star (NS) or a black hole candidate (BHC), accretes matter via Roche lobe overflow from a normal companion of a mass M $\la$  $1~M_{\odot}$; a peculiar characteristic of this type of system is the formation of an accretion disk in the orbital plane near the compact object. In this paper we studied persistently bright NS LMXBs ( $L_{\rm X}\approx 10^{37}{-}10^{38}$ erg s-1) which grant long-lasting observability with instruments operating in the soft/hard X-ray range. The spectra of these sources are usually described as the sum of two components (e.g. White et al. 1988; Barret 2001; Mitsuda et al. 1984): a soft component often associated with the accretion disk or NS and a hard component interpreted as thermal Comptonization of soft seed photons from the disk and/or the NS by high temperature plasma of electrons near the compact object (so-called corona). The advent of broad-band X-ray missions, such as BeppoSAX, RXTE, INTEGRAL, revealed the presence of a spectral hardening (so-called ``hard tails'') above $\sim$30 keV on top of otherwise soft spectra (e.g. Di Salvo & Stella 2002; Paizis et al. 2006, hereafter P06, and references therein). These hard tails, mostly fit with phenomenological models such as a powerlaw, have been detected in Z sources (e.g. Frontera et al. 1998; Di Salvo et al. 2002) and also in the bright Atoll source GX 13+1 (P06).

To explain the origin of these hard tails, different models have been proposed across the years, such as direct synchrotron emission from a jet (Markoff et al. 2005), hybrid thermal/non-thermal Comptonization (Di Salvo et al. 2006; Coppi 1999) or more recently bulk motion Comptonization (Farinelli et al. 2008; Titarchuk et al. 1997, hereafter TMK97 and F08, respectively). The adoption of different models which satisfactorily fit the hard X-ray component in NS LMXBs clearly shows that it is necessary to look for other observable quantities in these systems, such as their timing properties or correlation among the spectral parameters.

For black-hole sources, a fundamental step forward came with the unambiguous discovery of the saturation of the spectral index (as a function of either the low QPO frequency or seed photon BB normalization) when sources move from the low/hard to the high/soft state (e.g. Shaposhnikov & Titarchuk 2009, and references therein). Such a saturation can be naturally explained in terms of the presence of a converging flow close to the compact object.

For NS systems the situation is more complex because of the presence of a firm surface in the compact object that plays a fundamental role in determining the hydrodynamical and radiative system configuration with, in turn, a different spectral appearance. However, given that a PL-like emission can be seen in both BH and NS systems and on the basis of the above reported results for BHs, it is a reasonable working hypothesis that converging flow (with unavoidable qualitative and quantitative differences) is a characteristic of NS systems too, at least in some particular accretion rate states. Close to the NS surface, the radial component of the velocity of matter ($V_{\rm R}$) dominates over the azimuthal one, and it is straightforward to find that $V_{\rm R}$ $\sim$ 0.56 c at  $R_{\rm NS}$, a factor that is actually reduced by the presence of pressure gradients (due to radiation, gas and magnetic field). Our interpretation is that multiple thermal plus bulk Compton scatterings, which occur in a high optical depth environment are at the origin of the hard tails observed in NS LMXBs, extending over the thermal continuum up to at least 100 keV. A self-consistent physical treatment of the innermost region in the case of neutron stars is presently being developed by Titarchuk & Farinelli (in preparation, see Sect. 4.1). In this paper we adopt the bulk motion Comptonization scenario which also enables a consistent interpretation with previous works (e.g. P06, Farinelli et al. 2008,2009,2007).

\begin{figure} \par\includegraphics[angle=270,width=8.5cm,clip]{12921fig1.ps} \end{figure} Figure 1:

Schematic view of the proposed scenario for thermal and bulk Comptonization regions in LMXBs hosting NSs.

Open with DEXTER

P06 proposed for the first time a unified physical scenario to explain the spectral evolution of NS LMXBs, including the peculiar transient hard tail. All the observed spectral states could be well fit in terms of the interplay of thermal and bulk Comptonization (TC and BC, respectively), using the $\mathsf{BMC}$ model (Titarchuk et al. 1996,1997, hereafter TMK96 and TMK97) in XSPEC. Thermal Comptonization operates in a region where a hot plasma is present and acts on a population of soft seed photons, hardening the injected seed photon spectrum (from the accretion disk, Fig. 1); the resulting spectrum is extended to higher energies depending on the Comptonization efficiency. Bulk Comptonization operates in the inner part of the system between the Keplerian accretion disk and the NS surface, the transition layer, hereafter TL (Fig. 1). In the inner part of the TL, matter falls towards the NS surface with a preferred (bulk) motion, acting on the inner seed photons of the system; the result is a powerlaw-shape spectrum at high energies due to the energy transfer from the matter kinetic energy to the photon field (TMK96, TMK97). P06 found evidence that bulk motion is always present, its strength is related to the accretion rate and is suppressed only in the presence of high local luminosity. This scenario has been confirmed also by Farinelli et al. (2007, hereafter F07), who re-analyzed broad-band BeppoSAX data, applying the $\mathsf{BMC}$ model to GX 17+2.

In the quest to study in a quantitative way the evolution of the parameters that describe the innermost physical conditions of NS LMXBs, Farinelli et al. (2008, hereafter F08), developed a new Comptonization model, $\mathsf{compTB}$[*]. We recall here the basics of this recent model, referring the reader to F08 for a more detailed description.

The total emerging spectrum is given by

\begin{displaymath}% F(E)=\frac{C_{\rm n}}{A+1}(\underbrace{{\rm BB}}_{(a)} + \underbrace{A \times {\rm BB} \ast G}_{(b)}), \end{displaymath} (1)

where $C_{\rm n}$ is the normalization constant, A is the illumination factor, $C_{\rm n}~{\rm BB}/(A+1)$ is the seed photon spectrum directly seen by the observer and not modified by Comptonization processes. $C_{\rm n}~A/(A+1)$ $\times$  ${\rm BB} \ast G$ is the Comptonized spectrum obtained by convolution of a seed photon spectrum (blackbody, BB) with the Green's function[*], to evaluate the effect of TC and BC on the seed photon field.

Parameters of the $\mathsf{compTB}$ XSPEC model are the seed photon temperature  $kT_{\rm s}$, the electron plasma temperature  $kT_{\rm e}$, the spectrum energy slope (i.e. overall Comptonization efficiency) $\alpha$ (photon index $\Gamma=\alpha+1$), the bulk parameter $\delta$ that quantifies the efficiency of BC over TC and $\log A$, which assigns a different weight to the two components (a) and (b). This model enables the co-existence of the direct seed photon component and its Comptonized part, all obtained in a self-consistent way. In Eq. (1) we note that for $\log A = -8$ we have only (a), i.e. the direct seed photon component, while for $\log A = 8$ the direct component is no longer visible and we have only thermal plus bulk Comptonization. In the case of $\delta=0$, the BC contribution is neglected, retaining only the TC effects (equivalent to compTT, Titarchuk 1994).

\begin{figure} \par\includegraphics[width=18cm,clip]{12921fig2.ps} \end{figure} Figure 2:

IBIS/ISGRI 20-40 keV mosaic in Galactic coordinates of the Galactic Bulge (about 3.3 Ms). Only the sources studied in this paper are labeled.

Open with DEXTER

The first application of the $\mathsf{compTB}$ model and of the proposed physical scenario to the spectral evolution of a single NS LMXB, to trace the evolution of the physical parameters in a quantitative way, was presented in Farinelli et al. (2009, hereafter F09) on Cyg X-2, using BeppoSAX data. F09 fitted the spectra of the source with two $\mathsf{compTB}$ models. The first one, with the bulk parameter $\delta=0$, was the dominant component and described a pure thermal Comptonization process. This component, due to the Comptonization of cold disk photons by the outer TL, is roughly constant with time and the accretion rate. The second $\mathsf{compTB}$ model describes the overall Comptonization (thermal plus bulk, variable $\delta$ parameter) of hotter seed photons close to the neutron star surface by the inner region of the TL (Fig. 1). This component is highly variable with time (and local accretion rate), ranging from significant Comptonization of the hot seed photons (thermal and bulk) to a simple blackbody-like spectrum.

In this work we extend the above study to five persistently bright NS LMXBs (GX 5-1, GX 349+2, GX 13+1, GX 3+1 and GX 9+1). The choice of sources was driven by the validity range of the $\mathsf{compTB}$ model (diffusion regime, see F08), associated to a high accretion rate where the transient hard tail can be appreciated. The selected sources are located in the Galactic Center where angular resolution is an issue because of the presence of a large number of X-ray sources. The imager IBIS (Ubertini et al. 2003) and the X-ray instrument JEM-X (Lund et al. 2003) on-board INTEGRAL (Winkler et al. 2003) have the necessary angular resolution to disentangle the different contributions, allowing us to build good quality broad-band X-ray spectra (3-200 keV).

2 Observations and data analysis

2.1 Analysis process

The sample of the NS LMXB chosen is given in Table 1 and comprises five bright (``GX'') bulge sources. We have analyzed INTEGRAL pointings collected from September 2006 to September 2007 from the AO4 and AO5 INTEGRAL Key Programmes. The exposure time for each pointing is variable ( $\Delta t \sim 2000$ s). The selected pointings satisfy the condition that every source is ${\leq}3^{\circ}$ from the pointing direction. Analysis was performed on JEM-X1 and IBIS/ISGRI (Lebrun et al. 2003) data with the software package OSA, version 7.0.

The energy bands selected for the JEM-X1 imaging analysis are 3-10 keV and 10-20 keV while the energy band selected for the IBIS/ISGRI imaging analysis is 20-40 keV. The mosaic of the Galactic Center (Fig. 2) was constructed using all available pointings in the IBIS/ISGRI energy band: as expected, all the sources studied were active and detectable. We used the official INTEGRAL catalog to extract spectra for the single sources as well as the JEM-X default response matrix (256 bins) and a new re-binned (57-bins) IBIS/ISGRI response matrix.

Table 1:   The five bright NS LMXBs studied in this paper.

2.2 Spectral classification with HR

In order to study the spectral evolution of the sources, we associated a numeric parameter to the spectrum of each pointing, the hardness ratio (hereafter HR). The HR is computed from the counts per second extracted from the two energy bands of the JEM-X analysis as follows

\begin{displaymath}% \rm HR= \frac{S}{H}, \end{displaymath} (2)

where S (soft) is the count rate for the 3-10 keV energy band, while H (hard) is the count rate for the 10-20 keV energy band. HR is an indicator of the source spectral state: the lower the HR the harder the spectrum. Despite its unusual/counterintuitive form, we adopted the definition (2) because the good statistics showed by JEM-X granted us integer values for a more facile management of HR boundaries and as explained in Sect. 4.1, we wanted to connect the increase of HR with the increase of the accretion rate.

Considering the overall behavior, each source presents a characteristic HR variability that covers wide ranges (for example see Fig. 3 for GX 5-1). From a morphological evaluation of the spectral characteristics together with HR values, we classified every spectrum and averaged similar spectra to improve the overall statistics.

\begin{figure} \par\includegraphics[angle=90,width=8.5cm,clip]{12921fig3.ps} \end{figure} Figure 3:

Example of the HR variation for the source GX 5-1 considering all available pointings.

Open with DEXTER

2.3 The spectral fitting

Before spectral fitting, all the spectra were re-binned so as to contain at least 25 counts in every channel; we considered only the counts within the interval 5-18 keV for JEM-X1 spectra and the counts starting at 22 keV for IBIS/ISGRI. Systematic errors of $2\%$ for IBIS/ISGRI data and $3\%$ for JEM-X1 data were added. Instrumental cross-calibration factors were allowed to vary between 0.8 and 1.2 (IBIS/ISGRI) with JEM-X1 frozen at 1. In all cases the value of the constant stabilized itself at the maximum value, 1.2. For the spectral analysis, we used XSPEC version 12.

In all cases we started the fitting process with the simplest general model, considering only one  $\mathsf{compTB}$, and for more complex cases, we added a second  $\mathsf{compTB}$, as in F08. Hence (excluding the cross-calibration constant) we used in the most complex cases

\begin{displaymath}% F(E)=\mathsf{wabs}\ast(\mathsf{compTB[1]} + \mathsf{compTB[2]}), \end{displaymath} (3)

where $\mathsf{wabs}$ (Morrison & McCammon 1983) is the multiplicative model that takes into account the interstellar absorption at low X-ray energies; the column-density $N_{\rm H}$ was fixed during the fitting to the values shown in Table 1, as the absence of data below 5 keV does not allow the correct determination of this parameter through the fitting process.

We note that $\mathsf{compTB[1]}$, with parameters set to $\log A = 8$ and $\delta=0$, is a thermal $\mathsf{compTB}$ accounting only for TC processes (equivalent to  $\mathsf{compTT}$). Instead, $\mathsf{compTB[2]}$, when present, is either a mixed $\mathsf{compTB}$ (shape-wise equivalent to ${\approx}\mathsf{bbody}+ \mathsf{PL}$, where we consider both TC and BC processes), or a  $\mathsf{bbody}$ (neither TC nor BC setting $\log A = -8$). For the cases in which the fit required two $\mathsf{compTB}$ components, a single temperature of the plasma  $kT_{\rm e}$ was considered (see Sect. 3 for details).

2.4 Other parameters

Some other quantities can be obtained from the fit processes to gain more information about the system and the environment around the NS:

  • $\vec {F_{\rm tot}}$: the unabsorbed total flux (erg s-1 cm-2) in the interval 0.1-200 keV and relative luminosity $L_{\rm tot}=4\pi D^2 F_{\rm tot}$ (using distances in Table 1);

  • CAF: the Compton amplification factor that allows us to evaluate the total energy gain of the seed photons through the TC process. It is defined as $\rm {CAF}=flux1/flux2$, where flux1 (erg s-1 cm-2) is the unabsorbed energy flux associated to the thermally Comptonized photons (calculated on compTB[1] with $N_{\rm H}=0$), and flux2 (erg s-1 cm-2) is the unabsorbed energy flux associated to the seed photons (calculated on compTB[1] with $\log A = -8$ and $N_{\rm H}=0$) in the energy interval 0.1-200 keV;

  • the optical depth $\mathbf{\tau}$: the Comptonization parameter  $\mathbf{\alpha}$ from the fit is linked to  $kT_{\rm e}$ and $\tau$ as

    \begin{displaymath}% \alpha=-\frac{3}{2}+\sqrt{\frac{9}{4}+\frac{\pi^2m_{\rm e}c^2}{C_{\tau}kT_{\rm e} (\tau + \frac{2}{3})^2}}, \end{displaymath} (4)

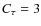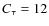    where $C_{\tau} =3$ for a spherical geometry with an optical radius $\tau$, while $C_{\tau} =12$ for a ``slab'' geometry (Titarchuk & Lyubarskij 1995). In this paper we presumed a slab geometry corresponding to a reduced corona (see also F08);

  • $\vec{R}_{\rm bb}$: the blackbody radius of  $\mathsf{compTB[2]}$, computed using $L_{\rm bb}=4\pi~R_{\rm bb}^2~\sigma T^4$.

3 Results

The detailed results per source are given in the next subsections, while here we note a few general trends and issues. Each source shows a given range of variability for HR values which enabled us to identify a different number of intervals (see Table 2) and spectral states per source. Our sources showed all types of behaviors, and hence we used a model with two  $\mathsf{compTB}$s in which the first is thermal and the second mixed (GX 5-1 and GX 13+1); two $\mathsf{compTB}$s in which the first is thermal and the second a blackbody (GX 9+1 and GX 349+2); one thermal  $\mathsf{compTB}$ (GX 3+1). The absence of data below 5 keV led to a high uncertainty in determining  $kT_{\rm s}$ in the $\mathsf{compTB[1]}$ component (the softest). In fact, for the majority of cases only an upper limit could be determined.

As already experienced in F08 and F09, in the cases where we applied a mixed  $\mathsf{compTB[2]}$, the lack of an observable cut-off prevented us to allow $\alpha$, $\delta$ and $\log A$ to be free during the fit: indeed, if the number of the free parameters exceeds the number of the observable quantities (normalization, cut-off and the PL slope), a degeneration of model parameters occurs, and hence more than one model solution can be obtained. The degeneration can be reduced: as in F08, the  $kT_{\rm e}$ value for  $\mathsf{compTB[2]}$ was set equal to the $\mathsf{compTB[1]}$ one, considering a single plasma temperature (indeed a preliminary fit provided similar values for both  $kT_{\rm e}$). Furthermore, we fixed $\log A$ (GX 5-1) or $\alpha$ (GX 13+1) to the values corresponding to a $\chi^2$ minimum (chosen inside an interval calculated with the XSPEC command steppar). We left $\delta$ free during the fit to evaluate the bulk efficiency.

Table 2:   The number of pointings and exposition time for each HR interval for the NS LMXBs studied in this paper.

3.1 GX 5-1

The variability range of HR (definition (2)) spans between $\sim$5-18 (as shown in Fig. 3). By classifying the spectral shapes, we obtained four mean spectra: the first spectrum, the hardest one, corresponding to HR < 7, shows as expected a hard tail between 40 and 150 keV. Indeed a hard tail in the spectra of GX 5-1 had already been detected by previous observations (Paizis et al. 2005; Asai et al. 1994, P06). The second spectrum (7 < HR < 10) shows a weaker hard tail between 40 and 150 keV; the third one (10 < HR < 12) does not show a hard tail and is soft; the last spectrum is the softest (HR > 12), again with no hard tail (see also Paizis et al. 2005; Kuulkers et al. 2007, on the variability of GX 5-1).

As required by the data, we used the two-component model for all spectra in the fitting process and obtained the following results (see Table 3):

  • with the $\mathsf{compTB[1]}$ component we describe the presence of the TC process as the dominant mechanism in all the four spectra. For higher values of HR we observe that the CAF decreases, while $\alpha$ increases. This is consistent with a reduction in the efficiency of the TC process;

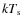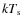  • the seed photon temperatures $kT_{\rm s}$ of the two components are different: in the thermal  $\mathsf{compTB[1]}$, $kT_{\rm s}$ remains always below 1 keV, while in the mixed  $\mathsf{compTB[2]}$ it has higher values of ${\ga}1.5$ keV;

  • considering the errors associated, the plasma temperature  $kT_{\rm e}$ remains within the interval 3-4 keV;

  • with $\mathsf{compTB[2]}$ in all spectra, we describe an additional component that shows a specific evolution: in the first two spectra (HR < 7, 7 < HR < 10) we obtained a mixed  $\mathsf{compTB}$ that allows us to evaluate the BC contribution with the parameter $\delta\neq0$. The spectra are representative of the intermediate state (according to the definition given by P06). 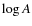For increasing values of HR, $\log A$ shows a decreasing trend that assigns less importance to the mixed component. In fact we found a best-fit using the  $\mathsf{compTB[2]}$ in the blackbody mode ($\log A = -8$) in the third and fourth spectra (10 < HR < 12, HR > 12);

  • with increasing values of HR, the size of the blackbody-emitting region 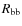 $R_{\rm bb}$ in  $\mathsf{compTB[2]}$ increases, remaining compatible with the NS and/or TL dimensions.
In Fig. 4 we show the EF(E) spectra (keV cm-2 s-1) of GX 5-1 for two of the four selected HR intervals (corresponding to the hardest and the softest case).

Table 3:   Best-fit parameters of the multi-component model $\mathsf{wabs\cdot(compTB[1]+compTB[2])}$ for the source GX 5-1.

\begin{figure} \par\includegraphics[angle=270,width=8.5cm,clip]{12921fig4.ps}\hspace*{5mm} \includegraphics[angle=270,width=8.5cm,clip]{12921fig5.ps} \end{figure} Figure 4:

Unabsorbed EF(E) spectra of GX 5-1 for the HR intervals: HR < 7 ( left), and HR > 12 ( right). The dotted lines are the two separated $\mathsf{compTB}$ components: dash for $\mathsf{compTB[1]}$, dash-dot $\mathsf{compTB[2]}$.

Open with DEXTER

3.2 GX 13+1

Examining the shape of the GX 13+1 JEM-X1 and IBIS/ISGRI spectra, we identified three intervals in which we recognized different phases of the spectral evolution, and so we obtained three mean spectra: the first mean spectrum corresponding to HR < 10 shows a hard tail between 30 and 150 keV, which characterizes an intermediate state. A hard tail in the spectra of GX 13+1 had been discovered using INTEGRAL data by P06. The mean spectrum corresponding to 10 < HR < 13 shows a high/soft state, deprived of the hard tail, similar to the mean spectrum corresponding to HR > 13. Spectral analysis was carried out using a double-component model only for the HR < 10 spectrum, while the other two were fit with one thermal  $\mathsf{compTB}$ (see Table 4, Fig. 5). Looking at the parameters we note that

  • the $\mathsf{compTB[1]}$ component, present in all spectra, describes the TC process. Again, for increasing values of HR we observe a strong decrease of the CAF values and an increase of $\alpha$, a signature of decreasing efficiency of the TC process;

  • the seed photon temperatures 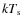$kT_{\rm s}$ in the two components are different in the first spectrum (in the other two spectra only one thermal  $\mathsf{compTB}$ was needed);

  • the plasma temperature $kT_{\rm e}$ remains within the range of 3-4 keV;

  • we applied the $\mathsf{compTB[2]}$ component only to the first spectrum as a mixed  $\mathsf{compTB}$: we detected a hard tail and an active BC process with $\delta\neq0$; the $\alpha$ value was fixed to a value that corresponds to a minimum $\chi^2$ (see Sect. 3);

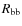
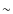  • the luminosity of the blackbody $L_{\rm bb}$ is very low with respect to the total X-ray luminosity of the source; the dimension of the blackbody emission region $R_{\rm bb}$ $\sim$ 2 km is compatible with part of the NS surface and/or TL dimensions.

\begin{figure} \par\includegraphics[angle=270,width=8.5cm,clip]{12921fig6.ps}\hs... ...{0.5cm} \includegraphics[angle=270,width=8.5cm,clip]{12921fig7.ps} \end{figure} Figure 5:

Unabsorbed EF(E) spectra of GX 13+1 for the HR intervals: HR < 10 ( left), HR > 13 ( right). The dotted lines are the two separated $\mathsf{compTB}$ components: dash for $\mathsf{compTB[1]}$, dash-dot $\mathsf{compTB[2]}$.

Open with DEXTER

Table 4:   Best-fit parameters of the multi-component model $\mathsf{wabs\cdot(compTB[1]+compTB[2])}$ for the source GX 13+1.

3.3 GX 9+1

We classified every JEM-X1 and IBIS/ISGRI spectrum of GX 9+1 according to their shape and identified three HR intervals (HR < 7.5, 7.5 < HR < 8.5 and HR > 8.5), obtaining three mean spectra. All spectra showed the high/soft state; in fact, the spectral analysis was carried out with a double-component model using a thermal  $\mathsf{compTB}$ plus a second  $\mathsf{compTB}$ as a pure blackbody (see Table 5, Fig. 6):

  • the TC process was described with $\mathsf{compTB[1]}$ in all three spectra;

  • similarly to the previous cases, the seed photon temperatures 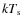 $kT_{\rm s}$ differ in the two components: about 0.6 keV for the first one and near 2 keV for the second one;

  • in this case, the plasma temperature $kT_{\rm e}$ is badly constrained by the data;

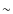  • the presence of the second component  $\mathsf{compTB[2]}$ reveals a constant blackbody contribution. Below 20 keV the blackbody emission is more important than the TC one. The size of the blackbody-emitting region is nearly constant ($\sim$3.4 km), as is the corresponding X-ray luminosity (0.2 $\times$ 1038 erg s-1). Despite the different HR selection, these spectra do not show a dramatic evolution, as shown in the previous cases.

Table 5:   Best-fit parameters of the multi-component model $\mathsf{wabs\cdot(compTB[1]+compTB[2])}$ for the source GX 9+1.

\begin{figure} \par\includegraphics[angle=270,width=8.5cm,clip]{12921fig8.ps} \end{figure} Figure 6:

Unabsorbed EF(E) spectrum for the HR interval 7.5 < HR < 8.5 for GX 9+1. The dotted lines are the two separated $\mathsf{compTB}$ components: dash for $\mathsf{compTB[1]}$, dash-dot $\mathsf{compTB[2]}$.

Open with DEXTER

3.4 GX 349+2

For GX 349+2, we identified two intervals (HR < 7 and HR > 7) that showed similar spectra from which we obtained two mean spectra: both are of the high/soft state well described with a double-component model consisting of a thermal  $\mathsf{compTB}$ and a second  $\mathsf{compTB}$ as blackbody. We obtained the following results (see Table 6, Fig. 7):

  • with $\mathsf{compTB[1]}$, we describe the TC process; for higher values of HR we do not observe the typical $\alpha$ growth, but instead it is constant, which results in a constant CAF value and invariant TC efficiency;

  • similarly to previous sources, the seed photon temperatures are different when two $\mathsf{compTB}$ components are taken into consideration: $kT_{\rm s}<1$ keV for the thermal  $\mathsf{compTB}$, higher temperature for the blackbody photons;

  • the plasma temperature stays always around 3 keV;

  • using $\mathsf{compTB[2]}$, we detected the presence of a blackbody component: the blackbody luminosity  $L_{\rm bb}$ does not vary (0.3 $\times$ 1038 erg s-1) and its emission region is of a dimension compatible with the NS and/or TL.

Table 6:   Best-fit parameters of the multi-component model $\mathsf{wabs\cdot(compTB[1]+compTB[2])}$ for the source GX 349+2.

\begin{figure} \par\includegraphics[angle=270,width=8.5cm,clip]{12921fig9.ps} \end{figure} Figure 7:

Unabsorbed EF(E) spectrum of GX 349+2 for HR < 7. The dotted lines are the two separated $\mathsf{compTB}$ components: dash for $\mathsf{compTB[1]}$, dash-dot $\mathsf{compTB[2]}$.

Open with DEXTER

3.5 GX 3+1

In the case of GX 3+1, we identified three intervals of HR in which we recognized different phases of spectral evolution in the JEM-X1 and IBIS/ISGRI spectra: the three mean spectra obtained (HR < 8, 8 < HR < 9.5 and HR > 9.5) all represent the high/soft state. The spectral fitting was carried out on all spectra with a single component model, a thermal  $\mathsf{compTB}$ (see Table 7, Fig. 8):

  • as usual with $\mathsf{compTB[1]}$ we describe the TC process; similarly to previous sources we see a decreasing of the TC efficiency (decrease of CAF and increase of $\alpha$) for increasing HR values;

  • the seed photon temperature 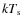$kT_{\rm s}$ is of the order of 1 keV;

  • the plasma temperature $kT_{\rm e}$ is of the order of 3-4 keV.

Table 7:   Best-fit parameters of the model $\mathsf{wabs\cdot(compTB[1])}$ for the source GX 3+1.

4 Discussion

In this work we have studied the spectral evolution of five NS LMXBs, using the new Comptonization model  $\mathsf{compTB}$ (Farinelli et al. 2008). The  $\mathsf{compTB}$ model is formed by two components: one component is a pure blackbody directly seen by the observer while the other one takes into account the contribution of thermal and bulk Comptonization of the blackbody seed photons. To fit the INTEGRAL broad band spectra we applied two $\mathsf{compTB}$ models.

Every source has shown a different spectral evolution: for GX 5-1 and GX 13+1 increasing values of the HR correspond to spectral changes from the intermediate state (high-energy hard tail), to the high/soft state (no hard tail), while in the other three sources we did not observe dramatic spectral changes despite a progressive softening for an increasing accretion rate (i.e. HR, see below).

\begin{figure} \par\includegraphics[angle=270,width=8.5cm,clip]{12921fig10.ps} \end{figure} Figure 8:

Unabsorbed EF(E) spectrum for the HR interval HR < 8 for GX 3+1. The overall spectrum is well described by a single component, $\mathsf{compTB[1]}$, see text.

Open with DEXTER

The total energetic budget is in all sources, regardless of HR, dominated by the thermal Comptonization component of $kT_{\rm s} \la 1$ keV BB-like seed photons off warm electrons with the temperature  $kT_{\rm e}$ typically of 3-4 keV and the optical depth of a few ( $\tau \la 5$). This component, described with a thermal  $\mathsf{compTB}$ (equivalent to a  $\mathsf{compTT}$) is probably associated to the region between the geometrically thin accretion disk and the NS surface, the so-called transition layer, where most of the gravitational energy release takes place (Titarchuk & Fiorito 2004, F08).

When a second $\mathsf{compTB}$ model is required by the data, a second hotter seed photon population ($\sim$1-2 keV) can be identified, interpreted as the BB-like contribution from the innermost region of the system, the NS and the inner TL (Fig. 1).

A rough estimation of the apparent emitting radius of this BB region actually provides results which are consistent with a NS and/or TL radius, with $R_{\rm bb}$ $\sim$ 2-12 km. In the case of GX 5-1, for which we have the best statistics, we can see (Table 3) an increase of the emitting BB region with the HR (hence $\dot M$, see next section).

Where a single $\mathsf{compTB}$ model has been applied, we observe that $kT_{\rm s}$ has values very close to 1 keV, unlike the other cases where  $kT_{\rm s}$ is either below this energy ($\la$0.6 keV) or higher (always >1 keV). In the single $\mathsf{compTB}$ model case, it is likely that a part of the seed photons come from the disk (very soft photons $\la$0.5 keV), but emission from the TL and NS surface can contaminate the seed photon population thereby increasing its overall temperature ($\sim$1 keV). As none of the observed sources reached the hard state (see, e.g. Fig. 2 in P06) where an increased height-scale of the TL may provide a high geometrical coverage of the central compact object, the lack of a second component in the case of a single $\mathsf{compTB}$ component in the fit is likely due to poor statistics in addition to small energy coverage in the band where most of the BB-like emission is present.

In terms of the observable quantities which may trace the source spectral evolution, it is important to focus on the $\alpha$-parameter, which is related to the slope of the Green's function of the Comptonization region. As already pointed out in F08, for intermediate state sources we are dealing in fact with two observable indexes, one related to the pure TC process while the second is related to the TC+BC efficiency. The first index only depends on the system temperature and optical depth and is actually directly related to the Comptonization parameter y[*], while the second index contains an additional dependence on the bulk parameter $\delta$ (see Eq. (23) in TMK97). In both cases, the slope of the Green's function depends on the first eigenvalue of the spatial problem for a bounded medium. In fact, when BC is present, it is possible to treat the two regions (internal bulk-dominated TL, external TC dominated TL plus innermost accretion disk) in a separate way, each one with its own spatial configuration and associated eigenvalue problem and derived spectral index. This translates into two different observable quantities (the thermal index $\alpha$ and the TC+BC index). For systems where BC is suppressed or strongly reduced, $\delta$ goes to zero, and according to Eq. (13) in TMK97, the two indexes tend to be coincident, and one single TC component is observed.

The $\alpha$parameter measures the slope of the spectrum and can quantify the effective efficiency of the overall Comptonization processes, i.e. how much energy has been exchanged between the photon field and the electrons. In the first  $\mathsf{compTB}$ (the thermal one), $\alpha$ becomes higher as HR increases: we can always observe the spectral evolution in the direction of a progressive softening, a smaller quantity of energy is gained by the photon field reducing the maximum energy of the spectra. Indeed, the energy gained by thermal Comptonization, CAF, decreases as $\alpha$ increases, giving a physical evaluation of the energy gain through the TC process. The $\alpha$ value related to the mixed  $\mathsf{compTB}$ is generally higher with respect to the thermal one. It encloses both the BC and TC contributions coming from the TL, the NS itself and possibly the inner accretion disk.

4.1 The transient nature of the hard tail

Bulk Comptonization acts in the TL, where the orbits of the in-falling matter deviate from the Keplerian behavior to adjust to the NS rotation speed. Here the matter interacts during its bulk motion ( $v_{\rm b}\sim 0.1~c$, Titarchuk & Farinelli, in prep.) with the photon field that originates in the inner disk, in the TL itself and from the impact of matter onto the NS.

Since the physical conditions of the interaction region strongly influence the BC, this produces the transient high energy hard tail behavior. Indeed, the local accretion rate of the source determines the resulting radiation pressure in the inner TL and in turn influences its hydrodynamical configuration.

At very high values of the accretion rate, the radiation pressure behaves like an intense photon wind (Bradshaw et al. 2007), able to efficiently break the accreting matter, abating the $v_{\rm b}$, hence suppressing (or strongly reducing) the Fermi first-order process in photon energy gain, which is responsible for the generation of the hard X-ray tail. In the $\mathsf{compTB}$ model, the quantity that allows us to evaluate the hard tail-$\dot M$ link is the bulk parameter $\delta$, which is defined as

\begin{displaymath}% \delta \equiv \frac{\left\langle \Delta E_{\rm Bulk} \right... ...e \Delta E_{\rm th} \right\rangle}= \frac{1-l}{\dot m \Theta}, \end{displaymath} (5)

where $l \equiv L/L_{\rm Edd}$ and $\dot m \equiv \dot M/\dot M_{\rm Edd}$ are local luminosity and accretion rate in Eddington's units, respectively, and $\Theta \equiv kT_{\rm e}/m_{\rm e}c^2$ is the adimensional electron temperature[*].

Increasing the accretion rate leads the system to a state closer to thermal equilibrium between electrons and the background radiation field through a more efficient Compton cooling of the electrons themselves (lower average energy gain of the photons and CAF decreasing).

In this work this spectral evolution has been observed for increasing values of HR with a slow spectral softening starting from the intermediate state (low HR) to the high/soft state (high HR values). Given the spectral evolution observed in all the sources, we can reasonably associate the increase of HR to an increasing accretion rate. As already pointed out by previous authors (e.g. Lin et al. 2009; van der Klis 2001; Homan et al. 2007), the role of $\dot M$ in the spectral evolution of these sources is not straightforward. Furthermore, from the observational results of a detailed time-resolved BeppoSAX spectral analysis of the Z source Cyg X-2, F09 proposed to split the general definition of the accretion rate $\dot M$ into two quantities, $\dot M_{\rm disk}$ and  $\dot M_{\rm TL}$, which obey the condition $\dot M_{\rm TL} \la \dot M_{\rm disk}$. The reason for this is that the total measured source bolometric luminosity does not follow the expected $\dot M$ trend from the source position in the hardness intensity diagram and thus cannot be used as a tracer of the total mass accretion rate. Moreover, as also reported in Bradshaw et al. (2007), for high (Eddington-like) accretion rates a strong radiation pressure may originate in the accretion disk, which may eventually eject part of the accreting material, so that the mass flow at the disk/TL radius is actually lower than the one flowing through the Roche lobe. In this picture the key role in the innermost system is played by  $\dot M_{\rm TL}$.

We can thus read the observed spectral variability of our sources as the interplay of TC and BC processes according to the aforementioned considerations and increasing HR:

1.
for a low $\dot M_{\rm TL}$, the hard tail results to be absent or too weak because of a lack of a sufficiently high number of BC scatterings able to elevate the hard tail contribution over the sensitivity instrument threshold. The observed spectrum is due mainly to the TC of soft seed photons from the disk and NS in the hot corona plasma (tens of keV). This is the case of low-dim Atolls not considered here (see F08);

2.
for higher $\dot M_{\rm TL}$, the corona starts to be efficiently cooled and the overall spectrum is dominated by TC in a cold corona ( $kT_{\rm e}$ of a few keV). BC may not be strong enough to be detected (GX 3+1, GX 9+1, GX 349+2, but see also point 4);

3.
for increasing $\dot M_{\rm TL}$ we can observe the intermediate state (GX 5-1, GX 13+1 in this work), in which the hard tail is visible. Its importance and intensity are strongly influenced by the accretion rate value. Indeed, only within a narrow range of  $\dot M_{\rm TL}$, the number of BC interactions is high enough to produce the hard tail, and at the same time the radiation pressure is so high as to reduce the BC efficiency. The fine-tuning of these two quantities could be the reason why we observe a little number of sources hosting NS displaying hard tails, and even more, only a given spectral state within a given source (the intermediate state, corresponding to the so-called horizontal branch of Z sources);

4.
in the case of very high values of $\dot M_{\rm TL}$, the hard tail disappears or its contribution becomes negligible as it is below the sensitivity threshold. The pressure in the TL increases because a large amount of matter releases a lot of energy at the impact onto the NS or within the TL itself, and this can inhibit the bulk motion. The source moves to the high/soft spectral state in which the spectrum is mainly defined by the TC process with eventually a variable contribution of a blackbody component emitted from the TL and/or the NS surface (GX 3+1, GX 9+1, GX 349+2).
In the case of GX 5-1, for which we have the best statistics and HR evolution, we can relate the increasing trend of the $R_{\rm bb}$ value (size of the BB emitting region) to the rising values of HR/$\dot M$: at high values of local accretion rates, i.e. radiation pressure, the bulk motion is inhibited and the matter falls at lower speed, following a complex behavior which lets it arrive on the NS surface and spread over a larger area (Inogamov & Sunyaev 1999). The high amount of matter covering the NS can produce a layer able to suppress the radio emission (P06).

4.2 The absence of the hard tail in most bright Atoll ``GX'' sources

From the spectral states observed and the information obtained by the fitting process, it is difficult to say whether the permanent absence of hard X-ray tail in sources like GX 3+1, GX 9+1 is due to a locally high-enough accretion rate which is able to suppress BC or rather to the opposite case, where BC is present but too low to be detected. In these sources such a transient feature has as yet never been observed, even with the past missions.

In GX 5-1, a transient hard X-ray tail was instead previously detected by Ginga (Asai et al. 1994) and INTEGRAL (Paizis et al. 2005), in GX 13+1 it was detected for the first time by INTEGRAL (P06), while in GX 349+2, the feature was observed by BeppoSAX (Di Salvo et al. 2001) when the source was out-of-flare. Also taking into account previous results on other Z sources (GX 17+2, Sco X-1, GX 340+0, see e.g. P06 for a complete list of references), it is currently difficult to provide a global self-consistent picture which may explain this variate phenomenology. We still do not have an observable parameter which may help to unambiguously determine at least phenomenologically which the threshold for triggering the hard X-ray tail is.

In the accretion scenario, where the production of high-energy photons is inhibited by high local levels of the accretion rate (bulk stopping through radiation pressure), one should look with particular care at the contribution of the BB-like emission to the total luminosity. If this BB-like emission is due to an energy release of the accreting matter both to the NS surface and in the TL (through viscous dissipation), one would expect that hard tail quenching would be correlated to a higher percentage of the BB contribution to the total luminosity.

Using $L_{\rm bb}/L_{\rm tot}$ as a possible tracer of the local accretion rate and thus of the BC efficiency would have the advantage of being distance-independent, an important issue when comparing the estimated luminosity among sources. Such a quantity may however be significantly different among sources which show a hard X-ray tail ranging from $\sim$2% (in GX 13+1, this work) to $\sim$25% in Cyg X-2 (F08). Of course, a satisfactory energy coverage below 1 keV is of prime importance to give unbiased estimations of this contribution. In this sense the reported values of  $L_{\rm tot}$ and  $L_{\rm bb}/L_{\rm tot}$in the present work must be treated very cautiously, as the energy band covered by JEM-X1 starts from 5 keV and is thus above the threshold where most of BB energy is emitted.

With these prescriptions in mind, we follow the spectral evolution of GX 5-1 with increasing HR and note that the presence of the hard X-ray tail is anti-correlated with the total source luminosity and the percentage of the energetic budget carried-out by the BB-like component, even though the latter change is marginal (see Fig. 4 and Table 3). The other sources for which we can detect two components in the spectrum along the observed HR range, but with no bulk contribution detected, unlike for GX 5-1, are GX 9+1 and GX 349+2 (see Figs. 6 and 7). In this case the BB-like component contributes about 20% and 10% of the source luminosity, respectively. Little can be said though for GX 3+1 or GX 13+1, for which we do not have the double component evolution along with HR.

5 Conclusions

Despite an increasing amount of theoretical and observational results, the picture which outlines to the presence of variable PL-like hard X-ray emission in NS LMXBs is far from being completely clear. Investigating the physical conditions of the innermost region of these sources is very critical. The bulk Comptonization approach together with the physical scenario proposed can be considered an important step forward in trying to understand what is at the origin of the transient hard tail behavior. Nevertheless, it is currently not easy to satisfactorily explain why sources like GX 9+1 and GX 5-1, which do have a similar X-ray spectrum and related parameters ( $kT_{\rm e}$, $kT_{\rm s}$ of the disk and NS-TL, $\tau$) yet differ for such an important feature as the presence of the transient hard tail.

Even if we were able to quantify $\dot M_{\rm TL}$ (disentangling it from the overall $\dot M$), we would face the problem of  $\dot M_{\rm TL}$change in the different cases, i.e. the origin of the inflow anisotropy. In fact, a theoretical and/or observational quantity, which may unambiguously trigger or dump the hard X-ray emission, has not yet been identified. Of course it is possible that we are dealing with a multi-parametric problem.

A possible highly speculative explanation could reside in the different composition of the disk: in Atoll sources the orbital period is in general relatively short ($\la$5 h) and in the Z sources for which it is known it is long ($\ga$10 h). This would indicate that Z sources may contain an evolved companion star (e.g. Cyg X-2, GX 1+4 Liu et al. 2007, and references therein), while Atolls contain a main sequence star (e.g. Aql X-1, Ser X-1 Liu et al. 2007, and references therein). This is consistent with the fact that the number of known Atoll sources (25) is higher than the number of known Z sources (8, Liu et al. 2007), since the main sequence phase of a star is much longer than the one of an evolved star, which renders the detection of Atolls more likely (Verbunt & van den Heuvel 1995). The accretion disk coming from an evolved companion (Z-like system) would be Helium-rich (i.e. heavier), hence a higher luminosity would be required to stop the bulk flow, which in turn makes the detection of BC more likely.

The chemical composition of the disk could be inferred by the duration of type I X-ray bursts: long bursts are thought to be due to mixed H/He burning, triggered by thermally unstable He ignition, expected at inferred near-Eddington accretion rates (Kuulkers et al. 2007). However, the observed behavior is far from being satisfactorily interpreted within the current bursting theory due to the presence of unexpected short bursts or even absence thereof, in a regime where long bursts would be expected (Kuulkers et al. 2007). The reason of this could be that in the case of high accretion rates accretion is unlikely through a plain disk, and the TL configuration may have an extra effect on the bursting behavior.

Additional or concurring effects could reside in the presence of a counter-rotating NS with respect to the Keplerian disk rotation, whose main effect could be the presence of a higher level of gravito-kinetic energy release in the TL in the region where the angular velocity adjusts from the Keplerian regime to that of the slowly spinning NS. Such higher energy release would in turn produce a higher local radiation pressure gradient, more efficient to stop bulk. Unfortunately, this is highly speculative and currently difficult to prove. A first approach to tackle the problem would be a more detailed study of the spectral evolution together with the long-term behavior of these sources (Savolainen et al., in prep.).

Understanding the origin of the hard tails in NS LMXBs is important to make a decisive step forward from phenomenology (powerlaw) to physics. This step forward will not make us understand hard tails alone, on the contrary, hard tails could be the observational feature that gives us the means to understand the mechanism of accretion flows in general, see e.g. Shrader & Titarchuk (1998) and Ferrigno et al. (2009) for an application of bulk motion Comptonization in black hole LMXBs and high mass X-Ray binaries, respectively.

Acknowledgements
Based on observations with INTEGRAL, an ESA project with instruments and science data center funded by ESA member states (especially the PI countries: Denmark, France, Germany, Italy, Spain, and Switzerland), Czech Republic and Poland, and with the participation of Russia and the USA. L.M., A.P. and R.F. acknowledge L. Titarchuk for useful discussions. A.P. acknowledges the Italian Space Agency financial support via contract I/008/07/0. This work has been partially supported by the grant from Italian PRIN-INAF 2007, ``Bulk motion Comptonization models in X-ray binaries: from phenomenology to physics'', PI M. Cocchi.

References

  1. Asai, K., Dotani, T., Mitsuda, K., et al. 1994, PASJ, 46, 479 [NASA ADS] [Google Scholar]
  2. Bandyopadhyay, R. M., Shahbaz, T., Charles, P. A., & Naylor, T. 1999, MNRAS, 306, 417 [NASA ADS] [CrossRef] [Google Scholar]
  3. Barret, D. 2001, Adv. Space Res., 28, 307 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bradshaw, C. F., Titarchuk, L., & Kuznetsov, S. 2007, ApJ, 663, 1225 [NASA ADS] [CrossRef] [Google Scholar]
  5. Chenevez, J., Falanga, M., Brandt, S., et al. 2006, A&A, 449, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Coppi, P. S. 1999, in High Energy Processes in Accreting Black Holes, ed. J. Poutanen, & R. Svensson, ASP Conf. Ser., 161 [Google Scholar]
  7. Di Salvo, T., & Stella, L. 2002, in Proc. of the XXXVIIth Rencontres de Moriond, The Gamma-Ray Universe, ed. A. Goldwurm, D. N. Neumann, & J. Tran Thanh Van, 67 [Google Scholar]
  8. Di Salvo, T., Robba, N. R., Iaria, R., et al. 2001, ApJ, 554, 49 [NASA ADS] [CrossRef] [Google Scholar]
  9. Di Salvo, T., Farinelli, R., Burderi, L., et al. 2002, A&A, 386, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Di Salvo, T., Goldoni, P., Stella, L., et al. 2006, ApJ, 649, L91 [NASA ADS] [CrossRef] [Google Scholar]
  11. Farinelli, R., Titarchuk, L., & Frontera, F. 2007, ApJ, 662, 1167 (F07) [NASA ADS] [CrossRef] [Google Scholar]
  12. Farinelli, R., Titarchuk, L., Paizis, A., & Frontera, F. 2008, ApJ, 680, 602 (F08) [NASA ADS] [CrossRef] [Google Scholar]
  13. Farinelli, R., Paizis, A., Landi, R., & Titarchuk, L. 2009, A&A, 498, 509 (F09) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Ferrigno, C., Becker, P. A., Segreto, A., Mineo, T., & Santangelo, A. 2009, A&A, 498, 825 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Frontera, F., dal Fiume, D., Malaguti, G., et al. 1998, in The Active X-ray Sky: Results from BeppoSAX and RXTE, ed. L. Scarsi, H. Bradt, P. Giommi, & F. Fiore, 286 [Google Scholar]
  16. Grimm, H.-J., Gilfanov, M., & Sunyaev, R. 2002, A&A, 391, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Homan, J., van der Klis, M., Wijnands, R., et al. 2007, ApJ, 656, 420 [NASA ADS] [CrossRef] [Google Scholar]
  18. Iaria, R., di Salvo, T., Robba, N. R., et al. 2004, Nucl. Phys. B Proc. Suppl., 132, 608 [Google Scholar]
  19. Iaria, R., di Salvo, T., Robba, N. R., et al. 2005, A&A, 439, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Inogamov, N. A., & Sunyaev, R. A. 1999, Astron. Lett., 25, 269 [NASA ADS] [Google Scholar]
  21. Kuulkers, E., & van der Klis, M. 2000, A&A, 356, L45 [NASA ADS] [Google Scholar]
  22. Kuulkers, E., Shaw, S. E., Paizis, A., et al. 2007, A&A, 466, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Lebrun, F., Leray, J. P., Lavocat, P., et al. 2003, A&A, 411, L141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Lin, D., Remillard, R. A., & Homan, J. 2009, ApJ, 696, 1257 [NASA ADS] [CrossRef] [Google Scholar]
  25. Liu, Q. Z., van Paradijs, J., & van den Heuvel, E. P. J. 2007, A&A, 469, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Lund, N., Budtz-Jørgensen, C., Westergaard, N. J., et al. 2003, A&A, 411, L231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Markoff, S., Nowak, M. A., & Wilms, J. 2005, ApJ, 635, 1203 [NASA ADS] [CrossRef] [Google Scholar]
  28. Mitsuda, K., Inoue, H., Koyama, K., et al. 1984, PASJ, 36, 741 [NASA ADS] [Google Scholar]
  29. Morrison, R., & McCammon, D. 1983, ApJ, 270, 119 [NASA ADS] [CrossRef] [Google Scholar]
  30. Paizis, A., Ebisawa, K., Tikkanen, T., et al. 2005, A&A, 443, 599 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Paizis, A., Farinelli, R., Titarchuk, L., et al. 2006, A&A, 459, 187 (P06) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Shaposhnikov, N., & Titarchuk, L. 2009, ApJ, 699, 453 [NASA ADS] [CrossRef] [Google Scholar]
  33. Shrader, C., & Titarchuk, L. 1998, ApJ, 499, L31 [NASA ADS] [CrossRef] [Google Scholar]
  34. Titarchuk, L. 1994, ApJ, 434, 570 [NASA ADS] [CrossRef] [Google Scholar]
  35. Titarchuk, L., & Fiorito, R. 2004, ApJ, 612, 988 [NASA ADS] [CrossRef] [Google Scholar]
  36. Titarchuk, L., & Lyubarskij, Y. 1995, ApJ, 450, 876 [NASA ADS] [CrossRef] [Google Scholar]
  37. Titarchuk, L., Mastichiadis, A., & Kylafis, N. D. 1996, A&AS, 120, 171 [Google Scholar]
  38. Titarchuk, L., Mastichiadis, A., & Kylafis, N. D. 1997, ApJ, 487, 834 (TMK97) [NASA ADS] [CrossRef] [Google Scholar]
  39. Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A, 411, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Ueda, Y., Murakami, H., Yamaoka, K., Dotani, T., & Ebisawa, K. 2004, ApJ, 609, 325 [NASA ADS] [CrossRef] [Google Scholar]
  41. Ueda, Y., Mitsuda, K., Murakami, H., & Matsushita, K. 2005, ApJ, 620, 274 [NASA ADS] [CrossRef] [Google Scholar]
  42. van der Klis, M. 2001, ApJ, 561, 943 [NASA ADS] [CrossRef] [Google Scholar]
  43. Verbunt, F., & van den Heuvel, E. P. J. 1995, in X-ray binaries, ed. W. H. G. Lewin, J. van Paradijs, & E. P. J. van den Heuvel, 457 [Google Scholar]
  44. White, N. E., Stella, L., & Parmar, A. N. 1988, ApJ, 324, 363 [NASA ADS] [CrossRef] [Google Scholar]
  45. Winkler, C., Courvoisier, T. J.-L., Di Cocco, G., et al. 2003, A&A, 411, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Footnotes

...$\mathsf{compTB}$[*]
http://heasarc.gsfc.nasa.gov/docs/xanadu/xspec/models/comptb.html
... function[*]
The Green's function, G, is the response of the system to the injection of a monochromatic line, see F08 for details.
...y[*]
The Comptonization parameter is defined as 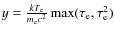$y = \frac{kT_{\rm e}}{m_{\rm e}c^2}\max(\tau_{\rm e},\tau_{\rm e}^2)$, where the optical depth of the scattering region in NS LMXBs is typically $\tau_{\rm e}^2\gg 1$.
... temperature[*]
We note that the correct expression of the $\delta$ parameter is the one written in the text. In Farinelli et al. (2008), Eq. (2) erroneously indicates a square root in the right term.

All Tables

Table 1:   The five bright NS LMXBs studied in this paper.

Table 2:   The number of pointings and exposition time for each HR interval for the NS LMXBs studied in this paper.

Table 3:   Best-fit parameters of the multi-component model $\mathsf{wabs\cdot(compTB[1]+compTB[2])}$ for the source GX 5-1.

Table 4:   Best-fit parameters of the multi-component model $\mathsf{wabs\cdot(compTB[1]+compTB[2])}$ for the source GX 13+1.

Table 5:   Best-fit parameters of the multi-component model $\mathsf{wabs\cdot(compTB[1]+compTB[2])}$ for the source GX 9+1.

Table 6:   Best-fit parameters of the multi-component model $\mathsf{wabs\cdot(compTB[1]+compTB[2])}$ for the source GX 349+2.

Table 7:   Best-fit parameters of the model $\mathsf{wabs\cdot(compTB[1])}$ for the source GX 3+1.

All Figures

  \begin{figure} \par\includegraphics[angle=270,width=8.5cm,clip]{12921fig1.ps} \end{figure} Figure 1:

Schematic view of the proposed scenario for thermal and bulk Comptonization regions in LMXBs hosting NSs.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=18cm,clip]{12921fig2.ps} \end{figure} Figure 2:

IBIS/ISGRI 20-40 keV mosaic in Galactic coordinates of the Galactic Bulge (about 3.3 Ms). Only the sources studied in this paper are labeled.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8.5cm,clip]{12921fig3.ps} \end{figure} Figure 3:

Example of the HR variation for the source GX 5-1 considering all available pointings.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8.5cm,clip]{12921fig4.ps}\hspace*{5mm} \includegraphics[angle=270,width=8.5cm,clip]{12921fig5.ps} \end{figure} Figure 4:

Unabsorbed EF(E) spectra of GX 5-1 for the HR intervals: HR < 7 ( left), and HR > 12 ( right). The dotted lines are the two separated $\mathsf{compTB}$ components: dash for $\mathsf{compTB[1]}$, dash-dot $\mathsf{compTB[2]}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8.5cm,clip]{12921fig6.ps}\hs... ...{0.5cm} \includegraphics[angle=270,width=8.5cm,clip]{12921fig7.ps} \end{figure} Figure 5:

Unabsorbed EF(E) spectra of GX 13+1 for the HR intervals: HR < 10 ( left), HR > 13 ( right). The dotted lines are the two separated $\mathsf{compTB}$ components: dash for $\mathsf{compTB[1]}$, dash-dot $\mathsf{compTB[2]}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8.5cm,clip]{12921fig8.ps} \end{figure} Figure 6:

Unabsorbed EF(E) spectrum for the HR interval 7.5 < HR < 8.5 for GX 9+1. The dotted lines are the two separated $\mathsf{compTB}$ components: dash for $\mathsf{compTB[1]}$, dash-dot $\mathsf{compTB[2]}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8.5cm,clip]{12921fig9.ps} \end{figure} Figure 7:

Unabsorbed EF(E) spectrum of GX 349+2 for HR < 7. The dotted lines are the two separated $\mathsf{compTB}$ components: dash for $\mathsf{compTB[1]}$, dash-dot $\mathsf{compTB[2]}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8.5cm,clip]{12921fig10.ps} \end{figure} Figure 8:

Unabsorbed EF(E) spectrum for the HR interval HR < 8 for GX 3+1. The overall spectrum is well described by a single component, $\mathsf{compTB[1]}$, see text.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.