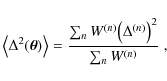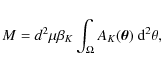| Issue |
A&A
Volume 512, March-April 2010
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 14 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200912670 | |
| Published online | 02 April 2010 | |
2MASS wide field extinction maps
III. The Taurus, Perseus, and California cloud complexes
M. Lombardi1,2 - C. J. Lada3 - J. Alves4
1 - European Southern Observatory, Karl-Schwarzschild-Straße 2,
85748 Garching bei München, Germany
2 -
University of Milan, Department of Physics, via Celoria 16, 20133
Milan, Italy (on leave)
3 -
Harvard-Smithsonian Center for Astrophysics, Mail Stop 72, 60 Garden
Street, Cambridge, MA 02138, UK
4 -
Calar Alto Observatory - Centro Astronómico Hispano Alemán,
C/Jesús Durbán Remón 2-2, 04004 Almeria, Spain
Received 9 June 2009 / Accepted 20 October 2009
Abstract
We present a near-infrared extinction map of a large region in the
sky (![]() 3500 deg2) in the general directions of
Taurus, Perseus, and Aries. The map has been obtained using robust
and optimal methods to map dust column density at near-infrared
wavelengths (N ICER, described in
Lombardi & Alves 2001, A&A, 377, 1023 and N ICEST, described in
Lombardi 2009, A&A, 493, 735) toward
3500 deg2) in the general directions of
Taurus, Perseus, and Aries. The map has been obtained using robust
and optimal methods to map dust column density at near-infrared
wavelengths (N ICER, described in
Lombardi & Alves 2001, A&A, 377, 1023 and N ICEST, described in
Lombardi 2009, A&A, 493, 735) toward ![]() 23 million stars from
the Two Micron All Sky Survey (2MASS) point source catalog. We
measure extinction as low as
23 million stars from
the Two Micron All Sky Survey (2MASS) point source catalog. We
measure extinction as low as
![]() with a
1-
with a
1-![]() significance, and a resolution of
significance, and a resolution of
![]() in
our map. A
in
our map. A
![]() section of our map encompasses the
Taurus, Perseus, and California molecular cloud complexes. We
determine the distances of the clouds by comparing the observed
density of foreground stars with the prediction of galactic models,
and we obtain results that are in excellent agreement with recent
VLBI parallax measurements. We characterize the large-scale
structure of the map and find a
section of our map encompasses the
Taurus, Perseus, and California molecular cloud complexes. We
determine the distances of the clouds by comparing the observed
density of foreground stars with the prediction of galactic models,
and we obtain results that are in excellent agreement with recent
VLBI parallax measurements. We characterize the large-scale
structure of the map and find a ![]()
![]() region close to the galactic plane (
region close to the galactic plane (
![]() ,
,
![]() )
with small extinction (
)
with small extinction (
![]() ); we
name this region the Perseus-Andromeda hole. We find that over the
region that encompasses the Taurus, Perseus, and California clouds
the column density measurements below
); we
name this region the Perseus-Andromeda hole. We find that over the
region that encompasses the Taurus, Perseus, and California clouds
the column density measurements below
![]() are
perfectly described by a log-normal distribution, and that a
significant deviation is observed at larger extinction values. If
turbulence models are invoked to justify the log-normal
distribution, the observed departure could be interpreted as the
result of the effect of gravity that acts on the cores of the
clouds. Finally, we investigate the cloud structure function, and
show that significant deviations from the results predicted by
turbulent models are observed in at least one cloud.
are
perfectly described by a log-normal distribution, and that a
significant deviation is observed at larger extinction values. If
turbulence models are invoked to justify the log-normal
distribution, the observed departure could be interpreted as the
result of the effect of gravity that acts on the cores of the
clouds. Finally, we investigate the cloud structure function, and
show that significant deviations from the results predicted by
turbulent models are observed in at least one cloud.
Key words: ISM: clouds - dust, extinction - ISM: individual objects: Taurus molecular complex - ISM: structure - methods: statistical
1 Introduction
This paper is the third of a series where we apply an optimized
multi-band technique dubbed Near-Infrared Color Excess Revisited
(N ICER Lombardi & Alves 2001, hereafter Paper 0) to
study the structure of nearby molecular dark clouds using the Two
Micron All Sky Survey (2MASS; Kleinmann et al. 1994).
Previously, we considered the Pipe nebula (see
Lombardi et al. 2006, hereafter Paper I) and the Ophiuchus
and Lupus complexes (Lombardi et al. 2008,
hereafter Paper II). In
this paper we present a wide field extinction map, constructed from
23 million JHK 2MASS photometric measurements, of a large region
covering
![]()
![]() ,
and including the Taurus, Perseus, and
California complexes, as well as the high-galactic latitude clouds
MBM 8, MBM 12, and MBM 16 and the M 31 and M 33 galaxies.
,
and including the Taurus, Perseus, and
California complexes, as well as the high-galactic latitude clouds
MBM 8, MBM 12, and MBM 16 and the M 31 and M 33 galaxies.
The main aim of our coordinated study of nearby molecular clouds is to investigate in detail the large-scale structure of these clouds, down to the lowest column densities measurable with this technique, which are below the column density threshold required for the detection of the CO molecule (e.g. Lombardi et al. 2006; Alves et al. 1999). In addition, the use of an uniform dataset and of a consistent and well tested pipeline allows us to characterize many properties of molecular clouds and to identify cloud-to-cloud variations in such properties.
The advantages of using near-infrared dust extinction as a column density tracer have been discussed elsewhere (Alves et al. 2001; Lombardi et al. 2006; Lada et al. 1994; Alves et al. 1999). Indeed, Goodman et al. (2008) used data from the COMPLETE survey (Ridge et al. 2006) to assess and compare three methods for measuring column density in molecular clouds, namely, near-infrared extinction (N ICER), thermal emission in the far-IR (IRAS), and CO line emission. They found that observations of dust are a better column density tracer than observations of molecular gas (CO), and that observations of dust extinction in particular provide more robust measurements of column density than observations of dust emission, mainly because of the dependence of the latter measurements on uncertain knowledge of dust temperatures and emissivities.
This paper is the first to use, in some key analyses, the improved N ICEST method (Lombardi 2009), which copes well with the sub-pixel inhomogeneities present in the high-column density regions of the maps. The inhomogeneities can either be due to steep gradients in the column density map, to the effect of turbulent fragmentation, or to the increased presence of foreground stars, and they bias the measurements towards lower column densities. All these effects are expected to be most severe in the densest regions of dark complexes, i.e. in very limited parts of the large areas considered in this paper. Nevertheless, because of the relevance of these regions in the process of star formation, it is important to understand this bias and to correct for it.
Taurus is one of the best studied molecular cloud complexes in the
Galaxy. It has about 200 young low-mass stars and it is one of the
Rosetta stones of star formation research with the identification,
about 60 years ago, of irregular, emission-line variable (T-Tauri)
stars physically associated with the cloud (Joy 1945)
and the subsequent recognition of their extreme youth
(Herbig 1962). Taurus is also the prototype low-mass,
distributed star forming region where stars appear to form in relative
isolation compared to the more common embedded cluster mode of
formation that characterizes regions such as Orion and Perseus. The
Taurus cloud complex has also been the prototype for molecular-line
studies of dense proto-stellar and pre-stellar cores
(e.g. Myers et al. 1979). Most recently, a 100 deg2 survey of the Taurus molecular cloud region in 12CO and
13CO J=1-0 and with at a resolution of
![]() and
and
![]() respectively was presented in Narayanan et al. (2008) and
Goldsmith et al. (2008). There have also been extensive dust
extinction studies done of the Taurus dark clouds
(Cernicharo & Guelin 1987; Dobashi et al. 2005; Cernicharo et al. 1985; Cernicharo & Bachiller 1984; Meistas & Straizys 1981; Straizys & Meistas 1980; Cambrésy 1999) using either star counts or color-excesses. The
current best estimate of the distance to the Taurus complex, using
VLBI, is
respectively was presented in Narayanan et al. (2008) and
Goldsmith et al. (2008). There have also been extensive dust
extinction studies done of the Taurus dark clouds
(Cernicharo & Guelin 1987; Dobashi et al. 2005; Cernicharo et al. 1985; Cernicharo & Bachiller 1984; Meistas & Straizys 1981; Straizys & Meistas 1980; Cambrésy 1999) using either star counts or color-excesses. The
current best estimate of the distance to the Taurus complex, using
VLBI, is
![]() (Loinard et al. 2007). These authors also found that the
thickness of the complex is comparable to its extent, or about
(Loinard et al. 2007). These authors also found that the
thickness of the complex is comparable to its extent, or about
![]() .
.
Like Taurus, Perseus is a well known star forming region. It is the prototype intermediate mass star forming region, with young B-stars and two clusters, IC 348 (Muench et al. 2007) and NGC 1333 (Lada et al. 1996). The complex seems to be associated with the Perseus OB2 association (de Zeeuw et al. 1999) at a distance of about 250 pc (Bally 2008).
The California molecular cloud is not as well known as Taurus and
Perseus. Only recently, and as a by-product of the analysis presented
in this paper, it has been recognized as a major cloud complex and
studied in detail by Lada et al. (2009). In that paper we estimated
the distance of this massive giant molecular complex to be
![]() ,
and stressed that this cloud is surprisingly similar
in mass, distance, and shape to the much better studied Orion
molecular cloud; interestingly, however, the California cloud displays
much less star formation.
,
and stressed that this cloud is surprisingly similar
in mass, distance, and shape to the much better studied Orion
molecular cloud; interestingly, however, the California cloud displays
much less star formation.
The area considered in this paper also includes the two spiral galaxies M 31 and M 33, and a few high galactic latitude clouds (MBM 8, MBM 12, and MBM 16). However, the limited angular resolution achievable using the 2MASS archive does not allow to study in detail the properties of these clouds, and therefore here we focus our efforts to the three main clouds mentioned above.
This paper is organized as follows. In Sect. 2 we briefly describe the technique used to map the dust and we present the main results obtained. A statistical analysis of our results and a discussion of the bias introduced by foreground stars and unresolved substructures is presented in Sect. 3. Section 4 is devoted to the mass estimate of the cloud complexes. The structure functions and the scaling index ratio of the three clouds are presented and discussed in Sect. 5. Finally, we summarize the results obtained in this paper in Sect. 6.
2 N ICER and N ICEST extinction maps
We carried out the data analysis using the N ICER and
N ICEST methods described in Paper 0 and in
Lombardi (2009). Near infrared J (1.25 ![]() m), H (1.65
m), H (1.65 ![]() m), and
m), and ![]() band (2.17
band (2.17 ![]() m) magnitudes of stars in a large region of the sky
which includes the dark clouds were taken from the Two Micron All Sky
Survey
m) magnitudes of stars in a large region of the sky
which includes the dark clouds were taken from the Two Micron All Sky
Survey![]() (2MASS; Kleinmann et al. 1994). In particular, we selected all
2MASS reliable point sources within the boundaries
(2MASS; Kleinmann et al. 1994). In particular, we selected all
2MASS reliable point sources within the boundaries
Our selection criteria excluded sources that are likely to be contaminated by extended objects (
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12670f01}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg48.png)
|
Figure 1:
Color-color diagram of the stars in the whole field, as a
density plot. The contours are logarithmically spaced, i.e. each
contour represents a density ten times larger than the enclosing
contour; the outer contour detects single stars and clearly shows
a bifurcation at large color-excesses. The dashed lines identify
the regions in the color space defined in Eqs. (2) and
(3), as indicated by the corresponding letters. Only
stars with accurate photometry in all bands (maximum 1- |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{12670f02}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg49.png)
|
Figure 2: Spatial distribution of the samples of sources as defined by Eqs. (2) and (3). Sample A is shown as filled circles, while sample B is shown as crosses (see also Fig. 1). Sample A appears to be strongly clustered in high-column density regions of the cloud, and is thus interpreted as genuine reddened stars; sample B seems not to be associated with the cloud, and is instead preferentially located at low galactic latitudes. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{12670f03}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg50.png)
|
Figure 3: The histogram of the K band magnitude for the two star subsets A and B of Eqs. (2) and (3). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{12670f04}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg51.png)
|
Figure 4: The extinction-corrected color-color diagram. |
| Open with DEXTER | |
We then generated a preliminary extinction map which, as described in Paper 0, was mainly used as a first check of the parameters adopted, to select a control region on the field, and to obtain the photometric parameters to be used in the final map. We identified a large region that is apparently affected by only a negligible extinction (see below), and used the colors of stars in this control field as reference ones.
Using the information provided by the control field, we generated a
second map, which is thus ``calibrated'' (i.e., provides already, for
each position in our field, a reliable estimate of the column
density). In this step we used the Indebetouw et al. (2005) 2MASS
reddening law. Similar to Paper I, we then considered the
color-color diagram for the stars in the catalog to check for possible
signs of anomalous star colors. The result, presented in
Fig. 1, shows two trails of stars parallel to the reddening
vector for
![]() .
.
As discussed in detail in Paper I, the bifurcation is likely to be due
to Asymptotic Giant Branch (AGB) stars. We verified this assumption
by considering the spatial distribution of two subsets of stars
defined in the color-color diagram as
Figure 2 shows the results obtained and proves that as expected, sample A is associated with the densest regions of the molecular cloud, while sample B is distributed on the whole field with a strong preference for low galactic latitude regions. We also considered in Fig. 3 the two histograms of the K-band magnitude distribution for the two samples. As expected, sample Ashows a broad distribution, which can be essentially described as a simple power-law luminosity function up to
Following Paper II, we then investigated the extinction-corrected color-color diagram (see Fig. 4), obtained by estimating, for each star, its ``intrinsic'' colors, i.e. the extinction corrected colors from the extinction at the star's location as provided by the N ICER map. In other words, we computed for each star
where
![]() is the N ICER
estimated extinction in the direction
is the N ICER
estimated extinction in the direction
![]() of the star
from the angularly close objects, as given by Eq. (7) below.
A comparison of Fig. 4 with Fig. 1 shows that the
many stars in upper branch, sample A, are moved toward the peak of
the density in the lower-left part of the plot, while the lower
branch, sample B, is largely unaffected, a result in agreement with
Fig. 2. Note that the residual stars appearing in the upper
branch are likely to be the effect of an inaccurate extinction
correction due to small-scale inhomogeneities not captured by our
analysis; similarly, the tail at negative colors is due to
``over-corrected'' stars (for example foreground stars observed in
projection to a cloud). In any case, Fig. 2 shows that the
number of contaminating AGB stars is negligible, and that no
noticeable effects are expected in the 2MASS extinction map. For this
reason, we decided not to correct for this contamination and to use
the whole 2MASS input catalog for the analysis (in contrast, we
proceeded with a correction in Paper II because of the much more
pronounced contamination).
of the star
from the angularly close objects, as given by Eq. (7) below.
A comparison of Fig. 4 with Fig. 1 shows that the
many stars in upper branch, sample A, are moved toward the peak of
the density in the lower-left part of the plot, while the lower
branch, sample B, is largely unaffected, a result in agreement with
Fig. 2. Note that the residual stars appearing in the upper
branch are likely to be the effect of an inaccurate extinction
correction due to small-scale inhomogeneities not captured by our
analysis; similarly, the tail at negative colors is due to
``over-corrected'' stars (for example foreground stars observed in
projection to a cloud). In any case, Fig. 2 shows that the
number of contaminating AGB stars is negligible, and that no
noticeable effects are expected in the 2MASS extinction map. For this
reason, we decided not to correct for this contamination and to use
the whole 2MASS input catalog for the analysis (in contrast, we
proceeded with a correction in Paper II because of the much more
pronounced contamination).
![\begin{figure}
\par\includegraphics[width=17cm]{12670f05}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg68.png)
|
Figure 5:
The N ICER extinction map of the region
considered in this paper. The resolution is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12670f06}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg69.png)
|
Figure 6: A zoom of Fig. 5 showing the Taurus, Perseus, and California, complexes. The several well studied objects are marked. |
| Open with DEXTER | |
Figure 5 shows the final 2MASS/N ICER extinction map
of the whole region considered here. We recall that in N ICER
the final map can be generated using different smoothing techniques
(see Lombardi 2002, for a discussion on the
characteristics and merits of various interpolators). As pointed out
in Paper 0, generally these techniques produce comparable results, and
thus we focused here on the simple moving weight average:
where
Hence, the weight for the nth star is composed by two factors: (i)
The map of Fig. 5 was generated on a grid of approximately
![]() points, with scale
points, with scale
![]() per
pixel, and with Gaussian smoothing characterized by
per
pixel, and with Gaussian smoothing characterized by
![]() .
Note that in the weighted average of
Eq. (7) we also introduced an iterative
.
Note that in the weighted average of
Eq. (7) we also introduced an iterative ![]() -clipping at
3-
-clipping at
3-![]() error (see Paper 0). The average, effective
density of stars is
error (see Paper 0). The average, effective
density of stars is ![]() 2.8 stars per pixel, but as noted above
this value changes significantly with galactic latitude; this density
guarantees an average (1-
2.8 stars per pixel, but as noted above
this value changes significantly with galactic latitude; this density
guarantees an average (1-![]() )
error on AK of 0.04 mag in the marked box of Fig. 5.
)
error on AK of 0.04 mag in the marked box of Fig. 5.
We also constructed a N ICEST extinction map (not shown here,
but used in some of the results presented below), obtained by using
the modified estimator (Lombardi 2009)
where the modified weight
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12670f07}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg88.png)
|
Figure 7:
A lower resolution version of Fig. 5. This
image was constructed by convolving Fig. 5 with a
Gaussian kernel. Also plotted are contour levels of (smoothed)
extinction at
|
| Open with DEXTER | |
As expected, we observe a significant gradient along the galactic latitude. Other variations in the expected errors can be associated with bright stars, galaxies, and the cloud itself (dark areas). Because of the relatively large variations on the noise of the extinction map, clearly a detailed analysis of Fig. 5 should be carried out using in addition the noise map. Figure 6 shows in greater detail the absorption maps we obtain for the Taurus, Perseus, and California complexes, and allows us to appreciate better the details that we can obtain by applying the N ICER method to the good quality 2MASS data. In this figure we also displayed the boundaries that we use throughout this paper and that we assign to the three clouds considered in this paper. In particular, we define
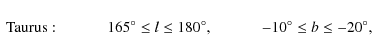

We show in Fig. 7 a very low resolution extinction map of the whole field. By averaging the extinction with a Gaussian kernel at
- the area studied in this paper is very large,
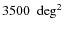 ,
and extends from the galactic plane to high galactic
latitudes. Therefore it is very likely that at least in some region
of our map the extinction is negligible;
,
and extends from the galactic plane to high galactic
latitudes. Therefore it is very likely that at least in some region
of our map the extinction is negligible;
- the DSS-based Dobashi et al. (2005) maps show low extinction at the location of the ``hole'';
- the IRAS measurements for the region that occupies the
Perseus-Andromeda hole have been translated from
Schlegel et al. (1998) into a visual extinction
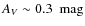 ,
corresponding to
,
corresponding to
 ;
a
similar extinction can be derived from the
;
a
similar extinction can be derived from the
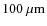 IRIS
map (Miville-Deschênes & Lagache 2005). If these values are taken, our
overall bias would be
IRIS
map (Miville-Deschênes & Lagache 2005). If these values are taken, our
overall bias would be
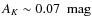 .
This is of
course possible, but note also that possible systematic
uncertainties present in these IRAS estimates, and in particular the
uncertainties inherent to the DIRBE calibration and to the zodiacal
model, are likely to be of the order of one tenth of a visual
magnitude, i.e. comparable to the detection itself.
.
This is of
course possible, but note also that possible systematic
uncertainties present in these IRAS estimates, and in particular the
uncertainties inherent to the DIRBE calibration and to the zodiacal
model, are likely to be of the order of one tenth of a visual
magnitude, i.e. comparable to the detection itself.
Finally, the low statistical uncertainty expected for the map of
Fig. 7 can be used to check the presence of systematic
errors. In this respect, the only significant anomaly we could detect
is a general pattern that extends along lines of equal right
ascension, and that is visible as stripes in the lower part of
Fig. 7 (see also Fig. 5). This pattern is a known
systematic effect of the 2MASS point source catalog, and is directly
related to the observing strategy used (which is based on
![]() tiles aligned with the equatorial coordinates, further split
in
tiles aligned with the equatorial coordinates, further split
in
![]() images). This problem is most likely due to
errors on the determination of the zero-points for the various
observation stripes, or to other effects induced by the different
observational conditions (and, in some cases, also to data reduction
issues present in high density regions; see Paper I).
images). This problem is most likely due to
errors on the determination of the zero-points for the various
observation stripes, or to other effects induced by the different
observational conditions (and, in some cases, also to data reduction
issues present in high density regions; see Paper I).
3 Statistical analysis
3.1 Reddening law
![\begin{figure}
\par\includegraphics[width=9cm]{12670f08}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg112.png)
|
Figure 8: The reddening law as measured on the analyzed region. The plot shows the color excess on J - K as a function of the color excess on H - K (the constant 0.170 and 0.498 represent, respectively, the average of H - K and of J - H colors in magnitudes for the control field). Error bars are uncertainties evaluated from the photometric errors of the 2MASS catalog. The solid line shows the normal infrared reddening law (Indebetouw et al. 2005). |
| Open with DEXTER | |
The use of two different colors, J-H and H-K, allows us to verify
that the reddening law used throughout this paper is consistent with
the data. For this purpose, we partitioned all stars with complete,
reliable measurements in all bands, into different bins corresponding
to the individual original
![]() measurements (we used a
bin size of
measurements (we used a
bin size of
![]() ). Then, we evaluated the average NIR
colors in each group of stars in the same bin and the corresponding
statistical uncertainties (estimated from on the photometry errors of
the 2MASS catalog). The results obtained are shown in
Fig. 8 together with the normal infrared reddening law in
the 2MASS photometric system (Indebetouw et al. 2005). This plot
shows that there are no significant deviations from the normal
reddening law over the whole range of extinctions and directions
investigated here.
). Then, we evaluated the average NIR
colors in each group of stars in the same bin and the corresponding
statistical uncertainties (estimated from on the photometry errors of
the 2MASS catalog). The results obtained are shown in
Fig. 8 together with the normal infrared reddening law in
the 2MASS photometric system (Indebetouw et al. 2005). This plot
shows that there are no significant deviations from the normal
reddening law over the whole range of extinctions and directions
investigated here.
3.2 Foreground star contamination and cloud distance
Foreground stars observed in projection on a dark cloud do not carry
any information on the cloud column density, and thus they dilute the
signal and add noise. Both effects are proportional to the fraction f of foreground stars, and it is thus important to verify that fis sufficiently small. For nearby molecular clouds, f is usually
very small and negligible on the outskirts of the clouds (typical
values are ![]()
![]() ), but increases significantly on the very dense
regions, where the density of observed background stars decreases
dramatically. In addition, many dense cores host young stellar
objects: these stars, if moderately embedded, show only a fraction of
the true, total column density of the cloud. As a result, the
extinction in the direction of dense regions can be severely
underestimated.
), but increases significantly on the very dense
regions, where the density of observed background stars decreases
dramatically. In addition, many dense cores host young stellar
objects: these stars, if moderately embedded, show only a fraction of
the true, total column density of the cloud. As a result, the
extinction in the direction of dense regions can be severely
underestimated.
![\begin{figure}
\par\includegraphics[width=17cm]{12670f09}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg117.png)
|
Figure 9:
The local density of foreground stars, averaged over
connected regions with extinction
|
| Open with DEXTER | |
Table 1: The average value of foreground stars found in the various complexes.
In order to evaluate quantitatively the fraction f of foreground
stars we selected high-extinction regions characterized by
![]() .
We then flagged all stars in these regions that show
``no'' extinction, i.e. stars with column densities less than
3-
.
We then flagged all stars in these regions that show
``no'' extinction, i.e. stars with column densities less than
3-![]() above the background, compatible with no or negligible
extinctions. We performed these tests for the whole area shown in
Fig. 6, and calculated the local density of foreground stars
by taking into account the area in the sky occupied by regions with
above the background, compatible with no or negligible
extinctions. We performed these tests for the whole area shown in
Fig. 6, and calculated the local density of foreground stars
by taking into account the area in the sky occupied by regions with
![]() .
Figure 9 shows the local density
of foreground stars, averaged over connected regions of high
extinction. For Perseus, we measure an anomalous density of
foreground stars around the reflection nebula NGC 1333, which is known
to contain several embedded young stellar objects (YSOs). It is
evident that the each of the three regions shows a rather uniform
density, a strong indication that the clouds are connected structures
at about the same distance. A possible exception is the Perseus
cloud, which seems to show rather large differences in
Fig. 9. Therefore, we performed a detailed analysis by
dividing the Perseus region into three areas: one, to the North, that
includes B3, B4, and B5; one, to the South, that includes B1, L1455,
and L1448; and a third, which includes NGC 1333, and is only considered
to isolate the effects of the YSO cluster from the estimate of the
density of foreground stars.
.
Figure 9 shows the local density
of foreground stars, averaged over connected regions of high
extinction. For Perseus, we measure an anomalous density of
foreground stars around the reflection nebula NGC 1333, which is known
to contain several embedded young stellar objects (YSOs). It is
evident that the each of the three regions shows a rather uniform
density, a strong indication that the clouds are connected structures
at about the same distance. A possible exception is the Perseus
cloud, which seems to show rather large differences in
Fig. 9. Therefore, we performed a detailed analysis by
dividing the Perseus region into three areas: one, to the North, that
includes B3, B4, and B5; one, to the South, that includes B1, L1455,
and L1448; and a third, which includes NGC 1333, and is only considered
to isolate the effects of the YSO cluster from the estimate of the
density of foreground stars.
A visual inspection of Fig. 9 also shows that California has a significantly higher density of foreground stars, suggesting that this cloud is located at a significantly higher distance than the other two complexes (see Lada et al. 2009). The results of a more quantitative analysis are presented in the Table 1, were we also report the cloud distances evaluated by comparing the observed densities with the values inferred from the Galactic model by Robin et al. (2003) at different distances (see Fig. 10).
As shown by the second and third line from the bottom of this table,
the Northern regions of the Perseus cloud has an average density of
foreground stars of that appears to be significantly larger than the
one found in the Southern regions. In order to better quantify this
result, we note that from simple error propagation the
difference between the two densities is
![]() ,
which is consistent with zero only at
1.8-
,
which is consistent with zero only at
1.8-![]() .
In other words, the data seem to suggest a genuine,
although relatively small, difference between the distances of the
Northern and Southern regions of the Perseus cloud. We also note the
extent covered by this cloud in the sky, approximately
.
In other words, the data seem to suggest a genuine,
although relatively small, difference between the distances of the
Northern and Southern regions of the Perseus cloud. We also note the
extent covered by this cloud in the sky, approximately ![]() ,
corresponds to approximately
,
corresponds to approximately
![]() ,
at the cloud distance, a
value smaller but comparable to the measured distance difference. In
summary, even if the distance difference is real (a claim that we
cannot make here), the various regions could still be physically
connected if the Perseus complex is extending along the line of sight.
,
at the cloud distance, a
value smaller but comparable to the measured distance difference. In
summary, even if the distance difference is real (a claim that we
cannot make here), the various regions could still be physically
connected if the Perseus complex is extending along the line of sight.
The agreement between the distances estimated for the Perseus and
Taurus clouds and the results known from the literature is amazing and
shows that the Galactic model used here (Robin et al. 2003) is
extremely accurate and reliable. For example, the Perseus distance is
in excellent agreement with recent multi-epoch VLBI maser observations
of the YSO SVS 13 in NGC 1333 (Hirota et al. 2008), which
provide
![]() .
Similarly,
the Taurus distance is in excellent agreement with a VLBI
determination,
.
Similarly,
the Taurus distance is in excellent agreement with a VLBI
determination,
![]() (Loinard et al. 2007).
(Loinard et al. 2007).
Finally, we note that the accuracy and reliability of the distances based on the density of foreground stars suggests that we can use this technique for clouds for which no VLBI distance is available (such as the California cloud) or possible (for example because of the lack of maser sources or of the large distance of the clouds). A further advantage of the technique used in this paper is that its accuracy is mainly driven by the number of foreground stars, a quantity that for equally-sized clouds is almost independent of the cloud distance. Indeed, the density of foreground stars increases quadratically (at least up to distances of a few kpc, cf. Fig. 10) with the distance of the cloud, while the area covered by the cloud decreases quadratically, thus leaving their product, the number of foreground stars, unchanged.
![\begin{figure}
\par\includegraphics[width=9cm]{12670f10}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg139.png)
|
Figure 10:
The distances of the Taurus (solid lines) and Perseus
(dashed lines) clouds deduced from the density of foreground
stars. The plots show the density of foreground of stars as a
function of the cloud distance, as predicted from the
Robin et al. (2003) Galactic model (the two curves are
slightly different because of the different Galactic coordinates
of the clouds). The grey areas show the |
| Open with DEXTER | |
3.3 Column density probability distribution
![\begin{figure}
\par\includegraphics[width=9cm]{12670f11}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg141.png)
|
Figure 11:
The probability distribution of star pixel extinctions
for the whole map shown in Fig. 6; the gray, smooth
curve represents the best-fit with a log-normal distribution,
smoothed with a Gaussian kernel of
|
| Open with DEXTER | |
The probability distribution for the volume density in molecular clouds is expected to be log-normal for isothermal, turbulent flows (e.g. Passot & Vázquez-Semadeni 1998; Scalo et al. 1998; Padoan et al. 1997b; Vazquez-Semadeni 1994). Under certain assumptions, verified in relatively ``thin'' molecular clouds, the probability distribution for the column density, i.e. the volume density integrated along the line of sight, is also expected to follow a log-normal distribution (Vázquez-Semadeni & García 2001).
Figure 11 reports the probability distributions of column
densities for the Taurus, Perseus, and California region, i.e. the
relative probability of column density measurements for each pixel of
Fig. 6. This probability is thus calculated for the
N ICER map, but we stress that no differences would be
observed for a N ICEST map up to
![]() (which, as noted above, only differ from the N ICER map in the
high column density regions). We fitted the column density histograms
with log-normal distributions of the form
(which, as noted above, only differ from the N ICER map in the
high column density regions). We fitted the column density histograms
with log-normal distributions of the form
convolved with a Gaussian kernel characterized by a standard deviation
Two features of Fig. 11 are evident. First, we note that
there is a significant number of column density estimates with
negative values. These can only partially be attributed to the
broadening due to the uncertainties on the column density measurement,
which are expected to be of the order of
![]() .
Rather,
this analysis, which we stress is based solely in the area shown in
Fig. 6, suggests again that our extinction values are
slightly under-estimated. If one believes, from theoretical or
observational grounds, that the log-normal distribution is a good fit
to the column density measurements, than the amount of this bias is
provided by the fit parameter A0, because this is the quantity
directly responsible for a pure shift in the column density in
Eq. (11). If we follow this path, then we can estimate the
bias in the extinction values reported in our map to be
.
Rather,
this analysis, which we stress is based solely in the area shown in
Fig. 6, suggests again that our extinction values are
slightly under-estimated. If one believes, from theoretical or
observational grounds, that the log-normal distribution is a good fit
to the column density measurements, than the amount of this bias is
provided by the fit parameter A0, because this is the quantity
directly responsible for a pure shift in the column density in
Eq. (11). If we follow this path, then we can estimate the
bias in the extinction values reported in our map to be
![]() .
This value agrees well with our previous results
on the Perseus-Andromeda hole: it is smaller than
.
This value agrees well with our previous results
on the Perseus-Andromeda hole: it is smaller than
![]() ,
as it should be (because we actually detect a
,
as it should be (because we actually detect a
![]() extinction in the hole) and it actually would predict a
extinction in the hole) and it actually would predict a
![]() extinction in the hole, which is very close to the IRAS
measurements (see above Sect. 2).
extinction in the hole, which is very close to the IRAS
measurements (see above Sect. 2).
A second feature visible in Fig. 11 is the excess of flux at
the higher column densities, approximately for
![]() .
We tentatively interpret this as the signature of relatively
dense cores, where the original assumptions of a turbulent flow are
likely to break down (e.g. Lada et al. 2008; Barranco & Goodman 1998). In particular, the clear break at
.
We tentatively interpret this as the signature of relatively
dense cores, where the original assumptions of a turbulent flow are
likely to break down (e.g. Lada et al. 2008; Barranco & Goodman 1998). In particular, the clear break at
![]() suggests that gravity might start playing a dominant role
for these relatively dense structures, and that for the even higher
column densities the effects of turbulence might be almost completely
canceled by the large gravitational fields.
suggests that gravity might start playing a dominant role
for these relatively dense structures, and that for the even higher
column densities the effects of turbulence might be almost completely
canceled by the large gravitational fields.
Table 2:
The best-fit parameters and their 1-![]() errors for
the log-normal distribution used to fit the column density
probability shown in Fig. 11 (see Eq. (11) for the
meaning of the various quantities).
errors for
the log-normal distribution used to fit the column density
probability shown in Fig. 11 (see Eq. (11) for the
meaning of the various quantities).
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12670f12}
\vspace*{-2mm}\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg151.png)
|
Figure 12:
The joint distributions for any combination of two
fitting parameters of Eq. (11). The
|
| Open with DEXTER | |
3.4 Small-scale inhomogeneities
Sub-pixel inhomogeneities play an important role in extinction maps of molecular clouds, especially at the resolution achievable from the 2MASS data. Lada et al. (1994) first recognized that the local dispersion of extinction measurements increases with the column density: in a small patch of the sky, the scatter of the individual star column density estimates is proportional to the average local column density estimate. The observed scatter in the column density is mainly due to the photometric errors, to the intrinsic scatter in the NIR star colors, and to the effect of unresolved structure on scales smaller than the resolution of the smoothed maps. The latter effect could be due to either small-scale random inhomogeneities in the cloud projected density or unresolved but otherwise systematic density gradients. The presence of any random inhomogeneities is important because they might contain signatures of turbulent motions (see, e.g. Padoan et al. 1997a; Miesch & Bally 1994), and because they are bound to bias the extinction measurements in high-column density regions (and, especially, in the very dense cores; see Lombardi 2009).
In order to better quantify the effect of unresolved structure on small
scales, consider the quantity (cf. Paper II)
This quantity estimates the observed scatter in column densities which, as mentioned above, also includes the effects of photometric errors and intrinsic scatter of star colors. As shown in Paper II, one can instead use a different estimator, the
where the definitions of Eqs. (8), (10), and (12) have been used. In Paper II we showed that the
where
![\begin{figure}
\par\includegraphics[width=9cm]{12670f13}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg156.png)
|
Figure 13:
The |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{12670f14}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg162.png)
|
Figure 14:
The distribution of the |
| Open with DEXTER | |
We evaluated the ![]() map for the whole field and identified
regions with large small-scale inhomogeneities. The results, shown in
Fig. 13, confirm our expectations: inhomogeneities are
mostly present in high column density regions, while at low
extinctions (approximately below
map for the whole field and identified
regions with large small-scale inhomogeneities. The results, shown in
Fig. 13, confirm our expectations: inhomogeneities are
mostly present in high column density regions, while at low
extinctions (approximately below
![]() )
substructures are either on scales large enough to be detected at our
resolution (
)
substructures are either on scales large enough to be detected at our
resolution (
![]() ), or are negligible.
), or are negligible.
Figure 14 shows the average ![]() as a function of the
local extinction AK for the map in Fig. 5. If we compare
the dashed line, representing the average value of
as a function of the
local extinction AK for the map in Fig. 5. If we compare
the dashed line, representing the average value of ![]() in bins
of
in bins
of
![]() in AK, with the average variance
in AK, with the average variance
![]() on the estimate of
on the estimate of ![]() from a single star, which is approximately
from a single star, which is approximately
![]() ,
we can see that local inhomogeneities start to be the prevalent source
of errors in extinction maps for
,
we can see that local inhomogeneities start to be the prevalent source
of errors in extinction maps for
![]() .
.
As for the Papers I and II, we note here that a complete
characterization of the properties of inhomogeneities cannot be
performed using the results shown in Fig. 14 alone.
However, this plot can be used very efficiently to validate specific
models for inhomogeneities. For example, the contamination from
foreground stars shows up in the AK-![]() diagram as separate
trails with parabolic shapes that divert from the main
diagram as separate
trails with parabolic shapes that divert from the main
![]() locus of points.
locus of points.
4 Mass estimate
Table 3: The masses of the Taurus, Perseus, and California dark complexes.
The cloud mass M can be derived from the AK extinction map using
the following simple relation
where d is the cloud distance,
![\begin{figure}
\par\includegraphics[width=9cm]{12670f15}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg186.png)
|
Figure 15:
The cumulative mass enclosed in iso-extinction contours
for the Taurus, Perseus, and California molecular clouds. All
plots have been obtained from the region shown in
Fig. 5 (but with the N ICEST estimator), and
have thus the same resolution angular limit (
|
| Open with DEXTER | |
Figure 15 shows the relationship between the integrated mass
distribution and the extinction in AK, calculated using the
N ICEST technique. Note that regions with extinction larger
than
![]() account for
account for ![]()
![]() in Taurus, for
in Taurus, for ![]()
![]() in Perseus, and for less than
in Perseus, and for less than ![]() for in California. Hence,
we do not expect any significant underestimation in the cloud mass due
to unresolved dense cores. Note that the apparent difference between
the curve presented in Fig. 15 and in Fig. 4 of
Lada et al. (2009) is due to the different resolution of the
extinction maps used to produce the cumulative mass fraction plots.
for in California. Hence,
we do not expect any significant underestimation in the cloud mass due
to unresolved dense cores. Note that the apparent difference between
the curve presented in Fig. 15 and in Fig. 4 of
Lada et al. (2009) is due to the different resolution of the
extinction maps used to produce the cumulative mass fraction plots.
Although Fig. 15 is valuable to understand the distribution of column densities and its impact on the mass estimates of the various clouds, it is not particularly useful to make comparisons on the physical properties of the various clouds. Indeed, the measured cloud cumulative mass distribution depends on the resolution of the map used to compute it (a low resolution map will be unable to trace the high density peaks, and will produce a cumulative mass distribution truncated at large column densities). In addition, other factors such as the density of background stars available for the extinction map and the contamination by foreground stars play a role in the final measured cumulative mass distribution. Hence, in order to be able to make a comparison among the various clouds, we made an effort to produce maps that probe, as much as possible, the various clouds under the same physical conditions. In particular, we imposed the following constraints:
- 1.
- the physical resolution of the various maps is identical, so that we probe the same physical scales. In practice, this forces us to degrade the angular resolutions of the maps of the nearby clouds to match the physical resolution of the most distant complex (California in our case). We perform this step by using, for each cloud, a pixel scale proportional to the inverse of its estimated distance;
- 2.
- all maps have, on average, the same density of stars per pixel, so that the noise properties of the various maps are comparable. In order to reach this goal, we discard a fraction of stars in the clouds that have a large density of background stars per pixel;
- 3.
- the expected number of foreground stars per pixel is identical for all clouds. We ensure this by adding in the star catalogs of the various clouds an appropriate number of artificial foreground stars, with colors randomly chosen from the observed color distribution of sources in the control field. Note that in this process we make use of the estimated density of foreground stars reported in Table 1.
For the clouds considered in this paper, the ``standard'' for all
constraints considered above is set by the California cloud, the most
distant of the three. Figure 16 shows the cumulative mass
fraction for the three clouds observed in these ``calibrated''
extinction maps; clearly, because of the previous considerations, the
cumulative plot for California is identical to the one in
Fig. 15. A comparison with Fig. 15 shows that as
a result of the degradation of our data we drastically change the
Taurus and Perseus curves, especially at high extinction values. For
example, for both clouds we originally measured peaks in extinction
exceeding
![]() in AK (Fig. 15), which
eventually reduced to
in AK (Fig. 15), which
eventually reduced to ![]()
![]() (Fig. 16);
however, differences are evident even for moderate values of
extinction.
(Fig. 16);
however, differences are evident even for moderate values of
extinction.
Finally, we stress the importance of using an identical physical scale, density of background, and density of foreground stars per pixels when analyzing quantities such as the cumulative mass fraction plotted in Fig. 16. It is clear from a comparison of Figs. 15 and 16 that a direct comparison of cumulative mass profiles of clouds observed at different physical resolutions does not make sense, because these profiles can change dramatically, especially if the clouds are located at different distances from us. However, our tests have also shown that the other, presumably less important, parameters such as the number of foreground stars per pixel, if not properly taken into account, can bias the results significantly.
![\begin{figure}
\par\includegraphics[width=9cm]{12670f16}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg196.png)
|
Figure 16:
Same as Fig. 15, but the extinction maps for
the various clouds were degraded as described in
Sect. 4 in order to have the same key
parameters for all clouds (physical resolution
|
| Open with DEXTER | |
5 Cloud structure functions
The structure functions of the extinction map of a molecular cloud are
defined as
where the average is carried over all positions
The structure functions of the velocity field have been one
of the early focuses of turbulence theory. One of the main
assumptions of turbulence theory is that the energy provided by
external forces acting on very large scales is transferred to smaller
and smaller scales until viscosity (which acts on very small scales)
dissipates it. This ``energy cascade'' naturally leads to leads to
random, isotropic motions (because the imprint of the large scale
flows is likely to be lost during the energy transfer). It is natural
then, in such a stochastic process, to use the velocity
structure functions
(defined similarly to ![]() of Eq. (16)) to characterize the properties of the energy
cascade. In his seminal paper, Kolmogorov (1941) considered the
first two structure velocity functions S2 and S3, and showed
that both are simple power laws of the separation
of Eq. (16)) to characterize the properties of the energy
cascade. In his seminal paper, Kolmogorov (1941) considered the
first two structure velocity functions S2 and S3, and showed
that both are simple power laws of the separation ![]() ,
with
exponents 2/3 and 1. Since Kolmogorov's theory implicitly assumes
that turbulence is statistically self-similar at different scales, one
can actually extend this result to any order p, and show that the
structure functions of the velocity field must be simple power laws of
the angular distance parameter
,
with
exponents 2/3 and 1. Since Kolmogorov's theory implicitly assumes
that turbulence is statistically self-similar at different scales, one
can actually extend this result to any order p, and show that the
structure functions of the velocity field must be simple power laws of
the angular distance parameter ![]() ,
i.e.
,
i.e.
where
There is no equivalent model for the (projected) density of molecular
clouds, but the continuity equation suggests that the density
structure functions must be simply related to the velocity structure
function. As customary in the literature, we thus assume that the
same scaling law ![]() applies to both the velocity and density
fields.
applies to both the velocity and density
fields.
![\begin{figure}
\par\includegraphics[width=9cm]{12670f17a} \vskip 1em
\includegr...
...cm]{12670f17b} \vskip 1em
\includegraphics[width=9cm]{12670f17c}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg203.png)
|
Figure 17:
The structure functions for the Taurus ( top), Perseus
( middle), and California ( bottom) clouds. The plots show the
measured |
| Open with DEXTER | |
We analysed the structure functions ![]() and scaling law
and scaling law ![]() for the three clouds discussed in this paper using the
N ICEST maps. Figure 17 shows the observed
structure functions up to p = 20, together with the best exponential
fits, needed for the estimation of the scaling law
for the three clouds discussed in this paper using the
N ICEST maps. Figure 17 shows the observed
structure functions up to p = 20, together with the best exponential
fits, needed for the estimation of the scaling law ![]() .
We
first stress that the structure functions seem to follow an
exponential profile only on a limited range of p, and that at large
scales significant deviations are observed. Interestingly, the range
where the exponential fit approximates the data differs substantially
for each cloud. This makes the derivation of the scaling laws
.
We
first stress that the structure functions seem to follow an
exponential profile only on a limited range of p, and that at large
scales significant deviations are observed. Interestingly, the range
where the exponential fit approximates the data differs substantially
for each cloud. This makes the derivation of the scaling laws ![]() rather tricky, because the results can change appreciably
depending on the exact choice of the range of the especially at high
indexes p. With these caveats in mind, we plot in Fig. 18
the scaling indexes for all clouds. We immediately note that the
Taurus scaling law, and to a lesser degree the Perseus law, are very
well approximated by the Boldyrev (2002) prediction. This
is in agreement with what was found by Padoan et al. (2003) and
Padoan et al. (2002), although the results are not perfectly
identical because of the differences in the area selection and in the
methodology used to produce the extinction maps.
rather tricky, because the results can change appreciably
depending on the exact choice of the range of the especially at high
indexes p. With these caveats in mind, we plot in Fig. 18
the scaling indexes for all clouds. We immediately note that the
Taurus scaling law, and to a lesser degree the Perseus law, are very
well approximated by the Boldyrev (2002) prediction. This
is in agreement with what was found by Padoan et al. (2003) and
Padoan et al. (2002), although the results are not perfectly
identical because of the differences in the area selection and in the
methodology used to produce the extinction maps.
![\begin{figure}
\par\includegraphics[width=9cm]{12670f18}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg204.png)
|
Figure 18:
The scaling index ratio
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12670f19}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg205.png)
|
Figure 19:
Similarly to Fig. 18, the plot shows the scaling index ratio
|
| Open with DEXTER | |
The results are much less encouraging for the California cloud, which
shows very large differences from the predictions for p > 10. From
a theoretical point of view this result is rather surprising, since in
this analysis we considered the ratio
![]() ,
which
according to Benzi et al. (1993) (see
also Dubrulle 1994) should show a universal behaviour also at
relatively small Reynolds numbers. However, we note that in earlier
results (see in particular the Ophiuchus complex in Paper II) we found
already a number of clouds that did show completely different
behaviours in their scaling indexes.
,
which
according to Benzi et al. (1993) (see
also Dubrulle 1994) should show a universal behaviour also at
relatively small Reynolds numbers. However, we note that in earlier
results (see in particular the Ophiuchus complex in Paper II) we found
already a number of clouds that did show completely different
behaviours in their scaling indexes.
In order to investigate whether the poor description of the California cloud in terms of turbulent models might be related to the larger distance of this cloud, and thus to the decreased effective physical resolution we reach there, we performed a test similar to the one described in Sect. 4. In particular, we considered extinction maps of the three clouds having the physical resolution, the same number of background, and the same number of foreground stars per pixel. As explained in Sect. 4, this procedure degrades the quality of the Taurus and of the Perseus maps to mach the one of the California. We then evaluated again the structure functions on these maps and their scaling index ratio. The results, reported in Fig. 19, show that this process moves the data for Taurus and Perseus away from both the Boldyrev prediction and the data for the California cloud. This shift now puts the Taurus and Perseus data very close to the She & Leveque (1994) model, i.e. for both clouds increases their scaling index ratios at high p. Hence, this experiment suggests that the results of the scaling index ratio analysis can be very sensitive to the the resolving power of the maps and distance of the clouds, and therefore should be interpreted with great care. However, the experiment also indicates that the discrepancy between the California cloud data and the model predictions is likely not due to a lack of resolving power in the map of that cloud.
In summary, the data collected so far show that, although the Boldyrev (2002) seems to describe the scaling index ratio for some clouds, there is by no means a general scaling relation that can be applied to all clouds. Specifically, we found clouds that are well described by the She & Leveque (1994) model (such as the Lupus cloud) and clouds that cannot be described by any of the models considered here (Ophiuchus and California).
6 Conclusions
The main results of this paper can be summarized as follows:
- We used approximately 23 million stars from the 2MASS point
source catalog to construct a 3500 square degree
N ICER/N ICEST extinction map of a large region of
the sky that includes the Taurus, Perseus, and California dark
nebulæ, as well as the high-galactic latitude clouds MBM 8,
MBM 12, and MBM 16. The map has a resolution of
 and an average
and an average  detection level of 0.2 visual magnitudes.
detection level of 0.2 visual magnitudes.
- We calculated the distances of the Taurus and Perseus clouds by comparing the density of foreground stars with the prediction of the Robin et al. (2003) Galactic model. The values obtained are in excellent agreement with recent independent VLBI parallax measurements.
- We characterize the large-scale structure of the map and find a

 region close to the galactic plane
(
region close to the galactic plane
(
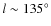 ,
,
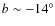 )
with extinction smaller
than
)
with extinction smaller
than
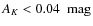 .
.
- We considered in detail the effect of sub-pixel inhomogeneities,
and derived an estimator useful to quantify them. We also showed
that inhomogeneities play a significant role only in the densest
cores with AK > 6-
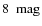 .
.
- We measured the probability distribution for column-density
measurements, and showed that it can be fit with exquisite accuracy
with a log-normal distribution, as expected from turbulence models.
The fit breaks down at
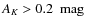 ,
a fact that suggests
that gravitational effects (typically ignored in turbulence models)
are starting to be important at these level of extinction.
,
a fact that suggests
that gravitational effects (typically ignored in turbulence models)
are starting to be important at these level of extinction.
- We evaluated the structure functions and scaling index ratios for the three clouds and compared them with the predictions of three turbulent models. We find the three clouds to have differing structural properties and no one model can explain the underlying structure of all the clouds.
It is a pleasure to thank Tom Dame for many useful discussions. This research has made use of the 2MASS archive, provided by NASA/IPAC Infrared Science Archive, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. C.J.L. acknowledges support from NASA ORIGINS Grant NAG 5-13041.
References
- Alves, J., Lada, C. J., & Lada, E. A. 1999, ApJ, 515, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Alves, J., Lada, C. J., & Lada, E. A. 2001, Nature, 409, 159 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bally, J. 2008, in Handbook of Star Forming Regions, ed. B. Reipurth, 1 [Google Scholar]
- Barranco, J. A., & Goodman, A. A. 1998, ApJ, 504, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Benzi, R., Ciliberto, S., Tripiccione, R., et al. 1993, Phys. Rev. E, 48, 29 [Google Scholar]
- Bhatt, H. C. 2000, A&A, 362, 715 [NASA ADS] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Boldyrev, S. 2002, ApJ, 569, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Boldyrev, S., Nordlund, Å., & Padoan, P. 2002, ApJ, 573, 678 [NASA ADS] [CrossRef] [Google Scholar]
- Cambrésy, L. 1999, A&A, 345, 965 [NASA ADS] [Google Scholar]
- Cernicharo, J., & Bachiller, R. 1984, A&AS, 58, 327 [NASA ADS] [Google Scholar]
- Cernicharo, J., & Guelin, M. 1987, A&A, 176, 299 [NASA ADS] [Google Scholar]
- Cernicharo, J., Bachiller, R., & Duvert, G. 1985, A&A, 149, 273 [NASA ADS] [Google Scholar]
- de Zeeuw, P. T., Hoogerwerf, R., de Bruijne, J. H. J., Brown, A. G. A., & Blaauw, A. 1999, AJ, 117, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Dobashi, K., Uehara, H., Kandori, R., et al. 2005, PASJ, 57, 1 [Google Scholar]
- Dubrulle, B. 1994, Phys. Rev. Lett., 73, 959 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Goldsmith, P. F., Heyer, M., Narayanan, G., et al. 2008, ApJ, 680, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Pineda, J. E., & Schnee, S. L. 2009, A&A, 692, 91 [Google Scholar]
- Herbig, G. H. 1962, Adv. A&A, 1, 47 [Google Scholar]
- Hirota, T., Bushimata, T., Choi, Y. K., et al. 2008, PASJ, 60, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Indebetouw, R., Mathis, J. S., Babler, B. L., et al. 2005, ApJ, 619, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Joy, A. H. 1945, ApJ, 102, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Kleinmann, S. G., Lysaght, M. G., Pughe, W. L., et al. 1994, Exp. Astron., 3, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Kolmogorov, A. N. 1941, Dokl. Akad. Nauk SSSR, 30, 301 [Google Scholar]
- Lada, C. J., Lada, E. A., Clemens, D. P., & Bally, J. 1994, ApJ, 429, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Alves, J., & Lada, E. A. 1996, AJ, 111, 1964 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Muench, A. A., Rathborne, J., Alves, J. F., & Lombardi, M. 2008, ApJ, 672, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lombardi, M., & Alves, J. F. 2009, ApJ, 703, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Lilley, A. E. 1955, ApJ, 121, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Loinard, L., Torres, R. M., Mioduszewski, A. J., et al. 2007, ApJ, 671, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M. 2002, A&A, 395, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M. 2009, A&A, 493, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., & Alves, J. 2001, A&A, 377, 1023 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., Alves, J., & Lada, C. J. 2006, A&A, 454, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., Lada, C. J., & Alves, J. 2008, A&A, 489, 143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnani, L., Hartmann, D., Holcomb, S. L., Smith, L. E., & Thaddeus, P. 2000, ApJ, 535, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Meistas, E., & Straizys, V. 1981, Acta Astron., 31, 85 [NASA ADS] [Google Scholar]
- Miesch, M. S., & Bally, J. 1994, ApJ, 429, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Miville-Deschênes, M.-A., & Lagache, G. 2005, ApJS, 157, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Muench, A. A., Lada, C. J., Luhman, K. L., Muzerolle, J., & Young, E. 2007, AJ, 134, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C., Benson, P. J., & Ho, P. T. P. 1979, ApJ, 233, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Narayanan, G., Heyer, M. H., Brunt, C., et al. 2008, ApJS, 177, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Jones, B. J. T., & Nordlund, A. P. 1997a, ApJ, 474, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Nordlund, A., & Jones, B. J. T. 1997b, MNRAS, 288, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Cambrésy, L., & Langer, W. 2002, ApJ, 580, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Boldyrev, S., Langer, W., & Nordlund, Å. 2003, ApJ, 583, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Passot, T., & Vázquez-Semadeni, E. 1998, Phys. Rev. E, 58, 4501 [NASA ADS] [CrossRef] [Google Scholar]
- Ridge, N. A., Di Francesco, J., Kirk, H., et al. 2006, AJ, 131, 2921 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savage, B. D., & Mathis, J. S. 1979, ARA&A, 17, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Scalo, J., Vazquez-Semadeni, E., Chappell, D., & Passot, T. 1998, ApJ, 504, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- She, Z.-S., & Leveque, E. 1994, Phys. Rev. Lett., 72, 336 [Google Scholar]
- Straizys, V., & Meistas, E. 1980, Acta Astron., 30, 541 [NASA ADS] [Google Scholar]
- Vazquez-Semadeni, E. 1994, ApJ, 423, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez-Semadeni, E., & García, N. 2001, ApJ, 557, 727 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ...
Survey
![[*]](/icons/foot_motif.png)
- See http://www.ipac.caltech.edu/2mass/
- ... field
![[*]](/icons/foot_motif.png)
- Note that the control field has been chosen to correspond approximately to the Perseus-Andromeda hole, but it also includes some areas from the nearby regions.
All Tables
Table 1: The average value of foreground stars found in the various complexes.
Table 2:
The best-fit parameters and their 1-![]() errors for
the log-normal distribution used to fit the column density
probability shown in Fig. 11 (see Eq. (11) for the
meaning of the various quantities).
errors for
the log-normal distribution used to fit the column density
probability shown in Fig. 11 (see Eq. (11) for the
meaning of the various quantities).
Table 3: The masses of the Taurus, Perseus, and California dark complexes.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12670f01}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg48.png)
|
Figure 1:
Color-color diagram of the stars in the whole field, as a
density plot. The contours are logarithmically spaced, i.e. each
contour represents a density ten times larger than the enclosing
contour; the outer contour detects single stars and clearly shows
a bifurcation at large color-excesses. The dashed lines identify
the regions in the color space defined in Eqs. (2) and
(3), as indicated by the corresponding letters. Only
stars with accurate photometry in all bands (maximum 1- |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12670f02}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg49.png)
|
Figure 2: Spatial distribution of the samples of sources as defined by Eqs. (2) and (3). Sample A is shown as filled circles, while sample B is shown as crosses (see also Fig. 1). Sample A appears to be strongly clustered in high-column density regions of the cloud, and is thus interpreted as genuine reddened stars; sample B seems not to be associated with the cloud, and is instead preferentially located at low galactic latitudes. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12670f03}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg50.png)
|
Figure 3: The histogram of the K band magnitude for the two star subsets A and B of Eqs. (2) and (3). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12670f04}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg51.png)
|
Figure 4: The extinction-corrected color-color diagram. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm]{12670f05}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg68.png)
|
Figure 5:
The N ICER extinction map of the region
considered in this paper. The resolution is
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12670f06}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg69.png)
|
Figure 6: A zoom of Fig. 5 showing the Taurus, Perseus, and California, complexes. The several well studied objects are marked. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12670f07}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg88.png)
|
Figure 7:
A lower resolution version of Fig. 5. This
image was constructed by convolving Fig. 5 with a
Gaussian kernel. Also plotted are contour levels of (smoothed)
extinction at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12670f08}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg112.png)
|
Figure 8: The reddening law as measured on the analyzed region. The plot shows the color excess on J - K as a function of the color excess on H - K (the constant 0.170 and 0.498 represent, respectively, the average of H - K and of J - H colors in magnitudes for the control field). Error bars are uncertainties evaluated from the photometric errors of the 2MASS catalog. The solid line shows the normal infrared reddening law (Indebetouw et al. 2005). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm]{12670f09}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg117.png)
|
Figure 9:
The local density of foreground stars, averaged over
connected regions with extinction
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12670f10}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg139.png)
|
Figure 10:
The distances of the Taurus (solid lines) and Perseus
(dashed lines) clouds deduced from the density of foreground
stars. The plots show the density of foreground of stars as a
function of the cloud distance, as predicted from the
Robin et al. (2003) Galactic model (the two curves are
slightly different because of the different Galactic coordinates
of the clouds). The grey areas show the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12670f11}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg141.png)
|
Figure 11:
The probability distribution of star pixel extinctions
for the whole map shown in Fig. 6; the gray, smooth
curve represents the best-fit with a log-normal distribution,
smoothed with a Gaussian kernel of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12670f12}
\vspace*{-2mm}\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg151.png)
|
Figure 12:
The joint distributions for any combination of two
fitting parameters of Eq. (11). The
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12670f13}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg156.png)
|
Figure 13:
The |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12670f14}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg162.png)
|
Figure 14:
The distribution of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12670f15}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg186.png)
|
Figure 15:
The cumulative mass enclosed in iso-extinction contours
for the Taurus, Perseus, and California molecular clouds. All
plots have been obtained from the region shown in
Fig. 5 (but with the N ICEST estimator), and
have thus the same resolution angular limit (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12670f16}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg196.png)
|
Figure 16:
Same as Fig. 15, but the extinction maps for
the various clouds were degraded as described in
Sect. 4 in order to have the same key
parameters for all clouds (physical resolution
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12670f17a} \vskip 1em
\includegr...
...cm]{12670f17b} \vskip 1em
\includegraphics[width=9cm]{12670f17c}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg203.png)
|
Figure 17:
The structure functions for the Taurus ( top), Perseus
( middle), and California ( bottom) clouds. The plots show the
measured |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12670f18}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg204.png)
|
Figure 18:
The scaling index ratio
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12670f19}
\end{figure}](/articles/aa/full_html/2010/04/aa12670-09/Timg205.png)
|
Figure 19:
Similarly to Fig. 18, the plot shows the scaling index ratio
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.





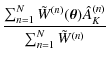
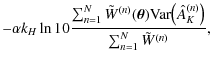
![\begin{displaymath}
\sigma^2_{\hat A_K}(\vec \theta) \equiv \frac{\sum_{n=1}^N ...
...bigr)}{\Bigl[ \sum_{n=1}^N W^{(n)}(\vec\theta) \Bigr]^2} \cdot
\end{displaymath}](/articles/aa/full_html/2010/04/aa12670-09/img91.png)
![\begin{displaymath}
h(A_K) = \frac{a}{A_K - A_0}
\exp\left[- \frac{\bigl(\ln (A_K - A_0) - \ln A_1 \bigr)^2}%
{2 (\ln \sigma)^2} \right] ,
\end{displaymath}](/articles/aa/full_html/2010/04/aa12670-09/img143.png)
![\begin{displaymath}
\hat\sigma^2_{\hat A_K}(\vec\theta) = \frac{\sum_{n=1}^N W^...
... - \hat A_K(\vec\theta)
\bigr]^2}{\sum_{n=1}^N W^{(n)}} \cdot
\end{displaymath}](/articles/aa/full_html/2010/04/aa12670-09/img152.png)