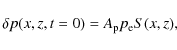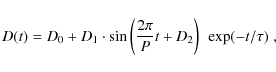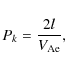| Issue |
A&A
Volume 512, March-April 2010
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200912603 | |
| Published online | 08 April 2010 | |
Excitation of vertical kink waves in a solar coronal arcade loop by a periodic driver
M. Selwa1,![]() - K. Murawski2
- S. K. Solanki3, 4 - L. Ofman1
- K. Murawski2
- S. K. Solanki3, 4 - L. Ofman1
1 - Department of Physics, The Catholic University of America,
620 Michigan Avenue, NE, 200 Hannan Hall, Washington, DC 20064;
NASA Goddard Space Flight Center, Code 671, Greenbelt, MD 20771, USA
2 - Group of Astrophysics and Gravity Theory,
Institute of Physics, UMCS, ul. Radziszewskiego 10, 20-031 Lublin,
Poland
3 - Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Str. 2,
37191 Katlenburg-Lindau, Germany
4 - School of Space Research, Kyung Hee University, Yongin, Gyeonggi
446-701, Korea
Received 29 May 2009 / Accepted 21 October 2009
Abstract
Context. We study an oscillatory driver as a
possible excitation mechanism of vertical kink loop oscillations in the
ideal MHD regime.
Aims. We consider a solar coronal magnetic arcade
with a dense photospheric layer. The two-dimensional numerical model
that we implement includes the effects of nonlinearity and line
curvature on the excitation and attenuation of fast magnetosonic kink
waves. We investigate the effects of a driven sinusoidal pressure pulse
and compare it with the impulsive excitation by a pressure pulse that
impacts the overlying loop.
Methods. Our numerical simulations reveal wave
signatures that are reminiscent of vertical loop oscillations seen in
TRACE observational data.
Results. We conclude that attenuation of vertical
kink oscillations can be reduced to the value observed by adopting an
oscillatory instead of an impulsive excitation. An oscillatory driver
also naturally explains why only a small subset of all loops is excited
to oscillate transversally in an active region.
Key words: magnetohydrodynamics (MHD) - Sun: corona - Sun: oscillations
1 Introduction
Sensitive instruments such as SUMER on SOHO (Wilhelm et al. 1995) and TRACE (Handy et al. 1999) have detected of various modes of oscillation in solar coronal loops. The identified wave modes include both slow propagating (De Moortel et al. 2002) and slow standing (Wang et al. 2002; 2003a,b; 2005; Ofman & Wang 2002) waves, sausage waves (Nakariakov et al. 2003; Aschwanden et al. 2004), and two polarizations of kink oscillations called horizontal (Aschwanden et al. 1999; Nakariakov et al. 1999; Schrijver et al. 2002) and vertical (Wang & Solanki 2004). Although these two polarizations are similar in nature, they differ in some properties (e.g., signs of compressibility are displayed by the vertical kink oscillations only). Note that some of the oscillations identified as horizontal may in fact be vertical (Wang et al. 2005).
The current work is motivated by the rapid attenuation of magnetohydrodynamic waves through leakage found by Selwa et al. (2005, 2006, 2007a) and Gruszecki et al. (2006, 2008) in earlier 2D simulations. The simulated oscillations are damped considerably more rapidly than the observed oscillations. The authors modeled impulsively excited vertical kink oscillations in a solar arcade. In this paper, we propose a new excitation mechanism for vertical kink waves: an oscillatory driver instead of a single pulse. This driver can be considered as a flare that contains quasi-periodic pulsations (Ofman & Sui 2006; Nakariakov et al. 2006; Nakariakov & Melnikov 2009).
Properties of waves in 2D and 3D straight loops/slabs were
described by Edwin & Roberts (1982, 1983) and Roberts
et al. (1984).
Several papers also describe the effect of the excitation of different
kinds of oscillations by a periodic driver. Murawski & Goossens
(1994)
excited fast waves in a 2D slab by means of periodic
photospheric shearing motions. They found that the type of excited wave
(kink or sausage) depends on the polarization of the driver.
Ruderman et al. (1997)
studied resonant Alfvén oscillations in coronal arcades driven by
toroidal footpoint motions. The authors calculated expressions for both
the total amount of dissipated wave energy and its spatial distribution
within the resonant magnetic surface. Tirry & Poedts (1998) studied the
heating of 2D coronal arcades by linear
resonant Alfvén waves that are excited directly by photospheric
toroidally polarised footpoint motions. Taroyan et al. (2005) studied the
excitation of slow standing waves in a 1D loop by footpoint
heat deposition.
They found that the time profile of the long-lasting pulse determines
whether a
standing or propagating wave is excited. Zaqarashvili et al. (2005)
suggested that the periodic shaking of coronal magnetic field lines due
to photospheric motions may induce the excitation of slow
magnetoacoustic waves in short coronal magnetic structures.
They found that harmonics of slow magnetoacoustic waves with half the
frequency of the photospheric driver had an exponential growth in time
that was proportional to the amplitude of photospheric motions and to
the value of the plasma ![]() in the corona. Brady & Arber (2005) studied
numerically the excitation of vertical kink waves in a
2D curved loop with a velocity driver at one of its
footpoints.
They found that the maximum wave period, which can successfully be
excited by the footpoint driving mechanism, corresponds
to the fifth harmonic of the loop. In this paper, we extend the
approaches of both Selwa et al. (2005, 2006, 2007a) and Brady
& Arber (2005)
by
perturbing the loop with an oscillatory pressure that acts on the
whole loop from the ambient medium. Ballai et al. (2008) studied kink
waves in straight cylindrical loop excited by EIT waves. The authors
found that for a harmonic driver the dominant period in the generated
oscillation belongs to the driver while in the case of a non-harmonic
driver (modelling a shock wave) the generated oscillations in the loop
are of natural periods only. This paper is devoted to a 2D MHD
study. A review of 3D MHD studies of coronal loop
oscillations can be found in Ofman (2009).
in the corona. Brady & Arber (2005) studied
numerically the excitation of vertical kink waves in a
2D curved loop with a velocity driver at one of its
footpoints.
They found that the maximum wave period, which can successfully be
excited by the footpoint driving mechanism, corresponds
to the fifth harmonic of the loop. In this paper, we extend the
approaches of both Selwa et al. (2005, 2006, 2007a) and Brady
& Arber (2005)
by
perturbing the loop with an oscillatory pressure that acts on the
whole loop from the ambient medium. Ballai et al. (2008) studied kink
waves in straight cylindrical loop excited by EIT waves. The authors
found that for a harmonic driver the dominant period in the generated
oscillation belongs to the driver while in the case of a non-harmonic
driver (modelling a shock wave) the generated oscillations in the loop
are of natural periods only. This paper is devoted to a 2D MHD
study. A review of 3D MHD studies of coronal loop
oscillations can be found in Ofman (2009).
This paper is organized as follows. The numerical model is described in Sect. 2. The numerical results are presented in Sect. 3. This is followed by a summary and discussion of the main results in Sect. 4.
2 Numerical model
We describe coronal plasma by the ideal magnetohydrodynamic
equations with polytropic index
![]() :
:
Here
Since the vertical pressure-scale height of
2.1 Equilibrium configurations
We adopt and modify the coronal arcade model described in Selwa
et al. (2005,
2006, 2007a). In this
model, the coronal arcade is embedded in a two-dimensional motionless
environment (
![]() ;
all variables referring to the
environment are denoted by subscript ``e'') in which mass
density
;
all variables referring to the
environment are denoted by subscript ``e'') in which mass
density
![]() and gas pressure
and gas pressure ![]() has to be constant. Here
has to be constant. Here ![]() is
the sound speed in the ambient medium. From the momentum Eq. (2), it follows that
in this equilibrium configuration the Lorentz force must vanish, i.e.,
is
the sound speed in the ambient medium. From the momentum Eq. (2), it follows that
in this equilibrium configuration the Lorentz force must vanish, i.e.,
This equation can be solved by a potential magnetic field
Since we limit our discussion to a two-dimensional magnetically structured atmosphere for which the plasma quantities are independent of the spatial coordinate y, i.e.,
Here
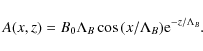
|
(11) |
This method leads to the equilibrium magnetic field components
|
|
= | (12) | |
| = | (13) |
where
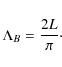
|
(14) |
Here L is the horizontal half-width of the arcade. In this model, the Alfvén speed in the environment is given by
Following Selwa et al. (2005,
2006, 2007a) we model a
denser loop
that is embedded in the arcade
in such a way that its edges follow two specific magnetic field lines.
We choose ![]() as footpoints of the loop and
w=0.0125 L
as its half-width at the footpoints. Such a loop does
not have a perfect circular shape, but its average radius and length
can be estimated to be 70 Mm and 190 Mm,
respectively. The mass
density is enhanced in the loop compared to the ambient medium.
Initially a top-hat density profile is introduced into the loop. For
the mass density contrast, we choose
as footpoints of the loop and
w=0.0125 L
as its half-width at the footpoints. Such a loop does
not have a perfect circular shape, but its average radius and length
can be estimated to be 70 Mm and 190 Mm,
respectively. The mass
density is enhanced in the loop compared to the ambient medium.
Initially a top-hat density profile is introduced into the loop. For
the mass density contrast, we choose ![]() ,
where
,
where ![]() denotes the mass
density within the loop and
denotes the mass
density within the loop and ![]() corresponds to the
ambient medium. This density contrast was chosen to
remain consistent with our earlier computations (Selwa et al. 2005,
2006, 2007a). Note that
the Alfvén speed within the loop is smaller than in the ambient medium
(
corresponds to the
ambient medium. This density contrast was chosen to
remain consistent with our earlier computations (Selwa et al. 2005,
2006, 2007a). Note that
the Alfvén speed within the loop is smaller than in the ambient medium
(
![]() ).
As a consequence, the loop forms a wave guide
for fast magnetosonic waves (as described in Edwin & Roberts
1982). Because
of the decrease in magnetic field strength with height and the constant
pressure loop, the plasma
).
As a consequence, the loop forms a wave guide
for fast magnetosonic waves (as described in Edwin & Roberts
1982). Because
of the decrease in magnetic field strength with height and the constant
pressure loop, the plasma
![]() grows from 0.048 at the loop
foot-points to 0.125 at the loop apex and the loop is cooler
than
the surrounding corona. It may affect slow waves evolution as their
speed is lower inside the loop than in the outer part of arcade. The
influence of the sound speed on fast magnetosonic speed is minor in low
grows from 0.048 at the loop
foot-points to 0.125 at the loop apex and the loop is cooler
than
the surrounding corona. It may affect slow waves evolution as their
speed is lower inside the loop than in the outer part of arcade. The
influence of the sound speed on fast magnetosonic speed is minor in low
![]() plasma, and therefore the lower loop temperature is not expected to
affect our results significantly.
Recently Ugarte-Urra et al. (2009) found that
cooler loops, e.g., at
transition region temperatures are observed in active regions
(mainly peripheral parts) and reach heights of 150 Mm in the
corona
above the limb. All equilibrium parameters are listed in Table 1.
plasma, and therefore the lower loop temperature is not expected to
affect our results significantly.
Recently Ugarte-Urra et al. (2009) found that
cooler loops, e.g., at
transition region temperatures are observed in active regions
(mainly peripheral parts) and reach heights of 150 Mm in the
corona
above the limb. All equilibrium parameters are listed in Table 1.
Table 1: Equilibrium and normalization parameters for the potential arcade and the loop.
3 Numerical simulations
We adopt the numerical code Athena developed by Gardiner & Stone (2005). This code implements a higher-order Godunov method for solving time-dependent ideal MHD equations. This algorithm, which is based on the piecewise parabolic method, is second-order accurate in space and time. Equation (5) is satisfied by using a constrained transport scheme.
Equations (1)-(5) are solved
numerically in an Eulerian box with the x- and z-dimensions
![]() .
This box is covered by a uniform grid of
.
This box is covered by a uniform grid of ![]() numerical
cells.
Grid convergence studies have shown that this resolution is sufficient
for obtaining results independent of the grid.
numerical
cells.
Grid convergence studies have shown that this resolution is sufficient
for obtaining results independent of the grid.
We apply open boundary conditions with a zero-gradient
extrapolation of all plasma variables at all the boundaries to allow a
wave signal to freely leave the simulation region. Instead of adopting
the line-tying boundary conditions at the bottom of the simulation
region implemented by Selwa et al. (2005, 2006, 2007a), we model
wave reflection from the bottom boundary by implementing a dense
photosphere-like layer for z < 0 region
given by
Here
![\begin{figure}
\par\includegraphics[scale=0.525, angle=0,clip]{12603fg1.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa12603-09/Timg62.png)
|
Figure 1: Initial mass density profile. Note the logarithmic scale on the vertical axis. |
| Open with DEXTER | |
3.1 Perturbations
To excite the oscillations, we implement a damped oscillatory driver in
gas pressure given by
where
| S(x,z) | = | ![$\displaystyle \exp\left[-\left(\frac{x-x_{\rm o}}{w}\right)^2\right]\exp\left[-\left(\frac{z-z_{\rm o}}{w}\right)^2\right]\; ,$](/articles/aa/full_html/2010/04/aa12603-09/img64.png)
|
(17) |
| S(t) | = | ![$\displaystyle \frac{1}{2}\left[1+\cos\left(\frac{2\pi}{P_{\rm o}}t\right)\right]\exp\left(-\frac{t}{\tau_{\rm o}}\right)\cdot$](/articles/aa/full_html/2010/04/aa12603-09/img65.png)
|
(18) |
Here
![\begin{figure}
\par\includegraphics[scale=0.45, angle=0,clip]{12603fg2.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa12603-09/Timg74.png)
|
Figure 2:
Several time signatures of an oscillator with
wave period |
| Open with DEXTER | |
Table 2:
Impulse over unit area![]() equivalent to the oscillator with parameters
equivalent to the oscillator with parameters
![]() ,
,
![]() s.
s.
To be able to compare with the results of Selwa
et al. (2005,
2006, 2007a), we also
perturb the static solution of
Eqs. (1)-(5) by launching a
hot pulse in the
gas pressure, i.e.,
where
3.2 Results
We begin our studies by launching an initial pulse in gas pressure
according to Eq. (18).
Since this case will be used for
comparison purposes with excitation by an oscillatory driver, we
choose an amplitude that provides a comparable integral over time as
an osillatory driver until the first minimum in its time signature:
![]() (see Table 2).
Next we excite
oscillations by an oscillatory driver (Eq. (15)). As a
reference value, we choose
(see Table 2).
Next we excite
oscillations by an oscillatory driver (Eq. (15)). As a
reference value, we choose ![]() ,
,
![]() s.
Figure 3
shows the time signatures of mass
density collected at the loop apex for impulsive (top panel) and
oscillatory (middle panel) excitation, respectively. The oscillations
excited by the oscillatory driver (middle panel) are less attenuated
than those produced by impulsive excitation (top panel)
as we demonstrate by means of the analysis in this section (although
the difference is not clearly visible from Fig. 3).
s.
Figure 3
shows the time signatures of mass
density collected at the loop apex for impulsive (top panel) and
oscillatory (middle panel) excitation, respectively. The oscillations
excited by the oscillatory driver (middle panel) are less attenuated
than those produced by impulsive excitation (top panel)
as we demonstrate by means of the analysis in this section (although
the difference is not clearly visible from Fig. 3).
![\begin{figure}
\par\includegraphics[scale=0.45, angle=0]{12603f3a.eps}\par\inclu...
...par\includegraphics[scale=0.45, angle=0]{12603f3c.eps}\vspace{-3mm}
\end{figure}](/articles/aa/full_html/2010/04/aa12603-09/Timg78.png)
|
Figure 3:
Time-signatures of the mass density
(color scale; units of |
| Open with DEXTER | |
To identify the excited mode of oscillations, we plot difference images of the loop between the initial state (t=0) and the first maximum observed in the time series of loop apex height (t=250 s) (top panel of Fig. 4) and between the first maximum (t=250 s) and the following minimum (t=400 s) (bottom panel of Fig. 4). We clearly see that the fundamental mode of the vertical kink oscillation is excited. This matches both the observational data (compare with Fig. 3 in Wang & Solanki 2004) and impulsively excited oscillations (compare with Fig. 2 in Selwa et al. 2005). Local enhancements (white patches), seen among yellow arcs indicating the new position in time of the loop in the lower panel, correspond to slow magnetosonic waves that propagate along the legs of the loop (Selwa et al. 2006). These waves are produced by magnetic compression of the loop that also leads to the evacuation of part of the mass from the apex, which can be seen in both panels of Fig. 3 and the bottom panel of Fig. 4. At a later stage of the evolution, the mass density at the loop's apex is again enhanced (not shown) after the reflection of the slow waves from the footpoints of the loop - this process leads to the formation of a slow standing wave (Selwa et al. 2007b). The other feature that amplifies the effect of mass rarefication at the apex is numerical diffusion discussed qualitatively and quantitatively by Selwa et al. (2006, 2007a).
![\begin{figure}
\par\includegraphics[scale=0.45, angle=0]{12603f4a.eps}\par\includegraphics[scale=0.45, angle=0]{12603f4b.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa12603-09/Timg79.png)
|
Figure 4:
Difference images of the loop in the case of oscillatory excitation (
|
| Open with DEXTER | |
We trace the global oscillations of the loop discussed above by
following the position of the loop apex in time estimated by the
maximum of a Gaussian function fitted to the mass density profile
across the loop's cross-section at its apex
![\begin{displaymath}G(z)=G_{\rm0} \cdot \exp\left[-\frac{(z-G_1)^2} {2{G_{\rm 2}}^2}\right]+G_{\rm 3},
\end{displaymath}](/articles/aa/full_html/2010/04/aa12603-09/img80.png)
|
(20) |
where G1 denotes the position of the loop apex,
where P denotes the wave period of the oscillation and
![\begin{figure}
\par\includegraphics[scale=0.45, angle=0,clip]{12603fg5.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa12603-09/Timg84.png)
|
Figure 5:
Offset of the loop's apex (measured in units of L)
versus amplitude of the oscillator with |
| Open with DEXTER | |
We begin our parametric studies with an impulsively excited wave.
The fitting described by Eq. (20)
provides ![]() (440) s and
(440) s and ![]() (0.97) for a fit to part of the oscillation time series
containing 2 (3) maxima (top panel of Fig. 3). The
subscript p identifies the
quantities related to the excitation by the pulse. Although this
wave period is about two times longer than the observed
(0.97) for a fit to part of the oscillation time series
containing 2 (3) maxima (top panel of Fig. 3). The
subscript p identifies the
quantities related to the excitation by the pulse. Although this
wave period is about two times longer than the observed ![]() s
period of the displacement oscillations (Wang &
Solanki 2004),
it can be reduced to the exact
observational value with a different choice of the Alfvén speed,
s
period of the displacement oscillations (Wang &
Solanki 2004),
it can be reduced to the exact
observational value with a different choice of the Alfvén speed,
![]() ,
in the corona, which is a free parameter in our model.
However, the attenuation time is approximately three times shorter
than the observed value of
,
in the corona, which is a free parameter in our model.
However, the attenuation time is approximately three times shorter
than the observed value of ![]() (Wang & Solanki 2004),
irrespective of the choice of Alfvén speed,
(Wang & Solanki 2004),
irrespective of the choice of Alfvén speed, ![]() .
The dimensionless ratio
.
The dimensionless ratio ![]() is expected to be independent of
is expected to be independent of ![]() in the linear regime.
Parameters such as the amplitude or width of the pulse also influence
the wave period and attenuation time: e.g., a narrower and smaller
amplitude pulse results in shorter wave periods and less attenuated
oscillations (Selwa et al. 2006), which,
however are still
attenuated too quickly. The inferred period is close to the kink
period of the loop, which in 2D is given by
in the linear regime.
Parameters such as the amplitude or width of the pulse also influence
the wave period and attenuation time: e.g., a narrower and smaller
amplitude pulse results in shorter wave periods and less attenuated
oscillations (Selwa et al. 2006), which,
however are still
attenuated too quickly. The inferred period is close to the kink
period of the loop, which in 2D is given by
where l is the loop length. The choice of external Alfvén speed for calculation of the period is not so straightforward. Since the equilibrium magnetic field exponentially decreases with height, we decided to estimate the period with the mean value of Alfvén speed outside the loop, e.g.,
The top panel of Fig. 6 displays the
wave period P versus the relative amplitude of a
driver ![]() (for
(for ![]() s)
in the case of a fit based on 2 (squares) or 3 (crosses)
maxima in the corresponding time signature (middle panel of
Fig. 3).
In Figs. 6-8, points
corresponding to impulsive excitation are plotted in green. They are
shown for comparison purposes.
We clearly see that for a low amplitude driver, the wave period of the
oscillations is close to the wave period of the oscillation excited
impulsively,
s)
in the case of a fit based on 2 (squares) or 3 (crosses)
maxima in the corresponding time signature (middle panel of
Fig. 3).
In Figs. 6-8, points
corresponding to impulsive excitation are plotted in green. They are
shown for comparison purposes.
We clearly see that for a low amplitude driver, the wave period of the
oscillations is close to the wave period of the oscillation excited
impulsively, ![]() ,
because only the first peak of the driver is significant enough to
excite oscillations. For a larger driver amplitude, the wave period of
the oscillations tends toward the wave period of the driver (
,
because only the first peak of the driver is significant enough to
excite oscillations. For a larger driver amplitude, the wave period of
the oscillations tends toward the wave period of the driver (
![]() s). Up to
s). Up to ![]() ,
the trends based on 2 and 3 maxima fits in
,
the trends based on 2 and 3 maxima fits in ![]() are consistent. However, for larger amplitudes they exhibit the
converse behavior, because a stronger pulse produces a higher shift of
the loop apex and the entire loop is more stretched so that its length
changes significantly. As a consequence of that, the distance
between the loop and the driver increases resulting in a decrease in
the observed wave frequency (increase in wave period)
between the first and the second maxima in time signatures.
In this way, we observe the influence of the Doppler effect. Because
the loop is shifted mainly between the 1st and the
2nd maximum, the Doppler effect influence is visible mainly
for the fit with 2 maxima (squares).
We estimated analytically the change in observed period,
are consistent. However, for larger amplitudes they exhibit the
converse behavior, because a stronger pulse produces a higher shift of
the loop apex and the entire loop is more stretched so that its length
changes significantly. As a consequence of that, the distance
between the loop and the driver increases resulting in a decrease in
the observed wave frequency (increase in wave period)
between the first and the second maxima in time signatures.
In this way, we observe the influence of the Doppler effect. Because
the loop is shifted mainly between the 1st and the
2nd maximum, the Doppler effect influence is visible mainly
for the fit with 2 maxima (squares).
We estimated analytically the change in observed period, ![]() ,
caused by the Doppler effect
,
caused by the Doppler effect
where
As shown by Selwa et al. (2007a), a major
attenuation mechanism of vertical kink oscillations in a 2D ideal MHD
model is energy leakage.
It was found that energy leakage causes attenuation to increase for
longer period oscillations.
Since the excitation mechanism does not change the properties of the
plasma, we expect that the attenuation mechanism should be the same for
both impulsive and oscillatory excitation.
Indeed, the middle and bottom panels of Fig. 6 show the
attenuation time measured in units of wave period, ![]() ,
versus the relative amplitude of the driver,
,
versus the relative amplitude of the driver, ![]() ,
and versus wave period, P.
It is clear that the normalized attenuation time,
,
and versus wave period, P.
It is clear that the normalized attenuation time, ![]() ,
falls off for longer period oscillations. This agrees with the findings
of Selwa et al. (2007a) for the energy leakage mechanism
(compare with the top panel of their Fig. 8). We plot only
crosses in this panel to avoid the results being too strongly affected
by the Doppler effect. Note the high
,
falls off for longer period oscillations. This agrees with the findings
of Selwa et al. (2007a) for the energy leakage mechanism
(compare with the top panel of their Fig. 8). We plot only
crosses in this panel to avoid the results being too strongly affected
by the Doppler effect. Note the high ![]() values reached for large
values reached for large ![]() .
.
![\begin{figure}
\par\includegraphics[scale=0.4, angle=0]{12603f6a.eps}\par\includ...
...ar\includegraphics[scale=0.4, angle=0]{12603f6c.eps}
\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/04/aa12603-09/Timg103.png)
|
Figure 6:
Wave period, P, ( top panel) and
the ratio of attenuation time |
| Open with DEXTER | |
Next we hold the amplitude and attenuation time of the driver fixed: ![]() ,
,
![]() s, and vary its
period
s, and vary its
period ![]() .
Figure 7
displays the wave period P and attenuation ratio
.
Figure 7
displays the wave period P and attenuation ratio ![]() of the oscillations versus the period of the oscillator.
For this value of
of the oscillations versus the period of the oscillator.
For this value of ![]() ,
we expect the oscillatory driver to behave like a single, long-lasting
pulse that is almost independent of
,
we expect the oscillatory driver to behave like a single, long-lasting
pulse that is almost independent of ![]() except at the shortest periods
(e.g., red and yellow curves in Fig. 2).
From the top panel of Fig. 7, we see
that a short-period strongly attenuated driver excites oscillations
with wave periods
close to the value obtained by an impulsive excitation (green). As
the period of the oscillator increases, we observe a small change
(decreasing trend) in the periods of the oscillations (<
except at the shortest periods
(e.g., red and yellow curves in Fig. 2).
From the top panel of Fig. 7, we see
that a short-period strongly attenuated driver excites oscillations
with wave periods
close to the value obtained by an impulsive excitation (green). As
the period of the oscillator increases, we observe a small change
(decreasing trend) in the periods of the oscillations (<![]() ).
If
).
If ![]() ,
then the driver acts like a real oscillator (note the high
,
then the driver acts like a real oscillator (note the high ![]() value in the bottom panel of Fig. 7 for small
value in the bottom panel of Fig. 7 for small ![]() ). However,
as
). However,
as ![]() increases we indeed find a long-lasting single pulse and
increases we indeed find a long-lasting single pulse and ![]() drops to the value expected for a pulse excitation. Note that the
driver periods were chosen to be close to a fraction or a multiple of
the loop's eigenperiod. Drivers with periods that do not fulfill this
criterion (e.g. 300 s) do not excite an eigenmode and give
rise to extremely strongly damped oscillations.
drops to the value expected for a pulse excitation. Note that the
driver periods were chosen to be close to a fraction or a multiple of
the loop's eigenperiod. Drivers with periods that do not fulfill this
criterion (e.g. 300 s) do not excite an eigenmode and give
rise to extremely strongly damped oscillations.
![\begin{figure}
\par\includegraphics[scale=0.4, angle=0]{12603f7a.eps}\par\includegraphics[scale=0.4, angle=0]{12603f7b.eps}
\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/04/aa12603-09/Timg106.png)
|
Figure 7:
Wave period, P, ( top panel) and
the ratio of attenuation time |
| Open with DEXTER | |
Next we vary the attenuation time of the oscillator with its amplitude
(
![]() )
and period (
)
and period (
![]() s) fixed.
The top panel of Fig. 8
shows yet again
that the strongly attenuated oscillator (
s) fixed.
The top panel of Fig. 8
shows yet again
that the strongly attenuated oscillator (
![]() )
acts like a single pulse and both the wave period of the excited
oscillation and its attenuation time tend to the values for an
impulsive excitation (green color).
For higher values of the attenuation time of the oscillator (less
attenuated driver), the wave period of the excited oscillation tends to
the period of the driver,
)
acts like a single pulse and both the wave period of the excited
oscillation and its attenuation time tend to the values for an
impulsive excitation (green color).
For higher values of the attenuation time of the oscillator (less
attenuated driver), the wave period of the excited oscillation tends to
the period of the driver, ![]() .
The middle panel of Fig. 8
shows
that the oscillations are less attenuated for a less attenuated driver.
The steady increase in
.
The middle panel of Fig. 8
shows
that the oscillations are less attenuated for a less attenuated driver.
The steady increase in ![]() with
with ![]() is particulary striking.
The bottom panel of Fig. 8
shows a similar trend as the bottom panel of Fig. 6, which again
agrees with the findings of Selwa et al. (2007a,
their Fig. 8) that energy leakage is a viable attenuation
mechanism for vertical kink oscillations.
is particulary striking.
The bottom panel of Fig. 8
shows a similar trend as the bottom panel of Fig. 6, which again
agrees with the findings of Selwa et al. (2007a,
their Fig. 8) that energy leakage is a viable attenuation
mechanism for vertical kink oscillations.
![\begin{figure}
\par\includegraphics[scale=0.4, angle=0]{12603f8a.eps}\par\includ...
...ar\includegraphics[scale=0.4, angle=0]{12603f8c.eps}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/04/aa12603-09/Timg108.png)
|
Figure 8:
Wave period, P, ( top panel) and
the ratio of attenuation time |
| Open with DEXTER | |
4 Summary
We have carried out the first study of vertical kink oscillations in a 2D curved loop excited by an oscillatory driver outside the loop. This driver could model a shock with a wave train behind it excited by a flare. Our numerical results show that the oscillations excited by the attenuated periodic driver are in general less attenuated than those excited by a pulse. The ratio ofTypically, an external oscillatory driver with a given frequency in an active region will be able to excite transverse oscillations only in a small subset of loops, namely those whose eigenfrequencies are close to the frequency of the driver. This can explain why only very few loops of an active region are excited to oscillate transversally after an energetic event such as a flare. An impulsive driver, which harbours a very wide range of frequencies, should excite a much larger fraction of all loops.
We also showed that a rapidly damped oscillator acts like a single pulse. By varying the period of the driver it is possible to excite oscillations that resemble a fundamental vertical kink mode, but which are just a very strongly attenuated simple response of the loop to a periodic driver. In addition, our results are consistent with the findings of Selwa et al. (2007a) that vertical kink oscillations are attenuated because of energy leakage.
In this study, we did not change the properties of the loop,
such as the spectrum of eigenfrequencies, ![]() ,
by switching between
impulsive excitation and the excitation by the damped oscillatory
driver. However, the observed change in decay rates (and periods)
can be explained in terms of changing the convolution
,
by switching between
impulsive excitation and the excitation by the damped oscillatory
driver. However, the observed change in decay rates (and periods)
can be explained in terms of changing the convolution ![]() ,
where
,
where ![]() is the response function of the
loop for the excitation mechanism. Although the oscillator is
characterized by a single wave-period
is the response function of the
loop for the excitation mechanism. Although the oscillator is
characterized by a single wave-period ![]() ,
it corresponds to
a more complex Fourier spectrum. This is partly related to the decay of
its amplitude with time and also its spatial structure. So,
the oscillator launches a continuous spectrum of
wave-periods centered around
,
it corresponds to
a more complex Fourier spectrum. This is partly related to the decay of
its amplitude with time and also its spatial structure. So,
the oscillator launches a continuous spectrum of
wave-periods centered around ![]() .
If
.
If ![]() fits
the eigenperiod of the loop,
fits
the eigenperiod of the loop, ![]() ,
then the excited
oscillations will be magnified by the oscillator. On the other hand,
in the case of a mismatch between
,
then the excited
oscillations will be magnified by the oscillator. On the other hand,
in the case of a mismatch between ![]() and
and ![]() ,
loop oscillations
receive signals from waves produced because the oscillator is out
of phase (at unsuitable moments of time). As a result, loop
oscillations
are incoherent to the oscillator and the loop exhibits more complex
oscillations, which are more attenuated.
,
loop oscillations
receive signals from waves produced because the oscillator is out
of phase (at unsuitable moments of time). As a result, loop
oscillations
are incoherent to the oscillator and the loop exhibits more complex
oscillations, which are more attenuated.
In the applied model, we have neglected several important factors such as the three-dimensional geometries of loops and the flare site, radiative losses, and gravitational stratification. A 2D model is more apropriate to the excitation of vertical oscillations than other transverse oscillation modes, since the source of the initial pulse must be located in or near the loop plane. However, the absence of the third dimension may result in higher leakage, especially with initial top-hat loop density profile becoming diffused with time, and smooth loop edges being another factor that increases the leakage.
One possible extension of our model is to study more realistic
drivers such as with random parameters (![]() or
or ![]() ).
A possible way of reducing the offset is to replace the pressure driver
by a vertical (or perpendicular to the loop) velocity driver, which,
according to Gruszecki et al. (2008, private
communication), results in a lower offset because it is not associated
with an internal energy (slow waves).
).
A possible way of reducing the offset is to replace the pressure driver
by a vertical (or perpendicular to the loop) velocity driver, which,
according to Gruszecki et al. (2008, private
communication), results in a lower offset because it is not associated
with an internal energy (slow waves).
M.S. thanks Dr. Tongjiang Wang for his comments. The magnetohydrodynamics code used in this study was developed at Princeton University by Tom Gardiner, Jim Stone, Peter Teuben and John Hawley with support of the NSF Information Technology Research (ITR) program. M.S.'s & L.O.'s work was financially supported by the NASA SEC Theory program and NASA grant NNG06GI55G. K.M.'s work was supported by a grant from the State Committee for Scientific Research Republic of Poland, with MNiN grant for years 2007-2010. S.K.S.'s work has been partially supported by the WCU grant No. R31-10016 funded by the Korean Ministry of Education, Science and Technology.
References
- Aschwanden, M., Fletcher, L., Schrijver, C., et al. 1999, ApJ, 520, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M., Nakariakov, V., & Melnikov, V. F. 2004, ApJ, 600, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Ballai, I., Douglas, M., & Marcu, A. 2008, A&A, 488, 1125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brady, C. S., & Arber, T. D. 2005, A&A, 438, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Moortel, I., Ireland, J., Walsh, R. W., et al. 2002, Sol. Phys., 209, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Edwin, P. M., & Roberts, B. 1982, Sol. Phys., 76, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Gardiner, T. A., & Stone, J. M. 2005, J. Comput. Phys., 205, 509 [Google Scholar]
- Gruszecki, M., Murawski, K., Selwa, M., et al. 2006, A&A, 460, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gruszecki, M., Murawski, K., & McLaughlin, J. 2008, A&A, 489, 413 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Handy, B. N., Tarbell, T. D., Wolfson, C. J., Korendyke, C. M., & Vourlidas, A. 1999, Sol. Phys., 190, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Murawski, K., & Goossens, M. 1994, A&A, 286, 952 [NASA ADS] [Google Scholar]
- Nakariakov, V., & Melnikov, V. 2009, Space Sci. Rev., DOI: 10.1007/S11214-009-9536-3 [Google Scholar]
- Nakariakov, V. M., Ofman, L., Deluca, E. E., Roberts, B., & Davila, J. M. 1999, Science, 285, 5429, 862 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nakariakov, V. M., Melnikov, V. F., & Reznikova, V. E. 2003, A&A, 412, 7 [Google Scholar]
- Nakariakov, V. M., Foullon, C., Verwichte, E. & Young, N. P. 2006, A&A, 452, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ofman, L., & Wang, T. J. 2002, ApJ, 580, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., & Sui, L. 2006, ApJ, 644, L1490 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L. 2009, Sp. Sci. Rev., 149, 153 [Google Scholar]
- Roberts, B., Edwin, P. M., & Benz, A. O. 1984, ApJ, 279, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., Goossens, M., Ballester, J. L., et al. 1997, A&A, 328, 361 [NASA ADS] [Google Scholar]
- Schrijver, C. J., Aschwanden, M. J., & Title, A. M. 2002, Sol. Phys., 206, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Selwa, M., Murawski, K., Solanki, S. K., Wang, T. J., & Tóth, G. 2005, A&A, 440, 385 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Selwa, M., Solanki, S. K., Murawski, K., Wang, T. J., & Shumlak, U. 2006, A&A, 454, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Selwa, M., Murawski, K., Solanki, S. K., et al. 2007a, A&A, 462, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Selwa, M., Ofman, L., & Murawski, K. 2007b, ApJ, 668, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. M., Roberts, B., & Oliver, R. 1997, A&A, 317, 752 [NASA ADS] [Google Scholar]
- Taroyan, Y., Erdélyi, R., Doyle, J. G., et al. 2005, A&A 438, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tirry, W. J., & Poedts, S. 1998, A&A, 329, 754 [NASA ADS] [Google Scholar]
- Ugarte-Urra, I., Warren, H. P., & Brooks, D. H. 2009, ApJ, 695, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T. J., Solanki, S. K., Curdt, W., Innes, D. E., & Dammash, I. E. 2002, ApJ, 574, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T. J., Solanki, S. K., Curdt, W., et al. 2003a, A&A, 406, 1105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, T. J., Solanki, S. K., Innes, D. E., Curdt, W., & Marsch, E. 2003b, A&A, 402, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, T. J., & Solanki, S. K. 2004, A&A, 421, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, T. J., Solanki, S. K., Innes, D. E., et al. 2005, A&A, 435, 753 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, T. J., Solanki, S. K., & Selwa, M. 2008, A&A, 489, 1307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilhelm, K., Curdt, W., Marsch, E., et al. 1995, Sol. Phys., 162, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Zaqarashvili, T. V., Oliver, R., & Ballester, J. L. 2005, A&A, 433, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Footnotes
- ...
![[*]](/icons/foot_motif.png)
- Present address: School of Mathematics and Statistics, University of St Andrews, North Haugh, St Andrews, Fife, KY16 9SS, UK
- ...
![[*]](/icons/foot_motif.png)
- Calculated to be the area beneath the curve within the time interval 0< t < 200 s.
All Tables
Table 1: Equilibrium and normalization parameters for the potential arcade and the loop.
Table 2:
Impulse over unit area![]() equivalent to the oscillator with parameters
equivalent to the oscillator with parameters
![]() ,
,
![]() s.
s.
All Figures
![\begin{figure}
\par\includegraphics[scale=0.525, angle=0,clip]{12603fg1.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa12603-09/Timg62.png)
|
Figure 1: Initial mass density profile. Note the logarithmic scale on the vertical axis. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.45, angle=0,clip]{12603fg2.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa12603-09/Timg74.png)
|
Figure 2:
Several time signatures of an oscillator with
wave period |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.45, angle=0]{12603f3a.eps}\par\inclu...
...par\includegraphics[scale=0.45, angle=0]{12603f3c.eps}\vspace{-3mm}
\end{figure}](/articles/aa/full_html/2010/04/aa12603-09/Timg78.png)
|
Figure 3:
Time-signatures of the mass density
(color scale; units of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.45, angle=0]{12603f4a.eps}\par\includegraphics[scale=0.45, angle=0]{12603f4b.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa12603-09/Timg79.png)
|
Figure 4:
Difference images of the loop in the case of oscillatory excitation (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.45, angle=0,clip]{12603fg5.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa12603-09/Timg84.png)
|
Figure 5:
Offset of the loop's apex (measured in units of L)
versus amplitude of the oscillator with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.4, angle=0]{12603f6a.eps}\par\includ...
...ar\includegraphics[scale=0.4, angle=0]{12603f6c.eps}
\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/04/aa12603-09/Timg103.png)
|
Figure 6:
Wave period, P, ( top panel) and
the ratio of attenuation time |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.4, angle=0]{12603f7a.eps}\par\includegraphics[scale=0.4, angle=0]{12603f7b.eps}
\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/04/aa12603-09/Timg106.png)
|
Figure 7:
Wave period, P, ( top panel) and
the ratio of attenuation time |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.4, angle=0]{12603f8a.eps}\par\includ...
...ar\includegraphics[scale=0.4, angle=0]{12603f8c.eps}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/04/aa12603-09/Timg108.png)
|
Figure 8:
Wave period, P, ( top panel) and
the ratio of attenuation time |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



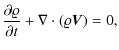
![$\displaystyle \frac{\partial E}{\partial t} + \nabla \cdot\left[\left( E + p + ...
...mu}\right)
{\vec V}- \frac{{\vec B} {\vec B} \cdot {\vec V}}{\mu}\right] = 0\;,$](/articles/aa/full_html/2010/04/aa12603-09/img16.png)

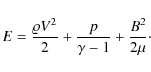
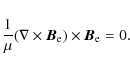
![\begin{displaymath}
\varrho_{\rm0}(z)=\varrho_{\rm e}\left\{1+\frac{d_{\rm ph}-1...
...1-\tanh\left( \frac{z}{s_{\rm ph}}\right) \right]\right\}\cdot
\end{displaymath}](/articles/aa/full_html/2010/04/aa12603-09/img59.png)