| Issue |
A&A
Volume 512, March-April 2010
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 18 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200811486 | |
| Published online | 18 March 2010 | |
Diagnostics of energetic electrons with anisotropic distributions in solar flares
I. Hard X-rays bremsstrahlung emission
V. V. Zharkova1 - A. A. Kuznetsov2 - T. V. Siversky1
1 - Department of Computing and Mathematics,
University of Bradford,
Bradford BD7 1DP, UK
2 -
Institute of Solar-Terrestrial Physics,
Irkutsk, Lermontov str. 126a, 664033, Russia
Received 8 December 2008 / Accepted 12 November 2009
Abstract
Aims. The paper aims are to simulate steady-state
distributions of electrons beams precipitating in collisional and Ohmic
losses with pitch angle anisotropy into a flaring atmosphere with
converging magnetic field and to apply these to the interpretation of
HXR photon spectra, directivity and polarization observed for different
photon energies and flare positions on the solar disk.
Methods. Summary approximation method is applied to a
time-dependent Fokker-Planck equation by splitting the temporal
derivative equally between the derivatives in depth, energy and pitch
angles and finding the solutions in forward and backward directions for
each variable.
Results. For softer beams, there is a noticeable flattening of
the photon spectra at lower energies caused by the self-induced
electric field that increases for larger viewing angles. For the models
with an electric field, the HXR emission with lower energies
(30 keV) becomes directed mainly upwards at upper atmospheric
levels owing to the increased number of particles moving upwards, while
in deeper layers it again becomes directed downwards. The polarization
maximum shifts to higher energies with every precipitation depth
approaching 25 keV for the models with pure collisions and
100 keV for the models with return currents. At deeper layers, the
polarization decreases because of the isotropization of electrons by
collisions. The maximum polarization is observed at the viewing angle
of
![]() ,
becoming shifted to lower angles for softer beams. The integrated
polarization and directivity shows a dependence on a magnetic field
convergence for harder beams, while for softer beams the directivity is
strongly affected by the self-induced electric field changing from a
downward motion to an upward one at upper atmospheric depths.
,
becoming shifted to lower angles for softer beams. The integrated
polarization and directivity shows a dependence on a magnetic field
convergence for harder beams, while for softer beams the directivity is
strongly affected by the self-induced electric field changing from a
downward motion to an upward one at upper atmospheric depths.
Conclusions. The proposed precipitation model for an electron
beam with wider pitch angle dispersion of 0.2 taking into account
collisional and Ohmic losses allowed us to fit the double power law HXR
photon spectra with a spectrum flattening at lower energies observed in
the flares of 20 and 23 July 2002. The observed directivity of HXR
photons of 20 keV derived for a large number of flares located
from the disk center to limb is also reproduced well by the theoretical
directivity calculated for an electron beam with a very narrow pitch
angle dispersion of 0.02. The simulated polarization of this
narrowly-directed electron beam fits up to 90![]() of all the available polarimetric observations carried out at various locations across the solar disk.
of all the available polarimetric observations carried out at various locations across the solar disk.
Key words: Sun: flares - Sun: X-rays, gamma rays
1 Introduction
RHESSI observations have allowed us to enhance in the quantitative interpretation of hard X-ray emission (Lin et al. 2003; Holman et al. 2010; Brown et al. 2006; Holman et al. 2003; Krucker et al. 2008) by providing not only light curves but the locations and shapes of hard X-ray sources on the solar disk, in addition to photon and electron spectra and their evolution during a flare. The observations show that flare events sometimes comprise one loop with two footpoints and one coronal source (Sui et al. 2002; Masuda et al. 1994) or several sets of loops with a number of footpoints and coronal sources (Battaglia & Benz 2006; Krucker et al. 2008). The analyses of observations of solar flares by TRACE and RHESSI found that the areas of flaring loops decrease and, thus, their magnetic fields increase with depth of the solar atmosphere (Kontar et al. 2008).A very close temporal correlation is detected between the lightcurves across the full electromagnetic range: HXR, microwave (MW), ultraviolet (UV), and optical emission assuming some common agents which deliver the energy to different atmospheric levels within a timescale shorter than 1 s (see for example, Holman et al. 2010; White et al. 2010; Fletcher et al. 2010). Although the spatial configurations of flaring sites in HXR and MW emission are not always similar, furthermore, they are very different in optical emission. Assuming that the HXR and MW emission is caused by the same population of electrons, these spatial differences may be indicative of different transport scenarios for high-energy particles precipitating into loop footpoints and different shapes of the flaring atmospheres where this emission occur (Bastian et al. 1998; Vilmer et al. 2002; Kundu et al. 2001a,2004; Willson & Holman 2003; Aschwanden 2005; Kundu et al. 2001b).
The mechanisms of transport affecting the HXR and MW emission substantially differ: MW radiation is related to gyro-synchrotron emission of high-energy electrons with energies from few tens keV (Kundu et al. 2001a,b) up to several MeV (Kundu et al. 2004; Bastian 1999), while HXR radiation is often produced by electrons of much lower energy from 10 to 300 keV (see for example, Lin et al. 2003; Holman et al. 2003). Although, occasionally, the accelerated electrons can reach energies of a few hundred MeV as observed for the flare of 28 October 2003 (Kuznetsov et al. 2006).
It is now well accepted that the agents delivering the energy required to account for the observed features in HXR, MW, and other emission are sub-relativistic charged particles (beams of electrons (Brown 1971; Brown et al. 2006), possibly, mixed with protons (Simnett 1995) accelerated somewhere in the corona. These particle precipitate downwards to the lower solar atmosphere, while depositing their energy into the ambient plasma. Obviously, the diagnostics of this precipitation from different types of emission can provide a valuable insight into the complicated processes, in which these particles deposit their energy at various depths of flaring loops. The variety of observations has led to the development of different models of particle acceleration and transport for different types of flaring events (see the reviews by Zharkova et al. 2010; Holman et al. 2010, in the forthcoming RHESSI book), which can account for the observed patterns in high energy emission.
These include double power-law elbow-type spectra of HXR photon emission deduced with the RHESSI payload from powerful flares with flattening towards lower energies (Holman et al. 2003), confirming earlier findings by the SMM observations (Brown & Loran 1985; Benz 1977) and the soft-hard-soft temporal profile of photon spectral indices below the energy of 35 keV (Grigis & Benz 2004) during the duration of the same flare. The spectral flattening at lower photon energies was first interpreted by an increase of the lower cutoff energy of beam electrons (Sui et al. 2005) that was later overturned by Sui et al. (2007) in favor of the Ohmic losses caused by the self-induced electric field of precipitating electrons (Zharkova & Gordovskyy 2006). In this case, the beam electrons producing HXR emission have different initial energy fluxes and, thus, different Ohmic losses: the higher the flux the greater the losses leading to larger spectral flattening in photon spectrum at lower energies (Zharkova & Gordovskyy 2006). Because of these dependences, the soft-hard-soft patterns in the temporal profile of HXR photon spectra (Krucker et al. 2008) can be easily reproduced by a triangle temporal profile (low-high-low) of the beam energy flux during flaring events (Zharkova & Gordovskyy 2006).
Another pattern that can be derived from observed MW and HXR emission is related to pitch-angle distributions of the beam electrons producing this emission and to the locations of flares on the solar disk. This pitch angle anisotropy of precipitating particles can be detected by polarimetric observations in flares located between close to the solar center and the limb. These observations are rather scattered since they were carried out over many years in different energy bands: e.g., 15 keV in the early rocket observations by Tindo et al. (1972b,1970,1972a), 16-21 keV later by Tramiel et al. (1984), 100-350 keV in the RHESSI observations Suarez-Garcia et al. (2006), and at 200-400 keV in the ACT observations by Boggs et al. (2006).
The polarimetric observations are indicative of the high variability of the HXR polarization degrees in different events: from a few percent (Tramiel et al. 1984) up to 40% (Suarez-Garcia et al. 2006; Tindo et al. 1976), or even above 50% as observed for the flare of 23 July 2002 (McConnell et al. 2003) or 75% as observed by the CORONAS payload (Zhitnik et al. 2006). The bulk of observations also detect a noticeable increase of the HXR polarization and directivity in flares located closer to the limb, although some deviations from this trend have been recently observed by RHESSI (Suarez-Garcia et al. 2006). The similar increase in the HXR directivity at 20-150 keV in flares located towards the limb is reported by Kasparová et al. (2007).
The theory describing generation of bremsstrahlung hard X-ray emission has significantly progressed due to improvements in the mechanisms for emitting this radiation: from pure Coulomb collisions (Brown 1971; Brown et al. 2006; Kontar & Brown 2006) to collisions and converging magnetic fields (McClements 1992; Leach & Petrosian 1981), or to combined collisional and Ohmic energy losses in the electric field induced by precipitating electrons (Zharkova et al. 1995; Zharkova & Gordovskyy 2005,2006). Further progress was achieved by considering relativistic bremsstrahlung cross-sections (Kontar et al. 2006) and taking into account various aspects of the photospheric albedo effects, while deriving mean electron spectra from the observed bremsstrahlung photon spectra (Kontar et al. 2006).
However, in spite of a large number of simulations for interpreting HXR or MW emission (see for example, reviews by Holman et al. 2010; White et al. 2010; Krucker et al. 2008, and references therein), no simultaneous simulations have been developed yet that account for these two types of emission with the same distributions of electrons. If one assumes that HXR and MW emissions are generated by different energy loss mechanisms of the same beam electrons, a rather challenging task is to account for the temporal variations of their depth distributions and the total areas of a given intensity covered in each precipitation site. This imposes strict limitations on the proposed models of electron precipitation that require us to correctly account for electron energy losses, such as Coulomb collisions, Ohmic losses and anisotropic scattering and changes in the electron pitch angles caused by a magnetic field that converges with depth.
The motivation of the present paper is to simulate electron distributions during their precipitation into a flaring atmosphere by taking into account all possible energy losses, and to produce HXR spectra and polarization matching those inferred from observations. This paper deals with the precipitation mechanisms of electrons with a wide range of energies from 10 keV to 1.2 MeV and their effect on HXR emission and polarization. This approach significantly extends the steady solutions for electron distribution functions found by Zharkova & Gordovskyy (2005), considering a magnetic field convergence, in addition to self-induced electric field, to much higher energies of electrons: from 384 keV to 1.2 MeV, required to account correctly for a magnetic mirroring, and to the inclusion of a pitch-angle diffusion term, in order to account for the particle and photon anisotropy, similar to the approach by Zharkova et al. (1995). In addition, in contrast to the angle-independent cross-section (averaged over all pitch angles) used by Zharkova & Gordovskyy (2005), the simulations of HXR bremsstrahlung emission are performed by using the relativistic angle-dependent photon cross-sections that are similar to those of Bai & Ramaty (1978).
The kinetic problem of precipitation of high-energy electrons from the source within the corona into a converging coronal loop with pitch-angle diffusion and energy losses in the induced electric field is described in Sect. 2. The depth, energy and pitch-angular variations in electron distribution functions of the injected and returning beams, resulting hard X-ray photon spectra and their polarization are discussed in Sect. 3 with conclusions being drawn in Sect. 4.
2 Electron precipitation: Fokker-Planck approach
2.1 The basic equations
We consider the time-dependent Fokker-Planck approach to the precipitation of high-energy electrons injected into a cold hydrogen plasma confined in a converging magnetic field structure. However, since high-density electron beams precipitating into a flaring atmosphere are expected to be rather dense, so they can carry a strong electric field. This electric field forms a return current from both the ambient plasma (van den Oord 1990; Knight & Sturrock 1977) and precipitating electrons returning to the source in the corona (Zharkova et al. 1995; Emslie 1980). Therefore, to accurately consider the beam electron kinetics during precipitation, one needs to include this induced electric field because it increases pitch-angle anisotropy of precipitating beam electrons as described by McClements (1992); Diakonov & Somov (1988); Zharkova & Gordovskyy (2005) and Siversky & Zharkova (2009).
Thus, one needs to solve simultaneously the kinetic Fokker-Planck equation for beam electron precipitation and Ohm's law for the electric field carried by the beams themselves at every depth. In the kinetic equation, we neglect the interaction of beam electrons with waves occurring in the ambient plasma since the energy exchange between electrons and plasma waves does not significantly affect the energy balance of fast electrons (Benz 2002; Aschwanden 2005). In the equation for the electric field we assume that the electric field induced by beam electrons is fully compensated by the electrons of the ambient plasma.
The Fokker-Planck, or Landau, equation, which describes the variations of distribution function f of beam electron, can be written in the form (Landau 1937; Siversky & Zharkova 2009)
where E and
2.1.1 The initial and boundary conditions
We assume that there are no beam electrons inside the atmosphere at the moment of injection, e.g.,
![]() .
.
The distribution function on the top boundary where
![]() is defined by the formula
is defined by the formula
which assumes the power-law energy distribution in the energy range from
Let us consider an electron beam injected with a power-law
dependence in energy and a narrow normal distribution in pitch angle with the angle dispersion (
![]() )
centered on
)
centered on ![]() (or
(or ![]() ). The coefficient A is inferred from the normalization condition for a
distribution function on a beam density on the top boundary (Siversky & Zharkova 2009). The additional index of 0.5 is added to index
). The coefficient A is inferred from the normalization condition for a
distribution function on a beam density on the top boundary (Siversky & Zharkova 2009). The additional index of 0.5 is added to index ![]() in the the energy dependence, in order to account for the spectral index
in the the energy dependence, in order to account for the spectral index ![]() being referred to the electron flux (
being referred to the electron flux (![]() vf = E0.5f) and not to the electron density, by which f is normalized. U(t) defines a temporal profile of the electron beam injection, which denotes the initial beam flux variations
during a required time interval, accepted in our simulations to be equal to
unity (a steady injection). The boundary conditions are the same as those described by Siversky & Zharkova (2009).
vf = E0.5f) and not to the electron density, by which f is normalized. U(t) defines a temporal profile of the electron beam injection, which denotes the initial beam flux variations
during a required time interval, accepted in our simulations to be equal to
unity (a steady injection). The boundary conditions are the same as those described by Siversky & Zharkova (2009).
2.1.2 Energy losses
The Fokker-Planck equation presented here in Eq. (1) takes into account the energy loss factors such as:- 1.
- particle collisions and anisotropic pitch angle scattering (the term
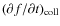 );
);
- 2.
- return current (caused by the self-induced electric field
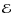 );
);
- 3.
- inhomogeneity (convergence) of a magnetic field (the term
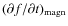 ).
).
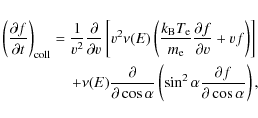
where
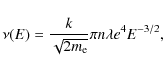
where
The magnetic field convergence is considered in the following form (McClements 1992)

where B(z) is the magnetic field at a given depth z.
Instead of the physical coordinate z, it is convenient to express the distance
passed by particles in terms of the column density ![]() ,
e.g.,
,
e.g.,
![]() .
A magnetic field convergence B can be then described by the hybrid model from Siversky & Zharkova (2009)
.
A magnetic field convergence B can be then described by the hybrid model from Siversky & Zharkova (2009)
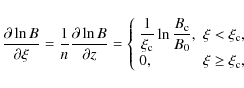
|
(3) |
which defines the magnetic field to increase by the factor
2.1.3 Self-induced electric field
The electric current carried by beam electrons can be determined as
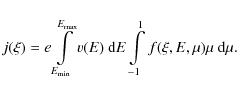
At each precipitation depths this electric field causes preferential scattering of beam electrons towards negative
Therefore, the electric field carried by the beams themselves at every
depth, which is used in the Fokker-Plank equation (Eq. (1)) can be written as follows
where
where X is the ionization degree.
2.1.4 Method of solution and accepted parameters
The set of Eqs. (1) and (4)
define the electron beam precipitation into a flaring atmosphere.
Unlike the stationary solutions found by Zharkova & Gordovskyy
(2005) (e.g., excluding the time derivative), we solve the full
time-dependent Fokker-Planck (FP) equation above. In the solution we
also include the term with pitch angle diffusion (a second derivative
by ![]() )
and magnetic field
convergence and yet exclude the diffusion in energy (the first term in the
collisional integral). For the FP solutions, we use the summary approximation
method (Samarskii 2001) by applying the iteration method by dividing the temporal
difference evenly between three other variables (depth, energy and pitch angles);
this method already has proven to give reliable time-dependent solutions for both
short impulses and steady injection (Zharkova et al. 1995; Siversky & Zharkova 2009).
)
and magnetic field
convergence and yet exclude the diffusion in energy (the first term in the
collisional integral). For the FP solutions, we use the summary approximation
method (Samarskii 2001) by applying the iteration method by dividing the temporal
difference evenly between three other variables (depth, energy and pitch angles);
this method already has proven to give reliable time-dependent solutions for both
short impulses and steady injection (Zharkova et al. 1995; Siversky & Zharkova 2009).
The converging magnetic field acts as a magnetic mirror that can
increase the number of electrons moving upwards. We determine the
magnetic convergence parameter,
![]() by selecting a characteristic column depth that defines the scale of
the magnetic field change in the selected flaring atmospheres. By
comparing the 4 models currently considered in the literature (Siversky & Zharkova 2009), in the current paper, we adopt the convergence model with a scale column depth of
by selecting a characteristic column depth that defines the scale of
the magnetic field change in the selected flaring atmospheres. By
comparing the 4 models currently considered in the literature (Siversky & Zharkova 2009), in the current paper, we adopt the convergence model with a scale column depth of
![]() cm-2 which closely corresponds to values deduced from observations (Kontar et al. 2008).
cm-2 which closely corresponds to values deduced from observations (Kontar et al. 2008).
In the current paper we consider relatively long beam injection times
of a few seconds, and, therefore, seek the solutions of the
quasi-stationary Eq. (1), i.e. those obtained for the time-dependent
equation after the time interval when the stationary injection is established
and fully compensated by returning electrons. This steady state is normally achieved for a beam with ![]() and an
initial energy flux F=1010 erg
cm-2
s-1 at about 0.07 s after the onset of beam injection (Siversky & Zharkova 2009).
and an
initial energy flux F=1010 erg
cm-2
s-1 at about 0.07 s after the onset of beam injection (Siversky & Zharkova 2009).
2.2 Hard X-ray bremsstrahlung emission and polarization
The parameters of X-ray emission from a homogeneous source in the solar corona (observed at the Earth) are determined by the equation (Leach & Petrosian 1983; Elwert & Haug 1970; Brown 1972)where I and Q are the Stokes parameters of bremsstrahlung radiation,
We assume that the X-ray source can be represented by a cylindrical magnetic tube in which
the magnetic field is aligned along the tube axis. All the parameters of the
plasma, magnetic field, and accelerated particles depend only on the coordinate
z along the tube. In this case, the total (integrated over all layers of
the source) emission is determined by the equation
where S is the cross-section area of a fluxtube. In a converging magnetic field, the cross-sectional area varies (due to the conservation of the magnetic flux) as
The degree of the linear polarization of the emission is defined by
and the angular distribution of the emission can be characterized by the so-called directivity parameter (Leach & Petrosian 1983; Brown 1972)
where
3 Results and discussion
3.1 Dynamics of electron beams
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{11486Fig01a.eps}\hspace*{4...
...s}\hspace*{4mm}
\includegraphics[width=5.5cm,clip]{11486Fig01f.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg75.png)
|
Figure 1:
Electron distribution functions (in the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{11486Fig02a.eps}\hspace*{4...
...s}\hspace*{4mm}
\includegraphics[width=5.5cm,clip]{11486Fig02f.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg76.png)
|
Figure 2:
Electron distribution functions at the column depth of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{11486Fig03a.eps}\hspace*{4...
...s}\hspace*{4mm}
\includegraphics[width=5.5cm,clip]{11486Fig03f.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg77.png)
|
Figure 3:
Electron distribution functions at the column depth of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11486Fig04a.eps}\hspace*{4mm}
\includegraphics[width=8.5cm,clip]{11486Fig04b.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg78.png)
|
Figure 4:
Dependencies of the density of precipitating electrons on a
column density of the ambient plasma. Dotted line: downward propagating particles ( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{11486Fig05a.eps}\par\includ...
...par\includegraphics[width=17cm,clip]{11486Fig05f.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg79.png)
|
Figure 5:
Intensity (in relative units) and polarization of the hard X-ray
emission for the different energies. Initial power-law indices of the
accelerated particles are: |
| Open with DEXTER | |
In all calculations, anisotropic scattering is considered, i.e, a dependence
of electron distributions on the pitch angle at scattering. A few precipitation
models were used to investigate the combined effects of different energy
losses: a) C - only collisions with charged particles and neutrals, b) CE -
collisions and self-induced electric field, c) CB - collisions and converging
magnetic field, and d) CEB - collisions, a self-induced electric field, and a converging
magnetic field. In the simulations, we used the following parameters: initial
energy flux of the accelerated electrons F=1010 erg
![]()
![]() ,
electron energy range defined by
,
electron energy range defined by
![]() keV,
keV,
![]() keV, initial pitch-angle dispersion of the electrons
keV, initial pitch-angle dispersion of the electrons
![]() ,
and a
transition region boundary at
,
and a
transition region boundary at
![]()
![]() .
The initial
power-law index of the accelerated electrons was taken to be either
.
The initial
power-law index of the accelerated electrons was taken to be either ![]() or
or
![]() .
The convergence factor
.
The convergence factor
![]() was equal
to
was equal
to
![]() and the characteristic column depth to
and the characteristic column depth to
![]()
![]() (for details of the selection rule, see Siversky & Zharkova 2009).
(for details of the selection rule, see Siversky & Zharkova 2009).
Examples of the distribution functions of electron for a few column depths are
shown in Figs. 1-3: a) for the column density of
![]()
![]() (Fig. 1), b) for the column density
of
(Fig. 1), b) for the column density
of
![]()
![]() (Fig. 2), and c) for the column
density
(Fig. 2), and c) for the column
density
![]()
![]() (Fig. 3).
One can see that both the self-induced electric and the converging
magnetic fields produce a particle stream that propagates upwards, or
returns back to the coronal source, from which it is injected. This
stream significantly exceeds a random stream of particles scattered
isotropically and becomes comparable to the stream of the particles
propagating downwards, or precipitating particles.
(Fig. 3).
One can see that both the self-induced electric and the converging
magnetic fields produce a particle stream that propagates upwards, or
returns back to the coronal source, from which it is injected. This
stream significantly exceeds a random stream of particles scattered
isotropically and becomes comparable to the stream of the particles
propagating downwards, or precipitating particles.
The self-induced electric field of the beam produces a stream of returning beam electrons
(Figs. 1a and 1d) that
compensates for the charge of precipitating electrons from Eq. (4).
The self-induced electric field at all depths comprises an electric
field of precipitating electrons minus the electric field of the beam
electrons, which changed their propagation direction at the depths
above to the negative ![]() .
This electric field corresponds to one that is then compensated for by the ambient electrons known as a return current (van den Oord 1990).
We note that for electron beams with extended energy ranges up
to 1.2 MeV, the effect of a self-induced electric field
remains more important at upper atmospheric depths for beams with
softer energy spectra (compare the left graphs (a, d) in Figs. 1-3), confirming the conclusions of Zharkova & Gordovskyy (2005,2006). One can also see that
the self-induced electric field is able to accelerate the returning beam particles
to rather high energies (up to 50-100 keV), while their number drops to zero at higher energies.
.
This electric field corresponds to one that is then compensated for by the ambient electrons known as a return current (van den Oord 1990).
We note that for electron beams with extended energy ranges up
to 1.2 MeV, the effect of a self-induced electric field
remains more important at upper atmospheric depths for beams with
softer energy spectra (compare the left graphs (a, d) in Figs. 1-3), confirming the conclusions of Zharkova & Gordovskyy (2005,2006). One can also see that
the self-induced electric field is able to accelerate the returning beam particles
to rather high energies (up to 50-100 keV), while their number drops to zero at higher energies.
The distributions of returning electrons also depart from power laws
resembling quasi-thermal distributions. The variations in power-law index
![]() in the energy distributions of injected particles lead to a number of
precipitating electrons that decreases with energy much faster for
in the energy distributions of injected particles lead to a number of
precipitating electrons that decreases with energy much faster for ![]() than
for
than
for ![]() .
As a result, for
.
As a result, for ![]() ,
at some atmospheric depths (Fig. 1), the number of returning particles with energies
below 100 keV can even exceed the number of precipitating particles with the
same energies, which dramatically affects the properties of the X-ray emission,
as discussed in Sect. 3.2.
,
at some atmospheric depths (Fig. 1), the number of returning particles with energies
below 100 keV can even exceed the number of precipitating particles with the
same energies, which dramatically affects the properties of the X-ray emission,
as discussed in Sect. 3.2.
On the other hand, a converging magnetic field produces the well-known loss-cone distributions by reflecting the precipitating electrons being scattered to pitch angles within the loss-cone defined by the magnetic convergence factor (Figs. (1-3)b and (1-3)e). The energy spectrum of the returning particles (reflected by a converging magnetic field) does not differ significantly from the initial energy spectrum of precipitating particles. However, the effect of magnetic mirroring is more significant for higher energy electrons than other energy losses (collisions or Ohmic losses) (compare Figs. 3a, d and c, f with Fig. 1a, d and c, f, respectively). This is because energy losses depend inversely on the particle energies, thus becoming with depth (and energy loss) much smaller than the energy losses in magnetic mirroring (convergence). In real events (e.g., solar flares), all the energy loss factors operate simultaneously, producing the beam electron distributions in energy and pitch angles perhaps similar to those shown in Figs. (1-3)c and (1-3)f.
At depths of
![]()
![]() where the bulk of
electrons lose their energy, the magnetic field convergence and
collisions govern the remaining electron distributions (Fig. 2).
The electrons are distributed almost isotropically at all energies (due to
collisional scattering) and the converging magnetic field makes the isotropisation process faster. In deeper layers (Fig. 3),
the number of particles decreases rapidly with depth because of collisions. Since the
collisional losses are more significant for low-energy electrons, the
``humped'' distribution (with a maximum at about 100 keV) is formed.
where the bulk of
electrons lose their energy, the magnetic field convergence and
collisions govern the remaining electron distributions (Fig. 2).
The electrons are distributed almost isotropically at all energies (due to
collisional scattering) and the converging magnetic field makes the isotropisation process faster. In deeper layers (Fig. 3),
the number of particles decreases rapidly with depth because of collisions. Since the
collisional losses are more significant for low-energy electrons, the
``humped'' distribution (with a maximum at about 100 keV) is formed.
Figure 4 shows the
density variations of energetic electrons, where the
distance from the injection point is expressed as a column density. If
the self-induced electric field is not taken into account (see the
panels labeled C and C+B), then the electric currents directed upwards
and
downwards do not compensate each other because only some of the
precipitating electrons
are scattered to negative pitch angle cosines, as described by
Eq. (4) for
the self-induced electric field. The beam densities of returning electrons
depend on the energy loss mechanisms of precipitating electrons. We
note that in the corona (at
![]() cm-2), the electron energy losses
due to
collisions are
insignificant, while Ohmic losses can play a dominant role (compare the
magnitudes of collisional and electric stopping depths defined in Table 1 of
Zharkova & Gordovskyy 2006). Thus, the number of returning
particles (integrated over all energies) is always slightly less than
that of the total precipitating particles.
cm-2), the electron energy losses
due to
collisions are
insignificant, while Ohmic losses can play a dominant role (compare the
magnitudes of collisional and electric stopping depths defined in Table 1 of
Zharkova & Gordovskyy 2006). Thus, the number of returning
particles (integrated over all energies) is always slightly less than
that of the total precipitating particles.
At every precipitation depth in the corona, there is a substantial increase
in the numbers of particles that propagate upwards (as shown in the panels labeled C+E and
C+E+B in Figs. 1-3), this increase becoming higher for the
beams with larger spectral indices (compare Figs. 4a and 4b). In other words, the electric current is not simply proportional
to the density of precipitating particles as discussed in Sect. 2
but depends on the spectral characteristics of beam electrons indicated by Eq. (4). Our simulations confirm the well-known fact that electron beams
with harder spectra can reach deeper layers of the solar atmosphere (Zharkova & Gordovskyy 2005; Siversky & Zharkova 2009; Zharkova & Kobylinskii 1993). This produces higher densities at deeper atmospheric levels for the electron beams with ![]() than for those with
than for those with ![]() ,
while at upper atmospheric levels the densities
of returning electrons are higher for the
electrons with
,
while at upper atmospheric levels the densities
of returning electrons are higher for the
electrons with ![]() ,
reflecting the Ohmic loss dependence of the power-law index (Zharkova & Gordovskyy 2006).
The effect of magnetic mirroring for the C+E+B models only enhances the
number of returning electrons across the entire energy range as
represented by Figs. 1-3.
,
reflecting the Ohmic loss dependence of the power-law index (Zharkova & Gordovskyy 2006).
The effect of magnetic mirroring for the C+E+B models only enhances the
number of returning electrons across the entire energy range as
represented by Figs. 1-3.
3.2 Variations in HXR bremsstrahlung intensity and polarization
3.2.1 Depth variations of HXR bremsstrahlung emission
The hard X-ray bremsstrahlung intensity and polarization produced by electrons injected with power-law spectral indices
of ![]() (red lines) and
(red lines) and ![]() (blue lines) are shown in Fig. 5. The first three columns present the X-ray photon spectra for the different simulation models and propagation directions, at
three distances from the electron injection point. We note that the curves for
different electron power-law indices are drawn by using a different scaling
factor, so the direct comparison of HXR emission caused by these beams with
their assigned spectral indices is infeasible. The last column of Fig. 5
shows the polarization of HXR emission calculated for a pitch angle
(blue lines) are shown in Fig. 5. The first three columns present the X-ray photon spectra for the different simulation models and propagation directions, at
three distances from the electron injection point. We note that the curves for
different electron power-law indices are drawn by using a different scaling
factor, so the direct comparison of HXR emission caused by these beams with
their assigned spectral indices is infeasible. The last column of Fig. 5
shows the polarization of HXR emission calculated for a pitch angle
![]() ,
where it is the highest.
,
where it is the highest.
We first consider the emission from the electron beams with ![]() (shown by red lines in Fig. 5). The spectrum of emission from the initial electron beam (at the injection
point) with a power-law distribution is shown in Fig. 5a.
Hard X-ray emission, especially at higher energies, is emitted preferably
in the direction of electron propagation (
(shown by red lines in Fig. 5). The spectrum of emission from the initial electron beam (at the injection
point) with a power-law distribution is shown in Fig. 5a.
Hard X-ray emission, especially at higher energies, is emitted preferably
in the direction of electron propagation (
![]() ). Thus,
with increasing viewing, or pitch, angle
). Thus,
with increasing viewing, or pitch, angle ![]() ,
the emission
intensity is expected to decrease, and the spectrum becomes softer, if
the bulk of electrons continue to propagate downwards. However, as the scattering
intensity of electrons increases with depth, the above conclusion becomes not valid
because the electrons emit far more isotropically.
,
the emission
intensity is expected to decrease, and the spectrum becomes softer, if
the bulk of electrons continue to propagate downwards. However, as the scattering
intensity of electrons increases with depth, the above conclusion becomes not valid
because the electrons emit far more isotropically.
The intensity plots in Figs. 5b-5e illustrate the effects of
collisions, a self-induced electric field, or a converging
magnetic field on the emission, at some distance from the injection
point (
![]() cm-2 corresponding to the corona).
Figure 5b illustrates the effect of collisions with pitch-angle
scattering on the HXR emission emitted by the downward (dotted line) and upward
(dashed line) moving particles. As we established in Sect. 3.1, the
number of particles scattered by pure collisions to large angles (when
cm-2 corresponding to the corona).
Figure 5b illustrates the effect of collisions with pitch-angle
scattering on the HXR emission emitted by the downward (dotted line) and upward
(dashed line) moving particles. As we established in Sect. 3.1, the
number of particles scattered by pure collisions to large angles (when ![]() changes sign) remains very small. This explains why the coronal emission from
precipitating electrons is an order of magnitude higher than those in the
chromosphere (compare rows b and f), while the shape of the energy spectrum does
not change much with depth. The emission from returning electrons (dashed
line) is much smaller than for the precipitating ones. Emission from returning
electrons becomes closer to those from precipitating ones as the viewing
angle increases.
changes sign) remains very small. This explains why the coronal emission from
precipitating electrons is an order of magnitude higher than those in the
chromosphere (compare rows b and f), while the shape of the energy spectrum does
not change much with depth. The emission from returning electrons (dashed
line) is much smaller than for the precipitating ones. Emission from returning
electrons becomes closer to those from precipitating ones as the viewing
angle increases.
Figure 5c shows the effect of a self-induced electric field and the appearance of the electrons of a return current (moving with ![]() ), which have a considerable effect on the resulting HXR emission spectra. This effect is strongest at
), which have a considerable effect on the resulting HXR emission spectra. This effect is strongest at
![]() keV, but is noticeable at the higher energies as well (up to
300 keV) for beams with an upper energy cutoff of 1.2 MeV. The upward emission
(
keV, but is noticeable at the higher energies as well (up to
300 keV) for beams with an upper energy cutoff of 1.2 MeV. The upward emission
(
![]() )
is generated entirely by electrons of the return
current. The emission intensity (especially at energies of about 30-100 keV)
is much higher than for collisions with anisotropic scattering
without the return current. The emission spectrum at a depth
of 1018
)
is generated entirely by electrons of the return
current. The emission intensity (especially at energies of about 30-100 keV)
is much higher than for collisions with anisotropic scattering
without the return current. The emission spectrum at a depth
of 1018
![]() differs from a power-law, the spectrum apparently flattening at lower
energies while keeping its power-law shape at higher energies. This
effect was noted previously by Zharkova & Gordovskyy (2005,2006).
differs from a power-law, the spectrum apparently flattening at lower
energies while keeping its power-law shape at higher energies. This
effect was noted previously by Zharkova & Gordovskyy (2005,2006).
The spectral flattening at low energies is also
visible at the viewing angle
![]() ,
although is much
weaker. The contributions of the downward and upward electrons become
almost equal. For the downward emission
(
,
although is much
weaker. The contributions of the downward and upward electrons become
almost equal. For the downward emission
(
![]() ), the contribution of the downward electrons always far exceeds
that of the upward electrons. Nevertheless, even in this case the return
current electrons affect the spectrum shape at energies below 50 keV.
), the contribution of the downward electrons always far exceeds
that of the upward electrons. Nevertheless, even in this case the return
current electrons affect the spectrum shape at energies below 50 keV.
The effect of a converging magnetic field is illustrated in Fig. 5d.
The convergence effect is strongest at
![]() ,
where emission at
higher energies is produced entirely by reflected electrons, and at
lower energies (<30 keV) the contribution of the reflected particles
dominates. The emission intensity is about two times higher than in the case
of pure collisions (Fig. 5b), and the spectrum is harder. For the
transversal propagation (
,
where emission at
higher energies is produced entirely by reflected electrons, and at
lower energies (<30 keV) the contribution of the reflected particles
dominates. The emission intensity is about two times higher than in the case
of pure collisions (Fig. 5b), and the spectrum is harder. For the
transversal propagation (
![]() ), the contributions of the downward
and reflected electrons are comparable, and the spectra of emission produced
by these electron populations are almost identical. For the downward emission
propagation (
), the contributions of the downward
and reflected electrons are comparable, and the spectra of emission produced
by these electron populations are almost identical. For the downward emission
propagation (
![]() ), the contribution of the reflected electrons
into X-ray emission is negligible.
), the contribution of the reflected electrons
into X-ray emission is negligible.
The intensities and polarization calculated for the most realistic case that
includes all the energy loss effects, e.g., collisions, return current, and
magnetic field convergence, are plotted in Fig. 5e. One can see
that two factors that produce the upward electron flux are now
combined: the return current electrons increase the upward emission
intensity at lower energies (<100 keV), while the reflected (by the
converging magnetic field) particles enhance the high-energy tail of the
emission spectrum. We note that the converging magnetic
field removes the spectral flattening at lower energy
as seen in Fig. 5c (for the beam with ![]() ). The emission
spectra at all viewing directions become similar to that in Fig. 5d.
We conclude that for hard electron beams, the influence of the
converging magnetic field is stronger than that of the self-induced electric
field.
). The emission
spectra at all viewing directions become similar to that in Fig. 5d.
We conclude that for hard electron beams, the influence of the
converging magnetic field is stronger than that of the self-induced electric
field.
The emission spectra for deeper layers of the solar atmosphere (in the
chromosphere) are plotted in Fig. 5f. Our calculations show that
the spectrum shape is almost independent of the simulation model. This means
that the effects of either a converging magnetic field or a
self-induced electric field become less significant than collisions,
which are the principal mechanism responsible for HXR emission at this level. In the directions
![]() and
and
![]() ,
the contribution of the emission produced by
downward electrons dominates. For the direction
,
the contribution of the emission produced by
downward electrons dominates. For the direction
![]() ,
the
contributions of the emission produced by either downward or upward (scattered) electrons are almost
equal.
,
the
contributions of the emission produced by either downward or upward (scattered) electrons are almost
equal.
The relative contributions of the scattered and returning electrons into the
hard X-ray emission become higher for softer beams (that is shown by blue lines
in Fig. 5). In the model taking into account the effects of
collisions and self-induced electric field (Fig. 5c), the relative
contribution of the return current electrons is more significant for the beam
with ![]() than for the beam with
than for the beam with ![]() .
This is particularly clear
for the viewing angles
.
This is particularly clear
for the viewing angles
![]() (where the emission at 20-100 keV is
produced mainly by the return current electrons) and
(where the emission at 20-100 keV is
produced mainly by the return current electrons) and
![]() (where
contributions of the upward and downward electrons are nearly the same at 20-50 keV); at
(where
contributions of the upward and downward electrons are nearly the same at 20-50 keV); at
![]() ,
the emission from the return current
electrons is strongly dominant both in the hard and soft beams, and a
spectral flattening at low energies is observed.
,
the emission from the return current
electrons is strongly dominant both in the hard and soft beams, and a
spectral flattening at low energies is observed.
The effect of a converging magnetic field on a softer beam with ![]() is
similar to that of a harder electron beam with
is
similar to that of a harder electron beam with ![]() (see Fig. 5d), both qualitatively and quantitatively.
(see Fig. 5d), both qualitatively and quantitatively.
The plots of HXR emission caused by electron beam scattering in the model with
collisions + return current + magnetic field convergence (Fig. 5e,
blue lines) are similar to those calculated for the model with collisions
+ return current (Fig. 5c). This implies that for softer beam
(![]() ), the effect of a self-induced electric field far exceeds all
other factors. In particular, the converging magnetic field does not remove the
spectral flattening entirely (although it reduces the energy range,
where the flattening takes place). The HXR polarization will also be significantly
affected, as discussed in Sect. 3.2.2.
), the effect of a self-induced electric field far exceeds all
other factors. In particular, the converging magnetic field does not remove the
spectral flattening entirely (although it reduces the energy range,
where the flattening takes place). The HXR polarization will also be significantly
affected, as discussed in Sect. 3.2.2.
In the deeper layers of the solar atmosphere (see Fig. 5f), the
emission parameters again become almost insensitive to the simulation model
used, because the parameters of the accelerated particles are determined
mainly by the collisions here. However, it should be noted that for the beam
with ![]() ,
only a small fraction of particles can reach the chromosphere. The
electrons at greater precipitation depths produce far lower HXR
emission intensities (compare the magnitudes of intensity in Figs. 5a and 5f).
,
only a small fraction of particles can reach the chromosphere. The
electrons at greater precipitation depths produce far lower HXR
emission intensities (compare the magnitudes of intensity in Figs. 5a and 5f).
3.2.2 Depth variations of the HXR bremsstrahlung polarization
With respect to the depth variation in the electron distributions discussed in Sect. 3.1, the polarization degree viewed in a perpendicular direction (right panels at Fig. 5) infers also a strong dependence on precipitation depth and the beam parameters.
At the injection point (Fig. 5a), the polarization degree steadily
decreases (by absolute value) with energy for both hard and soft beams. At intermediate
precipitation depth, for a harder beam (![]() ,
shown by red lines)
in the model with pure collisions (Fig. 5b), the polarization degree
has a maximum near the lowest photon energy (at about 15 keV) and
decreases as the energy increases.
,
shown by red lines)
in the model with pure collisions (Fig. 5b), the polarization degree
has a maximum near the lowest photon energy (at about 15 keV) and
decreases as the energy increases.
For the same beam parameters (![]() )
and at the same depth, the model with a magnetic field
convergence (Fig. 5d)
exhibits an increase in the polarization degree at higher energies (the
polarization degree decreases with energy more slowly than without the
converging magnetic field) because of the reflected electrons. In
contrast, the return current (Fig. 5c)
decreases the polarization degree at lower energies, such that the hard
electron beam produces emission with nearly constant (
)
and at the same depth, the model with a magnetic field
convergence (Fig. 5d)
exhibits an increase in the polarization degree at higher energies (the
polarization degree decreases with energy more slowly than without the
converging magnetic field) because of the reflected electrons. In
contrast, the return current (Fig. 5c)
decreases the polarization degree at lower energies, such that the hard
electron beam produces emission with nearly constant (
![]() )
polarization in the energy range 12-100 keV. A combination of these two factors (see Fig. 5e) results in a weak polarization maximum, which occurs at an energy of about 30 keV.
In deeper layers (Fig. 5f), the polarization
degree decreases in all the models considered, since the electron distribution
becomes more isotropic, in general, owing to collisions and pitch-angle
diffusion.
)
polarization in the energy range 12-100 keV. A combination of these two factors (see Fig. 5e) results in a weak polarization maximum, which occurs at an energy of about 30 keV.
In deeper layers (Fig. 5f), the polarization
degree decreases in all the models considered, since the electron distribution
becomes more isotropic, in general, owing to collisions and pitch-angle
diffusion.
The polarization of the emission from the beam with ![]() (shown by blue
lines) is higher than those from beams with
(shown by blue
lines) is higher than those from beams with ![]() .
This is partially caused by the different numbers of high-energy
particles and the properties of the bremsstrahlung cross-sections. For
the initially injected beam (Fig. 5a), the difference in polarization is caused only by the two aforementioned factors. Another reason is the
increase in the degree of scattering of beam electrons for
.
This is partially caused by the different numbers of high-energy
particles and the properties of the bremsstrahlung cross-sections. For
the initially injected beam (Fig. 5a), the difference in polarization is caused only by the two aforementioned factors. Another reason is the
increase in the degree of scattering of beam electrons for ![]() =7, e.g., a larger
number of lower energy electrons moves not downwards but in a
perpendicular direction. This, in turn,
happens owing to the joint effect of collisions and Ohmic losses (Zharkova & Gordovskyy 2005,2006).
=7, e.g., a larger
number of lower energy electrons moves not downwards but in a
perpendicular direction. This, in turn,
happens owing to the joint effect of collisions and Ohmic losses (Zharkova & Gordovskyy 2005,2006).
The converging magnetic field (see Fig. 5d) affects the emission from beams with ![]() and
and ![]() in the same way. The effect of a return current (Fig. 5c)
for the soft beams is far more significant than for the harder ones:
the polarization degree is reduced significantly at lower energies, so
we can see the polarization maximum at about 150 keV. The combined
effects of collisions, converging magnetic field, and return current
(Fig. 5e) produce a clearly
defined polarization maximum at 50-60 keV; the polarization
degree at that point exceeds (in absolute value) 60%. The similar
polarization maximum, but shifted to lower energies (about 50 keV)
and with lower magnitude, can be seen even in deeper layers (Fig. 5f).
in the same way. The effect of a return current (Fig. 5c)
for the soft beams is far more significant than for the harder ones:
the polarization degree is reduced significantly at lower energies, so
we can see the polarization maximum at about 150 keV. The combined
effects of collisions, converging magnetic field, and return current
(Fig. 5e) produce a clearly
defined polarization maximum at 50-60 keV; the polarization
degree at that point exceeds (in absolute value) 60%. The similar
polarization maximum, but shifted to lower energies (about 50 keV)
and with lower magnitude, can be seen even in deeper layers (Fig. 5f).
For other viewing angles, the depth variations in HXR polarization
produced by a hard beam are, in general, rather complex (see Fig. 6).
It can be noted that the precipitation depth of the emitting electrons
is the key factor in defining the magnitude of polarization produced.
The highest polarization degree (-46% at 30 keV and -37%
at 100 keV, for a beam with ![]() )
for the initially injected collimated beam is observed in the transversal (
)
for the initially injected collimated beam is observed in the transversal (
![]() )
propagation direction. As the electron beam propagates downwards, the
polarization dependence on the propagation direction becomes
asymmetric, although, in general, the polarization maximum does not
deviate much from
)
propagation direction. As the electron beam propagates downwards, the
polarization dependence on the propagation direction becomes
asymmetric, although, in general, the polarization maximum does not
deviate much from
![]() .
The polarization values depend on the simulation model. For the model with collisions and return current (Fig. 6a),
at 30 keV, the polarization degree steadily decreases with depth,
which shifts the maximum to lower viewing angles. At 100 keV, the
polarization degree firstly increases slightly, and then decreases
again.
.
The polarization values depend on the simulation model. For the model with collisions and return current (Fig. 6a),
at 30 keV, the polarization degree steadily decreases with depth,
which shifts the maximum to lower viewing angles. At 100 keV, the
polarization degree firstly increases slightly, and then decreases
again.
The converging magnetic field increases the rate of electron
isotropization leading, thus, to a HXR polarization decrease with depth
(see Figs. 6b and 6c)
that occurs far more rapidly than in the homogeneous magnetic field. In
the deepest layers, we can see small positive polarization values at
the propagation angles >
![]() ,
which are caused by reflected particles with large pitch-angles.
,
which are caused by reflected particles with large pitch-angles.
Softer electron beams (Figs. 6d-6f) exhibit a similar dependence of the HXR polarization on the depth and the simulation model. The polarization degree is higher now (up to -62% at 30 keV and -58% at 100 keV). As for harder beams, evolution in the polarization degree with depth is governed mainly by the convergence of the magnetic field, but the effect of the return current is now stronger (compare Figs. 6e and 6f).
It can be seen that the HXR polarization calculated even for all energy losses
above can still reach ![]() at the right viewing angle (
at the right viewing angle (
![]() )
(see Figs. 5-6). This helps one to understand that the
position of a flaring atmosphere on the solar surface and the viewing angle from
which it is observed can be factors defining the total observed outcome.
For example, this can explain the very high polarization degrees (up to 50
)
(see Figs. 5-6). This helps one to understand that the
position of a flaring atmosphere on the solar surface and the viewing angle from
which it is observed can be factors defining the total observed outcome.
For example, this can explain the very high polarization degrees (up to 50![]() )
reported for
the flare 23 July 2002 (McConnell et al. 2003), which was located
very close to the limb, and thus seen from the viewing angle close to
)
reported for
the flare 23 July 2002 (McConnell et al. 2003), which was located
very close to the limb, and thus seen from the viewing angle close to
![]() and
at small integration depth because seen from a side.
and
at small integration depth because seen from a side.
3.2.3 Depth variation of the HXR bremsstrahlung directivity
The variations with depth of X-ray emission directivity can be explored in
detail from Fig. 6.
Firstly, we consider the case of ![]() (Figs. 6a-6c)
when the directivity is the highest. If one
includes only the effects of collisions and self-induced electric field (Fig. 6a), then the changes in the X-ray directivity reflect the evolution
of electron isotropization via collisions and return current. At the injection
point (
(Figs. 6a-6c)
when the directivity is the highest. If one
includes only the effects of collisions and self-induced electric field (Fig. 6a), then the changes in the X-ray directivity reflect the evolution
of electron isotropization via collisions and return current. At the injection
point (![]() ), the emission is highly directed and is radiated mainly
downwards. As long as the stream of returning electrons develops at deeper
column depths (
), the emission is highly directed and is radiated mainly
downwards. As long as the stream of returning electrons develops at deeper
column depths (
![]() and 1019
and 1019
![]() ), the intensity of emission into the upward hemisphere
(towards an observer) increases due to the increased number of particles moving upwards
(see Sect. 3.1).
), the intensity of emission into the upward hemisphere
(towards an observer) increases due to the increased number of particles moving upwards
(see Sect. 3.1).
Thus, at lower energies (30-40 keV), the emission becomes almost isotropic. In the deeper layers of the solar atmosphere (
![]() and 1021
and 1021
![]() ),
the HXR photon flux decreases because of the lower total number of
electrons losing
their energy in collisions. This results, in turn, in the density and
the energies of the returning electrons decreasing considerably, and
the X-ray
emission (at 30 keV) becoming again directed mainly downwards. At
higher energies (>100 keV), this decrease is much less
noticeable because only particles with energies much higher than
100 keV can reach this energy at a given depth. These higher
energy electrons do not lose their energy fast enough because the Ohmic
losses become negligible owing to the lower number of electrons, while
collisional losses are reduced because the ambient plasma becoming
partially ionized, so the particles can precipitate to deeper
atmospheric levels.
),
the HXR photon flux decreases because of the lower total number of
electrons losing
their energy in collisions. This results, in turn, in the density and
the energies of the returning electrons decreasing considerably, and
the X-ray
emission (at 30 keV) becoming again directed mainly downwards. At
higher energies (>100 keV), this decrease is much less
noticeable because only particles with energies much higher than
100 keV can reach this energy at a given depth. These higher
energy electrons do not lose their energy fast enough because the Ohmic
losses become negligible owing to the lower number of electrons, while
collisional losses are reduced because the ambient plasma becoming
partially ionized, so the particles can precipitate to deeper
atmospheric levels.
Figure 6b shows the
hard X-ray directivity and polarization for the models with collisions
and converging magnetic field. One can see that at lower energy
(30 keV), the directivity pattern steadily becomes more isotropic
when the electron beam propagates to deeper atmospheric layers. At
higher energy (100 keV), the process of isotropization is slower.
At the level
![]() cm-2, we can see the emission of two beams, the direct and the mirrored ones.
cm-2, we can see the emission of two beams, the direct and the mirrored ones.
In Fig. 6c, both the collisions, return current, and magnetic field
convergence are taken into account. In this case, the relative contribution
of the upward particles into emission increases compared with two previous cases. Now the upward emission can even
dominate at
![]() and 1019 cm-2 for the energy 30 keV, and at
and 1019 cm-2 for the energy 30 keV, and at
![]() cm-2for the energy 100 keV.
cm-2for the energy 100 keV.
It was noted in Sects. 3.1, 3.2, and 3.2.2
that the effects of the self-induced electric field become much stronger for
softer electron beams (with ![]() ). This conclusion is also confirmed
by the directivity plots (Figs. 6d-6f). In Fig.
6d (collisions + return current), one can see that the X-rays are
emitted mainly upwards at
). This conclusion is also confirmed
by the directivity plots (Figs. 6d-6f). In Fig.
6d (collisions + return current), one can see that the X-rays are
emitted mainly upwards at
![]() cm-2
and 30 keV; the upward emission at the same depth at 100 keV
is comparable to the downward one. The converging magnetic field
(Fig. 6e) has almost the same effect as for the harder beam. In Fig. 6f
(collisions + return current + magnetic field
convergence), the upward emission strongly dominates at the levels of
cm-2
and 30 keV; the upward emission at the same depth at 100 keV
is comparable to the downward one. The converging magnetic field
(Fig. 6e) has almost the same effect as for the harder beam. In Fig. 6f
(collisions + return current + magnetic field
convergence), the upward emission strongly dominates at the levels of
![]() and 1019 cm-2 for both considered energies. These effects need to be incorporated into the integrated polarization
to be compared with those measured by the RHESSI instruments.
and 1019 cm-2 for both considered energies. These effects need to be incorporated into the integrated polarization
to be compared with those measured by the RHESSI instruments.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{11486Fig06a.eps}\hspace*{4...
...s}\hspace*{4mm}
\includegraphics[width=8.1cm,clip]{11486Fig06f.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg96.png)
|
Figure 6:
Directivity and polarization of the hard X-ray emission for different
propagation directions. The electron distribution functions are
obtained with taking into account different factors (see Fig. 1), the initial power-law indices of beam electrons
are |
| Open with DEXTER | |
| Figure 7:
Integrated by column depth intensity (in relative units) and polarization of hard X-ray
emission for different energies. The initial power-law indices of the
beam electrons are: |
|
| Open with DEXTER | |
3.2.4 Integrated HXR bremsstrahlung emission and polarization
The total emission from the considered coronal magnetic tube with the emission
parameters integrated over all layers using Eq. (7), is
shown in Figs. 7 and 8. As in Fig. 5,
the emission parameters for the electron beams with different power-law
indices in Fig. 7 are shown in different colors (red for ![]() and blue for 7).
We note that in Fig. 7, the intensity plots for
and blue for 7).
We note that in Fig. 7, the intensity plots for ![]() and
and ![]() are
drawn for different scalings (shown at the left axis for
are
drawn for different scalings (shown at the left axis for ![]() and at the right axis for
and at the right axis for ![]() ).
).
One can note from Fig. 7
that a harder beam exhibits a strong dependence on magnetic field
convergence (compare the models with a constant magnetic field (C, C+E)
with those taking into account a magnetic field convergence (C+B,
C+E+B)). In the converging magnetic field, the emission intensity is
lower than in the homogeneous magnetic field, because the magnetic
mirroring reduces the number of electrons reaching the deepest layers
of the solar atmosphere. For the softer beams, this dependence is less
significant, as the number of electrons reaching the deepest layers is
small in any case due to collisional damping. A small spectral
flattening at lower energies is evident, although it is less pronounced
than for the emission from the individual layers in the corona (compare
with Fig. 5); the ``break'' energy (for the C+E+B model and for the upward emission) is found to be about 100 keV for the beam with ![]() and about 50 keV for
and about 50 keV for ![]() .
This confirms the analytical predictions for a simplified precipitation model done by Zharkova & Gordovskyy (2006).
.
This confirms the analytical predictions for a simplified precipitation model done by Zharkova & Gordovskyy (2006).
The integrated HXR directivity and polarization are found to be even more sensitive to the beam parameters and viewing angles. One can see that for harder beams, the return current almost does not change the integrated directivity (in comparison with the purely collisional model), but reduces the integrated polarization at both energies considered. The converging magnetic field reduces the directivity and polarization significantly, and the results for the C+E+B model are similar to those for C+B.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11486Fig08.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg98.png)
|
Figure 8:
Directivity and polarization of the hard X-ray emission for the
different propagation directions. The emission parameters are integrated
over all layers of coronal magnetic tube. Initial power-law indices of the
accelerated particles are: |
| Open with DEXTER | |
For softer beams, the effect of the return current is much stronger.
We can see that the combination of the converging magnetic field and
return current changes the directivity at 30 keV, so the
integrated emission is directed mainly upwards. The integrated
polarization in this case can become higher than for the purely
collisional model. At 100 keV, the downward emission always
dominates, but the upward emission in C+E+B model is considerably
stronger than in the other three models. It can be seen from Figs. 7, 8 that the maximal polarization degree (about -36%) is achieved for the beam with ![]() ,
in the model with collisions, return current, and converging magnetic
field, at the energy of about 30 keV and transversal propagation
direction.
,
in the model with collisions, return current, and converging magnetic
field, at the energy of about 30 keV and transversal propagation
direction.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11486Fig09a.eps}\hspace*{4...
...s}\hspace*{4mm}
\includegraphics[width=8.5cm,clip]{11486Fig09d.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg99.png)
|
Figure 9:
The hard X-ray double power-law spectra observed by RHESSI for the flares of 23 July 2002 ( upper plots) and 20 July 2002 ( lower plots) for the times plotted in the top right corners of each plot. The top left and right plots correspond to the electron energy fluxes of
|
| Open with DEXTER | |
The current study has also established that the measurements of HXR integrated polarization combined with those of photon flux can derive far more precise electron beam parameters and provide far deeper insight into the mechanisms of particle transport in the deeper atmospheric levels than the pure emission measurements.
3.2.5 Comparison with observations
We now compare our simulation results with the available observations of HXR bremsstrahlung emission, polarization, and directivity.
HXR bremsstrahlung photon spectra
We first consider the deduced photon energy spectra and determine how they can be reproduced by the theoretical calculations (Fig. 9). It can be seen that the observed energy spectra for the flares 20 and 23 July 2002 have distinctive double power-law energy spectra where the lower energy part is flattened to much lower spectral indices (e.g., 4.6 and 4.4 for the 23 July flare (Sui et al. 2007) and 4.5 and 5.0 for the 20 July flare) compared to the higher energy parts (6.1-6.2 for the 23 July flare (Holman et al. 2003) and 7-7.7 for the 20 July flare). The observed HXR photon spectra can be well reproduced by the simulated ones produced by the distribution functions of precipitating and returning electrons by using Eq. (8) for the relativistic cross-sections from Appendix A and taking into account the self-induced electric field that causes the photon spectrum flattening at lower energies (Zharkova & Gordovskyy 2006) as discussed below.
![\begin{figure}
\par\mbox{\includegraphics[width=7.8cm,clip]{polar_20keV_bw.eps}\...
...*{4mm}
\includegraphics[width=7.8cm,clip]{polar_200keV_bw.eps} }\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg101.png)
|
Figure 10:
Comparison of the simulations of HXR bremsstrahlung polarization for 20 keV ( left plot) and 200 keV ( right plot) produced for different position angle on the solar disk (
|
| Open with DEXTER | |
This means that for the flare on 23 July 2002, where the
lower energy index changes from 4.6 to 4.4 in the left and
right top plots of Fig. 9, respectively (Holman et al. 2003), one observes an increase in the initial energy flux of beam electrons in the two consecutive times by a factor 2 - from
![]() to
to
![]() erg cm-2
s-1,
which is confirmed by the light curves for this flare (Holman et al. 2003).
This increase in the electron energy flux for the two observed cases
results in a stronger flattening of the photon spectrum in the second
case than in the first.
erg cm-2
s-1,
which is confirmed by the light curves for this flare (Holman et al. 2003).
This increase in the electron energy flux for the two observed cases
results in a stronger flattening of the photon spectrum in the second
case than in the first.
A spectral difference between the lower and upper spectral indices
![]() and
and
![]() of the observed photon spectra for these instances (fits to the simulated spectra plotted by dashed lines in Fig. 9)
increased from 1.5 (6.1-4.6) to 1.6 (6.0-4.4). For the
20 July 2002 flare, the spectral index difference in the
photon spectra produced by beam electrons plotted in the bottom graphs
of Fig. 9 increases from 4.5 to 5.0.
This
confirms that the energy flux of beam electrons increased in time from
of the observed photon spectra for these instances (fits to the simulated spectra plotted by dashed lines in Fig. 9)
increased from 1.5 (6.1-4.6) to 1.6 (6.0-4.4). For the
20 July 2002 flare, the spectral index difference in the
photon spectra produced by beam electrons plotted in the bottom graphs
of Fig. 9 increases from 4.5 to 5.0.
This
confirms that the energy flux of beam electrons increased in time from
![]() to
to
![]() erg cm-2
s-1 as indicated in Fig. 11
and Table 2 in the paper by Zharkova & Gordovskyy (2006).
Thus, we reckon that the observed spectral flattening at lower energies
and the soft-hard-soft pattern in the lower energy spectral indices of
photon spectra can be naturally explained by the low-high-low
variations in the initial energy flux of beam electrons.
erg cm-2
s-1 as indicated in Fig. 11
and Table 2 in the paper by Zharkova & Gordovskyy (2006).
Thus, we reckon that the observed spectral flattening at lower energies
and the soft-hard-soft pattern in the lower energy spectral indices of
photon spectra can be naturally explained by the low-high-low
variations in the initial energy flux of beam electrons.
We note that the above-mentioned spectral flattening of the X-ray spectra at lower energies caused by the returning beam electrons is qualitatively similar to the expected influence of the so-called albedo effect (e.g., Kontar et al. 2006; Bai & Ramaty 1978). Part of the downwardly emitted photons should be reflected from the photosphere up to the observer, thus distorting the primary emission spectra. The albedo contribution should be highest for photon energies of about 30-50 keV (owing to the energy dependence of the Compton scattering probability) and for events occurring close to the solar disk center (due to the geometrical reasons). The same can be said about the contribution of the returning electrons. In both cases we consider the reflection process, but either the photons or the precipitating electrons (and photons emitted by them) can change their propagation direction.
HXR bremsstrahlung directivity and polarization
Other properties of the HXR bremsstrahlung emission that can help us to understand more clearly the mechanisms of
electron precipitation into a flaring atmosphere is linear polarization calculated from Eq. (8) and
directivity obtained from Eq. (9).
To achieve a closer fit to observations, we considered the electron
beam with all energy losses (collisions, convergence, and Ohmic losses)
and with wider and narrower pitch angle dispersion
![]() in the initial distribution defined by Eq. (2).
The polarization calculated for HXR bremsstrahlung photon energies of
20 keV and 200 keV for different models of electron beam
precipitation and flare locations on the solar disk is plotted in
Fig. 10 and the directivity in Fig. 11.
The simulations are tested by numerous observations of HXR polarization
and directivity plotted in each figure with their error bars as
discussed below.
in the initial distribution defined by Eq. (2).
The polarization calculated for HXR bremsstrahlung photon energies of
20 keV and 200 keV for different models of electron beam
precipitation and flare locations on the solar disk is plotted in
Fig. 10 and the directivity in Fig. 11.
The simulations are tested by numerous observations of HXR polarization
and directivity plotted in each figure with their error bars as
discussed below.
We note that the polarization is higher by up to a factor 2 for
lower energy photons (20 keV) than for higher energy ones
(200 keV), which may be caused by the smaller number of high
energy photons compared to the lower energy ones because of the
power-law dependence on energy. For both photon energies (20 and
200 keV), the simulated HXR polarization smoothly increases
towards the solar limb. For beam electrons with a wider pitch-angle
dispersion
![]() ,
this increase is greater for a higher spectral index of 7 compared to 3
and for the models C+E+B taking into account magnetic field convergence
in addition to the model with collisions plus electric field (C+E). The
same is valid for the polarization in high energy band of 200 keV
produced by beams with higher energy flux of 1012 erg cm-2
s-1 in the right plot of Fig. 10.
For the polarization at lower energy of 20 keV, the higher the
initial energy flux of beam electrons, the lower the polarization (see
left plot in Fig. 10). The
latter is a clear electric field effect that causes more beam electrons
to return back to the corona and a greater spectral flattening for
,
this increase is greater for a higher spectral index of 7 compared to 3
and for the models C+E+B taking into account magnetic field convergence
in addition to the model with collisions plus electric field (C+E). The
same is valid for the polarization in high energy band of 200 keV
produced by beams with higher energy flux of 1012 erg cm-2
s-1 in the right plot of Fig. 10.
For the polarization at lower energy of 20 keV, the higher the
initial energy flux of beam electrons, the lower the polarization (see
left plot in Fig. 10). The
latter is a clear electric field effect that causes more beam electrons
to return back to the corona and a greater spectral flattening for ![]() as discussed above. For a narrower electron beam, HXR polarization increases closer to the limb by 30-40%.
as discussed above. For a narrower electron beam, HXR polarization increases closer to the limb by 30-40%.
![\begin{figure}
\par\mbox{\includegraphics[width=7.8cm,clip]{direct_20keV_bw_lege...
...*{4mm}
\includegraphics[width=7.8cm,clip]{direct_200keV_bw.eps} }\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg107.png)
|
Figure 11:
A comparison of the directivity estimations inferred for energies
20-200 keV from the statistical survey of different flare
positions at the solar disk (
|
| Open with DEXTER | |
Although, there are some discrepancies between the simulations and
observations located at the disk center, which can be caused by the
loop tilts which lead to the resulting viewing angle being higher than
their position angle on the disk. Nevertheless, at lower (20 keV)
and higher energy (>200 keV), the fit is significantly improved
(see the right plots in Fig. 10) by consideration of a narrower electron beam, which leaves only one measurement at
![]() not covered by the simulated curves. The only measurement that is not fitted by the simulations is that of the heliocentic
angle of about 50 degrees, which can be produced by even more focused beams, say
with
not covered by the simulated curves. The only measurement that is not fitted by the simulations is that of the heliocentic
angle of about 50 degrees, which can be produced by even more focused beams, say
with
![]() ,
or by the albedo effect (which, according to
Bai & Ramaty 1978, can also increase the visible polarization).
,
or by the albedo effect (which, according to
Bai & Ramaty 1978, can also increase the visible polarization).
The fit of our theoretical predictions of the HXR bremsstrahlung
directivity to those measured by Kasparová et al. (2007) is plotted in Fig. 11. The simulations are carried out for both wide and narrow electron
beams with
![]() and 0.02 for the same beam parameters discussed for polarization (Fig. 10).
It can be noted that the directivity of lower energy photons of
20 keV is lower and less widely dispersed over locations across
the solar disk than those of higher energy, e.g. 200 keV. The
directivity is at its highest approaching 2.5 at the solar limb,
while it smoothly decreases to 0.5 at the solar disk center. The
directivity of harder beams (
and 0.02 for the same beam parameters discussed for polarization (Fig. 10).
It can be noted that the directivity of lower energy photons of
20 keV is lower and less widely dispersed over locations across
the solar disk than those of higher energy, e.g. 200 keV. The
directivity is at its highest approaching 2.5 at the solar limb,
while it smoothly decreases to 0.5 at the solar disk center. The
directivity of harder beams (![]() )
for models with either pure collisions or collisions and electric field, is higher than for softer beams (
)
for models with either pure collisions or collisions and electric field, is higher than for softer beams (![]() ),
and for models considering also a magnetic field convergence. The
directivity of higher energy photons produced by a narrower beam with a
higher initial energy flux becomes much lower than that for a wider
beam with lower energy flux.
),
and for models considering also a magnetic field convergence. The
directivity of higher energy photons produced by a narrower beam with a
higher initial energy flux becomes much lower than that for a wider
beam with lower energy flux.
The fit to the observed directivity to the theoretical curve of directivity produced for the models C+E by a narrower electron beam with higher energy flux of 1012 erg cm-2 s-1, is satisfactory for higher energy emission (the right plot in Fig. 11). We emphasize that in the current paper we have not taken into account any albedo effects, and considered only the non-isotropic pitch angle scattering of beam electrons during their precipitation in a converging magnetic field and self-induced electric field. The effect of particle kinetics is exhibited in their emission properties and, in particular, its polarization and directivity.
However, when interpreting solar X-ray observations, the albedo and electric field effects can substantially change the HXR directivity and polarization since they act on HXR emission in similar ways. This explains why Kasparová et al. (2007) concluded that the observed deviations of the RHESSI flare X-ray spectra from the power-law ones can be well explained by the albedo effect, as for our current and previous conclusions about electric field effect (Zharkova & Gordovskyy 2006). Sui et al. (2007) found that the albedo correction is usually insufficient to explain the observations, and the remaining difference is most probably due to the return current. A clearer differentiation between the albedo and return current effects can be achieved, on the one hand, by using the spatially resolved observations of very compact X-ray sources (the albedo source should be larger than the primary X-ray source). However, simultaneous simulations of the albedo and return current contributions are urgently required and will be presented in a forthcoming paper.
4 Conclusions
The distribution functions of power-law beam electrons within the energy range of 12 keV to 1.2 MeV are simulated during their precipitation into a flaring atmosphere by using the Fokker-Planck approach and taking into account collisional and Ohmic energy losses in a converging magnetic field. By using the obtained electron distributions, the resulting HXR emission with relativistic bremsstrahlung cross-sections, directivity and polarization are also calculated for precipitating and returning particles with the positive and negative pitch angle cosines, respectively, at various depths and for different viewing angles. The conclusions of their comparison are summarized below.The distributions of beam electrons are shown to be strongly affected by their
self-induced electric field and magnetic field convergence at given depths
leading to a formation of particle streams moving upwards to the source where
they were injected from. The self-induced electric field produces the
returning electrons, or return current, which compensates the electric field
induced by precipitating electrons. For the extended upper cutoff energy of
1.2 MeV, the energy of returning electrons cover the range up to 300 keV and
their distributions are quasi-thermal-like with wide maxima being caused by
pitch-angle diffusion at 80 keV for ![]() and 120 keV for
and 120 keV for ![]() .
For a softer beam, the number of returning electrons at some depths can exceed
the number of precipitating ones.
.
For a softer beam, the number of returning electrons at some depths can exceed
the number of precipitating ones.
A converging magnetic field with a reasonable convergence coefficient (a factor of 2-3) towards the
characteristic depth in the upper chromosphere (
![]()
![]() )
produces a stream of mirrored electrons that are reflected by the
magnetic field within the loss cone defined by this convergence. The
effect of a converging magnetic field becomes noticeable only after the
initial well-collimated beam electrons (with the pitch-angle dispersion
)
produces a stream of mirrored electrons that are reflected by the
magnetic field within the loss cone defined by this convergence. The
effect of a converging magnetic field becomes noticeable only after the
initial well-collimated beam electrons (with the pitch-angle dispersion
![]() centered about
centered about ![]() )
become scattered by collisions to larger pitch angles,
or smaller
)
become scattered by collisions to larger pitch angles,
or smaller ![]() that only happens after quite a
few steps in the precipitation depth and lasts until the convergence exists.
The energy spectra of electrons reflected by a converging magnetic field
remain the same (power-law like) as for the precipitating electrons. The convergence
effect is found to be more important for a harder beam than for a softer one
which is more affected by a self-induced electric field.
The joint effect of self-induced electric and converging magnetic fields
at all precipitation depths creates more electrons that return back to the
corona, whose numbers are higher for softer beams.
that only happens after quite a
few steps in the precipitation depth and lasts until the convergence exists.
The energy spectra of electrons reflected by a converging magnetic field
remain the same (power-law like) as for the precipitating electrons. The convergence
effect is found to be more important for a harder beam than for a softer one
which is more affected by a self-induced electric field.
The joint effect of self-induced electric and converging magnetic fields
at all precipitation depths creates more electrons that return back to the
corona, whose numbers are higher for softer beams.
The beams, both precipitating and returning, produce HXR bremsstrahlung emission throughout their precipitation depths.
It was found that at higher atmospheric levels (
![]()
![]() )
the emission from precipitating electrons is
often comparable or even lower than those from the returning electrons. This is caused
by the self-induced electric field (for softer beams) or by the magnetic field convergence (for harder beams).
)
the emission from precipitating electrons is
often comparable or even lower than those from the returning electrons. This is caused
by the self-induced electric field (for softer beams) or by the magnetic field convergence (for harder beams).
The effect of a converging magnetic field is strongest for a viewing angle
of
![]() and decreases for smaller viewing angles. Similarly, the effect of a self-induced
electric field is strongest for the viewing angles about
and decreases for smaller viewing angles. Similarly, the effect of a self-induced
electric field is strongest for the viewing angles about
![]() ,
but
is significant for other directions as well. The joint effects of all
energy losses on HXR emission are defined by the dominant mechanisms of
energy losses, e.g., Ohmic losses prevailing for softer beams and
converging magnetic field prevailing for harder beams. The HXR emission
observed in the upper corona at small viewing angles (less then
,
but
is significant for other directions as well. The joint effects of all
energy losses on HXR emission are defined by the dominant mechanisms of
energy losses, e.g., Ohmic losses prevailing for softer beams and
converging magnetic field prevailing for harder beams. The HXR emission
observed in the upper corona at small viewing angles (less then
![]() )
is produced predominantly by returning
electrons, not by the precipitating ones. For lower atmospheric depths, the
effects of external fields are reduced and the emission is defined by
collisions only.
)
is produced predominantly by returning
electrons, not by the precipitating ones. For lower atmospheric depths, the
effects of external fields are reduced and the emission is defined by
collisions only.
The depth and viewing angle variations of HXR polarization are far more
pronounced than those of the emission. Near the electron injection site, the polarization is maximal
at the lower energy cutoff and then shifts to higher energies with every
precipitation depth, approaching 25 keV for models with pure collisions and
100 keV for models with collisions and a return current. In deeper
layers, the polarization decreases because of the isotropization of electrons
by collisions. The maximum polarization is observed at the viewing angle of
![]() and shifts to lower angles for softer beams. The polarization
of HXR emission caused by soft electron beams at
and shifts to lower angles for softer beams. The polarization
of HXR emission caused by soft electron beams at ![]() at higher depths
is higher than those produced by harder beams because the former have more electrons scattered
to larger pitch angles at smaller depths. In deeper atmospheric levels, the
polarization for harder beams becomes higher that for softer ones, as
defined by the electron isotropization by collisions, which is higher for
softer electrons.
at higher depths
is higher than those produced by harder beams because the former have more electrons scattered
to larger pitch angles at smaller depths. In deeper atmospheric levels, the
polarization for harder beams becomes higher that for softer ones, as
defined by the electron isotropization by collisions, which is higher for
softer electrons.
The HXR directivity, which determines the relative importance of
downward and upward emission, is also shown to be a function of
precipitating depth and viewing angle being controlled by a combination
of the flare position on the solar disk and the tilt of the flaring
loop towards the solar surface. At the injection point (![]() ), the emission is highly directed and
radiated mainly downwards. For all simulation models, in the deeper
atmospheric layers (about
), the emission is highly directed and
radiated mainly downwards. For all simulation models, in the deeper
atmospheric layers (about
![]()
![]() ),
a stream develops from the electrons returning upwards to the source
resulting in an increase in the HXR intensity and directivity for small
viewing angles in the upward direction (towards an observer).
),
a stream develops from the electrons returning upwards to the source
resulting in an increase in the HXR intensity and directivity for small
viewing angles in the upward direction (towards an observer).
For the models with an electric field and collisions, at upper atmospheric levels,
the HXR emission at lower energies (30 keV) is directed more upwards
than downwards, owing to the increased number of particles moving upwards. In the deeper layers of the solar atmosphere (
![]() and 1021
and 1021
![]() ), the
upward HXR photon flux (at 30 keV) is lower because of a considerably
lower number of returning electrons leading to the X-ray emission being
again directed mainly downwards. At higher energies (100 keV), this
emission is directed downwards because this effect is less pronounced and the
particles do not lose their energy fast enough in the partially ionized plasma,
so they can precipitate to deeper atmospheric levels.
), the
upward HXR photon flux (at 30 keV) is lower because of a considerably
lower number of returning electrons leading to the X-ray emission being
again directed mainly downwards. At higher energies (100 keV), this
emission is directed downwards because this effect is less pronounced and the
particles do not lose their energy fast enough in the partially ionized plasma,
so they can precipitate to deeper atmospheric levels.
For the models with collisions and converging magnetic field, the directivity pattern of HXR bremsstrahlung emission remains nearly the same when the electron beam propagates into deeper atmospheric layers showing that the emission is directed mainly downwards. For models including collisions, return current, and magnetic field convergence, the relative contribution into the HXR emission of the particles moving upwards increases compared to the case of collisions and Ohmic losses. In this case, the directivity is also governed by the self-induced electric field and collisions, but at smaller viewing angles (towards the observer) it becomes slightly higher owing to magnetic mirroring. At larger viewing angles, the emission parameters are fully defined by the electric field and collisions, so the directivity is very different from that caused by magnetic convergence. This difference can be used to diagnose these effects in the observations.
The total (spatially integrated) HXR emission spectra and directivity
also show a dependence on both the beam parameters and the energy losses. For softer beams, there is a noticeable flattening of
the photon spectra at lower energies caused by the self-induced electric field,
which increases for larger viewing angles approaching a maximum at the angle of
![]() .
There is also some dependence
on magnetic field convergence for harder beams that makes the corresponding photon
spectra softer at smaller viewing angles, while at larger angles they show no
significant dependence on the convergence factor. These dependencies are clearly controlled by the dynamics of
energy losses for harder and softer beams, the former being more sensitive to magnetic mirroring and the latter
to Ohmic losses.
.
There is also some dependence
on magnetic field convergence for harder beams that makes the corresponding photon
spectra softer at smaller viewing angles, while at larger angles they show no
significant dependence on the convergence factor. These dependencies are clearly controlled by the dynamics of
energy losses for harder and softer beams, the former being more sensitive to magnetic mirroring and the latter
to Ohmic losses.
The proposed precipitation model with collisional and Ohmic losses for
an electron beam with wider pitch angle dispersion of 0.2 allowed us to
fit the double power law HXR photon spectra with a spectrum flattening
at lower energies observed in the flares of 20 and
23 July 2002. The observed spectral flattening at lower
energies and the soft-hard-soft pattern in the lower energy spectral
indices of photon spectra can be naturally explained by the
low-high-low variations in the initial energy flux of injected beam
electrons.
The observed directivity of HXR photons of 20 keV derived for a
large number of flares located between the disk center and limb is also
reproduced well by the theoretical directivity calculated for an
electron beam with a very narrow pitch angle dispersion of 0.02. The
simulated polarization of this narrow-directed electron beam fits up to
90![]() of all the available polarimetric and directivity observations carried out at various locations on the solar disk.
of all the available polarimetric and directivity observations carried out at various locations on the solar disk.
Thus, the current study allows us to establish that polarization measurements combined with the observations of HXR photon flux can help researchers to extract the electron beam parameters far more precisely and to obtain a much deeper insight into the mechanisms of particle transport into deeper atmospheric levels than attainable from only measurements of HXR bremsstrahlung emission (such as light curves and energy spectra).
AcknowledgementsThe authors would like also to express their deepest gratitude to the Royal Society (UK) for providing a visiting grant for AK to visit the University of Bradford in March-April 2008 where the paper was initiated. The authors would like to thank the anonymous referee and the Editor for their constructive comments from which paper strongly benefited. The work was partially supported by the Royal Society (UK), the Science, Technology and Facilities Council (UK) (grant PP/E001246/1) and the Russian Foundation of Basic Research (grant 09-02-92610).
Appendix A: Hard X-ray bremsstrahlung cross-section
The parameters ![]() and
and ![]() in Eqs. (6), (7) can be
expressed using the bremsstrahlung cross-sections (Bai & Ramaty 1978; Leach & Petrosian 1983)
in Eqs. (6), (7) can be
expressed using the bremsstrahlung cross-sections (Bai & Ramaty 1978; Leach & Petrosian 1983)
where
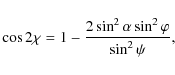
where
The expressions for the bremsstrahlung cross-sections in the relativistic case are given in the articles of Gluckstern & Hull (1953) and Bai & Ramaty (1978) by
In the above formulae, Z is the ion charge, r0 is the classical electron radius, k is the normalized photon impulse
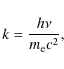
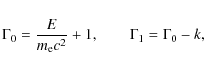
p0 and p1 are the normalized electron impulses before and after scattering, respectively
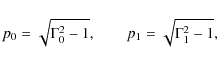
and the angle
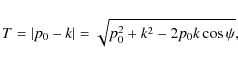
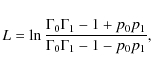
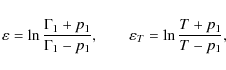
The factor QE is the Coulomb correction (Koch & Motz 1959):
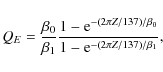
where
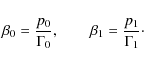
References
- Aschwanden, M. J. 2005, Physics of the Solar Corona. An Introduction with Problems and Solutions, 2nd edn., ed. M. J. Aschwanden [Google Scholar]
- Bai, T., & Ramaty, R. 1978, ApJ, 219, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, T. S. 1999, in Proceedings of the Nobeyama Symposium, held in Kiyosato, Japan, Oct. 27-30, 1998, ed. T. S. Bastian, N. Gopalswamy, & K. Shibasaki, NRO Rep., 479, 211 [Google Scholar]
- Bastian, T. S., Benz, A. O., & Gary, D. E. 1998, ARA&A, 36, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Battaglia, M., & Benz, A. O. 2006, A&A, 456, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benz, A., 2002, Plasma Astrophysics, second edition, Ap&SS Library, 279, [Google Scholar]
- Benz, A. O. 1977, ApJ, 211, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Boggs, S. E., Coburn, W., & Kalemci, E. 2006, ApJ, 638, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C. 1971, Sol. Phys., 18, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C. 1972, Sol. Phys., 26, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., & Loran, J. M. 1985, MNRAS, 212, 245 [NASA ADS] [Google Scholar]
- Brown, J. C., Emslie, A. G., Holman, G. D., et al. 2006, ApJ, 643, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Diakonov, S. V., & Somov, B. V. 1988, Sol. Phys., 116, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Elwert, G., & Haug, E. 1970, Sol. Phys., 15, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Emslie, A. G. 1978, ApJ, 224, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Emslie, A. G. 1980, ApJ, 235, 1055 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L., et al. 2010, Space Sci. Rev., submitted [Google Scholar]
- Gluckstern, R. L., & Hull, M. H. 1953, Phys. Rev., 90, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Grigis, P. C., & Benz, A. O. 2004, A&A, 426, 1093 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holman, G. D., Aschwanden, M. J., Aurass, H., et al. 2010, Space Sci. Rev., subm. [Google Scholar]
- Holman, G. D., Sui, L., Schwartz, R. A., & Emslie, A. G. 2003, ApJ, 595, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Kasparová, J., Kontar, E. P., & Brown, J. C. 2007, A&A, 466, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knight, J. W., & Sturrock, P. A. 1977, ApJ, 218, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, H. W., & Motz, J. W. 1959, Rev. Mod. Phys., 31, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P., & Brown, J. C. 2006, ApJ, 653, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P., MacKinnon, A. L., Schwartz, R. A., & Brown, J. C. 2006, A&A, 446, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kontar, E. P., Hannah, I. G., & MacKinnon, A. L. 2008, A&A, 489, L57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krucker, S., Battaglia, M., Cargill, P. J., et al. 2008, A&A Rev., 16, 155 [Google Scholar]
- Kundu, M. R., Grechnev, V. V., Garaimov, V. I., & White, S. M. 2001a, ApJ, 563, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Kundu, M. R., Nindos, A., White, S. M., & Grechnev, V. V. 2001b, ApJ, 557, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Kundu, M. R., Nindos, A., & Grechnev, V. V. 2004, A&A, 420, 351 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuznetsov, S. N., Kurt, V. G., Myagkova, I. N., Yushkov, B. Y., & Kudela, K. 2006, Sol. Sys. Res., 40, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Landau, L. D. 1937, Zh. Eksp. Teor. Fiz., 7, 203 [Google Scholar]
- Leach, J., & Petrosian, V. 1981, ApJ, 251, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Leach, J., & Petrosian, V. 1983, ApJ, 269, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, R. P., Krucker, S., Hurford, G. J., et al. 2003, ApJ, 595, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Masuda, S., Kosugi, T., Hara, H., Tsuneta, S., & Ogawara, Y. 1994, Nature, 371, 495 [NASA ADS] [CrossRef] [Google Scholar]
- McClements, K. G. 1992, A&A, 253, 261 [NASA ADS] [Google Scholar]
- McConnell, M. L., Smith, D. M., Emslie, A. G., et al. 2003, in BAAS, 35, 850 [Google Scholar]
- Samarskii, A. A. 2001, Monographs and Textbooks in Pure and Applied Mathematics, The theory of difference schemes (New York: Marcel Dekker Inc.), 240, translated from the Russian [Google Scholar]
- Simnett, G. M. 1995, Space Sci. Rev., 73, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Siversky, T. V., & Zharkova, V. V. 2009, A&A, in press [Google Scholar]
- Spicer, D. S. 1977, Sol. Phys., 54, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Suarez-Garcia, E., Hajdas, W., Wigger, C., et al. 2006, Sol. Phys., 239, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Sui, L., Holman, G. D., & Dennis, B. R. 2005, ApJ, 626, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Sui, L., Holman, G. D., & Dennis, B. R. 2007, ApJ, 670, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Sui, L., Holman, G. D., Dennis, B. R., et al. 2002, Sol. Phys., 210, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Tindo, I. P., Ivanov, V. D., Mandel'Stam, S. L., & Shuryghin, A. I. 1970, Sol. Phys., 14, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Tindo, I. P., Ivanov, V. D., Mandel'Stam, S. L., & Shuryghin, A. I. 1972a, Sol. Phys., 24, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Tindo, I. P., Ivanov, V. D., Valnícek, B., & Livshits, M. A. 1972b, Sol. Phys., 27, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Tindo, I. P., Shurygin, A. I., & Steffen, W. 1976, Sol. Phys., 46, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Tramiel, L. J., Novick, R., & Chanan, G. A. 1984, ApJ, 280, 440 [NASA ADS] [CrossRef] [Google Scholar]
- van den Oord, G. H. J. 1990, A&A, 234, 496 [NASA ADS] [Google Scholar]
- Vilmer, N., Krucker, S., Lin, R. P., & The Rhessi Team 2002, Sol. Phys., 210, 261 [NASA ADS] [CrossRef] [Google Scholar]
- White, S., et al. 2010, Space Sci. Rev., subm. [Google Scholar]
- Willson, R. F., & Holman, G. 2003, in BAAS, 35, 836 [Google Scholar]
- Zharkova, V. V., & Kobylinskii, V. A. 1993, Sol. Phys., 143, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V., Azner, K., Benz, A., et al. 2010, Space Sci. Rev., submitted [Google Scholar]
- Zharkova, V. V., Brown, J. C., & Syniavskii, D. V. 1995, A&A, 304, 284 [NASA ADS] [Google Scholar]
- Zharkova, V. V., & Gordovskyy, M. 2005, A&A, 432, 1033 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zharkova, V. V., & Gordovskyy, M. 2006, ApJ, 651, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Zhitnik, I. A., Logachev, Y. I., Bogomolov, A. V., et al. 2006, Sol. Sys. Res., 40, 93 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{11486Fig01a.eps}\hspace*{4...
...s}\hspace*{4mm}
\includegraphics[width=5.5cm,clip]{11486Fig01f.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg75.png)
|
Figure 1:
Electron distribution functions (in the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{11486Fig02a.eps}\hspace*{4...
...s}\hspace*{4mm}
\includegraphics[width=5.5cm,clip]{11486Fig02f.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg76.png)
|
Figure 2:
Electron distribution functions at the column depth of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{11486Fig03a.eps}\hspace*{4...
...s}\hspace*{4mm}
\includegraphics[width=5.5cm,clip]{11486Fig03f.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg77.png)
|
Figure 3:
Electron distribution functions at the column depth of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11486Fig04a.eps}\hspace*{4mm}
\includegraphics[width=8.5cm,clip]{11486Fig04b.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg78.png)
|
Figure 4:
Dependencies of the density of precipitating electrons on a
column density of the ambient plasma. Dotted line: downward propagating particles ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{11486Fig05a.eps}\par\includ...
...par\includegraphics[width=17cm,clip]{11486Fig05f.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg79.png)
|
Figure 5:
Intensity (in relative units) and polarization of the hard X-ray
emission for the different energies. Initial power-law indices of the
accelerated particles are: |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{11486Fig06a.eps}\hspace*{4...
...s}\hspace*{4mm}
\includegraphics[width=8.1cm,clip]{11486Fig06f.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg96.png)
|
Figure 6:
Directivity and polarization of the hard X-ray emission for different
propagation directions. The electron distribution functions are
obtained with taking into account different factors (see Fig. 1), the initial power-law indices of beam electrons
are |
| Open with DEXTER | |
| In the text | |
| |
Figure 7:
Integrated by column depth intensity (in relative units) and polarization of hard X-ray
emission for different energies. The initial power-law indices of the
beam electrons are: |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11486Fig08.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg98.png)
|
Figure 8:
Directivity and polarization of the hard X-ray emission for the
different propagation directions. The emission parameters are integrated
over all layers of coronal magnetic tube. Initial power-law indices of the
accelerated particles are: |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11486Fig09a.eps}\hspace*{4...
...s}\hspace*{4mm}
\includegraphics[width=8.5cm,clip]{11486Fig09d.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg99.png)
|
Figure 9:
The hard X-ray double power-law spectra observed by RHESSI for the flares of 23 July 2002 ( upper plots) and 20 July 2002 ( lower plots) for the times plotted in the top right corners of each plot. The top left and right plots correspond to the electron energy fluxes of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=7.8cm,clip]{polar_20keV_bw.eps}\...
...*{4mm}
\includegraphics[width=7.8cm,clip]{polar_200keV_bw.eps} }\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg101.png)
|
Figure 10:
Comparison of the simulations of HXR bremsstrahlung polarization for 20 keV ( left plot) and 200 keV ( right plot) produced for different position angle on the solar disk (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=7.8cm,clip]{direct_20keV_bw_lege...
...*{4mm}
\includegraphics[width=7.8cm,clip]{direct_200keV_bw.eps} }\end{figure}](/articles/aa/full_html/2010/04/aa11486-08/Timg107.png)
|
Figure 11:
A comparison of the directivity estimations inferred for energies
20-200 keV from the statistical survey of different flare
positions at the solar disk (
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



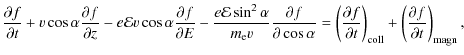
![\begin{displaymath}
\left.f(E, \mu, t)\right\vert _{z=z_{\min}}=\left\{\begin{ar...
...>0,~t\ge 0,\\ [10pt]
0,~\textrm{elsewhere},
\end{array}\right.
\end{displaymath}](/articles/aa/full_html/2010/04/aa11486-08/img32.png)
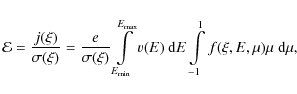
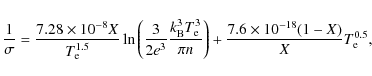
$](/articles/aa/full_html/2010/04/aa11486-08/img59.png)
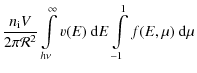
~{\rm d}\varphi,$](/articles/aa/full_html/2010/04/aa11486-08/img61.png)
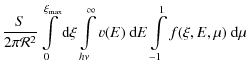
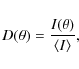
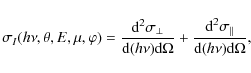
![\begin{displaymath}
\sigma_Q(h\nu, \theta, E, \mu, \varphi)=\left[
\frac{\textrm...
..._{\Vert}}{\textrm{d}(h\nu)\textrm{d}\Omega}
\right]\cos 2\chi,
\end{displaymath}](/articles/aa/full_html/2010/04/aa11486-08/img116.png)
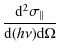
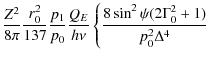
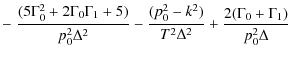
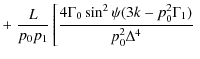
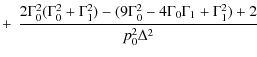
![$\displaystyle +\left.\left.
\frac{k(\Gamma_0^2+\Gamma_0\Gamma_1)}{p_0^2\Delta}\right]\right.$](/articles/aa/full_html/2010/04/aa11486-08/img128.png)
![$\displaystyle +\left.\frac{\varepsilon^T}{p_1T}\left[\frac{4}{\Delta^2}-\frac{7...
...
\frac{k(p_0^2-k^2)}{T^2\Delta}-4\right]-\frac{4\varepsilon}{p_1\Delta}
\right.$](/articles/aa/full_html/2010/04/aa11486-08/img129.png)
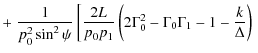
![$\displaystyle -\left.\left.\frac{4\varepsilon^T(\Delta-\Gamma_1)^2}{p_1T}-
\frac{2\varepsilon(\Delta-\Gamma_1)}{p_1}\right]\right\},$](/articles/aa/full_html/2010/04/aa11486-08/img131.png)
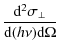
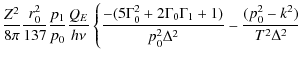
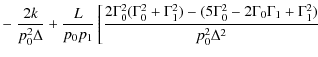
![$\displaystyle +\left.\left.
\frac{k(\Gamma_0^2+\Gamma_0\Gamma_1-2)}{p_0^2\Delta...
...^T}{p_1T}\left[\frac{k}{\Delta}-
\frac{k(p_0^2-k^2)}{T^2\Delta}+4\right]\right.$](/articles/aa/full_html/2010/04/aa11486-08/img135.png)
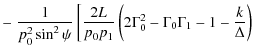
![$\displaystyle -\left.\left.\frac{4\varepsilon^T(\Delta-\Gamma_1)^2}{p_1T}-
\frac{2\varepsilon(\Delta-\Gamma_1)}{p_1}\right]\right\}\cdot$](/articles/aa/full_html/2010/04/aa11486-08/img137.png)