EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 511 (February 2010) A&A, 511 (2010) L6 Full HTML
Free Access
Issue
A&A
Volume 511, February 2010
Article Number L6
Number of page(s) 4
Section Letters
DOI https://doi.org/10.1051/0004-6361/200913878
Published online 05 March 2010
A&A 511, L6 (2010)

LETTER TO THE EDITOR

Spectral signatures of ultra-rapidly varying objects in spectroscopic surveys

E. F. Borra

Centre d'Optique, Photonique et Laser, and Centre de Recherche en Astrophysique du Québec, Département de Physique, Université Laval, Québec, Qc, Canada G1K 7P4

Received 15 December 2009 / Accepted 11 February 2010

Abstract
Context. Astronomy is an observationally-led subject where chance discoveries play an important role. The time domain is the least explored in astronomy.
Aims. We alert spectroscopists, particularly those involved in surveys, that rapidly varying sources can induce periodic patterns in spectra.
Methods. The analytical treatment is based on standard Fourier theory. It is used to predict the shapes of features introduced by intensity pulses in spectra. These are the shapes that one must look for in spectral surveys. The theoretical analysis is supported by published experiments that measured the spectral modulation, in the visible wavelength region, caused by pairs of 150 femtosecond laser pulses separated by time periods varying between $ \ 5\times 10^{-13}\ $ s and $ 3 \times 10^{-11} $ s.
Results. Detection of spectral signatures would allow the detection of new classes of objects that emit bursts of pulses separated by time intervals that are too short to be detected with conventional techniques. The principal advantage of the technique is that there is no need for specialized instruments or surveys: one must only incorporate algorithms capable of searching for periodic spectroscopic signals, such as those shown in a figure in this article, into existing data analyzis software and use it with standard spectroscopic surveys (including existing ones).

Key words: techniques: spectroscopic - methods: data analysis - radiation mechanisms: general

1 Introduction

Astronomy is an observationally-led subject where chance discoveries play an important role. In an article entitled ``Serendipity in Astronomy'' Fabian (2009) discusses at length the role that serendipity has historically played in astronomy and remarks that the time domain is the least explored in astronomy yet continues to be rich in discoveries. Pulsars appear to have the most rapid time variations. The Crab pulsar emits nanoshots with durations of nanoseconds (Hankins & Eilek 2007). Hankins & Eilek (2007) find extreme cases of nanoshots that are unresolved at the 0.4 ns instrumental resolution. These short time scales exclude thermal processes as the cause of the variability because they imply brightness temperatures of $2 \times 10^{41}~\rm K $ (an energy density $ \ 10^{136}\ $ times the energy density at the center of the sun). These pulses are evidently generated by unknown exotic physical processes.

Present techniques for observing variable objects measure intensity time variations and cannot detect time variations shorter than a fraction of a nanosecond. It is therefore possible that there are some classes of exotic astronomical objects undergoing ultra-rapid periodic pulsations that have yet to be discovered. The bandwidth of observation places a fundamental limitation on the timescales that can be measured. For example, the 1 GHz bandwidth typically used with observations in the GHz radio region limits one to times longer than 1 nanosecond (Hankins et al. 2003). The optical region, where bandwidths are typically much broader than thousands of GHz, is suitable for detecting objects that vary on timescales significantly shorter than nanoseconds. Astronomical spectroscopic surveys occur increasingly frequently. Most spectroscopists are probably unaware that periodic time variations in the intensity signal originating in a pulsating source modulate its spectrum with periodic structures. The main purpose of this article is to alert spectroscopists, in particular those carrying out spectroscopic surveys, to search for periodic structures in spectra. Ultra-rapid pulsators may also be detected from their peculiar colors in multi-color narrow-band surveys.

2 Spectral modulations from pulsating objects

The theory that follows is supported by the experiments of Chin et al. (1992). With a grating spectrometer, they measured spectral modulation in the visible wavelength region caused by pairs of 150 femtosecond laser pulses separated by times varying between $ \ 5\times 10^{-13}\ $ s and $ 3 \times 10^{-11} $ s. The pairs of pulses were periodically emitted at intervals of $ 1.3\times 10^{-8} $ s. We use standard Fourier theory to predict the shapes of the features that pulses introduce in spectra.

We begin by considering the simple model of a periodically pulsating source which can be extended to more complex time variations. We consider a pulsating source with a time dependent electric field E(t) sending a burst that consists of N pulses V(t) separated by a time interval $ \tau $. It can be modeled by the convolution of V(t) with a comb function $\sum\limits_{m = 1}^N {\delta (t - t_m } ) $ giving

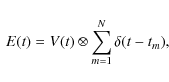
\begin{displaymath}\ E(t) = V(t) \otimes \sum\limits_{m = 1}^N {\delta (t - t_m } ) ,\end{displaymath} (1)

where $ \delta (t-t_{m}) $ is the delta function, $ t_{m}= (m-1)\tau $, and m an integer number.

We follow a mathematical treatment, similar to that used to model diffraction gratings found in many optics textbooks (e.g., Chap. 5 of Klein & Furtak 1986). The Fourier transform of E(t) infers that

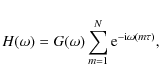
\begin{displaymath}H(\omega ) = G(\omega )\sum\limits_{m = 1}^N {{\rm e}^{ - {\rm i}\omega (m\tau )} } ,\end{displaymath} (2)

where $ \omega $ is the frequency of the observation. Equation (2) reduces to

\begin{displaymath}H(\omega ) = G(\omega ){\rm e}^{{\rm i}(N - 1)\omega \tau /2}... ...ft[ {\sin (\omega N\tau /2)/(\sin (\omega \tau /2))} \right] .\end{displaymath} (3)

Astronomical spectrographs detect the time average of $ S(\omega)=H(\omega)H^{*}(\omega)$, where the asterisk indicates complex conjugation. Using Eq. (3), we obtain

\begin{displaymath}S(\omega ) = S_1 (\omega )\left[ {\sin (\omega N\tau /2)/(\sin (\omega \tau /2))} \right]^2 .\end{displaymath} (4)

The experiments of Chin et al. (1992) illustrate the sinusoidal modulation of $ S( \omega ) $ predicted for 2 pulses by Eq. (4) with N = 2 as

\begin{displaymath}S(\omega ) = S_1 (\omega )\left[ {2\cos(\omega \tau /2)} \right]^2 .\end{displaymath} (5)

With increasing N, Eqs. (3) and (4) predict comb-like shapes with sharp peaks separated by $ 2\pi/\tau $. Figure 1 shows $ S( \omega ) $ for N = 2, 5 and 10, where N gives the number of pulses that generated the spectrum and $ \tau $ the time between pulses. The teeth of the comb become increasingly sharper as N increases, such that $ S( \omega ) $ will closely resemble a comb function consisting of $ \delta $ functions for very large N. We note that this resembles the basic physics of frequency comb technology, where a rapidly pulsed laser generates a sequence of very short optical pulses that produce an optical spectrum made of a series of Dirac delta functions. Steinmetz et al. (2008) describe astronomical applications of frequency combs.

\begin{figure} \par\includegraphics[width=9cm,clip]{13878fg1.eps} \end{figure} Figure 1:

This figure provides examples of spectra from pulsating sources. It shows the spectral signature $ S( \omega ) $, given by Eq. (4), for N = 2, 5, and 10. The signal could also be superimposed on a continuous spectrum, thereby decreasing the contrast.

Open with DEXTER

Equations (3)-(5) show that the periodic frequency spacing is inversely proportional to the time between pulses $ \tau $. This would allow us to directly observe pulses separated by times shorter than 10-10 s with standard spectroscopic equipment in the visual-infrared regions of the spectrum. One could measure time separations orders of magnitude shorter than the nanosecond time separation limits of current techniques (e.g., Howard et al. 2004).

This opens up the possibility of finding astronomical objects that pulsate with extremely short periods undetectable with presently used techniques. It would also be possible to detect either non-periodic sources that send bursts of periodic signals or periodic sources with relatively long periods that emit bursts of short-period signals. An example of this would be a source that sends random bursts of pairs of pulses. The time separation between pulses also does not have to be rigorously constant. A variation of $ \tau $ would simply decrease the contrast predicted by Eq. (4) and seen in Fig. 1.

Because Fourier theory predicts that the period between spectral maxima is inversely proportional to the time between pulses $ \tau $, very short periods will generate spectral features widely separated in frequency. Because spectra are usually limited in frequency by the detector, it is possible that only a single sharp emission feature may be found if $ N \gg 2 $. It may then be mistaken as the spectral emission line of a peculiar object (e.g., a high-redshift quasar). When $ \tau $ is small and N= 2, the spectral limitations of the detector may not enable an entire cycle to be studied and only give a curved spectrum.

Widely separated spikes may also be detected in broad-band photometric surveys because of their generation of peculiar colors. An object detected in a single filter would be particularly suspicious.

3 Discussion of the applicability of the spectral modulation theory

Although the basic theory on which this article is based is validated by the experiments of Chin et al. (1992), one may argue that the pairs of pulses in Chin et al. (1992) are coherent, since the division was performed by a Michelson interferometer, while the pulses in an astronomical source may not be coherent. One may then proceed to argue that while coherent light beams interfere, it is ``well-known'' that incoherent ones do not.

Firstly, we note that exotic objects capable of generating ultra-rapid pulses may generate pulses that are coherent in the classical sense. Secondly, the ``well-known'' statement of the opening paragraph, sometimes contained in optics books, is wrong. Interference between independent optical sources has been experimentally demonstrated since Magyar & Mandel (1963) detected interference effects by using integration times shorter than the coherence time. The reason why classical interference experiments do not detect interference is that they use integration times considerably longer than the coherence time of the light used: they therefore time-average over times significantly longer than the coherence time. Because phase randomly fluctuates over times longer than the coherence time, the long-term time-average of the interference pattern is not modulated. Furthermore, coherence can be artificially induced by periodic pulsation, allowing interference to be detected even after time-averaging. This was demonstrated by the experiment of Alford & Gold (1958) which detected interference between two beams originating in two orthogonal directions of the same periodically pulsating thermal source (an electric spark). For all essential purposes, the interfering beams in Alford & Gold (1958) originate in independent light sources. Coherence is artificially induced by pulsation because pulsation ensures that the 2 beams generated at orthogonal directions, hence incoherent in the classical sense, are emitted with synchronized phases. In an ultra-rapidly pulsating source, the constancy of $ \tau $ would ensure phase synchronization. Givens (1961) provides a theoretical analysis of the Alford & Gold (1958) experiment.

Intuitively, one may expect that searches for picosecond variability would require detection precisions of the order of one photon per picosecond and therefore photon count rates of the order of terahertzs. However, this is not the case because spectroscopic techniques use interference effects and a correct treatment must therefore use quantum mechanical wavefunctions and not the particle model. Hussain, Imoto & Loudon (1992) discuss in detail the quantum theory of interference effects, concluding that wave-interaction effects provided a correct description and not, as they write, ``the expectations of the naive particle model''. Compared to the particle model, this has highly non-intuitive consequences for interaction effects at low photon counting rates. For example, Godzinzki (1991) carried out optical interference experiments at extremely low intensities, finding that the fringe contrast is independent of intensity. He finds full contrast at counting rates as low as 12 photons/second, which implies mean inter-photon distances of 24 000 km (Godzinzki 1991). He concludes that the experiments fully confirm the validity of the wavefunction picture of the light phenomenon. We note that Godzinzki (1991) uses classical interferometry where, in particle language, ``the photon interferes with itself''. In the quantum mechanical interpretation, the words between quotes signify a source that interferes with itself by the means of a beam splitter. Experiments (Magyar & Mandel 1963) show that independent sources (``independent photons'') also interfere with each other.

Because pulsations induce spectral modulations, the signal-to-noise ratio (S/N) is given by the usual relations valid for stellar spectroscopy. Because it depends on several parameters (e.g., spectral resolution, telescope diameter, seeing, sky background) a detailed discussion would be too lengthy. We thus confine ourselves to a single example that adequately represents the problem: a source of magnitude B =22 that sends pulses separated by 1 picosecond. At 5500 $\AA$, there is a spectral modulation consisting of spikes with shapes given by the instrumental function and separated by 10 $\AA$. I estimated the S/N with the CTIO observatory exposure calculator for the R-C spectrograph and the KPGL3 grating (527 lines/mm, 1st order 5500 $\AA$ blaze) of the 4-m Blanco telescope. With a 1.2 arcsec slit, 1 arcsec seeing and no moonlight, it predicts a S/N of 4.8 per resolution element (2.92 $\AA$) at 5500 $\AA$ for B = 22. With a 10 $\AA$ separation between peaks, the spectral modulation would thus be clearly visible, especially considering that the S/N = 4.8 is for a uniform energy distribution, while in our case the energy is distributed among spikes. The S/N of a spectral spike would thus be about 8. The S/N of the signature will be even greater since there would be 100 spikes within a 1000 $\AA$ spectral window. This single example shows that faint pulsating objects could be readily identified. Given similar parameters, a multislit survey would have a comparable performance.

Spectral modulations may also be generated by well-known effects. For example, instrumental effects would be easily identified because they would be presented in all objects. Pulsating sources may have some particular signatures, for example, the shapes shown in Fig. 1 or their constant frequency separation $ \Delta\omega=2\pi/\tau $. Non-thermal sources may also be polarized.

Scattering effects from the interstellar medium can be severe for very distant objects (Howard et al. 2004), thus reducing the contrast of the spectral modulation, but are negligible for nearby objects. The effect will depend on position and distance, being worse in the direction of the Galactic plane and minimum near the Galactic poles. In the worse-case scenario (in the Galactic disk) the reduction in pulse height is modest (less than 10%) at visible wavelengths for distances less than 500 pc but becomes unmanageable, within the Galactic disk, at substantially greater distances (Howard et al. 2004). The effect would be negligible in the direction of the Galactic poles.

One also must consider the effect of the terrestrial atmosphere. Kelly et al. (1998) studied the temporal broadening of ultra-short space-time Gaussian pulses. Their analysis includes the effect of pulse wander because of both seeing and scattering effects. Broadening is important for 10 femtosecond pulses but becomes negligible for 100 femtoseconds and beyond. Broadening is of lesser importance for data taken at astronomical observatories, usually located on mountaintops. There is no broadening effect for data obtained with space telescopes (e.g., Hubble).

One must beware that instrumental effects can possibly induce spurious spectral modulations, for example caused by standing waves in the detector or the telescope. Fortunately, they can be readily detected from the spectra of bright sources.

4 Comparison with other optical search techniques

Any novel technique must answer two questions: what are its advantages and disadvantages over existing techniques?

The physical parameters of many astronomical objects vary in time. Variable objects are commonly detected by observing how intensity varies as a function of time. While this is effective for sources that have sufficiently slow time variations, it becomes inefficient and eventually inadequate as the timescale of variation decreases. Optical searches for rapid variations in astronomical objects have been proposed and carried out, principally to search for extraterrestrial intelligence (Howard et al. 2004; Stone et al. 2005; Hanna et al. 2009). They search for optical intensity pulses detected with fast electronics. In practice, they are limited to nanosecond timescales and bright objects (a few tens of thousands of nearby stars at most). The next generation of instruments that uses photon correlation effects capable of high time resolutions will be very complex and require very large telescopes (Barbieri et al. 2007; Dravins et al. 2006). Furthermore, instruments that measure intensity variations are limited by being unable to detect time variations shorter than some fundamental limits set by detectors and electronics.

This article proposes detection in the spectrum and not in the intensity versus time domain. The spectral technique is effective on timescales at which the intensity techniques gives up (nanoseconds) and goes down to picoseconds and beyond.

While the current intensity-based searches for rapid time variations use photomultipliers can only observe one object at a time and are limited to a few tens of thousands of bright objects, the spectral modulation technique can go considerably fainter and observe billions of objects, since the search is performed in spectra from standard surveys (e.g., SDSS or upcoming LSST). Spectroscopic surveys observe large numbers of objects that fit inside two-dimensional detectors (e.g., CCDs). They therefore make more efficient use of telescope time.

A small advantage that allows reaching fainter magnitudes is that surveys are insensitive to readout noise because of their long integration times, which is a problem with the shorter than nanosecond times needed with intensity techniques.

However, the main advantage of the technique is its simplicity. There is no need for specialized instruments or surveys. All one has to do is to incorporate simple signal-finding algorithms that detect the type of spectral signature predicted by Eq. (4) (see also Fig. 1) into existing software and use them with existing databases and future spectroscopic surveys.

5 Energy density considerations

Although, at this point in time, serendipity is the only justification for a search, it must make a minimum of physical sense, while at the same time one must not be too narrow-minded. For example, we must not forget that astronomical phenomena with periods of fractions of seconds were not known before 1950 and that the discovery of pulsars was totally unexpected. A detailed discussion of physical phenomena is beyond the scope of this article and, furthermore, would be an exercise in futility since serendipity is the principal justification. We therefore only briefly consider the physical limits involved.

One may question the basic physics responsible for the pulses, the energy requirements, and the energy density. The experiments of Chin et al. (1992) show that there is no violation of basic physical principles. However, a potential problem is that short timescales are indicative of small volumes and consequently high energy densities for distant objects that thermal sources and well-understood physics may have problems explaining. However, we first note that the pulsating objects may be relatively faint nearby objects (e.g. within the solar system itself), thereby relieving the energy requirement. We also note that the basic physics of several serendipitously discovered astronomical sources that also have energy density problems, is not understood. In particular, the 2 nanosecond radio bursts observed in pulsars by Hankins et al. (2003) cannot be explained with conventional physics. At 2 nanoseconds, we are near the lower limit of the timescales detectable in spectra. Hankins et al. (2003) speculate about the physics involved. The extreme nanopulses discussed by Hankins & Eilek (2007) are particularly puzzling. They are unresolved at 0.4 ns resolution and have an implied brightness temperature of $2 \times 10^{41}~\rm K $. By considering that the energy density of the brightness temperature increases with the fourth power of the temperature, $ 10^{41}~\rm K $ implies an energy density 10136 times the energy density at the center of the Sun! Hankins & Eilek (2007) conclude that exotic non-thermal mechanisms are obviously responsible. We note that the narrower than 0.4 ns width of the nanopulses is comparable to the separations detectable in optical spectra.

In conclusion, although no astronomical object is presently expected to pulsate below the nanosecond timescales, there are no fundamental reasons for excluding that such sources may exist.

6 Conclusion

That a periodic variation in the light intensity of a source generates a periodic modulation in its spectrum opens up the possibility of findings new classes of objects undergoing extremely rapid time variations. Extremely rapid pulsators that emit pulses with time separations between 10-13 and 10-10 s could be detected. One could also detect objects that emit bursts of short-period signals. The modulation could be superimposed on a continuous spectrum, thereby decreasing the contrast shown in Fig. 1.

Fabian (2009) discusses at length the important role that serendipity has historically played in astronomy. Indeed, serendipity is the only justification for carrying out a search for ultra-rapid variations in spectra. At this point in time, there is no indication of any astronomical object that would emit the type of signal that could be detected in spectra and it probably would not be worth the effort if specialized surveys or instruments were needed. However, all one has to do is to incorporate signal-finding algorithms (e.g., Fourier transforms) to detect the type of spectral features predicted by Eqs. (4) and (5) into existing software and use them with existing databases and future spectroscopic or multicolor surveys. It is a very small amount of work worth doing because finding rapidly pulsating objects is of enormous interest. This would particularly be the case if the pulses originated from extraterrestrial intelligence. It would be a small effort, especially considering the impact of this discovery.

Finally, even if no ultra-rapid pulsator is found, the lack of detection may be used to eliminate exotic theories.

Acknowledgements
This research has been supported by the Natural Sciences and Engineering Research Council of Canada

References

  1. Alford, W. P., & Gold, A. 1958, Am. J. Phys., 26, 481 [NASA ADS] [CrossRef] [Google Scholar]
  2. Barbieri, C., Dravins, D., Occhipinti, T., et al. 2007, J. Mod. Opt., 54, 191 [NASA ADS] [CrossRef] [Google Scholar]
  3. Chin, S. L., Francois, V., Watson, J. M., & Delisle, C. 1992, Applied Optics, 31, 3383 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  4. Dravins, D., Barbieri, C., Fosbury, R. A. E., et al. 2006, IAU Symp., 232, 502 [NASA ADS] [Google Scholar]
  5. Fabian, A. C. 2009 [arXiv:0908.2784] [Google Scholar]
  6. Givens, M. P. 1961, J. Opt. Soc. Am., 51, 1030 [CrossRef] [Google Scholar]
  7. Godzinzki, Z. 1991, Phys. Lett. A, 153, 291 [NASA ADS] [CrossRef] [Google Scholar]
  8. Hankins, T. H., & Eilek, J. A. 2007, ApJ, 670, 693 [NASA ADS] [CrossRef] [Google Scholar]
  9. Hankins, T. N., Kern, J. S., Weatherall, J. C., & Ellek, J. A. 2003, Nature, 422, 141 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  10. Hanna, D. S., Ball, J., Covault, C. E., et al. 2009, Astrobiology, 9, 345 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  11. Howard, A. W., Horowitz, P., Wilkinson, D. T., et al. 2004, ApJ, 613, 1270 [NASA ADS] [CrossRef] [Google Scholar]
  12. Hussain, N., Imoto, N., & Loudon, R. 1992, Phys. Rev. A, 45, 1987 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  13. Kelly, D. E., Young, C. Y., & Andrews, L. 1998, Proc. SPIE, 3266, 231 [NASA ADS] [CrossRef] [Google Scholar]
  14. Klein, M. V., & Furtak, T. E. 1986 (New York: Optics, John Wiley & Sons) [Google Scholar]
  15. Magyar, G., & Mandel, L. 1963, Nature, 198, 256 [NASA ADS] [CrossRef] [Google Scholar]
  16. Steinmetz, T., Wilken, T., Araujo-Hauck, C., et al. 2008, Science, 321, 1335 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  17. Stone, R. P. S., Wright, S. A., Drake, F., et al. 2005, Astrobiology, 5, 604 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{13878fg1.eps} \end{figure} Figure 1:

This figure provides examples of spectra from pulsating sources. It shows the spectral signature $ S( \omega ) $, given by Eq. (4), for N = 2, 5, and 10. The signal could also be superimposed on a continuous spectrum, thereby decreasing the contrast.

Open with DEXTER
In the text
Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.