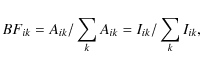| Issue |
A&A
Volume 511, February 2010
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 5 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/200913672 | |
| Published online | 11 March 2010 | |
The FERRUM project: laboratory-measured
transition probabilities for Cr II![[*]](/icons/foot_motif.png)
J. Gurell1 - H. Nilsson2 - L. Engström3 - H. Lundberg3 - R. Blackwell-Whitehead2 - K. E. Nielsen4,5 - S. Mannervik1
1 - Department of Physics, Stockholm University, AlbaNova University
Center, 10691 Stockholm, Sweden
2 - Lund Observatory, Lund University, Box 43, 22100 Lund, Sweden
3 - Atomic Physics, Department of Physics, Lund University, Box 118,
22100 Lund, Sweden
4 - Catholic University of America, Washington, DC 20064, USA
5 - Astrophysics Science Division, Code 667, Goddard Space
Flight Center, Greenbelt, MD 20771, USA
Received 16 November 2009 / Accepted 15 December 2009
Abstract
Aims. We measure transition probabilities for Cr II
transitions from the z 4HJ,
z 2DJ,
y 4FJ,
and y 4GJ
levels in the energy range 63 000 to
68 000 cm-1.
Methods. Radiative lifetimes were measured using
time-resolved laser-induced fluorescence from a laser-produced plasma.
In addition, branching fractions were determined from
intensity-calibrated spectra recorded with a UV Fourier transform
spectrometer. The branching fractions and radiative lifetimes were
combined to yield accurate transition probabilities and oscillator
strengths.
Results. We present laboratory measured transition
probabilities for 145 Cr II lines and
radiative lifetimes for 14 Cr II levels.
The laboratory-measured transition probabilities are compared to the
values from semi-empirical calculations and laboratory measurements in
the literature.
Key words: atomic data - line: identification - methods: laboratory - techniques: spectroscopic
1 Introduction
Spectral analysis of astrophysical objects depends on the availability of accurate laboratory data including radiative lifetimes and transition probabilities. Lines of Cr II are observed in a broad range of stellar and nebular spectra (e.g. Merrill 1951; Shevchenko 1994; Andrievsky et al. 1994), and accurate Cr data are required for stellar abundance studies (Babel & Lanz 1992; Dimitrijevic et al. 2007). In particular, several chemically peculiar stars show unexpectedly high abundances of Cr (Rice & Wehlau 1994; López-García et al. 2001).
Radiative lifetimes in Cr II have been measured with the beam-foil technique by Pinnington et al. (1973) and Engman et al. (1975) and with the time-resolved laser-induced fluorescence (TRLIF) technique by Schade et al. (1990), Pinnington et al. (1993), and Nilsson et al. (2006). In addition, branching fraction (BF) measurements were combined with radiative lifetimes to yield transition probabilities (Bergeson & Lawler 1993; Spreger et al. 1994; Gonzalez et al. 1994; Nilsson et al. 2006), and oscillator strengths were measured by Musielok & Wujec (1979), Goly & Weniger (1980) and Wujec & Weniger (1981) using a wall-stabilized arc. Semi-empirical oscillator strengths have been calculated by Kurucz (1988) using the Cowan code, by Luke (1988) using the R matrix method, and by Raasen & Uylings (1997) using the orthogonal operator method.
Several studies have found that the stellar chromium abundance determined from Cr I lines is significantly different to the abundance using Cr II lines (McWilliam et al. 1995; Sobeck et al. 2007; Lai et al. 2008). This difference is greater than the uncertainty in the stellar observations and measured oscillator strengths. Furthermore, the difference increases as the metallicity of the star decreases. Sobeck et al. (2007) indicate that one possible explanation of this discrepancy could be non-LTE effects not included in the stellar model. Sobeck et al. (2007) propose that, in order to resolve this issue additional laboratory investigations of chromium should focus on weak branches of Cr II and that the Cr abundance should be reanalyzed with a three-dimensional hydrodynamical model. In addition, the need for more laboratory measured Cr II transition probabilities is discussed by Wallace & Hinkle (2009).
![\begin{figure}
\par\includegraphics[width=13cm,clip]{13672fg1.eps}\end{figure}](/articles/aa/full_html/2010/03/aa13672-09/Timg6.png)
|
Figure 1:
Partial energy level diagram of Cr II (Ralchenko et al. 2009). Only terms belonging to the |
| Open with DEXTER | |
In this paper we present transition probabilities for 145 lines in Cr II from 14 upper levels, see the partial energy level diagram of Cr II in Fig. 1. The lifetimes of the upper levels have been measured with the TRLIF technique.
2 Laboratory measurements
The lifetime of an upper state i can be
written as
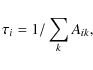
|
(1) |
where Aik is the transition probability of a line from upper level i to lower level k. The BF of the line is defined as
where Iik is the measured intensity corrected for the instrumental response. Combining these two equations gives the transition probabilities as
The following subsections describe the measurements of the lifetimes and BFs.
2.1 Radiative lifetimes
We measured lifetimes for 14 odd parity levels in Cr II
belonging to the ![]() configuration. The lifetimes were measured using the TRLIF technique at
the Lund High Power Laser Facility. This technique has been described
in detail in the literature (see Bergström
et. al. 1988;
Xu et al. 2003), so only a brief description
is given here.
configuration. The lifetimes were measured using the TRLIF technique at
the Lund High Power Laser Facility. This technique has been described
in detail in the literature (see Bergström
et. al. 1988;
Xu et al. 2003), so only a brief description
is given here.
Table 1: Lifetimes in Cr II.
A laser-produced ``plasma-cone'' containing Cr atoms and ions in metastable levels was created by focusing a Nd:YAG laser (Continuum Surelite) onto a target of pure Cr. Cr+ ions in metastable states were excited to levels of opposite parity using a pump laser and the fluorescence from the excited levels was recorded as a function of time. The excitation pulses were created by pumping a Continuum Nd-60 dye laser with a Nd:YAG Continuum NY-82 laser. The pulses from the Nd:YAG pump laser were shortened from 10 to 1.5 ns using stimulated Brillouin scattering. The Nd-60 dye laser used a DCM dye to produce light between 6000 and 6700 Å. A broader wavelength coverage was achieved by using nonlinear effects in KDP and BBO crystals and Raman shifts in a H2 cell.
A 1/8 m monochromator was used to select the observable fluorescence wavelength. The fluorescence signal was recorded with a micro-channel plate photomultiplier tube with a rise time of 0.2 ns. The shape of the excitation pulse was measured with the same system as the fluorescence signal. The lifetimes were extracted by fitting the fluorescence data with a single exponential convoluted with the shape of the laser pulse. Each lifetime curve was averaged over 1000 laser shots, and the final lifetimes given in Table 1 are averages of at least 10 lifetime curves. The uncertainties in the lifetimes include both statistical and systematic errors.
2.2 Branching fractions
The BFs were measured from spectra recorded with the Chelsea Instrument FT500 UV FT spectrometer at Lund Observatory. The light source was a Penning discharge lamp with pure Cr cathodes and operated with Ne as buffer gas. The light source was operated at a current between 0.8 and 1.3 A, and with at a carrier gas pressure of 40 mTorr. The Penning discharge lamp provides an intensity stable emission spectrum over several hours enabling high signal-to-noise (S/N) spectra to be recorded. Figure 2 shows part of the observed spectrum.
Three separate spectral regions were recorded to cover the wavenumber region between 20 000 and 52 000 cm-1. The spectra were intensity-calibrated with standard lamps with known spectral radiances and by Cr II BFs previously measured by Nilsson et al. (2006). A continuous deuterium (D2) lamp was used in the wavenumber range 32 000-52 000 cm-1. A tungsten strip lamp was used in the wavenumber range 20 000-28 000 cm-1 and the 28 000-32 000 cm-1 wavenumber region was calibrated using previously intensity-calibrated Cr II BFs from the data of Nilsson et al. (2006). The calibration was performed with a software routine implemented in the program XGremlin (Nave et al. 1997). In addition, the spectra were wavenumber-calibrated using an average of nine unblended Ne II lines, which have been measured with high accuracy and suggested as suitable transitions for wavenumber calibration by Öberg (2007).
However, the wavelengths and wavenumbers in Tables 2 and 3 are Ritz values determined from the energy levels in Ralchenko et al. (2009).
The spectral lines were fitted with Voigt profiles to determine the integrated intensity using the commercially available software PeakFit. The uncertainty in the integrated intensity is determined from the standard deviation in the fitted values and the S/N of the lines. The majority of the fitted Cr II line profiles were unblended. However, a small number of Cr II lines were partially blended with other lines. The blended features were identified, and a fit of both line profiles was performed when possible. The blended Cr II lines are given with larger uncertainties in the integrated intensity.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13672fg2.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13672-09/Timg18.png)
|
Figure 2: A section of the FT spectrum showing five Cr II lines indicated by their respective wavenumber. |
| Open with DEXTER | |
3 Results
Our experimental lifetimes are compared to previous measurements and calculations in Table 1. Table 2 shows our laboratory measured BFs, A-values and semi-empirical BFs. The complete line list for all Cr II lines measured in this paper with comparisons to semi-empirical log gf values in the literature is shown in Table 4. A comparison between our measured A-values and values presented in the literature is shown in Table 4.
3.1 Lifetimes
Table 4: A comparison between our A-values and the A-values in the literature.
In Table 1 we report radiative lifetimes for 14 levels in Cr II compared with values from the literature. Our experimental lifetimes of the z 4H term agree, within the uncertainties, with the beam-foil measurements by Pinnington et al. (1973) and by Engman et al. (1975), and the experimental lifetimes of Warner (1967). There is a good agreement between our lifetimes and the values from Raasen & Uylings (1997); however, the calculated values by Warner (1967) and Luke (1988) are shorter than our lifetimes by approximately four standard deviations.
There is a a three-sigma difference between our lifetimes for the y 4G term and the measured values of Pinnington et al. (1973). The difference may come from the improved wavelength resolution of our measurements. Pinnington et al. (1973) were not able to resolve the four individual levels y 4G and measured an average lifetime determined from a blend of transitions from these levels. Pinnington et al. (1973) also states that the assignment of the transition from the y 4G term at 2700 Å is one of the ``less certain'' ones presented. In our measurements we have resolved the individual decay channels.
There is good agreement between our work and the lifetimes calculated by Raasen & Uylings (1997) for the y 4F 9/2, 7/2 levels. However, there is a discrepancy between our lifetimes and the values of Raasen & Uylings (1997) for y 4F 5/2, 3/2 and the z 2D 5/2, 3/2. This may be due to a difference in the predicted level mixing, which is difficult to reproduce in semi-empirical calculations for complex atomic systems such as Cr II. In addition, an increase in the predicted level mixing may explain the discrepancy between our experimental BFs and the calculated BFs by Raasen & Uylings (1997) for transitions from the y 4F 5/2, 3/2 and the z 2D 5/2, 3/2 levels.
3.2 Transition probabilities
In Table 2 we present our BFs and A-values.
The BF residual value in Table 2 is
determined from the semi-empirical calculations of
Raasen & Uylings (1997). The residual value is used to
estimate the BF contribution from transitions that
were not observed in our spectra. The
missing lines are very weak transitions, ![]() ,
and for most upper levels in Table 2, the residual value is at
most a few percent, which is less
than the uncertainty in the BFs. The uncertainty in
the A-values is determined from the BF
and lifetime uncertainty using the method discussed by
Sikström et al. (2002), which include
uncertainties from the line-fitting, intensity calibration of each
spectra, intensity cross
calibration between separate spectra and the uncertainty in the fit of
the decay curve.
,
and for most upper levels in Table 2, the residual value is at
most a few percent, which is less
than the uncertainty in the BFs. The uncertainty in
the A-values is determined from the BF
and lifetime uncertainty using the method discussed by
Sikström et al. (2002), which include
uncertainties from the line-fitting, intensity calibration of each
spectra, intensity cross
calibration between separate spectra and the uncertainty in the fit of
the decay curve.
The log gfs in Table 4 are compared to the semi-empirical results by Kurucz (1988) and Raasen & Uylings (1997) and a graphical comparison is given in Figs. 3 and 4. The comparison between our laboratory log gfs and those of Raasen & Uylings (1997), Fig. 4, has a smaller deviation than those in Fig. 3.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13672fg3.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13672-09/Timg29.png)
|
Figure 3:
Comparison between |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13672fg4.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13672-09/Timg30.png)
|
Figure 4:
Comparison between |
| Open with DEXTER | |
There is good agreement between our experimental log gf
values and the semi-empirical log gf values
of Kurucz (1988) for lines
from the z 4HJ
levels as well as for lines from the y 4G5/2
and the z 2D3/2
levels, see Table 4.
However, there is
a larger deviation between our ![]() values and the semi-empirical calculations of Kurucz
(1988) for lines from the
y 4FJ
levels, the y 4G
7/2, 9/2, 11/2
levels, and the z 2D5/2
level. This may be due to inaccurate level mixing in the
semi-empirical calculations of Kurucz
(1988). The semi-empirical
calculations of Raasen & Uylings
(1997) agree more
consistently with our laboratory log gf
values.
values and the semi-empirical calculations of Kurucz
(1988) for lines from the
y 4FJ
levels, the y 4G
7/2, 9/2, 11/2
levels, and the z 2D5/2
level. This may be due to inaccurate level mixing in the
semi-empirical calculations of Kurucz
(1988). The semi-empirical
calculations of Raasen & Uylings
(1997) agree more
consistently with our laboratory log gf
values.
In Table 4 we compare our A-values with A-values in the literature. In general our A-values agree to within the uncertainties with the results in the literature; however, the A-values of Corliss & Bozman (1962) are significantly different to the other A-values in the literature. The compilation of Corliss & Bozman (1962) includes many values determined from a wall-stabilized arc. Inaccuracies in the wall temperature measurement for the wall-stabilized arc method can significantly increase the uncertainty in the measurement, so we recommend that the A-values in Corliss & Bozman (1962) are used with caution.
4 Summary
We present experimental lifetimes for 14 highly excited energy levels in Cr II and BFs for 145 transitions from these levels, yielding experimental transition probabilities for lines that are strong features in stellar spectra. For the majority of the Cr II transitions in this paper, the experimental transition probabilities agree with the semi-empirical calculations within the uncertainty of the measurements. In particular, we note that the semi-empirical orthogonal operator calculations of Raasen & Uylings (1997) have a one standard deviation difference to our experimental log gf values of 0.21. However, the semi-empirical Cowan code calculations of Kurucz (1988) have a one standard deviation difference to our experimental log gf values of 0.61. In addition, different semi-empirical calculations produce different term labels for the energy levels because of the large amount of level mixing. We suggested that further theoretical calculations for Cr II would benefit studies of this ion.
AcknowledgementsJ.G. and S.M. are very grateful for the warm hospitality shown by the staff at Lund Observatory. Financial support from the Swedish Research Council (VR), a Linnaeus grant to the Lund Laser Centre and the Knut and Alice Wallenberg Foundation, is gratefully acknowledged. RBW acknowledges a Euopean Commision Marie Curie Intra-European fellowship.
References
- Andrievsky, S. M., Kovtyukh, V. V., & Usenko, A. 1994, A&A, 281, 465 [NASA ADS] [Google Scholar]
- Babel, J., & Lanz, T. 1992, A&A, 263, 232 [NASA ADS] [Google Scholar]
- Bergeson, S. D., & Lawler, J. E. 1993, ApJ, 408, 382 [NASA ADS] [CrossRef] [Google Scholar]
- Bergström, H., Faris, H., Hallstadius, G. W., et al. 1988, Z. Phys. D 8, 17 [Google Scholar]
- Corliss, C. H., & Bozman, W. R. 1962, Nat. Bur. Std. Monograph, 53 [Google Scholar]
- Dimitrijevic, M. S., Ryabchikova, T., Simic, Popovic, L. C., et al. 2007, A&A, 469, 681 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Engman, B., Gaupp, A., Curtis, L. J., et al. 1975, Phys. Scr., 12, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Goly, A., & Weniger, S. 1980, J. Quant. Spectrosc. Radiat. Transfer, 24, 335 [Google Scholar]
- Gonzalez, A. M., Ortiz, M., & Campos, J. 1994, Can. J. Phys., 72, 57 [NASA ADS] [Google Scholar]
- Kurucz, R. L. 1988, Trans. IAU, XXB, ed. M. McNally (Dordrecht: Kluwer), 168 [Google Scholar]
- Lai, D. K., Bolte, M., Johnson, J. A., et al. 2008, ApJ, 681, 1524 [NASA ADS] [CrossRef] [Google Scholar]
- López-García, Z., Adelman, S. J., & Pintado, O. I. 2001, A&A, 367, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luke, T. M. 1988, J. Phys. B, 21, 4049 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., Preston, G. W., Sneden, C., et al. 1995, AJ, 109, 2757 [NASA ADS] [CrossRef] [Google Scholar]
- Merrill, P. W. 1951, ApJ, 114, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Musielok, J., & Wujec, T. 1979, A&AS, 38, 119 [NASA ADS] [Google Scholar]
- Nave, G., Sansonetti, C. J., & Griesmann, U. 1997, Optical Society of America Technical Digest, 3, 38 [Google Scholar]
- Nilsson, H., Ljung, G., Lundberg, H., et al. 2006, A&A, 445, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinnington, E. H., Lutz, H. O., & Carriaveao, G. W. 1973, Nucl. Instrum. Methods, 110, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Pinnington, E. H., Guo, Q., Jl., B., et al. 1993, Can. J. Phys., 71, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Raasen, A. J. J., & Uylings, P. H. M. 1997, unpublished data available at: ftp://ftp.wins.uva.nl/pub/orth/chromium [Google Scholar]
- Ralchenko, Yu., Kramida, A. E., Reader, J., & NIST ASD Team, 2009, NIST Atomic Spectra Database (version 3.1.5), [Online]. Available: http://physics.nist.gov/asd3, October 12, National Institute of Standards and Technology, Gaithersburg, MD [Google Scholar]
- Rice, J. B., & Wehlau, W. H. 1994, A&A, 291, 825 [NASA ADS] [Google Scholar]
- Schade, W., Mundt, B., & Helbig, V. 1990, Phys. Rev. A, 42, 3 [Google Scholar]
- Shevchenko, V. S. 1994, Astron. Zh., 71, 572 [NASA ADS] [Google Scholar]
- Sikström, C. M., Nilsson, H., Litzén, U., Blom, A., & Lundberg, H. 2002, J. Quant. Spectrosc. Radiat. Transfer, 74, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Sobeck, J. S., Lawler, J. E., & Sneden, C. 2007, ApJ, 667, 1267 [NASA ADS] [CrossRef] [Google Scholar]
- Spreger, R., Schelm, B., Kock, M., Neger, T., & Ulbel, M. 1994, J. Quant. Spectrosc. Radiat. Transfer, 51, 779 [Google Scholar]
- Wallace, L., & Hinkle, K. 2009, ApJ, 700, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B. 1967, Mem. Roy. Astron. Soc., 70, 165 [NASA ADS] [Google Scholar]
- Wujec, T., & Weniger, S. 1981, J. Quant. Spectrosc. Radiat. Transfer, 25, 167 [Google Scholar]
- Xu, H. L., Svanberg, S., Quinet, P., Garnir, H. P., & Biémont, É. 2003, J. Phys. B: At. Mol. Opt. Phys. 36 4773 [Google Scholar]
- Öberg, K. J. 2007, Eur. Phys. J. D, 41, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Footnotes
- ... II
![[*]](/icons/foot_motif.png)
- Tables 2 and 3 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/511/A68
All Tables
Table 1: Lifetimes in Cr II.
Table 4: A comparison between our A-values and the A-values in the literature.
All Figures
![\begin{figure}
\par\includegraphics[width=13cm,clip]{13672fg1.eps}\end{figure}](/articles/aa/full_html/2010/03/aa13672-09/Timg6.png)
|
Figure 1:
Partial energy level diagram of Cr II (Ralchenko et al. 2009). Only terms belonging to the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13672fg2.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13672-09/Timg18.png)
|
Figure 2: A section of the FT spectrum showing five Cr II lines indicated by their respective wavenumber. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13672fg3.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13672-09/Timg29.png)
|
Figure 3:
Comparison between |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13672fg4.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13672-09/Timg30.png)
|
Figure 4:
Comparison between |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.