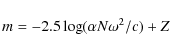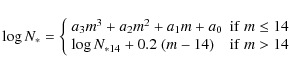| Issue |
A&A
Volume 511, February 2010
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 11 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200913629 | |
| Published online | 02 March 2010 | |
ASTEP South: an Antarctic Search for Transiting ExoPlanets around the celestial south pole
N. Crouzet1 - T. Guillot1 - A. Agabi2 - J.-P. Rivet1 - E. Bondoux2,5 - Z. Challita2,5 - Y. Fanteï-Caujolle2 - F. Fressin3 - D. Mékarnia2 - F.-X. Schmider2 - F. Valbousquet4 - A. Blazit2 - S. Bonhomme1 - L. Abe2 - J.-B. Daban2 - C. Gouvret2 - T. Fruth6 - H. Rauer6,7 - A. Erikson6 - M. Barbieri8 - S. Aigrain9 - F. Pont9
1 - Université de Nice Sophia Antipolis, CNRS UMR 6202, Observatoire de la Côte d'Azur, 06304 Nice Cedex 4, France
2 -
Université de Nice Sophia Antipolis, CNRS UMR 6525, Observatoire de la Côte d'Azur, 06108 Nice Cedex 2, France
3 -
Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, United States
4 -
Optique et Vision, 6 bis avenue de l'Estérel, BP 69, 06162 Juan-Les-Pins, France
5 -
Concordia Station, Dome C, Antarctica
6 -
DLR Institute for Planetary Research, Rutherfordstrasse 2, 12489 Berlin, Germany
7 -
Center for Astronomy and Astrophysics, TU Berlin, Hardenbergstr. 36, 10623 Berlin, Germany
8 -
Università di Padova, Dipartimento di Astronomia, vicolo dell'Osservatorio 5, 35122 Padova, Italia
9 -
School of Physics, University of Exeter, Stocker Road, Exeter EX4 4QL, UK
Received 9 November 2009 / Accepted 2 December 2009
Abstract
Context. The Concordia base in Dome C, Antarctica, is
an extremely promising site for photometric astronomy due to the
3-month long night during the Antarctic winter, favorable weather
conditions, and low scintillation.
Aims. The ASTEP project (Antarctic Search for Transiting
ExoPlanets) is a pilot project to discover transiting planets and
understand the limits of visible photometry from the Concordia site.
Methods. ASTEP South is the first phase of the ASTEP project. The instrument is a fixed 10 cm refractor with a 4k ![]() 4k CCD camera in a thermalized box, pointing continuously a
4k CCD camera in a thermalized box, pointing continuously a
![]() 2 field of view centered on the celestial south pole. We describe the project and report results of a preliminary data analysis.
2 field of view centered on the celestial south pole. We describe the project and report results of a preliminary data analysis.
Results. ASTEP South became fully functional in June 2008 and
obtained 1592 hours of data during the 2008 Antarctic winter. The
data are of good quality but the analysis has to account for changes in
the PSF (point spread function) due to rapid ground seeing variations
and instrumental effects. The pointing direction is stable within
10 arcsec on a daily timescale and drifts by only 34 arcsec
in 50 days. A truly continuous photometry of bright stars is
possible in June (the noon sky background peaks at a magnitude
![]() on June 22), but becomes challenging in July (the noon sky background magnitude is
on June 22), but becomes challenging in July (the noon sky background magnitude is
![]() on July 20). The weather conditions are estimated from the number
of stars detected in the field. For the 2008 winter, the statistics are
between 56.3% and 68.4% of excellent weather, 17.9%
to 30% of veiled weather (when the probable presence of thin
clouds implies a lower number of detected stars) and 13.7% of bad
weather. Using these results in a probabilistic analysis of transit
detection, we show that the detection efficiency of transiting
exoplanets in one given field is improved at Dome C compared to a
temperate site such as La Silla. For example we estimate that a
year-long campaign of 10 cm refractor could reach an efficiency
of 69% at Dome C versus 45% at La Silla for detecting
2-day period giant planets around target stars from magnitude 10
to 15. The detection efficiency decreases for planets with longer
orbital periods, but in relative sense it is even more favorable to
Dome C.
on July 20). The weather conditions are estimated from the number
of stars detected in the field. For the 2008 winter, the statistics are
between 56.3% and 68.4% of excellent weather, 17.9%
to 30% of veiled weather (when the probable presence of thin
clouds implies a lower number of detected stars) and 13.7% of bad
weather. Using these results in a probabilistic analysis of transit
detection, we show that the detection efficiency of transiting
exoplanets in one given field is improved at Dome C compared to a
temperate site such as La Silla. For example we estimate that a
year-long campaign of 10 cm refractor could reach an efficiency
of 69% at Dome C versus 45% at La Silla for detecting
2-day period giant planets around target stars from magnitude 10
to 15. The detection efficiency decreases for planets with longer
orbital periods, but in relative sense it is even more favorable to
Dome C.
Conclusions. This shows the high potential of Dome C for photometry and future planet discoveries.
Key words: methods: observational - methods: data analysis - site testing - techniques: photometric
1 Introduction
Dome C offers exceptional conditions for astronomy thanks to a
3-month continuous night during the Antarctic winter and a very dry
atmosphere. Dome C is located at
![]() at an altitude of 3233 meters on a summit of the high Antarctic
plateau, 1100 km away from the coast. After a pioneering summer
expedition in 1995, the site testing for astronomy begun in the early
2000's. It revealed a very clear sky, an exceptional seeing and very
low wind-speeds (Geissler & Masciadri 2006; Aristidi et al. 2003,2005; Ashley et al. 2005b; Lawrence et al. 2004).
The French-Italian base Concordia was constructed at Dome C from
1999 to 2005 to hold various science experiments. Summer time astronomy
experiments have been carried out (e.g. Guerri et al. 2007).
The study of Dome C for astronomy during night-time has
considerably expanded since the first winter-over at Concordia in 2005.
The winter site testing has shown an excellent seeing above a thin
boundary layer (Trinquet et al. 2008; Agabi et al. 2006; Aristidi et al. 2009), a very low scintillation (Kenyon et al. 2006) and a high duty cycle (Mosser & Aristidi 2007). Low sky brightness and extinction are also expected (Kenyon & Storey 2006).
at an altitude of 3233 meters on a summit of the high Antarctic
plateau, 1100 km away from the coast. After a pioneering summer
expedition in 1995, the site testing for astronomy begun in the early
2000's. It revealed a very clear sky, an exceptional seeing and very
low wind-speeds (Geissler & Masciadri 2006; Aristidi et al. 2003,2005; Ashley et al. 2005b; Lawrence et al. 2004).
The French-Italian base Concordia was constructed at Dome C from
1999 to 2005 to hold various science experiments. Summer time astronomy
experiments have been carried out (e.g. Guerri et al. 2007).
The study of Dome C for astronomy during night-time has
considerably expanded since the first winter-over at Concordia in 2005.
The winter site testing has shown an excellent seeing above a thin
boundary layer (Trinquet et al. 2008; Agabi et al. 2006; Aristidi et al. 2009), a very low scintillation (Kenyon et al. 2006) and a high duty cycle (Mosser & Aristidi 2007). Low sky brightness and extinction are also expected (Kenyon & Storey 2006).
Time-series observations such as those implied by the detection of transiting exoplanets should benefit from these atmospherical conditions and the good phase coverage. This could potentially greatly improve the photometric precision when compared to other temperate sites (Pont & Bouchy 2005). A first photometric instrument, PAIX (Chadid et al. 2007), was installed at Concordia in December 2006. A lightcurve of the RR Lyrae variable star S Ara over 16 nights in August 2007 is presented in Chadid et al. (2008), and results of the whole campaign from June to August 2007 have been submitted. The sIRAIT instrument also obtained lightcurves over 10 days on the stars V841 Cen and V1034 Cen (Briguglio et al. 2009; Strassmeier et al. 2008).
The ASTEP project (Antarctic Search for Transiting ExoPlanets) aims at determining the quality of Dome C as a site for future photometric surveys and to detect transiting planets (Fressin et al. 2005). The main instrument is a 40 cm Newton telescope entirely designed and built to perform high precision photometry from Dome C. The observations will start in winter 2010. A first instrument already on site, ASTEP South, has observed during the 2008 and 2009 winters.
We present here the ASTEP South project and results from the preliminary analysis of the 2008 campaign. We first describe the instrument, the observation strategy and the field of view. Section 3 discusses the main features obtained when running this simple instrument from Dome C: influence of the Sun and the Moon, PSF and pointing variations, as well as temperature effects. In Sect. 4 we detail our duty cycle and infer the weather statistics at Dome C for the 2008 winter. These results are combined to a probabilistic analysis to infer the potential of ASTEP South for planet detection and to evaluate Dome C as a site for future planet discoveries.
2 Instrumental setup
2.1 The instrument
ASTEP South consists of a 10 cm refractor, a front-illuminated 4096 ![]() 4096 pixels
CCD camera, and a simple mount in a thermalized enclosure. The
refractor is a commercial TeleVue NP101 and the camera is a ProLines
series by Finger Lake Instrumentation equipped with a KAF-16801E CCD by
Kodak. For the choice of the camera see Crouzet et al. (2007).
Its quantum efficiency peaks at 63% at 660 nm and is
above 50% from 550 to 720 nm. The pixel size is 9
4096 pixels
CCD camera, and a simple mount in a thermalized enclosure. The
refractor is a commercial TeleVue NP101 and the camera is a ProLines
series by Finger Lake Instrumentation equipped with a KAF-16801E CCD by
Kodak. For the choice of the camera see Crouzet et al. (2007).
Its quantum efficiency peaks at 63% at 660 nm and is
above 50% from 550 to 720 nm. The pixel size is 9 ![]() m
and the total CCD size is 3.7 cm. The pixel response
non-uniformity is around 0.5%. Pixels are coded on 16 bits, implying a
dynamic range of 65535 ADU. The gain is 2 e-/ADU. A filter
whose transmission starts at 600 nm is placed before the camera to
eliminate blue light. Given the CCD quantum efficiency, the overall
transmission (600 to 900 nm) is equivalent to that of a large R band.
We use a GM 8 equatorial mount from Losmandy. A thermalized enclosure
is used to avoid temperature fluctuations. The sides of this enclosure
are made with wood and polystyrene. A double glass window reduces
temperature variations and its accompanying turbulence on the optical
path. Windows are fixed together by a teflon part and separated by a
3 mm space filled with nitrogen to avoid vapour mist. The
enclosure is thermalized to -20
m
and the total CCD size is 3.7 cm. The pixel response
non-uniformity is around 0.5%. Pixels are coded on 16 bits, implying a
dynamic range of 65535 ADU. The gain is 2 e-/ADU. A filter
whose transmission starts at 600 nm is placed before the camera to
eliminate blue light. Given the CCD quantum efficiency, the overall
transmission (600 to 900 nm) is equivalent to that of a large R band.
We use a GM 8 equatorial mount from Losmandy. A thermalized enclosure
is used to avoid temperature fluctuations. The sides of this enclosure
are made with wood and polystyrene. A double glass window reduces
temperature variations and its accompanying turbulence on the optical
path. Windows are fixed together by a teflon part and separated by a
3 mm space filled with nitrogen to avoid vapour mist. The
enclosure is thermalized to -20
![]() C and fans are used for air circulation. The ASTEP South instrument is shown at Dome C in Fig. 1.
C and fans are used for air circulation. The ASTEP South instrument is shown at Dome C in Fig. 1.
In order to characterize the quality of Dome C for
photometric observations, we have to avoid as much as possible
instrumental noises and in particular jitter noise, leading to a new
observation strategy: the instrument is completely fixed and points
towards the celestial south pole continuously. This allows also a low
and constant airmass. The observed field of view is
![]() 2,
leading to a pixel size of 3.41 arcsec on the sky. This
observation setup leads to stars moving on the CCD from frame to frame
and to a widening of the PSF (point spread function) in one direction,
depending on the exposure time.
2,
leading to a pixel size of 3.41 arcsec on the sky. This
observation setup leads to stars moving on the CCD from frame to frame
and to a widening of the PSF (point spread function) in one direction,
depending on the exposure time.
Test observations were made at the Calern site (Observatoire de la Côte d'Azur) observing the celestial north pole, in order to choose the exposure time and the PSF size. A 30 s exposure time and a 2 pixel PSF FWHM (full width half maximum) lead to only 2 saturated stars and a limit magnitude around 14 (from Dome C the limit magnitude is increased to 15). An analysis of the celestial south pole field from the Guide Star Catalog GSC2.2 with these parameters taking into account the rotation of the star during each exposure leads to less than 10% of blended stars. Therefore we adopted these parameters.
Software programs were developed by our team to control the camera, to run the acquisitions and to transfer and save the data. The instrument was set up at the Concordia base in January 2008.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{images/13629-01.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg14.png)
|
Figure 1: ASTEP South at Dome C, Antarctica, January 2008. |
| Open with DEXTER | |
2.2 The south pole field
The distribution of stars in our field of view is shown in Fig. 2.
From the GSC2.2 catalog, we find nearly 8000 stars up to our limit
magnitude of 15. We also simulate stellar populations in a field
of 3.88 ![]() 3.88
3.88
![]() 2 centered on the celestial south pole using the Besançon model of the Galaxy
2 centered on the celestial south pole using the Besançon model of the Galaxy![]() (Robin et al. 2003) for R-band
magnitudes between 10 and 18 to calculate the dwarf ratio in
the field. The comparison shows that the Besançon model overestimates
the number of stars in the field by a factor
(Robin et al. 2003) for R-band
magnitudes between 10 and 18 to calculate the dwarf ratio in
the field. The comparison shows that the Besançon model overestimates
the number of stars in the field by a factor ![]() 2.
However, we believe that the ratio of dwarfs to the total number of
stars is, by construction of the model, better estimated. The bottom
panel of Fig. 2 shows that most of the stars brighter than magnitude
R=12 are giants (or more accurately larger than twice our Sun).
2.
However, we believe that the ratio of dwarfs to the total number of
stars is, by construction of the model, better estimated. The bottom
panel of Fig. 2 shows that most of the stars brighter than magnitude
R=12 are giants (or more accurately larger than twice our Sun).
Table 1 details
the number of stars per magnitude range; the total number of stars is
obtained from the GSC2.2 catalog and the number of dwarfs is estimated
using the relative fractions from the Besançon model. From
magnitude 10 to 15 we have 73.6% of dwarf stars with
radius
![]() .
This ratio is higher than in other typical fields used in the search
for transiting planets such as Carina. Based on CoRoTlux simulations (Fressin et al. 2007),
we expect that about one F, G, K dwarf in 1100 to 1600
should harbor a transiting giant exoplanet. The south pole field
observed by ASTEP South is thus, in principle, populated enough for the
detection of transiting planets (see also Crouzet et al. 2009). We will come back to a realistic estimate of the number of detectable exoplanets in Sect. 5.
.
This ratio is higher than in other typical fields used in the search
for transiting planets such as Carina. Based on CoRoTlux simulations (Fressin et al. 2007),
we expect that about one F, G, K dwarf in 1100 to 1600
should harbor a transiting giant exoplanet. The south pole field
observed by ASTEP South is thus, in principle, populated enough for the
detection of transiting planets (see also Crouzet et al. 2009). We will come back to a realistic estimate of the number of detectable exoplanets in Sect. 5.
The advantages of the south pole field are hence of course a continuous airmass, a high ratio of dwarfs to giant stars and a very low contamination by background stars. On the other hand, the field is less dense than regions closer to the galactic plane, so that the actual number of transiting planets in the field is smaller.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{images/13629-02.ps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg17.png)
|
Figure 2:
Top panel: cumulative distribution of the number of stars in the south pole field as a function of their magnitude in the R band. The plain line shows results from the Besançon model. The dashed line indicates output from the GSC2.2 catalog. Bottom panel: ratio of dwarf stars with selected radii (less than 2, 1 and 0.5 |
| Open with DEXTER | |
2.3 Temperature conditions
The instrument was set up during the Dome C 2008 summer campaign.
The external temperature varied at this time between -20 and -30
![]() C.
It was let outside without thermal control until the observations
started at the end of April. In winter the external temperature varies
between -50 and -80
C.
It was let outside without thermal control until the observations
started at the end of April. In winter the external temperature varies
between -50 and -80
![]() C. During the observations, the thermalized box is set to a temperature of -20
C. During the observations, the thermalized box is set to a temperature of -20
![]() C and the CCD to -35
C and the CCD to -35
![]() C. Because of self-heating, the electronics of the camera is around +5
C. Because of self-heating, the electronics of the camera is around +5
![]() C with some variations (see Sect. 3.7).
C with some variations (see Sect. 3.7).
3 Preliminary data analysis
ASTEP South generates around 60 gigabytes of data per day. Since internet facilities at Dome C are limited to a low stream connection only few hours a day, a whole data transfer is impossible. Data are stored in external hard disks and repatriated at the end of the winter-over, leading to at least a 6 month delay between the observations and a full data analysis. We thus developed a software program for on-site preliminary data analysis, in order to have a day-to-day feedback of the observations. We detail here the results of this preliminary analysis.
3.1 Preliminary data analysis software program
We developed a software program running on the data at Concordia.
For each image of a given day the mean intensity is computed. We then
process only the
![]() pixel central part of the frame (
pixel central part of the frame (
![]() )
for faster calculations. First, a point source identifier gives the
number of detected stars and their location on the CCD. The
200 brightest stars are matched to the GSC 2.2 catalog using
a home-made algorithm, in order to identify the south pole on the CCD.
The 30 brightest stars are fitted with a Gaussian to derive the
PSF size. Last, basic aperture photometry is performed for a set of
10 stars without any image calibration. The identification of
point sources, the Gaussian fit and the aperture photometry use an IDL
version of DAOPHOT (Stetson 1987).
A point source is considered as a star if its flux is 5 times larger
than the sky noise. Aperture photometry is made with large apertures of
diameter 12 and 20 pixels, allowing to get all the flux for
bright stars. Although these large apertures are not adapted to faint
stars, the low crowding in our field allows to get reasonable
lightcurves. Of course this will be optimized during the complete
analysis of data. The camera and CCD temperature are also recorded. A
small size binary file with these results is sent everyday by email.
Plots shown in the following are in UTC time as recorded by the
software program (local time at Dome C is UTC +8).
)
for faster calculations. First, a point source identifier gives the
number of detected stars and their location on the CCD. The
200 brightest stars are matched to the GSC 2.2 catalog using
a home-made algorithm, in order to identify the south pole on the CCD.
The 30 brightest stars are fitted with a Gaussian to derive the
PSF size. Last, basic aperture photometry is performed for a set of
10 stars without any image calibration. The identification of
point sources, the Gaussian fit and the aperture photometry use an IDL
version of DAOPHOT (Stetson 1987).
A point source is considered as a star if its flux is 5 times larger
than the sky noise. Aperture photometry is made with large apertures of
diameter 12 and 20 pixels, allowing to get all the flux for
bright stars. Although these large apertures are not adapted to faint
stars, the low crowding in our field allows to get reasonable
lightcurves. Of course this will be optimized during the complete
analysis of data. The camera and CCD temperature are also recorded. A
small size binary file with these results is sent everyday by email.
Plots shown in the following are in UTC time as recorded by the
software program (local time at Dome C is UTC +8).
Table 1:
Number of stars in the 3.88 ![]() 3.88
3.88
![]() 2 celestial south pole field.
2 celestial south pole field.
3.2 Magnitude calibration
In order to convert ADU into magnitudes, we perform a preliminary magnitude calibration: we measure the flux of the stars on a typical image taken under dark sky and convert them into instrumental magnitudes. We then compare these magnitudes to the ones from the GSC2.2 catalog and obtain the so-called zero point. The image used is a raw image, but the local background including bias is subtracted when calculating the flux of each star.
We estimate that the error on these magnitudes should be ![]() 0.3 mag
or less. First a comparison of the result for all the stars in a given
image to that obtained with only the stars in the
0.3 mag
or less. First a comparison of the result for all the stars in a given
image to that obtained with only the stars in the
![]() pixel
central part yields a 0.2 mag difference. We estimate that the
absence of a flat-field procedure is responsible for that difference
and that its impact on our inferred sky brightness magnitude should be
smaller. Second, while one may estimate that the GSC2.2 errors on the
magnitudes of individual stars can be as large as 0.5, the large
number of stars (
pixel
central part yields a 0.2 mag difference. We estimate that the
absence of a flat-field procedure is responsible for that difference
and that its impact on our inferred sky brightness magnitude should be
smaller. Second, while one may estimate that the GSC2.2 errors on the
magnitudes of individual stars can be as large as 0.5, the large
number of stars (![]() 7000)
implies that the mean error should be quite smaller. A 0.3 error on the
inferred magnitudes hence appears to be a conservative estimate.
7000)
implies that the mean error should be quite smaller. A 0.3 error on the
inferred magnitudes hence appears to be a conservative estimate.
In what follows, we will use this ADU to magnitude conversion only for the noon and full-moon sky brightness, not for the dark sky. This is because our preliminary analysis is based on data processed on the fly in Concordia which have not been de-biased. Variations in the bias level are of the order of 40 ADU. Given that uncertainty, we estimate that any measurement of magnitudes larger than 18 may have a bias error larger than 0.3 mag and therefore refrain from mentioning those.
A refined analysis of the full ASTEP South data with all available data is under way and will include an accurate de-biasing and magnitude calibration.
3.3 Influence of the Sun
We first consider the influence of the Sun on the photometry. It is
important to notice that although the Sun disappears below the horizon
from May 4 to August 9, the sky background is always higher
each day in the period around noon which is therefore less favorable
for accurate photometric measurements. The minimum altitude of the Sun
at noon occurs on June 21 and is
![]() below the horizon. The height and width of the peak of intensity are
the smallest around the winter solstice and increase before and after
this date (Fig. 3). The increase is not linear but varies from one day to another, as also observed with the sIRAIT instrument (Strassmeier et al. 2008).
We attempted to check whether this may be due to high altitude clouds
but no correlation was found between the sky brightness and the quality
of the night derived by studying the number of detected stars (see
Sect. 4).
below the horizon. The height and width of the peak of intensity are
the smallest around the winter solstice and increase before and after
this date (Fig. 3). The increase is not linear but varies from one day to another, as also observed with the sIRAIT instrument (Strassmeier et al. 2008).
We attempted to check whether this may be due to high altitude clouds
but no correlation was found between the sky brightness and the quality
of the night derived by studying the number of detected stars (see
Sect. 4).
Figure 4 shows
variations of the mean intensity as a function of time for 3 clear
days: June 22, July 20 and August 20. On June, 21 the
height is typically 1600 ADU and images are affected during 4
to 6 h. From our calibration this corresponds to a magnitude of
![]() in the standard R band.
The residual noise calculated from the actual number of photons
received from the sky in an aperture of 20 pixels (corresponding
to a radius equal to a FWHM of 2.5 pixels) is
in the standard R band.
The residual noise calculated from the actual number of photons
received from the sky in an aperture of 20 pixels (corresponding
to a radius equal to a FWHM of 2.5 pixels) is
![]() .
For larger apertures the noise will be smaller. Therefore this effect
will have a moderate impact on the photometry. In July the height grows
to typically 20 000 ADU, i.e. magnitude
.
For larger apertures the noise will be smaller. Therefore this effect
will have a moderate impact on the photometry. In July the height grows
to typically 20 000 ADU, i.e. magnitude
![]() ,
and a noticeable brightness increase lasts for 7 to 9 h. In August, this brightness increase lasts 9 to
12 h.
,
and a noticeable brightness increase lasts for 7 to 9 h. In August, this brightness increase lasts 9 to
12 h.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{images/13629-03-NEW.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg27.png)
|
Figure 3: Image intensity for all the winter. The bias level is around 2480 ADU and the scale is half of the CCD dynamics. Peaks around noon will affect the photometry. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{images/13629-04-NEW.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg28.png)
|
Figure 4: Image intensity during 3 typical days in June, July and August. The bias level is around 2480 ADU and the scale is half of the CCD dynamics. Due to the Sun, the sky background increases around noon. The corresponding magnitude for June 22 is 15.3 mag/arcsec2. |
| Open with DEXTER | |
The mean intensity of each image and the number of detected stars are plotted against the height of the Sun in Fig. 5. The fact that the sky intensity drops to an undetectable level when the Sun is below
![]() appears to be in line with the result from Moore et al. (2008)
that the Dome C sky may be darker than other sites. However, this
conclusion is at most tentative due to the absence of a bias removal
and dark sky magnitude determination. We notice that the R-band sky magnitude averaged over all observations for a Sun altitude of
appears to be in line with the result from Moore et al. (2008)
that the Dome C sky may be darker than other sites. However, this
conclusion is at most tentative due to the absence of a bias removal
and dark sky magnitude determination. We notice that the R-band sky magnitude averaged over all observations for a Sun altitude of
![]() is
is
![]() ,
very similar to that obtained close to the zenith for Paranal in the R-band, i.e. 16 to
,
very similar to that obtained close to the zenith for Paranal in the R-band, i.e. 16 to
![]() (Patat et al. 2006, see their Fig. 6).
(Patat et al. 2006, see their Fig. 6).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{images/13629-05-NEW.eps}\par...
...udegraphics[width=8cm,clip]{images/13629-06-NEW.eps}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg33.png)
|
Figure 5:
Mean intensity of each image and number of stars as a function of the Sun altitude when it is between
|
| Open with DEXTER | |
3.4 Influence of the Moon
The influence of the Moon is shown in Fig. 6.
The Moon is full on June 18, July 18, August 16 and
September 15. An increased sky background is clearly seen around
these days, up to 80 ADU in June, 100 ADU in July,
500 ADU in August and 70 ADU in September. The full Moon in
June, July, and September corresponds to a good weather, without
clouds, and the increase in intensity is low enough to allow
photometric observations. In contrast, during the full Moon of August
the weather was very bad with high temperature (up to -30
![]() C),
strong wind at ground level (up to 11 m/s), and a very cloudy sky.
The very high background is thus interpreted as due to the reflection
of moonlight by clouds. A typical increase of 80 ADU during the
full Moon leads to a sky brightness of
C),
strong wind at ground level (up to 11 m/s), and a very cloudy sky.
The very high background is thus interpreted as due to the reflection
of moonlight by clouds. A typical increase of 80 ADU during the
full Moon leads to a sky brightness of ![]() 18.1 mag / arcsec2. As discussed in Sect. 3.2, this magnitude estimate may change by a fraction of a magnitude with a precise bias subtraction.
18.1 mag / arcsec2. As discussed in Sect. 3.2, this magnitude estimate may change by a fraction of a magnitude with a precise bias subtraction.
3.5 Point spread function variations
PSF variations are a crucial issue for photometry. We investigate here the PSF variations in the ASTEP South data. For each image, the 30 brightest stars are fitted with a Gaussian PSF and their FWHM in both direction is calculated using DAOPHOT. The mean of the FWHM across the entire image is shown as a function of time in Fig. 7. This mean FWHM varies between 1.5 and 3.5 pixels over the winter.
Two kinds of variations are present. First, PSF variations on a timescale smaller than one day are observed. We compare them to independent seeing measurements at Dome C provided by three dedicated differential image motion monitors (DIMM), two of them forming a generalized seeing monitor (GSM) (for a description of these instruments see Ziad et al. 2008). In order to consider only the PSF variations of period smaller than one day we subtract to the FWHM the difference between the median FWHM and the median seeing for each day. Figure 8 shows that on this day timescale the corrected FWHM and the seeing are clearly correlated: the PSF variations on short timescales are mostly due to seeing variations. As previously discussed, the seeing at the ground level where ASTEP South is placed is rather poor: the median value in winter at 3 m high reported by Aristidi et al. (2009) is 2.37 arcsec with stability periods of 10 to 30 min. This explains the short-term variations of our PSFs.
On a timescale larger than one day the correlation is not true anymore. This shows that another cause of PSF variations is present. For this larger timescale, two regimes seem to be present, one with a PSF around 1.5 pixels and another with a PSF around 3.0 pixels. These variations are associated with an asymmetrical deformation of the PSF. This suggests an instrumental cause of PSF variations such as astigmatism and decollimation. Indeed, temperature inhomogeneities in the thermal enclosure cause mechanical and optical deformations. Unfortunately these large timescale variations prevent us from estimating the seeing at the ground level directly from our photometric data.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{images/13629-07-NEW.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg35.png)
|
Figure 6: Image intensity. The bias level is around 2480 ADU and the scale is 1% of the CCD dynamics. The sky background increases during 10 days around the full Moon up to typically 18.1 mag / arcsec2. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{images/13629-08-NEW.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg36.png)
|
Figure 7: Mean values of the size of the stars ( FWHM) on the CCD in pixels ( top panels) and their asymmetry ( bottom panels) as a function of the observing day for the months of June ( top left), July ( top right), August ( bottom left) and September ( bottom right). In the top panels, the blue and green curves correspond to the values of the FWHM in the x and y directions, respectively. The mean FWHM values are obtained through a spatial average on the CCD. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{images/13629-09-NEW.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg37.png)
|
Figure 8: Correlation between the PSF FWHM and independent seeing measurements at Dome C, for timescales smaller than one day (the FWHM is corrected for larger timescale variations). Direct seeing measurements from three differential image motion monitors are shown in blue, green and red. A linear regression gives a slope a = 0.59 with a correlation coefficient r = 0.65. The PSFs are clearly affected by seeing variations at the ground level. |
| Open with DEXTER | |
3.6 Astrometry and pointing variations
Ideally the pointing should remain stable during all the winter, meaning that the south pole must stay at the same place on the CCD. The position of the south pole on the CCD is found on each image using a home-made field-matching algorithm. The precision of this algorithm is typically 0.2 pixels. The results for a typical day and for all the winter are shown in Fig. 9.
First we have a variation of this position with a period of one sidereal day. This is due to an incomplete correction of astrometric effects. Indeed, the star coordinates from the GSC2.2 catalog were corrected only for the precession of the equinox from the J2000 epoch to January 1, 2008. The remaining error on the star coordinates led to an error of 10 pixels (34 arcsec) in the determination of the position of the pole. We then corrected the GSC2.2 coordinates from the precession of the equinox using the real observation date, and from the nutation and the aberration of light (or Bradley effect). After these astrometric corrections the pole stays within 2 or 3 pixels during the day.
Second, the pole is drifting during the winter. The amplitude is 10 pixels (34 arcsec) in 50 days, from June 12 to July 31. From the orientation of the CCD we find that this drift is oriented vertically towards the north. This may be due to mechanical deformations of the instrument, atmospheric changes or a motion of the ice under the instrument. In any case this effect is very small.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{images/13629-10.eps}\par\includegraphics[width=8cm,clip]{images/13629-11.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg38.png)
|
Figure 9: Position of the pole on the CCD. Top: 9 images on July 11 after various astrometric corrections (blue: approximate correction of the precession of the equinox, green: improved correction of the precession of the equinox, brown: correction of the nutation, red: correction of the Bradley effect). Bottom: 7 days between June 12 and July 30, showing a drift over the winter (dark blue: June 12, light blue: June 24, green: July 2, yellow: July 11, orange: July 17, red: July 30). |
| Open with DEXTER | |
3.7 Camera temperature variations
The CCD is cooled down to -35
![]() C without any variation. In contrast the electronic part of the camera oscillates between +4 and +8
C without any variation. In contrast the electronic part of the camera oscillates between +4 and +8
![]() C with a one hour period (Fig. 10).
A threshold effect explains these variations: the thermalized enclosure
is not heated continuously but only when it passes below a threshold
temperature. A direct consequence is seen on the bias images. The bias
level oscillates with the same period and an amplitude of 10 ADU.
The mean intensity of science images is affected in the same way. The
bias level is plotted against the camera temperature in Fig. 11
and shows a hysteresis behavior. For a given temperature, the bias
level is lower if the temperature is increasing than if the temperature
is decreasing. The hysteresis amplitude is around 5 ADU. An
explanation can be that the temperature sensor is not exactly on the
electronics but is stuck on a camera wall which may be sensitive to
temperature variations with a time lag compared to the electronics. It
may also be due to the electronics and sensor having different thermal
inertia.
C with a one hour period (Fig. 10).
A threshold effect explains these variations: the thermalized enclosure
is not heated continuously but only when it passes below a threshold
temperature. A direct consequence is seen on the bias images. The bias
level oscillates with the same period and an amplitude of 10 ADU.
The mean intensity of science images is affected in the same way. The
bias level is plotted against the camera temperature in Fig. 11
and shows a hysteresis behavior. For a given temperature, the bias
level is lower if the temperature is increasing than if the temperature
is decreasing. The hysteresis amplitude is around 5 ADU. An
explanation can be that the temperature sensor is not exactly on the
electronics but is stuck on a camera wall which may be sensitive to
temperature variations with a time lag compared to the electronics. It
may also be due to the electronics and sensor having different thermal
inertia.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{images/13629-12-NEW.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg39.png)
|
Figure 10:
Camera temperature, bias level and image intensity on July 11. The camera temperature varies between +4 and +8
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{images/13629-13-NEW.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg40.png)
|
Figure 11: Bias level against the camera temperature for July 11. The blue points correspond to an increasing temperature and the red points to a decreasing temperature, showing a hysteresis behavior. |
| Open with DEXTER | |
4 Duty cycle
A main objective of ASTEP South is to qualify the duty cycle for winter observations at Dome C. The observation calendar for the whole 2008 campaign is shown in Fig. 12. April and May were mainly devoted to setting up the instrument and software programs. Continuous observations started around mid-June. Since then, very few interruptions occurred and data were acquired until October. The effect of the Sun and of the Moon has already been discussed in Sect. 3. We present here some technical limitations to the duty cycle, and quantify the photometric quality of the Dome C site for this campaign.
4.1 Technical issues
Technical issues encountered during this campaign limited the duty cycle. We show here typical issues that instruments at Dome C have to face with. We believe these can be mostly overcome with appropriate technical solutions:
- first, the shutter did not close and got damaged at temperatures below 0
 C. We had to change the shutter and build a special thermalization device to warm it;
C. We had to change the shutter and build a special thermalization device to warm it;
- in order to install the camera again after changing the
shutter, the thermalized box was opened and suddenly cooled by the
ambient air at
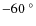 C. As a result, cables not made in teflon broke as well as the camera USB connection. These had to be replaced;
C. As a result, cables not made in teflon broke as well as the camera USB connection. These had to be replaced;
- outside instruments are affected by power cuts lasting for a few minutes to a few hours. The fraction of time lost for observations is negligible, however next instruments should be equipped with converters to avoid possible damages;
- the instrument is submitted to temperature gradients inside the thermal enclosure, and to the external temperature during power cuts or when opening the box. This leads to mechanical constraints resulting in decollimation and astigmatism.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{images/13629-14.ps}\par\in...
...29-18.ps}\par\includegraphics[width=8.5cm,clip]{images/13629-19.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg43.png)
|
Figure 12: ASTEP South observation calendar for the 2008 campaign. April and May were mainly dedicated to solving technical problems. Continuous observations started mid-June with very few interruptions until the end of the winter. |
| Open with DEXTER | |
4.2 Weather conditions at Dome C
A first experiment to measure the winter clear sky fraction at Dome C was made by Ashley et al. (2005a) with ICECAM, a CCD camera with a lens of
![]() field of view. Every 2 h from February to November 2001, ten
images of the sky were taken and averaged. An analysis of all the
images yielded a fraction of 74% of cloud-free time. An analysis
by Mosser & Aristidi (2007)
for the 2006 winter yielded an estimate of 92% of clear sky
fraction by reporting several times a day the presence of clouds with
the naked eye. Moore et al. (2008)
derive a clear sky fraction of 79% for the winter 2006 from the
Gattini instrument using the number of stars and the extinction across
the images. In a previous work, we derived a clear sky fraction
of 74% for the 2008 winter from the ASTEP South data, considering
that the sky is clear if we have more than half of the stars detected
on the best images (Crouzet et al. 2010).
However this result is dependent on this ad hoc criterion. We
reevaluate here this fraction by avoiding such an arbitrary limit.
field of view. Every 2 h from February to November 2001, ten
images of the sky were taken and averaged. An analysis of all the
images yielded a fraction of 74% of cloud-free time. An analysis
by Mosser & Aristidi (2007)
for the 2006 winter yielded an estimate of 92% of clear sky
fraction by reporting several times a day the presence of clouds with
the naked eye. Moore et al. (2008)
derive a clear sky fraction of 79% for the winter 2006 from the
Gattini instrument using the number of stars and the extinction across
the images. In a previous work, we derived a clear sky fraction
of 74% for the 2008 winter from the ASTEP South data, considering
that the sky is clear if we have more than half of the stars detected
on the best images (Crouzet et al. 2010).
However this result is dependent on this ad hoc criterion. We
reevaluate here this fraction by avoiding such an arbitrary limit.
4.2.1 Method
A new measurement of the clear sky fraction is made with ASTEP South using a method sensitive to thin clouds, based on the number of stars detected in the field. In order to do so, we need to evaluate the number of stars that should be detected on any given image if the weather was excellent. Our PSF size varies due to fluctuations of the seeing and of the instrument itself, and the background level also changes due to the presence of the Moon and the Sun. Since these are not directly related to weather, we need to derive how the number of detectable stars changes as a function of these parameters. (Note that thin clouds should affect the seeing in some way, however a posteriori examination of the data shows that this effect is small compared to the global attenuation due to clouds).
4.2.2 Identifying point sources with DAOPHOT
The
![]() pixel sub-images contain up to 500 stars of varying magnitude. Our
automatic procedure for finding point sources uses the FIND routine
from DAOPHOT. Specifically, in this procedure a star is detected if the
central height of the PSF is above the local background by a given
number of standard deviations of that background. This threshold
parameter
pixel sub-images contain up to 500 stars of varying magnitude. Our
automatic procedure for finding point sources uses the FIND routine
from DAOPHOT. Specifically, in this procedure a star is detected if the
central height of the PSF is above the local background by a given
number of standard deviations of that background. This threshold
parameter ![]() is chosen by the user. We choose
is chosen by the user. We choose ![]() .
.
4.2.3 A model to evaluate the expected number of stars
The full width half maximum ![]() of our PSFs is typically 2.5 pixels. To evaluate whether a star is detected or not we compare the amplitude A of the PSF to the noise in the central pixel. We consider two kind of noises: the photon noise from the sky background
of our PSFs is typically 2.5 pixels. To evaluate whether a star is detected or not we compare the amplitude A of the PSF to the noise in the central pixel. We consider two kind of noises: the photon noise from the sky background
![]() and the read-out noise
and the read-out noise
![]() .
The noise in the central pixel is hence
.
The noise in the central pixel is hence
![]() .
In order to obtain A as a function of
.
In order to obtain A as a function of ![]() we consider a Gaussian PSF. The amplitude A of a Gaussian is
we consider a Gaussian PSF. The amplitude A of a Gaussian is
![]() with F beeing the total flux under the PSF and
with F beeing the total flux under the PSF and
![]() .
The condition to detect a star
.
The condition to detect a star
![]() can thus be expressed as
can thus be expressed as
![]() .
The limit magnitude m is therefore:
.
The limit magnitude m is therefore:
with Z being the photometric calibration constant. We have
To derive the number of stars N* expected in a
![]() pixel
sub-image from this limit magnitude we use a typical image taken under
excellent weather conditions. We calculate the distribution in
magnitude of the detected stars and fit it with a
pixel
sub-image from this limit magnitude we use a typical image taken under
excellent weather conditions. We calculate the distribution in
magnitude of the detected stars and fit it with a ![]() order polynomial. For magnitudes larger than 14 the number of
stars increases more slowly because they are becoming too faint to be
all detected. We therefore extend the fitting function with a constant
slope. The following relation provides our assumed number of stars as a
function of the limit magnitude:
order polynomial. For magnitudes larger than 14 the number of
stars increases more slowly because they are becoming too faint to be
all detected. We therefore extend the fitting function with a constant
slope. The following relation provides our assumed number of stars as a
function of the limit magnitude:
where a3=0.013, a2=-0.664, a1=11.326, a0=-61.567 and N*14 is the number of stars detected for m=14. Equations (1) and (2) thus provide the number of stars that should be detected for a clear sky given a value of sky background and FWHM. In order to test the validity of this relation, we compare this to the maximum number of stars detected in our images for given values of FWHM and sky background. (By choosing the maximum number of stars, or more precisely the number of stars which is exceeded only 1% of the time, we ensure that we consider only images taken under excellent weather conditions.) We find that both agree with a standard error of 6.6% and a maximum error of 15%.
4.2.4 Comparison to the measured number of stars
We use this model to compare the measured to the expected number of stars for each data point, given its FWHM and sky background. The resulting distribution in Fig. 13 shows two features: a main peak centered around 1 with most of the points, meaning that for these points the weather is excellent, and a tail for which the measured number of stars is smaller than expected, corresponding to veiled weather.
The spread around the main peak of the histogram is partly due to measurement errors in the sky background and FWHM.
The limit between this natural spread and the veiled weather data
points must be defined to calculate the weather statistics. To do this
we use a large set of sky background and FWHM values coherent with our measurements, and calculate the expected number of stars for each point
![]() according to our model. We then add some random errors to this set of
values and calculate again the expected number of stars. For each point
according to our model. We then add some random errors to this set of
values and calculate again the expected number of stars. For each point
![]() we compare the expected number of stars obtained with the added errors
to the one without errors. This yields a theoretical distribution of
the number of stars that accounts for measurement errors.
we compare the expected number of stars obtained with the added errors
to the one without errors. This yields a theoretical distribution of
the number of stars that accounts for measurement errors.
The sky background value is typically around 40 ADU. We estimate the error to be around 10% of this value, i.e. only 4 ADU. This error is not dominant and the spread of the theoretical distribution is mainly due to the error on the FWHM. The FWHM is typically between 2 and 3 pixels, and we suppose again an error of 10%, i.e. 0.25 pixels. However the shape of the theoretical distribution does not fit perfectly to the data. Instead we find that we can fit the two sides of the main peak in Fig. 13 with two different errors on the FWHM, corresponding to a low and a high measurement error, respectively 0.17 and 0.25 pixels.
The data points fitting into the theoretical distribution with the low error are considered as excellent weather (red part in Fig. 13). Those between the low and high error distributions can be either due to a large measurement error or to veiled weather, thus they are considered as uncertain weather (orange part). The data points outside the low error distribution correspond to veiled weather (yellow part).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{images/13629-20.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg62.png)
|
Figure 13: Ratio between the measured and the expected number of stars (black line). Theoretical histograms taking into account low and high measurement errors allow to identify 3 parts in the data: excellent weather in red, uncertain weather in orange and veiled weather in yellow. |
| Open with DEXTER | |
4.2.5 Weather statistics for the winter 2008
This analysis gives a fraction of time between 65.2% and 79.2% with
excellent weather and between 20.8% and 34.8% of veiled
weather. Only the periods with data when at least few stars are visible
are considered here, excluding in particular the white-out periods.
During the winter the acquisitions were stopped during 13.7% of
time because of very bad weather, so the previous numbers must be
multiplied by 1-0.137 = 0.863. The weather
statistics for the 2008 winter at Dome C are
therefore: between 56.3% and 68.4% of excellent weather,
17.9 to 30% of veiled weather during which stars are still visible
and 13.7% of bad weather (Fig. 14).
For comparison the fraction of photometric weather during night-time
is 62% at La Silla and 75% at Paranal as provided by Sarazin![]() (see also Ardeberg et al. 1990), whereas it is only 45% at Mauna Kea (Ortolani 2003, and references therein) though more recent results report 56% (Steinbring et al. 2009). Dome C is therefore very competitive compared to other observing sites.
(see also Ardeberg et al. 1990), whereas it is only 45% at Mauna Kea (Ortolani 2003, and references therein) though more recent results report 56% (Steinbring et al. 2009). Dome C is therefore very competitive compared to other observing sites.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{images/13629-21.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg63.png)
|
Figure 14: Cumulative histogram of the ratio between the measured and the expected number of stars. The data are distributed between excellent, uncertain and veiled weather. The white part is the fraction of time during which the acquisitions where stopped because of very bad weather (white-out). |
| Open with DEXTER | |
4.2.6 Validation
To validate the method, we compare the number of stars to the intensity
received from the stars, as both should be smaller if clouds are
present. We measure the intensity received from nine stars of
magnitude 8 to 12 and sum them after dividing each star by
its median value. We then normalize this sum by the maximum value, more
precisely by the mean of the 1% highest values. We use only the
periods with a moderate sky background i.e. when the Sun is below
![]() and excluding the full Moon periods (the result is however very similar using all data points). Figure 15
shows the normalized star intensity as a function of the ratio between
the measured and the expected number of stars. As expected, both
parameters are directly correlated, thus validating the method. We
further note that for data points taken under excellent or intermediate
weather conditions, i.e. when
and excluding the full Moon periods (the result is however very similar using all data points). Figure 15
shows the normalized star intensity as a function of the ratio between
the measured and the expected number of stars. As expected, both
parameters are directly correlated, thus validating the method. We
further note that for data points taken under excellent or intermediate
weather conditions, i.e. when
![]() ,
the normalized intensity received from the stars is
,
the normalized intensity received from the stars is
![]() .
Both parameters are thus good indicators of the cloud cover in the field of view.
.
Both parameters are thus good indicators of the cloud cover in the field of view.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{images/13629-22-NEW.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg66.png)
|
Figure 15: Normalized intensity of a selected sample of nine stars as a function of the ratio between the measured and the expected number of stars based on theoretical estimates (see text). |
| Open with DEXTER | |
4.3 Auroras
Aurorae were first feared to be a source of contamination for long-term photometric data. However, it is to be noted that Concordia is a favorable site in that respect: auroras occur mainly in the auroral zone, a ring-shaped region with a radius of approximately 2500 km around the magnetic pole. The Concordia site is located well within this ring, only 1300 km from the south magnetic pole, and thus has a much lower auroral activity than other sites (e.g. Dome A).
During the winter-over 2008, the Concordia staff reported 2 auroras on July 30 and 31. On July 30, a careful examination of the ASTEP South data indicates a possibility of auroral contamination between 14:12 and 14:24 UTC, but it cannot be distinguished from thin clouds. The July 31 data were unfortunately lost during the copy, probably because of a hard drive glitch (the only instance of that occurring) so that we could not attempt to check the images for that day.
In any case, the ASTEP South 2008 data were not contaminated by auroras, confirming the low contribution of auroras to the sky brightness as suggested by Dempsey et al. (2005). It will be interesting to see whether it remains true when progressively moving towards a maximum solar activity in 2012.
4.4 Observing time and photometric quality of Dome C
The duty cycle for the 2008 campaign of ASTEP South is represented in Fig. 16.
The limit due to the Sun, the observing time and the excellent and
intermediate weather fractions are shown for each day, as well as the
white-out periods. We acquired 1592 h of data with ASTEP South on
a single field during the 2008 campaign. From the previous analysis we
have 1034 h with excellent or uncertain weather. As a comparison,
simulations based on the method described in Rauer et al. (2008)
show that the time usable for photometry in one year at La Silla for
the field with the best observability is typically 820 h (see
Sect. 5
for more details). Moreover, the white-out periods at Dome C last
typically from one to a few days, allowing extended periods of
continuous observations between them. For example we observed every day
during one month between July 9 and August 8. Considering the
excellent and uncertain weather and the hours lost because of the Sun,
the fraction of time usable for photometry for this one month period
is 52%. In La Silla the fraction of time usable for photometry for
all one month periods between 1991 and 1999 has a mean of 27% with
a maximum of 45% in April 1997 (from the La Silla weather
statistics![]() multiplied by the night-time fraction). This shows the very high
potential of Dome C for continuous observations during the
Antarctic winter.
multiplied by the night-time fraction). This shows the very high
potential of Dome C for continuous observations during the
Antarctic winter.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{images/13629-23.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg67.png)
|
Figure 16: Daily observing time
fraction for ASTEP South in 2008 as a function of the observation
period. The light blue and dark blue regions indicate the fraction of
time for which the Sun is lower than |
| Open with DEXTER | |
5 Planet detection probability
As shown by Pont & Bouchy (2005), the high phase coverage at Dome C should improve the efficiency of a transit survey. Here we investigate the potential of ASTEP South for transit detection using CoRoTlux and compare the Dome C and La Silla observing sites. CoRoTlux performs statistical simulations of transit events for a survey given the star distribution in the field of view, the instrumental parameters and the observation windows (Fressin et al. 2007,2009). In all simulations, the star distribution is the one of the south pole field (see Sect. 2.2). We use the GSC2.2 catalog for stars from magnitude 10 to 14.5 completed with a distribution from the Besançon model up to magnitude 18 (after scaling it to the GSC2.2 catalog for low magnitude stars). The target stars range from magnitude 10 to 15 and the background stars from magnitude 15 to 18. The instrumental parameters are always those of ASTEP South. We perform three simulations corresponding to three survey configurations differing only by their observation windows.
The first set of observation windows that we have used in our simulations corresponds to the periods during which ASTEP South actually ran in excellent or uncertain weather conditions in 2008, i.e. the red and orange parts of the duty cycle in Fig. 16. This provides us with the potential yield of the 2008 campaign in terms of detections of transiting planets.
We also want to compare Dome C and La Silla. In that purpose we consider an ideal campaign for an ASTEP South-like instrument for which the observation windows are determined only from the altitude of the Sun and weather statistics at that site. For Dome C, we apply the weather statistics presented in Sect. 4.2.5 to an entire winter season in order to generate the second set of observation windows. For this second simulation, we incorporate over the Sun limited duty cycle 13.7% of white-out periods and 17.9% of randomly distributed cloudy periods lasting less than one day.
For La Silla, we generate a third set of observation windows using the monthly weather statistics acquired from 1987 to 2007![]() .
The weather statistics for each month is taken as the mean of the
photometric fraction for this given month over all years. At La Silla,
one cannot simply stare at the south pole field continuously because it
is low over the horizon. A best pointing can be found that maximizes
the observation time as a combination of weather statistics, night-time
and airmass (for a complete description of the method see Rauer et al. 2008). The resulting field with the best observability is centered on RA = 18h30
.
The weather statistics for each month is taken as the mean of the
photometric fraction for this given month over all years. At La Silla,
one cannot simply stare at the south pole field continuously because it
is low over the horizon. A best pointing can be found that maximizes
the observation time as a combination of weather statistics, night-time
and airmass (for a complete description of the method see Rauer et al. 2008). The resulting field with the best observability is centered on RA = 18h30![]() and
DE =-58
and
DE =-58
![]() 54
54![]() .
For consistency with the other simulations we use the same stellar
population as for the south pole field, and consider that photometric
observations are possible when the Sun is less than
.
For consistency with the other simulations we use the same stellar
population as for the south pole field, and consider that photometric
observations are possible when the Sun is less than
![]() below the horizon. The resulting duty cycles for weather and Sun
limited observations of a single field over one year are shown in
Fig. 17
for both Dome C and La Silla. The total observing time is
typically 2240 h for Dome C and 820 h for La Silla.
below the horizon. The resulting duty cycles for weather and Sun
limited observations of a single field over one year are shown in
Fig. 17
for both Dome C and La Silla. The total observing time is
typically 2240 h for Dome C and 820 h for La Silla.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{images/13629-24.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg69.png)
|
Figure 17:
Observing time fraction as a function of observing period at Concordia and
La Silla. The blue and grey envelopes indicate values obtained by imposing a Sun altitude lower than |
| Open with DEXTER | |
A large number of runs (![]() 3000)
are performed for each survey configuration in order to have a
significant statistic. The results of the simulations provide the
number of detectable planets. We assume that only transiting planets
with a signal to noise ratio higher than 10 are detectable. This
yields 1.08 planets for the ASTEP South 2008 campaign (i.e.
3244 planets over 3000 runs), 1.62 planets for a whole
winter at Dome C, and 1.04 planet for La Silla. These numbers
are low because ASTEP South is a small instrument, however the number
of planets is notably higher for a survey from Dome C than from
La Silla. The resulting planet detection efficiency is shown in
Fig. 18.
The detection efficiency is defined as the number of detectable planets
divided by the total number of simulated planets. In spite of technical
problems at the beginning of the winter, the detection efficiency for
the ASTEP South 2008 campaign is equivalent to the one obtained for one
year at La Silla. When comparing an instrument that would run for the
entire observing season, the detection efficiency is found to be
significantly higher at Dome C than at La Silla both in terms of
planet orbital period and transit depth. For example we have an
efficiency of 69% at Dome C vs. 45% at La Silla for a 2-day
period giant planet, and 76% at Dome C vs. 45% at
La Silla for a 2% transit depth. The detection efficiency
decreases for planets with longer orbital periods, but is even more
favorable to Dome C relatively to La Silla. On the other hand, it
is true that a mid-latitude site offers more available targets.
However, we believe that this shows the high potential of Dome C
for future planet discoveries.
3000)
are performed for each survey configuration in order to have a
significant statistic. The results of the simulations provide the
number of detectable planets. We assume that only transiting planets
with a signal to noise ratio higher than 10 are detectable. This
yields 1.08 planets for the ASTEP South 2008 campaign (i.e.
3244 planets over 3000 runs), 1.62 planets for a whole
winter at Dome C, and 1.04 planet for La Silla. These numbers
are low because ASTEP South is a small instrument, however the number
of planets is notably higher for a survey from Dome C than from
La Silla. The resulting planet detection efficiency is shown in
Fig. 18.
The detection efficiency is defined as the number of detectable planets
divided by the total number of simulated planets. In spite of technical
problems at the beginning of the winter, the detection efficiency for
the ASTEP South 2008 campaign is equivalent to the one obtained for one
year at La Silla. When comparing an instrument that would run for the
entire observing season, the detection efficiency is found to be
significantly higher at Dome C than at La Silla both in terms of
planet orbital period and transit depth. For example we have an
efficiency of 69% at Dome C vs. 45% at La Silla for a 2-day
period giant planet, and 76% at Dome C vs. 45% at
La Silla for a 2% transit depth. The detection efficiency
decreases for planets with longer orbital periods, but is even more
favorable to Dome C relatively to La Silla. On the other hand, it
is true that a mid-latitude site offers more available targets.
However, we believe that this shows the high potential of Dome C
for future planet discoveries.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{images/13629-25.ps}\par\includegraphics[width=8.3cm,clip]{images/13629-26.ps}\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg70.png)
|
Figure 18:
Calculated efficiency of detection of transiting giant planets for a
single field as observed by an ASTEP-South like survey during a full
season, and as a function of the orbital period ( top) and transiting depth ( bottom). Dotted blue lines: detection efficiency for the ASTEP South 2008 campaign. Plain blue line:
detection efficiency for a full winter at Dome C for a circumpolar
field limited only by the weather statistics and the constraint of a
Sun altitude below |
| Open with DEXTER | |
6 Conclusion
ASTEP South, the first phase of the ASTEP project observed 1592 h of data during the 2008 winter. Night-time photometric observations started in a nearly continuous way around mid-June and proceeded to the end of September, when the sky became too bright even at midnight local-time. Our preliminary analysis showed that the Sun affects our photometric measurements when it is at an altitude higher thanAn identification of the stars in the field allowed us to retrieve the precise location of the celestial south pole on the images and show that the pointing direction is stable within 10 arcsec on a daily timescale for a drift of only 34 arcsec in 50 days. On the basis of the number of identified stars and of a model to account for PSF variations and sky brightness, we retrieved the weather statistics for the 2008 winter: between 56.3% and 68.4% of excellent weather, 17.9% to 30% of veiled weather (when the probable presence of thin clouds implies a lower number of detected stars) and 13.7% of bad weather.
An analysis of the yield of transit surveys with our weather statistics at Dome C compared to those at La Silla showed that the efficiency to detect transiting planets in one given field is significantly higher at Dome C (69% vs. 45% for 2-day period giant planets with an ASTEP South-like instrument in one season). The prospects for the detection and characterization of exoplanets from Dome C are therefore very good. Future work will be focused on a detailed analysis of the full ASTEP South images. The second phase of the project includes the installation of ASTEP 400, a dedicated automated 40-cm telescope at Concordia and its operation in 2010.
AcknowledgementsThe ASTEP project is funded by the Agence Nationale de la Recherche (ANR), the Institut National des Sciences de l'Univers (INSU), the Programme National de Planétologie (PNP), and the Plan Pluri-Formation OPERA between the Observatoire de la Côte d'Azur and the Université de Nice-Sophia Antipolis. The entire logistics at Concordia is handled by the French Institut Paul-Emile Victor (IPEV) and the Italian Programma Nazionale di Ricerche in Antartide (PNRA). The research grant for N. Crouzet is supplied by the Région Provence Alpes Côte d'Azur and the Observatoire de la Côte d'Azur. We wish to further thank E. Fossat for his helpful remarks on the manuscript. See http://fizeau.unice.fr/astep/ for more information about the ASTEP project.
References
- Agabi, A., Aristidi, E., Azouit, M., et al. 2006, PASP, 118, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Ardeberg, A., Lundstrom, I., & Lindgren, H. 1990, A&A, 230, 518 [NASA ADS] [Google Scholar]
- Aristidi, E., Agabi, A., Vernin, J., et al. 2003, A&A, 406, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aristidi, E., Agabi, K., Azouit, M., et al. 2005, A&A, 430, 739 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aristidi, E., Fossat, E., Agabi, A., et al. 2009, A&A, 499, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ashley, M. C. B., Burton, M. G., Calisse, P. G., Phillips, A., & Storey, J. W. V. 2005a, Highlights of Astronomy, 13, 932 [NASA ADS] [Google Scholar]
- Ashley, M. C. B., Lawrence, J. S., Storey, J. W. V., & Tokovinin, A. 2005b, EAS Pub. Ser. 14, ed. M. Giard, F. Casoli, & F. Paletou, 19 [Google Scholar]
- Briguglio, R., Tosti, G., Strassmeier, K. G., et al. 2009, Mem. Soc. Astron. It., 80, 147 [NASA ADS] [Google Scholar]
- Chadid, M., Vernin, J., Trinquet, H., et al. 2007, EAS Pub. Ser. 25, ed. N. Epchtein, & M. Candidi, 73 [Google Scholar]
- Chadid, M., Vernin, J., Jeanneaux, F., Mekarnia, D., & Trinquet, H. 2008, SPIE Conf. Ser., 7012 [Google Scholar]
- Crouzet, N., Agabi, K., Blazit, A., et al. 2009, IAU Symp., 253, 336 [NASA ADS] [Google Scholar]
- Crouzet, N., Guillot, T., Agabi, K., et al. 2010, EAS Pub. Ser. 40, ed. L. Spinoglio, & N. Epchtein, in press [Google Scholar]
- Crouzet, N., Guillot, T., Fressin, F., Blazit, A., & the A STEP team 2007, Astron. Nachr., 328, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Dempsey, J. T., Storey, J. W. V., & Phillips, A. 2005, PASA, 22, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Fressin, F., Guillot, T., Bouchy, F., et al. 2005, EAS Pub. Ser. 14, ed. M. Giard, F. Casoli, & F. Paletou, 309 [Google Scholar]
- Fressin, F., Guillot, T., Morello, V., & Pont, F. 2007, A&A, 475, 729 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fressin, F., Guillot, T., & Nesta, L. 2009, A&A, 504, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geissler, K., & Masciadri, E. 2006, SPIE Conf. Ser., 6267 [Google Scholar]
- Guerri, G., Abe, L., Aristidi, E., et al. 2007, EAS Pub. Ser. 25, ed. N. Epchtein, & M. Candidi, 339 [Google Scholar]
- Kenyon, S. L., Lawrence, J. S., Ashley, M. C. B., et al. 2006, PASP, 118, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. L., & Storey, J. W. V. 2006, PASP, 118, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Lawrence, J. S., Ashley, M. C. B., Tokovinin, A., & Travouillon, T. 2004, Nature, 431, 278 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Moore, A., Allen, G., Aristidi, E., et al. 2008, in SPIE Conf. Ser., 7012 [Google Scholar]
- Mosser, B., & Aristidi, E. 2007, PASP, 119, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Ortolani, S. 2003, ESPAS Site Summary Ser. 1.2, Mauna Kea (Garching: ESO), 2 [Google Scholar]
- Patat, F., Ugolnikov, O. S., & Postylyakov, O. V. 2006, A&A, 455, 385 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pont, F., & Bouchy, F. 2005, EAS Pub. Ser., 14, ed. M. Giard, F. Casoli, & F. Paletou, 155 [Google Scholar]
- Rauer, H., Fruth, T., & Erikson, A. 2008, PASP, 120, 852 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steinbring, E., Cuillandre, J., & Magnier, E. 2009, PASP, 121, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Briguglio, R., Granzer, T., et al. 2008, A&A, 490, 287 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trinquet, H., Agabi, A., Vernin, J., et al. 2008, PASP, 120, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Ziad, A., Aristidi, E., Agabi, A., et al. 2008, A&A, 491, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Footnotes
- ... Galaxy
![[*]](/icons/foot_motif.png)
- http://bison.obs-besancon.fr/modele/
- ... Sarazin
![[*]](/icons/foot_motif.png)
- http://www.eso.org/gen-fac/pubs/astclim/paranal/clouds/statcloud.gif
- ... statistics
![[*]](/icons/foot_motif.png)
- http://www.ls.eso.org/sci/facilities/lasilla/astclim/weather/tablemwr.html
- ... 2007
![[*]](/icons/foot_motif.png)
- http://www.eso.org/gen-fac/pubs/astclim/paranal/clouds/statcloud.lis.
All Tables
Table 1:
Number of stars in the 3.88 ![]() 3.88
3.88
![]() 2 celestial south pole field.
2 celestial south pole field.
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{images/13629-01.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg14.png)
|
Figure 1: ASTEP South at Dome C, Antarctica, January 2008. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{images/13629-02.ps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg17.png)
|
Figure 2:
Top panel: cumulative distribution of the number of stars in the south pole field as a function of their magnitude in the R band. The plain line shows results from the Besançon model. The dashed line indicates output from the GSC2.2 catalog. Bottom panel: ratio of dwarf stars with selected radii (less than 2, 1 and 0.5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{images/13629-03-NEW.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg27.png)
|
Figure 3: Image intensity for all the winter. The bias level is around 2480 ADU and the scale is half of the CCD dynamics. Peaks around noon will affect the photometry. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{images/13629-04-NEW.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg28.png)
|
Figure 4: Image intensity during 3 typical days in June, July and August. The bias level is around 2480 ADU and the scale is half of the CCD dynamics. Due to the Sun, the sky background increases around noon. The corresponding magnitude for June 22 is 15.3 mag/arcsec2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{images/13629-05-NEW.eps}\par...
...udegraphics[width=8cm,clip]{images/13629-06-NEW.eps}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg33.png)
|
Figure 5:
Mean intensity of each image and number of stars as a function of the Sun altitude when it is between
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{images/13629-07-NEW.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg35.png)
|
Figure 6: Image intensity. The bias level is around 2480 ADU and the scale is 1% of the CCD dynamics. The sky background increases during 10 days around the full Moon up to typically 18.1 mag / arcsec2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{images/13629-08-NEW.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg36.png)
|
Figure 7: Mean values of the size of the stars ( FWHM) on the CCD in pixels ( top panels) and their asymmetry ( bottom panels) as a function of the observing day for the months of June ( top left), July ( top right), August ( bottom left) and September ( bottom right). In the top panels, the blue and green curves correspond to the values of the FWHM in the x and y directions, respectively. The mean FWHM values are obtained through a spatial average on the CCD. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{images/13629-09-NEW.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg37.png)
|
Figure 8: Correlation between the PSF FWHM and independent seeing measurements at Dome C, for timescales smaller than one day (the FWHM is corrected for larger timescale variations). Direct seeing measurements from three differential image motion monitors are shown in blue, green and red. A linear regression gives a slope a = 0.59 with a correlation coefficient r = 0.65. The PSFs are clearly affected by seeing variations at the ground level. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{images/13629-10.eps}\par\includegraphics[width=8cm,clip]{images/13629-11.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg38.png)
|
Figure 9: Position of the pole on the CCD. Top: 9 images on July 11 after various astrometric corrections (blue: approximate correction of the precession of the equinox, green: improved correction of the precession of the equinox, brown: correction of the nutation, red: correction of the Bradley effect). Bottom: 7 days between June 12 and July 30, showing a drift over the winter (dark blue: June 12, light blue: June 24, green: July 2, yellow: July 11, orange: July 17, red: July 30). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{images/13629-12-NEW.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg39.png)
|
Figure 10:
Camera temperature, bias level and image intensity on July 11. The camera temperature varies between +4 and +8
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{images/13629-13-NEW.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg40.png)
|
Figure 11: Bias level against the camera temperature for July 11. The blue points correspond to an increasing temperature and the red points to a decreasing temperature, showing a hysteresis behavior. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{images/13629-14.ps}\par\in...
...29-18.ps}\par\includegraphics[width=8.5cm,clip]{images/13629-19.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg43.png)
|
Figure 12: ASTEP South observation calendar for the 2008 campaign. April and May were mainly dedicated to solving technical problems. Continuous observations started mid-June with very few interruptions until the end of the winter. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{images/13629-20.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg62.png)
|
Figure 13: Ratio between the measured and the expected number of stars (black line). Theoretical histograms taking into account low and high measurement errors allow to identify 3 parts in the data: excellent weather in red, uncertain weather in orange and veiled weather in yellow. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{images/13629-21.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg63.png)
|
Figure 14: Cumulative histogram of the ratio between the measured and the expected number of stars. The data are distributed between excellent, uncertain and veiled weather. The white part is the fraction of time during which the acquisitions where stopped because of very bad weather (white-out). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{images/13629-22-NEW.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg66.png)
|
Figure 15: Normalized intensity of a selected sample of nine stars as a function of the ratio between the measured and the expected number of stars based on theoretical estimates (see text). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{images/13629-23.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg67.png)
|
Figure 16: Daily observing time
fraction for ASTEP South in 2008 as a function of the observation
period. The light blue and dark blue regions indicate the fraction of
time for which the Sun is lower than |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{images/13629-24.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg69.png)
|
Figure 17:
Observing time fraction as a function of observing period at Concordia and
La Silla. The blue and grey envelopes indicate values obtained by imposing a Sun altitude lower than |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{images/13629-25.ps}\par\includegraphics[width=8.3cm,clip]{images/13629-26.ps}\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/03/aa13629-09/Timg70.png)
|
Figure 18:
Calculated efficiency of detection of transiting giant planets for a
single field as observed by an ASTEP-South like survey during a full
season, and as a function of the orbital period ( top) and transiting depth ( bottom). Dotted blue lines: detection efficiency for the ASTEP South 2008 campaign. Plain blue line:
detection efficiency for a full winter at Dome C for a circumpolar
field limited only by the weather statistics and the constraint of a
Sun altitude below |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.