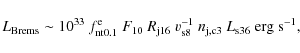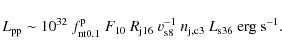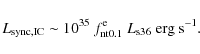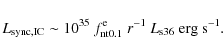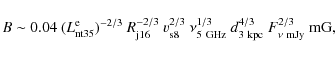| Issue |
A&A
Volume 511, February 2010
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/200913488 | |
| Published online | 19 February 2010 | |
Massive protostars as gamma-ray sources
V. Bosch-Ramon1
- G. E. Romero2,3,![]() ,
A. T. Araudo2,3 - J. M. Paredes1
,
A. T. Araudo2,3 - J. M. Paredes1
1 - Departament d'Astronomia i Meteorologia and Institut de Ciències
del Cosmos (ICC), Universitat de Barcelona (UB/IEEC),
Martí i Franquès 1,
08028 Barcelona, Spain
2 - Instituto Argentino de
Radioastronomía (CCT La Plata, CONICET), C.C.5, (1894) Villa Elisa,
Buenos Aires,
Argentina
3 - Facultad de Ciencias Astronómicas y Geofísicas,
Universidad Nacional de La Plata, Paseo del Bosque, 1900 La Plata,
Argentina
Received 16 October 2009 / Accepted 24 November 2009
Abstract
Context. Massive protostars have associated bipolar
outflows with velocities of hundreds of km s-1.
Such outflows can produce strong shocks when they interact with the
ambient medium leading to regions of nonthermal radio emission.
Aims. We aim at exploring under which conditions
relativistic particles are accelerated at the terminal shocks of the
protostellar jets and whether they can produce significant gamma-ray
emission.
Methods. We estimate the conditions necessary for
particle acceleration up to very high energies and gamma-ray production
in the nonthermal hot spots of jets associated with massive protostars
embedded in dense molecular clouds.
Results. We show that relativistic bremsstrahlung
and proton-proton collisions can make molecular clouds with massive
young stellar objects detectable by the Fermi
satellite at MeV-GeV energies and by Cherenkov telescope arrays in the
GeV-TeV range.
Conclusions. Gamma-ray astronomy can be used to
probe the physical conditions in star-forming regions and particle
acceleration processes in the complex environment of massive molecular
clouds.
Key words: stars: formation - gamma rays: stars - stars: early-type - ISM: clouds
1 Introduction
Massive stars are formed in the dense cores of massive cold clouds (Garay & Lizano 1999, and references therein). The accumulation of gas in the core might proceed through previous stages of fragmentation and coalescence with the progressive result of a massive protostar that then accretes from the environment (e.g. Bonnell et al. 1997; Stahler et al. 2000) or through direct accretion onto a central object of very high mass (e.g. Rodríguez et al. 2008 - RMF08 -; see Shu et al. 1987, for the basic mechanism). In either case, the prestellar core is expected to have angular momentum, which would lead to the formation of an accretion disk. The strong magnetic fields inside the cloud that thread the disk should be pulled toward the protostar and twisted by the rotation, giving rise to a magnetic tower with the consequent outflows, as shown by numerical simulations (e.g. Banerjee & Pudritz 2006, 2007).
Evidence of molecular outflows is found through methanol masers, which are likely associated with shocks formed by the interaction with the external medium (e.g. Plambeck & Menten 1990). However, the most important evidence of outflows comes from the detection of thermal radio jets. These jets are observed to propagate through the cloud material along distances of a fraction of a parsec (e.g. Martí et al. 1993 - MRR93 -). At the end point of the jets, hot spots due to the terminal shocks are observed in several sources. In a few cases, these hot spots are clearly nonthermal, indicating the presence of relativistic electrons that produce synchrotron radiation (e.g. Araudo et al. 2007 - ARA07 -, 2008).
A population of relativistic electrons in the complex environment of the massive molecular cloud in which the protostar is being formed will produce high-energy radiation through a variety of processes: inverse Compton (IC) scattering of infrared (IR) photons from the cloud, relativistic bremsstrahlung, and, if protons are accelerated at the shock as well, inelastic proton-proton (pp) collisions. If such radiation is detectable, gamma-ray astronomy can be used to shed light on the star-forming process, the protostar environment, and cosmic ray acceleration inside molecular clouds.
This work is devoted to discussing under what conditions the terminal shocks of jets from massive protostars can efficiently accelerate particles and produce gamma rays that may be detectable by the Fermi satellite and Cherenkov telescopes in the near future. The model developed for the calculations is essentially different from the phenomelogical model presented by ARA07, since now the dynamics of the jet termination region is characterized, the shock power estimated, the conditions for particle acceleration analyzed, and the role of hydrodynamical instabilities for nonthermal radiation explored. In short, the acceleration and emission are consistently modeled together with the hydrodynamics in a more physical scenario. Our study is partially based on early works on nonthermal emission in young stellar objects (YSO), as those by Crusius-Watzel (1990) and Henriksen et al. (1991), but we develop further some important aspects of the hydrodynamics-radiation relation, and focus on massive YSOs and the feasibility of their detection with the present observational facilities.
2 Physical scenario
A massive YSO, or a group of them, are deeply embedded in a molecular
cloud. The protostar heats the cloud in such a way
that it can be detected as a strong IR source, with luminosities in the
range
![]() erg s-1,
whereas the optical counterpart is obscured by the cloud. Masses and
sizes of these clouds are
erg s-1,
whereas the optical counterpart is obscured by the cloud. Masses and
sizes of these clouds are ![]() 103
103 ![]() and a few pc, respectively (e.g. Garay & Lizano 1999), and the
densities in the regions
in which the massive YSOs are found typically span
and a few pc, respectively (e.g. Garay & Lizano 1999), and the
densities in the regions
in which the massive YSOs are found typically span
![]() cm-1
(see Araudo et al. 2008
and references
therein).
cm-1
(see Araudo et al. 2008
and references
therein).
As already mentioned, collimated outflows are present in most
massive YSOs, and thermal radiation has been detected up
to distances of 1016-1018 cm
from the central star. These jets have temperatures of ![]() 104 K
and move at
speeds (
104 K
and move at
speeds (![]() )
from several hundred to
)
from several hundred to ![]() 1000 km s-1
(e.g. MRR93, Martí et al. 1995
-MRR95-). This shows that they are strongly supersonic flows with Mach
numbers
1000 km s-1
(e.g. MRR93, Martí et al. 1995
-MRR95-). This shows that they are strongly supersonic flows with Mach
numbers ![]() .
The kinetic luminosities of these
jets are expected to be
.
The kinetic luminosities of these
jets are expected to be
![]() erg s-1
(e.g. MRR95, ARA07).
erg s-1
(e.g. MRR95, ARA07).
In some cases (see Araudo et al. 2008),
nonthermal radio lobes have been detected
at distances of ![]() pc,
with sizes of
pc,
with sizes of ![]() 1%
of this distance (MRR93, Garay et al. 2003 -
GAR03 -). Given the directions, sizes, and distances from the
core, the lobes are compatible with being produced
by the head of the jet. These radio lobes are probably generated by the
strong terminal shocks of the jets, which also ionize
the shocked material. Magnetic fields should also be present, since
they play an important role in supporting the
cloud before the gravitational collapse, allowing the required high
densities in the cores to be achieved (e.g. McKee &
Ostriker 2007).
Estimates from Zeeman measurements of the cloud magnetic field give
values of
1%
of this distance (MRR93, Garay et al. 2003 -
GAR03 -). Given the directions, sizes, and distances from the
core, the lobes are compatible with being produced
by the head of the jet. These radio lobes are probably generated by the
strong terminal shocks of the jets, which also ionize
the shocked material. Magnetic fields should also be present, since
they play an important role in supporting the
cloud before the gravitational collapse, allowing the required high
densities in the cores to be achieved (e.g. McKee &
Ostriker 2007).
Estimates from Zeeman measurements of the cloud magnetic field give
values of
![]() mG
(e.g. Crutcher 1999),
where
mG
(e.g. Crutcher 1999),
where
![]() is the cloud density. Under these
conditions, particles can be accelerated up to relativistic energies
via diffusive shock (Fermi I) acceleration (DSA, e.g. Bell 1978;
see Drury 1983,
for a review). These particles would produce the radiation of
nonthermal nature found in the lobes, and could generate
significant emission in a broad spectral range, from radio to gamma
rays.
is the cloud density. Under these
conditions, particles can be accelerated up to relativistic energies
via diffusive shock (Fermi I) acceleration (DSA, e.g. Bell 1978;
see Drury 1983,
for a review). These particles would produce the radiation of
nonthermal nature found in the lobes, and could generate
significant emission in a broad spectral range, from radio to gamma
rays.
Some amount of thermal ultraviolet (UV)/X-ray photons is expected from the shocked material. This radiation will suffer strong photo-electric absorption in the regions of the cloud next to the jet head and will ionize the surrounding material improving the conditions for efficient particle acceleration (e.g. Drury et al. 1996). On the other hand, fast radiative cooling of the shocked material can affect the lobe dynamics and also reduce the efficiency of DSA, but could increase the detectability of massive YSO at high energies because of the density enhancement. Finally, ionization losses of radio emitting electrons and free-free absorption by the ionized medium could significantly affect the radio spectrum. In some sources, free-free emission may dominate the radio band.
In Fig. 1 we sketch the scenario in which nonthermal emission is produced through the acceleration of electrons and protons in the jet termination regions.
| Figure 1: Sketch of the termination region of the jet of a massive YSO. Two shocks of different strengths and velocities will form depending on the jet-medium properties. Electrons and protons can be accelerated in the shocks, and generate nonthermal emission via interaction with the ambient matter, magnetic, and radiation fields. The shocked material will also produce thermal radiation. |
|
| Open with DEXTER | |
3 Physical nature of the lobes
We assume that the nonthermal radio lobes are the regions in which the protostellar jets terminate. The action of the jet head on the external medium leads to two shocks, one moving in the cloud material and another one in the jet itself: the bow shock and the reverse shock, respectively. These shocks would be the accelerators of the relativistic particles generating the observed nonthermal radio emission.
3.1 Dynamics of the jet termination shocks
An important parameter determining the shock characteristics is the jet
(j) to cloud (c) density ratio
![]() .
For fiducial values of the jet properties, say
.
For fiducial values of the jet properties, say
![]() cm s-1,
cm s-1,
![]() erg s-1
and jet radius
erg s-1
and jet radius
![]() cm
(assuming that lobe and jet radii are similar), we obtain jet densities
in the range
cm
(assuming that lobe and jet radii are similar), we obtain jet densities
in the range ![]() cm-3
at the location of the lobe; then,
cm-3
at the location of the lobe; then,
![]() .
.
The value of ![]() ,
together with
,
together with ![]() ,
determines the speed of the
bow shock (e.g. Blondin et al. 1989):
,
determines the speed of the
bow shock (e.g. Blondin et al. 1989):
|
|
|||
| (1) |
where
and
Equations (2) and (3) show that the jet advances in two different regimes depending on the jet-medium density ratio, which depends in turn on the source age. As long as the jet lateral pressure is stronger than that of the surrounding medium, the jet expands freely and thus,
At some point, the jet expansion is stopped by the external
pressure, and the jet density becomes roughly constant. When it happens
depends on the shocked jet material pressure away from the reverse
shock,
but it is expected that ![]() .
If values as low as
.
If values as low as ![]() are reached,
the bow shock will move with a speed below the Alfven speed (
are reached,
the bow shock will move with a speed below the Alfven speed (![]() )
in the cloud and will not be a shock anymore.
)
in the cloud and will not be a shock anymore.
The luminosity crossing the shock surface in the jet and the
cloud (reverse and bow shock, respectively) is
|
|
= | ||
| (4) |
where
When ![]() ,
the reverse shock to bow shock luminosity ratio is
,
the reverse shock to bow shock luminosity ratio is ![]()
![]() .
This and
.
This and ![]() -t
dependence mentioned above imply that most of the time the reverse
shock will
be more powerful than the bow shock. On the other hand, for
-t
dependence mentioned above imply that most of the time the reverse
shock will
be more powerful than the bow shock. On the other hand, for ![]() the reverse shock will be very weak and the bow shock
radiation very faint. Therefore, lobe detection is favored when the jet
has expanded enough to reach
the reverse shock will be very weak and the bow shock
radiation very faint. Therefore, lobe detection is favored when the jet
has expanded enough to reach ![]() ,
being the reverse shock
the best place for particle acceleration unless
,
being the reverse shock
the best place for particle acceleration unless
![]() ,
when both shocks have similar properties.
,
when both shocks have similar properties.
3.2 The postshock regions
For purely adiabatic jet-medium interactions, the formation of the
reverse shock is accompanied by a strong widening of the jet
termination region as in extragalactic FRII sources (e.g. Kaiser
& Alexander 1997)
and possibly in microquasars (e.g. Bordas et al. 2009).
However, the conditions in massive YSOs are likely to be different. As
noted by Blondin et al. (1989), if the
cooling length ![]() of the
shocked material in either the reverse, the bow shock, or in both, is
<
of the
shocked material in either the reverse, the bow shock, or in both, is
<![]() ,
the jet head will not expand significantly. If using the cooling
function
,
the jet head will not expand significantly. If using the cooling
function
![]() (e.g. Myasnikov et al. 1998) at the
temperatures relevant here, adopting a density and speed downstream
right after the shock of
(e.g. Myasnikov et al. 1998) at the
temperatures relevant here, adopting a density and speed downstream
right after the shock of
![]() and
and
![]() ,
respectively (strong, nonrelativistic and lowly magnetized shock), and
assuming full ionization
in that region,
,
respectively (strong, nonrelativistic and lowly magnetized shock), and
assuming full ionization
in that region, ![]() is
is
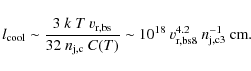
|
(5) |
A specific-case treatment and detailed simulations would be required to characterize the fine evolution of the jet head. However, there is a wide range of realistic parameters for which the bow shock, and even the reverse shock, can be radiative. This is compatible with the relatively small size of nonthermal radio lobes (see Sect. 2). In case one or both shocks are not radiative, the material cools through adiabatic expansion farther than
Because of radiative cooling, the compression ratio
When ![]() ,
the material downstream is
,
the material downstream is ![]() to
to ![]() times denser in the bow shock
than in the reverse shock. Since a force is exerted by the downstream
material of the reverse shock on that of the bow shock, Rayleigh-Taylor
(RT) instabilities in the contact discontinuity between both shocks can
develop. This phenomenon will distort the jethead on a timescale
times denser in the bow shock
than in the reverse shock. Since a force is exerted by the downstream
material of the reverse shock on that of the bow shock, Rayleigh-Taylor
(RT) instabilities in the contact discontinuity between both shocks can
develop. This phenomenon will distort the jethead on a timescale
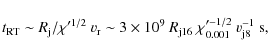
|
(7) |
where
Concerning the dynamic role of the jet and cloud magnetic
fields at the jet termination region, ![]() and
and ![]() ,
respectively, we assume
hereafter that they are negligible. This applies as long as
,
respectively, we assume
hereafter that they are negligible. This applies as long as
![]() ,
where
,
where
is the magnetic field of equipartition between the magnetic and the jet kinetic energy density. If
4 Particle acceleration in the lobes
4.1 Acceleration and cooling processes
The energies and luminosities that nonthermal particles may achieve
depend on the efficiency of particle acceleration, which
depends in turn on the lobe properties. As noted above, DSA can operate
in the fast strong shocks at the termination of the jets
accelerating particles up to relativistic energies. For a parallel,
barely magnetized (i.e.
![]() upstream), non-relativistic strong shock, in the test particle
approximation and with diffusion coefficient D, the
acceleration rate is (e.g. Protheroe 1999)
upstream), non-relativistic strong shock, in the test particle
approximation and with diffusion coefficient D, the
acceleration rate is (e.g. Protheroe 1999)
|
|
= | 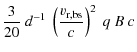
|
|
| (9) |
where e and p stand for electrons and protons, respectively, and
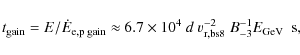
|
(10) |
where
At the maximum energy of particles,
![]() becomes equal to the shortest timescales among
synchrotron, IC (Thomson regime), and relativistic bremsstrahlung
losses for electrons
(see Blumenthal & Gould 1970),
inelastic pp collision losses for protons (see Kelner et al. 2006), and
diffusive particle escape and jet lifetime for both electrons and
protons. The relevant loss timescales,
becomes equal to the shortest timescales among
synchrotron, IC (Thomson regime), and relativistic bremsstrahlung
losses for electrons
(see Blumenthal & Gould 1970),
inelastic pp collision losses for protons (see Kelner et al. 2006), and
diffusive particle escape and jet lifetime for both electrons and
protons. The relevant loss timescales,
![]() ,
are given by the following expressions:
,
are given by the following expressions:
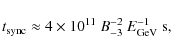
|
(11) |
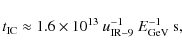
|
(12) |
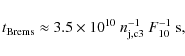
|
(13) |
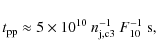
|
(14) |
where
From the timescales presented above, we obtain the following
maximum energies depending on the dominant energy loss mechanism and
source age:
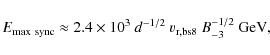
|
(17) |
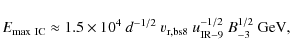
|
(18) |
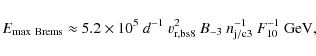
|
(19) |
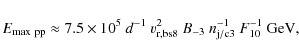
|
(20) |
This shows that, if
4.2 Required conditions for efficient DSA
In DSA particles are scattered by magnetic inhomogeneities back to the
shock before escaping downstream/upstream. These
inhomogeneities should not move faster than the shock itself, since
otherwise the particles would not be affected by the
shock velocity jump. If it were the case, stochastic Fermi II
particle acceleration could be at work (Fermi 1949). However,
in that case most of the jet kinetic energy will not be available, and
little energy will go to nonthermal particles. Therefore,
efficient particle acceleration requires the shock to be super-Alfvenic
in the upstream region, i.e.
![]() ,
where
,
where
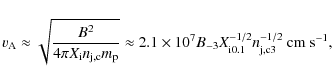
|
(23) |
and
Downstream of the shock, the material is likely ionized
through particle collisions, and the magnetic field is expected to
be quite disordered. Upstream of the shock, UV/X-ray radiation produced
in the shock region can photo-ionize the medium
unless ![]() cm s-1
(or
cm s-1
(or ![]() ),
since then photons cannot ionize hydrogen. From the recombination and
photo-ionization timescales,
),
since then photons cannot ionize hydrogen. From the recombination and
photo-ionization timescales,
![]() s
and
s
and
![]() s,
respectively (the recombination rate and ionization
cross section are given in Seaton 1959; and
Morrison & McCammon 1983;
L35 corresponds here to the
ionizing photon field
luminosity), it seems likely that upstream of the shock
s,
respectively (the recombination rate and ionization
cross section are given in Seaton 1959; and
Morrison & McCammon 1983;
L35 corresponds here to the
ionizing photon field
luminosity), it seems likely that upstream of the shock
![]() ,
and therefore
,
and therefore ![]() .
In
the radiative regions downstream of the shock,
.
In
the radiative regions downstream of the shock, ![]() may become much smaller than 1.
may become much smaller than 1.
As noted, the magnetic field should have some level of inhomogeneity: the scattering centers that isotropise particles in both sides of the shock. Magnetic inhomogeneities can develop upstream because of relativistic particle streaming (e.g. Lucek & Bell 2000), but they should not be suppressed by wave damping (see Reville et al. 2007). These inhomogeneities would be advected downstream of the shock, thus they would be also present there.
For very high densities, Coulombian/ionization energy losses
should not suppress acceleration from suprathermal energies (e.g. Drury
et al. 1996).
For that, the following condition should be provided:
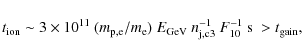
|
(24) |
which implies
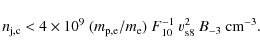
|
(25) |
The detection of radio emission from electrons with energy,
where
5 nonthermal emission in the lobes
5.1 The fate of accelerated particles
The electrons and protons accelerated by DSA have an uncooled energy
spectrum ![]() up to
up to ![]() ,
with
,
with ![]() (e.g. Drury 1983)
and total luminosity
(e.g. Drury 1983)
and total luminosity
![]() .
They mainly accumulate downstream of the shock,
in a region that here will be considered homogeneous with a typical
size
.
They mainly accumulate downstream of the shock,
in a region that here will be considered homogeneous with a typical
size ![]()
![]() .
When protons are present,
secondary electrons and positrons (
.
When protons are present,
secondary electrons and positrons (
![]() )
are injected from pp collisions with almost a powerlaw in energy in the
region in which these
protons interact significantly. The injection luminosity and the
maximum effective energy of
)
are injected from pp collisions with almost a powerlaw in energy in the
region in which these
protons interact significantly. The injection luminosity and the
maximum effective energy of ![]() will be about a
half of the luminosity going to
will be about a
half of the luminosity going to ![]() -decay gamma rays and
-decay gamma rays and ![]() 0.1 the
energy of protons (see Kelner et al. 2006). All these
particles evolve under the downstream magnetic, matter, and radiation
fields, losing energy in the form
of synchrotron radiation, relativistic bremsstrahlung, and IC emission
in the case of electrons, and high-energy photons,
neutrinos,
0.1 the
energy of protons (see Kelner et al. 2006). All these
particles evolve under the downstream magnetic, matter, and radiation
fields, losing energy in the form
of synchrotron radiation, relativistic bremsstrahlung, and IC emission
in the case of electrons, and high-energy photons,
neutrinos, ![]() ,
and other secondary particles via pp collisions in the case of
protons.
,
and other secondary particles via pp collisions in the case of
protons.
Only the radiation from a region closer than ![]() from the shock is computed. At distances greater than
from the shock is computed. At distances greater than
![]() ,
particles cool through adiabatic losses due to the re-expansion of the
shocked material, producing scarce
emission. If densities are large enough (i.e. strongly radiative
shocks,
,
particles cool through adiabatic losses due to the re-expansion of the
shocked material, producing scarce
emission. If densities are large enough (i.e. strongly radiative
shocks, ![]() ),
electrons will cool fast via
ionization/Coulombian losses and relativistic bremsstrahlung, and
protons through pp collisions, and they will not reach
the adiabatic cooling region far downstream.
),
electrons will cool fast via
ionization/Coulombian losses and relativistic bremsstrahlung, and
protons through pp collisions, and they will not reach
the adiabatic cooling region far downstream.
Far upstream of the bow shock, particles with
![]() shorter than the dominant cooling timescale
shorter than the dominant cooling timescale
![]() could
escape into the cloud. Some of the highest energy electrons and protons
would escape from the accelerator in this way.
could
escape into the cloud. Some of the highest energy electrons and protons
would escape from the accelerator in this way.
The particle distribution, N(E,t),
can be obtained solving the transport equation (e.g. Ginzburg &
Syrovatskii 1964):
where Q(E) is assumed to be constant in time and b(E) includes all the cooling rates
5.2 Radiation luminosities and spectral energy distributions
5.2.1 Luminosities
Adopting an efficiency
![]() for transferring shock luminosity to nonthermal particles (electrons or
protons), where
for transferring shock luminosity to nonthermal particles (electrons or
protons), where ![]() ,
we get
,
we get
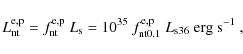
|
(28) |
where
These luminosities cannot be higher than
![\begin{displaymath}r(E_{\rm max})=t_{\rm sync,IC}/{\rm min}[t_{\rm esc},t_{\rm Brems},t_{\rm IC,sync}]<1{:}
\end{displaymath}](/articles/aa/full_html/2010/03/aa13488-09/img144.png)
|
(31) |
Otherwise,
The IC luminosities will be a minor component unless
The highest energy electrons and protons may escape from the lobe and radiate in the cloud, although the corresponding luminosities depend on the escape probability, which is difficult to quantify.
5.2.2 Spectral energy distributions
If synchrotron or IC losses dominate at
![]() for electrons, there is a break in the particle energy distribution
N(E,t) at
for electrons, there is a break in the particle energy distribution
N(E,t) at
![]() ,
in which
,
in which ![]() becomes the shortest timescale. Above
becomes the shortest timescale. Above ![]() ,
,
![]() ,
which yields a spectral energy distribution (SED) of the radiation that
is
,
which yields a spectral energy distribution (SED) of the radiation that
is
![]() for
synchrotron and IC dominance, and
for
synchrotron and IC dominance, and ![]()
![]() for
relativistic
bremsstrahlung (
for
relativistic
bremsstrahlung (![]() is the photon energy).
is the photon energy).
For electron energies
![]() ,
and at any energy for protons,
advection, and relativistic bremsstrahlung or pp collisions,
lead to
,
and at any energy for protons,
advection, and relativistic bremsstrahlung or pp collisions,
lead to ![]() ,
which yields an
SED
,
which yields an
SED ![]()
![]() (synchrotron/IC),
and
(synchrotron/IC),
and ![]()
![]() (both
relativistic bremsstrahlung and pp collisions).
Below
(both
relativistic bremsstrahlung and pp collisions).
Below ![]() MeV
and
MeV
and ![]() MeV,
the SEDs of relativistic
bremsstrahlung and pp collisions roughly become
MeV,
the SEDs of relativistic
bremsstrahlung and pp collisions roughly become ![]()
![]() and
and ![]()
![]() ,
respectively. Dominant
ionization/Coulombian losses, relevant only for electrons in our
context, lead to
,
respectively. Dominant
ionization/Coulombian losses, relevant only for electrons in our
context, lead to
![]() ,
yielding an SED
,
yielding an SED ![]()
![]() and
and ![]()
![]() for
synchrotron/IC and relativistic
bremsstrahlung, respectively.
for
synchrotron/IC and relativistic
bremsstrahlung, respectively.
5.2.3 Requirements from observed spectra
The nonthermal nature of the observed radio spectra in several specific
cases implies that strong free-free
absorption of radio emission should not occur in the lobe or in the
surroundings. Far from the lobe,
the ionization degree should be low. Close to the lobe, the medium is
ionized and
it is necessary to account for free-free
absorption, which is expected to be large downstream the bow shock. The
free-free opacity there can be written as (Rybicki & Lightman 1979):
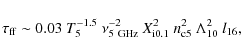
|
(34) |
where T5=T/105 K, and
Another condition that should be fulfilled given the observed
radio spectra is that either electron escape or relativistic
bremsstrahlung should dominate Coulombian/ionization losses at low
electron energies, i.e. ![]() (
(
![]() ).
From the timescale ratios,
).
From the timescale ratios,
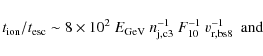
|
(35) |
| (36) |
it is seen that upstream and downstream of the shock, radio emitting electrons are dominated by escape or relativistic bremsstrahlung losses. Sources with spectra harder than
5.3 Deriving the magnetic field strength
Assuming a value for ![]() ,
plus some additional simplifying assumptions, a formula has been
obtained to derive the magnetic field strength consistent with the
observed radio fluxes.
Taking the radio fluxes at a certain frequency,
a particle energy distribution with
,
plus some additional simplifying assumptions, a formula has been
obtained to derive the magnetic field strength consistent with the
observed radio fluxes.
Taking the radio fluxes at a certain frequency,
a particle energy distribution with
![]() and normalized with the total energy
and normalized with the total energy
![]()
![]() ,
the synchrotron
power for one electron (
,
the synchrotron
power for one electron (
![]() erg s-1),
and the reasonable
simplification that electrons of energy E produce
only photons of frequency
erg s-1),
and the reasonable
simplification that electrons of energy E produce
only photons of frequency
![]() Hz,
we obtain
Hz,
we obtain
where
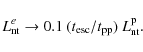
|
(38) |
6 Thermal emission in the lobes
The shocked material is heated up to
![]() K
(
K
(
![]() keV) and generates
line
and thermal bremsstrahlung continuum emission. The total luminosity
cannot overcome
keV) and generates
line
and thermal bremsstrahlung continuum emission. The total luminosity
cannot overcome ![]() ,
and it might be much lower
if the reverse shock is adiabatic and the bow shock relatively slow.
This radiation can be absorbed in the cloud core, since
the photo-electric opacity coefficient is
,
and it might be much lower
if the reverse shock is adiabatic and the bow shock relatively slow.
This radiation can be absorbed in the cloud core, since
the photo-electric opacity coefficient is
![]() (within a factor of 2
in the relevant energy range; see Morrison & McCammon 1983), where
(within a factor of 2
in the relevant energy range; see Morrison & McCammon 1983), where
![]() is the photon
energy and
is the photon
energy and
![]() cm-2
the neutral hydrogen column density of
the lobe surroundings.
cm-2
the neutral hydrogen column density of
the lobe surroundings.
The density in the shock regions should neither be too high,
to avoid suppression of the acceleration due to strong cooling,
nor too low, to avoid
![]() .
Actually, there is room for the shocks to be radiative, producing
thermal X-rays that may
escape the cloud, without necessarily suppressing particle
acceleration.
.
Actually, there is room for the shocks to be radiative, producing
thermal X-rays that may
escape the cloud, without necessarily suppressing particle
acceleration.
That thermal radio emission should not overcome the nonthermal
component at the same frequencies put some
constraints on the scenario. The thermal SED peaks at energies up to ![]() keV and is
harder than the synchrotron SED,
which should generally peak at lower energies. This means that the
total
keV and is
harder than the synchrotron SED,
which should generally peak at lower energies. This means that the
total ![]() must be
must be ![]()
![]() (
(
![]() for
for
![]() ),
if the nonthermal radio emission is to be dominated by the thermal one.
This
condition is hard to fulfill unless
),
if the nonthermal radio emission is to be dominated by the thermal one.
This
condition is hard to fulfill unless
![]() .
It is worth noting that a radio spectra harder than
.
It is worth noting that a radio spectra harder than
![]() may be
nonthermal radiation contaminated by a thermal component.
may be
nonthermal radiation contaminated by a thermal component.
As mentioned in Sect. 1, several massive YSOs present nonthermal radio emission. Two among the most relevant of them are studied in the next section: IRAS 16547-4247 and the complex source HH 80-81.
7 Application to IRAS 16547-4247 North and HH 80
The model described in Sect. 5.1 is now applied to the northern radio lobe of the massive YSO IRAS 16547-4247 (IRAS-N) and to the radio lobe HH 80 in the complex source HH 80-81. Both lobes have a clear nonthermal nature (e.g. GAR03; MRR93). IRAS-N shows also an extended structure pointing to the southeast, and HH 80 has a similar nonthermal source very nearby, HH 81. We consider here neither the southeast extension of IRAS-N nor HH 81; however, the extension in IRAS-N may in fact be a fore/background object (RMF08), and HH 81 could be part of the expected complex structure of the jet termination region (see Sect. 3; see also Heathcote et al. 1998 -HRR98- for a detailed optical study of the HH 80-81 complex).
7.1 IRAS-N and HH 80 properties
We focus on IRAS-N and HH 80 because both sources are at the
two extremes of the density parameter range presented above.
IRAS-N is embedded in a very dense cloud, with
![]() cm-3
(GAR03), whereas HH 80 is thought to be
close to the border of a cloud, in a more diluted medium with
cm-3
(GAR03), whereas HH 80 is thought to be
close to the border of a cloud, in a more diluted medium with
![]() cm-3
(e.g. MRR93; HRR98; Pravdo
et al. 2004
- PTM04 -). The distances to IRAS-N and HH 80 are
cm-3
(e.g. MRR93; HRR98; Pravdo
et al. 2004
- PTM04 -). The distances to IRAS-N and HH 80 are ![]() kpc
and
kpc
and ![]() 1.7 kpc
(RMF08; MRR93), and the central
stars show luminosities of
1.7 kpc
(RMF08; MRR93), and the central
stars show luminosities of
![]() and
and ![]() erg s-1
(GAR03; MRR93). This
radiation provides the main contribution to the infrared emission in
the lobes, yielding photon energy densities there of
erg s-1
(GAR03; MRR93). This
radiation provides the main contribution to the infrared emission in
the lobes, yielding photon energy densities there of
![]() erg cm-3
for IRAS-N, and
erg cm-3
for IRAS-N, and ![]() erg cm-3
for HH 80. The distances from the
central star to the lobes are
erg cm-3
for HH 80. The distances from the
central star to the lobes are
![]() cm
for IRAS-N, accounting for a jet inclination angle of
84
cm
for IRAS-N, accounting for a jet inclination angle of
84![]() (Garay et al. 2007),
and
(Garay et al. 2007),
and ![]() 1019 cm
for HH 80, with a not so well constrained jet inclination (see
however
HRR98). The lobe sizes for IRAS-N and HH 80 are about
1019 cm
for HH 80, with a not so well constrained jet inclination (see
however
HRR98). The lobe sizes for IRAS-N and HH 80 are about
![]() cm
and
cm
and ![]() cm,
(RMF08; MRR93), the velocities of the jets are expected to be around
cm,
(RMF08; MRR93), the velocities of the jets are expected to be around
![]() cm s-1and
cm s-1and
![]() 108 cm s-1,
and the velocities of the bow shocks would be
108 cm s-1,
and the velocities of the bow shocks would be
![]() cm s-1
and
cm s-1
and ![]()
![]() cm s-1
(RMF08; MRR93, MRR95, HRR98). IRAS-N has not been detected in X-rays
(see ARA07), whereas HH 80
has been detected by XMM (PTM04).
cm s-1
(RMF08; MRR93, MRR95, HRR98). IRAS-N has not been detected in X-rays
(see ARA07), whereas HH 80
has been detected by XMM (PTM04).
7.1.1 Derived parameters
The values of ![]() for IRAS-N imply that
for IRAS-N imply that ![]() and
and ![]() .
In fact, from the inferred age of
IRAS-N,
.
In fact, from the inferred age of
IRAS-N, ![]() s
(Garay et al. 2007),
s
(Garay et al. 2007),
![]() and
and ![]() ,
a particle density of
,
a particle density of
![]() cm-3
can be derived, i.e.
cm-3
can be derived, i.e. ![]() and
and ![]() cm s-1,
consistent with
the limit given above. Such a value for
cm s-1,
consistent with
the limit given above. Such a value for ![]() ,
together with
,
together with ![]() and
and ![]() ,
renders an
,
renders an ![]() erg s-1
for IRAS-N. Given that
erg s-1
for IRAS-N. Given that
![]() in this source, it is the case that
in this source, it is the case that
![]() in the reverse shock. The bow-shock luminosity will be
in the reverse shock. The bow-shock luminosity will be ![]()
![]() erg s-1.
erg s-1.
For HH 80, since
![]() ,
then
,
then ![]() ,
and therefore we have
,
and therefore we have
![]() .
In the
case of HH 80, this means that both the reverse shock and the
bow shock may contribute to the nonthermal radiation (see also
HRR98). Accounting for
.
In the
case of HH 80, this means that both the reverse shock and the
bow shock may contribute to the nonthermal radiation (see also
HRR98). Accounting for ![]() and
and ![]() ,
it can be inferred
,
it can be inferred
![]() s,
not far from the
value discussed in MRR93; also,
s,
not far from the
value discussed in MRR93; also,
![]() .
Taking
.
Taking ![]() erg s-1
(MRR95), we
get
erg s-1
(MRR95), we
get ![]() cm-3
and, since
cm-3
and, since ![]() ,
,
![]() cm-3.
This value
is between those inferred from X-ray and optical observations (see the
discussion in PTM04). We treat the bow shock and
the reverse shock in HH 80 as a single physical system, with
speed
cm-3.
This value
is between those inferred from X-ray and optical observations (see the
discussion in PTM04). We treat the bow shock and
the reverse shock in HH 80 as a single physical system, with
speed ![]() cm s-1
and
cm s-1
and ![]() .
The
full list of the relevant properties of IRAS-N and HH 80,
together with the derived parameters, is presented in
Table 1.
.
The
full list of the relevant properties of IRAS-N and HH 80,
together with the derived parameters, is presented in
Table 1.
Interestingly, the central star is brighter in IRAS-N than in
HH 80, but ![]() seems less in the former. This
could be related to the higher density of the environment in IRAS-N.
This may have induced jet deceleration through, e.g.,
medium mass entrainment in the jet. Nevertheless, the uncertainties are
large and no strong conclusions can be derived in
this regard.
seems less in the former. This
could be related to the higher density of the environment in IRAS-N.
This may have induced jet deceleration through, e.g.,
medium mass entrainment in the jet. Nevertheless, the uncertainties are
large and no strong conclusions can be derived in
this regard.
It is worth mentioning that very powerful, slow molecular
outflows with luminosities
10-100 times higher than ![]() have been detected in the two sources (see RMF08 and references
therein).
have been detected in the two sources (see RMF08 and references
therein).
Table 1: IRAS-N and HH 80 properties and derived parameters (see the text for details).
7.2 Estimates of the emission in IRAS-N and HH 80
7.2.1 Constraints on the nonthermal population
To model the radio emission from IRAS-N and HH 80 and to
compute the radiation at high and very high energies, the
values of B and
![]() for both sources are required. The value of B
should be well below
for both sources are required. The value of B
should be well below ![]() (see Eq. (8)).
The nonthermal luminosity
(see Eq. (8)).
The nonthermal luminosity
![]() will be taken equal to
will be taken equal to ![]() ,
or
,
or ![]() .
The observed radio
fluxes and spectral indices are
.
The observed radio
fluxes and spectral indices are ![]() 8.7 and 3 mJy at
8 GHz and
8.7 and 3 mJy at
8 GHz and ![]() and 0.3, respectively (GAR03; MRR93). The
value of the index
and 0.3, respectively (GAR03; MRR93). The
value of the index ![]() for the radio emitting particles can be obtained from
for the radio emitting particles can be obtained from ![]() ,
as shown in Sect. 5.1.
Fixing
,
as shown in Sect. 5.1.
Fixing
![]() and knowing the radio fluxes, B
can be estimated to
zeroth order with Eq. (37).
We note that
equipartition with the relativistic particles would lead to magnetic
fields of about 0.1-1 mG in the emitting regions
(see ARA07 for the case of IRAS-N).
and knowing the radio fluxes, B
can be estimated to
zeroth order with Eq. (37).
We note that
equipartition with the relativistic particles would lead to magnetic
fields of about 0.1-1 mG in the emitting regions
(see ARA07 for the case of IRAS-N).
The nature of the radio emitting particles may be primary
electrons accelerated in the shock, or secondary e![]() from
pp collisions. If primary electrons dominate the production of
the radio emission, the relativistic proton population will
be constrained by secondary radiation not being able to overcome that
of primary electrons (although pp collisions may
still be a significant source of high-energy emission). If secondary e
from
pp collisions. If primary electrons dominate the production of
the radio emission, the relativistic proton population will
be constrained by secondary radiation not being able to overcome that
of primary electrons (although pp collisions may
still be a significant source of high-energy emission). If secondary e![]() were the origin of the radio emission, the
value of
were the origin of the radio emission, the
value of ![]() for protons should be slightly softer than that of secondary e
for protons should be slightly softer than that of secondary e![]() (Kelner et al. 2006),
and the radio
contribution from primary electrons should be minor.
(Kelner et al. 2006),
and the radio
contribution from primary electrons should be minor.
7.2.2 The emission in IRAS-N
Given the values of ![]() and
and ![]() in IRAS-N, it seems unlikely that the bow shock is accelerating these
electrons. This shock will be strongly radiative, peaking the thermal
emission in the optical/UV, with a luminosity of a few
times 1034 erg s-1.
On the other hand, the reverse shock is marginally radiative because
in IRAS-N, it seems unlikely that the bow shock is accelerating these
electrons. This shock will be strongly radiative, peaking the thermal
emission in the optical/UV, with a luminosity of a few
times 1034 erg s-1.
On the other hand, the reverse shock is marginally radiative because
![]() ,
peaking at 0.5 keV with a bolometric luminosity
,
peaking at 0.5 keV with a bolometric luminosity ![]() 1035 erg s-1.
As mentioned above, the photoelectric
absorption
1035 erg s-1.
As mentioned above, the photoelectric
absorption ![]() is very large, likely >100, implying an almost complete
suppression of X-rays, which would
explain the non-detection of the source. Concerning the nonthermal
radiation, from
is very large, likely >100, implying an almost complete
suppression of X-rays, which would
explain the non-detection of the source. Concerning the nonthermal
radiation, from ![]() one obtains
one obtains
![]() erg s-1.
erg s-1.
If primary electrons produced the radio emission, the magnetic
field should be ![]() mG
for the adopted
mG
for the adopted ![]() ,
and the maximum energy, limited by diffusive escape,
,
and the maximum energy, limited by diffusive escape,
![]() GeV
for both electrons and protons. If
secondary
GeV
for both electrons and protons. If
secondary ![]() produced the radio emission, B>
0.5 mG, and
produced the radio emission, B>
0.5 mG, and
![]() GeV
(only protons), limited
again by diffusive escape.
GeV
(only protons), limited
again by diffusive escape.
The density downstream of the bow shock may be up to 104
times higher than downstream of the reverse shock due to strong
radiative cooling in the former region. Since
![]() should be much shorter than
should be much shorter than ![]() ,
we assume that the RT
instabilities have time to develop mixing reverse and bow shock
downstream material, effectively increasing the density in
the reverse shock. We have adopted a value for F
such that the resulting luminosities due to relativistic bremsstrahlung
and pp collisions be close to
,
we assume that the RT
instabilities have time to develop mixing reverse and bow shock
downstream material, effectively increasing the density in
the reverse shock. We have adopted a value for F
such that the resulting luminosities due to relativistic bremsstrahlung
and pp collisions be close to
![]() .
In this way, F is used as a free parameter that is
optimized to get
high gamma-ray luminosities, not to suppress acceleration, and that
accounts for the constraints given by the observational data
at lower energies and the F-limits provided in
Sect. 3.2.
Following this approach we have adopted
.
In this way, F is used as a free parameter that is
optimized to get
high gamma-ray luminosities, not to suppress acceleration, and that
accounts for the constraints given by the observational data
at lower energies and the F-limits provided in
Sect. 3.2.
Following this approach we have adopted ![]() .
Despite the high density, the Tsytovich-Razin effect may be neglected,
since the entrained dense bow shock
material should be cold and hardly fully ionized.
.
Despite the high density, the Tsytovich-Razin effect may be neglected,
since the entrained dense bow shock
material should be cold and hardly fully ionized.
7.2.3 The emission in HH 80
In the case of HH 80, both the reverse and the bow shocks are
adiabatic. We predict thermal X-rays peaking at ![]() 0.5 keV
with intrinsic luminosities of
0.5 keV
with intrinsic luminosities of ![]()
![]() erg s-1.
This value is
erg s-1.
This value is
![]() 100 times
higher than that given by PTM04, where no intrinsic absorption was
assumed. However, if an intrinsic
100 times
higher than that given by PTM04, where no intrinsic absorption was
assumed. However, if an intrinsic
![]() cm-2
in the surroundings of HH 80 were adopted, the factor of 100
could be explained with
photoelectric absorption (see the strong dependence of
cm-2
in the surroundings of HH 80 were adopted, the factor of 100
could be explained with
photoelectric absorption (see the strong dependence of
![]() and
and ![]() on photon energy and
on photon energy and ![]() ). To
compute the nonthermal emission, as noted, the two shocks are treated
as just one with
). To
compute the nonthermal emission, as noted, the two shocks are treated
as just one with
![]() ,
i.e.,
,
i.e.,
![]() erg s-1.
erg s-1.
In the case dominated by primary particles, the magnetic field
would be ![]() mG
for the adopted
mG
for the adopted ![]() ,
with a
maximum energy limited by diffusive escape
,
with a
maximum energy limited by diffusive escape
![]() GeV
for both electrons and protons. In the case of dominance
by secondaries, B>0.02 mG, and
GeV
for both electrons and protons. In the case of dominance
by secondaries, B>0.02 mG, and
![]() GeV
(only protons), limited again by diffusive escape. Since the
medium is quite diluted, relativistic bremsstrahlung and
pp collisions are not as efficient as in IRAS-N, but
that
GeV
(only protons), limited again by diffusive escape. Since the
medium is quite diluted, relativistic bremsstrahlung and
pp collisions are not as efficient as in IRAS-N, but
that ![]() and
and ![]() are both larger renders not very different values for
are both larger renders not very different values for
![]() .
.
7.3 Computed spectral energy distributions
In Figs. 2-5, the SEDs computed
for IRAS-N and HH 80 are shown. Two scenarios
are adopted for both sources, one in which the radio emission is
dominated by primary electrons and another one in which the
dominant radio emitters are secondary e![]() .
In the former,
.
In the former, ![]() and
and ![]() were taken as equal yielding
were taken as equal yielding ![]() ;
in the latter, we derived just a lower-limit for a
to avoid primary emission to be
significant. In IRAS-N, if secondary
;
in the latter, we derived just a lower-limit for a
to avoid primary emission to be
significant. In IRAS-N, if secondary
![]() were the source of radio emission, a should be
>10. In HH 80, given
the relatively low densities and high magnetic fields of the secondary e
were the source of radio emission, a should be
>10. In HH 80, given
the relatively low densities and high magnetic fields of the secondary e![]() scenario, the proton-to-electron number
ratio a should be >1000.
scenario, the proton-to-electron number
ratio a should be >1000.
It is remarkable that the high-energy components in the SEDs, associated with relativistic bremsstrahlung and/or pp collisions, have significant luminosities in the high-energy and very high-energy ranges and fulfill the X-ray constraints. The synchrotron emission peaks in the optical/UV, and can be the dominant cooling channel of electrons only if the magnetic field is rather high and densities low. Interestingly, in the primary electron scenario of HH 80, the electron component does not achieve energies beyond those for emitting radio synchrotron emission, but relativistic bremsstrahlung and pp emission may still be significant at GeV energies.
The list of the parameter values adopted to calculate the SEDs, together with the radio properties of the sources, is presented in Table 1. The parameter values have been adjusted numerically and are slightly different from those given in Sect. 7.2.
![\begin{figure}
\par\includegraphics[angle=0, width=8.8cm,clip]{13488f2.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13488-09/Timg267.png)
|
Figure 2:
Spectral energy distribution of the nonthermal emission for IRAS-N in
the primary electron scenario. The IC contribution is negligible and
not shown here. Observational points are from IRAS 16547-4247
(radio, Rodríguez et al. 2005;
X-rays, ARA07). The 1 yr/5 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=0, width=8.8cm,clip]{13488f3.eps}\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/03/aa13488-09/Timg268.png)
|
Figure 3:
The same as in Fig. 2
but for the secondary e |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=0, width=8.8cm,clip]{13488f4.eps}\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/03/aa13488-09/Timg269.png)
|
Figure 4: The same as in Fig. 2 but for HH 80. Observational points are from Martí et al. (1993) (radio) and PTM04 (X-rays). The X-ray detected point is shown as an upper-limit. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=0, width=8.8cm,clip]{13488f5.eps}\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/03/aa13488-09/Timg270.png)
|
Figure 5: The same as in Fig. 3 but for HH 80. |
| Open with DEXTER | |
Table 2: Radio data and parameters of the nonthermal emitter.
8 Detectability
The SEDs presented in Figs. 2-5 show that massive
YSOs can produce significant amounts of gamma rays,
although the results are quite sensitive to the available densities
downstream. For sources with high densities like IRAS-N,
if the development of RT instabilities does not interfere with particle
acceleration, relativistic bremsstrahlung and pp collisions
will be quite efficient. For low-density sources like HH 80,
the efficiency of relativistic bremsstrahlung and
pp collisions is lower, but the lobe sizes are expected to be
large, increasing the escape timescales and thus the
radiation outcome (see Sect. 5.2).
Therefore, for
![]() ,
it can be expected that the termination regions
of massive YSO jets will be eventually detected by Fermi and also by
Cherenkov telescopes through long enough exposures.
,
it can be expected that the termination regions
of massive YSO jets will be eventually detected by Fermi and also by
Cherenkov telescopes through long enough exposures.
In our calculations, the magnetic field strength B
and ![]() were adjusted for both to explain the radio
fluxes and to obtain significant gamma-ray fluxes. The magnetic field
assumed for high-density, IRAS-N-like sources
agrees with estimates derived through Zeeman measurements (e.g.
Crutcher 1999).
In the case of low-density, HH 80-like,
sources, the situation may be more complicated.
were adjusted for both to explain the radio
fluxes and to obtain significant gamma-ray fluxes. The magnetic field
assumed for high-density, IRAS-N-like sources
agrees with estimates derived through Zeeman measurements (e.g.
Crutcher 1999).
In the case of low-density, HH 80-like,
sources, the situation may be more complicated.
The primary electron scenario of HH 80 requires a
very low magnetic field in the shocked regions. As noted, low densities
imply large lobes, hence lower magnetic fields in the jet head.
However, the value of B in the bow shock can hardly
be lower than in the cloud, which is expected given the cloud densities
to be several times higher than the one
adopted in our calculations. Therefore, in such a scenario and source
type, if detected, gamma rays would likely come from
the reverse shock. Otherwise, in the secondary e![]() scenario in HH 80, the magnetic field must be quite high,
scenario in HH 80, the magnetic field must be quite high, ![]() 2.5 mG,
regardless of the shock involved, below but close to the maximum value
(see Eq. (8)).
Furthermore, the value
for a required in this case,
2.5 mG,
regardless of the shock involved, below but close to the maximum value
(see Eq. (8)).
Furthermore, the value
for a required in this case, ![]() 1000, may be
too high. Also, the hard particle energy distribution required may be
difficult to explain in the context of the linear theory of
Fermi I particle acceleration. Such a hard radio spectrum may
be
explained by marginal free-free absorption or by an additional thermal
component, but then the expected nonthermal fluxes at
higher energies would be smaller because of a softer particle energy
distribution. In either case, despite these caveats, one still cannot
rule out HH 80 and similar objects as gamma-ray emitters.
1000, may be
too high. Also, the hard particle energy distribution required may be
difficult to explain in the context of the linear theory of
Fermi I particle acceleration. Such a hard radio spectrum may
be
explained by marginal free-free absorption or by an additional thermal
component, but then the expected nonthermal fluxes at
higher energies would be smaller because of a softer particle energy
distribution. In either case, despite these caveats, one still cannot
rule out HH 80 and similar objects as gamma-ray emitters.
It is worth noting that the assumptions adopted in this work are quite conservative. The parameter uncertainties are relatively large, and a more optimistic (but still consistent with observations) choice of densities, shock velocities, and jet luminosities could easily move the SED curves up by a factor of several.
9 Discussion
Romero (2008) points out that the detection of massive protostars at gamma-ray energies would open a new window to star formation studies. The detection of the cutoff in the SED would give insight into the acceleration efficiency in the terminal shocks of the outflows. The SED can also shed light on the densities, magnetic fields, velocities, and diffusion coefficients in the shocked regions. Although we do not expect that massive protostars would be among the bright sources detected by Fermi (Abdo et al. 2009), our calculations show that they could show up in further analysis of weaker sources after a few years of observation. The emission levels above 100 GeV, close to 0.01 Crab, could be detectable by current and future Cherenkov telescopes for observation times moderately longer than 50 h.
However, not only massive protostars, but also the regions in
which they form, may be gamma-ray emitters. As mentioned in
Sect. 4,
some amount of the highest energy particles may escape to the cloud far
upstream of the bow shock. It is hard
to estimate the fraction of electrons and protons that would be
released in the cloud, which strongly depends on the
diffusion coefficient of the pre-shock cloud medium and the bow shock
velocity and size. However, they might carry a
non-negligible fraction of
![]() if
if ![]() .
In fact, in case
.
In fact, in case
![]() were in the cloud, massive YSOs may inject some protons well above the
average galactic level at several hundred
GeV, and the radiation resulting from pp may be detectable
(for a general case, see Aharonian & Atoyan 1996),
competing
with that produced in the lobe itself. For leptons, the emission at
high energies may be relevant for low magnetic fields,
i.e. when the maximum energy is determined by diffusive escape and
dominant relativistic bremsstrahlung in the cloud. The
spectrum of the gamma rays, generated by pp collisions for
protons and relativistic bremsstrahlung for electrons, should be
very hard since only the highest energy particles escape, peaking at
were in the cloud, massive YSOs may inject some protons well above the
average galactic level at several hundred
GeV, and the radiation resulting from pp may be detectable
(for a general case, see Aharonian & Atoyan 1996),
competing
with that produced in the lobe itself. For leptons, the emission at
high energies may be relevant for low magnetic fields,
i.e. when the maximum energy is determined by diffusive escape and
dominant relativistic bremsstrahlung in the cloud. The
spectrum of the gamma rays, generated by pp collisions for
protons and relativistic bremsstrahlung for electrons, should be
very hard since only the highest energy particles escape, peaking at
![]() .
The cloud synchrotron
emission should be quite diluted and dominated by the lobe.
.
The cloud synchrotron
emission should be quite diluted and dominated by the lobe.
A clustering of gamma-ray sources should be present in regions with large molecular clouds and star formation, as already inferred from EGRET data (e.g. Romero et al. 1999). The accumulation of cosmic rays accelerated in the radio lobes into the molecular cloud can produce extended gamma-ray sources. These radio lobes may be difficult to detect. Neither UV nor hard X-ray counterparts related to thermal bremsstrahlung produced in the shock downstream regions are expected to be observed from these sources because of the large absorption and/or low emission levels. Deep inside the cloud, even radio emission may be missing because of strong free-free absorption, so the exact number of accelerators could be hard to estimate. Also, cosmic-ray re-acceleration caused by magnetic turbulence inside the clouds (e.g. Dogiel et al. 2004) could result in stronger sources. Therefore, the combined effect of several protostars deeply embedded in giant clouds might be responsible for GeV-TeV sources found in star-forming regions by EGRET, Fermi, AGILE, and Cherenkov telescopes. We conclude that massive clouds with high IR luminosities and maser emission (tracers of massive star formation) deserve detailed study with Fermi and ground-based Cherenkov telescopes.
AcknowledgementsWe thank an anonymous referee for his/her constructive and useful comments that helped to improve the manuscript. V.B-R., G.E.R., and J.M.P. acknowledge support by the Ministerio de Educación y Ciencia (Spain) under grant AYA 2007-68034-C03-01, FEDER funds. V.B-R. wants to thank the Insituto Argentino de Astronomía and the Facultad de Ciencias Astronómicas y Geofísicas de la Universidad de La Plata for their kind hospitality. G.E.R. and A.T.A. are supported by CONICET and the Argentine agency ANPCyT (grant BID 1728/OC-AR PICT 2007-00848). A.T.A. thanks Max Planck Institut fuer Kernphysik for kind hospitality and support.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJS, 183, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A., & Atoyan, A. M. 1996, A&A, 309, 917 [NASA ADS] [Google Scholar]
- Araudo, A. T., Romero, G. E., Bosch-Ramon, V., & Paredes, J. M. 2007, A&A, 476, 1289 (ARA07) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Araudo, A. T., Romero, G. E., Bosch-Ramon, V., & Paredes, J. M. 2008, IJMP D, 17, 1889 [arXiv:0805.1898] [Google Scholar]
- Banerjee, R., & Pudritz, R. E. 2006, ApJ, 641, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, R., & Pudritz, R. E. 2007, ApJ, 660, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 1978, MNRAS, 182, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, J. M., Konigl, A., & Fryxell, B. A. 1989, ApJ, 337, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., Bate, M. R., & Zinnecker, H. 1998, MNRAS, 298, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Bordas, P., Bosch-Ramon, V., Paredes, J. M., & Perucho, M. 2009, A&A, 497, 325 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crusius-Watzel, A. R. 1990, ApJ, 361, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M. 1999, ApJ, 520, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Dogiel, V. A., Gurevich, A. V., Istomin, Ya. N., & Zybin, K. P. 2005, Ap&SS, 297, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Drury, L. O'C. 1983, Reports on Progress in Physics, 46, 973 [Google Scholar]
- Drury, L. O'C., Duffy, P., & Kirk, J. G. 1996, A&A, 309, 1002 [NASA ADS] [Google Scholar]
- Fermi, E. 1949, Phys. Rev., 75, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Garay, G., & Lizano, S. 1999, PASP, 111, 1049 [Google Scholar]
- Garay, G., Brooks, K., Mardones, D., & Norris, R. P. 2003, ApJ, 537, 739 (GAR03) [NASA ADS] [CrossRef] [Google Scholar]
- Garay, G., Mardones, D., Bronfman, L., et al. 2007, A&A, 463, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginzburg, V. L., & Syrovatskii, S. I. 1964, The Origin of Cosmic Rays (New York: Pergamon Press) [Google Scholar]
- Henriksen, R. N., Mirabel, I. F., & Ptuskin, V. S. 1991, A&A, 248, 221 [NASA ADS] [Google Scholar]
- Kaiser, C. R., & Alexander, P. 1997, MNRAS, 286, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Kelner, S. R., Aharonian, F. A., & Vugayov, V. V. 2006, Phys. Rev. D, 74, 034018 [NASA ADS] [CrossRef] [Google Scholar]
- Lucek, S. G., & Bell, A. R. 2000, MNRAS, 314, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Martí, J., Rodríguez, L. F., & Reipurth, B. 1993, ApJ, 416, 208 (MRR93) [NASA ADS] [CrossRef] [Google Scholar]
- Martí, J., Rodríguez, L. F., & Reipurth, B. 1995, ApJ, 449, 184 (MRR95) [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Morrison, R., & McCammon, D. 1983, ApJ, 270, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Myasnikov, A. V., Zhekov, S. A., & Belov, N. A. 1998, MNRAS, 298, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Plambeck, R. L., & Menten, K. M. 1990, ApJ, 364, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Pravdo, S. H., Tsuboi, Y., & Maeda, Y. 2004, ApJ, 605, 259 (PTM04) [NASA ADS] [CrossRef] [Google Scholar]
- Protheroe, R. J. 1999, in: Topics in Cosmic-Ray Astrophysics, 247 [arXiv:9812055] [Google Scholar]
- Reville, B., Kirk, J. G., Duffy, P., & O'Sullivan, S. 2007, A&A, 475, 435 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodríguez, L. F., Garay, G., Brooks, K., & Mardones, D. 2005, ApJ, 626, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez, L. F., Moran, J. M., Franco-Hernández, R., et al. 2008, AJ, 135, 2370 (RMF08) [NASA ADS] [CrossRef] [Google Scholar]
- Romero, G. E. 2008, in: High-Energy Gamma-Ray Astronomy, ed. Aharonian et al., AIP Conf. Proc., 1085, 97 [Google Scholar]
- Romero, G. E., Benaglia, P., & Torres, D. F. 1999, A&A, 348, 868 [NASA ADS] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Radiative processes in astrophysics (New York: Wiley-Interscience) [Google Scholar]
- Seaton, M. J. 1959, MNRAS, 119, 81 [NASA ADS] [Google Scholar]
- Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 23 [Google Scholar]
- Stahler, S. W., Palla, F., & Ho, P. T. P. 2000, in: Protostars and Planets IV, ed. V. Mannings, A. P. Boss, & S. S. Russell (Tucson: University of Arizona Press), 327 [Google Scholar]
Footnotes
- ...
![[*]](/icons/foot_motif.png)
- Member of CONICET, Argentina.
- ...

![[*]](/icons/foot_motif.png)
- Note that
 relates
to the jet kinetic energy density, not to the energy density of the (unshocked) cloud.
In the latter, the magnetic field may indeed be more important dynamically.
relates
to the jet kinetic energy density, not to the energy density of the (unshocked) cloud.
In the latter, the magnetic field may indeed be more important dynamically.
All Tables
Table 1: IRAS-N and HH 80 properties and derived parameters (see the text for details).
Table 2: Radio data and parameters of the nonthermal emitter.
All Figures
| |
Figure 1: Sketch of the termination region of the jet of a massive YSO. Two shocks of different strengths and velocities will form depending on the jet-medium properties. Electrons and protons can be accelerated in the shocks, and generate nonthermal emission via interaction with the ambient matter, magnetic, and radiation fields. The shocked material will also produce thermal radiation. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0, width=8.8cm,clip]{13488f2.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13488-09/Timg267.png)
|
Figure 2:
Spectral energy distribution of the nonthermal emission for IRAS-N in
the primary electron scenario. The IC contribution is negligible and
not shown here. Observational points are from IRAS 16547-4247
(radio, Rodríguez et al. 2005;
X-rays, ARA07). The 1 yr/5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0, width=8.8cm,clip]{13488f3.eps}\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/03/aa13488-09/Timg268.png)
|
Figure 3:
The same as in Fig. 2
but for the secondary e |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0, width=8.8cm,clip]{13488f4.eps}\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/03/aa13488-09/Timg269.png)
|
Figure 4: The same as in Fig. 2 but for HH 80. Observational points are from Martí et al. (1993) (radio) and PTM04 (X-rays). The X-ray detected point is shown as an upper-limit. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0, width=8.8cm,clip]{13488f5.eps}\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/03/aa13488-09/Timg270.png)
|
Figure 5: The same as in Fig. 3 but for HH 80. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



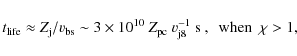
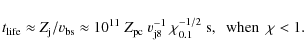
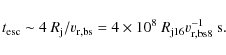
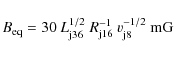
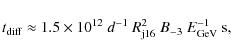
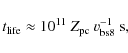
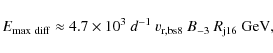
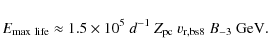
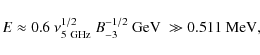
![\begin{displaymath}\frac{\partial N\left(t,E\right)}{\partial t}+\frac{\partial ...
...ght]}{\partial E}+\frac{N\left(t,E\right)}{t_{\rm esc}}=Q(E) ,
\end{displaymath}](/articles/aa/full_html/2010/03/aa13488-09/img130.png)