| Issue |
A&A
Volume 511, February 2010
|
|
|---|---|---|
| Article Number | A18 | |
| Number of page(s) | 13 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200913183 | |
| Published online | 24 February 2010 | |
Peering through the veil: near-infrared photometry and extinction for the Galactic nuclear star cluster
Accurate near infrared H, Ks, and L' photometry and
the near-infrared extinction-law toward the central parsec of the
Galaxy![[*]](/icons/foot_motif.png)
R. Schödel1 - F. Najarro2 - K. Muzic3 - A. Eckart3
1 - Instituto de Astrofísica de Andalucía - CSIC,
Glorieta de la Astronomía S/N, 18008 Granada, Spain
2 -
Centro de Astrobiología (CSIC/INTA), Instituto
Nacional de Técnica Aeroespacial, Ctra de Torrejón a Ajalvir,
km 4, 28850 Torrejón de Ardoz, Madrid, Spain
3 -
I. Physikalisches Institut, Universität zu Köln, Zülpicher Strasse 77,
50937 Köln, Germany
Received 26 August 2009 / Accepted 2 December 2009
Abstract
Context. The nuclear star cluster of the Galaxy is an
important template for understanding its extragalactic counterparts,
which can currently not be resolved into individual stars. Important
drawbacks of observations of the Galactic center are, however, the
presence of strong and spatially highly variable interstellar
extinction and extreme crowding of the sources, which makes the use of
adaptive optics techniques necessary. Both points pose serious
obstacles to precise photometry that is needed for analyzing the
stellar population.
Aims. The aims of this work are to provide accurate photometry
in multiple near-infrared broadband filters, to determine the power-law
index of the extinction-law toward the central parsec of the Galaxy, to
provide measurements of the absolute extinction toward the Galactic
center, and finally to measure the spatial variability of extinction on
arcsecond scales.
Methods. We use observations of the central parsec of the Milky
Way that were obtained with the near-infrared camera and adaptive
optics system NAOS/CONICA at the ESO VLT unit telescope 4. The
photometric method takes into account anisoplanatic effects and limits
the corresponding systematic uncertainties to ![]() 2%. Absolute values for the extinction in the H,
2%. Absolute values for the extinction in the H, ![]() ,
and L'-bands as well as of the power-law indices of the H to
,
and L'-bands as well as of the power-law indices of the H to ![]() and
and ![]() to L'
extinction-laws are measured based on the well-known properties of red
clump stars. Extinction maps are derived based on
to L'
extinction-laws are measured based on the well-known properties of red
clump stars. Extinction maps are derived based on
![]() and
and
![]() colors.
colors.
Results. We present ![]() -band photometry for
-band photometry for ![]() 7700 stars, and additionally photometry for stars detected in the H and/or L'-bands. From a number of recently published values we compute a mean distance of the Galactic center of
7700 stars, and additionally photometry for stars detected in the H and/or L'-bands. From a number of recently published values we compute a mean distance of the Galactic center of
![]() kpc, which has an uncertainty of just
kpc, which has an uncertainty of just ![]() .
Based on this R0 and on the RC method, we derive absolute mean extinction values toward the central parsec of the Galaxy of
.
Based on this R0 and on the RC method, we derive absolute mean extinction values toward the central parsec of the Galaxy of
![]() mag,
mag,
![]() mag, and
mag, and
![]() mag. We estimate values of the power-law indices of the extinction-law of
mag. We estimate values of the power-law indices of the extinction-law of
![]() and
and
![]() .
A
.
A ![]() -band extinction map for the Galactic center is computed based on this extinction law and on stellar
-band extinction map for the Galactic center is computed based on this extinction law and on stellar
![]() colors. Both its statistical and systematic uncertainties are estimated
to be <10%. Extinction in this map derived from stellar color
excesses is found to vary on arcsecond scales, with a mean value of
colors. Both its statistical and systematic uncertainties are estimated
to be <10%. Extinction in this map derived from stellar color
excesses is found to vary on arcsecond scales, with a mean value of
![]() mag. Mean extinction values in a circular region with 0.5'' radius centered on Sagittarius A* are
mag. Mean extinction values in a circular region with 0.5'' radius centered on Sagittarius A* are
![]() ,
,
![]() ,
and
,
and
![]() .
.
Key words: Galaxy: nucleus - dust, extinction - Galaxy: center - stars: horizontal-branch
1 Introduction
Nuclear star clusters (NSCs) are located at the photometric and dynamical centers of almost all spiral galaxies. Their detailed study has only become possible via HST observations in the 1990s, but they are of great interest because they are the densest and most massive clusters in their host galaxies. Frequently they contain supermassive black holes at their centers. They show signs of recurring star formation, and the discovery of rotation of the NSCs of NGC 4244 (Seth et al. 2008) and of the Milky Way (Schödel et al. 2009; Trippe et al. 2008) indicates that NSCs may at least partially form by accretion of material from their host galaxy. A concise review of the properties of NSCs and hypotheses on their formation is given in Böker (2008).
Studying the NSC at the Galactic center (GC) is of great importance for the understanding of NSCs in general because in the next decades it will remain impossible to resolve any but the brightest individual stars in extragalactic NSCs, even with 50m-class telescopes. A further reason for the importance of the GC NSC is that the existence of the supermassive black hole, Sagittarius A*, at the GC is well established and the mass of this black hole has been determined with high precision (e.g., Gillessen et al. 2009; Ghez et al. 2008). Strong interest in the stellar population at the GC was raised by spectroscopic observations, which have revealed the existence of numerous massive, young stars within 0.5 pc of Sagittarius A*. Those young stars are witnesses of a starburst event that occurred about 4 million years ago. The young stars are arranged in a non-isotropic pattern and at least 50% of them are located in a rotating disk (see Lu et al. 2009; Bartko et al. 2009).
Unfortunately, there are two important drawbacks in observational
studies of the Milky Way's NSC: extreme crowding and high
extinction. While the great progress made in adaptive optics
techniques at 8-10 m-class telescopes in the past years has been highly
successful in reducing the problem of crowding, it nevertheless
remains a serious issue. Even with instruments such as NACO at the ESO
VLT, strong crowding limits the point-source sensitivity within
![]() 0.5 pc of Sagittarius A* so significantly that only stars more
massive than
0.5 pc of Sagittarius A* so significantly that only stars more
massive than ![]() 2
2 ![]() can be detected in this region. This
means that we can still detect only of the order
can be detected in this region. This
means that we can still detect only of the order ![]() of the stars
in the NSC (Schödel et al. 2007a). Additionally, it is notoriously
difficult to extract accurate photometric measurements from AO
observations of crowded fields, particularly when the field-of-view
exceeds the size of the isoplanatic angle.
of the stars
in the NSC (Schödel et al. 2007a). Additionally, it is notoriously
difficult to extract accurate photometric measurements from AO
observations of crowded fields, particularly when the field-of-view
exceeds the size of the isoplanatic angle.
As concerns extinction, we can consider ourselves lucky that we can
observe the GC at all. Within 2-3 pc of Sagittarius A* there exist
plenty of clouds that are almost or completely opaque even in the
near-infrared (for example, see Fig. 1
in Schödel et al. 2007a). Average extinction toward the central parsec in
the K-band reaches
![]() .
As concerns extinction at visual
wavelengths, Rieke & Lebofsky (1985) found
.
As concerns extinction at visual
wavelengths, Rieke & Lebofsky (1985) found
![]() ,
but more
recent studies indicate higher values of
,
but more
recent studies indicate higher values of
![]() (Nishiyama et al. 2008), or even
(Nishiyama et al. 2008), or even
![]() (Gosling et al. 2009). Therefore, the stellar population at the GC
becomes observable only at near-infrared wavelengths. Only the
brightest stars can be seen in the J-band. Reasonable S/N on the
stars is only reached in the H, K, and L bands. This restriction
to a tight wavelength window, where most stars show only small color
indices, combined with the fact that the extinction toward the GC is
not only high, but also variable on small spatial scales of a few
arcseconds (Schödel et al. 2007a; Gosling et al. 2006; Scoville et al. 2003), makes photometric
studies of the stellar population at the GC extremely difficult.
(Gosling et al. 2009). Therefore, the stellar population at the GC
becomes observable only at near-infrared wavelengths. Only the
brightest stars can be seen in the J-band. Reasonable S/N on the
stars is only reached in the H, K, and L bands. This restriction
to a tight wavelength window, where most stars show only small color
indices, combined with the fact that the extinction toward the GC is
not only high, but also variable on small spatial scales of a few
arcseconds (Schödel et al. 2007a; Gosling et al. 2006; Scoville et al. 2003), makes photometric
studies of the stellar population at the GC extremely difficult.
Although adaptive optics assisted integral field spectroscopy has
resulted in the classification of hundreds of stars within
![]() 0.5 pc of Sagittarius A*
(e.g., Maness et al. 2007; Paumard et al. 2006; Do et al. 2009a), this technique is extremely time
consuming in both observations and data analysis. In order to
efficiently probe large fields in the Galactic center for the presence
of young, massive stars, it is therefore desirable to improve the
photometric observations in a way that enables us to at least crudely
distinguish whether a star in the GC is of early or of late spectral
type. How this can be done in spite of the difficulties described
above has been demonstrated recently by Buchholz et al. (2009). They
used intermediate band filters across the K-band, calibrated
photometry locally with the help of red clump stars, and used the CO
bandhead absorption feature of late-type stars as a distinguishing
criterion.
0.5 pc of Sagittarius A*
(e.g., Maness et al. 2007; Paumard et al. 2006; Do et al. 2009a), this technique is extremely time
consuming in both observations and data analysis. In order to
efficiently probe large fields in the Galactic center for the presence
of young, massive stars, it is therefore desirable to improve the
photometric observations in a way that enables us to at least crudely
distinguish whether a star in the GC is of early or of late spectral
type. How this can be done in spite of the difficulties described
above has been demonstrated recently by Buchholz et al. (2009). They
used intermediate band filters across the K-band, calibrated
photometry locally with the help of red clump stars, and used the CO
bandhead absorption feature of late-type stars as a distinguishing
criterion.
Accurate knowledge of extinction has impact in many different aspects of GC research: the stellar surface number density is not only a function of distance from Sagittarius A*, but is also dependent on local extinction (Schödel et al. 2007a); extinction is an important ingredient for modeling stellar atmospheres (e.g., Martins et al. 2007; Najarro et al. 1997); extinction in the infrared is also important for estimating the intrinsic brightness of the near-infrared emission from the accretion flow or outflow related to Sagittarius A* (e.g., Eckart et al. 2006; Do et al. 2009b; Genzel et al. 2003). The mentioned examples show that one must know not only the absolute value of extinction, but also how it changes as a function of wavelength and how it varies on spatial scales as small as one to a few arcseconds.
Until just about a decade ago, the extinction law from near- to
mid-infrared wavelengths (![]() 1-8
1-8 ![]() m) was thought to be described
well by a ``universal'' power-law,
m) was thought to be described
well by a ``universal'' power-law,
![]() ,
with a power-law index of
,
with a power-law index of
![]() (e.g., Draine 1989). First doubts were shed on this model
by spectroscopic observations of the GC with ISO SWS that showed clear
deviations from this model at wavelengths
(e.g., Draine 1989). First doubts were shed on this model
by spectroscopic observations of the GC with ISO SWS that showed clear
deviations from this model at wavelengths ![]() 3
3 ![]() m
(Lutz et al. 1996). Subsequent studies have confirmed that the near-
to mid-infrared extinction-law is more complex than a simple
power-law. While it seems well established by now that a simple
power-law is an adequate description of the wavelength dependence of
extinction in the near-infrared, albeit with a stronger wavelength
dependence as previously thought, the situation is less clear longward
of
m
(Lutz et al. 1996). Subsequent studies have confirmed that the near-
to mid-infrared extinction-law is more complex than a simple
power-law. While it seems well established by now that a simple
power-law is an adequate description of the wavelength dependence of
extinction in the near-infrared, albeit with a stronger wavelength
dependence as previously thought, the situation is less clear longward
of ![]() 3
3 ![]() m. Recent investigation shows that the extinction law
decreases much less rapidly at
m. Recent investigation shows that the extinction law
decreases much less rapidly at
![]() m than suggestd by
earlier estimates and may actually be almost constant at 5-10
m than suggestd by
earlier estimates and may actually be almost constant at 5-10 ![]() m
(see Nishiyama et al. 2009, for an extensive discussion of these
points). Taking the problem even a step further, in
a recent study of extinction toward the nuclear bulge
Gosling et al. (2009) find that the index of the power-law
extinction-law can change on spatial scales as small as
5 arcsec. This signifies that we may be forced to abandon the
concept of a universal extinction-law.
m
(see Nishiyama et al. 2009, for an extensive discussion of these
points). Taking the problem even a step further, in
a recent study of extinction toward the nuclear bulge
Gosling et al. (2009) find that the index of the power-law
extinction-law can change on spatial scales as small as
5 arcsec. This signifies that we may be forced to abandon the
concept of a universal extinction-law.
It is evident that the topic of extinction toward the central parsec
of the Galaxy needs to be re-visited. Extinction maps for the central
0.5-1 pc were recently presented by Schödel et al. (2007a) and
Buchholz et al. (2009). However, these papers were not mainly
focused on extinction and the extinction maps were rather
side-products. Both papers used the old
![]() extinction-law (Draine 1989). Neither the
extinction law nor absolute extinction were examined in depth. Also,
the absolute photometric calibration in our previous works was of limited
accuracy because the PSF for the stars was either truncated
(Schödel et al. 2007a) or because complex local calibration procedures
had to be adopted (Buchholz et al. 2009).
extinction-law (Draine 1989). Neither the
extinction law nor absolute extinction were examined in depth. Also,
the absolute photometric calibration in our previous works was of limited
accuracy because the PSF for the stars was either truncated
(Schödel et al. 2007a) or because complex local calibration procedures
had to be adopted (Buchholz et al. 2009).
The aim of this paper is to carry us a step forward in observational
studies of the GC NSC by addressing two of the above described
problems: accurate photometry with AO over a large FOV and accurate
measurements of extinction. Schödel (2010)
has recently presented a method for the photometric
analysis of AO data with spatially variable PSF, but a very limited
number of suitable PSF reference stars. Based on this method, in this
paper we analyze imaging observations of the GC in the H, ![]() ,
and
L' bands and provide accurate photometry (with both statistical and
systematic uncertainties of the order
,
and
L' bands and provide accurate photometry (with both statistical and
systematic uncertainties of the order ![]() 5% at
5% at ![]() )
for several
thousand sources observed in these bands within
)
for several
thousand sources observed in these bands within ![]() 1 pc of
Sagittarius A*. We determine both the absolute extinction and the
extinction law at the various bands and provide a detailed extinction
map (resolution of 1''-2'') for the central parsec of the GC.
1 pc of
Sagittarius A*. We determine both the absolute extinction and the
extinction law at the various bands and provide a detailed extinction
map (resolution of 1''-2'') for the central parsec of the GC.
Table 1: Details of the imaging observations used in this work.
2 Observations
The observations used in this work were obtained with the
near-infrared camera and adaptive optics (AO) system NAOS/CONICA
(short NACO) at the ESO VLT unit telescope 4![]() . The
. The
![]() supergiant IRS 7 was used to close the loop
of the AO, using the NIR wavefront sensor. The sky background was
measured on a largely empty patch of sky, a dark cloud about 400''north and 713'' east of the target. Sky subtraction, bad pixel
correction, and flat fielding were applied to the individual
exposures. The NACO S27 camera, with a pixel scale of
supergiant IRS 7 was used to close the loop
of the AO, using the NIR wavefront sensor. The sky background was
measured on a largely empty patch of sky, a dark cloud about 400''north and 713'' east of the target. Sky subtraction, bad pixel
correction, and flat fielding were applied to the individual
exposures. The NACO S27 camera, with a pixel scale of
![]() ,
was used for both H and
,
was used for both H and ![]() band observations. The
field-of-view (FOV) of a single exposure is thus
band observations. The
field-of-view (FOV) of a single exposure is thus
![]() .
The
observations were dithered by applying a rectangular dither pattern
with the center of the dithered exposures positioned approximately at
(8.0'',-2.6''),
(-6.1'',-2.7''),
(-6.1'',11.2''), and
(8.1'',11.3'') east and north of Sgr A*. In the text we refer to
these four offsets as dither positions 1, 2, 3, and 4. The combined
FOV of the observations is about
.
The
observations were dithered by applying a rectangular dither pattern
with the center of the dithered exposures positioned approximately at
(8.0'',-2.6''),
(-6.1'',-2.7''),
(-6.1'',11.2''), and
(8.1'',11.3'') east and north of Sgr A*. In the text we refer to
these four offsets as dither positions 1, 2, 3, and 4. The combined
FOV of the observations is about
![]() and is offset to the
north with respect to Sgr A* because the guide star IRS 7 is located
about 5.6'' north of Sgr A*.
and is offset to the
north with respect to Sgr A* because the guide star IRS 7 is located
about 5.6'' north of Sgr A*.
Seeing in the optical ranged between 0.6'' and 1.0'' for both H and ![]() observations. According to the ESO Ambient Conditions Database
observations. According to the ESO Ambient Conditions Database![]() sky
transparency variations during the observations were below 1%.
The achieved Strehl ratio ranged between
sky
transparency variations during the observations were below 1%.
The achieved Strehl ratio ranged between ![]() 20% (
20% (![]() 15%) near
the guide star and
15%) near
the guide star and ![]() 8% (
8% (![]() 8%) at 25'' distance from the
guide star in the
8%) at 25'' distance from the
guide star in the ![]() -(H-)band. The Strehl ratio was estimated
using the Strehl algorithm of the ESO eclipse software
package (Devillard 1997) on PSFs extracted at various
positions in the image. From the multiple measurements we estimate the
1
-(H-)band. The Strehl ratio was estimated
using the Strehl algorithm of the ESO eclipse software
package (Devillard 1997) on PSFs extracted at various
positions in the image. From the multiple measurements we estimate the
1![]() uncertainty of the measured Strehl ratio to
uncertainty of the measured Strehl ratio to ![]() 3%.
Table 1 summarizes the observations. The detector
integration time (DIT) was set to 2.0 s in order to avoid
saturation of the brightest stars. The central pixels of a small
number of the brightest stars were saturated in
3%.
Table 1 summarizes the observations. The detector
integration time (DIT) was set to 2.0 s in order to avoid
saturation of the brightest stars. The central pixels of a small
number of the brightest stars were saturated in ![]() .
Their cores were
repaired using nearby unsaturated stars and the PSF extraction routine
of StarFinder. After 28 DITs, the instrument averaged the data
to a single exposure (
.
Their cores were
repaired using nearby unsaturated stars and the PSF extraction routine
of StarFinder. After 28 DITs, the instrument averaged the data
to a single exposure (
![]() ). In this way, 8 individual exposures
were obtained per dither position. The exposures of each respective
dither position were aligned (to compensate for small residual shifts)
with the jitter algorithm of the ESO eclipse software
package (Devillard 1997). We show the combined FOV of the
). In this way, 8 individual exposures
were obtained per dither position. The exposures of each respective
dither position were aligned (to compensate for small residual shifts)
with the jitter algorithm of the ESO eclipse software
package (Devillard 1997). We show the combined FOV of the
![]() -band observations in Fig. 1. Note that the
photometry and astrometry in this work was done on the combined images
of each dither position and not on the combined mosaic of
all images (as shown in Fig. 1) in order to have a
constant signal-to-noise ratio over the entire images. The
-band observations in Fig. 1. Note that the
photometry and astrometry in this work was done on the combined images
of each dither position and not on the combined mosaic of
all images (as shown in Fig. 1) in order to have a
constant signal-to-noise ratio over the entire images. The
![]()
![]() overlap area between the four dither positions
is indicated by the rectangle in Fig. 1.
overlap area between the four dither positions
is indicated by the rectangle in Fig. 1.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13183fg1.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg43.png)
|
Figure 1:
Mosaic image of the |
| Open with DEXTER | |
Seeing in the optical ranged between 1.0'' and 2.0'' for the L'observations. The NACO L27 camera, with a pixel scale of
![]() ,
was used for the L' observations. According
to the ESO Ambient Conditions Database sky transparency variations
during the observations were below
,
was used for the L' observations. According
to the ESO Ambient Conditions Database sky transparency variations
during the observations were below ![]() .
The observations were
random jittered, with a jitter box width of 20''. Offsets by 60'' in
random directions were alternated with observations of the target. The
frames taken on the offsets frames, where the stellar density is
lower, were used to construct sky frames. The 7 offset frames nearest
in time to a given exposure on the target were median combined and
subtracted as sky measurement. Flat fielding and bad pixel correction
were applied. Finally, all exposures were combined with the jitter algorithm of the ESO eclipse software package. The
resulting mosaic image is shown in Fig. 2.
.
The observations were
random jittered, with a jitter box width of 20''. Offsets by 60'' in
random directions were alternated with observations of the target. The
frames taken on the offsets frames, where the stellar density is
lower, were used to construct sky frames. The 7 offset frames nearest
in time to a given exposure on the target were median combined and
subtracted as sky measurement. Flat fielding and bad pixel correction
were applied. Finally, all exposures were combined with the jitter algorithm of the ESO eclipse software package. The
resulting mosaic image is shown in Fig. 2.
3 Photometry
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13183fg2.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg46.png)
|
Figure 2: Mosaic image of the L'-band observations. North is up and east is to the left. Offsets are given in arcseconds from Sgr A*. |
| Open with DEXTER | |
Due to the extreme source density at the GC aperture photometry cannot
be applied accurately to GC imaging data. Therefore PSF fitting
techniques must be used. In AO imaging anisoplanatic effects can lead
to a systematic bias in the photometry of point sources when PSF
fitting is used for estimating the flux of the stars. This bias depends
on various factors such as distance from the guide star, observing
wavelength, and atmospheric conditions at the time of the
observations. In case of the H-band data used in this work the
systematic error of the photometry can reach 0.25 mag across the
FOV, if a single, non-variable PSF is used (see Schoedel, A&A,
2009, accepted for publication). For example, anisoplanatic effects
make stars at distances larger than the isoplanatic angle appear
elongated, with their major axes pointing toward the guide star. This
can be nicely seen in the image shown in Fig. 2
(note: usually anisoplanatic effects are stronger at shorter
wavelengths, but in the observations used for this paper, it happens
that those effects are stronger in the L'-band than in the ![]() -band
image). Various methods for dealing with anisoplanatic effects have
been suggested. A straightforward and effective method to deal with
anisoplanatic effects is presented in a companion paper (Schoedel,
A&A, 2009, accepted for publication). It not only provides accurate
point source photometry but also reliable estimation of the diffuse
background emission. In brief, the method consists of two steps: (a)
Wiener deconvolution, using a point spread function (PSF) extracted
from the guide star (or bright stars near the guide star), in this
case IRS 7; (b) photometry and astrometry on the deconvolved image
via PSF fitting with the StarFinder (Diolaiti et al. 2000)
program package. The image is partitioned into overlapping sub-frames
that are smaller than the isoplanatic angle. Those sub-frames are
analyzed independently. As shown in Schoedel (A&A, 2009, accepted for
publication) this method minimizes the systematic uncertainty of the point source
photometry due to anisoplanatic effects to
-band
image). Various methods for dealing with anisoplanatic effects have
been suggested. A straightforward and effective method to deal with
anisoplanatic effects is presented in a companion paper (Schoedel,
A&A, 2009, accepted for publication). It not only provides accurate
point source photometry but also reliable estimation of the diffuse
background emission. In brief, the method consists of two steps: (a)
Wiener deconvolution, using a point spread function (PSF) extracted
from the guide star (or bright stars near the guide star), in this
case IRS 7; (b) photometry and astrometry on the deconvolved image
via PSF fitting with the StarFinder (Diolaiti et al. 2000)
program package. The image is partitioned into overlapping sub-frames
that are smaller than the isoplanatic angle. Those sub-frames are
analyzed independently. As shown in Schoedel (A&A, 2009, accepted for
publication) this method minimizes the systematic uncertainty of the point source
photometry due to anisoplanatic effects to ![]() 0.02 mag across
the
0.02 mag across
the
![]() FOV of the images at each dither position.
FOV of the images at each dither position.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{13183fg3.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg47.png)
|
Figure 3:
Statistical photometric uncertainty vs. magnitude
for the H- ( top), |
| Open with DEXTER | |
After deconvolution with PSFs extracted from IRS 7, the H- and
![]() -band images from the four dither positions were partitioned into
-band images from the four dither positions were partitioned into
![]() overlapping sub-frames of
overlapping sub-frames of
![]() pixel2(
pixel2(![]()
![]() ). The shifts between sub-frames were thus just
64 pixels in x- and/or y-direction to assure large overlap between
the sub-frames. We used the following StarFinder parameters:
). The shifts between sub-frames were thus just
64 pixels in x- and/or y-direction to assure large overlap between
the sub-frames. We used the following StarFinder parameters:
![]() ,
thresh=[5.,5.], and
,
thresh=[5.,5.], and
![]() .
In order to
avoid spurious detections, point source detection was also run on
non-deconvolved images and only sources that were discovered in both
the deconvolved and non-deconvolved images were included in the final
list of detected stars. The images for the diffuse background and
residuals were obtained by recombining the corresponding
sub-frames. The method provides two kinds of uncertainties for the
photometric and astrometric measurements: formal uncertainties,
computed by the StarFinder algorithm from Gaussian and photon
noise, and PSF uncertainties, resulting from incomplete
knowledge of the local PSF. The latter is calculated by comparing
multiple measurements of the stars because they are present in several
sub-frames. For stars without multiple measurements we adopted a PSF
uncertainty of 0.02 mag for the H-band and 0.015 mag for the
.
In order to
avoid spurious detections, point source detection was also run on
non-deconvolved images and only sources that were discovered in both
the deconvolved and non-deconvolved images were included in the final
list of detected stars. The images for the diffuse background and
residuals were obtained by recombining the corresponding
sub-frames. The method provides two kinds of uncertainties for the
photometric and astrometric measurements: formal uncertainties,
computed by the StarFinder algorithm from Gaussian and photon
noise, and PSF uncertainties, resulting from incomplete
knowledge of the local PSF. The latter is calculated by comparing
multiple measurements of the stars because they are present in several
sub-frames. For stars without multiple measurements we adopted a PSF
uncertainty of 0.02 mag for the H-band and 0.015 mag for the
![]() -band (see Fig. 3). The results of multiple
measurements were averaged. Since deconvolution changes the noise
properties of the image, the formal uncertainties computed by StarFinder are too small (for details see Schoedel, A&A, 2009, accepted for
publication). Monte Carlo simulations were used to determine a correction
factor with which we scaled the formal uncertainties. The final
uncertainties were calculated by quadratically combining the re-scaled
formal fit uncertainties with the PSF uncertainties. The data in the
overlap region between the four dither positions were averaged. Stars
present in the overlap region between the dithered fields in the Hand
-band (see Fig. 3). The results of multiple
measurements were averaged. Since deconvolution changes the noise
properties of the image, the formal uncertainties computed by StarFinder are too small (for details see Schoedel, A&A, 2009, accepted for
publication). Monte Carlo simulations were used to determine a correction
factor with which we scaled the formal uncertainties. The final
uncertainties were calculated by quadratically combining the re-scaled
formal fit uncertainties with the PSF uncertainties. The data in the
overlap region between the four dither positions were averaged. Stars
present in the overlap region between the dithered fields in the Hand ![]() observations were used to check the photometric
accuracy. Photometry on the stars in the overlapping fields shows that
the uncertainties estimated by the applied method are correct (see
Schoedel, A&A, 2009, accepted for publication).
observations were used to check the photometric
accuracy. Photometry on the stars in the overlapping fields shows that
the uncertainties estimated by the applied method are correct (see
Schoedel, A&A, 2009, accepted for publication).
Photometry on the L' image was performed in a very similar way, except
that there was only one combined frame to be examined. The PSF for
initial linear deconvolution was extracted from IRS 7. The size of
the sub-frames for local PSF fitting was
![]() pixel2,
with a shift of 50 pixels between the frames. Since the L' data are
very rich in structure as concerns the diffuse emission, we set the
pixel2,
with a shift of 50 pixels between the frames. Since the L' data are
very rich in structure as concerns the diffuse emission, we set the
![]() to a smaller value (20 pixels).
to a smaller value (20 pixels).
Zero points for the NACO instrument for various combinations of
cameras, filters, and dichroics (that split the light between
wavefront sensor and camera) are determined routinely within the ESO
instrument calibration plan. Zero points for all filters used in this
work and for the corresponding setup (camera S27, dichroic N20C80)
were determined via observation of a standard star during the same
night as the observations:
![]() ,
,
![]() ,
and
,
and
![]() .
Additional
uncertainty of the zero point is caused by the uncertainty of the PSF
that is used for deconvolution. From experiments (choosing different
PSF sizes) we estimate this additional uncertainty to
.
Additional
uncertainty of the zero point is caused by the uncertainty of the PSF
that is used for deconvolution. From experiments (choosing different
PSF sizes) we estimate this additional uncertainty to
![]() 0.03 mag. We combine this additional uncertainty
quadratically with the previous uncertainties and obtain final zero
point uncertainties of
0.03 mag. We combine this additional uncertainty
quadratically with the previous uncertainties and obtain final zero
point uncertainties of
![]() ,
,
![]() ,
and
,
and
![]() .
The annual mean and standard deviation
of the zero points corresponding to the year and the setups used for
the observations in this work are
.
The annual mean and standard deviation
of the zero points corresponding to the year and the setups used for
the observations in this work are
![]() ,
,
![]() ,
and
,
and
![]() .
This agrees well with the zero
points and corresponding 1
.
This agrees well with the zero
points and corresponding 1![]() used for the photometry in this
work.
used for the photometry in this
work.
Plots of photometric uncertainty vs. magnitude for all point sources
discovered in the individual bands are shown in
Fig. 3. We combined the photometric results to a
final list, requiring that each star must be detected in at least two
different bands. The final lists of detected point sources was
aligned with the coordinate system of the ![]() -observations. The full
list of all stars and their fluxes in the different bands is given in
Table A.2, available online.
-observations. The full
list of all stars and their fluxes in the different bands is given in
Table A.2, available online.
Because of the non-standard photometric methodology applied here (deconvolution and extraction of local PSFs) it was not straightforward to determine incompleteness due to crowding via the standard method of inserting and recovering artifical stars. The main difficulty here is the change of the PSF across the FOV. We therefore estimated completeness directly from the data using the methodology suggested by Eisenhauer et al. (1998) and further described in Harayama et al. (2008). In brief, it consists of deriving a critical distance for each possible magnitude difference between two given stars. A star closer to a brighter one than the critical distance will not be detected. Once the critical distance is known for all relevant magnitude differences, completeness maps can be created. Table 2 gives the completeness of our data for different magnitudes and bands. Some of the assumptions of the methodology suggested by Eisenhauer et al. (1998) may be violated in our case, particularly becase the stellar density in the GC FOV changes strongly because of effects of extinction and cluster structure. For this reason we estimated the critical distances in various ways, e.g. by analysing different parts of the FOV. In Table 2 we therefore give two values for estimated completeness, a high and a low one, for each magnitude and band. Fortunately it turns out (see following section) that completeness correction does not have any significant influence on our results.
Table 2: Completeness levels in percent for given bands andmagnitudes.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13183fg4.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg64.png)
|
Figure 4:
Color-magnitude diagrams, with |
| Open with DEXTER | |
4 Constraining extinction with the red clump
Color-magnitude diagrams of our data are shown in Fig. 4. The
densely populated area around
![]() and
and
![]() is due to red clump (RC) stars, which are the
equivalent to horizontal branch stars in metal-rich populations. The
luminosities and colors of RC stars are narrowly distributed and are
only weakly dependent on age and metallicity, particularly for
clusters older than
is due to red clump (RC) stars, which are the
equivalent to horizontal branch stars in metal-rich populations. The
luminosities and colors of RC stars are narrowly distributed and are
only weakly dependent on age and metallicity, particularly for
clusters older than ![]() 1.6 Gyr
(e.g., Castellani et al. 1992; Alves 2000; Grocholski & Sarajedini 2002).
1.6 Gyr
(e.g., Castellani et al. 1992; Alves 2000; Grocholski & Sarajedini 2002).
The completeness corrected luminosity functions (LFs) in the H,
![]() ,
and L' bands are shown in the bottom panel of
Fig. 4. The RC feature is clearly visible as a bump in
all LFs. We fitted all LFs with the combination of exponentials plus
Gaussians. The locations of the peaks of the RC as derived from these
fits are
,
and L' bands are shown in the bottom panel of
Fig. 4. The RC feature is clearly visible as a bump in
all LFs. We fitted all LFs with the combination of exponentials plus
Gaussians. The locations of the peaks of the RC as derived from these
fits are
![]() ,
,
![]() ,
and
,
and
![]() .
Values in brackets are the
results obtained if no crowding completeness correction is
applied. The uncertainties of the fits are smaller than the
uncertainty of the absolute photometric calibration (0.06 mag for
H and
.
Values in brackets are the
results obtained if no crowding completeness correction is
applied. The uncertainties of the fits are smaller than the
uncertainty of the absolute photometric calibration (0.06 mag for
H and ![]() ,
and 0.15 mag for L'). In the following analysis we
will use the numbers based on the completeness corrected LFs. We note
however, that this crowding completeness corection has a negligible
effect, of the order 10% of the uncertainty, on the final results. We
attribute this to two reasons: (a) the RC is located in a magnitude
range where completeness is fairly high; (b) the dominating
uncertainty is the one of the absolute photometric calibration. That
incompleteness due to crowding is not a serious issue can also be seen
when comparing the
,
and 0.15 mag for L'). In the following analysis we
will use the numbers based on the completeness corrected LFs. We note
however, that this crowding completeness corection has a negligible
effect, of the order 10% of the uncertainty, on the final results. We
attribute this to two reasons: (a) the RC is located in a magnitude
range where completeness is fairly high; (b) the dominating
uncertainty is the one of the absolute photometric calibration. That
incompleteness due to crowding is not a serious issue can also be seen
when comparing the ![]() LF from this paper with the one shown in
Fig. 10 of Schödel et al. (2007a). A different, slightly deeper data
set was used for the latter work, but we can see that the RC bump in
the
LF from this paper with the one shown in
Fig. 10 of Schödel et al. (2007a). A different, slightly deeper data
set was used for the latter work, but we can see that the RC bump in
the ![]() LF is negligibly affected by incompleteness. Note, however,
that absolute calibration was not a goal of Schödel et al. (2007a),
therefore, there RC peak is shifted by
LF is negligibly affected by incompleteness. Note, however,
that absolute calibration was not a goal of Schödel et al. (2007a),
therefore, there RC peak is shifted by ![]() 0.3 mag to brighter
magnitudes. Finally, we may ask whether the strong extinction toward
the GC may affect the RC peak in the LFs of the different filters and
thus bias the peak toward brighter values. RC stars are, however, well
within the sensitivity of the observing setup used, at all bands. For
example, an isolated
0.3 mag to brighter
magnitudes. Finally, we may ask whether the strong extinction toward
the GC may affect the RC peak in the LFs of the different filters and
thus bias the peak toward brighter values. RC stars are, however, well
within the sensitivity of the observing setup used, at all bands. For
example, an isolated
![]() source would be detected with NACO
and the settings used for this work at a level of
source would be detected with NACO
and the settings used for this work at a level of
![]() 10
10![]() .
The only incompleteness that affects us here is the
one due to crowding, which has fortunately a negligible effect on our
results.
.
The only incompleteness that affects us here is the
one due to crowding, which has fortunately a negligible effect on our
results.
Since RC stars can be found in large numbers toward the Galactic bulge
and center, they are highly useful for studying Galactic extinction
and structure
(e.g., Nishiyama et al. 2005; Udalski 2003; Nishiyama et al. 2006b,a; Wozniak & Stanek 1996; Sumi 2004).
The absolute magnitude of RC stars has been estimated to
![]() (in the 2MASS system) by
Groenewegen (2008) and to
(in the 2MASS system) by
Groenewegen (2008) and to
![]() by
Alves (2000). Both values are based on the Hipparcos
catalogue. Here we adopt the more recent value for MK. The
difference between the K and
by
Alves (2000). Both values are based on the Hipparcos
catalogue. Here we adopt the more recent value for MK. The
difference between the K and ![]() -magnitude is
-magnitude is ![]() 0.01 mag
(see discussion in Nishiyama et al. 2006b).
Nishiyama et al. (2006b) estimated the distance to the GC based on
photometry of RC stars, calculating the distance modulus as
0.01 mag
(see discussion in Nishiyama et al. 2006b).
Nishiyama et al. (2006b) estimated the distance to the GC based on
photometry of RC stars, calculating the distance modulus as
| (1) |
where
Numerous efforts to determine the distance of the GC have been made
recently (the cited uncertainties are the quadratically combined
statistical and systematic uncertainties given in the respective
works):
![]() kpc (bulge red clump
stars, Nishiyama et al. 2006b),
kpc (bulge red clump
stars, Nishiyama et al. 2006b),
![]() kpc (stellar orbit
around Sagittarius A*, Gillessen et al. 2009),
kpc (stellar orbit
around Sagittarius A*, Gillessen et al. 2009), ![]() kpc
(stellar orbit around Sagittarius A*, Ghez et al. 2008),
kpc
(stellar orbit around Sagittarius A*, Ghez et al. 2008),
![]() kpc (Population II Cepheids and RR Lyrae
stars Groenewegen et al. 2008),
kpc (Population II Cepheids and RR Lyrae
stars Groenewegen et al. 2008),
![]() kpc (proper motion
and line-of-sight velocity dispersion of late-type stars in central
parsec, Trippe et al. 2008),
kpc (proper motion
and line-of-sight velocity dispersion of late-type stars in central
parsec, Trippe et al. 2008), ![]() kpc (trigonometric
parallaxes of masers measured with VLBI, Reid et al. 2009a),
kpc (trigonometric
parallaxes of masers measured with VLBI, Reid et al. 2009a),
![]() kpc (Mira stars, Matsunaga et al. 2009), and
kpc (Mira stars, Matsunaga et al. 2009), and
![]() kpc (trigonometric parallax of Sgr B2 measured with
VLBI, Reid et al. 2009b). These distance estimates are based on
different data sets and different methods and can probably be
considered largely independent measurements. It appears therefore
justified to combine these measurements to a weighted mean of
kpc (trigonometric parallax of Sgr B2 measured with
VLBI, Reid et al. 2009b). These distance estimates are based on
different data sets and different methods and can probably be
considered largely independent measurements. It appears therefore
justified to combine these measurements to a weighted mean of
![]() kpc. This corresponds to a distance modulus of
kpc. This corresponds to a distance modulus of
![]() .
This simple exercise demonstrates that - under the
assumption that these measurements are indeed statistically
independent - R0 is already known with the surprisingly small
uncertainty of just
.
This simple exercise demonstrates that - under the
assumption that these measurements are indeed statistically
independent - R0 is already known with the surprisingly small
uncertainty of just ![]() .
Using this value we obtain a reddening
free magnitude of the RC bump at the GC of
.
Using this value we obtain a reddening
free magnitude of the RC bump at the GC of
![]() .
All uncertainties have been quadratically
combined (
.
All uncertainties have been quadratically
combined (
![]() mag,
mag,
![]() mag,
mag,
![]() mag).
mag).
The fit of the RC bump in the ![]() LF with a Gaussian (plus an
exponential to fit the underlying luminosity function) results in
LF with a Gaussian (plus an
exponential to fit the underlying luminosity function) results in
![]() .
Here, the uncertainties from the fit of
the RC peak and from the absolute photometric calibration have been
combined quadratically. From the difference with the theoretical
reddening free magnitude of the RC bump, this results in an average
extinction of
.
Here, the uncertainties from the fit of
the RC peak and from the absolute photometric calibration have been
combined quadratically. From the difference with the theoretical
reddening free magnitude of the RC bump, this results in an average
extinction of
![]() toward the GC.
toward the GC.
Assuming
![]() and
and
![]() for the RC stars,
we obtain in the same way estimates for
for the RC stars,
we obtain in the same way estimates for
![]() and
and
![]() .
Note that these values depend only on the
well-known properties of RC stars and on the GC distance. They are
independent of any assumptions on the extinction-law.
.
Note that these values depend only on the
well-known properties of RC stars and on the GC distance. They are
independent of any assumptions on the extinction-law.
Assuming the validity of a power-law for the extinction law between
H and ![]() and between
and between ![]() and L', respectively (see,
e.g., Nishiyama et al. 2009), we can derive from the above measurements
the respective power-law indices
and L', respectively (see,
e.g., Nishiyama et al. 2009), we can derive from the above measurements
the respective power-law indices
![]() and
and
![]() .
Here the uncertainties include the
uncertainties of the effective wavelengths at the corresponding
bands. The effective wavelengths adopted in this work are
.
Here the uncertainties include the
uncertainties of the effective wavelengths at the corresponding
bands. The effective wavelengths adopted in this work are
![]() m,
m,
![]() m, and
m, and
![]() m. Details on how these effective
wavelengths have been calculated are given in
Appendix A.
m. Details on how these effective
wavelengths have been calculated are given in
Appendix A.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13183fg5.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg99.png)
|
Figure 5:
Peak |
| Open with DEXTER | |
As can be seen in the color-magnitude diagram shown in
Fig. 4 (top left) there is a clear dependency of the
![]() peak magnitude of the RC feature on
peak magnitude of the RC feature on
![]() .
Because of the narrow
intrinsic distribution of colors and magnitudes of the RC stars we
expect this trend to be almost exclusively due to differential
extinction. In order to quantify this relation, we extracted the
.
Because of the narrow
intrinsic distribution of colors and magnitudes of the RC stars we
expect this trend to be almost exclusively due to differential
extinction. In order to quantify this relation, we extracted the
![]() LF in narrow ranges of
LF in narrow ranges of
![]() .
The peaks of the RC features were
then fitted with a Gaussian. This method is very similar to the one
applied by Nishiyama et al. (2006a), who examined the location of the
RC feature in different fields toward the GC in order to derive the
reddening law. Figure 5 shows the thus measured RC
.
The peaks of the RC features were
then fitted with a Gaussian. This method is very similar to the one
applied by Nishiyama et al. (2006a), who examined the location of the
RC feature in different fields toward the GC in order to derive the
reddening law. Figure 5 shows the thus measured RC
![]() peak magnitude vs.
peak magnitude vs.
![]() along with a linear fit. Assuming
along with a linear fit. Assuming
![]() ,
the slope of the line
gives
,
the slope of the line
gives
![]() .
This value agrees within the
uncertainties with the one derived from the RC bump in the
H and
.
This value agrees within the
uncertainties with the one derived from the RC bump in the
H and ![]() luminosity functions (see above) and thus
serves as a cross-check. However, we consider the value
luminosity functions (see above) and thus
serves as a cross-check. However, we consider the value
![]() derived from the RC as more reliable
(see discussion section).
derived from the RC as more reliable
(see discussion section).
The ![]() vs.
vs.
![]() color magnitude diagram shows a decreasing
completeness with increasing reddening. This is reflected in
Fig. 4 by the increasing faint magnitude limit of the
cloud of dots toward redder colors. We have seen above that
incompleteness does not significantly affect the measured peak of the
RC in the
color magnitude diagram shows a decreasing
completeness with increasing reddening. This is reflected in
Fig. 4 by the increasing faint magnitude limit of the
cloud of dots toward redder colors. We have seen above that
incompleteness does not significantly affect the measured peak of the
RC in the ![]() LF. We have not used any completeness correction for
the fit of the RC peak in the color magnitude diagram, but tested its
reliability by omitting the two ``reddest'', i.e. highest
LF. We have not used any completeness correction for
the fit of the RC peak in the color magnitude diagram, but tested its
reliability by omitting the two ``reddest'', i.e. highest
![]() ,
data
points. The fit then results in
,
data
points. The fit then results in
![]() .
If we
additionally omit the bluest data point from the fit, which may be an
outlier, we obtain
.
If we
additionally omit the bluest data point from the fit, which may be an
outlier, we obtain
![]() .
We conclude that
incompleteness due to reddening does not have any significant
influence on the value of
.
We conclude that
incompleteness due to reddening does not have any significant
influence on the value of
![]() derived from the
color-magnitude diagram in Fig. 5.
derived from the
color-magnitude diagram in Fig. 5.
As can be seen in the middle panel of Fig. 4,
there is no clear trend of the RC visible in the plot of L'vs.
![]() .
This is mainly because the number of stars measured in
L' is smaller (smaller FOV) and because the range spanned by the
.
This is mainly because the number of stars measured in
L' is smaller (smaller FOV) and because the range spanned by the
![]() colors is limited due to the weak extinction in L' . We can
therefore not apply this method to determine
colors is limited due to the weak extinction in L' . We can
therefore not apply this method to determine
![]() (see
below for a different method, however).
(see
below for a different method, however).
5 An extinction map for the GC
![\begin{figure}
\par\includegraphics[width=15cm,clip]{13183fg6.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg106.png)
|
Figure 6:
Top left: map of
|
| Open with DEXTER | |
We produced an extinction map for the FOV of the H and ![]() observations of the GC by using the median of the
observations of the GC by using the median of the
![]() colors of
the 20 nearest stars at each position. For this purpose we used
all stars from our list, but excluded extremely blue (
colors of
the 20 nearest stars at each position. For this purpose we used
all stars from our list, but excluded extremely blue (
![]() )
or
red (
)
or
red (
![]() )
ones as fore- or background stars. The intrinsic colors
of almost all stellar types observable at the GC are similar at these
wavelengths. Nevertheless, we tried to improve the estimates
by applying a 0th order correction for different intrinsic stellar colors.
Stars fainter than
)
ones as fore- or background stars. The intrinsic colors
of almost all stellar types observable at the GC are similar at these
wavelengths. Nevertheless, we tried to improve the estimates
by applying a 0th order correction for different intrinsic stellar colors.
Stars fainter than
![]() were assigned
were assigned
![]() and stars
brighter than this value were assigned
and stars
brighter than this value were assigned
![]() .
Known
early-type stars (taken from Buchholz et al. 2009) were assigned
.
Known
early-type stars (taken from Buchholz et al. 2009) were assigned
![]() .
In order to assign these intrinsic colors, we used
the GC distance, approximate extinction, and the magnitude of the stars to roughly
guess their type (see, e.g., Table 3 in Buchholz et al. 2009) and
assigned colors from Tables 7.6 and 7.7 in Cox (2000).
.
In order to assign these intrinsic colors, we used
the GC distance, approximate extinction, and the magnitude of the stars to roughly
guess their type (see, e.g., Table 3 in Buchholz et al. 2009) and
assigned colors from Tables 7.6 and 7.7 in Cox (2000).
In order to check the importance of distinguishing different intrinsic
stellar colors we also created a map of
![]() assuming just one
uniform intrinsic color,
assuming just one
uniform intrinsic color,
![]() for all stars. The resulting map
looks almost identical to the one including the more refined
corrections (the mean difference between the two maps is
for all stars. The resulting map
looks almost identical to the one including the more refined
corrections (the mean difference between the two maps is
![]() ). We conclude that it would be, in
principle, acceptable to assume just one common intrinsic color for
our entire sample of stars because only
). We conclude that it would be, in
principle, acceptable to assume just one common intrinsic color for
our entire sample of stars because only ![]() 16% of our sample of
stars are brighter than
16% of our sample of
stars are brighter than
![]() .
The majority are, in fact, red
clump stars. Although this shows that distinguishing different types
of stars in the 0th order color correction is almost negligible, we
nevertheless include this correction in order to avoid bias in regions
where certain types of stars may be crowded. For example, the majority
of stars within 0.5'' of Sgr A* are of early-type
(e.g. Eisenhauer et al. 2005).
.
The majority are, in fact, red
clump stars. Although this shows that distinguishing different types
of stars in the 0th order color correction is almost negligible, we
nevertheless include this correction in order to avoid bias in regions
where certain types of stars may be crowded. For example, the majority
of stars within 0.5'' of Sgr A* are of early-type
(e.g. Eisenhauer et al. 2005).
The map of color excesses,
![]() ,
was converted to an
extinction map by assuming a power-law extinction-law with an index
,
was converted to an
extinction map by assuming a power-law extinction-law with an index
![]() for the effective wavelengths of
for the effective wavelengths of
![]() m and
m and
![]() m. The uncertainty of these three
parameters combined with the uncertainty of the photometric zero
points and of the intrinsic stellar colors results in a combined
systematic uncertainty of
m. The uncertainty of these three
parameters combined with the uncertainty of the photometric zero
points and of the intrinsic stellar colors results in a combined
systematic uncertainty of ![]() 9% on the calculated values of
9% on the calculated values of
![]() .
The extinction map based on
.
The extinction map based on
![]() colors is shown in the
top left panel of Fig. 6. The top right panel of this
figure shows the resolution of the extinction map, i.e. the radius at
each position within which 20 stars were detected. The
statistical uncertainty,
colors is shown in the
top left panel of Fig. 6. The top right panel of this
figure shows the resolution of the extinction map, i.e. the radius at
each position within which 20 stars were detected. The
statistical uncertainty,
![]() (with N=20), of the
extinction at each point in the map is shown in the bottom right
panel of Fig. 6. It is <0.1 mag for the entire map.
As a cross-check, we also created an extinction map based on
(with N=20), of the
extinction at each point in the map is shown in the bottom right
panel of Fig. 6. It is <0.1 mag for the entire map.
As a cross-check, we also created an extinction map based on
![]() colors, in a completely analogous way. It is presented in the bottom
left panel of Fig. 6 and shows the same patterns as
the extinction map based on
colors, in a completely analogous way. It is presented in the bottom
left panel of Fig. 6 and shows the same patterns as
the extinction map based on
![]() colors. Note that details will be
more reliable in the map based on
colors. Note that details will be
more reliable in the map based on
![]() because of the higher point
source density measured in these bands. Based on the assumption that
the extinction law between
because of the higher point
source density measured in these bands. Based on the assumption that
the extinction law between ![]() and L' is a power-law, we determined
the corresponding power-law index,
and L' is a power-law, we determined
the corresponding power-law index,
![]() ,
by requiring that
the average
,
by requiring that
the average
![]() must be the same, based on
must be the same, based on
![]() or
or
![]() colors. A value of
colors. A value of
![]() has been obtained, with a
statistical uncertainty of 0.12 and a systematic uncertainty - due
to uncertainties in the effective wavelengths and overall photometric
calibration - of 0.29. This value of
has been obtained, with a
statistical uncertainty of 0.12 and a systematic uncertainty - due
to uncertainties in the effective wavelengths and overall photometric
calibration - of 0.29. This value of
![]() agrees
very well with the one derived from the location of the RC bump in
the
agrees
very well with the one derived from the location of the RC bump in
the ![]() and L' luminosity functions.
and L' luminosity functions.
A histogram of the values of
![]() measured based on the
measured based on the
![]() colors is shown in Fig. 7. The histogram is fit well
by a Gaussian with a mean value of
colors is shown in Fig. 7. The histogram is fit well
by a Gaussian with a mean value of
![]() mag and a
standard deviation of 0.30 mag.
mag and a
standard deviation of 0.30 mag.
The extinction map was used to produce a differential extinction
corrected color magnitude diagram of ![]() vs.
vs.
![]() .
It is shown in
Fig. 8, after exluding all stars with
.
It is shown in
Fig. 8, after exluding all stars with
![]() as
foreground and
as
foreground and
![]() as background stars. It can be seen how the
extinction correction significantly reduces the scatter in the diagram
(compare with the uncorrected diagram in the upper left panel of
Fig. 4). The red clump is very well defined and the
giant sequence can be perceived clearly to the right of the dashed
line, which indicates the median
as background stars. It can be seen how the
extinction correction significantly reduces the scatter in the diagram
(compare with the uncorrected diagram in the upper left panel of
Fig. 4). The red clump is very well defined and the
giant sequence can be perceived clearly to the right of the dashed
line, which indicates the median
![]() color. Stars on the left of
the dashed line are expected to be either foreground or early-type
stars. Known early-type stars (Buchholz et al. 2009) are marked with
blue circles. They provide a sanity check on the reliability of
identifying early-type stars via extinction corrected
color. Stars on the left of
the dashed line are expected to be either foreground or early-type
stars. Known early-type stars (Buchholz et al. 2009) are marked with
blue circles. They provide a sanity check on the reliability of
identifying early-type stars via extinction corrected
![]() colors.
At
colors.
At
![]() about 65% of the known early-type stars are identified
correctly. How high is the probability to misidentify late-type stars
as early-type with this method? Since the FOV of our work is larger
than in comparable work, we limit the analysis for investigating this
question to the region within 12'' of Sgr A* and to magnitudes
brighter than
about 65% of the known early-type stars are identified
correctly. How high is the probability to misidentify late-type stars
as early-type with this method? Since the FOV of our work is larger
than in comparable work, we limit the analysis for investigating this
question to the region within 12'' of Sgr A* and to magnitudes
brighter than
![]() .
With these limits we can reasonably assume that
the number of known and correctly classified stars (as early- or
late-type) from literature is close to 100%. Within 12'' of
Sgr A* we find that about 30% of the stars brighter than
.
With these limits we can reasonably assume that
the number of known and correctly classified stars (as early- or
late-type) from literature is close to 100%. Within 12'' of
Sgr A* we find that about 30% of the stars brighter than
![]() identified by the extinction corrected
identified by the extinction corrected
![]() colors may be erroneous
identifications. Potential important sources of error are, for
example, photometric errors and inaccuracies of the extinction map
because of variability at scales below the resolution of our
extinction map or because of locally different extinction related
possibly with individual sources, e.g. due to circumstellar material.
Nevertheless, considering the crudenes of the method presented here, a
success rate of
colors may be erroneous
identifications. Potential important sources of error are, for
example, photometric errors and inaccuracies of the extinction map
because of variability at scales below the resolution of our
extinction map or because of locally different extinction related
possibly with individual sources, e.g. due to circumstellar material.
Nevertheless, considering the crudenes of the method presented here, a
success rate of ![]() 2/3 appears reasonable and suggests that our
method may be useful for large-scale surveys in order to identify
candidates for massive, young stars in highly extincted areas. At
magnitudes
2/3 appears reasonable and suggests that our
method may be useful for large-scale surveys in order to identify
candidates for massive, young stars in highly extincted areas. At
magnitudes
![]() the extinction corrected
the extinction corrected
![]() criterion is too
crude and does not allow to separate early- and late-type stars in our
sample. However, future work may provide more accurate colors and
extinction values.
criterion is too
crude and does not allow to separate early- and late-type stars in our
sample. However, future work may provide more accurate colors and
extinction values.
We have marked all stars with
![]() and a color bluer than the
median
and a color bluer than the
median
![]() (after excluding foreground stars, see above) with
crosses in the
(after excluding foreground stars, see above) with
crosses in the ![]() image shown in Fig. 1. Many
early-type stars reported by
Paumard et al. (2006); Do et al. (2009a); Buchholz et al. (2009) and other authors are
correctly identified. Following the error analysis in the
preceding paragraph of the order 30% of the stars may be
spurious identifications and a similar number of early-type stars may
be missed by this method. Nevertheless, this is the first time that
early-type stars at the GC can be identified via broad-band
imaging. Even taking into account the large estimated uncertainties,
this rather crude method confirms the finding of
Buchholz et al. (2009) that there exists a population of early-type
stars beyond a projected radius of 0.5 pc from Sagittarius A*.
image shown in Fig. 1. Many
early-type stars reported by
Paumard et al. (2006); Do et al. (2009a); Buchholz et al. (2009) and other authors are
correctly identified. Following the error analysis in the
preceding paragraph of the order 30% of the stars may be
spurious identifications and a similar number of early-type stars may
be missed by this method. Nevertheless, this is the first time that
early-type stars at the GC can be identified via broad-band
imaging. Even taking into account the large estimated uncertainties,
this rather crude method confirms the finding of
Buchholz et al. (2009) that there exists a population of early-type
stars beyond a projected radius of 0.5 pc from Sagittarius A*.
Finally, we have used the extinction map to produce a ![]() luminosity function corrected for differential extinction (fore- and
background stars excluded, mean extinction
luminosity function corrected for differential extinction (fore- and
background stars excluded, mean extinction
![]() ,
no
incompleteness correction applied). It is shown in
Fig. 9. By comparing the power-law fit (dashed line)
with the data, one can estimate that in the shallow observations used
in this work (in order to avoid saturating the brightest stars) the
completeness drops below 50% already at
,
no
incompleteness correction applied). It is shown in
Fig. 9. By comparing the power-law fit (dashed line)
with the data, one can estimate that in the shallow observations used
in this work (in order to avoid saturating the brightest stars) the
completeness drops below 50% already at
![]() (see also
Table 2).
(see also
Table 2).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13183fg7.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg125.png)
|
Figure 7:
Histogram of the extinction,
|
| Open with DEXTER | |
6 Discussion
For comparison of the derived photometry and extinction with other work, it is important to refer to an effective wavelength, i.e. to take into account such factors as the SED of the stars, extinction, and the filter transmission curves. The measured value of the exponent of the power-law extinction-law is strongly dependent on the effective wavelength (see, e.g., Stead & Hoare 2009; Nishiyama et al. 2006a; Gosling et al. 2009). The transmission curves of the NACO filters are available at the ESO website. In order to facilitate comparison of our work, we have calculated the effective wavelengths for the photometry presented here, using Eq. (A3) of Tokunaga & Vacca (2005).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13183fg8.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg126.png)
|
Figure 8:
Differential extinction corrected
color-magnitude diagram for the GC (assumed mean extinction is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13183fg9.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg127.png)
|
Figure 9:
|
| Open with DEXTER | |
We have found a significantly steeper extinction law at NIR
wavelengths than in earlier work (e.g., Draine 1989; Mathis 1990; Rieke & Lebofsky 1985, see the latter paper
for a review). There
exists, however, very good agreement between the values for
![]() (and
(and
![]() ,
respectively) and
,
respectively) and
![]() (and
(and
![]() ,
respectively) found in this work and the
respective values from other recent research. Gosling et al. (2009)
report
,
respectively) found in this work and the
respective values from other recent research. Gosling et al. (2009)
report
![]() based on NIR observations of the
nuclear bulge. Note that they find variability of this power-law index
along the line-of-sight, on scales as small as 5''. We have not
examined spatial variability of the power-law index in our work. Since
we do not have J-band observations available and since the
extinction law appears to be clearly different between J and
based on NIR observations of the
nuclear bulge. Note that they find variability of this power-law index
along the line-of-sight, on scales as small as 5''. We have not
examined spatial variability of the power-law index in our work. Since
we do not have J-band observations available and since the
extinction law appears to be clearly different between J and ![]() and
and ![]() and L', we cannot determine the extinction-law toward
individual stars or small groups of stars like Gosling et al. (2009).
Nishiyama et al. (2009) find
and L', we cannot determine the extinction-law toward
individual stars or small groups of stars like Gosling et al. (2009).
Nishiyama et al. (2009) find
![]() and
and
![]() ,
based on NIR observations of the Galactic
nuclear bulge. Stead & Hoare (2009) examined 8 regions from the UKIDDS
Galactic Plane Survey and report
,
based on NIR observations of the Galactic
nuclear bulge. Stead & Hoare (2009) examined 8 regions from the UKIDDS
Galactic Plane Survey and report
![]() .
These values agree with our results within the
.
These values agree with our results within the ![]() - combined
statistical and systematic - uncertainties. An exception is the value
- combined
statistical and systematic - uncertainties. An exception is the value
![]() determined from the color dependence of
the RC in the
determined from the color dependence of
the RC in the
![]() vs.
vs. ![]() color-magnitude diagram. Nevertheless,
this error lies within the
color-magnitude diagram. Nevertheless,
this error lies within the ![]() uncertainty of the value
uncertainty of the value
![]() that we have derived in this work from the
RC positions in the
that we have derived in this work from the
RC positions in the ![]() and H luminosity functions. We consider the
latter value more trustworthy because it is more straightforward to
determine (no cutting out of regions from the color-magnitude
diagram), is based on large numbers of stars, and agrees very well with
the recent works cited above.
and H luminosity functions. We consider the
latter value more trustworthy because it is more straightforward to
determine (no cutting out of regions from the color-magnitude
diagram), is based on large numbers of stars, and agrees very well with
the recent works cited above.
The extinction map based on
![]() colors from this work
resembles closely the one presented in Buchholz et al. (2009). The
overall extinction we find in the present work is, however, lower than the
one reported by Buchholz et al. (2009) -
colors from this work
resembles closely the one presented in Buchholz et al. (2009). The
overall extinction we find in the present work is, however, lower than the
one reported by Buchholz et al. (2009) -
![]() compared to
compared to
![]() .
The reason for this difference is
the assumption of a flatter extinction law (based
on Draine 1989) in Buchholz et al. (2009). The extinction map
presented by Schödel et al. (2007a) is also similar to the one
presented here, but shows a smaller FOV and is also based on a
different extinction law. Agreement can also be seen between the
extinction map produced in this work and the one presented by
Scoville et al. (2003). The map in the latter paper encompasses a
much larger region, but is less homogeneous than the one produced here
because it is derived from the line emission of ionized gas. Due to
the strong radio emission from Sagittarius A* the latter authors
could not reliably constrain the extinction in the immediate
surroundings of Sagittarius A*. Scoville et al. (2003) used an
extinction-law of the form
.
The reason for this difference is
the assumption of a flatter extinction law (based
on Draine 1989) in Buchholz et al. (2009). The extinction map
presented by Schödel et al. (2007a) is also similar to the one
presented here, but shows a smaller FOV and is also based on a
different extinction law. Agreement can also be seen between the
extinction map produced in this work and the one presented by
Scoville et al. (2003). The map in the latter paper encompasses a
much larger region, but is less homogeneous than the one produced here
because it is derived from the line emission of ionized gas. Due to
the strong radio emission from Sagittarius A* the latter authors
could not reliably constrain the extinction in the immediate
surroundings of Sagittarius A*. Scoville et al. (2003) used an
extinction-law of the form
![]() ,
significantly different from what is found here and in other recent
work on this subject.
,
significantly different from what is found here and in other recent
work on this subject.
A caveat may apply to the regions with the strongest extinction.
As can be seen in Fig. 1, there are some regions
(e.g. at an offset of ![]() +12'' E and
+12'' E and ![]() -13'' S of Sagittarius A*)
with very high extinction and consequently few stars. Extinction may
be under-estimated by our method in these patches of extremely high
extinction because the number of stars that can be detected behind a
strong extinction screen may be very small.
-13'' S of Sagittarius A*)
with very high extinction and consequently few stars. Extinction may
be under-estimated by our method in these patches of extremely high
extinction because the number of stars that can be detected behind a
strong extinction screen may be very small.
Finally, useful for analyses of the so-called ``S-cluster'' of stars
that are tightly bound to Sagittarius A* and of the NIR emission of
Sgr A* itself, we can use the extinction map presented in
Fig. 6 to calculate the mean extinction and its
standard deviation toward Sagittarius A*. For a circular region with
a radius of 0.5'' centered on Sagittarius A* we obtain
![]() ,
,
![]() ,
and
,
and
![]() .
The uncertainty of
.
The uncertainty of
![]() corresponds to the standard deviation of extinction within the
circular aperture. The uncertainties for
corresponds to the standard deviation of extinction within the
circular aperture. The uncertainties for
![]() and
and
![]() include additionally the uncertainties of
include additionally the uncertainties of
![]() and
and
![]() .
These extinction values are different from the
ones that have typically been used in the analysis of NIR
lightcurves from Sgr A*, e.g., AH=4.3, AK=2.8,
AL'=1.8(Eckart et al. 2006; Genzel et al. 2003), AK=3.3 (Do et al. 2009b), or
AL'=1.8 (Ghez et al. 2004). While the impact on
emission/accretion models of Sgr A* will probably be minor, we point
out that the new extinction values at
.
These extinction values are different from the
ones that have typically been used in the analysis of NIR
lightcurves from Sgr A*, e.g., AH=4.3, AK=2.8,
AL'=1.8(Eckart et al. 2006; Genzel et al. 2003), AK=3.3 (Do et al. 2009b), or
AL'=1.8 (Ghez et al. 2004). While the impact on
emission/accretion models of Sgr A* will probably be minor, we point
out that the new extinction values at ![]() and L' imply that the
de-reddened emission from Sgr A* may be weaker than assumed by a
factor 1.4-2.2 at
and L' imply that the
de-reddened emission from Sgr A* may be weaker than assumed by a
factor 1.4-2.2 at ![]() and a factor of
and a factor of ![]() 1.7 at L'.
1.7 at L'.
A correct estimate of the extinction is crucial to address one of the
long standing issues in the central parsec, namely the apparent
incompatibility between the ionizing flux arising from the massive
stars and the ionisation of the gas
(Najarro et al. 1997; Lutz 1999). Further, these authors found that
the population of HeI stars, displaying fairly large luminosities was
unusually high. Such incompatibility was recently claimed to be
solved by Martins et al. (2007) with the inclusion of line-blanketing
in the models, leading to lower bolometric luminosities and lower UV
fluxes for the HeI stars. However, we attribute most of the
discrepancy between the results of Najarro et al. (1997) and
Martins et al. (2007) for the HeI stars to the estimate of AKbetween both investigations. Indeed, the final AK values computed
by Najarro et al. (1997) were 50% larger than the ones adopted by
Martins et al. (2007) from the extinction map of
Schödel et al. (2007a). Such difference was translated into roughly
one magnitude in luminosity and was responsible for the much lower
luminosity of the HeI stars revised by Martins et al. (2007).
Similarly, the nature of the ``S'' stars is also affected. While
Martins et al. (2008) adopted
AK=2.25 for S2 it turns out that
the extinction map they used was calibrated on S2 with an
AK =
2.8 Schödel et al. (2007a). That would have changed S2 from being a
dwarf to being a giant. It turns out that the actual value of
![]() toward S2 is not too different from the value assumed
(erroneously) by Martins et al. (2008). As we show in this work, and
as other similar recent investigation has shown, the solution and key
to these problems is that the power-law slope of the NIR extinction
law is significantly steeper than what was assumed in earlier work. This
leads to lower extinction in the K-band, but significantly stronger
extinction at shorter wavelengths.
toward S2 is not too different from the value assumed
(erroneously) by Martins et al. (2008). As we show in this work, and
as other similar recent investigation has shown, the solution and key
to these problems is that the power-law slope of the NIR extinction
law is significantly steeper than what was assumed in earlier work. This
leads to lower extinction in the K-band, but significantly stronger
extinction at shorter wavelengths.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13183fg10.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg140.png)
|
Figure 10:
Ilustration of the relation between
the stars detected at |
| Open with DEXTER | |
In Fig. 10 we show a color composite image of the
stars, detected at ![]() ,
the
,
the
![]() extinction, and the MIR (PAH I)
emission (data from Schödel et al. 2007b). It can be seen how the
extinction is low in a region running roughly from SW to NE. This
creates an apparent high stellar density and therefore elongation of
the NSC along the galactic plane (as was also shown
by Schödel et al. 2007a). Similarly, the lower extinction to the NW of
Sgr A* is responsible for the higher stellar density observed in that
region. The strong influence that extinction has on the appearance of
the nuclear star cluster can also be nicely seen in Fig. 1 of Scoville et al. (2003).
There appears to be no obvious relation between the warm dust
emitting in the mid-infrared and the extinction. This is no surprise
because the surface density of HI and H2 and the warm dust
associated with it in the mini-spiral is just of the order a few
extinction, and the MIR (PAH I)
emission (data from Schödel et al. 2007b). It can be seen how the
extinction is low in a region running roughly from SW to NE. This
creates an apparent high stellar density and therefore elongation of
the NSC along the galactic plane (as was also shown
by Schödel et al. 2007a). Similarly, the lower extinction to the NW of
Sgr A* is responsible for the higher stellar density observed in that
region. The strong influence that extinction has on the appearance of
the nuclear star cluster can also be nicely seen in Fig. 1 of Scoville et al. (2003).
There appears to be no obvious relation between the warm dust
emitting in the mid-infrared and the extinction. This is no surprise
because the surface density of HI and H2 and the warm dust
associated with it in the mini-spiral is just of the order a few
![]() cm-3 (see, e.g., discussion of this topic
in Moultaka et al. 2009). The extinction toward the GC is largely
produced by clouds in the foreground, with the possible exception of
some dust-enshrouded individual objects (Moultaka et al. 2009).
cm-3 (see, e.g., discussion of this topic
in Moultaka et al. 2009). The extinction toward the GC is largely
produced by clouds in the foreground, with the possible exception of
some dust-enshrouded individual objects (Moultaka et al. 2009).
For our analysis we have used a weighted average of recent
measurements of the distance to the GC, assuming that all those
measurements are independent. We did not investigate this assumption
in depth. However, we took into account the systematic uncertainties
of the individual measurements when computing the weighted average. As
a further simple test we can use sub-samples of the measurements and
check the resulting values of R0 for consistency. Using only
geometrical estimates
(Gillessen et al. 2009; Reid et al. 2009b,a; Trippe et al. 2008; Ghez et al. 2008)
we obtain
![]() kpc (emitting the
estimate from the S0-2/S2 orbit by Ghez et al. 2008) and
kpc (emitting the
estimate from the S0-2/S2 orbit by Ghez et al. 2008) and
![]() kpc (emitting the estimate from the S0-2/S2 orbit
by Gillessen et al. 2009). Using only measurements based on variable and
RC stars, we obtain
kpc (emitting the estimate from the S0-2/S2 orbit
by Gillessen et al. 2009). Using only measurements based on variable and
RC stars, we obtain
![]() kpc. As an
additional test we computed the unweighted average of all
measurements:
kpc. As an
additional test we computed the unweighted average of all
measurements:
![]() kpc. It agrees within
the uncertainties with the weighted average. If we remove the
measurement with the strongest apparent deviation
(
kpc. It agrees within
the uncertainties with the weighted average. If we remove the
measurement with the strongest apparent deviation
(
![]() kpc, Nishiyama et al. 2006b), we obtain
kpc, Nishiyama et al. 2006b), we obtain
![]() kpc. The unweighted averages of the
sub-sets of distance measurements considered above agree also well
with the weighted results. We therefore believe that the value for
kpc. The unweighted averages of the
sub-sets of distance measurements considered above agree also well
with the weighted results. We therefore believe that the value for
![]() kpc derived in this work and its related
uncertainty can be considered reliable.
kpc derived in this work and its related
uncertainty can be considered reliable.
We believe that future work should focus on deriving the power-law index for the NIR extinction-law toward the GC with higher precision and examine its variability over the central parsecs. This could be achieved, for example, by deep AO imaging using a large number of narrow band filters across the near-infrared. The main limitation for this kind of work may come from the still limited performance of AO systems at short NIR wavelengths (J-band), combined with the long exposure times required by the high extinction. An additional great difficulty, in fact the main source of uncertainty in this work, is the difficulty to obtain precise and accurately calibrated photometry from AO data (crowding, large seeing foot of PSF, spatial variability of PSF). We have, however, no doubt that there will be significant technical progress in AO techniques and related data processing software in the next few years.
7 Summary
We provide photometry for ![]() 7700 point sources extracted from
adaptive optics observations of the central parsec of the Galactic
center in the
7700 point sources extracted from
adaptive optics observations of the central parsec of the Galactic
center in the ![]() ,
and for many of them also in the H and L' bands. The data are made publicly available as electronic
on-line material. Adaptive optics photometry has been published
previously in some papers. However, we believe that the data presented
in this work supersede those earlier results or are complementary to
them because of reasons such as: (a) limited field-of-view of previous
observations or focus on the central few 0.1 pc; (b) isoplanatic
effects were not taken properly into account; (c) bias by the
application of methods such as Lucy-Richardson deconvolution (the
companion paper to this work, by Schoedel, A&A, 2009, accepted for
publication, explains our photometric method and points out the bias
introduced by the Lucy-Richardson method); (d) no transparent
explanation of the photometric calibration. This data set is the most
comprehensive one published so far.
,
and for many of them also in the H and L' bands. The data are made publicly available as electronic
on-line material. Adaptive optics photometry has been published
previously in some papers. However, we believe that the data presented
in this work supersede those earlier results or are complementary to
them because of reasons such as: (a) limited field-of-view of previous
observations or focus on the central few 0.1 pc; (b) isoplanatic
effects were not taken properly into account; (c) bias by the
application of methods such as Lucy-Richardson deconvolution (the
companion paper to this work, by Schoedel, A&A, 2009, accepted for
publication, explains our photometric method and points out the bias
introduced by the Lucy-Richardson method); (d) no transparent
explanation of the photometric calibration. This data set is the most
comprehensive one published so far.
Based on the photometric results, we analyze extinction toward the
central parsec of the GC. Absolute values of extinction in the three
examined bands are derived based on the well-known properties of red
clump stars, without the need to measure stellar colors and without
having to assume an extinction law. The values obtained are
![]() mag,
mag,
![]() mag, and
mag, and
![]() mag. This results in
mag. This results in
![]() .
Assuming the validity of a
power-law extinction law between H and
.
Assuming the validity of a
power-law extinction law between H and ![]() and between
and between ![]() and
L', this is equivalent to power-law indices of
and
L', this is equivalent to power-law indices of
![]() and
and
![]() .
This is
significantly steeper than in earlier work
(e.g. Draine 1989; Rieke & Lebofsky 1985), but agrees with recent
studies of extinction toward the nuclear bulge
(Gosling et al. 2009; Nishiyama et al. 2009) and other targets in the
Galactic plane (Stead & Hoare 2009). We also confirm the flattening of
the extinction law beyond
.
This is
significantly steeper than in earlier work
(e.g. Draine 1989; Rieke & Lebofsky 1985), but agrees with recent
studies of extinction toward the nuclear bulge
(Gosling et al. 2009; Nishiyama et al. 2009) and other targets in the
Galactic plane (Stead & Hoare 2009). We also confirm the flattening of
the extinction law beyond ![]() 3
3 ![]() m (see
also Lutz et al. 1996; Flaherty et al. 2007; Indebetouw et al. 2005; Viehmann et al. 2005; Nishiyama et al. 2009).
m (see
also Lutz et al. 1996; Flaherty et al. 2007; Indebetouw et al. 2005; Viehmann et al. 2005; Nishiyama et al. 2009).
Based on
![]() colors of the stars, we provide a detailed
extinction map for a FOV of
colors of the stars, we provide a detailed
extinction map for a FOV of
![]() (
(![]() 1.5
1.5
![]() )
centered roughly on Sagittarius A*. The
spatial resolution of the map is
)
centered roughly on Sagittarius A*. The
spatial resolution of the map is ![]() 1''. Both statistical and
systematic uncertainties of the extinction map are smaller than
10%. The extinction map is made publicaly available as
electronic on-line material. We find that extinction varies
significantly on arcsecond scales. The mean extinction based on
stellar colors is found to be
1''. Both statistical and
systematic uncertainties of the extinction map are smaller than
10%. The extinction map is made publicaly available as
electronic on-line material. We find that extinction varies
significantly on arcsecond scales. The mean extinction based on
stellar colors is found to be
![]() mag, in good
agreement with the value of mean extinction based on the RC method. An
extinction map based on
mag, in good
agreement with the value of mean extinction based on the RC method. An
extinction map based on
![]() colors, although less accurate because
of lower point source surface density and possible contamination by
diffuse emission from dust in the mini-spiral, confirms the patterns
seen in the extinction map based on
colors, although less accurate because
of lower point source surface density and possible contamination by
diffuse emission from dust in the mini-spiral, confirms the patterns
seen in the extinction map based on
![]() colors. Requiring the mean
extinction between the two maps to be the same, we derive
colors. Requiring the mean
extinction between the two maps to be the same, we derive
![]() ,
in excellent agreement with the value of
this parameter derived from the mean magnitudes of the RC bump (see
above).
,
in excellent agreement with the value of
this parameter derived from the mean magnitudes of the RC bump (see
above).
Applying the derived extinction map to the observed
![]() colors
of the stars, we are able to correct the corresponding
color-magnitude diagram. This reduces the scatter in the diagram
considerably and makes it possible to distinguish between stars in the giant
branch and young, massive stars. We confirm recent findings of the presence of
of young, massive stars at projected distances >0.5 pc from
Sagittarius A*.
colors
of the stars, we are able to correct the corresponding
color-magnitude diagram. This reduces the scatter in the diagram
considerably and makes it possible to distinguish between stars in the giant
branch and young, massive stars. We confirm recent findings of the presence of
of young, massive stars at projected distances >0.5 pc from
Sagittarius A*.
A minor, but very interesting by-product of this work is a weighted
average of recent (years 2006-2009) estimates of R0. We find that
the distance of the GC is constrained with an uncertainty of just 2%:
![]() kpc.
kpc.
For a circular region with a radius of 0.5'' centered on
Sagittarius A* we obtain
![]() ,
,
![]() ,
and
,
and
![]() .
These values
imply that the NIR emission from Sgr A* in the
.
These values
imply that the NIR emission from Sgr A* in the ![]() and L'-bands
may be weaker than previously assumed, by factors 1.4-2.2.
and L'-bands
may be weaker than previously assumed, by factors 1.4-2.2.
We have used the following effective wavelengths in this work:
![]() m,
m,
![]() m,
and
m,
and
![]() m. Note that the
effective wavelength is a complex function of the transmission
functions of the atmosphere, the filter, the optical system,
extinction, and stellar type. For discussions of this problem,
see, for example, Espinoza et al. (2009) and Stead & Hoare (2009).
The uncertainties cited for the effective
wavelengths are based on best-estimates of the variablity of these
values for the case of Galactic center observations and the observing
conditions and instruments used in this work.
m. Note that the
effective wavelength is a complex function of the transmission
functions of the atmosphere, the filter, the optical system,
extinction, and stellar type. For discussions of this problem,
see, for example, Espinoza et al. (2009) and Stead & Hoare (2009).
The uncertainties cited for the effective
wavelengths are based on best-estimates of the variablity of these
values for the case of Galactic center observations and the observing
conditions and instruments used in this work.
R.S. acknowledges the Ramón y Cajal programme of the Spanish Ministerio de Ciencia e Innovación (MICINN) and support by the MICINN project AYA2007-64052. We thank the anonymous referee for his helpful comments. We are grateful to Andrea Ghez and her group at UCLA for providing detailed comments on this work.
Appendix A: Effective wavelength
Table A.1:
Effective wavelengths in units of ![]() m for the NACO H,
m for the NACO H,
![]() ,
and L' filters for blackbodies with different effective temperatures
and extinction,
,
and L' filters for blackbodies with different effective temperatures
and extinction,
![]() .
.
Table A.2:
List of detected point sources in the
NACO H, ![]() ,
and L'-band observations. We only include the
first ten lines of the table in the printed edition of this work.
,
and L'-band observations. We only include the
first ten lines of the table in the printed edition of this work.
We calculated the effective wavelengths of our
observations following Eq. (A3) of Tokunaga & Vacca (2005). The
transmission curves for the NACO H and ![]() filters were downloaded
from the instrument web site
filters were downloaded
from the instrument web site![]() .
Spectra of the atmospheric transmission were downloaded from the Gemini
telescope web site
.
Spectra of the atmospheric transmission were downloaded from the Gemini
telescope web site![]() . They are
based on models with the ATRAN software (Lord 1992). The
transmission curves for 3 mm precipitable water vapor were used
because humidity was high during the H and
. They are
based on models with the ATRAN software (Lord 1992). The
transmission curves for 3 mm precipitable water vapor were used
because humidity was high during the H and ![]() observations.
observations.
We did not use any particular stellar atmosphere model for the
calculations. Instead, simple extincted blackbody models were used.
Table A.1 lists the values of the effective
wavelength for various values of AK and effective temperatures of
the blackbodies. A power-law
![]() (Nishiyama et al. 2009) was used to calculate the extinction at
different wavelengths. We assumed
(Nishiyama et al. 2009) was used to calculate the extinction at
different wavelengths. We assumed
![]() for the
extinction between H and
for the
extinction between H and ![]() , and
, and
![]() for the
extinction between
for the
extinction between ![]() and L'
and L'![]() . The majority (>90%) of stars in the images analyzed in this work are of late-type, with a large
percentage of RC stars (see, e.g., Buchholz et al. 2009). We
therefore adopt as effective wavelengths
. The majority (>90%) of stars in the images analyzed in this work are of late-type, with a large
percentage of RC stars (see, e.g., Buchholz et al. 2009). We
therefore adopt as effective wavelengths
![]() m,
m,
![]() m, and
m, and
![]() m for an average extinction of
m for an average extinction of
![]() .
.
The uncertainty introduced by the choice for the amount of
precipitable water vapor is low. Choosing 1.6 mm instead of 3.0 mm will
change the effective wavelengths by ![]() 0.003
0.003 ![]() m for H,
m for H, ![]() 0.001
0.001 ![]() m
for
m
for ![]() ,
and
,
and ![]() 0.01
0.01 ![]() m for L'. Changing the power-law index for
the extinction curve between H and
m for L'. Changing the power-law index for
the extinction curve between H and ![]() to
to
![]() (Nishiyama et al. 2009) results in a change of
(Nishiyama et al. 2009) results in a change of ![]() 0.003
0.003 ![]() m for
m for
![]() ,
and
,
and ![]() 0.009
0.009 ![]() m for
m for
![]() .
Changing the
power-law index for the extinction curve between
.
Changing the
power-law index for the extinction curve between ![]() and L' to
and L' to
![]() (Nishiyama et al. 2009) results in a change of <0.001
(Nishiyama et al. 2009) results in a change of <0.001 ![]() m for
m for
![]() .
The uncertainty in extinction introduces an
uncertainty of
.
The uncertainty in extinction introduces an
uncertainty of ![]() 0.015
0.015 ![]() m for H,
m for H, ![]() 0.01
0.01 ![]() m for
m for
![]() ,
and
,
and ![]() 0.002
0.002 ![]() m for L'. The
unknown effective temperature of the stars introduces uncertainties of
m for L'. The
unknown effective temperature of the stars introduces uncertainties of
![]() 0.005
0.005 ![]() m for H,
m for H, ![]() 0.006
0.006 ![]() m for
m for ![]() ,
and
,
and
![]() 0.001
0.001 ![]() m for L'.
m for L'.
We estimate the combined 1![]() uncertainty of the effective
wavelengths to 0.018
uncertainty of the effective
wavelengths to 0.018 ![]() m for H, 0.012
m for H, 0.012 ![]() m for
m for ![]() ,
and
,
and
![]() m for L'.
m for L'.
References
- Alves, D. R. 2000, ApJ, 539, 732
- Bartko, H., Martins, F., Fritz, T. K., et al. 2009, ApJ, 697, 1741
- Böker, T. 2008, J. Phys. Conf. Ser., 131, 012043
- Buchholz, R. M., Schödel, R., & Eckart, A. 2009, A&A, 499, 483
- Castellani, V., Chieffi, A., & Straniero, O. 1992, ApJS, 78, 517
- Cox, A. N. (ed.) 2000, Allen's astrophysical quantities
- Devillard, N. 1997, The Messenger, 87, 19
- Diolaiti, E., Bendinelli, O., Bonaccini, D., et al. 2000, in SPIE Conf. Ser. 4007, ed. P. L. Wizinowich, 879
- Do, T., Ghez, A. M., Morris, M. R., et al. 2009a, ApJ, 703, 1323
- Do, T., Ghez, A. M., Morris, M. R., et al. 2009b, ApJ, 691, 1021
- Draine, B. T. 1989, in Infrared Spectroscopy in Astronomy, ed. E. Böhm-Vitense, ESA SP-290, 93
- Eckart, A., Baganoff, F. K., Schödel, R., et al. 2006, A&A, 450, 535
- Eisenhauer, F., Quirrenbach, A., Zinnecker, H., & Genzel, R. 1998, ApJ, 498, 278
- Eisenhauer, F., Genzel, R., Alexander, T., et al. 2005, ApJ, 628, 246
- Espinoza, P., Selman, F. J., & Melnick, J. 2009, A&A, 501, 563
- Flaherty, K. M., Pipher, J. L., Megeath, S. T., et al. 2007, ApJ, 663, 1069
- Genzel, R., Schödel, R., Ott, T., et al. 2003, Nature, 425, 934
- Ghez, A. M., Wright, S. A., Matthews, K., et al. 2004, ApJ, 601, L159
- Ghez, A. M., Salim, S., Weinberg, N. N., et al. 2008, ApJ, 689, 1044
- Gillessen, S., Eisenhauer, F., Trippe, S., et al. 2009, ApJ, 692, 1075
- Gosling, A. J., Blundell, K. M., & Bandyopadhyay, R. 2006, ApJ, 640, L171
- Gosling, A. J., Bandyopadhyay, R. M., & Blundell, K. M. 2009, MNRAS, 394, 2247
- Grocholski, A. J., & Sarajedini, A. 2002, AJ, 123, 1603
- Groenewegen, M. A. T. 2008, A&A, 488, 935
- Groenewegen, M. A. T., Udalski, A., & Bono, G. 2008, A&A, 481, 441
- Harayama, Y., Eisenhauer, F., & Martins, F. 2008, ApJ, 675, 1319
- Indebetouw, R., Mathis, J. S., Babler, B. L., et al. 2005, ApJ, 619, 931
- Lord, S. 1992, Tech. Rep.
- Lu, J. R., Ghez, A. M., Hornstein, S. D., et al. 2009, ApJ, 690, 1463
- Lutz, D. 1999, in The Universe as Seen by ISO, ed. P. Cox, & M. Kessler, ESA SP-427, 623
- Lutz, D., Feuchtgruber, H., Genzel, R., et al. 1996, A&A, 315, L269
- Maness, H., Martins, F., Trippe, S., et al. 2007, ApJ, 669, 1024
- Martins, F., Genzel, R., Hillier, D. J., et al. 2007, A&A, 468, 233
- Martins, F., Gillessen, S., Eisenhauer, F., et al. 2008, ApJ, 672, L119
- Mathis, J. S. 1990, ARA&A, 28, 37
- Matsunaga, N., Kawadu, T., Nishiyama, S., et al. 2009, MNRAS, 399, 1709
- Moultaka, J., Eckart, A., & Schödel, R. 2009, ApJ, 703, 1635
- Najarro, F., Krabbe, A., Genzel, R., et al. 1997, A&A, 325, 700
- Nishiyama, S., Nagata, T., Baba, D., et al. 2005, ApJ, 621, L105
- Nishiyama, S., Nagata, T., Kusakabe, N., et al. 2006a, ApJ, 638, 839
- Nishiyama, S., Nagata, T., Sato, S., et al. 2006b, ApJ, 647, 1093
- Nishiyama, S., Nagata, T., Tamura, M., et al. 2008, ApJ, 680, 1174
- Nishiyama, S., Tamura, M., Hatano, H., et al. 2009, ApJ, 696, 1407
- Paumard, T., Genzel, R., Martins, F., et al. 2006, ApJ, 643, 1011
- Reid, M. J., Menten, K. M., Zheng, X. W., et al. 2009a, ApJ, 700, 137
- Reid, M. J., Menten, K. M., Zheng, X. W., Brunthaler, A., & Xu, Y. 2009b, ApJ, 705, 1548
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618
- Schödel, R. 2010, A&A, 509, A58
- Schödel, R., Eckart, A., Alexander, T., et al. 2007a, A&A, 469, 125
- Schödel, R., Eckart, A., Muzic, K., et al. 2007b, A&A, 462, L1
- Schödel, R., Merritt, D., & Eckart, A. 2009, A&A, 502, 91
- Scoville, N. Z., Stolovy, S. R., Rieke, M., Christopher, M., & Yusef-Zadeh, F. 2003, ApJ, 594, 294
- Seth, A. C., Blum, R. D., Bastian, N., Caldwell, N., & Debattista, V. P. 2008, ApJ, 687, 997
- Stead, J. J., & Hoare, M. G. 2009, MNRAS, 400, 731
- Sumi, T. 2004, MNRAS, 349, 193
- Tokunaga, A. T., & Vacca, W. D. 2005, PASP, 117, 421
- Trippe, S., Gillessen, S., Gerhard, O. E., et al. 2008, A&A, 492, 419
- Udalski, A. 2003, ApJ, 590, 284
- Viehmann, T., Eckart, A., Schödel, R., et al. 2005, A&A, 433, 117
- Wozniak, P. R., & Stanek, K. Z. 1996, ApJ, 464, 233
Footnotes
- ... Galaxy
![[*]](/icons/foot_motif.png)
- Full Table A.2 is only available in
electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via
http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/511/A18
The extinction map shown in the top left of Fig. 6 can be obtained in electronic form at the same site. - ... telescope 4
![[*]](/icons/foot_motif.png)
- Based on observations made with ESO Telescopes at the La Silla or Paranal Observatories under programmes ID 077.B-0014 and 081.B-0648.
- ... Database
![[*]](/icons/foot_motif.png)
- http://archive.eso.org/asm/ambient-server?site=paranal
- ... site
![[*]](/icons/foot_motif.png)
- http://www.eso.org/sci/facilities/paranal/instruments/naco/index.html
- ... site
![[*]](/icons/foot_motif.png)
- http://www.gemini.edu/node/10781?q=node/10789
- ...'
![[*]](/icons/foot_motif.png)
- This value of
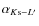 is from a preliminary estimate at the beginning of
this work and is smaller than the value
is from a preliminary estimate at the beginning of
this work and is smaller than the value
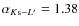 that
we derived in the end. However, the associated change of
that
we derived in the end. However, the associated change of
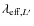 is minimal, see discussion of the uncertainties in the next paragraph.
is minimal, see discussion of the uncertainties in the next paragraph.
All Tables
Table 1: Details of the imaging observations used in this work.
Table 2: Completeness levels in percent for given bands andmagnitudes.
Table A.1:
Effective wavelengths in units of ![]() m for the NACO H,
m for the NACO H,
![]() ,
and L' filters for blackbodies with different effective temperatures
and extinction,
,
and L' filters for blackbodies with different effective temperatures
and extinction,
![]() .
.
Table A.2:
List of detected point sources in the
NACO H, ![]() ,
and L'-band observations. We only include the
first ten lines of the table in the printed edition of this work.
,
and L'-band observations. We only include the
first ten lines of the table in the printed edition of this work.
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13183fg1.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg43.png)
|
Figure 1:
Mosaic image of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13183fg2.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg46.png)
|
Figure 2: Mosaic image of the L'-band observations. North is up and east is to the left. Offsets are given in arcseconds from Sgr A*. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{13183fg3.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg47.png)
|
Figure 3:
Statistical photometric uncertainty vs. magnitude
for the H- ( top), |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13183fg4.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg64.png)
|
Figure 4:
Color-magnitude diagrams, with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13183fg5.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg99.png)
|
Figure 5:
Peak |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{13183fg6.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg106.png)
|
Figure 6:
Top left: map of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13183fg7.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg125.png)
|
Figure 7:
Histogram of the extinction,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13183fg8.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg126.png)
|
Figure 8:
Differential extinction corrected
color-magnitude diagram for the GC (assumed mean extinction is
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13183fg9.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg127.png)
|
Figure 9:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13183fg10.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13183-09/Timg140.png)
|
Figure 10:
Ilustration of the relation between
the stars detected at |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


