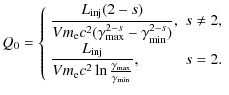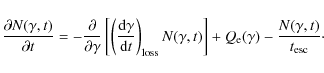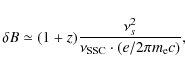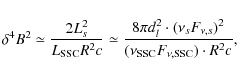| Issue |
A&A
Volume 511, February 2010
|
|
|---|---|---|
| Article Number | A11 | |
| Number of page(s) | 5 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200913035 | |
| Published online | 19 February 2010 | |
Mechanism of very high-energy radiation in BL Lacertae object 3C 66A
(Research Note)
J. Yang1,2,3 - J. Wang1,2
1 - National Astronomical Observatories, Yunnan Observatory, Chinese Academy
of Sciences, Kunming 650011, PR China
2 -
Key Laboratory for the Structure and Evolution of Celestial Objects,
Chinese Academy of Sciences, Kunming 650011, PR China
3 -
Yunnan Agricultural University, Kunming 650201, PR China
Received 31 July 2009 / Accepted 16 November 2009
Abstract
Aims. Our goal is to understand the nature of blazars and the mechanisms for generating high-energy ![]() -rays, through investigation of the blazar 3C 66A.
-rays, through investigation of the blazar 3C 66A.
Methods. We model the high-energy spectrum of 3C 66A, which was
observed recently with the Fermi-LAT and VERITAS telescopes. The
spectrum has a hard change from the energy range of 0.2-100 GeV to
200-500 GeV in recent almost contemporaneous observations of two
telescopes.
Results. The de-absorbed VERITAS spectrum depends strongly on redshift, which is highly uncertain. If z
= 0.444 is adopted, we are able to use the SSC model to produce the
Fermi-LAT component and the EC model to the VERITAS component. However,
if z = 0.1, the intrinsic VERITAS spectrum will be softer, and
there will be a smooth link between the Fermi-LAT and VERITAS spectra
that can be explained using an SSC model.
Key words: BL Lacertae objects: individual: 3C 66A
1 Introduction
Blazars are a peculiar class of active galactic nuclei (AGN), and
their jets point at small angles with respect to our line of sight.
Many of them have been observed at all wavelengths, from radio to
very high energy (VHE) ![]() -rays. Their spectral energy
distribution (SED) consists of two bumps that are attributed to the
synchrotron and the inverse Compton (IC) emission of
ultrarelativistic particles. The different soft-photon sources
deduce synchrotron self-Compton (SSC) and external Compton (EC)
models to produce high-energy emission. In the SSC model, the soft
photons are provided by the synchrotron emission of the same
electrons (Marscher 1980; Ghisellini & Maraschi 1989;
Marscher & Travis 1996); however, in the EC model, the soft photons
mostly come from the outside of the jet, such as outer disk,
broad-line region (BLR) clouds (etc. Dermer et al. 1993;
Sikora et al. 1994).
-rays. Their spectral energy
distribution (SED) consists of two bumps that are attributed to the
synchrotron and the inverse Compton (IC) emission of
ultrarelativistic particles. The different soft-photon sources
deduce synchrotron self-Compton (SSC) and external Compton (EC)
models to produce high-energy emission. In the SSC model, the soft
photons are provided by the synchrotron emission of the same
electrons (Marscher 1980; Ghisellini & Maraschi 1989;
Marscher & Travis 1996); however, in the EC model, the soft photons
mostly come from the outside of the jet, such as outer disk,
broad-line region (BLR) clouds (etc. Dermer et al. 1993;
Sikora et al. 1994).
In 3C 66A, Miller et al. (1978) give the redshift z=0.444 by a weak Mg II
emission line detection, but it is very uncertain (Bramel et al. 2005).
When 3C 66A is located at z=0.444, its TeV photons will suffer from
the strong pair production absorption of the extragalactic
background light (EBL). After correction by the EBL absorption, TeV
emission presents an inverted intrinsic spectrum (see the Acciari et al. 2009. Figure 2, the de-absorbed photon spectral index is
calculated as
![]() ). In this paper, we take z = 0.444 to
analyze TeV emissive mechanism and discuss the behavior of the
de-absorbed VERITAS spectrum in different redshifts. Generally, 3C
66A is classified as a low-frequency peaked BL Lac object (LBL). The
peak of the low-frequency component of LBLs usually lies in the IR
or optical regime, whereas the peak of high-energy component is
located at several GeV. The luminosity of
). In this paper, we take z = 0.444 to
analyze TeV emissive mechanism and discuss the behavior of the
de-absorbed VERITAS spectrum in different redshifts. Generally, 3C
66A is classified as a low-frequency peaked BL Lac object (LBL). The
peak of the low-frequency component of LBLs usually lies in the IR
or optical regime, whereas the peak of high-energy component is
located at several GeV. The luminosity of ![]() -ray is typically
comparable to or slightly higher than the luminosity of the
synchrotron component. Such as, Joshi & Bottcher (2007) argue that the peak
of the low-frequency component for 3C 66A is located at the optical
regime, and the peak of high-frequency component reaches a multi
MeV-GeV range. However, Perri et al. (2003) reveal that the synchrotron
peak is found between 1015 and 1016 Hz, then 3C 66A is
classified as an intermediate-frequency peaked BL Lac (IBL). From
the X-ray spectrum with the photon spectral index
-ray is typically
comparable to or slightly higher than the luminosity of the
synchrotron component. Such as, Joshi & Bottcher (2007) argue that the peak
of the low-frequency component for 3C 66A is located at the optical
regime, and the peak of high-frequency component reaches a multi
MeV-GeV range. However, Perri et al. (2003) reveal that the synchrotron
peak is found between 1015 and 1016 Hz, then 3C 66A is
classified as an intermediate-frequency peaked BL Lac (IBL). From
the X-ray spectrum with the photon spectral index
![]() (Bottcher et al. 2005; Donato et al. 2005; Foschini et al. 2006),
which might be the tail of the synchrotron emission, 3C 66A is
considered as an IBL in this paper. 3C 66A is observed in radio, IR,
optical, X-rays, and
(Bottcher et al. 2005; Donato et al. 2005; Foschini et al. 2006),
which might be the tail of the synchrotron emission, 3C 66A is
considered as an IBL in this paper. 3C 66A is observed in radio, IR,
optical, X-rays, and ![]() -rays and shows strong luminosity
variations. As described in Bottcher et al. (2005), the object exhibits
several outbursts in the optical band and the variations of
-rays and shows strong luminosity
variations. As described in Bottcher et al. (2005), the object exhibits
several outbursts in the optical band and the variations of
![]() over several days. Until now, the majority
of BL Lacs detected at VHE (very high energy: E > 100 GeV) are
HBLs (high-frequency peaked BL Lacs). Only IBL W Comae
(Acciari et al. 2008), LBL BL Lacertae (Albert et al. 2007), and 3C 279
(Albert et al. 2008) display the potential to enlarge the extragalactic
TeV source. For 3C 66A, the Crimean Astrophysical Observatory report
a 5.1
over several days. Until now, the majority
of BL Lacs detected at VHE (very high energy: E > 100 GeV) are
HBLs (high-frequency peaked BL Lacs). Only IBL W Comae
(Acciari et al. 2008), LBL BL Lacertae (Albert et al. 2007), and 3C 279
(Albert et al. 2008) display the potential to enlarge the extragalactic
TeV source. For 3C 66A, the Crimean Astrophysical Observatory report
a 5.1![]() detection above 900 GeV (Stepanyan et al. 2002).
detection above 900 GeV (Stepanyan et al. 2002).
Recently, VERITAS have carried out 14 h of observations for 3C
66A from September 2007 through January 2008 (hereafter, the
2007-2008 season) and from September through November 2008
(hereafter, the 2008-2009 season), a further 46 h of data were
taken (Acciari et al. 2009). Because of the limited spatial resolution
of Cherenkov telescopes, it is difficult to accurately identify the
emission region. The radio galaxy 3C 66B lies in the same view field
of 3C 66A at a separation of 0.12![]() and is also a plausible
source of VHE radiation (Tavecchio & Ghisellini 2008). The recent detection
by MAGIC favored 3C 66B as VHE source and excluded 3C 66A at an 85%
confidence level (Aliu et al. 2009). However, VERITAS have found that
3C 66A lies 0.01
and is also a plausible
source of VHE radiation (Tavecchio & Ghisellini 2008). The recent detection
by MAGIC favored 3C 66B as VHE source and excluded 3C 66A at an 85%
confidence level (Aliu et al. 2009). However, VERITAS have found that
3C 66A lies 0.01![]() from the fit position, while 3C 66B lies
0.13
from the fit position, while 3C 66B lies
0.13![]() away, and 3C 66A is VHE source. If 3C 66A has a
redshift of z = 0.444, its de-absorbed spectral index is
away, and 3C 66A is VHE source. If 3C 66A has a
redshift of z = 0.444, its de-absorbed spectral index is
![]() showing very hard intrinsic spectrum (Acciari et al. 2009). In the
first three months, the Fermi-LAT Gamma-ray Space Telescope have
observed 3C 66A (Abdo et al. 2009), almost at contemporaneous
observation with VERITAS in the 2008-2009 season. However, very soft
spectrum with the spectral index of
showing very hard intrinsic spectrum (Acciari et al. 2009). In the
first three months, the Fermi-LAT Gamma-ray Space Telescope have
observed 3C 66A (Abdo et al. 2009), almost at contemporaneous
observation with VERITAS in the 2008-2009 season. However, very soft
spectrum with the spectral index of
![]() appears in the
Fermi-LAT observing energy range. The
appears in the
Fermi-LAT observing energy range. The ![]() -ray spectrum suddenly
hardens from 0.2-100 GeV to 200-500 GeV and challenges the one-zone
homogeneous SSC model.
-ray spectrum suddenly
hardens from 0.2-100 GeV to 200-500 GeV and challenges the one-zone
homogeneous SSC model.
In Sect. 2 we present the jet models for application to 3C 66A. We use the observed data to constrain the model parameters in Sect. 3. We finish with discussions and conclusions in Sect. 4. Throughout this paper, we use a soft cosmology with a deceleration factor q0 = 0.5 and a Hubble constant H0 = 75 km s-1 Mpc-1.
2 The models
We use a public model of Georganopoulos et al. (2007)![]() to describe the
observed spectrum of 3C 66A. The emission region is assumed to be a
sphere (blob) with radius R, permeated by a homogeneous magnetic
field B. The blob moves with bulk Lorentz factor
to describe the
observed spectrum of 3C 66A. The emission region is assumed to be a
sphere (blob) with radius R, permeated by a homogeneous magnetic
field B. The blob moves with bulk Lorentz factor ![]() through
an external photon field with a black body spectrum, at an angle
through
an external photon field with a black body spectrum, at an angle
![]() (in this work
(in this work
![]() is assumed) with
respect to the line of sight, and has a Doppler factor
is assumed) with
respect to the line of sight, and has a Doppler factor
![]() .
The relativistic electrons are continuously injected into
the blob at a rate
.
The relativistic electrons are continuously injected into
the blob at a rate
![]() [cm-3 s-1]
between
[cm-3 s-1]
between
![]() and
and
![]() ,
where
,
where
![]() is the minimum Lorentz factor of the injected
electrons and should not be confused with the minimum Lorentz factor
of the emitting particles. The injection correspond to a luminosity
is the minimum Lorentz factor of the injected
electrons and should not be confused with the minimum Lorentz factor
of the emitting particles. The injection correspond to a luminosity
![]() ,
,
Where
The time-dependent evolution of the electron population
![]() [cm-3] inside the emission region is governed by
[cm-3] inside the emission region is governed by
Here,
The energy loss rates of electrons caused by the synchrotron are
given by
![]() ,
where
,
where
![]() is the magnetic
energy density. The energy loss rates of inverse Compton emission,
is the magnetic
energy density. The energy loss rates of inverse Compton emission,
![]() ,
have excellent analytical expressions for the
Thomson regime
,
have excellent analytical expressions for the
Thomson regime ![]() and for the deep Klein-Nishina (KN) regime
and for the deep Klein-Nishina (KN) regime
![]() ,
but do not have ones for the middle regime of
,
but do not have ones for the middle regime of
![]() (where
(where ![]() is the energy of the incoming
photon in units of the electron rest mass). To overcome this,
Georganopoulos et al. (2007)
modifies an analytical approximation used by
Moderski et al. (2005):
is the energy of the incoming
photon in units of the electron rest mass). To overcome this,
Georganopoulos et al. (2007)
modifies an analytical approximation used by
Moderski et al. (2005):
![]() ,
where
,
where ![]() is
the energy density of seed photons including synchrotron photons and
external photons (such as the reprocessed photons by broad line
region (BLR) Sikora et al. 1994),
is
the energy density of seed photons including synchrotron photons and
external photons (such as the reprocessed photons by broad line
region (BLR) Sikora et al. 1994),
![]() is given by
Moderski et al. (2005). In this paper, the latter photons are assumed to
be a blackbody radiation with peak frequency
is given by
Moderski et al. (2005). In this paper, the latter photons are assumed to
be a blackbody radiation with peak frequency
![]() and
energy density
and
energy density
![]() (all seen in the observer frame). For
the beaming of the EC emission, we use the recipe of
Georganopoulos et al. (2001).
(all seen in the observer frame). For
the beaming of the EC emission, we use the recipe of
Georganopoulos et al. (2001).
3 Modeling parameters
First of all, we use the observed quantities to estimate the physical parameters in the blob, and then use these values to reproduce the observed SED. Mastichiadis & Kirk (1997) and Konopelko et al. (2003) have estimated the parameter relations of the inverse Compton scattering in the Klein-Nishina regime in a homogeneous SSC scenario. However, Paggi et al. (2009) find that the simple relations of parameters in Thomson regime satisfy the observations of LBL or IBL sources and that the relations in the extreme KN limit are not suited to HBLs, indicating that the inverse Compton scattering for HBLs just borders the KN regime. For 3C 66A, the Fermi-LAT spectra showing flat and rising shapes and higher energy observations of VERITAS both indicate that the IC scattering of Fermi-LAT spectra are not likely to enter into the Klein-Nishina regime. Therefore, we assume that the Fermi-LAT spectrum just covers the peak of SSC emission, so use the parameter relations in Thomson regime to rudely estimate the parameters. In fact, we consider the Klein-Nishina effect in producing the high-energy spectra.
The size of the emitting region, R, can be constrained by
measurements of variability time scales, i.e.
![]() .
The observations of VERITAS have shown the
variability to be on a time scale of days (Acciari et al. 2009). The
multiwave campaign of 3C 66A by the Whole Earth Blazar Telescope
(WEBT) in 2007-2008 has observed several bright flares on time
scales of
.
The observations of VERITAS have shown the
variability to be on a time scale of days (Acciari et al. 2009). The
multiwave campaign of 3C 66A by the Whole Earth Blazar Telescope
(WEBT) in 2007-2008 has observed several bright flares on time
scales of ![]() 10 days (Bottcher et al. 2005). These observations
suggest that the size of the emitting region is about 1016 cm if
we assume
10 days (Bottcher et al. 2005). These observations
suggest that the size of the emitting region is about 1016 cm if
we assume ![]() is close to 10. From the peak frequencies of
synchrotron and inverse Compton radiation, we can estimate the
is close to 10. From the peak frequencies of
synchrotron and inverse Compton radiation, we can estimate the
![]() (i.e. the Lorentz factor of the electrons emitting
at the peaks of the synchrotron and SSC components) as
(Tavecchio et al. 1998)
(i.e. the Lorentz factor of the electrons emitting
at the peaks of the synchrotron and SSC components) as
(Tavecchio et al. 1998)
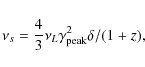
|
(3) |
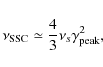
|
(4) |
and we obtain
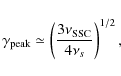
|
(5) |
and
where
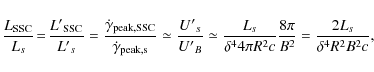
|
(7) |
we have
where Ls and
Table 1: Parameters for the SSC+EC or SSC model used to reproduce the SED (Figs. 1 and 3).
The steady state distribution of emitting electrons is given by
![\begin{displaymath}N(\gamma) = \frac{\int [Q_{\rm e}(\gamma)- N({\gamma})/t_{\rm esc}]
{\rm d}\gamma}{\dot\gamma }\cdot
\end{displaymath}](/articles/aa/full_html/2010/03/aa13035-09/img75.png)
|
(9) |
What is the criterion for steady state? The code of Georganopoulos et al. (2007) first takes a time step equal to the cooling time of the lowest energy electrons under the synchrotron and external Compton losses, and then calculates
We emphasize the selection of the spectral index s of injected
electrons. Based on the X-ray photon spectral index of
![]() (Bottcher et al. 2005;
Donato et al. 2005; Foschini et al. 2006), we deduce the spectral index of
emitting electrons to be 4. Assuming the observed X-rays to be from
synchrotron emission of the cooled electrons, the spectral index of
the injected electrons is given by s=3. Celotti & Ghisellini (2008) adopt
s=3.6 to model the SED of 3C 66A. Therefore, we use
(Bottcher et al. 2005;
Donato et al. 2005; Foschini et al. 2006), we deduce the spectral index of
emitting electrons to be 4. Assuming the observed X-rays to be from
synchrotron emission of the cooled electrons, the spectral index of
the injected electrons is given by s=3. Celotti & Ghisellini (2008) adopt
s=3.6 to model the SED of 3C 66A. Therefore, we use ![]() to
model the observed data. The particle injection, radiative cooling,
and escape from the emission region might yield a temporary
quasi-equilibrium state described by a broken power law. The balance
between escape and radiative cooling will lead to a break in the
equilibrium particle distribution at a break Lorentz factor
to
model the observed data. The particle injection, radiative cooling,
and escape from the emission region might yield a temporary
quasi-equilibrium state described by a broken power law. The balance
between escape and radiative cooling will lead to a break in the
equilibrium particle distribution at a break Lorentz factor
![]() ,
where
,
where
![]() .
The cooling time
scale is evaluated taking synchrotron, SSC, and EC cooling into
account. Depending on whether
.
The cooling time
scale is evaluated taking synchrotron, SSC, and EC cooling into
account. Depending on whether
![]() is greater than or less
than
is greater than or less
than
![]() ,
the system will be in the slow-cooling or
fast-cooling regime. In the fast-cooling regime (
,
the system will be in the slow-cooling or
fast-cooling regime. In the fast-cooling regime (
![]() ), the equilibrium distribution will be a broken power
law with
), the equilibrium distribution will be a broken power
law with
![]() for
for
![]() and
and
![]() for
for
![]() .
In the slow-cooling regime
(
.
In the slow-cooling regime
(
![]() ), the equilibrium distribution will be
), the equilibrium distribution will be
![]() for
for
![]() ,
,
![]() for
for
![]() ,
and
,
and
![]() for
for
![]() .
Since for thin synchrotron emission, the
energy spectral index is related to that of the emitting electrons
as
.
Since for thin synchrotron emission, the
energy spectral index is related to that of the emitting electrons
as
![]() ,
where q is the spectral index of the
emitting electron distribution, and can immediately be seen that the
peak in the
,
where q is the spectral index of the
emitting electron distribution, and can immediately be seen that the
peak in the
![]() spectrum occurs where q=3. When s>3 (in
this work s=3.4 and 3.3 are adopted),
spectrum occurs where q=3. When s>3 (in
this work s=3.4 and 3.3 are adopted),
![]() (the minimum
Lorentz factor of the injected electrons) almost corresponds to
(the minimum
Lorentz factor of the injected electrons) almost corresponds to
![]() (Ghisellini et al. 1998, 2002). Another input parameter,
(Ghisellini et al. 1998, 2002). Another input parameter,
![]() ,
presents the balance between the acceleration and
cooling and has a low impact upon the SED. It is usually taken to be
105-107 (Inoue & Takahara 1996).
,
presents the balance between the acceleration and
cooling and has a low impact upon the SED. It is usually taken to be
105-107 (Inoue & Takahara 1996).
Considering the EC emission of electrons, we need to estimate
![]() and
and
![]() by mainly considering the soft photons
reprocessed by the BLR. Usually
by mainly considering the soft photons
reprocessed by the BLR. Usually
![]() is considered to be
around optical-UV wavebands, so we let
is considered to be
around optical-UV wavebands, so we let
![]() Hz. The
Hz. The
![]() of FSRQ is easily estimated from emission
line spectra or UV-excesses, while it is difficult to estimate the
of FSRQ is easily estimated from emission
line spectra or UV-excesses, while it is difficult to estimate the
![]() of BL Lacs. Assuming the luminosity of the accretion disk
to be
of BL Lacs. Assuming the luminosity of the accretion disk
to be
![]() erg s-1, which is more than the
jet luminosity and does not produce a blue bump in the simulated SED
(Joshi & Bottcher 2007). Taking
erg s-1, which is more than the
jet luminosity and does not produce a blue bump in the simulated SED
(Joshi & Bottcher 2007). Taking
![]() cm
(Tavecchio & Ghisellini 2008), we get the upper limit
cm
(Tavecchio & Ghisellini 2008), we get the upper limit
![]() erg cm-3, assuming the reprocessing efficiency of
the BLR to be 0.1. In this work, we estimate
erg cm-3, assuming the reprocessing efficiency of
the BLR to be 0.1. In this work, we estimate
![]() through
modeling the spectrum under the condition of
through
modeling the spectrum under the condition of
![]() .
Taking
.
Taking
![]() erg cm-3, we can already reproduce the observed data of VERITAS.
Therefore the soft photons reprocessed by the BLR can provide the EC
emission of electrons to produce high-energy radiation.
erg cm-3, we can already reproduce the observed data of VERITAS.
Therefore the soft photons reprocessed by the BLR can provide the EC
emission of electrons to produce high-energy radiation.
In Fig. 1, we present the modeling results for the observed data of 3C 66A, which assemble the data of Perri et al. (2003), Bottcher et al. (2009), Fermi-LAT, and the VERITAS results corrected by EBL absorption according to Franceschini et al. (2008). We include a quasi-simultaneous data including the near-infrared, optical, UV-Optical, and X-ray observations (Reyes et al. 2009). We used the synchrotron emission model to model the lower energy part, and used the SSC model to reproduce the spectrum observed by the Fermi-LAT. Particularly we use the EC model to model the VERITAS spectrum. It is indicated that the harden spectrum from the Fermi-LAT to VERITAS energy ranges could exhibit an EC spectrum.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13035fg1.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13035-09/Timg101.png)
|
Figure 1: Modeling SED of 3C 66A with the SSC+EC model. The black triangles are the data of Perri et al. (2003), the open circles come from Bottcher et al. (2009), the cross blue bow-tie show the Fermi-LAT spectrum, the red squares denote the data of Reyes et al. (2009), and the green squares represent the VERITAS spectrum corrected by EBL absorption according to Franceschini et al. (2008). We use the synchrotron model to model the lower energy part (black solid line), the SSC model to reproduce the Fermi-LAT spectrum (red dash line), and the EC model to model the VERITAS spectrum (green dot line). |
| Open with DEXTER | |
4 Discussions and conclusions
The redshift of 3C 66A has an uncertain value (Bramel et al. 2005), and
is usually adopted as z = 0.444; however, the redshift is crucial in
constructing intrinsic high-energy spectrum because of the EBL
absorption (Hauser & Dwek 2001). This absorption decreases the observed
flux and softens the observed spectrum. If the redshift is less than
0.444, such as just ![]() 0.096 suggested by Finke et al. (2008), the
intrinsic spectrum in the VERITAS energy range will be softer. There
will be a smooth link spectrum between the Fermi-LAT and the VERITAS
energy ranges. In Fig. 2, we generate the intrinsic
spectra of VERITAS observations corrected by EBL absorption
according to Franceschini et al. (2008) model, assuming the source to be
at the different redshifts z=0.03, 0.1, 0.3, and 0.5. It is shown
that the de-absorbed spectrum strongly depends on the redshift. When
z=0.3, the de-absorbed spectrum has a little inverted, but it
becomes an inverted spectrum in z=0.5. If the redshift is less than
0.1, the de-absorbed spectrum will present the usual SED of an LBL
such as W Comae (Acciari et al. 2008). In Fig. 3, we show
the de-absorbed SEDs under z=0.1 and the modeling. A smooth spectrum
can link the Fermi-LAT and VERITAS data and be explained with an SSC
model, in which
0.096 suggested by Finke et al. (2008), the
intrinsic spectrum in the VERITAS energy range will be softer. There
will be a smooth link spectrum between the Fermi-LAT and the VERITAS
energy ranges. In Fig. 2, we generate the intrinsic
spectra of VERITAS observations corrected by EBL absorption
according to Franceschini et al. (2008) model, assuming the source to be
at the different redshifts z=0.03, 0.1, 0.3, and 0.5. It is shown
that the de-absorbed spectrum strongly depends on the redshift. When
z=0.3, the de-absorbed spectrum has a little inverted, but it
becomes an inverted spectrum in z=0.5. If the redshift is less than
0.1, the de-absorbed spectrum will present the usual SED of an LBL
such as W Comae (Acciari et al. 2008). In Fig. 3, we show
the de-absorbed SEDs under z=0.1 and the modeling. A smooth spectrum
can link the Fermi-LAT and VERITAS data and be explained with an SSC
model, in which
![]() erg cm-3 and
erg cm-3 and
![]() erg cm-3.
erg cm-3.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13035fg2.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13035-09/Timg105.png)
|
Figure 2: Intrinsic spectra of VERITAS observations corrected by EBL absorption according to the Franceschini et al. (2008) model in different redshifts, such as z=0.03 (cyan dash line), 0.1 (blue dot line), 0.3 (green dash-dot line), 0.5 (red dash-dot-dot line). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13035fg3.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13035-09/Timg106.png)
|
Figure 3: Modeling SED of 3C 66A with the SSC model. The black triangles are the data of Perri et al. (2003), the open circles come from Bottcher et al. (2009), the cross blue bow-tie show the Fermi-LAT spectrum, the red squares present the data of Reyes et al. (2009), and the green squares denote the VERITAS spectrum corrected by EBL absorption according to Franceschini et al. (2008). We use the synchrotron model to model the lower energy part (black solid line) and the SSC model to reproduce the Fermi-LAT and de-absorbed VERITAS spectra assuming z=0.1 (red dash line). |
| Open with DEXTER | |
In fact the bulk motion of the emitting blob affects the observed
SED (e.g., Dermer 1995; Georganopoulos et al. 2001). The peak
frequencies are given by
![]() ,
,
![]() ,
and
,
and
![]() .
We can see
that
.
We can see
that
![]() would be higher than
would be higher than
![]() provided the blob
has larger
provided the blob
has larger ![]() or
or ![]() (Usually the viewing angle
(Usually the viewing angle
![]() is assumed,
is assumed,
![]() .) From the
ratio of peak luminosity,
.) From the
ratio of peak luminosity,
![]() (
(
![]() is amplified by a
factor of
is amplified by a
factor of ![]() ,
see Sikora et al. 1994; and Dermer 1995), where
,
see Sikora et al. 1994; and Dermer 1995), where
![]() is the reproduced fraction of the
is the reproduced fraction of the
![]() ,
we show that
,
we show that
![]() is strongly affected by the bulk
motion of the blob.
In Fig. 1, using
is strongly affected by the bulk
motion of the blob.
In Fig. 1, using
![]() erg cm-3,
erg cm-3,
![]() erg cm-3, and
erg cm-3, and
![]() erg cm-3, we can model the SED.
erg cm-3, we can model the SED.
![]() is obviously lower than U'B; however, the EC
luminosity is comparable with the synchrotron ones (see Fig. 1).
In the observer frame, the beaming factor is different for EC
(
is obviously lower than U'B; however, the EC
luminosity is comparable with the synchrotron ones (see Fig. 1).
In the observer frame, the beaming factor is different for EC
(
![]() Dermer 1995; Georganopoulos et al. 2001),
synchrotron and SSC emission (
Dermer 1995; Georganopoulos et al. 2001),
synchrotron and SSC emission (
![]() ). The difference
of EC and synchrotron luminosity is reasonable by considering their
beaming factor.
). The difference
of EC and synchrotron luminosity is reasonable by considering their
beaming factor.
The EC emission is less clear for the BL Lac objects. The lack of
strong emission lines and UV excesses suggests that the external
photon density
![]() is very low, while the Lorentz factor
of BL Lac objects is typically less than that of quasars
(Piner et al. 2008). Their high-energy emission strongly favors the SSC
mechanism over the EC mechanism. But, 3C 66A might be an exception
and reveal higher bulk velocity in the high-energy emissive region.
Therefore, the high-energy emission caused by EC mechanism is likely
observed in the IBL. This possibility needs future Fermi-LAT and
VERTAS observations for 3C 66A and a precise redshift determination.
is very low, while the Lorentz factor
of BL Lac objects is typically less than that of quasars
(Piner et al. 2008). Their high-energy emission strongly favors the SSC
mechanism over the EC mechanism. But, 3C 66A might be an exception
and reveal higher bulk velocity in the high-energy emissive region.
Therefore, the high-energy emission caused by EC mechanism is likely
observed in the IBL. This possibility needs future Fermi-LAT and
VERTAS observations for 3C 66A and a precise redshift determination.
We thank the referee for a very helpful and constructive report that helped to improve our manuscript substantially. We acknowledge the financial supports from the National Natural Science Foundation of China 10673028 and 10778702, and the National Basic Research Program of China (973 Program 2009CB824800).
References
- Abdo, A. A., et al. 2009, ApJ, 701, 597 [Google Scholar]
- Acciari, V. A., Aliu, E., Beilicke, M., et al. 2008, ApJ, 684, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Aliu, E., Arlen, T., et al. 2009, ApJ, 693, L104 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007, ApJ, 666, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2008, Science, 320, 1752 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Albert, J., Anderhub, H., Antonelli, L. A., et al. 2009, ApJ, 692, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Bottcher, M., Harvey, J., Joshi, M., et al. 2005, ApJ, 631, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Bottcher, M., Fultz, K., Aller, H. D., et al. 2009, ApJ, 694, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Bramel, D. A., Carson, J., Covault, C. E., et al. 2005, ApJ, 629, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Celotti. A., & Ghisellini, G. 2008, MNRAS, 385, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Dermer, C. D. 1995, ApJ, 446, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Dermer, C. D., & Schlickeiser, R. 1993, ApJ, 416, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Donato, D., Sambruna, R. M., & Gliozzi1, M. 2005, A&A, 433, 1163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finke, J. D., Shields, J. C., Böttcher, M., & Basu, S. 2008, A&A, 477, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foschini, L., Ghisellini, G., Raiteri, C. M., et al. 2006, A&A, 453, 829 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Franceschini, A., Rodighiero, G., & Vaccari, M. 2008, A&A, 487, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georganopoulos, M., & Kazanas, D. 2003, ApJ, 594, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Georganopoulos, M., Kirk, J. G., & Mastichiadis, A. 2001, ApJ, 561, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., & Maraschi, L. 1989, ApJ, 340, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Celotti, A., Fossati, G., Maraschi, L., & Comastri, A. 1998, MNRAS, 301, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Celotti, A., & Costamante, L. 2002, A&A, 386, 833 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hauser, M. G., & Dwek, E. 2001, ARA&A, 39, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Mattox, J. R., et al. 2001, ApJS, 134, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Joshi, M., & Bottcher, M. 2007, ApJ, 662, 884J [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. G., Rieger, F. M., & Mastichiadis, A. 1998, A&A, 333, 452 [NASA ADS] [Google Scholar]
- Konopelko, A., Mastichiadis, A., Kirk, J., de Jager, O. C., & Stecker, F. W. 2003, ApJ, 597, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P. 1980, ApJ, 235, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., & Travis, J. P. 1996, A&AS, 120, 537 [NASA ADS] [Google Scholar]
- Mastichiadis, A., & Kirk, J. 1997, A&A, 320, 19 [NASA ADS] [Google Scholar]
- Miller, J. S., French, H. B., & Hawley, S. A. 1978, in Pittsburgh Conference on BL Lac Objects, ed. A. M. Wolfe (Pittsburgh: Univ. Pittsburgh), 176 [Google Scholar]
- Moderski, Sikora, M., Coppi, P. S., & Aharonian, F. 2005, MNNRAS, 363, 954 [Google Scholar]
- Paggi, A., Massaro, F., Vittorini, V., et al. 2009, A&A, 504, 821 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perri, M., Massaro, E., Giommi, P., et al. 2003, A&A, 407, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piner, B. G., Pant, N., & Edwards, P. G. 2008, ApJ, 678, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Reyes, L. C., et al. 2009, in The Proceedings of the 31st International Cosmic Ray Conference, [arXiv:astro-ph/0907.5175] [Google Scholar]
- Sikora, M., Begelman, M. C., & Rees, M. J. 1994, ApJ, 421, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Stepanyan, A. A., Neshpor, Yu. I., Andreeva, N. A., et al. 2002, Astron. Rep., 46, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., Maraschi, L., & Ghisellini, G. 1998, ApJ, 509, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., & Ghisellini, G. 2008, MNRAS, 386, 945 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... (2007)
![[*]](/icons/foot_motif.png)
- Georganopoulos, M., Kazanas D., Perlman, E., et al. 2007, http://jca.umbc.edu/ markos/cs/index.html
All Tables
Table 1: Parameters for the SSC+EC or SSC model used to reproduce the SED (Figs. 1 and 3).
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13035fg1.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13035-09/Timg101.png)
|
Figure 1: Modeling SED of 3C 66A with the SSC+EC model. The black triangles are the data of Perri et al. (2003), the open circles come from Bottcher et al. (2009), the cross blue bow-tie show the Fermi-LAT spectrum, the red squares denote the data of Reyes et al. (2009), and the green squares represent the VERITAS spectrum corrected by EBL absorption according to Franceschini et al. (2008). We use the synchrotron model to model the lower energy part (black solid line), the SSC model to reproduce the Fermi-LAT spectrum (red dash line), and the EC model to model the VERITAS spectrum (green dot line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13035fg2.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13035-09/Timg105.png)
|
Figure 2: Intrinsic spectra of VERITAS observations corrected by EBL absorption according to the Franceschini et al. (2008) model in different redshifts, such as z=0.03 (cyan dash line), 0.1 (blue dot line), 0.3 (green dash-dot line), 0.5 (red dash-dot-dot line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13035fg3.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa13035-09/Timg106.png)
|
Figure 3: Modeling SED of 3C 66A with the SSC model. The black triangles are the data of Perri et al. (2003), the open circles come from Bottcher et al. (2009), the cross blue bow-tie show the Fermi-LAT spectrum, the red squares present the data of Reyes et al. (2009), and the green squares denote the VERITAS spectrum corrected by EBL absorption according to Franceschini et al. (2008). We use the synchrotron model to model the lower energy part (black solid line) and the SSC model to reproduce the Fermi-LAT and de-absorbed VERITAS spectra assuming z=0.1 (red dash line). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.