EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 511 (February 2010) A&A, 511 (2010) A88 Full HTML
Free Access
Issue
A&A
Volume 511, February 2010
Article Number A88
Number of page(s) 11
Section Galactic structure, stellar clusters, and populations
DOI https://doi.org/10.1051/0004-6361/200912905
Published online 17 March 2010
A&A 511, A88 (2010)

White dwarfs with hydrogen-deficient atmospheres and the dark matter content of the Galaxy

S. Torres1,2 - J. Camacho1 - J. Isern3,2 - E. García-Berro1,2

1 - Departament de Física Aplicada, Universitat Politècnica de Catalunya, c/Esteve Terrades 5, 08860 Castelldefels, Spain
2 - Institute for Space Studies of Catalonia, c/Gran Capità 2-4, Edif. Nexus 104, 08034 Barcelona, Spain
3 - Institut de Ciències de l'Espai, CSIC, Campus UAB, Facultat de Ciències, Torre C-5, 08193 Bellaterra, Spain

Received 16 July 2009 / Accepted 16 December 2009

Abstract
Context. The nature of the several microlensing events observed by the MACHO team towards the Large Magellanic Cloud (LMC) is still a subject of debate. Low-mass substellar objects and stars with masses larger than $\sim$1  $M_{\hbox{$\odot$ }}$have been ruled out as major components of a massive astrophysical compact halo object (MACHO) galactic halo, while stars of half a solar mass seem to be viable candidates. Main sequence stars have been already discarded, and there are tight restrictions on the role played by white dwarfs with hydrogen-dominated atmospheres.
Aims. In this paper we evaluate the contribution to the dark matter content of the Galaxy of white dwarfs with hydrogen-deficient atmospheres.
Methods. For this purpose we use a Monte Carlo simulator which incorporates up-to-date evolutionary sequences of white dwarfs with hydrogen-rich and hydrogen-deficient atmospheres. We also take into account detailed descriptions of the thick disk and the halo of our Galaxy as well as of a reliable model of the LMC.
Results. We find that the contribution of white dwarfs with hydrogen-deficient atmospheres moderately increases the theoretical estimate of the optical depth with respect to the value obtained when only hydrogen-rich white dwarfs are considered. We also find that the contribution of the thick disk population of white dwarfs is comparable to the halo contribution. However, the contributions of both the halo and the thick disk white-dwarf populations are still insufficient to explain the number of events observed by the MACHO team.
Conclusions. Finally, we find that the contribution to the halo dark matter of the entire population under study is less than 10% at the 95% conficence level.

Key words: white dwarfs - stars: luminosity function - mass function - Galaxy: stellar content - Galaxy: halo - Galaxy: structure

1 Introduction

Since the pioneering observational detection of the first Galactic gravitational microlensing events by the MACHO team (Alcock et al. 1997, 2000), many efforts have been devoted to this issue. In fact, after these preliminary discoveries, many other teams pursued similar studies to either confirm or discard their results. Among these observational studies we mention those performed by the EROS (Lasserre et al. 2001; Goldman et al. 2002; Tisserand et al. 2007), OGLE (Udalski et al. 1994), MOA (Muraki et al. 1999) and SuperMACHO (Becker et al. 2005) teams. All of them have monitored millions of stars during several years in both the Large Magellanic Cloud (LMC) and the Small Magellanic Cloud (SMC) to search for microlensing events. One of the main results of these searches is that none of the microlensing events found so far has durations between a few hours and 20 days. This inmediately translates into tight contraints on the nature of the objects responsible for the microlensing events. Today it is known that most likely the objects responsible of the reported gravitational microlensing events are stars with masses ranging from $\sim$$0.1~M_{\hbox{$\odot$ }}$to $\sim$ $1.0~M_{\hbox{$\odot$ }}$. Thus, for this reason and because of their intrinsical faintness, white dwarfs seem to be the best candidates to explain the observed microlensing events and, consequently, they would also be obvious candidates to build up the baryonic dark matter content of the Galaxy.

In a series of previous papers we have exhaustively analyzed the contributions of the halo populations of carbon-oxygen (CO) and oxygen-neon (ONe) white dwarfs with pure hydrogen atmospheres (García-Berro et al. 2004; Camacho et al. 2007). We have also extended our previous studies to include the population of halo red dwarfs (Torres et al. 2008). Thus, these studies covered the full range of initial masses able to produce microlensing events compatible with the required durations, and nearly 90% of the stellar content. The main conclusion of these papers is that the entire population of these stars can account at most for $\sim$0.3 of the optical depth found by the MACHO team. This in turn implies that the contribution of the full range of masses between 0.08 and $10~M_{\hbox{$\odot$ }}$represents $\la$5% of the halo dark matter, with an average mass of $0.4~M_{\hbox{$\odot$ }}$. Even though, we also found that the expected number of events obtained in our simulations (three events at the 95% confidence level) is substantially below the number of events detected by the MACHO team. Thus these results support the idea previously pointed out in several other studies, that the optical depth found by the MACHO team is probably an overstimate, possibly due to contamination of self-lensing objects, variable stars and others.

In all previous studies in which the contribution of white dwarfs to the dark matter content of the Galaxy was analyzed, white-dwarf evolutionary sequences with pure hydrogen atmospheres (white dwarfs of the DA type) were employed, and the contribution of non-DA white dwarfs was disregarded. However, non-DA white dwarfs represent roughly 20% of the entire white dwarf population and consequently their contribution cannot be considered a priori negligible. Moreover, there is strong observational evidence that non-DA white dwarfs represent an even more important fraction of the cool white dwarf population (Bergeron et al. 2001), but the current simulations of the halo white dwarf population do not take this fact into account. Additionally, the colors and magnitudes of cool white dwarfs depend on their atmospheric composition - see Fig. 1. Indeed, it has been demonstrated (Hansen 1998) that white dwarfs with hydrogen-rich atmospheres experience a blue turn at low luminosities, which is the result of extremely strong ${\rm H}_2$ molecular absorption features in the infrared. This blue hook prevents DA white dwarfs from reaching very faint magnitudes. On the contrary, white dwarfs of the non-DA types cool as blackbodies and hence can reach extremely faint magnitudes within the age of the Galaxy. Again, this important fact has been overlooked in the most up-to-date models of the population of halo white dwarfs. Finally, the rate of cooling of white dwarfs is controlled by the thickness and composition of the atmospheric layers. It turns out that non-DA white dwarfs cool faster than their corresponding DA counterparts, another fact that has not been taken into account in previous simulations.

Another point which deserves attention is whether the lenses belong to the halo or to an extended thick disk population (Reid et al. 2001; Torres et al. 2002). After all, and as pointed out by Gyuk & Gates (1999), the thick disk population presents a reasonable alternative to a halo population of lenses. Several observational (Oppenheimer et al. 2001; Kilic et al. 2006; Harris et al. 2006; Vidrih et al. 2007) works have addressed this question, but this is still a controversial issue, and a definitive answer still requires more theoretical and observational efforts.

\begin{figure} \par\includegraphics[width=7.6cm,clip]{12905fg1.eps} \end{figure} Figure 1:

Color-magnitude diagram of a typical $0.6~M_{\hbox{$\odot$ }}$white dwarf. The solid line corresponds to a cooling sequence of a hydrogen-rich (DA) white dwarf (Salaris et al. 2000), while the dashed line corresponds to a helium-rich (non-DA) white dwarf (Benvenuto & Althaus 1997). The dots correspond to cooling ages of 6, 8, 10, 12 and 14 Gyr.

Open with DEXTER

In this paper we extend our previous studies of the populations of halo red and white dwarfs. In particular, we include the contribution of non-DA halo white dwarfs to the microlensing event rate and we analyze the role played by the thick-disk populations of these stars. Special emphasis has been put on the analysis of the simulated microlensing events as a function of the range of colors susceptible to be detected by surveys like EROS and to compare our results with those of the MACHO team. The paper is organized as follows. In Sect. 2 we summarize the main ingredients of our Monte Carlo code and other basic assumptions and procedures necessary to evaluate the microlensing optical depth towards the LMC. In this section we also describe in depth our thick disk model. Section 3 is devoted to the discussion of our main results, including the contribution of red dwarfs and DA and non-DA white dwarfs to the microlensing optical depth towards the LMC, and to compare our results with those of the EROS team. In this section we also estimate the probability that a microlensing event could be assigned to the thick disk or the halo, and we discuss the contribution of red and white dwarfs to the baryonic content of the Galaxy. Finally, in Sect. 4 our major findings are summarized and we draw our conclusions.

2 Building the model

A detailed description of our Monte Carlo simulator has been already presented in García-Berro et al. (1999), García-Berro et al. (2004), Camacho et al. (2007) and Torres et al. (2002). Consequently, we will only summarize the most important inputs here. At the core of any Monte Carlo simulator there is a pseudo-random number generator algorithm, for which we have used that of James (1990). It belongs to the linear congruential generator family. It provides excellent statistical properties and ensures a repetition period of $\ga$1018, which is virtually infinite for our purposes. Each one of the Monte Carlo simulations presented here consists of an ensemble of $\sim$ $5 \times 10^4$independent realizations of the synthetic star population, for which the average of any observational quantity and its corresponding standard deviation were computed. Here the standard deviation means the ensemble mean of the sample dispersions for a typical sample.

The main sequence mass is obtained by drawing a pseudo-random number according to an initial mass function. We have adopted the standard initial mass function of Scalo (1998). Other biased non-conventional initial mass functions (Adams & Laughlin 1996; Chabrier et al. 1996) have been disregarded since these mass functions are incompatible with the observed properties of the halo white dwarf population (Isern et al. 1998; García-Berro et al. 2004), with the contribution of thermonuclear supernovae to the metallicity of the Galactic halo (Canal et al. 1997), and with the observations of galactic halos in deep galaxy surveys (Charlot & Silk 1995). Once the mass of the star is chosen, its main-squence lifetime is derived (Iben & Laughlin 1989), and we are able to determine which stars have evolved into white dwarfs or remain in the main-squence as red dwarfs. We considered red dwarfs to have masses in the range of $0.08<M/M_{\hbox{$\odot$ }}<1$. For these stars we have adopted the evolutionary models of Baraffe et al. (1998). Stars with such small masses have long main-sequence lifetimes and, therefore, no post-main-sequence evolutionary tracks were required. For those stars which have had time enough to enter into the white dwarf cooling track and given a set of theoretical cooling sequences and the initial to final mass relationship (Iben & Laughlin 1989) their luminosities, effective temperatures and colors were obtained. The cooling sequences adopted here depend on the mass of the white dwarf. White dwarfs with masses smaller than $M_{\rm WD}=1.1~M_{\hbox{$\odot$ }}$are expected to have CO cores and, consequently, we adopt for them the cooling tracks of Salaris et al. (2000) if they belong to the DA spectral class. If, on the contrary, the white dwarf has a hydrogen-deficient atmosphere we use the cooling sequences of Benvenuto & Althaus (1997) - corresponding to pure helium atmospheres - and the bolometric corrections of Bergeron et al. (1995). These are our fiducial cooling sequences. However, to study the effects of different cooling sequences for hydrogen-deficient white dwarfs (and, hence, different cooling speeds) which may affect our results we also use the cooling sequences of Bergeron et al. (1995) - see below. White dwarfs with masses larger than $M_{\rm WD}=1.1~M_{\hbox{$\odot$ }}$most probably have ONe cores, and for these white dwarfs we adopt the cooling sequences of Althaus et al. (2007). All these cooling sequences incorporate the most accurate physical inputs for the stellar interior (including neutrinos, crystallization, phase separation and Debye cooling) and, for the case of DA white dwarfs, reproduce the blue turn at low luminosities (Hansen 1998).

2.1 The fraction of DA and non-DA white dwarfs

To assign a spectral type to each of the white dwarfs in the simulated sample we proceeded as follows. In a first set of simulations we adopted the canonical fraction of 80% of white dwarfs of the spectral type DA and 20% of the non-DA class, independently of the effective temperature of the white dwarf. We regard this as our fiducial model, and we refer to it as model A. However, several observations indicate that this ratio is a function of the effective temperature. For instance, the well-known DB-gap, where no white dwarfs of the DB spectral class can be found, occurs at effective temperatures between 45 000 K and 30 000 K. Additionally, Bergeron et al. (2001) found that most white dwarfs with effective temperatures ranging from 6000 K to 5000 K are DAs. Finally, Bergeron & Leggett (2002) argued that all white dwarfs cooler than 4000 K have mixed H/He atmospheres. Many of these early findings have been corroborated by the wealth of data obtained from recent large surveys, like the Sloan Digital Sky-Survey (Harris et al. 2006; Kilic et al. 2006). Accordingly, we have have produced a second set of simulations, and we refer to them as model B, following these observational results. Basically, in model B we adopt the same fraction of DA white dwarfs (80%) for temperatures above 6000 K. All white dwarfs in the range of effective temperatures between 6000 K and 5000 K were considered to be DA white dwarfs. Finally, for effective temperatures below this value we adopt a fraction of 50% (Bergeron & Legget 2002; Gates et al. 2004). We would like to note that we model the transitions between the different spectral classes in a purely heuristic way because currently there are no cooling sequences which correctly reproduce these transitions, as this is a long-standing problem, which is indicative of a failure of the theoretical cooling models. However, our model correctly reproduces the observations, and thus we consider it to be a fair approach. Finally, to check the sensitivity of our results to the adopted cooling tracks we have also computed a third set of simulations, based on model B, in which we use the cooling sequences of Bergeron et al. (1995). We refer to this model as model C.

2.2 The halo model

We have adopted a spherically symmetric halo. In particular the model used here is the typical isothermal sphere of a radius of 5 kpc, also called the ``S-model'', which has been extensively used by the MACHO collaboration (Alcock et al. 2000; Griest 1991). Despite the fact that other models as for instance the exponential power-law models or the Navarro et al. (1997) density profiles have been proposed, our studies (García-Berro et al. 2004) have shown that no relevant differences are found when these models are used. Furthermore, we do not consider non-standard models of the Galactic halo, such as models with flattened density profiles, oblate halo models and others because a thorough study of these models is beyond the scope of this paper.

The kinematical properties of the halo population have been modeled according to Gaussian laws (Binney & Tremaine 1987) with radial and tangential velocity dispersions accordingly related by the Jeans equation and fulfilling the flat rotation curve of our Galaxy. We have adopted standard values for the circular velocity $V_{\rm c}=220$ km s-1 as well as for the peculiar velocity of the Sun $(U_{\hbox{$\odot$ }}, V_{\hbox{$\odot$ }},W_{\hbox{$\odot$ }})=(10.0, 15.0, 8.0)$ km s-1 (Dehnen & Binney 1998). Besides, we have rejected stars with velocities higher than 750 km s-1, because they would have velocities exceeding 1.5 times the escape velocity. Finally, since white dwarfs usually do not have determinations of the radial component of the velocity, the radial velocity is eliminated when a comparison with the observational data is needed.

Finally, to compare the simulated results with the observational ones, a normalization criterion should be used. We have proceeded as in our previous papers (Camacho et al. 2007; García-Berro et al. 2004; Torres et al. 2008). That is, we have normalized our simulations to the local density of halo white dwarfs obtained from the halo white dwarf luminosity function of Torres et al. (1998), but taken into account the new halo white dwarf candidates found in the SDSS Stripe 82 (Vidrih et al. 2007). Nevertheless, we emphasize that when normalizing to the local density of halo white dwarfs obtained using the white dwarf luminosity function we only consider those stars with velocities higher than 250 km s-1, given that only those stars would be genuinely considered as halo members and would be used to build the observational halo luminosity function (Liebert et al. 1989; Torres et al. 1998). This is totally equivalent to the adopted cut in reduced proper motion employed by Flynn et al. (2001). Additionally, only the number density of DA white dwarfs was considered to normalize the simulations, since all but one of the white dwarfs used to obtain the luminosity function of Torres et al. (1998) were of the DA spectral type. Obviously, imposing this normalization we implicitly assume that the MACHO results and the direct surveys are complementary and seem to be probing the same populations, whatever the nature of those populations (Hansen & Liebert 2003).

2.3 The thick disk model

The structure and kinematics of the Galactic disk remain a source of controversy and discussion. In particular the nature of the thick disk is an active field of research. Consequently we have used two different models in our simulations. The first of these is a canonical thick disk model, which we consider as a starting reference model. However, there are alternative thick disk models based on the kinematics of metal-poor stars of the Galaxy - see Chiba & Beers (2000) and references therein - that challenge the canonical model. Accordingly, we also consider the most recent thick disk model of Carollo et al. (2010), which is based on the SDSS Data Release 7. We describe them separately.

The kinematical properties of the canonical model are well represented by an ellipsoid with constant values of the velocity and dispersions and an asymmetrical drift. Within this model the spatial distribution is generally assumed to follow exponential laws characterized by a scale height and a scale length with no vertical gradients. Thus we have choosen a double exponential law for the density profile of this model with a scale height of 1.5 kpc and a scale length of 3.0 kpc (Reid 2005). The kinematical properties of the synthetic thick disk stars have been modeled according to an ellipsoid with the standard dispersion $(\sigma_U, \sigma_V, \sigma_W)=(60, 45, 35)~{\rm km}~{\rm s}^{-1}$and an asymmetric velocity drift $V_\phi=-40~{\rm km}~{\rm s}^{-1}$(Reid 2005).

In a recent study, Carollo et al. (2010) analyzed the structure and kinematical properties of the Milky Way based on the Sloan Digital Sky Survey Data Release 7 and showed evidence that a sizeable fraction of the thick disk is composed by metal-weak stars with independent kinematical properties. Following Carollo et al. (2010) we use an ellipsoid with standard dispersions $(\sigma_U, \sigma_V, \sigma_W)=(59, 40, 44)~{\rm km}~{\rm s}^{-1}$, and a scale height and a scale length of 1.36 and 2.0 kpc, respectively. The most distinctive feature of the model of Carollo et al. (2010) is that the asymmetric drift varies as a function of height above the Galactic plane. Specifically, the gradient in the asymmetric drift is $\Delta\langle V_{\phi}\rangle/\Delta\vert z\vert=-36~{\rm km}~{\rm s}^{-1}~{\rm kpc}^{-1}$, which agrees with the previous studies of Chiba & Beers (2000). We note that although the observations indicate that only a fraction of the thick disk could be explained by the metal-weak thick disk population, we have considered a full metal-weak thick disk to obtain an upper limit to the possible contribution of this population to the microlensing experiments.

Additionally, in both cases we took into account the peculiar velocity of the Sun $(U_{\hbox{$\odot$ }}, V_{\hbox{$\odot$ }}, W_{\hbox{$\odot$ }})=(10.0, 15.0, 8.0)~{\rm km~s^{-1}}$(Dehnen & Binney 1998) and discarded those stars that escape the potential of the Galaxy. We also assumed that the thick disk formation started 12 Gyr ago with a maximum star formation rate occuring 10 Gyr ago and exponentially decreased since, following the model of Gilmore et al. (1995). Finally our thick disk models have been normalized assuming that the thick disk density represents 8.5% of the thin disk density (Reid 2005).

2.4 The LMC model

In order to mimic the microlensing experiments towards the LMC we have simulated it following closely the detailed LMC descriptions of Gyuk et al. (2000) and Kallivayalil et al. (2006). Our model takes into account among other parameters the scale length and scale height of the LMC, its inclination and its kinematical properties. This model provides us with a synthetic population of stars representative of the monitored point sources. Afterwards we evaluate which stars of the Galactic halo could be responsible of a microlensing event. We have only considered stars fulfilling a series of conditions. First of all the lensing stars should be fainter than a certain magnitude limit. In a second step we have checked if the lens is inside the Einstein tube of the monitored star. That is, we checked if the angular distance between the lens and the monitored star is smaller than the Einstein radius. We recall here that the Einstein radius is given by

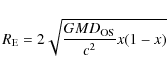
\begin{displaymath}R_{\rm E}=2\sqrt{\frac{GMD_{\rm OS}}{c^2}x(1-x)} \end{displaymath} (1)

where $D_{\rm OS}$ is the observer-source distance, $x\equiv D_{\rm OL}/D_{\rm OS}$ and $D_{\rm OL}$ is the observer-lens distance. Finally, we filtered those stars which are candidates to produce a microlensing event with the detection efficiency function, $\varepsilon(\hat t_i)$, where $\hat t_i$ is the Einstein ring diameter crossing time. The detection efficiency depends on the particular characteristics of the experiment. In our case we have reproduced the MACHO and EROS experiments. Specifically for the MACHO collaboration we have taken $1.1 \times 10^7$ stars during 5.7 yr and over $13.4~{\rm deg^2}$, whereas the detection efficiency has been modeled according to:

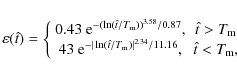
\begin{displaymath}\varepsilon(\hat{t})= \left\{ \begin{array}{cc} 0.43~{\rm e}... ...m})\vert^{2.34}/11.16}, &\hat{t}<T_{\rm m}, \end{array}\right. \end{displaymath} (2)

\begin{figure} \par\includegraphics[width=12cm,clip]{12905fg2.eps} \end{figure} Figure 2:

Microlensing optical depth towards the LMC as a function of the limiting magnitude. Solid and open squares represent the DA and non-DA white dwarf populations, respectively. Red dwarfs are represented by open triangles, while the entire population is shown by open circles.

Open with DEXTER

where $T_{\rm m}=250$ days. This expression provides a good fit to the results of Alcock et al. (2000). For the EROS experiment we have used $0.7\times 10^7$ stars over a wider field of $84~{\deg^2}$ and over a period of 6.7 yr. Regarding the detection efficiency we have adopted a numerical fit to the results of Tisserand et al. (2007).

For all the simulations presented here, we extracted the parameters relevant to characterize the microlensing experiments. A complete description of the various parameters which are of importance in discussing gravitational microlensing can be found in Mollerach & Roulet (2002) and Schneider et al. (2004). Among these parameters, perhaps the most important one for our purposes is the optical depth, $\tau$, which measures the probability of a star to be magnified by a lens at a given time by more than a factor of 1.34. From an observational point of view an estimate of this parameter can be obtained by the expression (Alcock et al. 2000):

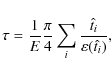
\begin{displaymath}\tau=\frac{1}{E}\frac{\pi}{4}\sum_i \frac{\hat t_i}{\varepsilon(\hat t_i)}, \end{displaymath} (3)

where E is the total exposure in star-years. The optical depth is independent of the lens motion and mass distribution. However, since the experiments measure the number of events and their durations, additional information can be obtained using the microlensing rate $\Gamma$ and its distribution as a function of the event durations. This parameter represents nothing else but the flux of lenses inside the microlensing tube. Finally, an estimate of the expected number of events can be achieved by the expression

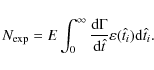
\begin{displaymath}N_{\rm exp}=E\int_{0}^{\infty}\frac{{\rm d} \Gamma}{{\rm d}\hat{t}}\varepsilon(\hat t_i){\rm d}\hat t_i. \end{displaymath} (4)

3 Results

3.1 The optical depth towards the LMC

The optical depth provides the most immediate and simple information about the microlensing experiments. Thus we compare our simulations with the optical depth derived by the MACHO collaboration. In Fig. 2 we show the contribution to the optical depth of the different populations under study as a function of the adopted magnitude cut, in the same manner as it was done in García-Berro et al. (2004) and subsequent papers. Our simulations have been normalized to the value derived by Alcock et al. (2000), $\tau_0=1.2\times 10^{-7}$. The contributions to the microlensing optical depth of the different populations are represented by solid and open squares for the populations of DA and non-DA white dwarfs respectively, while the contribution of the red dwarf population is displayed by open triangles. Finally, the contribution to the microlensing optical depth of the entire population is shown by open circles. For the sake of clarity, the contribution of the ONe white dwarf population is not shown in the top panels of Fig. 2, but it is taken into account when the total contribution (shown in the bottom panels of Fig. 2) is computed. As can be seen, for model A at bright magnitude cuts the contribution to the microlensing optical depth is roughly 7% for the population of non-DA white dwarfs and $\sim$15% for the DA white dwarf population (see the top left panel of Fig. 2). However, it is remarkable that as the magnitude cut increases, the contribution of non-DA white dwarfs remains almost constant, while the contribution of DA white dwarfs rapidly drops. This is a direct consequence of the faster cooling rate of non-DA white dwarfs and of the fact that non-DA white dwarfs do not experience the blue turn. The contribution of the red dwarf population is very similar to the one found in our previous studies, with a fairly constant decreasing slope as the magnitude cut increases. The decreasing contribution of red dwarfs to the microlensing optical depth for increasing magnitude cuts stems from the fact that in general red dwarfs are brighter than regular white dwarfs. When model B is considered, the overall contribution of DA white dwarfs is smaller than the contribution of non-DA white dwarfs - see the top central panel of Fig. 2. Note that for model A the opposite occurs, that is, the contribution of DA white dwarfs is more sizeable than the one of non-DA white dwarfs. The reason for this is easy to understand. Since the luminosity function of halo white dwarfs of Torres et al. (1998) only provides the density of relatively bright DA white dwarfs ( $\log(L/L_{\hbox{$\odot$ }})\ga -3.7$) and the fraction of low luminosity white dwarfs in model B is only 50% (in contrast with that of model A, for which a fraction of 80% was adopted independently of the effective temperature), the contribution of low luminosity white dwarfs to the optical depth decreases. Finally, the top right panel of Fig. 2 shows the relative contributions to the microlensing optical depth when model C is considered. As can be seen, the results are virtually indistinguishable of those obtained for model B, as one should expect given that the cooling tracks of Bergeron et al. (1995) are very similar to those of Benvenuto & Althaus (1997). In all cases it is important to realize that as far as the entire population is concerned, there is a noticeable increase in the contribution to the optical depth, which is exclusively due to the inclusion of non-DA white dwarfs in our calculations. Moreover, the global contribution of white dwarfs to the microlensing optical depth is very similar in both models - see the bottom panels of Fig. 2 - for magnitude cuts larger than $m_V \sim 23^{\rm mag}$, which is a reasonable value for current surveys. This value, roughly 30% of the observed optical depth obtained by the MACHO team, represents a 50% increment with respect to the value found in our previous studies, see Torres et al. (2008).

Table 1:   Summary of the results obtained for the entire population of microlenses towards the LMC for several magnitude cuts when the results of the MACHO collaboration are simulated.

A more detailed information can be obtained from our simulations. A summary is presented in Table 1, where we show several interesting parameters for the three models under study as a function of the adopted magnitude cut. In particular we show in this table the expected number of white dwarf microlensing events, the number of microlensing events produced by red dwarfs, the average mass of the microlenses for both the microlensing events produced by white and red dwarfs, the fraction of the white dwarf microlensing events produced by white dwarfs of the non-DA spectral type ($\eta$) over the total white dwarf microlensing events, the average proper motion, distance and tangential velocity of the lenses, the corresponding Einstein crossing times of the microlenses and finally the relative contribution to the microlensing optical depth. A close inspection of Table 1 reveals that all three models produce similar results except in one aspect, the fraction of microlensing events attributable to a non-DA white dwarf. As can be seen, the expected number of microlensing events is very small in all models, since in all cases no more than one microlensing event is expected to be found at the $1\sigma$confidence level. Additionally, the average masses of the microlenses are around $0.6~M_{\hbox{$\odot$ }}$in the case of white dwarfs, while for red dwarfs it is $\sim$ $0.2~M_{\hbox{$\odot$ }}$, the average distances to the microlenses are also very similar for both models, and there are no significant differences in the Einstein crossing times. The only relevant difference between the simulations is the spectral type of the white dwarf responsible for the simulated microlensing events. Whereas for model A the DA type prevails in $\sim$73% of the cases, for model B this fraction drops to $\sim$$20\%$ of the cases, while for model C we obtain a very similar value, $\sim$$21\%$. This can be understood by the same reasoning employed before. For models B and C, at low effective temperatures the fraction of hydrogen-rich white dwarfs is considerably smaller than for model A and, additionally, old DA white dwarfs are brighter than non-DAs. Thus for models B and C non-DA white dwarfs dominate at low luminosities and produce most of the microlensing events.

Additionally, from a detailed analysis of the data used to build Table 1, we have found that on average the microlenses produced by non-DA white dwarfs have slightly higher average masses ($\sim$ $0.61~M_{\hbox{$\odot$ }}$and $\sim$$0.56~M_{\hbox{$\odot$ }}$, respectively) and can be found at a smaller distances ($\sim$1.7 kpc and $\sim$2.9 kpc, respectively) than those produced by the population of DA white dwarfs. That is again a consequence of the different cooling rates and colors of non-DA white dwarfs. As previously mentioned, non-DA white dwarfs cool faster and moreover, as they cool, they become substantially dimmer than their corresponding DA counterparts. Hence, the population of non-DA white dwarfs can produce microlenses at significantly smaller distances. Also, these values do not depend significantly on the model adopted for the evolution of the atmospheric composition of white dwarfs. Since the distribution of velocities does not depend on the spectral type, the final result is that the Einstein crossing times are on average different for the microlensing events produced by non-DA and DA white dwarfs ($\sim$40 and $\sim$57 days, respectively).

3.2 The EROS experiment

The EROS experiment has monitored a wider solid angle and less crowded fields in LMC than the MACHO team. In addition, it has also monitored the SMC. For these reasons, self-lensing of the LMC should be less important in the EROS experiment than in the case of the MACHO collaboration. Consequently, a smaller value of the optical depth should be expected, and this is indeed the case. The EROS results, adopting a standard halo model and assuming $\tau_{\rm SMC}=1.4\tau_{\rm LMC}$indicate that the microlensing optical depth is $\tau_0=0.36\times10^{-7}$ (Tisserand et al. 2007), which is four times smaller than that obtainded by the MACHO team.

We have performed a set of simulations emulating the conditions of the EROS experiment using the same populations described previously. Although only small differences should be expected, this new series of simulations represents a test of the robustness of our numerical procedures. In Table 2 we summarize the results obtained for this set of simulations. Our simulations show that independently of the adopted model for the spectral type of white dwarfs, the joint population of red dwarfs and white dwarfs of the galactic halo provides at most $\sim$90% of the optical depth estimated by the EROS team. This value represents an increase of $\sim$20% with respect to the one obtained in our previous simulations (Torres et al. 2008). Obviously, the non-DA white dwarf population is responsible for this result, and this confirms our previous conclusion that there is a general agreement between the theoretical models and the results of the EROS team.

Moreover the EROS experiment used a set of selection criteria in the search of halo white dwarfs to distinguish halo objects from thick disk stars (Goldman et al. 2002). For those stars detectable by EROS, namely those with magnitudes brighter than V=21.5 and I=20.5, the selection criteria are implemented by two cuts. The first one uses the reduced proper motion and requires that the reduced proper motion of a halo object should be HV>22.5. The second cut is applied to the resulting sample and only selects those stars with large proper motions, $\mu>0.8''~{\rm yr^{-1}}$. In Fig. 3 we present a typical simulation of the halo white dwarf population adapted to the requirements of the EROS team. The previously mentioned criteria are displayed by dotted lines, while the resulting halo selection zone is represented by a bold solid line. For model A we obtain that at the 1$\sigma$ confidence level, $4 \pm 2$ DA white dwarfs and $1\pm1$ non-DA white dwarfs should be found in the selection zone, while for model B we obtain $1\pm1$ and $1\pm1$ white dwarfs, respectively, and the same occurs for model C. These results indicate that the models which take into account the temperature dependence of the white dwarf spectral type (models B and C) seem to yield a more realistic and consistent estimate, given that it agrees well with the null results of the EROS team. It is also worth noting that the applied selection criteria, in particular the proper motion cut ( $\mu>0.8''~{\rm yr^{-1}}$), are so restrictive that only a small (1%) fraction of the halo white dwarf population can be found in the selection zone.

\begin{figure} \par\includegraphics[width=8.2cm,clip]{12905fg3.eps} \end{figure} Figure 3:

Proper motion as a function of the V magnitude for the halo white dwarf population. The EROS selection zone is shown as a bold solid line.

Open with DEXTER

Table 2:   Summary of the results obtained for the entire population of microlenses towards the LMC for the EROS experiment, using models A, B and C and adopting an age of the halo of 14 Gyr and several magnitude cuts.

3.3 The thick disk contribution

As already mentioned, the thick disk is characterized by higher velocity distributions and a larger scale height than those of the thin disk. Several studies on halo white dwarfs have considered the thick disk population as a possible source of contamination (Oppenheimer et al. 2001; Reid et al. 2001; Torres et al. 2002), but a comprehensive theoretical study remains to be done. Accordingly we evaluate in this section the joint contribution of thick disk white dwarfs and red dwarfs to the microlensing optical depth. We do that for both the MACHO and EROS experiments in the same way as for the halo simulations presented in the previous section. The model of spectral evolution of white dwarfs adopted for this study is our model B, which we consider to be the most realistic one. Before starting the discussion of our results, we would like to emphasize that the calculation of the microlensing optical depth involves the addition of individual contributions, which are proportional to the Einstein crossing time corrected by the efficiency function - see Eq. (3). The efficiency function in turn depends on the crossing time, which is directly proportional to the Einstein radius and inversely proportional to the velocity perpendicular to the observer. For a thick disk object the average distance is smaller than that of a typical halo object. Thus there are two competing effects, smaller distances clearly imply smaller individual contributions to the optical depth. However, thick disk stars have also lower velocities than those of the halo, thus implying more important individual contributions. The precise balance between these two effects determines the final contribution.

\begin{figure} \par\includegraphics[width=12cm,clip]{12905fg4.eps} \end{figure} Figure 4:

Microlensing optical depth towards the LMC as a function of the limiting magnitude for the thick disk population. Solid and open squares represent the DA and non-DA white dwarf populations, respectively. Red dwarfs are represented by open triangles, while the entire population is shown by open circles.

Open with DEXTER

Table 3:   Summary of the results obtained for the thick disk population of microlenses towards the LMC for the MACHO experiment with a thick disk age of 12 Gyr and several magnitude cuts.

The results of these simulations are shown in Fig. 4 and Table 3. In the top panels of Fig. 4 we show the contribution of the different populations under study to the optical depth derived by the MACHO experiment for both the canonical thick disk - left panels - and the metal-weak thick disk of Carollo et al. (2010) - right panels. It is interesting to realize that in both cases DA and non-DA white dwarfs contribute by roughly the same amount. Additionally, the contribution of red dwarfs quickly decreases and becomes almost negligible for realistic magnitude cuts, while that of white dwarfs decreases only slightly. Consequently, for realistic magnitude cuts - say $m_v > 20^{\rm mag}$ - the contributions to the microlensing optical depth of both DA and non-DA white dwarfs are much more significant than that of red dwarfs. In the bottom panels of Fig. 4 we show the contribution of the entire population to the microlensing optical depth for both thick disk models. We obtain that in the case of the MACHO experiment and for a typical magnitude cut of $22.5^{\rm mag}$the contribution of the populations of the canonical thick disk white dwarfs and red dwarfs to the optical depth can be as large as 30%, which is slightly more than that of the metal-weak thick disk model, which is on the order of 20%. At first glance, this result may seem to be in contrast with other recent estimates. For instance, Alcock et al. (2000) estimated the contribution of thick disk stars to be $\sim$2% of the observed optical depth. This agrees with our model if we only consider the red dwarf population, for which we obtain a contribution to the optical depth of $\sim$3%, a value very similar to that obtained by Alcock et al. (2000). On the contrary, when thick disk white dwarfs are taken into account, the contribution of the thick disk is as large as that of the halo.

A more detailed analysis of the thick disk population can be done and reveals that in the case of the canonical thick disk the possible microlensing events have an Einstein crossing time $t_{\rm E}\approx 170$ days for a magnitude cut of $22.5^{\rm mag}$, while for the case of the metal-weak thick disk the average Einstein crossing time amounts to $t_{\rm E}\approx 120$ days. Both values are considerably higher than that of the halo population. Moreover, as can be seen in Table 3, the mean average tangential velocity is $\sim$$80~{\rm km~s^{-1}}$for both models - which is what we would expect for a thick disk population, but the mean average distance of the lenses is $\sim$4 kpc - which is comparable to that obtained for the halo population. This can be easily understood in terms of the selection criteria we use to decide when a star can be considered responsible of a microlensing event. In particular, we only consider as reliable microlensing events those in which the lens is dimmer than a certain magnitude cut and, given that the thick population is intrinsically brighter than the halo population, we only select those thick disk lenses which are far enough away. In any case, as can be seen in Table 3, our simulations show that the thick disk populations can produce at most one microlensing event. We emphasize that the results obtained using the canonical thick disk model appear to provide an upper limit for the contribution to the total microlensing optical depth - see Fig. 4.

We have also estimated the contribution to the optical depth of the thick disk populations in the case of the EROS experiment. The results are shown in Table 4. For a realistic magnitude cut of $22.5^{\rm mag}$, $1\pm1$microlensing event is expected at a 1$\sigma$confidence level. The confirmation of this microlensing event would increase the value of the optical depth measured by the EROS team by $\sim$40%. However, we point out that given the poor statistics, the number of microlensing events obtained in our simulations agrees reasonably well with the observations of the EROS team, who found none.

Table 4:   Same as table 3 for the EROS experiment.

3.4 The event rate distribution

\begin{figure} \par\includegraphics[width=12cm,clip]{12905fg5.eps} \end{figure} Figure 5:

Normalized distributions of the microlensing event rate as a function of the event duration for the different population under study (solid lines) and also for the observed microlensing events of the MACHO experiment (dashed lines). All the distributions have been computed for a magnitude cut of 22.5 $^{\rm mag}$.

Open with DEXTER

Besides the optical depth and the Einstein crossing time, a third quantity was proposed by Paczynski (1986) as relevant for the study of the microlensing experiments. This quantity is the microlensing event rate $\Gamma$, which provides the rate at which the lenses enter the microlensing tube. While the optical depth does not depend on the mass function, the event rate does, and consequently useful information about the different populations responsible for the micronlensing envents can be obtained by studying it.

In Fig. 5 we display with solid lines the normalized distributions of the microlensing event rate as a function of the event duration for the different populations of the canonical thick disk (left panels), the metal-weak thick disk (central panels) and the halo (right panels). We also show the results obtained by the MACHO team with a dashed line. The top panels show the distribution obtained for the population of red dwarfs, while the middle and the bottom panels show the distributions obtained for the populations of DA and non-DA white dwarfs respectively. To produce these distributions we have adopted a magnitude cut of $22.5^{\rm mag}$, which can be considered as representative of the current experiments. Although for this magnitude cut the contribution to the microlensing optical depth is approximately the same for the canonical thick disk (27.4%) and the halo populations (24.9%) and somewhat smaller for the metal-weak thick disk (20.3%), the event rate distributions are significantly different. We obtain for instance for the canonical thick disk population in all the cases very extended distributions with no clear maxima (except for the population of red dwarfs, which peaks at 70 days), while for the metal-weak thick disk population of red dwarfs a deficit of stars with long Einstein crossing times is found. Finally, for the halo populations the theoretical distributions of the microlensing event rate have clear maxima and moderate dispersions. Still, all the distributions are only marginally consistent with the observational distribution, which is characterized by event timescales in the range of 35 to 110 days. These results show the difficulty of explaining the MACHO microlensing events with a single population.

A more quantitative assesment of the compatibility of the different simulated populations with the observational data can be done using the Z2 compatibility test. The Z2 statistical test (Lucy 2000) is specifically designed to deal with meagre data sets and is thus especially well suited for our case. The results of this compatibility test are presented in Table 5 for the different populations under study and for different magnitude cuts. As can be seen, the probability that for our reference magnitude cut ( $22.5^{\rm mag}$) the distributions of microlensing timescales of the canonical thick disk populations are compatible with the observational data are $\sim$0.8, while those of the metal-weak thick disk are less probable ($\sim$0.7) and those of the halo populations are signifincantly smaller, $\sim$0.6. In particular it is to be noted that the population of red dwarfs and DA white dwarfs of a metal-weak thick disk is practically incompatible with the observational data when a magnitude cut of $30^{\rm mag}$ is adopted. As previously mentioned, the thick disk populations present wider timescale distributions than the halo (see Fig. 5) and, given that the observational results are to some extent spread over a wide range of timescales, the result is that the thick disk populations match the observational distribution better. Finally, it is interesting to realize that as the magnitude cut becomes larger, the compatibility of the thick disk population with the observational data substantially decreases, while those of the halo white dwarf populations remain almost constant. That is a clear consequence of the different nature of the thick disk and halo white dwarf populations: while the population of thick disk white dwarfs is constituted by bright objects at sufficiently far away distances, the halo white dwarf population is made of intrinsically dim and distant objects.

Table 5:   Z2 compatibility test between the Einstein crossing times obtained by the MACHO team and the simulated thick disk and halo populations for different magnitude cuts.

3.5 The joint contribution of the thick disk and halo populations

We have also computed the joint contribution to the microlensing optical depth of the thick disk and halo populations of red dwarfs and white dwarfs. A summary of our results is displayed in Table 6 where the same quantities are displayed as those in Table 1 for the case of the halo population and Table 3 for the case of the thick disk simulation. We present the outcome for both the cases in which a canonical thick disk (left section) and a metal-weak thick disk (right section) are adopted. Moreover, we only show in this table the results obtained for model B (which we remind is the most realistic model for the white dwarf population) when the results of the MACHO towards the LMC are simulated. The main effect is that the entire population under study can explain about half of the optical depth obtained by the MACHO experiment, irrespective of the adopted thick disk model. This value practically doubles the one obtained when only the halo population was considered. Clearly, these results indicate that the thick disk population must be taken into account as a potential source of contamination in the current experiments. For a realistic magnitude cut of $22.5^{\rm mag}$, a maximum of three microlensing events is expected at the $1\sigma$ confidence level, which is far below the $\sim$11 microlensing events of the MACHO experiment. Our results show that in the case in which a white dwarf is responsible of the microlensing event, the average mass of the lenses is approximately $0.6~M_{\hbox{$\odot$ }}$, whereas in the case in which the one responsible for the microlensing event is a red dwarf the average mass is $\sim$ $0.2~M_{\hbox{$\odot$ }}$. Both values are typical of their respective populations. Moreover, in the case of white dwarfs, half of the microlensing events are due to non-DA white dwarfs.

Table 6:   Summary of the results obtained for the thick disk and halo populations of microlenses towards the LMC for the MACHO experiment.

3.6 Halo dark matter

We have also computed the contribution of the halo populations to the baryonic dark matter density of the Galaxy. The fraction of dark matter in the form of MACHOs, f, can be directly obtained from the microlensing optical depth towards the LMC. Assuming a halo isothermal sphere we have $\tau_{\rm LMC}=5.1\times 10^{-7}f$. Thus we obtain from our simulations f=0.07 in the case of model A, whereas for model B we derive f=0.06. These values can be compared with our previous results of f=0.05 (Torres et al. 2008). Thus when we include the population of non-DA white dwarfs we find a modest increase, which is still not enough to account for the bulk of halo dark matter.

4 Conclusions

We have analyzed the contribution to the microlensing optical depth towards the LMC of the halo population of white dwarfs with both hydrogen-rich and hydrogen-deficient atmospheres. We have used three models to describe the atmospheric evolution of white dwarfs. In the first of these models we have assumed a canonical ratio of hydrogen-rich white dwarfs, to 80% independent of the effective temperature. In our second model, which we consider to be the most realistic one, we have adopted a fraction of white dwarfs with helium-rich atmospheres which depends on the effective temperature. In these two models the cooling sequences of Salaris et al. (2000) for DA white dwarfs and those of Benvenuto & Althaus (1997) for non-DA white dwarfs were used. In the third set of calculations the fraction of non-DA white dwarfs was assumed to depend on the effective temperature, but the cooling tracks of Bergeron et al. (1995) for non-DA white dwarfs were adopted. We have found that when the contribution of hydrogen-deficient white dwarfs is considered, the theoretical optical depth towards the LMC for both the MACHO and EROS experiments is substantially increased by nearly 34%, with respect to previous calculations. Nevertheless, we have also found that no more than one third of the microlensing optical depth found by the MACHO team can be explained by the halo population of white dwarfs at the 1$\sigma$ confidence level, and that no more than three microlensing events could be expected at the same confidence level in reasonable agreement with the results of the EROS experiment.

We have also studied the role played by the thick disk populations of white dwarfs and red dwarfs, thus extending our previous calculations. For this purpose we have used two thick disk models. The first one is a canonical thick disk model, while the second one corresponds to the most recent model of Carollo et al. (2010), which is based in the data of the Sloan Digital Sky Survey Data Release 7. We have obtained that for both thick disk models, the contribution of these populations to the microlensing optical depth is comparable to that of the halo populations, which is somewhat larger for the canonical thick disk model, which provides an upper limit to this contribution. In particular we have found that the thick disk contribution is dominated by the white dwarf population in both cases, as the contribution of thick disk red dwarfs is only half of that of halo red dwarfs. Besides, we have also found that the average distance of the simulated lenses is very similar for the thick and halo populations, $\sim$3 kpc. This unexpected result can be easily explained in terms of the selection criteria used to decide when a star can be considered responsible of a microlensing event. Since we only consider as reliable microlensing events those in which the lens is dimmer than a certain magnitude cut, intrinsically bright lenses must be located at larger distances. Consequently, since the thick population is intrinsically brighter than the halo population, we only select those thick disk lenses which are far enough away, at distances very similar to those of the halo population, which are naturally located at large distances. We have found as well that although both populations have similar average distances and thick disk objects have smaller average velocities, their event timescales are nearly three times more extended than those of the halo population. We have also assessed the compatibility of our simulated populations with the scarce observational data. We have found that the thick disk population agrees better with the MACHO observational distribution of event timescales than the halo population.

Finally, we found that when both the halo and the thick disk populations are considered, nearly half of the measured value of the microlensing optical depth towards the LMC can be explained at the 95% confidence level by our simulated halo and thick disk populations. According to our simulations, the fraction of halo dark matter that can be expected from MACHOs increases moderately (to f = 0.06) with respect to our previous simulations when hydrogen-deficient white dwarfs are taken into account.

Acknowledgements
Part of this work was supported by the MEC grants AYA08-04211-C02-01 and AYA08-1839/ESP, by the European Union FEDER funds and by the AGAUR.

References

  1. Adams, F. C., & Laughlin, G. 1996, ApJ, 468, 686 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alcock, C., Allsman, R. A., Alves, D. R., et al. 1997, ApJ, 486, 69 [Google Scholar]
  3. Alcock, C., Allsman, R. A., Alves, D. R., et al. 2000, ApJ, 542, 281 [NASA ADS] [CrossRef] [Google Scholar]
  4. Althaus, L. G., García-Berro, E., Isern, J., et al. 2007, A&A, 465, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Baraffe, I., Chabrier, G., Allard, F., et al. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
  6. Becker, A. C., Rest, A., Stubbs, C., et al. 2005, IAU Symp., 225, 357 [Google Scholar]
  7. Benvenuto, O. G., & Althaus, L. G. 1997, MNRAS, 288, 1004 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bergeron, P., & Leggett, S. K. 2002, ApJ, 580, 1070 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bergeron, P., Leggett, S. K., & Ruiz, M. T. 2001, ApJS, 133, 413 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bergeron, P., Wesemael, F., & Beauchamp, A. 1995, PASP, 107, 1047 [NASA ADS] [CrossRef] [Google Scholar]
  11. Binney, J., & Tremaine, H. 1987, Galactic Dynamics (Princeton: Princeton Univ. Press) [Google Scholar]
  12. Camacho, J., Torres, S., Isern, J., et al. 2007, A&A, 471, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Canal, R., Isern, J., & Ruiz-Lapuente, P. 1997, ApJ, 488, L35 [NASA ADS] [CrossRef] [Google Scholar]
  14. Carollo, D., Beers, T. C., Chiba, M., et al. 2010, ApJ, 712, 692 [NASA ADS] [CrossRef] [Google Scholar]
  15. Chabrier, G., Segretain, L., & Méra, D. 1996, ApJ, 468, 21 [Google Scholar]
  16. Charlot, S., & Silk, J. 1995, ApJ, 445, 124 [NASA ADS] [CrossRef] [Google Scholar]
  17. Dehnen, W., & Binney, J. 1998, MNRAS, 298, 387 [NASA ADS] [CrossRef] [Google Scholar]
  18. Flynn, C., Sommer-Larsen, J., Fuchs, B., et al. 2001, MNRAS, 322, 553 [NASA ADS] [CrossRef] [Google Scholar]
  19. García-Berro, E., Torres, S., Isern, J., et al. 1999, MNRAS, 302, 173 [NASA ADS] [CrossRef] [Google Scholar]
  20. García-Berro, E., Torres, S., Isern, J., et al. 2004, A&A, 418, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Gates, E., Gyuk, G., Harris, H. C., et al. 2004, ApJ, 612, L129 [NASA ADS] [CrossRef] [Google Scholar]
  22. Gilmore, G., Wyse, R. F. G., & Jones, J. B. 1995, AJ, 109, 1095 [NASA ADS] [CrossRef] [Google Scholar]
  23. Goldman, B., Afonso, A., Alard, Ch., et al. 2002, A&A, 389, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Griest, K. 1991, ApJ, 366, 412 [NASA ADS] [CrossRef] [Google Scholar]
  25. Gyuk, G., & Gates, E. 1999, MNRAS, 304, 281 [NASA ADS] [CrossRef] [Google Scholar]
  26. Gyuk, G., Dalal, N., & Griest, K. 2000, ApJ, 535, 90 [NASA ADS] [CrossRef] [Google Scholar]
  27. Hansen, B. M. S. 1998, Nature, 394, 860 [NASA ADS] [CrossRef] [Google Scholar]
  28. Hansen, B. M. S., & Liebert, J. 2003, ARA&A, 41, 465 [NASA ADS] [CrossRef] [Google Scholar]
  29. Harris, H. C., Munn, J. A., Kilic, M., et al. 2006, AJ, 131, 571 [NASA ADS] [CrossRef] [Google Scholar]
  30. Iben, I., & Laughlin, G. 1989, ApJ, 341, 312 [NASA ADS] [CrossRef] [Google Scholar]
  31. Isern, J., García-Berro, E., Hernanz, M., et al. 1998, ApJ, 503, 239 [NASA ADS] [CrossRef] [Google Scholar]
  32. James, F. 1990, Comput. Phys. Commun., 60, 329 [NASA ADS] [CrossRef] [Google Scholar]
  33. Kallivayalil, N., van der Marel, R. P., Alcock, C., et al. 2006, ApJ, 638, 772 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kilic, M., Munn, J. A., Harris, et al. 2006, ApJ, 131, 582 [Google Scholar]
  35. Lasserre, T., Afonso, C., Albert, J. N., et al. 2001, A&A, 355, L39 [Google Scholar]
  36. Liebert, J. 1989, in White Dwarfs, ed. G. Wegner (Berlin: Springer), 15 [Google Scholar]
  37. Lucy, L. 2000, MNRAS, 318, 92 [NASA ADS] [CrossRef] [Google Scholar]
  38. Mollerach, S., & Roulet, E. 2002, Gravitational Lensing and Microlensing (Singapore: World Scientific) [Google Scholar]
  39. Muraki, Y., Sumi, T., Abe, F., et al. 1999, Progr. Theor. Phys. Suppl., 133, 233 [NASA ADS] [CrossRef] [Google Scholar]
  40. Navarro, J. F., Frenck, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
  41. Oppenheimer, B. R., Hambly, N. C., Digby, A. P., et al. 2001, Science, 292, 698 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  42. Paczynski, B. 1986, ApJ, 304, 1 [NASA ADS] [CrossRef] [Google Scholar]
  43. Reid, I. N. 2005, ARA&A, 43, 247 [NASA ADS] [CrossRef] [Google Scholar]
  44. Reid, N. I., Sahu, K. C., & Hawley, S. L. 2001, ApJ, 559, 942 [NASA ADS] [CrossRef] [Google Scholar]
  45. Salaris, M., García-Berro, E., Hernanz, M., et al. 2000, ApJ, 544, 1036 [NASA ADS] [CrossRef] [Google Scholar]
  46. Scalo, J. 1998, in The Stellar Initial Mass Function, ed. G. Gilmore, & D. Howell (San Francisco: PASP Conf. Ser.), 142, 201 [Google Scholar]
  47. Schneider, P., Kochanek, C. S., & Wambsganss, J. 2004, in Saas-Fee lectures on Gravitational Lensing [Google Scholar]
  48. Tisserand, P., Le Guillou, L., Afonso, C., et al. 2007, A&A, 469, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Torres, S., García-Berro, E., & Isern, J. 1998, ApJ, 508, L71 [NASA ADS] [CrossRef] [Google Scholar]
  50. Torres, S., García-Berro, E., Burkert, A., et al. 2002, MNRAS, 336, 971 [NASA ADS] [CrossRef] [Google Scholar]
  51. Torres, S., Camacho, J., Isern, J., et al. 2008, A&A, 486, 427 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Udalski, A., Szymanski, M., Kaluzny, J., et al. 1994, Acta Astron., 44, 1 [NASA ADS] [Google Scholar]
  53. Vidrih, S., Bramich, D. M., Hewett, P. C., et al. 2007, MNRAS, 382, 515 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1:   Summary of the results obtained for the entire population of microlenses towards the LMC for several magnitude cuts when the results of the MACHO collaboration are simulated.

Table 2:   Summary of the results obtained for the entire population of microlenses towards the LMC for the EROS experiment, using models A, B and C and adopting an age of the halo of 14 Gyr and several magnitude cuts.

Table 3:   Summary of the results obtained for the thick disk population of microlenses towards the LMC for the MACHO experiment with a thick disk age of 12 Gyr and several magnitude cuts.

Table 4:   Same as table 3 for the EROS experiment.

Table 5:   Z2 compatibility test between the Einstein crossing times obtained by the MACHO team and the simulated thick disk and halo populations for different magnitude cuts.

Table 6:   Summary of the results obtained for the thick disk and halo populations of microlenses towards the LMC for the MACHO experiment.

All Figures

  \begin{figure} \par\includegraphics[width=7.6cm,clip]{12905fg1.eps} \end{figure} Figure 1:

Color-magnitude diagram of a typical $0.6~M_{\hbox{$\odot$ }}$white dwarf. The solid line corresponds to a cooling sequence of a hydrogen-rich (DA) white dwarf (Salaris et al. 2000), while the dashed line corresponds to a helium-rich (non-DA) white dwarf (Benvenuto & Althaus 1997). The dots correspond to cooling ages of 6, 8, 10, 12 and 14 Gyr.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12cm,clip]{12905fg2.eps} \end{figure} Figure 2:

Microlensing optical depth towards the LMC as a function of the limiting magnitude. Solid and open squares represent the DA and non-DA white dwarf populations, respectively. Red dwarfs are represented by open triangles, while the entire population is shown by open circles.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.2cm,clip]{12905fg3.eps} \end{figure} Figure 3:

Proper motion as a function of the V magnitude for the halo white dwarf population. The EROS selection zone is shown as a bold solid line.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12cm,clip]{12905fg4.eps} \end{figure} Figure 4:

Microlensing optical depth towards the LMC as a function of the limiting magnitude for the thick disk population. Solid and open squares represent the DA and non-DA white dwarf populations, respectively. Red dwarfs are represented by open triangles, while the entire population is shown by open circles.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12cm,clip]{12905fg5.eps} \end{figure} Figure 5:

Normalized distributions of the microlensing event rate as a function of the event duration for the different population under study (solid lines) and also for the observed microlensing events of the MACHO experiment (dashed lines). All the distributions have been computed for a magnitude cut of 22.5 $^{\rm mag}$.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.