| Issue |
A&A
Volume 511, February 2010
|
|
|---|---|---|
| Article Number | A7 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200912824 | |
| Published online | 19 February 2010 | |
Hanle signatures of the coronal magnetic field in the linear polarization of the hydrogen L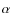 line
line
M. Derouich1,![]() - F. Auchère1 - J. C. Vial1 - M. Zhang2
- F. Auchère1 - J. C. Vial1 - M. Zhang2
1 - Institut d'Astrophysique Spatiale, CNRS-Université Paris-Sud 11, 91405 Orsay Cedex, France
2 -
National Astronomical Observatory, Chinese Academy of Sciences, Beijing 100012, PR China
Received 3 July 2009 / Accepted 21 October 2009
Abstract
Aims. This paper is dedicated to the assessment of the
validity of future coronal spectro-polarimetric observations and to
prepare their interpretation in terms of the magnetic field vector.
Methods. We assume that the polarization of the hydrogen coronal L![]() line is due to anisotropic scattering of an incident chromospheric
radiation field. The anisotropy is due to geometrical effects but also
to the inhomogeneities of the chromospheric regions which we model by
using Carrington maps of the L
line is due to anisotropic scattering of an incident chromospheric
radiation field. The anisotropy is due to geometrical effects but also
to the inhomogeneities of the chromospheric regions which we model by
using Carrington maps of the L![]() .
Because the corona is optically thin, we fully consider the effects of
the integration over the line-of-sight (LOS). As a modeling case, we
include a dipolar magnetic topology perturbed by a non-dipolar magnetic
structure arising from a prominence current sheet in the corona. The
spatial variation of the hydrogen density and the temperature is taken
into account. We determine the incident radiation field developed on
the tensorial basis at each point along the LOS. Then, we calculate the
local emissivity vector to obtain integrated Stokes parameters with and
without coronal magnetic field.
.
Because the corona is optically thin, we fully consider the effects of
the integration over the line-of-sight (LOS). As a modeling case, we
include a dipolar magnetic topology perturbed by a non-dipolar magnetic
structure arising from a prominence current sheet in the corona. The
spatial variation of the hydrogen density and the temperature is taken
into account. We determine the incident radiation field developed on
the tensorial basis at each point along the LOS. Then, we calculate the
local emissivity vector to obtain integrated Stokes parameters with and
without coronal magnetic field.
Results. We show that the Hanle effect is an interesting technique for interpreting the scattering polarization of the L![]()
![]() 1216
line in order to diagnose the coronal magnetic field. The difference
between the calculated polarization and the zero magnetic field
polarization gives us an estimation of the needed polarimetric
sensitivity in future polarization observations. We also obtain useful
indications about the optimal observational strategy.
1216
line in order to diagnose the coronal magnetic field. The difference
between the calculated polarization and the zero magnetic field
polarization gives us an estimation of the needed polarimetric
sensitivity in future polarization observations. We also obtain useful
indications about the optimal observational strategy.
Conclusions. Quantitative interpretation of the Hanle effect on the scattering linear polarization of L![]() line can be a crucial source of information about the coronal magnetic field at a height over the limb h
line can be a crucial source of information about the coronal magnetic field at a height over the limb h
![]() .
Therefore, one needs the development of spatial instrumentation to observe this line.
.
Therefore, one needs the development of spatial instrumentation to observe this line.
Key words: line: formation - Sun: corona - Sun: UV radiation - scattering
1 Introduction
One of the most powerful tools for the diagnostics of magnetic fields
in the Sun is the interpretation of polarimetric observations (e.g. the
monograph by Landi Degl'Innocenti & Landolfi 2004; and the recent review by Trujillo Bueno 2009).
However, these diagnostics are mostly concerned with the fields at the
photospheric and chromospheric levels. The coronal magnetic field
presents more intrinsic difficulties to measure and interpret. This is
especially true for the case of the UV coronal lines. Only rather
recently, Raouafi et al. (2002) performed the first measurement and interpretation of the linear polarization of a UV line (O VI ![]() 1032
line) polarized under anisotropic scattering by the underlying solar
radiation field. In addition, Manso Sainz & Trujillo Bueno (2009)
proposed a polarizing mechanism showing the adequate sensitivity of
other coronal UV lines to the direction of the magnetic field. These
successful works suggest that new UV polarimeters with high sensitivity
associated with theoretical and numerical modeling obtained with a high
degree of realism are a fundamental step to be performed in order to
extract information on the coronal plasmas. In this context, the Hanle
effect on the L
1032
line) polarized under anisotropic scattering by the underlying solar
radiation field. In addition, Manso Sainz & Trujillo Bueno (2009)
proposed a polarizing mechanism showing the adequate sensitivity of
other coronal UV lines to the direction of the magnetic field. These
successful works suggest that new UV polarimeters with high sensitivity
associated with theoretical and numerical modeling obtained with a high
degree of realism are a fundamental step to be performed in order to
extract information on the coronal plasmas. In this context, the Hanle
effect on the L![]() polarization constitutes an excellent opportunity which merits to be exploited.
polarization constitutes an excellent opportunity which merits to be exploited.
The scattering polarization of the coronal L![]() line of neutral hydrogen, which we are revisiting in this paper, has been computed by Bommier & Sahal-Bréchot (1982) and by Trujillo Bueno et al. (2005).
These authors, however, neglected the effects of the integration over
the line-of-sight (LOS) by considering a local position of the
scattering hydrogen atom. Since the corona is optically thin, the LOS
integration problem has to be solved. Fineschi et al. (1992)
treated the case of the L
line of neutral hydrogen, which we are revisiting in this paper, has been computed by Bommier & Sahal-Bréchot (1982) and by Trujillo Bueno et al. (2005).
These authors, however, neglected the effects of the integration over
the line-of-sight (LOS) by considering a local position of the
scattering hydrogen atom. Since the corona is optically thin, the LOS
integration problem has to be solved. Fineschi et al. (1992)
treated the case of the L![]() line polarization and took into account the LOS integration. However,
Fineschi et al. considered the effect of a deterministic magnetic
field vector having a direction and strength independent of the position of the scattering volume. They also treated the case of a random magnetic field.
line polarization and took into account the LOS integration. However,
Fineschi et al. considered the effect of a deterministic magnetic
field vector having a direction and strength independent of the position of the scattering volume. They also treated the case of a random magnetic field.
To improve upon these previous works, we take into account the
variation of the direction and the strength of the magnetic field for
each scattering event along the LOS. The calculation of the
polarization generated by scattering depends strongly on the level of
anisotropy of the incident radiation, which in turn depends strongly on
the geometry of the scattering process and the brightness variation of
the chromospheric regions. In order to accurately compute the degree of
the anisotropy at each scattering position, we use Carrington maps of
the chromospheric incident radiation of the L![]() line obtained by Auchère (2005).
In addition, the coronal density of the scattering atoms and the local
temperature are included according to a quiet coronal model (Cranmer
et al. 1999). We perform a comparison of the L
line obtained by Auchère (2005).
In addition, the coronal density of the scattering atoms and the local
temperature are included according to a quiet coronal model (Cranmer
et al. 1999). We perform a comparison of the L![]() linear polarization in the zero-field reference case with the amplitude
corresponding to the polarization in the presence of a magnetic field.
In our forward modeling, we adopt a dipolar magnetic distribution as a
first step and then we add a magnetic field associated to an equatorial
current sheet.
linear polarization in the zero-field reference case with the amplitude
corresponding to the polarization in the presence of a magnetic field.
In our forward modeling, we adopt a dipolar magnetic distribution as a
first step and then we add a magnetic field associated to an equatorial
current sheet.
The paper is organized as follows. We describe the theoretical
background and formulate the problem in Sect. 2. Section 3 deals
with the calculations of the Hanle effect without integration over the
LOS in order to compare with known results. The generalization of these
calculations to integrate over the LOS and the discussion of the
possibility of obtaining a coronal magnetic field through polarization
measurements are presented in Sect. 4. The technique that could be
used to measure the scattering polarization of the L![]() D2 line is given in Sect. 5; in particular we show how the linear scattering polarization could be measured using a L
D2 line is given in Sect. 5; in particular we show how the linear scattering polarization could be measured using a L![]() disk imager and coronagraph called LYOT (LYman Orbiting Telescope). In Sect. 6 we summarize our conclusions.
disk imager and coronagraph called LYOT (LYman Orbiting Telescope). In Sect. 6 we summarize our conclusions.
2 Formulation of the problem
2.1 Hanle effect
The term Hanle effect represents the ways in which the scattering polarization can be modified by weak magnetic fields. The well-known Zeeman effect and the Hanle effect are complementary because they respond to magnetic fields in very different parameter regimes. The Zeeman effect depends on the ratio between the Zeeman splitting and the Doppler line width. The Hanle effect though depends on the ratio between the Zeeman splitting and the inverse life time of the atomic levels involved in the process of the formation of the polarized line. For the permitted UV lines, the Zeeman effect is of limited interest for the determination of the magnetic fields in the quiet corona. This is because the ratio between the Zeeman splitting and the Doppler width is small due to the weakness of the magnetic field and the high Doppler width in such hot coronal plasmas. On the contrary, the measurement and physical interpretation of the scattering polarization of the UV lines are a very efficient diagnostic tool for determining the coronal magnetic field through its Hanle effect.
2.2 Atomic linear polarization
The possibility of the creation of a linear polarization by anisotropic scattering can be only explained correctly in the framework of the quantum-mechanical scattering theory. In fact, the intrinsic capacity of a line to be polarized is intimately linked to subtle quantum behaviors pertaining to the atomic levels involved in the transition. Let us denote by mJ the projection of the orbital angular momentum J of the hydrogen atom; mJ takes the values -J, J+1, ..., J. The term ``atomic linear polarization" in a J-level consists in (e.g. Cohen-Tannoudji & Kastler 1966; Omont 1977; Sahal-Bréchot 1977; Blum 1981):- -
- an unbalance of the populations of the Zeeman sub-levels having different absolute values |mJ|;
- -
- a presence of interferences between these Zeeman sub-levels.
2.3 Linear scattering polarization in the L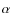 line
line
The so-called scattering polarization is simply the observational manifestation of the atomic polarization. The Hanle effect
is nothing but a perturbation of the atomic polarization by a magnetic
field. The Hanle signatures in the spectrum of the linear polarization
are a variation of the polarization degree and a rotation of the
polarization plane. These Hanle signatures can be used to retrieve
information on coronal magnetic fields. The two components D1 and D2 of the L![]() connect the hydrogen ground state
connect the hydrogen ground state
![]() to the electronic excited states
to the electronic excited states
![]() and
and
![]() ,
respectively. The upper level
,
respectively. The upper level
![]() of the D2 line can be polarized due to the difference of the populations between the Zeeman sub-levels with |mJ|=1/2 and |mJ|=3/2. However, the states
of the D2 line can be polarized due to the difference of the populations between the Zeeman sub-levels with |mJ|=1/2 and |mJ|=3/2. However, the states
![]() and
and
![]() cannot be polarized since |mJ|
is necessarily 1/2 implying that no difference of population inside
these states can be generated by anisotropic scattering. Consequently,
the D1 line is not linearly polarizable.
cannot be polarized since |mJ|
is necessarily 1/2 implying that no difference of population inside
these states can be generated by anisotropic scattering. Consequently,
the D1 line is not linearly polarizable.
It is useful to keep in mind that in the description of the emitting
hydrogen atom, we neglect the contribution of the hyperfine structure
(HFS). For instance if the HFS is not neglected, the level J = 1/2 of the ground state
![]() is split into hyperfine levels F = 0 and F = 1 due to coupling with the nuclear spin of the hydrogen I = 1/2. The hyperfine level F = 1 can be linearly polarized
is split into hyperfine levels F = 0 and F = 1 due to coupling with the nuclear spin of the hydrogen I = 1/2. The hyperfine level F = 1 can be linearly polarized![]() , which means that the D1 line can be polarized and the polarization of the D2 line can be affected. As previously suggested by Bommier & Sahal-Bréchot (1982), we neglect the effect of the HFS in the process of formation of L
, which means that the D1 line can be polarized and the polarization of the D2 line can be affected. As previously suggested by Bommier & Sahal-Bréchot (1982), we neglect the effect of the HFS in the process of formation of L![]() line.
line.
2.4 Expression of the Stokes parameters
The emission of the L![]()
![]() 1216 line in the solar corona has been discovered by Gabriel et al. (1971). They concluded that in most coronal structures the process responsible for the formation of the L
1216 line in the solar corona has been discovered by Gabriel et al. (1971). They concluded that in most coronal structures the process responsible for the formation of the L![]() line is the photo-excitation by underlying radiation. The creation of
population imbalances and the quantum interferences in the
line is the photo-excitation by underlying radiation. The creation of
population imbalances and the quantum interferences in the
![]() and thus the existence of the scattering polarization in the D2 L
and thus the existence of the scattering polarization in the D2 L![]() line are caused by the photo-excitation of coronal neutral hydrogen by anisotropic chromospheric radiation (see Fig. 1).
line are caused by the photo-excitation of coronal neutral hydrogen by anisotropic chromospheric radiation (see Fig. 1).
The components of the incident radiation field at a frequency ![]() are usually denoted by
are usually denoted by
![]() where k is the tensorial order and q represents the coherences in the tensorial basis (
where k is the tensorial order and q represents the coherences in the tensorial basis (
![]() ); the order k can be equal to 0 (with q=0) or 2 (with q=0,
); the order k can be equal to 0 (with q=0) or 2 (with q=0, ![]() 1,
1, ![]() 2).
This radiation field with six components constitutes a generalization
of the unpolarized light field where only the quantity
2).
This radiation field with six components constitutes a generalization
of the unpolarized light field where only the quantity
![]() is considered. In fact,
is considered. In fact,
![]() is proportional to the intensity of the radiation.
is proportional to the intensity of the radiation.
If the incident radiation is no longer anisotropic, the components
![]() become zero, which means that no linear polarization can be created as
a result of scattering processes. Regardless of the anisotropy of the
incident radiation, the radiation component associated with the
circular polarization usually denoted by
become zero, which means that no linear polarization can be created as
a result of scattering processes. Regardless of the anisotropy of the
incident radiation, the radiation component associated with the
circular polarization usually denoted by
![]() is negligible. This means that no odd order k can be created inside the scattering hydrogen atom. As a result, the Stokes V of the scattered radiation is zero.
is negligible. This means that no odd order k can be created inside the scattering hydrogen atom. As a result, the Stokes V of the scattered radiation is zero.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{figure1.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12824-09/Timg25.png)
|
Figure 1:
Geometry of the scattering of chromospheric L |
| Open with DEXTER | |
We denote by ![]() the angle between the direction of the incident light MP and the local
vertical through the scattering center OP. The incident radiation comes
from a chromospheric spherical cap limited by an angle
the angle between the direction of the incident light MP and the local
vertical through the scattering center OP. The incident radiation comes
from a chromospheric spherical cap limited by an angle
![]() corresponding to the tangent to the solar limb (see Fig. 1).
corresponding to the tangent to the solar limb (see Fig. 1). ![]() is the azimuth angle around the normal with respect to an arbitrary reference. Note that
is the azimuth angle around the normal with respect to an arbitrary reference. Note that ![]()
![]()
![]()
![]() and 0
and 0 ![]()
![]()
![]() 2
2 ![]() .
When the distance from the solar surface increases, the anisotropy of
the light becomes larger and the polarization degree increases. The
maximum of polarization is reached when the radiation is purely
directive, i.e. the spherical cap is seen by the scattering hydrogen
atom as a point. It is useful to notice that if the chromosphere is
assumed to be uniform the radiation has a cylindrical symmetry around
its preferred direction, implying that the coherence components with
.
When the distance from the solar surface increases, the anisotropy of
the light becomes larger and the polarization degree increases. The
maximum of polarization is reached when the radiation is purely
directive, i.e. the spherical cap is seen by the scattering hydrogen
atom as a point. It is useful to notice that if the chromosphere is
assumed to be uniform the radiation has a cylindrical symmetry around
its preferred direction, implying that the coherence components with ![]() are zero. In fact,
are zero. In fact,
![]() and
and
![]() components quantify the breaking of the cylindrical symmetry around the axis of quantification which is here the local vertical.
components quantify the breaking of the cylindrical symmetry around the axis of quantification which is here the local vertical.
In the framework of the two level approximation, where only the upper
level is polarized, the statistical equilibrium equations are solved
analytically. The upper level density matrix elements are simply
proportional to the incident radiation elements
![]() .
The emissivity vector is then expressed as a function of the incident
radiation field. Consequently, we do not explicitly calculate the
density matrix elements, but instead we determine the incident
radiation tensor at each scattering position along the line of sight.
For an unmagnetized atmosphere, in an arbitrary reference, the
emissivity vector can be written as (e.g. Landi Degl'Innocenti &
Landolfi 2004):
.
The emissivity vector is then expressed as a function of the incident
radiation field. Consequently, we do not explicitly calculate the
density matrix elements, but instead we determine the incident
radiation tensor at each scattering position along the line of sight.
For an unmagnetized atmosphere, in an arbitrary reference, the
emissivity vector can be written as (e.g. Landi Degl'Innocenti &
Landolfi 2004):
| (1) |
where
In order to determine the magnetic field one has to include its Hanle effect on the polarization of the L![]() light, then, for a given magnetic field vector
light, then, for a given magnetic field vector ![]() ,
,
![]() becomes (e.g. Landi Degl'Innocenti & Landolfi 2004):
becomes (e.g. Landi Degl'Innocenti & Landolfi 2004):
| (2) |
This expression of
| (3) |
where the Einstein coefficient for spontaneous emission AJuJl is given in [107 s-1], gu=4/3 is the Landé factor of the level
3 Hanle effect without integration over the LOS
We developed a numerical code allowing for the calculation of the
theoretical polarization taking into account the effects of the LOS. In
order to validate the code, we considered typical cases of a horizontal
magnetic field having different azimuth angles ![]() (angles between the magnetic field vector and the LOS). LOS
integrations are avoided in order to be able to compare our results
with well known Hanle effect results. We retrieve the Hanle behaviors
typically encountered in the literature, for instance:
(angles between the magnetic field vector and the LOS). LOS
integrations are avoided in order to be able to compare our results
with well known Hanle effect results. We retrieve the Hanle behaviors
typically encountered in the literature, for instance:
- -
- when the magnetic field is zero or very small or oriented along the symmetry axis of the radiation field, the polarization is not affected;
- -
- when the field increases until reaching the critical value corresponding to Hu=1, the polarization decreases rapidly. Moreover, for a very large Hu (i.e. very large magnetic field strength) we obtain an asymptotical curve of polarization
![$p[B \to \infty]$](/articles/aa/full_html/2010/03/aa12824-09/img46.png) which depends only on the value of
which depends only on the value of 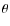 but not on the magnetic field strength. The asymptotic value of
but not on the magnetic field strength. The asymptotic value of
![$p[B \to \infty]$](/articles/aa/full_html/2010/03/aa12824-09/img46.png) divided by p[B =0] equals 1/5 when the distribution of the magnetic field is isotropic
divided by p[B =0] equals 1/5 when the distribution of the magnetic field is isotropic![[*]](/icons/foot_motif.png) and 1/4 when the field has a cylindrical symmetry (i.e. horizontal magnetic field with random azimuth);
and 1/4 when the field has a cylindrical symmetry (i.e. horizontal magnetic field with random azimuth);
- -
- no rotation of the plane of the polarization in the case of a highly symmetric distribution (e.g. isotropic or cylindrical) because the contributions of opposite magnetic polarities tend to cancel out;
- -
- we find that a meridian magnetic vector (i.e. horizontal with
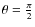 )
presents a depolarizing effect without rotation of the polarization direction.
)
presents a depolarizing effect without rotation of the polarization direction.
4 Hanle effect integrated over the LOS
The corona being an optically thin medium for the L![]() line,
it is then necessary to consider the effects of the integration over
the LOS. We adopt the analytical magnetic field model proposed by Fong
et al. (2002) and Low et al. (2003).
It is a sum of two terms: a purely dipolar term and a term
corresponding to the magnetic field of a current sheet structure. The
model is axisymmetric and the prominence is treated as a cold plasma
sheet forming a flat ring around the Sun. We take into consideration
that the current is in the equator and that it represents a prominence
sheet extending from
line,
it is then necessary to consider the effects of the integration over
the LOS. We adopt the analytical magnetic field model proposed by Fong
et al. (2002) and Low et al. (2003).
It is a sum of two terms: a purely dipolar term and a term
corresponding to the magnetic field of a current sheet structure. The
model is axisymmetric and the prominence is treated as a cold plasma
sheet forming a flat ring around the Sun. We take into consideration
that the current is in the equator and that it represents a prominence
sheet extending from
![]() to
to
![]() .
In the analytical expression of the magnetic field the contribution of
the current sheet, relative to the dipolar background field is
controlled by a constant ratio
.
In the analytical expression of the magnetic field the contribution of
the current sheet, relative to the dipolar background field is
controlled by a constant ratio ![]() (see Eq. (12)
of Low et al. 2003).
(see Eq. (12)
of Low et al. 2003).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{figure2.eps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12824-09/Timg51.png)
|
Figure 2:
A purely dipolar magnetic field structure presented in the plane (x,z) in units of the solar radius |
| Open with DEXTER | |
4.1 Purely dipolar magnetic field: 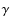 = 0
= 0
As a first step, we avoid the effect of the term associated to the current sheet by taking ![]() .
Figure 2
represents the dipolar term of the magnetic field. This configuration
represents a typical coronal magnetic field of 15 to 20 Gauss close to
the base of the corona. The Hanle effect of the dipolar magnetic field
depends on the angle
.
Figure 2
represents the dipolar term of the magnetic field. This configuration
represents a typical coronal magnetic field of 15 to 20 Gauss close to
the base of the corona. The Hanle effect of the dipolar magnetic field
depends on the angle ![]() between the axis of symmetry of the incident light
between the axis of symmetry of the incident light![]() and the axis of symmetry of the magnetic structure. It also depends on the height above the solar surface h mainly because the magnetic field strength decreases and the anisotropy of the incident light increases. The parameters
and the axis of symmetry of the magnetic structure. It also depends on the height above the solar surface h mainly because the magnetic field strength decreases and the anisotropy of the incident light increases. The parameters ![]() and h are represented in Fig. 3.
and h are represented in Fig. 3.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{figure3.eps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12824-09/Timg53.png)
|
Figure 3:
The polarization at each position P of the scattering event depends on the height over the limb h and the angle |
| Open with DEXTER | |
In theory, the expression of the emissivity vector is valid regardless
of the location of the scattering atom. However, the integration over
the LOS must take into account the inhomogeneities of the solar
conditions like the variation of the hydrogen density, the temperature,
the magnetic field and the variation of the incident radiation field.
The density of neutral hydrogen and the temperature are assumed to be a
function of the radial distance r and the latitude (see Cranmer et al. 1999, for details). In order to model the inhomogeneities of the chromospheric intensity, we use the Carrington maps of the L![]() chromospheric line built by Auchère (2005).
In the optically thin limit, the integrated Stokes parameters of the
scattered radiation reduce to a volume integration over the LOS:
chromospheric line built by Auchère (2005).
In the optically thin limit, the integrated Stokes parameters of the
scattered radiation reduce to a volume integration over the LOS:
| (4) |
then the polarization degree is
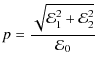
|
(5) |
and the rotation of the direction of the polarization
| (6) |
Figure 4 shows the variation of the linear polarization with the inclination
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{figure4.eps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12824-09/Timg62.png)
|
Figure 4:
Linear polarization degree obtained for a dipolar magnetic field divided by zero-field polarization versus the angle |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{figure5.eps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12824-09/Timg63.png)
|
Figure 5:
Rotation angle obtained after integration over the LOS versus the inclination |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.7cm,clip]{figure6.eps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12824-09/Timg64.png)
|
Figure 6: Perturbation of the lines
of the dipolar magnetic field due to an equatorial current sheet. The
calculations of the polarization given in Fig. 7 are obtained for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{figure7.eps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12824-09/Timg65.png)
|
Figure 7:
Linear polarization degree versus the height from the solar surface h.
We put together the results obtained in the zero-field case and these
obtained for (1) a purely dipolar magnetic field (2) the sum of a
dipolar field and a non-dipolar field associated to a current sheet
with
|
| Open with DEXTER | |
4.2 Perturbed dipolar field:
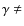 0
0
To the dipolar part of the magnetic field we now add the contribution
resulting from an equatorial current sheet. We adopt a ratio
![]() between the current sheet and the dipolar background field. In order to
highlight the Hanle effect of the equatorial current sheet, we
calculate the degree of polarization in a position located at
between the current sheet and the dipolar background field. In order to
highlight the Hanle effect of the equatorial current sheet, we
calculate the degree of polarization in a position located at
![]() ,
and we vary the height above the limb h (see Fig. 6). Figure 7
shows the difference between the linear polarization in the
zero-magnetic field case and the one in the presence of the magnetic
field,
,
and we vary the height above the limb h (see Fig. 6). Figure 7
shows the difference between the linear polarization in the
zero-magnetic field case and the one in the presence of the magnetic
field,
![]() .
A polarimetric sensitivity smaller than
.
A polarimetric sensitivity smaller than ![]() is needed in order to apply the Hanle effect as a technique of magnetic field investigations. Our results show that
is needed in order to apply the Hanle effect as a technique of magnetic field investigations. Our results show that
![]() %,
i.e. well within the typical measurement sensitivities of a new
generation of instruments such as LYOT (see Sect. 5). We point out that
by using the UV SUMER spectrometer aboard SoHO, Raouafi et al. (1999) measured the linear polarization of the O VI
%,
i.e. well within the typical measurement sensitivities of a new
generation of instruments such as LYOT (see Sect. 5). We point out that
by using the UV SUMER spectrometer aboard SoHO, Raouafi et al. (1999) measured the linear polarization of the O VI ![]() 1032
line with a polarimetric precision equal to 1.7%. We note in passing
that such an accuracy is reached although SUMER was not initially
designed to measure the polarization.
1032
line with a polarimetric precision equal to 1.7%. We note in passing
that such an accuracy is reached although SUMER was not initially
designed to measure the polarization.
5 Measurement of the linear polarization degree and its direction
5.1 Principle of the measurement
Raouafi et al. (1999) used the rotation of the SUMER spectrometer to measure the linear polarization of the D2 component of the O VI ![]() 1032 line. They extracted the polarization of the D2 line from a ratio of the intensities of the non-polarizable D1 line and of the D2 line (see the Fig. 3 of Raouafi et al. 1999).
This technique was possible because the wavelengths of the two components D1 and D2 are sufficiently different to be resolved (1031.93 Å for the D2 line and 1037.62 Å for the D1). However, the wavelengths of the D1 and D2 lines of the L
1032 line. They extracted the polarization of the D2 line from a ratio of the intensities of the non-polarizable D1 line and of the D2 line (see the Fig. 3 of Raouafi et al. 1999).
This technique was possible because the wavelengths of the two components D1 and D2 are sufficiently different to be resolved (1031.93 Å for the D2 line and 1037.62 Å for the D1). However, the wavelengths of the D1 and D2 lines of the L![]() line cannot be resolved since they are very close: in the vacuum
line cannot be resolved since they are very close: in the vacuum ![]() (D
1)= 1215.668 Å and
(D
1)= 1215.668 Å and ![]() (D
2)= 1215.674 Å. As a result, the technique presented by Fig. 3 of Raouafi et al. (1999) cannot be applied to measure the linear polarization of the D2 line of L
(D
2)= 1215.674 Å. As a result, the technique presented by Fig. 3 of Raouafi et al. (1999) cannot be applied to measure the linear polarization of the D2 line of L![]() .
.
Using the so-called Poincaré representation![]() ,
one can demonstrate that the intensity observed when the instrument is
placed at an arbitrary position referred by an angle
,
one can demonstrate that the intensity observed when the instrument is
placed at an arbitrary position referred by an angle ![]() around the LOS, is
around the LOS, is
In this expression the Stokes V is assumed to be zero. The quantity I denotes the unpolarized part of the intensity of the D1 and D2 L
Note that
On the other hand, generally speaking, the linear polarization is defined as
where
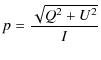
|
(10) |
and
In Eq. (11) we have three unknowns: I, p, and
| |
= | 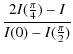
|
(12) |
| p | = | 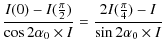
|
where the intensity of the unpolarized light is given by:
| (13) |
Obviously, more than three measurements of
5.2 The LYOT project
The LYOT project is a L6 Conclusion
Measurement and interpretation of the scattering polarization of UV coronal lines provide a largely unexplored diagnostic of the coronal magnetic field. The greatest difficulty facing the UV coronal spectropolarimetry is that the polarization measurements integrate radiation along the LOS over structures with different properties but also that the observations of these lines are impossible from ground-based telescopes; they can only be observed with the help of high-sensitivity instruments flown on space missions.We have performed a forward modeling of the coronal Hanle effect on the polarization of the L![]() line generated by anisotropic scattering of chromospheric light.
The main feature of this modeling consists in integrating the effect of
the LOS. We show that the information about the coronal magnetic field
is not lost through LOS integration. To confirm these results, we plan
to work with different families of maps of magnetic fields and to add
small scale magnetic perturbations. For instance, one can think of a
set of active loops whose field determination could be compared with
field extrapolations. One should however keep in mind that (1) a
realistic thermodynamic model is required in order to integrate along
the LOS and that (2) our modeling is limited to the case of optically
thin plasmas in the L
line generated by anisotropic scattering of chromospheric light.
The main feature of this modeling consists in integrating the effect of
the LOS. We show that the information about the coronal magnetic field
is not lost through LOS integration. To confirm these results, we plan
to work with different families of maps of magnetic fields and to add
small scale magnetic perturbations. For instance, one can think of a
set of active loops whose field determination could be compared with
field extrapolations. One should however keep in mind that (1) a
realistic thermodynamic model is required in order to integrate along
the LOS and that (2) our modeling is limited to the case of optically
thin plasmas in the L![]() line.
line.
Finally, we notice that it is suitable to combine measurements in L![]() with measurements in polarized lines like the Fe XIV
with measurements in polarized lines like the Fe XIV ![]() 5303
which have a different sensitivity to the magnetic field. An analysis
of combined measurements should give more information data to constrain
the magnetic field topology and strength (an example of the Hanle
effect in a multi-line approach is given in Landi Degl'Innocenti 1982). It is also of interest to remark that the ground level
5303
which have a different sensitivity to the magnetic field. An analysis
of combined measurements should give more information data to constrain
the magnetic field topology and strength (an example of the Hanle
effect in a multi-line approach is given in Landi Degl'Innocenti 1982). It is also of interest to remark that the ground level
![]() of L
of L![]() is non polarizable by radiation anisotropy, but that this is no longer
true in the presence of hyperfine structure and if the depolarizing
effect of the isotropic collisions is negligible. Because the
sensitivity to the Hanle effect depends on the level life-time, the
hyperfine polarization of such a long-lived level is much more
vulnerable to very weak magnetic fields than the short-lived upper
levels
is non polarizable by radiation anisotropy, but that this is no longer
true in the presence of hyperfine structure and if the depolarizing
effect of the isotropic collisions is negligible. Because the
sensitivity to the Hanle effect depends on the level life-time, the
hyperfine polarization of such a long-lived level is much more
vulnerable to very weak magnetic fields than the short-lived upper
levels ![]() .
Consequently, one could distinguish a very small perturbation of the
magnetic field (smaller than 1 Gauss) which corresponds for
instance to a current sheet with a very small
.
Consequently, one could distinguish a very small perturbation of the
magnetic field (smaller than 1 Gauss) which corresponds for
instance to a current sheet with a very small ![]() and a background field of the order of 10 Gauss or larger. In
particular, this could be the key to distinguish potential magnetic
field structures from non potential ones.
and a background field of the order of 10 Gauss or larger. In
particular, this could be the key to distinguish potential magnetic
field structures from non potential ones.
References
- Auchère, F. 2005, ApJ, 622, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, K. 1981, Density Matrix Theory and Applications (New York: Plenum Press) [Google Scholar]
- Bommier, V., & Sahal-Bréchot, S. 1982, Sol. Phys., 78, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R., Kohl, J. L., Noci, G., et al. 1999, ApJ, 511, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen-Tannoudji, C., & Kastler, A. 1966, in Progress in Optics, ed. E. Wolf, 5, 1 [Google Scholar]
- Fong, B., Low, B. C., & Fan, Y. 2002, ApJ, 571, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Gabriel, A. H., Garton, W. R. S., Goldberg, L., et al. 1971, ApJ, 169, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Judge, P. G., Low, B. C., & Casini, R. 2006, ApJ, 651, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Landi Degl'Innocenti, E. 1982, Sol. Phys., 79, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Landi Degl'Innocenti, E. 1982, Sol. Phys., 91, 1 [Google Scholar]
- Landi Degl'Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines (Dordrecht: Kluwer) [Google Scholar]
- Low, B. C., Fong, B., & Fan, Y. 2003, ApJ, 594, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Millard, A. A., Lemaire, P., & Vial, J. C., 2006, Proc. SPIE, 6266, 62662G [CrossRef] [Google Scholar]
- Manso Sainz, R., & Trujillo Bueno, J. 2009, in Solar Polarization 5, ed. S. Berdyugina, K. N. Nagendra, & R. Ramelli, ASP Conf. Ser., 405, 423 [Google Scholar]
- Omont A. 1977, Prog. Quantum Electronics, 5, 69 [Google Scholar]
- Raouafi, N.-E., Sahal-Bréchot, S., & Lemaire, P. 1999, 9th European Meeting on Solar Physics, ed. A. Wilson, European Space Agency, ESA SP-448, 1205 [Google Scholar]
- Raouafi, N.-E., Sahal-Bréchot, S., & Lemaire, P. 2002, A&A, 396, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahal-Bréchot, S. 1977, ApJ, 213, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo Bueno, J. 2009, in Magnetic Coupling between the Interior and the Atmosphere of the Sun, ed. S. S. Hasan, & R. J. Rutten, Astrophysics and Space Science Proceedings (Springer-Verlag), in press [arXiv0903.4372T] [Google Scholar]
- Trujillo Bueno, J., Landi degl'Innocenti, E., Casini, R., & Marítnez Pillet, V. 2005, 39th ESLAB Symposium on Trends in Space Science and Cosmic Vision 2020, ed. F. Favata, J. Sanz-Forcada, A. Gimnez, & B. Battrick, ESA SP-588, 203 [Google Scholar]
- Vial, J.-C., et al., 2002, The solar high resolution imager-coronograph LYOT mission, Astronomical telescopes and instrumentation, SPIE, 4853, 479 [Google Scholar]
- Vial, J.-C., Auchére, F., Chang, J., et al., 2008, Adv. Space Res., 41, 183 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ...
![[*]](/icons/foot_motif.png)
- Present address: Colorado Research Associates Division, NorthWest Research Associates, Inc., 3380 Mitchell Ln., Boulder, CO 80301, USA.
- ... polarized
![[*]](/icons/foot_motif.png)
- In other words, population imbalances and quantum interferences between the sub-levels having |mF|=1 and |mF|=0 can be created due to the scattering of anisotropic light. The same is true for the hyperfine levels of the upper states
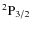 and
and
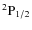 .
.
- ... isotropic
![[*]](/icons/foot_motif.png)
- The case of isotropic field distribution is encountered in the photosphere of the Sun (second solar spectrum) where the magnetic geometries are unresolved within the spatiotemporal resolution of the current observational capabilities.
- ... light
![[*]](/icons/foot_motif.png)
- Rigorously speaking, this is only the axis of symmetry of the spherical cap where the chromospheric radiation is uniform. The fact that the incident radiation is inhomogeneous implies that this symmetry around the preferred axis of radiation is broken.
- ... representation
![[*]](/icons/foot_motif.png)
- A suitable graphical representation of polarized light conceived by Henri Poincaré in 1892.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{figure1.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12824-09/Timg25.png)
|
Figure 1:
Geometry of the scattering of chromospheric L |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{figure2.eps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12824-09/Timg51.png)
|
Figure 2:
A purely dipolar magnetic field structure presented in the plane (x,z) in units of the solar radius |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{figure3.eps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12824-09/Timg53.png)
|
Figure 3:
The polarization at each position P of the scattering event depends on the height over the limb h and the angle |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{figure4.eps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12824-09/Timg62.png)
|
Figure 4:
Linear polarization degree obtained for a dipolar magnetic field divided by zero-field polarization versus the angle |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{figure5.eps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12824-09/Timg63.png)
|
Figure 5:
Rotation angle obtained after integration over the LOS versus the inclination |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4.7cm,clip]{figure6.eps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12824-09/Timg64.png)
|
Figure 6: Perturbation of the lines
of the dipolar magnetic field due to an equatorial current sheet. The
calculations of the polarization given in Fig. 7 are obtained for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{figure7.eps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12824-09/Timg65.png)
|
Figure 7:
Linear polarization degree versus the height from the solar surface h.
We put together the results obtained in the zero-field case and these
obtained for (1) a purely dipolar magnetic field (2) the sum of a
dipolar field and a non-dipolar field associated to a current sheet
with
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


