| Issue |
A&A
Volume 511, February 2010
|
|
|---|---|---|
| Article Number | A28 | |
| Number of page(s) | 5 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/200912744 | |
| Published online | 26 February 2010 | |
Rotational excitation and de-excitation of CH+ molecules by 4He atoms
F. Turpin - T. Stoecklin - A. Voronin
Institut des Sciences Moléculaires, UMR5255-CNRS, Université de Bordeaux, France
Received 22 June 2009 / Accepted 11 November 2009
Abstract
We present a quantum mechanical investigation of rotational energy
transfer in cold collisions of CH+ with 4He
atoms. We use a global 3D potential energy surface obtained using the
reproducing Kernel Hilbert Space (RKHS) method. Rotational deactivation
transition cross-sections are performed for collision energy ranging
from 10-6 to 3000 cm-1
and the corresponding rotational deactivation and excitation rate
coefficients are evaluated for the transitions of levels up to j
= 5 and temperatures up to 500 K. We also discuss the validity of the
rigid rotor approximation for this collision.
Key words: molecular data - molecular processes - ISM: molecules - astrochemistry
1 Introduction
The methylidyne cation (CH+), a key species of carbon chemistry in diffuse interstellar molecular clouds, was one of the first molecules to be detected in the interstellar medium (Douglas & Herzberg 1941). It has been the target of a very large number of subsequent observations (Federman 1982), but its observed over-abundance remains questionable. Several mechanisms have been proposed to explain its formation. Bates & Spitzer (1951) and later, Solomon & Klemperer (1972) first suggested radiative association (1) that produces CH+ given by
but the currently accepted value of the reaction rate coefficient
but again this hypothesis was not fully conclusive. Federman (1982) demonstrated that an empirical linear relation exists between the abundances of CH+and H I. However, the computed theoretical abundance does not agree with the observational results. When analysing high spectral resolution astronomical data, Weselak et al. (2004) also showed how difficult it is to discriminate CH+ from CH. In two previous works, we studied the H + CH+ reaction (Stoecklin & Halvick 2005; Halvick et al. 2007), and we focus our interest in the present article, on the rotational excitation of CH+ in collisions with 4He atoms, which we need to understand in modelling the CH+ molecular abundance of diffuse interstellar clouds.
At very low temperature, collisional rates are difficult to measure experimentally for both neutral and ionic species, and the lack of accurate values is currently a major source of uncertainty in interpreting astrophysical data. While the experimental and theoretical spectra of CH+ have been studied (Pearson & Drouin 2006; Hakalla et al. 2006), to our knowledge, no experimental data is available for the He-CH+ collisional rate.
On the theoretical side, rotationally inelastic close coupling calculations were performed for this system by Hammami et al. (2008), for collision energies ranging from 0 to 2500 cm-1. However, this study was limited to the rigid rotor approximation and their 2D surface did not include the long-range interactions that, are very important to ionic systems. The long-range charge-induced dipole potential is expected to strongly alter the threshold behaviour of the elastic and inelastic cross-sections. On the other hand, at higher temperatures, the energy transfer between the vibrational and the rotational modes, is not described by the rigid rotor approximation. We previously showed (Stoecklin & Voronin 2008) that the unusual geometry of the complex leads to a strong coupling between vibration and rotation. The vibrational and rotational quenching cross-sections are found to be of the same order of magnitude for this system. In the present work, we discuss both the validity of the rigid rotor approximation for this collision and the modifications of the results by the long-range potential. We use the 3D analytical representation of the potential-energy surface (Stoecklin & Voronin 2008) that we developed for the study of ro-vibrational energy transfer. This analytical model is based on a grid of potential-energy points calculated using the coupled cluster method (BCCD(T)) with Brueckner orbitals (Handy et al. 1989). The cc-pVQZ basis of Dunning (1993) was employed and complemented by a set of bound functions of Tao & Pan (1992). The analytical model of the potential-energy surface was obtained by using the reproducing kernel Hilbert space method (Ho & Rabitz 1996), which accurately describes the long-range part of the surface. This method has already been used in several other studies of Van der Waals systems such as He-HF (Reese et al. 2005) and is very effective in terms of precision.
In Sect. 2, we first describe the method and parameters used to complete the scattering calculations. The results are then presented and compared with those of the Langevin model in Sect. 3. Section 4 presents our conclusions.
2 Scattering calculations
The close-coupling calculations are performed using the Newmat code (Stoecklin & Voronin 2005), which is based on the Magnus propagator introduced by Light and coworkers (Anderson 1982; Stechel et al. 1978). The scattering equations are propagated in space-fixed coordinates and the asymptotic matching to diagonal spherical Bessel functions of the first and second kind follows the method described by Launay (1977).The cross-sections are calculated from the T
matrix elements obtained for a given transition from an initial
vibrational-rotational level, labelled by the quantum numbers ![]() to a final level labelled by the quantum numbers
to a final level labelled by the quantum numbers ![]() ,
,
where J and l are, respectively, the total and the orbital angular momentum quantum numbers. The wave vector is given by
The de-excitation rate coefficients are then calculated by
averaging
the cross-sections over a Boltzmann distribution of the relative
kinetic energy
The detailed balance relationship is eventually used to obtain the excitation rate coefficients
Because the rotational constant of CH+is
relatively large (around 14 cm-1), a basis
composed of 10 rotational states for both vibrational levels ![]() and
and ![]() considered in the calculations, was sufficient to obtain a convergence
of the cross-sections closer than 1 percent. The maximum propagation
distance was 300 Bohr and convergence was checked as a
function of the propagator step size. The matrix elements of the
potential were obtained by expanding the potential in terms of Legendre
polynomials retaining terms up to l=6 on a grid of
10 points, used to calculate the Gauss-Hermite quadrature of the
vibrational part of the integral. This operation is repeated for each
point of the propagation grid. We computed the diatomic wave function
by solving the diatomic equation, using an extended Hartree Fock fit of
the ab initio diatomic potential and the same numerical procedure
applied in our previous works (Reese
et al. 2005).
considered in the calculations, was sufficient to obtain a convergence
of the cross-sections closer than 1 percent. The maximum propagation
distance was 300 Bohr and convergence was checked as a
function of the propagator step size. The matrix elements of the
potential were obtained by expanding the potential in terms of Legendre
polynomials retaining terms up to l=6 on a grid of
10 points, used to calculate the Gauss-Hermite quadrature of the
vibrational part of the integral. This operation is repeated for each
point of the propagation grid. We computed the diatomic wave function
by solving the diatomic equation, using an extended Hartree Fock fit of
the ab initio diatomic potential and the same numerical procedure
applied in our previous works (Reese
et al. 2005).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig1New.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg15.png)
|
Figure 1: Comparison between the elastic cross-sections (in Angstrom2) of CH+ (v = 0, j=1) by collision with 4He and 3He as a function of the kinetic energy in cm-1. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig2New.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg16.png)
|
Figure 2: Elastic and rotational deactivation cross sections (in Angstrom2) of CH+ (v = 0, j=1) in collision with 4He as a function of the kinetic energy in cm-1. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig3New.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg17.png)
|
Figure 3: Elastic and rotational deactivation cross sections (in Angstrom2) of CH+ (v=0, j= 2) in collision with 4He as a function of the kinetic energy in cm-1. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig4New.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg18.png)
|
Figure 4: Elastic and rotational deactivation cross sections (in Angstrom2) of CH+ (v=0, j=3) in collision with 4He as a function of the kinetic energy in cm-1. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig5New.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg19.png)
|
Figure 5: Elastic and rotational deactivation cross sections (in Angstrom2) of CH+ (v=0, j=5) in collision with 4He as a function of the kinetic energy in cm-1. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig6New.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg20.png)
|
Figure 6: Comparison between the rotational deactivation and elastic rate coefficients of CH+ (v = 0, j = 1) in collision with 4He and 3He as a function of temperature. The inverse rotational transition-rate coefficients are also represented for the inelastic transitions. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig7New.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg21.png)
|
Figure 7: Rotational deactivation and elastic rate coefficients of CH+ (v=0, j=1) in collision with 4He as a function of temperature. The inverse rotational transition-rate coefficients are also represented for the inelastic transitions. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig8New.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg22.png)
|
Figure 8: Rotational deactivation and elastic rate coefficients of CH+ (v= 0, j= 2) in collision with 4He as a function of temperature. The inverse rotational transition rate coefficients are also represented for the inelastic transitions. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig9New.eps}\vspace*{2.22mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg23.png)
|
Figure 9: Rotational deactivation and elastic rate coefficients of CH+ (v=0, j=3) in collision with 4He as a function of temperature. The inverse rotational transition rate coefficients are also represented for the inelastic transitions. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig10New.eps} %
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg24.png)
|
Figure 10: Rotational deactivation and elastic rate coefficients of CH+ (v=0, j=5) in collision with 4He as a function of temperature. The inverse rotational transition rate coefficients are also represented for the inelastic transitions. |
| Open with DEXTER | |
3 Results and discussion
Close coupling calculations were performed for collision energies ranging from 10-6 cm-1 to 3000 cm-1. Convergence of the cross-section as a function of the total angular momentum J was checked for each value of the kinetic energy. The maximum value of total angular momentum used in the calculations was J=81.To evaluate the influence of the long-range potential, we compare our
results to those given by the classical Langevin
model, which is based on the long-range charge-induced dipole potential
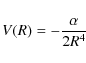
for singly charged ion-molecule reactions, where

where
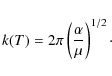
Figures 1-5 show the elastic and rotational de-excitation cross-sections for the rotational levels j respectively indicated in 1, 2, 3, and 5 of CH+. The agreement between our results and the Langevin formula (also reported on these figures) shows that the collision is controlled by the long range potential in a wide interval of energy. The profile of the different curves is typical of a very low energy regime following the Wigner law shown in Fig. 1, while the resonance regime characterized by numerous oscillations extends up to approximately 500 cm-1, which is close to the value of the Van der Waals well depth (513 cm-1). A more detailed analysis of these profiles can be found in our previous work (Stoecklin & Voronin 2008). Figure 1 also illustrates the very strong isotopic effect obtained for this system in the very low kinetic energy regime. Indeed, the elastic cross-sections involving a collision with 4He is three orders of magnitude larger than the one involving 3He. This feature, which is typical of the collisions involving ionic species (Stoecklin & Voronin 2005), results from the strong long-range potential. In these figures, we can also see that the rotational de-excitation cross-sections of this system do not obey the usual energy gap law. This unusual feature was analysed in our previous work (Stoecklin & Voronin 2008) and attributed to a Feshbach resonance.
Figures 6-10 show the
corresponding de-excitation and excitation rate coefficients as a
function of temperature in the range 1 K to 300 K.
The excitation rate coefficients increase monotonically as a function
of temperature, whereas the de-excitation rate coefficients exhibit
small fluctuations between 1 K and 10 K, which are
direct consequences of the resonances shown in 1-5. To analyse the
differences between our results and those of Hammami
et al. (2008), we also performed calculations with
our surface but this time using the rigid rotor approximation. In
Table 2,
our two sets of results are compared to those of Hammami et al. (2008)
for two temperatures 20 and 200 K. In this table, the rate coefficients
for the rotational transitions
![]() of CH+ (j = 5, 4, 3, 2, 1),
induced by collisions with 4He are presented.
The rate coefficients for rotational excitation of CH+
can be obtained using the detailed balance relationship. For each
temperature, in the first column we reported the results of Hammami et al. (2008)
(H), in the second our results using the rigid rotor approximation
(RR), and in the third those for the close coupling results (C).
If we first compare our two sets of results obtained when using or not
using the rigid rotor approximation we see that at 20 K the largest
relative difference is obtained for the
of CH+ (j = 5, 4, 3, 2, 1),
induced by collisions with 4He are presented.
The rate coefficients for rotational excitation of CH+
can be obtained using the detailed balance relationship. For each
temperature, in the first column we reported the results of Hammami et al. (2008)
(H), in the second our results using the rigid rotor approximation
(RR), and in the third those for the close coupling results (C).
If we first compare our two sets of results obtained when using or not
using the rigid rotor approximation we see that at 20 K the largest
relative difference is obtained for the
![]() transition and is equal to 22 percent, whereas it reaches 39 percent at
200 K for the
transition and is equal to 22 percent, whereas it reaches 39 percent at
200 K for the
![]() transition. These results indicate that the rigid rotor approximation
is not fully satisfactory for this system when the temperature
increases, as suggested by our previous study dedicated to the
rovibrational energy transfer. If we now compare our rigid rotor
calculations to those of Hammami
et al. (2008), we find that at 20 K the
largest difference is obtained for the
transition. These results indicate that the rigid rotor approximation
is not fully satisfactory for this system when the temperature
increases, as suggested by our previous study dedicated to the
rovibrational energy transfer. If we now compare our rigid rotor
calculations to those of Hammami
et al. (2008), we find that at 20 K the
largest difference is obtained for the
![]() transition and is equal to 33 percent, whereas it decreases to 20
percent at 200 K for the
transition and is equal to 33 percent, whereas it decreases to 20
percent at 200 K for the
![]() transition. The differences between the two sets of results are caused
by the inclusion of the long-range charge-induced dipole contribution
to the intermolecular potential, whose influence is stronger at low
temperature, which Hammami
et al. (2008) did not include. We conclude from
these comparisons that if the rigid rotor approximation and the neglect
of the long-range potential used by Hammami
et al. (2008) provide the correct order of magnitude
for the elastic rate coefficients between 20 K and
300 K, their results are sometimes discrepant by 40 percent
for the inelastic transitions.
transition. The differences between the two sets of results are caused
by the inclusion of the long-range charge-induced dipole contribution
to the intermolecular potential, whose influence is stronger at low
temperature, which Hammami
et al. (2008) did not include. We conclude from
these comparisons that if the rigid rotor approximation and the neglect
of the long-range potential used by Hammami
et al. (2008) provide the correct order of magnitude
for the elastic rate coefficients between 20 K and
300 K, their results are sometimes discrepant by 40 percent
for the inelastic transitions.
The values of our calculated rate coefficients for the rotational de-excitation of CH+ (j=5, 4, 3, 2, 1) are given in Table 1 for 8 temperatures in the [0.1 : 200] temperature interval. The rate coefficients for rotational excitation of CH+ can again be obtained using the detailed balance relationship.
Collision rate coefficients for other transitions and other temperatures are available on request from the corresponding author.
Table 1: Rate coefficients for rotational de-excitation of CH+ in collisions with 4He.
Table 2: Rate coefficients for rotational transitions in CH+ induced by collisions with 4He.
4 Conclusions
Rotational transition rate-coefficients, for levels of up to j= 5 and temperature of up to 300 K were computed for CH+in collision with 4He. As the unusual geometry of the He-CH+ complex leads to a strong coupling between vibration and rotation, we performed both rigid rotor calculations and others, taking fully into account the vibration of CH+ using the same 3D global potential energy surface. The close coupling results show that the Langevin model provides good estimates of the rotationally elastic-rate coefficients, for temperatures below 10 K. We have also found that the calculations of Hammami et al. (2008), which did not include neither the long-range potential nor the vibration of CH+, provide the correct order of magnitude for the elastic rate coefficients, but are discrepant by up to 40 percent for some of the inelastic transitions. At very low kinetic energy, we have also mentioned the strong isotopic effect obtained when replacing 4He by 3He, which suggests that this effect should also be seen when H atoms are replaced by D atoms.
References
- Anderson, R. W. 1982, J. Chem. Phys., 77, 5426 [NASA ADS] [CrossRef] [Google Scholar]
- Bates, D. R., & Spitzer, L. J. 1951, ApJ, 113, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Douglas, A. E., & Herzberg, G. 1941, ApJ, 94, 381 [Google Scholar]
- Elitzur, M., & Watson, W. D. 1978, A&A, 70, 443 [NASA ADS] [Google Scholar]
- Federman, S. R. 1982, ApJ, 257, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Hakalla, R., Kepa, R., & Szajna, W. 2006, EPJD, 38, 481 [Google Scholar]
- Halvick, P., Stoecklin, T., Larrgaray, P., & Bonnet, L. 2007, Phys. Chem. Chem. Phys., 9, 582 [CrossRef] [PubMed] [Google Scholar]
- Hammami, K., Owono Owono, L. C., Jaidane, N., & Ben Lakhdar, Z. 2008, J. Molecular Structure: THEOCHEM, 853, 18 [Google Scholar]
- Handy, N. C., Pople, J. A., Head-Gordon, M., Raghavachari, K., & Trucks, G. W. 1989, Chem. Phys. Lett., 164, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, T. S., & Rabitz, H. 1996, J. Chem. Phys., 104, 2584 [NASA ADS] [CrossRef] [Google Scholar]
- Launay, J. M. 1977, J. Phys. B, 10, 3665 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. C., & Drouin, B. J. 2006, ApJ, 647, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Prasad, S. S., & Huntress, Jr., W. T. 1980, ApJS, 43, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Reese, C., Stoecklin, T., Voronin, A., & Rayez, J. C. 2005, A&A, 430, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solomon, P. M., & Klemperer, W. 1972, ApJ, 178, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Stechel, E., Walker, R., & Light, J. 1978, J. Chem. Phys., 69, 3518 [NASA ADS] [CrossRef] [Google Scholar]
- Stoecklin, T., & Halvick, P. 2005, Phys. Chem. Chem. Phys., 7, 2446 [CrossRef] [PubMed] [Google Scholar]
- Stoecklin, T., & Voronin, A. 2005, Phys. Rev. A, 72, 042714 [NASA ADS] [CrossRef] [Google Scholar]
- Stoecklin, T., & Voronin, A. 2008, EPJD, 46, 259 [Google Scholar]
- Tao, F.-M., & Pan, Y.-K. 1992, J. Phys. Chem., 96, 5815 [CrossRef] [Google Scholar]
- Weselak, T., Galazutdinov, G. A., Musaev, F. A., & Kre▯owski, J. 2004, A&A, 414, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woon, D. E., & Thom H. Dunning, J. 1993, J. Chem. Phys., 99, 1914 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Table 1: Rate coefficients for rotational de-excitation of CH+ in collisions with 4He.
Table 2: Rate coefficients for rotational transitions in CH+ induced by collisions with 4He.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig1New.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg15.png)
|
Figure 1: Comparison between the elastic cross-sections (in Angstrom2) of CH+ (v = 0, j=1) by collision with 4He and 3He as a function of the kinetic energy in cm-1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig2New.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg16.png)
|
Figure 2: Elastic and rotational deactivation cross sections (in Angstrom2) of CH+ (v = 0, j=1) in collision with 4He as a function of the kinetic energy in cm-1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig3New.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg17.png)
|
Figure 3: Elastic and rotational deactivation cross sections (in Angstrom2) of CH+ (v=0, j= 2) in collision with 4He as a function of the kinetic energy in cm-1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig4New.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg18.png)
|
Figure 4: Elastic and rotational deactivation cross sections (in Angstrom2) of CH+ (v=0, j=3) in collision with 4He as a function of the kinetic energy in cm-1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig5New.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg19.png)
|
Figure 5: Elastic and rotational deactivation cross sections (in Angstrom2) of CH+ (v=0, j=5) in collision with 4He as a function of the kinetic energy in cm-1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig6New.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg20.png)
|
Figure 6: Comparison between the rotational deactivation and elastic rate coefficients of CH+ (v = 0, j = 1) in collision with 4He and 3He as a function of temperature. The inverse rotational transition-rate coefficients are also represented for the inelastic transitions. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig7New.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg21.png)
|
Figure 7: Rotational deactivation and elastic rate coefficients of CH+ (v=0, j=1) in collision with 4He as a function of temperature. The inverse rotational transition-rate coefficients are also represented for the inelastic transitions. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig8New.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg22.png)
|
Figure 8: Rotational deactivation and elastic rate coefficients of CH+ (v= 0, j= 2) in collision with 4He as a function of temperature. The inverse rotational transition rate coefficients are also represented for the inelastic transitions. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig9New.eps}\vspace*{2.22mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg23.png)
|
Figure 9: Rotational deactivation and elastic rate coefficients of CH+ (v=0, j=3) in collision with 4He as a function of temperature. The inverse rotational transition rate coefficients are also represented for the inelastic transitions. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12744fig10New.eps} %
\end{figure}](/articles/aa/full_html/2010/03/aa12744-09/Timg24.png)
|
Figure 10: Rotational deactivation and elastic rate coefficients of CH+ (v=0, j=5) in collision with 4He as a function of temperature. The inverse rotational transition rate coefficients are also represented for the inelastic transitions. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



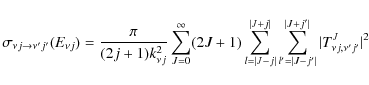
![\begin{displaymath}k^{\ln}_{\nu j \rightarrow \nu' j'}(T) = \sqrt[]{\frac{8}{\pi...
...j}) ~{\rm e}^{-\frac{E_{\nu j}}{k_{\rm B}T}}~{\rm d}E_{\nu j}.
\end{displaymath}](/articles/aa/full_html/2010/03/aa12744-09/img11.png)
![\begin{displaymath}k_{\nu' j' \rightarrow \nu j}^{\ln}(T) = \frac{\left(2j+1\rig...
... \right]}{k_{\rm B}T}}k_{\nu j \rightarrow \nu' j'}^{\ln}(T).
\end{displaymath}](/articles/aa/full_html/2010/03/aa12744-09/img12.png)