Recommended data on proton-ion collision rate coefficients for Fe X–Fe XXIII ions

I. Skobelev; I. Murakami; T. Kato

doi:10.1051/0004-6361/200912392

Home

All issues

Volume 511 (February 2010)

A&A, 511 (2010) A60

Full HTML

Free Access

Issue		A&A Volume 511, February 2010


Article Number		A60
Number of page(s)		13
Section		Atomic, molecular, and nuclear data
DOI		https://doi.org/10.1051/0004-6361/200912392
Published online		10 March 2010

A&A 511, A60 (2010)

Recommended data on proton-ion collision rate coefficients for Fe X-Fe XXIII ions

I. Skobelev^1,2 - I. Murakami¹ - T. Kato¹

1 - National Institute for Fusion Science, Oroshi-cho, Toki, Gifu, 509-5292, Japan
2 - Joint Institute for High Temperatures of RAS, Izhorskaya 13/19, 125412 Russia

Received 27 April 2009 / Accepted 4 December 2009

Abstract
Aims. Proton-ion collisions are important for excitation or de-excitation of certain excited states in a high-temperature low density astrophysical plasma.
Methods. In the present work an evaluation of data obtained for proton-induced transitions in Fe X-Fe XXIII ions is carried out with the help of different theoretical methods.
Results. A simple analytical formula with seven parameters is suggested. This formula allows us to describe the dependence of the proton rate coefficient on the proton temperature in a wide temperature range. The values of the free parameters have been determined by fitting the approximation formula to numerical data and are presented for recommended data together with fitting accuracies. By comparing proton collision rates with electron rates it is shown that proton impact excitation processes may be important for Fe X, XI, XIII-XV, XVII-XXIII ions. The results obtained can be used for plasma kinetics calculations and for the development of spectroscopic methods of astrophysical plasma diagnostics.

Key words: atomic processes - atomic data - plasmas

1 Introduction

The importance of proton-ion collisions for ion kinetic calculations was first demonstrated by Seaton (1964) for the case of the Fe XIV ion. It has been shown that proton excitation rates can become comparable to (or even larger than) the electron excitation rates for transitions for which the excitation energy $\Delta$ E is much smaller than the proton temperature $kT_{\rm p}$ . It should be noted that often proton-ion collisions are not important for populating ion levels even in the case $\Delta$ $E \ll kT_{\rm p}$ , i.e. this condition is necessary but is not sufficient. For example, such a situation occurs in dense plasma where closely spaced ionic levels are as a rule statistically populated. In low density plasma the importance of proton-ion collisions may be very high especially for transitions within the ground configuration of an ion. The number of such transitions is not very large and so, compared to the electron processes, relatively little data are required to account for proton processes in a particular ion.

In principle, proton collision can influence the population kinetics by increasing either excitation rates for some levels or their collision decay rates.

An increase of excitation rates can be important only for levels i near the ground ion state (or close to a strongly metastable state). In this case proton collision will be important for a plasma with an electron density $N_{\rm e}$ which satisfies the condition

$\begin{displaymath}N_{\rm e} < A_i/C_{i{\rm e}} \end{displaymath}$

(1)

(where A_i and $C_{i{\rm e}}$ are the probability of radiative and electron collision decay of level i, respectively), because at higher density electron collisions cause a Boltzmann population of the level i.

Increase of collision decay rates can be important for excited levels i if the proton density satisfies the reverse condition

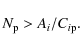
$\begin{displaymath}N_{\rm p} > A_i/C_{i{\rm p}}. \end{displaymath}$

(2)

If radiative decay of level i is allowed, the last condition can be valid only in a dense plasma (laser-produced plasma, Z-pinches, exploding wires), while for metastable levels it can be satisfied even in low density astrophysical or laboratory plasmas.

Thus, proton excitation/de-excitation of fine-structure transitions involving ground or low-lying ion metastable states are of primary interest.

At present there are a lot of papers where proton-ion collision rates C_ij have been calculated for different Fe ions. In these papers proton collision rate coefficients were published in a table form. Because positive ions repel protons, the rate coefficients fall sharply to zero at the threshold energy, and tabulated values of rate coefficients typically change by several orders of magnitude over a small temperature range. For many applications tabular data presentation is not very convenient, and some analytical representation $C_{ij}(T_{\rm p})$ would be preferable. Therefore the purpose of the present work was not only an evaluation of proton rates calculated for Fe X-Fe XXIII ions with the help of different methods, but also the choice of a simple function allowing us to describe dependencies $C_{ij}(T_{\rm p})$ for all transitions considered.

2 Methods used for calculations of proton rate coefficients

Several different methods, both semiclassical and quantal, can be employed in deriving proton rate coefficients (see for example reviews by Dalgarno 1983; Reid 1988; Copeland et al. 1997; Young et al. 2003).

The most basic is the semiclassical (or impact-parameter) approach in which the position of the proton relative to the ion is treated classically. This approach was originally applied to Coulomb excitation of nuclei by Alder et al. (1956) and first extended to the proton excitation of ions by Seaton (1964). In the case of semiclassical calculations, either first-order approximations or close-coupling approximations have been used.

At low proton energies the semiclassical first-order approximation is valid at all impact parameters because the interactions between the proton and electrons of an ion are weak due to Coulomb repulsion of proton and ion. At intermediate energies and low impact parameter values the first-order approximation fails, and it is necessary to adopt a different approximation or solve numerically the coupled differential equations describing the interaction. In the semiclassical close-coupling approximation, the transition probabilities are determined by means of the numerical solution of coupled differential equations, thereby removing the need for first-order approximations and hence the uncertainty in the intermediate energy range.

Generally speaking, the most accurate method is to treat the proton's trajectory quantum mechanically and solve the complete set of close-coupling equations. Such an approach is commonly used in R-matrix calculations of electron-ion collisions; however, it is computationally much more demanding for proton collisions, and only a few results were obtained for Fe ions by this method. Within the semiclassical approach, it has been shown that symmetrizing the problem with respect to the initial and final velocities (Alder et al. 1956), and including polarization effects (Heil et al. 1982, 1983), can improve the accuracy of the proton rates. In the paper of Faucher & Landman (1977) it has been shown that for highly charged ions both a quantum and a semiclassical close-coupling approach can give very close results.

It should be noted that an estimation of the accuracy of the computations is very difficult. In the best cases we can expect a data accuracy of about 10-25% (see also Copeland et al. 1997).

3 Analytical function for an approximation of the dependencies of proton collision rates on proton temperature

In the present work we have used a simple function to approximate calculated temperature dependencies $C_{ij}(T_{\rm p})$ :

$\begin{displaymath}C_{ij}(T_{\rm p})[{\rm cm^3~s^{-1}}] = 10^{-10}p_1\exp(-(p_2/... ... {{(T_{\rm p}/p_6)^{p_7}}\over{1+(T_{\rm p}/p_4)^{p_5}}}\cdot \end{displaymath}$

(3)

In Eq. (3) $T_{\rm p}, p_2, p_4$ and p₆ are in [eV], 1 eV = 11605 K.

It should be mentioned that Eq. (3) is not based on the known properties of the rate coefficients. It has a qualitatively correct behavior at low temperatures and absolutely incorrect behavior at high temperature. But in the temperature range that is most important for plasma applications, Eq. (3) allows us to describe numerical data with an accuracy better than 5% for all transitions in all ions considered. The values of the seven free parameters and the temperature ranges over which the fit is valid are presented in the present paper together with approximation accuracies. Note that functions with five to nine free parameters are now often used in different databases to store data on electron-ions collisions.

The values of the free parameters p_i were determined by the following two-stage procedure. In the first stage we chose manually initial values p_i(0) which gave the correct qualitative temperature-dependence of the rate coefficient. In the second stage we constructed a seven-dimensional grid around the point p_i(0) with steps of about 0.01p_i(0). The differences between the theoretically-calculated rate coefficients and the approximation Eq. (3) were then calculated at all given temparatures for all points of the grid. If for some grid point this difference was less than 5% for all temperatures, the calculation was stopped, and the coordinates of this grid point were taken as the required p_i values. The values of p_i determined in this way do not give the best fit of Eq. (3) to the theoretically-calculated values (which was not our purpose), but they provide approximations to the theoretically-calculated results with an accuracy better than the intrinsic accuracy of those theoretical results. Such simple approximations are currently employed to include detailed radiation-collisional ion kinetics in two- and three-dimensional plasma gas-dynamical calculations.

4 Results

4.1 Chlorine-like Fe X (3s²3p⁵ ²P)

For the Fe X ion proton collision excitation is important for only one transition $\rm 3s^23p^5\ ^2P_{3/2}$ - $\rm 3s^23p^5\ ^2P_{1/2}$ .

Bely & Faucher (1970) used a symmetrized first-order semiclassical approximation to calculate the proton cross section and rate coefficient for the $\rm 3s^23p^5\ ^2P_{3/2}{-}^2P_{1/2}$ transition in Fe X. In the intermediate energy range, where a first-order theory breaks down, an approximation referred to as Coulomb-Bethe II was employed, borrowed from the theory of electron excitation of positive ions, to determine the cross section. Bely & Faucher (1970) estimate their rate coefficients to be accurate to within 50% for the first ions in the chlorine isoelectronic sequence. The estimated error is smaller for the more highly charged ions.

Kastner (1977) and Kastner & Bhatia (1979) also used the first-order semiclassical approximation for low energies, while for intermediate energies a form for the cross section due to Bahcall & Wolff (1968) was used. From the comparison presented in Fig. 1 one can see that the results of Kastner (1977) and Kastner & Bhatia (1979) are on the whole lower than the earlier values of Bely & Faucher (1970). All results agree within 50% throughout the temperature range of 50-350 eV, while for temperatures <100 eV the agreement is very good. Because the first-order semiclassical approximation systematically overestimates the rates in the high energy region, we recommend to use the data of Kastner & Bhatia (1979), but we present in Table 1 the results of the approximation for both the data of Kastner & Bhatia (1979) and of Bely & Faucher (1970).

Table 1: The values of fitting parameters, defined in Eq. (3), for proton excitation rate coefficients of transitions in ions Fe X-Fe XV.

Bhatia & Doschek (1995) calculated the rate of this transition for a single temperature value of 10⁶ K. As we see from Fig. 1 this result agrees with both Bely & Faucher (1970) and Kastner & Bhatia (1979) as well as with our fitting.

In Fig. 1 the electron collision rate coefficient calculated by Aggarwal & Keenan (2005b) is also presented. It can be seen that proton collisions will influence the population of the $\rm 3s^23p^5\ ^2P_{1/2}$ level in plasmas with temperature higher than 100 eV.

$\begin{figure} \par\includegraphics[width=9cm]{12392f01.eps} \end{figure}$	Figure 1: Proton collision rate coefficient for transition $\rm 3s^23p^5\ ^2P_{3/2}{-}^2P_{1/2}$ in Cl-like Fe X: solid lines - Eq. (3), triangles - data Kastner & Bhatia (1979), $\diamond$ - data Bely & Faucher (1970), $\bullet$ - data Bhatia & Doschek (1995), dashed line - electron collision rate coefficient of Aggarwal & Keenan (2005b).
Open with DEXTER

4.2 Sulfur-like Fe XI (3s²3p⁴ ³P)

For the Fe XI ion proton collisions must be taken into account for three transitions between the fine structure components of the ground $\rm 3s^23p^4\ ^3P_{0,1,2}$ term. The corresponding rate coefficients have been calculated by Landman (1980) with the help of a symmetrized, semiclassical close-coupling method. This method retains the classical treatment for the proton trajectory, but the transition probabilities are determined by numerically solving the close-coupling equations, removing the uncertainties at intermediate energies of the first-order approximation. For the transitions $\rm ^3P_2{-}^3P_{1,0}$ at a temperature of $1.3 \times 10^6$ K the proton rates were calculated by Bhatia & Doschek (1996) with the help of the first-order semiclassical approach. It can be seen from Fig. 2 that the first-order approach significantly overestimates the collision rates.

We fitted the data of Landman (1980) by Eq. (3), and the results for p_i are presented in Table 1, while dependencies of the rate coefficients on the proton temperature are shown in Fig. 2.

In Fig. 2 the electron collision rate coefficients calculated by Gupta & Tayal (1999) are also presented. It can be seen that proton collisions will influence the population of the $\rm 3s^23p^4\ ^3P_{1,2}$ levels in plasma with a temperature higher than 100 eV.

$\begin{figure} \par\includegraphics[width=9cm]{12392f02.eps} \end{figure}$

Figure 2:

Proton collision rate coefficients for the transitions ${\rm 3s^23p^4\ ^3P}_J{-}^3{\rm P}_{J'}$ in S-like Fe XI: solid, dashed and doted lines - Eq. (3), diamonds - Bhatia & Doschek (1995) and triangle - Landman (1980) for $^3{\rm P}_2{-}^3{\rm P}_1$ transition; $\times$ - Bhatia & Doschek (1995) and + - Landman (1980) for the $\rm ^3P_2{-}^3P_0$ transition; $\circ$ - Bhatia & Doschek (1995) for the $\rm ^3P_1{-}^3P_0$ transition; solid thin lines with diamonds, $\times$ , $\circ$ - electron rate coefficients of Gupta & Tayal (1999) for the transitions $\rm ^3P_2{-}^3P_1,\ ^3P_2{-}^3P_0$ and $\rm ^3P_1{-}^3P_0$ , respectively.

Open with DEXTER

4.3 Phosphorus-like Fe XII (3s²3p³ ⁴S, ²D, ²P)

For the Fe XII ion proton collisions must be taken into account for ten transitions between fine structure components of the ground $\rm 3s^23p^3$ configuration. The corresponding rate coefficients have been calculated by Landman (1978) with the help of a symmetrized, semiclassical close-coupling method. We fitted the data of Landman (1978) by Eq. (3). The obtained values of p_i are presented in Table 1 and the dependencies of rate coefficients on proton temperature are shown in Figs. 3-5.

In Figs. 3-5 the electron collision rate coefficients calculated by Binello et al. (1998) are also presented. It can be seen that proton collisions are not important for the kinetics of the Fe XII ion in the plasma with any reasonable temperature.

$\begin{figure} \par\includegraphics[width=9cm]{12392f03.eps} \end{figure}$

Figure 3:

Proton collision rate coefficients for transitions in P-like Fe XII: thick solid, dashed and dot lines - formula (3), $\times$ - data for $\rm 3s^23p^3\ ^4S_{3/2}{-}^2D_{3/2}$ transition, diamonds - data for $\rm 3s^23p^3\ ^4S_{3/2}{-}^2D_{5/2}$ transition, $\bullet$ - data for $\rm 3s^23p^3\ ^4S_{3/2}{-}^2P_{3/2}$ transition, $\triangle$ - data for $\rm 3s^23p^3\ ^4S_{3/2}{-}^2P_{3/2}$ transition; thin solid lines with $\times$ , diamonds, $\bullet$ , $\triangle$ - electron rate coefficients of Binello et al. (1998) for $\rm ^4S_{3/2}{-}^2D_{3/2},\ ^4S_{3/2}{-}^2D_{5/2},\ ^4S_{3/2}{-}^2P_{3/2}$ , and $\rm ^4S_{3/2}{-}^2P_{3/2}$ transitions, respectively.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{12392f04.eps} \end{figure}$

Figure 4:

Proton collision rate coefficients for transitions in P-like Fe XII: solid, dashed and doted lines - Eq. (3), $\times$ - data for the $\rm 3s^23p^3\ ^2D_{3/2}{-}^2D_{5/2}$ transition, $\bullet$ - data for the $\rm 3s^23p^3\ ^2D_{3/2}{-}^2P_{3/2}$ transition, $\triangle$ - data for the $\rm 3s^23p^3\ ^2D_{3/2}{-}^2P_{1/2}$ transition; thin solid lines with $\times ,\ \bullet , \ \triangle$ - electron rate coefficients of Binello et al. (1998) for the $\rm ^2D_{3/2}{-}^2D_{5/2},\ ^2D_{3/2}{-}^2P_{3/2}$ , and $\rm ^2D_{3/2}{-}^2P_{1/2}$ transitions, respectively.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{12392f05.eps} \end{figure}$

Figure 5:

Proton collision rate coefficients for transitions in P-like Fe XII: solid, dashed and doted lines - Eq. (3), $\times$ - data for the $\rm 3s^23p^3\ ^2D_{5/2}{-}^2P_{1/2}$ transition, $\bullet$ - data for the $\rm 3s^23p^3\ ^2P_{1/2}{-}^2P_{3/2}$ transition, $\triangle$ - data for the $\rm 3s^23p^3\ ^2D_{5/2}{-}^2P_{3/2}$ transition; solid thin lines with $\times ,\ \bullet , \ \triangle$ - electron rate coefficients of Binello et al. (1998) for the $\rm ^2D_{5/2}{-}^2P_{1/2},\ ^2P_{1/2}{-}^2P_{3/2}$ , and $\rm ^2D_{5/2}{-}^2P_{3/2}$ transitions, respectively.

Open with DEXTER

4.4 Silicon-like Fe XIII (3s²3p² ³P, ¹D, ¹S)

For the Fe XIII ion it is necessary to consider ten transitions among the levels of the ground configuration $\rm 3s^23p^2$ . Cross sections and rate coefficients for these transitions have been obtained by using the semiclassical close-coupling theory (Masnou-Seeuws & McCarroll 1972; Landman 1975), a first-order semiclassical method (Sahal-Breshot 1974; Kastner 1977; Kastner & Bhatia 1979) and a quantal approach to the close-coupling method (Faucher 1977; Faucher & Landman 1977). The quantal approach is based on the work of Faucher (1975) which adapts the electron-ion quantum collision theory (Bely et al. 1963) to the proton-ion case. While such quantal calculations can model the short-range interaction more accurately, it is possible to expect that the accuracy of the data of Faucher (1977) and Faucher & Landman (1977) is higher than others (Masnou-Seeuws & McCarroll 1972; Landman 1975; Sahal-Brechot 1974; Kastner 1977).

In Fig. 6 the proton excitation cross-sections between the fine structure levels of ${\rm 3s^23p^2\ ^3P}_J$ are shown as a function of the incident proton energy. In this figure quantum results of Faucher (1975, 1977) and Faucher & Landman (1977) (square) are compared with semi-classical results of Landman (1975) (solid line) and of Masnou-Seeuws & McCarroll (1972) (dotted line). It can be seen from this figure that the semi-classical cross-sections obtained in Landman (1975) by directly solving Schrodinger's equation are very similar to those obtained by Faucher (1975) with a quantum method in the low and intermediate energy range.

$\begin{figure} \par\includegraphics[width=9cm]{12392f06.eps} \end{figure}$	Figure 6: Proton excitation cross sections for transitions in Si-like Fe XIII: squares - quantum results of Faucher (1977), solid line - semi-classical results of Landman (1975), dotted line - semi-classical results of Masnou-Seeuws & McCarroll (1972); for (1) the $\rm ^3P_0{-}^3P_1$ transition, (2) the $\rm ^3P_1{-}^3P_2$ transition, and (3) the $\rm ^3P_0{-}^3P_2$ transition.
Open with DEXTER

Among the two available calculations of Masnou-Seeuws & McCarroll (1972) and Landman (1975) we choose the data of Landman (1975) because these data agree better with the quantum calculations of Faucher (1977) and Faucher & Landman (1977) and are presented for a wider range of transitions. In Landman (1975) data are given for all transitions between the individual magnetic sublevels of the $\rm ^3P_{0,1,2},\ ^1D_2,$ and $\rm ^1S_0$ levels of the ground configuration. These rates have been summed over the magnetic sublevels and fitted to Eq. (3). Results obtained are presented in Table 1 and Figs. 7-9.

In Figs. 7-9 the electron collision rate coefficients calculated by Aggarwal & Keenan (2005a) are also presented. It can be seen that proton collisions will significantly influence the population of the $\rm 3s^23p^2\ ^3P_{1,2}$ and $\rm ^1D_2$ levels in plasma with a temperature higher than 200 eV and will not influence the population of the $\rm 3s^23p^2\ ^1S_0$ level.

$\begin{figure} \par\includegraphics[width=9cm]{12392f07.eps} \end{figure}$

Figure 7:

Proton collision rate coefficients for transitions in Si-like Fe XIII: thick solid, thin solid, dashed and doted lines - Eq. (3), diamonds - data of Landman (1975) for the $\rm 3s^23p^2\ ^3P_0{-}^3P_1$ transition, black triangles - data of Landman (1975) for the $\rm 3s^23p^2\ ^3P_0{-}^3P_2$ transition, $\times$ - data of Landman (1975) for the $\rm 3s^23p^2\ ^3P_0{-}^1D_2$ transition, + - data of Landman (1975) for the $\rm 3s^23p^2\ ^3P_0{-}^1S_0$ transition, $\triangle$ - data of Kastner & Bhatia (1979) for the $\rm 3s^23p^2\ ^3P_0{-}^3P_2$ transition; thin solid lines with diamonds, black triangles, $\times$ , $\triangle$ - electron rate coefficients of Aggarwal & Keenan (2005a) for the $\rm ^3P_0{-}^3P_1,\ ^3P_0{-}^3P_2,\ ^3P_0{-}^1D_2,\ ^3P_0{-}^1S_0$ , and $\rm ^3P_0{-}^3P_2$ transitions, respectively.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{12392f08.eps} \end{figure}$

Figure 8:

Proton collision rate coefficients for transitions in Si-like Fe XIII: solid, dashed and doted lines - Eq. (3), diamonds - data of Landman (1975) for the $\rm 3s^23p^2\ ^3P_1{-}^3P_2$ transition, triangles - data of Landman (1975) for the $\rm 3s^23p^2\ ^3P_1{-}^1D_2$ transition, + - data of Landman (1975) for the $\rm 3s^23p^2\ ^3P_1{-}^1S_0$ transition; thin solid lines with diamonds, triangles, + - electron rate coefficients of Aggarwal & Keenan (2005a) for the $\rm ^3P_1{-}^3P_2,\ ^3P_1{-}^1D_2$ , and $\rm ^3P_1{-}^1S_0$ transitions, respectively.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{12392f09.eps} \end{figure}$

Figure 9:

Proton collision rate coefficients for transitions in Si-like Fe XIII: solid, dashed and doted lines - Eq. (3), diamonds - data of Landman (1975) for the $\rm 3s^23p^2\ ^3P_2{-}^1D_2$ transition, triangles - data of Landman (1975) for the $\rm 3s^23p^2\ ^3P_2{-}^1S_0$ transition, + - data of Landman (1975) for the $\rm 3s^23p^2\ ^1D_2{-}^1S_0$ transition; thin solid lines with diamonds, triangles, + - electron rate coefficients of Aggarwal & Keenan (2005a) for the $\rm ^3P_2{-}^1D_2,\ ^3P_2{-}^1S_0$ , and $\rm ^1D_2{-}^1S_0$ transitions, respectively.

Open with DEXTER

4.5 Aluminium-like Fe XIV (3s²3p ²P)

For the Fe XIV ion the proton collision rates are important only for one transition $\rm 3s^23p\ ^2P_{1/2}{-}^2P_{3/2}$ . For this transition data calculated with the help of all methods considered above are available.

In the papers of Bely & Faucher (1970), Kastner & Bhatia (1979), and Burgess & Tully (2005) a first-order semiclassical theory has been used with different methods of a limitation of the transition probabilities for small values of the impact parameter. In the work of Landman (1975) the rate coefficient was calculated using a semi-classical close-coupling treatment analogous to Masnou-Seeuws & McCarroll (1972). Close-coupling quantal calculations have been carried out by Heil et al. (1983). The cross sections calculated in this paper are probably the most accurate for Fe XIV to date because of the approach (Heil et al. 1983) to model the interaction accurately not only by expressing the short-range term accurately, but also by including the polarization term for the long-range interaction as well as the quadrupole term. The results obtained in these papers are shown in Fig. 10. It can be seen that as usual the first-order semiclassical method overestimates the rate coefficient in medium and high energy regions, and the semiclassical close-coupling results are close enough to the quantal calculations. It should be noted that the results in Landman (1975) at higher temperatures are higher than the data in Heil et al. (1983). This is likely caused by the following reason. In Heil et al. (1983) the cross sections were calculated only for a proton energy of up to 900 eV, which is not large enough to obtain reliable rate coefficients at high temperatures. In Landman (1975) a wider energy range (up to 2900 eV) was considered. Therefore we have chosen the data of Landman (1975) as our recommended data and fit them in Eq. (3). The results obtained are presented in Table 1.

In Fig. 10 the electron collision rate coefficient calculated by Storey et al. (1996) is also presented. It can be seen that proton collisions will strongly influence the population of the $\rm 3s^23p\ ^2P_{3/2}$ level in the plasma with a temperature higher than 200 eV.

$\begin{figure} \par\includegraphics[width=9cm]{12392f10.eps} \vspace*{-2.3mm} \end{figure}$

Figure 10:

Proton collision rate coefficients for the transition $\rm 3s^23p\ ^2P_{1/2}{-}^2P_{3/2}$ in Al-like Fe XIV: solid line - Eq. (3), $\circ$ - data of Kastner & Bhatia (1979), triangles - data of Landman (1975), + - data of Bely & Faucher (1970), $\diamond$ - data of Heil et al. (1983), squares and $\times$ - data of Burgess & Tully (2005) for different methods considering the small impact parameter region; thin solid line - electron rate coefficient of Storey et al. (1996).

Open with DEXTER

4.6 Magnesium-like Fe XV (3s3p ³P)

Two calculations (Kastner 1977; Landman & Brown 1979) have been carried out for the fine-structure transitions ${\rm 3s3p\ ^3P}_J{-}{\rm ^3P}_{J'}$ in magnesium-like Fe XV. In Kastner (1977) a first-order semiclassical theory was used, while the calculations of Landman & Brown (1979) were based on the semiclassical close-coupling treatment. We recommend to use the results of Landman & Brown (1979) and corresponding fitting parameters are presented in Table 1. The dependencies of the proton rate coefficients on proton temperature are shown in Fig. 11.

In Fig. 11 the electron collision rate coefficients calculated by Aggarwal et al. (2003a,b) are also presented. It can be seen that proton collisions will significantly influence the population of the $\rm 3s3p\ ^3P_{0,1,2}$ levels in plasma with a temperature higher than 400 eV.

$\begin{figure} \par\includegraphics[width=9cm]{12392f11.eps} \end{figure}$

Figure 11:

Proton collision rate coefficients for the transitions in Mg-like Fe XV: solid, dashed and doted lines - Eq. (3), diamonds - data of Landman & Brown (1979) for the $\rm 3s3p\ ^3P_0{-}^3P_1$ transition, $\times$ - data of Landman & Brown (1979) for the $\rm 3s3p\ ^3P_0{-}^3P_2$ transition, $\circ$ - data of Landman & Brown (1979) for the $\rm 3s3p\ ^3P_1{-}^3P_2$ transition; thin solid lines with diamonds, $\times$ , $\circ$ - electron rate coefficients of Aggarwal et al. (2003a) for the $\rm ^3P_0{-}^3P_1,\ ^3P_0{-}^3P_2$ , and $\rm ^3P_1{-}^3P_2$ transitions, respectively.

Open with DEXTER

It should be noted that in the CHIANTI database (Young et al. 2003) for proton impact excitation of transitions in Fe XI, XII, XIII, and Fe XV ions, the data presented in the papers by Landman (1980, 1978, 1975), and Landman & Brown (1979) are used. These data are the same as we recommend in the present paper. For Fe X they use the data in Bely & Faucher (1970), while we recommend the data in Kastner & Bhatia (1979), and for Fe XIV they use unpublished calculations by Tully J. (2002, unpublished), while we recommend data in Landman (1975).

4.7 Ne-like Fe XVII ion (2s²2p⁵3s ^3,1P)

For Ne-like Fe XVII we know only one paper of Landman (1985) where proton collisional excitation rate coefficients have been calculated for transitions among the ${\rm 2p^53s}\ ^{(2S+1)}{\rm P}_J$ levels. The calculations have been performed according to a symmetrized semiclassical impact parameter theory in which the truncated Schrodinger equation for quadrupole excitation is directly integrated. Intermediate coupling wave functions for the J = 1 levels were determined using the observed $\rm 2p^53s$ energy levels; otherwise, the Slater and spin-orbit interaction integrals obtained with Froese Fischer's MCHF77 program (Froese Fischer 1978) were used. The LS-coupled quadrupole interaction matrix was then converted to intermediate coupling according to the derived transformation coefficients.

The results of Landman's calculations (Landman 1985) are presented in Figs. 12 and 13. Note that at present no other theoretical or experimental results are available for a comparison of the proton rate coefficients. It is possible to compare proton collision excitation with electron excitation. In Figs. 12 and 13 the electron rate coefficients calculated by extrapolation of the data of Aggarwal et al. (2003a,b) in the low energy region are presented. It should be noted that designations of energy levels used in the paper of Aggarwal et al. (2003a,b) (namely, $\rm ^3P_2,\ ^1P_1,\ ^3P_0$ , and $\rm ^3P_1$ ) differ from the designations used in paper of Landman (1985) (namely, $\rm ^3P_2,\ ^3P_1,\ ^3P_0$ , and $\rm ^1P_1$ ). Our presentation of the proton rate coefficients in Figs. 12 and 13 and in Table 2 corresponds to the designations of Aggarwal et al. (2003a,b). One can see from Figs. 12 and 13 that in the region $T \geqq 10^7$ K proton collisions are important for all levels considered.

Table 2: The values of fitting parameters, defined in Eq. (3), for proton excitation rate coefficients of transitions in ions Fe XVII-Fe XXIII.

$\begin{figure} \par\includegraphics[width=9cm]{12392f12.eps} \vspace*{2mm} \end{figure}$

Figure 12:

Collision rate coefficient for transition ${\rm 2s^22p^53s\ ^3P_2}{-}^{(2S+1)}{\rm P}_J$ in Ne-like Fe XVII: solid thick lines - Eq. (3) for protons, solid thin lines - electrons (Aggarwal et al. 2003b), triangles - data of Landman (1985) and Aggarwal et al. (2003b) for level $\rm ^1P_1$ , squares - data of Landman (1985) and Aggarwal et al. (2003b) for level $\rm ^3P_0$ , $\circ$ - data of Landman (1985) and Aggarwal et al. (2003b) for level $\rm ^3P_1$ .

Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{12392f13.eps} \vspace*{2mm} \end{figure}$

Figure 13:

Collision rate coefficient for the transition ${\rm 2s^22p^53s\ ^3P}_J{-}^{(2S+1)}{\rm P}_{J'}$ in Ne-like Fe XVII: solid thick lines - Eq. (3) for protons, solid thin lines - electrons (Aggarwal et al. 2003b), triangles - data of Landman (1985) and Aggarwal et al. (2003b) for the transition $\rm ^1P_1{-}^3P_0$ , squares - data of Landman (1985) and Aggarwal et al. (2003b) for the transition $\rm ^1P_1{-}^3P_1$ , $\circ$ - data of Landman (1985) and Aggarwal et al. (2003b) for the transition $\rm ^3P_0{-}^3P_1$ .

Open with DEXTER

We fitted the data of Landman (1985) by Eq. (3) and the values of p_i obtained are presented in Table 2.

It should be noted that proton collisions can not effectively excite $\rm 2s^22p^53s$ levels from the ground level. However, the $\rm ^3P_2$ and $\rm ^3P_0$ levels are metastable and can have substantial population densities in relatively low density plasma. Therefore, proton collisions can play a significant role at densities where the collision depopulation of these levels competes with their radiative decay. Under these conditions, for example, the relative intensities of the $\rm 2s^22p^53s\ ^3P_0{-}2s^22p^53s\ ^3P_1$ M1 and $\rm 2s^22p^53s\ ^3P_2{-}2p^6\ ^1S_0$ M2 lines relative to the $\rm 2s^22p^53s\ ^3P_1{-}2s^22p^6\ ^1S_0$ line may provide useful density diagnostics (Landman 1985). Because of the radiative probabilities $A({\rm 2s^22p^53s\ ^3P_0{-}2s^22p^53s\ ^3P_1}) = 1.6 \times 10^4\ \rm s^{-1}$ , $A({\rm 2s^22p^53s\ ^3P_0{-}2s^22p^53s\ ^3P_2}) = 2\ \rm s^{-1}$ , $A({\rm 2s^22p^53s\ ^3P_2{-}2s^22p^6\ ^1S_0}) = 1.7 \times 10^5\ \rm s^{-1}$ (see, for example, Landman 1985) it follows from the data presented in Figs. 12 and 13 and condition (2) that proton collision decay will be important for the $\rm 2s^22p^53s\ ^3P_0$ level at $N_{\rm p} \geqq 10^{14}\ \rm cm^{-3}$ and for the $\rm 2s^22p^53s\ ^3P_2$ level at $N_{\rm p} \geqq 10^{15}\ \rm cm^{-3}$ . Note that the CHIANTI database (Young et al. 2003) does not use proton impact de-excitation data.

4.8 F-like Fe XVIII ion (2s²2p⁵ ²P_3/2-²P_1/2)

Several semiclassical calculations, both first-order and close-coupling, have been performed for the Fe XVIII ion. The first-order semiclassical calculations have been done by Kastner & Bhatia (1979) and some later by Feldman et al. (1980).

The close-coupling semiclassical method of Reid & Schwarz (1969) has been used by several authors to calculate both proton collision excitation cross sections and rate coefficients for the $\rm 2s^22p^5\ ^2P_{3/2}{-}^2P_{1/2}$ transition in Fe XVIII (Keenan & Reid 1987, 1989; Foster et al. 1994). In the earlier paper of Keenan & Reid (1987) aspects like the polarization effects, symmetrization of coupled equations, or departures from LS-coupling were not considered. Later Keenan & Reid (1989) have developed this method to incorporate symmetrization with respect to channel velocities, and in a further development, Foster et al. (1994) have improved the accuracy of the calculations by considering both symmetrization and polarization effects, whereby they have included the $\rm 2s2p^6\ ^2S_{1/2}$ level by means of a polarization potential. The inclusion of these factors has resulted in a difference of 60% in the cross sections compared with those of Keenan & Reid (1989, see Fig. 14).

$\begin{figure} \par\includegraphics[width=9cm]{12392f14.eps} \vspace{-3mm} \end{figure}$	Figure 14: Proton collision cross section for the transition $\rm 2s^22p^5\ ^2P_{3/2}{-}^2P_{1/2}$ in F-like Fe XVIII: solid line - data of Foster et al. (1994), dashed line - data of Keenan & Reid (1989).
Open with DEXTER

The importance of including polarization effects in intramultiplet excitation collisions was noted in the papers of Heil et al. (1982, 1983) where a quantal molecular approach was used to describe the proton-ion interaction. In the calculations of Foster et al. (1994), the polarization was taken into account by the inclusion of the $\rm 2s2p^6\ ^2S_{1/2}$ state alone. For Fe XVIII ion the major component of the polarization can be really incorporated by a single state, because the next states that contribute to the polarization (i.e., states with configuration $\rm 2s^22p^43s$ ) have about six times larger excitation energies than $\rm 2s2p^6$ . This is a feature of highly charged F-like systems and, generally speaking, one would not expect that a single state could give a good representation of the polarization in a general case.

The excitation rate coefficients obtained in Kastner & Bhatia (1979), Feldman et al. (1980), Keenan & Reid (1989), and Foster et al. (1994) are presented in Fig. 15. It should be noted that results from Foster et al. (1994) are more than a factor of two smaller than the semiempirical results of Kastner & Bhatia (1979) and Feldman et al. (1980) over the narrow temperature range for which they present results, and are 30-36% lower than the results of Keenan & Reid (1989), where the effects of the $\rm ^2S$ state were not included. We recommend using the data of Foster et al. (1994), and present the corresponding values of fitting parameters in Table 2.

$\begin{figure} \par\includegraphics[width=9cm]{12392f15.eps} \end{figure}$	Figure 15: Proton collision rate coefficient for the transition $\rm 2s^22p^5\ ^2P_{3/2}{-}^2P_{1/2}$ in F-like Fe XVIII: solid line - Eq. (3), diamonds - data of Foster et al. (1994), opened squares - data of Keenan & Reid (1989), triangles - data of Kastner & Bhatia (1979), filled squares - data of Feldman et al. (1980).
Open with DEXTER

The extrapolation of the results obtained in Hummer et al. (1993) for the excitation of the transition $\rm 2s^22p^5\ ^2P_{3/2}{-}^2P_{1/2}$ by electron impact shows that in the temperature region $T \approx (2-6) \times 10^7$ K the electron rate coefficient is about $(1{-}2) \times 10^{-9}\ \rm cm^3s^{-1}$ . It means that in a plasma with $T_{\rm e} = T_{\rm p}$ the excitation by proton impact can increase the population of the $\rm 2s^22p^5\ ^2P_{1/2}$ level only by 10%. Of course, at $T_{\rm e} \neq T_{\rm p}$ the influence of the proton excitation may be more important.

Note also that the critical density in Eq. (1) for the transition considered is about $10^{14}\ \rm cm^{-3}$ (see, for example, Foster et al. 1994). It follows from this that the proton excitation process may be important for Fe XVIII ion only in the low density plasma with $N_{\rm e} \leqq 10^{14}\ \rm cm^{-3}$ , and it is not necessary to take this process into account for simulations of more dense plasma kinetics.

Foster et al. (1994) used their proton excitation rates to calculate the intensity ratio R for the spectral lines $\rm 2s^22p^5\ ^2P_{3/2}{-}2s^22p^5\ ^2P_{1/2}$ and $\rm 2s^22p^5\ ^2P_{3/2}{-}2s2p^6\ ^2S_{1/2}$ at plasma parameters determined independently in the experiment on the JIPP T-II-U tokamak (Nagoya, Japan) and showed that the modeling results agree very well with results observed by Sato et al. (1986).

The CHIANTI database uses data of Foster et al. (1994).

4.9 O-like Fe XIX ion (2s²2p⁴ ³P_J)

There is only one paper of Feldman et al. (1980) where data on the proton excitation of the $\rm ^3P_2{-}^3P_0$ and $\rm ^3P_2{-}^3P_1$ transitions in O-like Fe XIX ion were calculated by a first-order semiclassical method and are presented for one temperature value.

There are unpublished data calculated by Ryans et al. by using the semiclassical close-coupling approach of Reid & Schwarz (1969). These data are now used in the CHIANTI database (Young et al. 2003) and only these data have been fitted to Eq. (3) in the present work.

In Figs. 16-18 we present: 1) the result of our fit of the proton excitation rates; 2) the proton excitation rates calculated in Feldman et al. (1980); 3) the proton excitation rates calculated in Ryans, Keenan, & Reid (unpublished); and 4) the electron excitation rate coefficients obtained by Butler & Zeippen (2001b). It can be seen from Figs. 16 and 17 that proton-ion collisions will strongly influence the population of the $\rm ^3P_0$ and $\rm ^3P_1$ levels at practically all reasonable values of temperature. It is interesting that the electron rate coefficient for the $\rm ^3P_0{-}^3P_1$ transition (not presented in Fig. 18) is higher than the proton one by about two orders of magnitude. This means that collision mixing of the $\rm ^3P_0$ and $\rm ^3P_1$ levels will occur only by electron-ion collisions. The probabilities of radiative decay for the levels $\rm ^3P_0$ and $\rm ^3P_1$ are (Cheng et al. 1979): $A({\rm ^3P_0{-}^3P_2}) = 0.53\ \rm s^{-1}$ , and $A({\rm ^3P_1{-}^3P_2}) = 1.43 \times 10^4\ \rm s^{-1}$ . Because for temperatures about 10⁷ K the electron collision rate coefficient for the $\rm ^3P_0{-}^3P_1$ transition is about $2 \times 10^{-9}\ \rm cm^3~s^{-1}$ (Butler & Zeippen 2001b), it is possible to conclude that in a plasma with $N_{\rm e} \gg 10^{13}\ \rm cm^{-3}$ electrons will cause a Boltzmann equilibrium among the fine-structure levels, and proton collision will not be important for ion kinetics.

$\begin{figure} \par\includegraphics[width=9cm]{12392f16.eps} \end{figure}$	Figure 16: Collision rate coefficients for the transition $\rm 2s^22p^4\ ^3P_2{-}^3P_0$ in O-like Fe XIX: solid thick lines - Eq. (3) for protons, solid thin lines - electrons (Butler & Zeippen 2001b), triangle - data of Feldman et al. (1980), and squares - data of Ryans, Keenan, & Reid (unpublished).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{12392f17.eps} \end{figure}$	Figure 17: Collision rate coefficients for the transition $\rm 2s^22p^4\ ^3P_2{-}^3P_1$ in O-like Fe XIX: solid thick lines - Eq. (3) for protons, solid thin lines - electrons (Butler & Zeippen 2001b), triangle - data of Feldman et al. (1980), and squares - data of Ryans, Keenan, & Reid (unpublished).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{12392f18.eps} \vspace*{-2mm} \end{figure}$	Figure 18: Collision rate coefficient for the transition $\rm 2s^22p^4\ ^3P_0{-}^3P_1$ in O-like Fe XIX: solid thick lines - Eq. (3) for protons, and squares - data of Ryans, Keenan, & Reid (unpublished).
Open with DEXTER

4.10 N-like Fe XX ion (2s²2p³ ⁴S_3/2, ²D _3/2,5/2, ²P _1/2,3/2)

At present there is only one paper where Bhatia & Mason (1980) have used the semiclassical first-order method of Bely & Faucher (1970) to calculate proton impact excitation of fine-structure transitions in Fe XX ions. We have fitted these data to Eq. (3) and the results obtained are presented in Table 2. In Figs. 19, 21 the temperature dependencies of the proton excitation rates are shown together with the electron excitation rates calculated by Butler & Zeippen (2001a). It can be seen that for practically all transitions (except for $\rm ^4S_{3/2}{-}^2P_{1/2,3/2}$ ) the proton rate coefficients are comparable or larger than the electron ones at all reasonable temperatures. The density region where proton collisions are important for the population kinetics of the fine-structure levels can be estimated from Eq. (2) by using the radiative probabilities calculated in the paper of Bhatia & Mason (1980). Because the total radiative decay probabilities are $A({\rm ^2D_{3/2}}) = 1.56 \times 10^4\ \rm s^{-1}$ , $A({\rm ^2D_{5/2}}) = 1.68 \times 10^3\ \rm s^{-1}$ , $A({\rm ^2P_{1/2}}) = 3.53 \times 10^4\ \rm s^{-1}$ , and $A({\rm ^2P_{3/2}}) = 8.05 \times 10^4\ \rm s^{-1}$ , we find that it is necessary to take into account the proton collisions in the kinetic calculations for a plasma with an electron density of $N_{\rm e} \leqq 10^{16}~\rm cm^{-3}$ .

$\begin{figure} \par\includegraphics[width=9cm]{12392f19.eps} \vspace*{-3mm} \end{figure}$

Figure 19:

Collision rate coefficients for the transitions $\rm 2s^22p^3\ ^4S_{3/2}{-}^2D_{3/2}$ (filled squares), $\rm 2s^22p^3\ ^4S_{3/2}{-}^2D_{5/2}$ (opened squares), $\rm 2s^22p^3\ ^4S_{3/2}{-}^2P_{1/2}$ (triangles), $\rm 2s^22p^3\ ^4S_{3/2}{-}^2P_{3/2}$ ( $\diamond$ ) in N-like Fe XX: solid thick lines - Eq. (3) for protons, solid thin lines - electrons (Butler & Zeippen 2001a), triangles, filled squares, opened squares, $\diamond$ - data of Bhatia & Mason (1980).

Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{12392f20.eps} \end{figure}$

Figure 20:

Collision rate coefficients for the transitions $\rm 2s^22p^3\ ^2D_{3/2}{-}^2D_{5/2}$ (opened squares), $\rm 2s^22p^3\ ^2D_{3/2}{-}^2P_{1/2}$ (filled squares), $\rm 2s^22p^3\ ^2D_{3/2}{-}^2P_{3/2}$ (triangles) in N-like Fe XX: solid thick lines - Eq. (3) for protons, solid thin lines - electrons (Butler & Zeippen 2001a), opened squares, filled squares, triangles - data of Bhatia & Mason (1980).

Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{12392f21.eps} \end{figure}$

Figure 21:

Collision rate coefficients for the transitions $\rm 2s^22p^3\ ^2D_{5/2}{-}^2P_{1/2}$ (opened squares), $\rm 2s^22p^3\ ^2D_{5/2}{-}^2P_{3/2}$ (filled squares), $\rm 2s^22p^3\ ^2P_{1/2}{-}^2P_{3/2}$ (triangles) in N-like Fe XX: solid thick lines - Eq. (3) for protons, solid thin lines - electrons (Butler & Zeippen 2001a), opened squares, filled squares, triangles - data of Bhatia & Mason (1980).

Open with DEXTER

The CHIANTI database uses the data of Bhatia & Mason (1980).

4.11 C-like Fe XXI ion (2s²2p² ³P)

Several calculations, both semiclassical and quantal have been performed for the ground configuration of the Fe XXI ion.

Close-coupling semiclassical calculations have been done by Ryans et al. (1999a,b). They consider the $\rm ^3P_0{-}^3P_1$ , $\rm ^3P_0{-}^3P_2$ and $\rm ^3P_1{-}^3P_2$ transitions among the fine-structure levels ${\rm 2s^22p^2\ ^3P}_J$ of carbon-like Fe XXI and have calculated the proton rates using the symmetrized close-coupling semi-classical approach in which the interaction matrix elements were modified to give them the correct short-range forms, and the effects of dipole coupling to nearby terms were included by means of a polarization potential. A set of excited terms was selected which are coupled to the ground state by the E1 interaction. In the present case of the $\rm ^3P$ ground state, the terms that can contribute to the polarization have the symmetry $\rm ^3S$ , $\rm ^3P$ , or $\rm ^3D$ . Therefore the calculations in the paper of Ryans et al. (1999a) were made in two approximations: 1) when only the three excited terms $\rm 2s2p^3\ ^3D$ , $\rm ^3P$ , and $\rm ^3S$ were included in the calculation via the polarization potential and 2) when the terms $\rm 2s^22p3s\ ^3P$ and $\rm 2s^22p3d\ ^3D,\ ^3P$ were also included to test the convergence of the results. It has been shown that for the Fe XXI ion and for protons as perturbers the inclusion of the further excited terms had a small effect on the cross sections. For Fe XXI as well as for other heavy ions the polarization affects the cross sections significantly at all impact energies. However, for the heavy ions the polarization potential is dominated by the $\rm 2s2p^3$ terms, because the excitation energies of the ${\rm 2s^22p3}l$ , ${\rm 2s2p^23}l$ and higher configurations are much higher than the excitation energies of $\rm 2s2p^3$ . This means that the representation of the polarization by the $\rm 2s2p^3$ terms is adequate to calculate the ${\rm 2s^22p^2\ ^3P}_J{-}^3{\rm P}_{J'}$ transitions in the Fe XXI ions. Note that additionally including ${\rm 2p3}l$ terms does not allow us to increase the accuracy of the calculation, because in this case the includion of some other configurations (for example, $\rm 2s2p^23p$ ) is also needed. The results of the calculations of Ryans et al. (1999b) where only the $\rm 2s2p^3$ configuration was taken into account for the polarization potential are shown in Figs. 22-24. Note also that in the low energy tail of the cross sections, where the close-coupling calculations are difficult, the first-order cross sections modified to allow for polarization were used in the calculations of the proton rate coefficients by Ryans et al. (1999b). These rate coefficients were fitted to Eq. (3) and the results obtained are presented in Table 2. Note that the CHIANTI database uses the data of Ryans et al. (1999b).

$\begin{figure} \includegraphics[width=9cm]{12392f22.eps} \end{figure}$	Figure 22: Collision rate coefficients for the transition $\rm 2s^22p^2\ ^3P_0{-}^3P_1$ in C-like Fe XXI: solid thick line - Eq. (3) for protons, solid thin line - electrons (Butler & Zeippen 2000), triangles - data of Faucher (1977), squares - data of Ryans et al. (1999b).
Open with DEXTER

$\begin{figure} \includegraphics[width=9cm]{12392f23.eps} \end{figure}$	Figure 23: Collision rate coefficients for the transition $\rm 2s^22p^2\ ^3P_0{-}^3P_2$ in C-like Fe XXI: solid thick line - Eq. (3) for protons, solid thin line - electrons (Butler & Zeippen 2000), triangles - data of Faucher (1977), squares - data of Ryans et al. (1999b).
Open with DEXTER

$\begin{figure} \includegraphics[width=9cm]{12392f24.eps} \end{figure}$	Figure 24: Collision rate coefficients for the transition $\rm 2s^22p^2\ ^3P_1{-}^3P_2$ in C-like Fe XXI: solid thick line - Eq. (3) for protons, solid thin line - electrons (Butler & Zeippen 2000), triangles - data of Faucher (1977), squares - data of Ryans et al. (1999b).
Open with DEXTER

Earlier Faucher (1977) have considered a proton-impact excitation of C-like Fe XXI using a quantal formulation. For Fe XXI the differences between the results of Faucher (1977) and Ryans et al. (1999b) are significant, especially for the $\rm ^3P_0{-}^3P_1$ transition (see Figs. 22-24). In Faucher's calculations the electrostatic interaction potential was approximated by its long-range quadrupole part and no polarization effects were taken into account. Ryans et al. (1999a) have made a special calculation with the polarization omitted and with the same atomic data as Faucher (1977). This calculation differs from Faucher (1977) only in two respects: 1) in the collision treatment - semiclassical versus quantal, and 2) in the interaction between matrix elements - short-range modified forms versus purely asymptotic forms. For the $\rm ^3P_0{-}^3P_2$ and $\rm ^3P_1{-}^3P_2$ transitions these results are close to Faucher (1977) in the energy region of $E_{\rm p} < 3$ KeV, and for higher energies the progressive divergence in the two calculations is due to the difference in the short-range part of the interaction potential. For the $\rm ^3P_0{-}^3P_1$ transition the discrepancy is more pronounced because this strictly second-order process is more sensitive to the short-range forms of the matrix elements (Ryans et al. 1999a). Thus, in the calculations of Faucher (1977) two important effects (the modification of the interaction potential at short distances and polarization) were not taken into account, and we recommend to use the data of Ryans et al. (1999b).

Comparisons of proton and electron excitation rates are also shown in Figs. 22-24. It is clearly seen that only for the transition $\rm ^3P_0{-}^3P_1$ proton collisions are insignificant, while for the transitions $\rm ^3P_0{-}^3P_2$ and $\rm ^3P_1{-}^3P_2$ the proton rates dominate. According to the paper of Cheng et al. (1979) the total probabilities of the radiative decay of the $\rm ^3P_1$ and $\rm ^3P_2$ levels are: $A(\rm ^3P_1) = 6.52 \times 10^3\ s^{-1}$ and $A(\rm ^3P_2) = 1.04\ s^{-1}$ . This means (see Eq. (2)) that only in a plasma with $N_{\rm e} \gg 10^{15}\ \rm cm^{-3}$ electrons will cause a Boltzmann equilibrium among the fine-structure levels and the proton collision will be unimportant for ion kinetics.

4.12 B-like Fe XXII ion (2s²2p ²P, 2s2p² ⁴P)

At present for B-like Fe XXII there are only the calculations made by Foster et al. (1996, 1997a,b). In these papers cross sections and excitation rate coefficients for the fine-structure transitions within both the ground $\rm 2s^22p\ ^2P$ and the metastable $\rm 2s2p^2\ ^4P$ terms have been obtained by the same method as in Foster et al. (1994). In the former case (Foster et al. 1996), the $\rm 2s2p^2\ ^2S,\ ^2P$ , and $\rm ^2D$ terms were included, while in the latter (Foster et al. 1997a,b), the $\rm 2p^3\ ^4S^o$ term was also included. Additionally, in these calculations the interaction matrix elements were modified to give them the correct short-range forms. The values of the magnitudes of the required matrix elements have been derived from the best available oscillator strengths, while the signs of the matrix elements were taken to be those which would arise from LS-coupled hydrogenic orbitals. This means that errors might arise if the ion departs too far from LS-coupling. Therefore Foster et al. (1997b) estimated the accuracy of their data for Fe XXII to be 30% in the high temperature region. We have fitted the data of Foster et al. (1997b) to Eq. (3) and the values of the fitting parameters are presented in Table 2. The CHIANTI database uses the data of Foster et al. (1997b).

In Figs. 25 and 26 the temperature dependencies of proton excitation rates are shown together with the data of Zhang & Pradhan (1997) for the electron excitation rates. It is seen that for the transitions $\rm 2s^22p\ ^2P_{1/2}{-}^2P_{3/2}$ , $\rm 2s2p^2\ ^4P_{1/2}{-}^4P_{5/2}$ and $\rm 2s2p^2\ ^4P_{3/2}{-} ^4P_{5/2}$ the proton collisions dominate at practically all reasonable temperatures, and for the $\rm 2s2p^2\ ^4P_{1/2}{-}^4P_{3/2}$ transition the proton collisions are important at T > 10⁷ K.

$\begin{figure} \par\includegraphics[width=9cm]{12392f25.eps} \end{figure}$	Figure 25: Collision rate coefficients for the transition $\rm 2s^22p\ ^2P_{1/2}{-}^2P_{3/2}$ in B-like Fe XXII: solid thick line - Eq. (3) for protons, solid thin line - electrons (Zhang & Pradhan 1997), and squares - data of Foster et al. (1997b).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{12392f26.eps} \end{figure}$	Figure 26: Collision rate coefficients for the transition $\rm 2s2p^2\ ^4P_{1/2}{-}^4P_{5/2}$ ( $\bullet$ ), $\rm 2s2p^2\ ^4P_{3/2}{-} ^4P_{5/2}$ ( $\triangle$ ), $\rm 2s2p^2\ ^4P_{1/2}{-}^4P_{3/2}$ (squares), in B-like Fe XXII: solid thick line - Eq. (3) for protons, solid thin line - electrons (Zhang & Pradhan 1997), $\bullet$ , $\triangle$ , squares - data of Foster et al. (1997b).
Open with DEXTER

According to Cheng et al. (1979) the total probabilities of a radiative decay of the levels considered are: $A(\rm 2s^22p\ ^2P_{3/2}) = 1.48 \times 10^4\ s^{-1}$ , $A(\rm 2s2p^2\ ^4P_{1/2}) = 0.97 \times 10^8\ s^{-1}$ , $A(\rm 2s2p^2\ ^4P_{3/2}) = 1.02 \times 10^7\ s^{-1}$ , and $A(\rm 2s2p^2\ ^4P_{5/2}) = 0.67 \times 10^8\ s^{-1}$ . This means that proton collisions will be able to populate the $\rm 2s^22p\ ^2P_{3/2}$ level at plasma densities of $N_{\rm e} < 10^{16}\ \rm cm^{-3}$ (see Eq. (1)), and significantly influence the populations of the $\rm 2s2p^2\ ^4P_{1/2, 3/2, 5/2}$ levels at $N_{\rm p} > 10^{16}\ \rm cm^{-3}$ (see Eq. (2)). So in this case it is necessary to take the proton excitation processes into account in both low and high density plasma.

4.13 Be-like Fe XXIII ion (2s2p ³P_0,1,2)

$\begin{figure} \par\includegraphics[width=9cm]{12392f27.eps} \end{figure}$	Figure 27: Collision rate coefficients for the transition $\rm 2s2p\ ^3P_0{-}^3P_2$ (triangles), $\rm 2s2p\ ^3P_1{-}^3P_2$ (opened squares), $\rm 2s2p\ ^3P_0{-}^3P_1$ (filled squares) in Be-like Fe XXIII: solid thick line - Eq. (3) for protons, solid thin line - electrons (Chidichimo et al. 2005), and thick dashed lines - data of Doyle (1987).
Open with DEXTER

The excitation of Fe XXIII levels from the ground state by proton impact is not important because the first excited configuration lies too far from the ground configuration $\rm 2s^2$ . However, the first excited configuration contains the closely spaced metastable levels ${\rm 2s2p\ ^3P}_J$ , for which proton-induced transitions can be important. The are several papers concerned with the calculation of the proton rates for these transitions.

Feldman et al. (1980) used a first-order semiclassical approach (see above) and presented the proton rate only at one temperature value.

More sophisticated calculations based on the semiclassical close-coupling method were carried out by Doyle (1987). The calculations were split into two energy ranges: a low-energy and an intermediate-energy range. For both energy ranges, the perturbing proton follows a classical Coulomb trajectory, but for the first range the first-order theory was used and close-coupling equations were solved only for the second region. Calculations were carried out with different short-range forms of interaction matrix elements, but no polarization effects have been taken into account.

The importance of including the effects of higher-lying states in the calculation of proton rates via a polarization potential technique was demonstrated by Foster et al. (1994) and Ryans et al. (1999a,b) for the ground term fine-structure transitions in F-like and B-like ions. Ryans et al. (1998) have extended this approach to Be-like ions and calculated proton excitation cross sections and rate coefficients for the transitions among the $\rm 1s^22s2p\ ^3P$ fine-structure levels of Fe XXIII. The cross sections for the transitions ${\rm 2s2p\ ^3P}_J{-}^3{\rm P}_{J'}$ were calculated by the same symmetrized close-coupled semiclassical treatment that we have described above (F-like and B-like Fe ions): the interaction matrix elements are modified to have the correct short-range forms, and the effects of dipole coupling to nearby terms are included by means of a polarization potential. In the case of the Fe XIII ion dipole coupling to the $\rm 2p^2\ ^3P$ , $\rm 2s3s\ ^3S,$ and $2{\rm s}3{\rm d}\ ^3$ D terms were included in the polarization potential. Ryans et al. (1998) estimated the accuracy of their data for Fe XXII to be 20%. We have fitted the data of Ryans et al. (1998) to Eq. (3) and the values of fitting parameters are presented in Table 2. The CHIANTI database uses the data of Ryans et al. (1998).

In Fig. 27 the temperature dependencies of the proton excitation rates calculated in the papers of Feldman et al. (1980), Doyle (1987), and Ryans et al. (1998) are shown together with the data of Chidichimo et al. (2005) for electron excitation rates. It is seen that proton collisions are very important for the transitions $\rm 2s2p\ ^3P_0{-}^3P_2$ , $\rm 2s2p\ ^3P_1{-}^3P_2$ at T > 10⁷ K and are insignificant for the transition $\rm 2s2p\ ^3P_0{-}^3P_1$ at practically all reasonable temperatures.

Among the components of the $\rm 2s2p\ ^3P$ term, level $\rm ^3P_1$ has the largest probability of radiative decay: $A(\rm 2s2p\ ^3P_1{-}2s^2\ ^1S_0) = 4.91 \times 10^7\ s^{-1}$ (Cheng et al. 1979). This means that in plasma with $N_{\rm e} > 10^{18}\ \rm cm^{-3}$ the electron collisions alone can cause a Boltzmann population distribution among the states of the $\rm 2s2p\ ^3P$ term. In a lower density plasma it is necessary to take the proton excitation processes into account in collisional-radiative kinetic calculations.

5 Conclusions

In the present work the comparison of data obtained for proton-induced excitation transitions in Fe X-Fe XXIII ions by different theoretical methods is carried out. A simple analytical equation with seven parameters is proposed; this allows us to describe the proton temperature dependence of the proton rate coefficients in a wide temperature range. The values of the free parameters have been determined by fitting the equation with numerical data. The recommended data are presented together with the fitting accuracies. A comparison of the proton collision rates with the electron ones shows that the proton impact excitation processes may be important for the Fe X, XI, XIII-XV, and XVII-XXIII ions. The results obtained can be used for plasma kinetics calculations and for the development of spectroscopic methods of astrophysical plasma diagnostics.

Acknowledgements

Part of the present work was carried out when I.S. was a visiting professor at the National Institute for Fusion Science. The authors are grateful to Prof. R.M. More for a careful reading of the manuscript. Work of I.S. was partly supported by ISTC grant 3504.

References

Aggarwal, K. M., Keenan, F. P., & Msezane, A. Z. 2003a, A&A, 410, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Aggarwal, K. M., Keenan, F. P., & Msezane, A. Z. 2003b, ApJS, 144, 169 [NASA ADS] [CrossRef] [Google Scholar]
Aggarwal, K. M., & Keenan, F. P. 2005a, A&A, 429, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Aggarwal, K. M., & Keenan, F. P. 2005b, A&A, 439, 1215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Alder, K., Bohr, A., Huus T., Mottleson, B., & Winther A. 1956, Rev. Mod. Phys., 28, 432 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
Bahcall, J. N., & Wolff, R. A. 1968, ApJ, 152, 701 [NASA ADS] [CrossRef] [Google Scholar]
Bely, O., & Faucher, P. 1970, A&A, 6, 88 [NASA ADS] [Google Scholar]
Bely, O., Tully, J. A., & Van Regemorter, H. 1963, Ann. Phys. (Paris), 8, 303 [Google Scholar]
Bhatia, A. K., & Doschek, G. A. 1995, At. Data Nucl. Data Tables, 60, 97 [NASA ADS] [CrossRef] [Google Scholar]
Bhatia, A. K., & Doschek, G. A. 1996, At. Data Nucl. Data Tables, 64, 183 [NASA ADS] [CrossRef] [Google Scholar]
Bhatia, A. K., & Mason, H. E. 1980, A&A, 83, 380 [NASA ADS] [Google Scholar]
Binello, A. M., Mason, H. E., & Storey, P. J. 1998, A&AS, 127, 545 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
Burgess, A., & Tully, J. A. 2005, J. Phys. B., 38, 2629 [NASA ADS] [CrossRef] [Google Scholar]
Butler, K., & Zeippen, C. J. 2000, A&AS, 143, 483 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
Butler, K., & Zeippen, C. J. 2001a, A&A, 372, 1078 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Butler, K., & Zeippen, C. J. 2001b, A&A, 372, 1083 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cheng, T., Kim, Y.-K., & Desclaux, J. P. 1979, At. Data Nucl. Data Tables, 24, 111 [NASA ADS] [CrossRef] [Google Scholar]
Chidichimo, M. C., Del Zanna, G., Mason, H. E., et al. 2005, A&A, 430, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Copeland, F., Reid, R. H. G., & Keenan ,F. P. 1997, At. Data Nucl. Data Tables, 67, 179 [NASA ADS] [CrossRef] [Google Scholar]
Dalgarno, A. 1983, in Atoms in Astrophysics, ed. P. G. Burke, W. B. Eissner, D. G. Hummer, & I. C. Percival (New York: Plenum Press), 103 [Google Scholar]
Doyle, J. G. 1987, At. Data Nucl. Data Tables, 37, 441 [NASA ADS] [CrossRef] [Google Scholar]
Faucher, P. 1975, J. Phys. B, 8, 1886 [NASA ADS] [CrossRef] [Google Scholar]
Faucher, P. 1977, A&A, 54, 589 [NASA ADS] [Google Scholar]
Faucher, P., & Landman D. A. 1977, A&A, 54, 159 [NASA ADS] [Google Scholar]
Feldman, U., Doschek, G. A., Cheng Chung-Chieh, & Bhatia, A. K. 1980, J. Appl. Phys., 51, 190 [NASA ADS] [CrossRef] [Google Scholar]
Foster, V. J., Keenan, F. P., & Reid R. H. G. 1994, Phys. Rev. A, 49, 3092 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Foster, V. J., Keenan, F. P., & Reid R. H. G. 1996, A&A, 308, 1009 [NASA ADS] [Google Scholar]
Foster, V. J., Reid, R. H. G., & Keenan, F. P. 1997a, MNRAS, 288, 973 [NASA ADS] [Google Scholar]
Foster V. J., Keenan F. P., & Reid, R. H. G. 1997b, At. Data Nucl. Data Tables, 67, 99 [NASA ADS] [CrossRef] [Google Scholar]
Froese Fischer, C. 1978, Comp. Phys. Comm., 14, 145 [NASA ADS] [CrossRef] [Google Scholar]
Gupta, G. P., & Tayal, S. S. 1999, ApJ, 510, 1078 [NASA ADS] [CrossRef] [Google Scholar]
Heil, T. G., Green, S., & Dalgarno, A. 1982, Phys. Rev. A, 26, 3293 [NASA ADS] [CrossRef] [Google Scholar]
Heil, T. G., Kirby, K., & Dalgarno, A. 1983, Phys. Rev. A, 27, 2826 [NASA ADS] [CrossRef] [Google Scholar]
Hummer, D. G., Berrington, K. A., Eissner, W., et al. 1993, A&A, 279, 298 [NASA ADS] [Google Scholar]
Kastner, S. O. 1977, A&A, 54, 255 [NASA ADS] [Google Scholar]
Kastner, S. O., & Bhatia, A. K. 1979, A&A, 71, 211 [NASA ADS] [Google Scholar]
Keenan, F. P., & Reid, R. H. G. 1987, J. Phys. B, 20, L753 [NASA ADS] [CrossRef] [Google Scholar]
Keenan, F. P., & Reid, R. H. G. 1989, J. Phys. B, 22, L295 [NASA ADS] [CrossRef] [Google Scholar]
Landman, D. A. 1975, A&A, 43, 285 [NASA ADS] [Google Scholar]
Landman, D. A. 1978, ApJ, 220, 366 [NASA ADS] [CrossRef] [Google Scholar]
Landman, D. A. 1980, ApJ, 240, 709 [NASA ADS] [CrossRef] [Google Scholar]
Landman, D. A. 1985, J. Quant. Spectrosc. Radiat. Transf., 34, 365 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
Landman, D. A., & Brown, T. 1979, ApJ, 232, 636 [NASA ADS] [CrossRef] [Google Scholar]
Masnou-Seeuws, F., & McCarroll, R. 1972, A&A, 17, 441 [NASA ADS] [Google Scholar]
Reid, R. H. G. 1988, Adv. At. Mol. Phys., 25, 251 [CrossRef] [Google Scholar]
Reid, R. H. G., & Schwarz, J. H. 1969, in Proceedings of the Sixth International Conference on Physics of Electronic and Atomic Collisions, Cambridge, MA, ed. I. Amdur (Cambridge, MA: MIT), 236 [Google Scholar]
Ryans, R. S. I., Foster-Woods, V. J., Keenan, F. P., & Reid, R. H. G. 1999a, At. Data Nucl. Data Tables, 73, 1 [NASA ADS] [CrossRef] [Google Scholar]
Ryans, R. C. I., Foster-Woods, V. J., Reid, R. H. G., & Keenan, F. P. 1999b, A&A, 345, 663 [NASA ADS] [Google Scholar]
Ryans, R. S. I., Foster-Woods, V. J., Copeland, F., et al., 1998, At. Data Nucl. Data Tables, 70, 179 [NASA ADS] [CrossRef] [Google Scholar]
Sahal-Brechot, S. 1974, A&A, 32, 147 [NASA ADS] [Google Scholar]
Sato K., Mimura M., Ostuka M., et al. 1986, Phys. Rev. Lett., 56, 151 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Seaton, M. J. 1964, MNRAS, 127, 191 [NASA ADS] [Google Scholar]
Storey, P. J., Mason, H. E., & Saraph, H. E. 1996, A&A, 309, 677 [NASA ADS] [Google Scholar]
Young, P. R., Del Zanna, G., Landi, E., et al. 2003, ApJS, 144, 135 [NASA ADS] [CrossRef] [Google Scholar]
Zhang, H. L., & Pradhan, A. K. 1997, A&AS, 123, 575 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]

All Tables

Table 1: The values of fitting parameters, defined in Eq. (3), for proton excitation rate coefficients of transitions in ions Fe X-Fe XV.

Table 2: The values of fitting parameters, defined in Eq. (3), for proton excitation rate coefficients of transitions in ions Fe XVII-Fe XXIII.

All Figures

$\begin{figure} \par\includegraphics[width=9cm]{12392f01.eps} \end{figure}$	Figure 1: Proton collision rate coefficient for transition $\rm 3s^23p^5\ ^2P_{3/2}{-}^2P_{1/2}$ in Cl-like Fe X: solid lines - Eq. (3), triangles - data Kastner & Bhatia (1979), $\diamond$ - data Bely & Faucher (1970), $\bullet$ - data Bhatia & Doschek (1995), dashed line - electron collision rate coefficient of Aggarwal & Keenan (2005b).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f02.eps} \end{figure}$	Figure 2: Proton collision rate coefficients for the transitions ${\rm 3s^23p^4\ ^3P}_J{-}^3{\rm P}_{J'}$ in S-like Fe XI: solid, dashed and doted lines - Eq. (3), diamonds - Bhatia & Doschek (1995) and triangle - Landman (1980) for $^3{\rm P}_2{-}^3{\rm P}_1$ transition; $\times$ - Bhatia & Doschek (1995) and + - Landman (1980) for the $\rm ^3P_2{-}^3P_0$ transition; $\circ$ - Bhatia & Doschek (1995) for the $\rm ^3P_1{-}^3P_0$ transition; solid thin lines with diamonds, $\times$ , $\circ$ - electron rate coefficients of Gupta & Tayal (1999) for the transitions $\rm ^3P_2{-}^3P_1,\ ^3P_2{-}^3P_0$ and $\rm ^3P_1{-}^3P_0$ , respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f03.eps} \end{figure}$	Figure 3: Proton collision rate coefficients for transitions in P-like Fe XII: thick solid, dashed and dot lines - formula (3), $\times$ - data for $\rm 3s^23p^3\ ^4S_{3/2}{-}^2D_{3/2}$ transition, diamonds - data for $\rm 3s^23p^3\ ^4S_{3/2}{-}^2D_{5/2}$ transition, $\bullet$ - data for $\rm 3s^23p^3\ ^4S_{3/2}{-}^2P_{3/2}$ transition, $\triangle$ - data for $\rm 3s^23p^3\ ^4S_{3/2}{-}^2P_{3/2}$ transition; thin solid lines with $\times$ , diamonds, $\bullet$ , $\triangle$ - electron rate coefficients of Binello et al. (1998) for $\rm ^4S_{3/2}{-}^2D_{3/2},\ ^4S_{3/2}{-}^2D_{5/2},\ ^4S_{3/2}{-}^2P_{3/2}$ , and $\rm ^4S_{3/2}{-}^2P_{3/2}$ transitions, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f04.eps} \end{figure}$	Figure 4: Proton collision rate coefficients for transitions in P-like Fe XII: solid, dashed and doted lines - Eq. (3), $\times$ - data for the $\rm 3s^23p^3\ ^2D_{3/2}{-}^2D_{5/2}$ transition, $\bullet$ - data for the $\rm 3s^23p^3\ ^2D_{3/2}{-}^2P_{3/2}$ transition, $\triangle$ - data for the $\rm 3s^23p^3\ ^2D_{3/2}{-}^2P_{1/2}$ transition; thin solid lines with $\times ,\ \bullet , \ \triangle$ - electron rate coefficients of Binello et al. (1998) for the $\rm ^2D_{3/2}{-}^2D_{5/2},\ ^2D_{3/2}{-}^2P_{3/2}$ , and $\rm ^2D_{3/2}{-}^2P_{1/2}$ transitions, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f05.eps} \end{figure}$	Figure 5: Proton collision rate coefficients for transitions in P-like Fe XII: solid, dashed and doted lines - Eq. (3), $\times$ - data for the $\rm 3s^23p^3\ ^2D_{5/2}{-}^2P_{1/2}$ transition, $\bullet$ - data for the $\rm 3s^23p^3\ ^2P_{1/2}{-}^2P_{3/2}$ transition, $\triangle$ - data for the $\rm 3s^23p^3\ ^2D_{5/2}{-}^2P_{3/2}$ transition; solid thin lines with $\times ,\ \bullet , \ \triangle$ - electron rate coefficients of Binello et al. (1998) for the $\rm ^2D_{5/2}{-}^2P_{1/2},\ ^2P_{1/2}{-}^2P_{3/2}$ , and $\rm ^2D_{5/2}{-}^2P_{3/2}$ transitions, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f06.eps} \end{figure}$	Figure 6: Proton excitation cross sections for transitions in Si-like Fe XIII: squares - quantum results of Faucher (1977), solid line - semi-classical results of Landman (1975), dotted line - semi-classical results of Masnou-Seeuws & McCarroll (1972); for (1) the $\rm ^3P_0{-}^3P_1$ transition, (2) the $\rm ^3P_1{-}^3P_2$ transition, and (3) the $\rm ^3P_0{-}^3P_2$ transition.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f07.eps} \end{figure}$	Figure 7: Proton collision rate coefficients for transitions in Si-like Fe XIII: thick solid, thin solid, dashed and doted lines - Eq. (3), diamonds - data of Landman (1975) for the $\rm 3s^23p^2\ ^3P_0{-}^3P_1$ transition, black triangles - data of Landman (1975) for the $\rm 3s^23p^2\ ^3P_0{-}^3P_2$ transition, $\times$ - data of Landman (1975) for the $\rm 3s^23p^2\ ^3P_0{-}^1D_2$ transition, + - data of Landman (1975) for the $\rm 3s^23p^2\ ^3P_0{-}^1S_0$ transition, $\triangle$ - data of Kastner & Bhatia (1979) for the $\rm 3s^23p^2\ ^3P_0{-}^3P_2$ transition; thin solid lines with diamonds, black triangles, $\times$ , $\triangle$ - electron rate coefficients of Aggarwal & Keenan (2005a) for the $\rm ^3P_0{-}^3P_1,\ ^3P_0{-}^3P_2,\ ^3P_0{-}^1D_2,\ ^3P_0{-}^1S_0$ , and $\rm ^3P_0{-}^3P_2$ transitions, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f08.eps} \end{figure}$	Figure 8: Proton collision rate coefficients for transitions in Si-like Fe XIII: solid, dashed and doted lines - Eq. (3), diamonds - data of Landman (1975) for the $\rm 3s^23p^2\ ^3P_1{-}^3P_2$ transition, triangles - data of Landman (1975) for the $\rm 3s^23p^2\ ^3P_1{-}^1D_2$ transition, + - data of Landman (1975) for the $\rm 3s^23p^2\ ^3P_1{-}^1S_0$ transition; thin solid lines with diamonds, triangles, + - electron rate coefficients of Aggarwal & Keenan (2005a) for the $\rm ^3P_1{-}^3P_2,\ ^3P_1{-}^1D_2$ , and $\rm ^3P_1{-}^1S_0$ transitions, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f09.eps} \end{figure}$	Figure 9: Proton collision rate coefficients for transitions in Si-like Fe XIII: solid, dashed and doted lines - Eq. (3), diamonds - data of Landman (1975) for the $\rm 3s^23p^2\ ^3P_2{-}^1D_2$ transition, triangles - data of Landman (1975) for the $\rm 3s^23p^2\ ^3P_2{-}^1S_0$ transition, + - data of Landman (1975) for the $\rm 3s^23p^2\ ^1D_2{-}^1S_0$ transition; thin solid lines with diamonds, triangles, + - electron rate coefficients of Aggarwal & Keenan (2005a) for the $\rm ^3P_2{-}^1D_2,\ ^3P_2{-}^1S_0$ , and $\rm ^1D_2{-}^1S_0$ transitions, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f10.eps} \vspace*{-2.3mm} \end{figure}$	Figure 10: Proton collision rate coefficients for the transition $\rm 3s^23p\ ^2P_{1/2}{-}^2P_{3/2}$ in Al-like Fe XIV: solid line - Eq. (3), $\circ$ - data of Kastner & Bhatia (1979), triangles - data of Landman (1975), + - data of Bely & Faucher (1970), $\diamond$ - data of Heil et al. (1983), squares and $\times$ - data of Burgess & Tully (2005) for different methods considering the small impact parameter region; thin solid line - electron rate coefficient of Storey et al. (1996).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f11.eps} \end{figure}$	Figure 11: Proton collision rate coefficients for the transitions in Mg-like Fe XV: solid, dashed and doted lines - Eq. (3), diamonds - data of Landman & Brown (1979) for the $\rm 3s3p\ ^3P_0{-}^3P_1$ transition, $\times$ - data of Landman & Brown (1979) for the $\rm 3s3p\ ^3P_0{-}^3P_2$ transition, $\circ$ - data of Landman & Brown (1979) for the $\rm 3s3p\ ^3P_1{-}^3P_2$ transition; thin solid lines with diamonds, $\times$ , $\circ$ - electron rate coefficients of Aggarwal et al. (2003a) for the $\rm ^3P_0{-}^3P_1,\ ^3P_0{-}^3P_2$ , and $\rm ^3P_1{-}^3P_2$ transitions, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f12.eps} \vspace*{2mm} \end{figure}$	Figure 12: Collision rate coefficient for transition ${\rm 2s^22p^53s\ ^3P_2}{-}^{(2S+1)}{\rm P}_J$ in Ne-like Fe XVII: solid thick lines - Eq. (3) for protons, solid thin lines - electrons (Aggarwal et al. 2003b), triangles - data of Landman (1985) and Aggarwal et al. (2003b) for level $\rm ^1P_1$ , squares - data of Landman (1985) and Aggarwal et al. (2003b) for level $\rm ^3P_0$ , $\circ$ - data of Landman (1985) and Aggarwal et al. (2003b) for level $\rm ^3P_1$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f13.eps} \vspace*{2mm} \end{figure}$	Figure 13: Collision rate coefficient for the transition ${\rm 2s^22p^53s\ ^3P}_J{-}^{(2S+1)}{\rm P}_{J'}$ in Ne-like Fe XVII: solid thick lines - Eq. (3) for protons, solid thin lines - electrons (Aggarwal et al. 2003b), triangles - data of Landman (1985) and Aggarwal et al. (2003b) for the transition $\rm ^1P_1{-}^3P_0$ , squares - data of Landman (1985) and Aggarwal et al. (2003b) for the transition $\rm ^1P_1{-}^3P_1$ , $\circ$ - data of Landman (1985) and Aggarwal et al. (2003b) for the transition $\rm ^3P_0{-}^3P_1$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f14.eps} \vspace{-3mm} \end{figure}$	Figure 14: Proton collision cross section for the transition $\rm 2s^22p^5\ ^2P_{3/2}{-}^2P_{1/2}$ in F-like Fe XVIII: solid line - data of Foster et al. (1994), dashed line - data of Keenan & Reid (1989).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f15.eps} \end{figure}$	Figure 15: Proton collision rate coefficient for the transition $\rm 2s^22p^5\ ^2P_{3/2}{-}^2P_{1/2}$ in F-like Fe XVIII: solid line - Eq. (3), diamonds - data of Foster et al. (1994), opened squares - data of Keenan & Reid (1989), triangles - data of Kastner & Bhatia (1979), filled squares - data of Feldman et al. (1980).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f16.eps} \end{figure}$	Figure 16: Collision rate coefficients for the transition $\rm 2s^22p^4\ ^3P_2{-}^3P_0$ in O-like Fe XIX: solid thick lines - Eq. (3) for protons, solid thin lines - electrons (Butler & Zeippen 2001b), triangle - data of Feldman et al. (1980), and squares - data of Ryans, Keenan, & Reid (unpublished).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f17.eps} \end{figure}$	Figure 17: Collision rate coefficients for the transition $\rm 2s^22p^4\ ^3P_2{-}^3P_1$ in O-like Fe XIX: solid thick lines - Eq. (3) for protons, solid thin lines - electrons (Butler & Zeippen 2001b), triangle - data of Feldman et al. (1980), and squares - data of Ryans, Keenan, & Reid (unpublished).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f18.eps} \vspace*{-2mm} \end{figure}$	Figure 18: Collision rate coefficient for the transition $\rm 2s^22p^4\ ^3P_0{-}^3P_1$ in O-like Fe XIX: solid thick lines - Eq. (3) for protons, and squares - data of Ryans, Keenan, & Reid (unpublished).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f19.eps} \vspace*{-3mm} \end{figure}$	Figure 19: Collision rate coefficients for the transitions $\rm 2s^22p^3\ ^4S_{3/2}{-}^2D_{3/2}$ (filled squares), $\rm 2s^22p^3\ ^4S_{3/2}{-}^2D_{5/2}$ (opened squares), $\rm 2s^22p^3\ ^4S_{3/2}{-}^2P_{1/2}$ (triangles), $\rm 2s^22p^3\ ^4S_{3/2}{-}^2P_{3/2}$ ( $\diamond$ ) in N-like Fe XX: solid thick lines - Eq. (3) for protons, solid thin lines - electrons (Butler & Zeippen 2001a), triangles, filled squares, opened squares, $\diamond$ - data of Bhatia & Mason (1980).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f20.eps} \end{figure}$	Figure 20: Collision rate coefficients for the transitions $\rm 2s^22p^3\ ^2D_{3/2}{-}^2D_{5/2}$ (opened squares), $\rm 2s^22p^3\ ^2D_{3/2}{-}^2P_{1/2}$ (filled squares), $\rm 2s^22p^3\ ^2D_{3/2}{-}^2P_{3/2}$ (triangles) in N-like Fe XX: solid thick lines - Eq. (3) for protons, solid thin lines - electrons (Butler & Zeippen 2001a), opened squares, filled squares, triangles - data of Bhatia & Mason (1980).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f21.eps} \end{figure}$	Figure 21: Collision rate coefficients for the transitions $\rm 2s^22p^3\ ^2D_{5/2}{-}^2P_{1/2}$ (opened squares), $\rm 2s^22p^3\ ^2D_{5/2}{-}^2P_{3/2}$ (filled squares), $\rm 2s^22p^3\ ^2P_{1/2}{-}^2P_{3/2}$ (triangles) in N-like Fe XX: solid thick lines - Eq. (3) for protons, solid thin lines - electrons (Butler & Zeippen 2001a), opened squares, filled squares, triangles - data of Bhatia & Mason (1980).
Open with DEXTER
In the text

$\begin{figure} \includegraphics[width=9cm]{12392f22.eps} \end{figure}$	Figure 22: Collision rate coefficients for the transition $\rm 2s^22p^2\ ^3P_0{-}^3P_1$ in C-like Fe XXI: solid thick line - Eq. (3) for protons, solid thin line - electrons (Butler & Zeippen 2000), triangles - data of Faucher (1977), squares - data of Ryans et al. (1999b).
Open with DEXTER
In the text

$\begin{figure} \includegraphics[width=9cm]{12392f23.eps} \end{figure}$	Figure 23: Collision rate coefficients for the transition $\rm 2s^22p^2\ ^3P_0{-}^3P_2$ in C-like Fe XXI: solid thick line - Eq. (3) for protons, solid thin line - electrons (Butler & Zeippen 2000), triangles - data of Faucher (1977), squares - data of Ryans et al. (1999b).
Open with DEXTER
In the text

$\begin{figure} \includegraphics[width=9cm]{12392f24.eps} \end{figure}$	Figure 24: Collision rate coefficients for the transition $\rm 2s^22p^2\ ^3P_1{-}^3P_2$ in C-like Fe XXI: solid thick line - Eq. (3) for protons, solid thin line - electrons (Butler & Zeippen 2000), triangles - data of Faucher (1977), squares - data of Ryans et al. (1999b).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f25.eps} \end{figure}$	Figure 25: Collision rate coefficients for the transition $\rm 2s^22p\ ^2P_{1/2}{-}^2P_{3/2}$ in B-like Fe XXII: solid thick line - Eq. (3) for protons, solid thin line - electrons (Zhang & Pradhan 1997), and squares - data of Foster et al. (1997b).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f26.eps} \end{figure}$	Figure 26: Collision rate coefficients for the transition $\rm 2s2p^2\ ^4P_{1/2}{-}^4P_{5/2}$ ( $\bullet$ ), $\rm 2s2p^2\ ^4P_{3/2}{-} ^4P_{5/2}$ ( $\triangle$ ), $\rm 2s2p^2\ ^4P_{1/2}{-}^4P_{3/2}$ (squares), in B-like Fe XXII: solid thick line - Eq. (3) for protons, solid thin line - electrons (Zhang & Pradhan 1997), $\bullet$ , $\triangle$ , squares - data of Foster et al. (1997b).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{12392f27.eps} \end{figure}$	Figure 27: Collision rate coefficients for the transition $\rm 2s2p\ ^3P_0{-}^3P_2$ (triangles), $\rm 2s2p\ ^3P_1{-}^3P_2$ (opened squares), $\rm 2s2p\ ^3P_0{-}^3P_1$ (filled squares) in Be-like Fe XXIII: solid thick line - Eq. (3) for protons, solid thin line - electrons (Chidichimo et al. 2005), and thick dashed lines - data of Doyle (1987).
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Aggarwal, K. M., Keenan, F. P., & Msezane, A. Z. 2003a, A&A, 410, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[2] Aggarwal, K. M., Keenan, F. P., & Msezane, A. Z. 2003b, ApJS, 144, 169 [NASA ADS] [CrossRef] [Google Scholar]

[3] Aggarwal, K. M., & Keenan, F. P. 2005a, A&A, 429, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[4] Aggarwal, K. M., & Keenan, F. P. 2005b, A&A, 439, 1215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[5] Alder, K., Bohr, A., Huus T., Mottleson, B., & Winther A. 1956, Rev. Mod. Phys., 28, 432 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]

[6] Bahcall, J. N., & Wolff, R. A. 1968, ApJ, 152, 701 [NASA ADS] [CrossRef] [Google Scholar]

[7] Bely, O., & Faucher, P. 1970, A&A, 6, 88 [NASA ADS] [Google Scholar]

[8] Bely, O., Tully, J. A., & Van Regemorter, H. 1963, Ann. Phys. (Paris), 8, 303 [Google Scholar]

[9] Bhatia, A. K., & Doschek, G. A. 1995, At. Data Nucl. Data Tables, 60, 97 [NASA ADS] [CrossRef] [Google Scholar]

[10] Bhatia, A. K., & Doschek, G. A. 1996, At. Data Nucl. Data Tables, 64, 183 [NASA ADS] [CrossRef] [Google Scholar]

[11] Bhatia, A. K., & Mason, H. E. 1980, A&A, 83, 380 [NASA ADS] [Google Scholar]

[12] Binello, A. M., Mason, H. E., & Storey, P. J. 1998, A&AS, 127, 545 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]

[13] Burgess, A., & Tully, J. A. 2005, J. Phys. B., 38, 2629 [NASA ADS] [CrossRef] [Google Scholar]

[14] Butler, K., & Zeippen, C. J. 2000, A&AS, 143, 483 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]

[15] Butler, K., & Zeippen, C. J. 2001a, A&A, 372, 1078 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[16] Butler, K., & Zeippen, C. J. 2001b, A&A, 372, 1083 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[17] Cheng, T., Kim, Y.-K., & Desclaux, J. P. 1979, At. Data Nucl. Data Tables, 24, 111 [NASA ADS] [CrossRef] [Google Scholar]

[18] Chidichimo, M. C., Del Zanna, G., Mason, H. E., et al. 2005, A&A, 430, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[19] Copeland, F., Reid, R. H. G., & Keenan ,F. P. 1997, At. Data Nucl. Data Tables, 67, 179 [NASA ADS] [CrossRef] [Google Scholar]

[20] Dalgarno, A. 1983, in Atoms in Astrophysics, ed. P. G. Burke, W. B. Eissner, D. G. Hummer, & I. C. Percival (New York: Plenum Press), 103 [Google Scholar]

[21] Doyle, J. G. 1987, At. Data Nucl. Data Tables, 37, 441 [NASA ADS] [CrossRef] [Google Scholar]

[22] Faucher, P. 1975, J. Phys. B, 8, 1886 [NASA ADS] [CrossRef] [Google Scholar]

[23] Faucher, P. 1977, A&A, 54, 589 [NASA ADS] [Google Scholar]

[24] Faucher, P., & Landman D. A. 1977, A&A, 54, 159 [NASA ADS] [Google Scholar]

[25] Feldman, U., Doschek, G. A., Cheng Chung-Chieh, & Bhatia, A. K. 1980, J. Appl. Phys., 51, 190 [NASA ADS] [CrossRef] [Google Scholar]

[26] Foster, V. J., Keenan, F. P., & Reid R. H. G. 1994, Phys. Rev. A, 49, 3092 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]

[27] Foster, V. J., Keenan, F. P., & Reid R. H. G. 1996, A&A, 308, 1009 [NASA ADS] [Google Scholar]

[28] Foster, V. J., Reid, R. H. G., & Keenan, F. P. 1997a, MNRAS, 288, 973 [NASA ADS] [Google Scholar]

[29] Foster V. J., Keenan F. P., & Reid, R. H. G. 1997b, At. Data Nucl. Data Tables, 67, 99 [NASA ADS] [CrossRef] [Google Scholar]

[30] Froese Fischer, C. 1978, Comp. Phys. Comm., 14, 145 [NASA ADS] [CrossRef] [Google Scholar]

[31] Gupta, G. P., & Tayal, S. S. 1999, ApJ, 510, 1078 [NASA ADS] [CrossRef] [Google Scholar]

[32] Heil, T. G., Green, S., & Dalgarno, A. 1982, Phys. Rev. A, 26, 3293 [NASA ADS] [CrossRef] [Google Scholar]

[33] Heil, T. G., Kirby, K., & Dalgarno, A. 1983, Phys. Rev. A, 27, 2826 [NASA ADS] [CrossRef] [Google Scholar]

[34] Hummer, D. G., Berrington, K. A., Eissner, W., et al. 1993, A&A, 279, 298 [NASA ADS] [Google Scholar]

[35] Kastner, S. O. 1977, A&A, 54, 255 [NASA ADS] [Google Scholar]

[36] Kastner, S. O., & Bhatia, A. K. 1979, A&A, 71, 211 [NASA ADS] [Google Scholar]

[37] Keenan, F. P., & Reid, R. H. G. 1987, J. Phys. B, 20, L753 [NASA ADS] [CrossRef] [Google Scholar]

[38] Keenan, F. P., & Reid, R. H. G. 1989, J. Phys. B, 22, L295 [NASA ADS] [CrossRef] [Google Scholar]

[39] Landman, D. A. 1975, A&A, 43, 285 [NASA ADS] [Google Scholar]

[40] Landman, D. A. 1978, ApJ, 220, 366 [NASA ADS] [CrossRef] [Google Scholar]

[41] Landman, D. A. 1980, ApJ, 240, 709 [NASA ADS] [CrossRef] [Google Scholar]

[42] Landman, D. A. 1985, J. Quant. Spectrosc. Radiat. Transf., 34, 365 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]

[43] Landman, D. A., & Brown, T. 1979, ApJ, 232, 636 [NASA ADS] [CrossRef] [Google Scholar]

[44] Masnou-Seeuws, F., & McCarroll, R. 1972, A&A, 17, 441 [NASA ADS] [Google Scholar]

[45] Reid, R. H. G. 1988, Adv. At. Mol. Phys., 25, 251 [CrossRef] [Google Scholar]

[46] Reid, R. H. G., & Schwarz, J. H. 1969, in Proceedings of the Sixth International Conference on Physics of Electronic and Atomic Collisions, Cambridge, MA, ed. I. Amdur (Cambridge, MA: MIT), 236 [Google Scholar]

[47] Ryans, R. S. I., Foster-Woods, V. J., Keenan, F. P., & Reid, R. H. G. 1999a, At. Data Nucl. Data Tables, 73, 1 [NASA ADS] [CrossRef] [Google Scholar]

[48] Ryans, R. C. I., Foster-Woods, V. J., Reid, R. H. G., & Keenan, F. P. 1999b, A&A, 345, 663 [NASA ADS] [Google Scholar]

[49] Ryans, R. S. I., Foster-Woods, V. J., Copeland, F., et al., 1998, At. Data Nucl. Data Tables, 70, 179 [NASA ADS] [CrossRef] [Google Scholar]

[50] Sahal-Brechot, S. 1974, A&A, 32, 147 [NASA ADS] [Google Scholar]

[51] Sato K., Mimura M., Ostuka M., et al. 1986, Phys. Rev. Lett., 56, 151 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]

[52] Seaton, M. J. 1964, MNRAS, 127, 191 [NASA ADS] [Google Scholar]

[53] Storey, P. J., Mason, H. E., & Saraph, H. E. 1996, A&A, 309, 677 [NASA ADS] [Google Scholar]

[54] Young, P. R., Del Zanna, G., Landi, E., et al. 2003, ApJS, 144, 135 [NASA ADS] [CrossRef] [Google Scholar]

[55] Zhang, H. L., & Pradhan, A. K. 1997, A&AS, 123, 575 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]

Recommended data on proton-ion collision rate coefficients for Fe X-Fe XXIII ions

1 Introduction

2 Methods used for calculations of proton rate coefficients

3 Analytical function for an approximation of the dependencies of proton collision rates on proton temperature

4 Results

4.1 Chlorine-like Fe X (3s23p5 2P)

4.2 Sulfur-like Fe XI (3s23p4 3P)

4.3 Phosphorus-like Fe XII (3s23p3 4S, 2D, 2P)

4.4 Silicon-like Fe XIII (3s23p2 3P, 1D, 1S)

4.5 Aluminium-like Fe XIV (3s23p 2P)

4.6 Magnesium-like Fe XV (3s3p 3P)

4.7 Ne-like Fe XVII ion (2s22p53s 3,1P)

4.8 F-like Fe XVIII ion (2s22p5 2P3/2-2P1/2)

4.9 O-like Fe XIX ion (2s22p4 3PJ)

4.10 N-like Fe XX ion (2s22p3 4S3/2, 2D 3/2,5/2, 2P 1/2,3/2)

4.11 C-like Fe XXI ion (2s22p2 3P)

4.12 B-like Fe XXII ion (2s22p 2P, 2s2p2 4P)

4.13 Be-like Fe XXIII ion (2s2p 3P0,1,2)

5 Conclusions

References

All Tables

All Figures

4.1 Chlorine-like Fe X (3s²3p⁵ ²P)

4.2 Sulfur-like Fe XI (3s²3p⁴ ³P)

4.3 Phosphorus-like Fe XII (3s²3p³ ⁴S, ²D, ²P)

4.4 Silicon-like Fe XIII (3s²3p² ³P, ¹D, ¹S)

4.5 Aluminium-like Fe XIV (3s²3p ²P)

4.6 Magnesium-like Fe XV (3s3p ³P)

4.7 Ne-like Fe XVII ion (2s²2p⁵3s ^3,1P)

4.8 F-like Fe XVIII ion (2s²2p⁵ ²P_3/2-²P_1/2)

4.9 O-like Fe XIX ion (2s²2p⁴ ³P_J)

4.10 N-like Fe XX ion (2s²2p³ ⁴S_3/2, ²D _3/2,5/2, ²P _1/2,3/2)

4.11 C-like Fe XXI ion (2s²2p² ³P)

4.12 B-like Fe XXII ion (2s²2p ²P, 2s2p² ⁴P)

4.13 Be-like Fe XXIII ion (2s2p ³P_0,1,2)