EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 510 (February 2010) A&A, 510 (2010) A21 Full HTML
Free Access
Issue
A&A
Volume 510, February 2010
Article Number A21
Number of page(s) 4
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/200913675
Published online 02 February 2010
A&A 510, A21 (2010)

Stellar limb-darkening coefficients for CoRot and Kepler[*]
(Research Note)

D. K. Sing1,2

1 - Institut d'Astrophysique de Paris, CNRS/UPMC, 98bis boulevard Arago, 75014 Paris, France
2 - Astrophysics Group, School of Physics, University of Exeter, Stocker Road, Exeter EX4 4QL, UK

Received 16 November 2009 / Accepted 11 December 2009

Abstract
Transiting exoplanets provide unparalleled access to the fundamental parameters of both extrasolar planets and their host stars. We present limb-darkening coefficients (LDCs) for the exoplanet hunting CoRot and Kepler missions. The LDCs are calculated with ATLAS stellar atmospheric model grids and span a wide range of  $T_{\rm eff}$, log g, and metallically [M/H]. Both CoRot and Kepler use wide nonstandard photometric filters, and are producing a large inventory of high-quality transiting lightcurves, sensitive to stellar limb darkening. Comparing the stellar model limb darkening to results from the first seven CoRot planets, we find better fits are found when two model intensities at the limb are excluded in the coefficient calculations. This calculation method can help to avoid a major deficiency present at the limbs of the 1D stellar models.

Key words: stars: atmospheres - planetary systems - binaries: eclipsing

1 Introduction

Transiting exoplanets have provided an unprecedented opportunity to directly measure physical parameters of the planet and host star, such as mass and radius. The lightcurve shape of a transit (where the planet passes in front of the star as viewed from the Earth) is primarily determined by the planet-to-star radius ratio, impact parameter, and stellar limb darkening. Thus, an accurate treatment of limb darkening is critical when deriving planetary radii and transmission spectra from transit data.

With high signal-to-noise (S/N) transit light curves, the limb darkening can be fit and compared to theoretical stellar atmospheric models, providing a method to scrutinize and test different models (e.g. Southworth 2008). In a comparison with the sun, Sing et al. (2008) found that for the widely used Kurucz 1D ATLAS stellar models[*], the largest differences between existing limb-darkening data (Neckel & Labs 1994) and the 1D stellar models was at the limb, where ATLAS models predict a dramatic increase in the strength of limb darkening. For the sun, the ATLAS models over-predict the strength of limb darkening by >20% at $\mu=\cos(\theta)$ values below 0.05, though seemed to perform well otherwise, over-predicting the strength by only a few percent. While there remain few other observational constraints, theoretical atmospheric models have also been unable to provide a satisfactory fits to the observations of eclipsing binary stars (Claret 2008) and the transiting data of HD 209458 (Claret 2009). However, different LDC calculation methods may help improve the situation, with (Sing et al. 2009) recently fitting near-infrared LDCs to a level of a few percent with HST/NICMOS transit data of HD 189733, finding good agreement with the theoretical stellar models.

The exoplanet hunting missions CoRot and Kepler provide an excellent opportunity to further test these stellar models, as high S/N transits for a variety of spectral types are being discovered. Both CoRot and Kepler operate at optical wavelengths, where the effects of limb-darkening are strong, using wide band filters with wavelengths between $\sim$4000 and $\sim$9000 Å. Here we present stellar limb-darkening coefficients for both the CoRot and Kepler satellites, along with some initial results comparing different calculation methods to the observed stellar LD. We present our calculation methods in Sect. 2, compare our results to CoRot transit data in Sect. 3, and make concluding remarks in Sect. 4.

Table 1:   CoRot stellar limb-darkening coefficients.

2 The numerical methods

We calculate LDCs for the laws most commonly used in exoplanetary transit work:
The Linear law

\begin{displaymath}\frac{I(\mu)}{I(1)}=1 - u(1 - \mu).\end{displaymath} (1)

The Quadratic law

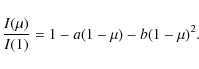
\begin{displaymath}\frac{I(\mu)}{I(1)}=1 - a(1 - \mu) - b(1 - \mu)^2 .\end{displaymath} (2)

The Non-Linear law

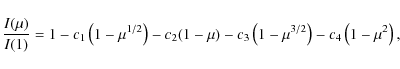
\begin{displaymath}\frac{I(\mu)}{I(1)}=1 - c_1\left(1 - \mu^{1/2}\right) - c_2(1... ...- c_3\left(1 - \mu^{3/2}\right) - c_4\left(1 - \mu^{2}\right), \end{displaymath} (3)

where I(1) is the intensity at the center of the stellar disk, $\mu=\cos(\theta)$ (which is the angle between the line of sight and the emergent intensity), while u, a, b, and cn are the LDCs. These laws can all be used along with the analytical transit light models of Mandel & Agol (2002), and the definitions of each law have been set to conform with the work of Claret (2000).

In addition to the above laws, we also calculate a variant of Eq. (3), which is a three parameter non-linear law,

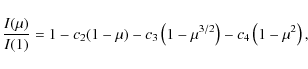
\begin{displaymath}\frac{I(\mu)}{I(1)}=1 - c_2(1 - \mu) - c_3\left(1 - \mu^{3/2}\right) - c_4 \left(1 - \mu^{2}\right), \end{displaymath} (4)

introduced by Sing et al. (2009) to improve the performance of the calculated LD at the limb, while still providing enough flexibility to capture the inherently non-linear nature of stellar LD. The $\mu^{1/2}$ term from the four parameter non-linear law mainly affects the intensity distribution at small $\mu$ values and is not needed when the intensity at the limb varies approximately linearly at small $\mu$ values. Dropping the c1 term is also further motivated by both solar data (Neckel & Labs 1994) and 3D stellar models (Bigot et al. 2006), which show the intensity distribution at the limb to vary smoothly to $\mu=0$, with no dramatic or sudden increases in limb-darkening strength as observed in the ATLAS models.

We choose a least squares method to fit for the limb-darkening coefficients from ATLAS models. The model specific intensities were first integrated at each angle using the CoRot PF white-light (Auvergne et al. 2009) and Kepler[*] response functions. We used only values of $\mu \geq 0.05$for the linear, quadratic, and three parameter non-linear laws (corresponding to 15 angles in the ATLAS model grids) while retaining all 17 angles, including the limb intensities, for the four-parameter non-linear law.

The four-parameter law best describes the tabulated ATLAS model grid intensities and should be analogous to the widely used LDCs of Claret (2000). Thus in our study, the four-parameter non-linear law is the best representation of the original stellar atmospheric models themselves, while the linear, quadratic and three-parameter non-linear laws are calculated with the intent of improving the limb intensities. The results of the calculations are given in Tables 1 and 2, with the full versions of these tables available[*]. In Fig. 1, we illustrate typical CoRot and Kepler model limb darkening profiles for F, G, and K main sequence stars.

Table 2:   Kepler stellar limb-darkening coefficients.

3 Comparisons with CoRot exoplanet transit results

We compared the calculated LDCs with results from six of the first seven CoRot exoplanets, four of which have LDCs determined from the transit light curve fit: CoRot-1 (Barge et al. 2008), CoRot-2 (Alonso et al. 2008), CoRot-3 (Deleuil et al. 2008), and CoRot-4 (Aigrain et al. 2008). The LDCs of CoRot-5 and CoRot-7 were not fit by the authors (Léger et al. 2009; Rauer et al. 2009), so no comparison was possible. With the limb intensities a potential source of disagreement between the observations and models, we compared the theoretical values of I($\mu=0$) with the CoRot results (see Fig. 2). This comparison is aided by the fact that for each law considered here, $I(0)=1-\Sigma$(Cn), making a direct comparison between different laws possible. In addition, the authors of CoRot 1, 2, and 3 choose to fit the LDC u+=a+b, for the quadratic law, which is directly related to the limb intensity, I(0)=1-u+. CoRot-4 was fit with the linear law. We also calculated the model uncertainty for the theoretical LDCs, incorporating the quoted uncertainty in stellar parameters ( $T_{\rm eff}$, log g, [M/H]) using the partial derivative of the coefficients as a function of the stellar parameters. We find that typical errors in $T_{\rm eff}$, log g, and [M/H] lead to only a small change in model LDCs for the linear and quadratic laws, with the model limb intensities uncertain by only a few percent or less. This error estimation breaks down for the higher-order laws, as fitting degeneracies between the coefficients lead to unrealistically large partial derivatives and large errors. In those cases, we used the uncertainty from the linear law as a reasonable estimate of the model I(0) error. However, the model error is small and much less important than the observational errors.

\begin{figure} \par\includegraphics[width=0.35\textwidth,angle=90]{13675fig1.eps} \end{figure} Figure 1:

Stellar limb darkening for CoRot (solid lines) and Kepler (dashed lines) calculated from Atlas models appropriate for a solar metallically F5V, G5V, and K5V star ( top to bottom: $T_{\rm eff}=6500$, 5500, 4500 K; log g = 4.5, [M/H] = 0.0). The Atlas models show earlier type stars exhibiting increasingly non-linear intensity distributions for the CoRot and Kepler bandpasses.

Open with DEXTER

From Fig. 2, the most obvious disagreement between the models and observations is with the active star CoRot-2 (Alonso et al. 2008). A determination of the planet-to-star radius ratio is affected by stellar activity, as shown for CoRot-2 by Czesla et al. (2009) who re-determined the planetary radius, taking into account stellar activity, finding a larger radius than either Alonso et al. (2008) or Gillon et al. (2009). However, as the radii and limb darkening are linked in a transit fit, the limb darkening coefficients are also affected by stellar activity, though these parameters were not re-determined. With these complications due to stellar activity, a proper comparison of limb darkening will likely have to wait until the limb darkening is also re-determined in conjunction with the planetary radii.

The three CoRot targets (1, 3 and 4) are sufficient to see a significant improvement in model limb intensities, when calculating LDCs with 15-angles and using lower order laws. For every CoRot target thus far, the calculated limb intensities of the ATLAS models are significantly lower than the observed transit fit values, further proof of the model limb deficiencies previously mentioned.

\begin{figure} \par {\includegraphics[angle=90,width=12cm]{13675fig2.eps} }\end{figure} Figure 2:

Limb intensity for the CoRot transiting planets (black circles) vs. effective stellar temperature. CoRot-5 and CoRot-7 did not have lightcurve-fit LDCs, and the adopted values without y-error bars are shown. The ATLAS model limb intensities for the linear (red), quadratic (orange), three-parameter non-linear (purple), and four-parameter non-linear (blue stars) laws are also shown, along with the error derived from the uncertainty in the stellar parameters. The model errors are small and typically less than the size of the plotted point. Our method of calculating for LDCs, with lower order laws and excluding the model limb intensities, shows a better agreement with the observations.

Open with DEXTER

There is a potential source of disagreement between comparing I(0) when different laws are used in the stellar model LD and transit-fit LD. In our model calculations, the general trend is to decrease I(0) when adopting a higher order law to describe the intensity. Higher order laws are increasingly sensitive to the shape of the falling intensity at the limb, thus reducing the fit value of I(0). However, we believe this to be a second order effect which should not seriously affect these results, especially as several of the CoRot LDCs are poorly constrained and are not sensitive to higher order terms.

Comparing the I(0) calculated from the different laws to the fit CoRot values, the 17-angle four parameter non-linear law has a $\chi^2_{\nu}$ of 5.15, the 15-angle 3-parameter law has a $\chi^2_{\nu}$ of 2.85, the quadratic law a $\chi^2_{\nu}$ of 1.67 and the linear law a $\chi^2_{\nu}$ of 0.63. For the lower order laws, a better fit to I(0) is obtained by using 15-angles to calculate the LDCs, disregarding the model limb values. Though the linear law represents the best fit for I(0) here, the expected deviations of the model $I(\mu)$ from a linear trend in F and G type stars (Fig. 1) will likely make higher order laws necessary to describe the full intensity distribution.

Determining which limb darkening law to use in a transit light curve fit is very dependent on the S/N of the data and the stellar type of the star being studied. From our model calculations, we expect that linear laws will likely fit transit light curves quite well for both CoRot and Kepler in cooler K type stars, or for earlier types at low S/N. Higher order terms will likely be needed in F and G type stars at high S/N, where multiple LDCs can be fit at good precision.

4 Conclusions

For use within the community, we present ATLAS model grid LDCs calculated for the CoRot and Kepler transiting exoplanet missions. We find better agreement between the existing CoRot observations and model LDC when two limb intensities are not used in the calculations, and incorporate this method in the presented LDCs.

The future catalog of transiting planets discovered by CoRot and Kepler offers the prospect of substantially improving the theoretical models of stellar limb darkening. The very high photometric precision of Kepler should allow for multiple LDCs to be fit at the percent level, which should open up many detailed comparisons with stellar atmospheric models. For instance, Kepler (at high temporal resolution) will be quite sensitive to non-linear LD terms, as there will be sufficient S/N to accurately fit for coefficients beyond just the linear term. The LDCs presented here are intended to aid in these studies and be of general use to the community.

Acknowledgements
D.K.S. is supported by CNES. We thank Robert Kurucz for making his grid of stellar models publicly available and the referee for their helpful comments.

References

  1. Aigrain, S., Collier Cameron, A., Ollivier, M., et al. 2008, A&A, 488, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Alonso, R., Auvergne, M., Baglin, A., et al. 2008, A&A, 482, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Barge, P., Baglin, A., Auvergne, M., et al. 2008, A&A, 482, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bigot, L., Kervella, P., Thévenin, F., & Ségransan, D. 2006, A&A, 446, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
  7. Claret, A. 2008, A&A, 482, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Claret, A. 2009, A&A, 506, 1335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Czesla, S., Huber, K. F., Wolter, U., Schröter, S., & Schmitt, J. H. M. M. 2009, A&A, 505, 1277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Deleuil, M., Deeg, H. J., Alonso, R., et al. 2008, A&A, 491, 889 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Gillon, M., Lanotte, A. A., Barman, T., et al. 2009, ArXiv e-prints [Google Scholar]
  12. Léger, A., Rouan, D., Schneider, J., et al. 2009, A&A, 506, 287 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  13. Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
  14. Neckel, H., & Labs, D. 1994, Sol. Phys., 153, 91 [NASA ADS] [CrossRef] [Google Scholar]
  15. Rauer, H., Queloz, D., Csizmadia, S., et al. 2009, A&A, 506, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Sing, D. K., Vidal-Madjar, A., Désert, J.-M., Lecavelier des Etangs, A., & Ballester, G. 2008, ApJ, 686, 658 [NASA ADS] [CrossRef] [Google Scholar]
  17. Sing, D. K., Désert, J., Lecavelier Des Etangs, A., et al. 2009, A&A, 505, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Southworth, J. 2008, MNRAS, 386, 1644 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... Kepler[*]
Full Tables 1 and 2 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/510/A21
... models[*]
http://kurucz.harvard.edu/
... Kepler[*]
http://keplergo.arc.nasa.gov/CalibrationResponse.shtml
... available[*]
at the CDS or at http://vega.lpl.arizona.edu/ singd/
Copyright ESO 2010

All Tables

Table 1:   CoRot stellar limb-darkening coefficients.

Table 2:   Kepler stellar limb-darkening coefficients.

All Figures

  \begin{figure} \par\includegraphics[width=0.35\textwidth,angle=90]{13675fig1.eps} \end{figure} Figure 1:

Stellar limb darkening for CoRot (solid lines) and Kepler (dashed lines) calculated from Atlas models appropriate for a solar metallically F5V, G5V, and K5V star ( top to bottom: $T_{\rm eff}=6500$, 5500, 4500 K; log g = 4.5, [M/H] = 0.0). The Atlas models show earlier type stars exhibiting increasingly non-linear intensity distributions for the CoRot and Kepler bandpasses.

Open with DEXTER
In the text

  \begin{figure} \par {\includegraphics[angle=90,width=12cm]{13675fig2.eps} }\end{figure} Figure 2:

Limb intensity for the CoRot transiting planets (black circles) vs. effective stellar temperature. CoRot-5 and CoRot-7 did not have lightcurve-fit LDCs, and the adopted values without y-error bars are shown. The ATLAS model limb intensities for the linear (red), quadratic (orange), three-parameter non-linear (purple), and four-parameter non-linear (blue stars) laws are also shown, along with the error derived from the uncertainty in the stellar parameters. The model errors are small and typically less than the size of the plotted point. Our method of calculating for LDCs, with lower order laws and excluding the model limb intensities, shows a better agreement with the observations.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.