| Issue |
A&A
Volume 510, February 2010
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 11 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/200913345 | |
| Published online | 05 February 2010 | |
First CoRoT light curves of RR Lyrae stars
Complex multiplet structure and
non-radial pulsation detections in V1127 Aquilae![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
M. Chadid1 - J. M. Benko2 - R. Szabó2 - M. Paparó2 - E. Chapellier1 - K. Kolenberg3 - E. Poretti4 - G. Bono5,6 - J.-F. Le Borgne7 - H. Trinquet1 - S. Artemenko8 - M. Auvergne9 - A. Baglin9 - J. Debosscher10 - K. N. Grankin8 - E. Guggenberger3 - W. W. Weiss3
1 - Observatoire de la Côte d'Azur, Université Nice Sophia-Antipolis,
UMR 6525, Parc Valrose, 06108 Nice Cedex 02, France
2 - Konkoly Observatory of the Hungarian Academy of Sciences, PO Box
67, 1525 Budapest, Hungary
3 - Institute of Astronomy, University of Vienna, Türkenschanzstrasse
17, 1180 Vienna, Austria
4 - INAF - Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807
Merate (LC), Italy
5 - INAF, Rome Astronomical Observatory, via Frascati 33, 00040 Monte
Porzio Catone, Italy
6 - Dipartimento di Fisica, Universita' di Roma Tor Vergata via Della
Ricerca Scientifica 1, 00133 Roma, Italy
7 - Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de
Toulouse, CNRS, 14 Av. Edouard Belin, 31400 Toulouse, France
8 - Scientific Research Institute Crimean Astrophysical Observatory
of the Ministries of Education and Sciences of Ukraine, 98409 Nauchny,
Crimea, Ukraine
9 - LESIA, Université Pierre et Marie Curie, Université Denis Diderot,
Observatoire de Paris, 92195 Meudon Cedex, France
10 - Instituut Voor Sterrenkunde, Catholic University of Leuven,
Celestijnenlaan 200D, 3001 Leuven, Belgium
Received 29 September 2009 / Accepted 17 November 2009
Abstract
Context. The CoRoT - Convection Rotation and
planetary Transits - space mission is a great opportunity for
monitoring stars with excellent time-sampling and unprecedented
photometric precision for up to 150 days. As an important
benefit, high-quality RR Lyrae light curves are obtained with a
quasi-uninterrupted coverage over several pulsation and Blazhko cycles.
Aims. The Blazhko effect in RR Lyrae stars is an
unsolved problem of astrophysics. We used the high-precision space data
to contribute more precise knowledge to explain the possible physical
processes behind the phenomenon.
Methods. We applied different period-finding
techniques including Period04, MuFrAn, PDM and SigSpec. Amplitude and
phase modulation were investigated by an analytical function method as
well as with the traditional O-C diagrams.
Results. The Blazhko modulation frequency is
directly detected in the spectrum, as well as its first and second
harmonics. It shows the non-linear nature of the Blazhko modulation.
Besides the triplets, further higher-order modulation side peaks appear
around the pulsation frequency as quintuplet, septuplet, nonuplet,
undecaplet, tredecaplet, quindecaplet and sepdecaplet structures.
Additional frequencies, not belonging to the classical multiplet
structures, are detected, as well as their linear combinations with the
fundamental radial mode. We interpret these additional terms as
non-radial modes. During the five consecutive Blazhko cycles, there is
a shift of the maximum phase around 0.011 pulsation phase
which is likely the consequence of a long term modulation.
Key words: stars: atmospheres - stars: variables: RR Lyr - techniques: photometric - methods: data analysis - hydrodynamics - space vehicles
1 Introduction
RR Lyrae stars have contributed to almost every branch of modern astronomy. They are the most important low-mass distance indicators (Del Principe et al. 2006; Sollima et al. 2008), they are present in all the stellar systems including a stellar population older than a few Gyrs (Sanna et al. 2009). Moreover, they are fundamental benchmarks to constrain the plausibility of the physical assumptions adopted to construct both evolutionary and pulsation models of low-mass stars (Del Principe et al. 2005). In recent years, their atmosphere has been considered as a laboratory of hypersonic shock wave simulation (Chadid et al. 2008). With their large amplitudes, the RR Lyrae stars have been known for more than a century. Although these stars are well studied, a few disturbing questions concerning their pulsation and their atmospheric dynamics remain to be answered. In particular the Blazhko modulation is known since about hundred years, while its physical origin remains an enigma. The Blazhko effect (Blazhko 1907) is a periodic modulation of both the amplitude and the phase of the main pulsation on timescales typically varying from dozens to hundreds of days. As discussed by Chadid & Chapellier (2006) and Chadid et al. (2004), none of the currently suggested models - the resonance model which involves the non-radial modes (Dziembowski & Mizerski 2004) and the magnetic oblique rotator (Shibahashi 2000) - is able to explain the complexity of the observed properties of the Blazhko modulation. Recently, Stothers (2006) gave a new interpretation of the modulating Blazhko effect in RR Lyrae stars. He explains the continuous amplitude and period changes of the main pulsation by a convective turbulent dynamo inside the hydrogen and helium ionization zones, where the dynamo period is identical to the Blazhko period. The Stothers theory does not require any non-radial mode, but it still remains a qualitative interpretation of the modulation which needs to be confirmed.
Many studies have been devoted to the light curve changes of RR Lyrae stars. Initially, the observations were biased in general towards the rising branch and maximum phase of the light curve (Walraven 1949). Even the best of them have some defects caused by the inaccuracy and data inhomogeneity. On the other hand, both photometric (e.g. Borkowski 1980; Smith et al. 2003; Kovács 1995) and spectroscopic observations (Chadid & Chapellier 2006; Struve & Blaauw 1949; Chadid et al. 1999; Preston et al. 1965) of well-studied field Blazhko stars, have yielded accurate frequency spectra which allow the study of the pulsation characteristics in detail. However, the large gaps typical of inadequately sampled earth-bound single-site observations sometimes hinder an unambiguous determination of the frequencies and their amplitudes and phases. Even if the outcome of large-scale studies such as microlensing surveys (OGLE, see Moskalik & Poretti 2003 and MACHO, see Alcock et al. 2000,2003) has yielded a much better picture of the general phenomenology of the Blazhko effect by the extensive multi-target surveys, these are not extended enough to study the modulation properties in full detail. Multisite campaigns (Kolenberg et al. 2006) and compact dedicated single-site multicolour observations (Jurcsik et al. 2009,2008,2005,2006) provided a higher-level knowledge on the Blazhko phenomenon, but the coverage is still not continuous on a long time base.
The CoRoT space mission (Convection Rotation and Planetary
Transits), successfully launched on 2006 December 27, is a
great opportunity for monitoring the pulsating stars with excellent
time-sampling and unprecedented photometric precision for up to
150 days. As an important consequence, several high-quality RR
Lyrae light curves are obtained with a quasi-uninterrupted coverage
over several pulsation and Blazhko cycles
with an excellent photometric accuracy. Our team, the
RR Lyrae-CoRoTeam![]() is an international collaboration focusing on a better understanding of
RR Lyrae stars using CoRoT data.
Our first RR Lyrae CoRoT study has been focused on
RR Lyrae stars found during the first long run of the CoRoT
mission, long run centre and anticentre - LRc01 and LRa01 - of the
Milky Way. We classified six RR Lyrae stars in LRc01, four of
them are RRab Blazhko stars (CoRoT ID: 0100689962, 0101128793,
0101503544 and 0100881648) one of them is an RRab monoperiodic (CoRoT
ID:0101370131) star and one is an RRd star (CoRoT ID:0101368812) and in
LRa01, there is also one RR ab monoperiodic star (CoRoT
ID:0102781750)
(see Chadid et al. 2009).
is an international collaboration focusing on a better understanding of
RR Lyrae stars using CoRoT data.
Our first RR Lyrae CoRoT study has been focused on
RR Lyrae stars found during the first long run of the CoRoT
mission, long run centre and anticentre - LRc01 and LRa01 - of the
Milky Way. We classified six RR Lyrae stars in LRc01, four of
them are RRab Blazhko stars (CoRoT ID: 0100689962, 0101128793,
0101503544 and 0100881648) one of them is an RRab monoperiodic (CoRoT
ID:0101370131) star and one is an RRd star (CoRoT ID:0101368812) and in
LRa01, there is also one RR ab monoperiodic star (CoRoT
ID:0102781750)
(see Chadid et al. 2009).
In this paper we present the results of the photometric CoRoT
data on the star with CoRoT ID: 0100689962, known as
V1127 Aql (
![]()
![]()
![]() ,
,
![]() = +01
= +01![]() 41
41![]() 48
48
![]() 9,
J2000).
9,
J2000).
The variability of the star was discovered by Hoffmeister (1966) on the Sonneberg plates. Since then, observations devoted to V1127 Aql have not been published apart from some early photographic maxima measurements (Gessner 1973).
The CoRoT data of V1127 Aql were obtained
continuously and regularly from 16 May 2007 to
05 October 2007.
Note that the CoRoTJD corresponds to
HJD 2 451 545.0 (January 1![]() ,
2000 at 12
,
2000 at 12![]() :00
:00![]() :00
:00![]() ).
In Sect. 2.
we present CoRoT observations.
Section 3.
is devoted to the description of data analysis and its results with new
findings. The specialities of the Blazhko phenomenon are discussed in
Sect. 4.
Finally some concluding remarks are given in Sect. 5.
).
In Sect. 2.
we present CoRoT observations.
Section 3.
is devoted to the description of data analysis and its results with new
findings. The specialities of the Blazhko phenomenon are discussed in
Sect. 4.
Finally some concluding remarks are given in Sect. 5.
![\begin{figure}
\par\includegraphics[angle=00,width=15cm,clip]{13345fg1.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg28.png)
|
Figure 1: Two-dimensional CoRoT light curve of V1127 Aql folded with the pulsation period (0.355996 d) over five Blazhko cycles. The variations in the light curve due to the Blazhko effect are clearly visible. |
| Open with DEXTER | |
2 Observations and data processing
The CoRoT data used in this study are the calibrated light curves, N2-level, that have been measured by the CoRoT Exoplanet CCDs during the first long run in the centre direction of the Galaxy. The total time span is 143 days. The time sampling of the light curves is 32 s, an average is taken on board over 16 such measurements, and these results in a nominal sampling time of 512 s. We used here the resulting ``white'' flux for our purpose, and we removed all measurements having non-zero quality flags in the N2 product delivery, retaining only valid flux measurements. These flagged measurements included the measurements which were taken during the South-Atlantic Anomaly passages. The bad data points account for 2% of the data and, their removal breaks the equidistancy of the time series and changes the behaviour of the window function. For more technical details on the satellite and data we refer to Auvergne et al. (2009). The CoRoT N2 data are affected by instrumental trends and jumps in the light curves due to changes in the amount of incident stray light during the run, periodic changes in flux caused by the satellite orbit, and discontinuities in the light curves due to cosmic ray hits on the CCDs. Then, after the removal of bad data points a trend and jump filtering code was used to the data. The trend filtering part of the process divides the data set into bins and within each bin the fluxes and times are averaged. The independently binned, averaged values of fluxes are interpolated in the original points of time and subtracted from the observed ones. The jump filtering process is based on the difference of the subsequent points of the light curve. A difference is regarded as a jump if it exceeds a certain factor of the standard deviation. The data are transformed into a zero averaged instrumental magnitude scale.![\begin{figure}
\par\includegraphics[angle=0,width=9cm]{13345fg2.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg29.png)
|
Figure 2: The main steps of prewhitening process. a) The amplitude spectrum. b) Prewhitened spectrum with main pulsation frequency, its harmonics and the triplets (see insert in panel a)). c) Prewhitened spectrum with modulation frequency, its harmonics and all higher-order side peaks (see insert in panel b)). d)) Residual spectrum when all frequencies in Table 1 are removed. (For better visibility only the lower frequency regions are shown.) |
| Open with DEXTER | |
3 Frequency analysis
As is well known, the Fourier spectra of classical Blazhko RR Lyrae
stars are dominated by equidistant triplets
with a frequency separation identical with the modulation
frequency (Kolenberg
et al. 2006; Chadid & Chapellier 2006;
Chadid
et al. 1999). Recently, Hurta
et al. (2008) found equidistant quintuplets in the
spectrum of RV UMa. The appearance of the Blazhko modulation
frequency ![]() itself was a long-standing debate.
However, it has always been detected in the spectra of extended enough
photometric data sets (Nagy
1998; Jurcsik
et al. 2009,2008,2005,2006; Kovács 1995). In the case of
MW Lyr it was found together with its first harmonics
itself was a long-standing debate.
However, it has always been detected in the spectra of extended enough
photometric data sets (Nagy
1998; Jurcsik
et al. 2009,2008,2005,2006; Kovács 1995). In the case of
MW Lyr it was found together with its first harmonics ![]() (Jurcsik et al. 2008).
(Jurcsik et al. 2008).
From a purely mathematical point of view, when an arbitrary periodic signal is modulated both in its amplitude and phase, its Fourier spectrum shows an infinite series of side peak structures with asymmetric amplitudes between the higher and lower frequency sides (Benko et al. 2009; Szeidl & Jurcsik 2009).
3.1 Detection of frequencies
The CoRoT data of V1127 Aql provide 400 consecutive pulsation cycles and a homogeneous coverage of five Blazhko cycles. The heights of maxima and minima of the light curves clearly indicate a modulation period of about 27 days (Fig. 1).
We used different algorithms to find frequencies, such as
Period04 (Lenz & Breger 2005),
the package MuFrAn (Kolláth 1990),
the CLEAN algorithm as introduced by Roberts
et al. (1987) and the PDM method (Stellingwerf 1978). The
frequency analyses all led to the same results with a slight difference
at higher orders. In this study, we present the results of the MuFrAn
frequency analysis. The Fourier decomposition consists of fitting the
magnitude measurements by means of the series
![\begin{displaymath}m(t) = A_0 + \sum_{i=1, N}A_i\sin[2 \pi F_i(t - T_0) + \Phi_i],
\end{displaymath}](/articles/aa/full_html/2010/02/aa13345-09/img31.png)
|
(1) |
where T0 is the initial epoch value of the data set CoRoTJD T0 = 2691.0.
The original spectrum is dominated by the main pulsation
frequency ![]() ,
its harmonics up to the 20th order (Fig. 2a)
and the modulation triplet structure
,
its harmonics up to the 20th order (Fig. 2a)
and the modulation triplet structure ![]() (as insert panel a).
After prewhitening the spectrum with the main pulsation frequency, its
harmonics and the triplet structure, the dominant peaks are at the
frequencies of higher-order side peaks
(as insert panel a).
After prewhitening the spectrum with the main pulsation frequency, its
harmonics and the triplet structure, the dominant peaks are at the
frequencies of higher-order side peaks ![]() ,
,
![]() (Fig. 2b) and at the
modulation frequency
(Fig. 2b) and at the
modulation frequency ![]() .
The unexpected amplitude ratio of the multiplets will be discussed
later.
The insert in panel b shows the higher-order side peak structure.
Figure 3
shows a map of harmonics and side peak structures, listed in
Tables 1.A.1, 1.A.3, 1.A.4, 1.A.5, 1.A.6, 1.A.7, 1.A.8, 1.A.9,
and 1.A.10. We plotted the order of side peaks k
versus
harmonic orders n in the formula
.
The unexpected amplitude ratio of the multiplets will be discussed
later.
The insert in panel b shows the higher-order side peak structure.
Figure 3
shows a map of harmonics and side peak structures, listed in
Tables 1.A.1, 1.A.3, 1.A.4, 1.A.5, 1.A.6, 1.A.7, 1.A.8, 1.A.9,
and 1.A.10. We plotted the order of side peaks k
versus
harmonic orders n in the formula ![]() .
Due to the high precision of the CoRoT data the number of observed side
peaks remarkably increased compared to numbers known up to now.
Altogether 161 side peaks were identified in the frequency
spectrum. Surprisingly, the
lower harmonics have fewer side peaks. At the same time we could
identify the multiplet structure around the higher harmonics where the
harmonic itself was not significantly detected.
.
Due to the high precision of the CoRoT data the number of observed side
peaks remarkably increased compared to numbers known up to now.
Altogether 161 side peaks were identified in the frequency
spectrum. Surprisingly, the
lower harmonics have fewer side peaks. At the same time we could
identify the multiplet structure around the higher harmonics where the
harmonic itself was not significantly detected.
Figure 2b
shows the presence of Blazhko modulation frequency as well.
We clearly detected not only the modulation
frequency ![]() but also its first
but also its first ![]() and second harmonics
and second harmonics ![]() in V1127 Aql (Fig. 4;
Table 1.A.2). Figure 2c shows the
spectrum after the prewhitening with modulation frequency, its
harmonics and all higher-order side peaks. The dominant peak
in V1127 Aql (Fig. 4;
Table 1.A.2). Figure 2c shows the
spectrum after the prewhitening with modulation frequency, its
harmonics and all higher-order side peaks. The dominant peak ![]() in the spectrum does not fit to the regular pattern of harmonics and
side peaks in an RR Lyrae star.
in the spectrum does not fit to the regular pattern of harmonics and
side peaks in an RR Lyrae star.
Figure 2d
shows the residual spectrum prewhitening of all the frequencies
we identified. To check our frequency solution we ran the program
package SigSpec.
It calculates the spectral significance defined by Reegen (2007) for each peak of
the spectrum. The critical point of where to stop in the frequency
analyses is a well-known, unsolved problem. Generally, the application
of a certain signal-to-noise ratio is used to be accepted as a
significance level. In our case sig = 5.2 value
served as an overall criterium. However, the regular behaviour of
harmonics and side peaks in the Blazhko RR Lyrae star helps to
identify even frequency peaks, intrinsic to the star's pulsation, with
a lower amplitude than the accepted value. Through a rigorous check in
the high-frequency region, where the noise level is lower, we were able
to detect the harmonics and their side peaks below the generally
accepted significance level. An example is presented in Fig. 5. Around the
17th harmonic among the marked peaks only the five highest amplitude
peaks have a higher value than the accepted significance level.
Nevertheless, the regularity of the Blazhko side peak structure can be
nicely followed among the lower amplitude peaks. We included these
frequencies in our solution.
Comparing our frequencies to the result of the SigSpec
we conclude that they are very similar if we set the parameter
Sig ![]() 5.
We add the spectral significances from SigSpec to the amplitudes and
phases of the finally accepted frequencies (Table 1).
5.
We add the spectral significances from SigSpec to the amplitudes and
phases of the finally accepted frequencies (Table 1).
Knowing the precise values of the pulsation and Blazhko period
we deduce the 2007 Blazhko ephemeris:
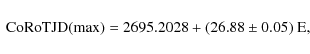
and the 2007 pulsation ephemeris:
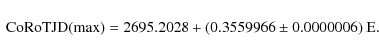
In this paper, the pulsation phase is
Table 1: Frequencies, Fourier amplitudes, phases, spectral significances and identification of the frequencies (this table can be found in its entirety at CDS).
![\begin{figure}
\par\includegraphics[angle=0,width=9cm]{13345fg3.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg47.png)
|
Figure 3:
Map of harmonics and side peaks in the Fourier spectrum of the
V1127 Aql.
The order of side frequencies (k) vs. harmonic
orders (n) is plotted according to the formula |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=0,width=9cm]{13345fg4.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg48.png)
|
Figure 4:
The Blazhko modulation frequency |
| Open with DEXTER | |
3.2 Blazhko multiplets
The complex side peak structure shown in Fig. 3 is highly connected to the amplitude value of certain peaks both in the case of harmonics and Blazhko side peaks. The amplitude of the harmonics of the main frequency seemingly decreases exponentially as it is obtained in RR Lyrae stars. However, presenting them on a logarithmic scale a standstill appears at the 6th, 7th and 8th harmonics (Fig. 6). The amplitude of these harmonics are the same while the lower-order harmonics and the higher-order harmonics are situated on straight lines with a slightly different inclination. An abrupt increase of the higher-order harmonics' amplitudes was reported only on the other CoRoT RR Lyrae star ID:0101370131 (Paparó et al. 2009).
Table 2: Complex multiplet structures, degree of deviation and degree of asymmetry.
![\begin{figure}
\par\includegraphics[angle=0,width=9cm]{13345fg4bis}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg51.png)
|
Figure 5: Top: a part of the unbiased Fourier spectrum around the harmonics of 17f0. Bottom: the same part of the window function in the same scale as the spectrum. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=00,width=9cm,clip]{13345fg5.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg52.png)
|
Figure 6:
a) Amplitude ratios of the harmonic
components of the radial pulsation given in decimal logarithmic scale (Anf0/Af0)
compared to the amplitude ratios of the modulation components |
| Open with DEXTER | |
Blazhko side peaks with non-significant amplitudes are omitted causing holes in the regular pattern in Fig. 3. Table 2 summarizes the type of multiplet structure of V1127 Aql. The triplet, quintuplet and septuplet structures are more numerous in agreement with the fact that these are more frequently obtained in lower quality data sets. For nonuplet (9 peaks) to septdecaplet (17 peaks) structures the number of findings is decreasing due to the lower amplitudes.
It is clear that more side peaks appear on the positive, higher-frequency sides (k>0, right) than on the negative, lower-frequency sides (left). The asymmetry is caused by the amplitude difference between right and left side peaks. The right-side peaks have always a higher amplitude than the corresponding left-side ones.
To see the regularity in a particular case Fig. 5 shows the part of the Fourier spectrum around the 17f0 harmonic. (The original unbiased spectrum is plotted without prewhitening.) Although the harmonic at 17f0 is not significant, its modulation side peaks are visible up to the 7th order. The asymmetry between positive and negative sides is clearly detected. The maximal amplitude of the side peaks is reached at the 5th side peak (undecaplet). This regularity is similar for the side peaks around the main pulsation mode and its harmonics.
The general amplitude behaviour of the side peaks is presented in Fig. 6 for different kinds of multiplet peaks. The amplitude of triplet side peaks (left and right) runs parallel along straight lines on the logarithmic scale. There is a slight difference in the amplitude of side peaks between the 9th and 14th harmonics (panel a). There is a remarkable difference in the amplitude of the left and right-side peaks in the quintuplet structure. The right-side amplitudes (open circles) are much higher than the left-side peaks, although the inclination of the lines are similar. Only the right-side peaks around the main frequency and the first harmonics have as small amplitude as the left side peaks, much lower than around the other harmonics (panel b). There is also a large difference in the left and right side peaks in the case of the septuplet structure. The decrease of the amplitude is not parallel anymore, but there are larger differences around medium-order harmonics (panel c). The shape of the amplitude ratio vs. the harmonic order relation is similar for higher-order side peaks and for the lower-orders ones (panel d).
To characterize the asymmetry of the side peaks a parameter Q=(A+-A-)/A++A-)was
calculated. In Table 2 we present
the Q values for the side peaks. This
indicates a higher than average asymmetry to the right in the case of a
triplet, nonuplet, undecaplet and quindecaplet structure,
whereas the quintuplet, septuplet and tredecaplet structure shows a
lower than average asymmetry to the right
(see also Fig. 6).
We computed the degree of deviation from the equidistant spacing of the
multiplet structure with an uncertainty of ![]() 0.0069. The values of the degree of deviation are
given in Table 2
with the uncertainties for all multiplet structures except for the
quindecaplet.
0.0069. The values of the degree of deviation are
given in Table 2
with the uncertainties for all multiplet structures except for the
quindecaplet.
We confirmed the previously known results obtained from ground-based observations for triplets and quintuplets. Our high-precision space data revealed new regularities in the higher-order side peaks, especially for the highest amplitude of the medium-order right-side peaks. A comparison with other RR Lyrae stars will reveal whether the difference from a purely exponential decrease is connected to the more general parameters of the star or if it is only accidental in V1127 Aql.
3.3 Additional frequencies
A dominant peak ![]() was found in the course of our frequency analysis.
A detailed analysis reveals a complex structure in the frequency domain
around the dominant peak and
around
was found in the course of our frequency analysis.
A detailed analysis reveals a complex structure in the frequency domain
around the dominant peak and
around ![]() presented in Fig. 7.
A list of additional frequencies is given in
Tables 1.B.1, 1.B.2, 1.B.3, 1.B.4, and 1.B.5. The
combination terms between f' and f0
exclude the possibility that
presented in Fig. 7.
A list of additional frequencies is given in
Tables 1.B.1, 1.B.2, 1.B.3, 1.B.4, and 1.B.5. The
combination terms between f' and f0
exclude the possibility that
![]() and
and
![]() are actually related to a background contact system,
measured with V1127 Aql in the CoRoT window.
are actually related to a background contact system,
measured with V1127 Aql in the CoRoT window.
As we see in the figure and the tables, the dominant modes in
the two regions are numerically connected to each other, ![]() or
or ![]() depending on what we
use as a reference frequency. Linear combination terms were also found
with
f0 (up to 6f0)
and
depending on what we
use as a reference frequency. Linear combination terms were also found
with
f0 (up to 6f0)
and ![]() or
or ![]() .
Many triplet, quintuplet, septuplet components of
.
Many triplet, quintuplet, septuplet components of ![]() and
and ![]() were identified
with the Blazhko modulation frequency
were identified
with the Blazhko modulation frequency ![]() .
Multiplet structures of these additional
frequencies and their linear combinations with the main period and its
harmonics
were also found.
.
Multiplet structures of these additional
frequencies and their linear combinations with the main period and its
harmonics
were also found.
We could infer the presence of a second modulation-like
frequency ![]() .
This frequency corresponds to a period of 6.289 d. We did not
observe this frequency itself in the Fourier spectrum, but many peaks
could be identified as
multiplet structures around the additional mode
.
This frequency corresponds to a period of 6.289 d. We did not
observe this frequency itself in the Fourier spectrum, but many peaks
could be identified as
multiplet structures around the additional mode ![]() and its linear combinations with the main pulsation frequency
and its linear combinations with the main pulsation frequency ![]() and
and ![]() (1<k<5, Table 1C). A triplet
structure was clearly detected and we always observed the right side
peak to have a higher amplitude than the left one. A quintuplet
structure was detected only around the
(1<k<5, Table 1C). A triplet
structure was clearly detected and we always observed the right side
peak to have a higher amplitude than the left one. A quintuplet
structure was detected only around the ![]() ,
,
![]() and
and
![]() frequencies and showed on the left side peak.
frequencies and showed on the left side peak.
A second modulation has been previously reported by Sódor (2009); Sódor et al. (2006), but it appeared around the main pulsation frequency, not around a rather low amplitude additional component. In our case second modulation peaks appear only in the interpretation of the additional modes and their linear combination of the main pulsation frequency.
![\begin{figure}
\par\includegraphics[angle=0,width=9cm]{13345fg6.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg65.png)
|
Figure 7:
Frequency pattern around the frequency of the additional mode
and its harmonic
|
| Open with DEXTER | |
It is a great challenge to find an answer to the origin of the
additional frequency ![]() ,
its subharmonic and its cyclic modulation
,
its subharmonic and its cyclic modulation ![]() .
There are several possible explanations:
.
There are several possible explanations:
- (1)
- the rotation period of V1127 Aql? But, the related
period
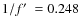 d
seems to be too short to be the rotation period of the RRab star
V1127 Aql.
Peterson et al. (1996)
measured the line-widths via cross-correlation for 27 field
RR Lyrae stars and obtained an upper limit for the projected
rotational velocity, which
corresponds to 10-100 d of the rotation period;
d
seems to be too short to be the rotation period of the RRab star
V1127 Aql.
Peterson et al. (1996)
measured the line-widths via cross-correlation for 27 field
RR Lyrae stars and obtained an upper limit for the projected
rotational velocity, which
corresponds to 10-100 d of the rotation period;
- (2)
- tidal effects in a binary system? If V1127 Aql has
a companion, the
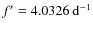 would be the orbital period, but it
seems to be too short to be connected to the orbital period.
We could hardly explain the side peaks' structure around
would be the orbital period, but it
seems to be too short to be connected to the orbital period.
We could hardly explain the side peaks' structure around 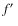 in this framework;
in this framework;
- (3)
- Is V1127 Aql a double mode RR Lyrae variable?
Additional frequencies with low amplitudes were also found in the
photometric data obtained with the MOST satellite of AQ Leo, a
``classical'' RRd star (Gruberbauer
et al. 2007).
A higher-order radial or resonant non-radial mode was suggested by
the authors to explain the two detected frequencies with a ratio
of 2:1.
In our case, V1127 Aql might be interpreted as oscillating in
the fundamental radial mode
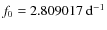 (0.355996 d) and the first or a higher-order radial overtone
mode
(0.355996 d) and the first or a higher-order radial overtone
mode 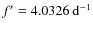 (0.247978 d). As in AQ Leo, the coupling terms are
clearly detected as well. Moreover, both modes show cyclic modulation
with
(0.247978 d). As in AQ Leo, the coupling terms are
clearly detected as well. Moreover, both modes show cyclic modulation
with 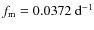 .
However, the ratio f0/f'
= 0.6965 and
.
However, the ratio f0/f'
= 0.6965 and 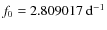 (0.355996 d) does not fit to the relation of the RR d
stars of our Galaxy.
(0.355996 d) does not fit to the relation of the RR d
stars of our Galaxy.
To demonstrate this, we computed convective linear RR Lyrae model grids on an extremely large parameter space (L=40, 50, 60 and 70
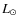 ,
M=0.50-0.80
,
M=0.50-0.80 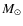 with
with 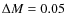
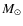 ,
,
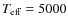 -8000 K,
-8000 K,
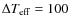 K,
Z=0.001, 0.003, 0.01, 0.02 and 0.04).
The other adopted parameters were standard RR Lyrae parameters
(see Szabó et al. 2004).
The Petersen diagram for different metallicities is shown in
Fig. 8.
The ``+'' sign marks the observed period ratio of
K,
Z=0.001, 0.003, 0.01, 0.02 and 0.04).
The other adopted parameters were standard RR Lyrae parameters
(see Szabó et al. 2004).
The Petersen diagram for different metallicities is shown in
Fig. 8.
The ``+'' sign marks the observed period ratio of 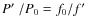 .
We note that nonlinearity introduces a negligible difference in the
periods and period
ratios in this figure.
Based on the large differences between the observed and computed
period ratios
we can exclude a radial-overtone explanation for the frequency
.
We note that nonlinearity introduces a negligible difference in the
periods and period
ratios in this figure.
Based on the large differences between the observed and computed
period ratios
we can exclude a radial-overtone explanation for the frequency 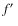 .
It can be neither the first radial overtone nor one of the higher
overtones, since the discrepancy between the computed higher-overtone
period ratios (Pi/P0)
and
.
It can be neither the first radial overtone nor one of the higher
overtones, since the discrepancy between the computed higher-overtone
period ratios (Pi/P0)
and 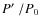 is even larger than for the first overtone;
is even larger than for the first overtone;
- (4)
- is V1127 Aql a multiperiodic RR Lyrae variable? In
this case, the frequency
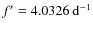 (0.248 d) is a non-radial mode with a subharmonic
(0.248 d) is a non-radial mode with a subharmonic 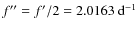 and a cyclic modulation of 6.289 d. In this scenario we have
to suppose that the additional frequencies are non-radial
modes.
and a cyclic modulation of 6.289 d. In this scenario we have
to suppose that the additional frequencies are non-radial
modes. 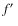 can be a non-radial p-mode while
can be a non-radial p-mode while 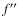 could be interpreted as a
g-mode, since it is longer than the radial fundamental mode. However,
the numerical
relation (
could be interpreted as a
g-mode, since it is longer than the radial fundamental mode. However,
the numerical
relation (
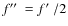 )
raised the possibility of
)
raised the possibility of 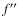 being a subharmonic. It would be interesting to
check the possibility of a 2:1 resonance between a p-mode and a g-mode.
For this purpose, however, non-radial non-linear codes for RR Lyrae
stars would be required.
being a subharmonic. It would be interesting to
check the possibility of a 2:1 resonance between a p-mode and a g-mode.
For this purpose, however, non-radial non-linear codes for RR Lyrae
stars would be required.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm]{13345fg7.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg78.png)
|
Figure 8:
Petersen diagram based on linear convective RR Lyrae models. The
symbols denote different metallicities. The ``+'' sign shows the
position
of V1127 Aql assuming that the frequency
|
| Open with DEXTER | |
3.4 Multimode pulsation
We propose a second explanation that avoids the second modulation
frequency.
The ![]() values are slightly different when considering the couples
4.0326, 4.1916 (0.1590 d-1)
and 4.0326, 3.8632 (0.1694 d-1).
Therefore,
the 3.8632, 4.0326 and 4.1916 terms could be independent
excited modes. Following this hypothesis,
V1127 Aql could be a multimode pulsator, showing up to nine
independent modes
spanning the narrow interval from 3.64 to 4.82 d-1
(Table 1.C.1).
Since the corresponding periods are shorter than the fundamental
radial period, these terms can be typified as both radial modes
belonging to a higher
n number (overtones) and non-radial modes.
Looking at Fig. 8,
we note that f4=3.722 d-1
and f8=3.749 d-1
supply period ratios compatible with the identification of one of them
as the first overtone.
Moreover, f6=4.825 d-1
supplies a period ratio compatible
with the expected ratio between the second overtone and the fundamental
mode.
But, due to the large number, most if not all of these frequencies are
likely related to non-radial modes. It it also noteworthy that the
independent terms show a signature of an almost regular spacing (i.e.,
that
between the 3.647, 3.674, 3.697, 3.722, and 3.749 d-1
frequencies),
which could be ascribed to effects (rotational splitting, large
separation)
typical of non-radial modes.
values are slightly different when considering the couples
4.0326, 4.1916 (0.1590 d-1)
and 4.0326, 3.8632 (0.1694 d-1).
Therefore,
the 3.8632, 4.0326 and 4.1916 terms could be independent
excited modes. Following this hypothesis,
V1127 Aql could be a multimode pulsator, showing up to nine
independent modes
spanning the narrow interval from 3.64 to 4.82 d-1
(Table 1.C.1).
Since the corresponding periods are shorter than the fundamental
radial period, these terms can be typified as both radial modes
belonging to a higher
n number (overtones) and non-radial modes.
Looking at Fig. 8,
we note that f4=3.722 d-1
and f8=3.749 d-1
supply period ratios compatible with the identification of one of them
as the first overtone.
Moreover, f6=4.825 d-1
supplies a period ratio compatible
with the expected ratio between the second overtone and the fundamental
mode.
But, due to the large number, most if not all of these frequencies are
likely related to non-radial modes. It it also noteworthy that the
independent terms show a signature of an almost regular spacing (i.e.,
that
between the 3.647, 3.674, 3.697, 3.722, and 3.749 d-1
frequencies),
which could be ascribed to effects (rotational splitting, large
separation)
typical of non-radial modes.
These additional terms show combinations with several
harmonics of f0 (up to 6f0)
with its Blazhko modulation (Table 1.C.2). We stress
that the frequencies as listed in Table 1.C are the same
listed in Table 1.B,
but they are identified in a different way. There are some relations
between the two solutions (
![]() ,
,
![]() ,
,
![]() )
and hence they could be considered to be very similar
from a mathematical point of view.
)
and hence they could be considered to be very similar
from a mathematical point of view.
It is very interesting to note
that the terms f1, f2,
and f6 show some complete
multiplet structures
![]() (k=2 for f1
and f-2, k=3 for f6;
Table 1.C.3). It is hard to say whether this directly means
that the Blazhko phenomenon
also affects other modes than the radial ones, or if these terms are
just
linear combinations since it could be, for instance,
(k=2 for f1
and f-2, k=3 for f6;
Table 1.C.3). It is hard to say whether this directly means
that the Blazhko phenomenon
also affects other modes than the radial ones, or if these terms are
just
linear combinations since it could be, for instance,
![]() .
In the former case
these terms would have a relevant impact
on the modelling of the underlying physical mechanism
of the Blazhko effect, since
.
In the former case
these terms would have a relevant impact
on the modelling of the underlying physical mechanism
of the Blazhko effect, since ![]() has been considered so far as
a modulation of the fundamental radial mode f0
only.
has been considered so far as
a modulation of the fundamental radial mode f0
only.
4 The Blazhko phenomenon
The most striking feature of V1127 Aql is the large amplitude and phase modulation of the light curve over five Blazhko cycles. We emphasize that five continuously covered Blazhko cycles have never been in anyone's hands for investigation. The present paper describes the regularity of the Blazhko modulation by traditional and new tools. Due to the proper sampling and high precision of the CoRoT data we were able to use distinguished points in the light curve to characterize the nature of the Blazhko modulation. Especially the use of the minimum of the light curve can be accounted as a new tool.
4.1 Amplitude modulation
Figure 9
shows the phased CoRoT light curve of V1127 Aql folded with
the Blazhko period, ![]() = 26.88 d.
The modulation of V1127 Aql is highly non-linear, as can be
judged from the non-sinusoidal modulation of the light curve in
Fig. 9.
= 26.88 d.
The modulation of V1127 Aql is highly non-linear, as can be
judged from the non-sinusoidal modulation of the light curve in
Fig. 9.
To assess the light variation characteristics of
V1127 Aql, we plotted
the maximum and minimum brightness as a function of time (i.e., the
envelopes of the light curve), as shown in Fig. 10.
Due to the non-linear nature of the modulation a third-order harmonic
series of the Blazhko modulation frequency (![]() )
is needed to separately fit the variations of the maxima and the
minima, respectively.
In this way, we obtain a total light variation of 0.753 mag.
The maximum pulsation amplitude is
0.744 mag, while the minimum pulsation amplitude is
0.352 mag. Hence, the modulation amplitude amounts to
0.392 mag, where the magnitudes are in the CoRoT instrumental
system.
)
is needed to separately fit the variations of the maxima and the
minima, respectively.
In this way, we obtain a total light variation of 0.753 mag.
The maximum pulsation amplitude is
0.744 mag, while the minimum pulsation amplitude is
0.352 mag. Hence, the modulation amplitude amounts to
0.392 mag, where the magnitudes are in the CoRoT instrumental
system.
![\begin{figure}
\par\includegraphics[angle=270,width=9cm]{13345fg8.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg85.png)
|
Figure 9: The CoRoT light curve of V1127 Aql folded by the Blazhko period. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=9cm]{13345fg9.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg86.png)
|
Figure 10: Maximum and minimum (shifted by -0.9 vertically) magnitudes. Both curves were fitted with third order harmonic series. There is a phase lag between the maximum of maxima and the minimum of minima denoted by small line segments. |
| Open with DEXTER | |
The light curve folded with the Blazkho period reveals a clear phase
lag: the lowest minimum occurs around ![]() and the highest maximum around
and the highest maximum around ![]() .
.
To visualize the phase lag between the maximum of maxima and the minimum of the minima, in Fig. 10 the minimum magnitudes were vertically shifted. From the fitted harmonic series we derive a shift of 3.4344 days which is equivalent to 0.1276 Blazhko phase.
4.2 Phase modulation
The O-C curve is a traditional tool for the investigation of period changes. In the case of a Blazhko star we use it for the investigation of period variation seemingly caused by the phase modulation. We constructed O-C curves of both the maxima and minima for the individual cycles (Fig. 11). Due to the higher scatter around the minimum of the light curve the minimum has never previously been used to construct an O-C diagram. Note that because of its double minimum caused during the bump (Gillet & Crowe 1988), the minimum is measured by fitting a polynomial of the 9th order. The same was found to give satisfactory results for the maxima, as well.
We used the epoch of the O-C values T0 = 2691.7543167 CoRoTJD and the pulsation period P0=0.355996 d. The variation of the maximum and minimum O-C values is of the order of 0.06 days. The phase modulation reaches 14% of the pulsation period (around 77 min). V1127 Aql exhibits one of the strongest phase modulations among all known Blazhko stars. Both the maximum and minimum O-C diagrams reveal the same behaviour of the phase modulation.
![\begin{figure}
\par\includegraphics[angle=270,width=9cm]{13345fg10.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg89.png)
|
Figure 11: The O-C diagram for the pulsation maxima and minima. |
| Open with DEXTER | |
4.3 Instantaneous amplitude and period
We interpret the phase modulation as a period variation. In order to find a connection between the amplitude modulation and the period variation we need to derive the time-dependent amplitude and period. As is well known, the O-C diagram contains the integrated effect of the period variation. However, the numerical derivation of the O-C data gives a rather noisy period value, which is an expected behaviour. One way to circumvent the problem is to fit the maximum (or minimum) O-C values by a polynomial.
In this work we applied another approach, namely the analytical
signal method (Kolláth
et al. 2002).
It uses the mathematical theorem that connects the real and imaginary
part of any complex function which is analytic in the upper half plane.
This relation makes it possible to unambiguously define the phase ![]() and the amplitude A(t) of a
signal
and the amplitude A(t) of a
signal ![]() .
Consequently it allows one to extract both the instantaneous amplitude
and period.
.
Consequently it allows one to extract both the instantaneous amplitude
and period.
Figure 12,
shows the instantaneous period and the amplitude of the first
Fourier-component of the dominant
pulsational mode. Note that the longest period occurs near the smallest
amplitude, and the shortest period is seen at the middle of the
descending phase of the amplitude modulation. The average delay between
the maximum period and maximum amplitude is ![]() days,
corresponding to
days,
corresponding to ![]() Blazhko phase.
Blazhko phase.
The accuracy of the analytical signal method was checked through Monte-Carlo simulations by generating 1000 artificial datasets. Each dataset contained a modulated sine wave with similar amplitudes to the V1127 Aql light curve, using the same original light curve sampling. A Gaussian random error was added to the simulated data. The formal error of both quantities is less than the width of the lines in Fig. 12.
![\begin{figure}
\par\includegraphics[angle=270,width=9cm]{13345fg11}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg94.png)
|
Figure 12: The instantaneous period (dotted line) and the amplitude of the first Fourier-component of the dominant pulsational mode A(f0), (solid line) during the Blazhko modulation. |
| Open with DEXTER | |
We applied the same analysis technique to three other Blazhko RR Lyrae
stars found in the LRc01 field: 0101128793, 0100881648, 0101503544
(Szabó et al. 2009).
The average phase delay between the
amplitude and phase maxima is ![]() ,
,
![]() and
and
![]() .
Note that the
four phase-lag values are confined to a relatively small interval
[0.39; 0.53]. Moreover, the phase lag in the case of MW Lyr
is 0.38, and 0.50 for DM Cyg (Jurcsik et al. 2009,2008).
.
Note that the
four phase-lag values are confined to a relatively small interval
[0.39; 0.53]. Moreover, the phase lag in the case of MW Lyr
is 0.38, and 0.50 for DM Cyg (Jurcsik et al. 2009,2008).
We argue that this quantity is an important parameter to study, because it is tightly connected to the physical mechanism of the amplitude and phase modulation. In addition, it strongly influences the multiplet structure of the modulated light curve (Benko et al. 2009; Szeidl & Jurcsik 2009).
The period variation emerges either due to a global parameter change in the star or because of non-linear effects or both, but its underlying cause and that of the amplitude modulation is not known. Therefore, the observed surprisingly small interval of the phase delay between the amplitude and the period variation presents a strong constraint for any model aiming to explain the Blazhko effect. The derivation of this quantity for more Blazhko stars is highly desirable.
From Fig. 12,
it also seems that there is a continuous change in the pulsation period
during the Blazhko cycle. The period change is antiphased with the
light amplitude, showing an elbow centred at the phase of the Blazhko
maximum. The full range of the period change is 0.006 d with ![]() P/P = +0.0169
(1.69% of the pulsation period). The amplitude variation of the
pulsation period is about 80% and the positive sign of
P/P = +0.0169
(1.69% of the pulsation period). The amplitude variation of the
pulsation period is about 80% and the positive sign of ![]() is consistent with the Stothers prediction (Stothers
2006).
is consistent with the Stothers prediction (Stothers
2006).
![\begin{figure}
\par\includegraphics[angle=270,width=9cm]{13345fg12}\par\includegraphics[angle=270,width=9cm]{13345fg13}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg99.png)
|
Figure 13: a) Maximum brightness vs. Blazhko phase b) The same for the maximum phase. |
| Open with DEXTER | |
4.4 Maximum brightness and maximum phase variation
The maximum brightness and maximum phase variation during the Blazhko
phase are
shown in Fig. 13.
The maximum phase curve shows an asymmetric shape
with a rapid increase on the rising branch (Blazhko phase
between 0.4 and 0.7). The maximum phase plot was
fitted using a 5th order Fourier-sum, and we fitted the maximum
brightness curve using a 3th order Fourier-sum. Table 3 lists the
Fourier components of the maximum brightness and maximum phase fits.
These differences show that the non-linearity is stronger in the phase
modulation than in the amplitude modulation.
The 0.0175 mag and 0.0090 phase rms scatter of the
residuals of the maximum brightness and maximum phase fits are too
large since the data are accurate within ![]() 0.005 mag and
0.005 mag and ![]() 0.0018 d, respectively. This means that
both the maximum brightness and maximum phase curves reflect the
imperfection of modelling the modulation using the Fourier sum of
discrete frequency components.
0.0018 d, respectively. This means that
both the maximum brightness and maximum phase curves reflect the
imperfection of modelling the modulation using the Fourier sum of
discrete frequency components.
The stability of the subsequent Blazhko cycles can be studied by plotting the maximum brightness values versus the maximum phase values. Figure 14 shows the curve for the first and the last observed Blazhko cycles, plotted with different symbols. The scatter is surprisingly large around the triangular shape curve and can neither be explained by the accuracy of the data nor by the procedure of determining the maximum phase and brightness values. We fitted the maximum brightness and the maximum phase values of each individual Blazhko cycle with a 5th order Fourier-sum, which allows us to discern a slight decrease in the maximum phase around 0.011 pulsation phase (5.6 min) during the five covered Blazhko cycles. This variation is quasi-linear, while there is a seemingly random variation in the maximum brightness values of the fits. A longer data set with the same accuracy would be necessary to decide whether the shift of the maximum phase continues or shows cyclic variations.
Table 3: Fourier amplitudes and phases of the fits to the maximum brightness and maximum phase data.
![\begin{figure}
\par\includegraphics[angle=270,width=9cm]{13345fg14}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg102.png)
|
Figure 14: a) Maximum brightness - maximum phase plot with 5th order harmonic fits. For clarity only the first (right, ``+'' symbols) and the fifth Blazhko cycles ( left, dots) are shown. |
| Open with DEXTER | |
5 Summary
The photometric observations of V1127 Aql analysed in this paper, produced which were in the framework of CoRoT Exoplanet programme, are the most accurate and continuous data set of a Blazhko star ever obtained.
Due to the proper data sampling and high precision we got new results on both the frequency content and the amplitude behaviour. We describe the still puzzling Blazhko phenomenon on a higher level, revealing more details to constrain the theoretical interpretation.
- We determined 18 harmonics of the main pulsation period. All of them have a complex structure of the Blazhko side peaks up to the septdecaplet (16 side peaks) distribution. Not all components of the side peaks' structure exceed the significance level.
- The
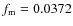 d-1
Blazhko modulation frequency as well as its first two
harmonics were identified in the frequency spectrum. That is, the
Blazhko modulation turned out to be non-linear both in amplitude and
phase.
We could determine that the phase modulation shows a higher
non-linearity than
the amplitude modulation.
d-1
Blazhko modulation frequency as well as its first two
harmonics were identified in the frequency spectrum. That is, the
Blazhko modulation turned out to be non-linear both in amplitude and
phase.
We could determine that the phase modulation shows a higher
non-linearity than
the amplitude modulation.
- A frequency peak
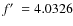 d-1
was found that does not fit the regular pattern
of harmonics and Blazhko side peaks. Additionally, with a 2:1 frequency
ratio
d-1
was found that does not fit the regular pattern
of harmonics and Blazhko side peaks. Additionally, with a 2:1 frequency
ratio
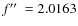 d-1
also appeared. Side peaks with the Blazhko modulation
frequency
d-1
also appeared. Side peaks with the Blazhko modulation
frequency 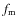 were
also found around these peaks up to the quintuplet structure. We argue
that rotation, tidal effects and
higher-order radial overtones can be excluded as an explanation for the
occurrence of those additional frequencies.
A small possible amplitude modulation
were
also found around these peaks up to the quintuplet structure. We argue
that rotation, tidal effects and
higher-order radial overtones can be excluded as an explanation for the
occurrence of those additional frequencies.
A small possible amplitude modulation 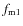 was also detected.
Since it is not connected to a radial mode, its interpretation is
ambiguous.
The most plausible interpretation is that non-radial p-modes are
excited in V1127 Aql.
We extended this explanation by removing
was also detected.
Since it is not connected to a radial mode, its interpretation is
ambiguous.
The most plausible interpretation is that non-radial p-modes are
excited in V1127 Aql.
We extended this explanation by removing
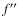 and
and 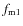 and providing a different identification of
the detected frequencies in terms of a set of nine additional modes.
These modes show linear combinations with the main pulsation period and
the Blazhko modulation.
and providing a different identification of
the detected frequencies in terms of a set of nine additional modes.
These modes show linear combinations with the main pulsation period and
the Blazhko modulation.
- Regarding the amplitude of the harmonics of the main frequency a special feature, a standstill, was observed at the medium-order harmonics. A similar feature was found in the monoperiodic non-Blazhko CoRoT star, ID:0101370131. Otherwise, the harmonics show an exponential decrease in amplitude. The distribution of Blazhko side peaks around the harmonics show a high-level asymmetry in favour of higher frequency side peaks because of the asymmetric amplitudes. The amplitude ratio of the lower- (left) and higher- (right) frequency side peaks have different values for the different components of the multiplet structure. The largest difference between the left and right components of the triplet side peaks is reached for medium-order harmonics (n). A similar behaviour is found for higher-order multiplets (k).
- As for the general characteristic of the Blazhko modulation, we derived the maximum value of the modulation of the light maximum (0.310) and at the minimum (0.100). Both values are robust compared to the 0.744 mag maximum amplitude brightness variation caused by the pulsation and are definitely not symmetrical to a constant mean brightness level. We derived a 3.4344 days (0.1276 Blazhko phase) phase lag between the maximum of maxima and minimum of minima. A strong 0.06 days modulation was derived, which amounts to 14% of the pulsation period. A long, 10.48 days (0.390 Blazhko phase) phase delay occured between the instantaneous period and amplitude during the Blazhko cycle.
- The phase delay between the amplitude and period modulation is 10.48 days (0.390 Blazhko phase) for V1127 Aql. This quantity is confined to a relatively small interval [0.38; 0.53] for all studied Blazkho stars which have a well covered light curve.
- The diagram of the maximum brightness and maximum phase over the five consecutive Blazhko cycles revealed a systematic shift. The shift between the first and the 5th cycle is 0.011 pulsational phase which means 5.6 min over 143 days.
We would like to thank the referee for helpful comments. M.Ch. thanks the CoRoTeam and the CoRoT Variability Classifier (CVC Team) for their help during the preparation of the CoRoT data. J.M.B., M.P. and R.Sz. acknowledge the support of the ESA PECS projects No. 98022 & 98114. K.K. and E.G. thank the project FWF T359 and FWF P19962, and E.P. the Italian ESS project (contract ASI/INAF/I/015/07/0, WP 03170) for financial support.
References
- Alcock, C., Allsman, R., Alves, D. R., et al. 2000, ApJ, 542, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Alcock, C., Alves, D. R., Becker, A., et al. 2003, ApJ, 598, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benko, J. M., Paparó, M., Szabó, R., Chadid, M., et al. 2009, AIP Conf. Proc., 1170, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Blazhko, S. 1907, Astr. Nachr., 175, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Bono, G., Caputo, F., Castellani, V., et al. 1997, ApJ, 483, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Borkowski, K. J. 1980, , 33, 393 [Google Scholar]
- Chadid, M., & Chapellier, E. 2006, A&A, 456, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chadid, M., & Gillet, D. 1997, A&A, 319, 154 [NASA ADS] [Google Scholar]
- Chadid, M., Kolenberg, K., Aerts, C., & Gillet, D. 1999, A&A, 352, 201 [NASA ADS] [Google Scholar]
- Chadid, M., Wade, G. A., Shorlin, S. L. S., & Landstreet, J. D. 2004, A&A, 413, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chadid, M., Vernin, J., & Gillet, D. 2008, A&A, 491, 537 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chadid, M., Baglin, A., Benko, J. M., et al. 2009, AIP Conf. Proc., 1170, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Del Principe, M., Piersimoni, A. M., & Bono, G. 2005, AJ, 129, 2714 [NASA ADS] [CrossRef] [Google Scholar]
- Del Principe, M., Piersimoni, A. M., Storm, J., et al. 2006, ApJ, 652, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Dziembowski, W. A., & Mizerski, T. 2004, , 54, 363 [Google Scholar]
- Gillet, D., & Crowe, R. A. 1988, A&A, 199, 242 [NASA ADS] [Google Scholar]
- Gessner, H. 1973, Veröff. Sternw. Sonneberg, 7, Heft 5, 525 [NASA ADS] [Google Scholar]
- Gruberbauer, M., Kolenberg, K., Rowe, J. F., et al. 2007, MNRAS, 379, 1498 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffmeister, C. 1966, AN, 289, 139 [Google Scholar]
- Hurta, Zs., Jurcsik, J., Szeidl, B., & Sódor, Á. 2008, AJ, 135, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Jurcsik, J., Sódor, Á., Váradi, M., et al. 2005, A&A, 430, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jurcsik, J., Szeidl, B., Sódor, Á., et al. 2006, AJ, 132, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Jurcsik, J., Sódor, Á., Hurta, Zs., et al. 2008, MNRAS, 391, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Jurcsik, J., Hurta, Zs., Sódor, Á., et al. 2009, MNRAS, 397, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Kolenberg, K., Smith, H. A., Gazeas, K. D., et al. 2006, A&A, 459, 577 [Google Scholar]
- Kolenberg, K., Guggenberger, E., Medupe, T., et al. 2009, MNRAS, 396, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Kolláth, Z. 1990, Occ. Tech. Notes Konkoly Obs., Budapest, 1 [Google Scholar]
- Kolláth, Z., Buchler, J. R., Szabó, R., & Csubry, Z. 2002, A&A, 385, 932 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovács, G. 1995, A&A, 295, 693 [NASA ADS] [Google Scholar]
- Lenz, P., & Breger, M. 2005, CoAst., 146, 53 [Google Scholar]
- Moskalik, P., & Poretti, E., 2003, A&A, 398, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nagy, A. 1998, A&A, 339, 440 [NASA ADS] [Google Scholar]
- Paparó, M., Szabó, R., Benko, J. M., et al. 2009, AIP Conf. Proc., 1170, 240 [NASA ADS] [Google Scholar]
- Peterson, R. C., Carney, B. W., & Latham, D. W. 1996, ApJ, 465, 47 [Google Scholar]
- Preston, G. W., Smak, J., & Paczynski, B. 1965, ApJS, 12, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Reegen, P. 2007, A&A, 467, 1353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roberts, D. H., Lehar, J., & Dreher, J. W. 1987, AJ, 93, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Sanna, N., Bono, G., Stetson, P. B., et al. 2009, ApJ, 699, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Shibahashi, H. 2000. ASP Conf. Ser., 203, 299 [Google Scholar]
- Smith, H. A., Church, J. A., Fournier, J., et al. 2003, PASP, 115, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Sódor, Á. 2009, CoAst, 159, 55 [Google Scholar]
- Sódor, Á., Vida, K., Jurcsik, J., et al. 2006, IBVS, 5705 [Google Scholar]
- Sollima, A., Cacciari, C., Arkharov, A. A. H., et al. 2008, MNRAS, 384, 1583 [NASA ADS] [CrossRef] [Google Scholar]
- Stellingwerf, R. F. 1978, ApJ, 224, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Stothers, R. B. 2006, ApJ, 652, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Struve, O., & Blaauw, A. 1949, ApJ, 108, 60 [Google Scholar]
- Szabó, R., Kolláth, Z., & Buchler, J. R. 2004, A&A, 425, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szabó, R., Paparó, M., Benko, J. M., Chadid, M., et al. 2009, AIP Conf. Proc., 1170, 291 [NASA ADS] [Google Scholar]
- Szeidl, B., & Jurcsik, J., 2009, CoAst, 160, 17 [Google Scholar]
- Walraven, Th. 1949, BAN, 11, 17 [Google Scholar]
Footnotes
- ... V1127 Aquilae
![[*]](/icons/foot_motif.png)
- Full Table 1 is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/510/A39
- ...
![[*]](/icons/foot_motif.png)
- The CoRoT space mission was developed and is operated by the French space agency CNES, with participation of ESA's RSSD and Science Programmes, Austria, Belgium, Brazil, Germany, and Spain.
- ...
RR Lyrae-CoRoTeam
![[*]](/icons/foot_motif.png)
- The dedicated website is http://fizeau.unice.fr/corot
All Tables
Table 1: Frequencies, Fourier amplitudes, phases, spectral significances and identification of the frequencies (this table can be found in its entirety at CDS).
Table 2: Complex multiplet structures, degree of deviation and degree of asymmetry.
Table 3: Fourier amplitudes and phases of the fits to the maximum brightness and maximum phase data.
All Figures
![\begin{figure}
\par\includegraphics[angle=00,width=15cm,clip]{13345fg1.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg28.png)
|
Figure 1: Two-dimensional CoRoT light curve of V1127 Aql folded with the pulsation period (0.355996 d) over five Blazhko cycles. The variations in the light curve due to the Blazhko effect are clearly visible. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=9cm]{13345fg2.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg29.png)
|
Figure 2: The main steps of prewhitening process. a) The amplitude spectrum. b) Prewhitened spectrum with main pulsation frequency, its harmonics and the triplets (see insert in panel a)). c) Prewhitened spectrum with modulation frequency, its harmonics and all higher-order side peaks (see insert in panel b)). d)) Residual spectrum when all frequencies in Table 1 are removed. (For better visibility only the lower frequency regions are shown.) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=9cm]{13345fg3.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg47.png)
|
Figure 3:
Map of harmonics and side peaks in the Fourier spectrum of the
V1127 Aql.
The order of side frequencies (k) vs. harmonic
orders (n) is plotted according to the formula |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=9cm]{13345fg4.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg48.png)
|
Figure 4:
The Blazhko modulation frequency |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=9cm]{13345fg4bis}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg51.png)
|
Figure 5: Top: a part of the unbiased Fourier spectrum around the harmonics of 17f0. Bottom: the same part of the window function in the same scale as the spectrum. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=00,width=9cm,clip]{13345fg5.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg52.png)
|
Figure 6:
a) Amplitude ratios of the harmonic
components of the radial pulsation given in decimal logarithmic scale (Anf0/Af0)
compared to the amplitude ratios of the modulation components |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=9cm]{13345fg6.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg65.png)
|
Figure 7:
Frequency pattern around the frequency of the additional mode
and its harmonic
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm]{13345fg7.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg78.png)
|
Figure 8:
Petersen diagram based on linear convective RR Lyrae models. The
symbols denote different metallicities. The ``+'' sign shows the
position
of V1127 Aql assuming that the frequency
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=9cm]{13345fg8.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg85.png)
|
Figure 9: The CoRoT light curve of V1127 Aql folded by the Blazhko period. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=9cm]{13345fg9.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg86.png)
|
Figure 10: Maximum and minimum (shifted by -0.9 vertically) magnitudes. Both curves were fitted with third order harmonic series. There is a phase lag between the maximum of maxima and the minimum of minima denoted by small line segments. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=9cm]{13345fg10.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg89.png)
|
Figure 11: The O-C diagram for the pulsation maxima and minima. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=9cm]{13345fg11}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg94.png)
|
Figure 12: The instantaneous period (dotted line) and the amplitude of the first Fourier-component of the dominant pulsational mode A(f0), (solid line) during the Blazhko modulation. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=9cm]{13345fg12}\par\includegraphics[angle=270,width=9cm]{13345fg13}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg99.png)
|
Figure 13: a) Maximum brightness vs. Blazhko phase b) The same for the maximum phase. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=9cm]{13345fg14}
\end{figure}](/articles/aa/full_html/2010/02/aa13345-09/Timg102.png)
|
Figure 14: a) Maximum brightness - maximum phase plot with 5th order harmonic fits. For clarity only the first (right, ``+'' symbols) and the fifth Blazhko cycles ( left, dots) are shown. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


