| Issue |
A&A
Volume 510, February 2010
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200913289 | |
| Published online | 10 February 2010 | |
XMM-Newton long-look observation of the narrow line Seyfert 1 galaxy PKS 0558-504
I. Spectral analysis
I. E. Papadakis1,2 - W. Brinkmann3 - M. Gliozzi4 - C. Raeth3 - F. Nicastro2,5,6 - M. L. Conciatore6
1 - Physics Department, University of Crete, PO Box 2208,
710 03 Heraklion, Crete, Greece
2 - IESL, Foundation for Research and Technology, 711 10, Heraklion, Crete,
Greece
3 - Max-Planck-Institut für extraterrestrische Physik,
Giessenbachstrasse, 85740 Garching, Germany
4 - George Mason University,
Department of Physics and Astronomy, MS 3F3, 4400 University Dr.,
Fairfax, VA 22030, USA
5 - Osservatorio Astronomico di Roma, INAF, Italy
6 - Harvard-Smithsonian Center for Astrophysics, 60 Garden Street,
Cambridge, MA 02138, USA
Received 14 September 2009 / Accepted 26 November 2009
Abstract
Context. PKS 0558-504 has been observed repeatedly by XMM-Newton
as a calibration and performance verification (PV) target. In this
work, we present results from the spectral analysis of a long
XMM-Newton observation of the radio loud Narrow Line Seyfert 1 galaxy
PKS 0558-504.
Aims. To study the soft excess component in this object, the
spectral variations it exhibits in both the hard and soft X-ray bands,
and their correlation.
Methods. We used mainly the PN data, and we fitted various
spectral models to the time average spectra of the individual orbits as
well as the spectra from data segments of shorter duration. We also
used the RGS data to search for signs of a warm absorber in the source.
Results. The source is highly variable, on all sampled time
scales. We did not observe any absorption features in either the soft
or hard band. We found weak evidence for the presence of an iron line
at ![]() 6.8 keV,
which is indicative of emission from highly ionized iron. The
2-10 keV band spectrum of the source is well fitted by a simple
power law model, whose slope steepens with increasing flux, similar to
what is observed in other Seyferts as well. The soft excess is variable
both in flux and shape, and it can be well described by a
low-temperature Comptonisation model, whose slope flattens with
increasing flux. Finally, the soft excess flux variations are
moderately correlated with the hard band variations, and we found weak
evidence that they are leading them by
6.8 keV,
which is indicative of emission from highly ionized iron. The
2-10 keV band spectrum of the source is well fitted by a simple
power law model, whose slope steepens with increasing flux, similar to
what is observed in other Seyferts as well. The soft excess is variable
both in flux and shape, and it can be well described by a
low-temperature Comptonisation model, whose slope flattens with
increasing flux. Finally, the soft excess flux variations are
moderately correlated with the hard band variations, and we found weak
evidence that they are leading them by ![]() 20 ks.
20 ks.
Conclusions. Our results rule out a jet origin for the bulk of
the X-ray emission in this object. We found no signals of a warm
absorber. The observed hard band spectral variations suggest intrinsic
continuum slope variations, caused by changes in the
``heating/cooling'' ratio of the hot corona. The low-temperature
Comptonising medium, responsible for the soft excess emission, could be
a hot layer in the inner disc of the source, which appears due to the
fact that the source is accreting at a super-Eddington rate. The soft
excess flux and spectral variations could be caused by random
variations of the accretion rate.
Key words: galaxies: active - galaxies: Seyfert - X-rays: galaxies
1 Introduction
Narrow Line Seyfert 1 galaxies (NLS1) are optically identified by their
emission line properties: the ratio of [O III]/H![]() is less than 3 and the
FWHM H
is less than 3 and the
FWHM H![]() less than 2000
less than 2000
![]() (Osterbrock & Pogge 1985;
Goodrich 1989). Their optical spectra are further characterised by the presence
of strong permitted Fe II, Ca II, and O I
(Osterbrock & Pogge 1985;
Goodrich 1989). Their optical spectra are further characterised by the presence
of strong permitted Fe II, Ca II, and O I ![]() 8446 ionisation lines
(Persson 1988). NLS1 have been rarely found to be radio-loud (Ulvestad et al. 1995; Siebert et al. 1999; Grupe et al. 1999). Recent
dedicated studies, in particular using the Sloan digital sky survey,
demonstrated that this is a consequence of the low radio-loud fraction of the
NLS1 population (
8446 ionisation lines
(Persson 1988). NLS1 have been rarely found to be radio-loud (Ulvestad et al. 1995; Siebert et al. 1999; Grupe et al. 1999). Recent
dedicated studies, in particular using the Sloan digital sky survey,
demonstrated that this is a consequence of the low radio-loud fraction of the
NLS1 population (![]() 7%, Komossa et al. 2006). The same authors found that
radio-loud NLS1 galaxies resemble GHz-peaked/compact steep spectrum sources,
and Yuan et al. (2008) suggested similarities with high-energy peaked BL Lac
Objects.
7%, Komossa et al. 2006). The same authors found that
radio-loud NLS1 galaxies resemble GHz-peaked/compact steep spectrum sources,
and Yuan et al. (2008) suggested similarities with high-energy peaked BL Lac
Objects.
PKS 0558-504 (
![]() )
is one of the best studied
radio loud NLS1 galaxies (
)
is one of the best studied
radio loud NLS1 galaxies (
![]() ;
Siebert et al. 1999). A peculiar property displayed by the source is its
unusually high X-ray to radio luminosity ratio (Brinkmann et al.
1997). It was optically identified on the basis of its X-ray position from
HEAO-1 (Remillard et al. 1986). It is an X-ray bright source, with a flux of
;
Siebert et al. 1999). A peculiar property displayed by the source is its
unusually high X-ray to radio luminosity ratio (Brinkmann et al.
1997). It was optically identified on the basis of its X-ray position from
HEAO-1 (Remillard et al. 1986). It is an X-ray bright source, with a flux of
![]()
![]() erg cm-2 s-1 in the 2-10 keV band. Its 2-10 keV spectrum
is rather steep (
erg cm-2 s-1 in the 2-10 keV band. Its 2-10 keV spectrum
is rather steep (
![]() Gliozzi et al. 2007). Its
spectral slope remains roughly constant on long time scales, despite the large
amplitude flux variations that the source exhibits (Gliozzi et al. 2007). PKS 0558-504 also exhibits strong flux variations on short time scales (Remillard et al.
1991; Gliozzi et al. 2000, 2001; Wang et al. 2001; Brinkmann
et al. 2004).
Gliozzi et al. 2007). Its
spectral slope remains roughly constant on long time scales, despite the large
amplitude flux variations that the source exhibits (Gliozzi et al. 2007). PKS 0558-504 also exhibits strong flux variations on short time scales (Remillard et al.
1991; Gliozzi et al. 2000, 2001; Wang et al. 2001; Brinkmann
et al. 2004).
PKS 0558-504 has been observed repeatedly by XMM-Newton as a calibration and performance
verification (PV) target. O'Brien et al. (2001) published the spectral analysis
of some preliminary data of the commissioning/CalPV phase. The 0.2-2 keV
spectrum was dominated by a large soft X-ray excess, which showed no evidence
for absorption or emission line features and was fitted by a model consisting
of three black body components. An analysis of all PV phase and calibration
observations performed by XMM-Newton up to orbit 341, with various instrumental
settings, was presented by Brinkmann et al. (2004). They found that all spectra
could be well fitted by two Comptonisation components, one at moderate
temperatures of
![]() keV and optical depths of
keV and optical depths of
![]() ,
the
other at high temperatures (
,
the
other at high temperatures (![]() keV) and low optical depths (
keV) and low optical depths (
![]() ). The same XMM-Newton data were recently used by Haba et al. (2008). The
spectra were fitted with a multicolour disc black body model (Mitsuda et al. 1984) plus a high energy power law. The results were interpreted in terms of a
super-critical accretion flow with significant photon trapping in the inner
regions of the accretion disc.
). The same XMM-Newton data were recently used by Haba et al. (2008). The
spectra were fitted with a multicolour disc black body model (Mitsuda et al. 1984) plus a high energy power law. The results were interpreted in terms of a
super-critical accretion flow with significant photon trapping in the inner
regions of the accretion disc.
In September 2008, PKS 0558-504 was observed with XMM-Newton for five consecutive orbits. The main objective of this long observation was to study its X-ray flux variability and in particular to investigate whether it exhibits any quasi-periodic signals. The results from this study will be presented in a companion paper (Papadakis et al., in preparation). In this paper we present the results from the spectral analysis of the XMM-Newton data. We used mainly the PN data because of the higher sensitivity of the PN camera, although we sometimes resorted to the RGS and MOS data as well, mainly for clarification purposes. We start with the observational details in the next section. Section 3 deals with the spectral analysis of the PN data, first in the hard band and then for the total band. In the same section we also present the results from a preliminary analysis of the RGS data. Temporal spectral variations and a time resolved spectroscopic analysis are discussed in Sects. 4 and 5. We then present a more detailed analysis of the full band spectra in selected time intervals in Sect. 6. Finally, in Sect. 7 we summarise our results and we present a short discussion of their potential implications.
2 Observations and data analysis
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{13289fg1.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg26.png)
|
Figure 1: The PN 0.4-10 keV light curve of PKS 0558-504 for all five observations with a binning of 100 s. The time counts from the beginning of the first observation. The points plotted with crosses at the bottom of the plot indicate the background count rate in the same energy range. |
| Open with DEXTER | |
PKS 0558-504 was observed with all instruments on board XMM-Newton for five consecutive orbits starting on 2008 September 9, 1:19 UT and ending on 2008 September 16, 12:02 UT. The observation identifiers range from 0555170201 (XMM revolution 1602) to 0555170601 (XMM revolution 1606). Below we will identify the individual observations by the last 3 digits (i.e. ``obs-201'', ``obs-301'', etc.). The PN was operated in Small Window mode (SW) with a thin filter, the MOS1 in Small Window mode with a thin filter, and the MOS2 in TIMING mode also thin filter. Both RGS were operated in spectroscopy mode.
For the following analysis we will rely mainly on data from the PN camera
(Strüder et al. 2001) due to its superior statistical quality. The PN data
have been processed using XMMSAS version 8.0. Source counts were
accumulated from a rectangular box of
![]() RAW pixels (1
RAW pixel
RAW pixels (1
RAW pixel ![]() 4.1
4.1
![]() )
around the position of the source.
Background data were extracted from a similar, source free region on the chip.
We selected single and double events ( PATTERN
)
around the position of the source.
Background data were extracted from a similar, source free region on the chip.
We selected single and double events ( PATTERN ![]() 4, FLAG = 0; for details of the instruments see Ehle et al. 2008). With an
average count rate of about 10 cts s-1 photon pile-up is negligible for
the PN detector, as verified using the XMMSAS task epatplot. The
data were screened for high background in both the soft and hard bands. After
rejection of time intervals affected by high background (usually at the end of
the individual orbits) and flaring activity, the total useful observation time
was 540 ks. For the spectral fits we employed for the PN the canned responses
from the MPE database.
4, FLAG = 0; for details of the instruments see Ehle et al. 2008). With an
average count rate of about 10 cts s-1 photon pile-up is negligible for
the PN detector, as verified using the XMMSAS task epatplot. The
data were screened for high background in both the soft and hard bands. After
rejection of time intervals affected by high background (usually at the end of
the individual orbits) and flaring activity, the total useful observation time
was 540 ks. For the spectral fits we employed for the PN the canned responses
from the MPE database.
As for the RGS data, for each observation we used the tool rgsproc to extract
calibrated first order spectra and responses for both RGS cameras. The RGS
spectra are affected by numerous instrumental features due to hot pixels and/or
bad columns in the read-out chips. To reduce the number of narrow spectral
intervals blocked by such features, and their width, we modified the default
rgsproc filtering parameters to exclude photons only from hot pixels and not
from their neighbouring pixels. The RGS data can be affected by high particle
background periods during parts of the XMM-Newton orbits, mostly caused by solar
activity. The high energy band is the most affected by background flares, and
high energy RGS photons are dispersed over the CCD-9 chip. We therefore
extracted background light curves of the CCD-9 chip and selected as
good-time-intervals of the processed observations only those during which the
background count rate deviated by ![]()
![]() from the average background
count rate of each observation. To improve and optimise the S/N of the RGS
spectra, we then used the tool
rgscombine to co-add the five RGS1 and RGS2
spectra. The final (after cleaning for high background time intervals) exposures
of the RGS1 and RGS2 spectra are 480 ks and 466 ks, respectively.
from the average background
count rate of each observation. To improve and optimise the S/N of the RGS
spectra, we then used the tool
rgscombine to co-add the five RGS1 and RGS2
spectra. The final (after cleaning for high background time intervals) exposures
of the RGS1 and RGS2 spectra are 480 ks and 466 ks, respectively.
The 0.4-10 keV PN light curve is shown in Fig. 1. The
data, plotted in 100 s time bins, represent the actual count rate on the
chip, i.e. they are not corrected for the live time of 0.71 of the SW mode. The
source exhibits large amplitude flux variations on all sampled time scales. On
long time scales, the source undergoes large intensity variations by a factor
of ![]() 5 (from
5 (from ![]() 5 counts/s at the start of obs-201 to
5 counts/s at the start of obs-201 to ![]() 24 counts/s at the beginning of obs-601). On shorter time scales of the order of
a few hours we still observe substantial and continuous variability with an
amplitude of the order of
24 counts/s at the beginning of obs-601). On shorter time scales of the order of
a few hours we still observe substantial and continuous variability with an
amplitude of the order of ![]() 2. A detailed analysis of the observed flux
variations will be presented in a forthcoming paper.
2. A detailed analysis of the observed flux
variations will be presented in a forthcoming paper.
3 Spectral analysis of the PN data
Previous studies of PKS 0558-504 have confirmed the presence of spectral components
which are typical of the X-ray spectra of NLS1 galaxies: i) a strong soft
excess below ![]() 2 keV, which appears over the extrapolation of a higher
energy power-law-like spectral component with a slope of
2 keV, which appears over the extrapolation of a higher
energy power-law-like spectral component with a slope of ![]() 2-2.4 (Gliozzi
et al. 2000; O'Brien et al. 2001; Brinkmann et al. 2004), and ii) a smooth
spectrum, with no obvious absorption and/or emission spectral features either at
higher energies or in the soft band. Given the presence of the soft component,
we first investigated the spectral shape of the source spectrum at energies
above 2 keV. We then proceeded to study the full band energy spectrum.
2-2.4 (Gliozzi
et al. 2000; O'Brien et al. 2001; Brinkmann et al. 2004), and ii) a smooth
spectrum, with no obvious absorption and/or emission spectral features either at
higher energies or in the soft band. Given the presence of the soft component,
we first investigated the spectral shape of the source spectrum at energies
above 2 keV. We then proceeded to study the full band energy spectrum.
For the spectral analysis, source counts were grouped with a minimum of 100
counts per energy bin. Spectral fits were performed with the XSPEC
v.12.5.0 software package. The errors on the best-fitting model parameters
represent the 90% confidence limits for one interesting parameter (unless
otherwise stated). The energies of emission or absorption features are given in
the rest frame of the source. We considered a model to provide an acceptable fit
to the data if the quality of the fit is better than the 5% confidence level,
and we accepted that the addition of a model component is significant if the
quality of the fit is improved at more than the 95% confidence level. For the
Galactic absorption we used the value of
![]() cm-2 (Kalberla et al. 2005).
cm-2 (Kalberla et al. 2005).
3.1 High energy power law fits
We first considered the average spectrum from each individual XMM-Newton observation. A simple power law model (PL) fitted well the 2-10 keV spectrum
of all observations, except for obs-301. That spectrum is rather noisy.
Figure 2 shows the best power law model fit for this
observation and the corresponding residuals. A broad, low-amplitude, line-like
feature does appear close to ![]() 6 keV (observers frame), but the addition of
a Gaussian component did not improve the quality of the fit significantly (see
the discussion in the next section). Possible absorption features also appear
around
6 keV (observers frame), but the addition of
a Gaussian component did not improve the quality of the fit significantly (see
the discussion in the next section). Possible absorption features also appear
around ![]() 7 keV. The addition of an EDGE component (in XSPEC
terminology) to the model improved the fit (we got a reduction of
7 keV. The addition of an EDGE component (in XSPEC
terminology) to the model improved the fit (we got a reduction of
![]() of 24.8 for the addition of 2 degrees of freedom, d.o.f.), however, the best-fit
edge energy turned out to be
of 24.8 for the addition of 2 degrees of freedom, d.o.f.), however, the best-fit
edge energy turned out to be ![]() 2.9 keV. It is difficult to spot this
feature in Fig. 2, and we did not detect a similar feature
in any of the average spectra of the other four observations. This fact casts
doubt on the possibility that such an absorption edge is an intrinsic feature in
the spectrum of the source.
2.9 keV. It is difficult to spot this
feature in Fig. 2, and we did not detect a similar feature
in any of the average spectra of the other four observations. This fact casts
doubt on the possibility that such an absorption edge is an intrinsic feature in
the spectrum of the source.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13289fg2}\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg34.png)
|
Figure 2:
Top panel: power law model fit to the total spectrum of obs-301 in the
2-10 keV band. Lower panel: the best-fit residuals plot (residuals are in
terms of |
| Open with DEXTER | |
The PL best-fit results are listed in Table 1. All spectra
show a slope of
![]() .
We did not observe significant
indications of any absorption features in the high energy band spectra. We did
not observe any spectral curvature in the hard energy band either.
Nevertheless, a Comptonisation model (compTT in XSPEC, Titarchuk
1994) provided a nearly identical fit to the data. The main model parameters are
the temperature, T0, of the soft photon input spectrum (which is assumed to
be the Wien part of a black body), the electron plasma temperature, kT, and
optical depth,
.
We did not observe significant
indications of any absorption features in the high energy band spectra. We did
not observe any spectral curvature in the hard energy band either.
Nevertheless, a Comptonisation model (compTT in XSPEC, Titarchuk
1994) provided a nearly identical fit to the data. The main model parameters are
the temperature, T0, of the soft photon input spectrum (which is assumed to
be the Wien part of a black body), the electron plasma temperature, kT, and
optical depth, ![]() .
Their best fit values (
.
Their best fit values (
![]() eV,
eV,
![]() keV, and
keV, and
![]() )
are subject to large uncertainties due to their
inherent degeneracy (in the absence of a the detection of the high energy
cut-off) but, in any case, they are similar to those found for broad line
Seyfert 1 galaxies (e.g. Petrucci et al. 2001).
)
are subject to large uncertainties due to their
inherent degeneracy (in the absence of a the detection of the high energy
cut-off) but, in any case, they are similar to those found for broad line
Seyfert 1 galaxies (e.g. Petrucci et al. 2001).
The average 2-10 keV flux of the source during the XMM-Newton observations is ![]()
![]() erg cm-2 s-1. This implies that PKS 0558-504 was at a rather low flux
state, when compared to its average flux level of
erg cm-2 s-1. This implies that PKS 0558-504 was at a rather low flux
state, when compared to its average flux level of ![]()
![]() erg cm-2 s-1, as determined from its long term RXTE monitoring observations (Gliozzi
et al. 2007). At a distance of 624 Mpc
erg cm-2 s-1, as determined from its long term RXTE monitoring observations (Gliozzi
et al. 2007). At a distance of 624 Mpc ![]() this
flux corresponds to an average luminosity of
this
flux corresponds to an average luminosity of ![]()
![]() erg s-1 during the XMM-Newton observations.
erg s-1 during the XMM-Newton observations.
Table 1: Results from the PL model fits to the 2-10 keV average spectra of the 5 observations.
Table 2: The iron-line best fit parameter values.
3.2 The iron line
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13289fg3.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg57.png)
|
Figure 3: Top panel: the best power law model fit to the total PN spectrum in the 4.5-8 keV band. Lower panel: the best-fit residuals plot. |
| Open with DEXTER | |
The previous XMM-Newton data of PKS 0558-504 yielded low upper limits on the equivalent width of an iron line, either from neutral or ionised material (O'Brien et al. 2001; Brinkmann et al. 2004). The present data are consistent with the results from these studies: the best PL fit residuals to the individual spectra of the five observations do not show clear evidence for the presence of an iron line.
To investigate this issue in a more quantitative way, we re-fitted the five
average spectra of each observation with the PL model in the 4.5-8 keV band. We
fixed the best-fit spectral slope and then added a narrow Gaussian component to
the model (the line width was kept fixed at a value of
![]() eV). The
best-fit results are listed in Table 2. The third column in
this table lists the improvement in the best-fit
eV). The
best-fit results are listed in Table 2. The third column in
this table lists the improvement in the best-fit ![]() (i.e.
(i.e.
![]() )
when we added the Gaussian component to the model. The numbers
in the parentheses indicate the degrees of freedom in the case of the PL model;
the addition of the Gaussian component reduces this number by 2. The small
)
when we added the Gaussian component to the model. The numbers
in the parentheses indicate the degrees of freedom in the case of the PL model;
the addition of the Gaussian component reduces this number by 2. The small
![]() values suggest that the addition of the Gaussian component is
not statistically significant (except perhaps in the case of obs-401). The
numbers in the parenthesis in the fourth column indicate the 90% upper limits
on the equivalent width (EW) of the line. In fact, the best-fit
values suggest that the addition of the Gaussian component is
not statistically significant (except perhaps in the case of obs-401). The
numbers in the parenthesis in the fourth column indicate the 90% upper limits
on the equivalent width (EW) of the line. In fact, the best-fit
![]() values turned out to be close to the starting values we chose. The rather low
90% upper limits imply that if there is an iron line in the energy spectrum of
PKS 0558-504, it is weak.
values turned out to be close to the starting values we chose. The rather low
90% upper limits imply that if there is an iron line in the energy spectrum of
PKS 0558-504, it is weak.
For that reason, we combined the data from all orbits into a single spectrum
and fitted it again with a power law model in the 4.5 to 8 keV energy range.
Figure 3 shows the best power law model fit to the data,
together with the residuals plot. The reduced ![]() value of 767/697 d.o.f.
implies a null hypothesis probability of 3.4%. The residuals indicate a
low-amplitude excess emission around
value of 767/697 d.o.f.
implies a null hypothesis probability of 3.4%. The residuals indicate a
low-amplitude excess emission around ![]() 6 keV. As before, we added a
Gaussian component to the model and repeated the fit (keeping the best-fit
spectral slope fixed). In this case, we also let the line's width,
6 keV. As before, we added a
Gaussian component to the model and repeated the fit (keeping the best-fit
spectral slope fixed). In this case, we also let the line's width, ![]() ,
be
a free parameter. The best-fit results are also listed in Table
2 (the best-fit
,
be
a free parameter. The best-fit results are also listed in Table
2 (the best-fit ![]() value was
0.19+0.24-0.09keV). The line's best-fit energy is indicative of emission from Fe XXV. However,
the large error of the line's equivalent width measurement suggests that the
detection of the line itself is only at the 90% significance level. We
therefore conclude that if there is an iron line in the spectrum of the source
it is very weak (
value was
0.19+0.24-0.09keV). The line's best-fit energy is indicative of emission from Fe XXV. However,
the large error of the line's equivalent width measurement suggests that the
detection of the line itself is only at the 90% significance level. We
therefore conclude that if there is an iron line in the spectrum of the source
it is very weak (
![]() eV), and an indication of emission from ionized
material.
eV), and an indication of emission from ionized
material.
3.3 The full band EPIC-PN spectrum
![\begin{figure}
\par\includegraphics[width=15.6cm,clip]{13289fg4.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg61.png)
|
Figure 4: Top panel: the 0.4-10 keV PN spectra of all observations. Black, open circles indicate the obs-201 spectrum; red, open triangles indicate the obs-301 spectrum, and green, open diamonds indicate the obs-401 spectrum. The obs-501 and obs-601 spectra are plotted with a continuous black and brown line. Some of the spectra are scaled for demonstration reasons (see text for details). The solid line indicates the best PL fit to the obs-201, 2-10 keV spectrum. Lower panel: the ``Data/the best hard band PL model fit'' plots for the same spectra (plotted using the same colour code as in the top panel). |
| Open with DEXTER | |
Various models have been proposed for the ``soft excess'' component in NLS1 galaxies. In PKS 0558-504 in particular, O'Brien et al. (2001) fitted three black body components to this excess, Brinkmann et al. (2004) used an extra Comptonisation component, while Haba et al. (2008) used a multicolour disc black body model. Finally, recent claims about the connection of strong radio loud NLS1 galaxies with BL Lac objects (Yuan et al. 2008) raise the possibility that the X-ray spectra in objects like PKS 0558-504 could be modelled by broken power laws.
To check which of the proposed models provides the best interpretation of the source's X-ray spectrum, we fitted the spectra from the five individual observations with various models. In Fig. 5 we show the data-to-model ratios for fits of four different models. The fits were performed in the 0.4-10 keV band, by keeping the PL spectral slopes fixed at the values listed in Table 1.
In the top panel of Fig. 5 we show the data-to-model ratio
when we used a bremsstrahlung component to account for the soft excess
(``PLBrems'' hereafter, for the combination of a ``hard power law plus a
bremsstrahlung component''). The residuals are similar in all five spectra (for
this reason it is difficult to spot the residuals for the individual spectra in
this panel). The best-fit resulted in a ![]() of 5796 for 5203 d.o.f. and is
formally not acceptable. The residuals show small amplitude absorption
structures near the O I edge and perhaps near
of 5796 for 5203 d.o.f. and is
formally not acceptable. The residuals show small amplitude absorption
structures near the O I edge and perhaps near ![]() 0.7 keV as well
(observers frame).
0.7 keV as well
(observers frame).
In the following panel we present the data-to-model ratio plot for the case for
which we fitted the full band spectrum with a broken PL model (``BKNPL'',
hereafter). For clarity reasons, we plot the data-to-model ratio only for the
obs-201 spectrum in this panel as well as the remaining panels of
Fig. 5. The model residuals are almost identical for the
other spectra as well. We foundthat the fit was slightly worse in this case
(
![]() d.o.f.). The best-fit soft band slope and break energy were
varying between 2.5 and 2.7, and 1.8-2 keV, respectively.
d.o.f.). The best-fit soft band slope and break energy were
varying between 2.5 and 2.7, and 1.8-2 keV, respectively.
In the bottom two panels, we show the data-to-model ratios when we used two
``physical'' models, namely the compTT and DISKBB models in XSPEC, to account for the soft excess. In the case of the compTT+PL model
(
![]() d.o.f.), we first fitted the spectra by letting
d.o.f.), we first fitted the spectra by letting ![]() free to vary. The resulting best-fit values were similar for the five spectra,
and for this reason we repeated the fit by forcing
free to vary. The resulting best-fit values were similar for the five spectra,
and for this reason we repeated the fit by forcing ![]() to be the same in
all cases. The best fit
to be the same in
all cases. The best fit ![]() value turned out to be
value turned out to be ![]() 0.14 keV,
while kT, and
0.14 keV,
while kT, and ![]() were varying between
were varying between ![]() 2-4.4 keV and
2-4.4 keV and ![]() 1.5-2.6,
respectively. In the case of the DISKBB+PL model (
1.5-2.6,
respectively. In the case of the DISKBB+PL model (
![]() d.o.f.), the best-fit temperature at the inner radius was
d.o.f.), the best-fit temperature at the inner radius was ![]() 0.16-0.18 keV. We
also tried models like a combination of two power laws, or a black body plus a
hard band PL, but these models resulted in significantly worse fits.
0.16-0.18 keV. We
also tried models like a combination of two power laws, or a black body plus a
hard band PL, but these models resulted in significantly worse fits.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13289f5-1.eps}\par\includegraphics[width=8.4cm,clip]{13289f5-2.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg66.png)
|
Figure 5: From top to bottom: data-to-model ratio in the 0.4-2 keV band for the best fits of a Brems+PL, a broken PL, a compTT+PL, and a DISKBB+PL model. In the top panel, we plot the data for the the average spectrum of each XMM-Newton observation (black, red, green, blue and brown points have been used for the obs-201, obs-301, obs-401, obs-501, and obs-601 spectra, respectively). For clarity reasons, in the following panels, we plot the data for the obs-201 spectrum only (the data-to-model ratios are very similar for the other spectra as well). |
| Open with DEXTER | |
The amplitude of the residuals becomes larger at energies below 0.4 keV. Using
the whole energy band, i.e. ![]() 0.2 keV, yielded much larger best fit
0.2 keV, yielded much larger best fit
![]() values. This indicates either a failure of the models at the
lowest energies, or an inherent detector calibration uncertainty. To check the
possibility of calibration uncertainties, we additionally performed fits (using
the PLBrems model) with the single events (PATTERN = 0) of the PN and with the
MOS1 data. Open circles, open squares and the filled diamonds in
Fig. 6 indicate the 0.25-10 keV best-fit data-to-model
residuals in the case of obs-601 for the MOS1, the single, and the
single+double PN events spectra, respectively (we obtained similar results for
the PN and MOS1 spectra of the other observations as well). The residuals for
the single and single+double PN spectra are quite similar. On the other hand,
there are differences between the PN and the MOS1 residuals below
values. This indicates either a failure of the models at the
lowest energies, or an inherent detector calibration uncertainty. To check the
possibility of calibration uncertainties, we additionally performed fits (using
the PLBrems model) with the single events (PATTERN = 0) of the PN and with the
MOS1 data. Open circles, open squares and the filled diamonds in
Fig. 6 indicate the 0.25-10 keV best-fit data-to-model
residuals in the case of obs-601 for the MOS1, the single, and the
single+double PN events spectra, respectively (we obtained similar results for
the PN and MOS1 spectra of the other observations as well). The residuals for
the single and single+double PN spectra are quite similar. On the other hand,
there are differences between the PN and the MOS1 residuals below ![]() 0.6 keV. At energies <0.4 keV, the MOS1 and PN residuals are quite different.
Their max-to-min difference is of the order of
0.6 keV. At energies <0.4 keV, the MOS1 and PN residuals are quite different.
Their max-to-min difference is of the order of ![]() 10%, a result which
indicates that there exist unresolved detector calibration uncertainties at
these low energies (it is for this reason that we considered the PN spectra at
energies above 0.4 keV).
10%, a result which
indicates that there exist unresolved detector calibration uncertainties at
these low energies (it is for this reason that we considered the PN spectra at
energies above 0.4 keV).
At higher energies, the difference between the MOS1 and the PN spectra is less
than ![]() 5% except for the 0.5-0.6 keV band (where we expect the
instrumental and the Galactic oxygen edges to appear). This result implies that
any ``dips'' in the residual plots at these energies (like the ones shown in
Fig. 5) may be due to additional calibration uncertainties.
Furthermore, the compTT+PL and DISKBB+PL residual plots in
Fig. 5 exhibit a further shallow flux deficit around
5% except for the 0.5-0.6 keV band (where we expect the
instrumental and the Galactic oxygen edges to appear). This result implies that
any ``dips'' in the residual plots at these energies (like the ones shown in
Fig. 5) may be due to additional calibration uncertainties.
Furthermore, the compTT+PL and DISKBB+PL residual plots in
Fig. 5 exhibit a further shallow flux deficit around ![]() 0.7 keV, which may correspond to low amplitude absorption features intrinsic to
the source. This possibility can be investigated with the study of the RGS
spectrum, which we describe below.
0.7 keV, which may correspond to low amplitude absorption features intrinsic to
the source. This possibility can be investigated with the study of the RGS
spectrum, which we describe below.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13289fg6.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg69.png)
|
Figure 6: ``Data-to-PLBrems model'' ratio in the 0.25-2 keV band, for the single PN events (open squares), single plus double PN events (filled circles), and the MOS1 spectra (open circles) of obs-601. |
| Open with DEXTER | |
3.4 The RGS data
We used the fitting package Sherpa, of the Chandra Interactive Analysis of
Observation (Ciao) software (vs. 4.1.2), to simultaneously fit the total
RGS1 and RGS2 spectra of PKS 0558-504. Both the RGS1 and RGS2 spectra are grouped at a
resolution of 20 mÅ (![]() 0.5 eV at 0.5 keV), thus allowing for three bins
for a RGS resolution element. For both the RGS1 and the RGS2 the photon count
rate of the background spectrum becomes comparable to the background-subtracted
source count rate at
0.5 eV at 0.5 keV), thus allowing for three bins
for a RGS resolution element. For both the RGS1 and the RGS2 the photon count
rate of the background spectrum becomes comparable to the background-subtracted
source count rate at ![]() keV (
keV (
![]() Å), and
Å), and ![]() keV
(
keV
(
![]() Å). Moreover, due to failures of two different read-out
detector chips early in the mission, both the RGS1 and the RGS2 lack response in
two different spectral intervals:
Å). Moreover, due to failures of two different read-out
detector chips early in the mission, both the RGS1 and the RGS2 lack response in
two different spectral intervals: ![]() 0.9-1.2 keV (RGS1) and
0.9-1.2 keV (RGS1) and ![]() 0.5-0.7 keV (RGS2). Finally, a visual inspection of the RGS2 spectrum and its effective
area revealed several regions where the modelling of effective area features
failed to properly reproduce the data. These were mostly concentrated at
0.5-0.7 keV (RGS2). Finally, a visual inspection of the RGS2 spectrum and its effective
area revealed several regions where the modelling of effective area features
failed to properly reproduce the data. These were mostly concentrated at ![]() keV and in two narrow regions at
keV and in two narrow regions at
![]() keV and
keV and
![]() keV. We
therefore considered the following two RGS1 and RGS2 spectral intervals for
spectral fitting purpose:
(0.4-0.9) + (1.2-2)] keV and
(0.69-0.82) +
(0.85-1.07) + (1.09-2)] keV, respectively.
keV. We
therefore considered the following two RGS1 and RGS2 spectral intervals for
spectral fitting purpose:
(0.4-0.9) + (1.2-2)] keV and
(0.69-0.82) +
(0.85-1.07) + (1.09-2)] keV, respectively.
Due to the EPIC-RGS cross calibration problems, the RGS data cannot be compared directly to the PN best-fit models. However, this is not a serious problem, as our main aim in this work is to identify any strong emission and/or absorption features in the RGS spectra that should be included in the models we use to fit the PN spectra. To this end, all we need is to model the continuum in the RGS spectrum as accurately as possible and search for any remaining residuals.
We first fitted a simple power law attenuated by neutral absorption, set to be
at least equal to the Galactic column along the line of sight. Although the fit
is statistically acceptable,
![]() d.o.f., a visual inspection of the
broad band 0.4-2 keV residuals shows a flattening at energies higher than
d.o.f., a visual inspection of the
broad band 0.4-2 keV residuals shows a flattening at energies higher than
![]() 1.2 keV, both in the RGS1 and RGS2. We therefore replaced the PL with a
broken power law model. This fitted the 0.4-2 keV continuum in the RGS
spectra very well (
1.2 keV, both in the RGS1 and RGS2. We therefore replaced the PL with a
broken power law model. This fitted the 0.4-2 keV continuum in the RGS
spectra very well (
![]() d.o.f.). The best-fit residuals are shown in
Fig. 7.
d.o.f.). The best-fit residuals are shown in
Fig. 7.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13289fg7.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg79.png)
|
Figure 7: RGS1 ( top panel) and RGS2 ( bottom panel) residuals to a broken power law fit attenuated by Galactic absorption. For clarity reasons, the data in this figure are binned by a factor of 8 when compared to the unbinned RGS pipeline data. Consequently, the spectra plotted in this figure are grouped at about 40 Å per resolution element, i.e. at about 1.5 bins per RGS resolution element. |
| Open with DEXTER | |
The residuals do not show any significant spectral features identifiable with
either absorption or emission transitions within ![]() km s-1 from the
systemic redshift of PKS 0558-504, that should be considered in the PN spectral
fits. In particular there are no signatures of ionised material (i.e. the
so-called ``warm absorbers''; WA) which are observed in other Seyferts. We tried
to investigate this in a more quantitative way by adding PHASE, i.e. the
warm absorber model of Krongold et al. (2003), to the broken power law model.
We fixed the turbulence velocity of the absorber to 200 km s-1 (unresolved
in the RGS), and left the ionisation parameter U (defined as the ratio between
the photon volume density at the location of the absorbing cloud and the
electron density in the cloud) and the equivalent column density of the
absorber,
km s-1 from the
systemic redshift of PKS 0558-504, that should be considered in the PN spectral
fits. In particular there are no signatures of ionised material (i.e. the
so-called ``warm absorbers''; WA) which are observed in other Seyferts. We tried
to investigate this in a more quantitative way by adding PHASE, i.e. the
warm absorber model of Krongold et al. (2003), to the broken power law model.
We fixed the turbulence velocity of the absorber to 200 km s-1 (unresolved
in the RGS), and left the ionisation parameter U (defined as the ratio between
the photon volume density at the location of the absorbing cloud and the
electron density in the cloud) and the equivalent column density of the
absorber, ![]() ,
free to vary. The redshift of the absorber was fixed to the
systemic redshift of PKS 0558-504, and its outflow/inflow velocity was allowed
to vary between -5000 km s-1 and +5000 km s-1.
,
free to vary. The redshift of the absorber was fixed to the
systemic redshift of PKS 0558-504, and its outflow/inflow velocity was allowed
to vary between -5000 km s-1 and +5000 km s-1.
The best model fit was achieved for log
![]() (the lowest tabulated value in
the model) and log(U)=1.37. At these column densities and for this ionisation
parameter, the gas is already fully transparent in the RGS band. The best-fit
parameter values are not well determined, but the allowed parameter values (for
example log(U)>2 for log(
(the lowest tabulated value in
the model) and log(U)=1.37. At these column densities and for this ionisation
parameter, the gas is already fully transparent in the RGS band. The best-fit
parameter values are not well determined, but the allowed parameter values (for
example log(U)>2 for log(![]() ) = 20-21, and log(U)>2.3 if log
) = 20-21, and log(U)>2.3 if log
![]() -22)
are incompatible with the parameter space which would be normally occupied by a
WA (i.e. log
-22)
are incompatible with the parameter space which would be normally occupied by a
WA (i.e. log
![]() -22 and log(U) < 1.1-2). We therefore conclude that the
presence of a warm absorber is not required by these data. A more detailed study
of the RGS spectrum of the source is presented in Nicastro et al. (submitted to
ApJ).
-22 and log(U) < 1.1-2). We therefore conclude that the
presence of a warm absorber is not required by these data. A more detailed study
of the RGS spectrum of the source is presented in Nicastro et al. (submitted to
ApJ).
4 Spectral variability
The discussion in the above sections suggests that unaccounted detector calibration
inaccuracies may be responsible for the ![]() 0.5-0.6 keV ``dip'' in the residual
plots shown in Fig. 5. However, such inaccuracies most probably
cannot explain the remaining residuals, such as the the ``wavy'' pattern we see in
the two lower panels of the same figure for example. The absence of warm absorbing
signatures cannot explain them either.
0.5-0.6 keV ``dip'' in the residual
plots shown in Fig. 5. However, such inaccuracies most probably
cannot explain the remaining residuals, such as the the ``wavy'' pattern we see in
the two lower panels of the same figure for example. The absence of warm absorbing
signatures cannot explain them either.
Before reaching conclusions regarding the quality of the model fits to the average spectra of each observation, we have to consider the fact that, as shown in Fig. 1, the source exhibits continuous, large amplitude flux variations on both short and long time scales. If these flux variations are associated with spectral variations as well (as it is usually the case in Seyfert galaxies), then model fitting of some kind of ``average'' spectrum may yield dubious results.
To illustrate the presence of spectral variations during the XMM-Newton observations,
we estimated the ratio of the 2-10 keV over the 0.4-1 keV count rates (i.e.
the ``hardness ratio'', or simply HR), using light curves binned in 100 and 1000 s. The top panel in Fig. 8 shows the HR values for the
obs-601. The respective light curve is plotted in the lower panel. The first
result from this plot is that the HR does not stay constant, i.e., the source
exhibits significant spectral variations, although of an amplitude smaller than
that of the flux variations: the max-to-min ratio for the HR values is ![]() 1.4, as opposed to
1.4, as opposed to ![]() 3.3 for that of the observed count rates.
3.3 for that of the observed count rates.
There is also an indication that the spectral variations are anti-correlated with the flux variations. For example, approximately 7-20 ks after the start of obs-601 the flux increases while HR decreases, and in the next 20 ks HR increased while the total source flux decreased. This ``HR-flux'' anti-correlation is not ``perfect'' though. For example, around 95-105 ks after the start of the observation, HR is positively correlated with the source flux: they both decrease with time. A similar behaviour (i.e. significant HR variations, which are mainly anti-correlated with flux) is seen in the other observations as well (a detailed study of the spectral variability of the source with the use of HR plots, together with a cross-correlation analysis, will be presented in a forthcoming paper).
5 Time resolved spectroscopy
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13289fg8.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg84.png)
|
Figure 8:
Top panel: HR plotted as a function of time (obs-601). Points shown in
grey indicate the HR using bins of the size of 100 s, while open diamonds
indicate the HR values using bins of the size of 1000 s (for clarity reasons
errors in the latter case are not plotted; they are of the order of |
| Open with DEXTER | |
Regarding the hard band (i.e. 2-10 keV) spectra, a PL model fitted them well.
However, it does not provide an acceptable fit to the 0.4-2 keV band as well. A
soft excess emission component was almost always present at energies below ![]() 2 keV. We therefore used the PLBrems model to fit the full band spectra. The
model fit was first performed in the 2-10 keV band. We then kept the PL slope
and normalisation fixed at their best-fit values when we fit the full band
spectrum.
2 keV. We therefore used the PLBrems model to fit the full band spectra. The
model fit was first performed in the 2-10 keV band. We then kept the PL slope
and normalisation fixed at their best-fit values when we fit the full band
spectrum.
The quality of this model fit was statistically acceptable in all cases: the
mean reduced ![]() of all 78 fitted spectra is
of all 78 fitted spectra is
![]() ,
with a standard deviation of
,
with a standard deviation of
![]() .
Figure 9
shows one of the worst PLBrems fits (
.
Figure 9
shows one of the worst PLBrems fits (
![]() d.o.f.); the data
shown correspond to the time interval between
d.o.f.); the data
shown correspond to the time interval between ![]() 51-70 ks after the
start of obs-301. The dotted lines in the top panel of this figure indicate the
PL component (
51-70 ks after the
start of obs-301. The dotted lines in the top panel of this figure indicate the
PL component (
![]() )
and the bremsstrahlung emission of
)
and the bremsstrahlung emission of ![]() 0.16 keV which best fitted the spectrum. In the bottom panel we show the contribution
to the total
0.16 keV which best fitted the spectrum. In the bottom panel we show the contribution
to the total ![]() per spectral bin. The residuals plot does not indicate
any systematic large amplitude deviations between the data and the best-fit
model. We reached a similar conclusion when we investigated the residual plots
for all the other spectra as well.
per spectral bin. The residuals plot does not indicate
any systematic large amplitude deviations between the data and the best-fit
model. We reached a similar conclusion when we investigated the residual plots
for all the other spectra as well.
Although bremsstrahlung emission cannot account for the soft excess emission in
PKS 0558-504 (if that were the case we would expect to detect a plethora of emission
lines in the RGS spectrum of the source) our results indicate that this model
can adequately parametrise the shape of this component. We therefore decided to
use the PLBrems best-fit results to study the spectral variability properties of
the source. In particular, we used the best PL spectral slope, ![]() ,
as a
representation of the hard band spectral shape, and the (un-absorbed) 2-10 keV
and 0.4-1 keV PL flux (Flux
,
as a
representation of the hard band spectral shape, and the (un-absorbed) 2-10 keV
and 0.4-1 keV PL flux (Flux
![]() and Flux
and Flux
![]() )
as a measure of the power law continuum flux in the hard
and soft bands, respectively. We also used the (un-absorbed) 0.4-1 keV flux of
the bremsstrahlung spectral component (Flux
)
as a measure of the power law continuum flux in the hard
and soft bands, respectively. We also used the (un-absorbed) 0.4-1 keV flux of
the bremsstrahlung spectral component (Flux
![]() )
as a representative
of the soft excess flux in this object (i.e. of the flux of the excess emission
on top of the hard band PL component, which is assumed to extend down to
)
as a representative
of the soft excess flux in this object (i.e. of the flux of the excess emission
on top of the hard band PL component, which is assumed to extend down to ![]() 0.4 keV with the same slope), and the Brems temperature, kT, as a
representative of the soft excess shape.
0.4 keV with the same slope), and the Brems temperature, kT, as a
representative of the soft excess shape.
As a simple ``sanity'' check that our model-fitting results agree with the
observed variations, Fig. 10 shows the ``total'' model flux
(i.e. the sum of Flux
![]() ,
Flux
,
Flux
![]() and Flux
and Flux
![]() )
plotted as a function of the mean, 0.4-10 keV count
rate of each segment. The expected one-to-one relation between these two
quantities is obvious from this plot.
)
plotted as a function of the mean, 0.4-10 keV count
rate of each segment. The expected one-to-one relation between these two
quantities is obvious from this plot.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{13289f9.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg91.png)
|
Figure 9: Plot of one of the worst PLBrems fits ( top panel), and of the respective residuals ( bottom panel) to the PN data of one of the individual spectra (see Sect. 5 for details). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13289f10.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg94.png)
|
Figure 10:
The ``total'' model flux (i.e. Flux
|
| Open with DEXTER | |
5.1 The hard band spectral variability results
The top panel in Fig. 11 displays ![]() as a function of time
measured from the start of the XMM-Newton observations. The power law spectral slope
is significantly variable; we find that
as a function of time
measured from the start of the XMM-Newton observations. The power law spectral slope
is significantly variable; we find that
![]() d.o.f., when we fit a
constant to the ``
d.o.f., when we fit a
constant to the ``![]() vs time'' plot. The average spectral slope is
vs time'' plot. The average spectral slope is
![]() .
The individual spectral slopes vary between
.
The individual spectral slopes vary between
![]() 2-2.3, which implies a max-to-min variability amplitude of
2-2.3, which implies a max-to-min variability amplitude of ![]() .
The
fractional root mean square variability amplitude (corrected for the
experimental noise) of the spectral slope variations is
.
The
fractional root mean square variability amplitude (corrected for the
experimental noise) of the spectral slope variations is
![]()
![]() . The small amplitude
. The small amplitude ![]() variations indicate that
the observed count rate variability is mainly caused by variations of the PL
normalisation. Figure 12 shows that this is indeed the
case.
variations indicate that
the observed count rate variability is mainly caused by variations of the PL
normalisation. Figure 12 shows that this is indeed the
case.
Filled and open circles in the lower panel of Fig. 11 indicate
Flux
![]() and Flux
and Flux
![]() .
A
comparison between the top and bottom panels shows that the spectral slope and
flux variations are highly correlated: the spectrum becomes steeper with
increasing flux. This correlation became clearer when we plotted
.
A
comparison between the top and bottom panels shows that the spectral slope and
flux variations are highly correlated: the spectrum becomes steeper with
increasing flux. This correlation became clearer when we plotted ![]() as a
function of the observed 0.4-10 keV count rate (top panel in
Fig. 13). This is the first time that such a positive
spectral-flux variability correlation (which is commonly detected in other
nearby Seyferts) is detected for this source.
as a
function of the observed 0.4-10 keV count rate (top panel in
Fig. 13). This is the first time that such a positive
spectral-flux variability correlation (which is commonly detected in other
nearby Seyferts) is detected for this source.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13289f11.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg100.png)
|
Figure 11:
Top panel: the best-fit spectral slope of the individual spectra of the
source, plotted as a function of time (measured from the start of the XMM-Newton observations). Lower panel: filled, open, and crosses indicate Flux
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13289f12.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg101.png)
|
Figure 12: The best PL model fit normalisation values plotted as a function of the observed 0.4-10 keV count rate. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13289f13.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg102.png)
|
Figure 13:
Top panel: the best-fit spectral slope of the individual spectra of the
source, plotted as the function of the 0.4-10 keV count rate. Filled
``up-triangles'' and open ``down-triangles'' indicate the
|
| Open with DEXTER | |
Filled (open) triangles in the top panel of Fig. 13 indicate the
spectral slope during the periods when the source flux increases (decreases),
![]() (
(
![]() ). On average, the source spectrum
appears to be steeper when the flux increases:
). On average, the source spectrum
appears to be steeper when the flux increases:
![]() and
and
![]() .
But this
difference is not highly significant (
.
But this
difference is not highly significant (
![]() .
The solid and dashed lines in the same panel indicate the best line fits to the
(
.
The solid and dashed lines in the same panel indicate the best line fits to the
(
![]() ,
CR) and the (
,
CR) and the (
![]() ,
CR) data sets,
respectively. The best-fit lines also imply that, on average, most of the time
,
CR) data sets,
respectively. The best-fit lines also imply that, on average, most of the time
![]() is steeper than
is steeper than
![]() ,
but the difference of the best-fit line parameters is not statistically significant. We therefore cannot
rule out that the shape of the X-ray continuum varies with flux in a similar
way, irrespective of whether the source flux increases or decreases.
,
but the difference of the best-fit line parameters is not statistically significant. We therefore cannot
rule out that the shape of the X-ray continuum varies with flux in a similar
way, irrespective of whether the source flux increases or decreases.
5.2 The soft excess spectral variability results
Points plotted with
crosses in the lower panel of Fig. 11 indicate Flux
![]() ,
plotted as a function of time. The average soft excess flux is
,
plotted as a function of time. The average soft excess flux is
![]() erg cm-2 s-1, which is smaller than the average PL flux in the
same band (
erg cm-2 s-1, which is smaller than the average PL flux in the
same band (
![]() erg cm-2 s-1).
Furthermore, the soft excess flux is significantly variable (
erg cm-2 s-1).
Furthermore, the soft excess flux is significantly variable (
![]() d.o.f.), but its average amplitude is smaller (
d.o.f.), but its average amplitude is smaller (
![]() %)
than the average PL variability amplitude in the 0.4-1 keV band (
%)
than the average PL variability amplitude in the 0.4-1 keV band (
![]() .
.
The shape of the soft excess is also variable. The best-fit kT values are not
consistent with the hypothesis of a constant temperature (
![]() d.o.f.).
These variations are of a rather small amplitude (
d.o.f.).
These variations are of a rather small amplitude (
![]() ). Crosses in the bottom panel of Fig. 13
indicate the best-fit kT values plotted as function of CR. The soft excess
shape appears to be broadly correlated with the source flux: the temperature
increases with increasing flux. Application of the Kendall's
). Crosses in the bottom panel of Fig. 13
indicate the best-fit kT values plotted as function of CR. The soft excess
shape appears to be broadly correlated with the source flux: the temperature
increases with increasing flux. Application of the Kendall's ![]() test
resulted in a value of
test
resulted in a value of ![]() ,
which implies a rather weak, but
significant, correlation between kT and the source flux (the probability of
the null hypothesis is less than
,
which implies a rather weak, but
significant, correlation between kT and the source flux (the probability of
the null hypothesis is less than
![]() ). We conclude that as the
source flux increases kT increases as well, i.e. the soft excess ``shifts'' to
higher energies. The average kT is
). We conclude that as the
source flux increases kT increases as well, i.e. the soft excess ``shifts'' to
higher energies. The average kT is
![]() keV, which remains the same
irrespective of whether the flux is increasing or decreasing. The best line
fits to the (
keV, which remains the same
irrespective of whether the flux is increasing or decreasing. The best line
fits to the (
![]() ,
CR) and the (
,
CR) and the (
![]() ,
CR) data sets are
also almost identical. We therefore conclude that the shape of the soft excess
varies with flux in a similar way, irrespective of whether the source flux
increases or decreases.
,
CR) data sets are
also almost identical. We therefore conclude that the shape of the soft excess
varies with flux in a similar way, irrespective of whether the source flux
increases or decreases.
5.3 Cross-correlation between soft excess and hard power law flux
The
bottom panel in Fig. 11 indicates that the PL and Brems flux
light curves are not highly correlated. To investigate this issue further, we
split up all five observations in segments of 2000 s long (278 in total) and
fitted their 0.4-10 keV band spectra with the PLBrems model. As above, the
2-10 keV band was first fitted with a PL model, and we kept the best-fit
![]() and PL normalisation values fixed when we added the Brems component to
fit the full band spectra. The model fitted all spectra well, and using the
best-fit model parameter values we calculated Flux
and PL normalisation values fixed when we added the Brems component to
fit the full band spectra. The model fitted all spectra well, and using the
best-fit model parameter values we calculated Flux
![]() ,
Flux
,
Flux
![]() ,
and Flux
,
and Flux
![]() .
.
We determined the cross-correlation between the PL and Brems flux light curves
using the ``Discrete Correlation Function'' (DCF) method of Edelson & Krolik
(1988). The DCF was calculated using lags of size 2000 s and in a way that a
significant correlation at positive lags will indicate that the Flux![]() variations are leading those in the Flux
variations are leading those in the Flux
![]() light curve. The
results are plotted in the top panel of Fig. 14, in the case of
the DCF between the Flux
light curve. The
results are plotted in the top panel of Fig. 14, in the case of
the DCF between the Flux
![]() and Flux
and Flux
![]() .
The maximum DCF amplitude reaches a value of DCF
.
The maximum DCF amplitude reaches a value of DCF
![]() at a lag of
lag
at a lag of
lag
![]() ks (the results are similar when we cross-correlated
Flux
ks (the results are similar when we cross-correlated
Flux
![]() and Flux
and Flux
![]() ,
except that DCF
,
except that DCF
![]() in this case).
in this case).
The DCF
![]() value of
value of ![]() 0.6 implies that the hard band continuum
and the soft excess flux variations are weakly correlated. The bottom panel in
Fig. 14 shows the Flux
0.6 implies that the hard band continuum
and the soft excess flux variations are weakly correlated. The bottom panel in
Fig. 14 shows the Flux
![]() and
Flux
and
Flux
![]() light curves (open squares and grey continuous line,
respectively), normalised to their mean. The soft excess light curve is shifted
by +20 ks, and we have plotted only these parts of the light curves which
overlap (i.e., those light curve parts which correspond to the estimation DCF
at lag =-20 ks). This plot clarifies why the correlation between the hard
band continuum and the soft excess variations is just moderate. The observed
variations agree reasonably well during obs-401, 501 and 601. But the soft and
hard band fluxes are not correlated during obs-301, while the situation is
unclear for obs-201. Furthermore, the difference in the variability amplitude
(even in those cases when the correlation is reasonably good) contributes to the
decrease in the DCF
light curves (open squares and grey continuous line,
respectively), normalised to their mean. The soft excess light curve is shifted
by +20 ks, and we have plotted only these parts of the light curves which
overlap (i.e., those light curve parts which correspond to the estimation DCF
at lag =-20 ks). This plot clarifies why the correlation between the hard
band continuum and the soft excess variations is just moderate. The observed
variations agree reasonably well during obs-401, 501 and 601. But the soft and
hard band fluxes are not correlated during obs-301, while the situation is
unclear for obs-201. Furthermore, the difference in the variability amplitude
(even in those cases when the correlation is reasonably good) contributes to the
decrease in the DCF
![]() amplitude. In any case, even if the two light
curves are indeed intrinsically correlated, the negative time lag implies that
it is the soft excess flux variations which lead the hard band continuum
variations.
amplitude. In any case, even if the two light
curves are indeed intrinsically correlated, the negative time lag implies that
it is the soft excess flux variations which lead the hard band continuum
variations.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13289f14.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg123.png)
|
Figure 14:
Top panel: the DCF between Flux
|
| Open with DEXTER | |
6 The full band PN spectrum revisited
Given the complex spectral variability of the source, we chose seven of the 78
segments into which we originally split the total XMM-Newton observation, based on
the following criteria: i) HR remained constant during the exposure of each
segment, ii) the average count rate is different and adequately samples the
observed flux variability amplitude of the source, and iii) there are enough
photons in the spectra to ensure a sufficiently high signal to noise ratio. The
first and second columns in Table 3 list the start time, the
exposure time, and the average count rate of the segments we chose (segments are
listed in a decreasing order of the average count rate). There are more than
![]() 60 000 photons in the 0.4-10 keV band of each one of these spectra.
60 000 photons in the 0.4-10 keV band of each one of these spectra.
First, we fitted the 2-10 keV spectrum of each segment with a PL model
(best-fit slopes,
![]() ,
are listed in the third column of
Table 3), which fitted the high energy part of the spectra
well. Then we kept
,
are listed in the third column of
Table 3), which fitted the high energy part of the spectra
well. Then we kept
![]() and the best-fit PL normalisation fixed,
and we fitted the 0.4-10 keV spectra with the following more physically
motivated additional models:
and the best-fit PL normalisation fixed,
and we fitted the 0.4-10 keV spectra with the following more physically
motivated additional models:
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13289f15.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg125.png)
|
Figure 15: From top to bottom: data-to-model ratio in the 0.4-2 keV band for the best fits of a DISKBB+PL, REFLION+PL, a broken PL, and a NTHCOMP+PL model to the seven individual spectra we considered in Sect. 6. The residuals for the spectra listed in Table 3 are plotted with points in black, red, green, blue, brown, magenta and orange, respectively. It is difficult to identify the individual residual plots for each spectrum, because they are similar for all of them. For clarity reasons, in the following panels we plot the best-fit residuals in the case of the spectrum of the fourth segment listed in Table 3 only. The residuals are similar for the other spectra as well. |
| Open with DEXTER | |
Table 3:
Results from the spectral fits of the
NTHCOMP+PL model to the 0.4-10 keV spectra of the seven short segments (see
section 6 for details), assuming the same electron temperature (
![]() keV), and disc-black body seed photon temperature (
keV), and disc-black body seed photon temperature (
![]() keV), in all cases.
keV), in all cases.
- a)
- a standard accretion disc, multi black body spectrum, i.e. DISKBB. The
best-fit temperature at the inner disc radius,
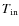 ,
turned out to be
similar in all cases. We therefore re-fitted the spectra simultaneously by
keeping
,
turned out to be
similar in all cases. We therefore re-fitted the spectra simultaneously by
keeping
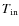 the same for all seven spectra. The model gave a poor fit
to the data (
the same for all seven spectra. The model gave a poor fit
to the data (
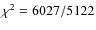 d.o.f.). The best-fit residuals are plotted in the
top panel of Fig. 15. They are plotted with points in black,
red, green, blue, brown, magenta and orange for the spectra as listed in
Table 3. They are very similar for all spectra, and for that reason it is
difficult to spot the residuals for each spectrum in this panel;
d.o.f.). The best-fit residuals are plotted in the
top panel of Fig. 15. They are plotted with points in black,
red, green, blue, brown, magenta and orange for the spectra as listed in
Table 3. They are very similar for all spectra, and for that reason it is
difficult to spot the residuals for each spectrum in this panel;
- b)
- a relativistically blurred photo-ionised reflection model. We used the model
of Ross & Fabian (2005) (which is available as an additional table model, REFLION, in XSPEC), in which a semi-infinite slab of optically thick cold
gas of a constant density is illuminated by a PL continuum. Although we did not
detect any significant evidence for disc reflection in the hard band spectrum
of the source, we considered this model, because strong blurring effects from
the relativistic accretion disc can smear the iron line almost completely and at
the same time result in a featureless soft excess emission. For each spectrum,
we kept the PL continuum slope fixed at the
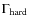 values listed
in Table 3, and we added the illuminating and reflected
components (with the amount of each free to vary). To simulate the blurring from
the disc, we convolved the total emission with a Laor (1991) line profile (KDBLUR model in XSPEC). We fitted the seven spectra simultaneously, with
the same iron abundance of the disc (relative to solar). We also fixed the inner
radius of the Laor profile to be 1.235 gravitational radii (the smallest radius
allowed in the case of a maximally rotating BH), and we also assumed a common
emissivity profile and the disc's inclination angle. The best-fit values were:
emissivity index
values listed
in Table 3, and we added the illuminating and reflected
components (with the amount of each free to vary). To simulate the blurring from
the disc, we convolved the total emission with a Laor (1991) line profile (KDBLUR model in XSPEC). We fitted the seven spectra simultaneously, with
the same iron abundance of the disc (relative to solar). We also fixed the inner
radius of the Laor profile to be 1.235 gravitational radii (the smallest radius
allowed in the case of a maximally rotating BH), and we also assumed a common
emissivity profile and the disc's inclination angle. The best-fit values were:
emissivity index  10 (which is the maximum value allowed in KDBLUR), inclination
10 (which is the maximum value allowed in KDBLUR), inclination  72 degrees, and iron abundance
72 degrees, and iron abundance  1.8. The
ionization parameter of the gas was decreasing from
1.8. The
ionization parameter of the gas was decreasing from
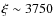 to
to
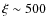 for the highest to the lowest flux spectrum, respectively. The final
best model fit was very poor (
for the highest to the lowest flux spectrum, respectively. The final
best model fit was very poor (
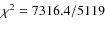 d.o.f.). In the second panel of
Fig. 15, we plot the best-fit residuals in the case of the
spectrum of the fourth segment listed in Table 3 only. The
residuals are similar for the other spectra as well, and for clarity reasons we
do not plot them;
d.o.f.). In the second panel of
Fig. 15, we plot the best-fit residuals in the case of the
spectrum of the fourth segment listed in Table 3 only. The
residuals are similar for the other spectra as well, and for clarity reasons we
do not plot them;
- c)
- a BKNPL model. This model is frequently used to parametrise the X-ray
spectra of BL Lac objects (see e.g. Brinkmann et al. 2005). The spectra were
fitted simultaneously by keeping the hard band slope fixed at
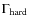 .
The best-fit ``break energy'',
.
The best-fit ``break energy'',
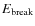 ,
turned out to be
,
turned out to be  2 keV in all cases, except for the highest flux spectrum, where
2 keV in all cases, except for the highest flux spectrum, where
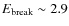 keV. The best-fit slope at soft energies was decreasing form
keV. The best-fit slope at soft energies was decreasing form
 2.7 to
2.7 to  2.5, from the low to the high flux spectra. The best model
fit is statistically acceptable in this case (
2.5, from the low to the high flux spectra. The best model
fit is statistically acceptable in this case (
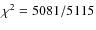 d.o.f.). The data
plotted in the third panel of Fig. 15 indicate the best-fit
residuals in the case of the spectrum of the fourth segment listed in
Table 3. The residuals have a similar shape and amplitude in
the other spectra as well;
d.o.f.). The data
plotted in the third panel of Fig. 15 indicate the best-fit
residuals in the case of the spectrum of the fourth segment listed in
Table 3. The residuals have a similar shape and amplitude in
the other spectra as well;
- d)
- a low-temperature Comptonisation model. We first fitted the spectra
individually, using the compTT model. The best-fit
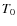 and
and 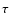 values turned out to be quite similar for all spectra. For that reason, we
re-fitted the spectra simultaneously, assuming the same
values turned out to be quite similar for all spectra. For that reason, we
re-fitted the spectra simultaneously, assuming the same 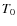 and
and 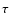 .
The resulting best-fit electron temperature values were increasing from
.
The resulting best-fit electron temperature values were increasing from
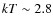 keV, in the case of the largest flux spectrum, to
keV, in the case of the largest flux spectrum, to  5.4 keV, for the
lowest flux spectrum. The fit was statistically acceptable, with a
5.4 keV, for the
lowest flux spectrum. The fit was statistically acceptable, with a 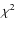 value of 5124 for 5120 d.o.f. However, the best-fit residuals plot was
qualitatively similar to the compTT+PL model residuals plotted in
Fig. 5: they had a similar ``wavy'' pattern, with a deficit
around 0.5-0.7 keV, although of significantly smaller amplitude.
value of 5124 for 5120 d.o.f. However, the best-fit residuals plot was
qualitatively similar to the compTT+PL model residuals plotted in
Fig. 5: they had a similar ``wavy'' pattern, with a deficit
around 0.5-0.7 keV, although of significantly smaller amplitude.
To further investigate the issue of low-temperature Comptonisation, we also
considered the model NTHCOMP in XSPEC (Zycki et al. 1999),
which also describes the continuum shape from thermal Comptonisation. The
parameters of the model are: a) the seed photon temperature,
![]() ,
b) the electron temperature,
,
b) the electron temperature,
![]() ,
and c) the asymptotic power law
photon index,
,
and c) the asymptotic power law
photon index,
![]() (which is set by the combination of the
electron scattering optical depth and
(which is set by the combination of the
electron scattering optical depth and
![]() ). We first fitted the seven
spectra separately (assuming a disc-black body soft photon input). We noticed
that the individual best-fit
). We first fitted the seven
spectra separately (assuming a disc-black body soft photon input). We noticed
that the individual best-fit
![]() and
and
![]() values were
similar. We therefore re-fitted the spectra simultaneously, assuming the same
values were
similar. We therefore re-fitted the spectra simultaneously, assuming the same
![]() and
and
![]() .
The model fit was very good, with a
.
The model fit was very good, with a
![]() of 4997 for 5120 d.o.f. (the best-fit residuals plot shown in the bottom
panel of Fig. 15 is for the spectrum of the fourth segment
listed in Table 3; similar residuals were observed for the
other spectra as well). The best-fit electron and seed photon temperatures were
of 4997 for 5120 d.o.f. (the best-fit residuals plot shown in the bottom
panel of Fig. 15 is for the spectrum of the fourth segment
listed in Table 3; similar residuals were observed for the
other spectra as well). The best-fit electron and seed photon temperatures were
![]() keV and
keV and
![]() keV.
The best-fit
keV.
The best-fit
![]() values for this model are listed in
Table 3.
values for this model are listed in
Table 3.
Both the BKNPL and the NTHCOMP+PL models gave a good fit to the data.
However, in the case of the latter model, we got a reduction in the best-fit
![]() value of
value of
![]() with a smaller number of model
parameters. Following Mushotzky (1982), we defined the ratio of the likelihood of
the best BKNPL fit,
with a smaller number of model
parameters. Following Mushotzky (1982), we defined the ratio of the likelihood of
the best BKNPL fit,
![]() ,
to the likelihood of the best NTHCOMP+PL model fit,
,
to the likelihood of the best NTHCOMP+PL model fit,
![]() ,
as:
,
as:
![]() [(
[(
![]() ]=exp
]=exp
![]() ,
in our case. This high value strongly suggests that the
Comptonisation model is much more likely than the BKNPL model to be the
``correct'' model for the soft excess in PKS 0558-504.
,
in our case. This high value strongly suggests that the
Comptonisation model is much more likely than the BKNPL model to be the
``correct'' model for the soft excess in PKS 0558-504.
7 Summary and discussion
We presented the results from the spectral analysis of a long XMM-Newton observation of the luminous, radio-loud, narrow line Seyfert 1 galaxy PKS 0558-504. The object was observed in September 2008 for 5 orbits, yielding data of unprecedented quality for this source. The main results from our work are summarised below:
- 1)
- The source exhibits continuous, large amplitude flux variations on all sampled time scales. A flux variability study with the use of the power spectrum analysis will be presented in a companion paper.
- 2)
- The 2-10 keV band spectrum of the source is well fitted by a simple PL
model, with a steep slope of
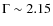 ,
which is typical of NLS1.
,
which is typical of NLS1.
- 3)
- The hard band slope is variable; the spectrum steepens as the flux increases. This is similar to what is commonly observed in other Seyferts as well (see e.g. Sobolewska & Papadakis 2009).
- 4)
- The hard band spectrum is very smooth; we did not observe any absorption
features (either lines or edges), and we found only weak evidence for the
presence of an iron line, which is indicative of emission from highly ionised
iron. The line's EW is small,
 20 eV, with an 90% upper limit of no more
than
20 eV, with an 90% upper limit of no more
than  45-50 eV.
45-50 eV.
- 5)
- At energies below
 2 keV a strong, steep, smooth, and broad soft
excess component appears. The soft excess flux is variable, but with an
amplitude which is smaller than the hard band continuum variability amplitude.
The soft excess spectra shape is also variable and becomes ``harder'' with
increasing flux.
2 keV a strong, steep, smooth, and broad soft
excess component appears. The soft excess flux is variable, but with an
amplitude which is smaller than the hard band continuum variability amplitude.
The soft excess spectra shape is also variable and becomes ``harder'' with
increasing flux.
- 6)
- The soft excess and the hard band flux variations are moderately correlated,
but with a delay: the former are leading the latter by
 20 ks.
20 ks.
- 7)
- We detected no signs of warm absorption features at energies below
 2 keV.
2 keV.
- 8)
- The average 0.4-10 keV spectra of the individual XMM-Newton, orbit-long observations cannot be fitted well by any of the models that are commonly used to fit similar data of other NLS1. This could be partly due to remaining uncertainties in the instrumental PN calibration. But we believe that the spectral variability of the source, and in particular the variable soft/hard flux ratio (even on time scales of the order of a few ks), significantly affects the the results from the spectral analysis of spectra which are averaged on time scales longer than 10-20 ks.
- 9)
- Model-fitting to the spectrum of a few short segments of the total observations showed that the soft excess can be well described by a low-temperature Comptonisation model of the disc photons, in agreement with the results of Brinkmann et al. (2004). Other alternatives like emission from a multicolour disc black body, or reflection from an ionised disc, could not fit the data well. A broken power law model also provided a statistically acceptable fit to the data, however, the low-temperature Comptonisation model is a more likely explanation of the source spectrum.
Although PKS 0558-504 is one of the few radio-loud NLS1, its X-ray spectrum seems to
be ``normal'' and rather similar to the spectra of other NLS1. Our results rule
out a jet origin for the bulk of the X-ray emission from this object: the hard
band slope of ![]() 2.15 is similar to the X-ray slope of most radio-quiet
NLS1s, the ``soften when brighter'' spectral variability trend of the power law
continuum is identical to what is observed in other radio-quiet Seyferts, and
even the weakness of the iron line emission is also consistent with what is
observed in other NLS1s. Furthermore, the fact that we found no evidence for
ionised absorption in either the soft or the hard X-ray bands implies that
the X-ray spectrum of PKS 0558-504 is essentially unmodified by intervening matter. As
a result, the present data set is ideal to study the intrinsic, X-ray emission
spectrum of this object, free from absorption effects. Given the similarity
between the X-ray emission properties between PKS 0558-504 and other NLS1s, some of
the results from the present study may have wider implications to NLS1 as a
class.
2.15 is similar to the X-ray slope of most radio-quiet
NLS1s, the ``soften when brighter'' spectral variability trend of the power law
continuum is identical to what is observed in other radio-quiet Seyferts, and
even the weakness of the iron line emission is also consistent with what is
observed in other NLS1s. Furthermore, the fact that we found no evidence for
ionised absorption in either the soft or the hard X-ray bands implies that
the X-ray spectrum of PKS 0558-504 is essentially unmodified by intervening matter. As
a result, the present data set is ideal to study the intrinsic, X-ray emission
spectrum of this object, free from absorption effects. Given the similarity
between the X-ray emission properties between PKS 0558-504 and other NLS1s, some of
the results from the present study may have wider implications to NLS1 as a
class.
However, PKS 0558-504 may still be a rather rare object, because it almost certainly
has a high mass accretion rate,
![]() .
To estimate this rate in
Eddington units,
.
To estimate this rate in
Eddington units,
![]() ,
we need to know the mass of the BH in
the nucleus of PKS 0558-504. We can estimate it by using the virial relation
,
we need to know the mass of the BH in
the nucleus of PKS 0558-504. We can estimate it by using the virial relation
![]() ,
where R and
,
where R and ![]() are the radius and velocity
dispersion of the broad line region. We measured the velocity dispersion from
the width of the broad H
are the radius and velocity
dispersion of the broad line region. We measured the velocity dispersion from
the width of the broad H![]() emission line (Corbin 1997) and the radius of
the broad line region from the radius-luminosity scaling relation of Bentz et al. (2009), using the 5100 Å luminosity measurement of Corbin & Smith
(2000), and we found that
emission line (Corbin 1997) and the radius of
the broad line region from the radius-luminosity scaling relation of Bentz et al. (2009), using the 5100 Å luminosity measurement of Corbin & Smith
(2000), and we found that
![]() .
The
average 2-10 keV flux of
.
The
average 2-10 keV flux of ![]()
![]() erg cm-2 s-1 (Gliozzi et al. 2007)
implies an average 2-10 keV luminosity of
erg cm-2 s-1 (Gliozzi et al. 2007)
implies an average 2-10 keV luminosity of ![]()
![]() ergs/s,
which is already
ergs/s,
which is already ![]()
![]() of the Eddington luminosity (
of the Eddington luminosity (
![]() )
for
this BH. Even if we use the lowest bolometric correction of
)
for
this BH. Even if we use the lowest bolometric correction of ![]() 20 of
Vasudevan & Fabian (2009), the bolometric accretion rate of the source turns
out to be larger than the Eddington accretion rate,
20 of
Vasudevan & Fabian (2009), the bolometric accretion rate of the source turns
out to be larger than the Eddington accretion rate,
![]() .
In
fact, the combined analysis of the present data set with simultaneous SWIFT
observations implies that the source is accreting at a rate which may be several
times larger than
.
In
fact, the combined analysis of the present data set with simultaneous SWIFT
observations implies that the source is accreting at a rate which may be several
times larger than
![]() (Gliozzi et al., in preparation).
Keeping this fact in mind, we present below a discussion of some of the results
we reported above.
(Gliozzi et al., in preparation).
Keeping this fact in mind, we present below a discussion of some of the results
we reported above.
The hard band X-ray spectral variability of PKS 0558-504. Despite the high accretion rate of the source, its hard band spectrum is not unusual. It has a power law shape, which, as we mentioned in Sect. 3.1, can be explained by thermal Comptonisation of seed photons by a hot electron corona whose parameters are similar to those which can also explain the hard band X-ray spectrum of most radio-quiet Seyferts.
In the case of thermal Comptonisation, the spectral slope ![]() is
determined by the so-called Compton amplification factor,
is
determined by the so-called Compton amplification factor,
![]() ,
where
,
where
![]() is the power dissipated in
the corona and
is the power dissipated in
the corona and ![]() is the intercepted soft luminosity. Obviously, if Avaries, then
is the intercepted soft luminosity. Obviously, if Avaries, then ![]() should also change as well. According to Beloborodov
(1999),
should also change as well. According to Beloborodov
(1999),
![]() ,
where
,
where
![]() ,
if the energy of the
input soft photons,
,
if the energy of the
input soft photons,
![]() ,
is of the order of a few eVs, and
,
is of the order of a few eVs, and
![]() ,
if
,
if
![]() is of the order of a few hundred eV.
is of the order of a few hundred eV.
The data plotted in the top panel of Fig. 11 can be well fitted
by a power law model of the form:
![]() X-ray
X-ray
![]() (here X-ray
(here X-ray
![]() stands for the observed 0.4-10 keV count
rate). A possible explanation then for the ``spectral slope - X-ray flux''
correlation is that the ``heating-to-cooling'' ratio of the corona,
stands for the observed 0.4-10 keV count
rate). A possible explanation then for the ``spectral slope - X-ray flux''
correlation is that the ``heating-to-cooling'' ratio of the corona,
![]() ,
decreases with increasing X-ray flux (or accretion rate, if
the X-ray flux is indicative of the accretion rate of the source), i.e.
,
decreases with increasing X-ray flux (or accretion rate, if
the X-ray flux is indicative of the accretion rate of the source), i.e.
![]() X-ray
X-ray
![]() .
In this case, we
would expect that
.
In this case, we
would expect that
![]() X-ray
X-ray
![]() ,
with
,
with
![]() in the case when the energy of the input photons is of the order of a
hundred eV or so, exactly as observed.
in the case when the energy of the input photons is of the order of a
hundred eV or so, exactly as observed.
The hard band spectral variations in PKS 0558-504 could also be explained by a
combination of a highly variable (in flux) power law continuum (with a fixed
slope) and a constant reflection component (e.g. Taylor et al. 2003; Ponti
et al. 2006; Miniutti et al. 2007), or by variations in the column density,
covering fraction, and/or the opacity of an absorber, while the continuum slope
remains constant (e.g. Miller et al. 2008; Turner et al. 2007).
Still, our results indicate that the X-ray spectrum of PKS 0558-504 is not modified by
intervening absorbing material, while the failure of the reflection model to
account well for the full band spectrum of the source (in various flux levels)
implies that the reflection component is probably minimal in the 2-10 keV band
(when compared to the PL continuum). For these reasons, we believe that the
observed spectral variations in this source indicate intrinsic ![]() variations. The fact that the ``steeper when brighter'' variability pattern of
PKS 0558-504 is similar to what is observed in many Seyfert galaxies suggests that
intrinsic
variations. The fact that the ``steeper when brighter'' variability pattern of
PKS 0558-504 is similar to what is observed in many Seyfert galaxies suggests that
intrinsic ![]() variations may also be responsible to a large extend for the
spectral variations we observe in these objects as well.
variations may also be responsible to a large extend for the
spectral variations we observe in these objects as well.
The iron emission line. We observe some weak evidence for the presence of
a line with an
![]() eV at
eV at
![]() keV, consistent with the
K
keV, consistent with the
K![]() line from He-like iron. PKS 0558-504 is not unusual among radio-quiet objects
in this respect, as similar lines have been observed in many AGN. Bianchi et al. (2009) for example report the detection of such a line with an EW less than 20
eV in at least 12 (broad and narrow line) objects in their sample. The weakness
of the line's strength may be easily explained if the disc is covered by a hot
layer which is up-scattering the disc photons to produce the observed
soft-excess (see below). If its optical depth is larger than unity, then even if
the disc is producing iron lines due to reflection, they will be significantly
suppressed by Compton scattering in this layer (Matt et al. 1997).
line from He-like iron. PKS 0558-504 is not unusual among radio-quiet objects
in this respect, as similar lines have been observed in many AGN. Bianchi et al. (2009) for example report the detection of such a line with an EW less than 20
eV in at least 12 (broad and narrow line) objects in their sample. The weakness
of the line's strength may be easily explained if the disc is covered by a hot
layer which is up-scattering the disc photons to produce the observed
soft-excess (see below). If its optical depth is larger than unity, then even if
the disc is producing iron lines due to reflection, they will be significantly
suppressed by Compton scattering in this layer (Matt et al. 1997).
We do not observe any evidence from iron line emission of neutral material. The
99% upper EW limit for a narrow iron K![]() line in the total spectrum of
the source is just 11 eV. This is significantly smaller than the EW of
line in the total spectrum of
the source is just 11 eV. This is significantly smaller than the EW of ![]() 40 eV that is expected from objects of luminosity
40 eV that is expected from objects of luminosity ![]()
![]() erg/s
(Bianchi et al. 2007). In the case of lines arising from reflection of X-rays
from the disc, this result can be explained from the fact that the disc
material is highly ionised, as discussed above. But iron lines can also be
produced by reprocessing of X-rays from distant, cold Compton-thick matter, as
for instance from the putative torus. The lack of a neutral iron K
erg/s
(Bianchi et al. 2007). In the case of lines arising from reflection of X-rays
from the disc, this result can be explained from the fact that the disc
material is highly ionised, as discussed above. But iron lines can also be
produced by reprocessing of X-rays from distant, cold Compton-thick matter, as
for instance from the putative torus. The lack of a neutral iron K![]() line
suggests that the covering factor of the Compton-thick torus in this object
must be significantly smaller than the covering factor in similar luminosity
Seyferts. On the other hand, the absence of this line agrees with the fact that
PKS 0558-504 is most probably accreting at a rate higher than
line
suggests that the covering factor of the Compton-thick torus in this object
must be significantly smaller than the covering factor in similar luminosity
Seyferts. On the other hand, the absence of this line agrees with the fact that
PKS 0558-504 is most probably accreting at a rate higher than
![]() .
Indeed, objects with
.
Indeed, objects with
![]() significantly higher than
significantly higher than
![]() show lines with an EW which is smaller than 20-10 eV (Bianchi et al. 2007). Perhaps the increase of the opening angle of the torus may then depend
mainly on the accretion rate and not just the luminosity of the source.
show lines with an EW which is smaller than 20-10 eV (Bianchi et al. 2007). Perhaps the increase of the opening angle of the torus may then depend
mainly on the accretion rate and not just the luminosity of the source.
The soft excess. We found that the soft excess emission below ![]() 2 keV is best explained by a low-temperature (
2 keV is best explained by a low-temperature (![]() 0.42 keV) Comptonisation
component, where the temperature of the seed photons is
0.42 keV) Comptonisation
component, where the temperature of the seed photons is ![]() 0.11 keV. This
agrees with the results of Brinkmann et al. (2004). The seed photons temperature
is not consistent with the expected maximum temperature in the innermost region
of a Shakura & Sunyaev, optically thick and geometrically thin accretion disc
around a
0.11 keV. This
agrees with the results of Brinkmann et al. (2004). The seed photons temperature
is not consistent with the expected maximum temperature in the innermost region
of a Shakura & Sunyaev, optically thick and geometrically thin accretion disc
around a ![]()
![]() BH (which should be
BH (which should be ![]() times
smaller than
times
smaller than ![]() 0.1 keV in the case when
0.1 keV in the case when
![]() ). However, in the case of super-Eddington accretion discs, the
accretion flow deviates from the thermodynamic equilibrium, and as a result the
accreted gas can be overheated in the central region. Beloborodov (1998) has
shown that the maximum temperature in the disc around a massive (Schwarzschild)
black hole can be as large as
). However, in the case of super-Eddington accretion discs, the
accretion flow deviates from the thermodynamic equilibrium, and as a result the
accreted gas can be overheated in the central region. Beloborodov (1998) has
shown that the maximum temperature in the disc around a massive (Schwarzschild)
black hole can be as large as ![]() 107 K, if the accretion rate is 100 times
107 K, if the accretion rate is 100 times
![]() .
Since the temperature of the gas in the disc determines
the emission spectrum to a large extent, it may not be surprising for the
spectrum of a disc with a super-Eddington accretion rate to extend up to 0.1 keV
or so, as observed.
.
Since the temperature of the gas in the disc determines
the emission spectrum to a large extent, it may not be surprising for the
spectrum of a disc with a super-Eddington accretion rate to extend up to 0.1 keV
or so, as observed.
Furthermore, Kawaguchi (2003) has demonstrated that a hot layer (where
Comptonisation becomes important) can be developped in the inner region of
super-Eddington discs when
![]() .
Perhaps then,
due to its super-Eddington accretion rate, there is a hot layer on top of the
disc in PKS 0558-504, which can be identified as the low-temperature Comptonising
medium responsible for its soft excess emission. Interestingly, low temperature
Comptonisation spectra can also fit well the soft excess emission in two AGN
which also have a super-Eddington rate, namely EX J0136.9-3510 and RE J1034+396
(Jon et al. 2009; Middleton et al. 2009). If this is the case, then perhaps the
physical origin of the soft excess in these objects may be different from the
origin of the same component in NLS1 with a sub-Eddington accretion rate,
because we would not expect the presence of hot layers in these objects where
significant Comptonisation can distort the underlying disc spectrum.
.
Perhaps then,
due to its super-Eddington accretion rate, there is a hot layer on top of the
disc in PKS 0558-504, which can be identified as the low-temperature Comptonising
medium responsible for its soft excess emission. Interestingly, low temperature
Comptonisation spectra can also fit well the soft excess emission in two AGN
which also have a super-Eddington rate, namely EX J0136.9-3510 and RE J1034+396
(Jon et al. 2009; Middleton et al. 2009). If this is the case, then perhaps the
physical origin of the soft excess in these objects may be different from the
origin of the same component in NLS1 with a sub-Eddington accretion rate,
because we would not expect the presence of hot layers in these objects where
significant Comptonisation can distort the underlying disc spectrum.
We also found that both the soft excess flux and shape are variable. Regarding
the spectral variability of this component, we found that its spectral shape
``hardens'' (i.e. it shifts to higher energies) with increasing flux (lower panel
in Fig. 11). According to the model-fit results presented in the previous
section, this spectral ``hardening'' can be explained by a decrease (i.e.
flattening) of
![]() at a constant electron temperature with
increasing flux. Since
at a constant electron temperature with
increasing flux. Since
![]() depends on the optical depth of the
Comptonising medium as well, the
depends on the optical depth of the
Comptonising medium as well, the
![]() flattening implies an
increase in
flattening implies an
increase in ![]() with increasing flux. Similar spectral variations were also
reported by Brinkmann et al. (2004), who also attributed them to
with increasing flux. Similar spectral variations were also
reported by Brinkmann et al. (2004), who also attributed them to ![]() variation.
variation.
In physical terms, an increase in the normalisation of the soft excess can be
achieved by an increase in the size of the emitting area. Indeed, the radial
extent of the hot disc layer, where Comptonisation effects become important,
does increases with increasing
![]() (i.e. increasing flux) according
to Kawaguchi (2003). At the same time the Compton y parameter (which depends
on the temperature and the optical depth due to scattering in the hot layer)
increases as well, and since
(i.e. increasing flux) according
to Kawaguchi (2003). At the same time the Compton y parameter (which depends
on the temperature and the optical depth due to scattering in the hot layer)
increases as well, and since
![]() (Beloborodov 1999),
(Beloborodov 1999),
![]() should flatten with increasing
should flatten with increasing ![]() ,
as observed.
Consequently, both the shape of the soft excess component and its flux and
spectral variations are consistent with the hypothesis that, due to the
super-Eddington accretion rate of the source, a hot disc layer exists in the
innermost region of PKS 0558-504, which significantly distorts the underlying disc
emission. An increase in the accretion rate will result in an increase of the
size of the hot layer as well as hence an increase in the flux of the soft
excess, and an increase in the Compton y parameter, which will in turn result
in the ``hardening'' of the shape of this component.
,
as observed.
Consequently, both the shape of the soft excess component and its flux and
spectral variations are consistent with the hypothesis that, due to the
super-Eddington accretion rate of the source, a hot disc layer exists in the
innermost region of PKS 0558-504, which significantly distorts the underlying disc
emission. An increase in the accretion rate will result in an increase of the
size of the hot layer as well as hence an increase in the flux of the soft
excess, and an increase in the Compton y parameter, which will in turn result
in the ``hardening'' of the shape of this component.
The delay between soft and hard band flux variations. Our results suggest
that the soft excess flux may lead the hard band X-ray flux variations by ![]() 20 ks. If real, such a correlation cannot be explained by reflection models;
therefore this result is another indication that such models cannot account for
the soft excess component in PKS 0558-504.
20 ks. If real, such a correlation cannot be explained by reflection models;
therefore this result is another indication that such models cannot account for
the soft excess component in PKS 0558-504.
We argued in the paragraph above that the soft excess flux variability may be
caused by
![]() perturbations. One possible explanation for the
correlation and the time delay between soft and hard band variations is that
the hard band X-rays are produced at a radius
perturbations. One possible explanation for the
correlation and the time delay between soft and hard band variations is that
the hard band X-rays are produced at a radius
![]() ,
which is smaller
than the radius where most of the soft excess emission originates,
,
which is smaller
than the radius where most of the soft excess emission originates,
![]() ,
and the
,
and the
![]() perturbations can propagate from
perturbations can propagate from
![]() to
to
![]() .
The time-delay between the soft excess and hard band X-rays
could then be identified with the propagation/diffusion time scale of the
perturbations, which should be of the order of
.
The time-delay between the soft excess and hard band X-rays
could then be identified with the propagation/diffusion time scale of the
perturbations, which should be of the order of
![]() ,
where vr is the radial drift velocity of the accretion flow.
For example, according to Kawaguchi (2003), in a
,
where vr is the radial drift velocity of the accretion flow.
For example, according to Kawaguchi (2003), in a
![]() source, the hot layer, which could be responsible for the soft
excess emission, should extend from
source, the hot layer, which could be responsible for the soft
excess emission, should extend from ![]() to
to ![]() (in units of the
Schwarzschild radius). If most of the 0.4-1 keV soft excess photons originate
at
(in units of the
Schwarzschild radius). If most of the 0.4-1 keV soft excess photons originate
at ![]() ,
then
,
then
![]() ks. If furthermore the hard
X-rays are mainly produced at
ks. If furthermore the hard
X-rays are mainly produced at ![]() ,
then the delay we detected could be
identified with this
,
then the delay we detected could be
identified with this
![]() value.
value.
We note though that even if this is indeed the case in PKS 0558-504, these
![]() perturbations should affect the soft and hard band Comptonising regions in a
different way; the soft excess ``hardens'' while the hard band spectrum
``softens'' with increasing flux (i.e.
perturbations should affect the soft and hard band Comptonising regions in a
different way; the soft excess ``hardens'' while the hard band spectrum
``softens'' with increasing flux (i.e. ![]() ). If the
). If the
![]() perturbations mainly affect the optical depth of the scattering media, they do
it in such a way that while
perturbations mainly affect the optical depth of the scattering media, they do
it in such a way that while ![]() increases in the hot disc layer, it should
decrease in the hot corona which is responsible for the hard band X-ray
continuum. Clearly, more work is needed to elaborate further on the relation
between the soft and hard band spectral and flux variations in PKS 0558-504, and other
Seyferts as well.
increases in the hot disc layer, it should
decrease in the hot corona which is responsible for the hard band X-ray
continuum. Clearly, more work is needed to elaborate further on the relation
between the soft and hard band spectral and flux variations in PKS 0558-504, and other
Seyferts as well.
I. E. and W. P. B. acknowledge partial support from the EU ToK grant 39965 and FP7-REGPOT 206469. M.G. acknowledges support by the XMM-Newton Guest Investigator Program under NASA grant 201593. This work is based on observations with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and the USA (NASA). This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
References
- Beloborodov, A. M. 1998, MNRAS, 297, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Beloborodov, A. M. 1999, in High Energy Processes in Accreting Black Holes, ASP Conf. Ser., 161, 295 [Google Scholar]
- Bentz, M. C., Peterson, B. M., Netzer, H., et al. 2009, ApJ, 697, 160 [Google Scholar]
- Bianchi, S., Guainazzi, M., Matt, G., & Fonseca Bonilla, N. 2007, A&A, 467, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, S., Guainazzi, M., Matt, G., Fonseca Bonilla, N., & Ponti, G. 2009, A&A, 495, 421 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brinkmann, W., Yuan W., & Siebert J. 1997, A&A, 319, 413 [NASA ADS] [Google Scholar]
- Brinkmann, W., Arevalo, P., Gliozzi, M., & Ferrero, E. 2004, A&A, 415, 959. [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brinkmann, W., Papadakis, I. E., Raeth, C., Mimica, P., & Haberl, F. 2005, A&A, 443, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corbin, M. R. 1997, ApJS, 113, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Corbin, M. R., & Smith, P. S. 2000, ApJ, 532, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Ehle, M., de la Calle, I., Diaz Trigo, M., et al. 2008, XMM-Newton Users Handbook, http://xmm.esac.esa.int/external/xmm_user_support/documentation/uhb_2.6/ [Google Scholar]
- Gliozzi, M., Boller, Th., Brinkmann, W., & Brandt, W. N. 2000, A&A, 356, L17 [NASA ADS] [Google Scholar]
- Gliozzi, M., Brinkmann, W., O'Brien, P. T., et al. 2001, A&A, 365, L128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gliozzi, M., Papadakis, I. E., & Brinkmann, W. 2007, ApJ, 656, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Goodrich, R. W. 1989, ApJ, 342, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Grupe, D., Beuermann, K., Mannhein, K., & Thomas, H.-C. 1999, A&A, 350, 805 [NASA ADS] [Google Scholar]
- Haba, Y., Terashima, Y., Kunieda, H., & Ohsuga, K. 2008, PASJ, 60, 487 [NASA ADS] [Google Scholar]
- Jon, C., Done, C., Ward, M., Gierlinski, M., & Mullaney, J. 2009, MNRAS, 398, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kawaguchi, T. 2003, ApJ, 593, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Komossa, S., Voges, W., Xu, D., et al. 2006, AJ, 132, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Krongold, Y., Nicastro, F., Brickhouse, N. S., et al. 2003, ApJ, 597, 832 [NASA ADS] [CrossRef] [Google Scholar]
- Laor, A. 1991, ApJ, 376, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, G., Fabian, A. C., & Reynolds, C. S. 1997, MNRAS, 289, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Middleton, M., Done, C., Ward, M., Gierlinski, M., & Schurch, N. 2009, MNRAS, 394, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, L., Turner, T. J., & Reeves, J. N. 2008, A&A, 483, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miniutti, G., Fabian, A. C., Anabuki, N., et al. 2007, PASJ, 59, 315 [NASA ADS] [Google Scholar]
- Mitsuda, K., Inoue, H., Koyama, K., et al. 1984, PASJ, 36,741 [NASA ADS] [Google Scholar]
- Mushotzki, R. F. 1982, ApJ, 256, 92 [NASA ADS] [CrossRef] [Google Scholar]
- O'Brien, P. T., Reeves, J. N., Turner, M. J. L., et al. 2001, A&A, 365, L122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osterbrock, D. E., & Pogge, R. W. 1985, ApJ, 297, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Persson S. E. 1988, ApJ, 330, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Petrucci P. O., Haardt F., Maraschi L., et al. 2001, ApJ, 556, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Ponti, G., Miniutti, G., Cappi, M., et al. 2006, MNRAS, 368, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., Bradt, H. V., Buckley, D. A. H., et al. 1986, ApJ, 301, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., Grossan, B., Bradt, H. V., et al. 1991, Nature, 350, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, R. R., & Fabian, A. C. 2005, MNRAS, 358, 211 [Google Scholar]
- Siebert, J., Leighly, K. M., Laurent-Muehleisen, S. A., et al. 1999, A&A, 348, 678 [NASA ADS] [Google Scholar]
- Sobolewska, M., & Papadakis, I. E. 2009, MNRAS, 399, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U. G., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, R. D., Uttley, P., & M Hardy, I. M. 2003, MNRAS, 342, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L. 1994, ApJ, 434, 313 [Google Scholar]
- Turner, T. J., Miller, L., Reeves, J. N., & Kraemer, S. B. 2007, A&A, 475, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ulvestad, J. S., Antonucci, R. R. J., & Goodrich, R. W. 1995, AJ, 109, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Vasudevan, R. V., & Fabian, A. C. 2009, MNRAS, 392, 1124 [NASA ADS] [CrossRef] [Google Scholar]
- Vaughan, S., Fabian, A. C., & Nandra, K. 2003, MNRAS, 339, 1273 [Google Scholar]
- Wang, T., Matsuoka, M., Kubo, H., Mihara, T., & Negoro, H. 2001, ApJ, 554, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, W., Zhou, H. Y., Komossa, S., et al.2008, ApJ, 685, 801 [Google Scholar]
- Zycki, P. T., Done, C., & Smith, D. A. 1999, MNRAS, 309, 561 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... Mpc
![[*]](/icons/foot_motif.png)
- This luminosity distance
estimate is taken from NASA/NED. It is calculated assuming
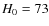 km s-1 Mpc-1,
km s-1 Mpc-1,
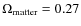 ,
and
,
and
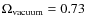 .
.
- ...
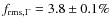
![[*]](/icons/foot_motif.png)
- The error, accounting only for the
measurement error of
 ,
has been calculated according to the prescription
of Vaughan et al. (2003).
,
has been calculated according to the prescription
of Vaughan et al. (2003).
All Tables
Table 1: Results from the PL model fits to the 2-10 keV average spectra of the 5 observations.
Table 2: The iron-line best fit parameter values.
Table 3:
Results from the spectral fits of the
NTHCOMP+PL model to the 0.4-10 keV spectra of the seven short segments (see
section 6 for details), assuming the same electron temperature (
![]() keV), and disc-black body seed photon temperature (
keV), and disc-black body seed photon temperature (
![]() keV), in all cases.
keV), in all cases.
All Figures
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{13289fg1.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg26.png)
|
Figure 1: The PN 0.4-10 keV light curve of PKS 0558-504 for all five observations with a binning of 100 s. The time counts from the beginning of the first observation. The points plotted with crosses at the bottom of the plot indicate the background count rate in the same energy range. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13289fg2}\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg34.png)
|
Figure 2:
Top panel: power law model fit to the total spectrum of obs-301 in the
2-10 keV band. Lower panel: the best-fit residuals plot (residuals are in
terms of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13289fg3.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg57.png)
|
Figure 3: Top panel: the best power law model fit to the total PN spectrum in the 4.5-8 keV band. Lower panel: the best-fit residuals plot. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15.6cm,clip]{13289fg4.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg61.png)
|
Figure 4: Top panel: the 0.4-10 keV PN spectra of all observations. Black, open circles indicate the obs-201 spectrum; red, open triangles indicate the obs-301 spectrum, and green, open diamonds indicate the obs-401 spectrum. The obs-501 and obs-601 spectra are plotted with a continuous black and brown line. Some of the spectra are scaled for demonstration reasons (see text for details). The solid line indicates the best PL fit to the obs-201, 2-10 keV spectrum. Lower panel: the ``Data/the best hard band PL model fit'' plots for the same spectra (plotted using the same colour code as in the top panel). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13289f5-1.eps}\par\includegraphics[width=8.4cm,clip]{13289f5-2.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg66.png)
|
Figure 5: From top to bottom: data-to-model ratio in the 0.4-2 keV band for the best fits of a Brems+PL, a broken PL, a compTT+PL, and a DISKBB+PL model. In the top panel, we plot the data for the the average spectrum of each XMM-Newton observation (black, red, green, blue and brown points have been used for the obs-201, obs-301, obs-401, obs-501, and obs-601 spectra, respectively). For clarity reasons, in the following panels, we plot the data for the obs-201 spectrum only (the data-to-model ratios are very similar for the other spectra as well). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13289fg6.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg69.png)
|
Figure 6: ``Data-to-PLBrems model'' ratio in the 0.25-2 keV band, for the single PN events (open squares), single plus double PN events (filled circles), and the MOS1 spectra (open circles) of obs-601. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13289fg7.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg79.png)
|
Figure 7: RGS1 ( top panel) and RGS2 ( bottom panel) residuals to a broken power law fit attenuated by Galactic absorption. For clarity reasons, the data in this figure are binned by a factor of 8 when compared to the unbinned RGS pipeline data. Consequently, the spectra plotted in this figure are grouped at about 40 Å per resolution element, i.e. at about 1.5 bins per RGS resolution element. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13289fg8.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg84.png)
|
Figure 8:
Top panel: HR plotted as a function of time (obs-601). Points shown in
grey indicate the HR using bins of the size of 100 s, while open diamonds
indicate the HR values using bins of the size of 1000 s (for clarity reasons
errors in the latter case are not plotted; they are of the order of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{13289f9.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg91.png)
|
Figure 9: Plot of one of the worst PLBrems fits ( top panel), and of the respective residuals ( bottom panel) to the PN data of one of the individual spectra (see Sect. 5 for details). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13289f10.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg94.png)
|
Figure 10:
The ``total'' model flux (i.e. Flux
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13289f11.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg100.png)
|
Figure 11:
Top panel: the best-fit spectral slope of the individual spectra of the
source, plotted as a function of time (measured from the start of the XMM-Newton observations). Lower panel: filled, open, and crosses indicate Flux
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13289f12.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg101.png)
|
Figure 12: The best PL model fit normalisation values plotted as a function of the observed 0.4-10 keV count rate. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13289f13.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg102.png)
|
Figure 13:
Top panel: the best-fit spectral slope of the individual spectra of the
source, plotted as the function of the 0.4-10 keV count rate. Filled
``up-triangles'' and open ``down-triangles'' indicate the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13289f14.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg123.png)
|
Figure 14:
Top panel: the DCF between Flux
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13289f15.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13289-09/Timg125.png)
|
Figure 15: From top to bottom: data-to-model ratio in the 0.4-2 keV band for the best fits of a DISKBB+PL, REFLION+PL, a broken PL, and a NTHCOMP+PL model to the seven individual spectra we considered in Sect. 6. The residuals for the spectra listed in Table 3 are plotted with points in black, red, green, blue, brown, magenta and orange, respectively. It is difficult to identify the individual residual plots for each spectrum, because they are similar for all of them. For clarity reasons, in the following panels we plot the best-fit residuals in the case of the spectrum of the fourth segment listed in Table 3 only. The residuals are similar for the other spectra as well. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


