| Issue |
A&A
Volume 510, February 2010
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 5 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200913272 | |
| Published online | 29 January 2010 | |
Mass loss out of close binaries
Case A Roche lobe overflow
W. Van Rensbergen - J. P. De Greve - N. Mennekens - K. Jansen - C. De Loore
Astrophysical Institute, Vrije Universiteit Brussel, Pleinlaan 2, 1050 Brussels, Belgium
Received 9 September 2009 / Accepted 18 November 2009
Abstract
Context. Matter leaving the donor during mass transfer spins
up the gainer and creates a hot spot in the impact area. If the kinetic
energy of the enhanced rotation combined with the radiative energy of
the hot spot exceeds the binding energy of the system, matter can
escape from the binary.
Aims. We calculate the amount of mass lost during eras of fast
mass transfer. We simulate the distribution of mass ratios and orbital
periods for interacting binaries with a B-type primary at birth where
mass transfer starts during hydrogen core burning of the donor.
Methods. We used the initial distributions of primary mass, mass
ratio and orbital period established in a previous paper. The amount of
time the binary shows Algol characteristics within different values of
mass ratio and orbital period was fixed from conservative and liberal
evolutionary calculations. We use these data to simulate the
distribution of mass ratios and orbital periods of Algols with the
conservative as well as the liberal model.
Results. Rapid rotation and hot spots are frequently observed at
the surface of the gainer in a semi-detached binary. The mass transfer
rate for low-mass binaries is never sufficiently large to achieve mass
loss from the system. Intermediate-mass binaries blow away a large
fraction of the transferred mass during short eras of rapid mass
transfer.
Conclusions. We compare mass ratios and orbital periods of
Algols obtained by conservative evolution with those obtained by our
liberal model. We calculate the amount of matter lost according to our
model by binaries with an early B-type primary at birth. Since binaries
with a late B-type primary evolve almost conservatively, the overall
distribution of mass ratios will only yield a few Algols more with high
mass ratios than conservative calculations do. Whereas the simulated
distribution of orbital periods of Algols fits the observations well,
the simulated distribution of mass ratios produces always too few
systems with high values.
Key words: binaries: eclipsing - stars: evolution - stars: mass-loss - stars: statistics
1 Introduction
Eggleton (2000) used the denomination liberal from Warner (1978) to distinguish binary evolution with a mass loss and subsequent angular momentum loss from the
conservative case where no mass leaves the system. A catalog
containing nowadays 240 conservative evolutionary tracks can be found
at the VUB-website![]() . Van Rensbergen et al. (2008)
developed a liberal scenario in which mass can be lost from a binary
during a short era of rapid mass transfer soon after the onset of Roche
Lobe OverFlow (RLOF). The joint online catalog with currently
356 liberal evolutionary tracks is available at the Centre de
Données Stellaires (CDS). The grid of calculations covers only binaries
with a B-type primary at birth and initial orbital periods so that RLOF
starts during hydrogen core burning of the donor: the case A of RLOF.
Systems undergoing a second era of RLOF after the onset of hydrogen
burning in the shell of the donor are designated as cases A/B.
. Van Rensbergen et al. (2008)
developed a liberal scenario in which mass can be lost from a binary
during a short era of rapid mass transfer soon after the onset of Roche
Lobe OverFlow (RLOF). The joint online catalog with currently
356 liberal evolutionary tracks is available at the Centre de
Données Stellaires (CDS). The grid of calculations covers only binaries
with a B-type primary at birth and initial orbital periods so that RLOF
starts during hydrogen core burning of the donor: the case A of RLOF.
Systems undergoing a second era of RLOF after the onset of hydrogen
burning in the shell of the donor are designated as cases A/B.
2 Initial conditions for binaries with a B-type primary
Van Rensbergen et al. (2006) used non-evolved systems in the 9th catalog of Spectroscopic Binaries of Pourbaix et al. (2004)
to establish the initial conditions for the evolution of binaries with
a B-type primary at birth. We distinguish between late B-type primaries
in the mass-range [2.5-7] ![]() and early B-type primaries in the range of [7-16.7]
and early B-type primaries in the range of [7-16.7] ![]() .
The subscript d is used throughout the paper for the binary component which is the donor during RLOF, whereas the subscript g is used for its mass-gaining companion. The following initial conditions were found:
.
The subscript d is used throughout the paper for the binary component which is the donor during RLOF, whereas the subscript g is used for its mass-gaining companion. The following initial conditions were found:
- future donors follow a normalized IMF:
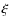 (
(
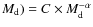 with
with
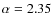 as given by Salpeter (1955);
as given by Salpeter (1955);
- initial orbital periods obey a normalized distribution:
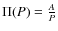 as given by Popova et al. (1982). Different distributions between short and long initial periods (Van Rensbergen et al. 2006) do not have to be taken into account since we consider only short periods leading to RLOF A in this paper;
as given by Popova et al. (1982). Different distributions between short and long initial periods (Van Rensbergen et al. 2006) do not have to be taken into account since we consider only short periods leading to RLOF A in this paper;
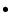
- initial mass ratios (
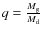 )
follow a normalized distribution:
)
follow a normalized distribution:
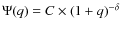 ;
;
 for non-evolved binaries with a late B primary and
for non-evolved binaries with a late B primary and
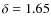 for non-evolved binaries with an early B primary, as given by Van Rensbergen et al. (2006).
for non-evolved binaries with an early B primary, as given by Van Rensbergen et al. (2006).
3 Amount of mass driven out of a close binary
Using a Monte-Carlo simulation starting from a large number of non-evolved binaries, the liberal binary evolutionary scenario of Van Rensbergen et al. (2008) was applied to binaries with a B-type primary at birth and undergoing RLOF A, i.e. during hydrogen core burning of the donor. The details used in the calculations can be found in that paper.
3.1 The contact phase
A hot spot is created on the gainer's equator or on the edge of its
accretion disk when the binary is semi-detached. For initial mass
ratios around 0.4 or lower (and in some cases for mass ratios as high
as 0.6), systems undergoing RLOF A evolve into contact soon after the
onset of mass transfer as a result of a rapid increase of the outer
surface layers of the gainer. The effect of an energy stream during
contact was studied by Nakamura ![]() Nakamura (1987a,b) and Packet (1988, available upon request). Packet (1988)
found that the effect has negligible influence on the evolution of the
binary if the energy stream goes from gainer to loser (i.e. if the
gainer is the hotter star, which is mostly the case in our systems).
Hence, we assume that mass transfer continues during this phase,
without any extra energy transfer.
Nakamura (1987a,b) and Packet (1988, available upon request). Packet (1988)
found that the effect has negligible influence on the evolution of the
binary if the energy stream goes from gainer to loser (i.e. if the
gainer is the hotter star, which is mostly the case in our systems).
Hence, we assume that mass transfer continues during this phase,
without any extra energy transfer.
No hot spot can be created or spin-up generated during contact since the geometrical impact parameter of the system vanishes in that case. The binary suffers then no mass loss and does not meet the Algol requirements. The contact phase does not last long and the system returns into the semi-detached state soon after mass ratio reversal, as a combined result of a decrease of the mass transfer rate and the increase of the distance between the components. Initial mass ratios smaller than 0.25 have been excluded from our statistical analysis because we assume that contact in those cases will provoke a merging of the system. Initial mass ratios larger than 0.25 undergoing contact have been included for the reasons given in this subsection and also because their exclusion would lead to the production of too few Algol type binaries.
3.2 The hot spot
The accuracy of the semi-detached scenario is restricted by the value of the radiative efficiency of accretion ![]() which defines the quantity
which defines the quantity
![]() exerting the radiation pressure of a hot spot.
exerting the radiation pressure of a hot spot.
![]() is that part of
is that part of
![]() which
is available after reduction due to the fact that matter impacting on
the gainer starts at the first Lagrangian point and not at infinity.
This accretion luminosity is weakened on the one hand by the fact that
only a fraction can be converted into radiation and strengthened on the
other because the energy of the impacting material is concentrated in a
hot spot which is significantly smaller than the entire gainer's
surface. Van Rensbergen et al. (2008) defined a quantity K
which enables us to calculate the contribution of the hot spot to the
total luminosity of the gainer. It is easier to visualize the action of
the hot spot using
which
is available after reduction due to the fact that matter impacting on
the gainer starts at the first Lagrangian point and not at infinity.
This accretion luminosity is weakened on the one hand by the fact that
only a fraction can be converted into radiation and strengthened on the
other because the energy of the impacting material is concentrated in a
hot spot which is significantly smaller than the entire gainer's
surface. Van Rensbergen et al. (2008) defined a quantity K
which enables us to calculate the contribution of the hot spot to the
total luminosity of the gainer. It is easier to visualize the action of
the hot spot using
![]() given by the relation (1):
given by the relation (1):
Unfortunately, there are only eleven reliable hot spot temperatures available in the literature. Eight systems (VW Cep, CN And, KZ Pav, V361 Lyr, RT Scl, U Cep, U Sge, and SV Cen) are direct impact systems, while the three others (SW Cyg, V356 Sgr and
The radiative efficiency
A numerical value can hence be calculated from relation (2) for the radiative efficiency of mass accretion by a main sequence gainer
The factor D is the geometric factor which takes into account that matter does not fall onto the gainer from infinity but from the first Lagarangian point. This factor is zero for a contact system and goes to unity as L1 goes to infinity. The factor S is the fractional surface area of the hot spot. Consequently we can compare the values of
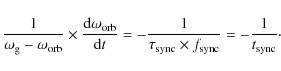
3.3 Tidal interaction
All the systems in the grid were calculated with both strong and weak
tidal interaction. The formalism for the tidal interaction was taken
from Zahn (1977), who gives a suitable approximation for the synchronization time-scale:
This expression uses the semi-major axis a of the binary and a mass ratio q, in which the star which has to be synchronized is in the denominator. This is the gainer in our case, so that
Tidal interactions modulate the angular velocity of the gainer
![]() with the angular velocity
with the angular velocity
![]() of the system. According to Tassoul (2000) one can write
of the system. According to Tassoul (2000) one can write
Tidal interactions spin the gainer down when
Strong tidal coupling should be preferable when the spherical shape of
the gainer is severely elongated due to rapid rotation. As a result we
found that binaries may lose matter during short eras of rapid RLOF
which occur soon after the onset of RLOF during hydrogen core burning
of the donor and sometimes also short after the subsequent onset of
RLOF during hydrogen shell burning of the donor. Binaries with initial
primary masses of below 6 ![]() certainly show a spinning up of the gainer and increased accretion
luminosities concentrated in hot spots, but the combined energies of
both events are never sufficient to overcome the binding energy of the
system: those systems evolve conservatively. Following increasing
values of the initial primary mass we find that binaries with initial
primary masses of below 8
certainly show a spinning up of the gainer and increased accretion
luminosities concentrated in hot spots, but the combined energies of
both events are never sufficient to overcome the binding energy of the
system: those systems evolve conservatively. Following increasing
values of the initial primary mass we find that binaries with initial
primary masses of below 8 ![]() do not lose a significant fraction of the transferred mass. Figures 1 to 3 show the amounts of mass lost by systems with initial primary masses from 8
do not lose a significant fraction of the transferred mass. Figures 1 to 3 show the amounts of mass lost by systems with initial primary masses from 8 ![]() on, respectively for
on, respectively for
![]() ,
0.6 and 0.9. Up to 9
,
0.6 and 0.9. Up to 9 ![]() are lost by systems with a 15
are lost by systems with a 15 ![]() primary mass at birth. There are no huge differences in mass loss
between similar cases calculated with weak and strong tidal interaction
respectively.
primary mass at birth. There are no huge differences in mass loss
between similar cases calculated with weak and strong tidal interaction
respectively.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13272fg1.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13272-09/Timg42.png)
|
Figure 1:
Amount of mass lost by a binary with a B-type primary at birth and an initial mass ratio
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13272fg2.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13272-09/Timg43.png)
|
Figure 2:
Amount of mass lost by a binary with a B-type primary at birth for
|
| Open with DEXTER | |
4 The distribution of mass ratios and orbital periods of Algols
4.1 The observed distributions
Van Rensbergen et al. (2008)
used the mass ratio and orbital period distribution of Algols out of a
sample of 303 observed systems. These systems were taken from the
catalog of Budding et al. (2004) and were extended with semi-detached Algols from the catalog of Brancewicz et al. (1996).
All these systems are issued from a binary with a B-type primary at
birth. A majority of 268 systems have a late B-type primary progenitor,
leaving only 35 systems with an early B-type primary at birth. The
initial conditions described in Sect. 2 use
![]() as a definition of the mass ratio, but since the gainer has become the most massive component of the Algol-system, we use
as a definition of the mass ratio, but since the gainer has become the most massive component of the Algol-system, we use
![]() as the definition of the mass ratio of an Algol-system. The observed
Algols combine a large fraction of systems where Algol characteristics
are at first produced during the hydrogen core burning of the donor
(case A and case A/B) and a smaller fraction where Algols are produced
only after the ignition of hydrogen shell burning in the donor (case
B).
as the definition of the mass ratio of an Algol-system. The observed
Algols combine a large fraction of systems where Algol characteristics
are at first produced during the hydrogen core burning of the donor
(case A and case A/B) and a smaller fraction where Algols are produced
only after the ignition of hydrogen shell burning in the donor (case
B).
4.2 The calculated distributions
Our conservative and liberal binary calculations consider a binary to be an Algol when the semi-detached system shows the typical characteristics as mentioned by Peters (2001):
- the less massive donor fills its Roche Lobe;
- the most massive gainer does not fill its Roche lobe and is still on the main sequence;
- the donor is the cooler, fainter and larger star.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13272fg3.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13272-09/Timg44.png)
|
Figure 3:
Amount of mass lost by a binary with a B-type primary at birth for
|
| Open with DEXTER | |
4.3 The mass ratio distribution of Algols with a late B-type primary at birth
Since binaries with a late B-type primary at birth hardly lose any
mass during their evolution, the mass ratio distribution as obtained
with the liberal assumptions will not differ very much from the one
obtained using the conservative binary evolutionary code. The fact that
![]() 45
45![]() out of a sample of 268 Algols are observed to have high mass ratios (
out of a sample of 268 Algols are observed to have high mass ratios (![]() 0.4-1])
is thus neither reproduced with the liberal binary evolutionary
scenario nor with the conservative code. All these codes produce only
0.4-1])
is thus neither reproduced with the liberal binary evolutionary
scenario nor with the conservative code. All these codes produce only ![]() 12
12![]() of Algols with a mass ratio q above 0.4. Figure 4
shows the mass ratio distribution of Algols with a late B-type primary
at birth as obtained from the theory with the conservative and the two
different liberal assumptions about the strength of the tidal
interaction. Since these binaries do not lose a large amount of mass,
the mass ratio distribution is approximately the same for the
conservative evolution compared to the liberal evolution, producing
only
of Algols with a mass ratio q above 0.4. Figure 4
shows the mass ratio distribution of Algols with a late B-type primary
at birth as obtained from the theory with the conservative and the two
different liberal assumptions about the strength of the tidal
interaction. Since these binaries do not lose a large amount of mass,
the mass ratio distribution is approximately the same for the
conservative evolution compared to the liberal evolution, producing
only ![]() 12
12![]() of Algols with high mass ratios:
of Algols with high mass ratios: ![]() 0.4-1].
0.4-1].
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13272fg4.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13272-09/Timg48.png)
|
Figure 4: Simulated distribution of mass ratios of Algols issued from a binary with a late B-type primary at birth and an initial orbital period so that case A RLOF occurs. |
| Open with DEXTER | |
4.4 The mass ratio distribution of Algols with an early B-type primary at birth
In Sect. 3 we showed
that binaries with an early B-type primary at birth lose a large
fraction of the transferred mass during their evolution. The short
liberal era during which mass is lost occurs when the mass transfer
rate is large, i.e. soon after the onset of RLOF when the binary is in
its pre- or early-Algol stage. The mass ratio distribution as obtained
with the liberal assumptions will now differ very much from the one
obtained using the conservative binary evolutionary code. The fact that
![]() 46
46![]() out of a sample of (only) 35 Algols are observed with high mass ratios (
out of a sample of (only) 35 Algols are observed with high mass ratios (![]() 0.4-1]) is reproduced with the liberal binary evolutionary scenario only (
0.4-1]) is reproduced with the liberal binary evolutionary scenario only (![]() 39
39![]() ). The large fraction of Algols observed with very high mass ratios (
). The large fraction of Algols observed with very high mass ratios (![]() 17
17![]() with
with ![]() 0.85-1]) remains still very hard to explain. Since the liberal era occurs mainly in the very early Algol-stage (when
0.85-1]) remains still very hard to explain. Since the liberal era occurs mainly in the very early Algol-stage (when
![]() ), it is clear that the Algol will populate the lower values of q
during the much longer lasting eras of quiet and slow mass transfer.
The binary loses mass during the short era of rapid mass transfer and
then shows Algol-characteristics during long-lasting eras of quiet and
slow mass transfer. Figure 5
shows the mass ratio distribution of Algols with an early B-type
primary at birth as obtained from theory with the conservative and the
two different liberal assumptions. These binaries lose a large amount
of mass so that the mass ratio distribution differs for the
conservative evolution compared to the liberal evolution, producing
), it is clear that the Algol will populate the lower values of q
during the much longer lasting eras of quiet and slow mass transfer.
The binary loses mass during the short era of rapid mass transfer and
then shows Algol-characteristics during long-lasting eras of quiet and
slow mass transfer. Figure 5
shows the mass ratio distribution of Algols with an early B-type
primary at birth as obtained from theory with the conservative and the
two different liberal assumptions. These binaries lose a large amount
of mass so that the mass ratio distribution differs for the
conservative evolution compared to the liberal evolution, producing ![]() 39
39![]() of Algols with high mass ratios (
of Algols with high mass ratios (![]() 0.4-1])
in the case of the liberal evolution only. These conclusions are
weakened by the fact that they are based on a comparison with only 35
Algols.
0.4-1])
in the case of the liberal evolution only. These conclusions are
weakened by the fact that they are based on a comparison with only 35
Algols.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13272fg5.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13272-09/Timg50.png)
|
Figure 5: Simulated distribution of mass ratios of Algols issued from a binary with an early B-type primary at birth and initial orbital periods so that case A RLOF occurs. |
| Open with DEXTER | |
4.5 Period distribution of Algols with a B-type primary at birth
Figure 6 shows the orbital
period distribution of Algols with an early B-type primary at birth as
obtained from theory with the conservative and the two different
liberal assumptions. We find no significant differences between the
conservative and liberal results. It will be very hard to reproduce by
theory the Algols observed with orbital periods with less than one day (![]() 9
9![]() )
since those systems always merge. Algols observed with orbital periods of more than 15 days (
)
since those systems always merge. Algols observed with orbital periods of more than 15 days (![]() 5
5![]() )
will be reproduced by theory when one includes the Algols which are
only formed after ignition of hydrogen in the shell of the donor. It
was e.g. illustrated for the conservative case by Van Rensbergen (2003)
that these cases B produce a large fraction of Algols with large
orbital periods. But these Algols will not influence the final global
distribution of mass ratios and orbital periods of Algols very much,
since their contribution to the Algol-population will not be very large
as the hydrogen shell burning duration will always last much shorter
than its previously lived hydrogen core burning time. Anticipating the
extension of our catalog of binary evolutionary calculations with the
cases B of RLOF, we may conclude that the theory reproduces the
observations well.
)
will be reproduced by theory when one includes the Algols which are
only formed after ignition of hydrogen in the shell of the donor. It
was e.g. illustrated for the conservative case by Van Rensbergen (2003)
that these cases B produce a large fraction of Algols with large
orbital periods. But these Algols will not influence the final global
distribution of mass ratios and orbital periods of Algols very much,
since their contribution to the Algol-population will not be very large
as the hydrogen shell burning duration will always last much shorter
than its previously lived hydrogen core burning time. Anticipating the
extension of our catalog of binary evolutionary calculations with the
cases B of RLOF, we may conclude that the theory reproduces the
observations well.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13272fg6.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13272-09/Timg51.png)
|
Figure 6: Simulated distribution of orbital periods of Algols issued from a binary with a B-type primary at birth and initial orbital periods so that case A RLOF occurs. |
| Open with DEXTER | |
5 Conclusions
Mass falling in from the donor spins the gainer up and creates a hot spot in its equatorial zone or at the edge of its accretion disk. The combined energy of the enhanced rotation and increased radiation from the hot spot may exceed the binding energy of the system. We present the results of liberal evolutionary calculations for binaries with a B-type primary at birth and with small initial orbital periods so that RLOF starts during the hydrogen core burning of the donor. A significant fraction of the transferred mass is lost by the system in the case of binaries with an early B-type primary at birth. Systems with a late B-type primary at birth hardly lose any matter.
The observed distribution of orbital periods of Algols is well reproduced by both conservative and liberal theoretical calculations.
Although the theoretically calculated liberal mass ratio
distribution of Algols with an initial early B-type primary fits the
observations much better, the overall observed mass ratio distribution
of Algols still shows too many systems with high mass ratios. This is
caused by the very short era of rapid mass tranfer as it results from
the calculation, which in turn causes the binary to rush through the
states with high mass ratios. Binary evolutionary calculations yielding
eras of rapid mass transfer which last for a longer time with somewhat
lower peak values of the mass transfer rate would produce more Algols
with high mass ratios, but have as yet not been published. We have
compared the mass transfer rates as obtained by our binary evolutionary
code in the conservative mode with mass transfer rates for conservative
evolution as produced by previous authors. According to Kippenhahn
et al. (1967a,b) a 9 ![]() donor transfers more than 5
donor transfers more than 5 ![]() to his initial 5
to his initial 5 ![]() gainer in
gainer in
![]() years during the hydrogen core burning of the donor and almost 7
years during the hydrogen core burning of the donor and almost 7 ![]() in
in
![]() years when RLOF starts after exhaustion of hydrogen in the core of the donor. A 2
years when RLOF starts after exhaustion of hydrogen in the core of the donor. A 2 ![]() donor transfers 0.45
donor transfers 0.45 ![]() to his 1
to his 1 ![]() companion in
companion in
![]() years in the rapid phase of mass transfer during hydrogen core burning of the donor. Paczynski et al. (1967a,b) calculated the conservative evolution of a binary with a 16
years in the rapid phase of mass transfer during hydrogen core burning of the donor. Paczynski et al. (1967a,b) calculated the conservative evolution of a binary with a 16 ![]() future donor at birth and a 10.67
future donor at birth and a 10.67 ![]() companion. With an initial orbital period leading to a case A RLOF they found that almost 8
companion. With an initial orbital period leading to a case A RLOF they found that almost 8 ![]() are transferred to the gainer in
are transferred to the gainer in
![]() years.
When RLOF starts after the exhaustion of hydrogen in the core of the
donor, a short era of mass transfer is found with a peak value as high
as
years.
When RLOF starts after the exhaustion of hydrogen in the core of the
donor, a short era of mass transfer is found with a peak value as high
as
![]()
![]() .
Our calculated durations of rapid mass transfer are very similar to
those mentioned above, whereas our peak values are somewhat lower. The
reason for this is that our stellar models are calculated with
Rogers-Iglesias opacities (1992),
which were not available previously. Therefore, our calculated
durations and peak values of mass transfer rates agree very well with
those published by Nelson & Eggleton (2001)
for a representative set of interacting binaries. The occurrence of
many observed Algols with high mass ratios thus remains unexplained.
Future investigations should explore other interactions between the
gravitational RLOF and the internal thermal structure driving the
evolution of the radius of the donor.
.
Our calculated durations of rapid mass transfer are very similar to
those mentioned above, whereas our peak values are somewhat lower. The
reason for this is that our stellar models are calculated with
Rogers-Iglesias opacities (1992),
which were not available previously. Therefore, our calculated
durations and peak values of mass transfer rates agree very well with
those published by Nelson & Eggleton (2001)
for a representative set of interacting binaries. The occurrence of
many observed Algols with high mass ratios thus remains unexplained.
Future investigations should explore other interactions between the
gravitational RLOF and the internal thermal structure driving the
evolution of the radius of the donor.
Podsiadlowski et al. (1992)
pointed out that liberal theoretical calculations depend very much on
the amount of mass lost from the system (characterized by the
parameter ![]() )
andthe amount of angular momentum taken away by this matter (characterized by the parameter
)
andthe amount of angular momentum taken away by this matter (characterized by the parameter ![]() ). Our liberal code calculates
). Our liberal code calculates ![]() self-consistently within the model and assumes that matter is lost from
the hot spot on the gainer (or the edge of its accretion disk) so that
the escaping matter takes only the angular momentum of the gainer's
orbit. It is clear that if matter would escape at another location
(another choice of the parameter
self-consistently within the model and assumes that matter is lost from
the hot spot on the gainer (or the edge of its accretion disk) so that
the escaping matter takes only the angular momentum of the gainer's
orbit. It is clear that if matter would escape at another location
(another choice of the parameter ![]() ,
e.g. characteristic for L2 as the position of mass loss from the system), the calculated population of Algols could be different.
,
e.g. characteristic for L2 as the position of mass loss from the system), the calculated population of Algols could be different.
We thank Peter Eggleton and the anonymous referee for their comments and suggestions.
References
- Brancewicz, H., & Dworak, T. 1980, AcA, 30, 501 (see also CDS, catalog: cats/II/150A) [NASA ADS] [Google Scholar]
- Budding, E., Erdem, A., Cicek, C., et al. 2004, A&A, 417, 263 (see also CDS, catalog: cats/J/A+A/417/263) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggleton, P. 2000, NewAR, 44, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1967, ZA, 65, 58 [Google Scholar]
- Kippenhahn, R., Kohl, L., & Weigert, A. 1967, ZA, 66, 58 [Google Scholar]
- Nakamura, M., & Nakamura, Y. 1987a, Ap&SS, 134, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, M., & Nakamura, Y. 1987b, Ap&SS, 134, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, C., & Eggleton, P. 2001, ApJ, 552, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Packet, W. 1988, Ph.D. dissertation, Vrije Universiteit Brussel, Brussels [Google Scholar]
- Paczynski, B. 1967a, AcA, 17, 193 [Google Scholar]
- Paczynski, B. 1967b, AcA, 17, 355 [Google Scholar]
- Peters, G. 2001, ASSL, 264, 79 [Google Scholar]
- Podsiadlowski, P., Joss, P., & Hsu, J. 1992, ApJ, 391, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Popova, E., Tutukov, A., & Yungelson, L. 1982, Ap&SS, 88, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Pourbaix, D., Tokovinin, A., Batten, A., et al. 2004, A&A, 424, 727 (see also CDS, The 9th catalog of Spectroscopic Binary orbits: cats/B/sb9) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rogers, F., & Iglesias, C. 1992, ApJS, 79, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. 1955, ApJ, 121, 161 [Google Scholar]
- Tassoul, J.-L. 2000, in Stellar Rotation (Cambridge University Press) [Google Scholar]
- Thorne, K. 1974, ApJ, 191, 507 [Google Scholar]
- Van Rensbergen, W. 2004, AASL, 298, 117 [Google Scholar]
- Van Rensbergen, W., De Loore, C., & Jansen, K. 2006, A&A, 446, 1071 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Rensbergen, W., De Greve, J. P., De Loore, C., & Mennekens, N. 2008, A&A, 487, 1129 (see also CDS, catalog: cats/J/A+A/487/1129) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warner, B. 1978, AcA, 28, 303 [Google Scholar]
- Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
Footnotes
- ... VUB-website
![[*]](/icons/foot_motif.png)
- VUB website, 2003-2009, http://www.vub.ac.be/astrofys.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13272fg1.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13272-09/Timg42.png)
|
Figure 1:
Amount of mass lost by a binary with a B-type primary at birth and an initial mass ratio
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13272fg2.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13272-09/Timg43.png)
|
Figure 2:
Amount of mass lost by a binary with a B-type primary at birth for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13272fg3.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13272-09/Timg44.png)
|
Figure 3:
Amount of mass lost by a binary with a B-type primary at birth for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13272fg4.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13272-09/Timg48.png)
|
Figure 4: Simulated distribution of mass ratios of Algols issued from a binary with a late B-type primary at birth and an initial orbital period so that case A RLOF occurs. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13272fg5.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13272-09/Timg50.png)
|
Figure 5: Simulated distribution of mass ratios of Algols issued from a binary with an early B-type primary at birth and initial orbital periods so that case A RLOF occurs. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13272fg6.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13272-09/Timg51.png)
|
Figure 6: Simulated distribution of orbital periods of Algols issued from a binary with a B-type primary at birth and initial orbital periods so that case A RLOF occurs. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}\tilde{K}~=~\frac{1}{K}~=~{{{\left[ \frac {R_{\rm g}} {R_{\od...
...t]} \over \frac{L_{\rm acc}}{L_{\odot}}\times (5770)^{4}}\cdot
\end{displaymath}](/articles/aa/full_html/2010/02/aa13272-09/img20.png)
![\begin{displaymath}\tilde{K} = 4.386 \times {{\left[\frac{M_{\rm d}}{M_{\odot}}+\frac{M_{\rm g}}{M_{\odot}}\right]}}^{1.735}\cdot
\end{displaymath}](/articles/aa/full_html/2010/02/aa13272-09/img26.png)
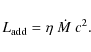
![\begin{displaymath}\eta~= 1.88\times{10^{-5}}\times {{\left[\frac{M_{\rm d}}{M_{...
...frac{M_{\rm g}}{M_{\odot}}\right]}}^{1.735}\times{D}\times{S}.
\end{displaymath}](/articles/aa/full_html/2010/02/aa13272-09/img31.png)
![\begin{displaymath}\tau_{\rm sync}~({\rm yr})={q^{-2}} \times {\left[ {a\over R_{\rm g}} \right]} ^{6}\cdot
\end{displaymath}](/articles/aa/full_html/2010/02/aa13272-09/img33.png)