| Issue |
A&A
Volume 510, February 2010
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200913187 | |
| Published online | 04 February 2010 | |
The XMM-Newton Wide Angle Survey (XWAS): the X-ray spectrum of type-1 AGN
S. Mateos1 - F. J. Carrera2 - M. J. Page3 - M. G. Watson1 - A. Corral4 - J. A. Tedds1 - J. Ebrero5 - M. Krumpe6 - A. Schwope7 - M. T. Ceballos2
1 - Department of Physics and Astronomy, University of Leicester, University Road, Leicester, UK
2 - Instituto de Física de Cantabria (CSIC-UC), 39005 Santander, Spain
3 - AA, Mullard Space Science Laboratory, University College London, Holmbury St Mary, Dorking, Surrey RH5 6NT, UK
4 - INAF - Osservatorio Astronomico di Brera, via Brera 28, 20121 Milan, Italy
5 - SRON - Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA, Utrecht, The Netherlands
6 - University of California, San Diego, Center for Astrophysics
& Space Sciences, 9500 Gilman Drive, La Jolla, CA 92093-0424, USA
7 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
Received 26 August 2009 / Accepted 11 December 2009
Abstract
Aims. We discuss the broad band X-ray properties of one of
the largest samples of X-ray selected type-1 AGN to date
(487 objects in total), drawn from the XMM-Newton Wide Angle Survey (XWAS). The objects presented in this work cover 2-10 keV (rest-frame) luminosities from
![]() and are detected up to redshift
and are detected up to redshift ![]() 4.
We constrain the overall properties of the broad band continuum, soft
excess and X-ray absorption, along with their dependence on the X-ray
luminosity and redshift. We discuss the implications for models of
AGN emission.
4.
We constrain the overall properties of the broad band continuum, soft
excess and X-ray absorption, along with their dependence on the X-ray
luminosity and redshift. We discuss the implications for models of
AGN emission.
Methods. We fitted the observed 0.2-12 keV broad band
spectra with various models to search for X-ray absorption and soft
excess. The F-test was used with a significance threshold of 99%
to statistically accept the detection of additional spectral
components.
Results. We constrained the mean spectral index of the broad band X-ray continuum to
![]()
![]() 0.02 with intrinsic dispersion
0.02 with intrinsic dispersion
![]() .
The continuum becomes harder at faint fluxes and at higher redshifts
and hard (2-10 keV) luminosities. The dependence of
.
The continuum becomes harder at faint fluxes and at higher redshifts
and hard (2-10 keV) luminosities. The dependence of ![]() with flux is likely due to undetected absorption rather than to
spectral variation. We found a strong dependence of the detection
efficiency of objects on the spectral shape. We expect this effect to
have an impact on the measured mean continuum shapes of sources at
different redshifts and luminosities. We detected excess absorption in
with flux is likely due to undetected absorption rather than to
spectral variation. We found a strong dependence of the detection
efficiency of objects on the spectral shape. We expect this effect to
have an impact on the measured mean continuum shapes of sources at
different redshifts and luminosities. We detected excess absorption in ![]() 3% of our objects, with rest-frame column densities
3% of our objects, with rest-frame column densities ![]() a few
a few
![]() .
The apparent mismatch between the optical classification and X-ray
properties of these objects is a challenge for the standard
orientation-based AGN unification model. We found that the
fraction of objects with detected soft excess is
.
The apparent mismatch between the optical classification and X-ray
properties of these objects is a challenge for the standard
orientation-based AGN unification model. We found that the
fraction of objects with detected soft excess is ![]() 36%. Using a thermal model, we constrained the soft excess mean rest-frame temperature and intrinsic dispersion to kT
36%. Using a thermal model, we constrained the soft excess mean rest-frame temperature and intrinsic dispersion to kT ![]() 100 eV and
100 eV and
![]()
![]() 34 eV. The origin of the soft excess as thermal emission from the
accretion disk or Compton scattered disk emission is ruled out on the
basis of the temperatures detected and the lack of correlation of the
soft excess temperature with the hard X-ray luminosity over more than
2 orders of magnitude in luminosity. Furthermore, the high
luminosities of the soft excess rule out an origin in the host galaxy.
34 eV. The origin of the soft excess as thermal emission from the
accretion disk or Compton scattered disk emission is ruled out on the
basis of the temperatures detected and the lack of correlation of the
soft excess temperature with the hard X-ray luminosity over more than
2 orders of magnitude in luminosity. Furthermore, the high
luminosities of the soft excess rule out an origin in the host galaxy.
Key words: galaxies: active - X-rays: galaxies - methods: observational - surveys - quasars: general
1 Introduction
It is now widely accepted that the emission of active galactic nuclei (AGN) in the X-ray band originates in the innermost regions, close to the energy source of the AGN, most probably an accreting supermassive black hole (SMBH). The study of the X-ray emission of AGN provides strong constraints on their powering mechanism and gives insight to the geometry and physical conditions of the matter surrounding the SMBH.
The typical spectrum of both low luminosity Seyfert galaxies and bright QSOs in the hard X-ray band (![]() 2 keV) is dominated by a power-law emission with a photon index
2 keV) is dominated by a power-law emission with a photon index ![]()
![]() 2 with intrinsic dispersion
2 with intrinsic dispersion
![]()
![]() 0.2-0.3 (e.g. Mainieri et al. 2007; Tozzi et al. 2006; Mateos et al. 2005b).
This hard X-ray spectral component is believed to originate in hot
plasma surrounding the accretion disk which Compton up-scatters UV-soft
X-ray thermal emission from the disk into the hard X-ray band (Haardt
& Maraschi 1991).
0.2-0.3 (e.g. Mainieri et al. 2007; Tozzi et al. 2006; Mateos et al. 2005b).
This hard X-ray spectral component is believed to originate in hot
plasma surrounding the accretion disk which Compton up-scatters UV-soft
X-ray thermal emission from the disk into the hard X-ray band (Haardt
& Maraschi 1991).
Part of the primary power-law continuum emission is then reprocessed in the disk producing
a reflection spectrum characterised by a hardening of the spectrum above ![]() 10 keV and a fluorescent Fe K
10 keV and a fluorescent Fe K![]() emission line around
emission line around ![]() 6.4 keV mostly detected in Seyfert-like luminosity objects (Pounds et al. 1990).
Signatures of ionised and/or cold gas have also been detected in high
signal-to-noise X-ray spectra of both Seyfert galaxies and QSOs
(e.g. Piconcelli et al. 2005). Moreover, an important fraction of AGN shows an excess of emission with respect to the power-law emerging below
6.4 keV mostly detected in Seyfert-like luminosity objects (Pounds et al. 1990).
Signatures of ionised and/or cold gas have also been detected in high
signal-to-noise X-ray spectra of both Seyfert galaxies and QSOs
(e.g. Piconcelli et al. 2005). Moreover, an important fraction of AGN shows an excess of emission with respect to the power-law emerging below ![]() 2 keV, the so-called soft excess,
whose nature is still debated. The soft excess has been interpreted as
the tail of the thermal emission from the accretion disk (Turner &
Pounds 1989) or Comptonization of EUV accretion disk photons (Kawaguchi et al. 2001).
However, when the soft excess is fitted with a thermal model, the
measured temperature is roughly constant over several orders of
magnitude in luminosity and BH mass (
2 keV, the so-called soft excess,
whose nature is still debated. The soft excess has been interpreted as
the tail of the thermal emission from the accretion disk (Turner &
Pounds 1989) or Comptonization of EUV accretion disk photons (Kawaguchi et al. 2001).
However, when the soft excess is fitted with a thermal model, the
measured temperature is roughly constant over several orders of
magnitude in luminosity and BH mass (
![]()
![]() 0.1 keV, Crummy et al. 2006; Gierlinski & Done 2004).
This is a major problem for models based on accretion disk continuum
emission because the disk temperature is expected to vary with both the
mass of the black hole and the accretion rate. Furthermore, the
measured soft excess temperatures are too high to be the high energy
tail of the accretion disk emission. In the past few years two
alternative models with very different geometries have been proposed to
explain the origin of the soft excess, both relating this spectral
component to atomic rather than continuum processes: the soft excess
could be produced by absorption from a relativistically outflowing warm
gas which is optically thin and in the line of sight, i.e. a wind
above the disk (Gierlinski & Done 2004), or by enhancement of reprocessing of disk emission in optically thick material out of the line of sight (Crummy et al. 2006). These two models are indistinguishable in the 0.2-10 keV band (see Ponti et al. 2008, and references therein).
0.1 keV, Crummy et al. 2006; Gierlinski & Done 2004).
This is a major problem for models based on accretion disk continuum
emission because the disk temperature is expected to vary with both the
mass of the black hole and the accretion rate. Furthermore, the
measured soft excess temperatures are too high to be the high energy
tail of the accretion disk emission. In the past few years two
alternative models with very different geometries have been proposed to
explain the origin of the soft excess, both relating this spectral
component to atomic rather than continuum processes: the soft excess
could be produced by absorption from a relativistically outflowing warm
gas which is optically thin and in the line of sight, i.e. a wind
above the disk (Gierlinski & Done 2004), or by enhancement of reprocessing of disk emission in optically thick material out of the line of sight (Crummy et al. 2006). These two models are indistinguishable in the 0.2-10 keV band (see Ponti et al. 2008, and references therein).
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{13187f1.eps}\hspace*{8mm}
...
...7f3.eps}\hspace*{7mm}
\includegraphics[width=8cm,clip]{13187f4.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg21.png)
|
Figure 1: Top: redshift distribution ( left) and 2-10 keV X-ray luminosity (corrected for absorption) vs. redshift ( right) of the XWAS type-1 AGN selected for our study. Bottom: distribution of EPIC 0.2-12 keV net counts in the X-ray spectra of the sources ( left) and 2-10 keV band flux distribution ( right). For clarity the last bin in the distribution of EPIC counts includes all objects with spectra with more than 2000 counts. The dashed vertical line indicates the limit in counts we used for this study. |
| Open with DEXTER | |
In most surveys AGN are optically classified as type-1 AGN if broad lines with velocity widths
![]() are present in their optical spectra. Objects where only narrow lines (velocity widths
are present in their optical spectra. Objects where only narrow lines (velocity widths
![]() )
are seen are classified as type-2 AGN. According to AGN unification
models the different properties observed for type-1 and type-2 AGN can
be explained solely as an orientation effect (e.g. Antonucci 1993; Urry & Padovani 1995).
In type-1 AGN our line of sight to the nucleus is not intercepted
by optically obscuring material, and therefore we see the central
engine and the broad line region. The line of sight in type-2 AGN
intercepts the obscuring material hiding both the central engine and
the broad line region. Therefore type-1 AGN are expected to show little
or no obscuration in X-rays while type-2 AGN should be more heavily
absorbed in X-rays. Spectral analyses have shown that the optical
type vs. X-ray properties for most AGN generally agree with the
predictions from AGN unification models. However, in recent years,
the number of cases where the predictions from AGN unification
models do not match the observations has increased substantially, as
significant absorption has been detected in
)
are seen are classified as type-2 AGN. According to AGN unification
models the different properties observed for type-1 and type-2 AGN can
be explained solely as an orientation effect (e.g. Antonucci 1993; Urry & Padovani 1995).
In type-1 AGN our line of sight to the nucleus is not intercepted
by optically obscuring material, and therefore we see the central
engine and the broad line region. The line of sight in type-2 AGN
intercepts the obscuring material hiding both the central engine and
the broad line region. Therefore type-1 AGN are expected to show little
or no obscuration in X-rays while type-2 AGN should be more heavily
absorbed in X-rays. Spectral analyses have shown that the optical
type vs. X-ray properties for most AGN generally agree with the
predictions from AGN unification models. However, in recent years,
the number of cases where the predictions from AGN unification
models do not match the observations has increased substantially, as
significant absorption has been detected in ![]() 10% type-1 AGN (Cappi et al. 2006; Mateos et al. 2005b; Akylas et al. 2004) while type-2 AGN have been detected without any signatures of X-ray absorption (Panessa et al. 2009; Bianchi et al. 2008; Corral et al. 2005; Panessa & Bassani 2002).
10% type-1 AGN (Cappi et al. 2006; Mateos et al. 2005b; Akylas et al. 2004) while type-2 AGN have been detected without any signatures of X-ray absorption (Panessa et al. 2009; Bianchi et al. 2008; Corral et al. 2005; Panessa & Bassani 2002).
It is still not clear whether the X-ray properties of AGN depend on the
luminosity or have any spectral variation with redshift. Various
studies of the X-ray photon index have produced different results. Some
authors claim an anti-correlation between the spectral photon
index ![]() and the X-ray luminosity (Young et al. 2009; Saez et al. 2008; Page et al. 2005) while other studies suggest the opposite correlation (Dai et al. 2004) or no correlation at
all (Winter et al. 2009; Mateos et al. 2005b; George et al. 2000; Reeves & Turner 2000).
Studies of the X-ray spectra of AGN have generally shown no clear
dependence of the AGN X-ray properties on the redshift (Mateos
et al. 2005a), although some exceptions have been found (Kelly et al. 2007).
and the X-ray luminosity (Young et al. 2009; Saez et al. 2008; Page et al. 2005) while other studies suggest the opposite correlation (Dai et al. 2004) or no correlation at
all (Winter et al. 2009; Mateos et al. 2005b; George et al. 2000; Reeves & Turner 2000).
Studies of the X-ray spectra of AGN have generally shown no clear
dependence of the AGN X-ray properties on the redshift (Mateos
et al. 2005a), although some exceptions have been found (Kelly et al. 2007).
Here we investigate the broad band X-ray properties of 487 type-1 AGN from the XMM-Newton Wide Angle Survey (XWAS). We selected only those objects having X-ray spectra with sufficient signal-to-noise ratio (hereafter S/N) to perform a basic spectral analysis. This is one of the largest X-ray selected samples of type-1 AGN assembled to date for which constraints on the X-ray properties of the sources can be directly derived from a spectral analysis. A study of the X-ray properties of 156 type-1 AGN observed by XMM-Newton was recently presented by Bianchi et al. (2008). As this study is based on type-1 AGN in targeted observations, it has the advantage that most of the spectra are characterised by high S/N, but it has the disadvantage of complex selection function, biased towards ``interesting'' objects, and it mainly samples AGN in the local Universe. The type-1 AGN from XWAS span more than 3 orders of magnitude in X-ray luminosity and are detected at redshifts from 0.08 to 3.9. Hence, our type-1 AGN sample is ideal to investigate whether the properties of the broad band continuum shape, X-ray absorption and soft excess in type-1 AGN depend on the X-ray luminosity of the objects and whether they have evolved with cosmic time.
This paper is organised as follows: in Sect. 2 we describe the XMM-Newton
Wide Angle Survey and the compilation of the sample of type-1 AGN. In
Sect. 3 we discuss the procedure for extraction of the X-ray
spectra of the objects and the spectral fitting. In Sect. 4 we
present and discuss the results of the spectral analysis. The summary
and conclusions of our analysis are reported in Sect. 5.
Throughout this paper we have adopted the WMAP derived cosmology with
![]() ,
,
![]() and
and
![]() (Spergel et al. 2003).
(Spergel et al. 2003).
2 The XMM-Newton Wide Angle Survey (XWAS)
The XMM-Newton Wide Angle Survey (XWAS) identification programme was
based on optical multi-fibre spectroscopy obtained at the Anglo
Australian Telescope (AAT) Two Degree Field (2dF; Lewis et al. 2002)
for the counterparts of serendipitous X-ray sources, originally
selected from 68 spatially distinct pointings made by XMM-Newton between June 2000 and May 2003. The fields targeted by XWAS cover a net sky area ![]()
![]() 11.5 deg2. A full description of this survey will be presented in a forthcoming paper.
11.5 deg2. A full description of this survey will be presented in a forthcoming paper.
The XMM-Newton field selection for XWAS prioritised those observations
with adjacent or overlapping coverage, to take optimum advantage of the
2 degree diameter of the 2dF spectrograph. Counterparts for
2dF spectroscopy were primarily selected from the SuperCOSMOS Sky
Survey (Hambly et al. 2001),
supplemented by additional counterparts extracted from Isaac Newton
Telescope Wide Field Camera (INT WFC) imaging. Only candidates
down to R ![]() 21 were selected, with priority given to X-ray sources with 0.5-4.5 keV flux
21 were selected, with priority given to X-ray sources with 0.5-4.5 keV flux
![]() .
The XWAS programme was primarily aimed at accumulating as large a
sample of X-ray sources identifications as possible and is not complete
to these magnitude and X-ray flux limits.
.
The XWAS programme was primarily aimed at accumulating as large a
sample of X-ray sources identifications as possible and is not complete
to these magnitude and X-ray flux limits.
Optical spectroscopy was obtained for the potential counterparts of a total of ![]() 3000 X-ray
sources (although, as the 2dF provides more fibres per field than
required for this programme, a significant fraction of the
spectroscopic fibres were placed on lower probability counterparts and
X-ray sources with lower detection likelihoods). The XWAS 2dF
spectroscopy provides an effective resolution
3000 X-ray
sources (although, as the 2dF provides more fibres per field than
required for this programme, a significant fraction of the
spectroscopic fibres were placed on lower probability counterparts and
X-ray sources with lower detection likelihoods). The XWAS 2dF
spectroscopy provides an effective resolution
![]() over a wavelength range
over a wavelength range ![]() 3850-8250 Å and
reaches a S/N of
3850-8250 Å and
reaches a S/N of ![]() 5 at 5500 Å for V=21 mag,
sufficient to provide reliable object classification and redshift
determination together with a reasonable characterisation of the
optical continuum shape.
5 at 5500 Å for V=21 mag,
sufficient to provide reliable object classification and redshift
determination together with a reasonable characterisation of the
optical continuum shape.
The XWAS survey provides data of sufficient quality for the optical spectroscopic identification of ![]() 980 of the sample X-ray sources. Of these, the majority,
980 of the sample X-ray sources. Of these, the majority, ![]() 65%, are identified as type-1 AGN (velocity widths
65%, are identified as type-1 AGN (velocity widths ![]() 1500 km s-1). The remainder comprise narrow emission line galaxies (NELGs;
1500 km s-1). The remainder comprise narrow emission line galaxies (NELGs; ![]() 16%, velocity widths
16%, velocity widths ![]() 1500 km s-1) absorption line galaxies (
1500 km s-1) absorption line galaxies (![]() 6%) and Galactic stars (
6%) and Galactic stars (![]() 13%).
13%).
Corral et al. (2008) computed the rest-frame X-ray averaged spectrum and constrained the mean Fe K![]() line emission properties for type-1 AGN up to redshift
line emission properties for type-1 AGN up to redshift ![]() 3.5 while Krumpe et al. (2008)
investigated the X-ray properties of the most luminous type-2 AGNs. In
this paper we concentrate on the X-ray spectral analysis of the
487 type-1 AGN in the sample with sufficient S/N in their X-ray
spectra (
3.5 while Krumpe et al. (2008)
investigated the X-ray properties of the most luminous type-2 AGNs. In
this paper we concentrate on the X-ray spectral analysis of the
487 type-1 AGN in the sample with sufficient S/N in their X-ray
spectra (![]() 75 EPIC
counts in the 0.2-12 keV energy band) to provide constraints on
their broad band X-ray properties. The top row in Fig. 1
shows the redshift distribution of the sources (left) and the
distribution of 2-10 keV luminosity vs. redshift (right). The
bottom row shows the distributions of 0.2-12 keV EPIC net counts
(left) and 2-10 keV fluxes (right). Fluxes and luminosities were
computed from the best-fit model and corrected for Galactic absorption.
Luminosities are also corrected for intrinsic X-ray absorption.
The great majority of AGN, including type-1 AGN, have X-ray-to-optical
flux ratios (X/O) in the range 0.1 < X/O < 10
(e.g. Brusa et al. 2007). The imposed limit of R
75 EPIC
counts in the 0.2-12 keV energy band) to provide constraints on
their broad band X-ray properties. The top row in Fig. 1
shows the redshift distribution of the sources (left) and the
distribution of 2-10 keV luminosity vs. redshift (right). The
bottom row shows the distributions of 0.2-12 keV EPIC net counts
(left) and 2-10 keV fluxes (right). Fluxes and luminosities were
computed from the best-fit model and corrected for Galactic absorption.
Luminosities are also corrected for intrinsic X-ray absorption.
The great majority of AGN, including type-1 AGN, have X-ray-to-optical
flux ratios (X/O) in the range 0.1 < X/O < 10
(e.g. Brusa et al. 2007). The imposed limit of R ![]() 21 for optical follow-up of the XWAS sources, implies that as we
approach the X-ray flux limit of the survey we are better sampling
type-1 AGN with typically lower X-ray to optical flux ratios than the
overall population. We note however that X-ray spectral analyses of AGN
samples not suffering from this identification bias do not find that
the X-ray properties of type-1 AGN vary with X/O (see e.g. Tozzi
et al. 2006).
Hence we do not expect the imposed limit for optical follow-up of the
XWAS sources to have any impact on the results of our analysis.
21 for optical follow-up of the XWAS sources, implies that as we
approach the X-ray flux limit of the survey we are better sampling
type-1 AGN with typically lower X-ray to optical flux ratios than the
overall population. We note however that X-ray spectral analyses of AGN
samples not suffering from this identification bias do not find that
the X-ray properties of type-1 AGN vary with X/O (see e.g. Tozzi
et al. 2006).
Hence we do not expect the imposed limit for optical follow-up of the
XWAS sources to have any impact on the results of our analysis.
We matched our type-1 sample with the 1.4-GHz NRAO VLA Sky Survey (NVSS, Condon et al. 1998). The survey covers the entire sky north to -40 deg declination, hence we have radio coverage for 410 out of the 487 objects in our sample. Only 10 objects were detected above the NVSS completeness limit of 2.5 mJy. Therefore we expect the contribution to our sample from radio-loud AGN to be less than 3%, and hence our sample to be dominated by radio quiet AGN.
2.1 The X-ray data
We searched the XMM-Newton archive for all the available observations of XWAS sources. The number of XMM-Newton fields that overlap with the original XWAS selected pointings at the time of this study was 119 observations in total.
In order to get the X-ray source list for each observation we used the same source detection
configuration as in the second XMM-Newton serendipitous source catalogue, 2XMM (see Watson et al. 2008,
for details). Source detection is carried out on data from the three
EPIC cameras (pn, MOS1 and MOS2) and on five energy bands
simultaneously (0.2-0.5 keV, 0.5-1 keV, 1-2 keV,
2-4.5 keV and 4.5-12 keV). The final XWAS X-ray source
catalogue includes all detections with EPIC 0.2-12 keV detection
likelihood ![]() 6 and contains
6 and contains ![]() 7000 unique X-ray sources.
7000 unique X-ray sources.
3 Spectral analysis
3.1 X-ray spectral extraction
Spectra were extracted for each detection and EPIC camera in circular regions centred at the source positions. The size of the source extraction regions was selected to optimise the S/N via the SAS task eregionanalyse. Background spectra were obtained in annular regions centred at the source position after masking out nearby sources falling in the extraction regions. If the background region did not have sufficient S/N we used source-free circular regions near the sources and in the same CCD. Appropriate response matrices and effective area curves were obtained for each detection using the SAS tasks rmfgen and arfgen respectively.
For each source all detections were merged to obtain a pn and a single
MOS spectrum over the observed energy range 0.2-12 keV.
As the differences between the MOS1 and MOS2 response
matrices are of just a few per cent we created combined MOS source
and background spectra and response matrices. Merged source and
background spectra were obtained by adding the individual spectra.
Backscale values (size of the regions used to extract the spectra)
and calibration matrices for the combined spectra were obtained
weighting the input data with the exposure times. In order to use
the ![]() minimisation during the spectral fitting spectra were grouped to a minimum of 15 counts per bin.
minimisation during the spectral fitting spectra were grouped to a minimum of 15 counts per bin.
3.2 Spectral fitting
The spectral fitting of the 487 XWAS type-1 AGN with more than
75 EPIC counts in the 0.2-12 keV band was carried out with
the XSPEC package (Arnaud 1996). Hereafter quoted errors refer to the 90% confidence level for one interesting parameter (i.e.
![]() = 2.71)
unless otherwise stated. We started with a joint fitting of MOS and
pn spectra with a power-law model with fixed Galactic absorption (
= 2.71)
unless otherwise stated. We started with a joint fitting of MOS and
pn spectra with a power-law model with fixed Galactic absorption (
![]()
![]()
![]() in
XSPEC). The spectral parameters were tied to the same value while the
normalisations were left free to vary in order to account for flux
cross-calibration discrepancies between the EPIC MOS and pn
cameras (see Mateos et al. 2009). The Galaxy H column density values for each field were obtained using the
ftool nh
in
XSPEC). The spectral parameters were tied to the same value while the
normalisations were left free to vary in order to account for flux
cross-calibration discrepancies between the EPIC MOS and pn
cameras (see Mateos et al. 2009). The Galaxy H column density values for each field were obtained using the
ftool nh![]() . The values are derived from the HI map of Dickey & Lockman (1990).
Two additional model components were added to the simple power-law
model to search for intrinsic absorption and soft excess emission:
a redshifted neutral absorption component (
. The values are derived from the HI map of Dickey & Lockman (1990).
Two additional model components were added to the simple power-law
model to search for intrinsic absorption and soft excess emission:
a redshifted neutral absorption component (
![]() in XSPEC) and a blackbody spectrum (
in XSPEC) and a blackbody spectrum (
![]() in XSPEC). We also used a partial covering model (
in XSPEC). We also used a partial covering model (
![]() in
XSPEC) to fit the spectral complexity observed in some of our sources,
but we found that the quality of the fits did not improve significantly
for any source with respect to the above models.
in
XSPEC) to fit the spectral complexity observed in some of our sources,
but we found that the quality of the fits did not improve significantly
for any source with respect to the above models.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13187f5.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg40.png)
|
Figure 2:
Best-fit |
| Open with DEXTER | |
The significance of the detection of additional components in the
X-ray spectra of our sources was measured with the F-test. The F-test
measures the significance of a change in ![]() when new components are added to the model. We used a significance
threshold of 99% to accept the detection of soft excess and/or
intrinsic absorption. No more spectral complexity was detected,
hence there was no need for additional model components. The lack of
detection of the Fe K
when new components are added to the model. We used a significance
threshold of 99% to accept the detection of soft excess and/or
intrinsic absorption. No more spectral complexity was detected,
hence there was no need for additional model components. The lack of
detection of the Fe K![]() line
emission is likely due to the fact that most spectra do not have
sufficient S/N to detect this spectral component. However,
it has also been shown that the most luminous AGN do not tend to
reveal iron emission (e.g. Corral et al. 2008; Krumpe et al. 2008; Iwasawa & Taniguchi 1993).
line
emission is likely due to the fact that most spectra do not have
sufficient S/N to detect this spectral component. However,
it has also been shown that the most luminous AGN do not tend to
reveal iron emission (e.g. Corral et al. 2008; Krumpe et al. 2008; Iwasawa & Taniguchi 1993).
Figure 2 shows the quality of the spectral fitting, where the best-fit ![]() values are shown as a function of the number of degrees of freedom (n d.o.f.) of the fits. The solid line indicates the value corresponding to
values are shown as a function of the number of degrees of freedom (n d.o.f.) of the fits. The solid line indicates the value corresponding to ![]() = n d.o.f. The upper and lower dashed lines indicate for a given number of n d.o.f. the range of
= n d.o.f. The upper and lower dashed lines indicate for a given number of n d.o.f. the range of ![]() above and below which we expect a 1% probability of finding such high/low values of
above and below which we expect a 1% probability of finding such high/low values of ![]() if the model is correct. We see that the quality of our fits is very good, only 5% and 1% of the fits have
if the model is correct. We see that the quality of our fits is very good, only 5% and 1% of the fits have ![]() values that lie above or below the region delineated by the dashed lines respectively.
values that lie above or below the region delineated by the dashed lines respectively.
Table 1: Summary of the results of the spectral fitting.
A summary of the results of the spectral fitting is presented in Table 1.
As expected most of our type-1 AGN are best fitted with a simple
power-law model corrected for Galactic absorption. Excess X-ray
absorption above the Galactic value and a soft excess emission were
detected in ![]() 4% and
4% and ![]() 9% of the sources respectivelly. We used the recipe in Mateos et al. (2005a)
to obtain the intrinsic fraction of objects with detected soft excess
and/or intrinsic absorption. The method takes into account the expected
number of spurious detections (1% expected for the chosen F-test
significance threshold) using Bayesian statistics. We found that
intrinsic absorption and soft excess emission were detected with a
significance
9% of the sources respectivelly. We used the recipe in Mateos et al. (2005a)
to obtain the intrinsic fraction of objects with detected soft excess
and/or intrinsic absorption. The method takes into account the expected
number of spurious detections (1% expected for the chosen F-test
significance threshold) using Bayesian statistics. We found that
intrinsic absorption and soft excess emission were detected with a
significance ![]() 99% in 3%
99% in 3% ![]() 1.5% and 7.3%
1.5% and 7.3% ![]() 2% of the sources respectively.
2% of the sources respectively.
4 Results and discussion
4.1 The broad band X-ray continuum
Figure 3 (top) shows the distribution of best-fit ![]() values (solid line). In order to constrain the mean continuum shape of our type-1 AGN,
values (solid line). In order to constrain the mean continuum shape of our type-1 AGN,
![]() ,
we have
assumed that the distribution of spectral slopes can be well reproduced with a Gaussian of mean
,
we have
assumed that the distribution of spectral slopes can be well reproduced with a Gaussian of mean
![]() and dispersion
and dispersion
![]() .
The best simultaneous estimates of the average photon index
.
The best simultaneous estimates of the average photon index
![]() and the intrinsic spread
and the intrinsic spread
![]() were obtained with a maximum likelihood technique accounting for both
the errors in the measurements and the intrinsic dispersion of values
(Maccacaro et al. 1988). Figure 3 shows the best-fit Gaussian distribution (top, dashed line) and the 1
were obtained with a maximum likelihood technique accounting for both
the errors in the measurements and the intrinsic dispersion of values
(Maccacaro et al. 1988). Figure 3 shows the best-fit Gaussian distribution (top, dashed line) and the 1![]() ,
2
,
2![]() and 3
and 3![]() contours for the two parameters together with the best-fit values,
contours for the two parameters together with the best-fit values,
![]()
![]() 0.02 and
0.02 and
![]() (cross). The errors in the parameters were obtained from the 1
(cross). The errors in the parameters were obtained from the 1![]() contour.
These values are in excellent agreement with recent measurements of the
mean photon index and intrinsic dispersion for type-1 AGN found in the
literature (e.g. Young et al. 2009; Dadina 2008; Mainieri et al. 2007; Page et al. 2006; Mateos et al. 2005a,b). We note that hard X-ray selected samples (
contour.
These values are in excellent agreement with recent measurements of the
mean photon index and intrinsic dispersion for type-1 AGN found in the
literature (e.g. Young et al. 2009; Dadina 2008; Mainieri et al. 2007; Page et al. 2006; Mateos et al. 2005a,b). We note that hard X-ray selected samples (![]() 20 keV) from the INTEGRAL and Swift satellites report marginally flatter spectral
slopes for bright type-1 AGN,
20 keV) from the INTEGRAL and Swift satellites report marginally flatter spectral
slopes for bright type-1 AGN, ![]()
![]() 1.7-1.8 (Molina et al. 2009; Winter et al. 2009; Panessa et al. 2008).
This could be explained if these surveys are biased towards sources
with flatter spectral slopes or with a substantial Compton reflection
component as these objects should be more easily detected at such high
X-ray energies.
1.7-1.8 (Molina et al. 2009; Winter et al. 2009; Panessa et al. 2008).
This could be explained if these surveys are biased towards sources
with flatter spectral slopes or with a substantial Compton reflection
component as these objects should be more easily detected at such high
X-ray energies.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13187f6.eps}\vspace*{5mm}
\includegraphics[width=8cm,clip]{13187f7.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg48.png)
|
Figure 3:
Top: distribution of best-fit photon indexes. The dashed line
shows the results of the maximum likelihood technique used to constrain
the mean spectral index of the broad band X-ray continuum and its
intrinsic dispersion (see text for details). Bottom: 1 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{13187f4n.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg50.png)
|
Figure 4:
Left: from top to bottom broad band continuum
shape vs. 0.5-2 keV flux, 2-10 keV luminosity and
redshift respectively. The error bars at the top of the plots indicate
the mean error in the measurements. Right: mean spectral index of the broad band X-ray continuum,
|
| Open with DEXTER | |
4.1.1 Dependence of 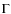 on the flux, luminosity and redshift
on the flux, luminosity and redshift
We have investigated whether the continuum shape of type-1 AGN depends
on the soft (0.5-2 keV) X-ray flux, hard (2-10 keV) X-ray
luminosity and redshift of the sources. Fluxes and luminosities were
computed from the best-fit model and corrected for Galactic absorption.
Luminosities are also corrected for intrinsic X-ray absorption. We use
hard X-ray luminosities because the measurements are less affected by
uncertainties in the detected amount of X-ray absorption. However,
to investigate the dependence of the spectral index on flux we
used fluxes in the 0.5-2 keV band. For samples of objects derived
by using different energy bands simultaneously in the source detection
procedure such as this, the number of objects detected only in the soft
band increases at faint hard (2-10 keV) fluxes. This is due to the
fact that at faint 2-10 keV fluxes it is more difficult to detect
sources with flat spectral slopes because their emission peaks at
energies above ![]() 2 keV where the sensitivity of the X-ray detectors is much lower. As already stated in Mateos et al. (2005a; see Fig. 6
in that paper) this produces an apparent softening of the objects' mean
spectral index as we approach the survey limit in the hard band.
2 keV where the sensitivity of the X-ray detectors is much lower. As already stated in Mateos et al. (2005a; see Fig. 6
in that paper) this produces an apparent softening of the objects' mean
spectral index as we approach the survey limit in the hard band.
The left column in Fig. 4 shows the distributions of best-fit ![]() values vs.
flux, luminosity and redshift. For reasons of simplicity error bars in
the individual measurements are not shown on the plot. The error bars
at the top of the plots indicate the mean error in
values vs.
flux, luminosity and redshift. For reasons of simplicity error bars in
the individual measurements are not shown on the plot. The error bars
at the top of the plots indicate the mean error in ![]() .
A Spearman rank correlation test indicates that
.
A Spearman rank correlation test indicates that ![]() correlates with the soft X-ray flux (
correlates with the soft X-ray flux (![]() = 0.18, prob = 1
= 0.18, prob = 1 ![]() 10-4), in the sense that fainter objects have flatter continuum slopes. On the other hand
10-4), in the sense that fainter objects have flatter continuum slopes. On the other hand ![]() seems to be anti-correlated with both the hard X-ray luminosity (
seems to be anti-correlated with both the hard X-ray luminosity (![]() = -0.17, prob = 1
= -0.17, prob = 1 ![]() 10-3) and redshift (
10-3) and redshift (![]() = -0.14, prob = 2
= -0.14, prob = 2 ![]() 10-3), i.e.
10-3), i.e. ![]() becomes flatter at higher luminosities and redshifts.
These trends become more evident when plotting
becomes flatter at higher luminosities and redshifts.
These trends become more evident when plotting
![]() instead of
instead of ![]() ,
binned in flux, luminosity and redshift (Fig. 4
right column). The bins were defined to have at least
50 measurements per bin. Note the different scales used on the
right hand plots in Fig. 4 compared to the corresponding figures on the left. Mean
,
binned in flux, luminosity and redshift (Fig. 4
right column). The bins were defined to have at least
50 measurements per bin. Note the different scales used on the
right hand plots in Fig. 4 compared to the corresponding figures on the left. Mean ![]() values
were obtained with the maximum likelihood method described before
(squares) while the corresponding errors are the measured intrinsic
dispersion of
values
were obtained with the maximum likelihood method described before
(squares) while the corresponding errors are the measured intrinsic
dispersion of ![]() for each bin. It is unlikely that the observed trends are affected by outliers in the distribution of
for each bin. It is unlikely that the observed trends are affected by outliers in the distribution of ![]() values
in each bin, as these typically correspond to spectra with
low S/N and hence larger associated uncertainties, and we
accounted for the uncertainties in the computations of
values
in each bin, as these typically correspond to spectra with
low S/N and hence larger associated uncertainties, and we
accounted for the uncertainties in the computations of
![]() .
.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13187f14.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg52.png)
|
Figure 5: Stacked rest-frame
unfolded spectra of our sources in redshift bins (data points). The
values at the top-left of each spectrum indicate the redshift range and
mean 2-10 keV luminosity of the objects on each bin. The
horizontal lines show a power-law model with photon index |
| Open with DEXTER | |
We have investigated whether the spectral complexity in type-1 AGN can explain the observed trends in ![]() .
At rest-frame energies below
.
At rest-frame energies below ![]() 2 keV,
intrinsic X-ray absorption and soft excess emission are important
contributors to the X-ray spectra of AGN. Nevertheless, at low
redshifts accurate constraints of
2 keV,
intrinsic X-ray absorption and soft excess emission are important
contributors to the X-ray spectra of AGN. Nevertheless, at low
redshifts accurate constraints of ![]() become more difficult especially in the low count statistics regime,
as the detection of soft excess or excess absorption might not be
significant enough to be accepted by our adopted detection threshold
(F-test
become more difficult especially in the low count statistics regime,
as the detection of soft excess or excess absorption might not be
significant enough to be accepted by our adopted detection threshold
(F-test ![]() 99%). Furthermore, the typical absorbing column densities detected in type-1 AGN do not exceed a few
99%). Furthermore, the typical absorbing column densities detected in type-1 AGN do not exceed a few
![]() ,
and hence are more difficult to detect especially at high
redshifts where the signatures of absorption shift outside the observed
band-pass. Undetected spectral complexity can have an important effect
on the measured values of
,
and hence are more difficult to detect especially at high
redshifts where the signatures of absorption shift outside the observed
band-pass. Undetected spectral complexity can have an important effect
on the measured values of ![]() as even moderate absorption (
as even moderate absorption (
![]() )
can still produce apparently flatter spectral slopes than the canonical value for type-1 AGN. In Fig. 4 (left) we see a number of objects in our sample with best-fit
)
can still produce apparently flatter spectral slopes than the canonical value for type-1 AGN. In Fig. 4 (left) we see a number of objects in our sample with best-fit ![]() values deviating more than 3
values deviating more than 3![]() from the mean. We found that all the objects with significantly flatter spectral slopes (31 objects with
from the mean. We found that all the objects with significantly flatter spectral slopes (31 objects with ![]()
![]() 1.4)
show curvature at the lowest energies, however the signatures of
absorption are not strong enough to be statistically detected in the
fitting process. Undetected X-ray absorption can explain the apparent
hardening of the mean continuum shape of our objects at faint soft
fluxes, as the S/N of the spectra decreases with the flux as indicated
in Fig. 4
(top-left). On the other hand a steepening of the spectra at the
softest energies, indicative of soft excess emission, was clearly
present in the objects with the softest spectral slopes in our sample.
However, in all cases the signature of this component was not strong
enough to be detected above our significance threshold.
1.4)
show curvature at the lowest energies, however the signatures of
absorption are not strong enough to be statistically detected in the
fitting process. Undetected X-ray absorption can explain the apparent
hardening of the mean continuum shape of our objects at faint soft
fluxes, as the S/N of the spectra decreases with the flux as indicated
in Fig. 4
(top-left). On the other hand a steepening of the spectra at the
softest energies, indicative of soft excess emission, was clearly
present in the objects with the softest spectral slopes in our sample.
However, in all cases the signature of this component was not strong
enough to be detected above our significance threshold.
In order to further investigate the scatter in the observed
![]() at different fluxes, redshifts and luminosities, we fitted the X-ray
spectra of the sources in the 2-10 keV rest-frame band a power-law
model as the measured hard X-ray continuum of type-1 AGN is expected to
be less affected by soft excess emission and/or absorption. We fitted
only sources with at least 50 EPIC counts in the 2-10 keV
rest-frame band (
at different fluxes, redshifts and luminosities, we fitted the X-ray
spectra of the sources in the 2-10 keV rest-frame band a power-law
model as the measured hard X-ray continuum of type-1 AGN is expected to
be less affected by soft excess emission and/or absorption. We fitted
only sources with at least 50 EPIC counts in the 2-10 keV
rest-frame band (![]() 60%
of the sources in the total sample). We checked that the objects with
enough S/N in their 2-10 keV rest-frame spectra have the same
0.5-2 keV flux, 2-10 keV luminosity and redshift
distributions as the total sample. The mean continuum shapes measured
in this way are shown in Fig. 4 (right column, circles). In this case we have not used the maximum likelihood analysis to compute
60%
of the sources in the total sample). We checked that the objects with
enough S/N in their 2-10 keV rest-frame spectra have the same
0.5-2 keV flux, 2-10 keV luminosity and redshift
distributions as the total sample. The mean continuum shapes measured
in this way are shown in Fig. 4 (right column, circles). In this case we have not used the maximum likelihood analysis to compute
![]() as the typical number of sources per bin is only
as the typical number of sources per bin is only ![]() 25-30.
The mean spectral slopes were obtained by weighting with the errors in
the individual measurements while the error bars correspond to the 1
25-30.
The mean spectral slopes were obtained by weighting with the errors in
the individual measurements while the error bars correspond to the 1![]() dispersion
in the values. We found that the spectral fitting in the 2-10 keV
rest-frame band returned a substantially harder
dispersion
in the values. We found that the spectral fitting in the 2-10 keV
rest-frame band returned a substantially harder
![]() at the lowest luminosities. Because these objects are detected at the
lowest redshifts sampled by our survey it is not surprising to find
that the 2-10 keV rest-frame fits returned a substantially harder
at the lowest luminosities. Because these objects are detected at the
lowest redshifts sampled by our survey it is not surprising to find
that the 2-10 keV rest-frame fits returned a substantially harder
![]() at low redshifts. It is interesting to note that we still find sources at high redshifts (
at low redshifts. It is interesting to note that we still find sources at high redshifts (![]() 2) to be marginally flatter than those at lower redshifts (
2) to be marginally flatter than those at lower redshifts (
![]() )
even when only rest-frame energies above 2 keV are used in the spectral fitting.
)
even when only rest-frame energies above 2 keV are used in the spectral fitting.
4.1.2 The mean type-1 AGN spectrum vs. redshift
In order to understand the origin of the variation of the mean
continuum shape of type-1 AGN as a function of redshift and luminosity
we stacked the spectra of the objects in each bin of redshift. The
co-addition of spectra in such a way blurs narrow features
(such as iron line emission), however this is not a problem for
our analysis as we are interested only in measuring broad band spectral
features. The co-added spectra were obtained following the recipe in
Appendix A in Mateos et al. (2005b).
At high energies the S/N of the spectra decreases substantially
and the uncertainties associated with background subtraction become
much larger. Hence we only stacked spectra from 0.5 keV
(to minimise EPIC calibration uncertainties at the lowest
energies) to 8 keV (observed frame). The stacked spectra were
shifted to rest-frame energies using the mean redshift of each bin.
Figure 5 shows both the unfolded stacked spectra (data points) and
a power-law model![]() in units of E2
in units of E2 ![]() f(E) (horizontal solid lines) with photon index
f(E) (horizontal solid lines) with photon index ![]() (
(![]() mean
spectral index of the broad band X-ray continuum of our objects). The
vertical line shows the energy where we expect the iron fluorescence
(Fe K
mean
spectral index of the broad band X-ray continuum of our objects). The
vertical line shows the energy where we expect the iron fluorescence
(Fe K![]() )
line emission. Also indicated are the redshift range and mean
2-10 keV luminosity of each bin. The normalisations are arbitrary.
We only show for clarity pn stacked spectra, however MOS and pn results
are consistent. We checked that the stacked spectra are not dominated
by bright objects in the bins.
)
line emission. Also indicated are the redshift range and mean
2-10 keV luminosity of each bin. The normalisations are arbitrary.
We only show for clarity pn stacked spectra, however MOS and pn results
are consistent. We checked that the stacked spectra are not dominated
by bright objects in the bins.
Table 2: Summary of the results of the spectral fitting of the type-1 AGN stacked spectra.
The results of fitting the co-added spectra are summarised in Table 2. The spectra of objects at redshifts above ![]() 0.9
were best fitted with a simple power-law model. Cold absorption was
required in all spectra, however the measured values were consistent
with typical Galactic values (
0.9
were best fitted with a simple power-law model. Cold absorption was
required in all spectra, however the measured values were consistent
with typical Galactic values (
![]() ).
At lower redshifts a soft excess component was detected with an
F-test significance >99.99%. We modelled this component with a
thermal blackbody. The measured temperatures are listed in Table 2. For comparison we also show in Table 2
the best-fit spectral slopes obtained by fitting the spectra with a
power-law in the 2-10 keV rest-frame band. The results of this
analysis show the same dependence of
).
At lower redshifts a soft excess component was detected with an
F-test significance >99.99%. We modelled this component with a
thermal blackbody. The measured temperatures are listed in Table 2. For comparison we also show in Table 2
the best-fit spectral slopes obtained by fitting the spectra with a
power-law in the 2-10 keV rest-frame band. The results of this
analysis show the same dependence of
![]() on the redshift as found in Fig. 4, i.e. the mean continuum shape of our objects becomes substantially harder (
on the redshift as found in Fig. 4, i.e. the mean continuum shape of our objects becomes substantially harder (
![]()
![]() 0.2-0.3) at the lowest and highest redshifts sampled by our survey.
0.2-0.3) at the lowest and highest redshifts sampled by our survey.
An apparently harder spectral slope could be ascribed to the net effect
of stacking spectra with different amounts of X-ray absorption and
marginally different redshifts. Another possible explanation for the
hard spectral slope could be a hardening of the continuum at the
highest energies due to the presence of the Compton reflection bump.
However, reflection is unlikely to explain the hard ![]() at the lowest redshifts as the reflection component only becomes important at rest-frame energies above
at the lowest redshifts as the reflection component only becomes important at rest-frame energies above ![]() 10 keV,
which are not sampled in our lowest redshift bin. Furthermore a
power-law fit to the stacked spectrum at rest-frame energies above
4 keV (where no effect from X-ray absorption is expected) resulted
in a steeper spectral slope,
10 keV,
which are not sampled in our lowest redshift bin. Furthermore a
power-law fit to the stacked spectrum at rest-frame energies above
4 keV (where no effect from X-ray absorption is expected) resulted
in a steeper spectral slope, ![]() = 1.9
= 1.9 ![]() 0.2. Therefore our results indicate that the overall harder spectral slope at the
lowest redshifts is an effect of X-ray absorption.
0.2. Therefore our results indicate that the overall harder spectral slope at the
lowest redshifts is an effect of X-ray absorption.
At high redshifts absorption is unlikely to explain the measured harder continuum of the objects, as at redshifts ![]() 2
we expect most of the spectral signatures of moderate absorption to be
shifted outside the observed band-pass. The flattening of
2
we expect most of the spectral signatures of moderate absorption to be
shifted outside the observed band-pass. The flattening of ![]() could be the result of the redshifting of the Compton reflection bump
into the observed band and/or the redshifting of the soft excess
outside the observed band. However, no strong indications for
spectral evolution of type-1 AGN have been detected so far, as the
power-law slopes of high redshift QSOs (out to
could be the result of the redshifting of the Compton reflection bump
into the observed band and/or the redshifting of the soft excess
outside the observed band. However, no strong indications for
spectral evolution of type-1 AGN have been detected so far, as the
power-law slopes of high redshift QSOs (out to ![]() )
have been constrained to a value
)
have been constrained to a value ![]()
![]() 2 (Just et al. 2007; Shemmer et al. 2006; Vignali et al. 2005).
It is therefore unlikely that the Compton reflection bump is
producing the overall flatter spectral slopes in our sources.
2 (Just et al. 2007; Shemmer et al. 2006; Vignali et al. 2005).
It is therefore unlikely that the Compton reflection bump is
producing the overall flatter spectral slopes in our sources.
4.1.3 Effect of the object detection efficiency on the measured

We have investigated whether the flatter spectral slope for high redshift sources can be explained by the dependence of the efficiency of detection of the XMM-Newton EPIC cameras on the spectral shape of the objects: in high redshift objects we are sampling rest-frame energies above 10 keV and hence harder sources might be more easily detected than steep spectrum sources or sources with no reflection component. This is related to the fact that source detection with X-ray telescopes is in photons rather than in flux, hence different flux limits are sampled for sources with different intrinsic spectra (Carrera et al. 2007; Della Ceca et al. 1999; Zamorani et al. 1988).
In order to constrain the importance of this effect we have simulated
power-law spectra with different continuum shapes at different
redshifts. We have performed the simulations using response files for
the EPIC pn camera only, although the results of this analysis also
apply to the EPIC MOS cameras. We required the simulated spectra
to have a 0.2-12 keV flux of
![]() ,
typical for the objects in our sample. At each redshift we found the
luminosity that corresponds to the selected flux for a typical spectral
slope
,
typical for the objects in our sample. At each redshift we found the
luminosity that corresponds to the selected flux for a typical spectral
slope
![]() .
Then we used that luminosity to obtain the normalisation of the
simulated spectra as a function of the spectral index. We then computed
the number of counts in the 0.2-12 keV band.
.
Then we used that luminosity to obtain the normalisation of the
simulated spectra as a function of the spectral index. We then computed
the number of counts in the 0.2-12 keV band.
The change in detection efficiency as a function of redshift and spectral slope is shown in Fig. 6, where the y-axis
represents the detected number of counts in the broad 0.2-12 keV
band normalised to the number of counts detected for a power-law
spectrum with ![]() = 1.9.
The top axis shows the luminosities that were used to normalise the
spectra at different redshifts. It is evident that there is a
strong dependence of the sensitivity of detection of objects on the
spectral shape and this also has a strong dependence on redshift. As we
move to higher redshifts the efficiency of detection of soft objects
decreases substantially while the efficiency of detection of hard
objects increases. Therefore in flux limited samples such as this, the
strong dependence of the efficiency of detection on the spectral shape
at different redshifts could produce the apparent hardening of the mean
continuum shape of objects detected at high redshifts: as we move
to higher redshifts, at the flux limit of the survey we better detect
objects in the ``hard tail'' of the distribution of continuum spectral
slopes. This effect was already noted by Francis et al. (1993),
who pointed out that the range of continuum slopes has an important
effect upon the measured spectral evolution of the AGN population.
Because of this important effect we cannot confirm whether the
intrinsic broad band continuum of type-1 AGN has any dependence on
redshift (and hence on the hard X-ray luminosity) without doing
extensive simulations, which are beyond the scope of this paper.
= 1.9.
The top axis shows the luminosities that were used to normalise the
spectra at different redshifts. It is evident that there is a
strong dependence of the sensitivity of detection of objects on the
spectral shape and this also has a strong dependence on redshift. As we
move to higher redshifts the efficiency of detection of soft objects
decreases substantially while the efficiency of detection of hard
objects increases. Therefore in flux limited samples such as this, the
strong dependence of the efficiency of detection on the spectral shape
at different redshifts could produce the apparent hardening of the mean
continuum shape of objects detected at high redshifts: as we move
to higher redshifts, at the flux limit of the survey we better detect
objects in the ``hard tail'' of the distribution of continuum spectral
slopes. This effect was already noted by Francis et al. (1993),
who pointed out that the range of continuum slopes has an important
effect upon the measured spectral evolution of the AGN population.
Because of this important effect we cannot confirm whether the
intrinsic broad band continuum of type-1 AGN has any dependence on
redshift (and hence on the hard X-ray luminosity) without doing
extensive simulations, which are beyond the scope of this paper.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13187f15.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg66.png)
|
Figure 6: Efficiency of detection
of objects with the EPIC-pn camera as a function of redshift and
spectral shape. We defined the efficiency as the detected number of
counts in the 0.2-12 keV band normalised to the number of counts
detected for a power-law spectrum with |
| Open with DEXTER | |
There have been claims in the literature of an anti-correlation between
the spectral slope and the hard X-ray luminosity, in the sense
that the X-ray spectral slope hardens at higher luminosities
(e.g. Young et al. 2009; Saez et al. 2008; Page et al. 2005).
However, other studies find the opposite correlation,
i.e. a softening of the spectral slope at higher luminosities
(Dai et al. 2004) or no correlation at all (e.g. George et al. 2000; Reeves & Turner 2000; Winter et al. 2009).
The detected hardening of the spectral slope at higher hard
luminosities in our sample is dominated by the two lowest luminosity
bins where the uncertainties in the measurements of ![]() are larger due to spectral complexity. Indeed, at luminosities above
are larger due to spectral complexity. Indeed, at luminosities above
![]()
![]() seems to remain fairly constant over
seems to remain fairly constant over ![]() two
orders of magnitude in luminosity, so we do not have strong
indications of a dependence of the spectral slope with the
2-10 keV luminosity. We note also that the strong dependence of
the sensitivity of detection of sources on the spectral shape must have
an impact on the measured mean continuum shapes at different
luminosities in flux limited samples due to the strong correlation of
the X-ray luminosity and redshift in these surveys.
two
orders of magnitude in luminosity, so we do not have strong
indications of a dependence of the spectral slope with the
2-10 keV luminosity. We note also that the strong dependence of
the sensitivity of detection of sources on the spectral shape must have
an impact on the measured mean continuum shapes at different
luminosities in flux limited samples due to the strong correlation of
the X-ray luminosity and redshift in these surveys.
4.2 X-ray absorption
We did not detect absorption in excess of the Galactic value in most
of our type-1 AGN. Only the spectra of 19 objects out of 487
showed strong enough signatures of absorption to be detected above our
significance threshold. This value corresponds to 3% of the
objects after taking into account the spurious detections for the
selected F-test significance. Furthermore, a number of objects in our
sample have best-fit ![]() values deviating more than 3
values deviating more than 3![]() from the mean (see Fig. 4). Using a fixed spectral slope of
from the mean (see Fig. 4). Using a fixed spectral slope of ![]() = 1.9 we detected substantial X-ray absorption in all sources with typical measured column densities
= 1.9 we detected substantial X-ray absorption in all sources with typical measured column densities
![]()
![]()
![]() .
Previous studies of type-1 AGN selected in the optical (Piconcelli et al. 2005) and X-ray band (Mainieri et al. 2007; Page et al. 2006; Mateos et al. 2005b; Mateos et al. 2005a; Caccianiga et al. 2004; Perola et al. 2004; Barcons et al. 2002)
report a fraction of absorbed type-1 AGN of 10% or less, i.e.
marginally higher than our reported value, however most of these
studies used lower confidence thresholds when applying the F-test.
However, accounting for all sources with measured flat spectral slopes,
the fraction of X-ray absorbed objects in our sample increases to
.
Previous studies of type-1 AGN selected in the optical (Piconcelli et al. 2005) and X-ray band (Mainieri et al. 2007; Page et al. 2006; Mateos et al. 2005b; Mateos et al. 2005a; Caccianiga et al. 2004; Perola et al. 2004; Barcons et al. 2002)
report a fraction of absorbed type-1 AGN of 10% or less, i.e.
marginally higher than our reported value, however most of these
studies used lower confidence thresholds when applying the F-test.
However, accounting for all sources with measured flat spectral slopes,
the fraction of X-ray absorbed objects in our sample increases to ![]() 8%, a value entirely consistent with previous measurements.
8%, a value entirely consistent with previous measurements.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13187f16.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg70.png)
|
Figure 7: Distribution of rest-frame absorbing column densities. |
| Open with DEXTER | |
The distribution of absorbing column densities for our type-1 AGN is shown in Fig. 7. The measured amounts of X-ray absorption are
![]()
![]()
![]() ,
i.e. lower than the amount of absorption typically detected for type-2 AGN (Krumpe et al. 2008; Mateos et al. 2005b). Only one object shows an absorbing column density substantially above
,
i.e. lower than the amount of absorption typically detected for type-2 AGN (Krumpe et al. 2008; Mateos et al. 2005b). Only one object shows an absorbing column density substantially above
![]() ,
but with very large uncertainty. Figure 8
shows the distribution of X-ray absorption as a function of redshift
and 2-10 keV luminosity. We do not see any clear correlation
amongst these parameters. We only find a marginal indication that the
minimum detected column density increases with redshift. However, this
effect can easily be explained in terms of absorption being redshifted
towards lower energies and further decreased by a factor
,
but with very large uncertainty. Figure 8
shows the distribution of X-ray absorption as a function of redshift
and 2-10 keV luminosity. We do not see any clear correlation
amongst these parameters. We only find a marginal indication that the
minimum detected column density increases with redshift. However, this
effect can easily be explained in terms of absorption being redshifted
towards lower energies and further decreased by a factor ![]() (1+z)2.7 (Barger et al. 2002).
(1+z)2.7 (Barger et al. 2002).
We found little or no evidence for X-ray absorption in the great
majority of our type-1 AGN, in line with AGN unification models.
However ![]() 3%
of type-1 AGN show substantial absorption in X-rays. The apparent
mismatch between the optical classification and the X-ray properties of
these objects is a challenge for the simplest AGN unification model
where the type-1/type-2 AGN classification is due solely to an
orientation effect.
3%
of type-1 AGN show substantial absorption in X-rays. The apparent
mismatch between the optical classification and the X-ray properties of
these objects is a challenge for the simplest AGN unification model
where the type-1/type-2 AGN classification is due solely to an
orientation effect.
Dedicated monitoring of a few bright AGN has found strong variations in X-ray absorption on time scales as short as a few hours (Risaliti et al. 2002). These results put tight constraints on the location of the X-ray absorber, suggesting that the toroidal obscuration region used in the AGN unification schemes to explain the observed AGN diversity might be co-spatial with the broad line region. In the clumpy torus models recently presented by Nenkova et al. (2008) there is a physical reason that could explain the detection of absorption in a fraction of type-1 AGN: the broad line region clouds located inside the dust sublimation radius are dust free, and hence affect X-rays but not the optical. In this scenario optical extinction should always be lower that the expected value assuming the Galactic dust-to-gas ratio as it is typically observed (Maiolino et al. 2001a). On the other hand, it has also been suggested that if the dust composition in the circumnuclear region of AGN has different properties than in the Galactic diffuse interstellar medium, for example if it is dominated by large grains, this medium will be less effective in absorbing the optical/UV radiation (Maiolino et al. 2001b).
![\begin{figure}
\par {\hspace*{1mm}\includegraphics[width=8cm,clip]{13187f17.eps}...
...1mm}}\vspace*{5mm}
\includegraphics[width=8.2cm,clip]{13187f18.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg73.png)
|
Figure 8: X-ray absorption vs. redshift ( top) and hard (2-10 keV) X-ray luminosity ( bottom). Errors are 90% confidence. |
| Open with DEXTER | |
A large fraction (![]() 50%)
of both Seyfert 1s and QSOs show signatures of highly ionised gas
along the line of sight, the so-called ``warm absorber'', in their
X-ray spectra (e.g. Piconcelli et al. 2005; George et al. 1998).
These absorbers, probably associated with outflowing winds, have been
found to show a wide range of ionisation, have typical outflowing
velocities of a few hundred km s-1 and have column densities in the range
50%)
of both Seyfert 1s and QSOs show signatures of highly ionised gas
along the line of sight, the so-called ``warm absorber'', in their
X-ray spectra (e.g. Piconcelli et al. 2005; George et al. 1998).
These absorbers, probably associated with outflowing winds, have been
found to show a wide range of ionisation, have typical outflowing
velocities of a few hundred km s-1 and have column densities in the range
![]() .
Warm absorption could also explain the apparent mismatch between the
optical and X-ray classification in our absorbed type-1 AGN.
.
Warm absorption could also explain the apparent mismatch between the
optical and X-ray classification in our absorbed type-1 AGN.
4.3 Soft excess
A strong broad excess emission at energies below ![]() 2 keV with respect to the extrapolation of the 2-10 keV continuum, known as soft excess,
is known to be an important component of the X-ray spectra of
Seyfert 1 galaxies and radio-quiet quasars (e.g. Porquet
et al. 2004).
The nature of the soft excess emission in unobscured AGN is still one
of the open questions in our understanding of the emission properties
of AGN.
2 keV with respect to the extrapolation of the 2-10 keV continuum, known as soft excess,
is known to be an important component of the X-ray spectra of
Seyfert 1 galaxies and radio-quiet quasars (e.g. Porquet
et al. 2004).
The nature of the soft excess emission in unobscured AGN is still one
of the open questions in our understanding of the emission properties
of AGN.
![\begin{figure}
\par {\hspace*{2mm}\includegraphics[width=7.8cm,clip]{13187f19.ep...
...mm}}\vspace*{5mm}
\includegraphics[width=8.2cm,clip]{13187f20.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg75.png)
|
Figure 9:
Top: distribution of rest-frame temperatures of the soft excess component when modelled with a thermal blackbody. Bottom: best-fit values of kT and its intrinsic dispersion
|
| Open with DEXTER | |
In order to search for this spectral component we have used a thermal
blackbody model that, to a first order approximation, can
model the thermal emission from an optically-thick accretion disk. We
also fitted soft excess signatures with a partial covering model but in
all cases we obtained better quality fits with the blackbody model.
Soft excess has been detected in 40 objects with an F-test
significance ![]() 99%.
Considering only objects at redshifts below 0.5, where most soft
excess emission is detected, we found that the fraction of objects with
detected soft excess increases to
99%.
Considering only objects at redshifts below 0.5, where most soft
excess emission is detected, we found that the fraction of objects with
detected soft excess increases to ![]() 36%.
A soft excess emission component seems to be very common in type-1
AGN. For example, studies based on ASCA (George et al. 2000; Reeves & Turner 2000) reported the detection of soft excess emission in
36%.
A soft excess emission component seems to be very common in type-1
AGN. For example, studies based on ASCA (George et al. 2000; Reeves & Turner 2000) reported the detection of soft excess emission in ![]() 50-60%
of the objects while in a more recent study of a sample of QSOs from
the Palomar-Green (PG) Bright Quasar Survey this spectral component was
detected in
50-60%
of the objects while in a more recent study of a sample of QSOs from
the Palomar-Green (PG) Bright Quasar Survey this spectral component was
detected in ![]() 90% of the objects (Piconcelli et al. 2005).
90% of the objects (Piconcelli et al. 2005).
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{13187f10n.eps} \vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg76.png)
|
Figure 10: Top row: temperature of the blackbody model used to fit the soft excess vs. redshift ( left) and hard (2-10 keV) luminosity ( right). Bottom row: luminosity of the soft excess vs. luminosity of the intrinsic power-law continuum ( left). Distribution of the strength of the soft excess measured as the ratio between the soft excess and power-law luminosities ( right). |
| Open with DEXTER | |
Taking into account the fraction of spurious detections we detected soft excess in 7.3% ![]() 2%
of the full sample of XWAS type-1 AGN at all redshifts. That this value
is so much lower that 36% is quite plausibly a consequence of the soft
excess being redshifted below the EPIC energy range for a large
fraction of our XWAS spectra, and hence 7.3% can be considered as a
very conservative lower limit to the fraction of type-1 AGN with soft
excess emission.
2%
of the full sample of XWAS type-1 AGN at all redshifts. That this value
is so much lower that 36% is quite plausibly a consequence of the soft
excess being redshifted below the EPIC energy range for a large
fraction of our XWAS spectra, and hence 7.3% can be considered as a
very conservative lower limit to the fraction of type-1 AGN with soft
excess emission.
We searched for warm absorbers in our objects with detected soft excess emission fitting the spectra with the warm absorber model absori in XSPEC. In all cases the warm absorber did not provide a good quality fit to the data. Therefore here we describe the properties of the soft excess emission fitted with the thermal blackbody model.
Figure 9 (top)
shows the distribution of measured temperatures of the soft excess
component. We clearly see that the values are narrowly distributed and
they tend to cluster around kT ![]() 0.1 keV in the rest-frame. We constrained the mean value of the
temperature of the soft excess and the amplitude of the intrinsic
scatter assuming that the distribution of temperatures can be
reproduced with a Gaussian of mean
0.1 keV in the rest-frame. We constrained the mean value of the
temperature of the soft excess and the amplitude of the intrinsic
scatter assuming that the distribution of temperatures can be
reproduced with a Gaussian of mean
![]() and
dispersion
and
dispersion
![]() .
The best simultaneous estimates were obtained with a maximum likelihood
technique accounting for both the errors in the measurements and the
intrinsic dispersion of values (Maccacaro et al. 1988). Figure 9 (bottom) shows the 1
.
The best simultaneous estimates were obtained with a maximum likelihood
technique accounting for both the errors in the measurements and the
intrinsic dispersion of values (Maccacaro et al. 1988). Figure 9 (bottom) shows the 1![]() ,
2
,
2![]() and 3
and 3![]() contours for the two parameters together with the best-fit values (cross). The mean blackbody temperature is kT = 0.093
contours for the two parameters together with the best-fit values (cross). The mean blackbody temperature is kT = 0.093 ![]() 0.007 keV with intrinsic dispersion
0.007 keV with intrinsic dispersion
![]() = 0.034
= 0.034 ![]() 0.005 keV. This value is in excellent agreement with recent estimates in the literature (e.g. Winter et al. 2009; Bianchi et al. 2009; Crummy et al. 2006; Piconcelli et al. 2005; Gierlinski & Done 2004).
We would like to note however that, although constraining the mean
temperature of the soft excess using thermal models is a helpful
measurement that can be compared with other data, it does not have
any physical meaning.
0.005 keV. This value is in excellent agreement with recent estimates in the literature (e.g. Winter et al. 2009; Bianchi et al. 2009; Crummy et al. 2006; Piconcelli et al. 2005; Gierlinski & Done 2004).
We would like to note however that, although constraining the mean
temperature of the soft excess using thermal models is a helpful
measurement that can be compared with other data, it does not have
any physical meaning.
As shown in Fig. 10
we find that the temperature of the thermal blackbody emission has no
dependence on the redshift of the objects and is uncorrelated with the
hard X-ray luminosity over more than two orders of magnitude in
luminosity. This result agrees with the recent finding that the
temperature of the soft excess is remarkably constant regardless of the
luminosity and mass of the objects (e.g. Bianchi et al. 2009; Crummy et al. 2006; Gierlinski & Done 2004). Figure 10
also shows the soft excess luminosity (rest-frame 0.5-2 keV,
corrected for absorption) vs. the power-law X-ray luminosity
(rest-frame 2-10 keV). If we use the ratio of the soft excess
and power-law X-ray luminosities to measure the strength of the soft
excess, we find that in most objects the strength of the soft excess is
under 60%. Furthermore, there seems to be a strong correlation
between the luminosities of the soft excess and power-law components,
with
![]()
![]()
![]() .
This result can be explained as the combination of two different
effects: first the lack of detections in the bottom-right of the plot
in Fig. 10 (bottom-left) is due to the fact that it is more difficult to detect weak soft excess (strength lower than
.
This result can be explained as the combination of two different
effects: first the lack of detections in the bottom-right of the plot
in Fig. 10 (bottom-left) is due to the fact that it is more difficult to detect weak soft excess (strength lower than ![]() 10%)
on top of a bright continuum. Second, the lack of detections in the
top-left of the plot suggests that there must be an upper limit in the
strength of the soft excess that exists in AGN. The strongest soft
excesses have been detected predominantly in narrow line Seyfert 1
galaxies (Boroson et al. 2002).
10%)
on top of a bright continuum. Second, the lack of detections in the
top-left of the plot suggests that there must be an upper limit in the
strength of the soft excess that exists in AGN. The strongest soft
excesses have been detected predominantly in narrow line Seyfert 1
galaxies (Boroson et al. 2002).
The measured soft excess blackbody temperatures are too high to be the
high energy tail of thermal emission from the hot inner accretion disk (kT ![]() 20-40 eV for a black hole mass of
20-40 eV for a black hole mass of
![]() accreting at the Eddington rate, Shakura & Sunyaev 1973).
Furthermore, the fact that the temperatures of the soft excess are
accreting at the Eddington rate, Shakura & Sunyaev 1973).
Furthermore, the fact that the temperatures of the soft excess are ![]() const.
(0.1-0.2 keV) over such a broad range of luminosities and black
hole masses is a major problem for models based on continuum emission,
such as optically-thick Comptonization of accretion disk emission,
because the disk temperature is expected to vary with both the mass of
the black hole and the accretion rate (see Fig. 1c in Gierlinski & Done 2004). However, see Kawaguchi et al. (2001)
for a model in which optically-thin Comptonization is invoked to
produce a soft excess with a shape that does not depend on the
temperature of the disk.
const.
(0.1-0.2 keV) over such a broad range of luminosities and black
hole masses is a major problem for models based on continuum emission,
such as optically-thick Comptonization of accretion disk emission,
because the disk temperature is expected to vary with both the mass of
the black hole and the accretion rate (see Fig. 1c in Gierlinski & Done 2004). However, see Kawaguchi et al. (2001)
for a model in which optically-thin Comptonization is invoked to
produce a soft excess with a shape that does not depend on the
temperature of the disk.
Alternative models relate the soft excess to atomic rather than
continuum processes which could easily explain the constancy of the
temperature by the abrupt increase in opacity in partially ionised
material between ![]() 0.7-3 keV especially due to
0.7-3 keV especially due to
![]() at 0.6-0.7 keV as well as Ly
at 0.6-0.7 keV as well as Ly![]() lines from C, N and Fe L shell transitions (Ross & Fabian 2005).
The result is a large increase in reflected/transmitted flux below
0.7 keV, which could produce the soft excess either from
absorption in an optically thin material in the line of sight, for
example in a wind from the disk (Gierlinski & Done 2004),
or from reflection in optically thick material out of the line of
sight, for example in the accretion disk (Crummy et al. 2006).
Both models predict sharp/strong atomic features from the partially
ionised material. To explain the featureless soft excess they both
require large velocity smearing which can only be produced in the
vicinity of the black hole. In order to fit the strongest soft
excesses detected these models require a fine tuning of the ionisation
state.
Because the reflected emission cannot exceed the illuminating flux,
this sets a tight limit on the strength of the soft excess in the
reflection model, while in the absorption model the range of measured
soft excess strength can be easily reproduced by changing the amount of
absorption. Both models have been found to fit the X-ray spectral
signatures of soft excess in bright AGN equally well.
lines from C, N and Fe L shell transitions (Ross & Fabian 2005).
The result is a large increase in reflected/transmitted flux below
0.7 keV, which could produce the soft excess either from
absorption in an optically thin material in the line of sight, for
example in a wind from the disk (Gierlinski & Done 2004),
or from reflection in optically thick material out of the line of
sight, for example in the accretion disk (Crummy et al. 2006).
Both models predict sharp/strong atomic features from the partially
ionised material. To explain the featureless soft excess they both
require large velocity smearing which can only be produced in the
vicinity of the black hole. In order to fit the strongest soft
excesses detected these models require a fine tuning of the ionisation
state.
Because the reflected emission cannot exceed the illuminating flux,
this sets a tight limit on the strength of the soft excess in the
reflection model, while in the absorption model the range of measured
soft excess strength can be easily reproduced by changing the amount of
absorption. Both models have been found to fit the X-ray spectral
signatures of soft excess in bright AGN equally well.
In an alternative scenario, it is possible that the soft excess
emission does not come from the AGN but from the host galaxy (X-ray
binaries, star formation, hot ionised gas). However this emission is
not expected to be more luminous than
![]() (Ranalli et al. 2003).
The majority of the measured luminosities of the soft excess for our
sources are at least an order of magnitude above this value, hence this
component is expected to originate from the AGN in our objects.
(Ranalli et al. 2003).
The majority of the measured luminosities of the soft excess for our
sources are at least an order of magnitude above this value, hence this
component is expected to originate from the AGN in our objects.
5 Conclusions
We have analysed the 0.2-12 keV broad band spectral properties of
one of the largest samples of X-ray selected type-1 AGN to date,
drawn from the XMM-Newton Wide Angle Survey. The sample contains 487 type-1 AGN detected up to redshift ![]() 4 and spanning more than 3 orders of magnitude in X-ray luminosity. The main results of our analysis are as follows.
4 and spanning more than 3 orders of magnitude in X-ray luminosity. The main results of our analysis are as follows.
- 1.
- The spectra of most type-1 AGN (
 90%)
are best-fitted with a simple power-law. Absorption and soft excess
emission are detected with an F-test significance >99% in 3%
and 7% of the objects respectively.
90%)
are best-fitted with a simple power-law. Absorption and soft excess
emission are detected with an F-test significance >99% in 3%
and 7% of the objects respectively.
- 2.
- We constrain the mean spectral index of the broad band X-ray continuum of type-1 AGN to a value of
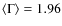
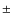 0.02 with intrinsic dispersion
0.02 with intrinsic dispersion
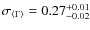 ,
in agreement with previous estimates in the literature. We find the
continuum to strongly depend on the 0.5-2 keV flux, in the sense
that the type-1 AGN population becomes marginally harder at
fainter fluxes. Our analysis indicates that this spectral
variation is likely due to undetected absorption in the faintest
sources in our sample rather than to changes in the intrinsic spectral
shape.
,
in agreement with previous estimates in the literature. We find the
continuum to strongly depend on the 0.5-2 keV flux, in the sense
that the type-1 AGN population becomes marginally harder at
fainter fluxes. Our analysis indicates that this spectral
variation is likely due to undetected absorption in the faintest
sources in our sample rather than to changes in the intrinsic spectral
shape.
- 3.
- The mean continuum shape of our type-1 AGN is found to become
harder at higher 2-10 keV luminosities and at higher redshifts.
At high redshifts undetected absorption is unlikely to explain the
harder continuum of the objects as we expect spectral signatures of
moderate absorption to be redshifted outside the observed band-pass.
The flattening of
 could be the result of redshifting of the Compton reflection bump into
the observed band and/or redshifting of the soft excess outside the
observed band. However, we find that there is a strong dependence of
the detection efficiency of sources on the spectral shape. Our analysis
indicates that at high redshifts the efficiency of detection of hard
objects increases while for soft sources it decreases substantially.
This effect must have an impact on the measured mean continuum shapes
of sources at different redshifts and also at different luminosities
due to the tight correlation between the X-ray luminosity and redshift
in flux limited surveys.
could be the result of redshifting of the Compton reflection bump into
the observed band and/or redshifting of the soft excess outside the
observed band. However, we find that there is a strong dependence of
the detection efficiency of sources on the spectral shape. Our analysis
indicates that at high redshifts the efficiency of detection of hard
objects increases while for soft sources it decreases substantially.
This effect must have an impact on the measured mean continuum shapes
of sources at different redshifts and also at different luminosities
due to the tight correlation between the X-ray luminosity and redshift
in flux limited surveys.
- 4.
- We find little or no evidence for X-ray absorption in the
great majority of our type-1 AGN, as expected from AGN unification
models. However
 3%
of our objects show substantial absorption in X-rays. The measured
amounts of X-ray absorption are typically lower than a
3%
of our objects show substantial absorption in X-rays. The measured
amounts of X-ray absorption are typically lower than a 
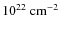 ,
i.e. in the low part of the column density distribution of type-2
AGN. The recently presented clumpy torus models, where the torus is a
smooth continuation of the broad line region, can provide a physical
explanation for the apparent mismatch between the optical
classification and the X-ray properties of these objects. In these
models X-ray absorption, dust obscuration and broad line emission are
produced in a single continuous distribution of clouds: the broad line
region is located inside the dust sublimation radius and hence the
dust-free clouds obscure the X-rays but not the optical while the torus
is located outside the dust sublimation radius (dusty clouds).
,
i.e. in the low part of the column density distribution of type-2
AGN. The recently presented clumpy torus models, where the torus is a
smooth continuation of the broad line region, can provide a physical
explanation for the apparent mismatch between the optical
classification and the X-ray properties of these objects. In these
models X-ray absorption, dust obscuration and broad line emission are
produced in a single continuous distribution of clouds: the broad line
region is located inside the dust sublimation radius and hence the
dust-free clouds obscure the X-rays but not the optical while the torus
is located outside the dust sublimation radius (dusty clouds). - 5.
- A soft excess component is detected in 40 objects in our sample, which corresponds to 7.3%
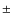 2% of our type-1 AGN after taking into account spurious
detections. This value should be taken as a lower limit as for high
redshift objects the signatures of soft excess will be redshifted
outside the observed band-pass. Indeed considering only objects at
redshifts below 0.5, where most soft excess emission is detected,
we found that the fraction of objects with detected soft excess
increases to
2% of our type-1 AGN after taking into account spurious
detections. This value should be taken as a lower limit as for high
redshift objects the signatures of soft excess will be redshifted
outside the observed band-pass. Indeed considering only objects at
redshifts below 0.5, where most soft excess emission is detected,
we found that the fraction of objects with detected soft excess
increases to  36%.
We constrain the properties of this spectral component with a thermal
blackbody which provided the best quality fits to the data. We
constrain the mean value of the temperature of the soft excess and the
amplitude of the intrinsic dispersion to kT
36%.
We constrain the properties of this spectral component with a thermal
blackbody which provided the best quality fits to the data. We
constrain the mean value of the temperature of the soft excess and the
amplitude of the intrinsic dispersion to kT 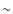 100 eV and
100 eV and
 34 eV. We find that the temperature of the thermal blackbody
emission has no dependence on the redshift of the objects and is
uncorrelated with the hard X-ray luminosity over more than two orders
of magnitude in luminosity. The measured strength of the soft excess,
defined as the ratio of the soft excess luminosity (rest-frame
0.5-2 keV, corrected for absorption) and the power-law X-ray
luminosity (rest-frame 2-10 keV), is under 60% for the great
majority of our objects. Direct thermal emission from the accretion
disk is ruled out as a possible origin of the soft excess on the basis
of the very high temperatures detected for this component and the
apparent lack of correlation of the temperature of the soft excess with
AGN parameters such as the X-ray luminosity. Compton scattered
disk emission is also ruled out on the basis that in the Comptonization
model the shape of the soft excess should be related to the disk
emission. The measured luminosities of the soft excess are at least an
order of magnitude above those expected if the soft excess originates
in the host galaxy (X-ray binaries, star formation, hot ionised gas)
hence this component is expected to originate from the AGN in our
objects.
34 eV. We find that the temperature of the thermal blackbody
emission has no dependence on the redshift of the objects and is
uncorrelated with the hard X-ray luminosity over more than two orders
of magnitude in luminosity. The measured strength of the soft excess,
defined as the ratio of the soft excess luminosity (rest-frame
0.5-2 keV, corrected for absorption) and the power-law X-ray
luminosity (rest-frame 2-10 keV), is under 60% for the great
majority of our objects. Direct thermal emission from the accretion
disk is ruled out as a possible origin of the soft excess on the basis
of the very high temperatures detected for this component and the
apparent lack of correlation of the temperature of the soft excess with
AGN parameters such as the X-ray luminosity. Compton scattered
disk emission is also ruled out on the basis that in the Comptonization
model the shape of the soft excess should be related to the disk
emission. The measured luminosities of the soft excess are at least an
order of magnitude above those expected if the soft excess originates
in the host galaxy (X-ray binaries, star formation, hot ionised gas)
hence this component is expected to originate from the AGN in our
objects.
We acknowledge Chris Done, Bozena Czerny, Gordon Stewart, Pilar Esquej and Ken Pounds for useful comments. We acknowledge the anonymous referee for a careful reading of the manuscript and for comments that improved the paper. S.M., M.W. and J.A.T. acknowledge support from the UK STFC research council. F.J.C. acknowledges financial support for this work from the Spanish Ministerio de Educación y Ciencia under project ESP2006-13608-C02-01. A.C. acknowledges financial support from the Spanish Ministerio de Educación y Ciencia fellowship and also from the MIUR and The Italian Space Agency (ASI) grants PRIN-MUR 2006-02-5203 and No. I/088/06/0. M.K. acknowledges support from the NASA grant NNX08AX50G and NNX07AG02G.
References
- Akylas, A., Georgakakis, A., & Georgantopoulos, I. 2004, MNRAS, 353, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Arnaud, K. 1996, Astronomical Data Analysis Software and Systems V., ed. G. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Barcons, X., Carrera, F. J., Watson, M. G., et al. 2002, A&A, 382, 522 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barger, A. J., Cowie, L. L., Brandt, W. N., et al. 2002, AJ, 124, 1839 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S., Corral, A., Panessa, F., et al. 2008, MNRAS, 385, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S., Guainazzi, M., Matt, G., et al. 2009, A&A, 495, 421 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bechtold, J., Siemiginowska, A., Shields, J., et al. 2003, A&A, 433, 855 [Google Scholar]
- Boroson, T. A. 2002, ApJ, 565, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Brusa, M., Zamorani, G., Comastri, A., et al. 2007, ApJS, 172, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Caccianiga, A., Severgnini, P., Braito, V., et al. 2004, A&A, 416, 901 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cappi, M., Panessa, F., Bassani, L., et al. 2006, A&A, 446, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carrera, F. J., Ebrero, J., Mateos, S., et al. 2007, A&A, 469, 27 [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Corral, A., Barcons, X., Carrera, F. J., et al. 2005, A&A, 431, 97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corral, A., Page, M. J., Carrera, F. J., et al. 2008, A&A, 492, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crummy, J., Fabian, A. C., Gallo, L., & Ross, R. R. 2006, MNRAS, 365, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Dadina, M. 2008, A&A, 485, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dai, X., Chartas, G., Eracleous, M., & Garmire, G. P. 2004, ApJ, 605, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Della Ceca, R., Castelli, G., Braito, V., et al. 1999, ApJ, 524, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Dickey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Francis, P. J. 1993, ApJ, 407, 519 [NASA ADS] [CrossRef] [Google Scholar]
- George, I. M., & Fabian, A. C. 1991, MNRAS, 249, 352 [NASA ADS] [CrossRef] [Google Scholar]
- George, I. M., Turner, T. J., Netzer, H., et al. 1998, ApJS, 114, 73 [NASA ADS] [CrossRef] [Google Scholar]
- George, I. M., Turner, T. J., Yaqoob, T., & Netzer, H. 2000, ApJ, 531, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Gierlinski, M., & Done, C. 2004, MNRAS, 349, 7 [Google Scholar]
- Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Hambly, N. C., MacGillivray, H. T., Read, M. A., et al. 2001, MNRAS, 326, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Iwasawa, K., & Taniguchi, Y. 1993, ApJ, 413, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Just, D. W., Brandt, W. N., Shemmer, O., et al. 2007, ApJ, 665, 1004 [Google Scholar]
- Kawaguchi, T., Shimura, T., & Mineshige, S. 2001, ApJ, 546, 966 [NASA ADS] [CrossRef] [Google Scholar]
- Kelly, B. C., Bechtold, J., Siemiginowska, A., & Aldcroft, T. 2007, ApJ, 657, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Krumpe, M., Lamer, G., Corral, A., et al. 2008, A&A, 483, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lewis, I. J., Cannon, R. D., Taylor, K., et al. 2002, MNRAS, 333, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Maccacaro, T., Gioia, I. M., Wolter, A., Zamorani, G., & Stocke, J. T. 1998, ApJ, 326, 680 [Google Scholar]
- Mainieri, V., Hasinger, G., Cappelluti, N., et al. 2007, ApJS, 172, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Marconi, A., Salvati, M., et al. 2001a, A&A, 365, 28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiolino, R., Marconi, A., & Oliva, E. 2001b, A&A, 365, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mateos, S., Barcons, X., Carrera, F. J., et al. 2005a, A&A, 433, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mateos, S., Barcons, X., Carrera, F. J., et al. 2005b, A&A, 444, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mateos, S., Saxton, R. D., Read, A. M., & Sembay, S. 2009, A&A, 496, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molina, M., Bassani, L., Malizia, A., et al. 2009, MNRAS, 399, 1293 [NASA ADS] [CrossRef] [Google Scholar]
- Nenkova, M., Sirocky, M. M., Nikutta, R., et al. 2008, ApJ, 685, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Page, K. L., Reeves, J. N., O'Brien, P. T., & Turner, M. J. L. 2005, MNRAS, 364, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Page, M. J., Loaring, N. S., Dwelly, T., et al. 2006, A&A, MNRAS, 369, 156 [Google Scholar]
- Panessa, F., & Bassani, L. 2002, A&A, 394, 435 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Panessa, F., Bassani, L., de Rosa, A., et al. 2008, A&A, 483, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Panessa, F., Carrera, F. J., Bianchi, S., et al. 2009, MNRAS, 398, 1951 [NASA ADS] [CrossRef] [Google Scholar]
- Perola, G. C., Puccetti, S., Fiore, F., et al. 2004, A&A, 421, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piconcelli, E., Jimenez-Bailón, E., Guainazzi, M., et al. 2005, A&A, 432, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ponti, G., Cappi, M., Genghini, M., et al. 2008, Mem. Soc. Astron. Ital., 79, 274 [NASA ADS] [Google Scholar]
- Porquet, D., Reeves, J. N., O'Brien, P., & Brinkmann, W. 2004, A&A, 422, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pounds, K. A., Nandra, K., Stewart, G. C., George, I. M., & Fabian, A. C. 1990, Nature, 344, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Ranalli, P., Comastri, A., & Setti, G. 2003, A&A, 399, 39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reeves, J. N., & Turner, M. J. L. 2000, MNRAS, 316, 234R [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., Elvis, M., & Nicastro, F. 2002, ApJ, 571, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, R. R., & Fabian, A. C. 2005, MNRAS, 358, 211 [Google Scholar]
- Saez, C., Chartas, G., Brandt, W. N., & Lehmer, B. D. 2008, AJ, 135, 1505 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shemmer, O., Brandt, W. N., Schneider, D. P., & Fan, X. 2006, ApJ, 644, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Sobolewska, M. A., & Done, C. 2007, MNRAS, 374, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Tozzi, P., Gilli, R., Mainieri, V., et al. 2006, A&A, 451, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turner, T. J., & Pounds, K. A. 1989, MNRAS, 240, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Vignali, C., Brandt, W. N., Schneider, D. P., & Kaspi, S. 2005, AJ, 129, 2519 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, M. G., Schröder, A. C., Fyfe, D., & Page, C. G. 2008, A&A, 493, 339 [Google Scholar]
- Wilkes, B. J., Schmidt, G. D., Cutri, R. M., & Ghosh, H. 2002, ApJ, 564, 65 [Google Scholar]
- Winter, L. M., Mushotzky, R. F., Reynolds, C. S., & Tueller, J. 2009, ApJ, 690, 1322 [NASA ADS] [CrossRef] [Google Scholar]
- Young, M., Elvis, M., & Risaliti, G. 2009, ApJS, 183, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Zamorani, G., Gioia, I. M., Maccacaro, T., & Wolter, A. 1988, A&A, 196, 39 [NASA ADS] [Google Scholar]
Footnotes
- ... nh
![[*]](/icons/foot_motif.png)
- http://heasarc.nasa.gov/lheasoft/ftools/
- ... model
![[*]](/icons/foot_motif.png)
-
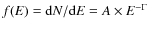 where N is the number of photons, E the photon energy, A the normalisation and
where N is the number of photons, E the photon energy, A the normalisation and  is the photon index.
is the photon index.
All Tables
Table 1: Summary of the results of the spectral fitting.
Table 2: Summary of the results of the spectral fitting of the type-1 AGN stacked spectra.
All Figures
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{13187f1.eps}\hspace*{8mm}
...
...7f3.eps}\hspace*{7mm}
\includegraphics[width=8cm,clip]{13187f4.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg21.png)
|
Figure 1: Top: redshift distribution ( left) and 2-10 keV X-ray luminosity (corrected for absorption) vs. redshift ( right) of the XWAS type-1 AGN selected for our study. Bottom: distribution of EPIC 0.2-12 keV net counts in the X-ray spectra of the sources ( left) and 2-10 keV band flux distribution ( right). For clarity the last bin in the distribution of EPIC counts includes all objects with spectra with more than 2000 counts. The dashed vertical line indicates the limit in counts we used for this study. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13187f5.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg40.png)
|
Figure 2:
Best-fit |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13187f6.eps}\vspace*{5mm}
\includegraphics[width=8cm,clip]{13187f7.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg48.png)
|
Figure 3:
Top: distribution of best-fit photon indexes. The dashed line
shows the results of the maximum likelihood technique used to constrain
the mean spectral index of the broad band X-ray continuum and its
intrinsic dispersion (see text for details). Bottom: 1 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{13187f4n.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg50.png)
|
Figure 4:
Left: from top to bottom broad band continuum
shape vs. 0.5-2 keV flux, 2-10 keV luminosity and
redshift respectively. The error bars at the top of the plots indicate
the mean error in the measurements. Right: mean spectral index of the broad band X-ray continuum,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13187f14.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg52.png)
|
Figure 5: Stacked rest-frame
unfolded spectra of our sources in redshift bins (data points). The
values at the top-left of each spectrum indicate the redshift range and
mean 2-10 keV luminosity of the objects on each bin. The
horizontal lines show a power-law model with photon index |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13187f15.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg66.png)
|
Figure 6: Efficiency of detection
of objects with the EPIC-pn camera as a function of redshift and
spectral shape. We defined the efficiency as the detected number of
counts in the 0.2-12 keV band normalised to the number of counts
detected for a power-law spectrum with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13187f16.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg70.png)
|
Figure 7: Distribution of rest-frame absorbing column densities. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\hspace*{1mm}\includegraphics[width=8cm,clip]{13187f17.eps}...
...1mm}}\vspace*{5mm}
\includegraphics[width=8.2cm,clip]{13187f18.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg73.png)
|
Figure 8: X-ray absorption vs. redshift ( top) and hard (2-10 keV) X-ray luminosity ( bottom). Errors are 90% confidence. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\hspace*{2mm}\includegraphics[width=7.8cm,clip]{13187f19.ep...
...mm}}\vspace*{5mm}
\includegraphics[width=8.2cm,clip]{13187f20.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg75.png)
|
Figure 9:
Top: distribution of rest-frame temperatures of the soft excess component when modelled with a thermal blackbody. Bottom: best-fit values of kT and its intrinsic dispersion
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{13187f10n.eps} \vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/02/aa13187-09/Timg76.png)
|
Figure 10: Top row: temperature of the blackbody model used to fit the soft excess vs. redshift ( left) and hard (2-10 keV) luminosity ( right). Bottom row: luminosity of the soft excess vs. luminosity of the intrinsic power-law continuum ( left). Distribution of the strength of the soft excess measured as the ratio between the soft excess and power-law luminosities ( right). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


