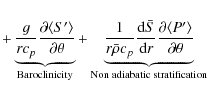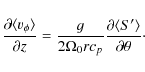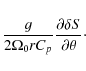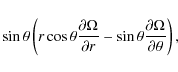| Issue |
A&A
Volume 510, February 2010
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200913166 | |
| Published online | 04 February 2010 | |
Is the solar convection zone in strict thermal wind balance?
A. S. Brun1,2 - H. M. Antia3 - S. M. Chitre4
1 - Laboratoire AIM, CEA/DSM-CNRS-Université Paris Diderot,
IRFU/SAp, 91191 Gif-sur-Yvette, France
2 -
LUTH, Observatoire de Paris, CNRS-Université Paris Diderot, Place Jules Janssen, 92195 Meudon, France
3 -
Tata Institute of Fundamental Research, Homi Bhabha Road,
Mumbai 400005, India
4 -
Centre for Basic Sciences, University of Mumbai, Mumbai 400098, India
Received 22 August 2009 / Accepted 14 October 2009
Abstract
Context. The solar rotation profile is conical rather than
cylindrical as it could be expected from classical rotating fluid
dynamics (e.g. Taylor-Proudman theorem). Thermal coupling to the
tachocline, baroclinic effects and latitudinal transport of heat have
been suggested to explain this peculiar state of rotation.
Aims. To test the validity of thermal wind balance in the solar
convection zone using helioseismic inversions for both the angular
velocity and fluctuations in entropy and temperature.
Methods. Entropy and temperature fluctuations obtained from 3D
hydrodynamical numerical simulations of the solar convection zone are
compared with solar profiles obtained from helioseismic inversions.
Results. The temperature and entropy fluctuations in 3D
numerical simulations have smaller amplitude in the bulk of the solar
convection zone than those derived from seismic inversions. Seismic
inversion provides variations of temperature from about 1 K at the
surface to up to 100 K at the base of the convection zone while in
3D simulations they are of an order of 10 K throughout the
convection zone up to 0.96 ![]() .
In 3D simulations, baroclinic effects are found to be important to tilt the isocontours of
.
In 3D simulations, baroclinic effects are found to be important to tilt the isocontours of ![]() away from a cylindrical profile in most of the convection zone, helped
by Reynolds and viscous stresses at some locations. By contrast the
baroclinic effect inverted by helioseismology is much larger than what
is required to yield the observed angular velocity profile.
away from a cylindrical profile in most of the convection zone, helped
by Reynolds and viscous stresses at some locations. By contrast the
baroclinic effect inverted by helioseismology is much larger than what
is required to yield the observed angular velocity profile.
Conclusions. The solar convection does not appear to be in
strict thermal wind balance, Reynolds stresses must play a dominant
role in setting not only the equatorial acceleration but also the
observed conical angular velocity profile.
Key words: Sun: interior - Sun: rotation - Sun: helioseismology - hydrodynamics - convection
1 Introduction
Helioseismic data from the Global Oscillation Network Group (GONG)
and the Michelson Doppler Imager (MDI) have been used to infer the
rotation profile in the solar interior (e.g., Thompson et al. 1996; Schou et al. 1998).
The inversion results show that isocontours of the differential rotation
![]() are conical
at mid-latitude rather than cylindrical as was expected from early
numerical simulations (e.g., Glatzmaier & Gilman 1982; Gilman & Miller 1986).
More recent theoretical work (Durney 1999; Kitchatinov & Rudiger 1995;
Brun & Toomre 2002, hereafter BT02; Rempel 2005; Miesch
et al. 2006, hereafter MBT06; Brun & Rempel 2008; Balbus et al. 2009)
indicates that in order to break the Taylor-Proudman constraint of
cylindrical
are conical
at mid-latitude rather than cylindrical as was expected from early
numerical simulations (e.g., Glatzmaier & Gilman 1982; Gilman & Miller 1986).
More recent theoretical work (Durney 1999; Kitchatinov & Rudiger 1995;
Brun & Toomre 2002, hereafter BT02; Rempel 2005; Miesch
et al. 2006, hereafter MBT06; Brun & Rempel 2008; Balbus et al. 2009)
indicates that in order to break the Taylor-Proudman constraint of
cylindrical ![]() ,
the Sun must either have a systematic latitudinal heat transfer in
its convection zone or thermal forcing from the tachocline or most likely both.
This is due to the so-called thermal wind balance (Pedlosky 1987), which means that the existence in the solar convection zone of
latitudinal entropy (or temperature) variation due to baroclinic
effect can result in a rotation state that breaks the Taylor-Proudman constraint.
Such latitudinal variations of the thermal properties at the solar surface have been looked for
observationally by several groups since the late 1960's (e.g., Dicke & Goldenberg 1967; Altroch & Canfield 1972; Koutchmy et al. 1977; Kuhn
et al. 1985, 1998; Rast et al. 2008,
to cite only a few). This is a difficult task since one has to compensate for limb
darkening effect, photospheric magnetic activity, instrument bias and many other subtle effects
to extract a relatively weak signal (see Rast et al. 2008).
In most cases a temperature contrast of a few degree K is found from
equator to pole at the surface, the pole being warmer. In some
observations a minimum at mid-latitude with a warm equator and hotter
polar regions is also found. The warm polar regions and cool equatorial
region pattern
is also found in 3D simulations of the solar convection zone with
temperature variation slightly larger (i.e., of order 10 K; BT02,
MBT06). At the surface a banded structure of the temperature field
(warm-cool-hot) is also found in 3D simulation of global scale
convection. While very useful and instructive, most observations are
confined to the solar surface and lack the information on the deep
thermal structure of the solar convection zone which is key to
characterise the dynamics of the deep solar convection zone. One way to
remedy that limitation is to rely on helioseismic inversions that allow
us to probe deeper into the Sun and to use 3D global simulations of the
solar convection zone
to guide our physical understanding.
,
the Sun must either have a systematic latitudinal heat transfer in
its convection zone or thermal forcing from the tachocline or most likely both.
This is due to the so-called thermal wind balance (Pedlosky 1987), which means that the existence in the solar convection zone of
latitudinal entropy (or temperature) variation due to baroclinic
effect can result in a rotation state that breaks the Taylor-Proudman constraint.
Such latitudinal variations of the thermal properties at the solar surface have been looked for
observationally by several groups since the late 1960's (e.g., Dicke & Goldenberg 1967; Altroch & Canfield 1972; Koutchmy et al. 1977; Kuhn
et al. 1985, 1998; Rast et al. 2008,
to cite only a few). This is a difficult task since one has to compensate for limb
darkening effect, photospheric magnetic activity, instrument bias and many other subtle effects
to extract a relatively weak signal (see Rast et al. 2008).
In most cases a temperature contrast of a few degree K is found from
equator to pole at the surface, the pole being warmer. In some
observations a minimum at mid-latitude with a warm equator and hotter
polar regions is also found. The warm polar regions and cool equatorial
region pattern
is also found in 3D simulations of the solar convection zone with
temperature variation slightly larger (i.e., of order 10 K; BT02,
MBT06). At the surface a banded structure of the temperature field
(warm-cool-hot) is also found in 3D simulation of global scale
convection. While very useful and instructive, most observations are
confined to the solar surface and lack the information on the deep
thermal structure of the solar convection zone which is key to
characterise the dynamics of the deep solar convection zone. One way to
remedy that limitation is to rely on helioseismic inversions that allow
us to probe deeper into the Sun and to use 3D global simulations of the
solar convection zone
to guide our physical understanding.
Indeed, helioseismic inversions can give us the rotation rate
as well as the sound speed and density in the solar interior as a function
of radius and latitude. Inside the convection zone the chemical composition is
uniform, and if we know the equation of state it is possible to determine
other thermodynamic quantities like the temperature and entropy from the
sound speed and density. Although there may be some uncertainty in the
equation of state, the OPAL equation of state (Rogers et al. 1996;
Rogers & Nayafonov 2002) is quite close to the equation of state of
solar material (e.g., Basu & Antia 1995; Basu & Christensen-Dalsgaard 1997). Consequently we
use the OPAL equation of state to calculate the perturbations in entropy
and temperature and assess how well a strict thermal wind balance is established in the
solar convective envelope. To achieve this goal we make use of 2D inversions of
![]() ,
using the GONG and MDI data for the full solar cycle 23 and analyse our findings using 3D
simulations obtained with the ASH (anelastic spherical harmonic) code (BT02; MBT06; Miesch
et al. 2008) supported by
theoretical considerations on the thermal wind balance and vorticity equations.
,
using the GONG and MDI data for the full solar cycle 23 and analyse our findings using 3D
simulations obtained with the ASH (anelastic spherical harmonic) code (BT02; MBT06; Miesch
et al. 2008) supported by
theoretical considerations on the thermal wind balance and vorticity equations.
The paper is organised as follows: in Sect. 2 we describe the data and technique used in this work while the results for the temperature and entropy inversions are described in Sect. 3 along with those of 3D simulations. In Sect. 4 we discuss at length the thermal wind balance and its generalisation and interpret our seismic inversion with 3D simulation of global scale convection. Finally, in Sect. 5 we put our results in perspective and conclude.
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{13166f1aN.eps}\hspace*{1mm...
...ncludegraphics[width=6.1cm,clip]{13166f1cN.eps}\hfill
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/02/aa13166-09/Timg14.png)
|
Figure 1:
The aspherical component of temperature fluctuation, |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{13166f2a.eps}\hspace*{1mm}
\...
...
\includegraphics[width=6cm,clip]{13166f2c.eps}\hfill
\vspace*{6mm}
\end{figure}](/articles/aa/full_html/2010/02/aa13166-09/Timg15.png)
|
Figure 2:
The aspherical component of entropy fluctuation, |
| Open with DEXTER | |
2 The helioseismic data and inversion technique
We use data from GONG (Hill et al. 1996) and SOI/MDI (Schou 1999). Each data set consists of mean frequencies of different (n,l) multiplets and the corresponding splitting coefficients. We use 130 temporally overlapping data sets from GONG, each covering a period of 108 days, starting from 1995 May 7 and ending on 2008 May 9, with a spacing of 36 days between consecutive data sets. The MDI data consist of 61 non-overlapping data sets, each covering a period of 72 days, starting from 1996 May 1 and ending on 2008 September 30. These data cover the solar cycle 23. For most of the work we use the temporal average over the available data to reduce the errors in inversion results. For this purpose we repeat the inversion process for all data sets and then take an average of all sets to get temporally averaged inversion results.
We use a 2D Regularised Least Squares (RLS) inversion
technique in the manner adopted by Antia et al. (1998) to infer the
angular velocity in the
solar interior from each of the available data sets.
Similarly, we use a 2D RLS inversion technique as described by
Antia et al. (2001) to infer the sound speed and density in the solar
interior. In practice, we calculate the differences
![]() and
and
![]() with respect to a reference solar model. We use the
solar model from Brun et al. (2002) with tachocline mixing as the
reference model. In this work, we are only interested in the latitudinal
variation in solar structure inside the convection zone. Thus the
fluctuation in sound speed can be converted to either temperature
or entropy using the relation:
with respect to a reference solar model. We use the
solar model from Brun et al. (2002) with tachocline mixing as the
reference model. In this work, we are only interested in the latitudinal
variation in solar structure inside the convection zone. Thus the
fluctuation in sound speed can be converted to either temperature
or entropy using the relation:
| |
= | (1) | |
| = | 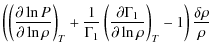
|
||
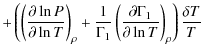
|
(2) | ||
| = | 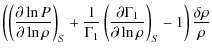
|
||
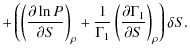
|
(3) |
Here S is the specific entropy, T is temperature, P is pressure and
3 Thermal perturbations in the solar convection zone
Convection is a macroscopic transport of heat and energy. It is directly associated to correlations between the velocity field and temperature fluctuations (Brun & Rempel 2008). Being able to infer the temperature and entropy perturbations in the solar convection zone is thus key to understanding its turbulent dynamics.
3.1 The inverted profiles
The aspherical part of temperature and entropy perturbations determined from
temporally averaged GONG and MDI data are shown in Figs. 1 and 2. The
maximum temperature fluctuation near the bottom of the convection zone is found to be about 100 K.
These fluctuations increase with depth initially, because of a steep increase in
the temperature with depth which can induce an artificially large value for ![]() .
The errors in
.
The errors in ![]() also increase with depth and the results may not be significant near the base of the convection zone.
If we consider the relative fluctuation
also increase with depth and the results may not be significant near the base of the convection zone.
If we consider the relative fluctuation
![]() ,
then the maximum would be much closer to the surface and the
value is of the order of 10-4 or less. Similarly, if the entropy fluctuation
is divided by its typical value of the order of Cp, then it too would be of
the same order. Both these relative perturbations are of the same order as
,
then the maximum would be much closer to the surface and the
value is of the order of 10-4 or less. Similarly, if the entropy fluctuation
is divided by its typical value of the order of Cp, then it too would be of
the same order. Both these relative perturbations are of the same order as
![]() .
A detailed look at Figs. 1 and 2
reveal that the fluctuations
are negative (relatively cold with respect to the spherically symmetric
mean) at low latitude and warm at mid latitudes. In the bulk of the
solar convection zone there is very little radial variation except near
the surface. In the GONG data a cool polar region is also apparent but
its significance is questionable given the relatively
poor resolution of inversion techniques at high latitude.
This feature is not clearly seen in the MDI data.
While this latitudinal variation imprints through the surface for
the entropy with little change in amplitude that is not the case for
the temperature. At the surface the seismic inversion of the
axisymmetric temperature fluctuations are very small which is in
agreement with previous photospheric studies (Rast et al. 2008).
It needs to be said that the inversions may not be reliable above the lower turning point of the modes, near the surface.
Around
.
A detailed look at Figs. 1 and 2
reveal that the fluctuations
are negative (relatively cold with respect to the spherically symmetric
mean) at low latitude and warm at mid latitudes. In the bulk of the
solar convection zone there is very little radial variation except near
the surface. In the GONG data a cool polar region is also apparent but
its significance is questionable given the relatively
poor resolution of inversion techniques at high latitude.
This feature is not clearly seen in the MDI data.
While this latitudinal variation imprints through the surface for
the entropy with little change in amplitude that is not the case for
the temperature. At the surface the seismic inversion of the
axisymmetric temperature fluctuations are very small which is in
agreement with previous photospheric studies (Rast et al. 2008).
It needs to be said that the inversions may not be reliable above the lower turning point of the modes, near the surface.
Around
![]() ,
where the inversions should be reliable, the temperature variations are of the order of 10 K.
,
where the inversions should be reliable, the temperature variations are of the order of 10 K.
3.2 The profiles realised in 3D models of large scale convection
Recent efforts to develop high resolution global simulations of the solar convection zone in
order to identify the physical processes at the origin of heat, energy and angular momentum transport have
been quite successful at reproducing the seismically inverted differential rotation profile (BT02; MBT06).
We display in Fig. 3 a typical solution of the solar convection zone and differential rotation obtained with the ASH code (case AB3 of MBT06).
We used a meridional cut to show the longitudinal and temporal average of the angular velocity ![]() along with the temperature
and entropy fluctuations with respect to a spherically symmetric background. We first note that the differential rotation in the
model is solar-like, with a fast equator and slow pole, and that the iso-contours of
along with the temperature
and entropy fluctuations with respect to a spherically symmetric background. We first note that the differential rotation in the
model is solar-like, with a fast equator and slow pole, and that the iso-contours of ![]() are constant along radial lines
at mid-latitude (i.e., the rotation profile is conical rather than
cylindrical). Its amplitude is also of the right order of magnitude. By
contrast it is important to note
that the temperature T' and entropy S' fluctuations
are constant along radial lines
at mid-latitude (i.e., the rotation profile is conical rather than
cylindrical). Its amplitude is also of the right order of magnitude. By
contrast it is important to note
that the temperature T' and entropy S' fluctuations![]() are smaller by a factor of about 10 with respect to the seismic inversion, with temperature variations of
about 10 K from equator to pole up to
are smaller by a factor of about 10 with respect to the seismic inversion, with temperature variations of
about 10 K from equator to pole up to
![]() .
A detailed analysis of the redistribution of heat and angular momentum
in the 3D models reveals that
the Reynolds stresses and the latitudinal enthalpy flux are key players
in establishing the profile of angular velocity and the variation of
temperature as well as entropy with latitude (Brun & Rempel 2008). Reynolds stresses transport angular momentum from the polar region down to the equator being opposed
by meridional circulation and viscous effect. The heat is transported poleward by the turbulent enthalpy flux (e.g.
.
A detailed analysis of the redistribution of heat and angular momentum
in the 3D models reveals that
the Reynolds stresses and the latitudinal enthalpy flux are key players
in establishing the profile of angular velocity and the variation of
temperature as well as entropy with latitude (Brun & Rempel 2008). Reynolds stresses transport angular momentum from the polar region down to the equator being opposed
by meridional circulation and viscous effect. The heat is transported poleward by the turbulent enthalpy flux (e.g.
![]() ,
with
,
with
![]() denoting an azimuthal average),
denoting an azimuthal average),
![]() the mean background density and
the mean background density and
![]() the fluctuating latitudinal component of the velocity field with
respect to the axisymmetric mean, (see for more details Brun &
Palacios 2009)
yielding a cool equator and hot poles in most of the domain. It is
opposed by the thermal diffusion which tries to make the entropy and
temperature field homogeneous. A careful study of the profile of the
temperature and entropy fluctuations reveals that the
entropy is monotonic with respect to latitude while near the surface
the temperature is banded (warm-cool-hot). Furthermore the entropy
profile is conical, as is the angular velocity at mid-latitude, whereas
the temperature profile is more cylindrical. In these stratified
(anelastic) simulations the difference between the two thermal
quantities is due to density (or pressure) fluctuations that cannot be
neglected. This confirms that entropy is the key quantity to consider
when studying the angular velocity profile of the Sun as is clearly
stated in the thermal wind equations detailed in Sect. 4.1.
Mean field 2D models also find axisymmetric temperature variations of
the order of a few Kelvin at the surface and in the bulk of the
convection zone (Kitchatinov & Rüdiger 1995; Küker & Rüdiger 2005).
Current global 3D numerical simulations of the solar convection zone do not model the very surface, but
stop at around 0.96 to 0.98
the fluctuating latitudinal component of the velocity field with
respect to the axisymmetric mean, (see for more details Brun &
Palacios 2009)
yielding a cool equator and hot poles in most of the domain. It is
opposed by the thermal diffusion which tries to make the entropy and
temperature field homogeneous. A careful study of the profile of the
temperature and entropy fluctuations reveals that the
entropy is monotonic with respect to latitude while near the surface
the temperature is banded (warm-cool-hot). Furthermore the entropy
profile is conical, as is the angular velocity at mid-latitude, whereas
the temperature profile is more cylindrical. In these stratified
(anelastic) simulations the difference between the two thermal
quantities is due to density (or pressure) fluctuations that cannot be
neglected. This confirms that entropy is the key quantity to consider
when studying the angular velocity profile of the Sun as is clearly
stated in the thermal wind equations detailed in Sect. 4.1.
Mean field 2D models also find axisymmetric temperature variations of
the order of a few Kelvin at the surface and in the bulk of the
convection zone (Kitchatinov & Rüdiger 1995; Küker & Rüdiger 2005).
Current global 3D numerical simulations of the solar convection zone do not model the very surface, but
stop at around 0.96 to 0.98 ![]() ,
and as a consequence can not be used yet to model the near surface shear layer
(see however the studies of Derosa et al. 2002; using a modified ASH code or of Robinson & Chan 2001, using a spherical wedge model).
,
and as a consequence can not be used yet to model the near surface shear layer
(see however the studies of Derosa et al. 2002; using a modified ASH code or of Robinson & Chan 2001, using a spherical wedge model).
![\begin{figure}
\par\includegraphics[angle=90,width=15cm,clip]{13166f3.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13166-09/Timg34.png)
|
Figure 3: Left panel: angular velocity (in nHz) achieved in model AB3 of Miesch et al. (2006). Middle panel: associated entropy S' (erg/g/K) and temperature T' (K) fluctuations with respect to the spherically averaged background. All quantities have been averaged over longitude and time (10 solar periods). Note the conical profile of the angular velocity at mid latitude and the latitudinal variation of the thermal variables possessing hot poles. Near the surface the temperature is banded with warm equator, cool mid latitudes and hot poles. Contrary to the helioseismic inversion no symmetry with respect to the equator is assumed and the quantities exhibit a small North-South asymmetry. |
| Open with DEXTER | |
4 Quality of thermal wind balance achieved in the Sun and 3D models
4.1 Theoretical considerations
In rotating convection, both radial and latitudinal heat transport
occurs, the latter establishing latitudinal gradients in
temperature and entropy within the convective zone as illustrated in Fig. 3.
A direct consequence of the existence of such gradients is that the
surfaces of pressure and density fluctuations will not coincide
anymore,
thereby yielding baroclinic effects. We can turn to the vorticity
equations
(Pedlosky 1987; Zahn 1992) to analyse the role of the turbulence and baroclinic effects
in setting the large scale flows shown in Fig. 3.
The thermal wind balance equation can be derived
from the vorticity equation as discussed in detail by BT02 and MBT06.
The equation for the vorticity in the purely hydrodynamical
case can be derived under the anelastic approximation by taking the
curl of the momentum equation (see also Fearn 1998; and Brun 2005,
for its MHD generalisation and the notion of magnetic wind):
with
![$\displaystyle {\cal D}_{ij}=-2\bar{\rho}\nu \left [e_{ij}-\frac{1}{3}(\mbox{\boldmath$\nabla$ }\cdot\vec{v})\delta_{ij} \right ],$](/articles/aa/full_html/2010/02/aa13166-09/img41.png)
|
(5) |
where eij is the strain rate tensor, and
This vorticity equation helps in understanding the relative importance of
the different processes acting in the meridional planes. In the
stationary case (
![]() ), and assuming an
azimuthal average (such that
), and assuming an
azimuthal average (such that
![]() vanishes),
the azimuthal component of Eq. (4) reads:
vanishes),
the azimuthal component of Eq. (4) reads:
where
| |
= | ![$\displaystyle \frac{1}{\bar{\rho}}\left \langle\left[\frac{1}{r^2}\frac{\partia...
...frac{ {\cal D}_{\theta \theta} + {\cal D}_{\phi \phi}}{r} \right]\right\rangle,$](/articles/aa/full_html/2010/02/aa13166-09/img52.png)
|
|
| = | ![$\displaystyle \frac{1}{\bar{\rho}}\Bigg \langle\left[\frac{1}{r^2}\frac{\partia...
...eta}\frac{\partial(\sin\theta{\cal D}_{\theta \theta})}{\partial\theta} \right]$](/articles/aa/full_html/2010/02/aa13166-09/img54.png)
|
(7) | |
![$\displaystyle + \frac{1}{\bar{\rho}}\left[ \frac{ {\cal D}_{\theta r} - {\rm cot} \theta {\cal D}_{\phi \phi}}{r} \right]\Bigg \rangle \cdot$](/articles/aa/full_html/2010/02/aa13166-09/img55.png)
|
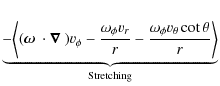
In the above equation we have identified several terms:
-
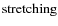 describes the stretching/tilting of the vorticity due to velocity gradients;
describes the stretching/tilting of the vorticity due to velocity gradients;
-
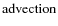 describes the advection of vorticity by the flow;
describes the advection of vorticity by the flow;
-
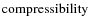 describes the change of vorticity due to the flow compressibility;
describes the change of vorticity due to the flow compressibility;
-
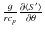 is the baroclinic term, characteristic of non-aligned density and pressure gradients;
is the baroclinic term, characteristic of non-aligned density and pressure gradients;
-
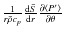 is part of the baroclinic term but arises from departure to adiabatic stratification;
is part of the baroclinic term but arises from departure to adiabatic stratification;
-
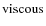 accounts for the diffusion of vorticity due to viscous effects.
accounts for the diffusion of vorticity due to viscous effects.
Under the assumption that the convection zone is adiabatic, the Rossby number
![]() is small, and that compressibility, Reynolds and viscous stresses can be neglected,
Eq. (6) simplifies to give:
is small, and that compressibility, Reynolds and viscous stresses can be neglected,
Eq. (6) simplifies to give:
This is the thermal wind equation. It simply states that baroclinic effect can break the Taylor-Proudman constraint of cylindrical differential rotation since otherwise
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13166f4.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13166-09/Timg69.png)
|
Figure 4:
Meridional cut of the terms discussed in Eq. (6) averaged over azimuth and 10 solar periods.
Shown are in turn:
|
| Open with DEXTER | |
4.2 Results from 3D models
Figure 4 displays for case AB3 the left-hand side of
Eq. (6),
along with the dominant terms of the right-hand side and their sum.
We clearly see that the sum of the dominant RHS term is
in very close agreement with the LHS. We have chosen to form the
temporal average over 10 solar periods because it corresponds to about
10 convective overturning times and leads to a very close balance
between the LHS and the RHS of Eq. (6).
Shorter averages do not
lead to such a good balance, whereas longer averages change neither the
quality of the balance obtained significantly nor the patterns of the
various terms. Our more detailed decomposition of the vorticity
equation is allowing us to
identify which term is contributing and where. First the baroclinic
term is found to be dominant in most of the bulk of
the convection zone as was found by BT02 and MBT06. Advection terms are
found to contribute both in the bulk and near the surface. Contrary to
the baroclinic term they do not possess a systematic dominant
contribution in each hemisphere. Their contribution leads to a change
in key places, yielding
a more structured profile of the RHS than the baroclinic term would
have yielded if considered alone. Since the Rossby number realised in
the simulation is less than one, we expect the
advection and stretching term to be small on average in the simulations
and indeed, their maximum amplitude is not as large as the baroclinic
term. As stressed above however this is not the case in all scales nor
in all locations and they do contribute in key places, leading to the
very good balance shown in Fig. 4 between the LHS and RHS of Eq. (6).
Finally, in our models a viscous shear layer is dominating the balance at the surface where the isocontours of ![]() possess
the strongest latitudinal shear. Durney (1989) and Kitchatinov & Ruediger (1999)
have also stressed that a strict thermal wind balance cannot be
realised everywhere in the convection zone and that viscous stresses
may play a role near the boundaries as observed in Fig. 4.
We can conclude accordingly that Eq. (8) is only partly satisfied in our 3D hydrodynamical simulations of the solar convective envelope.
Clearly baroclinic effects play a central role but these are far from being dominant everywhere, and considering only Eq. (8) instead of the full balance expressed in Eq. (6) would be misleading. We now turn to seismic inversion to see if
the thermal wind balance is strictly realised in the Sun or if other contributions must be invoked to explain the
peculiar solar rotation profile.
possess
the strongest latitudinal shear. Durney (1989) and Kitchatinov & Ruediger (1999)
have also stressed that a strict thermal wind balance cannot be
realised everywhere in the convection zone and that viscous stresses
may play a role near the boundaries as observed in Fig. 4.
We can conclude accordingly that Eq. (8) is only partly satisfied in our 3D hydrodynamical simulations of the solar convective envelope.
Clearly baroclinic effects play a central role but these are far from being dominant everywhere, and considering only Eq. (8) instead of the full balance expressed in Eq. (6) would be misleading. We now turn to seismic inversion to see if
the thermal wind balance is strictly realised in the Sun or if other contributions must be invoked to explain the
peculiar solar rotation profile.
4.3 Inverted solar thermal wind balance
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13166f5aN.eps}\hspace*{1.5mm}
\includegraphics[width=7cm,clip]{13166f5bN.eps} %
\end{figure}](/articles/aa/full_html/2010/02/aa13166-09/Timg70.png)
|
Figure 5:
The aspherical component of the latitudinal derivative of
the entropy fluctuation,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13166f6aN.eps}\hspace*{1.5mm}
\includegraphics[width=7cm,clip]{13166f6bN.eps} %
\end{figure}](/articles/aa/full_html/2010/02/aa13166-09/Timg72.png)
|
Figure 6:
The derivative of rotation velocity,
|
| Open with DEXTER | |
The entropy perturbations obtained in Sect. 3.1 can be differentiated to calculate the RHS of Eq. (8)
The result is shown in Fig. 5. We clearly see that the baroclinic term is non monotonic with respect to latitude, with large positive values near the poles and in a small region at the equator, whereas it is negative in mid latitudes. At the surface a surface thermal boundary layer is visible that yields strong radial gradients at high latitudes.
As we have done with the 3D model, the baroclinic term should be compared with
which is shown in Fig. 6. This quantity has much less structure in the bulk of the convection zone. Except for a slightly negative structure at mid depth and latitude, most of the action occurs in the surface shear layer where strong negative values are found due to strong radial gradient of rotation rate in the near surface shear layer. This near surface layer is not present in the simulations and hence cannot be compared with the results of 3D simulations. It is clear that contrary to what we have seen with the 3D model in the previous section, the two quantities do not agree with each other even slightly. In fact, these two terms differ by more than an order of magnitude. While the term involving
5 Discussion of results
What can be the source of the disagreement between the inverted baroclinic contribution and the z derivative of the angular velocity (i.e. Eqs. (8), or (9) and (10))?
The first and easiest solution is that the inversion of the thermal
quantities lacks the necessary accuracy, and given the increase by two
orders of magnitude of the background temperature and density with
depth, we end up with variations that are too large. The source of
discrepancy will then be due to an overestimation of ![]() and
and ![]() .
It is not easy to decide if these inverted thermal fluctuations are too
large or if the simulations (both 2D and 3D) underestimates
the fluctuations realised in the Sun, because of for instance their
limited Reynolds number. We must thus also consider the possibility
that these large thermal perturbations are genuine. If this is indeed
the case we need to see how we could resolve the discrepancy between
the seismically inverted LHS and RHS of Eq. (8).
As stated in Sect. 4.1, to obtain a strict thermal wind balance as expressed in Eq. (8),
one needs to make a certain number of assumptions:
adiabaticity, weak Rossby number, negligible compressibility, viscous
and Reynolds stresses, stationarity. By considering further only the
hydrodynamic contributions we have omitted those associated with
Maxwell stresses that are certainly present in the magnetic Sun. We are
confident that the Maxwell stresses are not the source of the large
observed discrepancy because we have formed temporal averages over a
maximum and minimum period of activity and the differences
between the two periods are about 10 times smaller than what would be
required if all the sources of discrepancy were coming from the Maxwell
stresses alone. We nevertheless intend to make a more systematic study
of the departure of the strict thermal wind balance linked to magnetic
effects (i.e. via the so called magnetic wind) by analysing the solar
cycle 23 in detail and by comparing the results with dynamo
simulations of the solar convection (Brun et al. 2004).
We must thus question the validity of the other hypothesis made in deriving Eq. (8).
It is clearly justified to consider the viscous terms as being
negligible, given the very low microscopic value of the solar kinematic
viscosity. This is clearly not the case in the 3D models where near the
surface they are major contributors to the overall balance (see
Fig. 4,
middle panel of the bottom row), but this is due to our large effective
viscosity. Assuming adiabaticity is certainly reasonable in most of the
convection zone, but clearly not near the surface. Since we are mostly
interested in understanding the bulk dynamics of the solar convection
zone, this term is indeed very small. The choice of a low Rossby number
that allows us to neglect
.
It is not easy to decide if these inverted thermal fluctuations are too
large or if the simulations (both 2D and 3D) underestimates
the fluctuations realised in the Sun, because of for instance their
limited Reynolds number. We must thus also consider the possibility
that these large thermal perturbations are genuine. If this is indeed
the case we need to see how we could resolve the discrepancy between
the seismically inverted LHS and RHS of Eq. (8).
As stated in Sect. 4.1, to obtain a strict thermal wind balance as expressed in Eq. (8),
one needs to make a certain number of assumptions:
adiabaticity, weak Rossby number, negligible compressibility, viscous
and Reynolds stresses, stationarity. By considering further only the
hydrodynamic contributions we have omitted those associated with
Maxwell stresses that are certainly present in the magnetic Sun. We are
confident that the Maxwell stresses are not the source of the large
observed discrepancy because we have formed temporal averages over a
maximum and minimum period of activity and the differences
between the two periods are about 10 times smaller than what would be
required if all the sources of discrepancy were coming from the Maxwell
stresses alone. We nevertheless intend to make a more systematic study
of the departure of the strict thermal wind balance linked to magnetic
effects (i.e. via the so called magnetic wind) by analysing the solar
cycle 23 in detail and by comparing the results with dynamo
simulations of the solar convection (Brun et al. 2004).
We must thus question the validity of the other hypothesis made in deriving Eq. (8).
It is clearly justified to consider the viscous terms as being
negligible, given the very low microscopic value of the solar kinematic
viscosity. This is clearly not the case in the 3D models where near the
surface they are major contributors to the overall balance (see
Fig. 4,
middle panel of the bottom row), but this is due to our large effective
viscosity. Assuming adiabaticity is certainly reasonable in most of the
convection zone, but clearly not near the surface. Since we are mostly
interested in understanding the bulk dynamics of the solar convection
zone, this term is indeed very small. The choice of a low Rossby number
that allows us to neglect ![]() over the planetary vorticity
over the planetary vorticity ![]() ,
is certainly not justified at all scales of the turbulent velocity
spectra, in particular for those scales much smaller than the Rossby
radius of deformation (Pedlosky 1987). In the
Sun the large range of convection scales implies that a subset of those
scales undergo different dynamics depending on how sensitive they are
to the Coriolis force. The subtle angular momentum and heat
redistribution realised in the Sun is in part captured in our 3D
models. We can thus analyse if the Reynolds stresses associated with
the turbulent motion indeed play a central role. As discussed in detail
in Brun & Toomre (2002) and in Sect. 4 we know that it is indeed
the case in our numerical simulations (see Fig. 4,
middle and right panel of the top row) even though our simulations do
not possess a Reynolds number and a degree of turbulence as high as
that in the Sun. We can thus expect, given the very large Reynolds
number of the solar convection zone, that Reynolds stresses must play a
central role in the Sun in shaping the differential rotation profile
and that they somehow in part compensate the baroclinic contribution to
yield the observed profile of angular velocity. This is a significant
result for two reasons: It confirms for one that the Reynolds stresses
are key to explain the equatorial acceleration of the
solar differential rotation (as anticipated by studying angular
momentum transport in our simulations as in BT02 or Miesch
et al. 2008).
Secondly
it indicates that they are also important to explain the conical
profile of the solar differential rotation, helping or opposing in some
regions the baroclinic effects to break Taylor-Proudman constraint. Of
course this conclusion only holds if the inverted large thermal
fluctuations are real.
,
is certainly not justified at all scales of the turbulent velocity
spectra, in particular for those scales much smaller than the Rossby
radius of deformation (Pedlosky 1987). In the
Sun the large range of convection scales implies that a subset of those
scales undergo different dynamics depending on how sensitive they are
to the Coriolis force. The subtle angular momentum and heat
redistribution realised in the Sun is in part captured in our 3D
models. We can thus analyse if the Reynolds stresses associated with
the turbulent motion indeed play a central role. As discussed in detail
in Brun & Toomre (2002) and in Sect. 4 we know that it is indeed
the case in our numerical simulations (see Fig. 4,
middle and right panel of the top row) even though our simulations do
not possess a Reynolds number and a degree of turbulence as high as
that in the Sun. We can thus expect, given the very large Reynolds
number of the solar convection zone, that Reynolds stresses must play a
central role in the Sun in shaping the differential rotation profile
and that they somehow in part compensate the baroclinic contribution to
yield the observed profile of angular velocity. This is a significant
result for two reasons: It confirms for one that the Reynolds stresses
are key to explain the equatorial acceleration of the
solar differential rotation (as anticipated by studying angular
momentum transport in our simulations as in BT02 or Miesch
et al. 2008).
Secondly
it indicates that they are also important to explain the conical
profile of the solar differential rotation, helping or opposing in some
regions the baroclinic effects to break Taylor-Proudman constraint. Of
course this conclusion only holds if the inverted large thermal
fluctuations are real.
We thank J. P. Zahn for useful comments on a draft version of this paper. We acknowledge funding by the Indian-French scientific network (IFAN). A.S.B. is grateful to the Tata Institute of Fundamental Research, Mumbai and the Indian Institute of Astrophysics, Bangalore and its director Prof. S. Hasan for their hospitality during his visit in November 2008. This work utilised data obtained by the Global Oscillation Network Group (GONG) project, managed by the National Solar Observatory, which is operated by AURA, Inc. under a cooperative agreement with the National Science Foundation. The data were acquired by instruments operated by the Big Bear Solar Observatory, High Altitude Observatory, Learmonth Solar Observatory, Udaipur Solar Observatory, Instituto de Astrofisico de Canarias, and Cerro Tololo Inter-American Observatory. This work also utilises data from the Solar Oscillations Investigation/Michelson Doppler Imager (SOI/MDI) on the Solar and Heliospheric Observatory (SOHO). SOHO is a project of international cooperation between ESA and NASA. A.S.B acknowledges funding by the European Research Council through ERC grant STARS2 207430 (www.stars2.eu).
References
- Altrock, R. C., & Canfield, R. C. 1972, Sol. Phys., 23, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Antia, H. M., Basu, S., & Chitre, S. M. 1998, MNRAS, 298, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Antia, H. M., Basu, S., Hill, F., et al. 2001, MNRAS, 327, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., Bonart, J., Latter, H. N., & Weiss, N. O. 2009, MNRAS, in press [Google Scholar]
- Basu, S., & Antia, H. M. 1995, MNRAS, 276, 1402 [NASA ADS] [Google Scholar]
- Basu, S., & Christensen-Dalsgaard, J. 1997, A&A, 322, L5 [NASA ADS] [Google Scholar]
- Brun, A. S. 2005, Habilitation à Diriger les Recherches, Physics Department, University of Paris VII Denis Diderot, France [Google Scholar]
- Brun, A. S., & Palacios, A. 2009, ApJ, 702, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Brun, A. S., & Rempel, M. 2008, Space Sci. Rev., 144, 151 [Google Scholar]
- Brun, A. S., & Toomre, J. 2002, ApJ, 570, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brun, A. S., Antia, H. M., Chitre, S. M., & Zahn, J.-P. 2002, A&A, 391, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brun, A. S., Miesch, M. S., & Toomre, J. 2004, ApJ, 614, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Derosa, M. L., Gilman, P., & Toomre, J. 2002, ApJ, 581, 1356 [NASA ADS] [CrossRef] [Google Scholar]
- Dicke, R. H., & Goldenberg, H. M. 1967, Phys. Rev. Lett., 18, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Durney, B. R. 1989, ApJ, 338, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Durney, B. R. 1999, ApJ, 511, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Fearn, D. R. 1998, Rep. Progr. Phys., 61, 3, 175 [Google Scholar]
- Gilman, P., & Miller, J. 1986, ApJS, 61, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Glatzmaier, G. A., & Gilman, P. 1982, ApJ, 256, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, F., Stark P. B., Stebbirs, R. T., et al. 1996, Science, 272, 1292 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kitchatinov, L. L., & Rüdiger, G. 1995, A&A, 299, 446 [NASA ADS] [Google Scholar]
- Kitchatinov, L. L., & Rüdiger, G. 1999, A&A, 344, 911 [NASA ADS] [Google Scholar]
- Koutchmy, S., Koutchmy, O., & Kotov, V. 1977, A&A, 59, 189 [NASA ADS] [Google Scholar]
- Kuhn, J. R., Libbrecht, K. G., & Dicke, R. H. 1985, ApJ, 290, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Kuhn, J. R., Bush, R. I., Scheick, X., et al. 1998, Nature, 392, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Küker, M., & Rüdiger, G. 2005, A. N., 326, 265 [Google Scholar]
- Miesch, M. S., Brun, A. S., & Toomre, J. 2006, ApJ, 641, 618 [Google Scholar]
- Miesch, M. S., Brun, A. S., DeRosa, M. L., & Toomre, J. 2008, ApJ, 673, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Pedlosky, J. 1987, Geophysical Fluid Dynamics (New York: Springer-Verlag) [Google Scholar]
- Rast, M. P., Ortiz, A., & Meisner, R. W. 2008, ApJ, 673, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M. 2005, ApJ, 622, 1320 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, F. J., & Chan, K. L. 2001, MNRAS, 321, 723 [Google Scholar]
- Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Schou, J. 1999, ApJ, 523, L181 [NASA ADS] [CrossRef] [Google Scholar]
- Schou, J., Antia, H. M., Basu, J., et al. 1998, ApJ, 505, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, M. J., Toomre, J., Anderson, E. R., et al. 1996, Science, 272, 1300 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
Footnotes
- ... fluctuations
![[*]](/icons/foot_motif.png)
- For the sake of clarity we make the distinction between the
seismic inversion of the temperature and entropy perturbations denoted with a
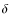 symbol and the one computed in the models denoted by a prime.
symbol and the one computed in the models denoted by a prime.
All Figures
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{13166f1aN.eps}\hspace*{1mm...
...ncludegraphics[width=6.1cm,clip]{13166f1cN.eps}\hfill
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/02/aa13166-09/Timg14.png)
|
Figure 1:
The aspherical component of temperature fluctuation, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{13166f2a.eps}\hspace*{1mm}
\...
...
\includegraphics[width=6cm,clip]{13166f2c.eps}\hfill
\vspace*{6mm}
\end{figure}](/articles/aa/full_html/2010/02/aa13166-09/Timg15.png)
|
Figure 2:
The aspherical component of entropy fluctuation, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=15cm,clip]{13166f3.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13166-09/Timg34.png)
|
Figure 3: Left panel: angular velocity (in nHz) achieved in model AB3 of Miesch et al. (2006). Middle panel: associated entropy S' (erg/g/K) and temperature T' (K) fluctuations with respect to the spherically averaged background. All quantities have been averaged over longitude and time (10 solar periods). Note the conical profile of the angular velocity at mid latitude and the latitudinal variation of the thermal variables possessing hot poles. Near the surface the temperature is banded with warm equator, cool mid latitudes and hot poles. Contrary to the helioseismic inversion no symmetry with respect to the equator is assumed and the quantities exhibit a small North-South asymmetry. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13166f4.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13166-09/Timg69.png)
|
Figure 4:
Meridional cut of the terms discussed in Eq. (6) averaged over azimuth and 10 solar periods.
Shown are in turn:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13166f5aN.eps}\hspace*{1.5mm}
\includegraphics[width=7cm,clip]{13166f5bN.eps} %
\end{figure}](/articles/aa/full_html/2010/02/aa13166-09/Timg70.png)
|
Figure 5:
The aspherical component of the latitudinal derivative of
the entropy fluctuation,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13166f6aN.eps}\hspace*{1.5mm}
\includegraphics[width=7cm,clip]{13166f6bN.eps} %
\end{figure}](/articles/aa/full_html/2010/02/aa13166-09/Timg72.png)
|
Figure 6:
The derivative of rotation velocity,
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



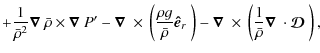
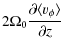
![$\displaystyle - \underbrace{\langle \omega_{\phi}v_r \rangle\frac{{\rm d}\ln \b...
...al}{\partial\theta}\langle {\cal A}_r \rangle \right]}_{\rm Viscous\; stresses}$](/articles/aa/full_html/2010/02/aa13166-09/img48.png)