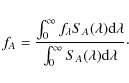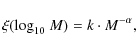EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 510 (February 2010) A&A, 510 (2010) A27 Full HTML
Free Access
Issue
A&A
Volume 510, February 2010
Article Number A27
Number of page(s) 14
Section Galactic structure, stellar clusters, and populations
DOI https://doi.org/10.1051/0004-6361/200913011
Published online 03 February 2010
A&A 510, A27 (2010)

Brown dwarfs and very low mass stars in the Praesepe open cluster: a dynamically unevolved mass function?[*],[*]

S. Boudreault1 - C. A. L. Bailer-Jones1 - B. Goldman1 - T. Henning1 - J. A. Caballero2

1 - Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
2 - Departamento de Astrofísica, Facultad de Física, Universidad Complutense de Madrid, 28040 Madrid, Spain

Received 29 July 2009 / Accepted 23 October 2009

Abstract
Context. Determination of the mass functions of open clusters of different ages allows us to infer the efficiency with which brown dwarfs are evaporated from clusters to populate the field.
Aims. In this paper we present the results of a photometric survey to identify low mass and brown dwarf members of the old open cluster Praesepe (age 590 +150-120 Myr, distance 190 +6.0-5.8 pc) from which we estimate its mass function and compare this with that of other clusters.
Methods. We performed an optical ($I_{\rm c}$-band) and near-infrared (J and $K_{\rm s}$-band) photometric survey of Praesepe covering 3.1 deg2. With 5$\sigma $ detection limits of $I_{\rm c}=23.4$ and J = 20.0, our survey is predicted to be sensitive to objects with masses from 0.6 to 0.05 $M_{\odot }$.
Results. We photometrically identify 123 cluster member candidates based on dust-free atmospheric models and 27 candidates based on dusty atmospheric models. The mass function rises from 0.6 $M_{\odot }$ down to 0.1 $M_{\odot }$ (a power law fit of the mass function gives $\alpha = 1.8 \pm 0.1$;  $\xi$(M)  $\propto M^{-\alpha}$ ), and then turns over at $\sim $0.1 $M_{\odot }$. This rise agrees with the mass function inferred by previous studies, including a survey based on proper motion and photometry. In contrast, the mass function differs significantly from that measured for the Hyades, an open cluster with a similar age ( $\tau \sim 600$ Myr). Possible reasons are that the clusters did not have the same initial mass function, or that dynamical evolution (e.g. evaporation of low mass members) has proceeded differently in the two clusters. Although different binary fractions could cause the observed (i.e. system) mass functions to differ, there is no evidence for differing binary fractions from measurements published in the literature. Of our cluster candidates, six have masses predicted to be equal to or below the stellar/substellar boundary at 0.072 $M_{\odot }$.

Key words: open clusters and associations: individual: Praesepe - stars: low-mass - stars: brown dwarfs - stars: luminosity function, mass function - stars: formation

1 Introduction

Several publications in the past decade have been concerned with the mass function (MF) of low mass stellar and substellar populations in open clusters, including $\sigma $ Orionis (Béjar et al. 2002; Caballero et al. 2007), the Orion Nebula Cluster (Hillenbrand & Carpenter 2000; Slesnick et al. 2004), IC 2391 (Barrado y Navascués et al. 2004; Boudreault & Bailer-Jones 2009), the Pleiades (Moraux et al. 2003; Lodieu et al. 2007), and the Hyades (Reid & Hawley 1999; Bouvier et al. 2008), to name just a few. Studies of relatively old open clusters (age $\gtrsim$ 100 Myr) are important for the following two reasons in particular. First, they permit a study of the intrinsic evolution of brown dwarfs (BDs), e.g. their luminosity and effective temperature, which constrains structural and atmospheric models. Second, together with younger clusters we can investigate how BD populations as a whole evolve and thus probe the efficiency with which BDs evaporate from clusters to populate the Galactic field. Numerical simulations of cluster evolution have demonstrated that the MFs can evolve through dynamical interaction (de la Fuente Marcos & de la Fuente Marcos 2000; Adams et al. 2002b). These interactions result in a decrease of the open cluster BD (and low-mass star) population. This has been observed by Bouvier et al. (2008) from a comparison of the Pleiades (120 Myr) and Hyades (625 Myr) mass functions.

Many earlier studies of the substellar MF have focused on young open clusters with ages less than $\sim $100 Myr, and in many cases much younger (<10 Myr). This is partly because BDs are bright when they are young (lacking a significant nuclear energy source, they cool as they age), thus easing detection of the least massive objects. However, youth presents difficulties. First, intra-cluster extinction plagues the determination of the intrinsic luminosity function from the measured photometry. Second, at these ages the BD models have large(r) uncertainties (Baraffe et al. 2002). Estimates of the substellar MF in very young clusters (age $\lesssim$ 1 Myr) might be unreliable due to these modelling uncertainties (Chabrier et al. 2005). BDs in older clusters suffer less from these problems, but have the disadvantage that much deeper surveys are required to detect them.

The old open cluster Praesepe is an interesting target considering its age and distance. It is located at a distance of 190 +6.0-5.8 pc (based on parallax measurements from the new Hipparcos data reduction, van Leeuwen 2009) and has an age of 590 +150-120 Myr (by isochrone fitting in the Hertzsprung-Russell diagram; Fossati et al. 2008). The extinction towards this cluster is low, $E(B-V) = 0.027 \pm 0.004$ mag (Taylor 2006), while determinations of the metallicity of Praesepe yield some discrepancies: [Fe/H] =  $0.038 \pm 0.039$, Friel & Boesgaard (1992); + $0.13 \pm 0.10$, Boesgaard & Budge (1988); $0.11 \pm 0.03$from spectroscopy and $0.20 \pm 0.04$ from photometry, An et al. (2007); + $0.27 \pm 0.10$, Pace et al. (2008). Hambly et al. (1995) presented a $\sim $19 deg2 survey of the Praesepe cluster down to masses of $\sim $0.1 $M_{\odot }$ and observed a rise of the MF at the lowest masses. They concluded that this implied a large population of BDs. A shallow survey complete to I = 21.2 mag, R = 22.2 mag over 800 arcmin2 uncovered one spectrally confirmed very low-mass star or BD (spectral type of M8.5V) with a model-dependent mass of 0.063-0.084 $M_{\odot }$ (Magazzú et al. 1998). A survey over the central 1 deg2 with 10$\sigma $ limits of R = 21.5, I = 20.0 and Z = 21.5 mag revealed 19 BD candidates and the first MF determination of Praesepe down to the substellar limit, but without spectral confirmation (Pinfield et al. 1997). Subsequent infrared photometry of the sample reduced this number to nine candidates (Hodgkin et al. 1999). Adams et al. (2002a) presented a 100 deg2 study of Praesepe using 2MASS (Two-Micron All Sky Survey) data and Palomar survey photographic plates, from which they derived proper motions. They determined the radial profile of this cluster but their MF does not reach the substellar regime. A more recent proper motion survey of Praesepe covers a much larger area (300 deg2; Kraus & Hillenbrand 2007), but does not reach the BD regime either (the limit is $\sim $0.12 $M_{\odot }$). Finally, the most recent substellar MF determination of Praesepe was published by González-García et al. (2006) and extends to a 5$\sigma $ detection limit of i = 24.5 mag corresponding to 0.050-0.055 $M_{\odot }$. They identified one new substellar candidate, but their survey covers only 1177 arcmin2.

In this paper, we present the results of a program to study, in detail, the MF of Praesepe down to the substellar regime. Our photometric survey is, as with González-García et al. (2006), the deepest so far in optical and near-infrared (NIR) bands, with 5$\sigma $ detection limits of $I_{\rm c}=23.4$ and J=20.0(corresponding to a mass limit of about 0.05 $M_{\odot }$), but covers more than nine times the area. Our paper is structured as follows. We first present the data set, reduction procedure and calibration in Sect. 2. We then discuss our candidate selection procedure in Sect. 3 and the survey results in Sect. 4 before discussing the derived MF in Sect. 5. We conclude in Sect. 6.

2 Observations, data reduction, calibration, and estimation of masses and effective temperatures

2.1 Observations

Table 1:   Description of observations with the O2k infrared camera.

Table 2:   Description of observations with WFI optical camera.

Our survey consists of 47 Omega 2000 (O2k) fields each of size $15.4 \times 15.4$ arcmin2 observed in J and $K_{\rm s}$, plus the same region observed in nine $I_{\rm c}$ Wide Field Imager (WFI) fields each of size $34 \times 33$ arcmin2. This gives a total coverage of 3.1 deg2 observed in all three bands, centred on RA(J2000) = 08$^{\rm h}$40$^{\rm m}$04$^{\rm s}$ and Dec(J2000) = + 19$^\circ$40'00''.

The near-infrared (NIR) observations were made on the 3.5m telescope at Calar Alto, Spain (with observation runs of several nights from February 2005 to January 2007). O2k (Bailer-Jones et al. 2000; Baumeister et al. 2003) comprises a HAWAII-2 detector with 2k $\times$ 2k pixels over a field of view of $15.4 \times 15.4$ arcmin delivering a pixel scale of 0.45 arcsec per pixel. The optical observations were carried out with the Wide Field Imager (WFI) on the MPG/ESO 2.2m telescope at La Silla, Chile (Baade et al. 1999) during 17-22 March 2007. The WFI is a mosaic camera of $4 \times 2$ CCDs, each with 2k $\times$ 4k pixels, covering a total field of view of $34 \times 33$ arcmin2 at 0.238 arcsec per pixel. All fields were observed in the broad band filter $I_{\rm c}$. A detailed list of the fields observed with pointing, filter, exposure time and 5$\sigma $ detection limits is given in Table 1 for the NIR data and in Table 2 for the optical data. The passband functions for the filters, multiplied with the quantum efficiency of the detectors, are shown in Fig. 1.

\begin{figure} \par\includegraphics[width=8cm,clip]{13011f01.eps} \end{figure} Figure 1:

Transmission curve of the filters used in our survey compared to the synthetic spectrum of a BD with $T_{\rm eff} = 2300$ K, $\log g = 4.5$ and solar metallicity (NextGen model). The transmission curves include the quantum efficiency of the detectors.

Open with DEXTER

2.2 Data reduction and astrometry

The standard data reduction steps (overscan subtraction, trimming and flat-fielding for the WFI data; dark subtraction and flat-fielding for O2k data) were performed on a nightly basis, using the ccdredpackage under IRAF[*]. For both WFI and O2k data we used superflats (obtained by combining science image frames for each night) for pixel-to-pixel variation correction and for correcting the global illumination. For our NIR data, the sky background was subtracted using the median-combined images for each filter and each field (on a nightly basis). For WFI data, we reduced each of the eight CCDs in the mosaic independently and in the final step scaled them to a common flux response level. We made an initial sky subtraction via a low-order fit to the optical data, and for the infrared data by subtracting a median combination of all (unregistered) images of the science frames. Fringes were visible for the $I_{\rm c}$-band photometry. They were removed in the way described by Bailer-Jones & Mundt (2001)[*]. Finally, the individual images of a given field were registered and median combined. We used the IRAF task daofind to automatically detect stellar objects in an image by approximating the stellar point spread function with a Gaussian. We visually inspected the images in order to remove from our cluster candidate list any extended sources (i.e. galaxies) that were mistakenly identified as stars by daofind (see Sect. 3.3). Sources were extracted and instrumental magnitudes assigned via aperture photometry with the IRAF task wphot. To this aperture photometry we have applied an aperture correction following the technique described in Howell (1989). An astrometric solution was obtained using the IRAF package imcoords and the tasks ccxymatch, ccmap and cctran. For each WFI field, this solution was computed for the $I_{\rm c}$-band image (and for each O2k field using the J-band image) using the 2MASS catalogue as a reference. The root mean square accuracy of our astrometric solution is 0.15-0.20 arcsec for both WFI and O2k data. For WFI data, the astrometry was performed on a CCD-by-CCD basis.

2.3 Photometric calibration

To correct for Earth-atmospheric absorption on the photometry, we calibrated the infrared data using the J and $K_{\rm s}$-band magnitudes of 2MASS objects which were observed in our science fields. By determining a constant offset between the magnitude of 2MASS and our instrumental magnitude, we obtained the zero point offset. Since this zero point offset was obtained with objects in the same field of view in each science frame, and since we found the difference between the 2MASS and O2k passbands to be insignificant, we did not need to perform an airmass or colour correction when reducing our NIR photometry. (That is, the determined coefficients were statistically consistent with zero).

We followed a similar approach for our $I_{\rm c}$-band photometry, but using observations in our fields for which r and i-band magnitudes are available in the Sloan Digital Sky Survey (SDSS) catalogue. We first transformed the i-band magnitudes of SDSS to $I_{\rm c}$-band magnitudes using the transformation equation of Jordi et al. (2006)

\begin{displaymath}I_{\rm c}=i-0.381{-}0.254 \times (r-i) \end{displaymath} (1)

We then determined the zero point offset between this $I_{\rm c}$magnitude and our instrumental $I_{\rm c}$ magnitude, again using the SDSS stars. A further colour correction was not necessary, and as this calibration is applied on a field-by-field basis (as with the NIR data), an airmass correction was likewise unnecessary.

2.4 Mass and effective temperature estimates based on photometry

After we identify candidates (Sect. 3) we will use the multiband photometry to derive their masses and effective temperatures, $T_{\rm eff}$. We use the evolutionary tracks from Baraffe et al. (1998) and atmosphere models from Hauschildt et al. (1999a) (assuming a dust-free atmosphere; the NextGen model) to compute an isochrone for Praesepe for an age of 590 Myr, a distance of 190 pc, a solar metallicity and assuming zero extinction. These models and assumptions provide us with a prediction of $f_{\lambda}$, the spectral energy distribution received at the Earth (in erg cm-2 s-1 Å-1) from the source. We need to convert these spectral energy distributions into magnitudes in the filters we used. Denoting as SA($\lambda$) the (known) total transmission function of filter A (including the CCD quantum efficiency and assuming telescope and instrumental throughput are flat), then the flux measured in the filter is

\begin{displaymath}f_{A}=\frac{\int_{0}^{\infty}f_{\lambda}S_{A}(\lambda){\rm d}\lambda}{\int_{0}^{\infty}S_{A}(\lambda){\rm d}\lambda}\cdot \end{displaymath} (2)

The corresponding magnitude mA in the Johnson photometric system is given by

\begin{displaymath}{m_{A}=-2.5\;{\rm log}\;f_{A}\;+\;c_{A}}, \end{displaymath} (3)

where cA is a constant (zero point) that remains to be determined in order to put the model-predicted magnitude onto the Johnson system. We derived this constant for each of the bands $I_{\rm c}$, J and $K_{\rm s}$ in the standard way, namely by requiring that the spectrum of Vega produce a magnitude mA of 0.03 in all bands. Using the Vega spectrum from Colina et al. (1992) we derive values of $c_{I_{\rm c}}=-22.6011$, cJ=-23.6865 and $c_{K_{\rm s}}=-25.9076$ mag. Applying the two equations above to a whole set of model spectra produces a theoretical isochrone in colour-magnitude space. Note that this procedure only provides us with the ``true'' magnitudes of the model spectra, not their instrumental ones. The photometric calibration procedure applied to the data converts the measured, instrumental magnitudes to the ``true'' magnitude plane where we then compare them with the isochrone.

Assuming that all our photometric candidates belong to Praesepe, we derive masses and effective temperatures from these isochrones using our three filter measurements in the following way. We first normalize the energy distribution of each object to the energy distribution of the model using the J filter. We then estimate the mass and effective temperature via a least squares fit of the measured spectral energy ``distribution'' (actually just two points) to the model spectral energy distribution from the isochrone. This involves estimating one parameter from two measurements, because mass and  $T_{\rm eff}$ are not independent.

The above assumption of a dust-free atmosphere is valid for $T_{\rm eff}$ $\geqslant$ 3000 K, but objects with 3000 K $\geqslant$  $T_{\rm eff}$ $\geqslant$ 1800 K are expected to have dust in equilibrium with the gas phase (Allard et al. 2001). We therefore perform a second selection of candidates (and determination of mass and $T_{\rm eff}$) based on isochrones predicted in the same way, but based on evolutionary tracks of Chabrier et al. (2000) and the AMES-dusty model of Allard et al. (2001). This give us a second dusty model list of candidates. A priori some observed stars could appear in both lists (and in fact two do), but in our later discussions of the mass function we do not mix stars from the two lists but rather make separate determinations of the mass function.

There are various sources of error in the estimation of mass and $T_{\rm eff}$. These are the photon noise, the photometric calibration, the least squares fitting (imperfect model) and the uncertainties in the age of and distance to Praesepe. The uncertainties in the age and distance are the most significant errors and given rise to uncertainties of $0.060 \pm 0.010~M_\odot$ and $1990 \pm 260$ K for a substellar object, $0.072 \pm 0.008~M_\odot$ and $2293 \pm 201$ K for an object at the hydrogen burning limit and $1.000 \pm 0.017~M_\odot$ and $5300 \pm 50$ K for a solar-type star.

3 Candidate selection procedure

The candidate selection procedure for BDs and very low-mass stars is as follows (and explained in more detail in the remainder of this section). Candidates were first selected based on colour-magnitude diagrams (CMDs) and this further refined using colour-colour diagrams. In the third and final selection, we used the known distance to Praesepe to reject objects based on a discrepancy between the observed magnitude in J and the magnitude in this band computed with the isochrones and our estimation of $T_{\rm eff}$. To be considered as a cluster member, an object has to satisfy all three of these criteria. We make two independent selections: one using dust-free and one using dusty atmospheric models.

3.1 First candidate selection step: colour-magnitude diagrams

Candidates were first selected from our CMDs by retaining only objects which are no more than 0.14 mag redder or bluer than the isochrone in all CMDs. This number accommodates errors in the magnitudes, uncertainties in the model isochrones plus uncertainties in the cluster age and distance estimates. We additionally include objects brighter than the isochrones by 0.753 mag in order to include unresolved binaries. In Figs. 2 and 3 we show two CMDs where candidates were selected based on $I_{\rm c}$vs. $I_{\rm c}$-J and $K_{\rm s}$ vs. $I_{\rm c}$-$K_{\rm s}$. These figures also show low-mass cluster member candidates from previous studies which we detected in our survey (Pinfield et al. 1997; Adams et al. 2002a; González-García et al. 2006; Kraus & Hillenbrand 2007). In Fig. 3, we can observe three structures in this CMD. The two structures at $I_{\rm c}-K_{\rm s} \sim 1$ mag and $I_{\rm c}-K_{\rm s} \sim 2$ mag are predominantly stars (Galactic disk turn-off, and disk late-type and giant stars respectively) while the structure at $I_{\rm c}-K_{\rm s} \sim 3$ mag is mostly composed of galaxies. From a total of 23 891 objects detected above the 5$\sigma $ detection limit in all filters, 800 are retained as candidate cluster members (96.7% are rejected). If we instead use dusty model isochrones, then out of the 23 891 objects, 357 are retained (98.5% are rejected) for our dusty model list.

\begin{figure} \par\includegraphics[width=7.8cm,clip]{13011f02.eps} \end{figure} Figure 2:

Colour-magnitude diagram showing an example of the first selection step using the $I_{\rm c}$ and J bands. The solid lines show the isochrone computed from an evolutionary model with a dust-free atmosphere (NextGen model) and the dashed lines show our selection band around this. The numbers indicate the masses (in $M_{\odot }$) of objects on the isochrone for various $I_{\rm c}$ magnitudes. Overplotted are measurements from our survey of candidate cluster members reported in Pinfield et al. (1997) (stars), Adams et al. (2002a) (triangles) [where we include objects which have a probability of being a real member higher than 10%], González-García et al. (2006) (squares) and Kraus & Hillenbrand (2007) (circles).

Open with DEXTER

\begin{figure} \par\includegraphics[width=7.8cm]{13011f03.eps} \end{figure} Figure 3:

As Fig. 2 but with the $I_{\rm c}$ and $K_{\rm s}$ bands.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{13011f04.eps} \end{figure} Figure 4:

Colour-colour diagram used in the second selection step. The solid line is the isochrone computed from an evolutionary model with a dust-free atmosphere (NextGen model, the masses in $M_{\odot }$ for each $I_{\rm c}-J$ colours are shifted up clarity) and the dashed lines show our selection band. Overplotted are the cluster candidate members from Pinfield et al. (1997) (stars), Adams et al. (2002a) (triangles), González-García et al. (2006) (squares) and from Kraus & Hillenbrand (2007) (circles), which we detected in our survey.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{13011f05.eps} \end{figure} Figure 5:

As Fig. 4, but now showing the theoretical colours of six galaxies as thick dotted lines and the theoretical colours of red giants as thick solid lines. The six galaxies are two starbursts, one Sab, one Sbc, and two ellipticals of 5.5 and 15 Gyr, with redshifts from z = 0 to z = 2 in steps of 0.25 (evolution not considered). We assume that all red giants have a mass of 5 $M_{\odot }$, $0.5 < \log g < 2.5$ and 2000 K < $T_{\rm eff} < 6000$ K.

Open with DEXTER

3.2 Second candidate selection step: colour-colour diagram

The second stage of candidate selection involves retaining just those objects which lie within 0.24 mag of the isochrone in the (single) colour-colour diagram. This value reflects the photometric errors plus uncertainty in the age estimation of Praesepe. One such colour-colour diagram with the selection limits is shown in Fig. 4. The two main sources of contamination beside field M dwarfs are background red giants and unresolved galaxies (Praesepe is at a Galactic latitude of $b =+32.5^{\circ}$). We show in Fig. 5 the theoretical colours for red giants using the atmosphere models of Hauschildt et al. (1999b) and theoretical colours of six galaxies from Meisenheimer et al. (in prep.). We see that red giants could be a source of contamination in the mass range of 0.09-0.2 $M_{\odot }$ and at $\sim $0.7 $M_{\odot }$, while unresolved galaxies should not be a major source of contamination below 0.6 $M_{\odot }$. In Fig. 5 we see the same three structures as in Fig. 3: from top to bottom galaxies, disk late-type and giant stars, and Galactic disk turn-off stars. Of the 800 objects selected in the first step, 291 are kept here (63.6% are rejected) assuming a dust-free atmosphere, and 110 out of 357 are kept (69.2% are rejected) when using the model for a dusty atmosphere.

3.3 Third candidate selection step: rejection based on observed magnitude vs. predicted magnitude discrepancy

As indicated in Sect. 2.4, our determination of $T_{\rm eff}$ is based on the spectral energy distribution of each object and is independent of the assumed distance. The membership status of an object can therefore be assessed by comparing its observed magnitude in a band with its magnitude predicted from its $T_{\rm eff}$ and Praesepe's isochrone (which assumes a distance). The premise is that the predicted magnitude of a background contaminant would be lower (brighter) than its observed magnitude and higher (fainter) for a foreground contaminant. In order to avoid removing unresolved binaries that are real members of the cluster, we keep all objects with a computed magnitude of up to 0.753 mag brighter than the observed magnitude. We also take into account photometric errors and uncertainties in the age and distance of Praesepe. This selection procedure is illustrated in Fig. 6. From 291 objects selected through CMDs and colour-colour diagrams in the first two steps, 144 are kept (50.5% are rejected) when using the dust-free atmospheres/models, and 35 out of 110 are kept (68.2% are rejected) when using the dusty atmosphere/models.

\begin{figure} \par\includegraphics[width=8cm,clip]{13011f06.eps} \end{figure} Figure 6:

Difference between the observed J magnitude and the model J magnitude computed from the derived mass and $T_{\rm eff}$, as a function of $T_{\rm eff}$. The two vertical lines are at the positions of L0 and M 5 dwarfs ( left to right), for orientation purposes. The dotted line (at -0.753 mag) represents the offset due to the possible presence of unresolved binaries, the dot-dash lines represents the error on the magnitude determination, and the curved, long-dashed lines represent the uncertainties on the age and distance of Praesepe.

Open with DEXTER

After this step, we perform a visual inspection directly on the images to reject resolved galaxies and spurious detections. This inspection removes 21 and 8 objects from the dust-free and dusty selection respectively.

4 Results of the survey

We now present the selected candidates, discuss contamination by cluster non-members and derive the magnitude and mass functions for Praesepe.

4.1 Selected photometric candidates

The final selection reveals 123 photometric candidates using an isochrone based on dust-free atmospheres, and 27 objects using an isochrone assuming dusty atmospheres[*]. This corresponds to $\sim $40 and $\sim $9 objects per deg2respectively. All our photometric candidates are presented in Table 3. Objects are given the notation PRAESEPE-YYY where YYY is a serial identification number (ID). Numbers above 900 indicate candidate members assuming a dusty atmosphere. Only the first 10 rows of the tables are shown, all other data are available online. We also note in Table 4 which objects are candidate cluster members also identified as such by Kraus & Hillenbrand (2007), Adams et al. (2002a) or Pinfield et al. (1997).

Table 3:   All photometric cluster member candidates of our survey. Table 3 is published in its entirety in the electronic edition of Astronomy & Astrophysics. A fraction is shown here for guidance regarding its form and content.

Some Praesepe members from previous studies are not detected in our work. This is the case for the objects from Pace et al. (2008) and Fossati et al. (2008), for example. Since those studies focused on bright objects, these stars saturate in our science images. (Pace et al. 2008; Fossati et al. 2008, were concerned with chemical abundances of A-type and solar-type stars, respectively, while our saturation occurs at $\sim $0.7 $M_{\odot }$).

Not all objects identified by other surveys as brown dwarfs or very low mass stellar member candidates - and detected in our survey - are members based on our criteria. The two objects from the work of González-García et al. (2006), who also used photometry in order to select candidate members, we detect above our 5$\sigma $ limit (Prae J084039.3+192840 and Prae J084130.4+190449). Yet both objects are non-members based on our selection criteria, because they have $I_{\rm c}-J$ colours bluer than our selection band. (Prae J084130.4+190449 is also too blue in $I_{\rm c}-K_{\rm s}$ for our selection band at $I_{\rm c}-K_{\rm s} = 3.0$ mag, whereas Prae J084039.3+192840 at $I_{\rm c}-K_{\rm s}= 4.0$ mag lies within it). González-García et al. (2006) did not report any NIR photometry for these two objects. Although the non-membership of Prae J084039.3+192840 can be debated (high membership probability based on González-García et al. 2006), Prae J084130.4+190449 is most likely an unresolved galaxy (low membership probability; González-García et al. 2006).

Table 4:   Photometric candidates in our survey that are also photometric candidates in previous surveys.

Of the candidates from the photometric survey of Pinfield et al. (1997), seven fall within our survey and are detected, of which six are identified as candidates by our selection criteria. The non-selected object is RIZpr6 in Hodgkin et al. (1999). It is bluer than the isochrones in both CMDs in Figs. 2 and 3. From its positions in the CMDs and in the colour-colour diagram in Fig. 4, we suspect that this object is an unresolved galaxy.

11 of the the 14 objects from a survey based on proper motion and photometry by Adams et al. (2002a) are identified by our selection. The objects not recovered fail the observed magnitude vs. predicted magnitude test. On the other hand, 27 cluster candidates of Kraus & Hillenbrand (2007) out of 37 detected in our survey are selected. The 10 non-selected objects have membership probabilities from Kraus & Hillenbrand (2007) based on proper motion greater than 95%, and are brighter than the 10$\sigma $ detection limit of the publicly available surveys used in their work. However, these objects failed our observed magnitude vs. predicted magnitude test and some are bluer than our isochrone of Praesepe in $J-K_{\rm s}$. With $I_{\rm c}-K_{\rm s}$colour of $\sim $2 mag, we suggest that these objects are more likely to be disk late-type stars or giant stars.

The 5$\sigma $ detection limits of our survey are $I_{\rm c}=23.4$ mag, J = 20.0 mag and $K_{\rm s} = 18.6$ mag (which correspond to $\sim $0.05 $M_{\odot }$ using the dust-free isochrone). However, we cannot expect to detect all objects down to these magnitudes. We estimate the survey completeness by taking the ratio of the number of objects detected to the predicted number of detections, the latter made by assuming a uniform distribution of stars along the line of sight in our survey fields. (This comparison distribution is somewhat crude, but it gives an approximate value without making too many assumptions). The predicted number of detections is obtained from the histogram of the number of detections as a function of magnitude (Fig. 7) and by observing where the distribution drops off compared to a straight line extrapolation. Based on this, the completeness of the survey down to the 5$\sigma $ detection limit is 90% in $I_{\rm c}$, 88% in J and 87% in $K_{\rm s}$. The overall detection completeness of our survey, from saturation to 5$\sigma $ detection corresponding to 0.05 $M_{\odot }$, is therefore $\sim $87%. In J band, we reach a completeness of 95% at J = 19.7 mag, which corresponds to $\sim $0.055 $M_{\odot }$.

4.2 Substellar candidates in Praesepe

Six objects in our survey are cluster candidates with theoretical masses equal to or below the stellar/substellar boundary at 0.072 $M_{\odot }$. We present the finding charts of the six objects in Fig. 8. In Table 5, we present their coordinates and physical parameters. These BD candidates have predicted masses between 0.064 and 0.072 $M_{\odot }$. A spectroscopic follow up (on a 8 m class telescope or larger) will be needed in order to confirm or refute their membership and their substellar status.

4.3 Contamination by non-members

As mentioned in Sect. 3.2, the two main sources of contamination are the background red giants, which are the dominant source at masses of 0.09-0.2 $M_{\odot }$ and $\sim $0.7 $M_{\odot }$, and unresolved galaxies, mostly affecting masses above 0.6 $M_{\odot }$. Other possible contaminants are field M dwarfs and high redshift quasars (for instance at $z \sim 6$; Caballero et al. 2008). However, as such quasars have spectral energy distributions similar to mid-T dwarfs whereas our faintest candidates are early L dwarfs, and given that they are rare (3.3 quasars at 5.5 < z < 6.5 in a 8 deg2 survey, Stern et al. 2007), the MF should not be affected by quasar contamination.

Let us estimate the contamination by M dwarfs, First, we consider that close to the open cluster Praesepe, the space density of M dwarfs is uniform. We assume that their density ($\rho$) drops exponentially with vertical distance from the galactic disk (h) such that

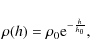
\begin{displaymath}\rho(h)=\rho_0 {\rm e}^{-\frac{h}{h_0}}, \end{displaymath} (4)

assuming a scale height of h0 = 500 pc. We use the local space density ($\rho_0$) for M dwarfs of $57 \times 10^{-3}$ pc-3 (from the Research Consortium on Nearby Stars; Henry et al. 2006). Given the Galactic latitude of Praesepe of b =+32.5 deg and its distance of 190 pc, the density of M dwarfs near Praesepe should be $47 \times 10^{-3}$ pc-3. If we define a volume corresponding to the area of our survey (3.1 deg2, 34 pc2) and use the distance uncertainties to the cluster (190 +6.0-5.8 pc) as its depth, we estimate that we have $\sim $19 M dwarf contaminants near the cluster. From a total of 150 photometric candidates, we estimate a contamination of $\sim $13% (or even less, as the cluster depth is presumably closer to $\sqrt{34}=5.8$ pc than to the 11.8 pc error span of the mean cluster distance). Therefore, we do not expect contamination by field M dwarfs to play a significant role in the determination of the MF.

4.4 Luminosity function and mass function

We present in Fig. 9 the luminosity function of Praesepe using the J-band magnitude of the cluster candidates. No correction is made for binaries, so this is the system rather than single-star luminosity function.

The mass function (MF), $\xi(\log_{10}~ M$), is generally defined as the number of stars per cubic parsec in the logarithmic mass interval $\log_{10}~ M$ to $\log_{10} M + {\rm d} \log_{10} ~M$. Here, we do not compute the volume of Praesepe so instead we define the MF as the total number of objects in each $0.1 \log_{10}~M$ bin per square degree. Since we do not make any corrections for binaries we compute here a system MF. Our inferred MF is shown in Fig. 10. The log-normal form for a MF is

\begin{displaymath}\xi({\log}_{10}~ {M})=k\cdot {\exp}{\biggl[-\frac{({\log}_{10}~ {M}- {\log}_{10}~ {M}_0)^2}{2\sigma^2}\biggr]}, \end{displaymath} (5)

where k = 0.086, $m_0 = 0.22~M_\odot$ and $\sigma = 0.57$ for the Galactic field system MF (Chabrier 2003). Fitting this function to both the dust-free and dusty MF data we obtain $k = 5.9 \pm 3.1$, $m_0 = 0.15 \pm 0.05~M_\odot$ and $\sigma = 0.51 \pm 0.12$. Figure 10 shows this result. If we instead fit a power law (Salpeter 1955)

\begin{displaymath} \xi({\log}_{10}~ {M})=k \cdot {M}^{-\alpha}, \end{displaymath} (6)

from the highest mass bin to the turn over at 0.1 $M_{\odot }$, we obtain $\alpha = 1.3 \pm 0.2$ (corresponding to $\xi( {M}) \propto M^{-2.3}$). If we exclude the two bins between 0.1 and 0.15 $M_{\odot }$ (possible contamination by red giants) and the two highest bins (possible incompleteness), the fit gives $\alpha = 0.8 \pm 0.1$.

5 Analysis and discussion of the stellar and substellar mass function of Praesepe

Our MF of Praesepe (Fig. 10) shows a rise in the number of objects from 0.6 $M_{\odot }$ down to 0.1 $M_{\odot }$, and then a turn-over at $\sim $0.1 $M_{\odot }$. This turn-over is not due to incompleteness since it occurs well above the 5$\sigma $ detection limit corresponding to 0.05 $M_{\odot }$. This behaviour is confirmed by the luminosity function in Fig. 9 which shows a rise from J = 13 to 16 mag (with candidates obtained using a dust-free atmosphere) and a drop at J = 17 mag (seen with both types of candidates). To help the analysis of these features in the mass function, we compare in Fig. 11 the mass functions of Praesepe obtained from several studies plus the MF for the old open cluster Hyades (age of 625 Myr).

The rise in our MF of Praesepe is also present in the MFs obtained in the three previous studies of Baker & Jameson (2009), Kraus & Hillenbrand (2007) and Hambly et al. (1995). On the other hand, we do not see this rise in the MF of Adams et al. (2002a). However, their MF is based on objects with a membership probability higher than only 1% and within a radius of 3.8 deg. Due to use of such a low probability threshold for selection, we expect that most of the objects used in the MF determination are simply field stars (which is their own conclusion in Sect. 5.4; Adams et al. 2002a), so further comparison is not warranted. As for the MFs of González-García et al. (2006) and Pinfield et al. (1997), since the highest mass bins are $\sim $0.11 and $\sim $0.15 $M_{\odot }$ (respectively), the rise observed from 0.6 $M_{\odot }$ to 0.1 $M_{\odot }$ cannot be discussed.

\begin{figure} \par\includegraphics[width=8cm,clip]{13011f07.eps} \end{figure} Figure 7:

Estimation of the completeness limit for our survey using the J band. The solid line is the best linear fit before the turn off, the vertical dashed line is the 5$\sigma $ detection limit and the vertical dotted line is the magnitude at which detector saturation occurs.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{13011f08.eps} \end{figure} Figure 8:

Finding charts of the six new BD candidates of Praesepe (J-band). We observed objects very close to PRAESEPE-099 and -909, although they do not influence the photometry. The panels are $50 \times 50$ arcsec with North up and East to the left.

Open with DEXTER

Table 5:   Same as Table 3, but only the BD candidates are given and we include the spectral type expected.

\begin{figure} \par\includegraphics[width=8cm,clip]{13011f09.eps} \end{figure} Figure 9:

J band luminosity function. The solid line histogram represents the luminosity function based on a selection using a dust-free atmosphere (NextGen model); the thick dotted histogram uses a dusty atmosphere (AMES-Dusty model). The stellar/substellar limit is at $J \sim 17.8$ mag for both models (0.072 $M_{\odot }$). For reference, the ordinate value of 1.11 at the histogram peak (magnitude bin J =15.25 mag) corresponds to 13 objects.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{13011f10.eps} \end{figure} Figure 10:

Mass function based on our survey photometry. Points with error bars represent the MF based on a selection and mass calibration assuming a dust-free atmosphere, whereas the open circles with error bars are the MF based on the dusty atmosphere model. We also overplot the log-normal and the power law MF fitted to our data (both solid line). Error bars are Poissonian arising from the number of objects observed in each bin. The vertical thin dotted lines are the mass limits at which detector saturation occurs in the $I_{\rm c}$, J and $K_{\rm s}$-bands ( from left to right). The vertical thick dashed line is the mass at the 5$\sigma $ detection limit (completeness of $\sim $87%). For reference, the ordinate value of 0.932 at the histogram peak (mass $\log_{10} M = - 0.85$ [0.142 $M_{\odot }$]) corresponds to 27 objects. The two dusty data points have been shifted to the right by $\log _{10} M = 0.05$ for clarity.

Open with DEXTER

Only four MFs, in addition to our work, reach masses below 0.1 $M_{\odot }$: Baker & Jameson (2009), González-García et al. (2006), Pinfield et al. (1997) and Hambly et al. (1995). While the MFs of Baker & Jameson (2009) and Hambly et al. (1995) show a turn-over at 0.1 $M_{\odot }$, the one obtained by Pinfield et al. (1997) does not. On the contrary, it presents a sudden rise at the stellar/substellar limit (with a ratio of $\sim $5 in the number of objects at the mass bin at 0.07 to the number in the bin at 0.11 $M_{\odot }$). They used RIZ photometry for their survey, but not all objects were observed in all bands, resulting in just one colour available for membership determination in some cases (Pinfield et al. 1997). From an analysis of MFs of other clusters and using a multi-band photometric survey, Boudreault & Bailer-Jones (2009) have shown that use of a narrow spectral coverage with few filters can lead to high contamination by field M dwarfs, and thus an apparent rise in the MF in the low mass regime. We suggest that this is the reason for the apparent rise at the low-mass end of the MF in Pinfield et al. (1997) (who also noted that only one colour is available for many objects in their two lowest bins). As for the MF of González-García et al. (2006), as they only have three points we cannot comment on any possible trend.

\begin{figure} \par\includegraphics[width=14cm,clip]{13011f11.eps} \end{figure} Figure 11:

MF of Praesepe from our present work (open dots assuming a dusty atmosphere and filled dots assuming a dust-free atmosphere), from previous work (open triangles for survey using proper motion and filled triangles for survey using photometry only), as well as the MF from the Hyades from Bouvier et al. (2008) (open squares). We also show the galactic field star MF from Chabrier (2003) as a thin dashed line and the substellar limit as a thick dashed line. We have normalized all the MFs to the log-normal fit of Chabrier et al. (2005) at $\sim $0.3 $M_{\odot }$ ( $\log M = - 0.5$), except for those of González-García et al. 2006; Pinfield et al. 1997) which have no data here.

Open with DEXTER

Although there are some discrepancies between the different MFs of Praesepe from previous works and our MF, none agrees with the MF of the Hyades ($\sim $625 Myr) obtained by Bouvier et al. (2008)[*], in which the MF is observed to turn-over and decrease already at 0.35 $M_{\odot }$. This is surprising, since Praesepe and the Hyades share a comparable age, size and mass: they have ages of 590 +150-120 Myr (Fossati et al. 2008) and $625 \pm 50$ Myr (Bouvier et al. 2008), tidal radii of $11.5 \pm 0.3$ pc ( $3.5 \pm 0.1$ deg, Kraus & Hillenbrand 2007) and 10.3 pc (12.5 deg, Bouvier et al. 2008), and masses of $550 \pm 40~M_\odot$ (Kraus & Hillenbrand 2007) and about 400 $M_{\odot }$(Bouvier et al. 2008), respectively. Therefore, we can expect that the potential well is the same (at least today). Only the metallicity may be slightly different, assuming the most recent measurement for Praesepe: [Fe/H] = + $0.27 \pm 0.10$ for the latest metallicity measurement of Praesepe (Pace et al. 2008) and [Fe/H] = + $0.14 \pm 0.05$ for the Hyades (Bouvier et al. 2008), although a metallicity as low as + $0.038 \pm 0.039$(Friel & Boesgaard 1992) has been reported for Praesepe. It is unclear how this metallicity difference could explain the significantly different mass functions.

It is a priori possible that different binary mass fractions in Praesepe and the Hyades could account for the difference in their observed (i.e. system, rather than star) mass functions. The binary fraction in Praesepe for different mass intervals was obtained by Pinfield et al. (2003): 17 +6-4% for 1.0-0.6 $M_{\odot }$, 31 +7-6% for 0.6-0.35 $M_{\odot }$, $44 \pm 6$% for 0.35-0.2 $M_{\odot }$ and 47 +13-11% for 0.11-0.09 $M_{\odot }$. As for the Hyades, Gizis & Reid (1995) observed a binary fraction of $27 \pm 16$% for their sample of stars ($\lesssim$0.4 $_\odot$), which is consistent with another determination of the Hyades binary fraction of $30 \pm 6$% from Patience et al. (1998) (for a primary mass of $\sim $0.6-2.8 $M_{\odot }$). From these figures we see no significant difference in the binary fractions of the two clusters (even if primarily because the uncertainties are quite large), so this cannot be used to explain the difference between in their mass functions. Of course, if the typical mass ratio in a binary system is different in the two clusters then this may be able to account for some difference in the mass functions, but their is also no evidence to support (or refute) this.

A distinction between the two clusters could be the spatial distribution of the members. Indeed, Holland et al. (2000) observed that the Praesepe cluster might be composed of two merged clusters with different ages, one main cluster of 630 $M_{\odot }$ and a second subcluster of 30 $M_{\odot }$. It was even proposed that faint low-mass members of the subcluster could appear as Praesepe brown dwarf candidates (Chappelle et al. 2005). However, Adams et al. (2002a) did not find evidence of a subcluster in Praesepe. Based on the spatial distribution of the main cluster and subcluster from Holland et al. (2000), our survey only overlaps the main cluster. In addition, a collision between two clusters could not explain alone an increase of the MF down to 0.1 $M_{\odot }$, as such a collision would rather remove low-mass member of the clusters.

By comparing the MF of the Hyades with the one of the Pleiades ($\sim $120 Myr), Bouvier et al. (2008) concluded that dynamical evolution was responsible for the deficiency observed in the very-low mass star and BD regime in the Hyades. However, this deficiency is not seen in Praesepe. One possible implication is that Praesepe has been less affected by dynamical evolution, i.e. evaporation of low mass members which are expected to have higher speeds based on equipartition of energy. On the other hand, if dynamical evolution has affected Praesepe in the same way, then it cannot have had the same initial mass function and/or initial conditions as the Hyades. Dynamical interaction between one of these clusters and another object (such as another open cluster in the past) could explain the discrepancies between the two MFs.

6 Conclusions

We have presented the results of a survey to study the mass function of the old open cluster Praesepe. The survey consisted of optical $I_{\rm c}$-band photometry and NIR J and $K_{\rm s}$-band photometry with a total coverage of 3.1 deg2, down to the substellar regime, with a 5$\sigma $ detection limit corresponding to 0.05 $M_{\odot }$ (the detection completeness to this level is $\sim $87%).

Our final sample yields 123 photometric cluster member candidates based on a selection assuming a dust-free atmosphere and 27 photometric cluster candidates based on a selection assuming a dusty atmosphere. We estimate the contamination by field M-dwarfs to be 13% or less. Among our cluster candidates, six objects have theoretical masses equal to or less than the stellar/substellar boundary at 0.072 $M_{\odot }$.

We observed that the MF of Praesepe is characterized by a rise in the number of objects from 0.6 $M_{\odot }$ down to 0.1 $M_{\odot }$, followed by a turn-over in the MF at $\sim $0.1 $M_{\odot }$. The rise is in agreement with the Praesepe MFs derived in several previous studies (Hambly et al. 1995; Kraus & Hillenbrand 2007; Baker & Jameson 2009) but disagrees with Adams et al. (2002a).

We have compared the mass function of Praesepe with one derived for the Hyades and have observed a significant difference: while the Hyades has a maximum at 0.35 $M_{\odot }$, Praesepe has a maximum at a much lower mass, 0.1 $M_{\odot }$. Assuming that they have similar ages (as main sequence fitting suggests), we conclude that the clusters either had different initial mass functions or that dynamical interaction has modified the evolution of one or both. More specifically, in the latter case, dynamical evaporation does not seem to have influenced the Hyades and Praesepe in the same way. A difference in the binary fraction or mass ratios could also cause a difference in the mass functions, but determinations of these are not yet precise enough to suggest any difference.

Acknowledgements
S.B. and C.B.J. acknowledge support from the Deutsche Forschungsgemeinschaft (DFG) grant BA2163 (Emmy-Noether Programme) to CBJ. S.B. thanks the Calar Alto observatory staff for support and Kester Smith for observations performed in January 2007. We are grateful to the referee, Nigel Hambly, for his constructive comments and suggestions. We acknowledge Klaus Meisenheimer and Marie-Hélène Nicol for useful discussions about galaxy contamination. IRAF is distributed by the National Optical Astronomy Observatories, which are operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation. Some data analysis in this article has made use of the freely available R statistical package, http://www.r-project.org. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.

References

  1. Adams, J. D., Stauffer, J. R., Skrutskie, M. F., et al. 2002a, AJ, 124, 1570 [NASA ADS] [CrossRef] [Google Scholar]
  2. Adams, T., Davies, M. B., Jameson, R. F., et al. 2002b, MNRAS, 333, 547 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  3. Allard, F., Hauschildt, P. H., Alexander, D. R., et al. 2001, ApJ, 556, 357 [NASA ADS] [CrossRef] [Google Scholar]
  4. An, D., Terndrup, D. M., Pinsonneault, M. H., et al., 2007, ApJ, 655, 233 [NASA ADS] [CrossRef] [Google Scholar]
  5. Baade, D., Meisenheimer, K., Iwert, O., et al. 1999, The Messenger, 95, 15 [NASA ADS] [Google Scholar]
  6. Bailer-Jones, C. A. L., & Mundt, R. 2001, A&A, 367, 218 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Bailer-Jones, C. A., Bizenberger, P., & Storz, C., 2000, SPIE Conf. Ser., 4008, 1305 [Google Scholar]
  8. Baker, D. E. A., & Jameson, R. F. 2009, Brown Dwarfs in Praesepe: A search for low mass members using UKIDSS, JENAM2009 meeting, poster No. 3-P03 [Google Scholar]
  9. Barrado y Navascués, D., Stauffer, J. R., & Jayawardhana, R. 2004, ApJ, 614, 386 [NASA ADS] [CrossRef] [Google Scholar]
  10. Baraffe, I., Chabrier, G., Allard, F., et al. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
  11. Baraffe, I., Chabrier, G., Allard, F., et al. 2002, A&A, 382, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Baumeister, H., Bizenberger, P., Bailer-Jones, C. A. L., et al. 2003, SPIE Conf. Ser., 4841, 343 [NASA ADS] [Google Scholar]
  13. Béjar, V. J. S., Martín, E. L., Zapatero Osorio, M. R., et al. 2001, ApJ, 556, 830 [NASA ADS] [CrossRef] [Google Scholar]
  14. Boesgaard, A. M., & Budge, K. G. 1988, ApJ, 332, 410 [NASA ADS] [CrossRef] [Google Scholar]
  15. Boudreault, S., & Bailer-Jones, C. A. L. 2009, ApJ, 706, 1484 [NASA ADS] [CrossRef] [Google Scholar]
  16. Bouvier, J., Kendall, T. T., Meeus, G., et al. 2008, A&A, 481, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Briceño, C., Luhman, K. L., Hartmann, L., Stauffer, J. R., & Kirkpatrick, J. D. 2002, ApJ, 580, 317 [NASA ADS] [CrossRef] [Google Scholar]
  18. Caballero, J. A., Béjar, V. J. S., Rebolo, R., et al. 2007, A&A, 470, 903 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Caballero, J. A., Burgasser, A. J., & Klement, R. 2008, A&A, 488, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Chabrier, G., Baraffe, I., Allard, F., et al. 2000, ApJ, 542, 464 [NASA ADS] [CrossRef] [Google Scholar]
  21. Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
  22. Chabrier, G., Baraffe, I., Allard, F., et al. 2005, Invited review Cancun [astro-ph/0509798] [Google Scholar]
  23. Chappelle, R. J., Pinfield, D. J., Steele, I. A., et al. 2005, MNRAS, 361, 1323 [NASA ADS] [CrossRef] [Google Scholar]
  24. Close, L. M., Lenzen, R., Guirado, J. C., et al. 2005, Nature, 433, 286 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  25. Colina, L., Bohlin, R., & Castelli, F. 1996, Instrument Science Report CAL/SCS, 8, 1 [Google Scholar]
  26. D'Antona, F., & Mazzitelli, I. 1985, ApJ, 296, 502 [Google Scholar]
  27. de la Fuente Marcos, R., & de la Fuente Marcos, C. 2000, Ap&SS, 271, 127 [NASA ADS] [CrossRef] [Google Scholar]
  28. Fossati, L., Bagnulo, S., Landstreet, J., et al. 2008, A&A, 483, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Friel, E. D., & Boesgaard, A. M. 1992, ApJ, 387, 170 [NASA ADS] [CrossRef] [Google Scholar]
  30. Gizis, J., & Reid, I. N. 1995, AJ, 110, 1248 [NASA ADS] [CrossRef] [Google Scholar]
  31. González-García, B. M., Zapatero Osorio, M. R., Béjar, V. J. S., et al. 2006, A&A, 460, 799 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Hambly, N. C., Steele, I. A., Hawkins, M. R. S., et al. 1995, MNRAS, 273, 505 [NASA ADS] [CrossRef] [Google Scholar]
  33. Hambly, N. C., Hodgkin, S. T., Cossburn, M. R., et al. 1999, MNRAS, 303, 835 [NASA ADS] [CrossRef] [Google Scholar]
  34. Harris, H. C., Vrba, F. J., Dahn, C. C., et al. 1999, AJ117, 339 [NASA ADS] [CrossRef] [Google Scholar]
  35. Hauschildt, P. H., Allard, F., & Baron, E. 1999a, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
  36. Hauschildt, P. H., Allard, F., Ferguson, J., Baron, E., & Alexander, D. R., 1999b, ApJ, 525, 871 [NASA ADS] [CrossRef] [Google Scholar]
  37. Henry, T. J., Jao, W.-C., Subasavage, J. P., et al. 2006, AJ, 132, 2360 [NASA ADS] [CrossRef] [Google Scholar]
  38. Hester, J. J., Scowen, P. A., Sankrit, R., et al. 1996, AJ, 111, 2349 [NASA ADS] [CrossRef] [Google Scholar]
  39. Hillenbrand, L. A., & Carpenter, J. M. 2000, ApJ, 540, 236 [NASA ADS] [CrossRef] [Google Scholar]
  40. Hodgkin, S. T., Pinfield, D. J., Jameson, R. F., et al. 1999, MNRAS, 310, 87 [NASA ADS] [CrossRef] [Google Scholar]
  41. Holland, K., Jameson, R. F., Hodgkin, S., et al. 2000, MNRAS, 319, 956 [NASA ADS] [CrossRef] [Google Scholar]
  42. Howell, S. B. 1989, PASP, 101, 616 [NASA ADS] [CrossRef] [Google Scholar]
  43. Jameson, R. F., Dobbie, P. D., Hodgkin, S. T. et al. 2002, MNRAS, 335, 853 [NASA ADS] [CrossRef] [Google Scholar]
  44. Johnstone, D., Hollenbach, D., & Bally, J. 1998, ApJ, 499, 758 [NASA ADS] [CrossRef] [Google Scholar]
  45. Jordi, K., Grebel, E. K., & Ammon, K. 2006, A&A, 460, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Kraus, A. L., & Hillenbrand, L. A. 2007, AJ, 134, 2340 [NASA ADS] [CrossRef] [Google Scholar]
  47. Kroupa, P., & Bouvier, J. 2003, MNRAS, 346, 369 [NASA ADS] [CrossRef] [Google Scholar]
  48. Kulkarni, S., & Golimowski, D. 1995, News Release Number: STScI-1995-48 [Google Scholar]
  49. Kumar, M. S. N., & Schmeja, S. 2007, A&A, 471, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. van Leeuwen, F. 2009, A&A, 497, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Lodieu, N., Dobbie, P. D., Deacon, N. R., et al. 2007, MNRAS, 380, 712 [NASA ADS] [CrossRef] [Google Scholar]
  52. Luhman, K. L. 2000, ApJ, 544, 1044 [NASA ADS] [CrossRef] [Google Scholar]
  53. Luhman, K. L. 2004, ApJ, 617, 1216 [NASA ADS] [CrossRef] [Google Scholar]
  54. Luhman, K. L., & Rieke, G. H. 1999, ApJ, 525, 440 [NASA ADS] [CrossRef] [Google Scholar]
  55. Mac Low, M.-M., & Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [NASA ADS] [CrossRef] [Google Scholar]
  56. Magazzú, A., Rebolo, R., Zapatero Osorio, M. R., et al. 1998, ApJ, 497, L77 [Google Scholar]
  57. Moraux, E., Bouvier, J., Stauffer, J. R., et al. 2003, A&A, 400, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Muench, A. A., Lada, E. A., Lada, C. J., et al. 2003, AJ, 125, 2029 [NASA ADS] [CrossRef] [Google Scholar]
  59. Nicol, M.-H., Ph.D. Thesis, University of Heidelberg (2009) [Google Scholar]
  60. Pace, G., Pasquini, L., & François, P. 2008, A&A, 489, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Patience, J., Ghez, A. M., Reid, I. N., et al. 1998, AJ, 115, 1972 [NASA ADS] [CrossRef] [Google Scholar]
  62. Pickett, B. K., Durisen, R. H., Cassen, P., et al. 2000, ApJ, 540, L95 [NASA ADS] [CrossRef] [Google Scholar]
  63. Pinfield, D. J., Hodgkin, S. T., Jameson, R. F., et al. 1997, MNRAS, 287, 180 [NASA ADS] [CrossRef] [Google Scholar]
  64. Pinfield, D. J., Dobbie, P. D., Jameson, R. F., et al. 2003, MNRAS, 342, 1241 [NASA ADS] [CrossRef] [Google Scholar]
  65. Reid, I. N., & Hawley, S. L. 1999, AJ, 117, 343 [NASA ADS] [CrossRef] [Google Scholar]
  66. Reipurth, B., & Clarke, C. 2001, AJ, 122, 432 [NASA ADS] [CrossRef] [Google Scholar]
  67. Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
  68. Slesnick, C. L., Hillenbrand, L. A., & Carpenter, J. M. 2004, ApJ, 610, 1045 [NASA ADS] [CrossRef] [Google Scholar]
  69. Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 23 [Google Scholar]
  70. Stern, D., Kirkpatrick, J. D., Allen, L. E., et al. 2007, ApJ, 663, 677 [NASA ADS] [CrossRef] [Google Scholar]
  71. Taylor, B. J. 2006, AJ, 132, 2453 [NASA ADS] [CrossRef] [Google Scholar]

Online Material

Table 3: All photometric cluster member candidates of our survey.

Footnotes

... function?[*]
Based in part on observations carried out at ESO/La Silla, Chile under proposal number 078.A-9055(A).
...[*]
Full Table 3 is only available in electronic form at http://www.aanda.org
... under IRAF[*]
The O2k camera suffers from a stray light problem. It appears on every image taken with the camera, forming a ring pattern centred in the middle of the detector (Nicol 2009). The stray light is removed via our global illumination correction and sky subtraction.
...Bailer-Jones & Mundt (2001)[*]
A fringe correction frame was created, which is a median combination of all science frames in a same filter with the same exposure time. This fringe correction frame was scaled by a factor, determined manually for each science frame, and subtracted from the science image.
... atmospheres[*]
Two objects in the dust-free atmosphere selection (PRAESEPE-089 and -093) were also identified in dusty atmosphere selection (PRAESEPE-915 and -917).
...Bouvier et al. (2008)[*]
Like the MF of Praesepe we present, the MF of the Hyades presented by Bouvier et al. (2008) is a system MF (no correction for binaries).
Copyright ESO 2010

All Tables

Table 1:   Description of observations with the O2k infrared camera.

Table 2:   Description of observations with WFI optical camera.

Table 3:   All photometric cluster member candidates of our survey. Table 3 is published in its entirety in the electronic edition of Astronomy & Astrophysics. A fraction is shown here for guidance regarding its form and content.

Table 4:   Photometric candidates in our survey that are also photometric candidates in previous surveys.

Table 5:   Same as Table 3, but only the BD candidates are given and we include the spectral type expected.

Full version

Table 3: All photometric cluster member candidates of our survey.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.