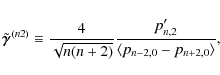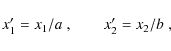| Issue |
A&A
Volume 510, February 2010
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 8 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200912785 | |
| Published online | 12 February 2010 | |
Limitations on shapelet-based weak-lensing measurements
P. Melchior1 - A. Böhnert2,3 - M. Lombardi3 - M. Bartelmann1
1 - Zentrum für Astronomie Heidelberg, Institut für Theoretische Astrophysik, Albert-Ueberle-Str. 2, 69120 Heidelberg, Germany
2 - Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
3 - European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching bei München, Germany
Received 29 June 2009 / Accepted 12 November 2009
Abstract
Aims. We seek to understand the impact on shape estimators
obtained from circular and elliptical shapelet models under two
realistic conditions: (a) only a limited number of shapelet modes are
available for the model, and (b) the intrinsic galactic shapes are not
restricted to shapelet models.
Methods. We create a set of simplistic simulations, in which the
galactic shapes follow a Sérsic profile. By varying the Sérsic index
and applied shear, we quantify the amount of bias on shear estimates
that arises from insufficient modeling. Additional complications from
PSF convolution, pixelation, and pixel noise are also discussed.
Results. Highly elliptical galaxy shapes cannot be accurately
modeled within the circular shapelet basis system and are biased
towards less elongated shapes. This problem can be cured by allowing
elliptical basis functions. Another problem occurs for galaxies whose
radial profile differs strongly from the Gaussian weighting function
employed in both the circular and the elliptical shapelet bases. For
galaxies with large Sérsic indices, shear estimates from circular
shapelets are biased low even for small apparent ellipticities because
of the preference for round models, and shear estimates from elliptical
shapelets depend critically on accurate ellipticity priors. Independent
of the particular form of the estimator, the bias depends on the true
intrinsic galaxy morphology, but also on the size and shape of the PSF.
Conclusions. As long as the issues discussed here are not
solved, we question that the shapelet method can provide weak-lensing
measurements for all observable galaxies (independent of their Sérsic
index) with an accuracy demanded by upcoming missions and surveys. An
accurate and reliable calibration, specific for the dataset under
investigation, would be required but is difficult to infer consistently
from the data.
Key words: gravitational lensing: weak - techniques: image processing - methods: numerical
1 Introduction
Shapelets have been proposed to describe the complex morphology of galaxies and to compress this information in a small number of expansion coefficients (Refregier 2003). Indeed, Massey et al. (2004) find that the shapelet decompositions of deep HST observations preserve the distribution of several morphological estimators so well that one can create simulations of a mock sky that are essentially indistinguishable from actual observations.
For weak-lensing measurements, it is furthermore important that shapelets can also faithfully describe the PSF shape (e.g. Bernstein & Jarvis 2002; Massey & Refregier 2005; Refregier 2003; Kuijken 2006). Additionally, deconvolution from the PSF is an analytic operation in shapelet space (Melchior et al. 2009; Refregier & Bacon 2003). Given shapelet models of the observed galaxy and the PSF, this means only linear algebra is required to obtain a shapelet model of the deconvolved galaxy shape. Finally, several estimators for gravitational shear and flexion can be directly formed from this model (Bernstein & Jarvis 2002; Massey et al. 2007). In summary, once a shapelet model of each galaxy has been obtained, all necessary steps for weak-lensing measurements can be performed very efficiently in shapelet space.
There is, however, an implicit assumption in the setup of such a shapelet-based weak-lensing pipeline: namely that the occurring shapes can be faithfully described by shapelet models. But this assumption is strictly valid only if the basis system is complete, which requires an infinite number of modes. In particular in weak lensing, the amount of modes that can be measured from the images is massively limited. For a limited number of modes, shapes that deviate from the characteristics of the employed basis functions can only have approximate representations.
This limitation applies to any complete basis function set. In this work, we want to understand the consequences particularly for weak-lensing measurements within the shapelet basis. We start by describing the simulated galaxy images in Sect. 2. As there are two general shapelet variants, namely circular and - as a generalization - elliptical ones, we discuss both of them in Sects. 3 and 4. We show the influence of PSF convolution, pixelation, and pixel noise in Sect. 5, and discuss the consequences of our findings in Sect. 6.
2 Test images
For this work we seek to answer the question, how well a shapelet model can recover the shear from a source whose shape cannot be entirely described by the model. To pin down the effects of an incomplete shape description and to isolate them from other systematics, we generate very simple test cases in which the galaxy shapes are - initially - not affected by PSF convolution and pixel noise.Often, the radial light profile of galaxies can be accurately described by the Sérsic profile (Sérsic 1963)
where
The profile G is sheared in real-space by transforming the coordinates by means of the linearized lens equation (e.g. Bartelmann & Schneider 2001)
![\begin{displaymath}\vec{x} = \left(
\begin{array}{cc}
1-\gamma_1 & -\gamma_2 \\ [1mm]
-\gamma_2 & 1+\gamma_1
\end{array}\right)
\vec{x^\prime}
\end{displaymath}](/articles/aa/full_html/2010/02/aa12785-09/img24.png)
|
(2) |
such that
The sheared profile ![]() is sampled at the final resolution of
is sampled at the final resolution of
![]() pixels. While
pixels. While
![]() is
already rather large for typical weak-lensing galaxies, we chose to
also simulate even larger ones so as to mimic higher resolution images
from which we can assess the impact of pixelation on the shear
estimates.
is
already rather large for typical weak-lensing galaxies, we chose to
also simulate even larger ones so as to mimic higher resolution images
from which we can assess the impact of pixelation on the shear
estimates.
Because there is no pixel noise in these test images and the resolution is very high, the ellipticity
![]() measured from unweighted quadrupole moments of the pixelated image is always compatible with the shear
measured from unweighted quadrupole moments of the pixelated image is always compatible with the shear
![]() .
Additionally, the centroid position can be computed with essentially arbitrary precision from the image.
.
Additionally, the centroid position can be computed with essentially arbitrary precision from the image.
3 Circular shapelets
According to Refregier (2003),
defines the two-dimensional shapelet basis function of order
with Hn the Hermite polynomial of order n.
From the shapelet coefficients of some two-dimensional function G
one can reconstruct a shapelet model
The model is found by minimizing
with respect to the parameters
One foreseeable problem of the shapelet decomposition stems from the Gaussian weighting function in Eq. (4). We have already discussed that galaxies typically have steeper profiles than a Gaussian, which means that an optimized shapelet model requires higher orders. However, because of the polynomial in Eq. (4), the largest oscillation amplitudes of high-order modes are located at rather large distances from the centroid. Models that include higher orders thus allow a better description of the outer parts of a galaxy, while they still fail to correctly reproduce the central region in the case of steep profiles. Additionally, in case of noisy image data, the number of modes must be limited to avoid overfitting spurious nearby noise fluctuations. As a result, galactic shapes with steeper profiles than a Gaussian are expected to be described by shapelet models with systematically shallower profiles.
Of similar concern is the circularity of the shapelet basis system. As the scale size for both dimensions in Eq. (3) is the same, the zeroth-order is round. If the shape to be described is stretched in a particular direction - as a result of its intrinsic shape or due to gravitational lensing - this elongation has to be carried by higher shapelet orders. Again, for a limited number of basis modes we must expect an inadequate representation of the true shape by the shapelet model. In particular, we have to consider an underestimation of the source elongation much more likely than an overestimation, as the basis system preferentially remains circular. These shortcomings are likely but do not have to affect the estimation of a weak shear. Whether a model with limited fidelity leads to a biased shear estimate depends an the construction of the estimator.
The most straightforward estimator is obtained from the complex ellipticity (e.g. Bartelmann & Schneider 2001)
where Qij are the quadrupole moments measured from the shapelet model
It is important to note that the Qij integrate over the entire shape of ![]() ,
consequently
,
consequently
![]() are linear combinations of all available shapelet coefficients of
are linear combinations of all available shapelet coefficients of
![]() (Bergé 2005), therefore this estimator critically relies on a decent shapelet model.
(Bergé 2005), therefore this estimator critically relies on a decent shapelet model.
3.1 Polar shapelets
For the problem of describing galactic shapes, it is often more convenient to use a polar coordinate framewhere nl and nr are the left-handed and right-handed modes, respectively, and
Bernstein & Jarvis (2002) show that, for nl<nr, one can relate
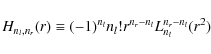
|
(11) |
to the associated Laguerre polynomial
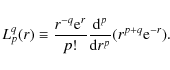
|
(12) |
Note the similarities between the Cartesian basis Eqs. (3) & (4) and the polar basis Eqs. (9) & (10): both share a Gaussian weighting function and are intrinsically circular.
As
Bnr,nl is a complex function if
![]() ,
it is computationally more efficient to decompose the galactic shape into Cartesian shapelets according to Eqs. (5)-(7) and then to perform a coordinate transformation
,
it is computationally more efficient to decompose the galactic shape into Cartesian shapelets according to Eqs. (5)-(7) and then to perform a coordinate transformation
![]() from Cartesian to polar shapelet space (cf. Eq. (69) in Refregier 2003),
from Cartesian to polar shapelet space (cf. Eq. (69) in Refregier 2003),
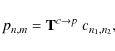
|
(13) |
where we introduced the convenient notation
Performing this transformation enables us to form a conceptionally different family of shear estimators. From Eq. (10) we can see that Bn,m behaves like a field with spin m. Since the shear behaves like a spin-2 field, its action on a circular source can be described by the m=2 modes of a polar shapelet model. Thus, the most basic one of these estimators,
only uses the m=2 mode of any even polar order n of
This approach differs drastically from measuring the quadrupole moment - in the sense that it depends only on a single lensed and two radial unlensed coefficients - and thus expected to behave in a different manner, even though the decomposition is done with Cartesian shapelets in both cases.
Alternatively, one can also form a shear estimator from the
amount of shear that is required to transform an initially circular
galaxy model - specified by pn,0 for
![]() - into one that fits the observed shape best (Bernstein & Jarvis 2002; Kuijken 2006). We refer to these papers for details.
- into one that fits the observed shape best (Bernstein & Jarvis 2002; Kuijken 2006). We refer to these papers for details.
3.2 Results
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12785fg1.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa12785-09/Timg63.png)
|
Figure 1:
( Left) Examples of Sérsic-type galaxy images with
|
| Open with DEXTER | |
The image of ![]() is decomposed into Cartesian shapelets of maximum order
is decomposed into Cartesian shapelets of maximum order
![]() ,
which is typical given the significance of weak-lensing images (cf. Kuijken 2006).
At first, we investigate the modeling fidelity visually. In Fig. 1,
we give four examples of Sérsic-type galaxy shapes and their shapelet
models. It is evident from the top row that, for modest ellipticities,
an elliptical Gaussian can be represented very well by its shapelet
model. But if either the ellipticity becomes stronger or the intrinsic
galactic profile becomes steeper, the shapelet decomposition performs
more poorly. For the Gaussian case shown in the third row, the overall
shape is evidently more compact and boxy rather than elliptical, and
affected by oscillatory artefacts. The images with
,
which is typical given the significance of weak-lensing images (cf. Kuijken 2006).
At first, we investigate the modeling fidelity visually. In Fig. 1,
we give four examples of Sérsic-type galaxy shapes and their shapelet
models. It is evident from the top row that, for modest ellipticities,
an elliptical Gaussian can be represented very well by its shapelet
model. But if either the ellipticity becomes stronger or the intrinsic
galactic profile becomes steeper, the shapelet decomposition performs
more poorly. For the Gaussian case shown in the third row, the overall
shape is evidently more compact and boxy rather than elliptical, and
affected by oscillatory artefacts. The images with
![]() (second and fourth rows) show prominent ring-shaped artefacts and are concentrated at the core region of G. It is striking that the drastic increase in ellipticity from
(second and fourth rows) show prominent ring-shaped artefacts and are concentrated at the core region of G. It is striking that the drastic increase in ellipticity from
![]() to
to
![]() causes almost no apparent change in the respective shapelet models.
causes almost no apparent change in the respective shapelet models.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12785fg2.eps} \vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12785-09/Timg68.png)
|
Figure 2:
Decomposition goodness-of-fit |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12785fg3.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa12785-09/Timg71.png)
|
Figure 3:
Shear estimates
|
| Open with DEXTER | |
The same trend can be seen quantitatively in Fig. 2, where we show the logarithm of the goodness-of-fit ![]() of the shapelet models. From this we infer that the modeling errors become stronger with increasing
of the shapelet models. From this we infer that the modeling errors become stronger with increasing ![]() and are almost independent of
and are almost independent of
![]() for
for
![]() .
In other words, while the shapelet decomposition is occupied with
modeling a steep profile, it misses most of the ellipticity
information. It is worth noting that an increase in
.
In other words, while the shapelet decomposition is occupied with
modeling a steep profile, it misses most of the ellipticity
information. It is worth noting that an increase in ![]() from 8 to 12 does not lead to substantially lower
from 8 to 12 does not lead to substantially lower ![]() ,
although the number of available modes is raised from 45 to 91. This
behavior can be explained by the shape of the higher-order shapelet
functions. As they tend to fit features in the outer regions, they only
improve the model in the low-flux regions.
,
although the number of available modes is raised from 45 to 91. This
behavior can be explained by the shape of the higher-order shapelet
functions. As they tend to fit features in the outer regions, they only
improve the model in the low-flux regions.
In the top panel of Fig. 3, we show the shear estimator
![]() as a function of the applied shear. We see that the bias is essentially a linear function of
as a function of the applied shear. We see that the bias is essentially a linear function of ![]() with a negative slope that increases with
with a negative slope that increases with ![]() .
It is important to note that the estimator is unbiased for
.
It is important to note that the estimator is unbiased for
![]() as long as
as long as ![]() remains moderate. But, for
remains moderate. But, for
![]() the same estimator is essentially shear-insensitive. Increasing the maximum order
the same estimator is essentially shear-insensitive. Increasing the maximum order ![]() from 8 to 12 improves the estimator, because the shape at large distances from the center is captured better by the model, and
from 8 to 12 improves the estimator, because the shape at large distances from the center is captured better by the model, and
![]() makes
use of all available orders. But the steeper the profiles, the less
high orders contribute to the shear estimation, because the quadrupole
moments become dominated by the inner region, which is governed by a
single central pixel with square shape, hence vanishing ellipticity
makes
use of all available orders. But the steeper the profiles, the less
high orders contribute to the shear estimation, because the quadrupole
moments become dominated by the inner region, which is governed by a
single central pixel with square shape, hence vanishing ellipticity![]() . From our prior discussion and Figs. 1 and 2, we anticipated this behavior, and it clearly confirms our theoretical expectations regarding steep galactic profiles.
. From our prior discussion and Figs. 1 and 2, we anticipated this behavior, and it clearly confirms our theoretical expectations regarding steep galactic profiles.
In the bottom panel of Fig. 3, the response of the shear estimator
![]() on the same set of galaxies is shown. We can see that the overall bias
is mitigated by roughly a factor 4, fairly independent of
on the same set of galaxies is shown. We can see that the overall bias
is mitigated by roughly a factor 4, fairly independent of ![]() .
This has to be expected because the shapelet basis is orthogonal and thus higher-orders do not change the value of
.
This has to be expected because the shapelet basis is orthogonal and thus higher-orders do not change the value of
![]() ,
which carries the shear signal of
,
which carries the shear signal of
![]() .
The differences that occur when changing
.
The differences that occur when changing ![]() are related to a different preferred scale size
are related to a different preferred scale size ![]() in the optimization.
in the optimization.
As before, galaxies with
![]() can be measured with high fidelity. For steeper profiles the estimator
has a - somewhat surprising - positive bias, while the shapelet model
itself underestimates the ellipticity. We do not fully understand why
this estimator overestimates the applied shear, but we can identify two
possible reasons:
can be measured with high fidelity. For steeper profiles the estimator
has a - somewhat surprising - positive bias, while the shapelet model
itself underestimates the ellipticity. We do not fully understand why
this estimator overestimates the applied shear, but we can identify two
possible reasons:
- The estimator has been derived from the action of a infinitesimal shear on a brightness distribution that is perfectly described by a shapelet model (Massey et al. 2007). In the tests performed here, we intentionally violate these unrealistic assumptions;
- Looking at the definition in Eq. (14) and the shapelet models in Fig. 1,
we see ring-shaped artefacts for steep profiles, corresponding to
radial shapelet modes. Exactly these modes are required for normalizing
the estimator. As we know from Fig. 2, the goodness-of-fit - hence the abundance of artefacts - is highly correlated with
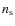 .
Thus, the denominator of Eq. (14) is probably also plagued by the poor reconstruction quality of steep profiles.
.
Thus, the denominator of Eq. (14) is probably also plagued by the poor reconstruction quality of steep profiles.
4 Elliptical shapelets
To assess the performance of all versions of shapelet image analysis, we also considered an elliptical implementation of the Gauss-Laguerre polynomials. To this purpose, we used a novel code that we have developed recently (Lombardi et al., in prep.). This implementation has many different operating modes for several key parameters, such as the truncation mode of the shapelet decomposition, the fitting of the object shape, and the masking method used. However, for the sake of simplicity, here we mostly discuss the results obtained by running the pipeline in a mode that closely follows the prescriptions of Bernstein & Jarvis (2002) and Nakajima & Bernstein (2007). We refer the reader to these two papers for all details that are not explicitly mentioned here.Elliptical shapelets are defined essentially like polar shapelets in a
suitably sheared reference system. For example, in the simple
case where the elliptical base is oriented along the Cartesian axes,
one can define a new coordinate system
(x'1, x'2) as
where a and b are two scales (the two semi-axes of the base system). This gives rise to a radial coordinate r', for which we evaluate the shapelet function Bnr,nl of Eq. (9) on this new system (by keeping
All further steps in the decomposition are essentially identical to
the circular shapelet one: for example, the shapelet coefficients are
still evaluated using a ![]() technique identical to Eq. (7).
technique identical to Eq. (7).
The elliptical shapelet decomposition just described, and the consequent shape estimation, is done using a sequence of individual steps in our pipeline.
- 1.
- First, we run SExtractor (Bertin & Arnouts 1996) on the input image (and associated weight map, if available) using a rather standard configuration. For each object, among other things, we measure its centroid, its shape, and its position angle.
- 2.
- The resulting SExtractor parameters of each objects are used as initial guesses for the shapelet decomposition. We first extract the images of each object, and mask them with an elliptical mask that follows the original SExtractor shape estimate (in particular, the mask ellipse has axes that are four times as big as the SExtractor ones). We then use the same SExtractor shape estimate as an initial guess for the shapelet elliptical basis.
- 3.
- We perform a forward fitting of all pixels contained within the
mask, and thereby obtain a set of shapelet parameters
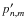 and
associated covariance matrix. To be able to compare with the circular shapelets, we
used a triangular truncation scheme by requiring that
and
associated covariance matrix. To be able to compare with the circular shapelets, we
used a triangular truncation scheme by requiring that
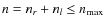 ,
where
,
where
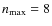 or 12 is the maximum order of the decomposition.
or 12 is the maximum order of the decomposition.
- 4.
- The next step is the estimation of the ellipticity. For this
purpose, we can either use the quadrupole moments as in Eq. (8)
or rely on an iterative approach that we call ``focusing'': we apply
a sequence of translations, scaling operations, and shear operations
to the object until it appears perfectly centered, with maximum
signal to noise, and round. As shown by
Bernstein & Jarvis (2002), these conditions can be fulfilled by
requiring that
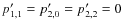 .
Since we are using an elliptical base for
our shapelets, the condition
.
Since we are using an elliptical base for
our shapelets, the condition
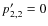 simply indicates that the
object is round in the elliptical base, i.e. has an ellipticity
and a position angle that are identical to the ones of the base.
simply indicates that the
object is round in the elliptical base, i.e. has an ellipticity
and a position angle that are identical to the ones of the base.
- 5.
- Finally, we compare the focusing parameters with the original SExtractor one, and we repeat the whole process with the newly determined parameters in case both parameter sets differ significantly. This step is typically executed only for a relatively small fraction of galaxies.
4.1 Results
To test the ability of our elliptical shapelet pipeline to
deal with inaccurate input catalogs, we biased the input ellipticity
by ![]() toward circular objects and measured the residual bias
left in the recovered ellipticity
toward circular objects and measured the residual bias
left in the recovered ellipticity
![]() .
As shown by Fig. 4, this test
produced conceptually similar results to circular shapelets:
for small Sérsic indices, we could recover the true ellipticity without any
significant bias, while the estimates degrade significantly as we approach
.
As shown by Fig. 4, this test
produced conceptually similar results to circular shapelets:
for small Sérsic indices, we could recover the true ellipticity without any
significant bias, while the estimates degrade significantly as we approach
![]() .
The situation is improved when
.
The situation is improved when ![]() is raised, because the transformations done during the focusing step
take all available orders into account, in contrast to the simpler
description underlying the construction of
is raised, because the transformations done during the focusing step
take all available orders into account, in contrast to the simpler
description underlying the construction of
![]() in Eq. (14). With
in Eq. (14). With
![]() (bottom panel of Fig. 4), galaxies with
(bottom panel of Fig. 4), galaxies with
![]() and 1 have shear estimates without bias. When raising
and 1 have shear estimates without bias. When raising ![]() beyond that, the bias is at first positive before it becomes negative.
beyond that, the bias is at first positive before it becomes negative.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{12785fg4.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa12785-09/Timg88.png)
|
Figure 4:
Shear estimate
|
| Open with DEXTER | |
Investigating this feature more closely, we find
that the Sérsic index has a strong impact on the ability of the method to choose a suitable optimal fitting size (a and b in Eq. (15)).
As discussed above, our code tries to maximize the detection
significance of the galaxy, i.e. the signal-to-noise ratio for
![]() ,
by requiring that
,
by requiring that
![]() .
If the fitted galaxy has an elliptical profile, this choice is indeed
optimal, and the resulting shapelet fitting size corresponds to a
Gaussian profile with the same half-light radius as the original
galaxy. However, as we increase the Sérsic index, the condition
.
If the fitted galaxy has an elliptical profile, this choice is indeed
optimal, and the resulting shapelet fitting size corresponds to a
Gaussian profile with the same half-light radius as the original
galaxy. However, as we increase the Sérsic index, the condition
![]() is fulfilled for increasingly smaller shapelet sizes, corresponding to
Gaussian profiles with half-light radii much smaller than the galaxy
half-light radius and eventually smaller than one pixel. At this point,
the estimate of all shapelet parameters, including the
is fulfilled for increasingly smaller shapelet sizes, corresponding to
Gaussian profiles with half-light radii much smaller than the galaxy
half-light radius and eventually smaller than one pixel. At this point,
the estimate of all shapelet parameters, including the
![]() is completely unreliable, and this usually triggers a re-try with a
large choice for the decomposition size, often much larger than the
galaxy. At the following iterations, the algorithm again tends to
progressively reduce the decomposition size, until a very small size is
reached again and the whole process is repeated.
is completely unreliable, and this usually triggers a re-try with a
large choice for the decomposition size, often much larger than the
galaxy. At the following iterations, the algorithm again tends to
progressively reduce the decomposition size, until a very small size is
reached again and the whole process is repeated.
An immediate consequence of this erratic behavior for the decomposition algorithm (highlighted in the bottom panel of Fig. 4) is that any ellipticity estimate obtained from peaked profiles is not robust and can lead to large errors. Although this observed behavior might be related to our particular implementation of the elliptical shapelet decomposition and to the method used to refine the initial elliptical decomposition basis, we still interpret it as a general difficulty for Gaussian-weighted decompositions (such as the circular shapelet one) to capture the essential shape information for peaked galaxy profiles.
In summary, it appears that the pipeline is unable to fully correct inaccuracies in the SExtractor catalog for galaxies showing a profile close to the De Vaucouleurs one.
5 Observational systematics
In more realistic simulations or observational data, the galactic shapes are recorded after convolution with the PSF, pixelation by the CCD, and degraded by pixel noise. We now discuss the impact of these effects on shear estimation with shapelets.
5.1 PSF convolution
Clearly, a convolution creates shallower profiles that can be better described by shapelet models. Therefore, the typical goodness-of-fit values, in particular for steeper profiles, are considerably lower than in the unconvolved case. If the PSF shape is perfectly described by its shapelet model, one can undo a convolution exactly in shapelet space. In such a case, the shape obtained by deconvolving a PSF-convolved galaxy model must approximate the true, unconvolved shapeTo verify this new hypothesis, we convolved Sérsic-type galaxies in pixel space with PSF shapes P obtained from shapelet models![]() ,
,
| (16) |
For circular shapelets, C is modeled with shapelets and explicitly deconvolved from
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{12785fg5.eps} \vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12785-09/Timg95.png)
|
Figure 5:
Similar to Fig. 3: solid lines show bias on shear estimate
|
| Open with DEXTER | |
In Fig. 5 we
compare the bias of the shear estimates from unconvolved galaxies
images and from the same set of galaxies after convolution with a
Gaussian PSF with an FWHM of 5 pixels - thus FWHM
![]() .
As expected, the overall shape of the convolved images - and thus also
their unconvolved shapes - can be better modeled with shapelets.
As a result, the shear estimator
.
As expected, the overall shape of the convolved images - and thus also
their unconvolved shapes - can be better modeled with shapelets.
As a result, the shear estimator
![]() profits manifestly because it makes use of the entire shape
information: its bias is lowered by a factor 3. We observed similar
improvements also for
profits manifestly because it makes use of the entire shape
information: its bias is lowered by a factor 3. We observed similar
improvements also for
![]() and
and
![]() .
.
We varied the size of the PSF and found that in general the bias is lower for larger PSFs. Additionally, we found
![]() and
and
![]() to be rather sensitive to changes of
to be rather sensitive to changes of ![]() and
and
![]() .
Finally, the bias of all estimators also depends in a non-trivial way
on the shape of the PSF, because the fidelity of the model for the
convolved galaxy image determines the accuracy of the estimators.
.
Finally, the bias of all estimators also depends in a non-trivial way
on the shape of the PSF, because the fidelity of the model for the
convolved galaxy image determines the accuracy of the estimators.
5.2 Pixelation
Images from CCDs are obtained by collecting the light within pixels of approximately square shape. For measuring shapes, pixelation has important consequences. If the size of the object is small compared to the pixel size, we cannot describe the true continuous shape of the object but rather its piecewise approximation with pixel-sized step functions. Modeling approaches like the shapelets method can take pixelation into account by integrating the model values within the pixels (Massey & Refregier 2005). In case of convolved images, the deconvolution procedures also treat pixelation consistently, if the PSF shape has been measured from images with the same pixelation (e.g. Bridle et al. 2009).For estimating the shear, an additional problem is of relevance. As the smallest piece of information within an image is given by a single pixel of square shape, we can only infer shear information from an object for which we can measure more than a single pixel. Particularly for galaxies with steep profiles, the largest fraction of the flux is registered in the pixel that is closest to the centroid. Then, the shear information is also dominated by this central pixel, which does not have any preferred direction, hence is biased low.
For this work, it is important to verify that the biases
related to steep profiles are not entirely a pixelation problem, but
stem from the shape mismatch as discussed before. Therefore, we also
made sets of images with
![]() .
Although there are some differences between the three tested
estimators, we found a common trend when increasing the size of the
galaxies: The results for galaxies with
.
Although there are some differences between the three tested
estimators, we found a common trend when increasing the size of the
galaxies: The results for galaxies with
![]() are essentially unchanged. In particular, the bias does not vanish when
the side length of a pixel is reduced to one quarter. This shows that
there is a profile-dependent bias even for very large galaxies.
The estimates for steeper profiles benefit from smaller pixel sizes,
but the results still remain more strongly biased than for shallower
profiles.
are essentially unchanged. In particular, the bias does not vanish when
the side length of a pixel is reduced to one quarter. This shows that
there is a profile-dependent bias even for very large galaxies.
The estimates for steeper profiles benefit from smaller pixel sizes,
but the results still remain more strongly biased than for shallower
profiles.
5.3 Pixel noise
There is an additional effect related to the discussion of pixelation. In the presence of pixel noise, fewer significant pixels remain for each galaxy. In particular, steep profiles therefore tend to be reduced to some pixels or even only a single pixel close to center of the galaxy, which is then fitted by the model. Thus, we expect pixel noise to behave in a similar way to strong pixelation.We performed the same tests again with realistic noise added to ![]() .
In fact, we can confirm that steep profiles are affected more strongly by pixel noise than shallower ones.
In any case, apart from additional statistical uncertainty, it did not lead to qualitatively different results.
.
In fact, we can confirm that steep profiles are affected more strongly by pixel noise than shallower ones.
In any case, apart from additional statistical uncertainty, it did not lead to qualitatively different results.
There is another important point to note. Increased pixel noise would normally lead to a lower ![]() ,
as the shapelet models are typically tuned such that they do not, or
only marginally, pick up noise fluctuations. Reducing the maximum order
typically leads to more prominent modeling problems, as already
discussed above, and consequently to poorer results from most shear
estimators.
,
as the shapelet models are typically tuned such that they do not, or
only marginally, pick up noise fluctuations. Reducing the maximum order
typically leads to more prominent modeling problems, as already
discussed above, and consequently to poorer results from most shear
estimators.
6 Conclusions
- Shear estimates from circular shapelets are biased if the shape to be described has too steep a profile (steeper than a Gaussian) or too large an ellipticity. Profile mismatch is the more important source of bias.
- For elliptical shapelets, profile mismatch still poses a considerable problem, because the shapelet models cannot fully correct biases of the ellipticity prior when the profile becomes steeper than exponential.
- Different shear estimators can mitigate the bias, but never eliminate it completely because the shape mismatch generally affects all shapelet modes.
- We are even more concerned for flexion estimates. While the overall octupole power might be lower than the quadrupole power, the bias introduced by the shape mismatch becomes more important for higher-order moments.
- Convolution with a PSF renders all observable shapes
shallower and allows the treatment of pixelation, hence facilitating a
more accurate description by shapelet models. For typical ground-based
observations, this may limit the bias to a tolerable level,
particularly for
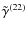 and
and
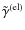 .
.
- The ellipticity estimates could be calibrated provided we have sufficiently detailed simulations to properly describe the distribution of intrinsic galaxy morphologies and the effect of PSF convolution on it. Furthermore, we would need to be able to infer the appropriate calibration parameters from observations. Achieving this is at least as hard as measuring the ellipticity.
- Even if an effective calibration for an entire galaxy ensemble could be achieved, it does not ensure unbiased results when the ensemble is sliced (e.g. in redshift bins for weak-lensing tomography or spatially for cluster-mass reconstructions).
- Lensing simulations with shapelet source models (e.g. Massey et al. 2004; Meneghetti et al. 2008) systematically favor shapelet pipelines for weak-lensing measurements as the shapelet basis forms the optimal way of describing these sources.
- The mentioned shortcomings are mostly relevant for small and faint galaxies that are described by shapelet models with low
 .
For objects with a high signal-to-noise ratio, modeling with high
.
For objects with a high signal-to-noise ratio, modeling with high  reduces
these effects. Additionally, the artefacts that can occur on bright
galaxies have a similar impact on shapelet models for galaxies that are
intrinsically similar. We conclude therefore that morphological
investigations of galaxy populations are still feasible with shapelets.
However, measures of e.g. their ellipticity or profile slope
distribution are potentially biased.
reduces
these effects. Additionally, the artefacts that can occur on bright
galaxies have a similar impact on shapelet models for galaxies that are
intrinsically similar. We conclude therefore that morphological
investigations of galaxy populations are still feasible with shapelets.
However, measures of e.g. their ellipticity or profile slope
distribution are potentially biased.
- PSF shapes typically follow the Moffat profile (Moffat 1969)
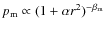 and can thus already be modeled very well with a pure Gaussian - which is the limiting case for
and can thus already be modeled very well with a pure Gaussian - which is the limiting case for
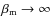 (Trujillo et al. 2001).
In particular for PSFs from ground-based observations with its at most
mild ellipticity, shapelets can in principle reach excellent modeling
accuracy. However, because of their Gaussian weighting function, they
cannot accurately describe PSF shapes with wide wings. This may
introduce additional systematics in the deconvolution step, which we
did not address in this work.
(Trujillo et al. 2001).
In particular for PSFs from ground-based observations with its at most
mild ellipticity, shapelets can in principle reach excellent modeling
accuracy. However, because of their Gaussian weighting function, they
cannot accurately describe PSF shapes with wide wings. This may
introduce additional systematics in the deconvolution step, which we
did not address in this work.
P.M. is supported by the DFG Priority Programme 1177. This work has gained substantially from the ideas, suggestions, and criticism of Massimo Meneghetti, René Andrae, Konrad Kuijken, and Ludovic van Waerbeke. The authors are particularly thankful to the referee, Gary Bernstein, for very constructive suggestions and comments.
References
- Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Bergé, J. 2005, An introduction to shapelets based weak lensing image processing, 1st edn. [Google Scholar]
- Bernstein, G. M., & Jarvis, M. 2002, ApJ, 123, 583 [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [Google Scholar]
- Bridle, S., Shawe-Taylor, J., Amara, A., et al. 2009, Annals of Applied Statistics, 3, 6 [Google Scholar]
- Capaccioli, M. 1989, in World of Galaxies (Le Monde des Galaxies), ed. H. G. Corwin, Jr., & L. Bottinelli, 208 [Google Scholar]
- de Vaucouleurs, G. 1948, Annales d'Astrophysique, 11, 247 [Google Scholar]
- Graham, A. W., & Driver, S. P. 2005, Publ. Astron. Soc. Austr., 22, 118 [Google Scholar]
- Kuijken, K. 2006, A&A, 456, 827 [Google Scholar]
- Massey, R., & Refregier, A. 2005, MNRAS, 363, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, R., Refregier, A., Conselice, C. J., & Bacon, D. J. 2004, MNRAS, 348, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, R., Rowe, B., Refregier, A., Bacon, D. J., & Bergé, J. 2007, MNRAS, 380, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Melchior, P., Meneghetti, M., & Bartelmann, M. 2007, A&A, 463, 1215 [Google Scholar]
- Melchior, P., Andrae, R., Maturi, M., & Bartelmann, M. 2009, A&A, 493, 727 [Google Scholar]
- Meneghetti, M., Melchior, P., Grazian, A., et al. 2008, A&A, 482, 403 [Google Scholar]
- Moffat, A. F. J. 1969, A&A, 3, 455 [Google Scholar]
- Nakajima, R., & Bernstein, G. 2007, AJ, 133, 1763 [NASA ADS] [CrossRef] [Google Scholar]
- Refregier, A. 2003, MNRAS, 338, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Refregier, A., & Bacon, D. 2003, MNRAS, 338, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, M. T., Carollo, C. M., Lilly, S. J., et al. 2007, ApJS, 172, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Sérsic, J. L. 1963, Boletin de la Asociacion Argentina de Astronomia La Plata Argentina, 6, 41 [Google Scholar]
- Trujillo, I., Aguerri, J. A. L., Cepa, J., & Gutiérrez, C. M. 2001, MNRAS, 328, 977 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... flux
![[*]](/icons/foot_motif.png)
- This is ensured by demanding of
 to satisfy the relation
to satisfy the relation

between the complete and the incomplete Gamma function (Graham & Driver 2005). The approximate solution for the equation above,
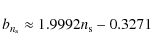
(Capaccioli 1989), is used throughout the paper. - ...
##) ![[*]](/icons/foot_motif.png)
- The exponential profile that describes the brightness
distribution of spiral galaxies and the de Vaucouleurs profile (de Vaucouleurs 1948) of
elliptical galaxies are special cases of the Sérsic profile with
 and
and 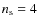 ,
respectively.
,
respectively.
- ...
![[*]](/icons/foot_motif.png)
- Of course, in reality galaxies show angular patterns (for example spiral arms) and substructures, but for simplicity we only consider the general radial shape.
- ...(Massey et al. 2007)
![[*]](/icons/foot_motif.png)
- We restrict ourselves to n=2 for the
following tests, so that we only discuss
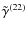 .
.
- ... ellipticity
![[*]](/icons/foot_motif.png)
- We will discuss the effects of pixelation in Sect. 5.2.
- ...
![[*]](/icons/foot_motif.png)
- For our argument, we only exploit that convolution with the PSF renders observed profiles shallower. Hence, the last statement is probably still true for imperfect shapelet models of the PSF - which are likely to introduce other systematics.
- ... models
![[*]](/icons/foot_motif.png)
- In the terminology of this work, that means
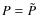 .
.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12785fg1.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa12785-09/Timg63.png)
|
Figure 1:
( Left) Examples of Sérsic-type galaxy images with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12785fg2.eps} \vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12785-09/Timg68.png)
|
Figure 2:
Decomposition goodness-of-fit |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12785fg3.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa12785-09/Timg71.png)
|
Figure 3:
Shear estimates
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{12785fg4.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa12785-09/Timg88.png)
|
Figure 4:
Shear estimate
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{12785fg5.eps} \vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12785-09/Timg95.png)
|
Figure 5:
Similar to Fig. 3: solid lines show bias on shear estimate
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}
p_{\rm s}(r) \propto \exp\left\lbrace -b_{n_{\rm s}}\left[\...
...frac{r}{R_{\rm e}}\right)^{1/n_{\rm s}}-1\right]\right\rbrace,
\end{displaymath}](/articles/aa/full_html/2010/02/aa12785-09/img12.png)
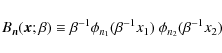
![\begin{displaymath}
\phi_{n}(x) \equiv [2^n \pi^{\frac{1}{2}} n!]^{-\frac{1}{2}}\ H_n(x)\
{\rm e}^{-\frac{x^2}{2}},
\end{displaymath}](/articles/aa/full_html/2010/02/aa12785-09/img38.png)
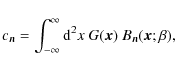
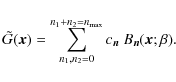
![\begin{displaymath}
\chi^2\propto \sum_{\vec{x}} [G(\vec{x}) - \tilde{G}(\vec{x})]^2
\end{displaymath}](/articles/aa/full_html/2010/02/aa12785-09/img41.png)
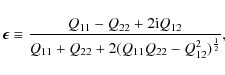
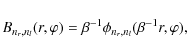
![\begin{displaymath}
\phi_{n_r, n_l}(r,\varphi) \equiv [\pi n_r! n_l!]^{-\frac{1}...
...r) {\rm e}^{-\frac{x^2}{2}} {\rm e}^{{\rm i}(n_r-n_l)\varphi}.
\end{displaymath}](/articles/aa/full_html/2010/02/aa12785-09/img51.png)