EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 510 (February 2010) A&A, 510 (2010) A30 Full HTML
Free Access
Issue
A&A
Volume 510, February 2010
Article Number A30
Number of page(s) 7
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/200912674
Published online 03 February 2010
A&A 510, A30 (2010)

Evidence of grain growth in the disk of the bipolar proto-planetary nebula M 1-92

K. Murakawa1 - T. Ueta2 - M. Meixner3

1 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
2 - Department of Physics and Astronomy, University of Denver, Denver, CO 80208, USA
3 - Space Telescope Science Institute, Baltimore, MD 21218, USA

Received 10 June 2009 / Accepted 20 November 2009

Abstract
Aims. We investigate the dust grain size and dust shell structure of the bipolar proto-planetary nebula M 1-92.
Methods. We performed radiative transfer modeling of the dust shells of M 1-92. Our models consists of a disk and bipolar lobes that are surrounded by an AGB shell, each component having different dust characteristics. The model parameters were constrained with the previously obtained spectral energy distribution, the intensity images, the polarization images based on HST/NICMOS archived data as well as the previous radio observations in the CO emission line.
Results. Our model geometries with the optically thick disk and lobes with a hollow structure reproduce the bright bipolar lobes of M 1-92. The upper limit of the grain size $a_{\max}$ in the lobes is estimated to be $0.5~\mu$m from the polarization value in the bipolar lobe. The $a_{\max}$ value of the disk is constrained with the disk mass (0.2 $M_{\odot}$), which was estimated from a previous CO emission line observation. We find a good model with $a_{\max}=1000.0~\mu$m, which provides an approximated disk mass of 0.15 $M_{\odot}$. Even taking into account uncertainties such as the gas-to-dust mass ratio, a significantly larger dust of $a_{\max}>100.0~\mu$m, comparing to the dust in the lobe, is expected. We also estimated the disk inner radius, the disk outer radius, the mass-loss rate, and the envelope mass to be 30 $R_\star$(=9 AU), 4500 AU, $7.5\times10^{-6}[v_{\exp}$ km s $^{-1}]~M_{\odot}$ yr-1, and 4 $M_{\odot}$, respectively, where $v_{\exp}$ is the expansion velocity.
Conclusions. If the dust existing in the lobes in large separations from the central star undergoes little dust processing, the dust sizes preserves the ones in the dust formation. Submicron-sized grains are found in many objects besides M 1-92, suggesting that the size does not depend much on the object properties, such as initial mass of the central star and chemical composition of the stellar system. On the other hand, the grain sizes in the disk do. Evidence of large grains has been reported in many bipolar PPNs, including M 1-92. This result suggests that disks play an important role in grain growth.

Key words: stars: AGB and post-AGB - planetary nebulae: individual: M 1-92 - radiative transfer - polarization

1 Introduction

Planetary nebula (PN) morphology represents a history of physical processes in the stellar/circumstellar environments. A large sample ($\sim$500) of galactic PNs has shown that 20-25% of them have spherical structures, but the others have asymmetric (elliptic, bipolar, and point-symmetric structures) (e.g. Corradi & Schwarz 1995; Manchado et al. 1996; Zuckerman & Aller 1986; Stanghellini et al. 1993; Soker 1997; Sahai & Trauger 1998). Several theoretical studies have been carried out to explain the PN morphologies (see review by Balick & Frank 2002). Widely accepted facts and physical processes are cool spots on the stellar surface (Soker & Clayton 1999; Frank 1995), the stellar rotation (Bjorkman & Cassinelli 1993), magnetic field (Matt et al. 2000; Mastrodemos & Morris 1999; Pascoli et al. 1992; Mastrodemos & Morris 1998), and binary interaction (Morris 1981; Soker & Livio 1994; Bond & Livio 1990; Morris 1987; Livio et al. 1979). While details are still unknown, these mechanisms one way or another cause the equatorially enhanced mass loss in the AGB phase (e.g. Meixner et al. 1999; Ueta et al. 2000). In the subsequent post-AGB phase, the central star blows away the low density fast wind, which inflates the lobe in the polar direction more than in the equatorial direction (Kwok 1982; Kwok et al. 1978). This interacting stellar wind (ISW) model explains various morphologies of elliptic and bipolar PNs (Balick 1987). In the above scenario, the binary interaction is thought to be one of the most promising mechanism to shape PNs with a narrow waist between the bipolar lobes because this can amplify the mass loss in the equatorial plane and make a disk-like structure (e.g. Soker & Rappaport 2000). In addition, the binary interaction is also thought to form asymmetric structures such as jets, ansae (e.g. Soker 1990,1992), and point-symmetric shapes such as a spiral and quadruple by precessing motion (Mauron & Hugins 2006; Manchado et al. 1996).

It is difficult to directly detect the effect of binary interaction on PN shaping using the current observing techniques. However, it would be possible to infer the presence of the effects due to the aforementioned scenario if the inner part of the circumstellar environment is investigated closely enough. Near-infrared imaging polarimetry is a powerful method to probe dust shells and to provide important information that can be derived in more details than non-polarimetric imaging. Previous observations and dust scattering modeling have revealed disk and bipolar lobe structures of evolved stars (e.g. Su et al. 2003; Scarrott & Scarrott 1995; Ueta et al. 2005; Gledhill 2005; Ueta et al. 2007; Murakawa et al. 2007,2005, hereafter UMM07). However, most previous experiments treated only a single grain model in the entire dust shell or SEDs were not considered simultaneously. These shortcomings have prohibited us from investigating into the grain and disk properties in detail. To resolve the situation, we considered both polarimetric images and SEDs in our recent radiative transfer modeling of the bipolar proto-PN (PPN) Frosty Leo, assuming two different dust models, one in the equatorial region (disk) and the other in the bipolar lobes (Murakawa et al. 2008a). From this modeling, we were able to derive evidence for grain growth in the disk region. In this paper, we use this technique for the bipolar PPN: M 1-92 (=IRAS 19343+2926), whose characteristics were discussed previously by us (UMM07). In Sect. 2, details of our radiative transfer modeling are described. We will discuss the implication of our model result in Sect. 3.

2 Radiative transfer calculations

The primary purpose of our modeling is to explore the parameter space of the disk geometry and the grain sizes in the circumstellar dust shells of our target. In order to do this, we applied model geometries with a disk and bipolar lobes and different dust models for them. We used our own three-dimensional Monte Carlo code STSH (Murakawa et al. 2008b), which solves radiative transfer problem of scattering and absorption by dust. This code can handle multiple dust models in an arbitrary model geometry and computes SEDs, dust temperatures, and the Stokes ${\it IQUV}$ parameters. We constrained the model parameters by comparing with the observed SEDs and polarimetric images from the HST NICMOS 2 data at a wavelength of 2 $\mu $m. We followed a similar modeling procedure as in the past (Murakawa et al. 2008a,b). We first tried several parameter sets to find an approximated solution and parameter ranges and determined some parameters, which can be estimated easily. The grain sizes in the bipolar lobe were determined from the polarization values in this region, which do not depend on the other parameters such as the model geometry and the masses of the disk and envelope. Then, we constructed a large number of models by SED fit and made model images of a few possible parameter sets. We find some good models with different dust sizes $a_{\max}$ in the disk, which reproduces the characteristics of the above observations well. To constrain the $a_{\max}$ value, we use the disk mass which was estimated from a previous CO emission line observation (Alcolea et al. 2007; Bujarrabal et al. 1998b). We will describe this grain size issue in detail below.

2.1 Model assumption and numerical simulation

M 1-92 is an oxygen-rich PPN known as Minkowski's footprint (Minkowski 1946). An optical spectrum suggests a 6500 K black body component and an 18 000 K component in shorter wavelengths. The latter is probably due to flux from the companion star (Arrieta et al. 2005). Because the 6500 K component dominates in the total flux, we assumed a blackbody spectrum with this temperature as the illumination source. The distance D was determined to be between 2.5 kpc (Cohen & Kuhi 1977) and 3.5 kpc (Eiroa & Hodapp 1989). We adopted 3.0 kpc, the average of the two. For the luminosity, although Cohen & Kuhi (1977) obtained a 1600 [D kpc] $^2~L_{\odot}$, which corresponds to $\sim$20 000 $L_{\odot}$ at 3.5 kpc, we found that 7000 $L_{\odot}$ fits the absolute flux in the SED better and adopted this value in our modeling.

The nebula has a waterlily petal-like shape with an $11\hbox{$^{\prime\prime}$ }\times6\hbox{$^{\prime\prime}$ }$extension (see also Bujarrabal et al. 1998a; Trammell et al. 1996), which extends towards the northwest and the southeast directions. The northwestern lobe is brighter than the southeastern one. Blue- and red-shifted components are detected in the northwestern and southeastern lobes, respectively, in the CO emission line data and the northwestern lobe is tilted towards us by $35\hbox{$^\circ$ }$(Bujarrabal et al. 1998b). In our modeling, we assume that the model geometry consisting of three components: (1) a disk in the innermost part, (2) a superwind shell in the outside of the disk, and (3) an AGB dust shell in the outermost part. The disk form chosen is one studied by Toomore (1982) and Fischer et al. (1996). For the superwind shell, the NICMOS 2 intensity image shows that the surface brightness at the outline of the bipolar lobes is slightly enhanced compared to the projected inner part (Ueta et al. 2007), suggesting a hollow structure, which is probably formed by the interaction with the ISW. The AGB shell is assumed to have a one-dimensional, spherically symmetric structure with a single power-law radial density gradient. The mass density distribution $\rho$ consists of the individual components of the disk $\rho_{\rm disk}$, the superwind shell $\rho_{\rm sw}$, and the AGB shell $\rho_{\rm AGB}$ and is given by

                                      $\displaystyle \rho$ = $\displaystyle \rho_{\rm disk}+\rho_{\rm sw}+\rho_{\rm AGB},$  
$\displaystyle \rho_{\rm disk}\left(r,z\right)$ = $\displaystyle \rho_{\rm d}\left(r/R_{\rm in}\right)^{-2} \exp\left[-\left\vert\frac{z}{Hr}\right\vert\right] \mbox{ for $R_{\rm in}\le R\le R_{\rm disk}$ },$  
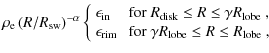
$\displaystyle \rho_{\rm sw}\left(R,\theta\right)$ = $\displaystyle \rho_{\rm e}\left(R/R_{\rm sw}\right)^{-\alpha} \left\{ \begin{ar... ...a R_{\rm lobe}\le R\le R_{\rm lobe}$ },\nonumber\\ \end{array}\right.\nonumber$  
$\displaystyle \rho_{\rm AGB}\left(R\right)$ = $\displaystyle \rho_{\rm e}\left(R/R_{\rm sw}\right)^{-2} \mbox{ for $R_{\rm sw}\le R\le R_{\rm out}$ },$  

where the coordinates of $\left(R,\theta\right)$ and $\left(r,z\right)=\left(R\sin\theta,R\cos\theta\right)$ are the two-dimensional spherical coordinate and cylindrical coordinate, respectively. We assume that the disk exists in a region between the inner radius $R_{\rm in}$ and the outer radius $R_{\rm disk}$. The value H is the ratio of the disk height to the disk radius. The $\rho_{\rm d}$ is the density coefficient and is derived from the optical depth in the equatorial plane instead of the disk mass $M_{\rm disk}$ as done before (Meixner et al. 2002; Murakawa et al. 2008a). We find that an optical depth of 30 at a wavelength of 2.0 $\mu $m fits well in the optical to NIR fluxes. We apply this value for further investigation of the grain size effect. The shape of the superwind is determined by $R_{\rm lobe}=R_{\rm sw}\left(\vert\theta/\pi-1/2\vert\right)^\beta$(Oppenheimer et al. 2005, and references therein). The density factors of $\epsilon_{\rm in}$ and $\epsilon_{\rm rim}$ produce the hollow structure of the lobe. In the above parameters, we adopted an $\alpha$ of 1.2, $\beta$ of 1.7, $\gamma$ of 0.7, $\epsilon_{\rm in}$ of 0.01, $\epsilon_{\rm rim}$ of 0.5, and $R_{\rm sw}$ of $7\hbox{$.\!\!^{\prime\prime}$ }5$, which fit well the appearance of the bipolar lobe. The AGB shell exists in the outermost part between the radii of  $R_{\rm sw}$ and  $R_{\rm out}$. The density coefficient $\rho_{\rm e}$is determined with the envelope mass $M_{\rm env}$. We applied a gas-to-dust mass ratio of 160, which is often used for oxygen-rich evolved stars (Knapp 1985). The model geometry is viewed at a viewing angle $\theta_{\rm view}$ measured from pole-on. The free parameters and their ranges are an  $R_{\rm in}$ of 30, 50, and 100 $R_\star$; H of 0.2, 0.3, and 0.4; $M_{\rm env}$ of 2, 4, 6, and 8 $M_{\odot}$; and $\theta_{\rm view}$ of 65$^\circ$, 55$^\circ$, and 45$^\circ$.

For the dust grains, we simplify the model as much as possible to focus on determining the grain sizes which characterize the optical properties of the dust the most. In our modeling, we assume spherical cores with a mantle and an MRN-like size distribution of $0.005~\mu$m  $\le a\le a_{\rm max}~\mu$m with $n\left(a\right)\propto a^{-3.5}$ (Mathis et al. 1977). The $a_{\rm max}$values are different for the disk and the envelope. The chemical compositions of the core and the mantle are astronomical silicate (Draine 1985) and crystalline water ice (Bertie et al. 1969), respectively. The water ice mantle is assumed to have a constant thickness proportional to the core radius, which is determined with a volume fraction of the water ice to the grain core $f_{\rm m}$. This value is chosen to be 0.2 which fits the 3 $\mu $m water ice absorption feature. The grain size in the lobe was estimated from the polarization values in the lobe, because the NIR polarization strongly depends on the grain size in cases of submicron size. In our NICMOS2 data, the 2 $\mu $m polarization is P=40-50% in the upper lobe and P=50-55% in the lower lobe. With a large inclination angle of $35\hbox{$^\circ$ }$, which is expected from CO observations, the calculated polarization becomes too low in the upper lobe and too high in the lower lobe. The average polarization between the upper and lower lobes for the $a_{\rm max}$ of 0.3, 0.5, and 0.7 $\mu $m are 60%, 45%, and 20%, respectively. We apply the $a_{\rm max}=0.5~\mu$m dust model in the envelope in the subsequent models. The free parameter is the $a_{\rm max}$ of the disk and the values to examine are 0.5 $\mu $m, 1.0 $\mu $m, 10.0 $\mu $m, 100.0 $\mu $m, 1000.0 $\mu $m, and 10 000.0 $\mu $m.

Table 1:   Model parameters of our radiative transfer calculations.

\begin{figure} \par\includegraphics[width=16.8cm,clip]{12674fig1.eps} \end{figure} Figure 1:

Mass density distribution of the selected model ( top left panel), dust temperature distribution ( top right panel), dust opacities as function of wavelength ( bottom left panel), and comparisons of model SEDs with observations ( bottom right panel). For the selected model, the attenuated stellar flux, thermal emission, and scattered light from the dust are also plotted with the dashed-curve, the dashed-dotted curve, and the dotted curve, respectively. The observed data are from Mermilliod & Mermilliod (1994) and USNO catalog for optical photometry, point source catalogs of 2MASS, MSX, and IRAS for infrared photometry, and ISO SWS and LWS for mid- and far-infrared spectra, respectively. In the opacity plot, the mean opacities of absorption $\kappa $, scattering $\sigma $, and extinction $\kappa +\sigma $ are indicated with dashed, dotted, and solid lines, respectively. Models with four different $a_{\max}$ values of 0.5 $\mu $m, 1.0 $\mu $m, 10.0 $\mu $m, and 1000.0 $\mu $m are compared. The $a_{\max}=0.5~\mu$m model, which is used in the superwind and AGB shells, is also presented for comparison. In the SED plots, several curves with different colors denote model results with different grain sizes ($a_{\max}$) in the disk.

Open with DEXTER

\begin{figure} \par\includegraphics[width=17.2cm,clip]{12674fig2.eps} \end{figure} Figure 2:

Model results of the intensity ( upper panels) and polarization ( bottom panels) images of M1-92 comparing with the HST/NICMOS 2 data from UMM07 ( left column). Models with grain sizes in the disk of $a_{\max}=1.0~\mu$m ( middle column) and $a_{\max}=1000.0~\mu$m ( right column) are presented to show the effects of grain sizes. In the polarization images, the polarization vector lines are also plotted.

Open with DEXTER

2.2 Result

From the aforementioned parameter sets, we selected a good model with the following parameters: $R_{\rm in}=30~R_\star$, H=0.3, $R_{\rm disk}=4500$ AU, $M_{\rm env}=4~M_{\odot}$, $R_{\rm out}=30\hbox{$^{\prime\prime}$ }$, $\theta_{\rm view}=55\hbox{$^\circ$ }$, and $a_{\rm max}=1000.0~\mu$m. These are summarized in Table 1.

The top panels of Fig. 1 show the cross section of the mass density distribution and the dust temperature distribution. As seen in the mass density distribution map, the superwind shell has a waterlily petal-shaped appearance. In the dust temperature distribution map, intermediate to high temperature components ( $T_{\rm d}\ga100$ K) are seen in the innermost low-density polar region. The rim of the superwind and AGB lobes has a low temperature of $\la$70 K, which characterizes the flux in the far-infrared (FIR) or longer wavelengths.

The bottom panels of Fig. 1 show the opacity (i.e. the size-averaged cross section per particle mass) of the modeled dust and the SEDs. To show the effect of grain sizes, we also present other dust models with $a_{\rm max}=1.0~\mu$m and $a_{\rm max}=10.0~\mu$m for comparison. In the opacity plot, the difference of the wavelength dependence for different dust models is clearly visible. As $a_{\rm max}$ increases, (1) the wavelength where the opacity drops becomes longer and (2) the strengths of water ice and silicate features become weaker. The SED plot compares the model results of different grain sizes of $a_{\rm max}=1.0~\mu$m, 10.0 $\mu $m, and 1000.0 $\mu $m to the observations. The model SEDs reproduce the water ice features at 3 $\mu $m, 44 $\mu $m, and 62 $\mu $m and the silicate features at 9.7 $\mu $m and 18 $\mu $m. Because the disk temperature is higher than the temperature of the superwind and AGB shells, in principle, the grain-size effect appears in the mid-infrared (MIR) flux, and it is possible to constrain the grain size by SED fit. On the longer wavelength side, the difference in the SED appears only for $\lambda\la50~\mu$m.

Figure 2 shows the model results of the intensity images (top panels) and polarization images (bottom panels). The results of two different dust models of $a_{\rm max}=1.0~\mu$m (middle column) and $a_{\rm max}=1000.0~\mu$m (right column) are compared with the observation (left column). The intensity images reproduce a waterlily petal-shaped bipolar appearance reasonably well. In the polarization images, the difference of the polarization values between the upper and lower lobes is too strong, as mentioned before. With respect to the effect of the grain size, we do not find any sufficient difference from our results.

Hence, it is difficult to determine the grain size in the disk of M 1-92 from the SED, intensity image, and polarization image, which we used in our modeling. The reason is explained as follows. The MIR flux F from the disk is approximately proportional to $M_{\rm disk}\kappa\left(a\right)$. Based on our assumption of a constant optical depth of the disk for different grain models, the optical depth $\tau$ is proportional to $M_{\rm disk}\left(\kappa\left(a\right)+\sigma\left(a\right)\right)$. Therefore, we obtain $F\propto \tau \kappa\left(a\right)\!/\!\left(\kappa\left(a\right)+\sigma\left(a\right)\right)$. For grain models with $a_{\rm max}>10~\mu$m, the $\kappa\left(a\right)\!/\!\left(\kappa\left(a\right)+\sigma\left(a\right)\right)$value becomes nearly constant. With the similar reason, the wavelength dependence of the dust scattering matrix elements become low in large grains, resulting that the effect of the grain size does not appear much in polarization images in the optical to NIR. Thus, the presence of large grains are examined often using a spectral index of dust opacity $\beta$ in longer wavelengths, i.e. the submillimeter and millimeter wavelength ranges (e.g. Jura et al. 1997). In objects with large grains in the disks, the spectral slopes of the flux in these wavelength ranges are shallower due to lower $\beta$ values (e.g. Draine 2006). However, since F and $\tau$ depend on the disk mass, if the disk mass is determined by other means, the grain size can be constrained. Bujarrabal et al. (1998b) obtained $\sim$ $1\hbox{$^{\prime\prime}$ }$ resolution images of M 1-92 in the 13CO J=2-1 emission line and an estimate of a gas disk mass of 0.2 $M_{\odot}$ (see also Alcolea et al. 2007). The calculated disk masses in our modeling are 0.022, 0.0098, 0.017, 0.049, 0.15, and 0.47 $M_{\odot}$ for dust models of $a_{\rm max}=0.5$, 1.0, 10.0, 100.0, 1000.0, and 10 000.0 $\mu $m, respectively. We find that the $a_{\rm max}=1000.0~\mu$m model provides the best estimate. However, facts such as the gas-to-dust mass ratio, a region that is considered to be the disk, and the dust size distribution can lead some uncertainties in the total disk mass. For example, the gas-to-dust mass ratio, which we adopted in our model is estimated from a number of mass-losing oxygen-rich giant stars (Knapp 1985). The value of individual objects varies with a factor of $\sim$2 in general (see also Olofsson et al. 1993). In a special case of objects with a long-lived disk, this value can be $\sim$0.01 times lower (Jura & Kahane 1999). It is not clear whether M 1-92 has such an extra ordinarily low value or not. However, the calculated disk mass is at least unlikely to be significantly higher than the aforementioned values. With models with small grains (micron size or smaller) in the disk, it is hard to explain the estimated CO disk mass. Taking into account the possible uncertainty by a factor of $\sim$2 in the gas-to-dust mass ratio, we conclude that dust in the M 1-92 disk is significantly larger than in the envelope and the $a_{\rm max}$ value is expected to be larger than $100.0~\mu$m.

3 Discussion

3.1 Grain size

For the last 20 years, grain growth in AGB stars and PPNs has been studied and several observational evidences has been reported. Of these, a particular interest to us lies in a series of studies in carbon stars that show silicate dust features such as the Red Rectangle, BM Gem, V 778 Cyg, and AC Her. In this class of objects, the dual chemistry is explained by the presence of a disk, in which oxygen-rich dust is stored (Barnbaum et al. 1991; Lloyd Evans 1990; Waters et al. 1998, and references therein). In fact, some observations have detected disk-like motions in CO emission line observations (e.g.  Fong et al. 2006; Kahane et al. 1998) and a spatially resolved Keplerian rotating motion in the Red Rectangle (Bujarrabal et al. 2005,2003). If such disks live for a long time, dust particles can coagulate by grain-grain collision and grow in size (Yamamura et al. 2000; Jura et al. 2000b). More recently, aforementioned evidence has been also found even in some single chemistry systems. For example, de Ruyter et al. (2006) found flux excesses in $\lambda\ga2.0~\mu$m in their 51 post-AGB stars which are known to have binary companions. These infrared excesses indicate small inner radii of dust structures, which are kept closer to the star due to their rotating motion of the disk rather than their expanding motion. They conclude that presence of disks are common phenomenon in binary post-AGB stars. Evidence for large grains has also been found in some PPNs such as AFGL 2688 (Jura et al. 2000a), IRAS 17150-3224 (Meixner et al. 2002), IRAS 18276-1431 (Sánchez Contreas et al. 2007), IRAS 19475+3119 (Sahai et al. 2007), IRAS 22036+5306 (Sahai et al. 2008), and IRAS 22272+5435 (Ueta et al. 2001) including our result of M 1-92. Fong et al. (2006) performed a survey observation of gas phase kinematics of 38 AGBs to PNs, which include some of aforementioned objects. The objects with evidence of grain growth, except IRAS 22272+5435 (and IRAS 19475+3119), have a disk-like motion or a bipolar appearance in the optical and NIR images and their initial masses are expected to be higher than those of spherical and elliptic PPNs and PNs with expanding motions (outflow) instead of rotating motions (disk) (Meixner et al. 2002; Corradi & Schwarz 1995). It is obvious that grain growth is affected by factors such as disk geometries, kinematics of the disk, evolution of the stellar system (i.e. duration time of the dust processes), and the stellar masses. Previous work has provided qualitative evaluations to determine if large grains exist or not and if a disk-like structure exist or not to explore the possibility of the disk hypothesis and grain growth. Future work should probably be focused on more qualitative, direct discussions on the disk hypothesis. For this purpose, a more systematic and self consistent analysis are required to estimate the physical parameters of the disk and dust.

\begin{figure} \par\includegraphics[width=12cm,clip]{12674fig3.eps} \end{figure} Figure 3:

Model results of thermal emission images. The top and bottom panels show images at the wavelength of 10.0 $\mu $m and 100.0 $\mu $m, and left and right columns correspond to dust models of $a_{\rm max}=1.0~\mu$m and $a_{\rm max}=1000.0~\mu$m in the disk, respectively. Each image is convolved with a Gaussian function with a 0 $.\!\!^{\prime\prime}$3 FWHM.

Open with DEXTER

With respect to dust, the presence of large dust grains in the nebulae is also intriguing. Optical to NIR imaging polarimetry offers a great advantage in this issue. In polarimetric images of circumstellar dust shells around AGB and post-AGB stars, a centro-symmetrically aligned polarization vectors are seen. If the dust shell geometry and the chemical composition of the dust are known, the degree of polarization would provide a good estimate of the grain size. Particularly, in an optically thin regime where most light from the central star is scattered only once by dust in the nebula, the upper limit can be provided (e.g. Pendleton et al. 1990; Dougados et al. 1990). It is possible to obtain a rough estimate even from a single wavelength data, under some circumstances, which is an advantage of polarimetric images compared to intensity images, visibility data, and SEDs. In most cases including our sample, intermediate to high polarizations ($P\ge20$%) in the NIR are detected and indicate submicron sizes in the shell. The dust in nebulae in large distances from the central star is thought to be ejected in the AGB mass-loss wind with mainly expanding motions instead of orbiting motions around the central stars. Thus, these grains are not expected to undergo physical processes such as grain-grain collision and ice formation on the grain core much. Thus, dust in this region is likely to preserve the original size distribution, which is determined in the dust formation process, as explained by the dust formation and stellar wind theories (e.g. Höfner 2008; Gautschy-Loidl et al. 2004). In previous observations, we did not find any significant difference in dust sizes or at least in the polarization values in various object classes (e.g. Jura 1996, UMM07). It appears that the initial mass of the stars (or the luminosity) and the chemical composition of the stellar system (i.e. oxygen-rich or carbon-rich) do not affect the dust particle size in the dust formation much.

3.2 Thermal emission images

In this section, we present some model images in the MIR and FIR. As is expressed in the radiative transfer theory, flux from objects in these wavelength regions (thermal emission regime) is characterized by a combination of the dust temperature and density distributions and the dust absorptive opacity, while optical and NIR fluxes are governed by scattered light. It is worth to take multiple wavelength data into account, which is based on different physics, to better constrain the model parameters. Unfortunately, observed images of M 1-92 in the MIR and FIR are not publicly available at this time. Thus, we use the model results to predict what we see in the nebulosity and what parameters can be constrained.

Figure 3 shows $\lambda=10.0~\mu$m and 100.0 $\mu $m images (top and bottom panels, respectively) of our selected model results with different grain populations of $a_{\rm max}=1.0~\mu$m and 1000.0 $\mu $m in the disk (left and right panels, respectively). In the 10.0 $\mu $m images, the surface brightness of the nebulosity is fainter by a factor of <10-5than the peak surface brightness of the central source. On the other hand, these are comparable in the 100.0 $\mu $m images. We find a clear correlation between the model images and the dust temperature and density distribution maps (Fig. 1). The appearance of the bright central source in the 10.0 $\mu $m images is due to the presence of a warm ($T\ga300$ K), high-density dust region (i.e. inner part of the disk). In fact, such results were also reproduced by previously reported modeling (e.g. Meixner et al. 2002; Ueta & Meixner 2003; Lopez et al. 2000). As explained in detail in these previous papers, in the bipolar case, i.e. optically thick case at a given wavelength, the inner part and polar region of the dust shell are heated well. Taking into account the dust density, MIR photons are mainly emitted from a central, compact region, but only a little from an envelope far from the central star. We illustrate the effect of dust temperature in the 100.0 $\mu $m images by comparing with the 10.0 $\mu $m images. As is expected in the radiative transfer theory, FIR photons are emitted more efficiently from cold dust ($T\sim30$ K) than warm dust. In the other words, a longer wavelength image traces generally more of the outer region. Therefore, in spite of a high density in the disk, the central source is faint in this wavelength. In contrast, the superwind shell, where cold dust exists, becomes brighter. In terms of the total flux, i.e. the flux seen in the SED plot, the total mass of the geometry components are also important because the flux is proportional to the dust mass. The estimated mass of the superwind shell is 2.6 $M_{\odot}$, which is much higher than the disk mass of 0.15 $M_{\odot}$. The FIR flux is governed much more by the flux from the superwind than the disk. The FIR data is useful for additional constraining of the dust mass of the superwind and AGB wind shell; however, it is unrealistic to probe the detailed structure using the present imagers because of a limitation of angular resolutions (a few arcsec).

The surface brightness of the central source would be useful to constrain the grain sizes in the disk. The 10.0 $\mu $m images show a brighter central source in the $a_{\rm max}=1000.0~\mu$m dust model than in the $a_{\rm max}=1.0~\mu$m dust model. As seen in Fig. 1, the 10 $\mu $m silicate feature (or opacity) becomes weaker in larger grains than in smaller grains. This results in lower extinction in larger grains. However, the wavelength dependence of the dust opacity becomes similar for large grains. In reality, we do not expect sufficient accuracy to determine the grain size with observed MIR/FIR images, if the $a_{\rm max}$ value exceeds $\sim$10.0 $\mu $m. Another possible method, besides the one we proposed in this paper, is to use the flux excess in the submillimeter and millimeter wavelengths. In these wavelength ranges, the flux from the superwind shell decreases by an order compared to FIR flux, as is expected in the SED, but flux from the disk does less if the dust in the disk is sufficiently grown in size (the spectral opacity index $\beta<1$). In further works, one can perform high angular resolution imaging in these wavelegnth ranges to better constrain the grain sizes and disk masses.

4 Conclusion

We performed two-dimensional radiative transfer modeling of the dust shells of the bipolar PPN M 1-92. Our modeling applied geometries with a disk and bipolar envelope surrounded by an AGB wind shell, each of which has different dust characteristics. The model parameters were constrained by comparing them with the previously observed SEDs, the intensity and polarization images from the HST NICMOS 2 archived data (UMM07), and a previous radio observation in the CO emission line (Alcolea et al. 2007; Bujarrabal et al. 1998b). With a waterlily-shaped hollow envelope, the bright bipolar lobes of M 1-92 were reproduced. For the dust sizes, we found submicron-sized grains ( $a_{\rm max}=0.5~\mu$m) in the bipolar lobes. The dust size in the disk was constrained with the disk mass, which was estimated from the CO emission line data. We obtained $a_{\rm max}=1000.0~\mu$m. Although this estimate includes some uncertainties in the gas-to-dust mass ratio, the grain size distribution, and the geometry of the region considered to be the disk, an $a_{\rm max}\la100.0~\mu$m is hard to explain the disk mass and a significantly large size of >$100.0~\mu$m is expected. We conclude that grain growth is likely to occur in the M 1-92 disk. Further works including submillimeter and millimeter wavelength imaging and photometry would provide better interpretations on grain growth. The small grains in the bipolar lobes are consistent with results of many other AGB and PPNs, suggesting that dust formed by AGB mass loss has a similar size, which does not depend on the object much. The formation of such submicron-sized dust is explained with dust formation and stellar wind theories. The presence of large grains in the disk should be explained with another mechanism, which is probably the long-lived disk hypothesis. The grain growth possibly depends on the disk geometry and the stellar temperature. Better understanding will be provided if a detailed systematic analysis is made for many other samples.

References

  1. Alcolea, J., Neri, R., & Bujarrabal, V. 2007, A&A, 468, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Arrieta, A., Torres-Peimbert, S., & Georgiev, L. 2005, ApJ, 623, 252 [NASA ADS] [CrossRef] [Google Scholar]
  3. Balick, B. 1987, AJ, 94, 671 [NASA ADS] [CrossRef] [Google Scholar]
  4. Balick, B., & Frank, A. 2002, ARA&A, 40, 439 [NASA ADS] [CrossRef] [Google Scholar]
  5. Barnbaum, C., Morris, M., Likkel, L., & Kastner, J. H. 1991, A&A, 251, 79 [NASA ADS] [Google Scholar]
  6. Bertie, J. E., Labbé, H. J., & Whalley, E. 1969, J. Chem. Phys., 50, 4501 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bjorkman, J. E., & Cassinelli, J. P. 1993, ApJ, 409, 429 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bond, H. E., & Livio, M. 1990, ApJ, 355, 568 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bujarrabal, V., Alcolea, J., Sahai, R., et al. 1998a, A&A, 331, 361 [NASA ADS] [Google Scholar]
  10. Bujarrabal, V., Alcolea, J., & Neri, R. 1998b, ApJ, 504, 915 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bujarrabal, V., Neri, R., Alcolea, J., & Kahane, C. 2003, A&A, 409, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bujarrabal, V., Castro-Carrizo, A., Alcolea, J., & Neri, R. 2005, ApJ, 441, 1031 [Google Scholar]
  13. Cohen, M., & Kuhi, L. V. 1977, ApJ, 213, 79 [NASA ADS] [CrossRef] [Google Scholar]
  14. Corradi, R. L. M., & Schwarz, H. E. 1995, A&A, 293, 871 [NASA ADS] [Google Scholar]
  15. de Ruyter, S., van Winckel, H., Maas, T., et al. 2006, A&A, 448, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Dougados, C., Rouan, D., Lacombe, et al. 1990, A&A, 227, 437 [NASA ADS] [Google Scholar]
  17. Draine, B. T. 1985, ApJS, 57, 587 [NASA ADS] [CrossRef] [Google Scholar]
  18. Draine, B. T. 2006, ApJ, 636, 1114 [NASA ADS] [CrossRef] [Google Scholar]
  19. Eiroa, C., & Hodapp, K.-W. 1989, A&A, 223, 271 [NASA ADS] [Google Scholar]
  20. Fischer, O., Henning, Th., & Yorke, H. W. 1996, A&A, 308, 863 [NASA ADS] [Google Scholar]
  21. Fong, D., Meixner, M., Sutton, E. C., et al. 2006, ApJ, 652, 1626 [NASA ADS] [CrossRef] [Google Scholar]
  22. Frank, A. 1995, AJ, 110, 2457 [NASA ADS] [CrossRef] [Google Scholar]
  23. Gautschy-Loidl, R., et al. 2004, A&A, 422, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Gledhill, T. M. 2005, MNRAS, 356, 883 [NASA ADS] [CrossRef] [Google Scholar]
  25. Höfner, S. 2008, A&A, 491, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Jura, M. 1996, ApJ, 472, 806 [NASA ADS] [CrossRef] [Google Scholar]
  27. Jura, M., & Kahane, C. 1999, ApJ, 521, 302 [NASA ADS] [CrossRef] [Google Scholar]
  28. Jura, M., Turner, J., & Balm, S. P. 1997, ApJ, 474, 741 [NASA ADS] [CrossRef] [Google Scholar]
  29. Jura, M., Turner, J. L., van Dyk, S., & Knapp, G. R. 2000a, ApJ, 528, L105 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  30. Jura, M., Chen, C., & Werner, M. W. 2000b, ApJ, 541, 264 [NASA ADS] [CrossRef] [Google Scholar]
  31. Jura, M., Webb, R. A., & Kahane, C. 2001, ApJ, 550, L71 [NASA ADS] [CrossRef] [Google Scholar]
  32. Kahane, C., Barnbaum, C., Uchida, K., et al. 1998, ApJ, 500, 466 [NASA ADS] [CrossRef] [Google Scholar]
  33. Knapp, G. R. 1985, ApJ, 293, 273 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kwok, S. 1982, ApJ, 258, 280 [NASA ADS] [CrossRef] [Google Scholar]
  35. Kwok, S., Purton, C. R., & Fitzgerald, P. M. 1978, ApJ, 219, L125 [NASA ADS] [CrossRef] [Google Scholar]
  36. Livio, M., Salzman, J., & Shaviv, G. 1979, MNRAS, 188, 1 [NASA ADS] [Google Scholar]
  37. Lloyd Evans, T. 1990, MNRAS, 243, 336 [NASA ADS] [Google Scholar]
  38. Lopez, B., & Perrin, J. M. 2000, A&A, 354, 657 [NASA ADS] [Google Scholar]
  39. Manchado, A., Stanghellini, L., & Guerrero, M. A. 1996, ApJ, 466, L95 [NASA ADS] [CrossRef] [Google Scholar]
  40. Mastrodemos, N., & Morris, M. 1998, ApJ, 497, 303 [NASA ADS] [CrossRef] [Google Scholar]
  41. Mastrodemos, N., & Morris, M. 1999, ApJ, 523, 357 [NASA ADS] [CrossRef] [Google Scholar]
  42. Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
  43. Matt, S., Balick, B., Winglee, R., & Goodson, A. 2000, ApJ, 545, 965 [NASA ADS] [CrossRef] [Google Scholar]
  44. Mauron, N., & Huggins, P. J. 2006, A&A, 452, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Meixner, M., Ueta, T., Dayal, A., et al. 1999, ApJS, 122, 221 [NASA ADS] [CrossRef] [Google Scholar]
  46. Meixner, M., Ueta, T., Bobrowsky, M., & Speck, A. 2002, ApJ, 571, 936 [NASA ADS] [CrossRef] [Google Scholar]
  47. Mermilliod, J.-C., & Mermilliod, M. 1994, Catalog of mean UBV data on stars (New York: Springer-Verlag) [Google Scholar]
  48. Minkowski, R. 1946, PASP, 58, 305 [NASA ADS] [CrossRef] [Google Scholar]
  49. Morris, M. 1981, ApJ, 249, 572 [NASA ADS] [CrossRef] [Google Scholar]
  50. Morris, M. 1987, PASP, 99, 1115 [NASA ADS] [CrossRef] [Google Scholar]
  51. Murakawa, K., Suto, H., Oya, S., et al. 2005, A&A, 436, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Murakawa, K., Nakashima, J., Ohnaka, K., & Deguchi, S. 2007, A&A, 470, 957 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Murakawa, K., Ohnaka, K., Driebe, T., et al. 2008a, A&A, 489, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Murakawa, K., Preibisch, T., Kraus, S., & Weigelt, G. 2008b, A&A, 490, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Olofsson, H., Eriksson, K., Gustafsson, B., & Carlstrom, U. 1993, ApJS, 87, 267 [NASA ADS] [CrossRef] [Google Scholar]
  56. Oppenheimer, B. D., Bieging, J. H., Schmidt, G. D., et al. 2005, ApJ, 624, 957 [NASA ADS] [CrossRef] [Google Scholar]
  57. Pascoli, G., Leclercq, J., & Poulain, B. 1992, PASP, 104, 182 [NASA ADS] [CrossRef] [Google Scholar]
  58. Pendleton, Y. J., Tielens, A. G. G. M., & Werner, M. W. 1990, ApJ, 349, 107 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  59. Sahai, R., & Trauger, J. T. 1998, AJ, 116, 1357 [NASA ADS] [CrossRef] [Google Scholar]
  60. Sahai, R., Sánchez Contreras, C., Morris, M., & Claussen, M. 2007, ApJ, 658, 410 [NASA ADS] [CrossRef] [Google Scholar]
  61. Sahai, R., Young, K., Patel, N., Sánchez Contreras, C., & Morris, M. 2008, Ap&SS, 313, 241 [NASA ADS] [CrossRef] [Google Scholar]
  62. Sánchez Contreas, C., Le Mignant, D., Sahai, R., et al. 2007, ApJ, 656, 1150 [NASA ADS] [CrossRef] [Google Scholar]
  63. Scarrott, S. M., & Scarrott, R. M. J. 1995, MNRAS, 277, 277 [NASA ADS] [Google Scholar]
  64. Soker, N. 1990, AJ, 90, 1869 [NASA ADS] [CrossRef] [Google Scholar]
  65. Soker, N. 1992, ApJ, 389, 628 [NASA ADS] [CrossRef] [Google Scholar]
  66. Soker, N. 1997, ApJS, 112, 487 [NASA ADS] [CrossRef] [Google Scholar]
  67. Soker, N., & Clayton, G. C. 1999, MNRAS, 307, 993 [NASA ADS] [CrossRef] [Google Scholar]
  68. Soker, N., & Livio, M. 1994, ApJ, 421, 219 [NASA ADS] [CrossRef] [Google Scholar]
  69. Soker, N., & Rappaport, S. 2000, ApJ, 538, 241 [NASA ADS] [CrossRef] [Google Scholar]
  70. Stanghellini, L., Corradi, R. L. M., & Schwarz, H. E. 1993, A&A, 276, 463 [NASA ADS] [Google Scholar]
  71. Su, K. Y. L., Hrivnak, B. J., Kwok, S., & Sahai, R. 2003, AJ, 126, 848 [Google Scholar]
  72. Toomre, A. 1982, ApJ, 259, 535 [NASA ADS] [CrossRef] [Google Scholar]
  73. Trammell, S. R., & Goodrich, R. W. 1996, ApJ, 468, L107 [NASA ADS] [CrossRef] [Google Scholar]
  74. Ueta, T., & Meixner, M. 2003, ApJ, 586, 1338 [NASA ADS] [CrossRef] [Google Scholar]
  75. Ueta, T., Meixner, M., & Bobrowsky, M. 2000, ApJ, 528, 861 [NASA ADS] [CrossRef] [Google Scholar]
  76. Ueta, T., Meixner, M., Hinz, P. M., et al. 2001, ApJ, 557, 831 [NASA ADS] [CrossRef] [Google Scholar]
  77. Ueta, T., Murakawa, K., & Meixner, M. 2005, AJ, 129, 1625 [NASA ADS] [CrossRef] [Google Scholar]
  78. Ueta, T., Murakawa, K., & Meixner, M. 2007, AJ, 133, 1345 [NASA ADS] [CrossRef] [Google Scholar]
  79. Waters, L. B. F. M., Cami, J., de Jong, T., et al. 1998, Nature, 391, 868 [NASA ADS] [CrossRef] [Google Scholar]
  80. Yamamura, I., Dominik, C., de Jong, T., et al. 2000, A&A, 363, 629 [NASA ADS] [Google Scholar]
  81. Zuckerman, B., & Aller, L. H. 1986, ApJ, 301, 772 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1:   Model parameters of our radiative transfer calculations.

All Figures

  \begin{figure} \par\includegraphics[width=16.8cm,clip]{12674fig1.eps} \end{figure} Figure 1:

Mass density distribution of the selected model ( top left panel), dust temperature distribution ( top right panel), dust opacities as function of wavelength ( bottom left panel), and comparisons of model SEDs with observations ( bottom right panel). For the selected model, the attenuated stellar flux, thermal emission, and scattered light from the dust are also plotted with the dashed-curve, the dashed-dotted curve, and the dotted curve, respectively. The observed data are from Mermilliod & Mermilliod (1994) and USNO catalog for optical photometry, point source catalogs of 2MASS, MSX, and IRAS for infrared photometry, and ISO SWS and LWS for mid- and far-infrared spectra, respectively. In the opacity plot, the mean opacities of absorption $\kappa $, scattering $\sigma $, and extinction $\kappa +\sigma $ are indicated with dashed, dotted, and solid lines, respectively. Models with four different $a_{\max}$ values of 0.5 $\mu $m, 1.0 $\mu $m, 10.0 $\mu $m, and 1000.0 $\mu $m are compared. The $a_{\max}=0.5~\mu$m model, which is used in the superwind and AGB shells, is also presented for comparison. In the SED plots, several curves with different colors denote model results with different grain sizes ($a_{\max}$) in the disk.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17.2cm,clip]{12674fig2.eps} \end{figure} Figure 2:

Model results of the intensity ( upper panels) and polarization ( bottom panels) images of M1-92 comparing with the HST/NICMOS 2 data from UMM07 ( left column). Models with grain sizes in the disk of $a_{\max}=1.0~\mu$m ( middle column) and $a_{\max}=1000.0~\mu$m ( right column) are presented to show the effects of grain sizes. In the polarization images, the polarization vector lines are also plotted.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12cm,clip]{12674fig3.eps} \end{figure} Figure 3:

Model results of thermal emission images. The top and bottom panels show images at the wavelength of 10.0 $\mu $m and 100.0 $\mu $m, and left and right columns correspond to dust models of $a_{\rm max}=1.0~\mu$m and $a_{\rm max}=1000.0~\mu$m in the disk, respectively. Each image is convolved with a Gaussian function with a 0 $.\!\!^{\prime\prime}$3 FWHM.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.