EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 510 (February 2010) A&A, 510 (2010) A68 Full HTML
Free Access
Issue
A&A
Volume 510, February 2010
Article Number A68
Number of page(s) 9
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/200912081
Published online 11 February 2010
A&A 510, A68 (2010)

The baryonic content and Tully-Fisher relation at z 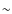$\sim $ 0.6

M. Puech - F. Hammer - H. Flores - R. Delgado-Serrano - M. Rodrigues - Y. Yang

GEPI, Observatoire de Paris, CNRS, University Paris Diderot, 5 Place Jules Janssen, 92190 Meudon, France

Received 16 March 2009 / Accepted 18 November 2009

Abstract
Context. Using the multi-integral-field spectrograph GIRAFFE at VLT, we previsouly derived the stellar-mass Tully-Fisher Relation (smTFR) at $z \sim 0.6$ for a representative sample of 63 emission-line galaxies. We found that the distant relation is systematically offset by roughly a factor of two toward lower masses from the local relation.
Aims. We extend the study of the evolution of the TFR by establishing the first distant baryonic TFR in a CDFS subsample of 35 galaxies. We also investigate the underlying cause of the large scatter observed in these distant relations.
Methods. To derive gas masses in distant galaxies, we estimate a gas radius and invert the Schmidt-Kennicutt law between star formation rate and gas surface densities. We consider the influence of velocity dispersion on the scatter of the relation, using the kinematic tracer S suggested by Kassin and collaborators.
Results. We find that gas extends farther out than the UV light from young stars, a median of $\sim $30%. We present the first baryonic TFR (bTFR) ever established at intermediate redshift and show that, within an uncertainty of $\pm$0.08 dex, the zeropoint of the bTFR does not appear to evolve between $z \sim 0.6$ and z = 0. On the other hand, we confirm that the difference between the local and distant smTFR is significant, even considering random and systematic uncertainties, and that accounting for velocity dispersion leads to a significant decrease in the scatter of the distant relation.
Conclusions. The absence of evolution in the bTFR over the past 6 Gyr implies that no external gas accretion is required for distant rotating disks to sustain star formation until z = 0 and convert most of their gas into stars. Finally, we confirm that the larger scatter found in the distant smTFR, and hence in the bTFR, is caused entirely by major mergers. This scatter results from a transfer of energy from bulk motions in the progenitors, to random motions in the remnants, generated by shocks during the merging. Shocks occurring during these events naturally explain the large extent of ionized gas found out to the UV radius in $z \sim 0.6$ galaxies. All the results presented in this paper support the ``spiral rebuilding scenario'' of Hammer and collaborators, i.e., that a large fraction of local spiral disks have been reprocessed during major mergers in the past 8 Gyr.

Key words: galaxies: evolution - galaxies: kinematics and dynamics - galaxies: high-redshift - galaxies: general - galaxies: interactions - galaxies: spiral.

1 Introduction

The stellar-mass Tully-Fisher Relation (smTFR) has received increased attention over the past decade, both at low (e.g., Bell & de Jong 2001; Pizagno et al. 2007; Meyer et al. 2008) and high redshift (Atkinson et al. 2007; Flores et al. 2006; Cresci et al. 2009; Kassin et al. 2007; Conselice et al. 2005; Puech et al. 2008). However, the smTFR does not allow us to homogeneously characterize all galaxy morphologies together. McGaugh (2000) showed that dwarf galaxies, which have a larger gas content that more massive galaxies, fall downward the smTFR. Considering the baryonic (i.e., stellar plus gas) content of galaxies, he showed that all galaxies, including dwarves, define a common TFR (see also Begum et al. 2008), which by then was dubbed the baryonic TFR (bTFR). Because the bTFR appears to hold over five decades in mass (McGaugh 2000), it can therefore be considered as being somehow more ``fundamental'' than the smTFR.

So far, the bTFR has been studied only in the local Universe (see Avila-Reese et al. 2008; Trachternach et al. 2009; Stark et al. 2009; McGaugh 2004; Bell & de Jong 2001; Geha et al. 2006; Goruvich et al. 2004; McGaugh 2005; Meyer et al. 2008; Noordermeer & Verheijen 2007; Verheijen 2001; De Rijcke et al. 2007). This was primarily because HI observations of galaxies are practically limited to z < 0.3 (Lah et al. 2007). To estimate the gas content of more distant galaxies, indirect methods were developed, such as the inversion of the Schmidt-Kennicutt (SK) law (Kennicutt 1989), which relates the gas surface and star formation rate (SFR) densities (e.g., Erb et al. 2006; Mannucci et al. 2009). Another difficulty in establishing a reliable bTFR (or even a smTFR) at high z is that it is not always very clear whether all distant samples are truly representative of the luminosity or mass function of galaxies at those epochs. At intermediate redshifts (i.e., z < 1), Flores et al. (2006) and Yang et al. (2008) assembled a representative sample of 63 $z \sim 0.6$emission-line galaxies observed by 3D spectroscopy for a project called IMAGES. The kinematics of the entire galaxy surface is probed by 3D spectroscopy, which allows us to classify them as a function of their relaxation state. Rotating Disks (RDs) are galaxies that exhibit regular rotation well-aligned along the morphological axis. Perturbed rotators (PRs) have large-scale rotation with a local perturbation in the velocity dispersion map that cannot be accounted for by rotation, while galaxies with complex kinematics (CKs) do not exhibit large-scale rotation, or have a strong misalignment between the dynamical and morphological axes (Yang et al. 2008). Using this new kinematical classification, Flores et al. (2006) showed that the larger dispersion of the distant TFR was due entirely to galaxies with non-relaxed kinematics, probably associated with mergers, as later confirmed by Puech et al. (2008, hereafter P08) as well as Kassin et al. (2007) and Covington et al. (2010). Restricting the smTFR to rotating disks (RDs), for which the TFR can be confidently established, for the first time P08 detected an evolution in zeropoint of the smTFR by 0.36 +0.21-0.06 dex between $z \sim 0.6$ and z = 0. However, $z \sim 0.6$ galaxies have a larger gas fraction than their local counterparts (i.e., $\langle f_{\rm gas} \rangle \sim 30$% at $z \sim 0.6$-0.8), as derived from the evolution of the gas-metallicity relation (Rodrigues et al. 2008). This led P08 to suggest that the bTFR, as opposed to the smTFR, might not be evolving.

In this paper, we take advantage of the representative IMAGES sample of intermediate-mass galaxies at $z \sim 0.6$ to establish the first bTFR at high redshift, using the SK inversion method. The paper is organized as follows: in Sect. 2, we present the sample and the data used in this paper; in Sect. 3, we extend the previous analysis of the smTFR by P08, obtaining new insight about its shift in zeropoint and its scatter; in Sect. 4, we estimate the gas content of intermediate-redshift galaxies and compare it to the stellar light from young stars; in Sect. 5, we establish the first bTFR at $z \sim 0.6$, which is discussed in Sect. 6. Throughout, we adopt H0 = 70 km s-1 Mpc-1, $\Omega_{\rm M} = 0.3$, and $\Omega _\Lambda=0.7$, and the AB magnitude system.

2 Data and sample

2.1 The sample

We started from the 3D sample of P08. Galaxies were selected using J-band absolute magnitudes as a proxy for stellar mass, such that $M_J \leq -20.3$, which roughly corresponds to $M_{\rm stellar}\geq 1.5\times 10^{10}~M_\odot$, using a ``diet'' Salpeter IMF and Bell et al. (2003) simplified recipes for deriving stellar mass from J-band luminosity. Additional practical constraints were imposed on their rest-frame [OII] equivalent width (i.e., $EW_0 \geq 15~\AA$) and redshift (i.e., z between 0.4 and 0.75), by observing with the multi-integral-field unit spectrograph FLAMES/GIRAFFE at the VLT. This provided a sample of 63 galaxies that represents the J-band luminosity function of galaxies at these redshifts (Yang et al. 2008). In the following, we restrict our study of the bTFR to galaxies within the CDFS (see Sect. 2.4). This sample of 35 galaxies is still representative of the luminosity function at $z \sim 0.6$ (Yang et al. 2008).

NIR photometry was derived from public images of the respective fields where galaxies were selected (i.e., CDFS, CFRS, and HDFS). Stellar masses $M_{\rm stellar}$ were estimated from $M_{\rm stellar}/L_K$ ratios using the method of Bell et al. (2003), assuming a ``diet'' Salpeter IMF. We estimated in P08 that this method, when applied to $z \sim 0.6$galaxies, provides us with estimates of the stellar mass with an associated random uncertainty of 0.3 dex, and a systematic uncertainty of -0.2 dex. We note that this comparison takes into account the influence of possible secondary bursts of star formation (Borch et al. 2006). In addition, the influence of TP-AGB stars on the derivation of stellar masses could overestimate the stellar mass by up to $\sim $0.14 dex (Pozzetti et al. 2007; Maraston et al. 2006) in a systematic way, but constant with redshift. In Hammer et al. (2009b), it is shown that the Bell et al. (2003) method, when applied to $z \sim 0.6$ galaxies, provides us with an upper limit to their stellar mass relative to the measurements determined by other stellar-population-synthesis models and IMF combinations, which is reflected by all systematic effects tending to lower these estimates. Using these stellar masses to study the TFR is therefore a quite conservative choice, leading to evolutionary trends measured being perhaps lower than in reality. We refer the reader to P08 and its Appendix for a clearer description of our adopted method, as well as Hammer et al. (2009b).

We note that the IMF used to derive stellar masses (i.e., the diet Salpeter IMF following Bell et al. 2003) differs from the IMF used in the next section to derive star formation rates (i.e., the regular Salpeter IMF). However, in Hammer et al. (2009b), we argue that stellar masses derived using Bell et al. (2003) recipes and a diet Salpeter are roughly equivalent (in a one-to-one correlation and not only in statistical sense) to stellar masses derived using the models of Bruzual & Charlot (2003) and a regular Salpeter IMF. Therefore, in the following, we make no attempt to correct for this difference in IMF, since the current generation of stellar population synthesis models is simply not accurate enough for difference caused by these two IMFs to be significant.

Compared to P08, we modified the classification of two galaxies in the sample. J033245.11-274724.0 was studied in detail by Hammer et al. (2009a), who found in HST/ACS images from the UDF a dust-enshrouded disk that had not previously been seen in GOODS images because of their shallower depth (see a comparison between GOODS and UDF images in their Fig. 1). Accounting for this disk, the dynamical axis was found to be strongly misaligned with the morphological axis. Hammer et al. (2009a) argued that the morpho-kinematic properties of J033245.11-274724.0 can only be reproduced by a major merger event. Similarly, Puech et al. (2009) carried out a detailed study of J033241.88-274853.9, whose morpho-kinematic properties also appeared to be far more closely reproduced by a major merger model than that of a simple rotating disk. Therefore, we shifted the classification of both objects from RD to CK.

2.2 Star formation rates

We estimated the total SFR $_{\rm tot}$ of each galaxy, following Puech et al. (2007b). Briefly, SFR $_{\rm tot}$ was taken to be the sum of SFR$_{\rm UV}$, derived from the 2800 Å luminosity L2800, and SFR$_{\rm IR}$, which was derived from Spitzer/MIPS photometry at 24 $\mu $m using the Chary & Elbaz (2001) calibration between rest-frame 15 $\mu $m flux and total IR luminosity $L_{\rm IR}$. To convert both $L_{\rm IR}$ and L2800 into SFRs, we used the calibrations of Kennicutt (1998), which rely on a Salpeter IMF. Uncertainties were estimated by propagating the flux uncertainty measurement using the SFR calibrations. About half of the galaxies in the sample were not detected by MIPS. In this case, we derived an upper limit to SFR$_{\rm IR}$ as a function of redshift using Fig. 9 of Le Floc'h et al. (2005). We assumed that SFR $_{\rm tot}$ is the mean of this limit and SFR$_{\rm UV}$. The corresponding uncertainty in this case is half the difference between SFR$_{\rm UV}$ and the limit to SFR$_{\rm IR}$, which infers a mean relative uncertainty of 50% for these objects (see Fig. 1 and Table 1).

\begin{figure} \par\includegraphics[width=8.5cm]{12081fg1.eps} \end{figure} Figure 1:

SFR as a function of stellar mass in a subsample of 35 CDFS galaxies. RDs are shown as blue dots, PRs as green squares, and CKs as red triangles. The open blue circle corresponds to the RD+ galaxy for which the velocity measurement is more uncertain (see P08). Uncertainties in stellar mass are discussed in Sect. 2.1, and are not shown for reasons of clarity.

Open with DEXTER

2.3 Gas mass estimates

To estimate the mass of gas within each galaxy, we used the SK relation between SFR and gas densities of Kennicutt (1989), which is given by $\Sigma _{\rm SFR}=2.5\times 10^{-4} \Sigma _{\rm gas}^{1.4}~M_\odot$/yr/kpc2. Bouché et al. (2007) derived a new calibration of the SK law, based on distant sources ( $z \sim 2{-}3$). They found that the SK law holds up to $z \sim 2.5$, but has a quite different power-law index (i.e., 1.7 instead of 1.4). For the CDFS sample, we find that $\Sigma _{\rm gas}$ ranges from 0.004 to 0.46 $M_\odot$/yr/kpc2. In this regime, the two SK laws are relatively similar, the discrepancy between the two relations being caused mostly by the higher star-formation densities found in $z \sim 2$ starbursts (see Fig. 3 of Bouché et al. 2007). This range corresponds to the star-formation densities of local (U)LIRGs, starbursts, and star-forming disks (Bouché et al. 2007). Finally, at z = 0.24, Lah et al. (2007) performed direct HI measurements of distant galaxies, and found that there is no evolution in the relation between HI mass and SFR. Therefore, we conclude that it is more appropriate to rely on the local SK law rather than the one at high-z to derive gas masses in a sample of $z \sim 0.6$ galaxies.

To do this, we first derived the SFR density $\Sigma _{\rm SFR}=SFR_{\rm total}/\pi R_{\rm gas}^2$, which was then converted into a gas density $\Sigma _{\rm gas}$ using the SK law. Gas masses were derived as $M_{\rm gas}=\Sigma _{\rm gas} \times \pi R_{\rm gas}^2$. The same radius $R_{\rm gas}$, which is defined in the next section, is assumed when normalizing both densities, following Kennicutt (1989). Uncertainties in $M_{\rm gas}$ were derived using standard methods of error propagation (see Table 1 and Fig. 2). It is noteworthy that gas masses derived this way are independent of the IMF, since the SK law and SFRs are derived using the same Salpeter IMF[*]. Gas masses and gas fractions in $z \sim 0.6$ galaxies are discussed further by Hammer et al. (2009b). Of particular interest here, is that the gas masses derived by inverting the SK law lead to a median gas fraction of 31% in $z \sim 0.6$ galaxies. We note that gas fractions, in contrast to gas masses, are not IMF independent. Strikingly, the same value is found using a completely different data set and methodology (i.e., based on the evolution of the mass-metallicity relation derived from FORS2 long-slit spectroscopy, see Rodrigues et al. 2008). It is therefore very unlikely that the gas fractions derived at $z \sim 0.6$ could be affected by any systematic effect, which makes us quite confident in our estimates of gas masses.

\begin{figure} \par\includegraphics[width=8.5cm]{12081fg2.eps} \end{figure} Figure 2:

Gas mass as a function of stellar mass in a subsample of 35 CDFS galaxies. RDs are shown as blue dots, PRs as green squares, and CKs as red triangles. The open blue circle corresponds to the RD+ galaxy for which the velocity measurement is more uncertain (see P08). Uncertainties in stellar mass are discussed in Sect. 2.1, and are not shown for reasons of clarity. The blue line represents equality between the stellar and gas masses, while the blue dashed line represents the local relation between these two quantities given by Schiminovich (2008). The median gas fraction is found to be 31%, or $M_{\rm gas}/M_{\rm stellar} = 0.45$, which is represented as a thin black line.

Open with DEXTER

Table 1:   Principle properties of the sample of 35 galaxies used in this study, in order of increasing RA (see Sect. 2.5).

\begin{figure} \par\includegraphics[width=8.5cm]{12081fg3.eps}\includegraphics[width=8.5cm]{12081fg4.eps} \end{figure} Figure 3:

Left: evolution of the stellar-mass TFR in the sample of 64 galaxies of P08 (RDs are shown as blue dots, PRs as green squares, and CKs as red triangles). The open blue circle correspond to the RD+ galaxies for which the velocity measurement is more uncertain, see P08). The two open red triangles correspond to the two galaxies that were changed from RD to CK compared to P08 (see Sect. 2.1). The black line is the local smTFR, while the blue dash-line represent a linear fit to the $z \sim 0.6$ smTFR. Left: same relation but using S. The black and blue-dashed lines are the same as in the left panel.

Open with DEXTER

2.4 [OII] gas radius estimates

To convert from density to mass, one needs to define and measure a gas radius $R_{\rm gas}$. To do this, we first constructed rest-frame UV images by summing observed B and V bands. Given that not all galaxies in the sample have homogeneous imaging (see Neichel et al. 2008), we decided to restrict the study of the bTFR to galaxies with the highest quality images. Therefore, we restricted the study of the bTFR to the subsample of 35 galaxies lying in the CDFS with HST/ACS images, which is still representative of the luminosity function at $z \sim 0.6$(Yang et al. 2008). This allowed us to limit uncertainties in the derivation of gaseous radii and therefore, gas masses.

From rest-frame UV images, we derived for each galaxy an axis ratio b/a and a PA using SExtractor (Bertin & Arnouts 1996). For each galaxy, these two parameters were used to generate a set of images with flat ellipses of increasing radii using the IDL procedure DIST_ELLIPSE. To account for the relatively coarse spatial sampling of the GIRAFFE IFU (0.52 arcsec/pix, which roughly corresponds to 3.5 kpc at $z \sim 0.6$), these high-resolution ellipses were then rebinned to the GIRAFFE pixel scale after determining as accurately as possible the position of the GIRAFFE IFU on the UV image (see, e.g., Puech et al. 2007b). These simulated [OII] GIRAFFE images were renormalized in terms of flux using the observed IFU-integrated [OII] value, and pixels with a resulting flux lower than the minimal [OII] flux detected within the GIRAFFE IFU for a given galaxy were disregarded, to account for GIRAFFE IFU pixels being selected in terms of signal-to-noise ratio (i.e., $S/N \geq 3$, see Flores et al. 2006). By identifying the simulated [OII] map that most closely reproduces the observed one, it is in principle possible to retrieve the underlying [OII] total-light radius. However, the exact position of the IFU, as well as the precise value of the seeing during the observations are subject to uncertainties (e.g., Puech et al. 2007b,2008) that prevent us from being able to determine the exact position of the IFU grid. The relatively coarse spatial resolution of the GIRAFFE IFU also makes it relatively difficult to retrieve precisely the underlying [OII] flux distribution. To mitigate the uncertainty associated with these effects, we did not use a classical chi-square minimization between the simulated and observed [OII] maps, but used a spatial cross-correlation to determine, for each galaxy, the subset of simulated [OII] maps that maximizes the number of pixels illuminated in both the observed and simulated [OII] maps. This subset of simulated maps corresponds to a range of ellipse radii that are deconvolved from the GIRAFFE coarse spatial sampling. We assumed that the mean value of this range is a measure of the total [OII] radius $R_{[{\rm OII}]}$, whose error-bars are equal to half this range. Finally, $R_{[{\rm OII}]}$ were quadratically deconvolved from a 0.8 arcsec mean seeing disk. The maximal value of the ratio of the errorbars to the corresponding radii is found to be 51%, while their distribution shows an average of 17% and a 1-$\sigma$ spread of 12%. The derived radii and errorbars in kpc are shown in Fig. 4 and listed in Table 1.

\begin{figure} \par\includegraphics[width=8.7cm]{12081fg5.eps} \end{figure} Figure 4:

Comparison between the [ OII] and UV radii for the CDFS sub-sample of galaxies. The two insets on the left (30-arcsec wide) show MIPS imaging at 24 $\mu $m of J033228.48-274826.6 ( upper one) and J033244.20-274733.5, while the two insets on the right show z-band HST/ACS images of J033230.78-275455.0 and J033226.23-274222.8 superimposed with the GIRAFFE IFU grid. RDs are shown as blue dots, PRs as green squares, and CKs as red triangles. The open blue circle corresponds to the RD+ galaxy for which the velocity measurement is more uncertain (see P08).

Open with DEXTER

3 Evidence that major mergers are responsible for the large scatter in the distant TFR

3.1 The z 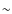$\sim $ 0.6 stellar-mass TFR

The smTFR in the IMAGES sample was initially derived in P08 (see their Appendix). We show in Fig. 3 (see left panel) a revised version of this relation, in which the classification of two objects has changed (see Sect. 2). We also show here all galaxies, including non-relaxed ones. The dispersion in this relation was shown to be caused entirely by non-relaxed systems by P08 (see next section). Maintaining the slope at its local value, we found a shift in the smTFR zeropoint of 0.34 +0.21-0.06 dex in stellar mass, or, equivalently, of $\sim $0.12 dex in velocity, between $z \sim 0.6$ and z = 0, consistent with the shift derived by P08. The errorbars account for possible systematic effects, which were quantified in detail by P08. Most of them are associated with the estimation of stellar mass. As we noted in Sect. 2.1, all these effects would tend to decrease the estimates of the stellar mass in $z \sim 0.6$ galaxies, since we ``maximized'' them by adopting the Bell et al. (2003) method. The only systematic effects that could reduce the shift in zeropoint are relatively insignificant (i.e., -0.06 dex), and are associated with the derivation of rotation velocities (see P08). In P08, we found that the shift of the smTFR with redshift cannot be interpreted as a pure evolution along the velocity axis, and that only half, at most, could be accounted for by a velocity shift caused by gas accretion within the optical radius. We then concluded that most of the shift in the smTFR reflects an increase in stellar mass in rotating disks over the past 6 Gyr.

Koen & Lombard (2009) performed a permutation test to demonstrate that the distant K-band TFR found by P08 was offset significantly from the local relation. We repeated their analysis for the smTFR and found a probability $\ll$1% that the two relations have identical slope and zeropoint. To test the reliability of this result in terms of systematic uncertainties, we shifted the distant smTFR in steps of 0.01 dex in stellar mass toward the local relation and repeated the permutation test. We found that for this probability to exceed 10% we would need to bias the stellar mass in the distant sample by +0.28 dex, which exceeds systematic uncertainties (see above). This means that, within the systematic effects on the zeropoint shift identified by P08, the two relations differ significantly, which secures the results of P08.

3.2 Origin of the scatter in the z 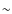$\sim $ 0.6 smTFR

In Flores et al. (2006), we showed that the dispersion in the $z \sim 0.6$smTFR was caused by non-relaxed galaxies. This result was confirmed by P08, who showed that the dispersion in the distant smTFR, once restricted to RDs (i.e., 0.12 dex), was similar to that in the local relation, with 0.15 dex. The galaxies contributing to the scatter in the distant smTFR exhibit strong perturbations in their kinematic maps (e.g., Yang et al. 2008), which led us to claim that most of them were probably associated with major mergers (see P08). This interpretation is also supported by the large scatter seen in the specific angular momentum versus rotation velocity plane, which could be produced by these events, as demonstrated by Puech et al. (2007a).

Interestingly, Weiner et al. (2006) defined a new kinematic tracer $S=\sqrt{0.5\times V_{\rm rot}^2+\sigma ^2}$ that combines rotation velocity and velocity dispersion. They found that velocity dispersion is an important component of the dynamical support in intermediate-redshift galaxies, especially for morphologically compact or disturbed systems. Their study confirmed the earlier finding of Puech et al. (2006) that the majority of compact galaxies have motions in which dispersion plays an important role (see also Puech et al. 2007a). Kassin et al. (2007) later showed that using S in the smTFR leads to a significant reduction in its scatter. In addition, Covington et al. (2010) showed, using hydro-dynamical simulations of major mergers, that this reduction in scatter is consistent with a (partial) transfer of energy between the kinetic energy associated with bulk motions to that associated with random motions. This transfer is driven by shocks and collisions generated during the merger events (e.g., Montero-Ibero et al. 2006).

That the ``merger-hypothesis'' is the underlying cause of the large scatter measured in the distant TFR can be tested by searching for specific objects and verifying whether this transfer of energy between bulk and random motions driven by interaction-driven shocks really occurs. Peirani et al. (2009) studied one CK galaxy of the sample (J033239.72-275154.7) in detail and they demonstrated that both its morphology and kinematics were reproduced well by a 1:3 major merger where the companion galaxy had been in a retrograde parabolic orbit and there had been an inclination angle of 15 degrees between the two orbital planes. This object is a perfect test-bed for the present discussion, since it is measured to have $\log{V_{\rm flat}} = 1.48$ km s-1and $M_{\rm stellar}=10.31~M_\odot$, i.e., to be among the CK galaxies in the distant smTFR that are the most deficient in rotation velocity (see left panel of Fig. 3). Peirani et al. (2009) showed that, because of the retrograde nature of interaction, the host galaxy can lose angular momentum to its companion, resulting in the deceleration of the main progenitor. This explains why the resulting merger remnant appears to have systematically smaller velocities in the smTFR than other objects. Shocks in the gaseous phase generated during the interaction produce an increase in the velocity dispersion, similar to that suggested by Covington et al. (2010) by their merger simulations (see their Fig. 1). If the scatter in the smTFR is really caused by a transfer of energy between bulk and random motions driven by merger events, then this object should fall back onto the TFR, once its velocity dispersion is taken into account.

To test this, we derived S in the IMAGES sample using $V_{\rm rot}=V_{\rm flat}$ and $\sigma = \sigma_{\rm disk}$, as defined by Puech et al. (2007a). We show the resulting S-TFR in Fig. 3 (see right panel). Using S results in the shifting of all RDs back onto the local smTFR, so we propose to use the local slope in all future investigations. We also note that several CK galaxies lie at relatively high S compared to the bulk of the sample. These galaxies were found to have large rotation velocity in the conventional smTFR. However, these galaxies do not seem to be present in the Kassin et al. (2007) smTFR, although Covington et al. (2010) managed to produce some of these galaxies in their merger simulations (see their Fig. 3). These differences seem to be related to different selection criteria involving inclination. We did not apply any selection of this type (see P08), while Kassin et al. (2007) removed galaxies with low inclinations (i.e., $inc \leq 30$ deg) because of the larger associated uncertainty, and those with high inclinations (i.e., $inc \geq 70$ deg), because of the effect of dust (see also Covington et al. 2010).

The total scatter in the resulting S-TFR is significantly lower than in the smTFR, since it decreases from 0.63 to 0.34 dex. This residual scatter is still a factor of two larger than the residual dispersion in the local relation, which is $\sigma_{\rm res} = 0.15$ dex (in mass). Looking at the dispersion in more detail, the scatter remains roughly constant in RDs and PRs (from 0.12 to 0.14 dex and 0.32 to 0.29 dex, respectively), but strongly decreases from 0.83 to 0.41 dex among CKs. That kinematically disturbed galaxies show a smaller but still large scatter compared to the local relation suggests that part of the remaining discrepancy is related to the greater uncertainty in rotation velocity of CKs (see P08). The median uncertainty in the rotation velocity of the sample is found to be 0.12 dex, which translates into $\sim $0.3 dex in stellar mass, i.e., the same order of magnitude as the residual scatter in the distant S-TFR.

As one can see in the right panel of Fig. 3, accounting for velocity dispersion brings the merger-test J033239.72-275154.7 back onto the S-TFR. This is the first direct observational evidence of the transfer of energy described by Covington et al. (2010). As shown above, this process can account for most of the scatter in the smTFR. Given the still relatively large uncertainties, we cannot exclude other process(es) playing a role in producing the scatter in the distant relation, but these results clearly indicate that this transfer of energy is the main underlying cause, and that mergers are the main cause of the large scatter seen in the $z \sim 0.6$ TFR, as initially argued by Flores et al. (2006; see also Kannappan & Barton 2004).

4 Gas content of intermediate-mass galaxies

4.1 Comparison between gas and stellar extents

We show the total-light [OII] radius $R_{[{\rm OII}]}$ as a function of 1.9 times the UV half-light radius $R_{\rm UV}$ in Fig. 4. For a thin exponential disk, 1.9 times the half-light radius is equal to the optical radius of the galaxy (Persic & Salucci 1991), which provides us with a useful comparison point[*]. Galaxies that have a $R_{[{\rm OII}]}$ significantly lower than $1.9 \times R_{\rm UV}$ are galaxies for which the UV light extents farther than the IFU FoV ( $3 \times 2$arcsec2). Two examples of these galaxies can be seen on the right side of Fig. 4. For these galaxies, it is clear that assuming $R_{[{\rm OII}]}$ to be a measure of the gaseous extent would lead to underestimating the gas mass. Therefore, we defined $R_{\rm gas}={\rm MAX}(R_{[{\rm OII}]},~1.9 \times R_{\rm UV})$ to be a conservative measure of the gaseous extent. We note that for galaxies with non-relaxed kinematics, this might still underestimate the gas radius. The uncertainties correspond to the respective uncertainties in $R_{[{\rm OII}]}$ or $1.9 \times R_{\rm UV}$ depending on which radius was the largest for a given galaxy.

Most RDs (see blue dots) fall relatively close to the equality line, which instills confidence in the estimate of $R_{\rm gas}$ in dynamically relaxed systems. To first order, one can assume that, at least on large spatial scales and for relaxed systems, the spatial distribution of UV light emitted by young OB stars is correlated with the emission from the [OII] ionized gas detected by GIRAFFE. However, in more disturbed galaxies, there is a clear trend in which the gas is more extended than the UV light. We find a median [OII]-to-UV radius ratio of $1.3 \pm 0.16$ (1-$\sigma$ bootstrapped uncertainty), which is consistent with the mean ratio of $\sim $1.2 of emission line to B-band scale-lengths found by Bamford et al. (2007) in a sample of field galaxies at similar redshifts. Using a Student t-test, the probability that this median ratio is equal to one (i.e., that the total [OII] and UV radii are statistically equivalent) is found to be 6%. This trend is even more pronounced for more compact systems: galaxies with a UV radius lower or equal to the median in the sample have a median ratio of $\sim $1.7, while those having a UV radius larger than the median value, have a ratio $\sim $0.9. We also examined the GOODS/MIPS (DR3) images of the four galaxies with a UV radius smaller that one GIRAFFE pixel. All were detected, although only three at a significantly high level for their flux to be measurable. Interestingly, two of them were resolved by MIPS (see the two insets on the left side of Fig. 4), which confirms that the gas content can be significantly more extended than the UV stellar light.

4.2 What causes the large gaseous extent in 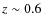$z \sim 0.6$ galaxies?

It is interesting to investigate what causes this discrepancy between the extents of the ionized gas and the UV ionizing stellar light from OB stars. Most of the ionizing stellar light is assumed to be emitted by stars earlier than B2 (Strömberg 1939), so to first order, one would expect conversely that the ionized gas is confined to within the UV radius. What mechanisms can explain our actual findings?

Supernovae (SN) and AGN feedback are two mechanisms that are known to be able to drive outflows in galaxies. If these mechanisms were responsible for ejecting ionized gas to the UV radius, we should detect offsets between absorption and emission lines in a large fraction of galaxies in the sample. For 20 galaxies in the GIRAFFE sample, we were able to retrieve FORS2 integrated spectra (see Rodrigues et al. 2008) that allowed us to measure absorption lines. Among these galaxies, we found systematic shifts in only three or possibly four of them (at a $\sim $100 km s-1 level in J033224.60-274428.1, J033225.26-274524.0, J033214.97-275005.5, and possibly in J033210.76-274234.6). Hence, we conclude that outflows, regardless of their powering mechanism, cannot explain why gas extends farther out than the UV stellar light.

If ionized gas is not pushed out of the UV disk by outflows, then the gas must be ionized by a mechanism other than the radiation of OB stars. Interestingly, for one object in the sample, Puech et al. (2009) observed a region that is completely devoid of stars, where ionized gas was detected. They concluded that this gas was ionized by shocks induced by a major merger. These interaction-driven shocks could be an important mean of ionizing gas in $z \sim 0.6$ galaxies. Hammer et al. (2009b) showed that the morpho-kinematics of most galaxies in the sample can be reproduced by the simulations of major mergers. We note that gas in all galaxies in the sample have lower $V/\sigma$ratios than their local counterparts, which might be a dynamical signature of these shocks (Puech et al. 2007a). In particular, most PRs show off-center velocity dispersion peaks (see Yang et al. 2008), which strengthens this interpretation.

5 The baryonic Tully-Fisher relation at z $\sim $ 0.6

5.1 The local relation

We used the local sample gathered by McGaugh (2005) to derive our local reference bTFR. McGaugh (2005) used $V_{\rm flat}$ and (amongst others) the Bell et al. (2003) method to estimate stellar mass, so their sample is particularly well suited to compare with our high-z bTFR. However, they used the B-band luminosity to derive stellar mass, which is a less accurate tracer than K-band luminosities. Hence, we rederived stellar mass from K-band luminosities by cross-correlating the McGaugh (2005) sample with the 2MASS database. Stellar masses were derived following the method outlined in P08 for their local sample, i.e., by accounting for k-corrections and extinction. We found that $\log{(M_{\rm baryonic}/M_\odot)} = 2.10 \pm 0.42 + (3.74 \pm 0.20)\times \log{(V_{\rm flat})}$ has a residual scatter of $\sigma = 0.25$ dex. In the following, we checked that by instead using the McGaugh (2005) stellar masses derived from the B-band luminosity (see his Table 2 with \ensuremath{{\cal P}} = 1) would not change significantly our results.

Stark et al. (2009) established a new calibration of the local bTFR using gas-dominated galaxies, which has the advantage of being less sensitive to a given estimator of the stellar mass. However, Stark et al. (2009) averaged the bTFR produced by various stellar mass estimators. Therefore, we chose to keep our own derived relation, which has the advantage of resulting from the same methodology used to derive the smTFR, both at low and high redshift, as well as the bTFR at high redshift, which minimizes possible systematic effects. We nevertheless note that our slope and zeropoint are consistent with their calibration. In contrast to the smTFR, whose calibration depends on the galaxy populations analyzed, the bTFR is found to be independent of galaxy type (Stark et al. 2009). We therefore do not expect any bias to be caused by the choice of a particular local sample and its level of representation in the local population.

5.2 The baryonic TFR at z $\sim $ 0.6

We show the first bTFR obtained at high redshift so far, in Fig. 5. Overall, the bTFR has the same structure as the smTFR, with non-relaxed galaxies associated with the greatest amount of dispersion. Holding the slope constant, we found a distant zeropoint of $2.16 \pm 0.07$, i.e., a shift of +0.06 dex in baryonic mass between the z = 0 bTFR and $z \sim 0.6$ RDs. This shift translates into a -0.02dex shift in rotation velocity. The scatter in the distant bTFR for RDs is found to be roughly similar to that in the local bTFR, with 0.14 dex, which suggests no evolution in slope. In comparison with the distant smTFR, the scatter in RDs is found to be roughly equivalent, with 0.14 dex in the bTFR instead of 0.12 dex in the smTFR (i.e., bootstrapping reveals that the 1-$\sigma$ spread of the scatter in RDs in the smTFR is $\sim $0.03 dex). In contrast, the total scatter is found to be significantly larger, with 0.83 dex in the bTFR instead of 0.63 in the smTFR. We used Monte-Carlo simulations to investigate whether the larger uncertainty associated with the gas mass, compared to the stellar mass, is responsible for the increase in scatter in the bTFR. To do this, we simulated 1000 smTFRs by moving the galaxies within the errorbars in their baryonic mass. We then refitted the resulting smTFRs, and found that the total scatter (as well as the scatter for RDs) does not increase significantly. Therefore, it appears that the bTFR has a significantly larger scatter than the smTFR, at least for the total galaxy population.

\begin{figure} \par\includegraphics[width=8.2cm,clip]{12081fg6.eps} \end{figure} Figure 5:

Evolution of the baryonic TFR in the CDFS subsample (see text). The black line is the local bTFR of McGaugh (2005), while the blue-dashed line is the fit to the distant relation. All panels have similar limits to ease the comparison between the different relations.

Open with DEXTER

In assessing whether there is an evolution in the intercept of the bTFR, it is important to account for possible systematic effects, which are usually more significant than random effects in the TFR (see P08 and Sect. 3). In the following, we express all systematic uncertainties in terms of their influence on the evolution of the zeropoint of the bTFR between $z \sim 0.6$ and z = 0. Systematic effects on the velocity estimates in the distant sample were found to be $\pm$0.02 dex, which corresponds to $\pm$0.08 dex once converted into $M_{\rm baryonic}$. Regarding the stellar mass, we identified in P08 two possible systematic effects, which are an evolution in the IMF (+0.05 dex), and an evolution in the K-band mass-to-light ratio (+0.1 dex) with redshift (see Appendix of P08). Finally, concerning gas masses, the only possible systematic effect could be an evolution of the SK law with redshift, since we argued in Sect. 2.3 that this quantity is derived independently of the IMF. As stated in Sect. 2.3, there is no evidence of an evolution in the SK law between $z \sim 0.6$ and z = 0, based on a comparison between their star-formation densities and those of local starbursts. Therefore, the main systematic effect that could affect the baryonic mass would be that related to stellar mass, which translates into a possible impact on the evolution of the bTFR zeropoint shift between $z \sim 0.6$ and z = 0 by +0.15 dex (0.05+0.1, see above). In conclusion, we find a bTFR zeropoint shift between $z \sim 0.6$ and z = 0 of $- 0.05 \pm 0.08$ (random, see above) +0.23-0.08 (systematic).

Using the permutation test of Koen & Lombard (2009), we find a probability of $\sim $62% that the local and distant relations have the same slope and intercept. Given that there are only six RDs in the distant bTFR, we also tested whether the local and distant intercepts are different, assuming that the slope does not evolve. To do this, we used a Welch t-test (Koen & Lombard 2009), and found that the probability that they are equal is 91%. We also found that this probability drops below 10% when we systematically increase the local bTFR zeropoint by at least 0.77 dex: this means that the local and distant bTFR zeropoints are not statistically different within systematic uncertainties (see above), assuming no evolution in slope. As stated above, the residual scatters of the local and distant relation are similar, which suggests that assuming there is no evolution in slope is a reasonable hypothesis. Therefore, we conclude that we do not detect any significant shift in the bTFR between $z \sim 0.6$ and z = 0.

6 Discussion and conclusions

There is now little doubt that the large scatter found in the $z \sim 0.6$ TFR is caused by non-relaxed systems associated with major mergers (Covington et al. 2010; Flores et al. 2006; Kassin et al. 2007; Puech et al. 2008; see also Kannappan & Barton 2004). Mergers provide a natural and coherent frame for interpreting the morpho-kinematics properties of $z \sim 0.6$galaxies (see Hammer et al. 2009b). In this paper, we have reported that ionized gas extends farther out than the ionizing light from OB stars: we indeed found a probability of 6% that the median ratio of the gas to stellar radius is equal to one. This can be seen as a natural consequence of shocks produced during these events. It is even difficult to figure out how gas lying significantly farther out than any radiation source could be ionized by any other process, given that a very negligible fraction of objects in the sample are found to contain evidence of gas outflows, which might spread ionized gas out to the UV radius.

Returning to the TFR, we confirm that, once restricted to rotating disks, the $z \sim 0.6$ smTFR appears to be shifted toward fainter masses by 0.34 dex. This shift is found to be very significant within the random and systematic uncertainties. In contrast, by including the gas fraction of the baryonic mass in the TFR, we found that, within the uncertainties, the $z \sim 0.6$ relation is consistent with the local relation derived for the McGaugh (2005) sample. This implies that star formation in rotating disks is mostly fed by gas that is already gravitationally bound to galaxies, otherwise we would have detected significant evolution in the bTFR. This does not mean that there is no external gas accretion: given the still relatively large associated uncertainties, there could be room for external gas accretion, at a level of up to roughly one third of the local baryonic mass. However, there is presently no need for this external gas accretion.

At higher redshifts, Cresci et al. (2009) found an evolution of 0.41 dex in the zeropoint of the smTFR between $z \sim 2.2$ and z = 0, i.e., of similar amplitude (within uncertainties) to the evolution found in this paper between $z \sim 0.6$ and z = 0. This would imply that the smTFR does not evolve significantly between $z \sim 2.2$ and $z \sim 0.6$, while it evolves significantly between $z \sim 0.6$ and z = 0. To try to understand this surprising result, we refitted the smTFR found by Cresci et al. (2009), but assumed that the local slope of reference is that used in the present study. The choice of the slope in the local relation is crucial for deriving the evolution in zeropoint as a function of redshift (see Sect. 5.1 of P08 for details). While the distant sample used by Cresci et al. (2009) seems to be representative of $z \sim 2$ galaxies, at least for galaxies with stellar masses higher than $\sim 2 \times 10^{10}~M_\odot$ (Förster Schreiber et al. 2009), they used the local relation derived by Bell & de Jong (2001), which relies on the sample of Verheijen (2001) that was shown to be biased toward an excess of low-mass, gas-rich galaxies by Hammer et al. (2007). In P08, we derived a local smTFR using a representative subsample of the SDSS from Pizagno et al. (2007). In this sample, the slope is found to be smaller, i.e., 2.8 (see Appendix of P08) instead of the value of 4.5 used by Cresci et al. (2009). By refitting the relation of Cresci et al. (2009) using the slope derived from this representative local sample, we find an evolution in zeropoint of $\sim $0.6 dex, instead of $\sim $0.4 dex found using the Bell & de Jong (2001) slope. We conclude that the shift found by Cresci et al. (2009) probably underestimates the evolution in zeropoint between $z \sim 2.2$ and z = 0.

Finally, Cresci et al. (2009) interpreted the shift of the $z \sim 2.2$ smTFR as the result of gas accretion onto the forming disks in filaments and cooling flows, as suggested by theoretical and numerical models. This gas accretion process could also play a role in feeding the outer regions of $z \sim 0.6$ galaxies with fresh gas, to within a limit of 30% of the local baryonic mass, as discussed above. However, it would remain unclear what the ionization source of this gas is (see Sect. 4). These models also clearly predict that these cold flows are strongly suppressed in the massive, $z \sim 0.6$ haloes that the galaxies studied in this paper inhabit (e.g., Dekel et al. 2009). In a companion paper (Hammer et al. 2009b), we explore another possibility that a large fraction of local spirals could have rebuilt their disk following a major merger at $z \leq 1$. This scenario, dubbed as ``spiral rebuilding disk scenario'', was proposed by Hammer et al. (2005), owing to the remarkable coincidence of the evolution of the merger rate, morphology, and fraction of actively star-forming galaxies. In this scenario, major mergers expel gas in, e.g., tidal tails, which is later re-accreted to rebuild a new disk (Hopkins et al. 2009; Barnes 2002; Robertson et al. 2006). It is tempting to associate a significant part of the gas reservoir with this process, which can therefore provide us with an evolutionary framework in which to intepret the non-evolution of the bTFR with redshift, and the finding that ionized gas extends farther out than the stellar UV light. A dynamical imprint of this accretion might already have been detected in terms of the lower $V/\sigma$ found in distant gaseous disks compared to local spirals (Puech et al. 2007a). Therefore, different physical mechanisms could be driving galaxy evolution and the shift in the smTFR, depending on redshift, which would complicate the interpretation of the evolution in the smTFR from very high redshift to z = 0.

Acknowledgements
This study made use of GOODS data in the CDFS field (MIPS and HST/ACS images), as well as of the 2MASS and the CDS databases. We thank X. Hernandez and L. Chemin for useful discussions about the subject of this paper.

References

  1. Atkinson, N., Conselice, C. J., & Fox, N. 2007, [arXiv:0712.1316], unpublished Avila-Reese, V., Zavala, J., Firmani, C., et al. 2008, AJ, 136, 1340 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bamford, S. P., Milvang-Jensen, B., & Aragon-Salamanca, A. 2007, MNRAS, 378, L6 [NASA ADS] [Google Scholar]
  3. Barnes, J. E. 2002, MNRAS, 333, 481 [NASA ADS] [CrossRef] [Google Scholar]
  4. Begum, A., Chengalur, J. N., Karachentsev, I. D., et al. 2008, MNRAS, 386, 138 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bell, E. F., & de Jong, R. S. 2001, ApJ, 550, 212 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bell, E. F., McIntosh, D. H., Katz, N., & Weinberg, M. D. 2003, ApJS, 149, 289 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Borch, A., Meisenheimer, K., Bell, E. F., et al. 2006, A&A, 453, 869 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bouch, N., Cresci, G., Davies, R., et al. 2007, ApJ, 671, 303 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chary, R., & Elbaz, D. 2001, ApJ, 556, 562 [NASA ADS] [CrossRef] [Google Scholar]
  12. Conselice, C. J., Bundy, K., Ellis, R. S., et al. 2005, ApJ, 628, 160 [NASA ADS] [CrossRef] [Google Scholar]
  13. Covington, M. D., Kassin, S. A., Dutton, A. A., et al. 2010, ApJ, 710, 279 [NASA ADS] [CrossRef] [Google Scholar]
  14. Cresci, G., Hicks, E. K. S., Genzel, R., et al. 2009, ApJ, 697, 115 [NASA ADS] [CrossRef] [Google Scholar]
  15. De Rijcke, S., Zeilinger, W. W., Hau, G. K. T., Prugniel, P., & Dejonghe, H. 2007, ApJ, 659, 1172 [NASA ADS] [CrossRef] [Google Scholar]
  16. Dekel, A., Birnboim, Y., Engel, G., et al. 2009, Nature, 457, 451 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  17. Erb, D. K., Steidel, C. C., Shapley, A. E., et al. 2006, ApJ, 646, 107 [NASA ADS] [CrossRef] [Google Scholar]
  18. Flores, H., Hammer, F., Puech, M., Amram, P., & Balkowski, C. 2006, A&A, 455, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Forster Schreiber, N. M., et al. 2009, ApJ, 706, 1364 [NASA ADS] [CrossRef] [Google Scholar]
  20. Geha, M., Blanton, M. R., Masjedi, M., & West, A. A. 2006, ApJ, 653, 240 [NASA ADS] [CrossRef] [Google Scholar]
  21. Gurovich, S., McGaugh, S. S., Freeman, K. C., et al. 2004, PASA, 21, 412 [Google Scholar]
  22. Hammer, F., Flores, H., Elbaz, D., et al. 2005, A&A, 430, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Hammer, F., Puech, M., Chemin, L., Flores, H., & Lehnert, M. 2007, ApJ, 662, 322 [NASA ADS] [CrossRef] [Google Scholar]
  24. Hammer, F., Flores, H., Yang, Y., et al. 2009a, A&A, 496, 381 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Hammer, F., Flores, H., Puech, M., et al. 2009b, A&A, 507, 1313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Hopkins, P. F., Cox, T. J., Younger, J. D., & Hernquist, L. 2009, ApJ, 691, 1168 [Google Scholar]
  27. Kannappan, S. J., & Barton, E. J. 2004, AJ, 127, 2694 [NASA ADS] [CrossRef] [Google Scholar]
  28. Kassin, S. A., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, 35 [Google Scholar]
  29. Kennicutt, R. 1989, ApJ, 344, 685 [NASA ADS] [CrossRef] [Google Scholar]
  30. Kennicutt, R. 1998, ARA&A, 36, 189 [Google Scholar]
  31. Koen, C., & Lombard, F. 2009, MNRAS, 395, 1657 [NASA ADS] [CrossRef] [Google Scholar]
  32. Lah, P., Chengalur, J. N., Briggs, F. H., et al. 2007, MNRAS, 376, 1357 [NASA ADS] [CrossRef] [Google Scholar]
  33. Le Floc'h, E., Papovich, C., Dole, H., et al. 2005, ApJ, 632, 169 [NASA ADS] [CrossRef] [Google Scholar]
  34. Mannucci, F., Cresci, G., Maiolino, R., et al. 2009, MNRAS, 398, 1915 [NASA ADS] [CrossRef] [Google Scholar]
  35. Maraston, C., Daddi, E., Renzini, A., et al. 2006, ApJ, 652, 85 [NASA ADS] [CrossRef] [Google Scholar]
  36. Marchesini, D., van Dokkum, P. G., Förster Schreiber, N. M., et al. 2009, ApJ, 701, 1765 [NASA ADS] [CrossRef] [Google Scholar]
  37. McGaugh, S. S. 2000, ApJ, 533, L99 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  38. McGaugh, S. S. 2004, ApJ, 609, 652 [NASA ADS] [CrossRef] [Google Scholar]
  39. McGaugh, S. S. 2005, ApJ, 632, 859 [NASA ADS] [CrossRef] [Google Scholar]
  40. Meyer, M. J., Zwaan, M. A., & Webster, R. L. 2008, MNRAS, 391, 1712 [NASA ADS] [CrossRef] [Google Scholar]
  41. Montero-Ibero, A., Arribas, S., & Colina, L. 2006, ApJ, 637, 138 [NASA ADS] [CrossRef] [Google Scholar]
  42. Neichel, B., Hammer, F., Puech, M., et al. 2008, A&A, 484, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Noordermeer, E., & Verheijen, M. A. W. 2007, MNRAS, 381, 1463 [NASA ADS] [CrossRef] [Google Scholar]
  44. Peirani, S., Hammer, F., Flores, H., et al. 2009, A&A, 496, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Persic M., & Salucci P. 1991, ApJ, 368, 60 [NASA ADS] [CrossRef] [Google Scholar]
  46. Pizagno, J., Prada, F., Weinberg, D. H., et al. 2007, AJ, 134, 945 [NASA ADS] [CrossRef] [Google Scholar]
  47. Puech, M., Hammer, F., Flores, H., Östlin, G., & Marquart, T. 2006, A&A, 455, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Puech, M., Hammer, F., Lehnert, M. D., & Flores, H. 2007a, A&A, 466, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Puech, M., Hammer, F., Flores, H., et al. 2007b, A&A, 476, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Puech, M., Flores, H., Hammer, F., et al. 2008, A&A, 484, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Puech, M., Hammer, F., Flores, H., et al. 2009, A&A, 493, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Pozzetti, L., Bolzonella, M., Lamareille, F., et al. 2007, A&A, 474, 443 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Ravikumar, C. D., Puech, M., Flores, H., et al. 2007, A&A, 465, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Robertson, B., Bullock, J. S., Cox, T. J., et al. 2006, ApJ, 645, 986 [NASA ADS] [CrossRef] [Google Scholar]
  55. Rodrigues, M., Hammer, F., Flores, H., et al. 2008, A&A, 492, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Schiminovich, D. 2008, The Evolution of Galaxies Through the Neutral Hydrogen Window, AIP Conf. Proc., 1035, 180 [Google Scholar]
  57. Stark, D. V., McGaugh, S. S., & Swaters, R. A. 2009, AJ, 138, 392 [NASA ADS] [CrossRef] [Google Scholar]
  58. Strömberg, B. 1939, ApJ, 89, 526 [NASA ADS] [CrossRef] [Google Scholar]
  59. Trachternach, C., de Blok, W. J. G., McGaugh, S. S., van der Hulst, J. M., & Dettmar, R. 2009, A&A, 505, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Verheijen, M. A. W. 2001, ApJ, 563, 694 [NASA ADS] [CrossRef] [Google Scholar]
  61. Weiner, B. J., Willmer, C. N. A., Faber, S. M., et al. 2006, ApJ, 653, 1027 [NASA ADS] [CrossRef] [Google Scholar]
  62. Yang, Y., Flores, H., Hammer, F., et al. 2008, A&A, 477, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Footnotes

... IMF[*]
The IMF affects the SFR calibration in such a way that both the SFR and the numerical factors in the SK relation change and cancel eachother. It is possible to derive a direct relation between UV and IR luminosities and gas densities, in a similar way to Erb et al. (2006) using the H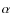$\alpha$ luminosity, therefore eliminating the SFR density, which is the IMF-dependant quantity.
... point[*]
For a thin exponential disk, this radius equals 3.2 times the disk scale-length, which defines the total stellar-light radius, and is statistically equivalent to the isophotal radius R25, see Persic & Salucci (1991).
Copyright ESO 2010

All Tables

Table 1:   Principle properties of the sample of 35 galaxies used in this study, in order of increasing RA (see Sect. 2.5).

All Figures

  \begin{figure} \par\includegraphics[width=8.5cm]{12081fg1.eps} \end{figure} Figure 1:

SFR as a function of stellar mass in a subsample of 35 CDFS galaxies. RDs are shown as blue dots, PRs as green squares, and CKs as red triangles. The open blue circle corresponds to the RD+ galaxy for which the velocity measurement is more uncertain (see P08). Uncertainties in stellar mass are discussed in Sect. 2.1, and are not shown for reasons of clarity.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm]{12081fg2.eps} \end{figure} Figure 2:

Gas mass as a function of stellar mass in a subsample of 35 CDFS galaxies. RDs are shown as blue dots, PRs as green squares, and CKs as red triangles. The open blue circle corresponds to the RD+ galaxy for which the velocity measurement is more uncertain (see P08). Uncertainties in stellar mass are discussed in Sect. 2.1, and are not shown for reasons of clarity. The blue line represents equality between the stellar and gas masses, while the blue dashed line represents the local relation between these two quantities given by Schiminovich (2008). The median gas fraction is found to be 31%, or $M_{\rm gas}/M_{\rm stellar} = 0.45$, which is represented as a thin black line.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm]{12081fg3.eps}\includegraphics[width=8.5cm]{12081fg4.eps} \end{figure} Figure 3:

Left: evolution of the stellar-mass TFR in the sample of 64 galaxies of P08 (RDs are shown as blue dots, PRs as green squares, and CKs as red triangles). The open blue circle correspond to the RD+ galaxies for which the velocity measurement is more uncertain, see P08). The two open red triangles correspond to the two galaxies that were changed from RD to CK compared to P08 (see Sect. 2.1). The black line is the local smTFR, while the blue dash-line represent a linear fit to the $z \sim 0.6$ smTFR. Left: same relation but using S. The black and blue-dashed lines are the same as in the left panel.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.7cm]{12081fg5.eps} \end{figure} Figure 4:

Comparison between the [ OII] and UV radii for the CDFS sub-sample of galaxies. The two insets on the left (30-arcsec wide) show MIPS imaging at 24 $\mu $m of J033228.48-274826.6 ( upper one) and J033244.20-274733.5, while the two insets on the right show z-band HST/ACS images of J033230.78-275455.0 and J033226.23-274222.8 superimposed with the GIRAFFE IFU grid. RDs are shown as blue dots, PRs as green squares, and CKs as red triangles. The open blue circle corresponds to the RD+ galaxy for which the velocity measurement is more uncertain (see P08).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.2cm,clip]{12081fg6.eps} \end{figure} Figure 5:

Evolution of the baryonic TFR in the CDFS subsample (see text). The black line is the local bTFR of McGaugh (2005), while the blue-dashed line is the fit to the distant relation. All panels have similar limits to ease the comparison between the different relations.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.