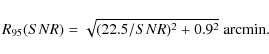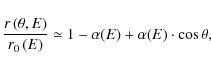| Issue |
A&A
Volume 510, February 2010
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 9 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200911779 | |
| Published online | 05 February 2010 | |
The Palermo Swift-BAT hard X-ray catalogue
I. Methodology
A. Segreto1 - G. Cusumano1 - C. Ferrigno2,3 - V. La Parola1 - V. Mangano1 - T. Mineo1 - P. Romano1
1 - INAF, Istituto di Astrofisica Spaziale e Fisica Cosmica,
via U. La Malfa 153, 90146 Palermo, Italy
2 -
Institut für Astronomie und Astrophysik Tübingen (IAAT), Germany
3 -
ISDC, Data Centre for Astrophysics, Chemin d'Écogia 16, 1290 Versoix, Switzerland
Received 2 February 2009 / Accepted 21 September 2009
Abstract
Aims. We develop a code, the BATIMAGER, for efficient data processing and image reconstruction of the Swift-BAT survey data.
Methods. The software performs image reconstruction via the
cross-correlation method and also generates source spectra and light
curves. The software is optimized for the direct production of all-sky
mosaics on an equi-area spherical grid. To reduce systematic errors, we
perform an accurate inflight calibration of the instrument, producing
an improved description of the mask pattern, time-dependent pixel
equalization maps, boresight misalignment correction, and energy
dependent off-axis count rate correction.
Results. The software is fully tested and used for the analysis of BAT survey data, demonstrating that the BATIMAGER is competitive in exploiting the BAT capabilities both for sensitivity and for position reconstruction.
Key words: method: data analysis - X-rays: general - surveys
1 Introduction
Imaging techniques based on focusing the X-ray radiation by grazing reflection from mirrors
become ineffective above ![]() 10 keV because of technological constraints. At higher energies,
coded mask imaging (e.g., Fenimore & Cannon 1978; Skinner et al. 1987a) is an efficient alternative
method, which allows medium resolution (arcmin) imaging.
10 keV because of technological constraints. At higher energies,
coded mask imaging (e.g., Fenimore & Cannon 1978; Skinner et al. 1987a) is an efficient alternative
method, which allows medium resolution (arcmin) imaging.
Several space observatories have been equipped with coded mask telescopes: Spacelab/XRT (Skinner et al. 1987b), MIR/KVANT/TTM (Sunyaev et al. 1991), GRANAT/ART-P (Pavlinsky et al. 1994,1992), GRANAT/SIGMA (Paul et al. 1991; Sunyaev et al. 1991), and BeppoSAX/WFC (Jager et al. 1997). Coded mask imagers now operate onboard INTEGRAL (the IBIS, JEM-X, and SPI telescopes; Winkler et al. 2003), Swift (the Burst Alert Telescope, BAT; Barthelmy et al. 2005), and AGILE (Super-AGILE; Feroci et al. 2007).
In these telescopes, the radiation originating in the sky sources is spatially modulated by a mask consisting of an array of opaque elements and recorded by a position-sensitive detector. To avoid ambiguities in the reconstruction of the sky image, the mask pattern is designed in such a way that the radiation from each sky direction casts a unique shadow on the detector. By knowing the orientation of the satellite in space and by analyzing the data from the detector, it is possible, using image reconstruction algorithms, to evaluate the position and the intensity of all cosmic sources and of the background level, thus reproducing the image of the observed sky.
The aim of this paper is to describe the code (BATIMAGER) that we developed to analyze the BAT survey data. The software performs image reconstruction, spectra, and light curve extraction, and has been optimized in particular for the direct production of all-sky mosaic skymaps on an equi-area spherical grid. The code is based on the widely used cross-correlation method and iterative removal of sources for the image reconstruction (Goldwurm et al. 2003; Jager et al. 1997; in 't Zand 1992); the reduction of systematic errors (which is the most difficult task when dealing with a real instrument) is treated with great care using novel approaches.
The paper is organized as follows. In Sect. 2, we describe the BAT telescope and the survey data set. In Sect. 3, we describe the BATIMAGER software in detail. In Sect. 4, we describe our instrument calibration solutions for the BAT boresight correction, the modeling of the coded mask pattern, the pixel efficiency map, and the off-axis energy correction. In Sect. 5, we describe the screening criteria applied to the data archive. In Sect. 6, we present the performance of our software and a comparison with the software developed by the BAT hardware team; finally, in Sect. 7, we summarize our results.
2 The BAT survey data
The BAT is a coded-mask detector sensitive in the 15-150 keV
band, with a field of view (FOV) of 1.4 steradian (half coded),
used as a GRB detector onboard Swift (Gehrels et al. 2004). While awaiting new GRBs, it continuously collects spectral and imaging data in survey mode, covering every day
a fraction of the sky between 50% and 80%. Data are immediately made available to the scientific community in
the public Swift data
archive![]() together with housekeeping and spacecraft
attitude information.
together with housekeeping and spacecraft
attitude information.
The Swift-BAT entrance window is a 2.7 m2 coded-aperture mask of
![]() mm2
elements
placed 1 m above the detector plane. The mask is designed with a
pseudo-random pattern that offers the advantage with respect to cyclic
patterns (like e.g., the one used for IBIS) that the reconstructed
images are unaffected by ghost sources, which can be completely
eliminated only by modeling the instrument at a level that is difficult
to obtain. On the other hand, this design is characterized by a non
optimal point spread function (PSF) with side lobes extending over the
whole image and inducing cross-contaminations among all the sources in
the same FOV.
mm2
elements
placed 1 m above the detector plane. The mask is designed with a
pseudo-random pattern that offers the advantage with respect to cyclic
patterns (like e.g., the one used for IBIS) that the reconstructed
images are unaffected by ghost sources, which can be completely
eliminated only by modeling the instrument at a level that is difficult
to obtain. On the other hand, this design is characterized by a non
optimal point spread function (PSF) with side lobes extending over the
whole image and inducing cross-contaminations among all the sources in
the same FOV.
The BAT detector plane consists of a 5200 cm2 array of 32 768 ![]() mm2
CdZnTe elements separated by thin (0.2 mm) gaps. Pixels are
organized into 128 element sub arrays (modules) and mounted onto
16 mechanical structures (blocks). The gaps between modules are
integer multiples (2 or 3) of the basic pixel pitch (Barthelmy et al. 2005). The ratio of the mask element size to the pixel pitch is
mm2
CdZnTe elements separated by thin (0.2 mm) gaps. Pixels are
organized into 128 element sub arrays (modules) and mounted onto
16 mechanical structures (blocks). The gaps between modules are
integer multiples (2 or 3) of the basic pixel pitch (Barthelmy et al. 2005). The ratio of the mask element size to the pixel pitch is ![]() 1.19 and the full width half maximum (FWHM) of the on-axis PSF is
1.19 and the full width half maximum (FWHM) of the on-axis PSF is ![]() 22 arcmin.
22 arcmin.
The BAT survey data are collected in the form of detector plane histograms (DPH, Markwardt et al. 2007). A DPH consists of a three-dimensional array, where an 80 channel spectrum is accumulated for each detector pixel over the integration period. A typical DPH integration time is five minutes, but longer integration times are sometimes possible (e.g., when telemetry reduction is needed) as well as shorter integration times since survey mode is always interrupted when the spacecraft begins a slew to a new target or when entering the South Atlantic Anomaly (SAA).
3 Software description
The main objective of BATIMAGER is to produce skymaps, light curves, and spectra, starting from a list of DPH and calibration files. To decrease the time required to process the huge BAT archive, all processing steps (from shadowgram accumulation to all-sky mosaicking) are integrated in one single executable, thus reducing the number of mathematical computations and unnecessary I/O operations.
Intermediate products are used to generate the calibration files needed to reduce the systematic errors in image reconstruction (Sect. 4). The main analysis steps implemented in the BATIMAGER are described in detail in the following subsections and illustrated in Fig. 1 with a flowchart.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11779_01.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg8.png)
|
Figure 1: Flowchart of the BATIMAGER software. All processing steps are integrated in a single executable to reduce the number of mathematical computations and unnecessary I/O operations. |
| Open with DEXTER | |
3.1 Shadowgram accumulation and cleaning
To obtain an image of the detector plane (shadowgram), each DPH file is integrated in a selected energy interval. Then, to identify the pixels that are disabled during the integration time or that are too noisy, the corresponding housekeeping enabled/disabled detector maps (taken at times immediately before and after the DPH acquisition time) are checked.
The code also analyzes the statistical distribution of the counts in the shadowgram and rejects the pixels corresponding to the histogram outliers. At this stage however, some noisy pixels can escape rejection because the shadowgram pixel distribution is broadened by the presence of bright sources and background spatial variations. For this reason, the pixel screening is repeated later (Sect. 3.5), after the subtraction of the contribution from all bright sources and the background spatial model.
3.2 Skymap reconstruction
A widely used method to obtain maps of the sky from a coded mask instrument is to cross-correlate the detector shadowgram with a decoding array derived from the projection of the mask pattern onto the detector plane. The balanced cross-correlation formula (as described e.g., in Fenimore & Cannon 1978) allows us to obtain background-subtracted sky images, however, this formula assumes an ideal detector plane with no gaps or dead pixels, perfectly uniform pixel efficiencies, and a flat background distribution across the detector plane. Any deviation from these ideal conditions produces fluctuations in the reconstructed skymap that can be much higher than those expected from the counting statistics. In the sky image reconstruction, we therefore adopted the balanced and renormalized cross-correlation formula described in Goldwurm et al. (2003), which allows us to take into account the differences in pixel efficiencies and the presence of gaps in the detection plane. The method that we used to obtain the pixel efficiencies used in the cross-correlation formula is described in Sect. 4.1.
To reduce the computation time, the skymaps of the entire FOV are
generated by performing the
cross-correlation by means of a Fast Fourier Transform (FFT) algorithm;
skymaps obtained in this way are defined on a rectangular grid of
points with an angular spacing corresponding to shifts of the mask
pattern projection of integer multiples of the detector pixel pitch.
This spacing is however too coarse with respect to the imaging PSF of
the instrument (![]() 1.56 pixels FWHM);
if a source position is not exactly on one of the points where the FFT
skymap is computed, it is observed with a signal to noise ratio (SNR)
that can be significantly reduced (
1.56 pixels FWHM);
if a source position is not exactly on one of the points where the FFT
skymap is computed, it is observed with a signal to noise ratio (SNR)
that can be significantly reduced (![]()
![]() lower in the worst case) with respect to the SNR that would be obtained
by using the cross-correlation formula at the exact source position.
lower in the worst case) with respect to the SNR that would be obtained
by using the cross-correlation formula at the exact source position.
To obtain skymaps with a finer grid spacing, BATIMAGER repeats the FFT cross-correlation process multiple times, each time using a decoding array obtained by shifting the coded mask pattern on-axis projection by a fraction of the detector pixel pitch; the set of skymaps obtained in this way are defined on grids of points shifted with respect to each other and can be merged into a single skymap. In this way, skymaps defined on a grid of points with angular spacing equivalent to any desired fraction of the detector pixel pitch can be obtained.
![\begin{figure}
\par\includegraphics[width=6.cm,angle=-90]{11779_02.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg10.png)
|
Figure 2: Scan of the Crab PSF (SNR) in a nearly on-axis BAT observation. The stepped line connects points from a skymap generated with a 1/2 pixel grid spacing, while the solid line connects values from a skymap generated with 1/10 pixel grid spacing. |
| Open with DEXTER | |
The SNR profile of the Crab extracted from a skymap with a very fine grid spacing is shown in Fig. 2;
as is evident, to sample the source PSF in an acceptable way, the BAT
skymaps must be computed on a grid with an angular spacing equivalent
to, at least, 1/2 of the detector pixel linear size. With this spacing,
the SNR loss due to finite skymap sampling is, in the worst case, ![]()
![]() ;
the SNR loss can be reduced to less than
;
the SNR loss can be reduced to less than ![]()
![]() by generating skymaps with a 1/3 pixel grid spacing.
While finer grid spacing of course provide higher quality images, the
increase in computational time must be considered when processing the
whole survey data archive.
by generating skymaps with a 1/3 pixel grid spacing.
While finer grid spacing of course provide higher quality images, the
increase in computational time must be considered when processing the
whole survey data archive.
We note that the method described above to produce skymaps on a grid finer than the detector pixel, does not need the introduction of any modification to the evaluation of the statistical uncertainty associated to the skymap signal, although, of course, values in neighboring pixels are highly correlated. By simulation of empty field observations, we verified that, independently of the grid resolution, the histogram of pixel SNR in skymap regions much larger than the PSF is always a Gaussian with a zero mean and a unitary standard deviation, as expected.
3.3 Identification and subtraction of the bright sources
In a coded mask instrument like BAT, the sidelobes of the source PSF extend over the whole reconstructed skymap, so that every bright source in the FOV increases the fluctuations in the reconstructed images above the noise expected from the counting statistics alone.
While the statistical noise associated with the increment of counts produced by the source (Poisson noise) cannot be eliminated, the fluctuations due to the source PSF spatial extension (coding noise) can be removed by subtracting the model of the source illumination pattern from the detector shadowgram.
The source detection in the skymap must then be implemented with an iterative cleaning algorithm (iterative removal of sources, IROS; Hammersley 1986; Hammersley et al. 1992; in 't Zand 1992).
In a preliminary skymap, the brightest sources are searched for by looking for pixels whose significance is well above the locally measured skymap noise. Then, using the cross-correlation formula, we produce a local skymap zoom with a very fine grid spacing (e.g., 1/10 pixel) centered on the preliminary source position; a local bidimensional fit is then used to obtain the refined source position. Using the local hyperfine grid, we eliminate any influence of the coarser grid spacing adopted (to reduce processing times) for the generation of the skymap of the entire FOV via FFT .
The source intensity is then computed and its simulated illumination pattern subtracted from the detector shadowgram. The resulting cleaned shadowgram is then used to generate a new skymap where, because of a lower noise level, other sources can be searched for. The process is then repeated until no more sources are detected.
The position of each detected source is then cross-correlated with a reference source catalogue for identification. If the source has a counterpart, its offset with respect to the nominal position is used to verify the pointing accuracy and is stored in a calibration file used to correct the boresight alignment (Sect. 4.3).
3.4 Background modeling and subtraction
The cross-correlation algorithm used for image reconstruction ensures a perfect subtraction of the background level only if this is uniform over the whole detector plane. In any real detector, however, the spatial distribution of the background (cosmic and instrumental) is influenced by several factors (e.g., scattering in the detector passive structure) that introduce an energy-dependent and non-uniform spatial distribution on the detector plane. Moreover, the spatial distribution is time-dependent since it is influenced by both the satellite pointing orientation and the external particle environment.
Figure 3 shows an example of the observed BAT background distribution averaged over a large set of shadowgrams, showing that the background count rate is much higher in the center than in the external regions. This is because the pixels in the central part of the detector are exposed to a larger sky solid angle and, as a consequence, collect more diffuse cosmic ray background (Ajello et al. 2008b). We also note that the pixels in the external perimeter of each module are affected by higher background count rates.
![\begin{figure}
\par\includegraphics[width=9cm]{11779_03.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg13.png)
|
Figure 3: An example of BAT detector background map (cts/s) in the 25-100 keV energy range. |
| Open with DEXTER | |
To avoid the appearance of large-scale structures in the reconstructed skymaps, the background spatial distribution must then be modeled and subtracted from the shadowgrams before image reconstruction. BATIMAGER derives a background spatial model for each pointing by performing a principal component analysis (PCA see e.g., Kendall 1980) of the shadowgram residual after the subtraction of the contribution from all the bright sources.
The PCA is an algorithm that allows us to decompose a data matrix in terms of an orthogonal basis vector set, the principal components (PCs), sorted so that the first ones account for as much of the variability in the data matrix as possible. The spatial variation on a large scale associated with the non-uniform background distribution can be reconstructed by means of the first few PCs; to better preserve the unsubtracted sources, the PCs selected for background modeling are replaced by their interpolation with a low-order polynomial. This method allows us to perform a flexible modeling of any kind of spatial distribution.
3.5 Final subtraction of sources and background
After subtraction of the illumination pattern of both the bright sources and the background model, the statistical distribution of values in the residual shadowgram is much narrower than the original one. This allows us to perform a more robust identification and rejection of bad pixels than in Sect. 3.1.
The BATIMAGER then recomputes the intensity of all the bright sources previously detected and of a list of sources included in an input catalog, directly from the shadowgram cleaned for the updated list of bad pixels, taking into account the cross-contamination between sources in the same FOV. This is achieved by computing (using the cross-correlation formula) the contribution of each source to the skymap intensity at the precise positions of all the other sources. A linear system is then obtained that, solved by matrix inversion, provides the corrected values for the source fluxes and the associated statistical uncertainty; these values are used to generate light curves and spectra.
We note that, being entirely algebraic, the method outlined above to remove source cross-contamination is much faster and numerically stable than other methods based e.g., on parametric fitting procedures.
The shadowgram, cleaned from both sources and background, is then converted into the final skymap, which, after the vignetting correction described in the next paragraph, is used to accumulate the all-sky mosaic.
3.6 Skymap flux off-axis corrections
The skymaps obtained by the balanced cross-correlation process, are normalized for both the number of active detector pixels and the partial coding. There are however other effects influencing the measured source flux as a function of the off-axis angle that must be corrected to obtain the optimum source detection in the final mosaic:
- the partial occultation of the FOV by the Earth, Sun, and Moon;
- off-axis geometric projection factor;
- absorption by the mask support layer.
The effects of the projection angle on the measured count rate are expressed by the cosine of the incident angle ![]() only when the detector pixels are assumed to entirely absorb the incident radiation.
At high energy, when the detection efficiency becomes lower than unity, using a simple cos
only when the detector pixels are assumed to entirely absorb the incident radiation.
At high energy, when the detection efficiency becomes lower than unity, using a simple cos![]() factor as a count rate correction would lead to a systematic overestimation in the source equivalent on-axis flux.
To avoid this effect, an energy-dependent geometric factor
factor as a count rate correction would lead to a systematic overestimation in the source equivalent on-axis flux.
To avoid this effect, an energy-dependent geometric factor
![]() should be used. This can be expressed
by the formula
should be used. This can be expressed
by the formula
where
Including the flux attenuation in the mask support layer, the measured source count rate,
![]() ,
as a function of the off-axis angle can be expressed by
,
as a function of the off-axis angle can be expressed by
where r0(E) is the on-axis count rate spectrum and
The off-axis correction factor for skymaps is obtained by averaging Eq. (2) in the skymap integration energy range; we note that in the averaging it is necessary to choose a reference count spectrum r0(E), thus introducing a systematic bias (significant if wide energy ranges are used) in the correction factor for sources with a different spectral indices. The procedure that we used to calibrate the parameters of the energy-dependent off-axis correction is described in Sect. 4.4.
3.7 Skymap projection and mosaicking
To accumulate a mosaic image, the skymaps obtained from individual detector pointing must be projected onto a common sky reference system. When analyzing the all-sky survey, the strong distortions present in any kind of plane projection systems (such as e.g., AITOFF) in regions far from the projection axis, introduce several problems.
The subdivision of the all-sky mosaic image into different local projection systems, reduces geometrical deformations but poses other problems. Since any individual pointing may contribute to more than one of the local projection mosaics, these are not entirely statistically independent. It is then not straightforward to merge the results obtained from the set of local projections into the global survey results.
These limitations can be overcome if the image mosaicking and any subsequent analysis adopts a spherical coordinate grid system in which each pixel covers the same area as every other pixel; in this way, besides avoiding angular distortion, the generation of all-sky statistical histograms (e.g., sky coverage) is straightforward. For visualization purposes, any selected regions or the entire mosaic sky map can be projected onto any conventional 2D plane projection system.
From the several spherical coordinate grid systems that have been defined, for our survey analysis we selected the Hierarchical Equal Area isoLatitude Pixelization (HEALPIX) (Górski et al. 2005), which was developed for the analysis of all-sky satellite data.
The HEALPIX-based all-sky spherical grid that we adopted in our analysis contains
![]()
![]() pixels, corresponding to a
pixels, corresponding to a ![]() 2.5 arcmin radius size for each
sky pixel, thus providing more than adequate oversampling of the BAT PSF.
The number of pixels in the all-sky mosaic map is high enough to make PSF distortions in
the projection procedure negligible, so the quality of the final all-sky mosaic is limited only by
the finite sampling resolution of single pointing skymaps (Sect. 3.2).
2.5 arcmin radius size for each
sky pixel, thus providing more than adequate oversampling of the BAT PSF.
The number of pixels in the all-sky mosaic map is high enough to make PSF distortions in
the projection procedure negligible, so the quality of the final all-sky mosaic is limited only by
the finite sampling resolution of single pointing skymaps (Sect. 3.2).
To accumulate the all-sky mosaic, the coordinates of the HEALPIX grid are projected onto the coordinate system of the skymap obtained from the individual pointings. Then, for each point in the projected HEALPIX grid, the intensity of the nearest skymap pixel, weighted by the inverse of the associated statistical variance, is accumulated and the associated statistical error propagated accordingly. By using simulated data, we verified that mosaics generated with this resampling method have a significance distribution that is a Gaussian with a unitary standard deviation independently of the grid spacing used for the single pointing skymaps.
Beside the nearest pixel resampling strategy, bilinear
interpolation can also be used to project the single pointing skymap
onto the final mosaic grid. When using this method it is necessary to
consider that it introduces a smoothing of the mosaic fluctuations so
the propagated statistical error overestimate the actual mosaic noise.
In simulated mosaics generated with this resampling method, we measured
a standard deviation of ![]() 0.9 if single pointing skymaps with a grid resolution of 1/2 pixel are used.
0.9 if single pointing skymaps with a grid resolution of 1/2 pixel are used.
3.8 Mosaic normalization
If a perfect subtraction of all sky sources and background is achieved, the histogram of values of the mosaic significance, which is defined as the ratio of the mosaic intensity to the associated statistical error, should be a Gaussian with a zero mean and a unitary standard deviation.
We checked the propagation of statistical errors in our code by providing as input to the BATIMAGER a set of simulated data (with both background and sources) with Poissonian distribution, and verified that the histogram of values in the final significance mosaic is the expected one. However, in the mosaic skymaps obtained from real survey data, a broadening of the histogram is still observed. This can be caused mainly by a non-perfect modeling of the source illumination pattern, that although negligible in any single skymap, becomes significant in the mosaic, and particularly evident in fields containing very bright sources.
Since the non-statistical spatial fluctuations can produce false source detections and wrong evaluation of source significance, it is necessary to measure the true fluctuations in the final mosaic rather than use the values obtained by the propagation of statistical errors.
To achieve this aim, the software computes the SNR mean values and standard deviations within a set of circular regions, with a radius much larger than the PSF (a few degrees), sampling the entire mosaic skymap. It then derives, by interpolation, the all-sky maps of the local mean values and local standard deviations, which are used to correct the mosaic intensity skymap and the associated statistical error. In Fig. 4, we show an example of the typical SNR distribution of the pixels in the all-sky mosaic map after the renormalization. This distribution can be described (except for the positive tail produced by unsubtracted sky sources) by a Gaussian distribution with unitary variance and zero mean.
![\begin{figure}
\par\includegraphics[width=6.cm,angle=-90,clip]{11779_04.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg25.png)
|
Figure 4: A typical distribution of pixel significances in BAT all-sky maps corrected using locally measured means and standard deviations. The Gaussian curve (a fit obtained by excluding the distribution tail) has a mean and standard deviation consistent with 0.0 and 1.0, respectively. |
| Open with DEXTER | |
3.9 Mosaic source detection
Source detection in the final significance all-sky mosaic is performed by applying a blind localization algorithm directly on the HEALPIX spherical grid. Pixels whose significance value is above a predefined threshold are identified and the source peak position refined with a local fit. The source localization accuracy that we obtained as a function of source significance is reported in Sect. 4.3.
The threshold usually adopted for source detection is ![]() ;
at this level, a few detections
caused by random fluctuations are however expected.
In a skymap without sources and a normal noise distribution, the probability of finding a pixel with
a significance higher than this threshold is
;
at this level, a few detections
caused by random fluctuations are however expected.
In a skymap without sources and a normal noise distribution, the probability of finding a pixel with
a significance higher than this threshold is
![]() =
=
![]() ;
in our all-sky HEALPIX skymap (with
;
in our all-sky HEALPIX skymap (with
![]()
![]() pixels), we then expect to find
pixels), we then expect to find ![]() 23 pixels
above the selected threshold. The number of spurious sources is however
lower than the number of pixels above this threshold, because of the
spatial correlation (on a scale of the order of the PSF FWHM) between
adjacent pixels.
23 pixels
above the selected threshold. The number of spurious sources is however
lower than the number of pixels above this threshold, because of the
spatial correlation (on a scale of the order of the PSF FWHM) between
adjacent pixels.
The correct number of expected spurious sources is evaluated by running the source detection algorithm on
several all-sky mosaics obtained from simulated empty field observations; in these simulations,
the typical number of spurious sources detected is ![]() 15. In mosaics obtained
from real observations, the negative side of the pixel SNR distribution is also analyzed to estimate
the effects of systematic errors on the number of spurious sources.
15. In mosaics obtained
from real observations, the negative side of the pixel SNR distribution is also analyzed to estimate
the effects of systematic errors on the number of spurious sources.
The source candidates are then cross-correlated with known catalogued source locations documented in the literature (e.g., Markwardt et al. 2005; Ajello et al. 2008a; Tueller et al. 2009) for identification.
3.10 Scientific products
Once the sources have been detected and their coordinates included in a catalogue, this can be adopted as input to the BATIMAGER for a second run to extract their light curves and spectra (Sect. 3.5). For these extractions, we use the same information used in the imaging analysis such as the non-uniform background distribution, the pixel efficiency maps, and the correction for the cross-contamination between sources.
For each pointing a spectrum is generated and corrected for the off-axis energy-dependent attenuation (Sect. 4.4). The total source spectrum is then accumulated by summing the single-pointing spectra weighted by the inverse of their variance.
Figure 5
shows a fit to the Crab spectrum generated by our software for the full
number of energy bins (80); the response matrix used in the fit
was obtained from the publicly available BAT response, slightly
modified to force the Crab fit to the canonical model adopted by the
BAT
team![]() ,
a power law with a photon index 2.15 and a normalization
of
,
a power law with a photon index 2.15 and a normalization
of
![]() at 1 keV (Kirsch et al. 2005).
at 1 keV (Kirsch et al. 2005).
![\begin{figure}
\par\includegraphics[width=6.cm,angle=-90,clip]{11779_05.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg30.png)
|
Figure 5: BAT Crab spectrum generated with BATIMAGER ( top panel), and fitting residuals ( bottom panel). |
| Open with DEXTER | |
4 Inflight calibration
The skymaps generated by a coded mask instrument are negatively affected by an imperfect knowledge of the real instrument. These systematic errors induce fluctuation in the skymaps that, for sufficiently long observations, inevitably become higher than thoses expected from the counting statistics.
To obtain a more in-depth knowledge of the instrument, we performed our own inflight calibration analysis. To achieve this aim, we perform preliminary runs of the software to produce the calibration files used as input to the image reconstruction process in subsequent runs.
In the following sections, we describe the calibration analysis that we performed.
4.1 Pixel efficiency maps
The pixel efficiency is expected to be inhomogeneous across the detector e.g., due to variations in the quality of the detector material, dead-time differences, or because of passive elements on a small scale (e.g., pixel electronics and cables).
Since in single-pointing shadowgrams the counting statistics is insufficient to allow us to measure any pixel-to-pixel differences, BATIMAGER accumulates the shadowgrams residual (after subtraction of the illumination pattern for all the bright sources and the background spatial model, Sect. 3.5), over a long series of consecutive satellite pointings; when statistics allow us to determine the detection efficiency in each pixel, the efficiency map is stored as a calibration file for subsequent runs.
Any residual unsubtracted contribution from bright sky sources or background does not influence the computation of the pixel efficiency maps, since it is averaged by the pointing strategy.
4.2 Modeling of the coded mask pattern
An imperfect representation of the coded mask pattern can generate systematic errors in the image reconstruction because of the imperfect subtraction of bright sources (Sect. 3.3). This error can be reduced by measuring the mask illumination pattern directly from the flight data, to infer any difference from the nominal mask pattern model.
The coded mask illumination pattern cannot however be obtained
with the required
accuracy by examining single-pointing shadowgrams. The counting
statistics at pixel level is very limited even by selecting the
pointings with the brightest sources and the longest exposures. In
addition, the spatial resolution of the detector plane (
![]() mm) is too coarse compared to the size of the coded-mask opaque elements (
mm) is too coarse compared to the size of the coded-mask opaque elements (
![]() mm) to allow us to resolve the fine details of the illumination pattern.
mm) to allow us to resolve the fine details of the illumination pattern.
To overcome these two problems, during the calibration runs the BATIMAGER software performs a proper mosaicking of the detector residual shadowgrams (Sect. 3.5) in a coded-mask coordinate system. In this way, by choosing a long set of pointings with bright sources in the field of view, the statistics can be improved to a very good level and, because of the different orientations of the detector pointings, fine details of the mask elements can be resolved at sub pixel resolution.
Figure 6, top panel, shows a small region of the mask illumination pattern reconstructed from BAT survey data, demonstrating that the single opaque elements of the coded mask are reconstructed with sub mm resolution; the image obtained as difference between the measured illumination pattern and the one expected from the nominal mask model (Fig. 6, bottom panel) shows clearly the presence of photon leakage caused by gaps between the coded mask and its support structure.
We then modified the mask model provided by the BAT team![]() ,
by taking into account all the residuals observed from our analysis,
and used our improved mask model in the skymap reconstruction process.
,
by taking into account all the residuals observed from our analysis,
and used our improved mask model in the skymap reconstruction process.
![\begin{figure}
\par\includegraphics[width=7.cm]{11779_06.eps}\\
~\\
\includegraphics[width=7.cm]{11779_07.eps}\\
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg31.png)
|
Figure 6: Top: a small detail of the BAT mask illumination pattern reconstructed by proper mosaicking of the shadowgrams relative to long series of pointings with strong sources in the FOV. Bottom: difference between the measured illumination pattern and the one expected from the mask model distributed with the BAT Calibration Database. The photon leakage between the coded mask and its support structure is evident. |
| Open with DEXTER | |
4.3 Boresight correction and localization accuracy
To obtain the highest source localization accuracy, the misalignment between the satellite star-trackers and the reference system of the BAT instrument must be accurately calibrated. This requires the evaluation of three parameters determining the rotation angles between the star-trackers and the BAT reference system. In our boresight correction, to take into account a possible deformation of the mask support structure, we add two other parameters that determine the translation between the coded mask axis and the detector plane axis.
The calibration is performed using the positions of known bright sources detected with high significance in the sky maps produced by the analysis of single pointings (Sect. 3.3). By minimizing the discrepancy between the measured and nominal source positions, we derived the five boresight correction parameters, which were then stored in calibration files for use in the scientific runs. The parameters are time dependent because of changes in the star-tracker configuration that occurred at some epochs.
Figure 7 shows the 95% error radius obtained from sources detected and identified in single pointings after boresight misalignment correction as a function of the measured detection significance. For comparison, we also show the localization accuracy obtained by running the localization software on a set of simulated shadowgrams with sources placed at their catalogue positions.
![\begin{figure}
\par\includegraphics[width=6cm,angle=-90]{11779_08.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg32.png)
|
Figure 7: The 95% BAT localization
error radius for near on-axis sources observed in individual pointings
as a function of the measured source significance.
The dashed line is the error radius derived from simulations (22.5/SNR arcmin). The solid line has been obtained
by adding a 0.9 |
| Open with DEXTER | |
The localization errors obtained from the simulations closely follow the theoretical (Gros et al. 2003)
dependence on the source SNR; in fact, the 95% localization error
radius obtained for near on-axis sources is consistent with
R95(SNR)=22.5/SNR arcmin. The localization accuracy obtained from observational
data is instead limited at high SNR values by a plateau and can be modeled by adding a ![]() 0.9 arcmin systematic error in quadrature to the simulation result:
0.9 arcmin systematic error in quadrature to the simulation result:
As we have found no significant correlation between the source localization errors and the spacecraft axis orientation, the observed systematic error is probably caused by the sum of small effects, such as imperfections in the mask or detector plane modeling, a non-uniform absorption in the mask support layer, or thermal deformations.
We note that mosaic images are less affected by the systematic
localization error found in individual pointing analysis because of the
overlap of skymaps with different orientations. As shown in
Fig. 8, source
localization offsets in RA and Dec coordinates have similar histograms
with a mean value that is consistent with zero, so the single pointing
offsets are averaged in the mosaics.
By comparing the position of known sources and those derived in the
mosaic images, we found that the 95% containment radius versus the
detection significance in mosaics images can be
modeled with a power law plus a constant:
![]()
![\begin{figure}
\par\includegraphics[width=6.cm,angle=-90]{11779_09.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg35.png)
|
Figure 8:
Distributions of localization errors of significant sources (> |
| Open with DEXTER | |
4.4 Off-axis energy calibration
By using Eqs. (1) and (2) in Sect. 3.6, the count-rate dependence on the off-axis angle can be approximated by
where the factor
In Fig. 9, we show the Crab count rates measured in different energy ranges as a function of
![]() .
The general trend is consistent with Eq. (4), although some systematic deviations are observed in particular in the low energy ranges. These deviations are related to
the non-uniformity of the mask support structure.
.
The general trend is consistent with Eq. (4), although some systematic deviations are observed in particular in the low energy ranges. These deviations are related to
the non-uniformity of the mask support structure.
![\begin{figure}\par\includegraphics[width=6.cm,angle=-90]{11779_10.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg39.png)
|
Figure 9:
Crab measured count rates versus the cosine of the off-axis angle |
| Open with DEXTER | |
In Fig. 10, upper curve, we show the value of the parameter ![]() obtained
from a linear fit to the Crab data as a function of
obtained
from a linear fit to the Crab data as a function of
![]() in narrow energy ranges. Considering
that in this plot a value of 1 is the contribute of the geometric projection factor,
in narrow energy ranges. Considering
that in this plot a value of 1 is the contribute of the geometric projection factor,
![]() ,
the additional contribute of the attenuation of the incident radiation in the mask support structure is clearly
evident in the low energy range; at high energy (>60 keV), the
decreasing of
,
the additional contribute of the attenuation of the incident radiation in the mask support structure is clearly
evident in the low energy range; at high energy (>60 keV), the
decreasing of ![]() because of the decreasing detection efficiency (as expressed by
Eq. (1)) is also clearly evident.
because of the decreasing detection efficiency (as expressed by
Eq. (1)) is also clearly evident.
To confirm the goodness of the off-axis energy correction implemented, in Fig. 10, (lower data), we show the values of ![]() measured on the Crab count rate corrected for the off-axis dependence by means of Eqs. (1) and (2) after optimization of the physical parameters.
measured on the Crab count rate corrected for the off-axis dependence by means of Eqs. (1) and (2) after optimization of the physical parameters.
![\begin{figure}\par\begin{overpic}[width=6.cm,angle=-90]{11779_11.ps}
\put(-5,40){\rotatebox{90}{$\alpha (E)$ } }
\end{overpic}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg40.png)
|
Figure 10: Slope of the dependency of the Crab count rate from the cosine of the off-axis angle as function of energy. The upper data are obtained from count rate without off-axis correction, while the lower data are the values measured after the correction. |
| Open with DEXTER | |
5 Data screening
Together with a set of accurate calibration files, an efficient procedure of data screening is fundamental to obtain the best scientific results from the BAT survey data.
The survey data set was preliminarily screened for time intervals with unstable/wrong spacecraft attitude (e.g., due to slews or to a loss of lock on the star-trackers) and very high count rates, (as it happens, e.g., just before entering or immediately after exiting the SAA). Moreover, to account for star-tracker loss of lock, or star-tracker lock on an incorrect nominal pointing direction, we screened out DPHs, whose reconstructed images showed bright sources with slew-deformed profiles or systematically misplaced from their known position.
Generally, consecutive DPHs with the same pointing are combined into a single shadowgram to improve the quality of the statistics, thus favoring the detection and removal of bright sources (Sect. 3.3) and the modeling and subtraction of the background distribution (Sect. 3.4). However, we have noted quite often, during intervals of stable pointing, strong increases in the total count rate lasting for a few hundreds of seconds, probably induced by short bursts of particle showers associated with solar activity. Skymaps obtained from these intervals have standard deviations that are much higher (by a factor of 2-5) than that expected from statistics and must then be excluded not to degrade the overall mosaic skymap quality.
6 Software performance validation
To validate the performance of the BATIMAGER, we compared the results
obtained with our software to those reported in Tueller et al. (2009) by processing the same
data set (22 months starting mid-December 2004) in the same energy range, and using the same detection threshold (![]() ).
).
In both analyses, the SNR distribution of the noise in the all-sky map is modeled well by a Gaussian profile with a mean zero and unitary standard deviation. This ensures that the source detection significance can be directly compared.
In the significance all-sky map generated with our software, we detected and identified 424 sources out of the 461 reported in Tueller et al. (2009). For the remaining 37 sources that were not detected in our mosaic, we verified that their significance in our sky map is just below the adopted detection threshold. We also detected and identified 193 sources not included in the Tueller catalogue.
In Fig. 11, we compare the significance reported in Table 5 of
Tueller et al. (2009) and the significance obtained with BATIMAGER for the same sources
(424). We find that the BATIMAGER achieves detection of greater significance for more than 90% of the sample with an improvement in significance of ![]()
![]() .
This is probably caused by different strategies in background modeling and systematic error correction.
.
This is probably caused by different strategies in background modeling and systematic error correction.
In Fig. 12, we compare the integrated distribution of the position offset
of the BAT sources: the BATIMAGER detects 95% of the sources with an offset lower than
![]() 2.4 arcmin, while using the position of Table 5 in Tueller et al. (2009),
we find that 95% of the sources are within
2.4 arcmin, while using the position of Table 5 in Tueller et al. (2009),
we find that 95% of the sources are within ![]() 4.2 arcmin of their counterpart. The inset
compares the differential distribution of the offset for the two data sets.
4.2 arcmin of their counterpart. The inset
compares the differential distribution of the offset for the two data sets.
![\begin{figure}
\par\includegraphics[width=7.5cm,height=5.5cm]{11779_12.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg42.png)
|
Figure 11: Comparison between the source significance reported in Tueller et al. (2009) (T) and the detection significance obtained with BATIMAGER (P) for the common sources sample ( top panel) and ratio of P to T significances ( bottom panel). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,height=5.5cm]{11779_13.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg43.png)
|
Figure 12: Integrated and differential (inset) distribution of the offset of the BAT sources with respect to their associated counterparts. The solid line represents the results obtained with BATIMAGER (P) while the dotted line refers to the results reported in Tueller et al. (2009) (T). |
| Open with DEXTER | |
7 Conclusions
We have developed a code, the BATIMAGER, to efficiently process Swift-BAT survey data. The software performs image reconstruction, and generates source spectra and light curves corrected for the off-axis energy dependence.
The processing speed of the software has been optimized by integrating all processing steps (from shadowgram accumulation to the all-sky mosaicking) in a single executable thusconsiderably decreasing the time required to process the enormous BAT archive. All-sky mosaics are generated on a spherical grid in which each pixel covers the same surface area as every other pixel (HEALPIX), thus greatly simplifying any all-sky subsequent analysis.
Systematic errors in image reconstruction have been reduced by performing an accurate inflight calibration of the instrument characteristics. In particular, original solutions are implemented to compute the background spatial model, and a new methodology to calibrate the mask pattern illumination at subpixel resolution has been used.
The software has been fully tested, and the results obtained demonstrate that the BATIMAGER is competitive in exploiting the BAT capabilities in terms of both sensitivity and position reconstruction. The data analysis and the complete catalogue for the first 39 months of the BAT mission are published in Cusumano et al. 2010.
AcknowledgementsThis work was supported by PRIN INAF grant CRA 1.06.10.07. C. F. has been supported by grant DLR 50 OG 0601. We would like to thank the anonymous referee for the valuable comments that significantly improved the quality of the paper.
References
- Ajello, M., Greiner, J., Kanbach, G., et al. 2008a, ApJ, 678, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Ajello, M., Greiner, J., Sato, G., et al. 2008b, ApJ, 689, 666 [Google Scholar]
- Barthelmy, S. D., Barbier, L. M., Cummings, J. R., et al. 2005, Space Sci. Rev., 120, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Cusumano, G., La Parola, V., Segreto, A., et al. 2010, A&A, 510, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fenimore, E. E., & Cannon, T. M. 1978, Appl. Opt., 17, 337 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Feroci, M., Costa, E., Soffitta, P., et al. 2007, Nucl. Instr. Meth. Phys. Res. A, 581, 728 [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Goldwurm, A., David, P., Foschini, L., et al. 2003, A&A, 411, L223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gros, A., Goldwurm, A., Cadolle-Bel, M., et al. 2003, A&A, 411, L179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Hammersley, A. 1986, Ph.D. Thesis, University of Birmingham [Google Scholar]
- Hammersley, A., Ponman, T., & Skinner, G. K. 1992, Nucl. Instr. Meth. Phys. Res. A, 311, 585 [NASA ADS] [CrossRef] [Google Scholar]
- in 't Zand, J. J. M. 1992, Ph.D. Thesis, University Utrecht [Google Scholar]
- Jager, R., Mels, W. A., Brinkman, A. C., et al. 1997, A&AS, 125, 557 [Google Scholar]
- Kendall M. G. 1980, Multivariate analysis, ed. Griffin & co. London [Google Scholar]
- Markwardt, C. B., Tueller, J., Skinner, G. K., et al. 2005, ApJ, 633, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B., Barthelmy, S., Cummings, J. R., et al. 2007, in The SWIFT BAT Software Guide (Version 6.3), http://swift.gsfc.nasa.gov/docs/swift/analysis/bat_swguide_v6_3.pdf [Google Scholar]
- Paul, J., Ballet, J., Cantin, M., et al. 1991, Adv. Space Res., 11, 289 [Google Scholar]
- Pavlinsky, M. N., Grebenev, S. A., & Syunyaev, R. A. 1992, Sov. Astron. Lett., 18, 116 [Google Scholar]
- Pavlinsky, M. N., Grebenev, S. A., & Sunyaev, R. A. 1994, ApJ, 425, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Skinner, G. K., Ponman, T. J., Hammersley, A. P., & Eyles, C. J. 1987a, Ap&SS, 136, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Skinner, G. K., Willmore, A. P., Eyles, C. J., Bertram, D., & Church, M. J. 1987b, Nature, 330, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., Churazov, E. M., Gil'Fanov, M. R., et al. 1991, Adv. Space Res., 11, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Tueller, J., Baumgartner, W. H., Markwardt, C. B., et al. 2009, ApJ, in press [arXiv:0903.3037] [Google Scholar]
- Winkler, C., Courvoisier, T. J.-L., Di Cocco, G., et al. 2003, A&A, 411, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirsch, M. G., Briel, U. G., Burrows, D., et al. 2005, Proc. SPIE, 5898, 22 [NASA ADS] [Google Scholar]
Footnotes
- ...
archive
![[*]](/icons/foot_motif.png)
- http://swift.gsfc.nasa.gov/cgi-bin/sdc/ql
- ...
team
![[*]](/icons/foot_motif.png)
- http://heasarc.gsfc.nasa.gov/docs/swift/nalysis/bat_digest.html
- ... team
![[*]](/icons/foot_motif.png)
- CALDB, http://heasarc.gsfc.nasa.gov/docs/heasarc/caldb/swift/
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11779_01.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg8.png)
|
Figure 1: Flowchart of the BATIMAGER software. All processing steps are integrated in a single executable to reduce the number of mathematical computations and unnecessary I/O operations. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.cm,angle=-90]{11779_02.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg10.png)
|
Figure 2: Scan of the Crab PSF (SNR) in a nearly on-axis BAT observation. The stepped line connects points from a skymap generated with a 1/2 pixel grid spacing, while the solid line connects values from a skymap generated with 1/10 pixel grid spacing. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{11779_03.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg13.png)
|
Figure 3: An example of BAT detector background map (cts/s) in the 25-100 keV energy range. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.cm,angle=-90,clip]{11779_04.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg25.png)
|
Figure 4: A typical distribution of pixel significances in BAT all-sky maps corrected using locally measured means and standard deviations. The Gaussian curve (a fit obtained by excluding the distribution tail) has a mean and standard deviation consistent with 0.0 and 1.0, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.cm,angle=-90,clip]{11779_05.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg30.png)
|
Figure 5: BAT Crab spectrum generated with BATIMAGER ( top panel), and fitting residuals ( bottom panel). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.cm]{11779_06.eps}\\
~\\
\includegraphics[width=7.cm]{11779_07.eps}\\
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg31.png)
|
Figure 6: Top: a small detail of the BAT mask illumination pattern reconstructed by proper mosaicking of the shadowgrams relative to long series of pointings with strong sources in the FOV. Bottom: difference between the measured illumination pattern and the one expected from the mask model distributed with the BAT Calibration Database. The photon leakage between the coded mask and its support structure is evident. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6cm,angle=-90]{11779_08.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg32.png)
|
Figure 7: The 95% BAT localization
error radius for near on-axis sources observed in individual pointings
as a function of the measured source significance.
The dashed line is the error radius derived from simulations (22.5/SNR arcmin). The solid line has been obtained
by adding a 0.9 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.cm,angle=-90]{11779_09.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg35.png)
|
Figure 8:
Distributions of localization errors of significant sources (> |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=6.cm,angle=-90]{11779_10.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg39.png)
|
Figure 9:
Crab measured count rates versus the cosine of the off-axis angle |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\begin{overpic}[width=6.cm,angle=-90]{11779_11.ps}
\put(-5,40){\rotatebox{90}{$\alpha (E)$ } }
\end{overpic}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg40.png)
|
Figure 10: Slope of the dependency of the Crab count rate from the cosine of the off-axis angle as function of energy. The upper data are obtained from count rate without off-axis correction, while the lower data are the values measured after the correction. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,height=5.5cm]{11779_12.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg42.png)
|
Figure 11: Comparison between the source significance reported in Tueller et al. (2009) (T) and the detection significance obtained with BATIMAGER (P) for the common sources sample ( top panel) and ratio of P to T significances ( bottom panel). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,height=5.5cm]{11779_13.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa11779-09/Timg43.png)
|
Figure 12: Integrated and differential (inset) distribution of the offset of the BAT sources with respect to their associated counterparts. The solid line represents the results obtained with BATIMAGER (P) while the dotted line refers to the results reported in Tueller et al. (2009) (T). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}
g\left(\theta,E\right) \approx \cos \theta \cdot \frac{1-\e...
... \theta\right]}{1-\exp\left[-\alpha_{D}\left(E\right)\right]},
\end{displaymath}](/articles/aa/full_html/2010/02/aa11779-09/img16.png)
![\begin{displaymath}
r\left(\theta,E\right) = r_{0} \left( E\right) \cdot g \lef...
...ft(E\right)\cdot \left(\frac{1}{\cos \theta} -1\right)\right],
\end{displaymath}](/articles/aa/full_html/2010/02/aa11779-09/img21.png)