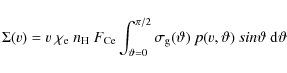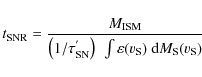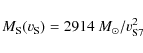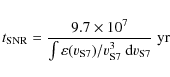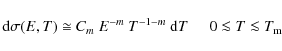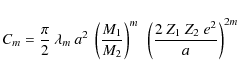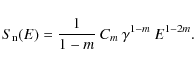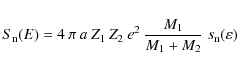| Issue |
A&A
Volume 510, February 2010
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 19 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200911682 | |
| Published online | 04 February 2010 | |
Polycyclic aromatic hydrocarbon processing in interstellar shocks
E. R. Micelotta1,2 - A. P. Jones2 - A. G. G. M. Tielens1,3
1 - Sterrewacht Leiden, Leiden University, PO Box 9513, 2300 RA Leiden,
The Netherlands
2 - Institut d'Astrophysique Spatiale, Université Paris Sud and CNRS
(UMR 8617), 91405 Orsay, France
3 - NASA Ames Research Center, MS 245-3, Moffett Field, CA 94035, USA
Received 20 January 2009 / Accepted 16
October 2009
Abstract
Context. PAHs appear to be an ubiquitous
interstellar dust component but the effects of shocks waves upon them
have never been fully investigated.
Aims. We study the effects of energetic (
![]() keV)
ion (H, He and C) and electron collisions on PAHs in
interstellar shock waves.
keV)
ion (H, He and C) and electron collisions on PAHs in
interstellar shock waves.
Methods. We calculate the ion-PAH and electron-PAH
nuclear and electronic interactions, above the threshold for carbon
atom loss from a PAH, in 50-200 km s-1
shock waves in the warm intercloud medium.
Results. Interstellar PAHs (
![]() )
do not survive in shocks with velocities greater than
100 km s-1 and larger PAHs (
)
do not survive in shocks with velocities greater than
100 km s-1 and larger PAHs (
![]() )
are destroyed for shocks with velocities
)
are destroyed for shocks with velocities ![]() km s-1.
For shocks in the
km s-1.
For shocks in the ![]() km s-1
range, where destruction is not complete, the PAH structure is likely
to be severely denatured by the loss of an important fraction (20-40%)
of the carbon atoms. We derive typical PAH lifetimes of the
order of a few
km s-1
range, where destruction is not complete, the PAH structure is likely
to be severely denatured by the loss of an important fraction (20-40%)
of the carbon atoms. We derive typical PAH lifetimes of the
order of a few
![]() yr for the Galaxy.
These results are robust and independent of the uncertainties in some
key parameters that have yet to be well-determined experimentally.
yr for the Galaxy.
These results are robust and independent of the uncertainties in some
key parameters that have yet to be well-determined experimentally.
Conclusions. The observation of PAH emission in
shock regions implies that that emission either arises outside the
shocked region or that those regions entrain denser clumps that, unless
they are completely ablated and eroded in the shocked gas, allow dust
and PAHs to survive in extreme environments.
Key words: shock waves - dust, extinction - supernovae: general
1 Introduction
Interstellar polycyclic aromatic hydrocarbon molecules (PAHs) are an
ubiquitous component of the interstellar medium. The mid-infrared
spectrum of the general diffuse interstellar medium as well as
energetic environments near massive stars such as H II regions
and reflection nebulae are dominated by broad emission features
at 3.3, 6.2, 7.7, and 11.2 ![]() m. These emission features are now generally
attributed to infrared fluorescence by large PAH molecules
containing 50-100 C-atoms, pumped by single
FUV photons (see Tielens
2008, for a recent review). The observed spectra also show
evidence for PAH clusters containing a few hundred C-atoms (Berné
et al. 2007; Rapacioli et al. 2005; Bregman
et al. 1989) as well as very small dust grains (
m. These emission features are now generally
attributed to infrared fluorescence by large PAH molecules
containing 50-100 C-atoms, pumped by single
FUV photons (see Tielens
2008, for a recent review). The observed spectra also show
evidence for PAH clusters containing a few hundred C-atoms (Berné
et al. 2007; Rapacioli et al. 2005; Bregman
et al. 1989) as well as very small dust grains (![]() 30 Å;
Désert et al. 1990).
It seems that the interstellar grain size distribution extends
all the way into the molecular domain (Draine & Li 2001; Allamandola
et al. 1989; Désert et al. 1990). The
origin and evolution of interstellar PAHs are somewhat controversial.
On the one hand, based upon extensive laboratory studies of soot
formation in terrestrial environments, detailed models have been made
for the formation of PAHs in the ejecta of C-rich giants (Cherchneff
et al. 1992; Frenklach & Feigelson 1989) -
as intermediaries or as side-products of the soot-formation
process - and studies have suggested that such objects might
produce enough PAHs to seed the ISM (Latter
1991). On the other hand, models have been developed where
PAHs (as well as very small grains) are the byproduct of the
grinding-down process of large carbonaceous grains in strong supernova
shock waves which permeate the interstellar medium (Borkowski &
Dwek 1995; Jones
et al. 1996). Grain-grain collisions shatter fast
moving dust grains into small fragments and, for graphitic progenitor
grains, these fragments might be more properly considered
PAH molecules. The destruction of interstellar PAHs is equally
clouded. Laboratory studies have shown that small (less than
16 C-atoms), (catacondensed) PAHs are rapidly photodissociated
by
30 Å;
Désert et al. 1990).
It seems that the interstellar grain size distribution extends
all the way into the molecular domain (Draine & Li 2001; Allamandola
et al. 1989; Désert et al. 1990). The
origin and evolution of interstellar PAHs are somewhat controversial.
On the one hand, based upon extensive laboratory studies of soot
formation in terrestrial environments, detailed models have been made
for the formation of PAHs in the ejecta of C-rich giants (Cherchneff
et al. 1992; Frenklach & Feigelson 1989) -
as intermediaries or as side-products of the soot-formation
process - and studies have suggested that such objects might
produce enough PAHs to seed the ISM (Latter
1991). On the other hand, models have been developed where
PAHs (as well as very small grains) are the byproduct of the
grinding-down process of large carbonaceous grains in strong supernova
shock waves which permeate the interstellar medium (Borkowski &
Dwek 1995; Jones
et al. 1996). Grain-grain collisions shatter fast
moving dust grains into small fragments and, for graphitic progenitor
grains, these fragments might be more properly considered
PAH molecules. The destruction of interstellar PAHs is equally
clouded. Laboratory studies have shown that small (less than
16 C-atoms), (catacondensed) PAHs are rapidly photodissociated
by ![]() 10 eV photons
(Jochims et al. 1994).
However, this process is strongly size-dependent as larger PAHs have
many more modes over which the internal energy can be divided and PAHs
as large as 50 C-atoms might actually be stable against
photodissociation in the ISM (Le Page et al. 2001; Allamandola
et al. 1989). While strong shock waves have been
considered as formation sites for interstellar PAHs, the destruction of
these PAHs in the hot postshock gas has not been evaluated. Yet, high
energy (
10 eV photons
(Jochims et al. 1994).
However, this process is strongly size-dependent as larger PAHs have
many more modes over which the internal energy can be divided and PAHs
as large as 50 C-atoms might actually be stable against
photodissociation in the ISM (Le Page et al. 2001; Allamandola
et al. 1989). While strong shock waves have been
considered as formation sites for interstellar PAHs, the destruction of
these PAHs in the hot postshock gas has not been evaluated. Yet, high
energy (![]() keV)
collisions of PAHs with ions and electrons are highly destructive.
keV)
collisions of PAHs with ions and electrons are highly destructive.
The observational evidence for PAHs in shocked regions is
quite ambiguous. The majority of supernova remnants does not show
PAH features (e.g. Cas A, Smith et al. 2009), but
observations of N132D (Tappe
et al. 2006) suggest the possibility of
PAH survival in shocks. Recent work by Andersen
et al. (2007) investigates the presence of PAHs in a
subset of galactic supernova remnants detected in the
GLIMPSE survey. Unfortunately the interpretation of such
observations is not straightforward, because of the difficulty in
disentangling the PAH features intrinsic to the shocked region
with those arising from the surrounding material. Another interesting
case is the starburst galaxy M 82, which
shows above and below the galactic plane a huge bipolar outflow of
shock-heated gas interwoven with PAH emission![]() (Armus et al. 2007).
PAHs have also been observed at high galactic latitudes in the edge-on
galaxies NGC 5907 and NGC 5529 (Irwin &
Madden 2006; Irwin
et al. 2007). Shock driven winds and supernovae can
create a so-called ``galactic fountain'' (Bregman
1980) transporting material into the halo and these
detections of PAHs suggests the possibility of survival or formation of
the molecules under those conditions. On the other hand O'Halloran
et al. (2008,2006) have found a strong
anti-correlation between the ratio [FeII]/[NeII] and PAH strenght in a
sample of low-metallicity starburst galaxies. Since [FeII] has
been linked primarly to supernova shocks, the authors attributed the
observed trend to an enhanced supernova activity which led to
PAH destruction.
(Armus et al. 2007).
PAHs have also been observed at high galactic latitudes in the edge-on
galaxies NGC 5907 and NGC 5529 (Irwin &
Madden 2006; Irwin
et al. 2007). Shock driven winds and supernovae can
create a so-called ``galactic fountain'' (Bregman
1980) transporting material into the halo and these
detections of PAHs suggests the possibility of survival or formation of
the molecules under those conditions. On the other hand O'Halloran
et al. (2008,2006) have found a strong
anti-correlation between the ratio [FeII]/[NeII] and PAH strenght in a
sample of low-metallicity starburst galaxies. Since [FeII] has
been linked primarly to supernova shocks, the authors attributed the
observed trend to an enhanced supernova activity which led to
PAH destruction.
In our previous study (Jones
et al. 1996), we considered the dynamics and
processing of small carbon grains with ![]()
![]() 100.
The processing of these grains by sputtering (inertial and thermal) in
ion-grain collisions and by vaporisation and shattering in grain-grain
collisions was taken into account for all the considered grain sizes.
In that work, the smallest fragments (
100.
The processing of these grains by sputtering (inertial and thermal) in
ion-grain collisions and by vaporisation and shattering in grain-grain
collisions was taken into account for all the considered grain sizes.
In that work, the smallest fragments (
![]() Å) were collected in
the smallest size bin and not processed. In this work we now consider
what happens to these smallest carbon grain fragments that we will here
consider as PAHs. In this paper, we will consider relatively
low velocity (
Å) were collected in
the smallest size bin and not processed. In this work we now consider
what happens to these smallest carbon grain fragments that we will here
consider as PAHs. In this paper, we will consider relatively
low velocity (![]() km s-1)
shocks where the gas cools rapidly behind the shock front but, because
of their inertia, PAHs (and grains) will have high velocity
collisions even at large postshock column densities. Collisions between
PAHs and the gas ions occur then at the PAH velocity which will slowly
decrease behind the shock front due to the gas drag. This relative
velocity is thus independent of the ion mass and, for dust grains,
destruction is commonly called inertial sputtering. Destruction of PAHs
in high velocity (
km s-1)
shocks where the gas cools rapidly behind the shock front but, because
of their inertia, PAHs (and grains) will have high velocity
collisions even at large postshock column densities. Collisions between
PAHs and the gas ions occur then at the PAH velocity which will slowly
decrease behind the shock front due to the gas drag. This relative
velocity is thus independent of the ion mass and, for dust grains,
destruction is commonly called inertial sputtering. Destruction of PAHs
in high velocity (![]() km s-1)
shocks - which cool slowly through adiabatic
expansion - is dominated by thermal sputtering and these
shocks are considered in a subsequent paper (Micelotta
et al. 2010, hereafter MJT).
km s-1)
shocks - which cool slowly through adiabatic
expansion - is dominated by thermal sputtering and these
shocks are considered in a subsequent paper (Micelotta
et al. 2010, hereafter MJT).
This paper is organized as follows: Sect. 2 describes the theory of ion interaction with solids, Sect. 3 illustrates the application of this theory to PAH processing by shocks and Sect. 4 presents our results on PAH destruction. The PAH lifetime in shocks and the astrophysical implications are discussed in Sect. 5 and our conclusions summarized in Sect. 6.
2 Ion interaction with solids
2.1 Nuclear interaction
The approach used in our earlier work is not valid for planar PAH molecules with of the order of tens of carbon atoms. Here, we assume that collisions are binary in nature, as is assumed in work on solids (Sigmund 1981; Lindhard et al. 1963,1968). If the energy transfer is above the appropriate threshold value, we assume that the carbon target is ejected from the molecule. For energy transfer below that threshold, the energy will become thermal energy and be radiated away.
In this description the ``bulk'' nature of the target enters only after the first interaction, when the projectile propagates into the material. We therefore consider only the first interaction, which is described in the binary collision approximation in a way that then conveniently allows us to take into account the ``molecular'' nature of the target.
In addition to the energy directly transferred to the target nucleus through elastic scattering (nuclear stopping or elastic energy loss), the energy loss to the atomic electrons (electronic stopping or inelastic energy loss) should also be considered (Lindhard et al. 1963,1968). In a solid the energy transferred via electronic excitation is distributed around the impact region. For a PAH, which has a finite size, the energy will be spread out over the entire molecule. This energy will either be radiated away or a fragment can be ejected.
Nuclear and electronic stopping are simultaneous processes
which can be treated separately (Lindhard
et al. 1963). Figure 11 illustrates
these effects and shows the PAH evolution following the loss
of carbon atoms, ![]() (lost),
for the two limiting cases: 1) where there is an instantaneous
and random removal of the lost carbon atoms and 2) where the
carbon atoms are removed only from the periphery in order to preserve
aromatic domain as much as possible. The reality of
PAH erosion in shocks probably lies somewhere between these
two extremes and will involve isomerisation and the formation of
five-fold carbon rings that distort the structure from a perfectly
two-dimensional form. This then begs the question as to the exact form
and structure of small carbon species once growth resumes by atom
insertion and addition. The full treatment of the nuclear stopping is
given here, for the electronic stopping only the results of the
calculations are shown, for the complete description of the phenomenon
we refer the reader to paper MJT.
(lost),
for the two limiting cases: 1) where there is an instantaneous
and random removal of the lost carbon atoms and 2) where the
carbon atoms are removed only from the periphery in order to preserve
aromatic domain as much as possible. The reality of
PAH erosion in shocks probably lies somewhere between these
two extremes and will involve isomerisation and the formation of
five-fold carbon rings that distort the structure from a perfectly
two-dimensional form. This then begs the question as to the exact form
and structure of small carbon species once growth resumes by atom
insertion and addition. The full treatment of the nuclear stopping is
given here, for the electronic stopping only the results of the
calculations are shown, for the complete description of the phenomenon
we refer the reader to paper MJT.
The treatment of PAH processing by shocks should also include
the effects of fast electrons present in the gas. Because of their low
mass, electrons can reach high velocities and hence high collision
rates even at relatively low temperatures (T ![]() 105 K),
leading to potentially destructive collisions. Again for a detailed
description of the electron-PAH interaction see paper MJT.
105 K),
leading to potentially destructive collisions. Again for a detailed
description of the electron-PAH interaction see paper MJT.
The theory of ion penetration into solids described here considers collisions where the transferred energy T goes from 0 to the maximum transferable energy. For this study, we are interested in only those collisions that are able to remove carbon atoms from the PAH, i.e. for which the energy transferred is greater than the minimum energy T0 required for C ejection. In Sect. 2.2 we present the modifications we introduce into the theory in order to treat the case of collisions above this threshold.
To describe the binary collision between a moving atom
(or ion) and a stationary target atom (e.g. Sigmund 1981), a pure
classical two-particle model using the Coulomb repulsion between the
nuclei (Rutherford scattering) is adequate only at high energies,
i.e. when ![]()
![]() 1,
where
1,
where
![]() is the dimensionless Lindhard's reduced energy
is the dimensionless Lindhard's reduced energy
where M1 and Z1 are the mass and atomic number of incident particle respectively, M2 and Z2 the mass and atomic number of target particle, E is the kinetic energy of incident particle and e is the electron charge, with e2 = 14.39 eV
where a0 = 0.529
To choose the appropriate formalism to describe our
interaction, we need to calculate the reduced energy for our
projectiles. For our study of the behaviour of PAHs in shocks, we
consider the binary
collision between H, He and C ions (projectiles) and
a carbon atom (target) in the PAH molecule. The
velocity ![]() of the projectile is determined by the shock velocity
of the projectile is determined by the shock velocity ![]() through the relation
through the relation ![]()
![]() .
We consider here shock velocities between 50 and
200 km s-1. The corresponding
projectile kinetic energies E and reduced
energies
.
We consider here shock velocities between 50 and
200 km s-1. The corresponding
projectile kinetic energies E and reduced
energies
![]() are reported in Table 1
for the two limiting cases
are reported in Table 1
for the two limiting cases ![]() (50) =
37.5 km s-1 and
(50) =
37.5 km s-1 and ![]() (200) = 150 km s-1.
(200) = 150 km s-1.
Table 1:
Kinetic energy E and reduced energy
![]() for H, He and C impacting on a carbon atom.
for H, He and C impacting on a carbon atom.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11682fg1.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg54.png)
|
Figure 1:
Scattering geometry for an elastic collision of particle 1
(mass M1, initial
velocity v0, impact
parameter p), on particle 2
(mass M2, initial
velocity zero). After the impact, the projectile particle 1 is
deflected by the angle |
| Open with DEXTER | |
The calculation clearly shows that for the shocks we are considering ![]()
![]() 1,
implying that our problem cannot be treated in terms of Rutherford
scattering but requires a different formalism, described by Sigmund (1981) and summarized below.
The scattering geometry for an elastic collision of the projectile
particle 1 on target particle 2 is illustrated in
Fig. 1.
Particle 1 has mass M1,
initial velocity v0
and impact parameter p, where the impact
parameter is the distance of closest approach of the centers of the
two atoms/ions that would result if the projectile trajectory was
undeflected. Particle 2 has mass M2
and is initially at rest. After the impact, the projectile is deflected
by the angle
1,
implying that our problem cannot be treated in terms of Rutherford
scattering but requires a different formalism, described by Sigmund (1981) and summarized below.
The scattering geometry for an elastic collision of the projectile
particle 1 on target particle 2 is illustrated in
Fig. 1.
Particle 1 has mass M1,
initial velocity v0
and impact parameter p, where the impact
parameter is the distance of closest approach of the centers of the
two atoms/ions that would result if the projectile trajectory was
undeflected. Particle 2 has mass M2
and is initially at rest. After the impact, the projectile is deflected
by the angle ![]() and continues its trajectory with velocity v1.
A certain amount of energy T is
transferred to the target particle which recoils at an angle
and continues its trajectory with velocity v1.
A certain amount of energy T is
transferred to the target particle which recoils at an angle ![]() with velocity v2.
The maximum transferable energy corresponds to a head-on collision
(impact parameter p = 0) and is
given by
with velocity v2.
The maximum transferable energy corresponds to a head-on collision
(impact parameter p = 0) and is
given by
An important quantity to consider is the nuclear stopping cross section
where
The nuclear stopping cross section can be expressed in terms
of the Lindhard's reduced energy
![]() and the dimensionless reduced nuclear stopping
cross section
and the dimensionless reduced nuclear stopping
cross section
![]() (Lindhard et al. 1968,
see Eqs. (A.4)
and (A.5)).
For this latter we adopt the Universal reduced
Ziegler-Biersack-Littmark (ZBL) nuclear stopping cross
section
(Lindhard et al. 1968,
see Eqs. (A.4)
and (A.5)).
For this latter we adopt the Universal reduced
Ziegler-Biersack-Littmark (ZBL) nuclear stopping cross
section
![]() (Ziegler et al. 1985),
which is an analytical approximation to a numerical solution that
reproduces well the experimental data. The ZBL reduced nuclear
stopping cross section has the form
(Ziegler et al. 1985),
which is an analytical approximation to a numerical solution that
reproduces well the experimental data. The ZBL reduced nuclear
stopping cross section has the form
and the nuclear stopping cross section
with the screening length
2.2 Nuclear interaction above threshold
For this study we are interested in destructive collisions, i.e., collisions for which the average transferred energy T exceeds the minimum energy T0 required to remove a carbon atom from the PAH. The theory discussed in Sect. 2.1 does not treat this situation and considers the specific case where T0 = 0 (no threshold). To include the treatment of collisions above threshold (T0 > 0) we developped the appropriate expressions for the relevant quantities described in the previous sections.
The definition of the nuclear stopping cross section ![]() (E)
can be written in a more general way as
(E)
can be written in a more general way as
where T0
In this case the threshold T0 must be strictly positive, otherwise
The condition
Table 2:
Threshold energy T0 and
critical kinetic energy
![]() for H, He and C ions impacting on a carbon atom.
for H, He and C ions impacting on a carbon atom.
Using d![]() from Eq. (A.1)
and evaluating the above integrals we obtain
from Eq. (A.1)
and evaluating the above integrals we obtain
To calculate the quantity m = m(E) we use the following expression from Ziegler et al. (1985)
with
Combining Eqs. (A.3)
and (A.4),
after some algebraic manipulation, we can rewrite the above expressions
for ![]() ,
,
![]() and
and
![]() in the more convenient form shown below. The full calculation is
reported in Appendix A. As explained in
Sect. 2.1, we adopt for the reduced stopping cross section the
ZBL function
in the more convenient form shown below. The full calculation is
reported in Appendix A. As explained in
Sect. 2.1, we adopt for the reduced stopping cross section the
ZBL function
![]() (Eq. (5))
with the appropriate screening length
(Eq. (5))
with the appropriate screening length ![]() .
.
Note that the term outside of the square brackets in Eqs. (14) and (15) is the stopping cross section
The nuclear stopping cross section ![]() (eV
(eV ![]() atom-1),
the total energy transfer cross section
atom-1),
the total energy transfer cross section ![]() (
(![]() atom-1)
and the average energy transferred
atom-1)
and the average energy transferred ![]() (eV),
for H, He and C ions impacting on a carbon atom,
calculated from the above expressions assuming a threshold T0 = 7.5 eV,
are shown in Fig. 2.
(eV),
for H, He and C ions impacting on a carbon atom,
calculated from the above expressions assuming a threshold T0 = 7.5 eV,
are shown in Fig. 2.
The sharp cut on the left-hand side of the curves arises from
the fact that we are treating collisions above threshold, and these
quantities are defined only for energies of the incident ion greater
than the critical value ![]() .
It can be seen that all quantities increase in absolute value
with increasing atomic number and mass of the projectile (Z1 and M1).
The two vertical lines indicate the minimum and maximum kinetic energy
of the projectile considered in our study, corresponding to the
PAH velocity in the 50 and 200 km s-1
shocks respectively. The values are those calculated
in Sect. 2.1 and reported in Table 1. The figure
cleary shows that for hydrogen the critical value
.
It can be seen that all quantities increase in absolute value
with increasing atomic number and mass of the projectile (Z1 and M1).
The two vertical lines indicate the minimum and maximum kinetic energy
of the projectile considered in our study, corresponding to the
PAH velocity in the 50 and 200 km s-1
shocks respectively. The values are those calculated
in Sect. 2.1 and reported in Table 1. The figure
cleary shows that for hydrogen the critical value ![]() is greater than the lower limit of energy range. This implies that in
the lower velocity shocks hydrogen is not energetic enough to cause
carbon ejection. The curves for
is greater than the lower limit of energy range. This implies that in
the lower velocity shocks hydrogen is not energetic enough to cause
carbon ejection. The curves for ![]() presents a characteristic convex shape with a maximum, illustrating
that nuclear energy transfer is important only for projectiles with
energy falling in a specific range. In particular, the nuclear
stopping becomes zero at high energies, with a limiting value depending
on projectile and target: in our case, going from H
to C impacting on carbon, the curves extend further to the
right, in the direction of higher energies. In the
high energy regime, the energy transfer is dominated by electronic
stopping (MJT).
presents a characteristic convex shape with a maximum, illustrating
that nuclear energy transfer is important only for projectiles with
energy falling in a specific range. In particular, the nuclear
stopping becomes zero at high energies, with a limiting value depending
on projectile and target: in our case, going from H
to C impacting on carbon, the curves extend further to the
right, in the direction of higher energies. In the
high energy regime, the energy transfer is dominated by electronic
stopping (MJT).
![\begin{figure}
\par\includegraphics[width=15cm,clip]{11682fg2.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg80.png)
|
Figure 2:
The nuclear stopping cross section
|
| Open with DEXTER | |
For a given incident ion energy, the difference between the values
of ![]() in the threshold and no-threshold cases results from the definition of
the nuclear stopping and from the properties of d
in the threshold and no-threshold cases results from the definition of
the nuclear stopping and from the properties of d![]() .
The differential cross section (cf. Eq. (A.1)) strongly
prefers collisions with low energy transfers (T
.
The differential cross section (cf. Eq. (A.1)) strongly
prefers collisions with low energy transfers (T ![]()
![]() )
and, moreover, decreases in absolute magnitute with increasing E.
For each E,
)
and, moreover, decreases in absolute magnitute with increasing E.
For each E, ![]() is defined as the
integral over the transferred energy T, of
the product between T and the corresponding
cross section d
is defined as the
integral over the transferred energy T, of
the product between T and the corresponding
cross section d![]() .
Choosing T0 >
0 means excluding from the integral all energy transfers T
< T0,
for which the cross section has the highest values. The
remaining terms have higher values of T but
lower values of d
.
Choosing T0 >
0 means excluding from the integral all energy transfers T
< T0,
for which the cross section has the highest values. The
remaining terms have higher values of T but
lower values of d![]() ,
then the integral gives a result smaller than the no-threshold case,
which includes all small energy transfers with their higher cross
sections.
,
then the integral gives a result smaller than the no-threshold case,
which includes all small energy transfers with their higher cross
sections.
The total cross section ![]() (E) clearly
shows that the projectiles can efficiently transfer energy to the
target atom only when their kinetic energy lies in the appropriate
window. In particular, it can be seen that the average energy
transferred
(E) clearly
shows that the projectiles can efficiently transfer energy to the
target atom only when their kinetic energy lies in the appropriate
window. In particular, it can be seen that the average energy
transferred
![]() increases with E, nevertheless at high
energies
increases with E, nevertheless at high
energies ![]() is close to zero (and the collision rate will be small). For a
fixed target atom (in our case, carbon), the width of the
is close to zero (and the collision rate will be small). For a
fixed target atom (in our case, carbon), the width of the ![]() curve,
and consequently the width of the energy window, increases
with Z and M of
the projectile. Heavier ions transfer more energy and in a more
efficient way.
curve,
and consequently the width of the energy window, increases
with Z and M of
the projectile. Heavier ions transfer more energy and in a more
efficient way.
2.2.1 The threshold energy T0
The threshold energy, T0, is
the minimum energy that must be transferred via nuclear excitation to a
carbon atom, in order to eject that same atom from the
PAH molecule. The choice for T0
for a PAH is unfortunately not well-constrained. There are no
experimental determinations, and the theoretical evaluation is
uncertain. The analog of T0
in a solid is the displacement energy ![]() ,
defined as the minimum energy that one atom in the lattice must receive
in order to be moved more than one atomic spacing away from its initial
position, to avoid the immediate hop back into the original site. For
graphite, the data on the threshold energy for atomic displacement
differ significantly, varying from
,
defined as the minimum energy that one atom in the lattice must receive
in order to be moved more than one atomic spacing away from its initial
position, to avoid the immediate hop back into the original site. For
graphite, the data on the threshold energy for atomic displacement
differ significantly, varying from ![]() 30 eV (Montet & Myers 1971; Montet 1967)
to 12 eV (Nakai
et al. 1991) largely depending on direction
(e.g., within or perpendicular to the basal plane). For
a PAH, the lower value (corresponding to the perpendicular
direction) seems then more appropriate. For amorphous carbon, Cosslett (1978) has found a low
value of 5 eV. Electron microscopy studies by Banhart (1997) on graphitic
nanostructures irradiated with electrons of different energies,
indicate that a value of
30 eV (Montet & Myers 1971; Montet 1967)
to 12 eV (Nakai
et al. 1991) largely depending on direction
(e.g., within or perpendicular to the basal plane). For
a PAH, the lower value (corresponding to the perpendicular
direction) seems then more appropriate. For amorphous carbon, Cosslett (1978) has found a low
value of 5 eV. Electron microscopy studies by Banhart (1997) on graphitic
nanostructures irradiated with electrons of different energies,
indicate that a value of ![]()
![]() 15-20 eV
seems appropriate for the perpendicular direction. The in-plane value,
however, could be much higher, presumably
above 30 eV.
15-20 eV
seems appropriate for the perpendicular direction. The in-plane value,
however, could be much higher, presumably
above 30 eV.
Instead of graphite, fullerenes and carbon nanotubes may be a
better analog for PAH molecules. For fullerene, ![]() has
been found between 7.6 and 15.7 eV (Füller & Banhart 1996).
Single walled nanotubes consist of a cylindrically curved graphene
layer. Unfortunately, also in this case the threshold for atomic
displacement is not precisely determined. However it is expected to be
lower than in a multi-layered tube, for which a value of
has
been found between 7.6 and 15.7 eV (Füller & Banhart 1996).
Single walled nanotubes consist of a cylindrically curved graphene
layer. Unfortunately, also in this case the threshold for atomic
displacement is not precisely determined. However it is expected to be
lower than in a multi-layered tube, for which a value of ![]()
![]() 15-20 eV has been found (Banhart
1997) close to the value of graphite. We note
that 4.5 and 7.5 eV are close to the energy of the
single and double C-bond.
15-20 eV has been found (Banhart
1997) close to the value of graphite. We note
that 4.5 and 7.5 eV are close to the energy of the
single and double C-bond.
Because we cannot provide a well-defined T0, we decided to explore a range of values, to study the impact of the threshold energy on the PAH processing. For our standard case, we adopt 7.5 eV that we consider a reasonable value consistent with all the experimental data. However, we have varied T0 from 4.5 to 15 eV.
Figure 3
shows the comparison between ![]() ,
,
![]() and
and ![]() calculated for He on C assuming T0 =
4.5, 7.5 and 15 eV. Coherently with their definition,
calculated for He on C assuming T0 =
4.5, 7.5 and 15 eV. Coherently with their definition, ![]() and
and
![]() increase
with decreasing threshold, because more collisions are effective and
the cross section increases with decreasing energy. Of course,
the average energy transferred will decrease when the threshold energy
is decreased.
increase
with decreasing threshold, because more collisions are effective and
the cross section increases with decreasing energy. Of course,
the average energy transferred will decrease when the threshold energy
is decreased.
In Sect. 4.1 we discuss the effect of the choice of different values for T0 on the PAH survival in shocks.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{11682fg3.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg84.png)
|
Figure 3:
The nuclear stopping cross section
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11682fg4.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg87.png)
|
Figure 4:
The structure of the 125 km s-1
shock: temperature T4
= T/104 K, hydrogen
density |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11682fg5.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg88.png)
|
Figure 5:
The velocity profile of a 50 C-atom PAH in a shock with
velocity |
| Open with DEXTER | |
3 PAHs in shocks
When grains and PAHs enter a shock they become charged and then gyrate around the compressed magnetic field lines. This leads to relative gas-particle velocities and hence to collisions with the gas (and other grains/PAHs). Collisions with the gas result in drag forces and therefore a decrease in the relative gas-particle velocity. However, these same collisions with the gas can also lead to the removal of atoms from the particle if the relative velocites are larger than the given threshold for an erosional process. The removal of carbon atoms from the PAH due to ion collisions, where the impact velocity is determined by the relative motion between the two partners, is the analog of the inertial sputtering of dust particles due to ion-grain collisions. In the following we will then refer to it using the term inertial, and the same will apply for all the related quantities.
In determining the processing of PAHs in shock waves,
as with all grain processing, it is the relative
gas-grain velocity profile through the shock that determines the level
of processing. In calculating the relative
ion-PAH velocity through the shock we use the same approach as
in our previous work (Jones
et al. 1994,1996), which is based on the
methods described in McKee
et al. (1987). The PAH velocity is
calculated using a 3D particle of the same mass as
the 50 carbon atom PAH under consideration. The
PAH velocity depends then on the PAH mass and average
geometric cross section. For a PAH with ![]() carbon atoms, these
are given by
carbon atoms, these
are given by
![]() and
and ![]() with
with ![]() given by
given by
![]() Å, appropriate for a
compact PAH (Omont 1986) and
the factor 1/2 in the cross section takes the averaging over
impact angle into account. The PAH and grain cross sections
are very close (to within 11% for
Å, appropriate for a
compact PAH (Omont 1986) and
the factor 1/2 in the cross section takes the averaging over
impact angle into account. The PAH and grain cross sections
are very close (to within 11% for ![]() = 50), thus
we are justified in using the same numerical approach even though we
are using a 3D grain to calculate the velocity
profile of a 2D PAH through the shock.
= 50), thus
we are justified in using the same numerical approach even though we
are using a 3D grain to calculate the velocity
profile of a 2D PAH through the shock.
The PAHs are injected into the shock with 3/4 of the shock
speed, as are all grains, and their trajectories are then calculated
self-consistently with their coupling to the gas, until the relative
gas-PAH veocity becomes zero. The velocity calculation
includes the effects of the direct drag with the gas due to atom and
ion collisions and the drag due to the ion-charged
PAH interaction in the post-shock plasma. We find that for
some shock velocities, in our case for ![]() and 100 km s-1, the PAHs (and
grains) experience betatron acceleration in the post-shock gas. All the
relevant expressions and assumptions for the calculation of the grain
velocity, betatron acceleration and grain charge are fully described in
McKee et al. (1987).
Thus, in
calculating the post-shock PAH velocity profiles, we follow
exactly the same methods as used in our previous work. The structure of
the 125 km s-1 shock is shown
in Fig. 4
as a function of the column density
and 100 km s-1, the PAHs (and
grains) experience betatron acceleration in the post-shock gas. All the
relevant expressions and assumptions for the calculation of the grain
velocity, betatron acceleration and grain charge are fully described in
McKee et al. (1987).
Thus, in
calculating the post-shock PAH velocity profiles, we follow
exactly the same methods as used in our previous work. The structure of
the 125 km s-1 shock is shown
in Fig. 4
as a function of the column density ![]() .
Figure 5
shows the velocity profile for a 50 carbon
atom PAH in the same shock, together with the effective charge
of the molecule, used to calculate the velocity profile itself. The
50 C-atoms PAH is positively charged (charge
between +2 and +3) during the whole slowing process,
and approaches neutrality at the end of the shock.
.
Figure 5
shows the velocity profile for a 50 carbon
atom PAH in the same shock, together with the effective charge
of the molecule, used to calculate the velocity profile itself. The
50 C-atoms PAH is positively charged (charge
between +2 and +3) during the whole slowing process,
and approaches neutrality at the end of the shock.
3.1 Ion collisions: nuclear interaction
Knowing the velocity profile of the PAH, we can then calculate the
inertial collision rate PAH-ions
![]() (s-1)
through the shock. This is given by the following equation
(s-1)
through the shock. This is given by the following equation
where
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11682fg6.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg102.png)
|
Figure 6:
The number of collisions |
| Open with DEXTER | |
The term ![]() is the cross section averaged over those collisions that transfer an
energy larger than the threshold energy T0
per C-atom and this cross section should therefore be multiplied by the
number of carbon atoms in the PAH,
is the cross section averaged over those collisions that transfer an
energy larger than the threshold energy T0
per C-atom and this cross section should therefore be multiplied by the
number of carbon atoms in the PAH, ![]() .
The factor 0.5 takes the angle averaged orientation into
account (see Appendix C).
.
The factor 0.5 takes the angle averaged orientation into
account (see Appendix C).
Because both collision partners are charged, the effect of the
Coulombian potential must be included as well. Depending on
whether the interaction is attractive or repulsive, the energy transfer
cross section will be increased or reduced by the coulombian
factor ![]() given by
given by
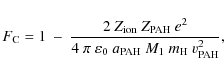
|
(18) |
where
where it should be understood that the postshock column density
Figure 6
illustrates the destructive collisions for
a 50 C-atom PAH behind
a 125 km s-1 shock
assuming T0=7.5 eV.
These results are plotted in such a way that equal areas under the
curve indicate equal contributions to the total number of destructive
collisions. ![]() drops
precipitously because of the drop in relative PAH-gas velocity. Because
heavier projectiles are more energetic in inertial collisions, this
drop off shifts to higher column densities for heavier species. The
results show that He is much more effective in destroying PAHs
than H because of the increased energy transferred for heavier
collision partners (cf. Fig. 2). The
low abundance of C depresses its importance in inertial sputtering.
drops
precipitously because of the drop in relative PAH-gas velocity. Because
heavier projectiles are more energetic in inertial collisions, this
drop off shifts to higher column densities for heavier species. The
results show that He is much more effective in destroying PAHs
than H because of the increased energy transferred for heavier
collision partners (cf. Fig. 2). The
low abundance of C depresses its importance in inertial sputtering.
The number of carbon atoms in a PAH is now given by
| (20) |
and the fraction of carbon atoms ejected from this PAH is
where
In the shocked gas, the velocity of the ions is not only
determined by the relative motion with respect to the PAH (inertial
case), but also by the temperature of the shocked gas. In principle,
the inertial and thermal velocity should be added vectorally and
averaged over the angle between the inertial motion and the (random)
thermal motion as well as over the thermal velocity distribution.
However, that becomes a quite cumbersome calculation and, hence, we
will follow calculations for sputtering of dust grains in interstellar
shocks (cf. Jones et al. 1994)
and evaluate these two processes (inertial and thermal sputtering)
independently. Studies have shown that this reproduces more extensive
calculations satisfactorily (Guillet
et al. 2007). The thermal destruction rate is
given by
with
3.2 Ion collisions: electronic interaction
As reported in the introduction of the paper, the collision between PAH and ions triggers two simultaneous process, which can be treated separately: the nuclear stopping (elastic energy loss) and the electronic stopping (inelastic energy loss). The first has been extensively discussed in the previous sections, while for the full treatment of the electronic interaction we refer the reader to MJT. For the sake of clarity, we report here the essential concepts and the principal equations which will be used in the following.
The energy transferred to the electrons is spread out over the
entire molecule, leaving the PAH in an excited state. De-excitation
occurs through two pricipal decay channels: emission of infrared
photons and dissociation and loss of a C2 fragment.
This latter is the process we are interested in, because it leads to
the PAH fragmentation. The dissociation probability p
(see Sect. 4.1 in MJT) depends on the
binding energy of the fragment E0,
on the PAH size, ![]() ,
and on the energy transferred, which in turns depends on the initial
energy (velocity) of the projectile.
,
and on the energy transferred, which in turns depends on the initial
energy (velocity) of the projectile.
For a fixed value of the transferred energy, the dissociation
probability decreases for increasing E0
and ![]() because either more energy is required in the bond that has to be
broken or because the energy is spread over more vibrational modes and
hence the internal excitation temperature is lower. On the
other hand, the more energy that is deposited in the PAH, the higher is
the dissociation probability. The energy transferred via electronic
excitation increases with the energy of the projectile up to a maximum
value, corresponding to an incident energy of 100 keV
for H (and higher for more massive particles), and decreases
for higher energies. The deposited energy also increases with the
path-length through the molecule
and will be higher for larger PAHs impacted at grazing collision
angles. For the shocks considered in this study, the energy transferred
increases with incident energy (velocity) and hence the dissociation
probability increases as well.
because either more energy is required in the bond that has to be
broken or because the energy is spread over more vibrational modes and
hence the internal excitation temperature is lower. On the
other hand, the more energy that is deposited in the PAH, the higher is
the dissociation probability. The energy transferred via electronic
excitation increases with the energy of the projectile up to a maximum
value, corresponding to an incident energy of 100 keV
for H (and higher for more massive particles), and decreases
for higher energies. The deposited energy also increases with the
path-length through the molecule
and will be higher for larger PAHs impacted at grazing collision
angles. For the shocks considered in this study, the energy transferred
increases with incident energy (velocity) and hence the dissociation
probability increases as well.
As for the nuclear stopping, also for the electronic
interaction we have to consider the effect of both inertial and thermal
velocities. The inertial collision rate is
given by
where
which reduces to
For the thermal collision rate we have
where the temperature T =
There is a clear distinction between the nuclear and electronic interactions. In nuclear interactions, a C-atom is ejected because a direct collision with the impacting ion transfers enough energy and momentum to kick out the impactee instantaneously. In electronic interaction, the impacting ion excites the electrons of the PAH. Internal conversion transfers this energy to the vibrational motions of the atoms of the PAH. Rapid intramolecular vibrational relaxation leads then to a thermalization of this excess energy among all the vibrational modes and this can ultimately lead to dissociation (or relaxation through IR emission). The threshold energy in the nuclear process, T0, differs therefore from the electronic dissociation energy, E0. The latter really is a parameter describing the dissociation rate of a highly excited PAH molecules using an Arrhenius law and this does not necessarily reflect the actual binding energy of the fragment to the PAH species (cf. Tielens 2005). Following MJT, we will adopt the canonical value of 4.6 eV for E0. However, this energy is very uncertain and we will evaluate the effects of reducing and increasing this parameter to a value of 3.65 and 5.6 eV respectively (MJT).
3.3 Electron collisions
For the full treatment of the PAH collisions with electrons, we refer again to the paper MJT, providing here a short summary of the basic concepts and equations.
Because of their small mass, the thermal velocity of the
electrons always exceeds the inertial velocity of the PAH. Hence, only
the thermal destruction needs to be evaluated. We follow the same
formalism used for the electronic interaction in
ion-PAH collisions. The energy dumped into the molecule during
collisions with electrons is spread over and determines (with E0
and ![]() )
the value of the dissociation probability. The electron energy loss
rises sharply with the electron energy, reaching its maximum for
incident energy around 100 eV. This energy range falls exactly
in the interval relevant for our shocks, implying that the electrons
optimally transfer their energy.
)
the value of the dissociation probability. The electron energy loss
rises sharply with the electron energy, reaching its maximum for
incident energy around 100 eV. This energy range falls exactly
in the interval relevant for our shocks, implying that the electrons
optimally transfer their energy.
The thermal electron collision rate can be
written as
where
4 Results
Figures 7 and 8 show the fraction of carbon atoms ejected from a 50 and 200 C-atoms PAH due to collisions with electrons and H, He and C, assuming the nuclear threshold energy T0 = 7.5 eV and the fragment binding energy E0 = 4.58 eV. The results concerning nuclear, electronic and electron interaction are discussed in the following sections.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{11682fg7.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg130.png)
|
Figure 7:
The fractional C-atom loss |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{11682fg8.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg131.png)
|
Figure 8: Same as Fig. 7 calculated for a 200 carbon atoms PAH. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{11682fg9.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg132.png)
|
Figure 9: Carbon atom loss due to collisions with thermal and inertial ions (H + He + C) via nuclear interaction. The figure shows the comparison betwen the three threshold values T0 = 4.5, 7.5 and 15 eV for a 50 carbon atom PAH. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{11682f10.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg133.png)
|
Figure 10:
The fractional C-atom loss |
| Open with DEXTER | |
4.1 PAH destruction via nuclear interactions
For the inertial nuclear interactions, the fraction
of ejected carbon atoms ![]() depends on both
depends on both ![]() and
and ![]() .
Hydrogen has the highest abundance (
.
Hydrogen has the highest abundance (
![]() = 1) but
the lowest absolute value for the cross section
(see Fig. 2).
In addition,
= 1) but
the lowest absolute value for the cross section
(see Fig. 2).
In addition, ![]() is
significantly different from zero only for the highest shock
velocities. This results in contribution to atom ejection which is only
relevant for
is
significantly different from zero only for the highest shock
velocities. This results in contribution to atom ejection which is only
relevant for ![]() above 150 km s-1. Helium is
ten times less abundant than hydrogen (
above 150 km s-1. Helium is
ten times less abundant than hydrogen (
![]() = 0.1), but
this is compensated for by a higher cross section for all shock
velocities. In particular, the C-atom ejection curve shows a peak
between 50 and 125 km s-1
due to betatron acceleration: because of the higher velocity, the
collision rate increases (cf. Eq. (17)) and then
the PAHs experience more destructive collisions. After the
peak, as expected the curve increases with the shock velocity. In the
case of carbon, the increased cross section is not sufficient to
compensate for the low abundance (
= 0.1), but
this is compensated for by a higher cross section for all shock
velocities. In particular, the C-atom ejection curve shows a peak
between 50 and 125 km s-1
due to betatron acceleration: because of the higher velocity, the
collision rate increases (cf. Eq. (17)) and then
the PAHs experience more destructive collisions. After the
peak, as expected the curve increases with the shock velocity. In the
case of carbon, the increased cross section is not sufficient to
compensate for the low abundance (
![]() = 10-4),
resulting in a totally negligible contribution to
PAH destruction. For all shock velocities, the fraction of
C-atoms removed because of inertial nuclear interaction does not exceed
the value of 20%.
= 10-4),
resulting in a totally negligible contribution to
PAH destruction. For all shock velocities, the fraction of
C-atoms removed because of inertial nuclear interaction does not exceed
the value of 20%.
Concerning the thermal nuclear
interaction, carbon does not contribute to PAH destruction
because of its very low abundance compared to H and He,
as for the inertial case. For hydrogen and helium, as expected
for low velocity shocks, the temperature is generally not sufficiently
high to provide the ions with the energy required to remove C-atoms.
Nevertheless, the ions in the high velocity tail of the Maxwellian
distribution can be energetic enough to cause C-atom ejection,
as can be seen for He at 100 km s-1.
This is less evident for hydrogen. In this case the critical
energy ![]() is higher than for helium and carbon. The corresponding critical
velocity v0 will be
higher as well. For the lower velocity shocks, the peak of the hydrogen
maxwellian function f(v,
T) is well below v0,
as a consequence the integrand of Eq. (22) is
close to zero over the integration range, and the same will be
true for the collision rate. At the highest shock velocities
the curves show a similar trend, with a steep rise beyond
125 km s-1 leading to complete
PAH destruction, i.e. removal of ALL carbon atoms,
for shock velocities above 150 km s-1.
At around 135 km s-1
the hydrogen contribution becomes larger than that for helium.
At these high velocities the He and H cross sections reach
approximately their maximum values (cf. Fig. 2) and the
abundance of H is a factor of 10 higher than
for He.
is higher than for helium and carbon. The corresponding critical
velocity v0 will be
higher as well. For the lower velocity shocks, the peak of the hydrogen
maxwellian function f(v,
T) is well below v0,
as a consequence the integrand of Eq. (22) is
close to zero over the integration range, and the same will be
true for the collision rate. At the highest shock velocities
the curves show a similar trend, with a steep rise beyond
125 km s-1 leading to complete
PAH destruction, i.e. removal of ALL carbon atoms,
for shock velocities above 150 km s-1.
At around 135 km s-1
the hydrogen contribution becomes larger than that for helium.
At these high velocities the He and H cross sections reach
approximately their maximum values (cf. Fig. 2) and the
abundance of H is a factor of 10 higher than
for He.
As discussed in Sect. 2.2.1, the threshold energy for carbon ejection via nuclear excitation is not well-constrained. We consider T0 = 7.5 eV to be a reasonable value, but experimental determinations are necessary. Figure 9 illustrates how the fraction of ejected C-atoms changes as a function of the adopted value for the threshold energy. The curves show the cumulative effect of H, He and C, calculated for T0 = 4.5, 7.5 and 15 eV in the inertial and thermal case. Both in the inertial and thermal case, the curves corresponding to the various thresholds follow the same trend, and for each value considered of T0 the inertial destruction dominates at low velocity and the thermal destruction at high velocities. As expected the fraction of ejected C-atoms increases for decreasing T0 in the inertial case, while the curves shift to the left in the thermal case, implying that the PAHs will start to experience significant damage at lower shock velocities. Our results also show that, even assuming a high threshold energy, PAHs experience a substantial loss of carbon atoms, which is complete for velocities above 175 km s-1 is all cases.
Finally, we investigated how the nuclear destruction process
depends on the size of the PAH. Figure 8 shows the
fraction of ejected carbon atoms from a big PAH with ![]() = 200.
The destruction of a 200 C-atom PAH follows the same
trends with shock velocity as for the 50 C-atom case and the
curves are almost identical. This is due to the fact that the velocity
and temperature profiles for the 50 and 200 C-atoms
molecules are quite similar, and the collision rate and
= 200.
The destruction of a 200 C-atom PAH follows the same
trends with shock velocity as for the 50 C-atom case and the
curves are almost identical. This is due to the fact that the velocity
and temperature profiles for the 50 and 200 C-atoms
molecules are quite similar, and the collision rate and ![]() scale
linearly with
scale
linearly with ![]() in both the inertial and thermal case (see Eqs. (17), (21) and (22)).
in both the inertial and thermal case (see Eqs. (17), (21) and (22)).
4.2 PAH destruction via electronic interaction by ion collisions
Inspection of Figs. 7
and 8
reveals that electronic excitation by impacting ions plays only a
marginal role in the destruction process. For both PAH sizes,
carbon is unimportant because of its very low abundance. In the
inertial case H does not contribute and He contributes
marginally at the highest shock velocities, while in the thermal case
they lead to a substantial atomic loss only for ![]() = 50 in the
highest velocity shock (200 km s-1).
For a 50 C-atom PAH, the low destruction rate due to
electronic excitation reflects the small cross section for this process
for these low velocity shocks. The inertial velocities of the PAH lead
to electronic excitation only being important for the highest shock
velocities where the impacting ions have a high enough temperature to
excite the PAHs sufficiently (cf. MJT). The larger number of
modes available in 200 C-atom PAHs, makes the electronic
excitation of such PAHs completely negligible over the full velocity
range of the shocks considered here.
= 50 in the
highest velocity shock (200 km s-1).
For a 50 C-atom PAH, the low destruction rate due to
electronic excitation reflects the small cross section for this process
for these low velocity shocks. The inertial velocities of the PAH lead
to electronic excitation only being important for the highest shock
velocities where the impacting ions have a high enough temperature to
excite the PAHs sufficiently (cf. MJT). The larger number of
modes available in 200 C-atom PAHs, makes the electronic
excitation of such PAHs completely negligible over the full velocity
range of the shocks considered here.
4.3 PAH destruction due to electron collisions
The fractional carbon atom loss ![]() due to collisions with thermal electrons is also
shown in Figs. 7
and 8.
For
due to collisions with thermal electrons is also
shown in Figs. 7
and 8.
For ![]() = 50,
the number of ejected carbon atoms rises sharply above
75 km s-1, leading to total
destruction above 100 km s-1.
For
= 50,
the number of ejected carbon atoms rises sharply above
75 km s-1, leading to total
destruction above 100 km s-1.
For ![]() = 200,
the damage is negligible up to 100 km s-1,
increases significantly beyond that and leads to complete destruction
above 150 km s-1.
= 200,
the damage is negligible up to 100 km s-1,
increases significantly beyond that and leads to complete destruction
above 150 km s-1.
The energy transferred by impacting electrons rises sharply
for velocities in excess of 2 ![]() 103 km s-1.
This results in a dissociation probability p
shaped as a step function: for v
103 km s-1.
This results in a dissociation probability p
shaped as a step function: for v ![]() 2
2 ![]() 103 km s-1
p jumps from values close to zero up
to 1. This limiting velocity applies to a 50 C-atoms
PAH; for
103 km s-1
p jumps from values close to zero up
to 1. This limiting velocity applies to a 50 C-atoms
PAH; for ![]() =
200 the value is higher (4
=
200 the value is higher (4 ![]() 103 km s-1),
due to the fact that for a bigger PAH more energy has to be transferred
for dissociation. These velocities correspond to electron temperatures
of 105 K and 3
103 km s-1),
due to the fact that for a bigger PAH more energy has to be transferred
for dissociation. These velocities correspond to electron temperatures
of 105 K and 3 ![]() 105 K, which are reached for shock
velocities of approximately 100 and 150 km s-1,
respectively.
105 K, which are reached for shock
velocities of approximately 100 and 150 km s-1,
respectively.
4.4 Summary
A summary of our findings from Figs. 7 and 8 is
presented in Fig. 10.
This shows the fractional atomic loss, ![]() ,
due to electron and ion collisions, calculated for the two PAH sizes
,
due to electron and ion collisions, calculated for the two PAH sizes ![]() =
50 and 200. To show how the fractional loss changes
as a function of the adopted value for E0,
we added the results obtained assuming for the electronic dissociation
energy the values 3.65 and 5.6 eV, lower and higher
respectively than our standard value 4.58 eV.
=
50 and 200. To show how the fractional loss changes
as a function of the adopted value for E0,
we added the results obtained assuming for the electronic dissociation
energy the values 3.65 and 5.6 eV, lower and higher
respectively than our standard value 4.58 eV.
For ionic collisions, ![]() is determined by nuclear interaction: inertial for low
is determined by nuclear interaction: inertial for low ![]() and thermal for high
and thermal for high ![]() .
For the 50 C-atoms PAH, the electronic contribution emerges
for the lowest value of E0,
3.65 eV. As already mentioned, the dissociation
probability increases for decreasing E0,
so we are not surprised to find
.
For the 50 C-atoms PAH, the electronic contribution emerges
for the lowest value of E0,
3.65 eV. As already mentioned, the dissociation
probability increases for decreasing E0,
so we are not surprised to find ![]() enhanced by electronic excitation (both inertial and thermal). The
electronic contribution desappears for higher dissociation energies,
as demonstrated by the coincidence between the curves for E0 =
4.58 and 5.6 eV. For
enhanced by electronic excitation (both inertial and thermal). The
electronic contribution desappears for higher dissociation energies,
as demonstrated by the coincidence between the curves for E0 =
4.58 and 5.6 eV. For ![]() = 200, all three
ionic curves are coincident, indicating that electronic excitation by
impacting ions does not contribute to PAH destruction below
150 km s-1. Above this value,
the carbon loss due to electronic interaction is covered by the other
processes.
= 200, all three
ionic curves are coincident, indicating that electronic excitation by
impacting ions does not contribute to PAH destruction below
150 km s-1. Above this value,
the carbon loss due to electronic interaction is covered by the other
processes.
The shift between the ionic curves for the two PAH sizes is
due to the small differences in the velocity profiles - due to
betatron acceleration -, which imply in the inertial case a
slightly higher damage for the bigger PAH. In the thermal case ![]() is instead independent on the PAH size because the number of ejected
C-atoms scales linearly with
is instead independent on the PAH size because the number of ejected
C-atoms scales linearly with ![]() (see Sect. 4.1). The resulting effect is an almost
linear rise for both PAH sizes up to 150 km s-1,
beyond which the destruction is complete.
(see Sect. 4.1). The resulting effect is an almost
linear rise for both PAH sizes up to 150 km s-1,
beyond which the destruction is complete.
The ``Electron'' curves reproduce the behaviour observed in
Figs. 7
and 8.
The comparison with the ionic ![]() clearly indicates that a 50 carbon atoms PAH
is already damaged in a non-negligible way in low velocity shocks
(50-75 km s-1, ion collisions)
and is totally destroyed above 100 km s-1
(electron collisions). When E0 =
3.65 eV, the fraction of ejected C-atom for
clearly indicates that a 50 carbon atoms PAH
is already damaged in a non-negligible way in low velocity shocks
(50-75 km s-1, ion collisions)
and is totally destroyed above 100 km s-1
(electron collisions). When E0 =
3.65 eV, the fraction of ejected C-atom for ![]() =
75 km s-1 increases
from 0.1 to
=
75 km s-1 increases
from 0.1 to ![]() 0.35 but the minimum shock velocity for complete
destruction is unchanged (100 km s-1).
For
0.35 but the minimum shock velocity for complete
destruction is unchanged (100 km s-1).
For ![]()
![]() 75 km s-1, the 5.6 eV
curve is almost parallel to the 3.65 eV curve and shifted by
25 km s-1 toward higher shock
velocities. For the 200 C-atom PAH, the carbon atom loss is
dominated by ionic collisions for shocks with velocity below
100 km s-1. Above this value,
the combined effect of ions and electrons leads to a complete
destruction. A lower electronic dissociation energy shifts
back by 25 km s-1 the minimum
shock velocity required for total carbon ejection. When E0 =
5.6 eV, destruction starts to be important only above
125 km s-1, and becomes almost
complete at 150 km s-1.
75 km s-1, the 5.6 eV
curve is almost parallel to the 3.65 eV curve and shifted by
25 km s-1 toward higher shock
velocities. For the 200 C-atom PAH, the carbon atom loss is
dominated by ionic collisions for shocks with velocity below
100 km s-1. Above this value,
the combined effect of ions and electrons leads to a complete
destruction. A lower electronic dissociation energy shifts
back by 25 km s-1 the minimum
shock velocity required for total carbon ejection. When E0 =
5.6 eV, destruction starts to be important only above
125 km s-1, and becomes almost
complete at 150 km s-1.
We adopt the quantity ![]() as destruction efficiency to calculate the PAH lifetime
in shocks.
as destruction efficiency to calculate the PAH lifetime
in shocks.
4.5 Uncertainties discussion
The main sources of uncertainties which have to be considered for this study are related to the adopted shock profiles, to the accuracy of the fitting function for the ZBL nuclear stopping cross section, and to the choice of an appropriate value for the nuclear threshold energy T0 and for the electronic dissociation energy E0.
The uncertainties related to the adopted shock profiles here are principally due to our assumption that we can equivalently treat a small, two-dimensional PAH molecule as a small three-dimensional grain. In the calculation of the PAH velocity profiles through the shocks we use the same formalism as for the grains (Jones et al. 1996), i.e., we assume that the PAH behaves as a three-dimensional grain of the same mass. Any uncertainties are then due to the inherent differences in the cross section to mass ratios for PAHs and grains. As mentioned in Sect. 3, once the PAH cross section is averaged over all possible orientations, the differences in the PAH and grain cross sections turn out to be only of the order of 11%, for a 50 carbon atom PAH, and are therefore rather small compared to the other uncertainties that we discuss here.
The accuracy of the ZBL nuclear stopping cross section depends on the accuracy of the single analytical function used by Ziegler et al. (1985) to calculate the interatomic potentials between atoms. This universal function has been compared with experimentally determined potentials, with a resulting standard deviation between theory and experiment of 5% (O'Connor & Biersack 1986). An additional test has been made comparing the results from the ZBL function with much more complex theoretical calculations including more effects. In this case as well the results agree within few percent (see Ziegler et al. 1985, and references therein).
The main source of uncertainty in the nuclear stopping
calculation is the choice of the threshold energy T0.
This quantity is not well constrained
(see Sect. 2.2.1) so we explored a set of plausible
values. In Fig. 9
we plotted together the values for ![]() resulting from the total effect of H, He and C,
calculated in both inertial and thermal case for three different
threshold energies T0 =
4.5, 7.5 and 15 eV. The curves corresponding to the highest
and lowest threshold
resulting from the total effect of H, He and C,
calculated in both inertial and thermal case for three different
threshold energies T0 =
4.5, 7.5 and 15 eV. The curves corresponding to the highest
and lowest threshold
![]() and
and
![]() identify a region which can be interpreted as the variation in the
amount of destruction due to the uncertainty in the threshold energy.
For the inertial case, this uncertainty introduces a variation in the
destruction efficiency of a factor less than about 2. For the
thermal case, the uncertainty introduces a shift of the critical shock
velocity above which thermal destruction is dominant from
about 100 to 150 km s-1
for T0 ranging
from 4.5 to 15 eV.
identify a region which can be interpreted as the variation in the
amount of destruction due to the uncertainty in the threshold energy.
For the inertial case, this uncertainty introduces a variation in the
destruction efficiency of a factor less than about 2. For the
thermal case, the uncertainty introduces a shift of the critical shock
velocity above which thermal destruction is dominant from
about 100 to 150 km s-1
for T0 ranging
from 4.5 to 15 eV.
Table 3: PAH destruction analytical fit parameters and survival timescales for electron and ion collisions.
An important issue for the electronic and electron stopping calculation is the choice of the value for the parameter E0. We adopt the value 4.58 eV, which has been extrapolated for interstellar conditions from experimental data. Unfortunately the extrapolation procedure is very model-dependent, so the same set of experimental data can lead to significantly different values for the interstellar E0. The problematic fragment binding energy is extensively discussed in MJT, the result of a different choice for E0 (3.65, 4.58 and 5.6 eV) on PAH processing by shocks is shown in Fig. 10. The differences are quite significant, indicating the importance of experimental studies on the critical energy E0 describing the dissociation probability of highly excited PAHs. To summarize, the errors related to the shock profiles and ZBL fitting function are quite small, for T0 we identified a range of plausible values, but experimental determinations would be desirable, while the choice of the parameter E0 is very uncertain and urgently requires a better determination.
5 Discussion
5.1 PAH lifetime in shocks
To calculate the timescale for supernova shock waves to destroy the
interstellar PAHs in the Galaxy, ![]() ,
we adopt the same approach used in our previous works (Jones
et al. 1994,1996), which is based on the
method of McKee (1989):
,
we adopt the same approach used in our previous works (Jones
et al. 1994,1996), which is based on the
method of McKee (1989):
where
were
Using our calculated fractional destruction data, we derived
analytical expressions for the destruction efficiency
![]() for electrons and ions. The ionic term represents the total
contribution of all considered ions (H, He and C) and
processes (nuclear and electronic
stopping, inertial and thermal). Below 150 km s-1,
we adopt a power law fit for
for electrons and ions. The ionic term represents the total
contribution of all considered ions (H, He and C) and
processes (nuclear and electronic
stopping, inertial and thermal). Below 150 km s-1,
we adopt a power law fit for ![]() and a linear fit for
and a linear fit for ![]() ,
while for the remaining velocities the efficiency is 1. For
electrons, for
,
while for the remaining velocities the efficiency is 1. For
electrons, for ![]() ,
the destruction efficiencies are well fit by two linear functions (
,
the destruction efficiencies are well fit by two linear functions (
![]() )
and a logarithmic function (
)
and a logarithmic function (
![]() ). The analytical fits
reproduce the calculated data within few percent. The functional form,
fitting parameters and corresponding timescales calculated from
Eq. (30)
are reported in Table 3.
). The analytical fits
reproduce the calculated data within few percent. The functional form,
fitting parameters and corresponding timescales calculated from
Eq. (30)
are reported in Table 3.
For electron collisions we find ![]() =
1.6
=
1.6 ![]() 108 yr for
108 yr for ![]() and 4.0
and 4.0 ![]() 108 yr for
108 yr for ![]() .
In case of ion collisions the lifetimes are 1.8
.
In case of ion collisions the lifetimes are 1.8 ![]() 108 yr and 1.4
108 yr and 1.4 ![]() 108 yr for the small and big molecule
respectively. The largest uncertainty in these lifetimes result from
the uncertainty in the values adopted for T0
and E0
(cf. Sect. 4.5). If we assume the lowest
values considered (4.5 and 3.65 eV), these lifetimes
decrease to 9.2
108 yr for the small and big molecule
respectively. The largest uncertainty in these lifetimes result from
the uncertainty in the values adopted for T0
and E0
(cf. Sect. 4.5). If we assume the lowest
values considered (4.5 and 3.65 eV), these lifetimes
decrease to 9.2 ![]() 107 yr and 8
107 yr and 8 ![]() 107 yr (for
107 yr (for
![]() and 200 respectively), while the maximum values considered for
these energies result in lifetimes of 2.5
and 200 respectively), while the maximum values considered for
these energies result in lifetimes of 2.5 ![]() 108 yr and 3.3
108 yr and 3.3 ![]() 108 yr for the small and
big PAH. Thus, while these parameters are quite uncertain, the
derived values for the lifetimes are quite robust. Essentially, PAHs
are destroyed by shocks larger than about 100 km s-1
and, typically, interstellar gas encounters such shocks once every
100 million years (McKee 1989).
108 yr for the small and
big PAH. Thus, while these parameters are quite uncertain, the
derived values for the lifetimes are quite robust. Essentially, PAHs
are destroyed by shocks larger than about 100 km s-1
and, typically, interstellar gas encounters such shocks once every
100 million years (McKee 1989).
From the results obtained assuming our standard values (T0 = 7.5 eV and E0 = 4.6 eV), we argue then that small PAHs are preferentially destroyed by electrons whereas big PAHs are more affected by ions.
Our derived values for ![]() for PAHs are significantly shorter than the 6
for PAHs are significantly shorter than the 6 ![]() 108 yr calculated by Jones et al. (1996) for
graphite/amorphous carbon grains in the warm intercloud medium.
Ignoring betatron acceleration, the total number of collisions per
C-atom required for stopping the inertial motion is independent of
grain size. The difference in lifetimes reflects then a difference in
sputtering efficiency. This is not surprising because of the different
approaches adopted for the ion-particle interactions for PAHs and
grains. In both cases, and for the shocks that we consider
here, it is the sputtering processes that completely dominate
dust destruction. In the case of grains not every atom that is
``knocked on'' by an incident ion is lost, i.e. sputtered,
from the grain. The displaced atom is often embedded deeper into the
grain and therefore not sputtered from the grain even when the
displacement energy significantly exceeds the threshold energy for
target atom displacement. This is reflected in the fact that, for
grains, the sputtering yield is usually much less that unity. The
shorter lifetime for the PAHs is then be ascribed to the fact that in
any incident ion interaction the target atom is always lost from the
PAH when the energy to displace it is greater that the required
threshold energy. In this case the equivalent PAH sputtering
yield is then unity.
108 yr calculated by Jones et al. (1996) for
graphite/amorphous carbon grains in the warm intercloud medium.
Ignoring betatron acceleration, the total number of collisions per
C-atom required for stopping the inertial motion is independent of
grain size. The difference in lifetimes reflects then a difference in
sputtering efficiency. This is not surprising because of the different
approaches adopted for the ion-particle interactions for PAHs and
grains. In both cases, and for the shocks that we consider
here, it is the sputtering processes that completely dominate
dust destruction. In the case of grains not every atom that is
``knocked on'' by an incident ion is lost, i.e. sputtered,
from the grain. The displaced atom is often embedded deeper into the
grain and therefore not sputtered from the grain even when the
displacement energy significantly exceeds the threshold energy for
target atom displacement. This is reflected in the fact that, for
grains, the sputtering yield is usually much less that unity. The
shorter lifetime for the PAHs is then be ascribed to the fact that in
any incident ion interaction the target atom is always lost from the
PAH when the energy to displace it is greater that the required
threshold energy. In this case the equivalent PAH sputtering
yield is then unity.
Our derived PAH lifetime is much closer to the value of ![]() 2
2 ![]() 108 yr found for a size distribution of
hydrogenated amorphous carbon (a-C:H) grains, typical of the
diffuse interstellar medium, by Serra
Díaz-Cano & Jones (2008). This is perhaps just
coincidental; it has its origin in lower average binding
energy of C-atoms in amorphous carbon than in graphite.
a-C:H grains are found, as we find for PAHs, to be more
susceptible to sputtering erosion than graphite/amorphous carbon grains
(Jones et al. 1996).
However PAHs are much more susceptible to erosion than a-C:H in fast
shocks (
108 yr found for a size distribution of
hydrogenated amorphous carbon (a-C:H) grains, typical of the
diffuse interstellar medium, by Serra
Díaz-Cano & Jones (2008). This is perhaps just
coincidental; it has its origin in lower average binding
energy of C-atoms in amorphous carbon than in graphite.
a-C:H grains are found, as we find for PAHs, to be more
susceptible to sputtering erosion than graphite/amorphous carbon grains
(Jones et al. 1996).
However PAHs are much more susceptible to erosion than a-C:H in fast
shocks (![]() km s-1)
and this is simply due to their small sizes. Thermal sputtering in the
hot post-shock gas of fast shocks is proportional to the surface area
and, small particles having a larger surface area per unit mass than
large particles, are more rapidly eroded.
km s-1)
and this is simply due to their small sizes. Thermal sputtering in the
hot post-shock gas of fast shocks is proportional to the surface area
and, small particles having a larger surface area per unit mass than
large particles, are more rapidly eroded.
5.2 Astrophysical implications
As shown in Sect. 5.1, the PAH lifetime against shock
destruction is much shorter than the stardust injection timescale into
the interstellar medium ![]() =
2.5
=
2.5 ![]() 109 yr. Gas shocked to velocities of
the order of 50-150 km s-1 is
observed in many regions of the interstellar medium:
e.g. toward the star
109 yr. Gas shocked to velocities of
the order of 50-150 km s-1 is
observed in many regions of the interstellar medium:
e.g. toward the star ![]() Ori (Welty et al. 2002),
in Herbig-Haro jets in the Orion and Vela star forming regions
(Podio et al. 2006),
and in the local interstellar cloud (Slavin
2008). Hence, according to our calculations,
PAH destruction should be widespread in the ISM.
Ori (Welty et al. 2002),
in Herbig-Haro jets in the Orion and Vela star forming regions
(Podio et al. 2006),
and in the local interstellar cloud (Slavin
2008). Hence, according to our calculations,
PAH destruction should be widespread in the ISM.
If we assume globally that the same ![]() holds for PAHs as for ``standard'' interstellar dust, i.e., that dust
and PAH formation are coeval in and around evolved stars, our
calculated survival times for PAHs, i.e.,
holds for PAHs as for ``standard'' interstellar dust, i.e., that dust
and PAH formation are coeval in and around evolved stars, our
calculated survival times for PAHs, i.e.,
![]() ,
indicate that they need to be re-formed in the ISM even more rapidly
than the larger interstellar grains. If PAHs are formed by the
fragmentation of larger carbonaceous grains then their ``effective''
survival time must just be the same as that of the larger grains from
which they originate. However, this can only be true for low velocity
shocks, or turbulent regions of the ISM, where grain-grain collisions
at relatively low velocities (of the order of a few
km s-1) can form PAHs via fragmentation
and where there is no associated destructive process
in operation.
,
indicate that they need to be re-formed in the ISM even more rapidly
than the larger interstellar grains. If PAHs are formed by the
fragmentation of larger carbonaceous grains then their ``effective''
survival time must just be the same as that of the larger grains from
which they originate. However, this can only be true for low velocity
shocks, or turbulent regions of the ISM, where grain-grain collisions
at relatively low velocities (of the order of a few
km s-1) can form PAHs via fragmentation
and where there is no associated destructive process
in operation.
On a region by region basis our results indicate that PAHs should not exist in environments shocked to high velocities (>100 km s-1). We conclude that PAHs that exist in unshocked regions do not survive the passage of shocks with velocities above 100-150 km s-1 (depending on their size). They are in fact destroyed rather early in in the shock at shocked column densities of the order of 1016-1017 cm-2. Any ``daughter'' PAHs produced in the post-shock region, by grain fragmentation in grain-grain collisions at shocked column densities of the order of 1017-1018 cm-2, will be destroyed by erosion due to their high injection velocities into the gas following the fragmentation of their larger, ``parent'' grains that undergo betatron-acceleration (Jones et al. 1996). Thus, high velocity shocks destroy all the PAHs that they both interact with and produce by fragmentation in high velocity grain-grain collisions.
In contrast observations show that PAHs lock up about 3% of the elemental carbon in the ISM (cf. Tielens 2008). Disentangling these two scenarios is not easy observationally. Here we now consider the case where the PAH emission is assumed to come from within the shocked region. This scenario requires an efficient (re)formation route for PAHs in the diffuse ISM (see above). However, this is difficult to understand since PAHs are a product of high temperature chemistry involving abundant carbon bearing precursors such as CH4 and C2H2. In the low temperature diffuse ISM, an O-rich environment, these precursor species are never really very abundant. This conundrum is very reminiscent of the general problem of rapid dust destruction in the ISM and the long injection time scale for freshly formed dust (Draine & Salpeter 1979; Dwek & Scalo 1980; Jones et al. 1994,1996). We note that, while dust grains may be rapidly covered by (thin)protective coatings between successive shock passages (cf. Tielens 1998), this is not a way out of this conundrum for PAHs. Perhaps, PAHs can be formed through prolonged photolysis of ice mantles accreted inside dense molecular clouds, although, presently, there is no experimental support for this suggestion. Lastly, observations have revealed the presence of PAHs associated with hot shocked gas in stellar (e.g., M 17) and galactic (e.g., M 82) wind regions (cf. Sect. 1). As will be discussed more extensively in MJT, these PAHs likely trace entrained cold gas which has not been fully exposed to the destructive effects of high velocity shocks.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{11682f11.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg168.png)
|
Figure 11:
The evolution of a 50 carbon atom PAH following the loss of |
| Open with DEXTER | |
For ![]() <
75 km s-1, PAH are
disrupted only by inertial ``sputtering'' due to nuclear interactions. Serra Díaz-Cano & Jones (2008)
have studied the erosion of hydrogenated amorphous carbon
(a-C:H) arising from ion irradiation in shocks in the warm
intercloud medium, using exactly the same shock profiles that we use
for our PAH study, and it is interesting to note that, for
a 50 carbon atom PAH molecule, the
percentage of destruction is the same as for a-C:H, indicating that the
lower density, more easily sputtered a-C:H and PAHs exhibit similar
erosion characteristics in lower velocity shocks (
<
75 km s-1, PAH are
disrupted only by inertial ``sputtering'' due to nuclear interactions. Serra Díaz-Cano & Jones (2008)
have studied the erosion of hydrogenated amorphous carbon
(a-C:H) arising from ion irradiation in shocks in the warm
intercloud medium, using exactly the same shock profiles that we use
for our PAH study, and it is interesting to note that, for
a 50 carbon atom PAH molecule, the
percentage of destruction is the same as for a-C:H, indicating that the
lower density, more easily sputtered a-C:H and PAHs exhibit similar
erosion characteristics in lower velocity shocks (
![]() km s-1),
as discussed in the previous section.
km s-1),
as discussed in the previous section.
We now consider what happens to a PAH as a result of the
ejection of aromatic carbon atoms, by the impacting ions,
as a function of the fraction of carbon atoms removed from the
structure. Our results show that ionic collisions severely modify PAH
in shocks with velocities between 75-150 km s-1.
Nuclear and electronic interaction lead to distinctly different
molecular destruction routes. Specifically, electronic excitation
(either by impacting ions or electrons) lead to a high vibrational
excitation of the PAH and this PAH will relax by ``losing'' the weakest
link in its skeleton. Initially, this will be the peripheral H-atoms or
other functional groups. For large PAHs (50-100 C-atoms), the
resulting ``pure-C'' may quickly isomerize to very stable carbon
cluster such as fullerenes. Fullerenes are very stable against C2 loss.
Measured dissociation energies of fullerenes are in the range
of 7 to 9.5 eV, with C60
itself at
![]()
![]() 0.1 eV
(Tomita et al. 2001).
0.1 eV
(Tomita et al. 2001).
In contrast, nuclear interaction will act on the C-atom hit by
the projectile ion. This will randomly remove C-atoms from the
C-skeleton of the PAH. Some isomerization may occur if internal
excitation energy is left behind. However, unless the C-atom loss in
the shock is very large, likely this is insufficient to affect the
overall PAH structure. In a simple ``geometrical'' analysis,
if one randomly removes C atoms from a PAH with ![]() ,
in the absence of any annealing of the PAH chemical structure,
we find that the loss of 10% of the C atoms leads to
a loss of of the order of
,
in the absence of any annealing of the PAH chemical structure,
we find that the loss of 10% of the C atoms leads to
a loss of of the order of ![]() % of the
aromatic character. However, the loss of
% of the
aromatic character. However, the loss of ![]() of the C atoms leads to the almost complete loss of aromatic
character and to the
onset of the fragmentation of the molecule. Figure 11 illustrates
these effects and shows the PAH evolution following the loss
of carbon atoms,
of the C atoms leads to the almost complete loss of aromatic
character and to the
onset of the fragmentation of the molecule. Figure 11 illustrates
these effects and shows the PAH evolution following the loss
of carbon atoms, ![]() (lost),
for the two limiting cases: 1) where there is an instantaneous
and random removal of the lost carbon atoms (appropriate for nuclear
interaction) and 2) where the carbon atoms are removed only
from the periphery in order to preserve aromatic domain as much as
possible (likely appropriate for electronic excitation through either
impact ions or electrons). The reality of PAH erosion in
shocks may well lie somewhere between these two extremes and may also
involve isomerisation and the formation of five-fold carbon rings that
distort the structure from a perfectly two-dimensional form. This then
begs the question as to the exact form and structure of small carbon
species once growth resumes by atom insertion and addition.
(lost),
for the two limiting cases: 1) where there is an instantaneous
and random removal of the lost carbon atoms (appropriate for nuclear
interaction) and 2) where the carbon atoms are removed only
from the periphery in order to preserve aromatic domain as much as
possible (likely appropriate for electronic excitation through either
impact ions or electrons). The reality of PAH erosion in
shocks may well lie somewhere between these two extremes and may also
involve isomerisation and the formation of five-fold carbon rings that
distort the structure from a perfectly two-dimensional form. This then
begs the question as to the exact form and structure of small carbon
species once growth resumes by atom insertion and addition.
After the shock wave has passed, the resulting PAH can react
chemically with impacting H, C, O, and N atoms.
A distinction can be made between H and O in the one hand and
C and N on the other hand, The latter can restore the stable aromatic
character of the PAH skeleton while the former lead only to
very unstable structures. Likely, then, H and O atom addition
can be reversed by UV photon absorption without loss of C (Allamandola et al. 1989).
Hence, the PAH carbon skeleton may be able to ``repair''
itself to an aromatic structure, possibly incorporating N-atoms. The
possible presence of N-atoms deeply in the C-skeleton of PAHs in the
diffuse medium (but not in C-dust birth sites such as C-rich
planetary nebulae) has been inferred from the peak position of the
6.2 ![]() m
band (Peeters et al. 2002).
It has also been suggested that the
m
band (Peeters et al. 2002).
It has also been suggested that the ![]() m band position variations can
be explained by a varying aliphatic to aromatic carbon content in
carbonaceous particles (Pino
et al. 2008). The difference in molecular structure
between circumstellar PAHs and the general ISM implies an active
chemistry in the ISM that is able to insert N atoms deeply in
the carbon skeleton. This is very puzzling given the very stable
character of the aromatic backbone and the low temperature of the ISM.
Here, we surmise that, unlike UV photolysis or chemical
attack, nuclear interactions in interstellar shocks may be a viable
pathway to promote N-incorporations deep inside PAHs. However, given
that the nitrogen abundance is a factor of a few lower than that for
carbon - depending on the fraction of carbon remaining in dust
and PAHs - carbon atom insertion ought to be favoured over
that for nitrogen, in the absence of any chemically-selective route for
nitrogen insertion.
m band position variations can
be explained by a varying aliphatic to aromatic carbon content in
carbonaceous particles (Pino
et al. 2008). The difference in molecular structure
between circumstellar PAHs and the general ISM implies an active
chemistry in the ISM that is able to insert N atoms deeply in
the carbon skeleton. This is very puzzling given the very stable
character of the aromatic backbone and the low temperature of the ISM.
Here, we surmise that, unlike UV photolysis or chemical
attack, nuclear interactions in interstellar shocks may be a viable
pathway to promote N-incorporations deep inside PAHs. However, given
that the nitrogen abundance is a factor of a few lower than that for
carbon - depending on the fraction of carbon remaining in dust
and PAHs - carbon atom insertion ought to be favoured over
that for nitrogen, in the absence of any chemically-selective route for
nitrogen insertion.
6 Conclusions
We have extensively studied the effects of PAH processing by shocks with velocities between 50 and 200 km s-1, in terms of collisions with ions and electrons which can lead to carbon atom loss, with a consequent disruption and destruction of the molecule.
An ionic collision consists of two simultaneous processes which can be treated separately: a binary collisions between the projectile and one single atom in the target (nuclear interaction) and the energy loss to the atomic electrons (electronic interaction). For the nuclear interaction, we modified the existing theory in order to treat collisions able to transfer energy above a specific threshold. This is the case we are interested in, which has not been treated in previous studies. For electronic interaction and collisions with electrons we developed specific models for PAH, described in MJT.
The PAH dynamics in the shocks is evaluated using the same
approach as in our previous work (Jones et al. 1994,1996).
For nuclear interaction, the level of carbon atom loss increases for
decreasing values of the threshold energy T0.
We adopt T0 =
7.5 eV as a reasonable value, but experimental determinations
are necessary. In ionic collisions, the carbon contribution to
PAH destruction is totally negligible because of its very low
abundance with respect to H and He. The fractional destruction
induced by nuclear excitation increases with the PAH size,
while in case of electronic excitation and electron collisions is lower
for higher ![]() values, i.e. bigger PAHs are more resistant than the smaller
ones against electron and electronic processing.
values, i.e. bigger PAHs are more resistant than the smaller
ones against electron and electronic processing.
The parameter E0 required for the evaluation of PAH destruction due to electron and electronic interaction is unfortunately not well constrained. We adopt a value of 4.58 eV consistent with extrapolations to interstellar conditions, but better determinations would be desirable.
Electronic interaction, both inertial and thermal, plays a
marginal role in PAH processing by shocks. We find that
50 carbon atoms PAHs are significantly disrupted in ionic
collisions for shock velocities below 75 km s-1,
mainly by inertial ``sputtering'' by helium during
nuclear interaction. Our results indicate ![]() C atom loss, sufficient to cause a severe de-naturation of the
PAH aromatic structure.
Above 100 km s-1 such
PAHs are instead totally
destroyed by collisions with thermal electrons. For
C atom loss, sufficient to cause a severe de-naturation of the
PAH aromatic structure.
Above 100 km s-1 such
PAHs are instead totally
destroyed by collisions with thermal electrons. For ![]() ,
PAHs experience increasing damaging caused by nuclear ionic collisions
up to 100 km s-1, which turns
into complete atomic loss for higher velocities. In this case the
destruction is due to the combined effect of electrons and nuclear
interaction with thermal ions.
,
PAHs experience increasing damaging caused by nuclear ionic collisions
up to 100 km s-1, which turns
into complete atomic loss for higher velocities. In this case the
destruction is due to the combined effect of electrons and nuclear
interaction with thermal ions.
The calculated PAH lifetime against destruction, ![]() , is
1.6
, is
1.6 ![]() 108 yr and 1.4
108 yr and 1.4 ![]() 108 yr for
108 yr for ![]() = 50
and 200 respectively. Small PAHs are preferentially destroyed
by electrons, big PAHs by ions. The calculated lifetimes are smaller
than the values found for carbonaceous grains (6
= 50
and 200 respectively. Small PAHs are preferentially destroyed
by electrons, big PAHs by ions. The calculated lifetimes are smaller
than the values found for carbonaceous grains (6 ![]() 108 yr)
but close to that for hydrogenated amorphous carbon (2
108 yr)
but close to that for hydrogenated amorphous carbon (2 ![]() 108 yr),
and far from the stardust injection timescale of 2.5
108 yr),
and far from the stardust injection timescale of 2.5 ![]() 109 yr. The presence of PAHs in shocked
regions therefore requires an efficient reformation mechanism and/or a
protective environment.
109 yr. The presence of PAHs in shocked
regions therefore requires an efficient reformation mechanism and/or a
protective environment.
We surmise that the molecular structure of PAHs is strongly affected by shock processing in the interstellar medium. Electronic excitation by impacting ions or electrons may lead to isomerization into stable pure-C species such as fullerenes. In contrast, nuclear interaction may lead to the formation of N-containing PAHs. Further laboratory studies are required to demonstrate the viability of these chemical routes.
Appendix A:
 ,
,
 and
and 
A fundamental quantity to describe the nuclear scattering is the energy
transfer cross section
![]() ,
which is function of the kinetic energy E
of the projectile and of the energy T
transferred to the target by the projectile in a single collision. At
low energies (
,
which is function of the kinetic energy E
of the projectile and of the energy T
transferred to the target by the projectile in a single collision. At
low energies (
![]()
![]() 1),
an approximated expression for the cross section can be
calculated using the power approximation to the Thomas-Fermi model of
interatomic interaction, i.e. with a potential of the form
1),
an approximated expression for the cross section can be
calculated using the power approximation to the Thomas-Fermi model of
interatomic interaction, i.e. with a potential of the form ![]() ,
where r is the distance between colliding
nuclei and m is a parameter related to the
steepness of the interatomic potential. The quantity m
can also be interpreted as an indicator of the energy of the
projectile, varying slowly from m = 1
at high energies to m
,
where r is the distance between colliding
nuclei and m is a parameter related to the
steepness of the interatomic potential. The quantity m
can also be interpreted as an indicator of the energy of the
projectile, varying slowly from m = 1
at high energies to m ![]() 0
at low energies (Winterbon
et al. 1970; Lindhard et al. 1968). We
have that
0
at low energies (Winterbon
et al. 1970; Lindhard et al. 1968). We
have that
with
where
The power approximation of the Thomas-Fermi cross section
(Eq. (A.1))
gives the following expression for the nuclear stopping cross section,
obtained evaluating the integral in Eq. (4)
between 0 and ![]() :
:
For Thomas-Fermi interaction, using Eqs. (1), (A.2), (3) and (A.3), this leads to
with
For heavy screening (
The nuclear stopping cross section above threshold is given by
Eq. (10).
Remembering that ![]() and
and ![]() ,
this can be rewritten as follows
,
this can be rewritten as follows

The first term in the right side of the equation is equal to the nuclear stopping cross section in the no-threshold case (T0 = 0)

In the second term we use the equality E-m = (E1-2m/E1-m) to obtain

Combining the two we obtain the following expression for
![\begin{eqnarray*}S_{\rm n}(E) & = & 4 \pi a Z_{1} Z_{2}~ e^{2} \frac{M_{1}}{M_{1...
...)
\left[1 - \left(\frac{E_{\rm0n}}{E}\right)^{1-m}\right]\cdot
\end{eqnarray*}](/articles/aa/full_html/2010/02/aa11682-09/img190.png)
The total cross section is given by Eq. (11)

The term (T0-m/m) can be rewritten as follows

Then we have

Using a similar approach we can write the term

Then second term in the right side of the equation then becomes

Combining the two terms we obtain for
![\begin{eqnarray*}\sigma(E) = 4 \pi a Z_{1} Z_{2} e^{2} \frac{M_{1}}{M_{1}+M_{2}}...
...mma~E}~
\left[\left(\frac{E_{\rm0n}}{E}\right)^{-m} - 1\right].
\end{eqnarray*}](/articles/aa/full_html/2010/02/aa11682-09/img197.png)
The expression for the average transferred energy

Appendix B: Low and high energy regime above threshold
In the low energy regime m can be taken equal
to 0, so the differential cross section d![]() becomes
becomes
| (B.1) |
The corresponding expressions for
| (B.2) | ||
| (B.3) | ||
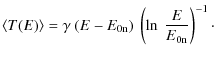
|
(B.4) |
In the high enery regime m = 1, then we have
| (B.5) |
and consequently
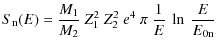
|
(B.6) | ||
| (B.7) | |||
| (B.8) |
Appendix C: Orientation correction
To calculate the orientation correction factor ![]() ,
let us consider the two versors
,
let us consider the two versors ![]() and
and ![]() ,
perpendicular to the PAH surface and forming between each
other the angle
,
perpendicular to the PAH surface and forming between each
other the angle ![]() .
This configuration defines two possible orientations for the molecule.
The average orientation is then given by the following integral:
.
This configuration defines two possible orientations for the molecule.
The average orientation is then given by the following integral:
where
Acknowledgements
We are grateful to L. Allamandola and L. Verstraete for useful discussions, and we acknowledge our referee Tom Hartquist for careful reading and helpful comments. E.R.M. thanks G. Lavaux for support and technical assistance and acknowledges financial support by the EARA Training Network (EU grant MEST-CT-2004-504604).
References
- Allamandola, L. J., Tielens, A. G. G. M., & Barker, J. R. 1989, ApJS, 71, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Andersen, M., Rho, J., Hewitt, J., & Reach, W. 2007, in BAAS, 38, 932 [Google Scholar]
- Armus, L., Draine, B., Engelbracht, C., et al. 2007, in BAAS, 38, 789 [Google Scholar]
- Banhart, F. 1997, J. Appl. Phys., 81, 3440 [NASA ADS] [CrossRef] [Google Scholar]
- Berné, O., Joblin, C., Deville, Y., et al. 2007, A&A, 469, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borkowski, K. J., & Dwek, E. 1995, ApJ, 454, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Bregman, J. D., Allamandola, L. J., Witteborn, F. C., Tielens, A. G. G. M., & Geballe, T. R. 1989, ApJ, 344, 791 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bregman, J. N. 1980, ApJ, 236, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Meyer, D. M., Jura, M., & Savage, B. D. 1996, ApJ, 467, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Cherchneff, I., Barker, J. R., & Tielens, A. G. G. M. 1992, ApJ, 401, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Cosslett, V. E. 1978, J. Microsc., 113, 113 [PubMed] [Google Scholar]
- Désert, F.-X., Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215 [NASA ADS] [Google Scholar]
- Draine, B. T., & Li, A. 2001, ApJ, 551, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Salpeter, E. E. 1979, ApJ, 231, 438 [Google Scholar]
- Dwek, E., & Scalo, J. M. 1980, ApJ, 239, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Frenklach, M., & Feigelson, E. D. 1989, ApJ, 341, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Füller, T., & Banhart, F. 1996, Chem. Phys. Lett., 254, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Guillet, V., Pineau Des Forêts, G., & Jones, A. P. 2007, A&A, 476, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Irwin, J. A., & Madden, S. C. 2006, A&A, 445, 123 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Irwin, J. A., Kennedy, H., Parkin, T., & Madden, S. 2007, A&A, 474, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jochims, H. W., Ruhl, E., Baumgartel, H., Tobita, S., & Leach, S. 1994, ApJ, 420, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P., Tielens, A. G. G. M., Hollenbach, D. J., & McKee, C. F. 1994, ApJ, 433, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P., Tielens, A. G. G. M., & Hollenbach, D. J. 1996, ApJ, 469, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Latter, W. B. 1991, ApJ, 377, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Le Page, V., Snow, T. P., & Bierbaum, V. M. 2001, ApJS, 132, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Lindhard, J., Scharff, M., & Schiott, H. E. 1963, Mat. Fys. Medd. Dan. Vid. Selsk., 33, 14 [Google Scholar]
- Lindhard, J., Nielsen, V., & Scharff, M. 1968, Mat. Fys. Medd. Dan. Vid. Selsk., 36, 10 [Google Scholar]
- McKee, C. 1989, in Interstellar Dust, ed. L. J. Allamandola, & A. G. G. M. Tielens, IAU Symp., 135, 431 [Google Scholar]
- McKee, C. F., & Ostriker, J. P. 1977, ApJ, 218, 148 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., Hollenbach, D. J., Seab, G. C., & Tielens, A. G. G. M. 1987, ApJ, 318, 674 [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2010, A&A, 510, A37 (MJT) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montet, G. L. 1967, Carbon, 5, 19 [CrossRef] [Google Scholar]
- Montet, G. L., & Myers, G. E. 1971, Carbon, 9, 179 [CrossRef] [Google Scholar]
- Nakai, K., Kinoshita, C., & Matsunaga, A. 1991, Ultramicroscopy, 39, 361 [CrossRef] [Google Scholar]
- O'Connor, D. J., & Biersack, J. P. 1986, Nucl. Instrum. Methods Phys. Res. B, 15, 14 [Google Scholar]
- O'Halloran, B., Satyapal, S., & Dudik, R. P. 2006, ApJ, 641, 795 [NASA ADS] [CrossRef] [Google Scholar]
- O'Halloran, B., Madden, S. C., & Abel, N. P. 2008, ApJ, 681, 1205 [NASA ADS] [CrossRef] [Google Scholar]
- Omont, A. 1986, A&A, 164, 159 [NASA ADS] [Google Scholar]
- Peeters, E., Hony, S., Van Kerckhoven, C., et al. 2002, A&A, 390, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Podio, L., Bacciotti, F., Nisini, B., et al. 2006, A&A, 456, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pino, T., Dartois, E., Cao, A.-T., et al. 2008, A&A, 490, 665 [CrossRef] [EDP Sciences] [Google Scholar]
- Rapacioli, M., Joblin, C., & Boissel, P. 2005, A&A, 429, 193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Serra Díaz-Cano, L., & Jones, A. P. 2008, A&A, 492, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sigmund, P. 1981, Sputtering by Particle Bombardment, 1, ed. R. Behrisch, in Topics in Applied Physics (Springer-Verlag), 47 [Google Scholar]
- Simmons, J. H. W. 1965, Radiation Damage in Graphite (Pergamon Press) [Google Scholar]
- Slavin, J. D. 2008, Space Sci. Rev., 50 [Google Scholar]
- Smith, J. D. T., Rudnick, L., Delaney, T., et al. 2009, ApJ, 693, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Sofia, U. J. 2009, in Cosmic Dust - Near and Far, ed. T. Henning, E. Grun, & J. Steinacker [Google Scholar]
- Tappe, A., Rho, J., & Reach, W. T. 2006, ApJ, 653, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 1998, ApJ, 499, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2005, The Physics and Chemistry of the Interstellar Medium (University of Cambridge Press) [Google Scholar]
- Tielens, A. G. G. M. 2008, ARA&A, 46, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tomita, S., Andersen, J. U., Gottrup, C., Hvelplund, P., & Pedersen, U. V. 2001, Phys. Rev. Lett., 87, 073401 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Welty, D. E., Jenkins, E. B., Raymond, J. C., Mallouris, C., & York, D. G. 2002, ApJ, 579, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Winterbon, K. B., Sigmund, P., & Sanders, J. B. 1970, Mat. Fys. Medd. Dan. Vid. Selsk., 37, 14 [Google Scholar]
- Ziegler, J. F., Biersack, J. P., & Littmark, U. 1985, The Stopping and Ranges of Ions in Matter, ed. J. F. Ziegler (Pergamon Press), 1 [Google Scholar]
Footnotes
- ... emission
![[*]](/icons/foot_motif.png)
- http://chandra.harvard.edu/photo/2006/m82/
All Tables
Table 1:
Kinetic energy E and reduced energy
![]() for H, He and C impacting on a carbon atom.
for H, He and C impacting on a carbon atom.
Table 2:
Threshold energy T0 and
critical kinetic energy
![]() for H, He and C ions impacting on a carbon atom.
for H, He and C ions impacting on a carbon atom.
Table 3: PAH destruction analytical fit parameters and survival timescales for electron and ion collisions.
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11682fg1.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg54.png)
|
Figure 1:
Scattering geometry for an elastic collision of particle 1
(mass M1, initial
velocity v0, impact
parameter p), on particle 2
(mass M2, initial
velocity zero). After the impact, the projectile particle 1 is
deflected by the angle |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{11682fg2.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg80.png)
|
Figure 2:
The nuclear stopping cross section
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{11682fg3.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg84.png)
|
Figure 3:
The nuclear stopping cross section
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11682fg4.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg87.png)
|
Figure 4:
The structure of the 125 km s-1
shock: temperature T4
= T/104 K, hydrogen
density |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11682fg5.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg88.png)
|
Figure 5:
The velocity profile of a 50 C-atom PAH in a shock with
velocity |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11682fg6.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg102.png)
|
Figure 6:
The number of collisions |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{11682fg7.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg130.png)
|
Figure 7:
The fractional C-atom loss |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{11682fg8.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg131.png)
|
Figure 8: Same as Fig. 7 calculated for a 200 carbon atoms PAH. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{11682fg9.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg132.png)
|
Figure 9: Carbon atom loss due to collisions with thermal and inertial ions (H + He + C) via nuclear interaction. The figure shows the comparison betwen the three threshold values T0 = 4.5, 7.5 and 15 eV for a 50 carbon atom PAH. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{11682f10.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg133.png)
|
Figure 10:
The fractional C-atom loss |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{11682f11.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11682-09/Timg168.png)
|
Figure 11:
The evolution of a 50 carbon atom PAH following the loss of |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



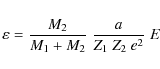
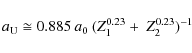
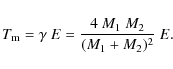
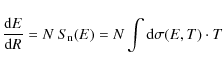
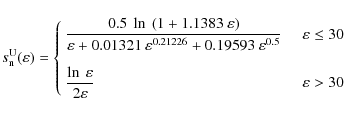
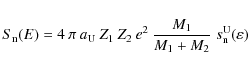
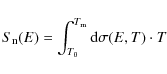
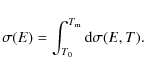
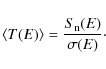
![\begin{displaymath}%
S_{\rm n}(E) = \frac{C_{m}~E^{-m}}{1-m} ~ [T_{\rm m}^{1-m} - T_{0}^{1-m}]
\end{displaymath}](/articles/aa/full_html/2010/02/aa11682-09/img68.png)
![\begin{displaymath}%
\sigma(E) = \frac{C_{m}~E^{-m}}{m} ~ [T_{0}^{-m} - T_{\rm m}^{-m}]
\end{displaymath}](/articles/aa/full_html/2010/02/aa11682-09/img69.png)
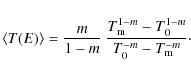
![\begin{displaymath}%
m(E) = 1 - \exp~\left[~-\exp \; \sum_{i=0}^{5}~a_{i}~\left(...
...rac{\varepsilon(E)}{\varepsilon_{1}}\right)^{i}~\right)\right]
\end{displaymath}](/articles/aa/full_html/2010/02/aa11682-09/img71.png)
![\begin{displaymath}%
S_{\rm n}(E) = 4 \pi a Z_{1} Z_{2}~ e^{2} \frac{M_{1}}{M_{1...
...ilon)
\left[1 - \left(\frac{E_{\rm0n}}{E}\right)^{1-m}\right]
\end{displaymath}](/articles/aa/full_html/2010/02/aa11682-09/img75.png)
![\begin{displaymath}%
\sigma(E) = 4 \pi a Z_{1} Z_{2} e^{2} \frac{M_{1}}{M_{1}+M_...
...gamma~E}
\left[\left(\frac{E_{\rm0n}}{E}\right)^{-m}-1\right]
\end{displaymath}](/articles/aa/full_html/2010/02/aa11682-09/img76.png)
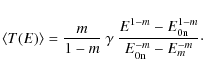
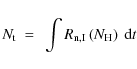
![\begin{displaymath}%
F_{\rm L}~ =~ \left(1~ -~ \exp\left[ -N_{\rm t}/N_{\rm C}\right]~ \right)
\end{displaymath}](/articles/aa/full_html/2010/02/aa11682-09/img113.png)