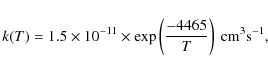The abundance of HNCO and its use as a diagnostic of environment

D. M. Tideswell; G. A. Fuller; T. J. Millar; A. J. Markwick

doi:10.1051/0004-6361/200810820

Free Access

Issue		A&A Volume 510, February 2010


Article Number		A85
Number of page(s)		9
Section		Interstellar and circumstellar matter
DOI		https://doi.org/10.1051/0004-6361/200810820
Published online		16 February 2010

A&A 510, A85 (2010)

The abundance of HNCO and its use as a diagnostic of environment

D. M. Tideswell¹ - G. A. Fuller¹ - T. J. Millar² - A. J. Markwick¹

1 - Jodrell Bank Centre for Astrophysics, Alan Turing Building, School of Physics and Astronomy, The University of Manchester, Oxford Road, Manchester M13 9PL, UK
2 - Astrophysics Research Centre, School of Mathematics and Physics, Queen's University Belfast, Belfast, BT7 1NN, UK

Received 18 August 2008 / Accepted 22 September 2009

Abstract
Aims. We aim to investigate the chemistry and gas phase abundance of HNCO and the variation of the HNCO/CS abundance ratio as a diagnostic of the physics and chemistry in regions of massive star formation.
Methods. A numerical-chemical model has been developed which self-consistently follows the chemical evolution of a hot core. The model comprises of two distinct stages. The first stage follows the isothermal, modified free-fall collapse of a molecular dark cloud. This is immediately followed by an increase in temperature which represents the switch on of a central massive star and the subsequent evolution of the chemistry in a hot, dense gas cloud (the hot core). During the collapse phase, gas species are allowed to accrete on to grain surfaces where they can participate in further reactions. During the hot core phase surface species thermally desorb back in to the ambient gas and further chemical evolution takes place. For comparison, the chemical network was also used to model a simple dark cloud and photodissociation regions.
Results. Our investigation reveals that HNCO is inefficiently formed when only gas-phase formation pathways are considered in the chemical network with reaction rates consistent with existing laboratory data. This is particularly true at low temperatures but also in regions with temperatures up to $\sim$ 200 K. Using currently measured gas phase reaction rates, obtaining the observed HNCO abundances requires its formation on grain surfaces - similar to other ``hot core'' species such as CH₃OH. However our model shows that the gas phase HNCO in hot cores is not a simple direct product of the evaporation of grain mantles. We also show that the HNCO/CS abundance ratio varies as a function of time in hot cores and can match the range of values observed. This ratio is not unambiguously related to the ambient UV field as been suggested - our results are inconsistent with the hypothesis of Martín et al. (2008, ApJ, 678, 245). In addition, our results show that this ratio is extremely sensitive to the initial sulphur abundance. We find that the ratio grows monotonically with time with an absolute value which scales approximately linearly with the S abundance at early times.

Key words: astrochemistry - stars: formation

1 Introduction

The molecule HNCO (isocyanic acid) was first detected in the interstellar medium over 30 years ago (Snyder & Buhl 1972) in the Sgr B2 molecular cloud complex where its distribution was found to be spatially extended with relatively strong emission. Since its discovery, HNCO has been subsequently observed in several other molecular clouds, including the dark cloud TMC-1 (e.g. Goldsmith et al. 1982; Brown 1981; Jackson et al. 1984). In the survey of 18 molecular clouds conducted by Jackson et al. (1984), HNCO emission was detected in seven sources with an average excitation temperature of 12 K, suggesting that this molecule was tracing cold gas. Jackson et al. (1984) proposed that HNCO was a dense gas tracer due to the coincidence of the emission with regions of high density ( $n \gtrsim 10^{6}~{\rm cm^{-3}}$ ). A larger survey of 81 molecular clouds was conducted by Zinchenko et al. (2000). They reported a 70% detection rate with typical fractional abundances relative to the total hydrogen number density, $n_{{\rm H}}$ , of $\sim$ 10^-9 and a wide range of rotational temperatures from 10 K to 500 K. Three of the objects were mapped and showed the emission region to be compact and centrally peaked.

Isocyanic acid has also been detected in hot cores (HCs), the sites of early stage, high mass star-formation including G34.3+0.15 (MacDonald et al. 1996), W3(H₂O) (Helmich & van Dishoeck 1997) and Sgr B2; in the N, M and NW cores (Nummelin et al. 2000). A survey towards seven high-mass star forming regions by Bisschop et al. (2007) identified HNCO with fractional abundances relative to $n_{{\rm H}}$ of between $6.4 \times10^{-9}$ and $5.4\times 10^{-8}$ and excitation temperatures from 64 K to 278 K. The observations suggested that HNCO can also trace much warmer gas - consistent with the findings of Zinchenko et al. (2000) and as such could be a potential indicator of star formation activity.

A recent multitransition study of 13 molecular clouds towards the Galactic Centre was conducted by Martín et al. (2008). The sources were selected to represent a range of physical conditions and included photodissociation regions (PDRs) along with HCs and giant molecular clouds. Martín et al. (2008) compared the CS abundance, a species used as a dense gas tracer and regarded as a tracer of star formation sites (Bronfman et al. 1996), to that of HNCO for each of the sources. They found that the ratio of the abundance of HNCO to that of CS (as traced by ¹³CS) was smaller for regions in which the FUV radiation is enhanced (PDRs), perhaps indicating that HNCO is more sensitive than CS to FUV photodissociation. The HNCO/CS ratio was systematically smaller in PDR-like regions by approximately two orders of magnitude than in the giant clouds. HCs were found to have intermediate values. It was therefore proposed that the HNCO/CS abundance ratio may provide a useful tool in distinguishing between shock and radiation (FUV) activity in molecular clouds. However, the Martín et al. (2008) survey only observed a limited sample towards the Galactic Centre and before the usefulness of this possible tracer can be established more complete surveys and a theoretical understanding of the processes involved are desirable.

Since the detection of HNCO there has been much speculation as to how this molecule forms but there have been few chemical models developed which incorporate an HNCO reaction network. Some authors have considered formation only in the gas phase (e.g. Iglesias 1977; Turner et al. 1999) whilst others have modelled the molecule's formation on grain surfaces (e.g. Garrod et al. 2008). Here we reconsider these processes and motivated by the observations of Martín et al. (2008), construct a model for a hot core including both gas phase and grain surface formation and destruction of HNCO. We set out to model both the HNCO abundance and the HNCO/CS ratio as a function of time for such a region. We also aim to explore the response of the gas-phase formation of HNCO to changing physical conditions. Besides modelling HNCO in hot cores, simple models of a dark cloud and PDRs are also presented for comparison.

2 Model descriptions

Our hot core model consists of two distinct stages. The first stage is the collapsing cloud (CC) phase which follows the isothermal collapse of a dark molecular cloud whilst the second stage follows the evolution at constant density and a specified temperature - this is the HC phase. Along with the CC and HC models simple dark cloud (DC) and PDR models were also produced. These models were similar to the HC models in that no collapse was included but different physical conditions were used. All the models described in this paper were single point models.

2.1 Physical model

The CC model begins at a time t = 0 with an homogeneous dark molecular cloud at a temperature, T and an initial total hydrogen number density of $2 \times 10^4~{\rm cm^{-3}}$ . The total hydrogen number density is defined as $n_{\rm H} = 2 n({\rm H_2})+n({\rm H})$ and is equal to the cloud's density. It was assumed that the cloud was shielded by a visual extinction, $A_{\rm v}$ , of 15 magnitudes and the standard Galactic UV radiation field and cosmic ray ionisation rates were adopted. These physical conditions were chosen to be representative of a typical Galactic molecular cloud (e.g. Millar & Herbst 1990). The cloud was then allowed to collapse isothermally following the modified free-fall collapse formula (see Spitzer 1978);

$\begin{displaymath} \frac{\textrm{d}n(t)}{\textrm{d}t} \!= \!B \left( \frac{n(t)... ...!-\! 1 \right] \right\}^{1/2}\textrm{cm}^{-3} \textrm{s}^{-1}, \end{displaymath}$

(1)

where B is the retardation factor and a value of 0.7 was adopted following Rawlings et al. (1992), $n_{\rm o}$ is the initial cloud density (total hydrogen number density) prior to the collapse being initiated, G is the Universal Gravitational constant and $m_{{\rm H}}$ is the atomic mass of hydrogen.

The collapse was halted once $n_{\rm H}=2\times10^7~{\rm cm^{-3}}$ which occurs after approximately $5 \times10^5$ years. This density was chosen to be representative of a typical hot core. As soon as this density was reached the model terminated and this was considered to be the end of the CC stage. The final chemical states of these collapse models were used as the initial chemistry of the subsequent hot core phases. A summary of the physical parameters adopted for the seven CC models used in this work is given in Table 1.

Table 1: Summary of the seven collapsing cloud models.

The HC model represents the second stage of the overall evolution. The HC was considered to be an homogeneous cloud at the final density reached at the end of the collapse phase, $n_{\rm H}=2\times10^7~{\rm cm^{-3}}$ , in which the $A_{\rm v}$ was high enough that the influence of external FUV photons is negligible. For the duration of the HC model these physical conditions remained fixed.

A total of 10 HC models were produced. Models 1 through 4 all had the same physical conditions including a temperature of 200 K, meant to represent the heating by a newly formed central star. The four models differ in their chemical networks. On the other hand, models 5 to 10 all had the same chemistry but differing temperatures (the temperature of the initial the collapsing clouds for these models also differed). A summary of these models can be seen in Table 2

In order to follow chemistry on dust surfaces it was necessary to include dust grains in the models. By assuming a gas mass to dust mass ratio of 100, the dust number density (relative to $n_{{\rm H}}$ ) was calculated to be $1.33 \times 10^{-12}$ . A single population of spherical dust grains was then assumed with each grain having a radius of 10^-5 cm. The total number of binding sites on each grain was approximately 10⁶ assuming a surface density of $7.9 \times10^{14}~{\rm cm^{-2}}$ .

The DC and PDR models were modelled in a similar fashion to the HC. The physical conditions were kept constant in each case and no collapse was included. The DC was modelled using a T=10 K, $n_{\rm H}=2\times10^4~{\rm cm^{-3}}$ and an $A_{\rm v}=15$ , whilst the PDR model adopted conditions representative of the Horsehead nebula (Habart et al. 2005); T=50 K, $n_{\rm H}=2\times10^4~{\rm cm^{-3}}$ , $A_{\rm v} = 1$ and an enhanced FUV radiation field equal to 60 times the interstellar value as used in all the other models. In order to mimic the effects of self-shielding of H₂ and CO, which is not explicitly included in the code, the photodissociation rates for both these species were set to zero in the PDR models. All the DC and PDR models produced in this work are also summarised in Table 2. A range of PDR models were run to demonstrate the effect of different aspects of the HNCO chemistry, different densities and different initial chemical compositions, either atomic or evolved from a collapsing cloud. A very dense PDR with an initially evolved chemistry such as models PDR4 and PDR5 were explored to represent clumps exposed to the UV radiation from a very nearby young massive star.

Table 2: Summary of the dark cloud (DC), hot core (HC) and PDR models used to model the time dependent HNCO gas-phase abundance.

Table 3: Standard initial chemical abundances relative to the total hydrogen number density.

Table 4: Key reactions included in the chemical network relevant to the formation of HNCO.

2.2 Chemical model

For the CC and DC models, along with PDR1, PDR2 and PDR3, all species were initially present in their elemental (atomic) form. The only exception was hydrogen which was assumed to be predominantly molecular with only a small fraction present as atoms. These initial abundances (relative to $n_{{\rm H}}$ ) are given in Table 3. For the HC models, along with PDR4 and PDR5, an evolved initial chemistry was used. The initial abundances at the start of these models used the abundances taken from a CC model. All the HC models and PDR4 used abundances taken from a CC at the final density, $2\times10^{7}$ cm^-3, whereas PDR5 used abundances from a CC model at an earlier stage in the collapse. In this case the density reached in the collapse was equal $2.4\times10^{5}$ cm^-3.

For all the models, once the chemistry had been initialised, the subsequent evolution of all species was followed via a chemical reaction network. This network included both reactions in the gas phase and on dust grain surfaces, along with the coupling mechanisms of accretion and thermal desorption only.

The gas-phase chemistry included all the reactions from the latest UMIST database for astrochemistry (UDfA), Rate06 (Woodall et al. 2007). For the grain-surface chemistry over 200 reactions were included from Allen & Robinson (1977), Hasegawa et al. (1992) and Hasegawa & Herbst (1993). Reactions on the surface were treated using the modified rate equation method as used by Ruffle & Herbst (2000).

In order to more completely model the HNCO gas-phase abundance some additional chemistry was included. Five surface reactions involving HNCO were taken from the expanded OSU gas-grain reaction network (Garrod et al. 2008) comprising of a single formation path (reaction b in Table 4) plus four destruction mechanisms. This surface chemistry was complemented by some gas phase reactions (also from Garrod et al. 2008) which followed the destruction of four new species (HNCHO, HNCOCHO, HNCONH and HNCOOH) formed from surface processing of HNCO. The destruction of HNCO in the gas phase was also included. This followed the treatment of Turner et al. (1999) and included the reactions between HNCO and the following species; H⁺, H₃⁺, He⁺, C⁺, H₃O⁺, CO⁺, HCO⁺, OCN⁺ and HNCO⁺. The rate coefficients for these reactions were taken from the ion-neutral reaction database compiled by Anicich (2004). The photodestruction of HNCO by FUV photons and cosmic ray induced photodissociation was also incorporated (Roberge et al. 1991; Gredel et al. 1989). Reactions with ions, particularly H₃⁺ and He⁺ dominate the destruction of HNCO in both dark clouds and hot cores.

Two gas-phase formation reactions for HNCO were added (reactions c and d in Table 4). The first reaction (c) is a neutral-neutral reaction whilst the second (d) is the dissociative recombination of H₂NCO⁺. For reaction c the rate coefficient is poorly known. Turner et al. (1999) adopted a value of 10^-13 cm³ s^-1 in their dark cloud model. However the energy barrier for this reaction may be much larger than suggested by this number and as such this reaction may only become significant in regions much warmer than dark clouds. The rate coefficient for this reaction has been measured but only at temperatures above 300 K (see the NIST chemical kinetics database). A fit to the available data provides an expression for the temperature dependent rate coefficient;

$\begin{displaymath} k(T) = 1.5 \times 10^{-11} \times {\rm exp}\left(\frac{-4465}{T}\right)~{\rm cm^3 s^{-1},} \end{displaymath}$

(2)

where T is the temperature. At 10 K this gives a considerably smaller value than that used by Turner et al. (1999). We used model DC1 to examine how the rate of reaction c affects the HNCO abundance - the model was run several times, each time using a different value for the rate coefficient ranging from 10^-22 cm³ s^-1 to 10^-8 cm³ s^-1 (increasing the value by two orders of magnitude each time). For all other models in which reaction c was included the rate was calculated using Eq. (2).

Three further reactions were added that form ``parent'' species needed for the formation of HNCO. Reactions e and f are ion-neutral reactions that are the first two reactions in a three stage process. The actual formation of HNCO in this reaction channel is via reaction d (Iglesias 1977). The rates of these reactions are calculated using the Langevin rate. The final reaction (g) is a charge exchange reaction between He⁺ and OCN which produces OCN⁺. This reaction represents a third, new, reaction channel between these two species since the UDfA already contains two reactions between He⁺and OCN. A rate coefficient of 10^-9 cm³ s^-1 was adopted for reaction g - representative of charge exchange reactions.

All models were allowed to evolve chemically for 10⁷ years, except for the collapsing cloud models which were stopped once the final density was reached.

3 Results

3.1 Gas phase formation of HNCO in dark clouds

For the first part of our investigation, using DC1, we explored the effect the rate coefficient for reaction c has on the abundance of HNCO in the gas phase. Figure 1 shows the HNCO abundance along with that of OCN for a range assumed rate coefficients for reaction c. For a rate coefficient of 10^-18 cm³ s^-1and above it is possible to achieve HNCO abundances within the observed range of $1.4\times 10^{-10}$ to $5.4\times 10^{-8}$ (MacDonald et al. 1996; Bisschop et al. 2007). Equation (2) implies that for the $\sim$ 4500 K barrier which laboratory data (NIST) infer for this reaction, temperatures above 277 K are required to reach this value of the rate coefficient for reaction c. Alternatively for this reaction to be effective at a gas temperature of 10 K, the barrier would have to be less than $\sim$ 165 K, much lower than measurements indicate. In other words, at the temperatures of dark molecular clouds these reactions do not occur.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{10820f1a.ps} \includegraphics[width=8.5cm,clip]{10820f1b.ps} \end{figure}$

Figure 1:

Time dependent, gas phase relative abundances for HNCO (top) and OCN (bottom) as a function of rate coefficient for reaction c in a non-collapsing dark cloud (model DC1). All other HNCO formation pathways are prohibited, both in the gas-phase and on grain surfaces. Reaction g has rate coefficient of 0.0. The shaded region defines the range of values for the observed HNCO abundance, $1.4\times 10^{-10}$ to $5.4\times 10^{-8}$ .

Open with DEXTER

Model DC2 illustrates how the other gas-phase formation route (via reaction d) influences the HNCO abundance. Reaction c was also included in this model and the rate was varied as before. Figure 2 shows the HNCO and OCN abundances along with those for OCN⁺. A lower limit for the fractional HNCO abundance (at steady state) is effectively set at $1.1 \times10^{-11}$ . This corresponds to the DC2 model with a rate cofficient of 0 for reaction c (the solid red line in Fig. 2). In this model HNCO is underabundant compared to observations by over 2 orders of magnitude. However, as seen for DC1, when the rate coefficient for reaction c increases, it is possible to achieve higher abundances. There is however very little difference between DC1 and DC2 for those models with non-zero rate coefficients for reaction c. Figure 3 shows the gas-phase abundance for the key reactants/products involved in the gas-phase production of HNCO (model DC3). This shows that there is OCN in the gas-phase but due to the low temperature this is not converted into HNCO. Instead, at low temperatures HNCO formation through reaction d (via reactions e and f) clearly dominates.

$\begin{figure} \par\includegraphics[width=8cm,clip]{10820f2a.ps} \includegraph... ...clip]{10820f2b.ps} \includegraphics[width=8cm,clip]{10820f2c.ps} \end{figure}$

Figure 2:

Time dependent, gas phase relative abundances for HNCO ( top), OCN ( middle) and OCN⁺ ( bottom) as a function of rate coefficient for reaction c in a non-collapsing dark cloud (model DC2). All gas-phase HNCO formation pathways are allowed; grain-surface reactions are prohibited. Reaction g has rate coefficient of 0.0. The shaded region defines the range of values for the observed HNCO abundance

Open with DEXTER

The fourth and final DC model, DC4, includes all the gas phase formation reactions listed in Table 4 (but in common with the other DC models, no grain surface processes) and the reaction rate for reaction c has been varied. The abundance profiles for this model are seen in Fig. 4. For small values of the rate coefficient of reaction c, the inclusion of reaction g increases the HNCO abundance. However, to achieve HNCO abundances in the observable range for ages less than 10⁶ years, the Turner rate must be greater than 10^-16 cm³ s^-1, which would imply temperatures of >370 K. At ages greater than $\sim$ 10⁶ years reaction g appears to be able to produce sufficient HNCO to match the observations even for a much reduced rate for reaction c (indeed even a rate of zero). However interpreting this late time rise in HNCO abundance needs to be treated with caution as these models only include gas phase reactions and so do not include the effect on the gas phase abundance of freeze-out on to the grains which will be very significant at these late times. This peak in HNCO abundance might occur earlier in models of denser clouds, but the effect of freeze-out on the gas phase abundances would also occur earlier.

$\begin{figure} \par\includegraphics[width=8cm,clip]{10820f3.ps} \end{figure}$	Figure 3: Time dependent, gas phase relative abundances for various species in a non-collapsing dark cloud using only reactions d, e and f to produce HNCO (model DC3).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{10820f4a.ps} \includegraphic... ...m,clip]{10820f4b.ps} \includegraphics[width=8cm,clip]{10820f4c.ps} \end{figure}$

Figure 4:

Time dependent, gas phase relative abundances for HNCO ( top), OCN ( middle) and OCN⁺ ( bottom) as a function of rate coefficient for reaction c in a non-collapsing dark cloud (model DC4). All gas-phase HNCO formation pathways are allowed but grain-surface reactions are prohibited. Reaction g has rate coefficient of $1.0 \times 10^{-9}$ cm³ s^-1. The shaded region defines the range of values for the observed HNCO abundance

Open with DEXTER

3.2 HNCO in photodissociation regions

Figure 5 shows the results for our PDR models. The HNCO abundances in PDR regions are even lower than those found in DC. For the three PDR models with an initially atomic chemistry (PDR1, PDR2 and PDR3) the largest late time abundance of HNCO (10^-17) is produced in the models with gas phase formation (PDR1 and PDR2), but these produce up to 9 orders of magnitude less HNCO than in a DC model. In model PDR3, which allows only surface reactions, HNCO is even less abundant, reaching a maximum value of 10^-20. The final two PDR models are also presented in Fig. 5. Both models follow a similar trend, that is the HNCO abundance is steadily decreasing with time, reaching a plateau at later times. However, the HNCO abundance in PDR4 is initially larger by about two orders of magnitude than in PDR5, although they ultimately reach similar abundances of about $2\times10^{-18}$ .

$\begin{figure} \par\includegraphics[width=8cm,clip]{10820f5.ps} \end{figure}$	Figure 5: Time dependent, relative gas phase abundance of HNCO for the five PDR models. For comparison the observed value is between $1.4\times 10^{-10}$ abd $5.4\times 10^{-9}$ . Note that curves for PDR1 and PDR2 are coincident.
Open with DEXTER

None of the PDR models ever approach the abundances of HNCO seen in DCs and HCs - even for the PDR models which start with previously evolved chemistries (PDR4 and PDR5).

The warmer conditions in these PDR models, largely due to the reduced optical depth and enhanced radiation field resulting in the heating of dust grains, lead to faster desorption meaning that once formed HNCO is never on the grains for long (at the 50 K used in these models the surface lifetime is approximately 100 years) so surface formation is limited. Furthermore, HNCO is efficiently destroyed by both FUV and cosmic ray induced photodestruction reactions. At no time during the evolution of any of our PDR models does the HNCO abundance come close to the $\sim$ 10^-9observed by Martín et al. (2008) towards PDR regions. As a consequence of this low HNCO abundance, the ratio of the abundance of HNCO to the CS abundance in these PDR models is also many orders of magnitude lower than seen by Martín et al. (2008) (Fig. 7). The origin of the HNCO observed by Martín et al. (2008) apparently in PDRs is therefore unclear, although it may be related to shielding of the molecular gas.

3.3 HNCO in hot cores

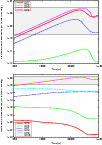
Figure 6 shows the HNCO gas-phase abundance as a function of time for all the hot core models 1 to 10. Only times between 1000 years to 1 Myr (since the HC's switch-on) are plotted as HCs are transient objects and are relatively short-lived phases of high-mass star formation lasting less than 1 Myr.

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{10820f6a.ps}} \resizebox{9cm}{!}{\includegraphics{10820f6b.ps}} \end{figure}$	Figure 6: Relative HNCO gas-phase abundance as a function of time for hot core models (HC) 1-4 ( top) and 5-10 ( bottom).
Open with DEXTER

HC1 includes the complete reaction network described earlier. The HNCO abundance for this model does reached observed levels. Beyond $\sim$ 10⁴ yrs values greater than 10^-9 are seen and a peak of $\sim$ $2 \times10^{-8}$ is reached at around 0.2-0.3 Myr. For the model with surface formation only (HC3) the lower observed limit for HNCO is reached but only beyond 10⁵ yr. The HNCO abundance in HC4 (which differs from HC1 only in the elemental sulphur abundance) is almost identical in behaviour as HC1. The major differences are that higher abundances are reached at slightly earlier times and the peak value of just over $2 \times10^{-8}$ remains for a further 0.1 Myr.

The gas-phase formation only HC model (HC2) shows that the abundance for HNCO remains relatively flat and never exceeds a few 10^-11, and even then only at HC ages greater than 0.3 Myr. As discussed above, this indicates that even the relatively high temperatures in hot cores, the gas-phase reactions by themselves are incapable of producing HNCO at observed levels.

The remaining HC models all had the same chemical networks (the full network with all reactions ``on''), it was only the initial and final temperatures that differed. In fact for the sake of comparison three of the models, HC5, HC7 and HC9, each had a constant temperature during the initial collapse and throughout subsequent constant density evolution. The first two models, HC5 and HC6, had the same post-collapse temperature (20 K), however HC6 used evolved abundances from a cloud collapsed at 10 K where as HC5 used abundances from a cloud at 20 K. HC5 never has a fractional HNCO abundance above 10^-19, whilst HC6 never really exceeds 10^-16. HC6 has consistently more HNCO throughout - due to a lower temperature collapse phase temperature. At lower temperatures the rate of thermal desoprtion is reduced such that the surface chemistry becomes more efficient. This means there is more NH, CO and OCN on grain surfaces - the key reactants for the surface formation of HNCO. For the models presented in this paper, the surface reaction between OCN and H is more important for the formation of HNCO than the reaction between CO and NH.

The next two models had post-collapse temperatures of 50 K. Again, the only difference being the collapse temperature (HC7 with T=50 K, HC8 with T=10 K). Both of these models have higher HNCO abundances compared to HC5 and HC6. Model HC8 is almost exactly the same as HC1, but HC7 has a relatively constant fractional abundance of around 10^-12. Model HC9 had a collapse and post-collapse temperature of 100 K. In this model the abundance of HNCO is roughly constant. At early times abundances just greater than 10^-11 are seen, falling slowly to just above 10^-12 beyond 0.1 Myr. The final model, HC10, also has a post-collapse temperature of 100 K but the collapse temperature is 10 K. This has an almost identical abundance profile as HC8. These results indicate that in order to achieve HNCO gas-phase abundances similar to those observed, post-collapse temperatures greater than 50 K are required.

3.4 The abundance of CS

Our models can also be used to investigate the abundance of CS as function of time in hot cores (and PDRs). A detailed discussion of the important pathways for the evolution of sulphur-bearing species, including CS, is given in Millar & Herbst (1990). As mentioned above, CS is often used as a tracer of dense gas associated with star formation and Martín et al. (2008) suggested the use of the ratio of the abundance of HNCO to that of CS as measure of the importance of UV radiation in a region.

Figures 7 and 8 show the evolution of the abundance of CS in our PDR and HC models respectively. All three PDR models which start with atomic compositions (PDR1, PDR2 and PDR3) show identical behaviour. From its initial value of $2\times10^{-10}$ the abundance of CS monotomically decreases by a factor of >10 over the period covered by the model. For PDR4 and PDR5 which start with evolved chemistries the CS abundance also monotomically decreases from a peak at early times, becoming approximately constant at later times. The highest abundance of CS in these models occurs are very early times in PDR5, where the peak abundance is $\sim$ 10^-9. In the HC models the CS abundance is initially relatively constant, rising to a peak after about 10⁵ yr before rapidly declining thereafter. Comparing models HC1 and HC4, which has a sulphur abundance ten times smaller that the other models, shows that the CS abundance throughout most the evolution of the HC scales nearly directly with the initial sulphur abundance.

$\begin{figure} \par\includegraphics[width=8cm,clip]{10820f7.ps} \end{figure}$	Figure 7: Time dependent, relative gas phase abundance of CS for the five PDR models.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{10820f8.ps} \end{figure}$	Figure 8: Time dependent, relative gas phase abundance of CS for four hot core models (HC1-4).
Open with DEXTER

4 Discussion

Hot core models HC1, HC2 and HC3 demonstrate that gas phase reactions alone can not produce a high enough abundance of HNCO to match observations. Reactions on the surfaces of grains are required. Of the models with a complete HNCO chemistry only models HC1, 8 and 10 achieve observed HNCO abundances. (Model HC4 can also match the observed abundance, but only differs from HC1 in its initial sulphur adundance.) These models all have a low collapse temperature combined with high post-collapse (hot core) temperatures. It appears that during the collapse phase cooler temperatures are essential. (A HC model identical to HC4, but with an inital collapse phase at 20 K, rather than 10 K, produces a peak HNCO abundance of only $\sim$ $3 \times 10^{-14}$ ). The cold collapse allows accretion on to the surface of grains and hence surface production of HNCO. However, during the hot core phase, high temperatures are needed to allow the desorption of the surface species back into the gas-phase. The models with constant temperatures across both stages 1 and 2 of the hot core model are seemingly incapable of producing HNCO at observed levels.

Interestingly, although grain surface reactions are clearly the ultimate source of the HNCO, the HNCO abundance does not follow the expected time dependent behaviour of a typical parent species ejected from grain mantles. In the log-log figures presented here the relative HNCO abundance is seen to linearly increase with time, reaching a peak value of $\sim$ 10^-8, consistent with the peak observed values, after about $2 \times10^{5}$ years (Fig. 6). This growth suggests that the gas phase HNCO is in fact a daughter product from the species ejected from the grain mantles.

Examining the grain mantle abundances shows that although it is efficiently formed, HNCO is also rapidly processed to more complex species. It is the destruction of these species after their ejection which produces the gas phase HNCO. In our models the HNCO is allowed to form several daughter products (HNCHO, HNCOCHO, HNCONH and HNCOOH) on grain surfaces during the collapse phase. Once the hot core stage is reached it is these species that are ejected and subsequently destroyed in the gas-phase thus returning HNCO. Such a possibility has been previously suggested by Zinchenko et al. (2000), although these authors prefered the explanation that the HNCO they observed was formed in the gas phase in post-shock gas. If the HNCO in our models was not destroyed on the grains it would be returned to the gas-phase as soon as the temperature is increased to 200 K with a relative abundance of $\sim$ $2\times10^{-5}$ . This abundance is several orders of magnitude overabundant compared to observations.

Based on its excitation temperature Bisschop et al. (2007) argue that HNCO is a ``first generation'' species ejected from grains. Our models indicate that this is not the case and suggest that this association of a molecular species with physical conditions on the basis of their excitation temperature alone can be misleading.

4.1 HNCO/CS abundance ratio

The HNCO/CS abundance ratio as a function of time is shown for the PDR models along with all the HC models in Fig. 9. The PDR models never reach values of the HNCO/CS abundance ratio >10^-6, orders of magnitude smaller than observed. For model HC1 the ratio increases from about $2\times10^{-4}$ at 10³ years, peaking at $\sim$ 3 around $3\times10^5$ years. Martín et al. (2008) observed ratios for HNCO/¹³CS in the range $\sim$ 1 to $\sim$ 100. Adopting a value of 77 for the abundance ratio to C/¹³C (Wilson & Rood 1994), this would imply HNCO/CS ratios of $\sim$ 0.013 to $\sim$ 1.3. The models span this ratio for times between approximately 10⁴ years to $2 \times10^{5}$ years showing that the time dependent evolution of the chemistry of hot cores alone can produce the entire range of observed HNCO/CS abundance ratios. Therefore, independent of its effect on the ratio, it is clear that HNCO/CS is not a unique tracer of UV radiation.

As the figure also shows, the underlying sulphur abundance also has a direct effect on the absolute value of the HNCO to CS abundance ratio. When S is reduced by a factor of 10, for a given time less than about few times 10⁵ years, the HNCO/CS ratio increases by a factor of 10. However for these times the evolution for different sulphur abundances is essentially independent of abundance. Overall the ratio monotonically increases with time up to a peak at a few times 10⁵ years. This generally monotonic behaviour suggests that for a given sulphur abundance this ratio could act as a ``chemical clock'' to constrain the ages of sources.

$\begin{figure} \par\includegraphics[width=8cm,clip]{10820f9a.ps}\par\includegrap... ...clip]{10820f9b.ps}\par\includegraphics[width=8cm,clip]{10820f9c.ps} \end{figure}$	Figure 9: HNCO/CS abundance ratio as a function of time for PDR models ( top), hot core models 1-4 ( middle) and hot core models 5-10 ( bottom). The shaded region defines the upper and lower limit for the HNCO/CS ratio as found by Martín et al. (2008).
Open with DEXTER

5 Summary

Our model shows that gas phase reactions appear incapable of producing HNCO in sufficient quantities (even at the $\sim$ 200 K temperature of hot cores) to match the observed abundance of this species. However the rate of a key gas phase reaction is uncertain and new laboratory determination of this rate coefficient is highly desirable. HNCO can be formed on icy surfaces by a variety of reactions. Despite the existence of these plausible mechanisms which can produce sufficient HNCO to match observations, laboratory data is again missing and should be obtained. Although it is produced on the grain surfaces in potentially large amounts, our models show that the gas phase HNCO is in fact a daughter product from the breakdown of more complex species to which the HNCO on the grains have been processed. This is contrary to recent speculation about the origin of this species (Bisschop et al. 2007). The model also shows that in PDRs HNCO can not be directly produced in sufficient quantities to match observations. In hot cores in particular it seems that surface chemistry during an earlier cold collapse phase followed by gas-phase processing (in the post-collapse regime) is important in the production of HNCO.

The ratio of HNCO to CS evolves strongly as a function of time while its absolute value is a sensitive function of the sulphur abundance. Whilst observations have suggested this ratio can be used to trace different physical conditions, our findings show that metallicity, choice of chemical network and hot core age can all also contribute to this value. Indeed, considering that HNCO contains three heavy elements one may expect the abundance of HNCO to be highly sensitive to the metallicity of a region.

Acknowledgements

D.M.T. wishes to acknowledge the receipt of an STFC studentship. Astrophysics at the JBCA and QUB is supported by grants from the STFC. This work has also been supported by the European Communitys human potential programme under contract MCRTNCT-512302 (The Molecular Universe). The authors would like to thank Paul Woods for his excellent proof reading ability.

References

Allen, M., & Robinson, G. W. 1977, ApJ, 212, 396 [NASA ADS] [CrossRef] [Google Scholar]
Anicich, V. G. 2004, JPL Publication 03-19 [Google Scholar]
Bisschop, S. E., Jørgensen, J. K., van Dishoeck, E. F., et al. 2007, A&A, 465, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bronfman, L., Nyman, L. A., & May, J. 1996, A&AS, 115, 81 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
Brown, R. L. 1981, ApJ, 248, L119 [NASA ADS] [CrossRef] [Google Scholar]
Garrod, R. T., Weaver, S. L. W., & Herbst, E. 2008, ApJ, 682, 283 [NASA ADS] [CrossRef] [Google Scholar]
Goldsmith, P. F., Snell, R. L., Deguchi, S., Krotkov, R., & Linke, R. A. 1982, ApJ, 260, 147 [NASA ADS] [CrossRef] [Google Scholar]
Gredel, R., Lepp, S., Dalgarno, A., et al. 1989, ApJ, 347, 289 [NASA ADS] [CrossRef] [Google Scholar]
Habart, E., Abergel, A., Walmsley, C. M., Teyssier, D., & Pety, J. 2005, A&A, 437, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Hasegawa, T. I. & Herbst, E. 1993, MNRAS, 261, 83 [NASA ADS] [CrossRef] [Google Scholar]
Hasegawa, T. I., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167 [NASA ADS] [CrossRef] [Google Scholar]
Helmich, F. P., & van Dishoeck, E. F. 1997, A&AS, 124, 205 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
Iglesias, E. 1977, ApJ, 218, 697 [NASA ADS] [CrossRef] [Google Scholar]
Jackson, J. M., Armstrong, J. T., & Barrett, A. H. 1984, ApJ, 280, 608 [NASA ADS] [CrossRef] [Google Scholar]
MacDonald, G. H., Gibb, A. G., Habing, R. J., et al. 1996, A&AS, 119, 333 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
Martín, S., Requena-Torres, M. A., Martín-Pintado, J., et al. 2008, ApJ, 678, 245 [NASA ADS] [CrossRef] [Google Scholar]
Millar, T. J., & Herbst, E. 1990, MNRAS, 242, 92 [NASA ADS] [Google Scholar]
Nummelin, A., Bergman, P., Hjalmarson, Å., et al. 2000, ApJS, 128, 213 [NASA ADS] [CrossRef] [Google Scholar]
Rawlings, J. M. C., Hartquist, T. W., Menten, K. M., et al. 1992, MNRAS, 255, 471 [NASA ADS] [CrossRef] [Google Scholar]
Roberge, W. G., Jones, D., Lepp, S., et al. 1991, ApJS, 77, 287 [NASA ADS] [CrossRef] [Google Scholar]
Ruffle, D. P., & Herbst, E. 2000, MNRAS, 319, 837 [NASA ADS] [CrossRef] [Google Scholar]
Snyder, L. E., & Buhl, D. 1972, ApJ, 177, 619 [NASA ADS] [CrossRef] [Google Scholar]
Spitzer, L. 1978, Physical processes in the interstellar medium, 2nd edn. (John Wiley and Sons) [Google Scholar]
Turner, B. E., Terzieva, R., & Herbst, E. 1999, ApJ, 518, 699 [NASA ADS] [CrossRef] [Google Scholar]
Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
Woodall, J., Agúndez, M., Markwick-Kemper, A. J., et al. 2007, A&A, 466, 1197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Zinchenko, I., Henkel, C., & Mao, R. Q. 2000, A&A, 361, 1079 [NASA ADS] [Google Scholar]

Footnotes

... (UDfA: UDfA; www.udfa.net
... database: The NIST chemical kinetics database; http://kinetics.nist.gov/kinetics/index.jsp

All Tables

Table 1: Summary of the seven collapsing cloud models.

Table 2: Summary of the dark cloud (DC), hot core (HC) and PDR models used to model the time dependent HNCO gas-phase abundance.

Table 3: Standard initial chemical abundances relative to the total hydrogen number density.

Table 4: Key reactions included in the chemical network relevant to the formation of HNCO.

All Figures

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{10820f1a.ps} \includegraphics[width=8.5cm,clip]{10820f1b.ps} \end{figure}$	Figure 1: Time dependent, gas phase relative abundances for HNCO (top) and OCN (bottom) as a function of rate coefficient for reaction c in a non-collapsing dark cloud (model DC1). All other HNCO formation pathways are prohibited, both in the gas-phase and on grain surfaces. Reaction g has rate coefficient of 0.0. The shaded region defines the range of values for the observed HNCO abundance, $1.4\times 10^{-10}$ to $5.4\times 10^{-8}$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{10820f2a.ps} \includegraph... ...clip]{10820f2b.ps} \includegraphics[width=8cm,clip]{10820f2c.ps} \end{figure}$	Figure 2: Time dependent, gas phase relative abundances for HNCO ( top), OCN ( middle) and OCN⁺ ( bottom) as a function of rate coefficient for reaction c in a non-collapsing dark cloud (model DC2). All gas-phase HNCO formation pathways are allowed; grain-surface reactions are prohibited. Reaction g has rate coefficient of 0.0. The shaded region defines the range of values for the observed HNCO abundance
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{10820f3.ps} \end{figure}$	Figure 3: Time dependent, gas phase relative abundances for various species in a non-collapsing dark cloud using only reactions d, e and f to produce HNCO (model DC3).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{10820f4a.ps} \includegraphic... ...m,clip]{10820f4b.ps} \includegraphics[width=8cm,clip]{10820f4c.ps} \end{figure}$	Figure 4: Time dependent, gas phase relative abundances for HNCO ( top), OCN ( middle) and OCN⁺ ( bottom) as a function of rate coefficient for reaction c in a non-collapsing dark cloud (model DC4). All gas-phase HNCO formation pathways are allowed but grain-surface reactions are prohibited. Reaction g has rate coefficient of $1.0 \times 10^{-9}$ cm³ s^-1. The shaded region defines the range of values for the observed HNCO abundance
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{10820f5.ps} \end{figure}$	Figure 5: Time dependent, relative gas phase abundance of HNCO for the five PDR models. For comparison the observed value is between $1.4\times 10^{-10}$ abd $5.4\times 10^{-9}$ . Note that curves for PDR1 and PDR2 are coincident.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{10820f6a.ps}} \resizebox{9cm}{!}{\includegraphics{10820f6b.ps}} \end{figure}$	Figure 6: Relative HNCO gas-phase abundance as a function of time for hot core models (HC) 1-4 ( top) and 5-10 ( bottom).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{10820f7.ps} \end{figure}$	Figure 7: Time dependent, relative gas phase abundance of CS for the five PDR models.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{10820f8.ps} \end{figure}$	Figure 8: Time dependent, relative gas phase abundance of CS for four hot core models (HC1-4).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{10820f9a.ps}\par\includegrap... ...clip]{10820f9b.ps}\par\includegraphics[width=8cm,clip]{10820f9c.ps} \end{figure}$	Figure 9: HNCO/CS abundance ratio as a function of time for PDR models ( top), hot core models 1-4 ( middle) and hot core models 5-10 ( bottom). The shaded region defines the upper and lower limit for the HNCO/CS ratio as found by Martín et al. (2008).
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.