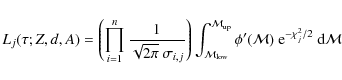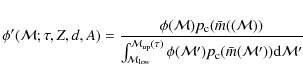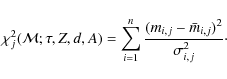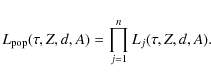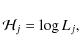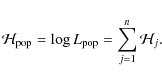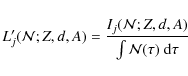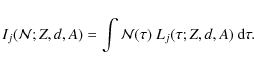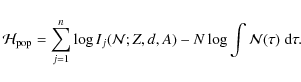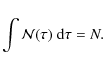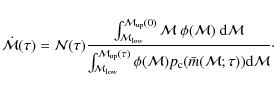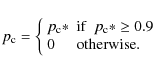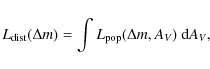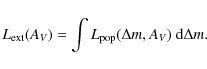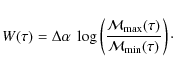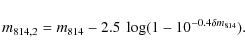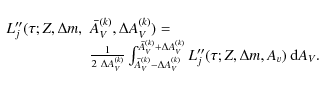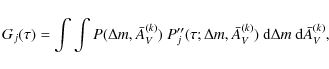EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 509 (January 2010) A&A, 509 (2010) A10 Full HTML
Free Access
Issue
A&A
Volume 509, January 2010
Article Number A10
Number of page(s) 12
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/20078239
Published online 12 January 2010
A&A 509, A10 (2010)

The distance to the C component of I Zw 18 and its star formation history

A probabilistic approach

L. Jamet1,2 - M. Cerviño1 - V. Luridiana1,3 - E. Pérez1 - T. Yakobchuk4

1 - Instituto de Astrofísica de Andalucía (CSIC), Camino bajo de Huétor, 50, Granada 18080, Spain
2 - Instituto de Astronomía, Universidad Nacional Autónoma de México, Apartado Postal 70-264, Ciudad Universitaria, México D.F. 04510, Mexico
3 - Instituto de Astrofísica de Canarias (IAC), c/Vía Láctea s/n, La Laguna, 38205 Tenerife, Spain
4 - Main Astronomical Observatory, Zabolotnoho 27, Kyiv 03680, Ukraine

Received 7 July 2007 / Accepted 20 August 2009

Abstract
Aims. We analyzed the resolved stellar population of the C component of the extremely metal-poor dwarf galaxy I Zw18 in order to evaluate its distance and star formation history as accurately as possible. In particular, we aimed at answering the question of whether this stellar population is young.
Methods. We developed a probabilistic approach to analyzing high-quality photometric data obtained with the Advanced Camera for Surveys of the Hubble Space Telescope. This approach gives a detailed account of the various stochastic aspects of star formation. We carried out two successive models of the stellar population of interest, paying attention to how our assumptions could affect the results.
Results. We found a distance to the C component of I Zw 18 as high as 27 Mpc, a significantly higher value than those cited in previous works. The star formation history we inferred from the observational data shows various interesting features: a strong starburst that lasted for about 15 Myr, a more moderate one that occurred $\approx$100 Myr ago, a continuous process of star formation between both starbursts, and a possible episode of low level star formation at ages over 100 Myr. The stellar population studied is likely $\approx$125 Myr old, although ages of a few Gyr cannot be ruled out. Furthermore, nearly all the stars were formed in the last few hundreds of Myr.

Key words: galaxies: individual: I Zw 18 - galaxies: photometry - galaxies: stellar content - galaxies: formation

1 Introduction

The study of dwarf galaxies is an important topic for the understanding of how galaxies form and evolve. Their presence in galaxy clusters and their physical properties put constraints on cosmological models, especially on the dark matter content of the Universe (e.g. Robertson et al. 2005). Furthermore, because their shallow gravitational potential well, dwarf irregular (dIrr) galaxies are ideal benchmarks for studing the effects of various processes, either internal (e.g., stellar winds and supernovae) or external (like gas infall and tidal forces), on the triggering and regulation of star formation (SF) in galaxies (Hunter et al. 1998; Hensler & Rieschick 2002). Finally, metal-deficient dIrr galaxies are expected to match the chemical composition of pristine galaxies, and efforts have been made to derive the primordial helium abundance of the Universe from the spectroscopic analysis of their ionized gas (Peimbert & Torres-Peimbert 1974, 1976; Izotov et al. 1997b, 2007; Peimbert et al. 2007).

Among the dIrr galaxies known, I Zw18 is arguably the most fascinating one. This object is the second lowest metallicity galaxy known (12 + log O/H = 7.2), corresponding to $\approx$1/30 of the solar value (e.g. Pagel et al. 1992; Skillman & Kennicutt 1993; Izotov & Thuan 1998; Izotov et al. 1999), being the lowest one SBS 0335-052 (West) (Izotov et al. 2004). Its blue color (van Zee et al. 1998) and its intense nebular emission (e.g. Vílchez & Iglesias-Páramo 1998; Cannon et al. 2002) bears witness to an intense ongoing SF episode. The galaxy presents a complex morphology; it is dominated by a two-lobed body (the ``main body'') with one companion, the ``C component'' (hereafter I Zw18 Dufour et al. 1996a).

In spite of many efforts, the distance and, more important, the age of the galaxy have not been well determined yet. By analyzing HST/WFPC2 color-magnitude diagrams (CMDs) and HST/FOS spectra, and assuming a distance of 10 Mpc (applying straightly the Hubble law to the redshift of the galaxy), Dufour et al. (1996b) detected a stellar population of up to 50 Myr in the main body of the galaxy and up to 300 Myr in the C component. They found no support for or against an old underlying population. Assuming the same distance and examining a larger set of HST/WFPC2 photometric data, Aloisi et al. (1999) decomposed the star formation history (SFH) in a continuous SF lasting over $\sim$1 Gyr and an ongoing starburst that started $\approx$15-20 Myr ago. By analyzing HST/WFPC2 CMDs jointly, ground-based spectra and the morphology of some nebular features, Izotov et al. (1999) find that a distance of 20 Mpc is necessary to explain the ionization state of the gas. They also state that the age of the galaxy, as derived from all three kinds of data, does not exceed 100 Myr, in agreement with the conclusion from Izotov & Thuan (1999) that very metal-deficient galaxies must all be young. Östlin (2000) carried out an analysis of HST/NICMOS photometric data and detected asymptotic giant branch stars (AGB) that, at the adopted distance of 12.6 Mpc (derived from the redshift corrected for the Virgocentric flow), are at least 1 Gyr old. From the surface distribution of the fluxes and colors of the galaxy, Kunth & Östlin (2000) argue that I Zw18 is an old galaxy whose age is likely $\sim$5 Gyr. A significant age of possibly several Gyr has also been advocated by Legrand et al. (2000) to account for the very homogeneous distribution of heavy elements throughout the ionized, optical-emitting gas of the galaxy. By studying the deep spectra of I Zw18C, Izotov et al. (2001) find that a distance of $\approx$15 Mpc is needed to reconcile ionized gas in this object with the apparent magnitudes of its brightest blue stars. This distance can actually be interpreted as a lower limit, since at larger distances these stars would be still considered as ionizing. Their spectra are well-fitted by models with a continuous star formation extending over the past 10-100 Myr, with no evidence of any older underlying stellar population. Papaderos et al. (2002) compared surface brightness maps obtained through various optical and near-infrared filters with the HST, which did not reveal any stellar population older than 0.5 Gyr. Such a population may exist, but most of the stellar content must be younger than this age. Izotov & Thuan (2004) carried out deep HST/ACS observations of I Zw18, improving by $\approx$2 mag the depth of stellar photometric data with respect to previous efforts. They concludes that the distance to I Zw18 should lie somewhere between 12.6 and 15 Mpc with the latter value being more likely, and claim that the absence of any detected red giant is proof that the galaxy is young ($\lesssim$500 Myr). Finally, by analyzing the same images as Izotov & Thuan (2004), along with other deep HST/ACS data, Aloisi et al. (2007) detected a red giant branch (RGB), as well as a confirmed, Cepheid star. They derived a distance of $\approx$18 Mpc and argue that the presence of RBG stars shows that the galaxy is old (at least 1 Gyr, but see also Tosi et al. 2007).

It is striking to see that similar approaches to the evaluation of the age of I Zw18 lead to contradictory results (e.g., Dufour et al. 1996b vs. Aloisi et al. 1999; or Kunth & Östlin 2000 vs. Papaderos et al. 2002). It turns out that the age estimates from the authors mentioned above go from a ten Myr to several Gyr! This might be explained at least partially by some uncertainties in the studies summarized above, such as the limited depth of the available data or the sensitivity of CMD analysis to the distance and extinction adopted. For this reason, we decided to carry out a new analysis of the deep HST/ACS observations performed by Izotov & Thuan (2004), focusing on I Zw18C. The latter has been little studied because of its faintness ($\approx$24 mag/ $\Box \hbox{$^{\prime\prime}$ }$ in the V band). However, there is a key difference between I Zw 18C and the main body that makes the C component more attractive for CMD studies: it is older.

1.
There is a significant absence of nebular emission. Because it is older, the observed surface brightness in the C component is lower than in the main body and is predominantly produced by the stellar component. The surface brightness in the main body is produced by both the stellar and nebular components (see, e.g. Vílchez & Iglesias-Páramo 1998). Also, compact clumps of ionized gas in the main component would mimic stellar sources, and the patchy ionized gas emission makes background subtraction more difficult.

2.
Isochrones (and their associated stellar luminosity functions) have a simpler structure at older (post Wolf-Rayet) ages, with well-defined structures excepting the blue loops that make a small contribution in the stellar luminosity function. In the case of the main component, there are identified Wolf-Rayet stars (Legrand et al. 1997; Izotov et al. 1997a) such a presence is difficult to explain in low-metallicity environment with standard evolutionary models Brown et al. (2002), so more complex evolutionary models (like the inclusion of rotation) would be required. However, current models including rotation produce evolutionary tracks with complex structures (see e.g. Fig. 3 in Meynet & Maeder 2005), so isochrones becomes strongly dependent on the assumed initial rotational velocity, the possible distribution of rotational velocities, and the (still unexplored) validity of homology relations between different stellar tracks for rotating stars.

There is an additional reason for choosing the C component instead of the main body. In the distance obtained by Izotov et al. (2001) from the integrated spectra of the galaxy the authors take the IMF sampling effects in the emission line spectrum into account (Cerviño et al. 2000, in its first version). However, they did not consider IMF sampling effects in the analysis of the continuum (Cerviño et al. 2002; Cerviño & Luridiana 2006) from which the distance of 15 Mpc to I Zw18C (and by extension, the main body) was obtained. It was also our intention to obtain an alternative value for the distance with a method where such sampling effects would be minimized (the CMD analysis).

For these reasons, we have decided to use study I Zw18C instead of the main body. We had built a new, improved CMD from the images of Izotov & Thuan (2004) and analyzed it with a probabilistic approach to evaluate the distance, the SFH, and the age of this component.

This paper is divided as follows. In Sect. 2, we define the probabilistic tools used in our approach. In Sect. 3, we describe the observational data and the theoretical isochrones on which our work was based. In Sect. 4, we present a first model of the stellar population studied. Section 5 is dedicated to a revision of the assumptions of this model, and in Sect. 6 we present a new model with improved reliability. We infer the minimum age of I Zw18C and discuss the estimate of its distance. Finally, we give our conclusions in Sect. 7.

2 A probabilistic approach

In considering a stellar population in which N individual stars are detected in a set of n photometric bands, note mi,jthe magnitude of the jth star in the ith photometric band. We first examine the case of a simple stellar population, i.e. a population where all the stars were formed at the same time and in the same conditions. The initial mass ${\cal{M}}_j$ of the jth star is considered a random variable and the initial mass function (IMF) $\phi({\cal{M}})$ is regarded as the probability density function (PDF) from which ${\cal{M}}_j$ is drawn. The expected magnitudes $\bar{m}_{i,j}$ of the star depend on ${\cal{M}}_j$ and on properties of the stellar population: the age $\tau$, the metallicity Z, the distance d and the interstellar extinction coefficients Ai. Furthermore, those magnitudes are affected by photometric errors, which we suppose follow Gaussian distributions of widths $\sigma_{i,j}$. Finally, the photometric data do not usually cover the whole IMF of the stellar population, since the faintest stars are not detected. Consequently, if we call $p_{\rm c}(m)$ the photometric completeness function of the data (the probability a star of magnitudes miis detected), then the observed magnitudes mi,j of the star jare associated to the following likelihood function (LF):

\begin{displaymath}L_j(\tau; Z,d,A) = \left( \prod_{i=1}^n \frac{1}{\sqrt{2\pi}~... ...}}} \phi'({\cal{M}})~ {\rm e}^{-\chi^2_j / 2}~{\rm d}{\cal{M}} \end{displaymath} (1)

with

\begin{displaymath}\phi'({\cal{M}}; \tau, Z,d,A) = \frac{\phi({\cal{M}}) p_{\rm ... ...({\cal{M}}') p_{\rm c}(\bar{m}({\cal{M}}')) {\rm d}{\cal{M}}'} \end{displaymath} (2)

and

\begin{displaymath}\chi^2_j({\cal{M}}; \tau, Z,d,A) = \sum_{i=1}^n \frac{(m_{i,j} - \bar{m}_{i,j})^2}{\sigma_{i,j}^2}\cdot \end{displaymath} (3)

In Eqs. (1) and (2), the upper limit ${{\cal{M}}_{{\rm up}}(\tau)}$ of the integrals is the maximum initial mass with which a $\tau$-old star still visible today could have been born.

Assuming that the initial masses of the stars are mutually independent, the LF $L_{\rm pop}$ associated to the distribution of magnitudes of the N stars is given by the product of the individual LFs Lj:

\begin{displaymath}L_{\rm pop}(\tau,Z,d,A) = \prod_{j=1}^n L_j(\tau,Z,d,A). \end{displaymath} (4)

In practice, it is preferable to work not with the LFs themselves, but rather with their logarithms. Hence, we introduce the following quantities:

\begin{displaymath}{\cal{H}}_j = \log L_j, \end{displaymath} (5)

\begin{displaymath}{\cal{H}}_{\rm pop} = \log L_{\rm pop} = \sum_{j=1}^n {\cal{H}}_j. \end{displaymath} (6)

In this section, we have limited the definition of Lj to the case of a simple stellar population. In what follows, we propose another definition that can be applied to composite populations.

2.1 Introducing the stellar formation history into the entropy

Many stellar populations show prolonged periods of star formation, in which case Eq. (1) cannot be used. It is necessary to introduce a function ${\cal{N}}(\tau)$ that describes the SFH of the population studied. Like their initial masses, the ages of the different stars are supposed to be independent random variables. As a result, we define ${\cal{N}}(\tau) ~ {\rm d}\tau$ as the expectancy of the number of stars observable today and whose ages are comprised between $\tau$ and $\tau + {\rm d}\tau$. Consequently, $L_j(\tau, Z, d, A)$ must be replaced by the following LF:

\begin{displaymath}L'_j({\cal{N}}; Z,d,A) = \frac{I_j({\cal{N}}; Z,d,A)}{\int {\cal{N}}(\tau) ~ {\rm d}\tau} \end{displaymath} (7)

with

\begin{displaymath}I_j({\cal{N}}; Z,d,A) = \int {\cal{N}}(\tau) ~ L_j(\tau; Z,d,A) ~{\rm d}\tau. \end{displaymath} (8)

The entropy ${\cal {H}}_{\rm pop}$ hence become:

\begin{displaymath}{\cal{H}}_{\rm pop} = \sum_{j=1}^n \log I_j({\cal{N}}; Z,d,A) - N \log \int {\cal{N}}(\tau) ~ {\rm d}\tau. \end{displaymath} (9)

For given values of Z, d, and A, maximizing ${\cal {H}}_{\rm pop}$ leads to the best-fit shape of ${\cal{N}}(\tau)$, not to absolute values of this function. The latter must then be normalized with the number of stars used:

\begin{displaymath}\int {\cal{N}}(\tau) ~ {\rm d}\tau = N. \end{displaymath} (10)

The mass rate $\dot{\cal{M}}(\tau)$ of star formation can be derived from ${\cal{N}}(\tau)$ by considering which part of the IMF is visible in the data at the age $\tau$:

\begin{displaymath}\dot{\cal{M}}(\tau) = {\cal{N}}(\tau) \frac{\int_{{\cal{M}}_{... ...M}}) p_{\rm c}(\bar{m}({\cal{M}};\tau)) {\rm d}{\cal{M}}}\cdot \end{displaymath} (11)

In some cases, a parametric model can be provided for the SFH. In this case, ${\cal{N}}(\tau)$ can be fitted using a Levenberg-Marquardt algorithm. In the case where no parametric model is assumed for the SFH, the latter must be inferred in a self-consistent way from the observed distribution of magnitudes mi,j. This can be achieved with the method developed by Hernández et al. (1999).

2.2 Comparison with other approaches

The variable ${\cal {H}}_{\rm pop}$ is an entropic tool whose maximization can be used to analyze resolved stellar populations. Contrary to simpler estimators (e.g., the chi-square one), it is sensitive not only to the shape of the tested isochrones in color-magnitude diagrams, but also to the density distribution of the stars along those isochrones, through the relations between the age, mass and magnitudes. This is particularly true for rapid stellar phases, where the magnitudes are very sensitive to the ages and initial masses of the stars. Other probabilistic methods have been developed to characterize resolved stellar populations, especially the comparison of star counts between observed and synthetic Monte-Carlo CMDs in different bins of the color-magnitude space (e.g. Gallart et al. 1999). However, the formalism proposed in this work is based on rigorous concepts, it is more accurate than the synthetic CMD approach. In particular, it avoids the biases and errors caused by the binning of data and the random content of simulated CMDs. Moreover, it bypasses expensive Monte-Carlo computations for the search of optimized parameters of the stellar population studied. In summary, ${\cal {H}}_{\rm pop}$allows a study of the stellar luminosity function as a whole, with its correlations among different luminosity bins, instead of only portions of the luminosity function without correlations among bins.

The approach we have presented is of course not free of drawbacks. In particular, there is no simple way to assess the goodness-of-fit, and Monte-Carlo simulations may be required to carry out this task (see Sect. 4.3). Furthermore, like other probabilistic methods, the results deeply depend on the input physics, in particular the stellar evolution models and the conversion of stellar parameters to magnitudes. Ideally, different evolutionary tracks and model atmospheres, or empirical magnitude calibrations, should be tested when analyzing an object, at the cost of simplicity and time.

3 Applications to I Zw18C

3.1 The photometric data

\begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig1.eps} \end{figure} Figure 1:

HST/ACS image of I Zw18C through the F555W filter. The two clusters ``C'' and ``NW'' mentioned by Izotov & Thuan (2004) are reported. The image display scale is logarithmic. North is up and East to the left. The ``white pixels'' are contaminated pixels that were rejected when performing the photometric measurements.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig2.eps} \end{figure} Figure 2:

Color-magnitude diagram of I Zw18C. The typical error bars as a function of F814W are reported for both the blue and red branches. The two clusters are annotated with open circles. The stars marked with crosses are those we rejected from the useful sample due to their extreme red color.We also report the 90% and 50% completeness limits as dashed lines.

Open with DEXTER

We carried out photometric measurements of the HST/ACS images obtained in the bands F555W ($\sim$V; Fig. 1) and F814W ($\sim$I) by Izotov & Thuan (2004). They performed photometric analysis of those images, obtaining data significantly deeper than those of previous works. However, their procedure, made use of a model point spread function (PSF) that was not optimal. For this reason, we performed our own measurements by using the well-suited DOLPHOT/ACS package (Dolphin 2000), which correctly accounts for the pixel undersampling of the instruments and uses accurate model PSFs.

The CMD that we obtained is shown in Fig. 2. The F555W and F814W magnitudes (hereafter m555 and m814, respectively) are expressed in the VEGAMAG system[*]. The CMD contains 965 sources going down to m555 = 29.8 and m814 = 29.0. We performed artificial star tests (ASTs) to assess the quality of the photometric data and evaluate their completeness. The latter shows a significant improvement with respect to the measurements of Izotov & Thuan (2004). Not only is the 50% completeness limit improved by nearly 1 mag, but the completeness is also maintained high closer to this limit (the completeness drop is more ``abrupt''). Furthermore, we used the ASTs to determine photometric errors that are more realistic than the default outputs by DOLPHOT/ACS and to evaluate the possible biases in the magnitudes retrieved.

We checked whether the stellar fluxes suffer from foreground Galactic extinction. Whereas the survey of Schlegel et al. (1998) yields a Galactic contribution of AV = 0.11 to the extinction toward I Zw18, the lower-resolution data of Burstein & Heiles (1982) indicate an extinction as small as AV = 0.01. Furthermore, an analysis of the nebular H$\alpha$/H$\beta$ line carried out by Cannon et al. (2002) shows that some regions of the main component of I Zw18 suffer very small extinction, if any. Consequently, we assumed that the Galactic extinction toward I Zw18C may be negligible and we did not correct our data for it.

3.2 Selection of the stars

Before carrying out the analysis of I Zw18C, we selected the stars for use. First, we limited the selection to the stars situated above the 90% completeness level. This threshold was chosen for two reasons: (i) the uncertainties in the photometric analysis (systematic and random errors in the magnitudes, evaluation of the completeness map) are small for the region of the CMD selected; and (ii) most of the stars situated below the 90% completeness limit are main-sequence (MS) objects that yield little useful information about the age and distance of the galaxy, compared with post-MS stars. Then, we rejected the sources situated within the two clusters annotated as ``C'' and ``NW'' by Izotov & Thuan (2004). Finally, we removed the five reddest remaining stars from the selection. According to Marigo & Girardi (2007), who revised the evolutionary models of asymptotic giant branch (AGB) stars, the presence of very red stars in the CMD is possible. However, the characteristics of these objects are still very sensitive to the physics used to model them. In principle, this problem concerns only extremely red stars. As a consequence, we decided to discard the stars with colors $m_{555} - m_{814} \gtrsim 2$. The final selection contains 408 stars, of which 315 are located in the blue ( $m_{555} - m_{814} \leq 0.6$) branch and 93 in the red one.

Given the selection procedure, the completeness function $p_{\rm c}$ for the selected stars can be written as a function of the ``real'' completeness $p_{\rm c}^*$ evaluated for the whole CMD:

\begin{displaymath}p_{\rm c} = \left\{ \begin{array}{l l} p_{\rm c}*& {\rm if~~... ...\rm c}* \geq 0.9 \\ 0& {\rm otherwise.}\\ \end{array}\right. \end{displaymath} (12)

3.3 Isochrones

An important assumption of this work regards the isochrones that we decided to use. We adopted the evolutionary tracks of Girardi et al. (2000) available for Z = 0.0004 and computed the theoretical absolute magnitudes through the ACS F555W and F814W filters[*] using the BaSeL 3.1 stellar library Westera et al. (2002).

4 A first model

4.1 Assumptions and procedure

We proceeded to a first measurement of the distance, extinction, and SFH of I Zw18C. The main assumptions of the calculus were the following:

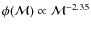  • a Salpeter IMF ( $\phi({\cal{M}}) \propto {\cal{M}}^{-2.35}$) in the 0.15-120 $M_\odot$ range;

  • the extinction to be uniform over the stellar population. Furthermore, since little work has been done regarding the extinction in I Zw18C (see, however Izotov et al. 2001), we decided to use the extinction AV as a free parameter;

  • no constraints on the SFH;

  • no concern for the possible effects of binary stars.
We explored the values of ${\cal {H}}_{\rm pop}$ in the $(\Delta m, A_V)$ space. For each examined point of this space, we computed the LFs $L_j(\tau; \Delta m, A_V)$. Using these coefficients, we evaluated the corresponding distribution ${\cal{N}}(\tau)$ with the algorithm of Hernández et al. (1999) and derived the entropy ${\cal{H}}_{\rm pop}(\Delta m, A_V)$. Furthermore, we calculated the entropies ${\cal{H}}_{\rm dist}(\Delta m) = \log L_{\rm dist}(\Delta m)$ and ${\cal{H}}_{\rm ext}(A_V) = \log L_{\rm ext}(A_V)$, where $L_{\rm dist}(\Delta m)$ and $L_{\rm ext}(A_V)$ are the LFs associated to the distance modulus and the amount of extinction, respectively. Those two LFs are defined by

\begin{displaymath}L_{\rm dist}(\Delta m) = \int L_{\rm pop}(\Delta m, A_V) ~ {\rm d}A_V, \end{displaymath} (13)

\begin{displaymath}L_{\rm ext}(A_V) = \int L_{\rm pop}(\Delta m, A_V) ~ {\rm d}\Delta m. \end{displaymath} (14)

4.2 Results

\begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig3.eps} \end{figure} Figure 3:

${\cal {H}}_{\rm dist}$ ( upper panel) and ${\cal {H}}_{\rm ext}$ ( lower panel) curves for the model of Sect. 4. The dashed lines indicate the best-fit values of $\Delta m$ and AV, while the dotted lines delineate the 99.9% confidence intervals.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig4.eps} \end{figure} Figure 4:

Observed CMD and theoretical isochrones for the model of Sect. 4. The observed data are corrected for interstellar extinction, using the best-fit value AV = 0.38. The dotted line shows the threshold above which we selected the stars to work with. The vertical axes show both apparent and absolute F814W magnitude scales, adopting the best-fit distance modulus $\Delta m = 32.12$.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig5.eps} \end{figure} Figure 5:

SFH derived from the approached explained in Sect. 4. The curve was slightly smoothed to limit the apparent statistic noise.

Open with DEXTER

The results are presented as follows. In Fig. 3, we present the curves of ${\cal{H}}_{\rm dist}(\Delta m)$ and ${\cal{H}}_{\rm ext}(A_V)$. Figure 4 shows the observed CMD along with some theoretical isochrones for the best-fit distance modulus and extinction. In Fig. 5, we show the mass rate $\dot{\cal{M}}(\tau)$ derived from ${\cal{N}}(\tau)$ at the best-fit distance and extinction.

The best-fit distance modulus is $\Delta m = 32.12$ (corresponding to a distance of 26.5 Mpc), and the 99.9% confidence interval for $\Delta m$ is 31.71-32.24. Such a distance modulus is higher than any previous estimate, by >1 mag for most of them and $\approx$0.8 mag for the newest (31.4, Aloisi et al. 2007). As for the extinction, the best-fit coefficient is AV = 0.38, and the 99.9% confidence interval is 0.30-0.45, a higher value than the different estimates of the foreground Galactic extinction (see Sect. 3.1). This value falls within the 0.20-0.65 interval derived by Izotov et al. (2001) from a spectroscopic study of I Zw18C and suggests the existence of dust clouds responsible for extinction inside this object.

The estimate of $\dot{\cal{M}}(\tau)$ shows various interesting features:

  • an intense episode of SF is visible at ages 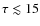$\tau \lesssim15$ Myr. This episode has already been detected by Izotov et al. (2001), who analyzed optical spectra of I Zw18C, and confirmed by Izotov & Thuan (2004) in their study of the resolved stellar population;

  • a lesser starburst is seen at 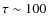$\tau \sim 100$ Myr;

  • approximately in the 15-70 Myr range the SFR is comparatively moderate but not negligible between those two bursts. Interestingly, the corresponding isochrones are those that fall between the two branches of the CMD, although they also cover populated regions of the CMD; that is, this empty zone of the CMD results not from an interruption in the SFH, but from the random filling of the CMD. Considering the estimated SFR, an average of 4 stars would be expected between the branches. The likelihood of observing no star there is about 6%, which is not small enough to discard the model;

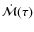  • the estimate of $\dot{\cal{M}}(\tau)$ suggests a low-rate, continuous SF that began at least a few hundreds Myr ago. However, the low number of stars benefit from the 300 Myr isochrone, and the uncertainty in their ages makes it impossible to confirm whether this SF process did occur.

Although this method seemed to yield accurate measurements of the distance, extinction, and SFH of I Zw18C, it was important to assess its reliability. Because of the complexity of the process, this could only be achieved by means of Monte-Carlo simulations. In the next section, we describe how we carried out this test.

4.3 Comparison to simulations

\begin{figure} \par\includegraphics[width=8.8cm,clip]{08239fig6.eps} \end{figure} Figure 6:

Synthetic CMD and theoretical isochrones for one of the simulations Sect. 4.3. The stars situated below the dotted line belong to the original observations of I Zw18C, whereas the others were simulated.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.8cm,clip]{08239fig7.eps} \end{figure} Figure 7:

${\cal {H}}_{\rm dist}$ ( upper panel) and ${\cal {H}}_{\rm ext}$ ( lower panel) curves for one of the simulations in Sect. 4.3. The dashed line indicates the best-fit value of $\Delta m$, while the dotted lines delineate the 99.9% confidence interval.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.8cm,clip]{08239fig8.eps} \end{figure} Figure 8:

SFH derived for one of the simulations in Sect. 4.3 (bold curve). The thin curve represents the SHF estimated for I Zw18C in Sect. 4 and is shown for comparison.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig9.eps} \end{figure} Figure 9:

Histogram of ${\cal {H}}_{\rm pop}$ for 100 simulations as described in Sect. 4.3. The superimposed curve is Gaussian and has the same mean and standard deviation as the distribution of ${\cal {H}}_{\rm pop}$.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig10.eps} \end{figure} Figure 10:

Histograms of $\Delta m - 31.12$ and AV - 0.38 for 100 simulations as described in Sect. 4.3.

Open with DEXTER

We ran a series of Monte-Carlo simulations of stellar populations, using the same assumptions as in Sect. 4.1 and the estimates of the distance, extinction, and SFH described in Sect. 4.2. For each simulation, we drew 408 stars with random ages and masses (using the SFH and the IMF as distribution functions) and photometric completeness above the 90% threshold.

We first analyzed 3 simulated populations using a large grid of points in the $(\Delta m, A_V)$ space to check the general behavior of our algorithm. The three simulations yielded very similar results. In Fig. 6, we present one of the synthetic CMDs, Fig. 7 shows the corresponding ${\cal {H}}_{\rm dist}$ and ${\cal {H}}_{\rm ext}$ curves, and Fig. 8 shows the mass rate computed at the best-fit distance and extinction. There is no significant discrepancy between the distance, extinction and SFH estimates obtained for I Zw18C and for the 3 simulations. In principle, this indicates that the probabilistic method we used suffers from no severe bias.

To check for small biases in our approach and verify the confidence level of our first model, we performed 100 new simulations, this time exploring a limited area of the $(\Delta m, A_V)$ space around the input values. The histograms of ${\cal{H}}_{\rm pop}, \Delta m - 32.12$ and AV - 0.38 are shown in Figs. 9 and 10. They show a possible bias in the estimation of $\Delta m$and AV, the first quantity being slightly overestimated and the second underestimated. However, the biases encountered are small ($\sim$0.03 mag) and do not exceed the respective dispersions of the simulations. As for the ${\cal {H}}_{\rm pop}$ distribution, the value obtained for I Zw18C falls well within the range of simulated values, an indication that the observations are well-fitted by the model shown in this section.

Although we have been able to satisfactorily describe the CMD of I Zw18C, it is important to review the assumptions so far. It is possible that modifying or relaxing some of them results in other satisfactory models of this stellar population.We discuss these modifications in the next section.

5 Towards a better model for I Zw18C

\begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig11.eps} \end{figure} Figure 11:

Function $W(\tau )$ as described in Sect. 5.2.

Open with DEXTER

There are at least four possible sources of error in our modeling of I Zw18C: the isochrones (via the evolutionary tracks, and the model atmospheres), the IMF, the treatment of the extinction and overlooking binarity.

5.1 Effects of the isochrones/stellar luminosity functions

As explained in Sect. 2.2, our method is related not just with the isochrones used, but also with the stellar luminosity function they produce: not only is the shape of the isochrone relevant, also the IMF (for MS stars) and the lifetime of different evolutionary phases (for post-MS stars)[*]. In this way, the method provides additional constraint to the ages and distances obtained, as we see in Sect. 6. In this situation, just the shape of the isochrones from different authors is not enough to assess the uncertainties of the isochrones used.

However, we can obtain a broad idea of how the results would differ by comparing just the mean value of the stellar luminosity function produced by different isochrones. By comparing of the results of evolutionary synthesis models (whose principal output is actually the mean value of the stellar luminosity function, Cerviño & Luridiana 2006). Such a comparison has been done by Buzzoni (2005), who in Fig. 1, shows the comparison of the evolution of U, V, K and bolometric luminosity for different synthesis models (which use different evolutionary tracks). In general, there is very good agreement between the different synthesis models, hence evolutionary tracks, except in the K band (which strongly depends on the synthesis model implementation of AGB, and post-AGB stars). For the given photometric bands we used, it is expected that using a different set of isochrones produces (at least in a global average) similar results.

5.2 Effects of the IMF

Changing the IMF shape modifies the values of the LFs Ljthrough Eq. (2). At a given age, this will be important if the minimum and maximum initial masses ``visible'' in the photometric data, respectively ${\cal{M}}_{\rm min}(\tau)$ and ${\cal{M}}_{\rm max}(\tau)$, are significantly different from each other. Let us examine the case where the IMF is a power law of slope $\alpha$. The ratio between the LFs $L_j(\tau)$ of a ${\cal{M}}_{\rm max}(\tau)$ mass star and a ${\cal{M}}_{\rm min}(\tau)$ one is nearly proportional to $({\cal{M}}_{\rm max}(\tau)/{\cal{M}}_{\rm min}(\tau) )^\alpha$. As a result, we can evaluate the impact of an uncertainty of $\Delta \alpha$ in the IMF slope on ${\cal{H}}_j(\tau)$ with the following function:

\begin{displaymath}W(\tau) = \Delta \alpha ~\log \left(\frac{{\cal{M}}_{\rm max}(\tau)}{{\cal{M}}_{\rm min}(\tau)}\right)\cdot \end{displaymath} (15)

Even though the Salpeter IMF ( $\alpha = -2.35$) is widely employed in the study of stellar populations, various authors have suggested the use of other IMFs. For example, according to Scalo (1998), the IMF slope may vary from $\alpha = -2.2$ to $\alpha = -2.8$ in the ${\cal{M}} \geq 1$ $M_\odot$ range. Thus, we computed $W(\tau )$using $\Delta \alpha = 0.5$ to check the importance of our choice of a Salpeter IMF. The curve is shown in Fig. 11. As seen, at any age (in particular at $\tau \geq 10$ Myr), the value of $W(\tau )$ is low. This reflects that our star sample is almost exclusively composed of post-MS objects whose properties, at a given age, are very sensitive to their initial masses, so the interval of initial masses they cover at this age is necessarily narrow. The consequence is that the exact choice of the IMF has no significant consequence on the calculation of the entropies ${\cal{H}}_j(\tau)$, and changing the IMF will have little impact on the model described in Sect. 4.

5.3 Effects of binary stars

Our results may be affected if a significant fraction of the point sources used are actually binary stars (either physical or optical) where the luminosities of both components are comparable. Assume that a given point source is a binary of integrated magnitude m814, with the magnitudes of the primary and secondary component m814,1 and m814,2, respectively ( m814,2 > m814,1). The magnitude of the secondary companion and the ``magnitude excess'' $\delta m_{814} = m_{814,1} - m_{814}$ caused by its presence are related by

\begin{displaymath}m_{814,2} = m_{814} - 2.5~ \log (1 - 10^{-0.4 \delta m_{814}}). \end{displaymath} (16)

The magnitude excess cannot be greater than $2.5 \log 2 = 0.753$ because we impose the condition that the secondary companion be fainter than the primary one.

In spite of various attempts, it has not been clearly demonstrated that the component masses in physical binaries are correlated (Kroupa et al. 1993), hence, we assumed that in a given binary star, the component masses are independently drawn from the IMF. For each point source, we computed the probability $P_{\rm bin}$ of the magnitude excess as $\delta m_{814} \geq \sigma_{814}$, where $\sigma_{814}$ is the photometric error on m814. We calculated this probability assuming the source to be either a physical binary (the two stars have the same age) or an optical double star (the ages of the two components are independent). For all the sources of our sample, we found $P_{\rm bin} < 0.15$%, which means that binarity is very unlikely to affect our results seriously. This is actually consistent with only looking at the very brightest stars of I Zw18C: the chance for a random star of the galaxy to be nearly as bright as them is small.

5.4 Effects of spacial variations in the intrinsic extinction

An arguable simplification of our first model is that we assumed the interstellar extinction is uniform. In principle, this is not the case since dust clouds may be present inside I Zw18C. The presence of such clouds is supported by the estimate of the extinction in our first model, and can cause the extinction to vary along the projected view of the galaxy. Large-scale fluctuations may exist, depending on the morphology of the dust clouds. Moreover, even on local scales, the extinction may be distributed, given that the stars can be located at different depths inside the clouds.

To our knowledge, the only work in which a heterogeneous extinction has been measured in I Zw18C is that of Izotov et al. (2001). They find the value of AV to range between 0.20 and 0.65. This supports the idea that treating the extinction with some detail would be useful for more exhaustive modeling of I Zw18C.

6 A model with detailed treatment of the extinction

\begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig12.eps} \end{figure} Figure 12:

HST/ACS image of I Zw18C through the F555W filter, with the boundaries of the 4 regions used in Sect. 6 overplotted. The two unresolved clusters are also reported.

Open with DEXTER

We carried out a second model of the stellar content of I Zw18C, based on the same assumptions and procedure as the first model, but chaning the treatment of extinction which was dealt with in the following fashion. We divided the galaxy into 4 regions, shown in Fig. 12, that contain 101, 121, 92, and 59 stars of the original selection, respectively. In each region k, we supposed the extinction of a given star is a random variable following a uniform probability law, with AV falling in the range $\bar{A}_V^{(k)} \pm \Delta A_V^{(k)}$. Mathematically, this was achieved by replacing $L_j(\tau; Z, d, A)$ by

\begin{displaymath}\begin{array}{rl} L_j''(\tau; Z, \Delta m, & \bar{A}_V^{(k)},... ...^{(k)}} L_j''(\tau; Z, \Delta m, A_v)~ {\rm d} A_V. \end{array}\end{displaymath} (17)

We determined the best-fit values of $\bar{A}_V^{(k)}$, $\Delta A_V^{(k)}$, and $\Delta m$ in the following way. For given values of $\Delta A_V^{(k)}$, we computed the ${\cal{H}}_{\rm dist}^{(k)}(\Delta m)$ curves, derived the ${\cal{H}}_{\rm dist}(\Delta m) = \sum_k {\cal{H}}_{\rm dist}^{(k)} (\Delta m)$ distribution, and picked the best-fit distance modulus $\Delta m$. At this distance modulus, we computed the maximum entropies ${\cal{H}}^{(k)}$as a function of $\bar{A}_V^{(k)}$. We repeated this operation for different sets of $\Delta A_V^{(k)}$ so as to maximize the values of ${\cal{H}}^{(k)}$.

6.1 Results

Table 1:   Best-fit values of $\Delta A_V^{(k)}$ and $\bar{A}_V^{(k)}$ for the three regions described in Sect. 6.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig13.eps} \end{figure} Figure 13:

${\cal {H}}_{\rm dist}$ curve for the model of Sect. 6. The dashed line indicates the best-fit value of $\Delta m$, while the dotted lines delineate the 99.9% confidence interval.

Open with DEXTER

The results are presented as follows. In Fig. 13, we show the curve ${\cal{H}}_{\rm dist}^{(k)}(\Delta m)$. The best-fit distance modulus is $\Delta m = 32.16$ (corresponding to a distance of 27.0 Mpc) and the 99.9% confidence interval is 31.78-32.29.We found that the best-fit value of $\Delta m$ is virtually insensitive to the adopted values of $\bar{A}_V^{(k)}$is actually close to that found with our first model. In Table 1, we summarize the values of $\bar{A}_V^{(k)}$ and $\Delta A_V^{(k)}$. All four extinction averages $\bar{A}_V^{(k)}$ fall within the 0.20-0.65 range of Izotov et al. (2001). Furthermore, the extinction spreads $\Delta A_V^{(k)}$ represent significant fractions of the averages for regions 1 and 3.

6.2 The SFH of I Zw18C and its spatial distribution

\begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig14.eps} \end{figure} Figure 14:

Dereddened CMDs for a) region 1, b) region 2, c) region 3, and d) region 4 (see Sect. 6). The isochrones are the same as in Fig. 4.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig15.eps} \end{figure} Figure 15:

SFH computed for region 1 (dashed line), regions 2 and 3 (dotted line), and all three regions (full line).

Open with DEXTER

\begin{figure} \par\includegraphics[width=17cm,clip]{08239fig16.eps} \end{figure} Figure 16:

Position of the stars falling in the following age ranges: a) 015 Myr, b) 1560 Myr, c) 60120 Myr. For reference, a surface brightness isocontour of the galaxy was also plotted in the panels.

Open with DEXTER

In Fig. 14, we show the CMDs for the individual regions at the adopted distance and average extinctions. Figure 15 shows the mass rate curves for the four regions together. Finally, Fig. 16 shows the position of the stars in different age ranges. The age $\tau_j$ of star j was defined as the age maximizing the LF $L_j''(\tau)$.

The global SFH shown in Fig. 15 is nearly identical the one discussed in Sect. 4. In particular, the two starbursts at $\tau \lesssim15$ Myr and $\tau \sim 100$ Myr and the continuous SF between them are confirmed with our new model. However, it is evident that the SFH is not homogeneous across the galaxy. The young stars ($\leq$15 Myr) tend to concentrate in the southwest tip of the object, while there is a slight excess of 60-120 Myr old stars in the northeast lobe. On the other hand, intermediate age stars (15-60 Myr) are distributed rather evenly through the component of the galaxy. This observation suggests that I Zw18C forms stars both through a continuous, global process and through local starbursts. The existence remains unconfirmed of the longlasting SF that started a few hundreds to thousands of Myr. Its possible contribution to the total mass of the stellar population is very small, about 10-3, and I Zw18C can be considered mostly as a young object.

6.3 The age of I Zw18C

\begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig17.eps} \end{figure} Figure 17:

Likelihood function of the age of I Zw18C, as computed in Sect. 6.3.

Open with DEXTER

So far, we have presented estimates of the SFH of I Zw18C where the stars could be as old as 14 Gyr. These estimates do not provide a precise constraint on the age of the stellar sample considered, i.e. the age of the oldest of its stars. To establish the age, we evaluated the distribution ${\cal{N}}(\tau)$ for a given tested age $\tau_{\rm pop}$, with the coefficients $G_j(\tau)$ defined as

\begin{displaymath}G_j(\tau) = \int \int P(\Delta m, \bar{A}_V^{(k)})~P_j''(\tau... ... m, \bar{A}_V^{(k)})~ {\rm d}\Delta m~{\rm d} \bar{A}_V^{(k)}, \end{displaymath} (18)

forcing ${\cal{N}}(\tau) = 0$ at $\tau > \tau_{\rm pop}$. We then retained the corresponding entropy ${\cal{H}}_{\rm age}(\tau_{\rm pop})$ and derived the LF $L_{\rm age}(\tau_{\rm pop})$. The definition of $G_j(\tau)$ has the advantage of properly accounting for the probabilistic distributions of $\Delta m$ and $\bar{A}_V^{(k)}$. With a few simulations, we checked that this procedure yields the correct LF.

In Fig. 17, we show the curve $L_{\rm age}(\tau_{\rm pop}$) obtained. If all the stars are considered as valid elements of the sample, then the most likely age of I Zw18C is 125 Myr, with a 99.9% confidence level interval of 110 Myr-7.6 Gyr. To ensure that ( $\tau_{\rm pop}) <$ 1 Gyr, it would be necessary to remove the oldest 20 stars from the sample. That is, I Zw18C is very likely a young object, but we cannot rule out the possibility that this object is several Gyr old.

6.4 A high distance estimate

Our estimate of the distance to I Zw18 is by far greater than those assumed or evaluated in all previous works published on this object, even considering the error bars of the different estimates. No modification to our model, including the removal of a large number of stars from the original sample, could alleviate this discrepancy. Whatever stars were removed, the distance estimate was found to be very similar to that described in Sect. 6.1. A good description of the distribution of the colors and magnitudes of the stars can be obtained by assuming the distance to I Zw18C to be 27 Mpc, as shown in Fig. 18. In particular, the fit of the magnitude distribution is excellent. Let us now adopt the distance modulus of 31.3, inferred from the RBG population by Aloisi et al. (2007). As shown in Fig. 19, where the extinction and the SFH were re-fitted, a significant excess of luminous AGB stars ( $m_{555} - m_{814} \approx 1.7$, $m_{814} \approx 24$) is predicted, while the expected number of MS stars at the faint end of the CMD ( $m_{555} - m_{814} \approx 0$, $m_{814} \approx 28$) is lower than the observed one. This scheme worsens if we assume an even shorter distance. Thus, it appears that the large distance modulus we computed is essential for explaining the distribution of colors and magnitudes of the stars observed.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig18.eps} \end{figure} Figure 18:

Color and magnitude histograms of the stars considered in Sect. 6. The thick curves represent the average distributions expected at the best-fit distance and extinction coefficients.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig19.eps} \end{figure} Figure 19:

Same as Fig. 18 but at a distance modulus of 31.3.

Open with DEXTER

7 Conclusions

In an attempt to evaluate the distance to the dwarf galaxy I Zw18C and its SFH, we carried out a detailed analysis of its resolved stellar content. We developed a probabilistic approach based on the current knowledge about SF and its random aspects, in order to exploit as much of the information held by the photometric data as possible.We used high-quality HST/ACS observations of the galaxy, on which we performed state-of-the art photometry to obtain high signal-to-noise and high completeness data.

We carried out a first model with a few simple assumptions about the stellar population studied. We found the distance to I Zw18C to be as high as 27 Mpc and detected several important features in the SFH: two starbursts of which an ongoing one ( $\tau \lesssim15$ Ma) dominates the SFH and the other occurred $\approx$100 Myr ago, a rather constant SF episode that has lasted for 100 Myr or so, and a possible low-rate SF process for larger ages. We performed Monte-Carlo simulations to assess those results. Although the simulations proved our approach to be efficient, some of our assumptions could limit the reliability of the model. We reviewed the assumptions and found that only the treatment of the extinction could yield a more robust depiction of the stellar population studied.

We performed a second model, accounting for the spatial variations and random fluctuations of the interstellar extinction inside I Zw18C.We could confirm the high estimate of the distance modulus of I Zw18C ( $\Delta m = 32.16^{+0.13}_{-0.38}$, i.e. d = 27.0+1.7-4.3 Mpc), significantly greater than any value previously published. The description of the SFH was also maintained. The spatial distribution of the stars in various age intervals suggests that the stellar content of I Zw18C has formed both through a global, continuous process and through a series of local starbursts.

That the distance we computed for I Zw18C is greater than those published in previous works is important for study the resolved stellar population of both this object and the main body of I Zw18. For example, the spectra assigned to the ionizing stars will be more intense if one adopts our distance instead of a more conservative one. The age estimate of the red stars is also sensitive to the adopted distance, because it is more at shorter distances. Another consequence of our distance estimate is that it explains why Izotov & Thuan (2004) did not detect any RGB stars in the galaxy.

An equally important result of our work regards the age of the galaxy. Our probabilistic approach allowed us to state that I Zw18C is most likely young, with a maximum likelihood age of 125 Myr, although we could not discard ages of several Gyr. A more accurate age could be inferred from photometric data that is either deeper or that covers a wider range of infrared wavelengths. In any case, our estimate of the SFH shows that nearly all the stellar content of I Zw18C has formed in the last few hundred Myr.

Let us finish the paper with a note about how its results have affected the authors of the paper (and maybe also the reader). Each of us had own expectations about this work. Some of us expected a shorter distance for I Zw18C and (by extension to the main body) more consistent with pre-Izotov et al. (2001) estimations: a lower distance implies one lower absolute luminosities and a higher impact from IMF sampling effects in the I Zw18 system studies. Others expected that this study would produce similar results to the ones by Izotov & Thuan (2004).

In all cases, our preconceptions (based in different readings and interpretations of previous works and our different personal history in I Zw18 studies) have not been satisfied.

Among us, a posteri criticism has arisen (maybe without being completely aware of our expectations and its impact on the interpretation of the results). As an example of potential problem that the reader might also have thought about, part of our analysis is based only in a few luminous red and MS stars. However, our solution is based on an overall analysis of both populations (i.e. the luminosity function) and not on a few stars in a particular box of the CMD in different areas (Figs. 18 and 19 and discussion in Sect. 6.4). We are not able to find any mistake in the methodology or in the results, and any possible criticism also applies (more strongly) to results from standard CMD methodology.

Independently of the particular expectations of each of the authors, we hope that the controversy about the I Zw18 system distance and I Zw18C star formation history will be solved with deeper observations of I Zw18C using future large observational facilities. But for the moment, against our expectations, it seems that current data point toward a distance of 27 Mpc to the I Zw18 system and maximum likelihood age of 125 Myr.

Acknowledgements
This work was supported by the Spanish Programa Nacional de Astronomía y Astrofísica through FEDER funding of the project AYA2004-02703 and AYA2007-64712. L.J. was supported by a UNAM post-doctoral grant.

References

  1. Aloisi, A., Tosi, M., & Greggio, L. 1999, AJ, 118, 302 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aloisi, A., Clementini, G., Tosi, M., et al. 2007, ApJ, 667, L151 [NASA ADS] [CrossRef] [Google Scholar]
  3. Brown, T. M., Heap, S. R., Hubeny, I., Lanz, T., & Lindler, D. 2002, ApJ, 581, L129 [NASA ADS] [CrossRef] [Google Scholar]
  4. Burstein, A., & Heiles, C. 1982, AJ, 87, 1165 [NASA ADS] [CrossRef] [Google Scholar]
  5. Buzzoni, A. 1989, ApJS, 71, 817 [NASA ADS] [CrossRef] [Google Scholar]
  6. Buzzoni, A. 2005, MNRAS, 361, 725 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cannon, J. M., Skillmann, E. D., Garnett, D. R., & Dufour, R. J. 2002, ApJ, 565, 931 [CrossRef] [Google Scholar]
  8. Cervino, M., & Luridiana, V. 2005, in Resolved Stellar Populations, ed. D. Valls-Gabaud, & M. Chávez, ASP Conf. Ser. (in press), [arXiv:astro-ph/0510411] [Google Scholar]
  9. Cerviño, M., & Luridiana, V. 2006, A&A, 451, 475 [Google Scholar]
  10. Cerviño, M., Luridiana, V., & Castander, F. J. 2000, A&A, 360, L5 [Google Scholar]
  11. Cerviño, M., Valls-Gabaud, D., Luridiana, V., & Mas-Hesse, J. M. 2002, A&A, 381, 51 [Google Scholar]
  12. Dolphin, A. 2000, PASP, 112, 1383 [NASA ADS] [CrossRef] [Google Scholar]
  13. Dufour, R. J., Esteban, C., & Castañeda, H. O. 1996a, ApJ, 471, L87 [NASA ADS] [CrossRef] [Google Scholar]
  14. Dufour, R. J., Garnett, D. R., Skillman, E. D., & Shields. G. A. 1996b, ASPC, 98, 358 [NASA ADS] [Google Scholar]
  15. Gallart, C., Freedman, W. L., Aparicio, A., Bertelli, G., & Chiosi, C. 1999, AJ, 118, 2245 [NASA ADS] [CrossRef] [Google Scholar]
  16. Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [Google Scholar]
  17. Hensler, G., & Rieschick, A. 2002, ASPC, 285, 341 [NASA ADS] [Google Scholar]
  18. Hernández, X., Valls-Gabaud, D., & Gilmore, G. 1999, MNRAS, 304, 705 [NASA ADS] [CrossRef] [Google Scholar]
  19. Hunter, D. A., Elmegreen, B. G., & Baker, A. L. 1998, ApJ, 493, 595 [NASA ADS] [CrossRef] [Google Scholar]
  20. Izotov, Y. I., & Thuan, T. X. 1998, ApJ, 497, 227 [NASA ADS] [CrossRef] [Google Scholar]
  21. Izotov, Y. I., & Thuan, T. X. 1999, ApJ, 511, 639 [NASA ADS] [CrossRef] [Google Scholar]
  22. Izotov, Y. I., & Thuan, T. X. 2004, ApJ, 616, 768 [CrossRef] [Google Scholar]
  23. Izotov, Y. I., Foltz, C. B., Green, R. F., Guseva, N. G., & Thuan, T. X. 1997a, ApJ, 487, L37 [NASA ADS] [CrossRef] [Google Scholar]
  24. Izotov, Y. I., Thuan, T. X., & Lipovetsky, V., 1997b, ApJS, 108, 1 [NASA ADS] [CrossRef] [Google Scholar]
  25. Izotov, Y. I., Chaffee, F. H., Foltz, C. B., et al. 1999, ApJ, 527, 757 [NASA ADS] [CrossRef] [Google Scholar]
  26. Izotov, Y. I., Chaffee, F. H., Foltz, C. B., et al. 2001, ApJ, 560, 222 [NASA ADS] [CrossRef] [Google Scholar]
  27. Izotov, Y. I., Stasinska, G., Guseva, N. G., & Thuan, T. X. 2004, A&A, 415, 87 [Google Scholar]
  28. Izotov, Y. I., Thuan, T. X., & Stasinska, G. 2007, ApJ, 662, 15 [NASA ADS] [CrossRef] [Google Scholar]
  29. Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
  30. Kunth, D., & Östlin, G. 2000, A&ARev., 10, 1 [Google Scholar]
  31. Legrand, F., Kunth, D., Roy, J.-R., Mas-Hesse, J. M., & Walsh, J. R. 1997, A&A, 326, L17 [Google Scholar]
  32. Legrand, F., Kunth, D., Roy, J. R., Mas-Hesse, J. M., & Walsh, J. R. 2000, A&A, 355, 891 [Google Scholar]
  33. Marigo, P., & Girardi, L. 2001, A&A, 377, 132 [Google Scholar]
  34. Marigo, P., & Girardi, L. 2007, A&A, 469, 239 [Google Scholar]
  35. Meynet, G., & Maeder, A. 2005, A&A, 429, 581 [Google Scholar]
  36. Östlin, G. 2000, ApJ, 535, L99 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  37. Pagel, B. E. J., Simonson, E. A., Terlevich, R. J., & Edmunds, M. G. 1992, MNRAS, 255, 325 [NASA ADS] [CrossRef] [Google Scholar]
  38. Papaderos, P., Izotov, Y. I., Thuan, T. X., et al. 2002, A&A, 3939, 461 [Google Scholar]
  39. Peimbert, M., & Torres-Peimbert, S. 1974, ApJ, 193, 327 [NASA ADS] [CrossRef] [Google Scholar]
  40. Peimbert, M., & Torres-Peimbert, S. 1976, ApJ, 203, 581 [NASA ADS] [CrossRef] [Google Scholar]
  41. Peimbert, M., Luridiana, V., & Peimbert, A. 2007, ApJ, 666, 636 [NASA ADS] [CrossRef] [Google Scholar]
  42. Renzini, A., & Buzzoni, A. 1984, Spectral Evolution of Galaxies, 86 [Google Scholar]
  43. Renzini, A., & Buzzoni, A. 1986, Spectral Evolution of Galaxies, 122, 195 [NASA ADS] [CrossRef] [Google Scholar]
  44. Robertson, B., Bullock, J. S., Font, A. S., Johnston, K. V., & Hernquist, L., 2005, ApJ, 632, 872 [NASA ADS] [CrossRef] [Google Scholar]
  45. Scalo, J. 1998, The stellar initial mass function, ASP Conf. Ser., 142, 202 [Google Scholar]
  46. Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
  47. Skillman, E. D., & Kennicutt, R. C., Jr. 1993, ApJ, 411, 655 [NASA ADS] [CrossRef] [Google Scholar]
  48. Tosi, M., Aloisi, A., Mack, J., & Maio, M. 2007, IAU Symp., 235, 65 [Google Scholar]
  49. van Zee, L., Westpfahl, D., Haynes, M. P., & Salzer, J. J. 1998, AJ, 115, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  50. Vílchez, J. M., & Iglesias-Páramo, J. 1998, ApJ, 508, 248 [NASA ADS] [CrossRef] [Google Scholar]
  51. Westera, P., Lejeune, T., Buser, R., Cuisinier, F., & Bruzual, G. 2002, A&A 381, 524 [Google Scholar]

Footnotes

... system[*]
See the HST/ACS zeropoints at http://www.stsci.edu/hst/acs/analysis/zeropoints.
... filters[*]
Tables of the ACS filter throughputs are available at http://acs.pha.jhu.edu/instrument/photometry.
... stars)[*]
Note that lifetimes of fast evolutionary phases and the amount of stars in a given evolutionary phase are linked by the fuel consumption theorem (Renzini & Buzzoni 1984, 1986; Buzzoni 1989); see also Marigo & Girardi (2001) and Cervino & Luridiana (2005) for the issues about obtain isochrones from evolutionary tracks and its relation with the stellar luminosity function.
Copyright ESO 2010

All Tables

Table 1:   Best-fit values of $\Delta A_V^{(k)}$ and $\bar{A}_V^{(k)}$ for the three regions described in Sect. 6.

All Figures

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig1.eps} \end{figure} Figure 1:

HST/ACS image of I Zw18C through the F555W filter. The two clusters ``C'' and ``NW'' mentioned by Izotov & Thuan (2004) are reported. The image display scale is logarithmic. North is up and East to the left. The ``white pixels'' are contaminated pixels that were rejected when performing the photometric measurements.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig2.eps} \end{figure} Figure 2:

Color-magnitude diagram of I Zw18C. The typical error bars as a function of F814W are reported for both the blue and red branches. The two clusters are annotated with open circles. The stars marked with crosses are those we rejected from the useful sample due to their extreme red color.We also report the 90% and 50% completeness limits as dashed lines.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig3.eps} \end{figure} Figure 3:

${\cal {H}}_{\rm dist}$ ( upper panel) and ${\cal {H}}_{\rm ext}$ ( lower panel) curves for the model of Sect. 4. The dashed lines indicate the best-fit values of $\Delta m$ and AV, while the dotted lines delineate the 99.9% confidence intervals.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig4.eps} \end{figure} Figure 4:

Observed CMD and theoretical isochrones for the model of Sect. 4. The observed data are corrected for interstellar extinction, using the best-fit value AV = 0.38. The dotted line shows the threshold above which we selected the stars to work with. The vertical axes show both apparent and absolute F814W magnitude scales, adopting the best-fit distance modulus $\Delta m = 32.12$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig5.eps} \end{figure} Figure 5:

SFH derived from the approached explained in Sect. 4. The curve was slightly smoothed to limit the apparent statistic noise.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{08239fig6.eps} \end{figure} Figure 6:

Synthetic CMD and theoretical isochrones for one of the simulations Sect. 4.3. The stars situated below the dotted line belong to the original observations of I Zw18C, whereas the others were simulated.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{08239fig7.eps} \end{figure} Figure 7:

${\cal {H}}_{\rm dist}$ ( upper panel) and ${\cal {H}}_{\rm ext}$ ( lower panel) curves for one of the simulations in Sect. 4.3. The dashed line indicates the best-fit value of $\Delta m$, while the dotted lines delineate the 99.9% confidence interval.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{08239fig8.eps} \end{figure} Figure 8:

SFH derived for one of the simulations in Sect. 4.3 (bold curve). The thin curve represents the SHF estimated for I Zw18C in Sect. 4 and is shown for comparison.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig9.eps} \end{figure} Figure 9:

Histogram of ${\cal {H}}_{\rm pop}$ for 100 simulations as described in Sect. 4.3. The superimposed curve is Gaussian and has the same mean and standard deviation as the distribution of ${\cal {H}}_{\rm pop}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig10.eps} \end{figure} Figure 10:

Histograms of $\Delta m - 31.12$ and AV - 0.38 for 100 simulations as described in Sect. 4.3.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig11.eps} \end{figure} Figure 11:

Function $W(\tau )$ as described in Sect. 5.2.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig12.eps} \end{figure} Figure 12:

HST/ACS image of I Zw18C through the F555W filter, with the boundaries of the 4 regions used in Sect. 6 overplotted. The two unresolved clusters are also reported.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig13.eps} \end{figure} Figure 13:

${\cal {H}}_{\rm dist}$ curve for the model of Sect. 6. The dashed line indicates the best-fit value of $\Delta m$, while the dotted lines delineate the 99.9% confidence interval.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig14.eps} \end{figure} Figure 14:

Dereddened CMDs for a) region 1, b) region 2, c) region 3, and d) region 4 (see Sect. 6). The isochrones are the same as in Fig. 4.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig15.eps} \end{figure} Figure 15:

SFH computed for region 1 (dashed line), regions 2 and 3 (dotted line), and all three regions (full line).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm,clip]{08239fig16.eps} \end{figure} Figure 16:

Position of the stars falling in the following age ranges: a) 015 Myr, b) 1560 Myr, c) 60120 Myr. For reference, a surface brightness isocontour of the galaxy was also plotted in the panels.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig17.eps} \end{figure} Figure 17:

Likelihood function of the age of I Zw18C, as computed in Sect. 6.3.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig18.eps} \end{figure} Figure 18:

Color and magnitude histograms of the stars considered in Sect. 6. The thick curves represent the average distributions expected at the best-fit distance and extinction coefficients.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{08239fig19.eps} \end{figure} Figure 19:

Same as Fig. 18 but at a distance modulus of 31.3.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.