EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 509 (January 2010) A&A, 509 (2010) A6 Full HTML
Free Access
Issue
A&A
Volume 509, January 2010
Article Number A6
Number of page(s) 15
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/200913290
Published online 12 January 2010
A&A 509, A6 (2010)

An optical spectroscopic survey of the 3CR sample of radio galaxies with z < 0.3

II. Spectroscopic classes and accretion modes in radio-loud AGN[*]

S. Buttiglione1 - A. Capetti2 - A. Celotti1 - D. J. Axon3,4 - M. Chiaberge5,6 - F. D. Macchetto5 - W. B. Sparks5

1 - SISSA-ISAS, via Beirut 2-4, 34151 Trieste, Italy
2 - INAF - Osservatorio Astronomico di Torino, Strada Osservatorio 20, 10025 Pino Torinese, Italy
3 - Department of Physics, Rochester Institute of Technology, 85 Lomb Memorial Drive, Rochester, NY 14623, USA
4 - School of Mathematical and Physical Sciences, University of Sussex, Falmer, Brighton BN1 9RH, UK
5 - Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
6 - INAF - Istituto di Radio Astronomia, via P. Gobetti 101, 40129 Bologna, Italy

Received 14 September 2009 / Accepted 29 October 2009

Abstract
In a previous paper we presented a homogeneous and 92% complete optical spectral dataset of the 3CR radio sources with redshift <0.3. Here we use the emission line measurements to explore the spectroscopic properties of the sample. The 3CR sources show a bimodal distribution of excitation index, a new spectroscopic indicator that measures the relative intensity of low and high excitation lines. This unveils the presence of two main sub-populations of radio-loud AGN to which we refer to, following previous studies, as high and low excitation galaxies (HEG and LEG, respectively). In addition to the two main classes, we find one source with a spectrum typical of star forming galaxies, and 3 objects of extremely low level of excitation. All broad-line objects are HEG from the point of view of their narrow emission line ratios and all HEG are FR II radio-galaxies with log L178 [erg s-1] $\ga$ 32.8. Conversely LEG cover the whole range of radio power encompassed by this 3CR subsample (30.7 $\la$ log L178 $\la$ 35.4) and they are of both FR I and FR II type. The brightest LEG are all FR II. HEG and LEG obey to two (quasi) linear correlations between the optical line and extended radio luminosities, with HEG being brighter than LEG in the [O III] line by a factor of $\sim$10. HEG and LEG are offset also in a plane that compares the black hole mass and the ionizing nuclear luminosity. However, although HEG are associated with higher nuclear luminosities, we find LEG among the brightest radio sources of the sample and with a clear FR II morphology, indistinguishable from those seen in HEG. This suggests that LEG are not simply objects with a lower level of accretion. We speculate that the differences between LEG and HEG are related to a different mode of accretion: LEG are powered by hot gas, while HEG require the presence of cold accreting material. The high temperature of the accreting gas in LEG accounts for the lack of ``cold'' structures (i.e. molecular torus and broad line region), for the reduced radiative output of the accretion disk, and for the lower gas excitation.

Key words: galaxies: active - galaxies: jets - galaxies: elliptical and lenticular, cD

1 Introduction

Radio galaxies (RG) are an important class of extragalactic objects for many reasons. Studies of radio-loud AGN are the key to understand the processes leading to the ejection of material in relativistic jets and its connection with gas accretion onto the central black holes, the way in which different levels of accretion are related to the process of jets launching, the origin of the AGN onset, and its lifetime. But the intense nuclear activity can also influence the star formation history and the properties of the ISM and ICM, thus representing a fundamental ingredient for the evolution of their hosts and their large scale environment.

RG have been historically classified according to their radio morphology, following the Fanaroff & Riley (1974) criteria: a FR I source has bright jets rising from the nucleus, while a FR II has two bright hot spots far from it. They also noted that FR II are mostly found at high radio luminosities, while FR I are associated to weaker radio sources. The two FR classes also differ, at least statistically, from several other points of view, such as the environment (Zirbel 1997) and host luminosities (Govoni et al. 2000). However, it soon became apparent that the transition between the two classes is continuous and objects of intermediate radio structure do exist (e.g. Capetti et al. 1995). A class of hybrid double sources, with a FR I jet on one side and a FR II lobe on the other, was also unveiled by Gopal-Krishna & Wiita (2000). This supports explanations for the FR dichotomy based upon jet interaction with the external medium, arguing against interpretations based on intrinsic differences in the central engine. Furthermore, the multi-wavelength behavior of the nuclear emission in RG does not appear to be directly related to the differences between the two FR classes, but it is more closely linked to their spectroscopic nuclear properties (e.g. Chiaberge et al. 2002,2000).

Optical spectroscopic information can clearly play a major role in gaining a better understanding of the properties of the central engines of RG. Heckman (1980) and Baldwin et al. (1981) proposed to use optical line ratios as diagnostic tools to classify emission-line objects in general and AGN in particular. They introduced diagnostic diagrams comparing selected emission line ratios, able to distinguish H II regions ionized by young stars from gas clouds ionized by nuclear activity. Moreover AGN were separated into Seyferts and Low Ionization Nuclear Emission-line Regions (LINERs, Heckman 1980) based on the relative ratios of the optical oxygen lines ([O I]$\lambda$6364, [O II]$\lambda$3727, and [O III]$\lambda$5007). Subsequently Veilleux & Osterbrock (1987) revised the definition of the diagnostic diagrams, using only ratios of lines with small separation in wavelength, thus reducing the problems related to reddening as well as to uncertainties on the flux calibration of the spectra. They used the following line combinations: [O III]/H$\beta $ as a function of [N II]$\lambda$6583/H$\alpha $, [S II] $\lambda\lambda$6716, 6731/H$\alpha $, and [O I]/H$\alpha $. The separation between AGN and HII regions, initially introduced empirically, was calibrated theoretically by Kewley et al. (2001). More recently, Kewley et al. (2006a, hereafter K06) selected a sample of ${\sim}85~000$ emission line galaxies from the SDSS, finding that Seyferts and LINERs form separated branches on the diagnostic diagrams. They suggested that the observed dichotomy corresponds to the presence of two sub-populations of AGN associated with different accretion states.

An attempt to adopt a similar scheme for the optical classification focusing on radio-loud galaxies was made by Laing et al. (1994) on a sub-sample of 3CR radio-galaxies, selected imposing z < 0.88, V < 20, and 0h < RA < 13h. They put on firmer ground the original suggestion by Hine & Longair (1979) that FR II sources can be distinguished into subclasses. They proposed a separation into high excitation galaxies (HEG, defined as galaxies with [O III]/H$\alpha $ > 0.2 and equivalent width (EW) of [O III] > 3 Å) and low excitation galaxies (LEG). Tadhunter et al. (1998) found a similar result from an optical spectroscopic study of the 2 Jy sample, in which a sub-class of Weak-Line Radio Galaxies (the sources with EW of [O III]) < 10 Å) stands out due to a low ratio between emission line and radio luminosities as well of [O III]/[O II] line ratio.

Emission line luminosities show a broad connection with radio power, as verified by many studies (e.g. Rawlings & Saunders 1991; Baum & Heckman 1989a,b; Rawlings et al. 1989). This relation holds also for compact steep spectrum (CSS) (Morganti et al. 1997) and GHz peaked spectrum (GPS) sources (Labiano 2008). Willott et al. (1999) demonstrated that the dominant effect is a strong positive correlation between $L_{\rm radio}$ vs. $L_{\rm line}$and not to a common dependence of these quantities on redshift. This relationship points to a common energy source for both the optical line and the radio emission, and suggests the radio and line luminosities of RG are determined, to first order, by the properties of their central engines. Baum & Heckman (1989b) noticed that the large scatter (roughly one order of magnitude) in $L_{\rm radio}$ for a given $L_{\rm line}$ suggests that other factors do play a secondary role, such as the environment. Another possibility is that the line and radio luminosities may be independently correlated with a third parameter, e.g. the amount of cold gas present on the kiloparsec scale. A correlation between emission lines and core radio powers, although weaker than that observed for $L_{\rm radio}$ and  $L_{\rm line}$, is also found (e.g. Rawlings & Saunders 1991; Baum & Heckman 1989b; Rawlings et al. 1989) suggesting that the total radio luminosity is separately correlated with the [O III] and the core radio power.

Morganti et al. (1992) extended the line-radio connection towards lower radio luminosities considering sources from the B2 sample, predominantly FR I, noting a flattening in the correlation. This result is supported also by the analysis by Zirbel & Baum (1995), who also report that FR II sources produce about 5-30 times more emission line luminosity than FR I for the same total radio power (see also Wills et al. 2004; Tadhunter et al. 1998).

In addition to the diagnostics derived from the narrow lines, optical spectra also reveal the presence of prominent permitted broad lines in a significant fraction of RG. Unifying models for active galaxies ascribe the lack of broad lines to selective obscuration and differences of orientation between narrow and broad lined AGN (see Urry & Padovani 1995; Antonucci 1993).

However, despite the massive amount of spectroscopic data collected over the last decades for RG, there are still several key questions waiting for clear answers: are there indeed two (or more) distinct populations of RG? On which basis they can be separated? Which are the physical parameters setting the division? Which is the relationship between the optical and radio properties? When are broad emission lines observed? Which processes set the presence and detectability of broad lines and how do they fit in the unified models for active nuclei? How do the spectroscopic properties of radio-loud and radio-quiet AGN compare?

A necessary ingredient required to enable a detailed exploration of spectroscopic properties of radio-loud AGN is a dataset as homogeneous and complete as possible. This is one of the aims of the optical spectroscopic survey that we performed with the Telescopio Nazionale Galileo, presented in Buttiglione et al. (2009, hereafter Paper I).

We considered the 113 3CR sources at redshift <0.3, with an effective coverage of the sub-sample of 92% (i.e. 104 sources). For 18 sources the spectra are available from the Sloan Digital Sky Survey (SDSS) database (York et al. 2000; Stoughton et al. 2002; Yip et al. 2004), Data Release 4-6. For these sources the observations provide uniform and uninterrupted coverage of the key spectroscopic optical diagnostics ratios. The data quality is such that the H$\alpha $ line is detected in all but 3 galaxies and in the majority (${\sim}75$%) of the objects all key emission lines (i.e. H$\beta $, [O III] $\lambda\lambda$ 4959, 5007 Å, [O I] $\lambda\lambda$ 6300, 64 Å, H$\alpha $, [N II] $\lambda\lambda$ 6548, 84 Å, [S II] $\lambda\lambda$ 6716, 31 Å) required to construct diagnostic diagrams are detected.

The attractiveness of the 3CR catalog of radio sources as a basis for such a study is obvious, being one of the best studied sample of RG. Its selection criteria are unbiased with respect to optical properties and orientation, and it spans a relatively wide range in redshift and radio power. A vast suite of observations is available for this sample, from multi-band HST imaging to observations with Chandra, Spitzer and the VLA, that can be used to address the issues listed above in a multiwavelength approach.

The paper is organized as follows: in Sect. 2 we derive and explore the spectroscopic diagnostic diagrams for the 3CR sample of sources with $z \leq 0.3$. In Sect. 3 we compare optical (line and host) luminosity and radio emission. Results are discussed in Sect. 4 and summarized in Sect. 5, where we also present our conclusions.

Throughout, we adopted H0 = 71 km s-1 Mpc-1, $\Omega_{\Lambda} = 0.73$ and $\Omega_{\rm m} = 0.27$.

2 Spectroscopic classification of 3CR sources

\begin{figure} \par\includegraphics[angle=90,width=5.8cm,clip]{13290f1a.ps}\hspa... ...cludegraphics[angle=90,width=5.8cm,clip]{13290f1i.ps} \vspace*{3mm} \end{figure} Figure 1:

Diagnostic diagrams. Left column: 3CR sources with symbol sizes increasing with [O III] luminosity (log  $L_{\rm [OIII]}$(erg s-1)); the galaxies showing a broad H$\alpha $ component are represented by crossed circles. Central column: the same plot with error bars. Right column: comparison between 3CR (black dots) and the density of SDSS emission line sources (contour lines) from K06. The ordinates are the ratio log [O III]/H$\beta $. The first row shows the log [N II]/H$\alpha $ ratio, the second row the log [S II]/H$\alpha $ ratio, while the third row shows log [O I]/H$\alpha $. The curves divide AGN (above the solid curved line) from star-forming galaxies. Between the dashed and solid curves there are the composite galaxies (K06). In the bottom two rows, the straight solid line divides Seyferts (upper left region) from LINERs (right region).

Open with DEXTER

2.1 Spectroscopic diagnostic diagrams

We used the emission lines intensities measured in Paper I[*] to explore the spectral properties of the 3CR sample taking advantage of the spectroscopic diagnostic diagrams (Kewley et al. 2006a). More specifically we constructed the diagrams that compare the [O III]$\lambda$5007/H$\beta $ ratio with [N II]$\lambda$6583/H$\alpha $, [S II] $\lambda\lambda$6716, 6731/H$\alpha $ and [O I]$\lambda$6364/H$\alpha $ shown in Fig. 1. Ratios involving line upper limits are not considered.

In the left hand panels of this figure, the 3CR sources are indicated by circles with sizes proportional to the [O III] luminosity, in the central panels the errors on the line ratios are shown and in the right panels the 3CR sources are compared with the SDSS emission line galaxies from K06. The solid lines divide sources into star-forming galaxies (lower left region of the diagram), Seyferts (top left region) and LINERs (bottom right region) according to K06.

In the first diagnostic diagram (first row) of Fig. 1, log [O III]/H$\beta $ versus log [N II]/H$\alpha $, all 3CR sources are located in the AGN region with only a few exceptions: one object (3C 198[*]) falls among the star-forming galaxies. Two objects (3C 028 and 3C 314.1) are located in the composite region and, together with 3C 348, have extremely low [O III]/H$\beta $ ratio (${\sim}0.5$); however, they are well into the AGN region in the other two diagrams. The location of the remaining sources appears to be related to their line luminosity. Powerful sources ( $L_{\rm [OIII]}\ga 10^{41.5}$ erg s-1) are mostly found along a horizontal strip around log[O III]/H$\beta $ $\sim$ 1. We also note that all 3CR galaxies in which we detected a broad H$\alpha $ component belong to this sub-group. In contrast, fainter sources ( $L_{\rm [OIII]}\la 10^{41.5}$ erg s-1) are instead generally distributed in a region around log[O III]/H$\beta $ $\sim$ 0.5. The sample divides roughly equally into powerful and faint sources. The horizontal spread is significantly broader for the bright galaxies as they extend to lower values of the [N II]/H$\alpha $ ratio.

In the second and third diagnostic diagrams, log [O III]/H$\beta $ versus log [S II]/H$\alpha $[*] and log [O I]/H$\alpha $, the sources show very similar distributions to that seen in the previous diagram. In these cases, we also take advantage of the separation into Seyfert and LINERs (i.e. into high and low ionization galaxies) proposed by K06 and graphically represented by the oblique solid lines. All powerful 3CR are located above the separation. Conversely, fainter sources straddle the Seyferts/LINERs divide. In particular, considering the log [O I]/H$\alpha $ ratio, they cover a region elongated along the Seyferts/LINERs separation line.

\begin{figure} \par\includegraphics[angle=90,width=8.5cm,clip]{13290f2.ps} \end{figure} Figure 2:

log [O III]/H$\beta $ versus log [O I]/H$\alpha $ diagram only for sources with $L_{\rm [OIII]}>10^{40}$ erg s-1: contour lines represent the SDSS sample while black circles indicate the 3CR sources. The symbol size increases with [O III] luminosity. As in Fig. 1, the curved line divides the star-forming galaxies and AGN, while the oblique line divides Seyferts and LINERs (according to K06).

Open with DEXTER

In the right column of Fig. 1 our data (circles) are compared with the SDSS data from K06 (contour lines): SDSS data are composed of $\sim$85 000 galaxies, mainly radio quiet AGN (Seyferts, LINERs) and star-bursts galaxies. As already mentioned most 3CR sources fall in the AGN region, but several differences can be seen comparing 3CR and SDSS AGN. First of all, a group of powerful 3CR sources cover a region with low values of [N II]/H$\alpha $ and [S II]/H$\alpha $ (top left of the diagrams): this group of sources seems to have no corresponding sources among SDSS objects. In the [O I]/H$\alpha $ diagram, 3CR sources are mainly distributed along the edge of the region covered by SDSS galaxies, both Seyfert and LINERs. In the other two diagrams the situation is less extreme, but many 3CR sources are located in areas of low AGN density.

These differences are probably not so surprising, considering the strong mismatch in line luminosity between the two samples. In fact, the mean [O III] luminosity of the SDSS sample is about 30 times lower than the 3CR sample. Indeed, the majority of LINERs has luminosities in the range $10^{38} \la L_{\rm [OIII]} \la 10^{39}$ erg s-1, the SDSS Seyferts are mostly in the range $10^{39}\la L_{\rm [OIII]}\la 10^{41}$ erg s-1 while half of the 3CR sources have luminosities in excess of $L_{\rm [OIII]}\sim10^{41}$ erg s-1. The luminosity mismatch is well visible in Fig. 2 where only sources with $L_{\rm [OIII]} \ga 10^{40}$ erg s-1 are plotted: among the SDSS sources, LINERs are substantially absent at these luminosities, and only a well defined Seyfert ``finger'' is present. Conversely, this threshold selects most 3CR galaxies, including those with low [O III]/H$\beta $ ratios.

An important consequence is that it is probably inappropriate to blindly apply the Seyferts/LINERs separation found by K06 to the 3CR sources. Similarly, we cannot guarantee that two sub-populations of radio-loud AGN exist based on the results found for (mostly) radio-quiet AGN of much lower activity level.

2.2 A new spectroscopic classification scheme

In addition to the points discussed in the previous section there are two further complications in the attempt to understand the spectroscopic properties of the 3CR radio-galaxies.

The first is related to the relatively large fraction of SDSS galaxies whose location with respect to the curves separating the various classes of emission line galaxies vary in the different diagnostic diagrams, defined by K06 as ``ambiguous galaxies''. While this does not represent a significant problem for the interpretation of the properties of the SDSS sources, thanks to the extremely large number of objects, this effect can have a strong impact due to the much smaller size of the 3CR sample. We decided to go beyond this complication by introducing new spectroscopic indicators. We estimate for all narrow line objects the average of the low ionization lines ratios, i.e. 1/3 (log [N II]/H$\alpha $ + log [S II]/H$\alpha $ + log [O I]/H$\alpha $) that we define as line ratios index (LRI) as well as the excitation index (EI), log [O III]/H$\beta $ - LRI. These indices are clearly more stable than the single line ratios. In particular, the excitation index represents the overall ratio of high and low excitation emission lines in each source.

The second issue is the presence of a substantial group of 3CR galaxies with strong broad emission lines. In these objects, the measurement of the narrow emission lines is less reliable due to the presence of the strong nuclear continuum and to the complexity of the profiles of the broad lines. In particular, as explained in Paper I, we expect a general over-estimate of the H$\beta $ line luminosity. For this reason we defer the discussion of broad lined objects to Sect. 2.3.

\begin{figure} \par\includegraphics[angle=90,width=8.5cm,clip]{13290f3.ps} \end{figure} Figure 3:

Line ratios index (LRI, see text for its definition). The contour lines indicate the distribution of the SDSS emission line galaxies (K06). The circles indicate the 3CR sources (the symbol size is proportional to the [O III] luminosity, see Fig. 1).

Open with DEXTER

In Fig. 3 we show the position of the 3CR sources in a new diagnostic plane where we compare log [O III]/H$\beta $ and LRI for the 59 narrow line objects for which we are able to measure both values. The sources are distributed along the edges of the distribution of the SDSS sources, similarly to the previous diagnostic diagrams. This diagram shows two groups of AGN: one group with -1 $\la$ LRI $\la$ 0 and log [O III]/H$\beta $ $\sim$ 1 and another one with -0.3 $\la$ LRI $\la$ 0.1 and 0.2 $\la$ log [O III]/H$\beta $ $\la$ 0.8.

The presence of two populations of AGN is clearly seen in the distribution of the values of the excitation index, shown in Fig. 4, where two separate distributions appear. This result is the analog of the two-horned histograms derived by K06 when slicing the density distribution of SDSS sources. Using the KMM test for bimodality (Ashman et al. 1994)[*] we estimated that the hypothesis of a single Gaussian distribution can be rejected at a confidence level of 98%. The significance level increases to 99.6% when the two galaxies with extremely low [O III]/H$\beta $ ratios are excluded from the analysis. The estimated means of the two populations are EI = 0.63 and EI = 1.40 for the low and high excitation sources respectively, with a standard deviation of 0.25. We also note that the average rate of correct classification of a galaxy within a given group is larger than 95%.

\begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{13290f4.ps} \end{figure} Figure 4:

Histogram of the number of 3CR sources as function of the excitation index (see text) representing the overall ratio of high and low excitation emission lines. Graphically, it is a coordinate axis parallel to the anti-bisectrix of Fig. 3.

Open with DEXTER

\begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{13290f5.ps} \end{figure} Figure 5:

Ratio of line and radio luminosities vs. excitation index.

Open with DEXTER

An additional distinction between objects of high and low excitation index is their radio emission. We will discuss the connection between radio and optical properties in more detail later on, but it is useful to anticipate this result. In Fig. 5 we compare the excitation index and $L_{\rm [OIII]}/\nu L_{178}$, i.e. the ratio between their line and total radio (at 178 MHz) luminosity. In this diagram, the two populations of galaxies at high and low values of EI are separated in two groups also from the point of view of the relative level of line emission with respect to their radio luminosity.

The median values of log ( $L_{\rm [OIII]}/\nu L_{178})$ are -0.1 for the galaxies with EI $\ga$ 1 and -1.1 for lower excitation galaxies.

\begin{figure} \par\includegraphics[angle=90,width=8.6cm,clip]{13290f6a.epsi}\hspace*{3mm} \includegraphics[angle=90,width=8.2cm,clip]{13290f6b.ps} \end{figure} Figure 6:

Left panel: LRI vs. log [O III]/H$\beta $ (as in Fig. 3) including the broad line objects (crossed circles) and zooming onto the 3CR populated region. HEG are represented by circles, LEG by squares. Right panel: comparison of the distributions of excitation index for narrow and broad line objects.

Open with DEXTER
\begin{figure} \par\includegraphics[angle=90,width=17cm,clip]{13290f7.epsi} \end{figure} Figure 7:

Diagnostic diagrams for 3CR sources after the classification into HEG (blue circles) and LEG (red squares) made using the excitation index. Crossed circles are broad line galaxies, green crosses are extremely low [O III]/H$\beta $ sources. Black triangles are sources for which the LRI cannot be estimated, as they lack the measurement of one or two diagnostic lines. The dotted lines mark the approximate boundaries between HEG and LEG in each diagram.

Open with DEXTER

We conclude that RG can be separated into two sub-populations based on their spectroscopic properties. The threshold can be located at a value of the excitation index of $\sim$0.95. This separation corresponds also to a difference related to $L_{\rm [OIII]}/\nu L_{178}$ (the ratio between line and radio luminosity) of a full order of magnitude. Following the terminology introduced by Laing et al. (1994) we define these classes as low and high excitation galaxies, LEG and HEG respectively.

There are sources which remain unclassified using the EI index. We will introduce alternative ways to classify these sources in Sects. 2.4 and 3.

2.3 Spectroscopic properties of broad line objects

We now include the broad line objects in our analysis[*]. In Fig. 6 (where we compare the line ratios index and the [O III]/H$\beta $ ratio) broad line objects (BLO), marked with crossed circles, are located in the region populated by HEG, although generally closer to the separation line between HEG and LEG. In fact, with respect to HEG, BLO have a slightly lower average level of the [O III]/H$\beta $ ratio. As discussed above this can be due to a general overestimate of the H$\beta $ intensity in this class of objects. The distribution of excitation index of BLO is compared with that of narrow line objects in Fig. 6, right panel, and again it shows a close overlap with high excitation galaxies. Although BLO show a larger dispersion in EI (0.44) than HEG (0.24), the median EI of the two classes differ by only $\sim$0.1. Similarly, the $L_{\rm [OIII]}/\nu L_{178}$ ratio of BLO is in the range 10-1-10, the same covered by HEG.

Based on these results, we conclude that BLO can be considered, from the point of view of their narrow lines intensity ratios and line over radio luminosities, as members of the HEG class.

Including the BLO into the HEG class, the KMM test for bimodality still rejects the hypothesis of a single Gaussian distribution at a confidence level of 96.7% (still excluding the two galaxies with extremely low [O III]/H$\beta $ ratios).

2.4 HEG and LEG in the diagnostic diagrams

In Fig. 7 we report the location of HEG (including broad line objects) and LEG in the standard diagnostic spectroscopic diagrams. As expected, HEG correspond generally to the objects with the highest values of [O III]/H$\beta $. They also have, on average, lower values of all ratios of low excitation lines with respect to H$\alpha $ (i.e. they are located to the top-left of LINERs). The two classes are completely separated in all diagrams with the exception of at most two BLO that fall among the LEG. As already mentioned this is most likely due to an overestimate of the H$\beta $ intensity and we note that a decrease of its luminosity by 20% would be sufficient to move them among the Seyferts.

In some cases it is possible to derive a rather robust classification also of the 3CR sources for which not all the diagnostic lines could be measured. These objects are represented by the black triangles. For example, two such galaxies (namely 3C 381 and 3C 436) fall in the HEG regions, but they lack a measurement of the [S II] or the [O I] line, due to the presence of a telluric absorption band. Based on their location in two of the diagrams a classification as HEG appears secure. In 3C 284, only upper limits can be derived for the [S II] and [O I] fluxes; however, these limits confirm the location of this object in the HEG region. Similarly, we can give a LEG classification for two sources, 3C 078 and 3C 357, whose spectra do not cover the [S II] spectral region.

In addition, the sample comprises a single galaxy characterized by a star forming spectrum (3C 198) and the three galaxies of extremely low excitation (ELEG) discussed above, namely 3C 028, 3C 314.1, and 3C 348. The spectroscopic classification of the sample is reported in Table 1. In Table 2 we provide the classification for each object.

More generally, due to the relatively narrow stripe covered by the 3CR sources in the diagnostic diagrams (and also by the relatively small number of objects), it is difficult to define a two-dimensional representation for the locus of the separation between LEG and HEG, such as those provided by K06. As already mentioned, HEG and LEG are optimally separated on the basis of a one-dimensional threshold in the excitation index at EI $\sim$ 0.95. However, when not all the required emission lines can be measured, considering the individual diagrams we note that LEG are located approximately at

\begin{eqnarray*}&& \log \; [{\rm O~III}]/{\rm H}\beta - \log \; [{\rm N~II}]/{\... ...~III}]/{\rm H}\beta - \log \; [{\rm O~I}]/{\rm H}\alpha \la 1.4. \end{eqnarray*}


Table 1:   Spectral classification breakdown.

3 On the line-radio relationship

3.1 Emission lines vs. radio luminosity

In Fig. 8, top panel, we compare the [O III] line luminosity with the total radio luminosity at 178 MHz. HEG are located in general at higher line luminosity with respect to LEG of similar radio luminosity. This reflects their higher value of the $L_{\rm [OIII]}/\nu L_{178}$ ratio already discussed in Sect. 2.2.

Table 2:   Multiwavelength data and spectroscopic classification.

There are two notable exceptions to this trend, namely 3C 084 and 3C 371. They are spectroscopically classified as LEG, but show an excess of a factor of $\sim$50 in line emission with respect to the sources of this class of similar radio power. Intriguingly, these are the two sources with the highest core dominance of the sample, with ratios  $P_{\rm core}$/L178 of 0.69 and 0.33 respectively. This implies that, by considering only their genuine extended radio emission, they would be stronger outliers, reaching ratios of line to radio emission even higher than observed in HEG.

While HEG are only found at radio luminosities larger than log L178 [erg/s] $\ga$ 32.8, LEG cover the whole range of radio power covered by the subsample of 3CR sources with z < 0.3, almost five orders of magnitude from log L178 $\sim$ 30.7 to log L178 $\sim$ 35.4.

There is a clear trend for increasing line luminosity with radio power, as already found and discussed by several authors and as reported in the introduction. However, we are now in the position of considering separately the sub-populations of HEG and LEG. More quantitatively, we find that HEG obey a linear correlation in the form:

\begin{eqnarray*}\log \; L_{\rm [O~III]} = 1.15 ~ \log \; L_{178} + 2.96. \end{eqnarray*}


The error in the slope is 0.11, while the rms around the correlation is 0.43 dex. We tested the possible influence of redshift in driving this correlation (both quantities depend on z2) estimating the partial rank coefficient, finding $r_{{\rm [O~III]} - L_{178},z}=0.41$. For 46 data-points, the probability that this results from randomly distributed data is P = 0.005. For LEG we find:

\begin{eqnarray*}\log \; L_{\rm [O~III]} = 0.99 ~ \log \; L_{178} + 7.65. \end{eqnarray*}


The error in the slope is 0.09 and the rms around the correlation is 0.50 dex. The partial rank coefficient is $r_{{\rm [O~III]} - L_{178},z}=0.51$, corresponding to a probability of a random distribution of P = 0.002.

The relations derived for HEG and LEG differ by a factor of $\sim$10 in the common range of radio power. The slopes of the line-radio luminosity correlations of HEG and LEG are instead consistent within the errors.

Considering instead the H$\alpha $ line, we find rather similar results, as shown in Fig. 8, middle panel. The form of the correlations are:

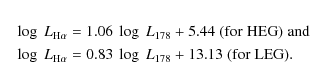
\begin{eqnarray*}&& \log \; L_{\rm {H\alpha}} = 1.06 ~ \log \; L_{178} + 5.44 \;... ...\alpha}} = 0.83 ~ \log \; L_{178} + 13.13 \; ({\rm for \; LEG}). \end{eqnarray*}


The main difference is the smaller offset between the two populations, reduced to a factor of $\sim$3. Also the spread among the two classes is reduced to 0.22 and 0.44 dex for HEG and LEG, respectively.

Finally, correlations are found also between radio core power and line luminosity (Fig. 8, bottom panel) with

\begin{eqnarray*}&& \log \; L_{\rm [O~III]} = 0.75 ~ P_{\rm core} + 18.71 \; ({\... ...\rm [O~III]} = 1.01 ~ P_{\rm core} + 9.28 \; ({\rm for \; LEG}). \end{eqnarray*}


The separation in terms of ratio between line and radio luminosity provides us with a further element to associate spectroscopically unclassified sources with the HEG and LEG sub-populations. For example, the narrow Balmer lines of two BLO, 3C 111 and 3C 445, could not be measured, due to the prominence of the broad component. Nonetheless, they are located at log L178 $\sim$ 33.5 and log  $L_{\rm [O~III]}$ $\sim$ 42.5, so the line luminosity factor is $\sim$100 times higher than LEG of similar radio luminosity, suggesting an identification of these two sources as HEG. Adopting this definition, all BLO belong to the HEG population.

Conversely, the nature of the relatively large population of unclassified sources remains ambiguous. In general, they show values (or upper limits) of the $L_{\rm [OIII]}/\nu L_{178}$ ratios significantly smaller than predicted by the line-radio correlation defined by HEG. However, a LEG classification is not granted since we cannot exclude that they are part of the ELEG population, as they lack a measurement of the [O III]/H$\beta $ ratio. While the H$\beta $ flux is never available, in a few cases the [O III] line can be measured leading to a ratio log [O III]/H$\beta $ > 0.1, inconsistent with a ELEG classification. This is the case of 3C 173.1, 3C 326, and 3C 430 which may then be considered as LEG.

3.2 Spectroscopic classes vs. radio morphology

We now examine the relationship between the spectroscopic classes and the radio morphological FR type. In Table 2 we report our own classification of the 3CR radio-sources based on the analysis of the best radio maps available in the literature. We adopted rather strict criteria for the inclusion of a given object into one of the FR morphological type, preferring a larger number of undefined sources with respect to a less secure identification. In particular, we include a radio source into the FR II group only when clear hot spots are visible in the radio maps, and considered as FR I only sources with a well defined twin-jets structure.

All sources of the HEG spectroscopic class belong to the FR II type, with only two exceptions. The first is 3C 433 that shows a peculiar radio morphology. The South radio lobe has the presence of a well defined hot-spot, while the northern radio jets bends dramatically toward the West, forming a rather diffuse lobe (Black et al. 1992). The second is 3C 93.1, a Compact Steep Spectrum source (Akujor et al. 1991) too compact ( ${\sim}0\hbox{$.\!\!^{\prime\prime}$ }2$ in size) to show any structure. As already noted, all HEG are found in radio-sources with log  $L_{178}\ga 32.8$.

\begin{figure} \par\includegraphics[angle=90,width=8.6cm,clip]{13290f8a.epsi}\pa... ...epsi}\par\includegraphics[angle=90,width=8.6cm,clip]{13290f8c.epsi} \end{figure} Figure 8:

[O III] and H$\alpha $ luminosity [erg s-1] ( top and middle panel, respectively) as a function of radio luminosity at 178 MHz [erg s-1 Hz-1]. Blue circles are HEG (crossed circles are BLO), red squares are LEG, green pluses are ELEG, the cyan asterisk is the star forming galaxy, while the black triangles are spectroscopically unclassified galaxies. The two solid lines represent the best linear fit obtained for the HEG and LEG sub-populations separately. When possible, we further mark the LEG according to their FR type: crossed squares are FR II/LEG and dotted squares are FR I/LEG. Bottom panel: [O III] luminosity as a function of radio core power.

Open with DEXTER

The situation for LEG is more complex. Of the 37 sources belonging to this spectroscopic class 16 are FR II, 12 are FR I, while the radio-morphology of the remaining 9 is not sufficiently well defined to include them in any FR group, such as, for example, 3C 317 (a core/halo source), 3C 371 (with a core/jet morphology), and the X-shaped 3C 315.

LEG with FR II morphology are associated with radio-sources with relatively large radio power, from log  $L_{178}\sim33.5$ to log  $L_{178} \ga 34.5$, with just one exception (3C 088) of lower luminosity, while the FR I/LEG all have log  $L_{178} \la 33$. We also stress that the excitation level of FR II/LEG (with a mean value of EI = 0.66 and a spread of 0.15) does not differ from the rest of the LEG population (for which the mean is EI = 0.63). This indicates that radio morphology does not affect the excitation levels.

For the objects not classified spectroscopically, we have 10 FRI, 4 FRII and 3 of uncertain FR type.

Conversely, by looking at the spectral classification of the different FR types, while there are FR II/HEG as well as FR II/LEG, all FR I for which we were able to derive a spectral type are LEG.

3.3 Broad emission lines and spectroscopic classes

Broad H$\alpha $lines are found in a sub-sample of 18 3CR sources. With the possible exception of 3C 273, where no narrow lines can be measured, all remaining sources are part of the HEG sub-population. The broad emission line fluxes are linked by a linear relation to the [O III] flux over 2.5 orders of magnitude, with an average ratio $F_{{\rm H\alpha(broad})} \sim 8 F_{\rm [O III]}$, and a scatter of a factor of $\sim$4 (see Fig. 9)[*]. This is expected since both lines are essentially proportional to the flux of ionizing photons. Differences in their relative intensities, from object to object, are most likely due to changes in the relative covering factor of the narrow and broad line regions.

\begin{figure} \par\includegraphics[width=8cm,clip]{13290f9.ps} \end{figure} Figure 9:

Comparison of the broad H$\alpha $and [O III] line fluxes for 17 RG showing a broad emission line component (we excluded 3C 273 since it lacks the [O III] flux). The solid line represents the locus of galaxies with $F_{{\rm H\alpha (broad})}$ = 8  $F_{\rm[O~III]}$. The dotted lines show the effect of varying this ratio by a factor 4. The outlier is 3C 234, whose broad lines are due to scattered light.

Open with DEXTER

Under the assumption that the flux of the H$\alpha $ broad component follows the relation with [O III] of Fig. 9 and with similar properties in terms of width and shape of the profile, one would have expected to detect a BLR in the objects with $F_{\rm {[O~III] }} \ga 2$ $\times$ 10-15 erg s-1 cm-2, the lowest [O III] flux among BLO, i.e. in $\sim$75% of the sample. This indicates that for these galaxies the $F_{{\rm H\alpha(broad})} / F_{\rm [O~III]}$ ratio must be lower than in BLO. For HEG lacking of a BLR this can be accounted for by selective absorption, i.e. to circumnuclear obscuring material, as predicted by the unified models (e.g. Urry & Padovani 1995). However, a BLR is never observed in LEG. This is difficult to account in a simple geometric scheme and it implies that BLR in LEG are intrinsically fainter, relative to the narrow line emission, than in HEG.

\begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{13290f10.epsi}\includegraphics[angle=90,width=8cm,clip]{13290f11.epsi} \end{figure} Figure 10:

Comparison of the radio luminosity at 178 MHz versus the magnitude in H band of the host galaxy for the various sub-populations of 3CR sources. Left panel: 3CR sources divided into FR I (green diamonds) and FR II (pink stars); right panel: comparison between HEG (blue circles) and LEG (FR I = crossed red squares, LEG FR II = filled red squares, LEG of uncertain FR type = empty red squares). The solid line marks the separation between FR I (below the line) and FR II (above the line) according to Ledlow & Owen (1996).

Open with DEXTER

3.4 Comparison with previous studies

We based our initial classification on the ratios of diagnostic emission lines. Previous studies used instead a combination of line ratios and equivalent widths (see the Introduction) that can be more affected (in particular when only upper limits can be derived) by the quality of the data and by the contrast with the continuum emission. Similarly, we only used ratios of lines with small wavelength separation, not affected by the possible effects of internal reddening, that can be particularly severe when considering e.g. the [O II]$\lambda$3727 line. Thus our procedure is expected to produce a rather robust method of spectral identification.

Nonetheless, our classifications are overall in good agreement with those found in the literature on a object by object basis. For example, comparing our results with those of Willott et al. (1999)[*] for the 3CRR sources we found 52 objects in common. Leaving aside 2 objects of the newly introduced class of ELEG, and 3 objects that we consider as unclassified (2 reported as LEG, namely 3C 035 and 3C 319, 1 as HEG, 3C 438) the identification in the various classes coincides with only 3 exceptions for the remaining 47 radio-galaxies. These are: 3C 388, a LEG from our analysis (with an excitation index of EI = 0.62) against the previous HEG identification, and two galaxies, 3C 079 and 3C 223, where we do not see a broad line component[*], contrasting with their suggested membership in the class of Weak Quasars.

3.5 The radio-host galaxy luminosity plane for FR I, FR II, LEG, and HEG

Ledlow & Owen (1996) compared the optical R band magnitude of the host galaxies with the total radio emission at 1.4 GHz. They found that sources locate in different areas of the plot depending on their radio morphology: as already known from the pioneering study of Fanaroff & Riley (1974) FR II sources have higher radio powers than FR I sources and they separate at a luminosity of ${\sim}2$ $\times$ 1025 W Hz-1 at 178 MHz. The novel result of Ledlow & Owen (1996) consists in the fact that the FR I/II division shows a dependence on  $M_{\rm host}$. FR I sources hosted by the more luminous galaxies can have radio powers higher than the average FR I/FR II separation. The separation between FR I and FR II is rather sharp over the whole range of radio power.

In Fig. 10 (left panel) we plotted the 3CR sources in the plane radio luminosity (at 178 MHz) versus the magnitude in H band of the host galaxy (reported in Table 2). We selected the H band since it provides the most complete coverage ($\sim$85%) for the 3CR sample by using measurements from the 2MASS (Skrutskie et al. 2006) or, when this is not available, from HST images (Donzelli et al. 2007). For the BLO we also corrected the host luminosity for the contribution of their bright IR nuclei, measured by Baldi et al. (2009). In order to compare our results with those of Ledlow & Owen (1996) we used the color correction from Mannucci et al. (2001), R - H = 2.5, and scaled the 1.4 GHz data to 178 MHz adopting a radio spectrum in the form $F_{\nu} \propto \nu^{-0.7}$.

The relative scarcity of FR I sources in the 3CR sample prevents us from exploring in detail the host magnitude-dependent separation between the FR classes. However, the FR location for our sample is consistent with the separation introduced by Ledlow & Owen (1996). We also checked that this result holds using radio luminosities at 1.4 GHz as well as host magnitude in other bands (i.e. V band). In line with their results we find a few exceptions, associated with FR I sources of extremely high radio powers in very massive hosts.

In the right panel we introduced the optical spectroscopic classification, separating the 3CR sources into HEG and LEG. For the LEG class we further consider the FR type. HEG and LEG/FR II sources are well mixed above the FR I/FR II separation, having the same median in terms of radio power, and only a small offset in the median host magnitude, with LEG $\sim$ 0.3 mag brighter. As originally suggested by Ghisellini & Celotti (2001, hereafter GC01) the radio - host galaxy luminosity plane can be translated into a jet-power vs. black hole mass diagram. The substantial superposition between HEG and LEG indicates that also the distribution of the estimated black hole masses and jet power for the two classes are similar.

GC01 also noted that the line luminosity can be used as indicator of the ionizing luminosity, $L_{\rm ion}$, that they estimated from the radio power (see e.g. Willott et al. 1999). We can now derive this quantity directly from the [O III] luminosity as[*]

\begin{eqnarray*}{\rm log} ~L_{{\rm ion}} \sim {\rm log} ~L_{\rm {[O~III]}} + 2.83. \end{eqnarray*}


We also derived the black hole mass from the host luminosity using the correlation of Marconi & Hunt (2003)

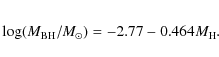
\begin{eqnarray*}{\rm log} (M_{\rm BH}/{M}_{\odot}) = -2.77 -0.464 M_{\rm H}. \end{eqnarray*}


In Fig. 11 we show the $L_{\rm [O~III]}-M_{\rm H}$ plane that, as explained above, can be translated into a $L_{\rm ion}-M_{\rm BH}$ plane. With respect to Fig. 10, the location of LEG and HEG are substantially offset. LEG/FR I are located at the bottom of the diagram and all have $L_{\rm ion}$/ $L_{\rm Edd} \la 10^{-4}$, where $L_{\rm Edd}= 1.3$ $\times$ $10^{38} M_{\rm BH}$/$M_{\odot}$ erg s-1 is the Eddington luminosity. LEG/FR II (and also LEG of uncertain FR type) lie in an intermediate area, while HEG cover the top region. In general LEG (regardless of the FR type) and HEG are rather well separated, but they coexist over the range 4 $\times$ 10-4 $\la$ $L_{\rm ion}$/ $L_{\rm Edd}$ $\la$ 2 $\times$ 10-3. The dividing line has apparently a positive slope, in the sense that LEG can be found at high values of $L_{\rm [O~III]}$ only in the brightest galaxies.

\begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{13290f12.epsi} \end{figure} Figure 11:

Comparison of [O III] line luminosity (in erg s-1) and H band host magnitude for 3CR sources. Symbols are as in the right panel of Fig. 10, i.e. HEG = blue circles, LEG = red squares (filled for FR II, crossed for FR I, empty for uncertain FR type. The right axis reports the ionizing luminosity (in erg s-1) while the upper axis reports the estimated black hole mass in solar units. The solid and dashed lines correspond to $L_{\rm ion} = 0.1 \cdot ~ L_{\rm Edd}$ and $0.001 \cdot ~ L_{{\rm Edd}}$, respectively.

Open with DEXTER

Marchesini et al. (2004) found that the bolometric luminosity for radio-loud AGN has a bimodal distribution, related to a different level of  $L_{\rm bol}$ for LEG and FR I with respect to BLO and radio-loud QSO, while, restricting only to RG, the evidence for bimodality was marginal. We find a similar marginal result ( $P \sim 0.1$) considering the ionizing luminosity or the $L_{\rm ion}$/ $L_{\rm Edd}$ ratio.

4 Discussion

4.1 On the origin of the spectroscopic sub-populations in radio-loud AGN

The main result derived from the spectroscopic properties of the 3CR sources is the presence of two dominant populations of galaxies, HEG and LEG, separated on the basis of the ratio between the intensity of high and low excitation emission lines. This finding confirms the original suggestion by Laing et al. (1994).

HEG and LEG differ also from the point of view of other properties: 1) we find prominent broad lines in $\sim$30% of HEG, but not in LEG; 2) HEG are brighter than LEG in the [O III] line by a factor of $\sim$10 at the same total radio luminosity; 3) the two classes are well offset in a plane that compares their ionizing luminosity and black hole mass; 4) the luminosity of the nuclear sources in LEG is on average $\sim$30 times fainter than in HEG (considering only HEG with broad lines, where the nucleus is not affected by obscuration) at both optical and infrared wavelengths (Chiaberge et al. 2002; Baldi et al. 2009) at a given radio core power; 5) HEG hosts are bluer than those of LEG, an indication that star formation is commonly associated with HEG while it rarely seen in LEG (Smolcic 2009; Baldi & Capetti 2008).

Conversely, the distribution of black hole masses for the two classes is not largely different. Actually, the overall black hole mass distribution of these RG is rather narrow, with the vast majority of the objects confined in the range 8.5 $\la$ log  $M_{\rm BH}$/$M_{\odot}$ $\la$ 9.5 (see also Marchesini et al. 2004). Thus, HEG nuclei are associated with a higher rate of radiative emission with respect to LEG, not only in absolute values, but also in terms of fraction of the Eddington level.

GC01 suggested that the transition from FR I to FR II can be associated with a threshold in the accretion rate that corresponds to a hange in the properties of the accretion disk, from ``standard'' to low radiative efficiency (hereafter RIAF). Nagao et al. (2002) argued that the differences in terms of emission line ratios between high and low excitation sources can be ascribed to a change in the Spectral Energy Distribution of the active nucleus, due to such a transition. In low efficiency disks, the emerging spectrum is presumably harder than for a radiatively efficient disk. This favors the emission of lower excitation lines, produced in the region of partially ionized gas, excited by the higher energy photons. This is consistent with the observed spectroscopic differences between HEG and LEG. Additional support for this conclusion is provided if we consider radio-quiet AGN. The photoionization models derived by K06 indicate that Seyferts require a higher ionization parameter than LINERs, but the optical line ratios of the more powerful objects of this latter class are better reproduced assuming also a harder nuclear continuum.

Nevertheless, the location of the various classes in the $L_{\rm ion}-M_{\rm BH}$ plane is not straightforward to interpret in this scenario. In fact, we lack of clear indications on how to convert the ionizing luminosity into accretion rate for the (putative) RIAF disks. The separation between FR I/LEG and FR II/HEG is sufficiently large (a factor of 100-1000 in  $L_{\rm ion}$/ $L_{\rm Edd}$) that one can probably infer that the latter class has not only a higher ionizing luminosity but also a higher accretion rate. Conversely, the brightest LEG overlap with FR II/HEG; in the case they were associated with RIAF, the superposition in terms of accretion rate would become even larger, due to their lower radiative efficiency.

Furthermore, LEG span the whole range of radio power covered by the subsample of 3CR sources with z < 0.3 and, actually, the brightest radio source of our sample (3C 123) is a LEG. Despite our rather strict criteria for the definition of the FR type, we found a substantial fraction (16 out of 37) of LEG with a FR II morphology. Moreover the radio core power of LEG is similar to that measured in HEG; restricting to the range of extended radio power 33 < log L178 < 34.5, where we have the bulk of the FR II population, the median core dominance is log  $P_{\rm core}$/L178 = -2.69 $\pm$ 0.13 in LEG and log  $P_{\rm core}$/L178 = -2.99 $\pm$ 0.14 in HEG. HEG and LEG/FR II are thus essentially indistinguishable from the point of view of their radio properties, suggesting that the two classes share the same range also in terms of jet power.

If the change in the spectral and nuclear properties from LEG to HEG are associated with a threshold in the accretion rate, the similarity of the radio properties of the two sub-populations requires a process of jet launching essentially decoupled from the level of accretion. This is the case, for example, in the Blandford & Znajek (1977) process where jets are shaped by the magnetic field and the black hole spin and not univocally by the accretion mechanism.

Focusing purely on those galaxies with FR II morphology, an alternative possibility is that the link between HEG and LEG is related to variability can be excluded. In fact, in response to a decrease in the accretion rate, the luminosity of the optical nucleus, of the BLR, and of the NLR, as well as its excitation level, will decline, possibly causing a change from a HEG to a LEG. However, this contrasts with the requirement that the radio core emission must remain essentially unaltered while this component reacts on very short timescales to changes of the central activity.

Based on the substantial difficulties in accounting for the similarities and differences between LEG and HEG based on different or time-varying accretion rates, we here propose a different interpretation for the origin of the spectroscopic sub-populations of radio-loud AGN. We speculate that the separation between LEG and HEG is not due to a different rate of accretion but, instead, to a different mode of accretion. In this scenario, HEG are powered by accretion of cold gas, e.g. provided by a recent merger with a gas rich galaxy (e.g. Baldi & Capetti 2008). Cold gas, approaching the central regions of the galaxy, forms the various structures commonly seen in these AGN, such as a molecular torus, a Broad Line Region, and a standard, geometrically thin, accretion disk. Conversely, LEG accrete hot material, provided by the ample reservoir of their X-ray emitting gaseous coronae. This process has been shown to be able to account for the nuclear activity of FR I radio-galaxies (Allen et al. 2006; Balmaverde et al. 2008) extending up to a radio power of log  $L_{178} \sim 33$. The temperature of the accreting gas is typically around 1 keV, ${\sim}10^7$ K. This prevents the formation of the ``cold'' structures, in particular of a molecular torus, but also of the clouds of the BLR, whose ionized portion has a temperature of ${\sim}10^5$ K, unless the in-flowing gas is able to cool dramatically on its way to the center of the galaxy. Indeed BLR are not seen in LEG and they also do not generally show the high level of absorption in the X-ray band expected if their nuclei were seen through an obscuring torus (e.g. Hardcastle et al. 2009).

Moreover, the properties of the accretion disk are likely to be substantially altered due to the high initial temperature of the gas. From a geometrical point of view, a ``cold'', standard accretion disk is flattened by rotation, while it remains geometrically thick for higher temperatures. While the radiative emission in a standard disk is dominated by UV and soft X-ray photons, a hotter disk emits most of the radiation at higher energies. The higher temperature in case of hot accretion corresponds also to a lower radiative efficiency due to the reduced gas cooling at these temperatures (but see Dumont 1992, for the effects of high density on the gas cooling function). At a given accretion rate, the number of ionizing photons is then reduced, due to the combination of higher average photon energy and lower overall emission. The emitted spectrum is harder and it produces lines of lower excitation, as discussed above. This effect can produce the spectral separation between LEG and HEG similarly to RIAF.

Furthermore, Capetti et al. (2005) showed that the non-thermal cores in FR I produce a sufficient flux of high energy photons to account for the ionization of their NLR. The radio and optical luminosities of the nuclei of FR I and FR II/LEG are linked by a common linear correlation (Chiaberge et al. 2002) and, as shown by Fig. 8, this applies also to radio cores and line luminosity. It is then possible that the dominant source of ionizing photons in LEG must be ascribed to non-thermal emission, associated with the base of their jets, rather then with their accretion disks.

The accretion rate in FR II/LEG can be estimated by extrapolating the scaling relation between jet and accretion power derived for low luminosity FR I/LEG to the objects of highest luminosity of this class. Balmaverde et al. (2008) estimated that the accretion rate needed to power a radio source with $L_{178} \sim 10^{33}$ erg s-1 is $P_{\rm accr} \sim 10^{44.6}$ erg s-1. This requires $P_{\rm accr} \sim 10^{46}$ erg s-1 for the most powerful LEG, corresponding to a fraction $\dot{m} \sim 0.1$ of the Eddington rate for a 10 $^9~{M}_{\odot}$ black hole. These hot flows at high accretion rate can be probably associated with the optically thin, geometrically thick solutions (e.g. Abramowicz et al. 1995) that can reach, for a viscosity parameter $\alpha =0.1$, a rate of the order of the Eddington one.

The mechanism of jet launching, likely to be determined by the disk structure in the region closer to the black hole, might not be sensitive to the gas history, but only to the final accretion rate. Provided that this reaches comparable high levels in HEG and LEG, radio structures of similar morphology and power can be formed in the two sub-classes.

4.2 Radio-loud vs. radio-quiet (SDSS) AGN

The separation between HEG and LEG is reminiscent of that found by K06 for the SDSS sources, mostly radio-quiet AGN. However, we find a significant number of LEG located above the line marking the transition between LINERs and Seyferts. The location of LEG shows an upward scatter with respect to the ``finger'' of highest LINERs density by $\sim$0.2 dex in the [O III]/H$\beta $ ratio. As already noted there is a substantial mismatch in luminosity between the 3CR and the SDSS sources. Our data are not sufficient to conclude whether this is due to a genuine difference between the (mostly) radio-quiet AGN of the SDSS and the radio-loud AGN of the 3CR sample (due e.g. to a contribution of jets emission to the line excitation) or simply to a luminosity difference.

Similarly, we noted that the 3CR sources are concentrated along the edges of the SDSS density distribution. The first possibility to account for the location of SDSS and 3CR sources is again a general difference in the spectroscopic behavior between radio-quiet and radio-loud AGN. Alternatively, the location of the SDSS sources could be due to the contamination of star forming regions. In this scenario, this results in a large spread in the line ratios, depending on the relative contribution of the line emission produced by the active nucleus and by star formation. The sources would be then distributed along a mixing region (possibly the ``fingers'' seen in Figs. 1 and 2), ranging from a ``pure'' AGN to a star forming spectrum. In the case of 3CR sources, the higher line luminosity is likely to be indication of a dominant AGN contribution, also considering the general weakness of star formation in their early type host with respect to later types.

The analysis of radio-loud AGN of lower luminosity can be used to test these alternative hypothesis.

5 Summary and conclusions

We used measurements of emission lines for a 92% complete survey of the 3CR sample of radio-galaxies with z < 0.3 to explore their spectroscopic properties. The different steps used to classify the 3CR sources in the various sub-populations can be summarized as follows:

$\bullet$
Excitation index diagram: we first considered a new spectroscopic indicator, the excitation index, defined as EI = log [O III]/H$\beta $ - 1/3 (log [N II]/H$\alpha $ + log [S II]/H$\alpha $ + log [O I]/H$\alpha $) and representing the relative intensity of high and low excitation lines. 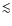The presence of a bimodal distribution of EI allows us to define two main spectroscopic classes, LEG and HEG, with LEG being sources with EI $\la$ 0.95. The drawback of this definition is that it requires the measurements of all 6 diagnostic lines.

$\bullet$
Diagnostic diagrams: the close correspondence between the excitation index and the location in the 3 ``standard'' diagnostic diagrams enabled us to define a class membership in a less ideal situation, i.e. when in addition to H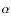$\alpha $, H$\beta $ and [O III], only one or two lines among [S II], [O I] or [N II] can be measured, defining as LEG all sources for which:

\begin{eqnarray*}&&\log~[{\rm O~III}]/{\rm H\beta} - \log ~ [{\rm N~II}]/{\rm H\... ...m O~III}]/{\rm H\beta} - \log~[{\rm O~I}]/{\rm H\alpha} \la 1.4. \end{eqnarray*}


$\bullet$
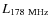Optical line-radio correlation. We also used the $L_{\rm [OIII]}$ vs. $L_{178~{\rm MHz}}$correlation to extend the classification for objects with the only requirement of a [O III] line measurement. This is due to the rather well defined separation in line emission, at fixed radio power, between HEG and LEG. In particular we found

\begin{eqnarray*}&& -1 \la {\rm log} ({L_{\rm [O~III]}}/\nu L_{178}) \la ~~ 0.5~... ...\rm log} ({L_{\rm [O~III]}}/\nu L_{178}) \la -0.5~{\rm for~LEG}. \end{eqnarray*}


Using this strategy we were able to associate a spectroscopic class to 87 sources, representing 84% of the sample. The breakdown in the various sub-classes is of 46 HEG (16 of which are BLO) and 37 LEG. In addition to the two main sub-classes, we found one object with a spectrum typical of star-forming galaxies, and 3 sources of extremely low excitation (ELEG). 17 galaxies remain spectroscopically unclassified. None of the unclassified sources is consistent with being a HEG, as they all have very low values of  $L_{\rm [OIII]}/\nu L_{178}$. However, we cannot conclude in general that they are LEG, since they could belong to the ELEG class.

The ELEG are particularly intriguing, being well offset from the rest of 3CR sample in all diagnostic diagrams. They are also characterized by very low values of the ratio between [O III] and radio luminosity as well as of core dominance. We defer to a forthcoming paper a more detailed analysis of these sources.

The dual population of HEG and LEG is reminiscent of the Seyfert and LINERs subclasses found in the SDSS emission line galaxies. Indeed, at zero-th order, the spectroscopic properties of radio-loud AGN of the 3CR and the (mostly) radio-quiet AGN of the SDSS are rather similar. However, looking at finer details, the separation between LEG and HEG shows an upward scatter by $\sim$0.2 dex in the [O III]/H$\beta $ ratio with respect to the transition from LINER to Seyfert. Furthermore, the 3CR sources are concentrated along the edges of the SDSS density distribution in the spectroscopic diagnostic diagrams. Both results could be related to the substantial mismatch in luminosity between the two samples, the 3CR being brighter by an average factor of 30 in emission line than the SDSS sources. However, we cannot exclude that the location of SDSS and 3CR source is an indication of a genuine difference in the spectroscopic behavior of radio-quiet and radio-loud AGN. The analysis of radio-loud AGN of lower luminosity can be used to test these alternative hypothesis.

Let us now summarize the similarities and differences between the two main spectroscopic classes of RG. All broad-line objects are HEG from the point of view of their narrow emission line ratios, but no LEG shows broad line in its spectrum. While all HEG are associated with FR II radio-galaxies, LEG are of both FR I and FR II type. HEG are only found in relatively bright radio sources, log  $L_{178}\ga 32.8$. Instead LEG cover the whole range of radio power (30.7 $\la$ log L178 $\la$ 35.4), the brightest of them being FR II. HEG and LEG obey to two linear correlations between line and radio emission, with a slope consistent with unity and a rms $\la$ 0.5 dex. HEG are brighter than LEG by a factor of ${\sim}10$ in [O III] line.

Conversely, the substantial superposition of the host galaxy luminosity of the two classes suggests that the distribution of their black hole masses is not strongly different, with the vast majority of the objects confined in the range 8.5 $\la$ log  $M_{\rm BH}$/$M_{\odot}$ $\la$ 9.5. Considering only the LEG with a FR II morphology, a further similarity with HEG emerges from the analysis of their radio structure. LEG/FR II extend over the same range of radio power of HEG and have the same level of radio core dominance. The fact that the radio properties of LEG/FR II and HEG are essentially indistinguishable is an indication that the two classes share the same range of jet power.

While the differences in terms of line intensities and line ratios (as well as in optical and IR nuclear luminosities) can be interpreted in a framework in which LEG are associated with a lower accretion rate than HEG, the similarity of the radio properties of the two sub-populations (having established that they do not differ in terms of black hole mass) would require that the process of jet launching is essentially decoupled from the level of accretion. This is the case, for example, of the Blandford-Znajek process that envisages jets powered by the extraction of rotational energy from a spinning black hole.

We instead speculated that the separation between LEG and HEG is due to a different mode of accretion: while HEG are powered by cold gas, LEG accrete hot gas, a mechanism that has been already demonstrated to be able to account for the activity of FR I radio-galaxies. The high initial temperature of the in-flowing gas in LEG prevents the formation of the various ``cold'' AGN structures, such as molecular tori and Broad Line Regions, seen in HEG but not in LEG. The radiative output of a ``hot'' accretion disk is reduced with respect to a standard geometrically thin disk, at a given accretion rate, due to the lower cooling at these temperatures and it will be emitted mostly at high energies. The harder spectrum and the lower number of ionizing photons gives rise to emission lines of lower luminosity and excitation, producing the spectral separation in lines properties between LEG and HEG. Since the mechanism of jet launching operates in the innermost regions of the accretion flow, it is likely that the memory of the initial gas conditions are effectively canceled and that the jet power is sensitive only to the final accretion rate.

The attractiveness of this scheme is that it can reproduce simultaneously, by only varying the initial temperature of the accreting gas, the various differences between LEG and HEG. Clearly this hypothesis must be analyzed in greater detail, exploring the properties of the proposed hot accretion flows combined to a high accretion rate. In particular a crucial requirement is that the coronal accreting gas must be able to remain hot during the inflow. The proposed scenario can also be tested and constrained using the limits on the nuclear LEG emission in the various observing bands. It is also of great interest to establish whether LEG can be found in objects of at most moderate redshift (and, consequently, power) such as those considered here, or, conversely, can be associated even with radio galaxies of the highest luminosity.

Summarizing, we found that the radio-galaxies in the 3CR sample are composed by two main populations, separated on the basis of their emission line properties. However, this does not correspond simply to a difference in their radio properties. We propose a scenario in which the two classes are associated with a different mode of accretion, set by the initial temperature of the inflowing gas.

Acknowledgements
S.B. and A.Ce. acknowledge the Italian MIUR for financial support. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.

References

  1. Abramowicz, M. A., Chen, X., Kato, S., Lasota, J.-P., & Regev, O. 1995, ApJ, 438, L37 [NASA ADS] [CrossRef] [Google Scholar]
  2. Akujor, C. E., Spencer, R. E., Zhang, F. J., et al. 1991, MNRAS, 250, 215 [NASA ADS] [CrossRef] [Google Scholar]
  3. Allen, S. W., Dunn, R. J. H., Fabian, A. C., Taylor, G. B., & Reynolds, C. S. 2006, MNRAS, 372, 21 [NASA ADS] [CrossRef] [Google Scholar]
  4. Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
  5. Antonucci, R. R. J. 1984, ApJ, 278, 499 [NASA ADS] [CrossRef] [Google Scholar]
  6. Ashman, K. M., Bird, C. M., & Zepf, S. E. 1994, AJ, 108, 2348 [NASA ADS] [CrossRef] [Google Scholar]
  7. Baldi, R., Chiaberge, M., Capetti, A., Macchetto, F., & Sparks, W. 2009, ApJ, submitted [Google Scholar]
  8. Baldi, R. D., & Capetti, A. 2008, A&A, 489, 989 [Google Scholar]
  9. Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Balmaverde, B., Baldi, R. D., & Capetti, A. 2008, A&A, 486, 119 [Google Scholar]
  11. Baum, S. A., & Heckman, T. 1989a, ApJ, 336, 681 [NASA ADS] [CrossRef] [Google Scholar]
  12. Baum, S. A., & Heckman, T. 1989b, ApJ, 336, 702 [NASA ADS] [CrossRef] [Google Scholar]
  13. Black, A. R. S., Baum, S. A., Leahy, J. P., et al. 1992, MNRAS, 256, 186 [NASA ADS] [Google Scholar]
  14. Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
  15. Buttiglione, S., Capetti, A., Celotti, A., et al. 2009, A&A, 495, 1033 [Google Scholar]
  16. Capetti, A., Fanti, R., & Parma, P. 1995, A&A, 300, 643 [Google Scholar]
  17. Capetti, A., Verdoes Kleijn, G. A., & Chiaberge, M. 2005, A&A, 439, 935 [Google Scholar]
  18. Chiaberge, M., Capetti, A., & Celotti, A. 2000, A&A, 355, 873 [Google Scholar]
  19. Chiaberge, M., Capetti, A., & Celotti, A. 2002, A&A, 394, 791 [Google Scholar]
  20. Donzelli, C. J., Chiaberge, M., Macchetto, F. D., et al. 2007, ApJ, 667, 780 [NASA ADS] [CrossRef] [Google Scholar]
  21. Dumont, A. M. 1992, A&A, 254, 454 [Google Scholar]
  22. Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 31P [Google Scholar]
  23. Ghisellini, G., & Celotti, A. 2001, A&A, 379, L1 (GC01) [Google Scholar]
  24. Gopal-Krishna, & Wiita, P. J. 2000, A&A, 363, 507 [Google Scholar]
  25. Govoni, F., Falomo, R., Fasano, G., & Scarpa, R. 2000, A&A, 353, 507 [Google Scholar]
  26. Hardcastle, M. J., Evans, D. A., & Croston, J. H. 2009, MNRAS, 396, 1929 [NASA ADS] [CrossRef] [Google Scholar]
  27. Heckman, T. M. 1980, A&A, 87, 152 [Google Scholar]
  28. Hine, R. G., & Longair, M. S. 1979, MNRAS, 188, 111 [NASA ADS] [Google Scholar]
  29. Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001, ApJ, 556, 121 [Google Scholar]
  30. Kewley, L. J., Groves, B., Kauffmann, G., & Heckman, T. 2006a, MNRAS, 372, 961 [NASA ADS] [CrossRef] [Google Scholar]
  31. Kewley, L. J., Groves, B., Kauffmann, G., & Heckman, T. 2006b, MNRAS, 372, 961 (K06) [NASA ADS] [CrossRef] [Google Scholar]
  32. Labiano, A. 2008, A&A, 488, L59 [Google Scholar]
  33. Laing, R. A., Jenkins, C. R., Wall, J. V., & Unger, S. W. 1994, in The Physics of Active Galaxies, ed. G. V. Bicknell, M. A. Dopita, & P. J. Quinn, ASP Conf. Ser., 54, 201 [Google Scholar]
  34. Ledlow, M. J., & Owen, F. N. 1996, AJ, 112, 9 [NASA ADS] [CrossRef] [Google Scholar]
  35. Mannucci, F., Basile, F., Poggianti, B. M., et al. 2001, MNRAS, 326, 745 [NASA ADS] [CrossRef] [Google Scholar]
  36. Marchesini, D., Celotti, A., & Ferrarese, L. 2004, MNRAS, 351, 733 [CrossRef] [Google Scholar]
  37. Marconi, A., & Hunt, L. K. 2003, ApJ, 589, L21 [NASA ADS] [CrossRef] [Google Scholar]
  38. Morganti, R., Ulrich, M.-H., & Tadhunter, C. N. 1992, MNRAS, 254, 546 [NASA ADS] [Google Scholar]
  39. Morganti, R., Tadhunter, C. N., Dickson, R., & Shaw, M. 1997, A&A, 326, 130 [Google Scholar]
  40. Nagao, T., Murayama, T., Shioya, Y., & Taniguchi, Y. 2002, ApJ, 567, 73 [NASA ADS] [CrossRef] [Google Scholar]
  41. Rawlings, S., & Saunders, R. 1991, Nature, 349, 138 [NASA ADS] [CrossRef] [Google Scholar]
  42. Rawlings, S., Saunders, R., Eales, S. A., & Mackay, C. D. 1989, MNRAS, 240, 701 [NASA ADS] [Google Scholar]
  43. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  44. Smolcic, V. 2009, ApJ, 699, L43 [NASA ADS] [CrossRef] [Google Scholar]
  45. Spinrad, H., Marr, J., Aguilar, L., & Djorgovski, S. 1985, PASP, 97, 932 [NASA ADS] [CrossRef] [Google Scholar]
  46. Stoughton, C., Lupton, R. H., Bernardi, M., et al. 2002, AJ, 123, 485 [NASA ADS] [CrossRef] [Google Scholar]
  47. Tadhunter, C. N., Morganti, R., Robinson, A., et al. 1998, MNRAS, 298, 1035 [NASA ADS] [CrossRef] [Google Scholar]
  48. Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
  49. Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295 [NASA ADS] [CrossRef] [Google Scholar]
  50. Willott, C. J., Rawlings, S., Blundell, K. M., & Lacy, M. 1999, MNRAS, 309, 1017 [NASA ADS] [CrossRef] [Google Scholar]
  51. Wills, K. A., Morganti, R., Tadhunter, C. N., Robinson, T. G., & Villar-Martin, M. 2004, MNRAS, 347, 771 [NASA ADS] [CrossRef] [Google Scholar]
  52. Yip, C. W., Connolly, A. J., Vanden Berk, D. E., et al. 2004, AJ, 128, 2603 [NASA ADS] [CrossRef] [Google Scholar]
  53. York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [Google Scholar]
  54. Young, S., Hough, J. H., Axon, D. J., Fabian, A. C., & Ward, M. J. 1998, MNRAS, 294, 478 [NASA ADS] [CrossRef] [Google Scholar]
  55. Zirbel, E. L. 1997, ApJ, 476, 489 [NASA ADS] [CrossRef] [Google Scholar]
  56. Zirbel, E. L., & Baum, S. A. 1995, ApJ, 448, 521 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... AGN[*]
Based on observations made with the Italian Telescopio Nazionale Galileo operated on the island of La Palma by the Centro Galileo Galilei of INAF (Istituto Nazionale di Astrofisica) at the Spanish Observatorio del Roque del los Muchachos of the Instituto de Astrofísica de Canarias.
... Paper I[*]
We removed 3C 270 from the list of observed objects since the SDSS fiber was not positioned on the galaxy's nucleus (Christian Leipski, private communication).
... (3C 198[*]
The source is not present in the middle diagram because the [S II] lines are not covered by its SDSS spectrum.
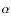
...$\alpha $[*]
For 3 sources (namely 3C 028, 3C 035, and 3C 066B) we could only measure the [S II]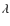$\lambda$6716 line. We estimated the total [S II] flux adopting equal intensities in the two lines and increased the line error to consider this approximation.
...(Ashman et al. 1994)[*]
Available at cas.umkc.edu/physics/ashman/blake.html
... analysis[*]
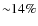We exclude 3C 234 from the sub-sample of Broad Lined Objects since for this source Antonucci (1984) reports a high level of polarization ( ${\sim}14\%$) for the broad emission line and continuum, at odds with the usually low level of polarization of Broad Line radio-galaxies. He interpreted this result as due to scattering of an otherwise hidden nucleus, at least in the optical band (Young et al. 1998). The observed broad line in this object represents only the small fraction of the intrinsic BLR emission that is reflected into our line of sight.
...)[*]
The only outlier from this trend is 3C 234, already discussed previously, and in which the observed broad lines are due to scattered light.
...Willott et al. (1999)[*]
Available at http://www.science.uottawa.ca/ cwillott/3crr/3crr.html
... component[*]
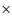
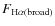We estimated a limit to their broad H$\alpha $ flux of 1.6 $\times$ 10-15 and 1.8 $\times$ $10^{-16}~\>{\rm erg}~{\rm s}^{-1}~{\rm cm}^{-2}$for 3C 079 and 3C 223 respectively. Given their [O III] fluxes, these limits correspond to a factor of 200-300 lower than the mean value $F_{{\rm H\alpha (broad})}$ = 8  $F_{\rm[O~III]}$reported in Sect. 3.3 (see also Fig. 9).
... as[*]
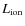
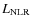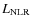Following Rawlings & Saunders (1991) the ionizing radiation is related to the NLR total luminosity as $L_{\rm ion}$ $\sim$ C  $L_{\rm NLR}$, where C is the covering factor of the NLR, for which we assume a value of 0.01. $L_{\rm NLR}$ is derived as $L_{\rm NLR} = 3 \cdot (3 L_{\rm [O~II]} + 1.5 L_{\rm [O~III]})$ and $L_{\rm [O~III]} = 4 L_{\rm [O~II]}$.
Copyright ESO 2010

All Tables

Table 1:   Spectral classification breakdown.

Table 2:   Multiwavelength data and spectroscopic classification.

All Figures

  \begin{figure} \par\includegraphics[angle=90,width=5.8cm,clip]{13290f1a.ps}\hspa... ...cludegraphics[angle=90,width=5.8cm,clip]{13290f1i.ps} \vspace*{3mm} \end{figure} Figure 1:

Diagnostic diagrams. Left column: 3CR sources with symbol sizes increasing with [O III] luminosity (log  $L_{\rm [OIII]}$(erg s-1)); the galaxies showing a broad H$\alpha $ component are represented by crossed circles. Central column: the same plot with error bars. Right column: comparison between 3CR (black dots) and the density of SDSS emission line sources (contour lines) from K06. The ordinates are the ratio log [O III]/H$\beta $. The first row shows the log [N II]/H$\alpha $ ratio, the second row the log [S II]/H$\alpha $ ratio, while the third row shows log [O I]/H$\alpha $. The curves divide AGN (above the solid curved line) from star-forming galaxies. Between the dashed and solid curves there are the composite galaxies (K06). In the bottom two rows, the straight solid line divides Seyferts (upper left region) from LINERs (right region).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8.5cm,clip]{13290f2.ps} \end{figure} Figure 2:

log [O III]/H$\beta $ versus log [O I]/H$\alpha $ diagram only for sources with $L_{\rm [OIII]}>10^{40}$ erg s-1: contour lines represent the SDSS sample while black circles indicate the 3CR sources. The symbol size increases with [O III] luminosity. As in Fig. 1, the curved line divides the star-forming galaxies and AGN, while the oblique line divides Seyferts and LINERs (according to K06).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8.5cm,clip]{13290f3.ps} \end{figure} Figure 3:

Line ratios index (LRI, see text for its definition). The contour lines indicate the distribution of the SDSS emission line galaxies (K06). The circles indicate the 3CR sources (the symbol size is proportional to the [O III] luminosity, see Fig. 1).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{13290f4.ps} \end{figure} Figure 4:

Histogram of the number of 3CR sources as function of the excitation index (see text) representing the overall ratio of high and low excitation emission lines. Graphically, it is a coordinate axis parallel to the anti-bisectrix of Fig. 3.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{13290f5.ps} \end{figure} Figure 5:

Ratio of line and radio luminosities vs. excitation index.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8.6cm,clip]{13290f6a.epsi}\hspace*{3mm} \includegraphics[angle=90,width=8.2cm,clip]{13290f6b.ps} \end{figure} Figure 6:

Left panel: LRI vs. log [O III]/H$\beta $ (as in Fig. 3) including the broad line objects (crossed circles) and zooming onto the 3CR populated region. HEG are represented by circles, LEG by squares. Right panel: comparison of the distributions of excitation index for narrow and broad line objects.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=17cm,clip]{13290f7.epsi} \end{figure} Figure 7:

Diagnostic diagrams for 3CR sources after the classification into HEG (blue circles) and LEG (red squares) made using the excitation index. Crossed circles are broad line galaxies, green crosses are extremely low [O III]/H$\beta $ sources. Black triangles are sources for which the LRI cannot be estimated, as they lack the measurement of one or two diagnostic lines. The dotted lines mark the approximate boundaries between HEG and LEG in each diagram.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8.6cm,clip]{13290f8a.epsi}\pa... ...epsi}\par\includegraphics[angle=90,width=8.6cm,clip]{13290f8c.epsi} \end{figure} Figure 8:

[O III] and H$\alpha $ luminosity [erg s-1] ( top and middle panel, respectively) as a function of radio luminosity at 178 MHz [erg s-1 Hz-1]. Blue circles are HEG (crossed circles are BLO), red squares are LEG, green pluses are ELEG, the cyan asterisk is the star forming galaxy, while the black triangles are spectroscopically unclassified galaxies. The two solid lines represent the best linear fit obtained for the HEG and LEG sub-populations separately. When possible, we further mark the LEG according to their FR type: crossed squares are FR II/LEG and dotted squares are FR I/LEG. Bottom panel: [O III] luminosity as a function of radio core power.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13290f9.ps} \end{figure} Figure 9:

Comparison of the broad H$\alpha $and [O III] line fluxes for 17 RG showing a broad emission line component (we excluded 3C 273 since it lacks the [O III] flux). The solid line represents the locus of galaxies with $F_{{\rm H\alpha (broad})}$ = 8  $F_{\rm[O~III]}$. The dotted lines show the effect of varying this ratio by a factor 4. The outlier is 3C 234, whose broad lines are due to scattered light.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{13290f10.epsi}\includegraphics[angle=90,width=8cm,clip]{13290f11.epsi} \end{figure} Figure 10:

Comparison of the radio luminosity at 178 MHz versus the magnitude in H band of the host galaxy for the various sub-populations of 3CR sources. Left panel: 3CR sources divided into FR I (green diamonds) and FR II (pink stars); right panel: comparison between HEG (blue circles) and LEG (FR I = crossed red squares, LEG FR II = filled red squares, LEG of uncertain FR type = empty red squares). The solid line marks the separation between FR I (below the line) and FR II (above the line) according to Ledlow & Owen (1996).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{13290f12.epsi} \end{figure} Figure 11:

Comparison of [O III] line luminosity (in erg s-1) and H band host magnitude for 3CR sources. Symbols are as in the right panel of Fig. 10, i.e. HEG = blue circles, LEG = red squares (filled for FR II, crossed for FR I, empty for uncertain FR type. The right axis reports the ionizing luminosity (in erg s-1) while the upper axis reports the estimated black hole mass in solar units. The solid and dashed lines correspond to $L_{\rm ion} = 0.1 \cdot ~ L_{\rm Edd}$ and $0.001 \cdot ~ L_{{\rm Edd}}$, respectively.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.