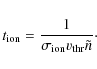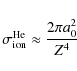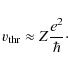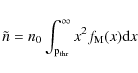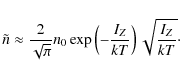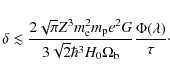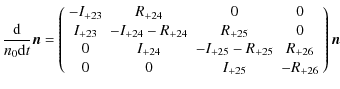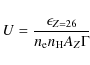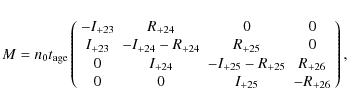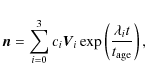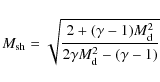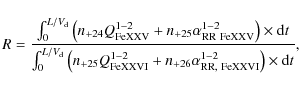EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 509 (January 2010) A&A, 509 (2010) A29 Full HTML
Free Access
Issue
A&A
Volume 509, January 2010
Article Number A29
Number of page(s) 6
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/200913195
Published online 14 January 2010
A&A 509, A29 (2010)

Non-equilibrium ionization states in galaxy clusters

D. A. Prokhorov1,2,3

1 - UPMC Université Paris 06, UMR 7095, Institut d'Astrophysique de Paris, 75014 Paris, France
2 - CNRS, UMR 7095, Institut d'Astrophysique de Paris, 75014 Paris, France
3 - Korea Astronomy and Space Science Institute, 61-1 Hwaam-dong, Yuseong-gu, Daejeon 305-348, Korea

Received 28 August 2009 / Accepted 28 October 2009

Abstract
Context. X-ray imaging observatories have revealed hydrodynamic structures with linear scales of $\sim$10 kpc in clusters of galaxies, such as shock waves in the 1E0657-56 and A520 galaxy clusters and the hot plasma bubble in the MKW 3s cluster. The future X-ray observatory IXO will for the first time resolve the metal distribution in galaxy clusters at the these scales.
Aims. Heating of plasmas by shocks and AGN activities can result in non-equilibrium ionization states of metal ions. We study the effect of the non-equilibrium ionization at linear scales of $\lesssim$50 kpc in galaxy clusters.
Methods. A condition for non-equilibrium ionization is derived by comparing the ionization time-scale with the age of hydrodynamic structures. Modeling of non-equilibrium ionization is performed at a point in time when the plasma temperature suddenly changes. An analysis of the relaxation processes of the FeXXV and FeXXVI ions by means of eigenvectors of the transition matrix is given.
Results. We conclude that the non-equilibrium ionization of iron can occur in galaxy clusters if the baryonic overdensity $\delta$ is smaller than $11.0/\tau$, where $\tau\ll1$ is the ratio of the hydrodynamic structure age to the Hubble time. Our modeling indicates that the emissivity in the helium-like emission lines of iron increases as a result of the deviation from the ionization equilibrium. A slow process of helium-like ionic fraction relaxation was analyzed. A new way to determine a shock velocity is proposed.

Key words: galaxies: clusters: general - atomic processes - shock waves

1 Introduction

Clusters of galaxies are gravitationally bound structures of a mass of $\sim$ $10^{14}{-}10^{15}~M_{\odot}$ and a size of $\sim$1-3 Mpc (for a review, see Kaastra et al. 2008). Their mass budget consists of dark matter ($\simeq$80%), hot diffuse intracluster plasma ($\lesssim$20%) and a small fraction of other components such as stars and dust. The mean baryonic overdensity in galaxy clusters equals $\delta=n_{{\rm H}}/\bar{n}_{{\rm H}}\simeq 200$, where $n_{{\rm H}}$ and $\bar{n}_{{\rm H}}$ are the mean hydrogen densities in galaxy clusters and in the Universe, respectively.

Many chemical elements reside in galaxy clusters. The plasma temperatures $kT \simeq 3{-}10$ keV in galaxy clusters are close to the values of the K-shell ionization potentials of heavy elements ( IZ=Z2 Ry, where Z is the atomic number and Ry the Rydberg constant). Emission lines from heavy elements were detected by X-ray telescopes in galaxy clusters. The current instruments (XMM-Newton, Chandra, and Suzaku) have largely enhanced our knowledge on the chemical abundances of many elements. The metal abundances of around 0.3 Solar Units in Anders & Grevesse (1989) were derived under the assumptions of a collisional ionization equilibrium (for a review, see Werner et al. 2008).

Non-equilibrium processes such as non-equilibrium ionization and relaxation of the ion and electron temperatures are usually taken into account only in the outskirts of galaxy clusters and in the warm-hot intergalactic medium (WHIM) where the baryonic overdensity $\delta$ is less than 200 (e.g. Yoshikawa & Sasaki 2006; Prokhorov 2008). However, we show that non-equilibrium ionization can also be produced as the result of merging processes and AGN activity in galaxy clusters where the baryonic overdensity $\delta \gtrsim 1000$.

Evidences for merging processes of galaxy clusters and AGN activity, such as shocks and hot plasma bubbles, were revealed by means of Chandra high-resolution observations. For example, strong shocks in the 1E0657-56 and A520 galaxy clusters propagating with a velocity of 4700 km s-1 and 2300 km s-1, respectively, were derived by Markevitch et al. (2002) and Markevitch et al. (2005). The corresponding Mach numbers of the shocks are 3.0 and 2.1. Hot plasmas inside bubbles arising from AGN activity were detected in galaxy clusters (e.g. Mazzotta et al. 2002). Heating of plasmas produced by shocks or AGNs can result in a non-equilibrium ionization state.

We study the effect of non-equilibrium ionization near merger shock fronts and in hot plasma bubbles. We give a theoretical analysis of collisional non-equilibrium ionization in Sect. 2. We show the importance of this effect in galaxy clusters numerically in Sect. 3. We analyze helium-like and hydrogen-like non-equilibrium ionization states by means of eigenvectors of the transition matrix in Sect. 4. A new approach to determine the value of the shock velocity is considered in Sect. 5, and our results are discussed in Sect. 6.

2 A condition for non-equilibrium ionization

Non-equilibrium ionization is often assumed in supernova remnants (e.g. Gronenschild & Mewe 1982; Masai 1994) and may be important in the WHIM (Yoshikawa & Sasaki 2006). The non-equilibrium ionization state in the linked region between the Abell 399 and Abell 401 clusters was also studied by Akahori & Yoshikawa (2008). We are going to show that non-equilibrium ionization can occur not only in the outskirts of galaxy clusters but also inside galaxy clusters, in which merging processes and AGN activity play a role. We derive here a condition on the baryonic overdensity for a deviation from collisional ionization equilibrium, by comparing the ionization time-scale with the age of hydrodynamic structures.

The number of collisions between electrons and an ion resulting in electron impact ionization per unit time is $\nu=\sigma_{{\rm ion}} v_{{\rm thr}} \tilde{n}$, where $\sigma_{{\rm ion}}$ is the characteristic value of the ionization cross-section, $v_{{\rm thr}}$ corresponds to the threshold velocity (energy) of the ionization process, and $\tilde{n}$ is the number density of electrons which have sufficient energy for electron impact ionization. The ionization time-scale is given by $t_{{\rm ion}}=1/\nu$, and therefore

\begin{displaymath}% t_{{\rm ion}}=\frac{1}{\sigma_{{\rm ion}} v_{{\rm thr}} \tilde{n}}\cdot \end{displaymath} (1)

As was noted by Yoshikawa & Sasaki (2006) and Akahori & Yoshikawa (2008), helium-like and hydrogen-like ions are interesting for the analysis of non-equilibrium ionization. Therefore, electron impact ionization of a helium-like ion will be considered in this section as a physically important case (a consideration of hydrogen-like ions is analogous).

For helium-like ions the characteristic value of the ionization cross-section is approximately (see Bazylev & Chibisov 1981)

\begin{displaymath}% \sigma^{{\rm He}}_{{\rm ion}}\approx\frac{2 \pi a^2_{{\rm0}}}{Z^4} \end{displaymath} (2)

where $a_{{\rm0}}=\hbar^2/m_{{\rm e}} e^2$ is the Bohr radius, Z is the atomic number.

Since the ionization potential of a He-like ion is approximately $I_{Z}\approx Z^2 m_{{\rm e}} e^4 \hbar^{-2}/2$[*], the electron threshold velocity $v_{{\rm thr}}=\sqrt{2 I_{{\rm Z}}/m_{{\rm e}}}$ can be approximated as

\begin{displaymath}v_{{\rm thr}}\approx Z \frac{e^2}{\hbar}\cdot \end{displaymath} (3)

The number density of electrons with energies higher than the ionization potential of a He-like ion is

\begin{displaymath}\tilde{n}= n_{0} \int^{\infty}_{{\rm p_{{\rm thr}}}} x^2 f_{{\rm M}}(x) {\rm d}x \end{displaymath} (4)

where n0 is the plasma number density, $p_{{\rm thr}}=\sqrt{2 I_{{\rm Z}}/kT}$ is the dimensionless threshold momentum and $f_{{\rm M}}(x)=\sqrt{2/\pi}\times\exp\left(-x^2/2\right)$ is the Maxwellian distribution.

If the dimensionless threshold momentum $p_{{\rm thr}}\gtrsim 1$, a simplified form of Eq. (4) is given by

\begin{displaymath}\tilde{n}\approx \frac{2}{\sqrt{\pi}} n_{0} \exp\left(-\frac{I_{{Z}}}{kT}\right) \sqrt{\frac{I_{{Z}}}{kT}}\cdot \end{displaymath} (5)

Using Eqs. (2), (3) and (5) we rewrite Eq. (1) as

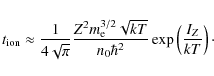
\begin{displaymath}t_{{\rm ion}}\approx \frac{1}{4\sqrt{\pi}} \frac{Z^2 m^{3/2}_... ...{kT}}{n_{0} \hbar^2} \exp\left(\frac{I_{ {Z}}}{kT}\right)\cdot \end{displaymath} (6)

It is most convenient to write the plasma number density in terms of the baryonic overdensity $n_{{\rm0}}=\delta \Omega_{{\rm b}} \rho_{{\rm crit}}/m_{{\rm p}}$, where the critical density is $\rho_{{\rm crit}}=3H^2_{{\rm0}}/(8\pi G)$, and to denote the ratio of the thermal energy kT and the ionization potential by $\lambda=kT/I_{{\rm Z}}$. Thus,

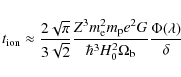
\begin{displaymath}% t_{{\rm ion}}\approx \frac{2\sqrt{\pi}}{3\sqrt{2}} \frac{Z^... ...3 H^{2}_{{\rm0}}\Omega_{{\rm b}}} \frac{\Phi(\lambda)}{\delta} \end{displaymath} (7)

where $\Phi(\lambda)=\sqrt{\lambda}\exp\left(1/\lambda\right)$.

Ionization states will be non-equilibrium if the ionization time-scale $t_{{\rm ion}}$ is longer than the hydrodynamic structure age $t = \tau H^{-1}_{{\rm0}}$, i.e. $t_{{\rm ion}} > \tau H^{-1}_{0}$. This condition is equivalent to the inequality

\begin{displaymath}\delta \lesssim \frac{2\sqrt{\pi} Z^3 m^{2}_{{\rm e}} m_{{\rm... ...^3 H_{{\rm0}}\Omega_{{\rm b}}} \frac{\Phi(\lambda)}{\tau}\cdot \end{displaymath} (8)

In an important case of the iron ions (Z = 26), the numerical value of the first dimensionless term on the right-hand side of Eq. (8) is

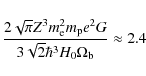
\begin{displaymath}\frac{2\sqrt{\pi} Z^3 m^{2}_{{\rm e}} m_{{\rm p}} e^2 G}{3\sqrt{2} \hbar^3 H_{{\rm0}}\Omega_{{\rm b}}}\approx 2.4 \end{displaymath} (9)

and, therefore,

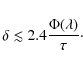
\begin{displaymath}\delta \lesssim 2.4 \frac{\Phi(\lambda)}{\tau}\cdot \end{displaymath} (10)

In rich galaxy clusters with a plasma temperature of $kT_{{\rm pl}}\approx 5$ keV, the value of the function $\Phi(kT_{{\rm pl}}/I_{{\rm Z}})$ is $\approx$4.6. Therefore we find in this case  $\delta \lesssim 11.0/\tau$ and conclude that, if the hydrodynamic structure age is on the order of 107-108years (i.e. $\tau$ lies in the range $6.6 \times 10^{-4} < \tau < 6.6 \times10^{-3}$), then non-equilibrium ionization occurs in galaxy clusters where the baryonic overdensity $\delta \approx 1000$ (see Eq. (8)).

Mazzotta et al. (2002) have estimated the age of a hot plasma bubble of a diameter of $\sim$50 kpc to be $t \approx 2.7 \times 10^7$ yr, which is much shorter than the age of the MKW 3s cluster. In the 1E0657-56 and A520 clusters the downstream velocities of the shocked gas flowing away from the shock are 1600 km s-1 and 1000 km s-1 (Markevitch et al. 2002, 2005), therefore the shocked gas covers a distance of 50 kpc in $3.1\times10^7$ and $4.7\times10^7$ yrs respectively. Thus, in light of the above conclusion non-equilibrium ionization can occur at linear scales of $\lesssim$50 kpc in galaxy clusters in which merging processes and AGN activity is present.

3 Modeling of non-equilibrium ionization

Non-equilibrium ionization occurs when the physical conditions of the plasma, such as the temperature, suddenly change. Shocks, for example, can lead to an almost instantaneous rise in temperature and to a deviation from the ionization equilibrium. However, it takes some time for the plasma to respond to an instantaneous temperature change, as the ionization balance is recovered by collisions.

In this section we consider the following situation: the plasma temperature instantaneously increases from kT1=3.4 keV to kT2=10.0 keV. Such a temperature change may correspond to a temperature jump at a shock with a Mach number M=2.6 or to plasma heating by AGN activity. We assume that the age of the hot plasma region is $3 \times 10^{7}$ yr and the baryonic overdensity is $\delta=4000$, which corresponds to the plasma number density in the post-shock region in the A520 cluster (see Fig. 2b of Markevitch et al. 2005). Following Markevitch (2006) we assume that the electron and ion temperatures are equal.

\begin{figure} \par\includegraphics[angle=0,width=8cm,clip]{13195fg1.eps} \end{figure} Figure 1:

Dependence of the He-like (solid line) and H-like (dashed line) ionic fractions of iron on the dimensionless time $t/(3\times 10^7$ yr).

Open with DEXTER

At the temperature kT1=3.4 keV the ionic fractions of Li-like, He-like and H-like ions of Fe relative to the total Fe abundance are $\approx$$12\%$, $\approx$$77\%$, and $\approx$$9\%$ respectively. Therefore we consider below four iron-ion-states Fe(+23), Fe(+24), Fe(+25) and Fe(+26). In that case the collisional ionization rate equation for each element is written as

$\displaystyle \frac{\rm d}{n_{0}{\rm d}t}\vec{n}= \left( \begin{array}{cccc} -I... ...+25}-R_{+25} & R_{+26}\\ 0 & 0 & I_{+25} & -R_{+26} \end{array}\right) \vec{n}$   (11)

where $\vec{n}$ is the vector with four components (n+23, n+24, n+25, n+26), normalized in a way that $\sum^{26}_{i =23} n_{+ i } =1$, which corresponds to the four iron-ion-states mentioned above, I+ z and R+ z represent the rate coefficients for ionization and recombination from an ion of charge z to charges z+1 and z-1, respectively. All the coefficients necessary to calculate the direct ionization cross sections are taken from Arnaud & Rothenflug (1985), the radiative recombination rates are taken from Verner & Ferland (1996), and the dielectronic recombination rates are taken from Mazzotta et al. (1998). To solve the system of Eq. (11), we use the fourth order Runge-Kutta method.

The time-dependence of the He-like and H-like ionic fractions of iron is shown in Fig. 1.

At the temperature kT2=10.0 keV the equilibrium ionic fractions of He-like and H-like ions of iron are $\approx$$27\%$ and $\approx$$45\%$ respectively. Therefore, the He-like ionic fraction, which equals 35% at a time of $3 \times 10^{7}$ yr, does not reach its equilibrium value and non-equilibrium ionization occurs. However, the H-like ionic fraction almost reaches its equilibrium value at a time of $3 \times 10^{7}$ yr.

We now show that the effect of non-equilibrium ionization on the helium-like emission lines of iron can be significant and that non-equilibrium ionization leads to the increase of volume emissivity in the helium-like spectral lines.

The helium-like volume emissivity for a chemical element of atomic number Z is given by

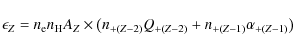
\begin{displaymath}\epsilon_{ {Z}}=n_{{\rm e}} n_{{\rm H}} A_{ {Z}}\times\left(n... ...{(Z-2)}} Q_{ {+(Z-2)}}+n_{+( {Z-1})} \alpha_{ {+(Z-1)}}\right) \end{displaymath} (12)

where $n_{{\rm e}}$ is the electron number density, $n_{{\rm H}}$ is the hydrogen number density, AZ is the abundance of the considered chemical element, n+( Z-2)and n+( Z-1) are the ionic fractions of helium-like and hydrogen-like ions respectively, Q +(Z-2) is the impact excitation rate coefficient and $\alpha_{ {+(Z-1)}}$ is the rate coefficient for the contribution from radiative recombination to the spectral lines. Excitation rate coefficients are taken from Prokhorov et al. (2009). Let us note the reduced volume emissivity in the iron helium-like emission lines as

\begin{displaymath}U=\frac{\epsilon_{ {Z=26}}}{n_{{\rm e}} n_{{\rm H}} A_{ {Z}} \Gamma} \end{displaymath} (13)

where $\Gamma=Z^{-4} \pi a^2_{0} \sqrt{I_{ {Z}}/m_{{\rm e}}}$ corresponds to the characteristic rate coefficient value (see also Prokhorov et al. 2009).

In Fig. 2 the reduced emissivity U, when the ionic fractions are in ionization equilibrium, is shown in the range of temperatures between 3.5 keV and 11 keV.

\begin{figure} \par\includegraphics[angle=0,width=8cm]{13195fg2.eps} \end{figure} Figure 2:

Dependence of the equilibrium-reduced iron volume emissivity in the helium-like lines on the plasma temperature.

Open with DEXTER

In the situation considered above we find that at temperatures of kT1=3.4 keV and kT2=10.0 keV the equilibrium values of the reduced volume emissivities are approximately equal. However, in the presence of non-equilibrium processes, the approximate equality of these volume emissivities does not remain the same. Since the fraction of electrons with an energy higher than the impact excitation threshold $E_{{\rm ex}}\approx 6.7$ keV is $27\%$ at the temperature kT1=3.4 keV and is in turn much less than 72% at a temperature of kT2=10.0 keV, the more effective impact excitation should be at a temperature of kT2=10.0 keV. Furthermore, the non-equilibrium ionic fraction of helium-like iron in the region of a temperature of kT2=10.0 keV is higher than the equilibrium ionic fraction (see Fig. 1) and, therefore, non-equilibrium ionization leads to an increase of the volume emissivity in the helium-like spectral lines.

Using the dependence of the ionic fractions of iron on the dimensionless time $t/(3\times 10^7$ yr) (see Eq. (11)), we study the time evolution of the reduced volume emissivity in the iron helium-like emission lines. This time-evolution is shown in Fig. 3.

\begin{figure} \par\includegraphics[angle=0,width=8cm,clip]{13195fg3.eps} \end{figure} Figure 3:

Evolution of the reduced iron volume emissivity in the iron helium-like lines in the region with a temperature of 10.0 keV. The dimensionless time is given by t/( $3 \times 10^{7}$ yr).

Open with DEXTER

Since the maximal value $U_{{\rm max}}$ of the equilibrium-reduced emissivity U(T) is at the temperature $kT \approx 6$ keV and equal to $\approx$1.25 (see Fig. 2), we conclude that the non-equilibrium value of U(t) (see Fig. 3) is higher than the maximal equilibrium value $U_{{\rm max}}$ up to a time $t=2 \times 10^7$ yr (up to a dimensionless time equal to 0.65). The value $U_{{\rm eq}}$ of the equilibrium-reduced emissivity at the temperature kT= 10.0 keV equal to $\approx$0.8 is less than the non-equilibrium value of U(t) during the time interval $t=3\times10^7$ yr. Therefore, the iron abundance AZ, eq, derived from the assumption that ionization states are in equilibrium, will be higher than the correct iron abundance value AZ (see Eq. (13)), which is given by

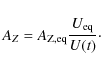
\begin{displaymath}A_{{Z}}= A_{{\rm Z, eq}} \frac{U_{{\rm eq}}}{U(t)}\cdot \end{displaymath} (14)

4 An analysis of He-like and H-like non-equilibrium ionization states by means of eigenvectors

In the previous section we showed that the ionic fraction of He-like iron ions can remain in non-equilibrium while the H-like iron ionic fraction almost achieves equilibrium. This somewhat paradoxical behavior can be more easily understood by the means of eigenvectors of the transition matrix M, which is (see Eq. (11))

\begin{displaymath}M=n_{0} t_{{\rm age}}\left(\begin{array}{cccc}-I_{+23} & R_{+... ...25} & R_{+26}\\ 0 & 0 & I_{+25} & -R_{+26}\end{array}\right), \end{displaymath} (15)

where $t_{{\rm age}}=3 \times 10^{7}$ yr is the age of the hydrodynamical structure (see Sect. 3).

Here we calculate the values of the eigenvalues of the transition matrix and the corresponding eigenvectors and show how the ionic fraction of He-like iron ions can remain in non-equilibrium longer than that of H-like iron ions.

The eigenvalues $\lambda$ of the transition matrix M are derived from the equation

\begin{displaymath}{\rm Det}(M-\lambda\times E)=0, \end{displaymath} (16)

where E is the unit matrix.

One of the eigenvalues of the transition matrix M is of the form Eq. (15) equal zero ( $\lambda_{0}=0$). Consequently, the ionization equilibrium is achieved in the end.

The solution of the system of differential equations (Eq. (11)) can be written as

\begin{displaymath}\vec{n}=\sum^{3}_{ {i=0}}c_{ {i}}\vec{V}_{ {i}} \exp\left(\frac{\lambda_{ {i}}t}{t_{{\rm age}}}\right), \end{displaymath} (17)

where c i are constants, $\vec{n}$ is the vector (n+23, n+24, n+25, n+26) and $\vec{V}_{ {i}}$are the eigenvectors of the transition matrix M.

At the temperature kT=10.0 keV we derive three eigenvalues which equal $\lambda_{1}\approx -17.80$, $\lambda_{2}\approx-3.40$ and $\lambda_{3}\approx-1.46$. Those eigenvectors which correspond to the derived eigenvalues are respectively

\begin{displaymath}\vec{V_1}=\left(\begin{array}{c} -0.66\\ 0.74\\ -0.08\\ 0.00... ...egin{array}{c}-0.03\\ -0.61\\ -0.14\\ 0.78\end{array}\right). \end{displaymath} (18)

The eigenvector which corresponds to the eigenvalue $\lambda_{0}$determines equilibrium ionic fractions at a temperature of kT=10.0 keV.

Since $\lambda_{3}$ is the smallest absolute value of the eigenvalues (excluding $\lambda_{0}$, which does not correspond to any relaxation process), the process which corresponds to the eigenvector $\vec{V_{3}}$ is the slowest (see Eq. (17)). This slow process corresponds to the increase in the FeXXVII ionic fraction due to decreases in the FeXXV and FeXXVI ionic fractions. However, the absolute value of the second component of $\vec{V_{3}}$, which corresponds to the decrease in the FeXXV ionic fraction and equals 0.61, is higher than the absolute value of the third component of $\vec{V_{3}}$, which corresponds to the decrease in the FeXXVI ionic fraction and equals 0.14. Therefore, the variation in the helium-like FeXXV ionic fraction which is proportional to the value of the second component of $\vec{V_{3}}$is more substantial during this relaxation process than the variation in the hydrogen-like FeXXVI ionic fraction.

\begin{figure} \par\includegraphics[angle=0,width=8cm]{13195fg4.eps} \end{figure} Figure 4:

Dependence of the He-like (solid line), H-like (dashed line) and fully ionized (dot-dashed line) ionic fractions of iron on the dimensionless time $t/(3\times 10^7$ yr).

Open with DEXTER

The quantitative difference between the variations in the He-like and H-like ionic fractions is illustrated in Fig. 4.

5 Mach number determination

Clusters of galaxies form via gravitational infall and mergers of smaller mass concentrations. In the course of a merger, a significant portion of the kinetic energy of the colliding subclusters, which carried by the gas, is dissipated by shocks.

The shocks in the A520 and 1E0657-06 clusters have the Mach numbers M=2-3, derived from the Rankine-Hugoniot jump-conditions (for a review, see Markevitch & Vikhlinin 2007), relating the density and temperature jumps at the shock and the Mach number, M=v/c1, where c1 is the velocity of sound in the pre-shocked gas and v is the velocity of the pre-shock gas in the reference frame of the shock. Thus, if the pre-shock and post-shock temperatures (T1 and T2, respectively) are determined from observations, the Mach number of the shock can be derived from the equation:

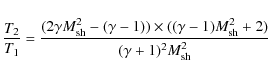
\begin{displaymath}\frac{T_{2}}{T_{1}}=\frac{(2\gamma M^2_{{\rm sh}}-(\gamma-1))\times((\gamma-1) M^2_{{\rm sh}}+2)}{(\gamma+1)^2 M^2_{{\rm sh}}} \end{displaymath} (19)

where $\gamma$ is the adiabatic index. It is usually assumed that the pre-shock velocity in the reference frame of the shock is equal to the shock velocity in the reference frame of the galaxy cluster, and that the adiabatic index is $\gamma=5/3$ (see Markevitch & Vikhlinin 2007).

The comparison of the X-ray image and the gravitational lensing mass map of the 1E0657-06 merging cluster (Clowe 2006) shows that the mass peak of the subcluster is offset from the baryonic mass peak. Clowe et al. (2006) interpret this as the first direct evidence for the existence of dark matter.

Such merging clusters offer the unique opportunity to study gas physics through direct comparison of the observed shock properties with the predictions of gas and dark matter modeling (e.g. Prokhorov & Durret 2007; Springel & Farrar 2007). In this section we provide a new way to derive shock parameters based on measurements of the flux ratio of the FeXXV and FeXXVI iron lines.

The fluxes of the FeXXV and FeXXVI lines have the same dependence on the metal abundance as on the emission measure, their ratio is independent of these parameters. This iron line ratio can therefore be used to determine the temperature of the intracluster gas (e.g. Nevalainen et al. 2003) and the presence of supra-thermal electrons (e.g. Prokhorov et al. 2009).

Taking into account both electron-impact-excitation and radiative recombination, the iron line flux ratio is given by

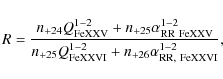
\begin{displaymath}R=\frac{n_{+24} Q^{1-2}_{{\rm FeXXV}} + n_{+25}\alpha^{1-2}_{... ...rm FeXXVI}} + n_{+26}\alpha^{1-2}_{{\rm RR},\ {\rm FeXXVI}} }, \end{displaymath} (20)

where the rate coefficients are $Q^{1-2}_{{\rm FeXXV}}=\sum\limits_{a}\sum\limits_{b (<a)} S^{1s^2-a}_{{\rm FeXXV}} B_{ab}$, $Q^{1-2}_{{\rm FeXXVI}}=\sum\limits_{a}\sum\limits_{b (<a)} S^{1s-a}_{{\rm FeXXVI}} B_{ab}$, and $S^{1s-a}_{{\rm FeXXVI}}$ are the impact-excitation rates. The excited states b correspond to the upper levels of the He-like triplet and the H-like doublet, and the radiative, branching ratios are given by,

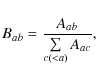
\begin{displaymath}B_{ab}=\frac{A_{ab}}{\sum\limits_{c (<a)} A_{ac}}, \end{displaymath} (21)

and $\alpha^{1-2}_{{\rm RR},\ {\rm FeXXV}}$ and $\alpha^{1-2}_{{\rm RR},\ {\rm FeXXVI}}$ are the rate coefficients for the contribution from radiative recombination to the spectral lines FeXXV (He-like triplet) and FeXXVI (H-like doublet), respectively, and $A_{\rm ac}$ are the transition probabilities.

Below we study the situation which was considered in Sects. 3 and 4. The variation of the iron line flux ratio in the region with temperature 10.0 keV as a function of dimensionless time is shown in Fig. 5.

\begin{figure} \par\includegraphics[angle=0,width=8cm]{13195fg5.eps} \end{figure} Figure 5:

Evolution of the iron line flux ratio in the region with a temperature of 10.0 keV. The dimensionless time is given by t/( $3 \times 10^{7}$ yr).

Open with DEXTER

Let the downstream velocity of the shocked gas which flows away from the shock be $V_{{\rm d}}$. Then the distance covered by the shocked gas is passed in a time t and is given by $L = V_{\rm d} t$. Therefore, if the iron line flux ratio R is known from observations at a distance L from the shock front, we can derive the value of the downstream velocity $V_{\rm d}=L/t(R)$ using the function R(t), where t(R) is the inverse function for R(t).

The Mach number of the shock and the downstream velocity are related by (e.g. Landau & Lifshitz 1959)

\begin{displaymath}M_{{\rm sh}}=\sqrt{\frac{2+(\gamma-1) M^2_{{\rm d}}}{2\gamma M^2_{{\rm d}}-(\gamma-1)}} \end{displaymath} (22)

where $M_{{\rm d}}=V_{{\rm d}}/c_{2}$ and c2 is the velocity of sound in the post-shocked gas.

On the observational side, it will be important to derive the flux ratio of the FeXXV and FeXXVI iron lines from the region between the shock front and the considered distance L which shocked gas covers in a time $t = L/V_{{\rm d}}$. Since non-equilibrium ionization can occur at a linear scale of $\lesssim$50 kpc (see Sect. 2), we choose L=25 kpc. The flux ratio of the iron lines FeXXV and FeXXVI from this region is then written as

\begin{displaymath}R=\frac{\int^{L/V_{{\rm d}}}_{0} \left(n_{+24} Q^{1-2}_{{\rm ... ...\alpha^{1-2}_{{\rm RR},\ {\rm FeXXVI}}\right)\times {\rm d}t}, \end{displaymath} (23)

using Eqs. (22) and (23), we find the Mach number Mof the shock as a function of the iron line flux ratio R. The dependence M(R) is plotted in Fig. 6.

\begin{figure} \par\includegraphics[angle=0,width=8cm,clip]{13195fg6.eps} \end{figure} Figure 6:

Dependence of the Mach number of the shock M on the iron line flux ratio R.

Open with DEXTER

Thus, we conclude that the Mach number of the shock can be derived from the iron line flux ratio. Methods based on the Rankine-Hugoniot jump conditions and on measuring the iron line flux ratio are independent for deriving the Mach number of the shock.

6 Conclusions

The currently operating X-ray imaging observatories provide us with a detailed view of the intracluster medium in galaxy clusters. Chandra's 1 $^{\prime\prime}$ angular resolution, the best among the current X-ray observatories, corresponds to linear scales of <1 kpc at z<0.05 and $\approx$4 kpc at z=0.3 (the redshift of the 1E065756 cluster). This enables us to study hydrodynamic phenomena in galaxy clusters, such as shock waves and hot plasma bubbles.

Metal observations are always limited by the number of X-ray photons. For diffuse low surface brightness objects like galaxy clusters, the effective area is a major issue, therefore in order to keep to a reasonable observation time, Chandra metal abundance maps will have lower spatial resolution than XMM-Newton (see Werner et al. 2008). IXO[*] is planned to be a follow-up mission of XMM-Newton and will have a sensitivity much higher than XMM-Newton. The expected effective area of the IXO mirror and focal plane instruments showing the large improvement at all energy levels (including the 6-7 keV band) in comparison with those of current X-ray observatories is plotted in a figure[*]. The larger effective area in the 6-7 keV band the higher the accuracy of the iron line flux measurements achieved. With IXO we will be able to resolve for the first time the metal distribution in the ICM on the scales of single galaxies in nearby clusters (simulations of metallicity maps, which will be provided by the next generation X-ray telescope are given by Kapferer et al. 2006). Therefore, the sensitivity of IXO will provide metal observations near shock fronts and in hot plasma bubbles.

We have considered in this paper the non-equilibrium ionization at linear scales of $\lesssim$50 kpc in galaxy clusters. The necessary condition on the baryonic overdensity (see Eq. (8)) for the existence of non-equilibrium ionization in regions of galaxy clusters where $\delta > 200$ holds for ions of iron. The reason for this is that the iron atomic number Z = 26 is high enough to reach the threshold value for the overdensity, which is proportional to Z3 (see Eq. (8)) and can therefore become higher than the mean cluster baryonic overdensity.

The dependence of the He-like and H-like ionic fractions of iron on time is given in Sect. 3. We found that the He-like ionic fraction of iron does not achieve its equilibrium value during the age of the hydrodynamical structures, and non-equilibrium ionization takes place.

We calculated the reduced emissivity in the He-like iron spectral lines and concluded that the iron abundance derived from the assumption that ionization states are in equilibrium, is predicted to be higher than the correct iron abundance value (see Fig. 3).

We found that the slowest relaxation process corresponds to the increase in the FeXXVII ionic fraction due to decreases in the FeXXV and FeXXVI ionic fractions. However, the decrease in the FeXXV ionic fraction is much higher than the decrease in the FeXXVI ionic fraction during this relaxation process.

A new way to derive the Mach number of a shock based on measurements of the flux ratio of the FeXXV and FeXXVI iron lines is proposed in Sect. 5. The advantage of this method over the method based on the Rankine-Hugoniot jump conditions is that ours is more accurate. Fortunately the iron line flux ratio is constrained without the effect of the hydrogen column density ( $N_{{\rm H}}$) uncertainties. In practice, the X-ray data can be fitted in a narrow band containing the FeXXV and FeXXVI lines, where the absorption is negligible (see Nevalainen et al. 2009). The drawback is that the number of photons is small in this narrow energy band, but the next-generation X-ray telescope IXO with larger effective area overcomes this drawback and will be ableto measure the flux ratio of the iron K $_{{\rm\alpha}}$ lines and, therefore, the Mach number of a shock with high precision. Using the narrow energy band instead of the full X-ray spectrum minimizes the dependence on calibration accuracy (see Nevalainen et al. 2003), therefore the FeXXV to FeXXVI lines are insensitive to the details of the effective area function compared to the continuum spectrum. Note that the method based on the Rankine-Hugoniot jump conditions uses the densities and temperatures derived from the continuum spectrum.

Another advantage of the proposed method is that it permits us to determine independently the Mach number of a shock by using measurements of the iron line flux ratio at different distances from a shock (see Sect. 5), since it takes into account an evolution of ionization states.

The effect of the apparent iron overabundance under the assumption of an ionization equilibrium and the slow process of helium-like ionic fraction relaxation should be analyzed in galaxy clusters by means of future X-ray observatories and may have implications in different astrophysical plasmas (e.g. in supernova remnants). New high-spectral-resolution instruments with higher sensitivity, such as IXO, are needed to measure the flux ratio of the iron K$\alpha$lines with the purpose of being independent in determining the shock parameters.

Acknowledgements
I am grateful to Joseph Silk, Florence Durret, Igor Chilingarian and Anthony Moraghan for valuable suggestions and discussions and thank the referee for very useful comments.

References

  1. Akahori, T., & Yoshikawa, K. 2008, PASJ, 60, L19 [NASA ADS] [CrossRef] [Google Scholar]
  2. Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
  3. Arnaud, M., & Rothenflug, R. 1985, A&ASS, 60, 425 [Google Scholar]
  4. Bazylev, V. A., & Chibisov, M. I. 1981, Sov. Phys. Usp., 4, 617 [Google Scholar]
  5. Clowe, D., Bradac, M., Gonzalez, A. H., et al. 2006, ApJ, 648, L109 [NASA ADS] [CrossRef] [Google Scholar]
  6. Gronenschild, E. H. B. M., & Mewe, R. 1982, A&ASS, 48, 305 [Google Scholar]
  7. Kaastra, J. S. 2008, Cluster of Galaxies: beyond the thermal view, SSRv (Springer) 134 [Google Scholar]
  8. Kapferer, W., Ferrari, C., Domainko, W. et al. 2006, A&A, 447, 827 [Google Scholar]
  9. Landau, L. D., & Lifshitz, E. M. 1959, Fluid Mechanics (Addison- Wesley Reading) [Google Scholar]
  10. Markevitch, M. 2006, ESA SP-604: The X-ray Universe 2005, 723 [Google Scholar]
  11. Markevitch, M, & Viklinin, A. 2007, Phys. Rep., 443, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Markevitch, M., Gonzalez, A. H., David, L., et al. 2002, ApJ, 567, L27 [NASA ADS] [CrossRef] [Google Scholar]
  13. Markevitch, M., Govoni, F., Brunetti, G., et al. 2005, ApJ, 627, 733 [NASA ADS] [CrossRef] [Google Scholar]
  14. Masai, K. 1994, ApJ, 437, 770 [NASA ADS] [CrossRef] [Google Scholar]
  15. Mazzotta, P., Mazzitelli, G., Colafrancesco, S., et al. 1998, A&AS, 133, 403 [Google Scholar]
  16. Mazzotta, P., Kaastra, J. S., Paerels, F. B. S., et al. 2002, ApJ, 567, L37 [NASA ADS] [CrossRef] [Google Scholar]
  17. Nevalainen, J., Lieu, R., Bonamente, M., et al. 2003, ApJ, 584, 716 [NASA ADS] [CrossRef] [Google Scholar]
  18. Nevalainen, J., Eckert, D., Kaastra, J., Bonamente, M., & Kettula, K. 2009, A&A, 508, 1161 [Google Scholar]
  19. Prokhorov, D. A. 2008, A&A, 492, 651 [Google Scholar]
  20. Prokhorov, D. A. 2009, A&A, 508, 69 [Google Scholar]
  21. Prokhorov, D. A., & Durret, F. 2007, A&A, 474, 375 [Google Scholar]
  22. Prokhorov, D. A., Durret, F., Dogiel, V. A., et al. 2009, A&A, 496, 25 [Google Scholar]
  23. Springel, V., & Farrar, G. R. 2007, MNRAS, 380, 911 [NASA ADS] [CrossRef] [Google Scholar]
  24. Verner, D. A., Ferland, G. J. 1996, ApJS, 103, 467 [NASA ADS] [CrossRef] [Google Scholar]
  25. Werner, N., Durret, F., Ohashi, T., et al. 2008, Space Sci. Rev., 134, 337 [NASA ADS] [CrossRef] [Google Scholar]
  26. Yoshikawa, K., & Sasaki, S. 2006, PASJ, 58, 641 [NASA ADS] [Google Scholar]

Footnotes

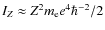
...$I_{Z}\approx Z^2 m_{{\rm e}} e^4 \hbar^{-2}/2$[*]
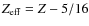The exact value of the ionized potential of a He-like ions is obtained by changing Z with $Z_{{\rm eff}}=Z-5/16$. We consider the case $Z \gg 1$ and, therefore, the approximate value is sufficient.
... IXO[*]
http://ixo.gsfc.nasa.gov/
... figure[*]
http://ixo.gsfc.nasa.gov/images/science/effective-area.jpg

All Figures

  \begin{figure} \par\includegraphics[angle=0,width=8cm,clip]{13195fg1.eps} \end{figure} Figure 1:

Dependence of the He-like (solid line) and H-like (dashed line) ionic fractions of iron on the dimensionless time $t/(3\times 10^7$ yr).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=0,width=8cm]{13195fg2.eps} \end{figure} Figure 2:

Dependence of the equilibrium-reduced iron volume emissivity in the helium-like lines on the plasma temperature.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=0,width=8cm,clip]{13195fg3.eps} \end{figure} Figure 3:

Evolution of the reduced iron volume emissivity in the iron helium-like lines in the region with a temperature of 10.0 keV. The dimensionless time is given by t/( $3 \times 10^{7}$ yr).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=0,width=8cm]{13195fg4.eps} \end{figure} Figure 4:

Dependence of the He-like (solid line), H-like (dashed line) and fully ionized (dot-dashed line) ionic fractions of iron on the dimensionless time $t/(3\times 10^7$ yr).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=0,width=8cm]{13195fg5.eps} \end{figure} Figure 5:

Evolution of the iron line flux ratio in the region with a temperature of 10.0 keV. The dimensionless time is given by t/( $3 \times 10^{7}$ yr).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=0,width=8cm,clip]{13195fg6.eps} \end{figure} Figure 6:

Dependence of the Mach number of the shock M on the iron line flux ratio R.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.