EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 509 (January 2010) A&A, 509 (2010) A81 Full HTML
Free Access
Issue
A&A
Volume 509, January 2010
Article Number A81
Number of page(s) 25
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/200913067
Published online 22 January 2010
A&A 509, A81 (2010)

Galaxy structure searches by photometric redshifts in the CFHTLS

C. Adami1 - F. Durret2,3 - C. Benoist4 - J. Coupon2,3 - A. Mazure1 - B. Meneux5 - O. Ilbert1 - J. Blaizot6 - S. Arnouts7 - A. Cappi8 - B. Garilli9 - L. Guennou1 - V. LeBrun1 - O. LeFèvre1 - S. Maurogordato4 - H. J. McCracken2,3 - Y. Mellier2,3 - E. Slezak4 - L. Tresse1 - M. P. Ulmer10

1 - LAM, OAMP, Pôle de l'Etoile Site Château-Gombert, 38 rue Frédéric Juliot-Curie, 13388 Marseille Cedex 13, France
2 - UPMC Université Paris 06, UMR 7095, Institut d'Astrophysique de Paris, 75014 Paris, France
3 - CNRS, UMR 7095, Institut d'Astrophysique de Paris, 75014 Paris, France
4 - OCA, Cassiopée, Boulevard de l'Observatoire, BP 4229, 06304 Nice Cedex 4, France
5 - MPE, Giessenbachstrasse, 85748 Garching, Germany
6 - CRAL (UMR 5574), Université Claude Bernard Lyon 1 (UCBL), École Normale Supérieure de Lyon (ENS-L), and Centre National de la Recherche Scientifique (CNRS), France
7 - Canada-France-Hawaii Telescope Corporation, Kamuela, HI-96743, USA
8 - INAF - Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
9 - INAF IASF - Milano, via Bassini 15, 20133 Milano, Italy
10 - Department Physics & Astronomy, Northwestern University, Evanston, IL 60208-2900, USA

Received 5 August 2009 / Accepted 20 October 2009

Abstract
Context. Counting clusters is one of the methods to constrain cosmological parameters, but has been limited up to now both by the redshift range and by the relatively small sizes of the homogeneously surveyed areas.
Aims. In order to enlarge publicly available optical cluster catalogs, in particular at high redshift, we have performed a systematic search for clusters of galaxies in the Canada France Hawaii Telescope Legacy Survey (CFHTLS).
Methods. We considered the deep 2, 3 and 4 CFHTLS Deep fields (each 1 $\times $ 1 deg2), as well as the wide 1, 3 and 4 CFHTLS Wide fields. We used the Le Phare photometric redshifts for the galaxies detected in these fields with magnitude limits of i'=25 and 23 for the Deep and Wide fields respectively. We then constructed galaxy density maps in photometric redshift bins of 0.1 based on an adaptive kernel technique and detected structures with SExtractor at various detection levels. In order to assess the validity of our cluster detection rates, we applied a similar procedure to galaxies in Millennium simulations. We measured the correlation function of our cluster candidates. We analyzed large scale properties and substructures, including filaments, by applying a minimal spanning tree algorithm both to our data and to the Millennium simulations.
Results. We detected 1200 candidate clusters with various masses (minimal masses between 1.0 $\times $ 1013 and 5.5 $\times $ 1013 and mean masses between 1.3 $\times $ 1014 and 12.6 $\times $ 10 $^{14}~M_\odot$) in the CFHTLS Deep and Wide fields, thus notably increasing the number of known high redshift cluster candidates. We found a correlation function for these objects comparable to that obtained for high redshift cluster surveys. We also show that the CFHTLS deep survey is able to trace the large scale structure of the universe up to $z \geq 1$. Our detections are fully consistent with those made in various CFHTLS analyses with other methods. We now need accurate mass determinations of these structures to constrain cosmological parameters.
Conclusions. We have shown that a search for galaxy clusters based on density maps built from galaxy catalogs in photometric redshift bins is successful and gives results comparable to or better than those obtained with other methods. By applying this technique to the CFHTLS survey we have increased the number of known optical high redshift cluster candidates by a large factor, an important step towards using cluster counts to measure cosmological parameters.

Key words: surveys - galaxies: clusters: general - large-scale structure of Universe

1 Introduction

The beginning of the 21st century is an exciting period for cosmological studies. Several methods now supply the means to put strong constraints on cosmological parameters. We can for example reconstruct Hubble diagrams (supernovae or tomography) or use directly the primordial fluctuation spectrum. In addition, the cluster count technique is probably the oldest one (see e.g. Gioia et al. 1990). Up to now this technique was penalized by the redshift range of detected clusters, which was too low to distinguish between flat and open universes. Distant cluster surveys have also been mainly conducted in areas too small or with inhomogeneous selection functions. Besides cluster mass knowledge, this technique requires indeed large fields of view of several dozen square degrees to provide large numbers of cluster detections at $z \geq 1$ (e.g. Romer et al. 2001). Recent X-ray cluster surveys are beginning to produce cluster catalogs at high z (e.g. the XMM-LSS survey, Pierre et al. 2007) and it is the goal of the present paper to contribute to the production of similar large cluster catalogs based on optical Canada France Hawaii Telescope Legacy Survey data.

The Canada-France-Hawaii Telescope Legacy Deep and Wide Surveys (CFHTLS-D and CFHTLS-W) respectively explore solid angles of 4 deg2 and 171 deg2 of the deep Universe, each in 4 independent patches (http://www.cfht.hawaii.edu/Science/CFHLS/). For both surveys, observations are carried out in five filters ( u*,g',r',i' and z'), providing catalogs of sources that are 80% complete up to $i_{\rm AB}$ = 26.0 (CFHTLS-D) and $i_{\rm AB}$ = 24.0 (CFHTLS-W) (Mellier et al. 2008, http://terapix.iap.fr/cplt/oldSite/Descart/CFHTLS-T0005-Release.pdf). The CFHTLS-W, in particular, encloses a sample of about 20 $\times $ 106 galaxies inside a volume size of ${\sim}1$ Gpc3, with a median redshift of $z \sim 0.92$ (Coupon et al. 2009). According to the standard cosmological model, the CFHTLS-W (W1, W2, W3, and W4 herafter) is then expected to contain 1000 to 5000 clusters of galaxies with accurate photometric redshifts, most of them in the 0.6<z<1.5 range. Likewise, the CFHTLS-D (D1, D2, D3, and D4 hereafter) should contain 50 to 200 clusters, with a significant fraction at higher redshift than the CFHTLS-W. The two surveys are therefore complementary data sets. Together, they can produce two homogeneous optically selected samples of clusters of galaxies that can be reliably compared and used jointly to explore the mass function, the abundance of clusters of galaxies and the evolution of cluster galaxy populations as a function of lookback time.

The construction of homogeneous catalogs of optically selected clusters of galaxies is not a simple task. Early searches for clusters of galaxies in the CFHTLS were performed by Olsen et al. (2007) based on a matched filter detection algorithm applied to the Deep fields (see also the recent paper by Grove et al. 2009). Galaxy density maps combined with photometric redshift catalogs were considered by Mazure et al. (2007) in the D1 field. Lensing techniques were also employed to detect massive structures in the CFHTLS (e.g. Cabanac et al. 2007; Gavazzi & Soucail 2007; Bergé et al. 2008). Other cluster studies based on the CFHTLS data (e.g. the CFHTLS-CARS survey: Erben et al. 2009; Hildebrandt et al. 2009) and based partly on the red sequence in the color magnitude diagram are also in progress. For example, Thanjavur et al. (2009) have very recently presented cluster catalogs for 161 deg2 of CFHTLS Wide data based upon a three filter (gri) colour plus position overdensity search.

We present here a systematic search for galaxy clusters in the D2, D3 and D4 Deep fields (the D1 field was already analyzed by Mazure et al. 2007) as well as in the regions of the W1, W3 and W4 Wide fields available in the T0004 release. Our approach is based on photometric redshifts computed for all the galaxies extracted in each field (Coupon et al. 2009). In this way, we take into account the full color information and not only two bands, as is done for example in red sequence searches. We divided the galaxy catalogs in slices of 0.1 in redshift, each slice overlapping the previous one by 0.05, and built density maps for each redshift slice. Structures in these density maps were then detected with the SExtractor software in the different redshift bins. We applied the same method to similar size mock samples built from the Millennium simulation, in order to estimate the reliability of our detections. We measured the clustering properties of our catalog. We then analyzed substructuring and filamentary large scale properties by applying a minimum spanning tree algorithm both to our data and to the Millennium simulation.

In this paper we assume H0 = 70 km s-1 Mpc-1, $\Omega_{\rm m}$ = 0.3, $\Omega_{\Lambda}$ = 0.7. All coordinates are given at the J2000 equinox, and magnitudes are given in the AB system.

2 Searching for clusters in the CFHTLS

A full description of the method applied to the D1 field is given in Mazure et al. (2007), and we adopt the same method here, which is briefly summarized below. We will not repeat the D1 analysis because the D1 photometric redshifts in Mazure et al. (2007) show a very similar quality compared to the present data. D1 cluster detections will only be considered for an internal crosscheck with the W1 detections of the present paper.

2.1 Photometric redshifts

We used the public photometric redshift catalogs from the CFHTLS data release T0004 (available at http://terapix.iap.fr/) in the D2, D3, D4, W1, W3 and W4 fields. The regions we selected inside the wide fields and present in T0004 are mosaics of 19, 4 and 11 Megacam fields for W1, W3 and W4 respectively. In order to avoid incompleteness effects and strong systematic biases in photometric redshift computations, the catalogs were limited to i'=25 and 23 for the Deep and Wide fields respectively. This is slightly deeper than the recommended cuts of Coupon et al. (2009) but proved to not be a problem in our analysis.

Our approach is based on photometric redshifts, which can be estimated with good precision up to $z\sim 1.5$ (Coupon et al. 2009) thanks to the optimal wavelength coverage achieved by the u*g'r'i'z' CFHTLS data. Photometric redshifts were computed for all the objects in the CFHTLS galaxy catalogs with the Le Phare software developed by Arnouts & Ilbert (Ilbert et al. 2006; also see http://www.ifa.hawaii.edu/ ilbert/these.pdf.gz, pages 50 and 142). Details of this computation are given in Mellier et al. (2008). Briefly, these photometric redshifts were computed with a large set of templates, covering a broad domain in parameter space (see Coupon et al. 2009, for a full description of the method and sample). Spectroscopic redshifts from the VVDS (e.g. LeFèvre et al. 2004) were used to optimize the photometric redshift estimates. This step is extensively described by Coupon et al. (2009), and the process consists in shifting the magnitude zero points until the difference between photometric and spectroscopic redshifts is minimized. These shifts were all lower than 0.1 mag, see Table 2 of Coupon et al. (2009). The resulting statistical errors (including the 1+z dependence) on the photometric redshifts are also given in Coupon et al. (2009). They continuously increase in the W1 field (between i'=20.5 and i'=24) for example from 0.025 to 0.053. At our limiting magnitude of i'=23, the redshift statistical error is 0.043. Deep fields have nearly constant redshift statistical errors on the order of 0.026 (maximum is 0.028) for i' magnitudes between 20.5 and 24.

We selected galaxies with photometric redshifts included in the range $0 \le z \le 1.5$ for the Deep fields and $0 \le z \le 1.2$ for the Wide fields.

For each CFHTLS field and subfield, we give the numbers of galaxies taken into account in Table 1. This table will be useful for comparisons with future data releases.

Table 1:   Number of galaxies in each CFHTLS field and subfield we studied.

2.2 Density maps

In order to obtain results directly comparable with those previously obtained by Mazure et al. (2007), we applied the same procedure as they. For each field, galaxy catalogs were built in running slices of 0.1 in redshift (see also Mazure et al. 2007), displaced by 0.05 (i.e. the first slice covers redshifts 0.0 to 0.1, the second 0.05 to 0.15 etc.). We assumed the most likely photometric redshift for each object in order to assign it to a redshift slice. Density maps were then computed for each redshift slice, based on an adaptative kernel technique described in Mazure et al. (2007). The highest redshift slices were 1.30-1.40 and 1.35-1.50 for the Deep fields and 1.05-1.15 for the Wide fields. An example of the density map obtained is displayed in Fig. 1.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13067fg1.ps} \end{figure} Figure 1:

Density maps for the D2 field for the z=0.65-0.75 redshift bin. Two clusters are detected at $S/N \geq 6$.

Open with DEXTER

The SExtractor software (Bertin & Arnouts 1996) was then applied to the galaxy density maps to detect structures at pre-defined significance levels (called hereafter S/N) of $2\sigma_{\rm S}$, $3\sigma_{\rm S}$, $4\sigma_{\rm S}$, $5\sigma_{\rm S}$ and $6\sigma_{\rm S}$ (where  $\sigma_{\rm S}$ is the SExtractor detection threshold).

The structures were then assembled in larger structures (called $\it detections$ in the following) using a friends-of-friends algorithm, as in Mazure et al. (2007). We assigned to a  $\it detection$ the redshift of its highest S/N component.

We had run several experimentations for the Mazure et al. (2007) preliminary work and found that the 0.1 redshift width of most of the studied slices was the best compromise between the redshift resolution and the possible dilution in the density signal due to photometric redshift uncertainties. We chose to keep the slice width larger than the maximal photometric redshift 1$\sigma$ uncertainty. For the Wide fields, assuming the worst possible photometric redshift statistical error of 0.043 $\times $ (1+z) (for i'=23, see Coupon et al. 2009) leads to a 1$\sigma$ error of 0.09 at z=1.15 (upper limit in redshift for the Wide field analyses). For the Deep fields, assuming a redshift statistical error lower than 0.028 $\times $ (1+z) leads to a 1$\sigma$ error of 0.07 at z=1.5. Both values are lower than the 0.1 slice width we choose.

By definition of a Gaussian function, ${\sim}32\%$ of the objects will have a true redshift differing by more than 1$\sigma$ from the most likely photometric redshift. This means that in the worst case (at the limiting magnitude and for the higher allowed redshift bin), slightly less than 30$\%$ of the objects (the slice width is slightly lower than the 1$\sigma$ value) will be assigned to a wrong redshift slice (mostly in the immediately higher or lower redshift slices). At lower redshifts and for brighter magnitudes, the percentage of such lost objects is low and is not a concern regarding our analysis. If we are close to the study limitations, it is then likely that the lost objects will be numerous enough to still be detected as part of a structure in the adjacent slices. The friends-of-friends algorithm described earlier will therefore associate these structures shifted in redshift to their true parent structure, and will therefore not significantly penalize our analysis.

2.3 Modified Millennium catalogs

With this method we obtained catalogs of galaxy cluster candidates in the various fields for a given significance level. In order to assess our detection levels we applied the same method to a modified version of the Millennium numerical simulation (e.g. Springel et al. 2005, http://www.mpa-garching.mpg.de/galform/virgo/millennium/) as follows:

  • We started from semi-analytic galaxy catalogs obtained by applying the prescriptions of De Lucia & Blaizot (2007) to the dark-matter halo merging trees extracted from the Millennium simulation (Springel et al. 2005). The Millennium run distributes particles in a cubic box of a size of 500 h-1 Mpc. The simulation was built with a 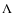$\Lambda$CDM cosmological model. For details on the semi-analytic model, we refer to De Lucia & Blaizot (2007) and references therein. Note that this model uses the Bruzual & Charlot (2003) population synthesis model and a Chabrier (2003) Initial Mass Function (IMF) to assign luminosities to model galaxies. The 1 $\times $ 1 deg2 light cones were generated with the MoMaF code (Blaizot et al. 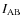2005) and are complete for an apparent magnitude of up to $I_{\rm AB}$ = 24. We used the 4 cones that had the most massive structures because they are more adequate for an investigating cluster search.

  • For each simulated galaxy, magnitude errors were computed in order to reproduce the (magnitude, magnitude error) mean relation obtained from the CFHTLS catalogs in all photometric bands. Magnitudes were then recomputed in order to reproduce the spread of the (magnitude, magnitude error) diagram assuming a gaussian distribution.

  • We took into account occultation effects of background galaxies by foreground galaxies. For a given galaxy, we searched for brighter galaxies located in the foreground which would be large enough to occult the given object (included within the disk size of the foreground galaxy as defined in the Millennium simulation). If such occulting objects were found, we removed the occulted objects from the simulation. This removed 8$\%$ of the objects of the Millennium simulation.

  • We took into account possible lensing effects which could potentially re-include occulted galaxies. In order to achieve this, we estimated the image displacement of a galaxy due to a foreground massive object. Assuming an isothermal gravitational potential for the lens galaxy, the deflexion of a background object is then given by:

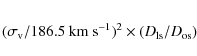
    \begin{eqnarray*}(\sigma _{\rm v} / 186.5~{\rm km~s}^{-1})^2 \times (D_{\rm ls}/D_{\rm os}) \end{eqnarray*}


    in arcsec, where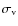 $\sigma_{\rm v}$ is the velocity dispersion of the lens, 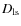$D_{\rm ls}$ the lens-source distance, and 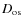 $D_{\rm os}$ the observer-source distance.

    We computed 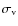$\sigma_{\rm v}$ from the values of M200 and r200 given in the Millennium simulation.

    If the deflexion amplitude was larger than the occulting object disk radius, we then re-included the lensed galaxy considered. This affected less than 1$\%$ of the Millennium simulation objects and the effect was therefore minor.

  • We added noise to the true redshift values of the Millennium simulation in order to mimic the photometric redshift distribution computed in the CFHTLS Wide and Deep fields. This means that we produced one modified Millennium simulation in order to compare with the CFHTLS Deep fields and another one to compare with the CFHTLS Wide fields. The process was done simply to compute the basic gaussian 1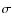$\sigma$ error of the CFHTLS photometric redshifts as a function of redshift, as a function of magnitude, and as a function of magnitude uncertainty. This produced a cubic grid of 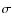$\sigma$'s with a resolution of 0.15 in redshift, 0.5 in magnitude, and 0.2 in magnitude uncertainty. This grid resolution is a good compromise between the computing time and the quality of the photometric redshifts. We then applied this grid to the true Millennium redshifts. These Millennium object redshifts were re-shuffled within a 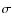$\sigma$ characterized gaussian function according to the object redshift, magnitude, and magnitude error. Figure 2 shows the resulting relations between true and photometric-like redshifts in the Millennium simulation.

    \begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067f21.ps}\vspace*{2mm} \includegraphics[angle=270,width=8cm,clip]{13067f22.ps} \end{figure} Figure 2:

    True redshift values for the modified Millennium simulation versus photometric redshifts according to the CFHTLS criteria. Upper figure: Wide parameters; lower figure: Deep parameters.

    Open with DEXTER

  • In order for the clusters detected in the Millennium simulations to be comparable to those in the Deep and Wide CFHTLS data, the catalogs of galaxies in the Millennium simulation were cut at R=25 and R=23 respectively. As previously described, galaxy catalogs were created in slices of photometric redshifts, density maps were computed, structures were identified with SExtractor, and the significance level was computed for each of them.
Several artificial galaxy concentrations in photometric redshifts appear in Fig. 2, mainly for the Wide survey characteristics. This is simply due to the characteristics of the CFHTLS data. We need to reproduce these biases in the Millenium simulations in order to properly quantify our false cluster detection rate in the CFHTLS data.

2.4 Detection rate assessments

We now need to estimate the $\it detection$ rate of our cluster detection method in the CFHTLS. This is complicated by the fact that the Millennium simulation has a very high spatial resolution compared to our galaxy density maps. This results in a multiplicity of Millennium halos which must be taken into account in a single $\it detection$ made with our technique. For a given $\it detection$, we can usually find more than one halo in the Millennium simulation. We must therefore investigate each of our $\it detections$ in the Millennium simulation (152 for the Wide parameters and 179 for the Deep parameters respectively) to check exactly how many Millennium halos can be associated.

For this purpose, and for a given $\it detection$:

  • we computed the density of Millennium halos in the $\it detection$ as a function of their mass.

  • for a given minimal mass, we compared this density to the mean density of Millennium halos included in the redshift range spanned by the $\it detection$ (and more massive than the given mass), but not spatially included in the $\it detection$.
If the ratio between these two densities was less than 0.1, we assumed that the density of halos present in a  $\it detection$ was significantly different from the mean density at the same redshift, which in turn meant that we had a significant mass concentration in our $\it detection$, i.e. our $\it detection$ was real. This means that we only kept $\it detections$ located in the highest 10$\%$ of the Millenium halo density regions. We did this exercise for several minimal Millenium halo masses (5 $\times $ 1012, 8 $\times $ 1012, 1013, 2 $\times $ 1013, 4 $\times $ 1013, and 6 $\times $ 10 $^{13}~M_\odot$). For clarity, we choose to express this with a significance parameter

\begin{eqnarray*}p = 100. \times (1. - {\rm density~ratio}) \end{eqnarray*}


A p value lower than 90$\%$ meant that a $\it detection$ is false. We considered a  $\it detection$ as real if none of the values of p (for various minimal masses) was lower than 90$\%$.

We give in Fig. 3 examples of the mass histograms of the Millennium halos present in two of our $\it detections$, one considered as a real $\it detection$ and the other considered as false.

\begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067f31.ps}\vspace*{2mm} \includegraphics[angle=270,width=8cm,clip]{13067f32.ps} \end{figure} Figure 3:

Mass histograms of the Millennium halos (Wide survey characteristics) present in a real $\it detection$ ( upper figure) and in a false $\it detection$ ( lower figure). Each figure gives the number of halos included in the $\it detection$, the total and maximal mass of these halos (in log 10 $^{10}~M_\odot$), and six significance parameters p for six different minimal masses (see text).

Open with DEXTER

Figure 4 gives the mean mass distributions of all the Millennium halos included in all our real $\it detections$ (CFHTLS Wide characteristics) as a function of mass for various $\it detection$ redshift bins.

\begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067fg4.ps} \end{figure} Figure 4:

Mass distributions of all the Millennium halos (CFHTLS Wide survey characteristics) included in real $\it detections$ as a function of mass for various $\it detection$ redshift bins.

Open with DEXTER

\begin{figure} \par\includegraphics[angle=270,width=6cm,clip]{13067f51.ps}\vspac... ...s[angle=270,width=6cm,clip]{13067f55.ps}\vspace*{2mm} \vspace*{3mm} \end{figure} Figure 5:

Percentages of all Millennium halos included in real $\it detections$for the Wide survey characteristics as a function of redshift for different mass limits.

Open with DEXTER

\begin{figure} \par\includegraphics[angle=270,width=6cm,clip]{13067f61.ps}\vspac... ...s[angle=270,width=6cm,clip]{13067f65.ps}\vspace*{2mm} \vspace*{3mm} \end{figure} Figure 6:

Percentages of all Millennium halos included in real $\it detections$for the Deep survey characteristics as a function of redshift for different mass limits.

Open with DEXTER

Considering the criterion described above, we are able to give success rates in the detection process. Figures 5 and 6 show the percentages of all Millennium halos identified with a real $\it detection$ as a function of mass.

\begin{figure} \par\includegraphics[angle=270,width=6cm,clip]{13067f71.ps}\vspac... ...s[angle=270,width=6cm,clip]{13067f75.ps}\vspace*{3mm} \vspace*{5mm} \end{figure} Figure 7:

Percentages of false $\it detections$ for the Wide survey characteristics as a function of redshift. From top to bottom: S/N of 2-6.

Open with DEXTER

\begin{figure} \par\includegraphics[angle=270,width=6cm,clip]{13067f81.ps}\vspac... ...s[angle=270,width=6cm,clip]{13067f85.ps}\vspace*{3mm} \vspace*{4mm} \end{figure} Figure 8:

Percentages of false $\it detections$ for the Deep survey characteristics as a function of redshift. From top to bottom: S/N of 2-6.

Open with DEXTER

We see that for the Wide survey we are only able to detect the Millennium halos more massive than 7.5 $\times $ 10 $^{13}~M_\odot$ with a success rate greater than $\sim$20$\%$. The detection rates become quite low at $z \geq 0.6{-}0.7$. For the Deep survey, we also detect halos more massive than 7.5 $\times $ 10 $^{13}~M_\odot$, but up to $z \geq 0.9$.

\begin{figure} \par\hspace*{1.5mm}\includegraphics[angle=270,width=7.85cm,clip]{... ...space*{3mm} \includegraphics[angle=270,width=8cm,clip]{13067f92.ps} \end{figure} Figure 9:

CFHTLS Wide-like Millennium simulation. Upper figure: shifts between true and estimated centers of the massive structures in the Millennium simulation as a function of the S/N. Open red circles with error bars are the values given in kpc, and filled black circles with error bars are the values given in arcmin. Lower figure: shifts between true and estimated redshifts of the massive structures in the Millennium simulation as a function of the S/N.

Open with DEXTER

\begin{figure} \par\hspace*{1.5mm}\includegraphics[angle=270,width=7.85cm,clip]{... ...space*{3mm} \includegraphics[angle=270,width=8cm,clip]{13067102.ps} \end{figure} Figure 10:

CFHTLS Deep-like Millennium simulation. Upper figure: shifts between true and estimated centers of the massive structures in the Millennium simulation as a function of the S/N. Open red circles with error bars are the values given in kpc, and filled black circles with error bars are the values given in arcmin. Lower figure: shifts between true and estimated redshifts of the massive structures in the Millennium simulation as a function of the S/N.

Open with DEXTER

We give in Figs. 7 and 8 the percentages of false $\it detections$ (following the criterion previously explained) as a function of S/N and redshift for the Wide and Deep surveys. For the Wide survey, false $\it detection$ rates are basically null for S/N $\geq $ 4 and remain small for S/N $\leq$ 3 and $z \leq 0.8$. For the Deep survey, false $\it detection$ rates are small whatever the S/N and for $z \leq 1$. We note however an unexpected local increase of this rate at $z \sim 0.5$ which is perhaps due to degeneracies in photometric redshift estimates producing an artificial clustering signal for example due to the discreteness of the templates.

As a compromise between true detection rate and false detection rate, we chose to not perform $\it detections$ at S/N lower than 2. We could also have limited our catalogs to S/N $\geq $ 3  $\it detections$ to have a more robust sample. However, only about 10$\%$ of the S/N = [2; 3[ $\it detections$ are false and this percentage decreases to 6$\%$ for the S/N = [3; 4[ $\it detections$. At the same time, the number of $\it detections$ is multiplied by $\sim$2.8 between S/N = [3; 4[ and S/N = [2; 3[. The number of real $\it detections$ therefore grows faster than the number of false $\it detections$. Hence, considering S/N = [2; 3[ $\it detections$allows to include numerous real clusters as well as to keep false $\it detections$ to a level lower than 10$\%$.

We now evaluate the coordinates and redshift precision of our $\it detections$. Using the Millennium simulation, we detected 97 candidate clusters at S/N = 2, 27 at S/N = 3, 16 at S/N = 4, 4 at S/N = 5, and 7 at S/N = 6, which turned out to be massive halos in the Millennium simulation. With these $\it detections$, we estimated that the typical uncertainty of the candidate cluster coordinates was smaller than $\sim$1 arcmin or $\sim$0.5 kpc and smaller than 0.025 in redshift (see Figs. 9 and 10). Several massive Millennium halos can be identified with a single $\it detection$ (see also next section). To compute the statistics given in Figs. 9 and 10, we considered the Millennium halo which is the closest to the considered $\it detection$. Error bars tend to increase with S/N. For the top figure, this can be explained by the fact that at high S/N we detect massive clusters, which are often heavily substructured which means that the definition of their center is not straightforward.

We also give a mass estimate based on the photometry. Each candidate cluster is detected at a given S/N. This detection threshold is a rough estimate of the cluster richness, being simply the net $\it flux$of the source, i.e. the number of galaxies in the source minus their background level. This criterion is not precise enough (we only took detection thresholds in steps of 1) and luminosity function based richnesses would be better tracers of the total mass of the structures. However, this criterion allows to assign a minimal mass to a detected structure. Table 2 therefore gives the relation between this detection threshold and the minimal cluster mass. We clearly see that when the detection threshold increases, the minimal mass also increases, both for the Deep and the Wide surveys.

Table 2:   Relation between the SExtractor detection threshold and the minimal and mean (over all the associated Millennium halos) cluster masses.

\begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067111.ps}\vspac... ...ncludegraphics[angle=270,width=8cm,clip]{13067112.ps}\vspace*{-2mm} \end{figure} Figure 11:

Percentage of $\it detections$ (S/N $\geq $ 2) with a ratio between the total included mass and the most massive halo mass lower than 3, as a function of total mass. Upper figure: Wide survey characteristics, lower figure: Deep survey characteristics.

Open with DEXTER

2.5 Level of substructuring

We now ask the question of the substructure level of our $\it detections$. As already explained, for a single $\it detection$ we have several attached Millennium halos most of the time. Each of these halos can be considered as a potential substructure of the $\it detection$. The question is to know what this level of substructure is. We therefore chose to compute for a given $\it detection$ the ratio of the total mass included in our $\it detection$ to the mass of the most massive Millennium halo included in the $\it detection$. We plot in Fig. 11 the percentage of $\it detections$ (S/N $\geq $ 2) for which the mass of the most massive included halo is at least 1/3 of the total mass (therefore with a low expected substructure level), as a function of the total mass. We see that halos in the Wide survey with a total mass lower than 5 $\times $ 10 $^{14}~M_\odot$ are not strongly substructured while more massive $\it detections$ are strongly substructured. In the Deep survey, the general tendency is similar.

When we investigated the potential effect of the S/N threshold on the substructure level, we did not find any significant tendency for S/N $\geq $ 3.

According to the hierarchical structure growth assumed in the Millennium simulation, we could also expect a higher level of substructures with increasing redshift. We do not detect a very clear tendency in the Millenium Wide-like catalog, but Fig. 12 (S/N $\geq $ 2) seems to show a reverse behavior for the Millenium Deep-like survey: high redshift $\it detections$ appear less substructured than nearby ones. However, this is at least partially a selection effect, explained by the fact that high redshift $\it detections$ are preferentially low mass structures, less substructured than high mass $\it detections$ by definition.

\begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067f12.ps}\vspace*{-1mm} \vspace*{-3mm} \end{figure} Figure 12:

Percentage of $\it detections$ (S/N $\geq $ 2) with a ratio between the total included mass and the most massive halo mass lower than 3, as a function of redshift for the Deep survey characteristics.

Open with DEXTER

\begin{figure} \par\hspace*{4.5mm}\includegraphics[angle=270,width=7.7cm,clip]{1... ...le=270,width=7.95cm,clip]{13067133.ps}\vspace*{-2mm} \vspace*{-3mm} \end{figure} Figure 13:

Spatial distribution of the detected structures in the three searched CFHTLS Deep fields. From top to bottom: D2, D3, and D4. The symbol sizes increase with the S/N of the $\it detection$.

Open with DEXTER

\begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067141.ps}\vspac... ...space*{2mm} \includegraphics[angle=270,width=8cm,clip]{13067143.ps} \end{figure} Figure 14:

Spatial distribution of the detected structures in the three searched CFHTLS Wide fields. From top to bottom: W1, W3, and W4. The symbol sizes increase with the S/N of the $\it detection$. Note the different sizes of the three fields, W1 being the largest one. Only W4 covers a full rectangle.

Open with DEXTER

\begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067f15.ps} \end{figure} Figure 15:

Redshift distribution of the detected structures (S/N $\geq $ 2) in the searched CFHTLS fields (thin dotted lines: Wide fields, thick continuous line: Deep fields).These histograms are not corrected for detection efficiency.

Open with DEXTER

\begin{figure} \includegraphics[angle=270,width=8cm,clip]{13067161.ps}\vspace*{2mm} \includegraphics[angle=270,width=7.9cm,clip]{13067162.ps} \end{figure} Figure 16:

Redshift distribution of the detected structures in the searched CFHTLS fields as a function of the S/N. Continuous black line: S/N = 6, dotted black line: S/N = 5, dashed green line: S/N = 4, dot-dashed blue line: S/N = 3, long-dashed blue line: S/N = 2. Upper figure: wide fields, lower figure: deep fields. These histograms are not corrected for detection efficiency.

Open with DEXTER

\begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067f17.ps} \end{figure} Figure 17:

Candidate cluster (S/N $\geq $ 2) density (per deg2) as a function of redshift. Continuous line: W1 field (computed over 15.73 deg2), dotted line: W3 field (3.24 deg2), dashed line: W4 field (8.87 deg2). Error bars are Poissonian. These curves are not corrected for detection efficiency.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{13067f18.ps} \end{figure} Figure 18:

Angular correlation function of our $\it detections$ in the W1 CFHTLS field for z = [0.4, 0.8] for S/N = 3. Error bars are Poissonian. The two straight lines are two power laws (see text).

Open with DEXTER

3 Spatial and redshift detection distributions


3.1 Detection counts

Tables A.1-A.6, give the $\it detections$ with their coordinates, redshift, and S/N for the Deep and Wide fields.

We show in Figs. 13 and 14 the spatial distributions and in Figs. 15-17 the redshift distributions of our $\it detections$.

We see in Fig. 16 a regular increase in the number of $\it detections$ as a function of S/N, in good agreement with the expected behavior of the detection method.

We see in Fig. 17 that the W4 field provides significantly fewer $\it detections$ (S/N $\geq $ 2) than W1 and W3. This is not due to a galaxy catalog incompleteness (see Coupon et al. 2009). As seen in Table 1 the numbers of galaxies per deg2 for the W1 (250 292 gal/deg2), W3 (272 147 gal/deg2), and W4 (263 685 gal/deg2) fields are similar. Coupon et al. (2009) also find slightly higher uncertainties in the W4 photometric redshift estimates, with a level of catastrophic errors $\sim$35$\%$ higher than in the W1 field. This could have an effect on the cluster detection level. However, this difference in the cluster density probably means that the W4 field is intrinsically poor in terms of structures and that this field probably does not include many massive large-scale structures due to cosmic variance.

3.2 Angular correlation function


The goal of this subsection is to consider the angular correlation of the distribution of our cluster candidates as a test of consistency of the catalog. If real, $\it detections$ should not be randomly distributed.

The spatial correlation function of clusters has been known for a long time to behave as a power-law (Bahcall & Soneira 1983; Nichol et al. 1992):

\begin{eqnarray*}\xi_{cc}(r) = (r/R_{0})^{-\gamma} \end{eqnarray*}


where the correlation length R0 depends on cluster richness and the slope is $\gamma$ $\sim$ 1.8. The angular correlation function is then also expected to show a power law behavior:

\begin{eqnarray*}\omega_{cc}(\theta) = (A_\omega (\theta))^{-\delta} \end{eqnarray*}


with $\delta = \gamma -1$.

To estimate the angular correlation of the distribution of our cluster candidates, we limited our sample to the 0.4-0.8 redshift range inside the W1 CFHTLS field in order to both take advantage of the large contiguous coverage of this field and to avoid the redshift range where the W1 field did not provide a high enough detection rate.

The angular two-point correlation function  $\omega(\theta)$ represents the excess probability for an object (here a detection) to have a neighbor located at an angular separation $\theta$ with respect to a random distribution of points (Peebles 1980).

We compute the angular correlation using the estimator of Landy & Szalay (1993):

\begin{eqnarray*}\omega(\theta)=\frac{DD(\theta) - 2DR(\theta) + RR(\theta)}{RR(\theta)} \end{eqnarray*}


where DD, RR and DR are in turn the normalised number of data-data, random-random and data-random pairs with an angular separation $\theta$ and $\theta_i\le \theta\le \theta_0 + i$ $\times $ $\Delta\theta$. We generate a random catalog of 10 000 points with the same geometry and masked as the data. Since the measurement is noisy, we consider several logarithmic binnings and zero points $\theta_0$. As a consequence, the measurement at a given angular scale is strongly correlated with the others, but the combined measurement gives us at least a qualitative trend to answer the question of whether or not our sample is randomly spatially distributed.

We do not correct our measurement for the integral constraint due to the finite size of the field (e.g. Cappi & Maurogordato 1995), as the scope of this work is not the clustering analysis itself, but the use of  $\omega(\theta)$ as a test of consistency. Our measurement is then a (moderate) underestimate of the real angular correlation function.

We estimate the uncertainty on each data point considering only Poisson errors on the data-data pairs. In the case of the Landy & Szalay estimator, they are given by:

\begin{eqnarray*}\delta\omega=\frac{1+\omega(\theta)}{\sqrt(DD(\theta))}\cdot \end{eqnarray*}


We show in Fig. 18 the combined angular 2-point correlation function in the W1 field for the S/N = 3 detection sample. We compare our measurements to two power laws conventionally defined as:

\begin{eqnarray*}\omega(\theta)=A_\omega (\theta/1^\circ)^{-\delta}. \end{eqnarray*}


The slope is fixed to $\delta=0.8$ (a reasonable approximation of the true slope) and the amplitude is arbitrarily chosen to guide the eye.

The sample of detections selected with S/N = 3 shows a clear signal at large angular scales. A power law with amplitude $A_\omega=0.025$ appears to be a good approximation on scales [0.15-1] degrees.

At small angular scales the signal is weaker and results are not significant, since they are based only on a small number of  $\it detections$, as shown by the large error bars.

This qualitative analysis shows that detections are dominated by structures showing a realistic clustering when compared to other high redshift analyses. Similar to our results, Papovich (2008) found for example an angular correlation function for his high redshift cluster sample consistent with a power-law fit over the interval [0.03, 1.7] deg. The slope of this power law was found to be 1.1 $\pm$ 0.1 in relatively good agreement with our slope of 0.8. Other works such as Bahcall et al. (2003, and references therein) or Brodwin et al. (2007) also show power-law angular correlation functions.

3.3 Tracing the large scale structure of the Universe

The Millennium simulation, among others, puts in evidence the increasing filament constrast (bridges joining massive clusters) with decreasing redshift. This is the well known hierarchical behavior of the Universe and could ultimately be used as a cosmological test, assuming that we are able to trace precisely this filamentary structure as a function of redshift. However, detecting large scale filaments is a very difficult task due to strong superposition effects and to the fact that they are only weak X-ray emitters (see e.g. the Abell 85 filament, Boué et al. 2008). We could in principle consider large scale galaxy surveys such as the CFHTLS combined with photometric redshift computations to try to detect these filaments. However, the galaxies populating these filaments can have very low masses and are therefore likely to be very faint. We must consequently assess the survey depth required to reach such a goal.

Rather than trying to detect individually the filaments present in the CFHTLS survey, we chose a statistical approach based on the Minimal Spanning Tree ($\it mst$ hereafter) technique. The $\it mst$ technique is a geometrical construction issued from the graph theory (e.g. Dussert 1988) which allows the quantitative characterization of a distribution of points (e.g. Adami & Mazure 1999). Very briefly put, it is a tree joining all the points of a given set, without any loop and with a minimal length; each point is visited by the tree only once. The main aspect here is the unity of such a construction. For a given set of points, there is more than one $\it mst$, but the histogram H of the length of the $\it mst$ edges is unique. This is fundamental because it is then possible to characterize completely a set of points with H. The details of the procedure and of the normalizations are given in Adami & Mazure (1999); we took into account the first three momenta mean, sigma and skewness of H to characterize this histogram.

\begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067f19.ps} \end{figure} Figure 19:

Variation of D as function of redshift. The continuous, dashed, dotted, and dash-dotted lines with error bars are for Millennium halos more massive than 10 $^{10}~M_\odot$, 3 $\times $ 10 $^{13}~M_\odot$, 5 $\times $ 10 $^{13}~M_\odot$, and 10 $^{14}~M_\odot$. Unconnected filled circles with error bars show the CFHTLS W1 galaxies limited to i'=23. The five horizontal blue lines correspond to the mean D value for clusters detected in the W1 field ( from top to bottom: S/N = 6, 5, 4, 3, and 2).

Open with DEXTER

\begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067f20.ps} \end{figure} Figure 20:

Variation of D as a function of redshift. The continuous, dashed, dotted, and dash-dotted lines with error bars are for Millennium halos more massive than 10 $^{10}~M_\odot$, 3 $\times $ 10 $^{13}~M_\odot$, 5 $\times $ 10 $^{13}~M_\odot$, and 10 $^{14}~M_\odot$. Unconnected filled circles with error bars show the CFHTLS D2 galaxies limited to i'=25. The four horizontal blue lines correspond to the mean D value for clusters detected in the D2 field ( from top to bottom: S/N = 5, 4, 3, and 2). S/N = 5 and 4 are overlapping.

Open with DEXTER

We chose to compute the distance D in the (mean, sigma, skewness) space between a given distribution of points and a uniform distribution for which the mean, sigma, and skewness values are well known (see Adami & Mazure 1999). The distance D is simply given by:

\begin{eqnarray*}D =\sqrt{\sum_{i=1}^n(p_i-q_i)^2} \end{eqnarray*}


with pi and qi being successively the mean, dispersion and skewness of the uniform distribution and of the considered distribution.

We computed D as a function of redshift in the Millennium simulation. Figures 19 and 20 show these variations for several halo classes: more massive than 10 $^{10}~M_\odot$ ($\sim$galaxies), more massive than 3 $\times $ 10 $^{13}~M_\odot$ ($\sim$groups of galaxies), more massive than 5 $\times $ 10 $^{13}~M_\odot$ ($\sim$major groups of galaxies), and more massive than 10 $^{14}~M_\odot$ ($\sim$clusters of galaxies). Based on these figures, a uniform distribution would be a horizontal line at minus infinity.

Firstly, our curves all decrease, meaning that the more distant the sample we consider, the closer to a uniform distribution it is. This is not surprising as the main ingredient of the Millennium simulation is a hierarchical Universe dominated by gravity.

Secondly, we plot on these figures the distance D computed with the CFHTLS galaxies in the W1 (Fig. 19) and D2 fields (Fig. 20) assuming the i'=23 and i'=25 mag limitations and the computed photometric redshifts. If the CFHTLS fields are good tracers of the large scale structure of the Universe (and if the Millennium simulation assumed the correct cosmology), distances D computed with the CFHTLS data should be included in the Millennium curve for objects more massive than 10 $^{10}~M_\odot$. We show in Figs. 19 and 20 that the CFHTLS Wide data become different from the expected Millennium behavior at $z \ge 0.5$. This means that the CFHTLS Wide survey is not able to recover properly the filamentary structure of the Universe above $z \sim 0.5$. The resulting galaxy distribution (penalized by galaxy detection incompleteness) then becomes too close to a uniform distribution. This also shows that the deep CFHTLS fields are good datasets to achieve such a goal up to z=1.25.

\begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{1306721.ps} \end{figure} Figure 21:

Variation of D as a function of redshift. The continuous and dotted lines with error bars are for Millennium halos more massive than 3 $\times $ 10 $^{13}~M_\odot$ with high and low levels of substructures. The three horizontal blue lines are the mean D value for clusters detected in the W1 field ( from top to bottom: S/N = 6, 5, and 4).

Open with DEXTER

In a third step, we add to these two figures the distances D computed for our cluster $\it detections$ and for several values of the S/N. We first note that the variation of D with redshift is not significant. We therefore chose to show only the mean value of D over the spanned redshift range (z = [0.1; 1.2] for the W1 and z = [0.1; 1.5] for the D2). We also find that the higher the S/N (hence the more massive the cluster), the more varied the cluster catalogs are from a random distribution. We finally note that the S/N $\geq $ 4 CFHTLS cluster $\it detections$ (which is to say with masses greater than 3.3 $\times $ 10 $^{13}~M_\odot$) show a different behavior than Millennium halos more massive than 3 $\times $ 10 $^{13}~M_\odot$. The Millennium halos considered are more clustered than the corresponding real clusters (in terms of mass). We now investigate the reason for such a difference.

\begin{figure} \par\hspace*{-3.5mm}\includegraphics[angle=270,width=8cm,clip]{13... ...ace*{2mm} \includegraphics[angle=270,width=7.7cm,clip]{13067222.ps} \end{figure} Figure 22:

Upper figure: center shifts in deg (blue filled circles: $z \leq 0.5$, green open circles: z=[0.5,0.8], red triangles: $z \geq 0.8$). Lower figure: histogram of redshift difference between our D1 and W1  $\it detections$ (S/N $\geq $ 2).

Open with DEXTER

Considering low mass Millennium halos implies that highly spatially correlated halos will be included in the $\it mst$ calculation. This will therefore artificially increase the D value because part of these halos are in fact subhalos of more massive structures. Our $\it detections$do not include such objects by definition. A way to exclude these highly spatially correlated sub-halos is to select only the less substructured Millennium halos. Therefore, we redid the previous exercise selecting only halos more massive than 3 $\times $ 10 $^{13}~M_\odot$ and with a substructure level lower than 20 subhalos included in the main halo. We generated Fig. 21 where we show the D value before and after considering low substructure level halos. We clearly see that removing halos with a high level of substructure makes the Millennium and CFHTLS D values compatible. This suggests that the Millennium simulation may exhibit higher than normal substructure levels in massive clusters.

4 Literature assessments of our detections

We computed in previous sections statistical assessments of our $\it detections$ based on simulations. We now try to compare our $\it detections$ with literature data, i.e. known clusters in the surveyed areas.

4.1 Internal assessment of our cluster detections

Among the searched CFHTLS fields, the W1 and D1 fields overlap (see Mazure et al. 2007), allowing us to compare $\it detections$based on Deep and Wide CFHTLS data. Wide field data exhibit lower detection rates compared to Deep fields, so we do not expect to recover in the present paper all the D1  $\it detections$ of Mazure et al. (2007). Assuming the success rates computed in the present paper via the Millennium simulations, we expect to detect 2.7 $\pm$1.4 times more clusters in the Deep D1 than in the W1 data (uncertainty from Poisson estimates). Experimentally, we detect 23 clusters in the W1 data out of the 44 detected in the D1 data by Mazure et al. (2007) with exactly the same method. The ratio is 1.9, in agreement with the expectations.

We show in Fig. 22 the position and redshift differences between the present W1 and D1  $\it detections$ of Mazure et al. (2007). The mean center shift is 0.01 $\pm$ 0.04 deg (0.6 arcmin) and the mean redshift difference is -0.002 $\pm$ 0.05. We also note that there is no significant variation in the center precision as a function of redshift. This demonstrates that we are limited by the pixel size used in the galaxy density map to define a cluster center.

4.2 External assessment of our cluster detections


As in Mazure et al. (2007), we compare our $\it detections$ with the XMM-LSS X-ray clusters published for the W1 field by Pacaud et al. (2007), limiting our comparison to the 15  $z \geq 0.1$ clusters of Pacaud et al. (2007) included in the portion of the W1 field we analysed. Ten of our $\it detections$are identified with these clusters. The remaining ones (but one) are all affected by masked areas in the optical data and we can reasonably assume that this renders their detection impossible by the present method.

We also compare our $\it detections$with the lensing searches made in the CFHTLS areas. Limousin et al. (private communication) discovered a galaxy cluster at $z \sim 0.88$ in the CFHTLS D3 field (SL2S J2214-1730) based on a strong lensing analysis. This cluster is also detected with our method (D4-7, S/N = 2) at z=0.90. A more complete list of group detections in the SL2S survey is given in Limousin et al. (2009). Among the 13 group detections of this paper, a single one (SL2S J2140-0532 at z=0.444) is included in our surveyed area (others are outside the area where photometric redshifts were computed), and we detect it at z=0.45 with S/N = 6.

We compared our $\it detections$ with the Gavazzi & Soucail (2007) cluster sample. If we limit our search to clusters with a photometric redshift in their paper (eight clusters), we redetect seven of these clusters with the present method. The last one is partially located in a masked region in our data, and this probably prevents its detection.

We finally compared our $\it detections$ with the matched filter detections of Olsen et al. (2008). Still limiting the comparison to clusters included in our surveyed area and at z $\geq $ 0.1, we detect 14 of the 16 Olsen et al. (2008) spectroscopically confirmed clusters.

These high recovery rates therefore put our detection method on a firm ground. We give in Fig. 23 the histograms of the center and redshift differences between our $\it detections$ and the clusters previously quoted in the literature. The mean center shift is 0.045 $\pm$ 0.03 deg (2.7 arcmin) and the mean redshift difference is -0.01 $\pm$ 0.08.

5 Discussion and conclusions

We have detected 1200 candidate clusters in the CFHTLS Deep and Wide fields. Statistically, more than 80$\%$ are real structures at $z \leq 1$. This is confirmed by internal and external comparisons with literature catalogs.

Table 3 gives the number and density of $\it detections$ as a function of S/N. Over an effective area of $\sim$28 deg2 (see Coupon et al. 2009) this means that we detect 19.2 candidate clusters per deg2 for mass $\geq $1.0 $\times $ 10 $^{13}~M_\odot$, 9.4 candidate clusters per deg2 for mass $\geq $1.3 $\times $ 10 $^{13}~M_\odot$, 6.1 candidate clusters per deg2 for mass $\geq $3.3 $\times $ 10 $^{13}~M_\odot$, 3.4 candidate clusters per deg2 for mass $\geq $3.5 $\times $ 10 $^{13}~M_\odot$, and 4.8 candidate clusters per deg2 for mass $\geq $5.5 $\times $ 10 $^{13}~M_\odot$. Given the typical uncertainty on detection rates, the two last candidate cluster densities are compatible. We note that these numbers are not corrected for detection efficiency. These numbers are also fully compatible with recent X-ray estimates (e.g. Pacaud et al. 2007) showing 5.8 clusters per deg2 for masses greater than 4.1 $\times $ 10 $^{13}~M_\odot$ (number scaled to our cosmology).

\begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067231.ps}\vspace*{2mm} \includegraphics[angle=270,width=8cm,clip]{13067232.ps} % \end{figure} Figure 23:

Histograms of the center shifts in degrees ( upper figure) and redshift differences ( lower figure) between our $\it detections$ (S/N $\geq $ 2) and the literature clusters quoted in the text.

Open with DEXTER

Table 3:   Number and density of detections as a function of S/N.

If we compare our results to published optically based cluster catalogs, our survey represents a major step forward (see Table 4). We have compiled a cluster catalog in the CFHTLS area most of the time deeper and larger by a factor of 10 than the ones previously published. We also basically provide the only cluster $\it detections$ at $z \geq 1$ using CFHTLS data. The comparison of our resuls with the well known MaxBCG SDSS catalog (Koester et al. 2007) provides similar numbers in terms of cluster spatial density. The present deep and wide surveys provide more than 13 000 and 10 500  $\it detections$ per Gpc3. This is comparable to the 16 735 clusters per Gpc3 of Koester et al. (2007), assuming the values of Table 4. This is also comparable to the results of Thanjavur et al. (2009) if we limit ourselves to similar lower redshifts.

Table 4:   Comparison of our cluster $\it detections$ with public CFHTLS optically based cluster catalogs and with the MaxBCG SDSS catalog.

These results illustrate the power of optical deep and wide field surveys to provide large samples of galaxy clusters. These samples could be used for pure cosmological applications (e.g. based on cluster counts, Romer et al. 2001) or more generally for the study of structures within a broad mass range. In particular, it is remarkable that our deep catalogs are among the first ones to provide numerous group $\it detections$ at redshifts greater than 1.

With these parameters, the perspectives of our work are:

  • To perform a more homogeneous comparison with matched filter detections across the Wide fields, and this will be the subject of a future paper. A by-product of this future work will be the center refinement of our candidate clusters.

  • To define a more precise optically-based mass estimator, via e.g. the galaxy luminosity functions. This requires however the previous match to have been performed.

  • To assess more precisely the detection rate for very massive clusters. The Millennium simulation as it is now does not provide a large enough number of very massive structures, which in turn leads to an unacceptably high uncertainty. This is prohibitive for any serious cosmological application based on cluster counts, since the most massive clusters are the most constraining for cosmology (e.g. Romer et al. 2001) and detection rates for these massive clusters need to be precisely evaluated. This aspect is currently under work and will also be developed in future papers.

  • Finally, the spectroscopic confirmation of the 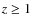$z \geq 1$ candidate clusters we have detected would be crucial for cosmology.
The cluster list will be available via the Cencos database at http://cencosw.oamp.fr/ in a near future.

Acknowledgements
The authors thank the referee for useful and constructive comments. The authors thank M. Limousin for useful discussions. We acknowledge support from the French Programme National Cosmologie, CNRS.

References

  1. Adami, C., & Mazure, A. 1999, A&AS, 134, 393 [Google Scholar]
  2. Bahcall, N. A., & Soneira, R. M. 1983, ApJ, 270, 20 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bahcall, N. A., Dong, F., Hao, L., et al. 2003, ApJ, 599, 814 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bergé, J., Pacaud, F., Réfrégier, A., et al. 2008, MNRAS, 385, 695 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [Google Scholar]
  6. Blaizot, J., Wadadekar, Y., Guiderdoni, B., et al. 2005, MNRAS, 360, 159 [NASA ADS] [CrossRef] [Google Scholar]
  7. Boué, G., Durret, F., Adami, C., et al. 2008, A&A, 489, 11 [Google Scholar]
  8. Brodwin, M., Gonzalez, A. H., Moustakas, L. A., et al. 2007, ApJ, 671, L93 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  10. Cabanac, R. A., Alard, C., Dantel-Fort, M., et al. 2007, A&A, 461, 813 [Google Scholar]
  11. Cappi, A., & Maurogordato, S. 1995, ApJ, 438, 507 [NASA ADS] [CrossRef] [Google Scholar]
  12. Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
  13. Coupon, J., Ilbert, O., Kilbinger, M., et al. 2009, A&A, 500, 981 [Google Scholar]
  14. De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [NASA ADS] [CrossRef] [Google Scholar]
  15. Dussert, C. 1988, Ph.D. Thesis, Université d'Aix-Marseille [Google Scholar]
  16. Erben, T., Hildebrandt, H., Lerchster, M., et al. 2009, A&A, 493, 1197 [Google Scholar]
  17. Gavazzi, R., & Soucail, G. 2007, A&A, 462, 459 [Google Scholar]
  18. Gioia, I. M., Henry, J. P., Maccacaro, T., et al. 1990, ApJ, 356, L35 [NASA ADS] [CrossRef] [Google Scholar]
  19. Grove, L. F., Benoist, C., & Martel, F. 2009, A&A, 494, 845 [Google Scholar]
  20. Hildebrandt, H., Pielorz, J., Erben, T., et al. 2009, A&A, 498, 725 [Google Scholar]
  21. Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [Google Scholar]
  22. Koester, B. P., McKay, T. A., Annis, J., et al. 2007, ApJ, 660, 239 [NASA ADS] [CrossRef] [Google Scholar]
  23. Landy, S. D., & Szalay, A. S. 1993, ApJ, 412, 64 [NASA ADS] [CrossRef] [Google Scholar]
  24. LeFèvre, O., Vettolani, G., Paltani, S., et al. 2004, A&A, 428, 1043 [Google Scholar]
  25. Limousin, M., Cabanac, R., Gavazzi, R., et al. 2009, A&A, 502, 445 [Google Scholar]
  26. Mazure, A., Adami, C., Pierre, M., et al. 2007, A&A, 467, 49 [Google Scholar]
  27. Mellier, Y., Bertin, E., Hudelot, P., et al. 2008, The CFHTLS T0005 Release, http://terapix.iap.fr/cplt/oldSite/Descart/CFHTLS-T0005-Release.pdf [Google Scholar]
  28. Nichol, R. C., Collins, C. A., Guzzo, L., & Lumsden, S. L. 1992, MNRAS, 255, 21 [NASA ADS] [CrossRef] [Google Scholar]
  29. Olsen, L. F., Benoist, C., Cappi, A., et al. 2007, A&A, 461, 81 [Google Scholar]
  30. Olsen, L. F., Benoist, C., Cappi, A., et al. 2008, A&A, 478, 93 [Google Scholar]
  31. Pacaud, F., Pierre, M., Adami, C., et al. 2007, MNRAS, 382, 1289 [NASA ADS] [CrossRef] [Google Scholar]
  32. Papovich, C. 2008, ApJ, 676, 206 [NASA ADS] [CrossRef] [Google Scholar]
  33. Peebles, P. J. E. 1980, The Large Scale Structure of the Universe (Princeton: Princeton University Press) [Google Scholar]
  34. Pierre, M., Chiappetti, L., Pacaud, F., et al. 2007, MNRAS, 382, 279 [NASA ADS] [CrossRef] [Google Scholar]
  35. Romer, A. K., Viana, P. T. P., Liddle, A. R., & Mann, R. G. 2001, ApJ, 547, 594 [NASA ADS] [CrossRef] [Google Scholar]
  36. Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  37. Thanjavur, K., Willis, J., & Crampton, D. 2009, ApJ, 706, 571 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Additional tables

Table A.1:   Candidate clusters detected in the D2 CFHTLS field. The first column is the cluster Id, the second and third columns are the J2000 coordinates given in decimal degrees, the fourth column is the mean redshift, and the fifth column is the SExtractor detection level.

Table A.2:   Same as Table A.1 for the D3 CFHTLS field.

Table A.3:   Same as Table A.1 for the D4 CFHTLS field.

Table A.4:   Same as Table A.1 for the W1 CFHTLS field.

Table A.5:   Same as Table A.1 for the W3 CFHTLS field.

Table A.6:   Same as Table A.1 for the W4 CFHTLS field.

Footnotes

... CFHTLS[*]
Based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l'Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS.

All Tables

Table 1:   Number of galaxies in each CFHTLS field and subfield we studied.

Table 2:   Relation between the SExtractor detection threshold and the minimal and mean (over all the associated Millennium halos) cluster masses.

Table 3:   Number and density of detections as a function of S/N.

Table 4:   Comparison of our cluster $\it detections$ with public CFHTLS optically based cluster catalogs and with the MaxBCG SDSS catalog.

Table A.1:   Candidate clusters detected in the D2 CFHTLS field. The first column is the cluster Id, the second and third columns are the J2000 coordinates given in decimal degrees, the fourth column is the mean redshift, and the fifth column is the SExtractor detection level.

Table A.2:   Same as Table A.1 for the D3 CFHTLS field.

Table A.3:   Same as Table A.1 for the D4 CFHTLS field.

Table A.4:   Same as Table A.1 for the W1 CFHTLS field.

Table A.5:   Same as Table A.1 for the W3 CFHTLS field.

Table A.6:   Same as Table A.1 for the W4 CFHTLS field.

All Figures

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13067fg1.ps} \end{figure} Figure 1:

Density maps for the D2 field for the z=0.65-0.75 redshift bin. Two clusters are detected at $S/N \geq 6$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067f21.ps}\vspace*{2mm} \includegraphics[angle=270,width=8cm,clip]{13067f22.ps} \end{figure} Figure 2:

True redshift values for the modified Millennium simulation versus photometric redshifts according to the CFHTLS criteria. Upper figure: Wide parameters; lower figure: Deep parameters.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067f31.ps}\vspace*{2mm} \includegraphics[angle=270,width=8cm,clip]{13067f32.ps} \end{figure} Figure 3:

Mass histograms of the Millennium halos (Wide survey characteristics) present in a real $\it detection$ ( upper figure) and in a false $\it detection$ ( lower figure). Each figure gives the number of halos included in the $\it detection$, the total and maximal mass of these halos (in log 10 $^{10}~M_\odot$), and six significance parameters p for six different minimal masses (see text).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067fg4.ps} \end{figure} Figure 4:

Mass distributions of all the Millennium halos (CFHTLS Wide survey characteristics) included in real $\it detections$ as a function of mass for various $\it detection$ redshift bins.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=6cm,clip]{13067f51.ps}\vspac... ...s[angle=270,width=6cm,clip]{13067f55.ps}\vspace*{2mm} \vspace*{3mm} \end{figure} Figure 5:

Percentages of all Millennium halos included in real $\it detections$for the Wide survey characteristics as a function of redshift for different mass limits.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=6cm,clip]{13067f61.ps}\vspac... ...s[angle=270,width=6cm,clip]{13067f65.ps}\vspace*{2mm} \vspace*{3mm} \end{figure} Figure 6:

Percentages of all Millennium halos included in real $\it detections$for the Deep survey characteristics as a function of redshift for different mass limits.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=6cm,clip]{13067f71.ps}\vspac... ...s[angle=270,width=6cm,clip]{13067f75.ps}\vspace*{3mm} \vspace*{5mm} \end{figure} Figure 7:

Percentages of false $\it detections$ for the Wide survey characteristics as a function of redshift. From top to bottom: S/N of 2-6.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=6cm,clip]{13067f81.ps}\vspac... ...s[angle=270,width=6cm,clip]{13067f85.ps}\vspace*{3mm} \vspace*{4mm} \end{figure} Figure 8:

Percentages of false $\it detections$ for the Deep survey characteristics as a function of redshift. From top to bottom: S/N of 2-6.

Open with DEXTER
In the text

  \begin{figure} \par\hspace*{1.5mm}\includegraphics[angle=270,width=7.85cm,clip]{... ...space*{3mm} \includegraphics[angle=270,width=8cm,clip]{13067f92.ps} \end{figure} Figure 9:

CFHTLS Wide-like Millennium simulation. Upper figure: shifts between true and estimated centers of the massive structures in the Millennium simulation as a function of the S/N. Open red circles with error bars are the values given in kpc, and filled black circles with error bars are the values given in arcmin. Lower figure: shifts between true and estimated redshifts of the massive structures in the Millennium simulation as a function of the S/N.

Open with DEXTER
In the text

  \begin{figure} \par\hspace*{1.5mm}\includegraphics[angle=270,width=7.85cm,clip]{... ...space*{3mm} \includegraphics[angle=270,width=8cm,clip]{13067102.ps} \end{figure} Figure 10:

CFHTLS Deep-like Millennium simulation. Upper figure: shifts between true and estimated centers of the massive structures in the Millennium simulation as a function of the S/N. Open red circles with error bars are the values given in kpc, and filled black circles with error bars are the values given in arcmin. Lower figure: shifts between true and estimated redshifts of the massive structures in the Millennium simulation as a function of the S/N.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067111.ps}\vspac... ...ncludegraphics[angle=270,width=8cm,clip]{13067112.ps}\vspace*{-2mm} \end{figure} Figure 11:

Percentage of $\it detections$ (S/N $\geq $ 2) with a ratio between the total included mass and the most massive halo mass lower than 3, as a function of total mass. Upper figure: Wide survey characteristics, lower figure: Deep survey characteristics.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067f12.ps}\vspace*{-1mm} \vspace*{-3mm} \end{figure} Figure 12:

Percentage of $\it detections$ (S/N $\geq $ 2) with a ratio between the total included mass and the most massive halo mass lower than 3, as a function of redshift for the Deep survey characteristics.

Open with DEXTER
In the text

  \begin{figure} \par\hspace*{4.5mm}\includegraphics[angle=270,width=7.7cm,clip]{1... ...le=270,width=7.95cm,clip]{13067133.ps}\vspace*{-2mm} \vspace*{-3mm} \end{figure} Figure 13:

Spatial distribution of the detected structures in the three searched CFHTLS Deep fields. From top to bottom: D2, D3, and D4. The symbol sizes increase with the S/N of the $\it detection$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067141.ps}\vspac... ...space*{2mm} \includegraphics[angle=270,width=8cm,clip]{13067143.ps} \end{figure} Figure 14:

Spatial distribution of the detected structures in the three searched CFHTLS Wide fields. From top to bottom: W1, W3, and W4. The symbol sizes increase with the S/N of the $\it detection$. Note the different sizes of the three fields, W1 being the largest one. Only W4 covers a full rectangle.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067f15.ps} \end{figure} Figure 15:

Redshift distribution of the detected structures (S/N $\geq $ 2) in the searched CFHTLS fields (thin dotted lines: Wide fields, thick continuous line: Deep fields).These histograms are not corrected for detection efficiency.

Open with DEXTER
In the text

  \begin{figure} \includegraphics[angle=270,width=8cm,clip]{13067161.ps}\vspace*{2mm} \includegraphics[angle=270,width=7.9cm,clip]{13067162.ps} \end{figure} Figure 16:

Redshift distribution of the detected structures in the searched CFHTLS fields as a function of the S/N. Continuous black line: S/N = 6, dotted black line: S/N = 5, dashed green line: S/N = 4, dot-dashed blue line: S/N = 3, long-dashed blue line: S/N = 2. Upper figure: wide fields, lower figure: deep fields. These histograms are not corrected for detection efficiency.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067f17.ps} \end{figure} Figure 17:

Candidate cluster (S/N $\geq $ 2) density (per deg2) as a function of redshift. Continuous line: W1 field (computed over 15.73 deg2), dotted line: W3 field (3.24 deg2), dashed line: W4 field (8.87 deg2). Error bars are Poissonian. These curves are not corrected for detection efficiency.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13067f18.ps} \end{figure} Figure 18:

Angular correlation function of our $\it detections$ in the W1 CFHTLS field for z = [0.4, 0.8] for S/N = 3. Error bars are Poissonian. The two straight lines are two power laws (see text).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067f19.ps} \end{figure} Figure 19:

Variation of D as function of redshift. The continuous, dashed, dotted, and dash-dotted lines with error bars are for Millennium halos more massive than 10 $^{10}~M_\odot$, 3 $\times $ 10 $^{13}~M_\odot$, 5 $\times $ 10 $^{13}~M_\odot$, and 10 $^{14}~M_\odot$. Unconnected filled circles with error bars show the CFHTLS W1 galaxies limited to i'=23. The five horizontal blue lines correspond to the mean D value for clusters detected in the W1 field ( from top to bottom: S/N = 6, 5, 4, 3, and 2).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067f20.ps} \end{figure} Figure 20:

Variation of D as a function of redshift. The continuous, dashed, dotted, and dash-dotted lines with error bars are for Millennium halos more massive than 10 $^{10}~M_\odot$, 3 $\times $ 10 $^{13}~M_\odot$, 5 $\times $ 10 $^{13}~M_\odot$, and 10 $^{14}~M_\odot$. Unconnected filled circles with error bars show the CFHTLS D2 galaxies limited to i'=25. The four horizontal blue lines correspond to the mean D value for clusters detected in the D2 field ( from top to bottom: S/N = 5, 4, 3, and 2). S/N = 5 and 4 are overlapping.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{1306721.ps} \end{figure} Figure 21:

Variation of D as a function of redshift. The continuous and dotted lines with error bars are for Millennium halos more massive than 3 $\times $ 10 $^{13}~M_\odot$ with high and low levels of substructures. The three horizontal blue lines are the mean D value for clusters detected in the W1 field ( from top to bottom: S/N = 6, 5, and 4).

Open with DEXTER
In the text

  \begin{figure} \par\hspace*{-3.5mm}\includegraphics[angle=270,width=8cm,clip]{13... ...ace*{2mm} \includegraphics[angle=270,width=7.7cm,clip]{13067222.ps} \end{figure} Figure 22:

Upper figure: center shifts in deg (blue filled circles: $z \leq 0.5$, green open circles: z=[0.5,0.8], red triangles: $z \geq 0.8$). Lower figure: histogram of redshift difference between our D1 and W1  $\it detections$ (S/N $\geq $ 2).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13067231.ps}\vspace*{2mm} \includegraphics[angle=270,width=8cm,clip]{13067232.ps} % \end{figure} Figure 23:

Histograms of the center shifts in degrees ( upper figure) and redshift differences ( lower figure) between our $\it detections$ (S/N $\geq $ 2) and the literature clusters quoted in the text.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.