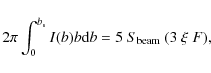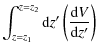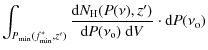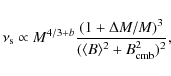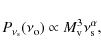| Issue |
A&A
Volume 509, January 2010
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 12 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200913063 | |
| Published online | 20 January 2010 | |
Unveiling radio halos in galaxy clusters in the LOFAR era
R. Cassano1 - G. Brunetti1 - H. J. A. Röttgering2 - M. Brüggen3
1 - INAF - Istituto di Radioastronomia, via P. Gobetti 101,I-40129 Bologna, Italy
2 - Leiden Observatory, Leiden University, Oort Gebouw, PO Box 9513, 2300 RA Leiden, The Netherlands
3 - Jacobs University Bremen, PO Box 750 651, 28725, Bremen, Germany
Received 4 August 2009 / Accepted 7 October 2009
Abstract
Aims. Giant radio halos are mega-parsec scale synchrotron
sources detected in a fraction of massive and merging galaxy clusters.
Radio halos provide one of the most important pieces of evidence of
non-thermal components in large-scale structure. Statistics of their
properties can be used to discriminate among various models for their
origin. Therefore, theoretical predictions of the occurrence of radio
halos are important as several new radio telescopes are about to begin
to survey the sky at low frequencies with unprecedented sensitivity.
Methods. We carry out Monte Carlo simulations to model the
formation and evolution of radio halos in a cosmological framework. In
the context of the turbulent re-acceleration model, we extend previous
work on the statistical properties of radio halos.
Results. We first compute the fraction of galaxy clusters that
show radio halos and derive the luminosity function of the radio halos.
We then derive differential and integrated number count distributions
of radio halos at low radio frequencies to explore the potential of the
upcoming LOFAR surveys. By restricting ourselves to clusters at
redshifts <0.6, we find that the planned LOFAR all-sky survey at
120 MHz is expected to detect about 350 giant radio halos.
About half of these halos have spectral indices greater than 1.9
and brighten substantially at lower frequencies. If detected they will
enable us to confirm that turbulence accelerates the emitting
particles. We also propose that commissioning surveys, such as MS3,
have the potential to detect about 60 radio halos in clusters of
the ROSAT brightest cluster sample and its extension (eBCS). These
surveys will allow us to constrain how the rate of formation of radio
halos in these clusters depends on cluster mass.
Key words: radiation mechanism: non-thermal - galaxies: clusters: general - radio continuum: general - X-rays: general
1 Introduction
Radio halos are diffuse Mpc-scale radio sources
observed at the center of ![]() 30% of massive galaxy clusters
(e.g., Feretti 2005; Ferrari et al. 2008, for reviews). These sources emit synchrotron radiation produced by GeV electrons diffusing through
30% of massive galaxy clusters
(e.g., Feretti 2005; Ferrari et al. 2008, for reviews). These sources emit synchrotron radiation produced by GeV electrons diffusing through ![]() G magnetic fields and provide the most important evidence of non-thermal components in the intra-cluster medium (ICM).
G magnetic fields and provide the most important evidence of non-thermal components in the intra-cluster medium (ICM).
Clusters hosting radio halos always display evidence of very recent or ongoing merger events (e.g., Buote 2001; Schuecker et al. 2001; Govoni et al. 2004; Venturi et al. 2008). This suggests a connection between the gravitational process of cluster formation and the origin of these halos. Cluster mergers are expected to be the most important sources of non-thermal components in galaxy clusters. A fraction of the energy dissipated during these mergers could be channelled into amplification of the magnetic fields (e.g., Dolag et al. 2002; Brüggen et al. 2005; Subramanian et al. 2006; Ryu et al. 2008) and into the acceleration of high energy particles by shocks and turbulence (e.g., Enßlin et al. 1998; Sarazin 1999; Blasi 2001; Brunetti et al. 2001, 2004; Petrosian 2001; Miniati et al. 2001; Fujita et al. 2003; Ryu et al. 2003; Hoeft & Brüggen 2007; Brunetti & Lazarian 2007; Pfrommer et al. 2008; Brunetti et al. 2009).
A promising scenario proposed to explain the origin of the synchrotron emitting electrons in radio halos assumes that electrons are re-accelerated by the interaction with MHD turbulence injected into the ICM in connection with cluster mergers (turbulent re-acceleration model, e.g., Brunetti et al. 2001; Petrosian 2001). An alternative possibility is that the emitting electrons are continuously injected by pp collisions in the ICM (secondary models; e.g., Dennison 1980; Blasi & Colafrancesco 1999).
In the picture of the turbulent re-acceleration
scenario, the formation and evolution of radio halos are tightly
connected with the dynamics and evolution of the hosting clusters.
Indeed, the occurrence of radio halos at any redshift depends on the
rate of cluster-cluster mergers and on the fraction of the merger
energy channelled into MHD turbulence and re-acceleration of high
energy particles. In the past few years, this has been modeled by Monte
Carlo procedures (Cassano & Brunetti 2005; Cassano et al. 2006a) that
provide predictions verifiable by future instruments.
In this scenario radio halos have a relatively short lifetime
(![]() 1 Gyr), and the fraction of galaxy clusters in which
radio halos are generated is expected to increase with cluster mass (or X-ray
luminosity), since the energy of the turbulence generated
during cluster mergers is expected to scale with the cluster thermal energy (which scales roughly as
1 Gyr), and the fraction of galaxy clusters in which
radio halos are generated is expected to increase with cluster mass (or X-ray
luminosity), since the energy of the turbulence generated
during cluster mergers is expected to scale with the cluster thermal energy (which scales roughly as ![]() M5/3; e.g., Cassano & Brunetti 2005). It has been shown that the predicted
occurrence of radio halos as a function of the cluster mass (or X-ray
luminosity) is in line with results obtained from a large observational
project, the ``GMRT radio halo survey'' (Venturi et al. 2007, 2008), and its combination with studies of nearby halos based on the NVSS survey (e.g., Cassano et al. 2008).
M5/3; e.g., Cassano & Brunetti 2005). It has been shown that the predicted
occurrence of radio halos as a function of the cluster mass (or X-ray
luminosity) is in line with results obtained from a large observational
project, the ``GMRT radio halo survey'' (Venturi et al. 2007, 2008), and its combination with studies of nearby halos based on the NVSS survey (e.g., Cassano et al. 2008).
The steep spectrum of radio halos makes these sources
ideal targets for observations at low radio frequencies suggesting
that present radio telescopes can only detect the tip of the iceberg
of their population (Enßlin & Röttgering 2002; Cassano et al. 2006a; Hoeft et al. 2008).
The discovery of the giant and ultra-steep spectrum radio halo
in Abell 521 at low radio frequencies (Brunetti et al. 2008)
allows a first confirmation of this conjecture and provides a glimpse
of what future low frequency radio telescopes, such as the Low
Frequency Array (LOFAR)![]() and the Long Wavelength Array (LWA, e.g., Ellingson et al. 2009), might find in upcoming years.
and the Long Wavelength Array (LWA, e.g., Ellingson et al. 2009), might find in upcoming years.
LOFAR promises an impressive gain of two orders of magnitude in sensitivity and angular resolution over present instruments in the frequency range 15-240 MHz, and as such will open up a new observational window to the Universe. In particular, LOFAR is expected to contribute significantly to the understanding of the origin and evolution of the relativistic matter and magnetic fields in galaxy clusters.
The main focus of the present paper is to provide a theoretical framework for the interpretation of future LOFAR data by quantifying expectations for the properties and occurrence of giant radio halos in the context of the turbulent re-acceleration scenario. In particular, in Sect. 2 we summarize the main ingredients used in the model calculations and provide an extension of the results of previous papers on the occurrence of radio halos in clusters (Sect. 2.1) and on the expected radio halo luminosity functions (Sect. 2.2). In Sect. 3, we derive the expected number counts of radio halos at 120 MHz and explore the potential of LOFAR surveys. Our conclusions are given in Sect. 4.
A ![]() CDM (
CDM (
![]()
![]() ,
,
![]() ,
,
![]() )
cosmology is adopted throughout the paper.
)
cosmology is adopted throughout the paper.
2 Statistical modelling of giant radio halos in galaxy clusters
Turbulence generated during cluster mergers may accelerate relativistic particles and produce diffuse synchrotron emission from Mpc regions in galaxy clusters (e.g., Brunetti et al. 2008). Diffuse radio emission in the form of giant radio halos should be generated in connection with massive mergers and fade away as soon as turbulence is dissipated and the emitting electrons cool due to radiative losses. It is likely that the generation of turbulence and the acceleration of particles persist for a few crossing times of the cluster-core regions, implying a lifetime of about 1 Gyr.
Since the physics of the proposed scenario is rather uncertain, we choose to model the properties of the halos and their cosmic evolution using a simple statistical approach. By means of Monte Carlo calculations, we take into account the main processes that play a role in this scenario. These include the rate of cluster-cluster mergers in the Universe and their mass ratios, and the fraction of the energy dissipated during these mergers that is channelled into MHD turbulence and acceleration of high energy particles (Cassano & Brunetti 2005; Cassano et al. 2006a). We refer the reader to these papers for details, here we briefly report the essential steps that enter into the calculations:
- i)
- The formation and evolution of galaxy clusters is computed by
the extended Press & Schechter approach (1974, hearafter PS;
Lacey & Cole 1993), which is based on the hierarchical theory of cluster formation. The PS mass function shows good agreement with that
derived from N-body simulations, at least for relatively low redshifts
and masses
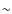
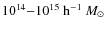 (e.g., Springel et al. 2005),
although it has the tendency to underestimate the number density
of systems with mass
(e.g., Springel et al. 2005),
although it has the tendency to underestimate the number density
of systems with mass 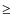
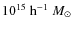 (e.g., Governato et al. 1999; Bode et al. 2001; Jenkins et al. 2001). Given the present-day mass and temperature of the parent clusters, the cluster merger history (merger trees) is obtained by using Monte Carlo simulations. We simulate the formation history of
(e.g., Governato et al. 1999; Bode et al. 2001; Jenkins et al. 2001). Given the present-day mass and temperature of the parent clusters, the cluster merger history (merger trees) is obtained by using Monte Carlo simulations. We simulate the formation history of 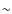 1000 galaxy clusters with present-day masses in the range
1000 galaxy clusters with present-day masses in the range
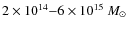 .
This allows a statistical description of the cosmological evolution of galaxy clusters and of
the merging events with cosmic time.
.
This allows a statistical description of the cosmological evolution of galaxy clusters and of
the merging events with cosmic time.
- ii)
- The generation of the turbulence in the ICM is estimated for each merger
identified in the merger trees.
The resulting turbulence is assumed to be generated and then dissipated
within a timescale of the order of the cluster-cluster crossing time in
that merger
![[*]](/icons/foot_motif.png) .
Furthermore, it is assumed that turbulence is generated in the volume
swept by the subcluster infalling into the main cluster and that a
fraction,
.
Furthermore, it is assumed that turbulence is generated in the volume
swept by the subcluster infalling into the main cluster and that a
fraction, 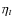 ,
of the
,
of the 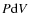 work done by this subcluster goes into the excitation of fast magneto-acoustic waves. The
work done by this subcluster goes into the excitation of fast magneto-acoustic waves. The 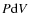 work is estimated to be
work is estimated to be 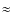
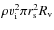 ,
where
,
where 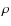 is the ICM density of the main cluster averaged over the swept cylinder,
is the ICM density of the main cluster averaged over the swept cylinder, 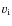 is the impact velocity of the two subclusters,
is the impact velocity of the two subclusters, 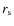 is the stripping radius (see also Sect. 2.1), and
is the stripping radius (see also Sect. 2.1), and 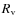 is the virial radius of the main cluster (see Cassano & Brunetti 2005, for details).
is the virial radius of the main cluster (see Cassano & Brunetti 2005, for details).
- iii)
- The resulting spectrum of MHD turbulence generated by the chain of mergers in any synthetic cluster and its evolution with cosmic time is computed by taking into account the injection of waves and their damping in a collisionless plasma. Acceleration of particles by this turbulence and their evolution is computed in connection with the evolution of synthetic clusters by solving Fokker-Planck equations and including the relevant energy losses.
- iv)
- This procedure allows for the exploration of the statistical properties of radio halos. Following Cassano et al. (2006a),
we consider homogeneous models, i.e., without spatial variation in
the turbulent energy, acceleration rate, and magnetic field in the halo
volume. We assume a value of the magnetic field, averaged over a region
of radius
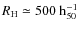 kpc, which scales with the virial mass of clusters,
kpc, which scales with the virial mass of clusters,  as
as
where b > 0 is a parameter that enters into the model calculations. Equation (1) is motivated by numerical cosmological (MHD) simulations that found a scaling of the magnetic field with temperature or mass of the simulated clusters (e.g., Dolag et al. 2002)![[*]](/icons/foot_motif.png) .
.
2.1 Occurrence of radio halos in galaxy clusters
Stochastic particle acceleration by MHD turbulence is believed
to be rather inefficient in the ICM. Consequently, electrons can
be accelerated only up to energies of
![]() several GeV, since at higher energies the radiation losses are
efficient and hence dominate. The resulting gradual steepening in the
theoretical synchrotron spectrum of radio halos at high frequencies is
consistent with the observed spectral shapes (or with the very steep
spectra) of several well studied halos (e.g., Schlickeiser
et al. 1987; Thierbach et al. 2003; Brunetti et al. 2008; Dallacasa et al. 2009).
several GeV, since at higher energies the radiation losses are
efficient and hence dominate. The resulting gradual steepening in the
theoretical synchrotron spectrum of radio halos at high frequencies is
consistent with the observed spectral shapes (or with the very steep
spectra) of several well studied halos (e.g., Schlickeiser
et al. 1987; Thierbach et al. 2003; Brunetti et al. 2008; Dallacasa et al. 2009).
This steepening makes it difficult to detect these sources
at frequencies higher than the frequency,
![]() ,
at which the
steepening becomes severe (see Fig. 1), where
,
at which the
steepening becomes severe (see Fig. 1), where
![]() is expected to be a few times higher than the break frequency,
is expected to be a few times higher than the break frequency,
![]() ,
and
,
and
![]() depends on the acceleration efficiency in the ICM,
depends on the acceleration efficiency in the ICM, ![]() ,
being defined by (e.g., Cassano et al. 2006a)
,
being defined by (e.g., Cassano et al. 2006a)
The transit time damping (TTD) is the most important collisionless resonance between the magnetosonic waves and particles, and is produced by the interaction of the compressible component of the magnetic field of these waves with the particles (e.g., Schlickeiser & Miller 1998; Cassano & Brunetti 2005; Brunetti & Lazarian 2007). In this case
where
Combined with Eq. (2), this implies that higher values of
![]() are expected in the more massive clusters,
are expected in the more massive clusters,
![]() (here considering
for simplicity a fixed value of B, see Cassano et al. 2006a for a more general discussion), and in connection with major merger events,
(here considering
for simplicity a fixed value of B, see Cassano et al. 2006a for a more general discussion), and in connection with major merger events,
![]() (
(![]() in Eq. (3) also increases with
in Eq. (3) also increases with
![]() ).
).
Monte Carlo simulations can now be used to follow cluster-mergers and
to explore how different mergers contribute to the acceleration
(efficiency) of relativistic particles in the ICM. Consequently, this
allows a statistical modeling of
![]() to be performed within a synthetic cluster sample and the derivation of
its statistical dependence on cosmic time and cluster mass.
to be performed within a synthetic cluster sample and the derivation of
its statistical dependence on cosmic time and cluster mass.
![\begin{figure}
\par\includegraphics[width=7.3cm,height=6.5cm,clip]{13063fg1.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg67.png)
|
Figure 1:
A schematic representation of the theoretical synchrotron spectra of radio halos with different values of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,height=7cm]{13063fg2.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg68.png)
|
Figure 2:
Ratio
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13063f3a.ps}\includegraphics[width=7.5cm,clip]{13063f3b.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg69.png)
|
Figure 3:
Fraction of clusters with radio halos, with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13063f4a.ps}\includegraphics[width=7.5cm,clip]{13063f4b.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg70.png)
|
Figure 4:
Fraction of clusters with radio halos
with
|
| Open with DEXTER | |
Surveys cannot detect radio halos that have
![]() lower
than the observing frequency, since the spectrum of these halos
should be very steep and their emission should fall below the
survey detection limit (Fig. 1).
To investigate the statistical behavior of the population of radio
halos at different frequencies, we only consider halos to be observable
when
lower
than the observing frequency, since the spectrum of these halos
should be very steep and their emission should fall below the
survey detection limit (Fig. 1).
To investigate the statistical behavior of the population of radio
halos at different frequencies, we only consider halos to be observable
when
![]() .
Figure 2 shows the ratio
.
Figure 2 shows the ratio
![]() calculated for homogeneous models of radio halos, defining
calculated for homogeneous models of radio halos, defining
![]() as the
frequency where the synchrotron spectrum of these
halos is
as the
frequency where the synchrotron spectrum of these
halos is
![]() (
(
![]() being calculated between
being calculated between
![]() and
and
![]() to mimic
600-1400 MHz spectra); since
to mimic
600-1400 MHz spectra); since
![]() is only mildly dependent on magnetic field strength and the assumed fraction of turbulent energy injected, we adopt
is only mildly dependent on magnetic field strength and the assumed fraction of turbulent energy injected, we adopt
![]() .
A statistical modeling of
.
A statistical modeling of
![]() provides a statistical evaluation of
provides a statistical evaluation of
![]() in the synthetic cluster sample.
in the synthetic cluster sample.
In the context of the turbulent acceleration model for giant radio
halos, energetics arguments imply that halos with
![]() GHz
must be generated in connection with the most energetic merger-events
in the Universe. Only these mergers can produce the efficient acceleration
necessary to have relativistic electrons emitting at these
frequencies (Cassano & Brunetti 2005).
Present surveys carried out at
GHz
must be generated in connection with the most energetic merger-events
in the Universe. Only these mergers can produce the efficient acceleration
necessary to have relativistic electrons emitting at these
frequencies (Cassano & Brunetti 2005).
Present surveys carried out at
![]() GHz
detect radio halos only in the most massive and merging
clusters (e.g., Buote 2001; Venturi et al. 2008), and their occurrence has been used to constrain the value of
GHz
detect radio halos only in the most massive and merging
clusters (e.g., Buote 2001; Venturi et al. 2008), and their occurrence has been used to constrain the value of
![]() in the models (Cassano & Brunetti 2005).
Similar energetics arguments can be used to
claim that radio halos with lower values of
in the models (Cassano & Brunetti 2005).
Similar energetics arguments can be used to
claim that radio halos with lower values of
![]() must be more common, since they can be generated in connection with less energetic phenomena, e.g., major mergers between
less massive systems or minor mergers in massive systems (e.g.,
Eqs. (2)-(3)), that are more common in the
Universe (e.g., Cassano et al. 2008).
must be more common, since they can be generated in connection with less energetic phenomena, e.g., major mergers between
less massive systems or minor mergers in massive systems (e.g.,
Eqs. (2)-(3)), that are more common in the
Universe (e.g., Cassano et al. 2008).
In Fig. 3, we plot the fraction of clusters that host radio halos with
![]() as a function of the cluster mass and by considering two redshift
ranges : 0-0.1 (left panel) and 0.4-0.5 (right panel); this is obtained
by assuming a reference set of model parameters, namely
as a function of the cluster mass and by considering two redshift
ranges : 0-0.1 (left panel) and 0.4-0.5 (right panel); this is obtained
by assuming a reference set of model parameters, namely
![]() G, b=1.5,
G, b=1.5,
![]() (see also Cassano et al. 2006a).
As expected, the fraction of clusters with halos increases at lower
values of
(see also Cassano et al. 2006a).
As expected, the fraction of clusters with halos increases at lower
values of
![]() ,
and the size of this increment depends on the
considered mass and redshift of the parent clusters, being greater at
lower cluster masses and at higher redshifts.
,
and the size of this increment depends on the
considered mass and redshift of the parent clusters, being greater at
lower cluster masses and at higher redshifts.
In Fig. 4, we plot the fraction
of radio halos with
![]() MHz (black upper line)
and the differential contribution to this
fraction from radio halos with
MHz (black upper line)
and the differential contribution to this
fraction from radio halos with
![]() in four frequency
ranges (see figure caption for details).
For nearby systems (Fig. 4, Left Panel), a
significant fraction of massive clusters,
in four frequency
ranges (see figure caption for details).
For nearby systems (Fig. 4, Left Panel), a
significant fraction of massive clusters,
![]() ,
is expected to host radio halos with
,
is expected to host radio halos with
![]() MHz; a sizeable
fraction of them with
MHz; a sizeable
fraction of them with
![]() MHz (blue and magenta lines).
On the other hand, the majority of radio halos in clusters with
mass
MHz (blue and magenta lines).
On the other hand, the majority of radio halos in clusters with
mass
![]() would have very steep spectra
if observed at GHz frequencies,
would have very steep spectra
if observed at GHz frequencies,
![]() MHz (red line and
black dot-dashed line).
Our calculations suggest that a similar situation is expected for
clusters at higher redshift (Fig. 4,
right panel). Radio halos with higher values of
MHz (red line and
black dot-dashed line).
Our calculations suggest that a similar situation is expected for
clusters at higher redshift (Fig. 4,
right panel). Radio halos with higher values of
![]() become much rarer with increasing
redshift, mainly because
the unavoidable inverse Compton losses at these redshifts
limit the maximum energy of the accelerated electrons in these
systems. At z > 0.5,
only merging clusters with mass
become much rarer with increasing
redshift, mainly because
the unavoidable inverse Compton losses at these redshifts
limit the maximum energy of the accelerated electrons in these
systems. At z > 0.5,
only merging clusters with mass
![]() have a sizeable chance of hosting giant
radio halos with
have a sizeable chance of hosting giant
radio halos with
![]() GHz, and an increasing contribution
to the percentage of radio halos at higher redshift comes from
halos with lower
GHz, and an increasing contribution
to the percentage of radio halos at higher redshift comes from
halos with lower
![]() .
.
2.2 The radio halo luminosity function
The luminosity functions of radio halos (RHLFs), i.e., the number of halos
per comoving volume and radio power, with
![]() GHz was
derived by Cassano et al. (2006a) to be
GHz was
derived by Cassano et al. (2006a) to be
where
The quantity
![]() can be estimated from the correlation between the 1.4 GHz radio power, P(1.4), and the mass of the
parent clusters that is observed for radio halos
(e.g., Govoni et al. 2001; Cassano et al. 2006a).
Cassano et al. (2006a) discussed the P(1.4)-
can be estimated from the correlation between the 1.4 GHz radio power, P(1.4), and the mass of the
parent clusters that is observed for radio halos
(e.g., Govoni et al. 2001; Cassano et al. 2006a).
Cassano et al. (2006a) discussed the P(1.4)-![]() correlation in the context of the turbulent acceleration model and demonstrated that
the slope is consistent with the observed value (
correlation in the context of the turbulent acceleration model and demonstrated that
the slope is consistent with the observed value (
![]() )
for a well constrained region of parameter space (
)
for a well constrained region of parameter space (
![]() ,
b, and
,
b, and ![]() ;
Fig. 7 in Cassano et al. 2006a); model parameters
adopted in the present paper, i.e.,
;
Fig. 7 in Cassano et al. 2006a); model parameters
adopted in the present paper, i.e.,
![]() G, b=1.5 and
G, b=1.5 and
![]() ,
fall in this range. In particular, the value of the derivative
,
fall in this range. In particular, the value of the derivative
![]() in Eq. (4) depends on the set of parameters (
in Eq. (4) depends on the set of parameters (
![]() ,
b) that, in the
case of the reference model we use in this paper, sets
,
b) that, in the
case of the reference model we use in this paper, sets
![]() .
.
To derive the RHLF at frequency
![]() ,
the
contribution of all radio halos with
,
the
contribution of all radio halos with
![]() should be
taken into account. We first obtained the RHLF for halos with
should be
taken into account. We first obtained the RHLF for halos with
![]() in a given frequency interval, e.g.,
in a given frequency interval, e.g.,
![]() ,
and then combined the different contributions from the considered
intervals
,
and then combined the different contributions from the considered
intervals
![]() :
:
To derive the contribution to the RHLF from radio halos with
where
We now consider the case of halos with
![]() GHz.
The bolometric synchrotron power of radio halos is expected to
scale with
GHz.
The bolometric synchrotron power of radio halos is expected to
scale with
![]() and B (e.g., Cassano et al. 2006a) such that
and B (e.g., Cassano et al. 2006a) such that
From Eqs. (2)-(3), it is clear that clusters of the same mass
This allows the evaluation of
We also note that from Eqs. (6) and (8), one has
i.e., radio halos with synchrotron spectra that steepen at lower frequencies will also have monochromatic radio powers at
As a relevant example, in Fig. 5 we report the expected RHLF at 120 MHz (black lines) for z=0-0.1 (solid thick lines) and
z=0.5-0.6
(dashed thick lines), where we also show the relative contributions
of halos with
![]() MHz (red lines) and
MHz (red lines) and
![]() MHz (blue lines).
MHz (blue lines).
As already discussed in Cassano et al. (2006a),
the shape of
the RHLF flattens at lower radio powers because of the decrease in the
efficiency of particle acceleration in less massive clusters. We note
that halos with
![]() MHz (blue lines,
Fig. 5) do not contribute to lower radio powers in the RHLF.
This is because higher-frequency halos are generated in very energetic
merger events, and must be extremely rare in smaller systems
and consequently their monochromatic radio power is greater
than that of halos with
MHz (blue lines,
Fig. 5) do not contribute to lower radio powers in the RHLF.
This is because higher-frequency halos are generated in very energetic
merger events, and must be extremely rare in smaller systems
and consequently their monochromatic radio power is greater
than that of halos with
![]() MHz (red lines, Fig. 5). Finally, we note that with increasing redshift the
RHLFs decrease due to the evolution with z of both the cluster mass function and the fraction of galaxy clusters with radio halos (Fig. 3, see also Cassano et al. 2006a).
The evolution of the RHLF with z is stronger at higher radio powers,
where the dominant contribution to the RHLF comes from halos
with higher
MHz (red lines, Fig. 5). Finally, we note that with increasing redshift the
RHLFs decrease due to the evolution with z of both the cluster mass function and the fraction of galaxy clusters with radio halos (Fig. 3, see also Cassano et al. 2006a).
The evolution of the RHLF with z is stronger at higher radio powers,
where the dominant contribution to the RHLF comes from halos
with higher
![]() and the fraction of clusters hosting these halos
decreases more rapidly with redshift (e.g., Fig. 4).
and the fraction of clusters hosting these halos
decreases more rapidly with redshift (e.g., Fig. 4).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13063fg5.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg107.png)
|
Figure 5:
Radio halo luminosity function at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13063fg6.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg108.png)
|
Figure 6: All-sky integrated RHNCs for: (1) z=0.044-0.2, obtained by considering a minimum mass of clusters constrained at any z by the XBACS X-ray flux limit (Ebeling et al. 1996) (dashed black line), and by combining the above mass-constraint with that implied by the NVSS sensitivity (following Cassano et al. 2008, see their Fig. 3) (solid upper black line); (2) z=0.2-0.32, obtained by considering the X-ray luminosity-range of the GMRT cluster sample (Venturi et al. 2007, 2008, red lower line). Black filled points are the observed RHNC of giant radio halos from NVSS-selected clusters in the redshift range 0.044-0.2, re-normalized to account for the NVSS and XBACS sky coverage (and XBACS completeness). Red open points are the observed RHNC of giant radio halos in the GMRT cluster sample (with redshift z=0.2-0.32), re-normalized to account for the sky coverage of the GMRT cluster sample. |
| Open with DEXTER | |
3 Number counts of radio halos and LOFAR surveys at 120 MHz
It has been shown that model expectations of the occurrence of radio halos
observed at
![]() GHz are consistent with the fraction of radio halos with cluster mass (Cassano et al. 2008) and with the number counts of nearby radio halos (Cassano et al. 2006a).
GHz are consistent with the fraction of radio halos with cluster mass (Cassano et al. 2008) and with the number counts of nearby radio halos (Cassano et al. 2006a).
As already discussed, in this paper we adopt a reference model
with parameters:
![]() G, b=1.5,
G, b=1.5,
![]() .
In Fig. 6,
we report number counts of giant radio halos expected with these
parameters compared with radio halo counts from the NVSS survey at low
redshift,
.
In Fig. 6,
we report number counts of giant radio halos expected with these
parameters compared with radio halo counts from the NVSS survey at low
redshift,
![]() (Giovannini et al. 1999) and from the GMRT radio halo survey at intermediate redshift,
z=0.2-0.32 (Venturi et al. 2007, 2008). The latter is a pointed survey down to
(Giovannini et al. 1999) and from the GMRT radio halo survey at intermediate redshift,
z=0.2-0.32 (Venturi et al. 2007, 2008). The latter is a pointed survey down to ![]() Jy/beam at 610 MHz of a sample of
Jy/beam at 610 MHz of a sample of ![]() 50 galaxy clusters extracted from the REFLEX (Böhringer et al. 2004) and eBCS (Ebeling et al. 1998, 2000) cluster catalogs. The clusters have
z=0.2-0.4 and
50 galaxy clusters extracted from the REFLEX (Böhringer et al. 2004) and eBCS (Ebeling et al. 1998, 2000) cluster catalogs. The clusters have
z=0.2-0.4 and
![]() erg/s (the X-ray sample is complete for
erg/s (the X-ray sample is complete for
![]() ;
see Cassano et al. 2008).
All halos in the survey have 1.4 GHz follow-up data. Beside the
fair agreement between expectations and observations
(see caption), we note that the GMRT radio halo survey is sufficiently
sensitive to detect relatively faint halos and constrain the flattening
of the distribution of number counts of radio halos (RHNC) at
lower fluxes.
;
see Cassano et al. 2008).
All halos in the survey have 1.4 GHz follow-up data. Beside the
fair agreement between expectations and observations
(see caption), we note that the GMRT radio halo survey is sufficiently
sensitive to detect relatively faint halos and constrain the flattening
of the distribution of number counts of radio halos (RHNC) at
lower fluxes.
Encouraged by these results, in this section we derive the expected RHNC at 120 MHz and explore the potential of upcoming LOFAR surveys.
Because in our simplified procedure the radio power of halos scales
with a spectral slope
![]() (Eqs. (6)-(9))
and the vast majority of halos is at
(Eqs. (6)-(9))
and the vast majority of halos is at
![]() -0.4,
in the following we neglect the K-correction
-0.4,
in the following we neglect the K-correction![]() .
.
3.1 LOFAR surveys
LOFAR will carry out surveys between 15 MHz and 210 MHz with
unprecedented sensitivity and spatial resolution
(e.g., Röttgering et al. 2006).
The unprecedented (u,v)
coverage of LOFAR on short baselines
also maximizes the instrument capability to detect extended sources of
low surface brightness such as radio halos.
These surveys will constrain models of diffuse radio emission in galaxy
clusters. In this paper, we assume an observing frequency
![]() MHz, at which LOFAR will carry out the deepest large-area radio surveys
(e.g., Röttgering et al. 2006).
MHz, at which LOFAR will carry out the deepest large-area radio surveys
(e.g., Röttgering et al. 2006).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13063f7a.ps}\includegraphics[width=7.5cm,clip]{13063f7b.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg118.png)
|
Figure 7:
Minimum flux ( left panel) and power ( right panel) of detectable radio halos at 120 MHz using Eq. (10) (solid lines) and Eq. (11) (dashed lines), where
|
| Open with DEXTER | |
The crucial step in our analysis is the estimate of the minimum
diffuse flux from giant radio halos (integrated over a scale
of ![]() 1 Mpc)
that is detectable by these surveys as a function of redshift. This
depends on the brightness profiles of radio halos that is known to
smoothly decrease with distance from the cluster center
(e.g., Govoni et al. 2001). Consequently, the outermost, low brightness, regions of halos will be difficult to detect.
1 Mpc)
that is detectable by these surveys as a function of redshift. This
depends on the brightness profiles of radio halos that is known to
smoothly decrease with distance from the cluster center
(e.g., Govoni et al. 2001). Consequently, the outermost, low brightness, regions of halos will be difficult to detect.
However what is important is the capability to detect the central,
brightest, regions of radio halos in the survey images. Following Brunetti et al. (2007),
we consider a shape of the radial profile of radio halos that is
obtained from the analysis of well studied halos. We assume a circular
observing beam =
![]() arcsec, and follow two complementary approaches
arcsec, and follow two complementary approaches![]() :
:
- i)
- Since radio halos emit about half of their total radio flux
within their half radius (Brunetti et al. 2007),
we estimate the minimum flux of a detectable halo,
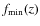 ,
by requiring that the mean brightness within
,
by requiring that the mean brightness within
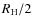 ,
,
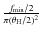 ,
is
,
is 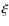 times the rms, F, of the survey, i.e.,
where
times the rms, F, of the survey, i.e.,
where![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13063f8a.ps}\includegraphics[width=7.5cm,clip]{13063f8b.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg125.png)
Figure 8: Number (all-sky) of radio halos with
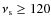 MHz
(black solid lines) as a function of redshift that can be expected at
the sensitivity of LOFAR surveys. Calculations are performed following
approaches i) in Sect. 2.1 ( left); and ii) ( right), assuming
MHz
(black solid lines) as a function of redshift that can be expected at
the sensitivity of LOFAR surveys. Calculations are performed following
approaches i) in Sect. 2.1 ( left); and ii) ( right), assuming
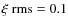 ,
0.25, 0.5, 1.0, 1.5 ( bottom to top). Red dashed lines give the number counts of radio halos with
,
0.25, 0.5, 1.0, 1.5 ( bottom to top). Red dashed lines give the number counts of radio halos with
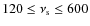 MHz.
MHz.
Open with DEXTER 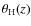 is the angular size of radio halos, in arcseconds, at a given redshift,
allowing for the detection of diffuse halo emission in the images
produced by the survey. Injection of fake radio halos in the (u,v) plane of interferometric
data from NVSS observations show that radio halos at
is the angular size of radio halos, in arcseconds, at a given redshift,
allowing for the detection of diffuse halo emission in the images
produced by the survey. Injection of fake radio halos in the (u,v) plane of interferometric
data from NVSS observations show that radio halos at
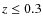 become
visible in the images as soon as their flux approaches that obtained
by Eq. (10) with
become
visible in the images as soon as their flux approaches that obtained
by Eq. (10) with
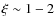 (Cassano et al. 2008).
(Cassano et al. 2008).
- ii)
- Following a second approach, we estimate the minimum flux of a
detectable halo by requiring that the average brightness within
5 observing beams is
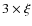 times the rms, F, of the survey. The minimum flux is obtained from the condition
times the rms, F, of the survey. The minimum flux is obtained from the condition
where I(b) is the typical radial profile of halos (Brunetti et al. 2007),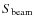 is the beam area, and
is the beam area, and
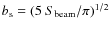 .
The aim of this second approach is to avoid any bias related to the
redshift of the halos since, in the first approach, the sensitivity
limit is reached across a fairly large area (many beams) for nearby
radio halos, but only within an area of few beams in the case of halos
at z = 0.5-0.6.
.
The aim of this second approach is to avoid any bias related to the
redshift of the halos since, in the first approach, the sensitivity
limit is reached across a fairly large area (many beams) for nearby
radio halos, but only within an area of few beams in the case of halos
at z = 0.5-0.6.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13063fg9.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg135.png)
|
Figure 9:
Spectral index distribution of radio halos, calculated for the range 120-330 MHz, for the number counts in Fig. 8 ( left panel) and assuming
|
| Open with DEXTER | |
Given the RHLF (
![]() ), the number counts of radio halos with
), the number counts of radio halos with
![]() in a redshift interval,
in a redshift interval,
![]() ,
is given by
,
is given by
In Fig. 8, we show the all-sky number of radio halos with
The LOFAR all-sky survey (e.g., Röttgering 2009, priv. comm.) is expected
to reach an rms = 0.1 mJy/beam at 120 MHz. Considering the
case i) (Fig. 8, left panel)
with
![]() ,
we predict that this survey will detect more than
350 radio halos at redshift
,
we predict that this survey will detect more than
350 radio halos at redshift ![]() 0.6, in the northern
hemisphere (
0.6, in the northern
hemisphere (
![]() )
and at high Galactic latitudes (
)
and at high Galactic latitudes (
![]() ).
This will increase the statistics of radio halos by about a factor of
20 with respect to that produced by the NVSS. The LOFAR
commissioning MS3
survey is expected to reach sensitivities of
).
This will increase the statistics of radio halos by about a factor of
20 with respect to that produced by the NVSS. The LOFAR
commissioning MS3
survey is expected to reach sensitivities of ![]() 0.5 mJy/b at 150 MHz.
Based on our results,
0.5 mJy/b at 150 MHz.
Based on our results, ![]() 100 radio halos are expected to be
discovered by this survey within a one year timescale.
100 radio halos are expected to be
discovered by this survey within a one year timescale.
The spectral properties of the population of radio halos
visible by the future radio surveys at low frequencies are expected
to change with the increasing sensitivity of these surveys.
In Fig. 8, we show the total number of halos with
![]() MHz (solid lines) and the number of halos with a spectral steepening at low frequencies,
MHz (solid lines) and the number of halos with a spectral steepening at low frequencies,
![]() MHz.
The latter class of radio halos has a synchrotron spectral
index
MHz.
The latter class of radio halos has a synchrotron spectral
index
![]() in the range 250-600 MHz, and would
become visible only at low frequencies,
in the range 250-600 MHz, and would
become visible only at low frequencies,
![]() MHz.
We find that about 55% of radio halos in the LOFAR all-sky survey
at 120 MHz is expected to belong to this class of ultra-steep spectrum
radio halos, while radio halos of higher
MHz.
We find that about 55% of radio halos in the LOFAR all-sky survey
at 120 MHz is expected to belong to this class of ultra-steep spectrum
radio halos, while radio halos of higher
![]() are expected to
dominate the population in shallower surveys. This is simply because,
for the reasons explained in Sect. 2.2, low frequency radio halos
are expected to populate the low power-end of the RHLF
(e.g., Fig. 5). Complementary information is given in Fig. 9 that shows the expected distribution of halo spectral indices, with reference to the number distributions in Fig. 8, and its evolution with sensitivity of radio observations; the spectra in Fig. 9 have been calculated for the range 120-300 MHz assuming homogeneous models.
are expected to
dominate the population in shallower surveys. This is simply because,
for the reasons explained in Sect. 2.2, low frequency radio halos
are expected to populate the low power-end of the RHLF
(e.g., Fig. 5). Complementary information is given in Fig. 9 that shows the expected distribution of halo spectral indices, with reference to the number distributions in Fig. 8, and its evolution with sensitivity of radio observations; the spectra in Fig. 9 have been calculated for the range 120-300 MHz assuming homogeneous models.
Ultra-steep spectrum halos are a unique prediction of the turbulent re-acceleration model (e.g., Brunetti et al. 2008) and our expectations demonstrate the potential of LOFAR to constrain present models for the origin of radio halos.
3.2 Application to X-ray selected cluster samples
Although unbiased surveys of radio halos provide an important way to measure the occurrence of these sources (Sect. 3.1), a potential problem with these approaches is the identification of both radio halos and their hosting clusters. This is because radio halos constitute only a very small fraction of the entire radio source population and need to be distinguished from confused regions produced by the superpositions of radio AGNs and starburst galaxies. Alternatively, an efficient approach is to exploit deep LOFAR surveys of X-ray selected samples of galaxy clusters. Here we derive the number of radio halos, and their flux and redshift distributions, that should be detected by LOFAR observations of X-ray selected clusters.
There are several catalogs of X-ray selected clusters in the northern
hemisphere that contain clusters extracted from the ROSAT All-Sky Survey (RASS, Trümper 1993).
At redshift ![]() 0.3, the ROSAT Brightest Cluster Sample and
its extension to lower X-ray fluxes (eBCS, Ebeling et al. 1998, 2000)
and the Northern ROSAT All-Sky (NORAS) Cluster Survey
(Böhringer et al. 2000) provide cluster catalogs with X-ray flux
0.3, the ROSAT Brightest Cluster Sample and
its extension to lower X-ray fluxes (eBCS, Ebeling et al. 1998, 2000)
and the Northern ROSAT All-Sky (NORAS) Cluster Survey
(Böhringer et al. 2000) provide cluster catalogs with X-ray flux
![]() ;
the eBCS is 75% complete down
to this flux limit. The extension of these catalogs to higher redshifts led to the Massive Cluster Survey (MACS, Ebeling
et al. 2001), which contains clusters with
;
the eBCS is 75% complete down
to this flux limit. The extension of these catalogs to higher redshifts led to the Massive Cluster Survey (MACS, Ebeling
et al. 2001), which contains clusters with
![]() at z
= 0.3-0.6. All these surveys have optical follow-ups and provide a
useful starting point for detecting radio halos in LOFAR surveys.
at z
= 0.3-0.6. All these surveys have optical follow-ups and provide a
useful starting point for detecting radio halos in LOFAR surveys.
A well-known correlation exists between the synchrotron power of giant radio
halos and the X-ray luminosity of the hosting clusters,
![]() ,
where
,
where
![]() (e.g., Liang et al. 2000; Bacchi et al. 2003; Enßlin & Röttgering 2002; Cassano et al. 2006a;
Brunetti et al. 2009). This implies that the X-ray flux limit of the survey,
(e.g., Liang et al. 2000; Bacchi et al. 2003; Enßlin & Röttgering 2002; Cassano et al. 2006a;
Brunetti et al. 2009). This implies that the X-ray flux limit of the survey, ![]() ,
is related to the radio flux of halos. The minimum flux of radio halos that can be detected at redshift z
is given by the maximum value of the minimum radio flux due to
the sensitivity of radio surveys (Sect. 3.1) and
that constrained by
,
is related to the radio flux of halos. The minimum flux of radio halos that can be detected at redshift z
is given by the maximum value of the minimum radio flux due to
the sensitivity of radio surveys (Sect. 3.1) and
that constrained by ![]() by the radio - X-ray correlation.
To address this issue at
by the radio - X-ray correlation.
To address this issue at
![]() MHz in the case of radio halos with
MHz in the case of radio halos with
![]() GHz, we assume a correlation between the monochromatic radio luminosity at 120 MHz and
GHz, we assume a correlation between the monochromatic radio luminosity at 120 MHz and
![]() rescaled from that at 1.4 GHz by means of Eq. (6).
For halos with lower
rescaled from that at 1.4 GHz by means of Eq. (6).
For halos with lower
![]() (yet
(yet
![]() MHz)
the correlation between the radio luminosity at 120 MHz and
MHz)
the correlation between the radio luminosity at 120 MHz and ![]() is obtained from Eq. (8), which accounts for the lower radio
power expected for halos with steeper spectra (Sect. 2.2).
is obtained from Eq. (8), which accounts for the lower radio
power expected for halos with steeper spectra (Sect. 2.2).
In this section, we model the sensitivity of LOFAR at 120 MHz
following the approach i) described in Sect. 3 (Eq. (10)).
More specifically, to detect radio halos, we consider 120 MHz LOFAR
follow-up of a cluster catalog obtained by combining the eBCS (at
![]() )
and the MACS (
0.3 <z <0.6) samples, and assume reference sensitivities of radio observations of
)
and the MACS (
0.3 <z <0.6) samples, and assume reference sensitivities of radio observations of
![]() and 1 mJy/beam.
The minimum
and 1 mJy/beam.
The minimum ![]() of cluster for which these radio observations
are expected to detect giant radio halos is evaluated by combining the above
radio sensitivity and the minimum
of cluster for which these radio observations
are expected to detect giant radio halos is evaluated by combining the above
radio sensitivity and the minimum ![]() in cluster catalogs at redshift z, and is shown in Fig. 10 by considering different
in cluster catalogs at redshift z, and is shown in Fig. 10 by considering different
![]() (see figure caption for details). One may note that at intermediate redshift and higher
redshift the luminosity-limit is driven by the X-ray flux limit of
the eBCS and MACS catalogs, respectively. On the other hand, we expect that in the redshift range where the minimum
(see figure caption for details). One may note that at intermediate redshift and higher
redshift the luminosity-limit is driven by the X-ray flux limit of
the eBCS and MACS catalogs, respectively. On the other hand, we expect that in the redshift range where the minimum ![]() is constrained
by the radio sensitivity, radio halos with
is constrained
by the radio sensitivity, radio halos with
![]() in the range
120-240 MHz (Fig. 10, black lines) can be detected
in clusters of X-ray luminosity about 3 times higher than that of clusters with
in the range
120-240 MHz (Fig. 10, black lines) can be detected
in clusters of X-ray luminosity about 3 times higher than that of clusters with
![]() GHz halos (Fig. 10, magenta lines).
GHz halos (Fig. 10, magenta lines).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13063f10.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg157.png)
|
Figure 10:
Minimum X-ray luminosity of clusters with detectable halos at
|
| Open with DEXTER | |
In Fig. 11, we show the cumulative and
differential number counts of radio halos expected from the
LOFAR follow-up of eBCS and MACS clusters at 120 MHz.
This is obtained from Eq. (12) and by taking into
account both the selection criteria illustrated in Fig. 10 and
the sky coverage of the eBCS and MACS surveys. The inflection in the number counts at z = 0.3 is caused by the change in the X-ray selection criteria (see Fig. 10) between the eBCS (
![]() )
and the MACS (
)
and the MACS (
![]() )
cluster sample. We expect that the LOFAR all-sky survey, with a planned sensitivity in line with the case
)
cluster sample. We expect that the LOFAR all-sky survey, with a planned sensitivity in line with the case
![]() mJy/beam (Fig. 11, upper panels), will discover about 130 radio halos out of the
mJy/beam (Fig. 11, upper panels), will discover about 130 radio halos out of the ![]() 400 clusters in the eBCS and MACS catalogs.
Remarkably, about 40% of these radio halos are expected to have
400 clusters in the eBCS and MACS catalogs.
Remarkably, about 40% of these radio halos are expected to have
![]() MHz,
thus to be halos with extreme steep spectra at GHz frequencies. The
majority of radio halos in eBCS and MACS clusters is expected to be
found at z = 0.2-0.4, while the small number of clusters at
MHz,
thus to be halos with extreme steep spectra at GHz frequencies. The
majority of radio halos in eBCS and MACS clusters is expected to be
found at z = 0.2-0.4, while the small number of clusters at
![]() with X-ray flux above the flux limit of the MACS catalog does not
allow a statistically solid expectations, although we may expect
a couple of radio halos hosted in MACS clusters at this redshift.
At this redshift, we expect that only major mergers in massive clusters (
with X-ray flux above the flux limit of the MACS catalog does not
allow a statistically solid expectations, although we may expect
a couple of radio halos hosted in MACS clusters at this redshift.
At this redshift, we expect that only major mergers in massive clusters (
![]() )
can generate radio halos with
)
can generate radio halos with
![]() GHz (Fig. 4, right panel). The powerful radio halo discovered in the cluster MACS J0717.5 +3745 (e.g., Bonafede et al. 2009; van Weeren et al. 2009) is consistent with these expectations.
GHz (Fig. 4, right panel). The powerful radio halo discovered in the cluster MACS J0717.5 +3745 (e.g., Bonafede et al. 2009; van Weeren et al. 2009) is consistent with these expectations.
Figure 11 (lower panels) shows the expected number counts of
radio halos assuming the more conservative case ![]() mJy/b that
is suitable for exploring the potential of the LOFAR MS3 commissioning survey. In this case, about 80 radio halos are expected to be found in eBCS
and MACS clusters, and about 20 of these halos are expected to have
mJy/b that
is suitable for exploring the potential of the LOFAR MS3 commissioning survey. In this case, about 80 radio halos are expected to be found in eBCS
and MACS clusters, and about 20 of these halos are expected to have
![]() MHz.
We note that the number of radio halos expected to be detected in
follow-up observations of eBCS and MACS clusters increases by less than
a factor of 2 because of a substantial drop in radio sensitivity
from
MHz.
We note that the number of radio halos expected to be detected in
follow-up observations of eBCS and MACS clusters increases by less than
a factor of 2 because of a substantial drop in radio sensitivity
from ![]() to 0.25 mJy/b. This is not surprising as the majority of radio
halos that are expected to be discovered by deep radio observations
should be found in galaxy clusters of X-ray luminosity below the
luminosity-threshold of the eBCS and MACS catalogs
(e.g., Fig. 10).
to 0.25 mJy/b. This is not surprising as the majority of radio
halos that are expected to be discovered by deep radio observations
should be found in galaxy clusters of X-ray luminosity below the
luminosity-threshold of the eBCS and MACS catalogs
(e.g., Fig. 10).
The eBCS cluster sample contains 300 galaxy clusters at z<0.3 and covers the northern hemisphere. The redshift and X-ray luminosity distribution of
eBCS clusters is public (Ebeling et al. 1998, 2000) and thus we can
provide a more quantitative expectation based
on e.g., the more conservative case, MS3-like that assumes that ![]() mJy/beam at 120 MHz
(in this case, the selection function of
clusters in the
mJy/beam at 120 MHz
(in this case, the selection function of
clusters in the ![]() -z plane is reported in Fig. 10,
solid lines at z<0.3).
-z plane is reported in Fig. 10,
solid lines at z<0.3).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13063f11a.ps}\includegraphic...
...m,clip]{13063f11c.ps}\includegraphics[width=8cm,clip]{13063f11d.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg163.png)
|
Figure 11:
Integrated ( left) and differential ( right) number counts of radio halos from radio follow up of eBCS and MACS clusters (see text). Calculations are shown for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13063f12a.ps}\includegraphics[width=8cm,clip]{13063f12b.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg164.png)
|
Figure 12:
Number distributions of radio halos in eBCS clusters from radio
follow-up are shown in different X-ray luminosity bins of the hosting
clusters and in two redshift bins : 0-0.2 ( left panel) and 0.2-0.3 ( right panel). Calculations are obtained assuming a sensitivity at 120 MHz,
|
| Open with DEXTER | |
In Fig. 12, we show the distribution of the expected
radio halos in the eBCS clusters in two redshift
intervals: 0-0.2 and 0.2-0.3 (left and right panels, respectively).
We find that radio observations at 120 MHz are expected to
discover radio halos in about 60 clusters, i.e., in about 20%
of eBCS clusters. In addition, about 12 of these halos are expected to have very steep radio spectra,
![]() MHz (magenta, shadowed
region in Fig. 12).
MHz (magenta, shadowed
region in Fig. 12).
Finally, the percentage of clusters with radio halos is expected to increase with the X-ray luminosity of the hosting clusters. This is particularly relevant in the redshift interval z=0-0.2 when comparing with expectations calculated based on the assumption that the fraction of clusters hosting radio halos is constant with cluster mass (Fig. 12 dashed lines, see caption). Consequently, LOFAR will be able to readily test this unique expectation of the turbulent re-acceleration model.
4 Summary and conclusions
We have performed Monte Carlo simulations to model the formation and
evolution of giant radio halos in the framework of the merger-induced
particle acceleration scenario (see Sect. 2). Following Cassano
et al. (2006a),
we have used homogeneous models that assume a) an average value of
the magnetic field strength in the radio halo volume that scales with
cluster mass as
![]() ;
and b) that a fraction,
;
and b) that a fraction, ![]() ,
of the
,
of the
![]() work done by subclusters crossing the main clusters during mergers goes into magneto-acoustic
turbulence. Although simple, these models reproduce the presently
observed fraction of galaxy clusters with radio halos and the scalings
between the monochromatic radio power of halos at 1.4 GHz and the
mass and X-ray luminosity of the host clusters (e.g., Cassano
et al. 2006a, 2008; Venturi et al. 2008), provided that the model parameters
work done by subclusters crossing the main clusters during mergers goes into magneto-acoustic
turbulence. Although simple, these models reproduce the presently
observed fraction of galaxy clusters with radio halos and the scalings
between the monochromatic radio power of halos at 1.4 GHz and the
mass and X-ray luminosity of the host clusters (e.g., Cassano
et al. 2006a, 2008; Venturi et al. 2008), provided that the model parameters
![]() lie within a fairly constrained range of values (Fig. 7 in Cassano et al. 2006a); in the present paper, we have adopted a reference set of parameters, i.e.,
lie within a fairly constrained range of values (Fig. 7 in Cassano et al. 2006a); in the present paper, we have adopted a reference set of parameters, i.e.,
![]() G, b=1.5,
G, b=1.5,
![]() ,
that fall in that range.
,
that fall in that range.
In Fig. 6, we show that the expected number counts of giant radio halos at
![]() GHz
obtained with this set of parameters are in good agreement with both
the data at low redshift (NVSS-XBACS selected radio halos, Giovannini
et al. 1999) and intermediate redshift (clusters in the ``GMRT radio halo survey'', Venturi et al. 2007, 2008).
GHz
obtained with this set of parameters are in good agreement with both
the data at low redshift (NVSS-XBACS selected radio halos, Giovannini
et al. 1999) and intermediate redshift (clusters in the ``GMRT radio halo survey'', Venturi et al. 2007, 2008).
The most important expectation of the turbulent re-acceleration scenario
is that the synchrotron spectrum of radio halos should become gradually steeper above a frequency,
![]() ,
that is determined by the energetics of the merger events that generate
the halos and by the electron radiative losses (e.g., Fujita
et al. 2003; Cassano & Brunetti 2005).
Consequently, the population of radio halos is expected to consist of a
mixture of halos with different spectra, steep-spectrum halos being
more common in the Universe than those with flatter spectra
(e.g., Cassano et al. 2006a). The discovery of these very steep-spectrum halos will allow us to test the above theoretical conjectures.
,
that is determined by the energetics of the merger events that generate
the halos and by the electron radiative losses (e.g., Fujita
et al. 2003; Cassano & Brunetti 2005).
Consequently, the population of radio halos is expected to consist of a
mixture of halos with different spectra, steep-spectrum halos being
more common in the Universe than those with flatter spectra
(e.g., Cassano et al. 2006a). The discovery of these very steep-spectrum halos will allow us to test the above theoretical conjectures.
In Sect. 2, we have
derived the expected radio halo luminosity functions
(RHLF) at frequency
![]() that account for the contributions
of the different populations of radio halos with
that account for the contributions
of the different populations of radio halos with
![]() .
The RHLF are obtained combining the theoretical mass function
of radio halos (of different
.
The RHLF are obtained combining the theoretical mass function
of radio halos (of different
![]() )
with the
radio power-cluster mass correlation (Eq. (4)).
The expected monochromatic radio power at
)
with the
radio power-cluster mass correlation (Eq. (4)).
The expected monochromatic radio power at
![]() of halos hosted
by clusters with mass
of halos hosted
by clusters with mass ![]() is extrapolated from the observed
P(1.4)-
is extrapolated from the observed
P(1.4)-![]() correlation by assuming simple scaling relations, appropriate for
homogeneous models, that account for the dependence of the emitted
synchrotron power on
correlation by assuming simple scaling relations, appropriate for
homogeneous models, that account for the dependence of the emitted
synchrotron power on
![]() (Eqs. (8), (9)).
(Eqs. (8), (9)).
As a relevant case, we calculate the expected RHLF at
![]() MHz
(Fig. 5).
The shape of the RHLF can be approximated by a power law over more than
two orders of magnitude in radio power. Homogeneous models imply that
scalings between
MHz
(Fig. 5).
The shape of the RHLF can be approximated by a power law over more than
two orders of magnitude in radio power. Homogeneous models imply that
scalings between
![]() ,
cluster mass and the radio luminosity at
,
cluster mass and the radio luminosity at
![]() ,
,
![]() are given by
are given by
and from Eq. (9) and the
i.e., radio halos with higher
In Sect. 3, we discussed the expected number counts of radio halos at 120 MHz that would allow us to explore most effectively the potential of upcoming LOFAR surveys in constraining present models.
A crucial step in this analysis is the estimate of the minimum
diffuse flux from giant radio halos that is detectable by these
surveys. Because the LOFAR capabilities will become clearer during the
upcoming commissioning phase, we exploit two complementary approaches:
i) we required that at least half of the radio halo emission is
above a fixed brightness-threshold, ![]() (F being the rms of LOFAR surveys; ii) we required that the signal from the radio halo is
(F being the rms of LOFAR surveys; ii) we required that the signal from the radio halo is ![]()
![]() in at least 5 beam areas of LOFAR observations. In both cases we
assume that the radial profile of radio halos has a fixed shape
calibrated by means of several well studied halos at 1.4 GHz,
which introduces a potential source of uncertainty.
in at least 5 beam areas of LOFAR observations. In both cases we
assume that the radial profile of radio halos has a fixed shape
calibrated by means of several well studied halos at 1.4 GHz,
which introduces a potential source of uncertainty.
Despite the uncertainties caused by the unavoidable simplifications
in our calculations, the expected number counts of radio halos
highlights the potential of future LOFAR surveys.
By assuming the expected sensitivity of the LOFAR all-sky
survey (e.g., Röttgering 2009; priv. comm.), rms = 0.1 mJy/b, and
![]() ,
we predict that about 350 giant radio halos (
,
we predict that about 350 giant radio halos (![]() 200 considering the case ii)) can be detected at redshift
200 considering the case ii)) can be detected at redshift ![]() 0.6. This means that LOFAR will increase the statistics of these sources by a factor of
0.6. This means that LOFAR will increase the statistics of these sources by a factor of ![]() 20 with respect to present-day surveys. About 55% of
these halos are predicted with a synchrotron spectral
index
20 with respect to present-day surveys. About 55% of
these halos are predicted with a synchrotron spectral
index
![]() in the range 250-600 MHz, and would brighten
only at lower frequencies, which are inaccessible to present observations.
Most important, the spectral properties of the population of radio halos
are expected to change with the increasing sensitivity
of the surveys as steep spectrum radio halos
are expected to populate the low-power end of the RHLF.
A large fraction of radio halos with spectra steeper than
in the range 250-600 MHz, and would brighten
only at lower frequencies, which are inaccessible to present observations.
Most important, the spectral properties of the population of radio halos
are expected to change with the increasing sensitivity
of the surveys as steep spectrum radio halos
are expected to populate the low-power end of the RHLF.
A large fraction of radio halos with spectra steeper than
![]() (e.g., Fig. 9)
is expected to allow a robust discrimination between different models
of radio halos, for instance in this case simple energetic arguments
would exclude a secondary origin of the emitting electrons
(e.g., Brunetti 2004; Brunetti et al. 2008).
(e.g., Fig. 9)
is expected to allow a robust discrimination between different models
of radio halos, for instance in this case simple energetic arguments
would exclude a secondary origin of the emitting electrons
(e.g., Brunetti 2004; Brunetti et al. 2008).
Because of the large number of expected radio halos, a potential
problem with these surveys is the identification of
halos and their hosting clusters. As a matter of fact, we expect that
LOFAR surveys will detect radio halos in galaxy clusters with masses
![]()
![]() at intermediate redshift. On the other hand, statistical samples of
X-ray selected clusters, which are unique tools for identifying the
hosting clusters, typically select more massive clusters at
intermediate z.
Consequently, we explored the potential of the first LOFAR surveys as
deep follow-ups of available X-ray selected samples of galaxy clusters.
at intermediate redshift. On the other hand, statistical samples of
X-ray selected clusters, which are unique tools for identifying the
hosting clusters, typically select more massive clusters at
intermediate z.
Consequently, we explored the potential of the first LOFAR surveys as
deep follow-ups of available X-ray selected samples of galaxy clusters.
We calculate the radio halo number counts expected from
the follow-up of clusters in the eBCS and MACS samples which contain ![]() 400 galaxy clusters in the redshift range 0-0.6.
We expect that the LOFAR all-sky survey, with a planned sensitivity in
line with
400 galaxy clusters in the redshift range 0-0.6.
We expect that the LOFAR all-sky survey, with a planned sensitivity in
line with
![]() mJy/b,
will discover about 130 radio halos in eBCS and MACS clusters and
that about 40% of these radio halos will have a very steep spectrum,
with
mJy/b,
will discover about 130 radio halos in eBCS and MACS clusters and
that about 40% of these radio halos will have a very steep spectrum,
with
![]() MHz.
The majority of radio halos in eBCS and MACS clusters are expected
to be at z = 0.2-0.4, while the small number of clusters at
MHz.
The majority of radio halos in eBCS and MACS clusters are expected
to be at z = 0.2-0.4, while the small number of clusters at
![]() in the MACS catalog does not allow us to form a statistically solid
expectations, although we expect a couple of radio halos to be hosted
by MACS clusters at this redshift.
in the MACS catalog does not allow us to form a statistically solid
expectations, although we expect a couple of radio halos to be hosted
by MACS clusters at this redshift.
The MS3 survey will be carried out in 2010,
covering the northern hemisphere, and is expected to reach a noise
level of about 0.5 mJy/b at 150 MHz, implying a sensitivity
to diffuse emission from galaxy clusters of about one order of
magnitude (assuming
![]() )
higher than present surveys (e.g., NVSS, Condon et al. 1998;
VLSS, Cohen et al. 2007, WENSS, Rengelink et al. 1997).
)
higher than present surveys (e.g., NVSS, Condon et al. 1998;
VLSS, Cohen et al. 2007, WENSS, Rengelink et al. 1997).
We considered MS3 pointings towards the fields of the about 300 galaxy clusters at
![]() in the eBCS catalogs.
We found that about 60 radio halos are expected to be detected by
MS3 observations in these clusters, 25% of them (10-15 halos) with
in the eBCS catalogs.
We found that about 60 radio halos are expected to be detected by
MS3 observations in these clusters, 25% of them (10-15 halos) with
![]() MHz. Fairly sensitive GMRT observations of eBCS clusters at
redshift 0.2-0.3 are already available (Venturi et al. 2007, 2008), and
in a few cases we expect that radio halos would be detectable in the MS3 images,
where no diffuse radio emission is detected at 610 MHz. We also find that MS3 observations of eBCS clusters at z=0-0.2
can be used to test the increase in the fraction of cluster with radio
halos, with the X-ray luminosity of the host clusters, which is a
unique prediction of our model (Fig. 12).
MHz. Fairly sensitive GMRT observations of eBCS clusters at
redshift 0.2-0.3 are already available (Venturi et al. 2007, 2008), and
in a few cases we expect that radio halos would be detectable in the MS3 images,
where no diffuse radio emission is detected at 610 MHz. We also find that MS3 observations of eBCS clusters at z=0-0.2
can be used to test the increase in the fraction of cluster with radio
halos, with the X-ray luminosity of the host clusters, which is a
unique prediction of our model (Fig. 12).
The most important simplification of our calculations is the use of
homogeneous models. Non-homogeneous approaches, which model the spatial
dependence of the acceleration efficiency and magnetic field in the
halo volume (e.g., Brunetti et al. 2004),
and possibly their combination with future numerical simulations, will
provide an additional step in interpreting LOFAR data. Also the use of
the extended PS theory is expected to introduce some biases. For
instance, it is well-known that the PS mass function underpredicts the
expected number of massive clusters (
![]() )
at higher redshift,
)
at higher redshift,
![]() ,
by a factor of
,
by a factor of ![]() 2 with respect to that found in N-body simulations (e.g., Governato et al. 1999; Bode et al. 2001; Jenkins et al. 2001).
In our model since the vast majority of halos at these redshift is
associated with massive clusters, the use of the PS mass function
implies that the RHNC at
z> 0.4-0.5 could be underestimated by a similar factor. A
refinement of the approach proposed in the present paper could be
achieved by using galaxy cluster merger trees extracted from N-body simulations. These would also allow a more realistic description of the merger events (e.g., spatially resolved, multiple mergers).
2 with respect to that found in N-body simulations (e.g., Governato et al. 1999; Bode et al. 2001; Jenkins et al. 2001).
In our model since the vast majority of halos at these redshift is
associated with massive clusters, the use of the PS mass function
implies that the RHNC at
z> 0.4-0.5 could be underestimated by a similar factor. A
refinement of the approach proposed in the present paper could be
achieved by using galaxy cluster merger trees extracted from N-body simulations. These would also allow a more realistic description of the merger events (e.g., spatially resolved, multiple mergers).
In the present paper, we focus on a reference set of model parameters. Cassano et al. (2006a)
discussed the dependence of model expectations at 1.4 GHz on these
parameters. Based on their analysis, we expect that all the general
results given in the present paper are independent of the adopted
parameter values. The expected number counts of halos should change by
a factor of ![]() 2-2.5 considering sets of model parameters within the region (
2-2.5 considering sets of model parameters within the region (
![]() ,
b,
,
b, ![]() )
that allow us to reproduce the observed
)
that allow us to reproduce the observed
![]() correlation. In this case, the number of halos that we expect decreases between super-linear sets of parameters (b>1 and
correlation. In this case, the number of halos that we expect decreases between super-linear sets of parameters (b>1 and
![]() G) and sub-linear cases (b<1 and
G) and sub-linear cases (b<1 and
![]() G) (see also Fig. 4 in Cassano et al. 2006b); a more detailed study will be presented in a future paper.
G) (see also Fig. 4 in Cassano et al. 2006b); a more detailed study will be presented in a future paper.
We thank the anonymous referee for useful comments. This work is partially supported by ASI and INAF under grants PRIN-INAF 2007, PRIN-INAF 2008 and ASI-INAF I/088/06/0.
References
- Bacchi, M., Feretti, L., Giovannini, G., et al. 2003, A&A, 400, 465 [Google Scholar]
- Blasi, P., 2001, APh, 15, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Blasi, P., & Colafrancesco, S. 1999, Astropart. Phys., 12, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Bode, P., Bahcall, N. A., Ford, E. B. et al. 2001, ApJ, 551, 15 [Google Scholar]
- Bonafede, A., Feretti, L., Giovannini, G., et al. 2009, A&A, 503, 707 [Google Scholar]
- Böhringer, H., Voges, W., Huchra, J. P., et al. 2000, ApJS, 129, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., Schuecker, P., Guzzo, L., et al. 2004, A&A, 425, 367 [Google Scholar]
- Brunetti, G. 2004, JKAS, 37, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., & Lazarian, A. 2007, MNRAS, 378, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., Setti, G., Feretti, L., et al. 2001, MNRAS, 320, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., Blasi, P., Cassano, R., et al. 2004, MNRAS, 350, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., Venturi, T., & Dallacasa, D., et al. 2007, ApJ, 670, 5 [Google Scholar]
- Brunetti, G., Giacintucci, S., Cassano, R., et al. 2008, Nature, 455, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, C., Cassano, R., Dolag, K., & Setti, G. 2009, A&A, 507, 661 [Google Scholar]
- Brüggen, M., Ruszkowski, M., Simionescu, A., et al. 2005, ApJ, 631, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Buote, D. A. 2001, ApJ, 553, 15 [Google Scholar]
- Cassano, R., & Brunetti, G. 2005, MNRAS 357, 1313 [NASA ADS] [CrossRef] [Google Scholar]
- Cassano, R., Brunetti, G., & Setti, G. 2006a, MNRAS 369, 1577 [NASA ADS] [CrossRef] [Google Scholar]
- Cassano, R., Brunetti, G., & Setti, G. 2006b, Astr. Nachr. 327, 557 [Google Scholar]
- Cassano, R., Brunetti, G., & Venturi, T. 2008, et al. A&A, 480, 687 [Google Scholar]
- Cohen, A. S., Lane, W. M., Cotton, W. D., et al. 2007, AJ, 134, 1245 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Dallacasa, D., Brunetti, G., Giacintucci, S., et al. 2009, ApJ, 699, 1288 [NASA ADS] [CrossRef] [Google Scholar]
- Dennison, B. 1980, ApJ, 239 [Google Scholar]
- Dolag, K., Bartelmann, M., & Lesch, H. 2002, A&A, 387, 383 [Google Scholar]
- Ebeling, H., Voges, W., Bohringer, H., et al. 1996, MNRAS, 281, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., Böhringer, H., et al. 1998, MNRAS, 301, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., Allen, S. W., et al. 2000, MNRAS, 318, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., & Henry, J. P. 2001, ApJ, 553, 668 [Google Scholar]
- Ellingson, S. W., Clarke, T. E., Cohen, A., et al. 2009, Proc. of the IEEE, 97, Issue8, 1421 [Google Scholar]
- Enßlin, T. A., Biermann, P. L., Klein, U., et al. 1998, A&A, 332, 395 [Google Scholar]
- Enßlin, T. A., & Röttgering, H. 2002, A&A, 396, 83 [Google Scholar]
- Feretti, L. 2005, in X-Ray and Radio Connections, published electronically by NRAO, ed. L.O. Sjouwerman, & K. K. Dyer [Google Scholar]
- Ferrari, C., Govoni, F., Schindler, S., Bykov, A. M., & Rephaeli, Y. 2008, Space Sci. Rev., 134, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Fujita, Y., Takizawa, M., & Sarazin, C. L. 2003, ApJ 584, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Giovannini, G., Tordi, M., & Feretti, L. 1999, NewA 4, 141 [Google Scholar]
- Governato, F., Babul, A., Quinn, T., et al. 1999, MNRAS, 307, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Govoni, F., Feretti, L., Giovannini, G., et al. 2001, A&A, 376, 803 [Google Scholar]
- Govoni, F., Markevitch, M., Vikhlinin, A., et al. 2004, ApJ, 605, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Hwang C.-Y. 2004, JKAS, 37, 461 [NASA ADS] [Google Scholar]
- Hoeft, M., & Brüggen, M. 2007, MNRAS, 375, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeft, M., Brüggen, M., Yepes, G., Gottlber, S., & Schwope, A. 2008, MNRAS, 391, 1511 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, A., Frenk, C. S., White, S. D. M., et al. 2001, MNRAS, 321, 372 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Liang, H., Hunstead, R. W., Birkinshaw, M., et al. 2000, ApJ, 544, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Lacey, C., & Cole, S. 1993, MNRAS, 262, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Miniati, F., Jones, T. W., Kang, H., et al. 2001, ApJ, 562, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Petrosian, V. 2001, ApJ, 557, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Pfrommer, C., Enßlin, T. A., & Springel, V. 2008, MNRAS, 385, 1211 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Rengelink, R. B., Tang, Y., de Bruyn, A. G., et al. 1997, A&AS, 124, 259 [Google Scholar]
- Röttgering, H. J. A., Braun, R., Barthel, P. D., et al. 2006, proceedings of the conference Cosmology, galaxy formation and astroparticle physics on the pathway to the SKA, Oxford, April 10-12 [astro-ph/0610596] [Google Scholar]
- Ryu, D., Kang, H., Hallman, E., et al. 2003, ApJ, 593, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Ryu, D., Kang, H., Cho, J., et al. 2008, Science, 320, 909 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sarazin, C. L. 1999, ApJ, 520, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R., Sievers, A., Thiemann, H. 1987, A&A, 182, 21 [Google Scholar]
- Schlickeiser, R., & Miller, J. A. 1998, ApJ, 492, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Schuecker, P., Böhringer, H., Reiprich, T. H., et al. 2001, A&A, 378, 408 [Google Scholar]
- Springel, V., White, S. D. M., & Jenkins, A. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Subramanian, K., Shukurov, A., & Haugen, N. E. L. 2006, MNRAS, 366, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Thierbach, M., Klein, U., & Wielebinski, R. 2003, A&A, 397, 53 [Google Scholar]
- Trümper, J., 1993, Science, 260, 1769 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Venturi, T., Giacintucci, S., Brunetti, G., et al. 2007, A&A, 463, 937 [Google Scholar]
- Venturi, T., Giacintucci, S., Dallacasa, et al. 2008, A&A, 484, 327 [Google Scholar]
- van Weeren, R. J., Röttgering, H. J. A., Bruggen M, et al. 2009, A&A, 505, 991 [Google Scholar]
Footnotes
- ... (LOFAR)
![[*]](/icons/foot_motif.png)
- http://www.lofar.org
- ... merger
![[*]](/icons/foot_motif.png)
- The cascading timescale of large-scale turbulence is expected to be of the same order as the cluster-cluster crossing time (e.g., Cassano & Brunetti 2005; Brunetti & Lazarian 2007).
- ...2002)
![[*]](/icons/foot_motif.png)
- Dolag et al. (2002) found a scaling
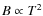 ,
which would imply that
,
which would imply that
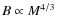 if the virial scaling
if the virial scaling
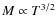 is assumed.
is assumed.
- ...-correction
![[*]](/icons/foot_motif.png)
- For simplicity,
we also consider as observables those halos with
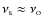 regardless of their redshift. This would slightly affect only the number counts of halos with
regardless of their redshift. This would slightly affect only the number counts of halos with
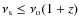 that represent a minimal fraction of our halo population.
that represent a minimal fraction of our halo population.
- ... approaches
![[*]](/icons/foot_motif.png)
- The 120 MHz LOFAR survey will have a full resolution of 5-6 arcsec, thus we are considering the case of tapered images that increase the sensitivity to extended emission without changing significantly the point source sensitivity (due to the large number of inner LOFAR stations).
All Figures
![\begin{figure}
\par\includegraphics[width=7.3cm,height=6.5cm,clip]{13063fg1.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg67.png)
|
Figure 1:
A schematic representation of the theoretical synchrotron spectra of radio halos with different values of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,height=7cm]{13063fg2.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg68.png)
|
Figure 2:
Ratio
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13063f3a.ps}\includegraphics[width=7.5cm,clip]{13063f3b.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg69.png)
|
Figure 3:
Fraction of clusters with radio halos, with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13063f4a.ps}\includegraphics[width=7.5cm,clip]{13063f4b.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg70.png)
|
Figure 4:
Fraction of clusters with radio halos
with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13063fg5.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg107.png)
|
Figure 5:
Radio halo luminosity function at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13063fg6.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg108.png)
|
Figure 6: All-sky integrated RHNCs for: (1) z=0.044-0.2, obtained by considering a minimum mass of clusters constrained at any z by the XBACS X-ray flux limit (Ebeling et al. 1996) (dashed black line), and by combining the above mass-constraint with that implied by the NVSS sensitivity (following Cassano et al. 2008, see their Fig. 3) (solid upper black line); (2) z=0.2-0.32, obtained by considering the X-ray luminosity-range of the GMRT cluster sample (Venturi et al. 2007, 2008, red lower line). Black filled points are the observed RHNC of giant radio halos from NVSS-selected clusters in the redshift range 0.044-0.2, re-normalized to account for the NVSS and XBACS sky coverage (and XBACS completeness). Red open points are the observed RHNC of giant radio halos in the GMRT cluster sample (with redshift z=0.2-0.32), re-normalized to account for the sky coverage of the GMRT cluster sample. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13063f7a.ps}\includegraphics[width=7.5cm,clip]{13063f7b.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg118.png)
|
Figure 7:
Minimum flux ( left panel) and power ( right panel) of detectable radio halos at 120 MHz using Eq. (10) (solid lines) and Eq. (11) (dashed lines), where
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13063f8a.ps}\includegraphics[width=7.5cm,clip]{13063f8b.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg125.png)
|
Figure 8:
Number (all-sky) of radio halos with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13063fg9.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg135.png)
|
Figure 9:
Spectral index distribution of radio halos, calculated for the range 120-330 MHz, for the number counts in Fig. 8 ( left panel) and assuming
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13063f10.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg157.png)
|
Figure 10:
Minimum X-ray luminosity of clusters with detectable halos at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13063f11a.ps}\includegraphic...
...m,clip]{13063f11c.ps}\includegraphics[width=8cm,clip]{13063f11d.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg163.png)
|
Figure 11:
Integrated ( left) and differential ( right) number counts of radio halos from radio follow up of eBCS and MACS clusters (see text). Calculations are shown for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13063f12a.ps}\includegraphics[width=8cm,clip]{13063f12b.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa13063-09/Timg164.png)
|
Figure 12:
Number distributions of radio halos in eBCS clusters from radio
follow-up are shown in different X-ray luminosity bins of the hosting
clusters and in two redshift bins : 0-0.2 ( left panel) and 0.2-0.3 ( right panel). Calculations are obtained assuming a sensitivity at 120 MHz,
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



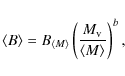
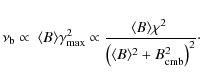
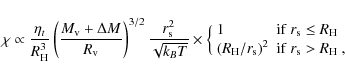
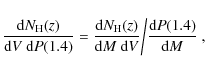
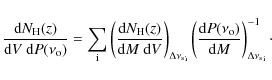

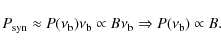
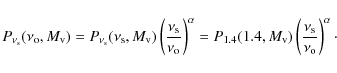
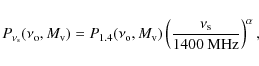
![\begin{displaymath}f_{\min}(z)\simeq 10^{-3}\Big(\frac{\xi ~ F}{0.5 {\rm mJy/beam}}\Big)~
\theta_{\rm H}^2(z)~~ [{\rm mJy}],
\end{displaymath}](/articles/aa/full_html/2010/01/aa13063-09/img123.png)