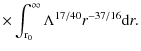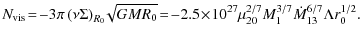| Issue |
A&A
Volume 509, January 2010
|
|
|---|---|---|
| Article Number | A45 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200912875 | |
| Published online | 15 January 2010 | |
The structure of thin accretion discs around magnetised stars
S. B. Tessema1,2 - U. Torkelsson2
1 - Department of Physics, Addis Ababa University,
PO Box 1176, Addis Ababa, Ethiopia
2 - Department of Physics, University of Gothenburg, SE 412 96 Gothenburg, Sweden
Received 13 July 2009 / Accepted 30 September 2009
Abstract
Aims. We determine the steady-state of an axisymmetric thin accretion disc with an internal dynamo around a magnetised star.
Methods. Starting from the vertically integrated equations of
magnetohydrodynamics we derive a single ordinary differential equation
for a thin accretion disc around a massive magnetic dipole and
integrate this equation numerically from the outside inwards.
Results. Our numerical solution shows that the torque between
the star and the accretion disc is dominated by the contribution from
the dynamo in the disc. The location of the inner edge of the accretion
disc varies between ![]() and
and
![]() depending mainly on the strength and direction of the magnetic field generated by the dynamo in the disc
depending mainly on the strength and direction of the magnetic field generated by the dynamo in the disc
Key words: accretion, accretion discs - magnetohydrodynamics (MHD) - magnetic fields - stars: neutron - X-rays: stars - stars: pre-main sequence
1 Introduction
In this paper we present a new solution for an accretion disc around a magnetic star. This star could be a neutron star, a white dwarf, or a T Tauri-star, but we assume that it is a neutron star since it is easy to measure the torque between the neutron star and the accretion disc by timing the X-ray pulses from the neutron star. The new feature of our solution is to include the effect of an internal dynamo in the accretion disc. By doing this we hope to be able to explain the torque reversals that have been observed in some X-ray pulsars.
Shakura & Sunyaev (1973) formulated the standard model of a geometrically thin,
optically thick accretion disc.
They were able to obtain an
analytical solution of the height-integrated hydrodynamic equations,
after having introduced the
![]() -prescription for the turbulent stress,
which transports the angular momentum outwards through the disc;
however, they did not explain why the disc is turbulent in the first place,
since a disc in Keplerian rotation is stable according to Rayleigh's criterion.
Balbus & Hawley (1991) instead showed that it is unstable if there is a
weak magnetic field in the disc.
Subsequent numerical simulations (e.g. Hawley et al. 1995; Balbus & Hawley 1998)
confirmed that this
instability generates turbulence and that the resulting
turbulent stresses transport
angular momentum outwards.
-prescription for the turbulent stress,
which transports the angular momentum outwards through the disc;
however, they did not explain why the disc is turbulent in the first place,
since a disc in Keplerian rotation is stable according to Rayleigh's criterion.
Balbus & Hawley (1991) instead showed that it is unstable if there is a
weak magnetic field in the disc.
Subsequent numerical simulations (e.g. Hawley et al. 1995; Balbus & Hawley 1998)
confirmed that this
instability generates turbulence and that the resulting
turbulent stresses transport
angular momentum outwards.
The interaction between a magnetised star and a surrounding accretion disc is one of the most poorly understood aspects of accretion. At the same time, it is central for our understanding of the spin evolution of objects as diverse as T Tauri stars and X-ray pulsars. The magnetic field of the star penetrates the surrounding accretion disc and couples the two. According to the Ghosh & Lamb (1979b,a) model, the part of the accretion disc that is located inside the corotation radius provides a spin up torque on the star, since it is rotating faster than the star, while the more slowly rotating outer part of the accretion disc brakes the star. The net torque is determined by the location of the inner edge of the disc, which moves inwards as the accretion rate increases, thereby increasing the spin up-torque on the star.
Campbell (1997) proposes physical descriptions of the magnetic diffusivity in terms of turbulence or buoyancy, and Campbell & Heptinstall (1998a,b) solve the resulting equations numerically. For both forms of diffusivity, the magnetic coupling between the disc and the star leads to an enhanced dissipation in the inner part of the accretion disc compared to the standard Shakura & Sunyaev (1973) model. This raises the temperature such that electron scattering dominates Kramer's opacity at larger radii than is otherwise the case, thus increasing the fraction of the disc that is subject to the (Lightman & Eardley 1974) instability. Brandenburg & Campbell (1998) considered a form of magnetic diffusivity that allows further analytical progress to be made, but the qualitative results remain the same.
All the models predict a positive correlation between the accretion rate and the torque on the neutron star and even predict a negative torque on the neutron star at very low accretion rates. Timing of X-ray pulsars during outbursts of Be/X-ray transients have provided at least some qualitative support for such a correlation (e.g. Parmar et al. 1989). The BATSE instrument on the Compton Gamma Ray Observatory made it possible to extend this database significantly (Bildsten et al. 1997). In particular there are a few X-ray pulsars with permanent discs that are oscillating between phases of constant spin-up and constant spin-down without a significant difference in the X-ray luminosity between these states, which appears to contradict the standard model for a disc-accreting X-ray pulsar.
Nelson et al. (1997) propose that these torque-reversals can be the result of transitions between co-rotating and counter-rotating accretion discs, though several other models have also been proposed. Torkelsson (1998) argue that the torque between an accreting star and its disc can be enhanced by the presence of a magnetic field generated by the turbulence in the accretion disc. The torque reversals are then the result of a reversal of the magnetic field generated by this dynamo. However, he did not construct a self-consistent model of the accretion disc. The aim of this paper is to construct such a model of an accretion disc with an internal dynamo around a magnetic star. We work in the spirit of Shakura & Sunyaev (1973) and assume that the disc is geometrically thin. In Sect. 2 we start from the equations of magnetohydrodynamics (MHD) and derive a single ordinary differential equation for the radial structure of the accretion disc. We then present numerical solutions of this equation in Sect. 3 and discuss the properties of these solutions in Sect. 4. Finally we summarise our conclusions in Sect. 5.
2 Mathematical formulation
We study a steady, thin axisymmetric Keplerian disc around a star with a magnetic dipole field. The basic equations describing the structure of the thin accretion disc can be derived from the equations of magnetohydrodynamics.
2.1 Conservation of mass
In steady state the continuity equation takes the form
where
where
and H is the halfthickness of the disc. For a steady disc the integral of Eq. (2) gives
which is the accretion rate.
2.2 Conservation of momentum
If assuming a steady state the Navier-Stoke's equation can be written as
where P is pressure,
The radial component of Navier- Stoke's equation is
For a thin accretion disc
which shows that the disc rotates in a Keplerian fashion.
In similar manner, the vertical component of the momentum equation for a
steady flow is
Neglecting vertical outflows and assuming the magnetic field to be weak the equation reduces to the equation of hydrostatic equilibrium
Using H as the halfthickness of the disc, the pressure at the midplane of the disc is
but the hydrostatic equilibrium can also be expressed as
which shows that the Keplerian velocity is highly supersonic in a thin accretion disc, as assumed above.
The azimuthal component of Navier-Stoke's equation
reduces to
We neglect
where the specific angular momentum
where
In this paper we consider the effect of adding
a large-scale toroidal field
that is generated by an internal dynamo in the accretion disc. Such
a dynamo is a natural consequence of the magnetohydrodynamic turbulence in the
accretion disc (e.g. Balbus & Hawley 1998). To estimate the size of
![]() ,
we assume for the moment that the viscous stress in the accretion disc is due to the internal magnetic stress
,
we assume for the moment that the viscous stress in the accretion disc is due to the internal magnetic stress
where we use the Shakura & Sunyaev (1973) prescription for the viscosity in the last equality. Based on the results of numerical simulations of magnetohydrodynamic turbulence in accretion discs (e.g. Brandenburg et al. 1995) Torkelsson (1998) argues that
where
where
We can now estimate the magnetic pressure in the accretion disc, to which
the toroidal magnetic field is the main contributor. According
to Eq. (17), the
pressure is approximately
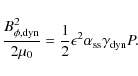
|
(18) |
Since we use
The vertical magnetic field can likewise be split up into two
components; (i) the stellar dipolar magnetic field, whose value in the stellar
equatorial plane is
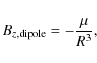
|
(19) |
where
We can now expand the product
![]() as
as
| |
= | ||
| = | |||
| (20) |
As we see below the term
2.3 Conservation of energy
For a slow inflow of matter through an optically thick disc,
the local viscous dissipation
![]() is balanced by the
radiative losses
is balanced by the
radiative losses
![]() This gives us
This gives us
where
and we assume that the opacity is given by Kramer's law
where
Equation (22) should also contain a term describing the
magnetic dissipation
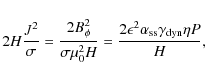
|
(25) |
where
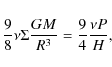
|
(26) |
so we see that the magnetic dissipation is negligible as long as
2.4 Structure equations
We reduce these equations to a single ordinary differential equation for the
radial structure of the accretion disc. First we assume the equation of state
of an ideal gas,
where
which gives us a relation between H and
The viscous stress tensor gives us the equation
which we solve for the density of the gas
The optical depth of the disc is
Using Eqs. (22) and (32) we get
where
The pressure is then given by
where
The
where
The magnetic field due to the shear can be written as:
where
is the corotation radius, at which the Keplerian angular velocity is the same as the stellar angular velocity. Here
Equation (21) gives us an ordinary differential equation for y
where
and
The solution of Eq. (41) approaches the Shakura-Sunyaev solution at large radii, thus giving us the boundary condition
We introduce the dimensionless variable ![]() through
through
and a dimensionless radial coordinate through
where
which is given by putting the magnetic pressure equal to the ram pressure of the accreting fluid (e.g. Frank et al. 2002). Here
where
and
is the fastness parameter.
3 Numerical solution
3.1 Global solutions
We integrate Eq. (47) inwards from a large radius, usually
![]() ,
to which we impose the boundary condition that
,
to which we impose the boundary condition that
![]() ,
which is similar to the approach by Brandenburg & Campbell (1998), but most studies
of accretion discs have rather applied a boundary condition
at the inner edge of the disc, and then integrated the equations outwards.
,
which is similar to the approach by Brandenburg & Campbell (1998), but most studies
of accretion discs have rather applied a boundary condition
at the inner edge of the disc, and then integrated the equations outwards.
There are two possible boundary conditions that can be applied at the inner
edge of the accretion disc, either that
![]() ,
which corresponds
to that
,
which corresponds
to that ![]() and
and ![]() at the inner edge (case D), or that
at the inner edge (case D), or that

|
(50) |
which means that the viscosity does not at all contribute to driving the accretion at this radius. Case D is the boundary condition that has been most widely used and that was adopted for instance by Shakura & Sunyaev (1973). In this case the density drops to zero because the inflow velocity becomes infinite, which is of course not realistic, and a more accurate treatment shows that the inflow becomes transonic close to this position Paczynski & Bisnovatyi-Kogan (1981). In case V the inflow at the inner edge of the accretion disc is driven completely by the transfer of excess angular momentum from the accreting matter to the stellar magnetic field (e.g. Wang 1995).
For our fiducial model, we take a neutron star of
![]() and a magnetic moment of 1020 T m3, which is accreting at
and a magnetic moment of 1020 T m3, which is accreting at
![]() .
The dimensionless parameters
.
The dimensionless parameters ![]() and
and
![]() are, respectively,
1 and 10 in
our fiducial model, while
are, respectively,
1 and 10 in
our fiducial model, while
![]() .
The exact values of
.
The exact values of
![]() and
and
![]() are unimportant, since we
vary the parameter
are unimportant, since we
vary the parameter ![]() below, but
below, but ![]() influences the solutions
in its own way as is shown at the end of this section.
We consider three different spin
periods with corresponding
corotation radii and fastness parameters (see Table 1). The system
goes into the propeller regime for
influences the solutions
in its own way as is shown at the end of this section.
We consider three different spin
periods with corresponding
corotation radii and fastness parameters (see Table 1). The system
goes into the propeller regime for
![]() (e.g. Illarionov & Sunyaev 1975;
Ghosh & Lamb 1979a,b).
(e.g. Illarionov & Sunyaev 1975;
Ghosh & Lamb 1979a,b).
Table 1: Spin parameters of the models.
Firstly, for a spin period of 7 s and
![]() and - 1,
we get the solutions shown from the top to the bottom of Fig. 1.
The
and - 1,
we get the solutions shown from the top to the bottom of Fig. 1.
The
![]() and -0.1 solutions have case D inner boundaries at 4.7 and 1.6
and -0.1 solutions have case D inner boundaries at 4.7 and 1.6 ![]() ,
respectively, while the other three
solutions have case V inner boundaries (Fig. 2).
The inner boundary is close to
,
respectively, while the other three
solutions have case V inner boundaries (Fig. 2).
The inner boundary is close to ![]() if
if
![]() which corresponds to the absence of an internal disc dynamo, but moves outwards
as
which corresponds to the absence of an internal disc dynamo, but moves outwards
as
![]() increases.
In case V, the solution continues inside
the inner edge of the accretion disc, but the viscosity counteracts the accretion,
which is instead driven by the magnetic stresses. This regime has been
described by Campbell (1998), who discusses how the disc is disrupted in this
region, we assume that this region belongs to a boundary layer
that we do not attempt to model in this paper.
On the other hand, all solutions approach the Shakura-Sunyaev solution at large radii, as
required by our boundary condition.
increases.
In case V, the solution continues inside
the inner edge of the accretion disc, but the viscosity counteracts the accretion,
which is instead driven by the magnetic stresses. This regime has been
described by Campbell (1998), who discusses how the disc is disrupted in this
region, we assume that this region belongs to a boundary layer
that we do not attempt to model in this paper.
On the other hand, all solutions approach the Shakura-Sunyaev solution at large radii, as
required by our boundary condition.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg1.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg155.png)
|
Figure 1:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg2.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg158.png)
|
Figure 2:
|
| Open with DEXTER | |
By increasing the spin peroid to 100 s, we see that the
![]() solution also develops a case V inner boundary (Fig. 3),
but there are only small quantitative
changes for the
solution also develops a case V inner boundary (Fig. 3),
but there are only small quantitative
changes for the
![]() and +1 solutions. (The inner boundary
of the
and +1 solutions. (The inner boundary
of the
![]() solution is now located at
solution is now located at
![]() .)
The dependence of the solution on the spin period can be better seen in
Fig. 4, where we vary the spin period, when
.)
The dependence of the solution on the spin period can be better seen in
Fig. 4, where we vary the spin period, when ![]() is fixed
to 0. Then
is fixed
to 0. Then ![]() has a local minimum for
has a local minimum for
![]() s, but this minimum
weakens and disappears as the spin period is increased. This is similar to
how
s, but this minimum
weakens and disappears as the spin period is increased. This is similar to
how ![]() depends on
depends on ![]() .
For
.
For
![]()
![]() has an
unphysical negative local minima at a small radius, such that the physical
solution has a case D boundary at several Alfvén radii. As
has an
unphysical negative local minima at a small radius, such that the physical
solution has a case D boundary at several Alfvén radii. As ![]() is
increased, the local minimum grows and the solution develops a case V inner boundary when the
minimum becomes positive. Increasing
is
increased, the local minimum grows and the solution develops a case V inner boundary when the
minimum becomes positive. Increasing ![]() removes the
local minimum further and the solution becomes a strictly decreasing function of r,
which asymptotically approaches
removes the
local minimum further and the solution becomes a strictly decreasing function of r,
which asymptotically approaches ![]() as required by our boundary
condition.
Increasing
as required by our boundary
condition.
Increasing ![]() has a similar effect to decreasing
has a similar effect to decreasing ![]() (Fig. 5).
(Fig. 5).
3.2 The structure of an accretion disc
The physical structure of the accretion disc can now be expressed
using ![]() and
and
![]() We have that
We have that
In Fig. 6 we show the surface density as a function of radius for the fiducial neutron star with a spin peroid of 7 s and
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg3.eps}
\par\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg178.png)
|
Figure 3:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg4.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg179.png)
|
Figure 4:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg5.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg182.png)
|
Figure 5:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg6.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg183.png)
|
Figure 6:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg7.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg184.png)
|
Figure 7:
VR as a function of r for the fiducial neutron star with
a spin period of 7 s
and
|
| Open with DEXTER | |
We plot the magnetic fields for our fiducial model with varying ![]() and
spin periods of 7 and 100 s, respectively,
in Figs. 9 and 10,
respectively. The corotation radius, at which
and
spin periods of 7 and 100 s, respectively,
in Figs. 9 and 10,
respectively. The corotation radius, at which
![]() changes sign, occurs inside of
the inner edge of the accretion disc for
changes sign, occurs inside of
the inner edge of the accretion disc for
![]() and -1, and for these values of
and -1, and for these values of ![]() ,
,
![]() is the dominant magnetic field everywhere inside the disc.
is the dominant magnetic field everywhere inside the disc.
In general the ratio of the magnetic field due to shear to that generated by the internal dynamo is
It is only during rather extreme conditions that the shear-induced field can dominate at small radii, and the dynamo is always dominant at large radii.
4 Discussion
4.1 The inner edge of the accretion disc
We have shown that there are two different forms of inner disc boundaries that
can be found among our solutions. We denote these as case D and V, respectively.
Case D occurs only for sufficiently negative ![]() ,
while case V covers a
larger part of the parameter domain that we have studied.
We summarise our values for the inner radius of the accretion disc in
Table 2. We see that the inner radius can be significantly
larger than the Alfvén radius when
,
while case V covers a
larger part of the parameter domain that we have studied.
We summarise our values for the inner radius of the accretion disc in
Table 2. We see that the inner radius can be significantly
larger than the Alfvén radius when
![]() is close to unity.
This is the result of the dynamo enhancing the coupling of the
stellar magnetic field to the accretion flow, such that it dominates
the viscous torque at larger radii than would otherwise be the case.
is close to unity.
This is the result of the dynamo enhancing the coupling of the
stellar magnetic field to the accretion flow, such that it dominates
the viscous torque at larger radii than would otherwise be the case.
4.2 The angular momentum balance
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg8.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg191.png)
|
Figure 8:
|
| Open with DEXTER | |
Table 2: The inner edge of the accretion disc and its torque on the fiducial neutron star.
To understand the exchange of angular momentum between the accretion disc and its environment we multiply Eq. (21) by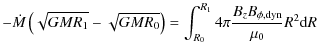
|
|||
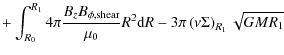
|
|||

|
(61) |
The lefthand side is the difference between the angular momentum that is advected out of the inner edge of the accretion disc and that which is fed into the disc at its outer edge and the righthand side describes the contribution of magnetic and viscous torques to the angular momentum balance. The term
Secondly, we have the magnetic torques on the neutron star, which we divide into one part due to the shear
and a second part due to the dynamo
Finally the viscous stress at the inner edge of the accretion disc transports angular momentum outwards away from the neutron star resulting in a torque
This torque vanishes for a case D inner boundary. We can now calculate the torques on our fiducial neutron star for our choices of spin periods and
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg9.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg282.png)
|
Figure 9:
The toroidal magnetic field for the fiducial neutron star with a
spin period of 7 s. The solid and dashed lines show the field generated by
the dynamo for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg0.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg283.png)
|
Figure 10:
The toroidal magnetic field for the fiducial neutron star with a
spin period of 100 s. The solid and dashed lines show the field generated by
the dynamo for
|
| Open with DEXTER | |
Let us now compare our results with the BATSE data (Bildsten et al. 1997).
The 7.6 s X-ray pulsar 4U1626-67 was observed to spin down at a rate
![]() and spin up at
and spin up at
![]() .
These spin
variations correspond to torques
.
These spin
variations correspond to torques
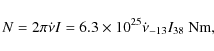
|
(66) |
where I is the moment of inertia of the neutron star, which we measure in 1038 kg m2, and we measure the spin acceleration in units of 10-13 Hz s-1. The required torque is significantly larger than what is produced by
We explain the torque reversals in the same way as in Torkelsson (1998), where
the dynamo undergoes a field
reversal, which in our model corresponds to ![]() changing sign. One
might speculate that, during this field reversal, the disc passes through a state
corresponding to
changing sign. One
might speculate that, during this field reversal, the disc passes through a state
corresponding to
![]() ,
in which the disc will have a smaller inner
radius than during the states with an active dynamo. The closer to the surface
of the neutron star that the accretion disc extends,
the more of the X-ray emission from the accretion columns it can absorb and
re-process.
Torkelsson (1998) showed that the observed time scales on which the torques
remain constant in the sources 4U1626-67, 4U1626-67, and
4U1626-67 are comparable
to the global viscous time scales of their accretion discs, which constrains
the mechanism that is responsible for the reversals of the magnetic field.
,
in which the disc will have a smaller inner
radius than during the states with an active dynamo. The closer to the surface
of the neutron star that the accretion disc extends,
the more of the X-ray emission from the accretion columns it can absorb and
re-process.
Torkelsson (1998) showed that the observed time scales on which the torques
remain constant in the sources 4U1626-67, 4U1626-67, and
4U1626-67 are comparable
to the global viscous time scales of their accretion discs, which constrains
the mechanism that is responsible for the reversals of the magnetic field.
5 Conclusions
We have investigated the interaction between a magnetic neutron star and its surrounding accretion disc in the case where the accretion disc is supporting an internal dynamo. The magnetic field that is produced by the dynamo can lead to a significant enhancement of the magnetic torque between the neutron star and the accretion disc, compared to what is seen in the model by Ghosh & Lamb (1979b,a). This extra magnetic torque can explain the large variations in spin frequencies of 4U1626-67 and 4U1626-67 (Bildsten et al. 1997). Furthermore, a reversal of the magnetic field that is generated by the dynamo, similar to the reversals that we see of the magnetic fields on the Sun, could explain the torque reversals in these objects.
From the way that we calculate the structure of the accretion disc, we find two kinds of solutions with different behaviours at the inner edge. A few of our solutions have case D boundaries at which the density and temperature go to 0 at finite radius, while most of our solutions have case V boundaries at whichthe accretion is driven entirely by the magnetic tension between the accreting matter and the neutron star. In this case there is a viscous stress between the accretion disc and the boundary layer, which can transfer angular momentum outwards at a rate that is comparable to the one at which it is advected inwards by the accreting matter itself.
We have also found that the dynamo leads to that the inner edge of the accretion disc occurs at a radius that is larger than the traditional Alfvén radius. This effect is weak, though, for a realistic value of the dynamo-generated magnetic field.
AcknowledgementsS.B.T. thanks the Department of Physics at the University of Gothenburg for hospitality and support during this project. SBT is supported in part by the Swedish Institute (SI) under their Guest Scholarship Programme. UT thanks the Department of Physics at Addis Ababa University for their hospitality. This research has made use of NASA's Astrophysics Data System. We thank an anonymous referee for comments that have improved the quality of the paper.
References
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [Google Scholar]
- Bardou, A., & Heyvaerts, J. 1996, A&A, 307, 1009 [Google Scholar]
- Bildsten, L., Chakrabarty, D., Chiu, J., et al. 1997, ApJS, 113, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., & Campbell, C. G. 1998, MNRAS, 298, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Nordlund, Å., Stein, R. F., & Torkelsson, U. 1995, ApJ, 446, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, C. G. 1997, Magnetohydrodynamics in binary stars (Dordrecht: Kluwer) [Google Scholar]
- Campbell, C. G. 1998, MNRAS, 301, 754 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, C. G., & Heptinstall, P. M. 1998a, MNRAS, 299, 31, [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, C. G., & Heptinstall, P. M. 1998b, MNRAS, 301, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J., King, A. R., & Raine, D. 2002, Accretion power in astrophysics (Cambridge University Press) [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979a, ApJ, 232, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979b, ApJ, 234, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1995, ApJ, 440, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Illarionov, A. F., & Sunyaev, R. A. 1975, A&A, 39, 185 [Google Scholar]
- Lightman, A. P., & Eardley, D. M. 1974, ApJ, 187, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, R. W., Bildsten, L., Chakrabarty, D., et al. 1997, ApJ, 488, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B., & Bisnovatyi-Kogan, G. 1981, Acta Astron., 31, 283 [NASA ADS] [Google Scholar]
- Parmar, A. N., White, N. E., Stella, L., Izzo, C., & Ferri, P. 1989, ApJ, 338, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [Google Scholar]
- Torkelsson, U. 1998, MNRAS, 298, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y. M. 1995, ApJ, 449, L153 [NASA ADS] [Google Scholar]
All Tables
Table 1: Spin parameters of the models.
Table 2: The inner edge of the accretion disc and its torque on the fiducial neutron star.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg1.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg155.png)
|
Figure 1:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg2.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg158.png)
|
Figure 2:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg3.eps}
\par\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg178.png)
|
Figure 3:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg4.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg179.png)
|
Figure 4:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg5.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg182.png)
|
Figure 5:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg6.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg183.png)
|
Figure 6:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg7.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg184.png)
|
Figure 7:
VR as a function of r for the fiducial neutron star with
a spin period of 7 s
and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg8.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg191.png)
|
Figure 8:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg9.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg282.png)
|
Figure 9:
The toroidal magnetic field for the fiducial neutron star with a
spin period of 7 s. The solid and dashed lines show the field generated by
the dynamo for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Paper1Figs/12875fg0.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12875-09/Timg283.png)
|
Figure 10:
The toroidal magnetic field for the fiducial neutron star with a
spin period of 100 s. The solid and dashed lines show the field generated by
the dynamo for
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



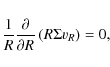
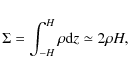
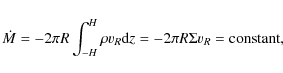


![$\displaystyle \rho\left[ v_R\frac{\partial v_R}{\partial R} -
\frac{v^{2}_\phi}{R}\right]$](/articles/aa/full_html/2010/01/aa12875-09/img31.png)
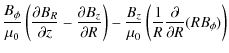
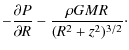
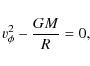
![$\displaystyle \rho \left[v_R \frac{\partial v_z}{\partial R} + v_z\frac{\partial v_z}{\partial
z}\right]$](/articles/aa/full_html/2010/01/aa12875-09/img36.png)
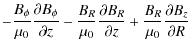
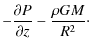

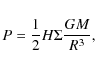
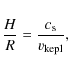
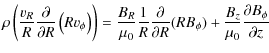
![$\displaystyle +
\frac{1}{R^{2}}\frac{\partial}{\partial R}
\left[R^{3}\rho\nu\frac{\partial}{\partial R}
\left(\frac{v_\phi}{R}\right)\right].$](/articles/aa/full_html/2010/01/aa12875-09/img43.png)
![\begin{displaymath}
\Sigma \left(v_R\frac{\partial l}{\partial R}\right) =
\le...
...ac{\partial}{\partial R}
\left(\frac{l}{R^{2}}\right)\right],
\end{displaymath}](/articles/aa/full_html/2010/01/aa12875-09/img45.png)
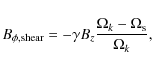
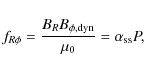

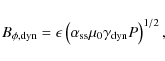

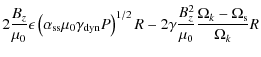
![$\displaystyle + \frac{1}{R}\frac{\mbox{d}}{\mbox{d} R}\left[R^{3}\nu\Sigma
\frac{\mbox{d}}{\mbox{d} R}
\left(\frac{l}{R^{2}}\right)\right].$](/articles/aa/full_html/2010/01/aa12875-09/img83.png)
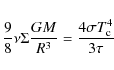
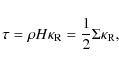
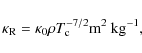

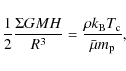

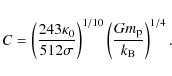
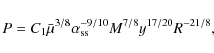
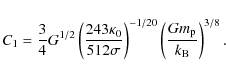
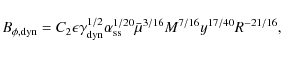
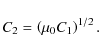
![\begin{displaymath}
B_{\phi,{\rm shear}} = \frac{\mu\gamma}{R^{3}}
\left[1- \left(\frac{R}{R_{{\rm c}}}\right)^{3/2}\right],
\end{displaymath}](/articles/aa/full_html/2010/01/aa12875-09/img112.png)
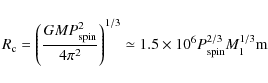
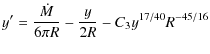
![$\displaystyle - C_{4}R^{-9/2}\left[1 - \left(\frac{R}{R_{\rm c}}\right)^{3/2}\right],$](/articles/aa/full_html/2010/01/aa12875-09/img120.png)
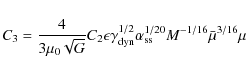
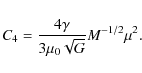
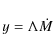
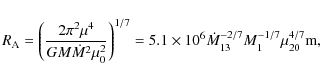

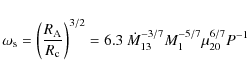

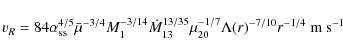
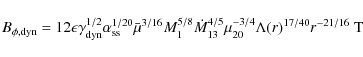
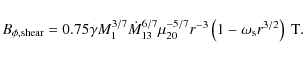
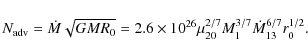
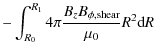
![$\displaystyle \times \int_{\rm r_{0}}^{\infty}\left[r^{-4}\left(1 - \omega_{\rm s}r^{3/2}\right)\right]\mbox{d}r$](/articles/aa/full_html/2010/01/aa12875-09/img276.png)