| Issue |
A&A
Volume 509, January 2010
|
|
|---|---|---|
| Article Number | A61 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200912805 | |
| Published online | 19 January 2010 | |
The old and heavy bulge of
M 31![[*]](/icons/foot_motif.png)
I. Kinematics and stellar populations
R. P. Saglia1,2 - M. Fabricius1,2 - R. Bender1,2 - M. Montalto2,1 - C.-H. Lee2,1 - A. Riffeser2,1 - S. Seitz2,1 - L. Morganti1,2 - O. Gerhard1,2 - U. Hopp2,1
1 - Max-Planck Institut für extraterrestrische Physik,
Giessenbachstrasse, Postfach 1312, 85741 Garching, Germany
2 - Universitäts-Sternwarte München, Scheinerstrasse 1, 81679 München,
Germany
Received 1 July 2009 / Accepted 28 October 2009
Abstract
We present new optical long-slit data along six position angles of the
bulge region of M 31. We derive accurate stellar and
gas kinematics reaching 5 arcmin from the center, where the
disk light contribution is always less than 30%, and out to
8 arcmin along the major axis, where the disk
provides 55% of the total light. We show that the velocity
dispersions of McElroy (1983) are severely underestimated (by up to
50 km s-1). As a consequence,
previous dynamical models have underestimated the stellar mass of
M 31's bulge by a factor of 2. As a further
consequence, the light-weighted velocity dispersion of the galaxy grows
to 166 km s-1 and to
170 km s-1 if rotation is also
taken into account, thus reducing the discrepancy between the predicted
and measured mass of the black hole at the center of
M 31 from a factor of 3 to a factor
of 2. The kinematic position angle varies with distance,
pointing to triaxiality, but a quantitative conclusion can be reached
only after simultaneous proper dynamical modeling of the bulge and disk
components is performed. We detect gas counterrotation near the bulge
minor axis. We measure eight emission-corrected Lick indices. They are
approximately constant on circles. Using simple stellar population
models we derive the age, metallicity and ![]() -element overabundance
profiles. Except for the region in the inner arcsecs of the galaxy, the
bulge of M 31 is uniformly old (
-element overabundance
profiles. Except for the region in the inner arcsecs of the galaxy, the
bulge of M 31 is uniformly old (![]() 12 Gyr,
with many best-fit ages at the model grid limit of 15 Gyr),
slightly
12 Gyr,
with many best-fit ages at the model grid limit of 15 Gyr),
slightly ![]() -elements
overabundant (
-elements
overabundant (
![]() )
and of solar metallicity, in agreement with studies of the resolved
stellar components. The predicted u-g,
g-r and r-i
Sloan color profiles match the dust-corrected observations reasonably
well, within the known limitations of current simple stellar population
models. The stellar populations have approximately radially constant
mass-to-light ratios (
)
and of solar metallicity, in agreement with studies of the resolved
stellar components. The predicted u-g,
g-r and r-i
Sloan color profiles match the dust-corrected observations reasonably
well, within the known limitations of current simple stellar population
models. The stellar populations have approximately radially constant
mass-to-light ratios (
![]() for a Kroupa IMF), which is in agreement with the stellar dynamical
estimates based on our new velocity dispersions. In the inner arcsecs
the luminosity-weighted age drops to 4-8 Gyr, while the
metallicity increases to above three times the solar value. Starting
from 6 arcmin from the center along the major axis, the mean
age drops to
for a Kroupa IMF), which is in agreement with the stellar dynamical
estimates based on our new velocity dispersions. In the inner arcsecs
the luminosity-weighted age drops to 4-8 Gyr, while the
metallicity increases to above three times the solar value. Starting
from 6 arcmin from the center along the major axis, the mean
age drops to ![]() 8 Gyr
with slight supersolar metallicity (
8 Gyr
with slight supersolar metallicity (![]() +0.1 dex) and
+0.1 dex) and ![]() -element
overabundance (
-element
overabundance (![]() +0.2 dex)
for a mass-to-light ratio
+0.2 dex)
for a mass-to-light ratio ![]() .
Diagnostic diagrams based on the [OIII]/H
.
Diagnostic diagrams based on the [OIII]/H![]() and [NI]/H
and [NI]/H![]() emission
line equivalent widths (EWs) ratios indicate that the gas is ionized by
shocks outside 10 arcsec, but an AGN-like ionizing source
could be present near the center. We speculate that a gas-rich minor
merger happened some 100 Myr ago, causing the observed minor
axis gas counterrotation, the recent star formation event and possibly
some nuclear activity.
emission
line equivalent widths (EWs) ratios indicate that the gas is ionized by
shocks outside 10 arcsec, but an AGN-like ionizing source
could be present near the center. We speculate that a gas-rich minor
merger happened some 100 Myr ago, causing the observed minor
axis gas counterrotation, the recent star formation event and possibly
some nuclear activity.
Key words: galaxies: kinematics and dynamics - galaxies: individual: M 31 - galaxies: stellar content
1 Introduction
This is the first of two papers presenting new optical spectra for the bulge of M 31 to study its stellar populations and assess its triaxiality through dynamical modeling. We present here the new data and constrain the stellar populations.
In the past 50 years papers studying the dynamics of our neighbor-galaxy M 31 have been published on a regular basis, discussing gas kinematics, both by optical spectroscopy (Boulesteix et al. 1987; Pellet 1976), and in HI (Kent 1989a; Braun 1991; Chemin et al. 2009, and references therein), stellar kinematics concentrating on the central regions to probe the black hole dynamics (Bender et al. 2005) or they were considering the whole bulge (McElroy 1983). The data were used to construct dynamical models of the galaxy (Widrow et al. 2003; Klypin et al. 2002) and possibly probe the tridimensional distribution of its stellar components. The question of the triaxiality of the M 31 bulge has been posed early on (Stark 1977; Gerhard 1986) and is of significant importance for the understanding of M 31, but a definitive quantitative modeling of both photometry and kinematics is still lacking. A bar could also be present (Athanassoula & Beaton 2006; Beaton et al. 2007). Moreover, investigations of the stellar populations of the central regions of M 31 through the measurement of Lick indices have been performed (Davidge 1997). They indicate the presence of a young and metal rich population in the inner arcsecs of the galaxy. Studies of the resolved stellar population of the bulge of M 31 have assessed at the same time that the global stellar population of the M 31 bulge must be as old as the bulge of the Milky Way and of solar metallicity, resolving previous claims of younger ages as due to crowding problems (Stephens et al. 2003; Sarajedini & Jablonka 2005).
Two considerations convinced us of the necessity to collect
new
optical spectroscopic information for the bulge of
M 31,
supplementary to the old age of the dataset of McElroy
(1983). The
first one is the start of PAndromeda, an
extensive monitoring campaign of M 31 with the
PanSTARRS-1 telescope
and camera system (Kaiser 2004),
which is in principle able
to deliver hundreds of pixel lensing events, probing both bulge and
disk regions. Detailed stellar population and dynamical models, based
on accurate spectral information, are needed to interpret these events
as due to a compact baryonic dark matter component (the so-called
MACHOs) rather than self-lensing of stellar populations (Kerins
et al. 2001;
Riffeser et al. 2006).
The second is
the development of new modeling techniques of both simple stellar
populations and stellar dynamical systems. On the one hand, the
interpretation of Lick indices (Worthey et al. 1994) in
terms of the most recent simple stellar population models (Maraston
1998, 2005) which
takes into account the
variation of ![]() Fe]
(Thomas et al. 2003),
allows for the accurate determination of the stellar population ages,
metallicities and overabundances, and therefore the prediction of
stellar mass-to-light ratios. On the other hand, new dynamical
modeling codes like N-MAGIC (De Lorenzi et al. 2007)
allow for the flexible dynamical modeling of triaxial structures,
optimally exploiting the information contained in the line-of-sight
velocity distributions that modern programs for the analysis of the
galaxy optical spectra are able to extract (Bender et al. 1994) well beyond the
mean velocities and velocity dispersions
of McElroy (1983).
Fe]
(Thomas et al. 2003),
allows for the accurate determination of the stellar population ages,
metallicities and overabundances, and therefore the prediction of
stellar mass-to-light ratios. On the other hand, new dynamical
modeling codes like N-MAGIC (De Lorenzi et al. 2007)
allow for the flexible dynamical modeling of triaxial structures,
optimally exploiting the information contained in the line-of-sight
velocity distributions that modern programs for the analysis of the
galaxy optical spectra are able to extract (Bender et al. 1994) well beyond the
mean velocities and velocity dispersions
of McElroy (1983).
In the following we discuss our new spectroscopic observations of the bulge of M 31. A future paper (Morganti et al., in prep.) will report on the dynamical modeling. In Sect. 2 we present the observations and the data reduction. In Sect. 3 we derive the stellar and gas kinematics and the strengths of the absorption and emission lines. In Sect. 4 we discuss the modeling of the new spectroscopic data. We analyze the stellar population in Sect. 4.1 and discuss previous axisymmetric dynamical models of the bulge of M 31 in Sect. 4.2. Section 4.3 considers the possible excitation sources compatible with the observed emission line EW ratios. We draw our conclusions in Sect. 5.
2 Observations and data reduction
We observed the bulge of M 31 using the Low
Resolution Spectrograph
(LRS, Hill et al. 1998)
at the Hobby-Eberly Telescope
equipped with a 1.5 arcsec wide, 3.5 arcmin long
slit, the E2 grism
and a Ford Aerospace CCD device, with ![]() 15
15 ![]() m pixels
(usable range 2750
m pixels
(usable range 2750 ![]() 900 pixels)
and a scale of 0.235 arcsec per
pixel. We covered the wavelength range
900 pixels)
and a scale of 0.235 arcsec per
pixel. We covered the wavelength range ![]() Å
with
0.36 Å per pixel and an instrumental resolution of
Å
with
0.36 Å per pixel and an instrumental resolution of
![]() km s-1.
During the period of August 10-19, 2007 (see
Table 1)
M 31 was observed in service mode along six position
angles. The seeing varied from 1.3 to 2.5 arcsec. At
each position
angle three 10-min exposures were taken, the first one centered on
the galaxy, the second one shifted to the west (decreasing RA)
3.5 arcmin in the slit direction, and the third one shifted to
the east
(increasing RA) 3.5 arcmin in the slit direction. Finally, on
the September 15, 2009 we collected a 20-min exposure along
the major
axis, shifted 5 arcmin from the center in the eastern
direction. Figure 1
shows the distribution of the
19 slit-M 31-pointings on
the sky with the naming convention given in Table 1, where
MJ is short for the major axis and MN for the minor axis. The position
angle of the bulge MJ axis
km s-1.
During the period of August 10-19, 2007 (see
Table 1)
M 31 was observed in service mode along six position
angles. The seeing varied from 1.3 to 2.5 arcsec. At
each position
angle three 10-min exposures were taken, the first one centered on
the galaxy, the second one shifted to the west (decreasing RA)
3.5 arcmin in the slit direction, and the third one shifted to
the east
(increasing RA) 3.5 arcmin in the slit direction. Finally, on
the September 15, 2009 we collected a 20-min exposure along
the major
axis, shifted 5 arcmin from the center in the eastern
direction. Figure 1
shows the distribution of the
19 slit-M 31-pointings on
the sky with the naming convention given in Table 1, where
MJ is short for the major axis and MN for the minor axis. The position
angle of the bulge MJ axis ![]() is fixed from our 2MASS photometry
(see Sect. 4.2
and Fig. 13).
Note that this is different from the position angleof the major axis of
the disk of
M 31 (
is fixed from our 2MASS photometry
(see Sect. 4.2
and Fig. 13).
Note that this is different from the position angleof the major axis of
the disk of
M 31 (![]() ,
de Vaucoulers 1958).
Apart from the MN
pointings, the slits with a given position angle are always well
aligned and have small overlaps, providing spectra out to
5 arcmin
from the center. In addition, the MJEE slit probes the major axis out
to 8 arcmin from the center. The MNE and MNW are slighly shifted from
the MNC central slit (by 34
,
de Vaucoulers 1958).
Apart from the MN
pointings, the slits with a given position angle are always well
aligned and have small overlaps, providing spectra out to
5 arcmin
from the center. In addition, the MJEE slit probes the major axis out
to 8 arcmin from the center. The MNE and MNW are slighly shifted from
the MNC central slit (by 34
![]() orthogonal to the slit to the west and
to the east respectively). Furthermore, 10-min exposures of empty
sky regions were also taken, as well as several kinematic and Lick
standard stars, wiggled and trailed along the slit.
orthogonal to the slit to the west and
to the east respectively). Furthermore, 10-min exposures of empty
sky regions were also taken, as well as several kinematic and Lick
standard stars, wiggled and trailed along the slit.
Table 1: Log of the observations.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12805f1.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg30.png)
|
Figure 1: The positions of the 19 M 31 slit pointings superimposed on a NOAO image of the Andromeda galaxy (credit Adma Block/NOAO/AURA/NSF). See Table 1 for the naming convention. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12805f2.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg31.png)
|
Figure 2: The anamorphic distortion of the LRS as mapped by tracing the peaks of the stellar spectra. The traces of nine stellar spectra are shown as full black lines and are compared to the corresponding straight lines (dashed). The interpolated differences (in pixel) between the stellar traces and the cartesian grid as a function of the position on the chip are shown coded by color. |
| Open with DEXTER | |
The data reduction followed the usual procedure described in Mehlert
et al. (2000)
under MIDAS with some additional steps
needed to correct for the spectral alignment and the anamorphism of
the LSR spectrograph. After bias subtraction and flatfielding,
the 2![]() tilt between the wavelength direction and the CCD was
removed through appropriate rebinning. Two bad columns at positions
corresponding to
tilt between the wavelength direction and the CCD was
removed through appropriate rebinning. Two bad columns at positions
corresponding to ![]() Å
were corrected by
interpolation. The wavelength calibration used Cd and Ne calibration
lamps frames taken at the end of each night, and a third order
polynomial fitting nine lines and gave a rms of less than one pixel.
Residual overall shifts in the used starting wavelength of the
wavelength
calibrated science frames were corrected by referencing to the
5577 Å sky line. After filtering cosmic ray hits, the science
frames
were rebinned to a logarithmic wavelength scale. The sky subtraction
for the M 31 frames was performed through the four
empty sky frames
available. The averaged sky continuum amounted to 3.5 counts
per
pixels (varying by at most 10% from frame to frame). This is
only 14% of the averaged flux measured at the extreme ends of
the MJE and
MJW slits, 23% at the end of the MJEE slit, but 44% at those
of the
MNE and MNW slits. In contrast, the flux per pixel in the strongest
sky line at 5577 Å is 160 counts with variations of
up to 50% from
frame to frame. We constructed a line-free and a line-only average sky
spectrum for each of the available sky frames and subtracted it with
proper scaling from the corresponding science frames. The average of
the available sky frames was used for the nights without empty sky
observations. Stars were extracted tracing the peaks corresponding to
their trails across the slit as a function of wavelength and averaging
over a 10 pixel wide window. The final spectra are averages of
the
extracted ones. This procedure also allowed us to map the anamorphic
distortions of the spectrograph, which at the short and long
wavelengths bend the spectra upwards in the upper end and downwards in
the lower end of the slit (see Fig. 2). Moreover,
the sky was estimated at the ends of the slit and subtracted. The
anamorphic mapping was used to rebin the sky subtracted frames of
M 31 on a cartesian grid. Finally, the
M 31 spectra were rebinned in
the radial direction to give approximately constant signal-to-noise
ratio.
Å
were corrected by
interpolation. The wavelength calibration used Cd and Ne calibration
lamps frames taken at the end of each night, and a third order
polynomial fitting nine lines and gave a rms of less than one pixel.
Residual overall shifts in the used starting wavelength of the
wavelength
calibrated science frames were corrected by referencing to the
5577 Å sky line. After filtering cosmic ray hits, the science
frames
were rebinned to a logarithmic wavelength scale. The sky subtraction
for the M 31 frames was performed through the four
empty sky frames
available. The averaged sky continuum amounted to 3.5 counts
per
pixels (varying by at most 10% from frame to frame). This is
only 14% of the averaged flux measured at the extreme ends of
the MJE and
MJW slits, 23% at the end of the MJEE slit, but 44% at those
of the
MNE and MNW slits. In contrast, the flux per pixel in the strongest
sky line at 5577 Å is 160 counts with variations of
up to 50% from
frame to frame. We constructed a line-free and a line-only average sky
spectrum for each of the available sky frames and subtracted it with
proper scaling from the corresponding science frames. The average of
the available sky frames was used for the nights without empty sky
observations. Stars were extracted tracing the peaks corresponding to
their trails across the slit as a function of wavelength and averaging
over a 10 pixel wide window. The final spectra are averages of
the
extracted ones. This procedure also allowed us to map the anamorphic
distortions of the spectrograph, which at the short and long
wavelengths bend the spectra upwards in the upper end and downwards in
the lower end of the slit (see Fig. 2). Moreover,
the sky was estimated at the ends of the slit and subtracted. The
anamorphic mapping was used to rebin the sky subtracted frames of
M 31 on a cartesian grid. Finally, the
M 31 spectra were rebinned in
the radial direction to give approximately constant signal-to-noise
ratio.
![\begin{figure}
\par\includegraphics[width=13cm,angle=270,clip]{12805f3a.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg34.png)
|
Figure 3:
The stellar kinematics along different position angles, folded with
respect to the center (at velocity -333.2 km s-1),
antisymmetrically for recessional velocities and H3
coefficients, symmetrically for velocity dispersions and H4
coefficients. Filled circles refer to radii with increasing RA (East),
stars to radii with decreasing RA (West). The number in the velocity
panel indicates the correction in km s-1
to the central velocity (-333.2 km s-1)
applied to achieve maximal symmetry. The plus or minus sign indicates
whether the velocities of the sides with increasing RA (the filled
dots) are receding or approaching. The vertical dotted lines mark the
transition from the central slit data to those from the outer two. For
the major axis, a further vertical dotted line marks the outer MJEE
dataset. The short-dashed vertical lines mark the seeing values of the
central slits (see Table 1).
The data of McElroy (1983,
at PA = 75, 45, 15, 165, 135 and
105 respectively) are indicated by green open circles and
triangles. The data of van der Marel et al. (1994, MJ at
PA = 55, MN at PA = 128) are shown
by the red continuous lines. The data of Kormendy & Bender (1999) are shown
in yellow (from their Calcium Triplet spectra) and magenta (from their H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12.4cm,angle=270,clip]{12805f3b.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg35.png)
|
Figure 3: continued. |
| Open with DEXTER | |
3 Kinematics and line strengths
The stellar kinematics were derived using the Fourier Correlation
Quotient technique (Bender 1990)
with the addition of an
iterative procedure to correct for the emission clearly detected in
the H![]() line
and the [OIII] and [NI] doublets similar to the
method of Sarzi et al. (2006).
The best fitting stellar
template convolved to the derived line-of-sight velocity distribution
(LOSVD) is subtracted from the galaxy spectra. Five Gaussian functions
are fitted to the residuum spectrum in correspondence to the two
doublets and the H
line
and the [OIII] and [NI] doublets similar to the
method of Sarzi et al. (2006).
The best fitting stellar
template convolved to the derived line-of-sight velocity distribution
(LOSVD) is subtracted from the galaxy spectra. Five Gaussian functions
are fitted to the residuum spectrum in correspondence to the two
doublets and the H![]() line.
Six parameters are derived: the
recessional velocity of the gas emission and its velocity dispersion
(determined by fitting just the [OIII] lines) plus five
normalization
factors. The best-fitting Gaussians are subtracted from the original
spectrum, and the stellar kinematics are derived a second time, using
the wavelength range of
4870-5470 Å. The final parameters of the
gas emission are derived by fitting the difference between the
original spectrum and the improved, iterated best-fitting stellar
kinematic template. The best-fitting template is chosen from a
pool of single star spectra and simple stellar population models from
Vazdekis (1999),
by minimizing the
line.
Six parameters are derived: the
recessional velocity of the gas emission and its velocity dispersion
(determined by fitting just the [OIII] lines) plus five
normalization
factors. The best-fitting Gaussians are subtracted from the original
spectrum, and the stellar kinematics are derived a second time, using
the wavelength range of
4870-5470 Å. The final parameters of the
gas emission are derived by fitting the difference between the
original spectrum and the improved, iterated best-fitting stellar
kinematic template. The best-fitting template is chosen from a
pool of single star spectra and simple stellar population models from
Vazdekis (1999),
by minimizing the ![]() between
the
galaxy and the LOSVD-convolved template, and this results in an almost
mismatch-free description of the galaxy spectrum. An eighth order
polynomial is used to subtract the continuum, and the first and last
three channels in the Fourier space are filtered out. Monte Carlo
simulations as described in Mehlert et al. (2000) are
performed to derive the final errors on the estimated parameters and
estimate the size of systematic errors. With the choice of the
continuum fitting and filtering given above the systematic errors are
always smaller than the statistical ones. Our tests have shown that
none of the results presented below depend on the precise order of the
continuum subtraction within the errors as soon as it is larger than
6. The measured kinematics are very precise, with statistical errors
on velocities of the order of 2 km s-1,
of the order of 3 km s-1
(i.e. 3%), on
between
the
galaxy and the LOSVD-convolved template, and this results in an almost
mismatch-free description of the galaxy spectrum. An eighth order
polynomial is used to subtract the continuum, and the first and last
three channels in the Fourier space are filtered out. Monte Carlo
simulations as described in Mehlert et al. (2000) are
performed to derive the final errors on the estimated parameters and
estimate the size of systematic errors. With the choice of the
continuum fitting and filtering given above the systematic errors are
always smaller than the statistical ones. Our tests have shown that
none of the results presented below depend on the precise order of the
continuum subtraction within the errors as soon as it is larger than
6. The measured kinematics are very precise, with statistical errors
on velocities of the order of 2 km s-1,
of the order of 3 km s-1
(i.e. 3%), on ![]() ,
less than 0.02 on H3
and H4. We investigated
the systematic effects of the sky subtraction by deriving the
kinematics from frames where
,
less than 0.02 on H3
and H4. We investigated
the systematic effects of the sky subtraction by deriving the
kinematics from frames where ![]() 10%
of the sky were additionally
subtracted. At the extreme ends of the slits differences in velocities
of up to 5 km s-1, in
10%
of the sky were additionally
subtracted. At the extreme ends of the slits differences in velocities
of up to 5 km s-1, in ![]() of up to 12 km s-1, in H3
of up to 0.03 and in H4
of up to 0.05 are seen.
of up to 12 km s-1, in H3
of up to 0.03 and in H4
of up to 0.05 are seen.
Figure 3
shows the derived stellar line of sight recessional
velocity V, the velocity
dispersion ![]() and the Hermite-Gauss
coefficients H3 and H4
following Bender, Saglia and Gerhard
(1994). Overall,
the kinematic data are symmetric with respect
to the center within the errors. Stellar rotation is detected at some
level at all position angles. Along the major axis (MJ) it keeps
rising with increasing distance from the center, reaching
and the Hermite-Gauss
coefficients H3 and H4
following Bender, Saglia and Gerhard
(1994). Overall,
the kinematic data are symmetric with respect
to the center within the errors. Stellar rotation is detected at some
level at all position angles. Along the major axis (MJ) it keeps
rising with increasing distance from the center, reaching ![]() 100 km s-1
at the last measured point at
100 km s-1
at the last measured point at ![]() 8 arcmin, where the
disk light dominates. The velocity dispersion reaches a maximum of
170 km s-1 at
8 arcmin, where the
disk light dominates. The velocity dispersion reaches a maximum of
170 km s-1 at ![]() 60 arcsec
from the center. Along or near the
major axis, where stellar rotation is clearly detected, the H3parameter
anticorrelates (as expected, see Bender et al.
1994) with the
stellar velocity out to
60 arcsec
from the center. Along or near the
major axis, where stellar rotation is clearly detected, the H3parameter
anticorrelates (as expected, see Bender et al.
1994) with the
stellar velocity out to ![]() 100 arcsec,
to change sign at larger distances (see the discussion in
Sect. 4.2).
In the inner arcsecs the signature of the central
supermassive black hole is clearly visible, with a steep increase in
velocity and in velocity dispersion. In the inner region, the
comparison
with the kinematics of van der Marel et al. (1994) along
the major and minor axis shows overall good agreement; but they
measure systematically (
100 arcsec,
to change sign at larger distances (see the discussion in
Sect. 4.2).
In the inner arcsecs the signature of the central
supermassive black hole is clearly visible, with a steep increase in
velocity and in velocity dispersion. In the inner region, the
comparison
with the kinematics of van der Marel et al. (1994) along
the major and minor axis shows overall good agreement; but they
measure systematically (![]() 0.05)
lower values of H4. Since we
agree with the data of Kormendy and Bender (1999) and we
do not expect residual systematics from our Monte Carlo tests (see
above), we trust our H4
profiles to be the correct ones. The
comparison with McElroy (1983)
shows that this old dataset
gives seriously underestimated velocity dispersions. The smallest
differences are observed along the minor axis. The discrepancy is
probably due to the sensitivity of McElroy analysis's method to the
disk light contamination (see discussion in Sect. 4.2). The
recessional velocities are in reasonable agreement.
0.05)
lower values of H4. Since we
agree with the data of Kormendy and Bender (1999) and we
do not expect residual systematics from our Monte Carlo tests (see
above), we trust our H4
profiles to be the correct ones. The
comparison with McElroy (1983)
shows that this old dataset
gives seriously underestimated velocity dispersions. The smallest
differences are observed along the minor axis. The discrepancy is
probably due to the sensitivity of McElroy analysis's method to the
disk light contamination (see discussion in Sect. 4.2). The
recessional velocities are in reasonable agreement.
As a consequence, the mean velocity dispersion used to predict
the
mass of the black hole at the center of M 31
(160 km s-1, Gültekin
et al. 2009,
corresponding to ![]() ,
three times smaller than the measured value) has to be
revised upwards. Figure 4, top, shows
that the
(angle averaged) light-weighted velocity dispersion converges to
166 km s-1 and to almost
170 km s-1 if the rotational
velocity is added in
quadrature. This results in a black hole mass only a factor of two
smaller
than the one observed. The same Figure, bottom, shows that lower values
are
derived as a function of the distance from the center if the
weighting is performed using the total isophotal light.
,
three times smaller than the measured value) has to be
revised upwards. Figure 4, top, shows
that the
(angle averaged) light-weighted velocity dispersion converges to
166 km s-1 and to almost
170 km s-1 if the rotational
velocity is added in
quadrature. This results in a black hole mass only a factor of two
smaller
than the one observed. The same Figure, bottom, shows that lower values
are
derived as a function of the distance from the center if the
weighting is performed using the total isophotal light.
The gas kinematics (
![]() and
and ![]() )
are shown in Fig. 5.
Gas velocities are almost a factor two higher than
stellar velocities, but less axisymmetric and regular. Gas velocity
dispersions are slightly larger than the instrumental resolution,
indicating intrinsic velocity dispersions of less than
80 km s-1. In the
inner 10-20 arcsec near the minor axis gas counterrotation
(i.e., the
orientation of the gas rotation changes) is observed. The gas
velocities compare reasonably well with the H
)
are shown in Fig. 5.
Gas velocities are almost a factor two higher than
stellar velocities, but less axisymmetric and regular. Gas velocity
dispersions are slightly larger than the instrumental resolution,
indicating intrinsic velocity dispersions of less than
80 km s-1. In the
inner 10-20 arcsec near the minor axis gas counterrotation
(i.e., the
orientation of the gas rotation changes) is observed. The gas
velocities compare reasonably well with the H![]() measurements of
Pellet (1976)
or Boulesteix et al. (1987).
measurements of
Pellet (1976)
or Boulesteix et al. (1987).
![\begin{figure}
\par\includegraphics[width=7cm,angle=0]{12805f4.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg41.png)
|
Figure 4:
Top: the full line shows the velocity
dispersion resulting from averaging all measured |
| Open with DEXTER | |
We measured Lick line strength index profiles on the
M 31
emission-corrected spectra as in Mehlert et al. (2000),
from H![]() to Fe5789.
to Fe5789.
As a first check, we verify that we measure line indices uniformly well across the slit. For this purpose, we analyse the spectra of the Lick standard star HD 72324 (=HR 3369) which was observed trailed along the slit. Figure 6 shows the variation of its line indices as a function of the position on the slit. The measured molecular indices Mg1 and Mg2 with their widely spread continuum windows are increasingly biased towards the ends of the slit, probably because of inaccurate spectral flat fielding where vignetting becomes important. In contrast, all the other indices are well determined and do not vary much . In the following discussion we do not consider Mg1 and Mg2 anymore. As a consequence, all (atomic) indices presented here below are measured in Angstrom.
As a second step, we assess how well we agree with the Lick
system,
since our spectra are not flux calibrated. Our indices are measured
following the bands definitions of Worthey et al. (1994)
with the corrections of Trager et al. (1998).
Figure 7
demonstrates that neither tilt nor shift are needed within
the errors, with a typical rms of 0.2 Å. The largest shift of
0.32 Å, which is significant at the 2.5 sigma level,
is observed for the H![]() line,
where, as discussed above, we have interpolated two bad columns.
We have added in quadrature the rms of each relation to the errors of
the galaxy indices.
line,
where, as discussed above, we have interpolated two bad columns.
We have added in quadrature the rms of each relation to the errors of
the galaxy indices.
Finally, Fig. 8
shows the typical effect of the
correction for a gas emission applied to the spectra. The plot shows
the
differences ![]() between the
emission-corrected index
between the
emission-corrected index ![]() and the values
and the values ![]() measured
before the correction. Before the correction, the H
measured
before the correction. Before the correction, the H![]() and Fe5015
indices are smaller (since the emission is present in the index
window) by typically 0.29 Å and 0.41 Å respectively,
and Mgb is
larger (since the emission is present in the redder continuum window)
by 0.07 Å. While the
and Fe5015
indices are smaller (since the emission is present in the index
window) by typically 0.29 Å and 0.41 Å respectively,
and Mgb is
larger (since the emission is present in the redder continuum window)
by 0.07 Å. While the ![]() H
H![]() and
and ![]() [NI] match
the EW of the emission fully,
[NI] match
the EW of the emission fully, ![]() [OIII] amounts to the
difference
between the EWs of the [OIII] doublet redder line (that falls in the
band window of the Fe5015 index) and the bluer line (that falls in the
bluer continuum window of the index). The other indices are not
affected. Again, we add in quadrature the errors on the emission EWs
of H
[OIII] amounts to the
difference
between the EWs of the [OIII] doublet redder line (that falls in the
band window of the Fe5015 index) and the bluer line (that falls in the
bluer continuum window of the index). The other indices are not
affected. Again, we add in quadrature the errors on the emission EWs
of H![]() ,
[OIII] and [NI] to the ones of the absorption line
strengths H
,
[OIII] and [NI] to the ones of the absorption line
strengths H![]() ,
Fe5015 and Mgb, respectively.
,
Fe5015 and Mgb, respectively.
Figure 9
shows the measured Lick indices profiles
for M 31. Apart from the central regions, where
rapid variations are
measured, the indices show very mild gradients, indicative of
homogeneous stellar populations (see discussion in Sect. 4.1). Along the
major axis and at distances larger than
![]() 5 arcmin
where the disk light starts to dominate, making 55% of the
total at 500 arcsec from the center, the strenght of the
5 arcmin
where the disk light starts to dominate, making 55% of the
total at 500 arcsec from the center, the strenght of the
![]() line increases,
indicative of a younger stellar population
(see the discussion in Sect. 4.1). Overall,
the indices
appear not only symmetric with respect to the center, but also
approximately circularly symmetric. As an example, if we compute
the rms of the differences of the Mgb index measured at the same
distance on the major axis and on one of the other slit positions, we
get values between 0.15 and 0.18 Å. If we now repeat
the procedure
interpolating at the same isophotal distance (using
the
ellipticity profile derived in Sect. 4.2, see
Fig. 13),
the rms increases to 0.20-0.25 Å. The same
applies to the H
line increases,
indicative of a younger stellar population
(see the discussion in Sect. 4.1). Overall,
the indices
appear not only symmetric with respect to the center, but also
approximately circularly symmetric. As an example, if we compute
the rms of the differences of the Mgb index measured at the same
distance on the major axis and on one of the other slit positions, we
get values between 0.15 and 0.18 Å. If we now repeat
the procedure
interpolating at the same isophotal distance (using
the
ellipticity profile derived in Sect. 4.2, see
Fig. 13),
the rms increases to 0.20-0.25 Å. The same
applies to the H![]() or the iron indices.
or the iron indices.
Davidge (1997)
measured Lick indices (not corrected for
gas emission) in a ![]() arcsec
area centered on M 31. His
values along the centered East-West slit are shown in
Fig. 8
on the plots for the P30 slit (nearest to the EW position).
The agreement is good.
arcsec
area centered on M 31. His
values along the centered East-West slit are shown in
Fig. 8
on the plots for the P30 slit (nearest to the EW position).
The agreement is good.
In Fig. 10
we plot the equivalent widths (EWs) of the
H![]() emission line in Å, together with the EW ratios [OIII]/H
emission line in Å, together with the EW ratios [OIII]/H![]() and [NI]/H
and [NI]/H![]() of the emission lines considered above in
logarithmic units. Note that we expect the EW ratios to vary by no
more than 10% with respect to the ratios of the emission line
fluxes,
due to the restricted wavelength range spanned by the three lines.
Given the logarithmic units, this does not affect the discussion given
in Sect. 4.3.
While the
H
of the emission lines considered above in
logarithmic units. Note that we expect the EW ratios to vary by no
more than 10% with respect to the ratios of the emission line
fluxes,
due to the restricted wavelength range spanned by the three lines.
Given the logarithmic units, this does not affect the discussion given
in Sect. 4.3.
While the
H![]() and [OIII] lines are almost always well detected, with a
signal to noise ratio larger than four, the [NI] doublets are often
weak, if not undetected. The H
and [OIII] lines are almost always well detected, with a
signal to noise ratio larger than four, the [NI] doublets are often
weak, if not undetected. The H![]() EW is approximately constant
with radius. At radii larger than
EW is approximately constant
with radius. At radii larger than ![]() 10 arcsec the same is
true for the [OIII]/H
10 arcsec the same is
true for the [OIII]/H![]() ratio
(at the value of 3) and the
[NI]/H
ratio
(at the value of 3) and the
[NI]/H![]() ratio
(at low values smaller than
ratio
(at low values smaller than ![]() 0.1). Near
the center [OIII]/H
0.1). Near
the center [OIII]/H![]() increases to
increases to ![]() ,
combined with an
increased [NI]/H
,
combined with an
increased [NI]/H![]() ratio (
ratio (![]() 1).
1).
Tables 2-4 give format examples of the measured stellar and gaseous kinematics and Lick indices as a function of distance and position angle, respectively. The full listing is available electronically at the CDS.
![\begin{figure}
\par\includegraphics[width=13cm,angle=270,clip]{12805f5.ps}
\vspace{-1mm}\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg46.png)
|
Figure 5: The gas kinematics along different position angles, folded with respect to the center, antisymmetrically for recessional velocities, symmetrically for velocity dispersions. Only data with errors smaller than 50 km s-1 are shown. Filled circles refer to radii with increasing RA, stars to radii with decreasing RA, with the same convention and zero-point shifts on radial velocities as in Fig. 3. The vertical dotted lines mark the transition from the central slit data to those from the outer two. For the major axis, a further vertical dotted line marks the outer MJEE dataset. The (red) short-dashed vertical lines mark the seeing values of the central slits (see Table 1). The data of Pellet (1976) are also shown for comparison as open circles (for increasing RA) and triangles (for decreasing RA). His 28 Å data are plotted in green, the 135 Å in red. We show his PA = 45 data as MJ, his PA = 128 as MN, his PA = 68 as P30. Moreover, the data at PA = 38 (his major axis) are shown in blue and also as MJ. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{12805f6.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg47.png)
|
Figure 6: The variation of the molecular Mg1 and Mg2 (in mag) and atomic (in Å, all the rest) line strengths as a function of position on the slit measured for the star HD 72324 (=HR 3369). The dotted line shows the values of Worthey et al. (1994). |
| Open with DEXTER | |
4 An old and massive bulge?
Before discussing the stellar populations (Sect. 4.1)
and dynamics (Sect. 4.2)
of the central 300 arcsec of M 31,
it is important to assess the light contribution of the bulge
and the disk of M 31 as a function of distance and
position angle.
According to the decomposition of Kormendy and Bender
(1999),
based on a Sersic plus exponential law fit to the
MJ photometry and very similar to the one of Kent (1989b),
the disk provides 1% of the total light at the center, 10% at
100 arcsec and 31% at a distance of
300 arcsec along the major axis, and 9%
and 25% along the minor axis respectively. The disk light
amounts
to <55% of the total at the end of the MJEE slit,
500 arcsec from
the center. The results discussed in Sect. 4.1 show
that generally old stellar populations are found out to
300 arcsec
from the center. In agreement with Stephens et al.
(2003), who
start detecting (younger) disk stars only at
distances larger than 7 arcmin from the center, we see the
effect of
the increasing importance of the younger disk component only at
distances of 400-500 arcsec from the center. In contrast, the
kinematic imprint of the disk stars is probably already visible at
distances of ![]() 100 arcsec,
especially on the major axis (see Fig. 3 and
Sect. 3).
We discuss it in Sect. 4.2.
100 arcsec,
especially on the major axis (see Fig. 3 and
Sect. 3).
We discuss it in Sect. 4.2.
4.1 Stellar populations
We study the stellar populations of the inner 5 arcmin of
M 31 (and out to 8 arcmin along the major
axis) using
the simple stellar population (SSP) models of Maraston
(1998, 2005) with a
Kroupa (2001)
IMF and the modeling of the Lick indices (LSSP) with
![]() -elements
overabundance of Thomas, Maraston and Bender
(2003). The
models cover ages t of up 15 Gyr, metallicities
[Z/H] from -2.25 dex to +0.67, and overabundances [
-elements
overabundance of Thomas, Maraston and Bender
(2003). The
models cover ages t of up 15 Gyr, metallicities
[Z/H] from -2.25 dex to +0.67, and overabundances [![]() /Fe]
from -0.3 to +0.5. We spline-interpolate the LSSP
models on a finer grid in
t, [Z/H] and [
/Fe]
from -0.3 to +0.5. We spline-interpolate the LSSP
models on a finer grid in
t, [Z/H] and [![]() /Fe] and
determine values of t, [Z/H] and [
/Fe] and
determine values of t, [Z/H] and [![]() /Fe] that
minimize the
/Fe] that
minimize the
![]() :
:
at each radius r, where
where
Figure 11
shows the resulting age, metallicity,
overabundance, color and M/L profiles along the different slit
positions. The corresponding best-fit lines to the measured indices
profiles are shown in Fig. 9. We fit
eight Lick
indices to derive three parameters, so the expected ![]() should
be
around 5. This matches the derived values rather well (see
bottom plot
of Fig. 9),
indicating that the SSP models are a
good representation of the data within their sizeable errors.
should
be
around 5. This matches the derived values rather well (see
bottom plot
of Fig. 9),
indicating that the SSP models are a
good representation of the data within their sizeable errors.
The six age, metallicity and overabundance slit profiles are very similar when overplotted as a function of radius. This is a consequence of the approximate constancy of the indices along the circles discussed above and indicates that the region with homogeneous stellar populations is not as flattened as a disk component would be, which is in agreement with what Davidge (1997) found for the inner 30 arcsec. Figure 12 shows the age, metallicity, overabundance and M/LR profiles averaged over the position angles and binned logarithmically in radius (for the MN profile, only the central slit data are included in the average).
The picture emerging from Figs. 11
and 12
is the following. At radii larger than a few arcsec
and out to ![]() 5 arcmin
from the center, the stars of the bulge
of M 31 are on average almost as old as the
universe, tend to solar
metallicity and are
5 arcmin
from the center, the stars of the bulge
of M 31 are on average almost as old as the
universe, tend to solar
metallicity and are ![]() overabundant
by 0.2-0.25 dex. This is in
agreement with Stephens et al. (2003) and
Sarjedini &
Jablonka (2005),
who find that the near infrared
luminosity function of the red giant stars of the bulge of
M 31 is
indistinguishable from the one of the Milky Way bulge and the mean
metallicity is solar. Of course, the point to point scattering in age
in the single slit profiles is large, and formally the 1-sigma lines
would sometimes allow ages as small as 5 Gyr. This is driven
by the
scattering in the H
overabundant
by 0.2-0.25 dex. This is in
agreement with Stephens et al. (2003) and
Sarjedini &
Jablonka (2005),
who find that the near infrared
luminosity function of the red giant stars of the bulge of
M 31 is
indistinguishable from the one of the Milky Way bulge and the mean
metallicity is solar. Of course, the point to point scattering in age
in the single slit profiles is large, and formally the 1-sigma lines
would sometimes allow ages as small as 5 Gyr. This is driven
by the
scattering in the H![]() ,
which ultimately correlates with the
emission correction applied. There is a metallicity gradient of
0.2 dex per radial decade out to 40 arcsec and
essentially no gradient at
larger distances where solar metallicity is reached. There is no
obvious radial variation in age or overabundance. This translates in
to moderate u-g and M/LB gradients
and almost no detectable
gradients in the g-r, r-i,
M/LV
and M/LR.
The exact values of
the stellar mass-to-light ratios depend on the assumed IMF (Kroupa
2001), which
has a slope
,
which ultimately correlates with the
emission correction applied. There is a metallicity gradient of
0.2 dex per radial decade out to 40 arcsec and
essentially no gradient at
larger distances where solar metallicity is reached. There is no
obvious radial variation in age or overabundance. This translates in
to moderate u-g and M/LB gradients
and almost no detectable
gradients in the g-r, r-i,
M/LV
and M/LR.
The exact values of
the stellar mass-to-light ratios depend on the assumed IMF (Kroupa
2001), which
has a slope ![]() for the mass range
for the mass range
![]() and
and ![]() at larger masses. Changing the
break mass from
at larger masses. Changing the
break mass from ![]() to
to ![]() lowers the M/LR
from 4
to 3.
lowers the M/LR
from 4
to 3.
Along the major axis and at distances larger than ![]() 6 arcmin,
the mean age of the stellar population drops to
6 arcmin,
the mean age of the stellar population drops to ![]() 8 Gyr, again in
agreement with Stephens et al. (2003),
who find disk
stars only at distances larger than 7 arcmin from the center.
The
metallicity is slightly supersolar (by
8 Gyr, again in
agreement with Stephens et al. (2003),
who find disk
stars only at distances larger than 7 arcmin from the center.
The
metallicity is slightly supersolar (by ![]() +0.1 dex). The
+0.1 dex). The
![]() overabundance remains high. As a consequence,
the derived mass-to-light ratio drops to
overabundance remains high. As a consequence,
the derived mass-to-light ratio drops to ![]() .
.
The situation is different in the inner arcsecs, where the
stellar
population age drops to 4-8 Gyr, the metallicity increases to
more
than three times the solar value, but the overabundance remains at
![]() 0.2 dex.
This is in agreement with the conclusions of
Davidge (1997),
who however hints at a possible further
increase of the overabundance towards the center, not seen here.
0.2 dex.
This is in agreement with the conclusions of
Davidge (1997),
who however hints at a possible further
increase of the overabundance towards the center, not seen here.
We compare the predicted Sloan color profiles to the ones
derived from
the Sloan survey, which have been dereddened using the extinction map
discussed in Montalto et al. (2009). Following
Maraston
(private communication), we apply a correction of -0.05 mag to
the
model g-r and of
+0.07 mag to the model r-i
colors. The comparison
is surprisingly good in u-g and
good in r-i, with deviations of
![]() 0.1 mag.
Some residual systematic deviations are still present in
g-r (where the models are too
red) and r-i (where the models
are
slightly too blue). This is in qualitative agreement with the
discussion of Maraston et al. (2009). This
overall match
provides an independent assessment of the line index analysis.
0.1 mag.
Some residual systematic deviations are still present in
g-r (where the models are too
red) and r-i (where the models
are
slightly too blue). This is in qualitative agreement with the
discussion of Maraston et al. (2009). This
overall match
provides an independent assessment of the line index analysis.
4.2 Axisymmetric dynamical modeling
The kinematics shown in Fig. 3 describe the light-averaged stellar motions of the bulge and disk components. In the inner arcmin this follows the bulge kinematics closely, but at larger distances the contamination by the disk becomes more and more important. Therefore, a dynamical model for the sum of the two components should be compared with Fig. 3. Qualitatively, we can expect the stellar disk to rotate much faster, possibly up to the 150 km s-1 observed in the gas (see Fig. 5) and to be colder (with velocity dispersions of the order of 60-70 km s-1) than the bulge. As a consequence, the true rotational velocity of the bulge could be smaller than, and the bulge velocity dispersion could be larger than shown in Fig. 3. Moreover, the line of sight velocity distribution in the outer regions will be dominated in the high velocity tail by disk stars. This can balance the intrinsic asymmetry of the bulge (which anticorrelates with the mean rotational velocity), possibly explaining the change in sign of the H3 coefficient observed near the major axis at distances larger than 100 arcsec. We have tested that a simple bulge plus disk kinematical model which follows the light-decomposition of Kent (1989b) can qualitatively reproduce this trend, but we postpone a quantitative analysis to Morganti et al. (in prep.).
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12805f7.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg62.png)
|
Figure 7:
The comparison between the line strengths measured here and the Lick
values for 20 stars. The dotted line shows the one-to-one
correlation, the full line the best fitting relation |
| Open with DEXTER | |
The blue lines in Fig. 3 show the fits to the data of McElroy (1983) by Widrow et al. (2003), model A (full) and model K1 (dashed). From the discussion given above, it is clear that it is dangerous to assume that McElroy's data describe the kinematics of the bulge component alone, as done by Widrow et al. (2003). Indeed, McElroy (1983) recognises that he might be underestimating the true stellar velocity dispersion due to how his analysis method reacts to disk light contamination (see his Table 3), but concludes that the effect is not large on the basis of the disk-to-bulge decomposition available at the time, which severely downplayed the role of the disk in the inner 5 arcmin.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12805f8.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg63.png)
|
Figure 8:
The effect of the gas emission correction on the H |
| Open with DEXTER | |
Apart from this intrinsic problem, the best-fit model A of Widrow
et al. (2003)
predicts a mass-to-light ratio for the bulge
(
![]() )
that is smaller than the one of the disk
(
)
that is smaller than the one of the disk
(
![]() ),
and this despite overestimating the
velocity dispersions along the minor axis. Only model K1, well
above
McElroy
),
and this despite overestimating the
velocity dispersions along the minor axis. Only model K1, well
above
McElroy ![]() s,
delivers
s,
delivers ![]() for the bulge.
Widrow et al. continue to discuss this, not taking into account
the possibility that McErloy velocities are in fact systematically too
small. Of course Widrow et al.'s model A fails to match our
kinematics,
while model K1 slightly overestimates our velocity dispersions.
Figure 11
shows that for r>10 arcsec the analysis of
the
Lick indices predicts
for the bulge.
Widrow et al. continue to discuss this, not taking into account
the possibility that McErloy velocities are in fact systematically too
small. Of course Widrow et al.'s model A fails to match our
kinematics,
while model K1 slightly overestimates our velocity dispersions.
Figure 11
shows that for r>10 arcsec the analysis of
the
Lick indices predicts ![]() ,
which is in line
with the model K1. As a consequence, the microlensing events
estimated by
Widrow et al. (2003),
which are based on their model A, are
clearly underestimates. Similarly, an upward revision of the event
rate estimates of Riffeser et al. (2006) is needed,
since this paper assumes a stellar mass-to-light ratio for the bulge
of M/LR=2.6.
The extremely low M/LR
value (0.8
,
which is in line
with the model K1. As a consequence, the microlensing events
estimated by
Widrow et al. (2003),
which are based on their model A, are
clearly underestimates. Similarly, an upward revision of the event
rate estimates of Riffeser et al. (2006) is needed,
since this paper assumes a stellar mass-to-light ratio for the bulge
of M/LR=2.6.
The extremely low M/LR
value (0.8
![]() )
favored by Chemin et al. (2009)
based on
a simple mass modeling of the HI velocities is completely ruled out
and points to the inadequacy of underlying modeling assumptions
(circular motions and spherical mass distributions).
)
favored by Chemin et al. (2009)
based on
a simple mass modeling of the HI velocities is completely ruled out
and points to the inadequacy of underlying modeling assumptions
(circular motions and spherical mass distributions).
Finally, a word on the triaxiality of the bulge or the
possible
presence of a bar. A rotating axisymmetric structure shows equal
velocity curves along slits inclined at positive or negative angles
with respect to the major or minor axis. In general, this does not
happen if the structure is triaxial or a bar is present (see
Fig. 12
of Athanassoula & Beaton 2006). In
the case of the bulge of M 31 the maximal rotation
velocity
achieved on the slits M60 and M30 are larger than the
ones reached
on slits P60 and P30 respectively, or, in other
words, the kinematic
minor axis of the M 31 bulge does not coincide with
its isophotal
minor axis. We quantify this effect by measuring how the position
angle of the kinematic major axis varies as a function of semi-major
distance. At each semi-major distance a
from the center we find
the parameters ![]() and
and ![]() which minimize the
which minimize the
![]() function:
function:
where the twelve angles
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12805f9a.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg79.png)
|
Figure 9:
The measured Lick indices profiles along the six slit positions of
M 31. The vertical dotted lines mark the ends of the
central slits. For the major axis, a further vertical dotted line marks
the outer MJEE dataset. The lines show the best-fit LSSP models (see
discussion in Sect. 4.1).
The bottom plots show the respective |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{12805f9b.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg80.png)
|
Figure 9: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13cm,angle=270,clip]{12805f10.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg81.png)
|
Figure 10:
The EW of the H |
| Open with DEXTER | |
Table 2: Format example of the measured stellar kinematics as a function of distance from the center (positive: east, negative: west) for the different position angles. The full table is available electronically at the CDS.
Table 3: Format example of the measured gas kinematics as a function of distance from the center (positive: east, negative: west) for the different position angles. The full table is available electronically at the CDS.
Table 4: Format example of the measured Lick indices as a function of distance from the center (positive: east, negative: west) for the different position angles. The full table is available electronically at the CDS.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12805f11.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg101.png)
|
Figure 11: The age, metallicity, overabundance, Sloan colors u-g (blue), g-r (green), r-i (red) and Johnson M/L profiles in the B (blue), V (green) and R (red) bands along the different slit positions. The dotted lines show the 1-sigma errors. The vertical dotted lines mark the ends of the central slits. For the major axis, a further vertical dotted line marks the outer MJEE dataset. The measured color profiles, corrected by extinction (Montalto et al. 2009), are shown as crosses. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12805f12.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg102.png)
|
Figure 11: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12805f13.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg103.png)
|
Figure 12: The age, metallicity, overabundance, and M/LR profiles (full lines) averaged over position angles and binned logarithmically in radius. The dotted lines and the bars show the corresponding rms and errors on the mean, respectively. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{12805f14.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg104.png)
|
Figure 13:
Top: the ellipticity profile as a function of
the semi-major axis distance a. Bottom:
the position angle of the kinematic major axis |
| Open with DEXTER | |
However, only a proper dynamical model that takes into account the disk contribution on top of the triaxiality of M 31's bulge and its possible figure rotation and fits not only the light distribution, mean velocities and velocity dispersion fields, but also the higher moments of the LOSVDs, can address these issues quantitatively. We postpone this discussion to Morganti et al. (in prep.).
4.3 The sources of ionizing radiation
Sarzi et al. (2009)
discuss in detail how to exploit the
[OIII]/H![]() vs. [NI]/H
vs. [NI]/H![]() diagram to constrain the properties
of the ionizing sources for the gas in elliptical and lenticular
galaxies. Their Fig. 1 shows that the diagram neatly separates
the
regions where dusty AGNs, shocks and startburst activity are
responsible for the production of emission lines, in analogy with the
standard [OI]/H
diagram to constrain the properties
of the ionizing sources for the gas in elliptical and lenticular
galaxies. Their Fig. 1 shows that the diagram neatly separates
the
regions where dusty AGNs, shocks and startburst activity are
responsible for the production of emission lines, in analogy with the
standard [OI]/H![]() vs. [OIII]/H
vs. [OIII]/H![]() diagram
of Veilleux and
Osterbrook (1987).
diagram
of Veilleux and
Osterbrook (1987).
As discussed by Sarzi et al. (2009), the
constancy of the
H![]() EW with the radius indicates that the H
EW with the radius indicates that the H![]() emission flux
follows the stellar light distribution. A a first approximation, this
should apply also to the case discussed here. Values of
emission flux
follows the stellar light distribution. A a first approximation, this
should apply also to the case discussed here. Values of ![]() [OIII]/H
[OIII]/H
![]() with low [NI]/H
with low [NI]/H![]() ratios occupy the
region where shocks are responsible for the gas excitation (see
Fig. 1
of Sarzi et al. 2009).
In contrast, [OIII]/H
ratios occupy the
region where shocks are responsible for the gas excitation (see
Fig. 1
of Sarzi et al. 2009).
In contrast, [OIII]/H![]() ratios
as high as 10, like the ones measured in the inner arcsecs of
M 31,
fall in the region where photoionization by a central AGN is the
working mechanism.
ratios
as high as 10, like the ones measured in the inner arcsecs of
M 31,
fall in the region where photoionization by a central AGN is the
working mechanism.
5 Discussion and conclusions
We presented new optical spectroscopic observations of the bulge of
M 31. We measured the stellar and gas kinematics,
emission line
strength ratios and absorption Lick indices profiles along six
position angles out to distances of 5 arcmin from the center. Along
the major axis we probed regions out to 8 arcmin. We show that the old
kinematics of McElroy (1983)
provide velocity dispersions
which are too small (by up to 30%), which in turn biases the
dynamical modeling to assign to the bulge a mass that is too small by a
factor of two. Moreover, the new higher averaged velocity dispersion
predicts a mass for the central supermassive black hole of
M 31 that is
only a factor of 2 below the measurements. The new velocity dispersion
profiles are now in better agreement with the axisymmetric dynamical
models with a large bulge mass-to-light ratio (Widrow et al.
2003), which
now match the values derived from stellar
population models (
![]() ,
see below).
This implies an upward revision of the predicted self-lensing
microlensing event rate of Widrow et al. (2003) and
Riffeser et al. (2006),
which are based on lower stellar
mass-to-light ratios.
,
see below).
This implies an upward revision of the predicted self-lensing
microlensing event rate of Widrow et al. (2003) and
Riffeser et al. (2006),
which are based on lower stellar
mass-to-light ratios.
The inner (![]() arcsec)
bulge is slowly
rotating, with a
arcsec)
bulge is slowly
rotating, with a ![]() .
At distances from the center
larger than
.
At distances from the center
larger than ![]() 100 arcsec
the measured kinematics become
increasingly influenced by the rapidly rotating stellar disk.
Therefore, the observed variation of the kinematic position angle is
suggestive of bulge triaxiality, but needs a proper dynamical modeling
of both disk and bulge components to be quantified. The measured gas
kinematics confirm the well studied large scale disk rotation.
However, a more complex structure, with gas minor axis
counter-rotation,
is detected in the inner bulge. This might be evidence for a (recent)
minor merger, possibly connected to the younger stellar population
detected in the inner arcsecs of the galaxy discussed below.
100 arcsec
the measured kinematics become
increasingly influenced by the rapidly rotating stellar disk.
Therefore, the observed variation of the kinematic position angle is
suggestive of bulge triaxiality, but needs a proper dynamical modeling
of both disk and bulge components to be quantified. The measured gas
kinematics confirm the well studied large scale disk rotation.
However, a more complex structure, with gas minor axis
counter-rotation,
is detected in the inner bulge. This might be evidence for a (recent)
minor merger, possibly connected to the younger stellar population
detected in the inner arcsecs of the galaxy discussed below.
The analysis of eight Lick index profiles shows that the bulge
of M 31
is old, of solar-metallicity and a factor of 2 overabundant in
![]() -elements,
which is in agreement with studies of its resolved stellar
component (Stephens et al. 2003; Sarajedini
& Jablonka 2005).
The line indices and stellar
population parameters appear approximately constant on circles, i.e.
their isocontours are rounder than the galaxy isophotes, as seen in
many ellipticals and bulges (Kuntschner et al. 2006;
Falcón-Barroso et al. 2006).
Together with the derived
old ages, this confirms that the stellar disk out to 5 arcmin
from the
center is either old (similar to what was found for other spiral
galaxies,
Peletier & Balcells 1996)
or not sufficiently probed by
the spectral features considered here. However, we do detect smaller
ages (
-elements,
which is in agreement with studies of its resolved stellar
component (Stephens et al. 2003; Sarajedini
& Jablonka 2005).
The line indices and stellar
population parameters appear approximately constant on circles, i.e.
their isocontours are rounder than the galaxy isophotes, as seen in
many ellipticals and bulges (Kuntschner et al. 2006;
Falcón-Barroso et al. 2006).
Together with the derived
old ages, this confirms that the stellar disk out to 5 arcmin
from the
center is either old (similar to what was found for other spiral
galaxies,
Peletier & Balcells 1996)
or not sufficiently probed by
the spectral features considered here. However, we do detect smaller
ages (![]() 8 Gyr)
along the major axis at distances of
8 Gyr)
along the major axis at distances of ![]() 6 arcmin.
The u-g SLOAN colors predicted
from our stellar population analysis
match the observed ones reasonably well. The redder colors g-rand
r-i are systematically offset, a
well known problem of the flux
calibration of current simple stellar population models (Maraston
et al. 2009).
The derived mass-to-light ratios (in the
Johnson R band and with a Kroupa IMF we
get
6 arcmin.
The u-g SLOAN colors predicted
from our stellar population analysis
match the observed ones reasonably well. The redder colors g-rand
r-i are systematically offset, a
well known problem of the flux
calibration of current simple stellar population models (Maraston
et al. 2009).
The derived mass-to-light ratios (in the
Johnson R band and with a Kroupa IMF we
get ![]() )
agree
with the dynamical estimates (see above). They drop to
)
agree
with the dynamical estimates (see above). They drop to ![]()
![]() along the major axis at distances of
along the major axis at distances of ![]() 6 arcmin,
where the disk light starts to dominate.
6 arcmin,
where the disk light starts to dominate.
In the inner arcsecs the situation changes and a population
with a
light-weighted younger age (![]() 8 Gyr inside the
seeing disk or
2 arcsec, with values as low as 4 Gyr) and metal
richer (
8 Gyr inside the
seeing disk or
2 arcsec, with values as low as 4 Gyr) and metal
richer (![]() 3
times solar) appears. This agrees with the findings of Davidge
(1997). In
addition, the emission line EW ratios
[OIII]/H
3
times solar) appears. This agrees with the findings of Davidge
(1997). In
addition, the emission line EW ratios
[OIII]/H![]() increase in this region. Their values are compatible
with being excited by shocks in the main body of the bulge, but near
the center they increase to levels pointing to the presence of an
AGN-like photo-ionizing source. Combined with the detection of
counterrotating gas along the minor axis of the galaxy (see above),
this suggests that a gas-rich minor merger probably happened some
100 Myr ago, which triggered an episode of star formation and
possibly
boosted the nuclear activity of the central supermassive black hole of
M 31. We estimate how broad a range of star burst
ages and masses can
be to give the measured mean value of 8 Gyr in the inner
2 arcsec,
when superimposed on the old bulge stars background. To this purpose
we compute composite spectra of an old (12.6 Gyr) plus a young
(from
100 Myr to 4 Gyr) simple stellar population, using
the Vazdekis
(1999)
library, and measure their SSP ages through the
analysis of the Lick indices observed here. We find that global ages
smaller than 8 Gyr are found when considering a young
component
younger than
increase in this region. Their values are compatible
with being excited by shocks in the main body of the bulge, but near
the center they increase to levels pointing to the presence of an
AGN-like photo-ionizing source. Combined with the detection of
counterrotating gas along the minor axis of the galaxy (see above),
this suggests that a gas-rich minor merger probably happened some
100 Myr ago, which triggered an episode of star formation and
possibly
boosted the nuclear activity of the central supermassive black hole of
M 31. We estimate how broad a range of star burst
ages and masses can
be to give the measured mean value of 8 Gyr in the inner
2 arcsec,
when superimposed on the old bulge stars background. To this purpose
we compute composite spectra of an old (12.6 Gyr) plus a young
(from
100 Myr to 4 Gyr) simple stellar population, using
the Vazdekis
(1999)
library, and measure their SSP ages through the
analysis of the Lick indices observed here. We find that global ages
smaller than 8 Gyr are found when considering a young
component
younger than ![]() 600 Myr
and a mass fraction lower than 10%.
Higher mass fractions are possible for older ages. From Kormendy and
Bender (1999),
inside an aperture of 2 arcsec diameter we
measure a V mag of 12.5, or
600 Myr
and a mass fraction lower than 10%.
Higher mass fractions are possible for older ages. From Kormendy and
Bender (1999),
inside an aperture of 2 arcsec diameter we
measure a V mag of 12.5, or ![]() .
In this region we
estimate
.
In this region we
estimate ![]() and therefore an enclosed
mass of
and therefore an enclosed
mass of ![]() .
As a consequence,
.
As a consequence, ![]()
![]() of some 100 Myr old stars would be needed. Note that in
the inner nucleus of M 31, at fractions of an
arcsec, a disk of 200 Myr
old stars is found (Bender et al. 2005), with a mass
of
of some 100 Myr old stars would be needed. Note that in
the inner nucleus of M 31, at fractions of an
arcsec, a disk of 200 Myr
old stars is found (Bender et al. 2005), with a mass
of
![]()
![]() .
Of course the spatial resolution of our
spectra is too low to probe this scale. Moreover, our result, based
on the H
.
Of course the spatial resolution of our
spectra is too low to probe this scale. Moreover, our result, based
on the H![]() line
as an age tracer, depends heavily on the details
of the emission correction and might be affected by the bad column's
interpolation (see Sect. 2).
Spectra of the higher order
Balmer lines, taken with better seeing, are needed to improve our
conclusions.
line
as an age tracer, depends heavily on the details
of the emission correction and might be affected by the bad column's
interpolation (see Sect. 2).
Spectra of the higher order
Balmer lines, taken with better seeing, are needed to improve our
conclusions.
In a second paper (Morganti et al., in prep.), a dynamical model of the data presented here, which takes into account the contributions of the bulge and disk components, will assess in a quantitative way the bulge triaxiality issue and will give a proper estimate of the microlensing event rates due to self-lensing.
AcknowledgementsThe Hobby-Eberly Telescope (HET) is a joint project of the University of Texas at Austin, the Pennsylvania State University, Stanford University, Ludwig-Maximilians-Universität München, and Georg-August-Universität Göttingen. The HET is named in honor of its principal benefactors, William P. Hobby and Robert E. Eberly. The Marcario Low Resolution Spectrograph is named for Mike Marcario of High Lonesome Optics who fabricated several optics for the instrument but died before its completion. The LRS is a joint project of the Hobby-Eberly Telescope partnership and the Instituto de Astronomía de la Universidad Nacional Autónoma de México. The grism E2 used for these observations has been bought through the DFG grant BE1091/9-1.
References
- Athanassoula, E., & Beaton, R. L. 2006, MNRAS, 370, 1499 [NASA ADS] [CrossRef] [Google Scholar]
- Beaton, R. L, Majewski, S. R., Guthakurta, P., et al. 2007, ApJ, 658, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Bender, R. 1990, A&A, 229, 441 [Google Scholar]
- Bender, R., & Möllenhoff, C. 1987, A&A, 117, 71 [Google Scholar]
- Bender, R., Saglia, R. P., & Gerhard, O. 1994, MNRAS, 269, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Bender, R., Kormendy, J., Bower, G., et al. 2005, ApJ, 631, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Boulesteix, J., Geolgelin, Y. P., Lecoarer, E., Marcelin, M., & Monnet, G. 1987, A&A, 178, 91 [Google Scholar]
- Braun, R. 1991, ApJ, 372, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Chemin, L., Carignan, C., & Foster, T. 2009, ApJ, 705, 1395 [NASA ADS] [CrossRef] [Google Scholar]
- Davidge, T. J. 1997, AJ, 113, 985 [NASA ADS] [CrossRef] [Google Scholar]
- De Lorenzi, F., Debattista, V. P., Gerhard, O., & Sambhus, N. 2007, MNRAS, 376, 71 [NASA ADS] [CrossRef] [Google Scholar]
- De Vaucouleurs, G. 1958, ApJ, 128, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Falcón-Barroso, J., Bacon, R., Bureau, M., et al. 2006, MNRAS, 369, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Gerhard, O. 1986, MNRAS, 219, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Gültekin, K., Richstone, D. O., Gebhardt, K. et al. 2009, ApJ, 698, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Kent, S. 1989a, PASP, 101, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Kent, S. 1989b, AJ, 97, 1614 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, G. J., Nicklas, H. E., MacQueen, P. J., et al. 1998, SPIE, 3355, 375 [Google Scholar]
- Kaiser, N. 2004, SPIE, 5489, 11 [Google Scholar]
- Kerins, E., Carr, B. J., Evans, N. W., et al. 2001, MNRAS, 323, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A., Zhao, H., & Somerville, R. S. 2002, ApJ, 573, 597 [Google Scholar]
- Kormendy, J., & Bender, R. 1999, ApJ, 522, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kuntschner, H., Emsellem, E., Bacon, R., et al. 2006, MNRAS, 369, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Maraston, C. 1998, MNRAS, 300, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Maraston, C. 2005, MNRAS, 362, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Maraston, C., Strömback, G., Thomas, D., et al. 2009, MNRAS, 394, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Mehlert, D., Saglia, R. P., Bender, R., & Wegner, G. 2000, A&AS, 141, 449 [Google Scholar]
- McElroy, D. B. 1983, ApJ, 270, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Montalto, M., Seitz, S., Riffeser, A., et al. 2009, A&A, 507, 283 [Google Scholar]
- Peletier, R. F., & Balcells, M. 1996, AJ, 111, 2238 [NASA ADS] [CrossRef] [Google Scholar]
- Pellet, A. 1976, A&A, 50, 421 [Google Scholar]
- Riffeser, A., Fliri, J., Seitz, S., & Bender, R. 2006, ApJS, 163, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Sarzi, M., Falcón-Barroso, J., Davies, R. L., et al. 2006, MNRAS, 366, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Sarajedini, A., & Jablonka, P. 2005, AJ, 130, 1627 [NASA ADS] [CrossRef] [Google Scholar]
- Sarzi, M., et al. 2009, MNRAS, in press, [arXiv:0912.0275] [Google Scholar]
- Stark, A. A. 1977, ApJ, 213, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, A. W., Frogel, J. A., DePoy, D. L., et al. 2003, AJ, 125, 2473 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Maraston, C., & Bender, R. 2003, MNRAS, 339, 897 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, R. P., Rix, H. W., Carter, D., et al. 1994, MNRAS, 268, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Trager, S. C., Worthey, G., Faber, S. M., Burstein, D., & Gonzalez, J. J. 1998, ApJS, 116, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Vazdekis, A. 1999, ApJ, 513, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Widrow, L. M., Perrett, K. M., & Suyu, H. S. 2003, ApJ, 588, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G., Faber, S. M., Gonzalez, J. J., & Burstein, D. 1994, ApJS, 94, 687 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... M 31
![[*]](/icons/foot_motif.png)
- Full Tables 2-4 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/509/A61
All Tables
Table 1: Log of the observations.
Table 2: Format example of the measured stellar kinematics as a function of distance from the center (positive: east, negative: west) for the different position angles. The full table is available electronically at the CDS.
Table 3: Format example of the measured gas kinematics as a function of distance from the center (positive: east, negative: west) for the different position angles. The full table is available electronically at the CDS.
Table 4: Format example of the measured Lick indices as a function of distance from the center (positive: east, negative: west) for the different position angles. The full table is available electronically at the CDS.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12805f1.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg30.png)
|
Figure 1: The positions of the 19 M 31 slit pointings superimposed on a NOAO image of the Andromeda galaxy (credit Adma Block/NOAO/AURA/NSF). See Table 1 for the naming convention. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12805f2.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg31.png)
|
Figure 2: The anamorphic distortion of the LRS as mapped by tracing the peaks of the stellar spectra. The traces of nine stellar spectra are shown as full black lines and are compared to the corresponding straight lines (dashed). The interpolated differences (in pixel) between the stellar traces and the cartesian grid as a function of the position on the chip are shown coded by color. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,angle=270,clip]{12805f3a.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg34.png)
|
Figure 3:
The stellar kinematics along different position angles, folded with
respect to the center (at velocity -333.2 km s-1),
antisymmetrically for recessional velocities and H3
coefficients, symmetrically for velocity dispersions and H4
coefficients. Filled circles refer to radii with increasing RA (East),
stars to radii with decreasing RA (West). The number in the velocity
panel indicates the correction in km s-1
to the central velocity (-333.2 km s-1)
applied to achieve maximal symmetry. The plus or minus sign indicates
whether the velocities of the sides with increasing RA (the filled
dots) are receding or approaching. The vertical dotted lines mark the
transition from the central slit data to those from the outer two. For
the major axis, a further vertical dotted line marks the outer MJEE
dataset. The short-dashed vertical lines mark the seeing values of the
central slits (see Table 1).
The data of McElroy (1983,
at PA = 75, 45, 15, 165, 135 and
105 respectively) are indicated by green open circles and
triangles. The data of van der Marel et al. (1994, MJ at
PA = 55, MN at PA = 128) are shown
by the red continuous lines. The data of Kormendy & Bender (1999) are shown
in yellow (from their Calcium Triplet spectra) and magenta (from their H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12.4cm,angle=270,clip]{12805f3b.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg35.png)
|
Figure 3: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,angle=0]{12805f4.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg41.png)
|
Figure 4:
Top: the full line shows the velocity
dispersion resulting from averaging all measured |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,angle=270,clip]{12805f5.ps}
\vspace{-1mm}\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg46.png)
|
Figure 5: The gas kinematics along different position angles, folded with respect to the center, antisymmetrically for recessional velocities, symmetrically for velocity dispersions. Only data with errors smaller than 50 km s-1 are shown. Filled circles refer to radii with increasing RA, stars to radii with decreasing RA, with the same convention and zero-point shifts on radial velocities as in Fig. 3. The vertical dotted lines mark the transition from the central slit data to those from the outer two. For the major axis, a further vertical dotted line marks the outer MJEE dataset. The (red) short-dashed vertical lines mark the seeing values of the central slits (see Table 1). The data of Pellet (1976) are also shown for comparison as open circles (for increasing RA) and triangles (for decreasing RA). His 28 Å data are plotted in green, the 135 Å in red. We show his PA = 45 data as MJ, his PA = 128 as MN, his PA = 68 as P30. Moreover, the data at PA = 38 (his major axis) are shown in blue and also as MJ. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{12805f6.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg47.png)
|
Figure 6: The variation of the molecular Mg1 and Mg2 (in mag) and atomic (in Å, all the rest) line strengths as a function of position on the slit measured for the star HD 72324 (=HR 3369). The dotted line shows the values of Worthey et al. (1994). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12805f7.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg62.png)
|
Figure 7:
The comparison between the line strengths measured here and the Lick
values for 20 stars. The dotted line shows the one-to-one
correlation, the full line the best fitting relation |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12805f8.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg63.png)
|
Figure 8:
The effect of the gas emission correction on the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12805f9a.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg79.png)
|
Figure 9:
The measured Lick indices profiles along the six slit positions of
M 31. The vertical dotted lines mark the ends of the
central slits. For the major axis, a further vertical dotted line marks
the outer MJEE dataset. The lines show the best-fit LSSP models (see
discussion in Sect. 4.1).
The bottom plots show the respective |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{12805f9b.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg80.png)
|
Figure 9: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,angle=270,clip]{12805f10.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg81.png)
|
Figure 10:
The EW of the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12805f11.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg101.png)
|
Figure 11: The age, metallicity, overabundance, Sloan colors u-g (blue), g-r (green), r-i (red) and Johnson M/L profiles in the B (blue), V (green) and R (red) bands along the different slit positions. The dotted lines show the 1-sigma errors. The vertical dotted lines mark the ends of the central slits. For the major axis, a further vertical dotted line marks the outer MJEE dataset. The measured color profiles, corrected by extinction (Montalto et al. 2009), are shown as crosses. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12805f12.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg102.png)
|
Figure 11: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12805f13.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg103.png)
|
Figure 12: The age, metallicity, overabundance, and M/LR profiles (full lines) averaged over position angles and binned logarithmically in radius. The dotted lines and the bars show the corresponding rms and errors on the mean, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{12805f14.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12805-09/Timg104.png)
|
Figure 13:
Top: the ellipticity profile as a function of
the semi-major axis distance a. Bottom:
the position angle of the kinematic major axis |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



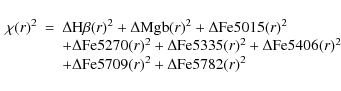
![\begin{displaymath}
\Delta {\rm Index} (r)^2=\left(\frac{{\rm Index}(r)-m{\rm Index}(t,\rm [Z/H],[\alpha/Fe])}
{d{\rm Index}(r)}\right)^2,
\end{displaymath}](/articles/aa/full_html/2010/01/aa12805-09/img51.png)
![\begin{displaymath}\chi(a)^2_\phi=\sum_{i=1}^{12}\left[\frac{V_i(a)-V_{\rm max}(a)\cos(\phi_i-\phi_0(a))}
{\delta V_i(a)}\right]^2,
\end{displaymath}](/articles/aa/full_html/2010/01/aa12805-09/img70.png)