EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 509 (January 2010) A&A, 509 (2010) A48 Full HTML
Free Access
Issue
A&A
Volume 509, January 2010
Article Number A48
Number of page(s) 6
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/200912712
Published online 15 January 2010
A&A 509, A48 (2010)

Probing the relation between the structure of initial proto-planetary disc and the Oort-cloud formation
(Research Note)

T. Paulech1 - M. Jakubík2 - L. Neslusan2 - P. A. Dybczynski3 - G. Leto4

1 - Astronomical Institute of the Slovak Academy of Sciences, Dúbravská cesta 9, 84504 Bratislava, Slovakia
2 - Astronomical Institute of the Slovak Academy of Sciences, 05960 Tatranská Lomnica, Slovakia
3 - Astronomical Observatory of the A. Mickiewicz University, S\loneczna 36, 60-286 Poznan, Poland
4 - Catania Astrophysical Observatory, via Santa Sofia 78, 95123 Catania, Italy

Received 17 June 2009 / Accepted 19 October 2009

Abstract
Aims. The Oort cloud consists of cometary nuclei which were ejected from the once existing proto-planetary disc to large heliocentric distances by the giant planets. The process of the cloud formation depended on the initial structure and mass of the disc. Considering four models of an initial proto-planetary disc, we roughly probe this dependence.
Methods. We use the resultant data of our previous simulation of the Oort cloud formation for the first two Gyr. The considered disc models consist of a set of representative test particles. The new models are created subtracting a fraction of the particles from the model considered in our previous work, in a way to obtain the required heliocentric-distance distribution. Specifically, we focus on the situations in which a part of the small bodies in the disc is assumed to be already spent in the previous process of the giant planet formation. We omit the particles from an originally smooth profile in the regions adjacent to the planet orbits. With the reduced data, we construct the comet cloud characteristics we are interested in.
Results. We find that it is difficult to construct the proto-planetary disc if (i) the amount of heavy chemical elements in Jupiter and Saturn is as high as currently accepted ($\approx$20 and $\approx$ $29~M_{\oplus}$; respectively) and (ii) the total mass of the minimum-mass solar nebula is assumed to be lower than $\approx$ $0.05~M_{\odot}$. The behaviour of the Oort cloud formation does not crucially depend on the initial disc model. Some quantitative differences in its structure are obvious: since the cloud is known to be filled mainly by Uranus and Neptune, the efficiency of its formation is higher if the initial amount of particles in the Uranus-Neptune region is relatively higher. The efficiency is also higher in the gapped-disc models because a less amount of particles experience a very close encounter with a planet resulting in their ejection into the interstellar space.

Key words: comets: general - Oort Cloud - solar system: formation

1 Introduction

The comet Oort cloud (OC), surrounding the Sun at large heliocentric distances, is now widely believed to originate in the once existing proto-planetary disc (PPD). Its formation and structure is still studied. The new, permanently enlarging observational databases of the reservoirs of small bodies in the solar system enable us to refine the model of the formation of this system.

In our previous work (Dybczynski et al. 2008; Leto et al. 2008, Paper I and II, hereinafter), we followed some earlier studies by other authors (especially direct numerical simulations by Dones et al. 2004; Duncan et al. 1987, 2005, private comm.), and dealt with the formation of the OC. The structure of this distant reservoir has been determined by several factors. Among others, it was influenced by the initial distribution of macroscopic solid bodies in the PPD.

In the simulation of the OC formation described in Paper I we assumed a smooth initial PPD, with the surface-density proportional to the heliocentric distance, r, as  ${\propto}r^{-3/2}$. This profile was found by Hayashi et al. (e.g. Hayashi et al. 1985) for the so-called minimum-mass solar nebula (MMSN) of gas and dust, and was adopted for the distribution of later-formed solid bodies by other authors (e.g. Morbidelli & Brown 2004). At the same time, we assumed that the giant (Jovian) planets were already formed and moved around the Sun in their current orbits. Therefore, a part of the material of the initial smooth-profile PPD had to be already spent for the planet formation in the beginning of the era, for which we performed the simulation. The process of the giant-planet formation could result in the occurrence of gaps in the PPD.

In this paper, we probe the possible impact of the PPD structure and mass on the process of the OC formation. Apart from the model of the smooth-profile PPD considered in our previous papers, we also consider three alternative models of the PPD, with the gaps around the giant-planet orbits. These models are described in Sect. 2. A comparison between the OC formation processes considering the various PPD models is given in Sect. 3 and the conclusion is stated in Sect. 4.

2 The models considered of the initial PPD

2.1 Some remarks on the modelling

As mentioned in Sect. 1, the structure of the PPD was obviously not smooth when the era of a massive OC formation began. A lot of its material was already spent for the formation of planets. Thus, the formation might lead to the occurrence of gaps around the orbits of planets. The gaps formation during the era of the gaseous solar nebula has been described in several papers (Papaloizou et al. 2004; Bryden et al. 1999; Lin & Papaloizou 1993; Papaloizou et al. 1999). Unfortunately, a detailed heliocentric-distance distribution of the planetesimals in the PPD after the gas was gone is not known. We simply assume a random depletion of the given planetary zone and, consequently, the Gaussian profile of each gap.

Before engaging in a further discussion, we recall the existing two different kinds of scenarios of the planet formation. The old scenarios assume a formation in situ, i.e. each planet formed in a heliocentric distance, approximately where its current orbit is situated. Fernández & Ip (1984) and several other author groups, recently Hahn & Malhotra (2005), Tsiganis et al. (2005), Morbidelli et al. (2005), and Gomes et al. (2005), suggested a scenario including a migration of especially the two outer-most planets, Uranus and Neptune. In our simulation, we considered the giant planets to have been in their current orbits and as having their current masses. Therefore, our results are fully consistent only with the first kind of scenarios.

The results can, however, be of a qualitative importance also within the second kind because we intend to study the effect of the presence or absence of comet nuclei in the orbits similar to those of perturbing giant planets. In this context, the planet migration does not appear to be important.

Some authors also considered the gas drag of solar nebula in the first stage of the OC formation (Brasser et al. 2007; Higuchi et al. 2002) and situated the Sun inside its birth star cluster for several million years in the beginning (Fernández 1997; Brasser et al. 2007; Kaib & Quinn 2008; Brasser et al. 2008,2006). Brasser et al. (2007) showed that the objects with their sizes comparable to the typical comet-nucleus size could not have been ejected into the OC distances during the gaseous phase of the solar nebula. The star cluster could influence the very early beginning of the OC formation. According to Fernández (1997) as well as to the simulations by Dones et al. (2004, 2005, private comm.) and our own (Papers I and II), the OC in the very early period (a few Myr) was populated however by the bodies which were on less stable orbits and abandoned the OC soon. The OC population that survives till the present was formed after the Sun escaped its birth star cluster. With respect to the initial assumptions, our work is mainly concerned with this surviving population.

In the current paper as in Papers I and II we assume that the PPD consists of a large number of test particles (TPs). To avoid another extensive computation, we utilize the resultant data of our former computation including the integration of the motion of 10 038 TPs, which was presented in Papers I and II. The new PPD models are created removing a part of TPs to reach a required initial-PPD profile.

The net mass of the TPs removed from a region close to the orbit of a given planet should be equal to the mass of heavy chemical elements (HCEs) that the planet contains at the present (when we assume a perfect accretion) or should be larger (if scattering of some material during the accretion process is assumed). Since the considered number of TPs, N = 10 038, represents the PPD in the range of a heliocentric distance from 4 to 50 AU, the average mass of a single TP is m1 = h M4-50/N, where h is the fraction of the HCE component of the solar nebula and M4-50 is the mass of this nebula between 4-50 AU. We consider here the HCE component because the planetesimals consisted of only a negligible fraction of hydrogen and helium. When calculating an average planetesimal mass, only the mass of HCEs is relevant.

The mass M4-50 can be calculated taking into account the surface-density profile of the MMSN and its total initial mass, $M_{\rm sn}$. Unfortunately, the latter is not exactly known. On the basis of the mass currently located in the planets, it is expected to be in the range from $\sim$0.01 to $\sim$ $0.1~M_{\odot}$(Weidenschilling 1977a). In our models introduced in the next subsections, we assume two values of  $M_{\rm sn}$: the one at the upper limit, i.e.  $0.1~M_{\odot}$and the half value, $0.05~M_{\odot}$. The latter was considered in the physical studies of the solar-system formation (e.g. Weidenschilling 1977b). We discuss why a lower value seems to be problematic.

2.2 A-model: a smooth r-3/2 surface-density profile, arbitrary Msn

This model of the initial PPD was considered in Papers I and II and is regarded as the reference model in the following. To recapitulate, it consists of 10 038 TPs in the heliocentric-distance interval between 4 and 50 AU. Their heliocentric-distance distribution (Fig. 1, plot labelled as Model-A, dashed curve) correlates with the ${\propto}r^{-3/2}$ surface-density profile (Morbidelli & Brown 2004). This PPD shares with all other here considered models that the initial distributions of the eccentricity and inclination of the TPs to the invariable plane of perturbing giant planets are Gaussian, centered at zero, with the half-width of $\sigma_{\rm e} = 0.01$ and $\sigma_{i} = 0.01$ rad, respectively. At the same time, the argument of perihelion, longitude of ascending node (both related to the coordinate system having the xy-plane identical to the invariable plane), as well as the true anomaly of the TPs are distributed randomly, in the entire interval from 0 to $2\pi$ rad.

The TPs reaching the OC can originate from various source regions. To characterise the origin of the TPs in the OC, we adopt the formal division by the initial semi-major axis $a_{\rm o}$ of the source regions: $a_{\rm o} < 8$ AU - Jupiter region, $8 \leq a_{\rm o} < 15$ AU - Saturn region, $15 \leq a_{\rm o} < 24$ AU - Uranus region, $24 \leq a_{\rm o} < 35$ AU - Neptune region, and $a_{\rm o} \geq 35$ AU - Edgeworth-Kuiper-belt (EKB) region. The relative abundances of the TPs considered are 16.2%, 20.7%, 20.2%, 20.1% and 22.9% in these regions, respectively. The initial $a_{\rm o}$ is approximately identified for almost circular initial orbits with the initial heliocentric distance, r, of TPs. Since we do not remove any TP in this model, we do not need to calculate the TP average mass and, thus, to know the mass  $M_{\rm sn}$of the MMSN.

\begin{figure} \par\includegraphics[angle=-90,width=7cm,clip]{12712f1a.eps}\vspa... ...pace*{1mm} \includegraphics[angle=-90,width=7cm,clip]{12712f1d.eps} \end{figure} Figure 1:

Distribution of the surviving TPs in the region of the PPD at 2 Gyr for A-, B-, C- and D-models of the initial PPD (Sect. 2). For every model, this distribution is illustrated with bars, each corresponding with 0.1 AU-wide interval of heliocentric distance. The corresponding initial distribution is illustrated with a dashed curve.

Open with DEXTER

2.3 B-model: Gaussian-like depleted r-3/2 profile, M sn = 0.1 M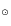${_{\odot }}$

In this model, we remove those TPs from the reference A-model, which are supposed to collide with the giant-planet embryos and, thus, are incorporated into the given planet. We assume that the accretion process was highly efficient during the nebular stage of the PPD environment and we can roughly identify the total mass of the removed TPs with the HCE mass inside the given planet. (This assumption does probably not fully apply in the case of ice-giants, Uranus and Neptune. For simplicity's sake we nevertheless keep the assumption also for these planets.)

The actual extent of the MMSN is not known. For the assumed r-3/2 surface-density profile we have to truncate the MMSN at an outer radius. We arbitrarily choose the outer border at the distance of 150 AU. This value is consistent with the outer-border distance considered by e.g. Kenyon (2002) or Kenyon & Bromley (2008).

Taking into account all adopted assumptions, the partial mass of the MMSN between 4 and 50 AU was $M_{4-50} \simeq 0.0414~M_{\odot} \simeq 13~800~M_{\oplus}$, if the total mass $M_{\rm sn} = 0.1~M_{\odot}$. Since the cometary nuclei prevailingly consists of HCEs, we further consider only the fraction of the MMSN mass corresponding with this component, the solar abundance of which is $h \simeq 2\%$. This fact implies that the HCE-PPD mass between 4 and 50 AU is equal to $\approx$ $276~M_{\oplus}$. As the corresponding part of the PPD consists of 10 038 TPs, the average mass of one TP is $\approx$ $0.0275~M_{\oplus}$.

According to the well-known models of the internal structure of giant planets (see e.g. the review by Weissman et al. 1999), we can deduce that the fractions of the HCEs in Jupiter, Saturn, Uranus and Neptune are approximately 20, 29, 13.5, and $16~M_{\oplus}$, respectively. To remove the corresponding mass from the appropriate region of a given planet, we must remove 727, 1055, 491 and 582 TPs, respectively.

At the removal, the Gaussian profile of given gap is centred at the current mean heliocentric distance of the given planet. The peak of the Gaussian corresponds to the number of TPs in the PPD at the given-planet distance (all TPs at the mean planet distance are removed), and its dispersion is fitted to remove the given above mentioned number of TPs. In more detail, the Gaussian profile is symmetric, but the heliocentric-distance distribution of the initial smooth disc is decreasing, therefore the centre of the Gaussian has to be slightly shifted towards the Sun to avoid an attempt to remove more TPs than those which are situated in the concerned distance interval. The initial heliocentric-distance distribution of TPs in the B-model can be seen in Fig. 1 (Model-B plot), dashed curve, together with this distribution at the end of the simulation.

2.4 C-model: Gaussian-like depleted r-3/2 profile, Msn = 0.05 M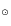${_{\odot }}$

Similar to the case of model B we obtain also model C. The TPs surface-density profile distribution maintains the distance TP distribution corresponding with the r-3/2 profile, but this time for the mass of MMSN equal to $0.05~M_{\odot}$. Since this mass is half of that in B-model, the average mass of a single TP is also about half of that in the B-model. Consequently, we need to remove more TPs, which are the equivalent of the mass of HCE component in the planets. Specifically, we now have to remove 1460, 2117, 985 and 1168 TPs from Jupiter, Saturn, Uranus and Neptune regions, respectively. The final heliocentric-distance TP distribution is illustrated in Fig. 1 (Model-C plot), dashed curve.

The initial distribution of the HCE component of the material in the accretion zone of Jupiter and Saturn, available to form the cores of these planets, can be seen in the first plot (Model-A, dashed curve) of Fig. 1. Let us assume the extent of the accretion zone of Jupiter to be from $\approx$3.5 to $\approx$7.5 AU and that of Saturn from $\approx$7.5 to $\approx$15 AU. (Within some recent models, as for instance the Nice model, Tsiganis et al. 2005, these zones are assumed to be narrower. In the given context, we tend to be conservative and assume the wide zones, corresponding to no planet migration.) In the third plot (Model-C) of Fig. 1, we can see only a small fraction of this material (a low peak centred at the heliocentric distance of about 7.5 AU) remaining after its main part was spent to constitute these planets. More exactly, $\sim$$80\%$ of the mass of solids had to be accreted so that the observed abundance of HCEs could be contained by Jupiter and Saturn (the corresponding value for Jupiter alone is $\sim$$90\%$). It implies the extremely high efficiency of the accretion. The efficiency was likely lower, and this fact implies, even for the considered total mass of the MMSN of $0.05~N_{\odot}$, a necessity of the flux of some material to the Jupiter-Saturn accretion zone from the adjacent regions of main-asteorid belt and Uranus. A radial flowing of solids during the nebular phase of the disc around the Sun is problematic, however, because of the gas drag. It is therefore hard to believe that a lower than $0.05~M_{\odot}$ total mass of the MMSN, which would imply an even more extensive radial flux, could be possible. This is the reason why we do not consider a lower mass of the MMSN than  $0.05~M_{\odot}$.

The problem with the high accretion efficiency would not appear if the amounts of HCEs in Jupiter and Saturn were lower than what is generally and also in this work accepted. A lower amount can be realistic, because the determination uncertainity is quite large. Guillot & Gladman (2000) demonstrated that the amount can be as low as 10 and $20~M_{\oplus}$ in Jupiter and Saturn, respectively (cf. 20 and $29~M_{\oplus}$, respectively, in this work).

2.5 D-model: Gaussian-like depleted r-2 profile, M 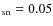${_{\rm sn} = 0.05}$M ${_{\odot }}$

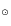
Another way to avoid the requirement of the unacceptably high formation efficiency of Jupiter and Saturn, in the case of C-model, is to assume a centrally more concentrated initial PPD. Kusaka et al. (1970) (see also Weidenschilling 1977b) demonstrated that the surface density of the MMSN may depend on the heliocentric distance as ${\propto}r^{-1}$ to  ${\propto}r^{-2}$with respect to the assumptions adopted.

\begin{figure} \par\includegraphics[angle=-90,width=7cm,clip]{12712f2a.eps}\vspa... ...pace*{1mm} \includegraphics[angle=-90,width=7cm,clip]{12712f2d.eps} \end{figure} Figure 2:

The evolution of the population of the OC as well as its inner (IOC) and outer (OOC) parts during the first 2 Gyr. The evolution is shown for the A-, B-, C- and D-models (Sect. 2) of the initial PPD.

Open with DEXTER

The D-model of the initial PPD is derived from the heliocentric-distance TP distribution corresponding with the r-2 surface-density profile, which is more centrally concentrated than the r-3/2 profile. Since we still intend to use only the data obtained within the large computation for the A-model, we create the r-2 surface-density profile of the PPD from the r-3/2 profile, considered in Papers I and II, removing the redundant TPs in the 4-50 AU range. The obtained initial heliocentric-distance distribution of the TPs in model D is illustrated in Fig. 1 (plot labelled correspondingly) with the dashed curve.

Table 1:   The amounts of comets (in per cents) from various source regions (Sect. 2.2), which reside in the inner and outer part of the OC, and the whole OC in 2 Gyr.

3 A comparison of results for the considered PPD models

In Papers I and II, we answered several questions about the evolution of the OC population as well as about the final cloud structure. Let us now compare the results from Papers I and II for the A-model of the initial PPD with the corresponding results for the other models introduced here. In Fig. 2 the evolution of the population of OC is shown. The evolutions of the sub-populations of the inner and outer OC (IOC and OOC, respectively) are distinguished. For our set of the initial conditions, without assuming any planet migration (as well as no presence of the solar-system-birth star cluster), the OOC population reaches its maximum at $\approx$200 Myr, while the IOC population does so at $\approx$1.2 Gyr, regardless of the considered specific PPD model. The height of the OOC-population peak depends on the amount of TPs in the Jupiter-Saturn region of the PPD, from where the TPs come to the OOC during the very early period. The peak is lowest for the C-model with a large amount of TPs spent for the Jupiter and Saturn formation and, consequently, a poor remnant of the TPs that remained for the first-stage OOC formation.

The final population of the OC as well as that of the sub-populations at 2 Gyr is given in Table 1 in per cents of the corresponding total initial PPD population for all considered PPD models. Specifically, we compare the results obtained for four models (A-D) of the initial PPD in Table 1. The abbreviations JR, SR, UR, NR, EKBR, and PPD stand for Jupiter, Saturn, Uranus, Neptune, and the Edgeworth-Kuiper-belt source region, as well as the whole considered PPD (from 4 to 50 AU), respectively. The uncertainity of the presented values is calculated applying the Poisson statistics. From the presented figures we can deduce that the efficiency of the formation of the OOC is a little higher for the gapped, B-, C- and D-models than for the smooth-profile A-model of the PPD (cf.  $0.18{-}0.19\%$and $0.14\%$). The OC-formation efficiency for the A-model is probably lower because of the existence of TP orbits being very close to the planetary orbits. Those TPs have a high probability to experience close encounters with the planets and consequently have a high probability to be ejected from the solar system rather than be sent to the comet cloud. Other details about the OC formation can be read in Table 1.

The absence of TPs in the gaps is obviously also a reason of a higher efficiency of IOC formation for the B- and C-models in comparison with the A-model. As found in the past (Safronov 1972), the comets surviving in the OC till today were delivered there mainly by Uranus and Neptune. The rate of the delivery by these two planets increases as the OC-comet semi-major axis decreases. Therefore, a larger amount of TPs should appear in the IOC in the case of the PPD models with a relatively larger amount of particles in the Uranus-Neptune region, i.e. in the B- and especially the C-model. For the A-model with the relatively lower amount of TPs in the Uranus-Neptune regions, some TPs are moreover ejected into the interstellar space at the close planetary encounters. The D-model, corresponding with r-2 initial surface-density profile, is centrally most concentrated and, therefore, the population of the IOC is the lowest in this case. The same conclusion is qualitatively valid for the entire OC, since only a relatively small number of TPs resides in its outer part.

The comparison of the way the OC is centrally concentrated between the considered models can also be done with the help of an analysis of the radial distribution of TPs at 2 Gyr. In the interval from the 5000 to 100 000 AU, we fit the radial number density with the power law $\rho (r) \propto r^{-s}$. The index s equals 3.53-0.02+0.03, 3.47-0.03+0.04, 3.39-0.04+0.06, and 3.72-0.05+0.10 for the A-, B-, C-, and D-model respectively. Although the value for the A-model is not statistically well separated from that for the B-model and likewise the value for the B-model from that for the C-model, there is a decreasing trend of s from the A- through B- to C-model with a distinct difference between the A- and finally the C-values of the index. One can state again, accordingly, that a relatively larger initial number of TPs in the Jupiter-Saturn region results in finally relatively more centrally concentrated OC (the order of the increase of central concentration is: model C, B, A and D).

Table 2:   The amounts (in per cents) of comets from various regions of their origin (Sect. 2.2), which were ejected into the interstellar space during the first 2 Gyr.

The cumulative ejection of the TPs at 2 Gyr, again in the per cents of the corresponding total initial PPD population, is presented in Table 2. In this table, TN stands for the total number of the TPs considered in the given model of the initial PPD. The abbreviations JR, SR, UR, NR, KBR, and PPD refer to the Jupiter, Saturn, Uranus, Neptune, Edgeworth-Kuiper-belt region of comet origin as weel as to the PPD as a whole. The amounts are presented for four (A-D) models of the considered initial PPD (Sect. 2). Since Jupiter and Saturn are the main planets ejecting the small bodies into the interstellar space, it is not surprising that the least number of TPs is ejected when the C-model with a very poor initial TP population in the Jupiter-Saturn region is considered.

Another question concerns the structure of surviving TPs in the planetary region. The appropriate distributions at 2 Gyr, for all considered models, are shown in the plots of Fig. 1. In the D-model, the number of trans-Neptunian TPs is reduced in comparison with the other models, therefore the total number of survival is proportionally lower. However, only small quantitative differences can be stated for all the other features of the trans-Neptunian belt. It is not surprising, because the models are practically identical in this part of the PPD and the appropriate population is only slightly contamined by bodies coming from part lying further inwards.

In all models one can also notice a thin belt of bodies at about 26 AU from the Sun. Another belt in the $\approx$14.5 AU distance consists of several TPs for a long period, during the simulation. At 2 Gyr, only a single stable orbit survives here, however. The 26 AU belt (as well as perhaps the 14.5 AU belt) can be regarded as an independent confirmation of the circular belt between the orbits of Uranus and Neptune (and between the Saturn and Uranus) as studied and theoretically proved by Duncan et al. (1989).

4 Conclusion

Comparing the characteristics of the OC and its sub-populations for 4 models of the initial PPD, we can conclude that the change of the assumption of the initial TP distribution in the PPD has no crucial impact on the formation of the OC as a whole or its inner and outer parts. Of course, there are quantitative differences. The efficiency of the OC formation is higher for the models of initial PPD with the particles removed from the regions adjacent to the planetary orbits. The formation efficiency of the relatively highly populated IOC and, consequently, of the whole OC rises with a relative increase of the abundance of TPs initially situated in the Uranus-Neptune region in comparison with those in the Jupiter-Saturn region. And a model with a relatively larger initial number of bodies in the Jupiter-Saturn region of the PPD results in a relatively more centrally concentrated, though less populated, OC.

The concept of MMSN and subsequent PPD is problematic if the amount of HCEs in Jupiter and Saturn is considered to be as high as currently accepted and if at the same time the mass of the MMSN is assumed to be lower than $\approx$ $0.05~M_{\odot}$. This combination of the two parameters does not yield enough material for the accretion of the HCE component inside the most massive planets.

Acknowledgements
T.P., M.J., and L.N. thank the project ``Enabling Grids for E-sciencE II'' (http://www.eu-egee.org/) for the provided computational capacity and support in the development of the computer code, which was necessary for the management of tasks on the GRID. They also acknowledge the partial support of this work by VEGA - the Slovak Grant Agency for Science (grant No. 7047). P.A.D. acknowledges the partial support of this work from Polish Ministry of Science and Higher Education (year 2009, grant No. N N203 302335). G.L. thanks PI2S2 Project managed by the Consorzio COMETA, http://www.pi2s2.it and http://www.consorzio-cometa.it for the computational resources and technical support.

References

  1. Brasser, R., Duncan, M. J., & Levison, H. F. 2006, Icarus, 184, 59 [NASA ADS] [CrossRef] [Google Scholar]
  2. Brasser, R., Duncan, M. J., & Levison, H. F. 2007, Icarus, 191, 413 [NASA ADS] [CrossRef] [Google Scholar]
  3. Brasser, R., Duncan, M. J., & Levison, H. F. 2008, Icarus, 196, 274 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bryden, G., Chen, X., Lin, D. N. C., Nelson, R. P., & Papaloizou, J. C. B. 1999, ApJ, 514, 344 [NASA ADS] [CrossRef] [Google Scholar]
  5. Dones, L., Weissman, P. R., Levison, H. F., & Duncan, M. J. 2004, in Comets II, ed. M. C. Festou, H. U. Keller, & H. A. Weaver (Arizona: Univ. Arizona Press), 153 [Google Scholar]
  6. Duncan, M., Quinn, T., & Tremaine, S. 1987, AJ, 94, 1330 [NASA ADS] [CrossRef] [Google Scholar]
  7. Duncan, M. J., Quinn, T., & Tremaine, S. 1989, Icarus, 82, 402 [NASA ADS] [CrossRef] [Google Scholar]
  8. Dybczynski, P. A., Leto, G., Jakubík, M., Paulech, T., & Neslusan, L. 2008, A&A, 487, 345 (Paper I) [Google Scholar]
  9. Fernández, J. A. 1997, Icarus, 129, 106 [NASA ADS] [CrossRef] [Google Scholar]
  10. Fernández, J. A., & Ip, W.-H. 1984, Icarus, 58, 109 [NASA ADS] [CrossRef] [Google Scholar]
  11. Gomes, R., Levison, H. F., Tsiganis, K., & Morbidelli, A. 2005, Nature, 435, 466 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  12. Guillot, T., & Gladman, B. 2000, in ASP Conf. Ser., 219, ed. F. Garzón, C. Eiroa, D. de Winter, & T. J. Mahoney, 475 [Google Scholar]
  13. Hahn, J. M., & Malhotra, R. 2005, AJ, 130, 2392 [NASA ADS] [CrossRef] [Google Scholar]
  14. Hayashi, C., Nakazawa, K., & Nakagawa, Y. 1985, in Protostars and planets II (Tucson: Univ. Arizona Press), 1100 [Google Scholar]
  15. Higuchi, A., Kokubo, E., & Mukai, T. 2002, in Proc. Asteroids, Comets, Meteors - ACM 2002 international conference, ed. B. Warmbein (Noordwijk: ESA Publications Division), ESA SP-500, 453 [Google Scholar]
  16. Kaib, N. A., & Quinn, T. 2008, Icarus, 197, 221 [NASA ADS] [CrossRef] [Google Scholar]
  17. Kenyon, S. J. 2002, PASP, 114, 265 [NASA ADS] [CrossRef] [Google Scholar]
  18. Kenyon, S. J., & Bromley, B. C. 2008, ApJS, 179, 451 [NASA ADS] [CrossRef] [Google Scholar]
  19. Kusaka, T., Nakano, T., & Hayashi, C. 1970, Prog. Theo. Phys., 44, 1580 [Google Scholar]
  20. Leto, G., Jakubík, M., Paulech, T., Neslusan, L., & Dybczynski, P. A. 2008, MNRAS, 391, 1350 (Paper II) [NASA ADS] [CrossRef] [Google Scholar]
  21. Lin, D. N. C., & Papaloizou, J. C. B. 1993, in Protostars and Planets III, ed. E. H. Levy, & J. I. Lunine (Tucson: Univ. Arizona Press), 749 [Google Scholar]
  22. Morbidelli, A., & Brown, M. E. 2004, in Comets II, ed. M. C. Festou, H. U. Keller, & H. A. Weaver (Arizona: Univ. Arizona Press), 174 [Google Scholar]
  23. Morbidelli, A., Levison, H. F., Tsiganis, K., & Gomes, R. 2005, Nature, 435, 462 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  24. Papaloizou, J. C. B., Terquem, C., & Nelson, R. P. 1999, in ASP Conf. Ser., 160, ed. J. A. Sellwood, & J. Goodman, 186 [Google Scholar]
  25. Papaloizou, J. C. B., Nelson, R. P., & Snellgrove, M. D. 2004, MNRAS, 350, 829 [NASA ADS] [CrossRef] [Google Scholar]
  26. Safronov, V. S. 1972, in The Motion, Evolution of Orbits, and Origin of Comets, ed. G. A. Chebotarev et al. (Dordrecht: Reidel), Proc. IAU Symp., 45, 329 [Google Scholar]
  27. Tsiganis, K., Gomes, R., Morbidelli, A., & Levison, H. F. 2005, Nature, 435, 459 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  28. Weidenschilling, S. J. 1977a, Ap&SS, 51, 153 [Google Scholar]
  29. Weidenschilling, S. J. 1977b, MNRAS, 180, 57 [Google Scholar]
  30. Weissman, P. R., McFadden, L.-A., & Johnson, T. V. 1999, Encyclopedia of the solar system (San Diego: Academic Press) [Google Scholar]

All Tables

Table 1:   The amounts of comets (in per cents) from various source regions (Sect. 2.2), which reside in the inner and outer part of the OC, and the whole OC in 2 Gyr.

Table 2:   The amounts (in per cents) of comets from various regions of their origin (Sect. 2.2), which were ejected into the interstellar space during the first 2 Gyr.

All Figures

  \begin{figure} \par\includegraphics[angle=-90,width=7cm,clip]{12712f1a.eps}\vspa... ...pace*{1mm} \includegraphics[angle=-90,width=7cm,clip]{12712f1d.eps} \end{figure} Figure 1:

Distribution of the surviving TPs in the region of the PPD at 2 Gyr for A-, B-, C- and D-models of the initial PPD (Sect. 2). For every model, this distribution is illustrated with bars, each corresponding with 0.1 AU-wide interval of heliocentric distance. The corresponding initial distribution is illustrated with a dashed curve.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=7cm,clip]{12712f2a.eps}\vspa... ...pace*{1mm} \includegraphics[angle=-90,width=7cm,clip]{12712f2d.eps} \end{figure} Figure 2:

The evolution of the population of the OC as well as its inner (IOC) and outer (OOC) parts during the first 2 Gyr. The evolution is shown for the A-, B-, C- and D-models (Sect. 2) of the initial PPD.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.