EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 509 (January 2010) A&A, 509 (2010) A20 Full HTML
Free Access
Issue
A&A
Volume 509, January 2010
Article Number A20
Number of page(s) 15
Section Galactic structure, stellar clusters, and populations
DOI https://doi.org/10.1051/0004-6361/200912687
Published online 12 January 2010
A&A 509, A20 (2010)

Chemical abundances of 11 bulge stars from high-resolution, near-IR spectra[*]

N. Ryde1,2 - B. Gustafsson2 - B. Edvardsson2 - J. Meléndez3 - A. Alves-Brito4 - M. Asplund5 - B. Barbuy4 - V. Hill6 - H. U. Käufl7 - D. Minniti8,9 - S. Ortolani10 - A. Renzini11 - M. Zoccali8

1 - Lund Observatory, Box 43, 221 00 Lund, Sweden
2 - Department of Physics and Astronomy, Uppsala University, Box 515, 751 20 Uppsala, Sweden
3 - Centro de Astrofisica da Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal
4 - Department of Astronomy, University of São Paulo, IAG, Rua do Matão 1226, São Paulo 05508-900, Brazil
5 - Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85748 Garching, Germany
6 - OCA, Boulevard de l'Observatoire, BP 4229, 06304 Nice Cedex 4, France
7 - ESO, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
8 - Department of Astronomy and Astrophysics, Universidad Catolica de Chile, Casilla 306, Santiago 22, Chile
9 - Vatican Observatory, V00120 Vatican City State, Italy
10 - Department of Astronomy, Padova University, Vicolo dell'Osservatorio 2, 35122 Padova, Italy
11 - Osservatorio Astronomico di Padova, Vicolo dell'Osservatorio 5, 35122 Padova, Italy

Received 12 June 2009 / Accepted 22 September 2009

Abstract
Context. It is debated whether the Milky Way bulge has characteristics more similar to those of a classical bulge than those of a pseudobulge. Detailed abundance studies of bulge stars are important when investigating the origin, history, and classification of the bulge. These studies provide constraints on the star-formation history, initial mass function, and differences between stellar populations. Not many similar studies have been completed because of the large distance and high variable visual extinction along the line-of-sight towards the bulge. Therefore, near-IR investigations can provide superior results.
Aims. To investigate the origin of the bulge and study its chemical abundances determined from near-IR spectra for bulge giants that have already been investigated with optical spectra. The optical spectra also provide the stellar parameters that are very important to the present study. In particular, the important CNO elements are determined more accurately in the near-IR. Oxygen and other ${\alpha }$ elements are important for investigating the star-formation history. The C and N abundances are important for determining the evolutionary stage of the giants and the origin of C in the bulge.
Methods. High-resolution, near-infrared spectra in the H band were recorded using the CRIRES spectrometer mounted on the Very Large Telescope. The CNO abundances are determined from the numerous molecular lines in the wavelength range observed. Abundances of the ${\alpha }$ elements Si, S, and Ti are also determined from the near-IR spectra.
Results. The abundance ratios [O/Fe], [Si/Fe], and [S/Fe] are enhanced to metallicities of at least [Fe/H] = -0.3, after which they decline. This suggests that the Milky Way bulge experienced a rapid and early burst of star formation similar to that of a classical bulge. However, a similarity between the bulge trend and the trend of the local thick disk seems to be present. This similarity suggests that the bulge could have had a pseudobulge origin. The C and N abundances suggest that our giants are first-ascent red-giants or clump stars, and that the measured oxygen abundances are those with which the stars were born. Our [C/Fe] trend does not show any increase with [Fe/H], which is expected if W-R stars contributed substantially to the C abundances. No ``cosmic scatter'' can be traced around our observed abundance trends: the measured scatter is expected, given the observational uncertainties.

Key words: stars: abundances - stars: carbon - Galaxy: bulge - infrared: stars - stars: late-type

1 Introduction

An unsolved problem in cosmology is how galaxies formed and obtained their stellar populations (see for instance Renzini 2006). Two scenarios have traditionally been presented for the formation of bulges, one leading to ``classical'' bulges, whereby they originate from merger-driven starbursts, and another leading to ``pseudobulges'', related to the ``secular'', dynamical evolution of disks (Kormendy & Kennicutt 2004). In the classical bulge scenario, most stars originate in a short phase of star formation when the universe was only a few Gyr old, and bulge formation may precede that of the disk, which possibly formed later. In the so-called ``pseudobulges'', stars form in the disk, over an extended period of time, and the bulge is produced by the secular evolution of the disk driven by the development of a bar. Thus, one expects classical bulges consist almost entirely of old stars, and stars in pseudobulges to have an age spread comparable to the Hubble time.

The bulges of early-type spirals (Sa and Sb) are generally considered to be ``classical'', while pseudobulges are thought to inhabit preferentially late-type spirals (Sc and Sd). The Sbc Milky Way (MW) galaxy sits morphologically on the borderline, hence it is no surprise that the origin of its bulge is currently a matter of debate. What is especially puzzling about the MW bulge is that it is dynamically ``pseudo'' (due to its boxy, peanut-shaped bar, Kormendy & Kennicutt 2004), while its stellar content is that expected of a ``classical'' bulge. Indeed, deep color-magnitude diagrams (CMD) of the MW bulge show no detectable trace of stellar populations younger than ${\sim}10$ Gyr (Zoccali et al. 2003; Ortolani et al. 1995), a conclusion for which compelling evidence was provided by the deep CMD obtained with HST for a proper-motion selected sample of bulge stars (Clarkson et al. 2008).

This sharp distinction between these two scenarios of bulge formation has been called into question: observations of disk galaxies at redshift ${\sim}2$ (a lookback time ${\sim}10$ Gyr) indicate that early disks have radically different physical properties from local disks of similar mass. The early disks are characterized by far higher velocity dispersions and gas fractions, and harbor massive, highly star-forming clumps (Förster Schreiber et al. 2009; Genzel et al. 2006). Thus, dynamical instabilities in these early disks appear to occur on much shorter timescales (few 108 years) than for local disks, with a secular, but rapid evolution of the early disks resulting in the early formation of a bulge (Genzel et al. 2008). In parallel to observations, theories have also envisaged the early production of bulges by the migration and central coalescence of gas-rich clumps in high-redshift disks (e.g., Immeli et al. 2004; Bournaud & Elmegreen 2009; Carollo et al. 2007; Elmegreen & Elmegreen 2005).

Determinations of detailed chemical compositions are key data for studies of the origin and evolution of stellar populations, since they provide characteristic signatures of the objects that enrich the interstellar gas. Abundance ratios are sensitive to both the time scales of star formation and the initial mass function (IMF), and may illustrate relations between different stellar groups, since different elements are synthesized by different processes and stars. For the bulge, a high ratio of ${\alpha }$-element abundances relative to Fe is observed, suggesting that the star-formation period was early and very short (Fulbright et al. 2007; Lecureur et al. 2007) and that the bulge formed more rapidly than the thin, and perhaps even the thick, Galactic disk (McWilliam et al. 2008).

Since stellar abundance ratios carry this genetic information on the origin of different stellar populations, Zoccali et al. (2006) compared the [O/Fe] ratios of bulge stars with those of thin disk and thick disk stars from Bensby et al. (2004). Finding bulge ratios that are systematically higher than disk ones, Zoccali et al. argued against the bulge having been appreciably contaminated by the migration of thick disk stars analogous to those in the solar neighborhood. A similar consideration was put forward by Lecureur et al. (2007), based on the much higher values of [Na/Fe], [Mg/Fe], and [Al/Fe] ratios in bulge stars compared to those in thin and thick disk stars measured by Bensby et al. (2005), Bensby & Feltzing (2006), and Reddy et al. (2006). However, differences in abundance ratios may also be caused by differences in systematic errors when the abundance analysis is completed by different groups, using different data and methods. For example, cool giants with crowded spectra are affected by many systematic uncertainties (see, for instance, Santos et al. 2009) and comparing abundances derived from metal-rich, cool giants with those of solar-type dwarfs could be uncertain because of relative systematic errors.

In this context, Meléndez et al. (2008) carried out a homogeneous abundance analysis of bulge, thick disk, and thin disk giant stars, confirming the [O/Fe] trend found by Zoccali et al. (2006) for bulge stars, but finding that [O/Fe] ratios for thick disk stars are much higher than those derived by Bensby et al. (2004). Thus, in the study by Meléndez et al., the high thick-disk [O/Fe]-ratios appear to be indistinguishable from those of the bulge. This similarity between the [O/Fe] ratios of bulge and thick disk stars weakens the conclusion of Zoccali et al. (2006) about the genetic difference between the bulge and the thick disk, although it remains to be seen whether this similarity also holds for other [${\alpha }$/Fe] ratios, that appear to be so different in Lecureur et al. (2007). If thick disk and bulge giants follow the same [O/Fe] versus [Fe/H] relation, the inference would be that both have formed ``rapidly''. The properties of $z \sim2$ disks, with their high velocity dispersion and high star formation rates, implies that we are witnessing thick-disk formation.

Determination of abundances for a large sample of red giant stars and planetary nebulae (cf. Chiappini et al. 2009) in various bulge fields as well as in the inner Galactic disk will obviously provide a most powerful method for constraining the chemical evolution and models of the bulge (Silk & Wyse 1993; Matteucci & Romano 1999). A way to achieve this is by high-resolution, near-IR spectroscopy of red-giant stars. In the IR, the obscuration in the direction of the bulge is considerably lower, offering us the opportunity to target heavily reddened regions. Furthermore, near-IR spectra are far less affected by line blending than spectra at optical wavelengths, which means that it is possible to accurately fit the continuum and avoid abundance criteria marred with blending lines, so important in abundance analysis. Moreover, only the IR offers, even within a small wavelength range, all the indicators necessary to accurately determine the CNO abundances by the simultaneous observations of many uncontaminated CO, CN, and OH lines. Here, we present the first data from our VLT/CRIRES program in which we study systematically the stellar abundance ratios in different parts of the Galactic bulge. In particular, we study the key elements C, N, and O, but also include some ${\alpha }$ elements.

2 Observations

In the VLT program ``Unveiling the secrets of the Galactic bulge: an infrared spectroscopic study of bulge giants'' we have as yet observed 8 bulge stars in the H band with the CRIRES spectrometer (Käufl et al. 2004; Moorwood 2005; Käufl et al. 2006). CRIRES is a cryogenic echelle spectrograph designed for high spectral resolution, near-infrared observations. Adaptive optics (MACAO - multi-applications curvature adaptive optics) was used, enhancing both the spatial resolution and the signal-to-noise ratio. The adaptive optics, which is only feasible and available in the near-IR, also has the advantage of rejecting diffuse starlight that may affect observations in regions of high star density.

The giants that we observed were chosen from the optical investigation of Lecureur et al. (2007), to be in three fields of the Galactic bulge at (l, b) = ($0^\circ$, $-6^\circ$), ($1^\circ$, $-4^\circ$) [Baade's Window], and ($5^\circ$, $-3^\circ$) [Globular Cluster NGC 6553]. Lecureur et al. (2007) analyzed UVES/FLAMES spectra and derived chemical abundances, but their determinations of the important C, N, and O elements can be improved. The K giants are chosen to be half way up along the red-giant branch (RGB), with 4000 K $\leq$ $T_{\rm eff}$ $\leq$ 4500 K, a range where molecular diagnostics can be optimally observed and where adequate S/N ratios can be achieved. Spectra of these stars may be modelled more accurately than those of stars higher in the RGB, making their abundance analysis much more reliable. The surface compositions are characteristic of the gas from which the stars once formed, with the exception of changes in C and N, the sums of which are, however, expected to be left unaltered by the dredge-up of CN-processed material from the stellar interiors. The H magnitudes and the total integration times (ranging from 32 to 80 min) for each of the program stars are given in Table 1. Our observations were performed between May 2007 and October 2008.

Zoccali et al. (2008) determined the iron abundance distribution of the Galactic bulge from approximately 800 K giants (including those we observed) in four fields toward the bulge with the VLT/FLAMES in the GIRAFFE mode at R=20 000. They detected a clear gradient toward lower latitudes. The iron distribution functions of the stars in the different fields are mainly in the range $-1.5 < {\rm [Fe/H]}< +0.5$, but the peaks of the distributions occur at lower [Fe/H] for lower latitudes. All of our stars in three fields in the bulge have metallicity less than solar.

The projected slit width on the sky was 0.30 $\pm$ $0.01\hbox{$^{\prime\prime}$ }$ yielding a spectral resolution of $R \sim \lambda/\Delta \lambda = 70~000$ with 3.0 pixels per spectral resolution element[*]. This allows us to resolve blends, define the continuum, and adequately take care of telluric lines. In principle, with ideal adaptive optics and perfect image quality the true effective entrance slit would be the diffraction-limited image of the star itself transmitted by the instrument[*]. However, CRIRES does not reach this limit because of the finite pixel size ( ${\sim}1500$ ms-1 equivalent) and the limited optical quality of the internal optics, mostly due to the relatively large ZnSe pre-dispersion prism. Indeed, the optical quality of the complete pre-disperser is just marginally sufficient for the nominal resolution of R=100 000. In addition, at the wavelength of interest here, the adaptive optics does not produce diffraction-limited images, but only a core with a halo. This implies that the finite slit width controls the effective spectral resolution. During the commissioning of the CRIRES-MACAO system, the effective point-spread function was analyzed in great detail, and even in the K-band in perfect conditions the energy fraction within the nominal 0.2'' slit never exceeded 60%, while for fainter stars and normal seeing conditions this fraction was similar to 40-50% (for more details, see Table 1 in Paufique et al. 2006).

The wavelength range expected from the ``36/-1/i''-setting of CRIRES (i.e., in Echelle order 36) was 1539.3-1565.4 nm over the detector arrays, consisting of a mosaic of four Aladdin III InSb arrays in the focal plane. At order 36, the blaze function of the grating limits the throughput of the detector arrays #1 and #4 markedly. We, therefore, concentrated our analysis on detector arrays #2 and #3. Data for the first and fourth detector arrays were used to check the abundances when possible. This is, nevertheless, an improvement in wavelength coverage compared with the Phoenix spectrometer (Hinkle et al. 1998) at the Gemini telescope, an instrument that inspired the design of the CRIRES spectrometer, with a total wavelength range that corresponds to approximately one of CRIRES's detector arrays ( $\Delta \lambda / \lambda = 0.5\%$). It should be noted that there are small gaps of approximately 2 nm between the spectra on the detector arrays.

Table 1:   Account of our observations.

Table 2:   Stellar parameters for the model atmospheres of our program stars given as $T_{\rm eff}/\log g/{\rm [Fe/H]}/\xi_{\rm micro}$.

The approximate signal-to-noise ratios (S/N) per pixel of the observed spectra at 1554.8 nm (a carefully selected continuum region in the third detector array) are also given in Table 1. The S/N per resolution element is close to being a factor of 2 higher. The S/N is difficult to measure because the many spectral lines make it difficult to find a large enough region of continuum in which it can be estimated. The numbers given here are therefore indicative. The S/N varies by a factor of two between the detector arrays, mainly because the blaze function. The S/N of the third detector array increases with wavelength from 90 to 110% of the S/N at the reference wavelength of the standard setting, here chosen to be at 1557.3 nm. For the second detector, the S/N varies linearly with wavelength from approximately 70% to 100% of the S/N at the reference wavelength.

The observed data were reduced with the ESO standard pipeline reduction package. The CRIRES pipeline is based on the general and coherent approach by ESO using common routines, also employed in other instruments (Ballester et al. 2006). The wavelength solution is based on a physical model approach for CRIRES (Kerber et al. 2008a) using telluric emission lines and the new infrared line catalog for ThAr hollow arc lamps (Kerber et al. 2008b). For the extraction of one-dimensional spectra, the data taken for different positions of the star along the slit (resulting from nodding and dithering) are corrected in the usual way for glitches and bad pixels and then rebinned in wavelength space before co-addition. The final extraction is based on the ``optimal extraction'' method, which preserves the flux without sacrificing S/N-ratio[*].

In addition to these eight giants, we reanalyzed the data of three bulge giants studied in Ryde et al. (2009). These were also observed with CRIRES, during its science verification, on 12 August 2006. The H magnitudes and the total integration times are given in Table 1. The observations and data are similar to those of our eight stars, although they were observed at R=50 000 and processed with routines in the reduction package IRAF (Tody 1993)[*] to obtain one-dimensional, continuum-normalized, and wavelength-calibrated stellar spectra.

3 Analysis

We analyze our spectra by modeling the stellar atmosphere and creating synthetic spectra for the observed spectral region. These are thereafter convolved to fit the shapes and widths of the lines, including the stellar macroturbulence and instrumental broadening. We then derive elemental abundances by fitting the synthetic to the observed spectra. In this section, we discuss the model atmospheres, the stellar parameters and their uncertainties, and the spectrum synthesis.

3.1 Model atmospheres

We derived model atmospheres with the MARCS code (Gustafsson et al. 2008) after adopting the stellar effective temperature, logarithmic surface gravity, metallicity, microturbulence, and [${\alpha }$/Fe] enhancement for the model of each of our stars (see Table 2, Col. 4). The MARCS standard models are hydrostatic and computed based on the assumptions of local thermodynamic equilibrium (LTE), chemical equilibrium, homogeneous spherically symmetric stratification (in our case with $M_{\rm star}=0.8~M_\odot$), and the conservation of the total flux (radiative plus convective, the convective flux being computed using the local mixing length recipe). The radiation field used in the model generation is calculated by assuming absorption from atoms and molecules by opacity sampling at approximately 100 000 wavelength points over the wavelength range $1300~\mbox{\AA}{-}20~\mu$m. The models are calculated with 56 depth points from a Rosseland optical depth of $\log \tau_{\rm Ross}=2.0$ to $\log \tau_{\rm Ross}=-5.0$. Data on absorption by atomic species are collected from the VALD database (Piskunov et al. 1995) and Kurucz and other authors (for details, see Gustafsson et al. 2008). The molecular-line opacity of CO, CN, CH, OH, NH, TiO, VO, ZrO, H2O, FeH, CaH, C2, MgH, SiH, and SiO is included and up-to-date dissociation energies and partition functions are used. It should be noted that, for our targeted elements, we iterate and specify these abundances for each new iteration of the model atmosphere calculation, in order to be self-consistent.

The atomic line absorption files used in a MARCS model calculation are precalculated within a grid. Those used for our models are thus files with metallicities closest to the metallicity of the stars. The grid is given in steps of $\Delta {\rm [Fe/H]} = 0.25~{\rm dex}$ within the relevant metallicity range. For stars with [Fe/H] < 0.0, [${\alpha }$/Fe] can be solar or ${\alpha }$-enriched by up to $0.4~{\rm dex}$. For more metal-rich stars, the abundance ratios are solar. Microturbulence parameters of 1 or $5~{\rm km~s^{-1}}$ were used in the model calculations.

3.2 Fundamental stellar parameters and their uncertainties

3.2.1 Deriving the fundamental parameters of our stars

The fundamental stellar parameters, i.e., $T_{\rm eff}$, $\log g$, [Fe/H], and $\xi_{\rm micro}$, are needed as input to our model photosphere and spectrum synthesis. Optical Fe I and Fe II equivalent widths were used to obtain spectroscopic surface gravities and effective temperatures by requiring a relative ionization and excitation equilibrium with respect to a set of standard bright giants (see Meléndez et al. 2008). The iron linelist was carefully chosen to avoid significant blends in K giants (Alves-Brito et al. 2009, in preparation) and is an extension of the linelist presented in Hekker & Meléndez (2007). It has an identical scale to that used by Meléndez et al. (2008), which means that the stellar parameters for our stars are on the same scale as those of well-studied nearby giants, which ultimately have effective temperatures determined from the infrared flux method temperature scale of Ramírez & Meléndez (2005a,b) and surface gravities based on absolute magnitudes inferred from Hipparcos parallaxes by adopting stellar masses from isochrones.

The equivalent widths ($W_\lambda$) of the iron lines for our new CRIRES stars were taken from Lecureur et al. (2007), who obtained automatic $W_\lambda$ measurements from spectra observed with VLT/FLAMES in the UVES mode, providing a spectral resolution of R=45 000. They used the DAOSPEC code, which is described in Stetson & Pancino (2008). For one star, B6-b8 (which can be considered as one of the most difficult cases, because the star is cool and metal-rich), we also measured the equivalent widths manually.

The microturbulence, $\xi_{\rm micro}$, was obtained by assuming that the derived Fe I abundances were independent of line strengths. This procedure also yields the iron abundances. The [${\alpha }$/Fe] used in our models are based on our preliminary optical analysis of different ${\alpha }$-elements in bulge stars (Alves-Brito et al. 2009, in preparation) and so is based on a preliminary mean bulge relationship between [${\alpha }$/Fe] and [Fe/H].

Our new stellar parameters for our bulge stars, including the three stars from Ryde et al. (2009) and our reference star Arcturus, are given in Table 2. In this table, we also give the [${\alpha }$/Fe] values that we use to determine the parameters and later adopt in the model calculations. The earlier determinations of the stellar parameters for these stars from the literature are also given in the table, namely those of Lecureur et al. (2007), the updated parameters based on UVES data as described in Zoccali et al. (2008), and finally Fulbright et al. (2006), the last set also being used by Ryde et al. (2009). The differences in the stellar parameters, which are sometimes quite large, are mainly caused by the different methods applied to the different stellar parameter determinations. For instance, the different line sets used and our relative ionization-equilibrium constraint to obtain the surface gravities, can cause differences. The different values illustrate the general uncertainty, in particular the difficulties in determining the fundamental parameters from the equivalent widths observed with UVES/FLAMES (Lecureur et al. 2007). Our new effective temperatures are systematically cooler (on average by 159 K) than the updated parameters based on the UVES data, as described in Zoccali et al. (2008). For the three stars from Fulbright et al. (2006), the differences are in both directions with a maximum of 144 K.

We redetermined the fundamental parameters of the stars from Ryde et al. (2009), which we also analyse here, based on the same scale used for other stars presented here. We also redetermined the fundamental parameters for our reference star Arcturus (${\alpha }$ Boo) in a similar way. The new parameters for these stars are given in the lower part of Table 2. The changes in the derived C, N, and O abundances for these stars compared with those derived by Ryde et al. (2009) agree with that expected from the sensitivities of these abundances to the stellar parameters, and keeping in mind that different solar C, N, and O values are used in our paper compared to Ryde et al. (2009).

It would be preferable to obtain accurate effective temperatures directly from our IR spectra because of the substantial extinction towards the bulge in the visual wavelength region. This is, however, a difficult task. Although we are exploring the use of other infrared wavelength regions to improve the determination of stellar parameters, the current infrared spectrographs available to us on 8 m-class telescopes cover only narrow regions, therefore requiring considerable amounts of telescope time to improve the stellar parameters based solely on infrared data. Furthermore, the limited ranges in excitation energy for lines of various molecular species limit their use for $T_{\rm eff}$ determination. Effective-temperature sensitive features are in particular the OH molecular lines used in oxygen abundance determinations. Other lines are only weakly sensitive. Carbon, which appears in numerous lines of four different species, should in principle be useful for the $T_{\rm eff}$ determination. Our tests show, however, that for a 100 K increase in  $T_{\rm eff}$ and for fundamental parameters typical of our targets the high-excitation C  I lines become only slightly stronger, the CN lines remain unchanged, the CO lines become slightly weaker, and the C2 lines remain almost unchanged. High S/N spectra or broad wavelength regions would therefore be necessary. In the near future, we, therefore, intend to rely on spectroscopic equilibrium based on optical FeI and FeII lines. Besides the current work of Alves-Brito et al. to define the zeropoints of the spectroscopic stellar parameters, we are currently acquiring more high resolution optical data of bright K giants, which will allow us to further improve our stellar parameter scale. We are also developing simulations to estimate realistic uncertainties in the atmospheric parameters of cool giants (Meléndez et al., in preparation).

3.2.2 Uncertainties in the fundamental parameters

Our $T_{\rm eff}$ values are uncertain, limited by the uncertainties in the $W_\lambda$ measurements. However, the small dispersion in the [O/Fe] versus [Fe/H] plot (Fig. 2) suggests that the random errors are of the order of 75 K. This is the value that we use to derive the impact of this uncertainty on the derived abundances (see Table 4). However, the uncertainty could be underestimated.

Our spectroscopic surface gravity determinations are also very uncertain with uncertainties estimated to be 0.3 dex (in some cases by as much as 0.5 dex), again mainly because of the quality of the $W_\lambda$ measurements of the few weak Fe II lines but also because we assume LTE in the ionization equilibrium, which may not be valid. However, our $\log g$ values more or less follow our expectations for giants with $T_{\rm eff} = 4000$ K ( $\log g \sim1.0$) and 4300 K ( $\log g = 2.0$). On the other hand, these gravities locate a few stars at distances incompatible with the bulge (all distances being between 4.5 and 12 kpc). Our stars are chosen from the bulge giants of Lecureur et al. (2007), which were selected to have a high probability of being bulge members. We therefore also calculated the photometric surface gravities, using the PARAM tool (see da Silva et al. 2006), by assuming the stars to be at a distance of 8 kpc (Reid 1993) and calculating the extinction in the same way as Lecureur et al. (2007). Our resulting gravities are given in Table 3 together with our spectroscopic ones. The $\log g$ values obtained by Zoccali et al. (and Lecureur et al.) are also determined photometrically and are given by 1.7 $\pm$ 0.1 dex, in good agreement with our photometric values. The main sources of uncertainty in the photometric gravities are that the true distances to the stars are not well known and the bulge has an extension of a few kpc. For a conservative uncertainty of ${\pm}2$ kpc in the distance of 8 kpc, we find an uncertainty in the gravities of 0.25 dex, only because of the distance uncertainty. The sensitivity of the determination of $\log g$ to the extinction and the differential reddening, of which the latter is not taken into account, is small (see Lecureur et al. 2007). The gravities based on the two methods, given in Table 3, are compatible with each other within the uncertainties, the differences being mostly <0.3 dex, except for one case, B6-b8, which is a cool, metal-rich giant. Fortunately, in our case, whichever $\log g$ determination we assume does not make a large difference, especially for the oxygen abundance from the OH lines, as can be seen from Table 4 and Fig. 2. The carbon abundance determined from the CO lines is, however, more affected (see also Fig. 4). In the following discussion, we have chosen to use the surface gravities determined spectroscopically.

Table 3:   Spectroscopically and photometrically determined surface gravities.

Finally, we estimate the uncertainty in the metallicity to be, in general, of the order of 0.05 dex and that in the microturbulence to be of the order of 0.25 km s-1.

The changes in the fundamental parameters caused only by the two different measurements of equivalent widths (automatic DAOSPEC or manually) of the cool, metal-rich giant, B6-b8, are 20 K in the temperature, 0.16 dex in $\log g$, -0.17 dex in [Fe/H], and 0.35 km s-1 in the microturbulence. The differences are within our estimated total uncertainties, except for  $\xi_{\rm micro}$ and the metallicity. This star is, however, particularly cool and metal-rich, which means that the iron line measurements are especially difficult for this star.

3.3 Synthetic spectra

For the analysis of the observed spectra, we generated synthetic spectra, calculated for spherical symmetry in our model photospheres. We sample the spectra with a resolution of R=600 000. With a microturbulence velocity of $1{-}2~{\rm km~s}^{-1}$, this ensures an adequate sampling. To fit the observed spectra, we finally convolve our synthetic spectra with a macroturbulent broadening, represented by a radial-tangential function (Gray 1992), and fitted to include the effects of both macroturbulence and the instrumental profile. The final macroturbulence parameters used are given in Table 2. The code used for calculating the synthetic spectra is BSYN v. 7.06, which is based on routines from the MARCS code. Full consistency with the model atmosphere is achieved by choosing the same fundamental parameters, [${\alpha }$/Fe], individual abundances and in both calculations, including the molecular equilibria. A  $^{12}\rm C/^{13}\rm C$ ratio of 24 (96%  $^{12}\rm C$) is used for the bulge stars, and 9 for Arcturus.

\begin{figure} \par\includegraphics[width=18cm,clip]{12687fig1.eps} \end{figure} Figure 1:

Sections of the observed CRIRES spectra of two of our bulge giants are shown with full, black lines. The observations are wavelength-shifted to laboratory wavelengths to enable a more direct comparison between the different stellar spectra. Therefore, our observed spectra cover slightly different wavelength ranges. For comparison, the Arcturus atlas spectrum (Hinkle et al. 1995b) is also shown. The parts of the spectra with the highest signal-to-noise ratios are shown. From these parts the C, N, and O elements can be determined. Our best-fit synthetic spectra is shown in red. All synthetic lines deeper than a factor of 0.97 of the continuum are identified. A few features cannot be identified in the Arcturus spectrum and are labeled with question marks. These features also show up in the bulge-star spectra. A few lines in BW-f6 are conspicuously stronger than expected. They are probably affected by cosmic rays in the detector array.

Open with DEXTER

The atomic linelist used in our calculations is compiled from the VALD database (Piskunov et al. 1995) and from Meléndez & Barbuy (1999). The stellar parameters of our bulge stars resemble those of ${\alpha }$ Boo, which is therefore a good choice of reference star. However, most of the lines used in our analysis can also be analyzed in the solar spectrum. We, therefore, primarily checked the linelist against the solar spectrum and corrected the line-strengths, if needed, by determining ``astrophysical $\log gf$-values'', and fitting the atomic lines in synthetic solar spectra to the observed ones (Livingston & Wallace 1991). Hence, in our linelist we adjusted the wavelengths of 96 lines based on the solar spectrum (see Table 7). The lines fitted were, among others, some Fe, Ni, Si, S and Ti lines. In addition, 4 Ti lines and 4 Si lines, which were too weak in the solar spectrum, were fitted to the ${\alpha }$ Boo spectrum from the Hinkle et al. (1995a) atlas. These 8 lines are also given in Table 7. To determine the astrophysical $\log gf$-values of these lines, we need to know the abundances of these elements in ${\alpha }$ Boo. Furthermore, apart from iron, Mg and Si are the most important electron donors in the continuum-forming regions, and therefore affect the line strengths by means of the continuous opacity (H $^-_{\rm ff}$). It is therefore also important to estimate the abundance of Fe and Mg, as reliably as possible. Hence, the Fe, Mg, Si, and Ti abundances of our Arcturus modeling are based on the optically determined abundances derived by Fulbright et al. (2007), but taking into consideration our slightly different fundamental parameters, which, however, increased these abundances by only 0.00, 0.01, 0.03, and 0.01 dex, respectively. The other Fe, Si, and Ti lines in our near-IR list, yield the same abundance for Arcturus, within a few tenth of a dex. To conclude, the linelist used here is similar to the one described in Ryde et al. (2009), except that some new lines are added, a few omitted, the strengths of nine lines were adjusted slightly (less than 0.1 dex), and the strengths of 2 Ti lines (15 334.84 and 15 543.78 Å) and one Si line (15 506.98 Å) strengths were adjusted by a larger amount. The latter three lines are all visible in the sun.

The molecular lists included are for CO (Goorvitch 1994), SiO (Langhoff & Bauschlicher 1993), CH (Jørgensen et al. 1996), CN (Jørgensen & Larsson 1990; and Plez 1998, private communications), OH (Goldman et al. 1998), and C2 (Querci et al. 1971; and Jørgensen 2001, private communications). For the molecules, the linelists were adopted as they were, leading to the following C, N, and O abundances for Arcturus from the spectra in the Arcturus atlas (Hinkle et al. 1995a): $\log\varepsilon_{\rm C}=8.08 \pm 0.11$ (from CO lines), $\log\varepsilon_{\rm N}=7.64\pm0.09$ (from CN lines), and $\log\varepsilon_{\rm O}=8.70 \pm 0.13$ (from OH lines), which are in excellent agreement with the values derived by Ryde et al. (2009) and by the optical work by Lecureur (2007), who derived $\log\varepsilon({\rm C})=7.96 \pm 0.10$, $\log\varepsilon({\rm N})=7.74 \pm 0.10$, and $\log\varepsilon({\rm O})=8.70 \pm 0.05$.

From our spectra, we determined elemental abundances from the CO [v=3-0] band, around 20 suitable CN lines, some 20 suitable OH [ v=4-2, 3-1, 2-0] lines, and numerous Fe  I lines. Silicon could be measured from 2 or 3 lines, sulfur from 2 lines, and titanium from only 1 line, which made the derived Ti abundance the most uncertain of the ${\alpha }$ elements. We derive the best fits, line by line, by synthesizing a grid of model spectra with incremental differences of 0.05 dex in the abundance sought for and finding the best fit by visual inspection. While for the OH and CN lines, and the atomic lines, every suitable line was inspected, for the CO band the entire band was fitted. In Fig. 1, we present two examples of spectra of our 8 bulge stars, namely those of B3-b8 and BW-f6. These are spectra for which we obtained the highest S/N. Only the third detector array, providing the highest S/N, is shown, but spectra from the other detector arrays were also used in the analysis. The reference spectrum of Arcturus is also shown in the figure.

Table 4:   Uncertainties in the derived abundances due to uncertainties in the stellar parameters.

Table 5:   [C/Fe]a,b, [N/Fe], [(C+N)/Fe], [O/Fe], [Si/Fe], [S/Fe], [Ti/Fe], and [Fe/H] for our 11 bulge giants and Arcturus.

3.4 Uncertainties in the derived abundances

The propagation of uncertainties in the stellar parameters to uncertainties in the C, N, and O abundances is presented in Table 4, based on the discussion in Ryde et al. (2009). These uncertainties are derived for a typical star of our sample, namely BW-f6. The uncertainty in the [${\alpha }$/Fe] ratio is included but ambiguous since the different ${\alpha }$-elements show different trends. We adopted a general enhancement of [${\alpha }$/Fe] = +0.2 in both the model calculations and the calculation of the synthetic spectra. We estimate the total internal uncertainties in the derived C, N, and O abundances to be approximately $\Delta A_{\rm C} = 0.11$, $\Delta A_{\rm N} = 0.09$, and $\Delta A_{\rm O} = 0.13$ dex. As a comparison, the standard deviations in the determinations of the C, N, and O abundances from the many observed CO, CN, and OH lines for a given model are small, less than 0.05 dex. For example, for a given star and model atmosphere, the determination of the oxygen abundances from each of the approximately 20 suitable OH lines provides a mean oxygen abundance with a standard deviation of 0.04 (line-to-line scatter) and a standard deviation of the mean of 0.01 dex. We note, however, that the error in the CNO abundances generated by errors in the fundamental parameters will correlate, e.g. according to Table 4 an underestimated effective temperature will lead to underestimated abundances of C, N, as well as O. For the ${\alpha }$ elements, represented here by sulfur, we estimate that $\Delta A_{\rm S} = 0.11$ dex, i.e., of the same order as the molecular lines. We see, however, that the oxygen abundance is affected by the largest uncertainty, which is mainly due to the uncertainties in the effective temperature.

The relatively low star-to-star scatter in the [O/Fe] versus [Fe/H] plot (see Fig. 2) confirms that our errorbar in the stellar parameters, especially  $T_{\rm eff}$, are reasonable. Although our [O/Fe] values are sensitive to  $T_{\rm eff}$, they are not affected much by the uncertainties in $\log g$ (compare Table 4 and the two panels in Fig. 2). On the other hand, the oxygen abundance of seven of our stars as derived by Zoccali et al. (2006) from the [O I] line at 6300 Å is not affected much by the effective temperature but far more by the surface gravity. For instance, a change in $\log g$ of +0.3 dex produces a change in the oxygen abundances of +0.13 dex from the [O I] line (cf.  ${\sim}0.00$ dex from the OH lines), whereas a change in the temperature of 100 K produces a change of +0.02 dex (cf. +0.16 dex from the OH lines).

Other systematic uncertainties that could affect the abundance results include those related to, for instance, the continuum placement, the model atmosphere assumptions (such as the treatment of convection and the assumption of spherical symmetry), the uncertainties in the line strengths ($\log gf$ values), and the dissociation energies of the molecules. Furthermore, possible non-LTE effects in the line formation of both atomic and molecular lines could affect the results in a systematic way. In the future, only a full non-LTE analysis of all relevant atoms and molecules would be able to disclose the magnitude of these systematic uncertainties that our LTE analysis might be plagued by. For abundance ratios, several uncertainties partly cancel leading to smaller uncertainties. The uncertainty due to the placement of the continuum is estimated to be relatively small, less than 0.03 dex.

\begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{12687fig2.eps} \end{figure} Figure 2:

Logarithmic ratios of oxygen to iron normalized by the solar value for bulge stars. Filled circles show all of our data from this paper, except for the special giant Arp 4203, which is denoted by an open circle. Crosses show the results of Meléndez et al. (2008). Typical uncertainties are indicated in the upper right corner. The upper panel shows the oxygen abundances we derive when we use our spectroscopically derived $\log g$ values with our stellar atmosphere models, whereas the lower panel shows the same values when we use instead our photometrically derived surface gravities.

Open with DEXTER

4 Results

In Table 5, we present our derived [C/Fe], [N/Fe], [O/Fe], [Si/Fe], [S/Fe], [Ti/Fe], and [Fe/H] for our eleven bulge giants. We also provide the derived C, N, C+N, O, and S abundances for Arcturus in addition to the Si, Ti, and Fe abundances used. Our iron abundances of the bulge stars, determined from 8 to 20 Fe-lines depending on the different S/N of the IR spectra, are systematically between 0.00 to 0.10 dex larger than the optically determined metallicity as given in Table 2, which is satisfactory. In Fig. 2, we plot the [O/Fe] versus metallicity for our 11 bulge giants, together with the bulge giants from Meléndez et al. (2008). These abundance ratios were also determined from near-IR spectra and the adopted stellar parameters were on the same scales. We find enhanced values of [O/Fe] $\sim$ +0.4 up to approximately [Fe/H] $\sim$ -0.3, after which they decrease. In the figure, we highlight the giant star Arp 4203 which shows a large depletion of carbon, a large enhancement of nitrogen, and a [C+N/Fe] that is far from solar, making this giant special. This was also noted by Fulbright et al. (2007), Meléndez et al. (2008), and Ryde et al. (2009), who concluded that the oxygen abundance in this star should probably not be used to represent the unprocessed [O/H] value of this bulge giant.

\begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{12687fig3.eps} \end{figure} Figure 3:

Logarithmic ratios of Si, S, and Ti to iron normalized by the solar value for our bulge stars are shown with filled circles. The [O/Fe] versus [Fe/H] trend is indicated by a full line for reference in all panels. The measured values for the special giant Arp 4203 are shown with an open circle. Typical uncertainties are indicated in the upper right corners.

Open with DEXTER

In Fig. 3, we plot our derived [Si/Fe], [S/Fe], and [Ti/Fe] versus our derived metallicity. For reference, we also plot the trend we estimate from our [O/Fe] versus [Fe/H] values. The abundances of the ${\alpha }$ elements are more uncertain than our derived C, N, O, and Fe abundances since there are much fewer lines to measure. The uncertainties are therefore larger for these elements than for the C, N, O, and Fe abundances. In spite of this, we find that the [${\alpha }$/Fe] values are enhanced for metallicities up to at least [Fe/H] $\sim$ -0.3 after which they appear to decline. Below this metallicity [Si/Fe] and [S/Fe] are enhanced at a level of [${\alpha }$/Fe] $\sim$ +0.3. For higher metallicities, they appear to decline and follow [O/Fe] for a given metallicity. The ratio [Ti/Fe] is generally lower for all metallicities. Our ${\alpha }$ element trends overall corroborate the [O/Fe] enhancement trend, although the [Ti/Fe] ratios are lower. In this figure, we also highlight Arp 4203.

All our stars except B3-b1 show significantly enhanced [N/Fe] values. If a star has experienced the first dredge-up, CN-cycled material is exposed at its surface. The abundances of C and N are then expected to change but their sum is left unaltered. In Table 5, we also provide the calculated [(C+N)/Fe]. This is plotted in Fig. 4 together with the [(C+N)/Fe] for the bulge giants from Meléndez et al. (2008). These two data sets show approximately the same pattern when it comes to the mean, standard deviation, and slope. We find a slope from a linear regression analysis for our data of k=+0.07 $\pm$ 0.09 and for both sets of k=+0.04 $\pm$ 0.04, i.e., both data sets are consistent with being sampled from a flat distribution. Furthermore, we find a mean for both data sets of $\langle$[(C+N)/Fe]$\rangle$ = 0.08 $\pm$ 0.09 (s.d.) and an error in the mean of 0.02 dex. Thus, both data sets show a systematic enhancement in the [(C+N)/Fe] ratios and they are therefore not consistent with being at solar values for all metallicities. Given our estimated uncertainties, our stars show no cosmic scatter. More stars and higher accuracy would be needed to judge whether an offset from solar values, the slight increase with metallicity, or the curved tendency in Fig. 4 are real. We note that the highest value, apart from that of Arp 4203, is that of Arcturus, with [(C+N)/Fe] = 0.23.

\begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{12687fig4.eps} \end{figure} Figure 4:

Logarithmic ratios of carbon+nitrogen to iron normalized by the solar value. Our data are shown by filled circles, except Arp 4203 which is shown by an open circle. Crosses show the results of Meléndez et al. (2008). The [(C+N)/Fe] value we derive for Arcturus is shown with a star. Typical uncertainties are indicated in the upper right corner. The upper panel shows the values we retrieve when assuming spectroscopically derived $\log g$ and the values presented in the lower panel assumes photometrically derived surface gravities.

Open with DEXTER

In Fig. 5, we plot C/N for our stars in the theoretical HR diagram and show how C/N varies with position in it. We see that the stars are aligned along the giant branch and that the C-N ratios decrease along it, as expected. Arp 4203 has evolved the furthest.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{12687fig5.eps} \end{figure} Figure 5:

C/N ratios plotted in the theoretical HR diagram. The dot diameters are proportional to C/N with a largest value of 4.6 for B3-b1, 2.8 for Arcturus, and 0.08 for Arp 4203. Stars with [Fe/H] < -0.4 are plotted as filled dots and the more metal-rich ones as open circles.

Open with DEXTER

5 Discussion

Here, we will discuss the trends of the ${\alpha }$ elements versus metallicity, and end with a discussion on our carbon and nitrogen abundances.

5.1 The [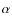${\alpha }$/Fe] trends

The trends of the ${\alpha }$ elements (O, Mg, Si, S, Ca, and Ti) are of particular interest, since accurate [${\alpha }$/Fe] ratios in pre-AGB bulge stars place strong constraints on the star-formation history.

5.1.1 Oxygen

Our oxygen abundances show good $\it general$ agreement in the downward [O/Fe] versus [Fe/H] trends with the results found by other authors. However, differences between these exist. In Fig. 6, we plot the [O/Fe] trends for the bulge stars based on analyses of near-IR spectra. These are, in addition to our new results, values from Cunha & Smith (2006), Rich & Origlia (2005), Meléndez et al. (2008), and Ryde et al. (2009). The [O/Fe] versus [Fe/H] trend of Rich & Origlia (2005) rises in value by 0.11 dex to adjust to the authors' assumed solar oxygen abundance of 8.83 compared to our value of 8.72.

It would be speculative to quantify the similarities between the different trends because of the small number of stars, but assuming a constant [O/Fe] versus [Fe/H] up to a metallicity of [Fe/H] = -0.3, and assuming a constant slope thereafter up to [Fe/H] $\sim$ +0.4, we find agreement between the slope of our data (k=-1.0 $\pm$ 0.3) and that of Meléndez et al. (2008) (k=-0.6 $\pm$ 0.15). Our data are also marginally consistent with the data of Rich & Origlia (2005), which are confined to a narrow range in metallicity. The Cunha & Smith (2006) data set seems, however, to infer a more shallow slope (k=-0.1 $\pm$ 0.2).

In Fig. 7, we plot the data points from the optical work of Fulbright et al. (2007), which also show an agreement in the slope (k=-0.8 $\pm$ 0.15). In Fig. 8 we plot the optical results from Zoccali et al. (2006), also presented in Lecureur et al. (2007) with a slope of k=-0.6 $\pm$ 0.15, together with our determinations. Our results are similar to these in scatter and slope.

\begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{12687fig6.eps} \end{figure} Figure 6:

Logarithmic ratios of oxygen to iron normalized by the solar value. The oxygen abundances are here all determined from near-IR spectra. Filled circles show our data from this paper, except that of Arp 4203. Arcturus at [Fe/H] = -0.53 is indicated with a black star at [O/Fe] = 0.51, in agreement with that of Lecureur (2007). Crosses show the results of Meléndez et al. (2008), green squares represent the abundances determined by Cunha & Smith (2006), and red squares the data from Rich & Origlia (2005). The blue star and plus signs represent thick disk and thin disk giants, respectively, from Meléndez et al. (2008).

Open with DEXTER

\begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{12687fig7.eps} \end{figure} Figure 7:

Logarithmic ratios of oxygen to iron normalized by the solar value. Filled circles show our data from this paper, except that of Arp 4203, and a black star indicates Arcturus at [Fe/H] = -0.53. Triangles show the optically determined values by Fulbright et al. (2007). The two small dots represent the stars from Fulbright et al. (2007), which were analyzed by Ryde et al. (2009) from near-IR lines and reanalyzed by us. The determinations by Fulbright et al. and our determinations are connected by full lines. The blue stars and plus signs represent thick disk and thin disk giants, respectively, from Meléndez et al. (2008).

Open with DEXTER

\begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{12687fig8.eps} \end{figure} Figure 8:

Logarithmic ratios of oxygen to iron normalized by the solar value. Filled black circles show our data from this paper, except that of Arp 4203, and a black star indicates Arcturus at [Fe/H] = -0.53. Filled green circles show the optically determined values by Lecureur et al. (2007) and Zoccali et al. (2006). The small black dots mark the stars from Lecureur et al. (2007) and Zoccali et al. (2006) for which we have determined the oxygen abundances from near-IR lines. These two determinations are connected. For the star B6-f7, there is only a near-IR determination of the oxygen abundance. When comparing these two determinations for the same stars, it should be noted that we have used new stellar parameters when determining the abundances from the near-IR spectra. The blue star and plus-sign symbols represent thick disk and thin disk giants, respectively, from Meléndez et al. (2008).

Open with DEXTER

Table 6:   [Fe/H] and [O/Fe] determined from near-IR lines in this paper and determinations based on optical lines.

All our stars are in common with the optical analyses of Zoccali et al. (2006) but for one of them it was impossible to determine an oxygen abundance from the [O I] lines at 6300 Å. The metallicities and [O/Fe] for these stars from our and their analyses are given in Table 6. We note that the stellar parameters differ between the two determinations. In Fig. 8, we mark and connect the two determinations for the same stars. When comparing the two analyses, we see that the metallicities are within the uncertainties, marginally also for B6-b8 ( $\Delta {\rm [Fe/H]}_{\rm B6-b8} = 0.13$ dex). The oxygen abundances generally agree within uncertainties, the largest difference being $\Delta {\rm [O/Fe]}_{\rm BW-f6} = 0.18$ dex. However, our abundances tend to be systematically lower. Given that our OH lines are very temperature sensitive, one reason for the differences could be that the effective temperatures are still not determined accurately enough. Another reason could be an overestimation of the line strengths in the optical spectra. Although the line strengths of the [O I] and the near-IR OH lines are comparable[*], the optical spectra used in Zoccali et al. (2006) reaches S/N $\sim$ 50 per resolution element, whereas our spectra have a S/N a factor of 2-4 higher and many more lines to use as oxygen criteria. Unknown blends might also affect the [O I] line.

Our [O/Fe] data suggest a high value of +0.4 up to [Fe/H] $\sim$ -0.3, after which the values decline rapidly with a slope of k=-1.0 $\pm$ 0.3. This is the mean trend plotted in Fig. 3. A combination of our [O/Fe] data and those of Meléndez et al. (2008) (see Fig. 2) corroborates our finding. This trend also fits well with the values found by Rich & Origlia (2005) (which are similar to those in Rich et al. 2007) and is consistent with the trends found by Fulbright et al. (2007).

In all the three comparison figures, we also plotted [O/Fe] versus [Fe/H] for the thin and thick disks from Meléndez et al. (2008). When studying all [O/Fe] determinations in Figs. 6 to 8, one obtains the impression that these together may suggest similar, or possibly even higher values than those of the local thick disk of Meléndez et al. (2008). We note that there may be important and different systematic errors in all of these comparisons.

All trends seem to show a scatter that is similar or larger than the trends found for the thick and thin disks by Meléndez et al. (2008). This might, however, be expected for analyses of bulge stars since these are more difficult to analyse; our scatter reflects the expected uncertainties, and a cosmic scatter, if any, must be smaller than that.

Table 7:   Linelist of metal lines with astrophysical oscillator strengths.

5.1.2 Mg, Si, S, Ca, and Ti

We find that [Si, S/Fe] $\sim$ +0.3 for metallicities up to at least [Fe/H] $\sim$ -0.3 above which they seem to decline. Although Si and S may exhibit slightly different trends, published abundance trends based on detailed abundance analyses for bulge stars all suggest that the ratio of ${\alpha }$-element abundances relative to Fe have more or less enhanced values for all metallicities [Fe/H] < 0.0 (e.g., Origlia et al. 2005b; McWilliam et al. 2008; Origlia et al. 2008; Cunha & Smith 2006; Origlia & Rich 2004; Fulbright et al. 2007; Origlia et al. 2002; McWilliam & Rich 2004; Rich et al. 2007; Origlia et al. 2005a; Lecureur et al. 2007; Rich & Origlia 2005; Carretta et al. 2001). For instance, Lecureur et al. (2007) found high [${\alpha }$/Fe] ratios in the bulge compared to the disks, which suggests an enrichment by mostly massive stars at all metallicities. Ryde et al. (2009) measured sulfur (a product of explosive nucleosynthesis) from near-IR spectra and found enhanced values. McWilliam & Rich (2004) demonstrated that Mg and Si are enhanced by 0.3-0.5 dex to super-solar metallicities. It should be noted here that our data do not support an enhanced [Si/Fe] and [S/Fe] values for [Fe/H] > -0.3. The McWilliam & Rich (2004) [Ti/Fe] and [Ca/Fe] trends show a steeper decline than for Mg and Si with metallicity but not as much as for oxygen. To reproduce the different trends, they suggest that the initial mass function (IMF) is skewed with more massive stars in the bulge. Fulbright et al. (2007) measured the abundances of O, Mg, Si, Ca, and Ti and found that these [${\alpha }$/Fe] decline as a function of metallicity but that they also retain higher values than those of the disks for all metallicities. Mg was found to be enhanced the most, while Si, Ca, and Ti (which are understood to be the products of the explosive nucleosynthesis phase of type II supernovae) follow each other well at lower enhancement levels. The sharp decline in Si, Ca, and Ti compared to that of Mg was assumed to be caused by a metallicity-dependent decline of the former yields.

Our results for the ${\alpha }$-elements do not support the existence of any significant ``cosmic scatter'' in the ${\alpha }$-element abundances relative to iron in the bulge, but this is hardly conclusive since the observational scatter is considerable. Alves-Brito et al. (2009, in prep.) show, however, that their measurement of the [${\alpha }$/Fe] ratio in both bulge and thick disk giants have a scatter of only 0.03 dex. Fulbright et al. (2007) also find a small scatter in their mean [$\langle$SiCaTi$\rangle$/Fe], much smaller than that of halo stars, and they interpret this as an indication that the bulge composition developed homogeneously, for example, due to efficient mixing.

5.1.3 The thick disk-bulge similarity

Fulbright et al. (2007), Lecureur et al. (2007), and Zoccali et al. (2006) find abundance trends, including those for oxygen, that differ from those of the thick disk dwarfs and turn-off stars measured by Bensby et al. (2004) and Reddy et al. (2005), and bulge giants measured from their own optical spectra. In contrast, Meléndez et al. (2008), by means of a homogeneous analysis of near-IR spectra of bulge and disk giants, find no chemical distinction between the local thick disk (up to [Fe/H] $\sim$ -0.2) and the bulge, suggesting that the two populations show a similar chemical evolution and that the star-formation rates should not differ significantly. As shown in Figs. 6 to 8, the abundances measured here for bulge giants are consistent, within the uncertainties, with previous ones, measured using data acquired in both optical and near-IR. In the comparison with the thick disk, we follow the approach of Meléndez et al., by restricting the comparison to giants in both components, measured in a fully consistent way. Our bulge stars have abundances similar to those of thick disk giants.

5.2 The carbon and nitrogen abundances

Estimates derived from the optical wavelength region of the carbon and nitrogen abundances are highly uncertain (in many cases only upper limits are known), whereas the CO, CN, and OH lines in the near-IR together easily infer these abundances. The C and N abundances might provide clues to, for instance, the importance of W-R winds and the evolutionary state of the giants, thereby indicating whether the measured oxygen abundances are the original, unprocessed ones.

5.2.1 First dredge-up and the measured oxygen abundance

Low-mass giants that have ascended the giant branch for the first time have only experienced the first dredge-up of CN-processed material from the interior. Thus, the CN cycle's products, which are mainly  $^{14}{\rm N}$ and some  $^{13}{\rm C}$ converted from $^{12}\rm C$, are dredged-up to their surfaces. This is not expected to alter the sum of the number of carbon and nitrogen nuclei, while the measured oxygen abundances should reflect the original abundances in the giants. From Table 5, we see that all stars (with the exception of Arp 4203) only show signs of the first dredge-up and thus no further processing of oxygen by means of the NO cycle, nor any increase in the C abundance characteristic of the third dredge-up on the asymptotic giant branch.

The galactic chemical evolution of carbon and nitrogen remains uncertain. Bensby & Feltzing (2006) find a constant [C/Fe] close to +0.1 for -0.9 < [Fe/H] < 0.0 for disk stars and the summarized observational trend of [N/Fe] versus [Fe/H] presented in Goswami & Prantzos (2000) is constant at a solar value. Thus, if the (C+N) abundances are expected to follow that of iron, one would expect the [(C+N)/Fe] to be slightly below +0.1 for all metallicities in the Galactic disk, which is consistent with what we find. If the atmospheres of our stars had also been exposed to ON-cycled material (in which $^{16}{\rm O}$ is converted to $^{14}{\rm N}$), their nitrogen abundances would have been higher (resulting in higher [(C+N)/Fe] ratios and a larger scatter) with an accompanying lower oxygen abundance. It therefore seems likely that our measured oxygen abundances can be taken as the stars original unprocessed abundance. This is also what is to be expected if the stars have relatively low masses, and are still in the H-shell burning or He-core burning phase, i.e., are on their first ascent along the giant branch or are clump stars.

5.2.2 The role of W-R stars

The oxygen abundance trends found from optical spectra of K giants in the bulge by McWilliam & Rich (2004), indicate a surprising interruption of oxygen production in the bulge for high metallicities. The decrease in oxygen abundance is consistent with the strange scenario of no oxygen production for ${\rm [Fe/H]}> -0.5$. McWilliam & Rich (2004) suggest that this could be connected to the onset of the Wolf-Rayet (W-R) phenomenon, which would be vital for the production of the CNO elements. Carbon is lost in metallicity-sensitive, radiation-driven stellar winds of metal-rich W-Rs preventing carbon being converted into oxygen, thereby reducing the oxygen production. Hence, the steep oxygen decline would not be specific for the stellar population(s) in the bulge, but a metal-dependent phenomenon, with metallicity-sensitive stellar yields from massive stars, playing an important role. Indeed, McWilliam et al. (2008) show that the Galactic bulge and the thin disk experience the same decline in the [O/Mg] versus [Mg/H] diagram, supporting this hypothesis (or the alternative hypothesis that the IMF is considerably metallicity dependent), since both oxygen and magnesium are synthesized in the hydrostatic cores of massive stars in a similar fashion. In this diagram, the effects of the Fe-producing type Ia supernovae are eliminated. The decline in the [O/Fe] versus [Fe/H] plot in the bulge would also reflect the decrease in oxygen yields due to W-R stars, and the onset of Fe production from type Ia supernovae which provide clues to the timescales of the rates and duration of the star formation in the early bulge. Similarly, Fulbright et al. (2007) also relate their low oxygen overabundances to lower oxygen yields at higher metallicities, because of metallicity-dependent W-R winds. This finds support in the calculations for rotating massive-star models by Meynet & Maeder (2005), who conclude that higher C/O abundances are expected from high-metallicity WR stars. This idea is strengthened by Cunha et al. (2008), who derive fluorine ( $^{19}{\rm F}$) abundances for a sample of bulge stars. Their results suggest that winds from metal-rich W-R stars contribute more to the production of this element than the AGB stars in the bulge do compared to the situation in the disk.

If the W-R hypothesis, invoked to explain the steeper decline of the [O/Fe] ratio compared to the other ${\alpha }$ elements is correct, it would mean a dramatic increase in the carbon yields and thereby of the carbon abundances versus metallicity, since the carbon lost from the star is material that would otherwise be expected to be transformed into oxygen at later stages and then expelled by supernovae explosions. However, it is fully conceivable that much of the matter, lost during the W-R stage, which would otherwise be transformed into oxygen, is as yet primarily helium. More detailed model calculations are needed to explore which type of C enrichment is expected. The mass loss in massive stars would, in any case, have a large impact on the formation of carbon and oxygen, especially in metal-rich populations. The carbon versus metallicity trend is therefore a crucial test of the W-R scenario. However, assuming that nitrogen is not affected, we are unable to detect a dramatic increase in carbon production from our data. The [(C+N)/Fe] ratio that we find has a mean of +0.08 $\pm$ 0.09 dex, and the [(C+N)/Fe] versus [Fe/H] trend shows a modest, if any, slope of $k= \frac{\partial{\rm [(C+N)/Fe]}}{\partial{\rm [Fe/H]}}=+0.07$ $\pm$ 0.09. Thus, our data do not provide strong support for this hypothesis.

6 Conclusions

The chemical abundance determinations of stars are known to be plagued by systematic errors that may be difficult to estimate. To discuss the properties of different stellar populations, homogeneous differential spectroscopic studies and detailed comparisons of results from different studies are significant. In the present study, we have tried to follow this route, and find satisfactory agreement with results obtained in the optical, as well as IR, when a common temperature scale is used for the stars. With our high-resolution IR spectroscopy, we have explored the CNO abundances, as well as the abundances of Si, S, Ti, and Fe for 11 bulge giants. We have found enhanced [O/Fe], [Si/Fe], and [S/Fe] values with increasing [Fe/H] up to approximately [Fe/H] $\sim$ -0.3, after which these abundance ratios relative to Fe decrease. This suggests an early and rapid star formation in the bulge. Our investigation is not designed to allow a detailed comparison with thick disk stars and to determine the relationship between these two populations; this type of study should be made differentially to minimise systematic uncertainties. Our abundance trends are, however, consistent with there being a similarity between these populations as found in the differential study by Meléndez et al. (2008). This type of similarity suggests that the picture of an isolated classical bulge may be oversimplified. Inner disk stars, at smaller galactocentric distances, should be explored to deepen the understanding of a possible physical connection between the bulge and the thick disk.

From our C and N abundances, we conclude that our stars are first-ascent red-giants or clump stars, suggesting that their oxygen abundances are unaffected by CNO cycling. Furthermore, we find that there is no significant increase in the carbon abundances at high metallicities, which is expected if W-R stars are responsible for the sharp decline in [O/Fe] versus metallicity.

We have demonstrated that for the same stars several different determinations of the stellar parameters from optical spectra produce significantly different results, implying that important systematic uncertainties exist. Attempts to reduce these should be made. We note also that Chiappini et al. (2009) compare, among others, the oxygen abundances derived from planetary nebulae (PNe) and giants in the bulge and find that the abundances determined from giant star spectra are systematically higher by 0.3 dex. They conclude that this discrepancy may be caused by systematic uncertainties in either the PNe or giant star abundance determinations, or both.

To fully clarify the situation of the origin and evolution of the galactic bulge, additional near-IR abundance surveys of elements (especially more ${\alpha }$ elements) are needed. Most previous investigations have been restricted to Baade's window. Different regions of the bulge are now being explored, and further systematic work is needed.

Acknowledgements
N.R. is a Royal Swedish Academy of Sciences Research Fellow supported by a grant from the Knut and Alice Wallenberg Foundation. Funds from Kungl. Fysiografiska Sällskapet i Lund are acknowledged. N.R., B.E., and B.G. acknowledge support from the Swedish Research Council, VR. J.M. acknowledge support from the Portuguese FCT (PTDC/CTE-AST/65971/2006, Ciencia 2007). M.Z. and D.M. are supported by FONDAP Center for Astrophysics 15010003, by BASAL CATA PFB 0609, and by FONDECYT. Kjell Eriksson is thanked for valuable help and discussions concerning the running of the MARCS program. The referee is thanked for valuable suggestions.

References

  1. Anstee, S. D., & O'Mara, B. J. 1995, MNRAS, 276, 859 [NASA ADS] [CrossRef] [Google Scholar]
  2. Ballester, P., Banse, K., Castro, S., et al. 2006, in SPIE Conf., 6270 [Google Scholar]
  3. Barklem, P. S., Piskunov, N., & O'Mara, B. J. 2000, A&AS, 142, 467 [Google Scholar]
  4. Bensby, T., & Feltzing, S. 2006, MNRAS, 367, 1181 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bensby, T., Feltzing, S., & Lundström, I. 2004, A&A, 415, 155 [Google Scholar]
  6. Bensby, T., Feltzing, S., Lundström, I., & Ilyin, I. 2005, A&A, 433, 185 [Google Scholar]
  7. Bournaud, F., & Elmegreen, B. G. 2009, ApJ, 694, L158 [NASA ADS] [CrossRef] [Google Scholar]
  8. Carollo, C. M., Scarlata, C., Stiavelli, M., Wyse, R. F. G., & Mayer, L. 2007, ApJ, 658, 960 [NASA ADS] [CrossRef] [Google Scholar]
  9. Carretta, E., Cohen, J. G., Gratton, R. G., & Behr, B. B. 2001, AJ, 122, 1469 [NASA ADS] [CrossRef] [Google Scholar]
  10. Chiappini, C., Górny, S. K., Stasinska, G., & Barbuy, B. 2009, A&A, 494, 591 [Google Scholar]
  11. Clarkson, W., Sahu, K., Anderson, J., et al. 2008, ApJ, 684, 1110 [NASA ADS] [CrossRef] [Google Scholar]
  12. Cunha, K., & Smith, V. V. 2006, ApJ, 651, 491 [NASA ADS] [CrossRef] [Google Scholar]
  13. Cunha, K., Smith, V. V., & Gibson, B. K. 2008, ApJ, 679, L17 [NASA ADS] [CrossRef] [Google Scholar]
  14. da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A&A, 458, 609 [Google Scholar]
  15. Elmegreen, B. G., & Elmegreen, D. M. 2005, ApJ, 627, 632 [NASA ADS] [CrossRef] [Google Scholar]
  16. Förster Schreiber, N. M., Genzel, R., Bouche, N., et al. 2009, ApJ, 706, 1364 [NASA ADS] [CrossRef] [Google Scholar]
  17. Fulbright, J. P., McWilliam, A., & Rich, R. M. 2006, ApJ, 636, 821 [NASA ADS] [CrossRef] [Google Scholar]
  18. Fulbright, J. P., McWilliam, A., & Rich, R. M. 2007, ApJ, 661, 1152 [NASA ADS] [CrossRef] [Google Scholar]
  19. Genzel, R., Burkert, A., Bouché, N., et al. 2008, ApJ, 687, 59 [NASA ADS] [CrossRef] [Google Scholar]
  20. Genzel, R., Tacconi, L. J., Eisenhauer, F., et al. 2006, Nature, 442, 786 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  21. Goldman, A., Schoenfeld, W., Goorvitch, D., et al. 1998, JQSRT, 59, 453 [NASA ADS] [CrossRef] [Google Scholar]
  22. Goorvitch, D. 1994, ApJS, 95, 535 [NASA ADS] [CrossRef] [Google Scholar]
  23. Goswami, A., & Prantzos, N. 2000, A&A, 359, 191 [Google Scholar]
  24. Gray, D. F. 1992, The observation and analysis of stellar photospheres (Cambridge; New York: Cambridge University Press), 2nd edn. [Google Scholar]
  25. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [Google Scholar]
  26. Hekker, S., & Meléndez, J. 2007, A&A, 475, 1003 [Google Scholar]
  27. Hinkle, K., Wallace, L., & Livingston, W. 1995a, PASP, 107, 1042 [NASA ADS] [CrossRef] [Google Scholar]
  28. Hinkle, K., Wallace, L., & Livingston, W. C. 1995b, Infrared atlas of the Arcturus spectrum, 0.9-5.3 microns (San Francisco, Calif.: ASP) [Google Scholar]
  29. Hinkle, K. H., Cuberly, R. W., Gaughan, N. A., et al. 1998, SPIE, 3354, 810 [Google Scholar]
  30. Immeli, A., Samland, M., Gerhard, O., & Westera, P. 2004, A&A, 413, 547 [Google Scholar]
  31. Jørgensen, U. G., & Larsson, M. 1990, A&A, 238, 424 [Google Scholar]
  32. Jørgensen, U. G., Larsson, M., Iwamae, A., & Yu, B. 1996, A&A, 315, 204 [Google Scholar]
  33. Käufl, H. U., Amico, P., Ballester, P., et al. 2006, The Messenger, 126, 32 [NASA ADS] [Google Scholar]
  34. Käufl, H.-U., Ballester, P., Biereichel, P., et al. 2004, in SPIE Conf. Ser. 5492, ed. A. F. M. Moorwood, & M. Iye, 1218 [Google Scholar]
  35. Kerber, F., Bristow, P., & Rosa, M. R. 2008a, in SPIE Conf., 7014 [Google Scholar]
  36. Kerber, F., Nave, G., & Sansonetti, C. J. 2008b, ApJS, 178, 374 [NASA ADS] [CrossRef] [Google Scholar]
  37. Kormendy, J., & Kennicutt, Jr., R. C. 2004, ARA&A, 42, 603 [Google Scholar]
  38. Langhoff, S. R., & Bauschlicher, C. W. 1993, Chem. Phys. Lett., 211, 305 [NASA ADS] [CrossRef] [Google Scholar]
  39. Lecureur, A. 2007, Ph.D. Thesis, GEPI, Observatoire de Paris, CNRS, Université Paris Diderot; Place Jules Janssen, 92190 Meudon, France [Google Scholar]
  40. Lecureur, A., Hill, V., Zoccali, M., et al. 2007, A&A, 465, 799 [Google Scholar]
  41. Livingston, W., & Wallace, L. 1991, an atlas of the solar spectrum in the infrared from 1850 to 9000 cm-1 (1.1 to 5.4 micrometer), NSO Technical Report, Tucson: National Solar Observatory, National Optical Astronomy Observatory [Google Scholar]
  42. Matteucci, F., & Romano, D. 1999, Ap&SS, 265, 311 [Google Scholar]
  43. McWilliam, A., & Rich, R. M. 2004, in Origin and Evolution of the Elements, ed. A. McWilliam, & M. Rauch [Google Scholar]
  44. McWilliam, A., Matteucci, F., Ballero, S., et al. 2008, AJ, 136, 367 [NASA ADS] [CrossRef] [Google Scholar]
  45. Meléndez, J., & Barbuy, B. 1999, ApJS, 124, 527 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  46. Meléndez, J., Asplund, M., Alves-Brito, A., et al. 2008, A&A, 484, L21 [Google Scholar]
  47. Meynet, G., & Maeder, A. 2005, A&A, 429, 581 [Google Scholar]
  48. Moorwood, A. 2005, in High Resolution Infrared Spectroscopy in Astronomy, ed. H. U. Käufl, R. Siebenmorgen, & A. F. M. Moorwood, 15 [Google Scholar]
  49. Origlia, L., & Rich, R. M. 2004, AJ, 127, 3422 [NASA ADS] [CrossRef] [Google Scholar]
  50. Origlia, L., Rich, R. M., & Castro, S. 2002, AJ, 123, 1559 [NASA ADS] [CrossRef] [Google Scholar]
  51. Origlia, L., Valenti, E., & Rich, R. M. 2005a, MNRAS, 356, 1276 [NASA ADS] [CrossRef] [Google Scholar]
  52. Origlia, L., Valenti, E., Rich, R. M., & Ferraro, F. R. 2005b, MNRAS, 363, 897 [NASA ADS] [CrossRef] [Google Scholar]
  53. Origlia, L., Valenti, E., & Rich, R. M. 2008, MNRAS, 388, 1419 [NASA ADS] [Google Scholar]
  54. Ortolani, S., Renzini, A., Gilmozzi, R., et al. 1995, Nature, 377, 701 [NASA ADS] [CrossRef] [Google Scholar]
  55. Paufique, J., Biereichel, P., Delabre, B., et al. 2006, in SPIE Conf. Ser., 6272, 36 [Google Scholar]
  56. Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [Google Scholar]
  57. Querci, F., Querci, M., & Kunde, V. 1971, A&A, 15, 256 [Google Scholar]
  58. Ramírez, I., & Meléndez, J. 2005a, ApJ, 626, 446 [Google Scholar]
  59. Ramírez, I., & Meléndez, J. 2005b, ApJ, 626, 465 [Google Scholar]
  60. Reddy, B. E., Lambert, D. L., & Allende Prieto, C. 2006, MNRAS, 367, 1329 [NASA ADS] [CrossRef] [Google Scholar]
  61. Reid, M. J. 1993, ARA&A, 31, 345 [Google Scholar]
  62. Renzini, A. 2006, ARA&A, 44, 141 [Google Scholar]
  63. Rich, R. M., & Origlia, L. 2005, ApJ, 634, 1293 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  64. Rich, R. M., Origlia, L., & Valenti, E. 2007, ApJ, 665, L119 [NASA ADS] [CrossRef] [Google Scholar]
  65. Ryde, N., Edvardsson, B., Gustafsson, B., et al. 2009, A&A, 496, 701 [Google Scholar]
  66. Santos, N. C., Lovis, C., Pace, G., Melendez, J., & Naef, D. 2009, A&A, 493, 309 [Google Scholar]
  67. Silk, J., & Wyse, R. F. G. 1993, Phys. Rep., 231, 293 [NASA ADS] [CrossRef] [Google Scholar]
  68. Stetson, P. B., & Pancino, E. 2008, PASP, 120, 1332 [Google Scholar]
  69. Tody, D. 1993, in Astronomical Data Analysis Software and Systems II, ed. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes, ASP Conf. Ser., 52, 173 [Google Scholar]
  70. Unsöld, A. 1955, Physik der Sternatmospharen, MIT besonderer Berucksichtigung der Sonne (Berlin: Springer), 2. Aufl. [Google Scholar]
  71. Zoccali, M., Hill, V., Lecureur, A., et al. 2008, A&A, 486, 177 [Google Scholar]
  72. Zoccali, M., Lecureur, A., Barbuy, B., et al. 2006, A&A, 457, L1 [Google Scholar]
  73. Zoccali, M., Renzini, A., Ortolani, S., et al. 2003, A&A, 399, 931 [Google Scholar]

Footnotes

... spectra[*]
Based on observations collected at the European Southern Observatory, Chile (ESO program 079.B-0338(A)).
... element[*]
The scale in dispersion direction is 0.10 $^{\prime\prime}$/pixel at the center of the order and 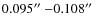$0.095\hbox{$^{\prime\prime}$ }{-}0.108\hbox{$^{\prime\prime}$ }$/pixel over the focal plane from the long wavelength-side to the short. In the spatial direction, the scale is 0.087 $^{\prime\prime}$/pixel. This change in scale is due to the change in the beam-diameter induced by the off-axis reflection at the Echelle grating, which produces an anamorphism.
... instrument[*]
In such a case, the spectrograph entrance slit would only be a technicality to reduce the background and to establish geometric alignment, here mostly compensating pointing errors.
...-ratio[*]
Full details of the pipeline can be found under http://www.eso.org/observing/dfo/quality/CRIRES/pipeline/pipe_reduc.html
...(Tody 1993)[*]
IRAF is distributed by the National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA) under cooperative agreement with the National Science Foundation.
... comparable[*]
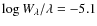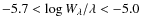For example, for the giant B3-b8 the [O I] line has a strength of approximately $\log W_\lambda/\lambda=-5.1$ and the OH lines have line-strengths in the approximate range of $-5.7<\log W_\lambda/\lambda< -5.0$.

All Tables

Table 1:   Account of our observations.

Table 2:   Stellar parameters for the model atmospheres of our program stars given as $T_{\rm eff}/\log g/{\rm [Fe/H]}/\xi_{\rm micro}$.

Table 3:   Spectroscopically and photometrically determined surface gravities.

Table 4:   Uncertainties in the derived abundances due to uncertainties in the stellar parameters.

Table 5:   [C/Fe]a,b, [N/Fe], [(C+N)/Fe], [O/Fe], [Si/Fe], [S/Fe], [Ti/Fe], and [Fe/H] for our 11 bulge giants and Arcturus.

Table 6:   [Fe/H] and [O/Fe] determined from near-IR lines in this paper and determinations based on optical lines.

Table 7:   Linelist of metal lines with astrophysical oscillator strengths.

All Figures

  \begin{figure} \par\includegraphics[width=18cm,clip]{12687fig1.eps} \end{figure} Figure 1:

Sections of the observed CRIRES spectra of two of our bulge giants are shown with full, black lines. The observations are wavelength-shifted to laboratory wavelengths to enable a more direct comparison between the different stellar spectra. Therefore, our observed spectra cover slightly different wavelength ranges. For comparison, the Arcturus atlas spectrum (Hinkle et al. 1995b) is also shown. The parts of the spectra with the highest signal-to-noise ratios are shown. From these parts the C, N, and O elements can be determined. Our best-fit synthetic spectra is shown in red. All synthetic lines deeper than a factor of 0.97 of the continuum are identified. A few features cannot be identified in the Arcturus spectrum and are labeled with question marks. These features also show up in the bulge-star spectra. A few lines in BW-f6 are conspicuously stronger than expected. They are probably affected by cosmic rays in the detector array.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{12687fig2.eps} \end{figure} Figure 2:

Logarithmic ratios of oxygen to iron normalized by the solar value for bulge stars. Filled circles show all of our data from this paper, except for the special giant Arp 4203, which is denoted by an open circle. Crosses show the results of Meléndez et al. (2008). Typical uncertainties are indicated in the upper right corner. The upper panel shows the oxygen abundances we derive when we use our spectroscopically derived $\log g$ values with our stellar atmosphere models, whereas the lower panel shows the same values when we use instead our photometrically derived surface gravities.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{12687fig3.eps} \end{figure} Figure 3:

Logarithmic ratios of Si, S, and Ti to iron normalized by the solar value for our bulge stars are shown with filled circles. The [O/Fe] versus [Fe/H] trend is indicated by a full line for reference in all panels. The measured values for the special giant Arp 4203 are shown with an open circle. Typical uncertainties are indicated in the upper right corners.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{12687fig4.eps} \end{figure} Figure 4:

Logarithmic ratios of carbon+nitrogen to iron normalized by the solar value. Our data are shown by filled circles, except Arp 4203 which is shown by an open circle. Crosses show the results of Meléndez et al. (2008). The [(C+N)/Fe] value we derive for Arcturus is shown with a star. Typical uncertainties are indicated in the upper right corner. The upper panel shows the values we retrieve when assuming spectroscopically derived $\log g$ and the values presented in the lower panel assumes photometrically derived surface gravities.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{12687fig5.eps} \end{figure} Figure 5:

C/N ratios plotted in the theoretical HR diagram. The dot diameters are proportional to C/N with a largest value of 4.6 for B3-b1, 2.8 for Arcturus, and 0.08 for Arp 4203. Stars with [Fe/H] < -0.4 are plotted as filled dots and the more metal-rich ones as open circles.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{12687fig6.eps} \end{figure} Figure 6:

Logarithmic ratios of oxygen to iron normalized by the solar value. The oxygen abundances are here all determined from near-IR spectra. Filled circles show our data from this paper, except that of Arp 4203. Arcturus at [Fe/H] = -0.53 is indicated with a black star at [O/Fe] = 0.51, in agreement with that of Lecureur (2007). Crosses show the results of Meléndez et al. (2008), green squares represent the abundances determined by Cunha & Smith (2006), and red squares the data from Rich & Origlia (2005). The blue star and plus signs represent thick disk and thin disk giants, respectively, from Meléndez et al. (2008).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{12687fig7.eps} \end{figure} Figure 7:

Logarithmic ratios of oxygen to iron normalized by the solar value. Filled circles show our data from this paper, except that of Arp 4203, and a black star indicates Arcturus at [Fe/H] = -0.53. Triangles show the optically determined values by Fulbright et al. (2007). The two small dots represent the stars from Fulbright et al. (2007), which were analyzed by Ryde et al. (2009) from near-IR lines and reanalyzed by us. The determinations by Fulbright et al. and our determinations are connected by full lines. The blue stars and plus signs represent thick disk and thin disk giants, respectively, from Meléndez et al. (2008).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{12687fig8.eps} \end{figure} Figure 8:

Logarithmic ratios of oxygen to iron normalized by the solar value. Filled black circles show our data from this paper, except that of Arp 4203, and a black star indicates Arcturus at [Fe/H] = -0.53. Filled green circles show the optically determined values by Lecureur et al. (2007) and Zoccali et al. (2006). The small black dots mark the stars from Lecureur et al. (2007) and Zoccali et al. (2006) for which we have determined the oxygen abundances from near-IR lines. These two determinations are connected. For the star B6-f7, there is only a near-IR determination of the oxygen abundance. When comparing these two determinations for the same stars, it should be noted that we have used new stellar parameters when determining the abundances from the near-IR spectra. The blue star and plus-sign symbols represent thick disk and thin disk giants, respectively, from Meléndez et al. (2008).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.