| Issue |
A&A
Volume 509, January 2010
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 20 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200912558 | |
| Published online | 14 January 2010 | |
The zCOSMOS redshift survey: how group
environment alters global downsizing trends![[*]](/icons/foot_motif.png)
A. Iovino1 - O. Cucciati1,2 - M. Scodeggio3 - C. Knobel4 - K. Kovac4 - S. Lilly4 - M. Bolzonella5 - L. A. M. Tasca2,3 - G. Zamorani5 - E. Zucca5 - K. Caputi4 - L. Pozzetti5 - P. Oesch4 - F. Lamareille6 - C. Halliday7 - S. Bardelli5 - A. Finoguenov8 - L. Guzzo1 - P. Kampczyk4 - C. Maier4 - M. Tanaka9 - D. Vergani5 - C. M. Carollo4 - T. Contini6 - J.-P. Kneib2 - O. Le Fèvre2 - V. Mainieri9 - A. Renzini10 - A. Bongiorno8 - G. Coppa5 - S. de la Torre2,1 - L. de Ravel2 - P. Franzetti3 - B. Garilli3 - J.-F. Le Borgne6 - V. Le Brun2 - M. Mignoli5 - R. Pellò6 - Y. Peng4 - E. Perez-Montero6 - E. Ricciardelli10 - J. D. Silverman4 - L. Tresse2 - U. Abbas11 - D. Bottini3 - A. Cappi5 - P. Cassata2,12 - A. Cimatti13 - A. M. Koekemoer15 - A. Leauthaud 14 - D. Maccagni3 - C. Marinoni16 - H. J. McCracken17 - P. Memeo3 - B. Meneux8,18 - C. Porciani4,19 - R. Scaramella20 - D. Schiminovich21 - N. Scoville22
1 - INAF - Osservatorio Astronomico di Brera, via Brera, 28, 20159
Milano, Italy
2 - Laboratoire d'Astrophysique de Marseille, CNRS-Université
d'Aix-Marseille, 38 rue Frederic Joliot Curie, 13388 Marseille, France
3 - INAF - IASF Milano, via Bassini 15, 20133, Milano, Italy
4 - Institute of Astronomy, ETH Zurich, 8093, Zürich, Switzerland
5 - INAF - Osservatorio Astronomico di Bologna, via Ranzani 1, 40127
Bologna, Italy
6 - Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de
Toulouse, CNRS, 14 Avenue Edouard Belin, 31400 Toulouse, France
7 - INAF - Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5,
50125 Firenze, Italy
8 - Max-Planck-Institut für extraterrestrische Physik, 84571 Garching
b. Muenchen, 85748, Germany
9 - European Southern Observatory, Karl-Schwarzschild-Strasse 2,
Garching b. Muenchen, 85748, Germany
10 - Dipartimento di Astronomia, Università di Padova, vicolo
Osservatorio 3, 35122 Padova, Italy
11 - INAF - Osservatorio Astronomico di Torino, Strada Osservatorio 20,
10025 Pino Torinese, Torino, Italy
12 - Dept. of Astronomy, University of Massachusetts, 710 North
Pleasant Street, Amherst, MA 01003-9305, USA
13 - Dipartimento di Astronomia, Universitá di Bologna, via Ranzani 1,
40127, Bologna, Italy
14 - Physics Division, MS 50 R5004, Lawrence Berkeley National
Laboratory, 1 Cyclotron Rd., Berkeley, CA 94720, USA
15 - Space Telescope Science Institute, 3700 San Martin Drive,
Baltimore, MD 21218, USA
16 - Centre de Physique Theorique, Campus de Luminy, Case 907 - 13288
Marseille, France
17 - Institut d'Astrophysique de Paris, UMR 7095 CNRS, Université
Pierre et Marie Curie, 98bis boulevard Arago, 75014 Paris, France
18 - Universitäts-Sternwarte, Scheinerstrasse 1, Munich 81679, Germany
19 - Argelander-Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn,
Germany
20 - INAF, Osservatorio di Roma via di Frascati, 33, 00040 Monte Porzio
Catone, Italy
21 - Department of Astronomy, Columbia University, 550 West 120th
Street, New York, NY 10027, USA
22 - California Institute of Technology, MC 105-24, 1200 East
California Boulevard, Pasadena, CA 91125, USA
Received 22 May 2009 / Accepted 8 October 2009
Abstract
Context. Groups of galaxies are a common
environment, bridging the gap between starforming field galaxies and
quiescent cluster galaxies. Within groups secular processes could be at
play, contributing to the observed strong decrease of star formation
with cosmic time in the global galaxy population.
Aims. We took advantage of the wealth of information
provided by the first ![]() galaxies
of the zCOSMOS-bright survey and its group catalogue to study in detail
the complex interplay between group environment and galaxy properties.
galaxies
of the zCOSMOS-bright survey and its group catalogue to study in detail
the complex interplay between group environment and galaxy properties.
Methods. The classical indicator
![]() ,
i.e., the fraction of blue galaxies, proved to be a simple but powerful
diagnostic tool. We studied its variation for different luminosity and
mass selected galaxy samples, divided as to define
groups/field/isolated galaxy subsamples.
,
i.e., the fraction of blue galaxies, proved to be a simple but powerful
diagnostic tool. We studied its variation for different luminosity and
mass selected galaxy samples, divided as to define
groups/field/isolated galaxy subsamples.
Results. Using rest-frame evolving B-band
volume-limited samples, the groups galaxy population exhibits
significant blueing as redshift increases, but maintains a systematic
difference (a lower
![]() )
with respect to the global galaxy population, and an even larger
difference with respect to the isolated galaxy population. However
moving to mass selected samples it becomes apparent that such
differences are largely due to the biased view imposed by the B-band
luminosity selection, being driven by the population of lower mass,
bright blue galaxies for which we miss the redder, equally low mass,
counterparts. By carefully focusing the analysis on narrow
mass bins such that mass segregation becomes negligible we find that
only for the lowest mass bin explored, i.e.,
)
with respect to the global galaxy population, and an even larger
difference with respect to the isolated galaxy population. However
moving to mass selected samples it becomes apparent that such
differences are largely due to the biased view imposed by the B-band
luminosity selection, being driven by the population of lower mass,
bright blue galaxies for which we miss the redder, equally low mass,
counterparts. By carefully focusing the analysis on narrow
mass bins such that mass segregation becomes negligible we find that
only for the lowest mass bin explored, i.e.,
![]() ,
does a significant residual difference in color remain as a
function of environment, while this difference becomes negligible
toward higher masses.
,
does a significant residual difference in color remain as a
function of environment, while this difference becomes negligible
toward higher masses.
Conclusions. Our results indicate that red galaxies
of mass
![]() are
already in place at
are
already in place at ![]() and do not exhibit any strong environmental dependence, possibly
originating from so-called nature or internal mechanisms.
In contrast, for lower galaxy masses and redshifts lower than
and do not exhibit any strong environmental dependence, possibly
originating from so-called nature or internal mechanisms.
In contrast, for lower galaxy masses and redshifts lower than ![]() ,
we observe the emergence in groups of a population of nurture red
galaxies: slightly deviating from the trend of the downsizing scenario
followed by the global galaxy population, and more so with cosmic time.
These galaxies exhibit signatures of group-related secular physical
mechanisms directly influencing galaxy evolution. Our analysis implies
that these mechanisms begin to significantly influence galaxy evolution
after
,
we observe the emergence in groups of a population of nurture red
galaxies: slightly deviating from the trend of the downsizing scenario
followed by the global galaxy population, and more so with cosmic time.
These galaxies exhibit signatures of group-related secular physical
mechanisms directly influencing galaxy evolution. Our analysis implies
that these mechanisms begin to significantly influence galaxy evolution
after ![]() ,
a redshift corresponding to the emergence of structures in
which these mechanisms take place.
,
a redshift corresponding to the emergence of structures in
which these mechanisms take place.
Key words: galaxies: clusters: general - galaxies: evolution - galaxies: interactions
1 Introduction
Groups and clusters are commonly viewed as sites where environmental influences can affect the colors, star formation histories and morphologies of their member galaxies. One of the first pieces of empirical evidence supporting this claim was the observation by Butcher & Oemler that clusters of galaxies contain a higher fraction of blue galaxies at progressively higher redshift, the so-called Butcher-Oemler effect (Butcher & Oemler 1984,1978). Their result provided direct observational evidence of strong, rapidly evolving galaxy population colors inside cluster cores with redshift.
Since these early papers, the Butcher-Oemler effect has been confirmed photometrically (Margoniner & de Carvalho 2000; Margoniner et al. 2001; Kodama & Bower 2001; Goto et al. 2003; Rakos & Schombert 1995), spectroscopically (Lavery & Henry 1988,1986; Poggianti et al. 1999; Ellingson et al. 2001; Dressler & Gunn 1982,1992; Fabricant et al. 1991; Poggianti et al. 2006), has been extended to groups (Wilman et al. 2005a; Gerke et al. 2007; Allington-Smith et al. 1993; Cucciati et al. 2009b), and critically discussed in the context of selection biases (Andreon et al. 2006,2004; Andreon & Ettori 1999).
In parallel to these studies, evidence has emerged that the Universe as a whole formed stars more actively in the past than today (Schiminovich et al. 2005; Hopkins 2004; Madau et al. 1998; Lilly et al. 1996) and that the typical mass of galaxies where the bulk of star formation occurs is higher in the past than today, the so-called downsizing effect (Cowie et al. 1996; Gavazzi et al. 1996).
These observations questioned whether the Butcher-Oemler phenomenon is caused by physical mechanisms typical of dense environments, that significantly alter global trends displayed by the global galaxy population in the coeval field, or reflects the evolution of the global galaxy population. Interestingly, with growing evidence that denser environments only suppress star formation (Balogh et al. 2004b,a), we have started to test in groups and/or clusters at higher redshifts whether we measure a higher fraction of blue galaxies that is nevertheless lower than the coeval field.
Since groups contain a large fraction of galaxies in the
nearby Universe, nearly ![]() (Berlind
et al. 2006; Eke et al. 2004; Huchra
& Geller 1982), while only a few percent of galaxies
are contained in the denser cluster cores, group-related
transformations may drive the observed strong decrease in star
formation with cosmic time, at least since
(Berlind
et al. 2006; Eke et al. 2004; Huchra
& Geller 1982), while only a few percent of galaxies
are contained in the denser cluster cores, group-related
transformations may drive the observed strong decrease in star
formation with cosmic time, at least since ![]() ,
when these structures started to become predominant according to the
hierarchical structure scenarios.
,
when these structures started to become predominant according to the
hierarchical structure scenarios.
In the cores of rich clusters phenomena such as ram pressure stripping have been widely documented in the literature, as for well studied galaxies in the Virgo cluster, (Vollmer et al. 2004; Kenney et al. 2004), and observed in simulations (Brüggen & De Lucia 2008).
In contrast, similar environment-dependent effects in groups are less clearly defined, although possibilities have been presented in the literature, including gradual cessation of star formation induced either by gentle gas stripping and starvation by a diffuse intragroup medium, or by slow group-scale harassment (Roediger & Hensler 2005; Gnedin 2003; Larson et al. 1980; Kawata & Mulchaey 2008; Moore et al. 1999).
From a theoretical perspective, numerical simulations incorporating the standard cosmological paradigm suggest that galaxy properties such as, e.g., colors, spin etc.) are primarily determined by the mass of the dark matter halo in which the galaxy resides (Cooray & Sheth 2002), and that, at a given mass, in overdense environments dark matter haloes assemble at higher redshifts than in underdense environments (Gao et al. 2005). This framework could provide a simple way of explaining the observed trends in colors with galaxy luminosity, mass and environment, at low (Blanton & Berlind 2007; De Propris et al. 2004) and also at high redshifts (Wilman et al. 2005a; Balogh et al. 2007), without resorting to any specific mechanisms acting in groups. Two large recent redshift surveys, VVDS and DEEP2, have addressed this problem by studying both groups (Gerke et al. 2007; Cucciati et al. 2009b) and local density field measurements (Cooper et al. 2007; Cucciati et al. 2006; Cooper et al. 2006), although both studies considered both luminosity selected samples, a choice that, as we discuss later, offers only partial insight into the problem.
The question of which variables are needed to fully define galaxy evolution therefore remains unanswered, and is usually considered in terms of either nature or nurture processes. This corresponds to asking whether: galaxy evolution is driven mainly by internal processes, imprinted at galaxy birth, that operate inside the average galaxy, or group environment has a specific effect on shaping galaxy evolution, because of specific mechanisms taking place in dense, possibly virialized regions, where secular influences have better chances to affect galaxy evolution.
To distinguish between the effects of environment and trends related to galaxy evolution with redshift, one needs homogeneous and sizeable group and field galaxy samples, covering a wide redshift range and with reliable measurements of galaxy rest-frame colors, luminosities and masses. These data would allow us to monitor with look-back time the evolutionary histories of galaxies located in different group/field environments, and to disentangle between the different dependencies and their relative importance.
The advantage of the data-set used in our analysis is that it
satisfies all of these requirements. zCOSMOS is a survey tailored for
studying the large scale structure and detecting groups up to ![]() (Lilly
et al. 2009,2007). Its large volume
coverage and small errors in galaxy redshift measurements enable the
production, even for the first batch of
(Lilly
et al. 2009,2007). Its large volume
coverage and small errors in galaxy redshift measurements enable the
production, even for the first batch of
![]() measured
redshifts, of a large group catalogue containing
102 groups with
measured
redshifts, of a large group catalogue containing
102 groups with ![]() spectroscopically confirmed members and a further
spectroscopically confirmed members and a further ![]() going
down to pairs (Knobel
et al. 2009). Furthermore this catalogue, because of
the precise fine tuning of the algorithm used for group detection,
is remarkably free from contamination and incompleteness,
especially at the low richness, low velocity dispersion end and, most
importantly, its quality is stable as a function of redshift (Knobel et al. 2009).
Last but not least, the large amount of precise photometric ancillary
data
available from the COSMOS survey (Scoville
et al. 2007), provides robust estimates of the
fundamental properties of each galaxy, such as rest-frame
luminosities, colors and masses. We are therefore in best position with
our data-set to investigate in detail which processes are the most
influential in shaping galaxy evolution.
going
down to pairs (Knobel
et al. 2009). Furthermore this catalogue, because of
the precise fine tuning of the algorithm used for group detection,
is remarkably free from contamination and incompleteness,
especially at the low richness, low velocity dispersion end and, most
importantly, its quality is stable as a function of redshift (Knobel et al. 2009).
Last but not least, the large amount of precise photometric ancillary
data
available from the COSMOS survey (Scoville
et al. 2007), provides robust estimates of the
fundamental properties of each galaxy, such as rest-frame
luminosities, colors and masses. We are therefore in best position with
our data-set to investigate in detail which processes are the most
influential in shaping galaxy evolution.
Complementary analyses of the same 10K-sampledata-set have been carried out in other papers. Kovac et al. (2009b) in a parallel paper study the influence of group environment in shaping galaxy morphologies. Using the density field measured in Kovac et al. (2009a), Zucca et al. (2009) and Bolzonella et al. (2009) study the galaxy luminosity and mass functions respectively as a function of environment, while Cucciati et al. (2009a) and Tasca et al. (2009) investigate the dependencies of galaxy colors and morphologies, respectively, from the general density field. Finally Silverman et al. (2009) and Vergani et al. (2010) study how environment plays a role in triggering active galactic nuclei activity and in quenching star-formation respectively. For more details, we refer the interested reader to those papers.
A concordance cosmology is adopted throughout our paper, with
h70
= H0/70 km s-1 Mpc-1,
![]() and
and ![]() .
All magnitudes are always quoted in the AB system.
.
All magnitudes are always quoted in the AB system.
2 Samples used in the analysis
2.1 The zCOSMOS 10K-sample
The zCOSMOS survey is a large spectroscopic survey undertaken
in the COSMOS field (Scoville
et al. 2007), using 600 h of observations
with the VIMOS spectrograph at VLT. It consists of two parts:
zCOSMOS-bright and zCOSMOS-deep. zCOSMOS-bright is a survey purely
magnitude limited in I-band; when complete it will
provide a sample of ![]() galaxies
in the range
galaxies
in the range ![]() from the HST ACS imaging (Koekemoer
et al. 2007) over the whole area of 1.7 deg2
of the COSMOS field. zCOSMOS-deep targets
from the HST ACS imaging (Koekemoer
et al. 2007) over the whole area of 1.7 deg2
of the COSMOS field. zCOSMOS-deep targets
![]() galaxies,
selected through color criteria to have
galaxies,
selected through color criteria to have
![]() within
the central 1 deg2.
At completion it will provide redshifts
for
within
the central 1 deg2.
At completion it will provide redshifts
for ![]() galaxies with
magnitudes
galaxies with
magnitudes ![]() .
.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12558F1.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg52.png)
|
Figure 1:
The left panel shows the
|
| Open with DEXTER | |
The analysis presented in this paper uses of the sample of 10 644 objects for which we obtained spectra during the first half of the zCOSMOS-bright observational campaign. This number corresponds to a total of 83 pointings of the VIMOS spectrograph, observed during ESO periods P75, P76, and P77 and includes compulsory, i.e., objects with forced slit positioning, and secondary targets, i.e., objects serendipitously falling inside the slit other than the primary target.
zCOSMOS-bright observations use the R =
600 MR grism and 1 h integrations to secure
redshifts with a high success rate. The wavelength range covered goes
from ![]() Å.
For more details of the survey strategy and characteristics we
refer the reader to Lilly
et al. (2007) and Lilly
et al. (2009).
Å.
For more details of the survey strategy and characteristics we
refer the reader to Lilly
et al. (2007) and Lilly
et al. (2009).
The distribution on the sky of the
![]() objects
observed in the first half of the zCOSMOS-bright survey is illustrated
in the left panel of Fig. 1. The
vertical banding visible in the external, less finely sampled, regions
reflects the
quadrant design of VIMOS and an additional pattern introduced by the
slit positioning software SPOC (Bottini
et al. 2005). This pattern should almost completely
disappear at survey completion, since the observational strategy
foresees an eight-pass coverage with two mask designs at each pointing.
The expected final sampling rate is around
objects
observed in the first half of the zCOSMOS-bright survey is illustrated
in the left panel of Fig. 1. The
vertical banding visible in the external, less finely sampled, regions
reflects the
quadrant design of VIMOS and an additional pattern introduced by the
slit positioning software SPOC (Bottini
et al. 2005). This pattern should almost completely
disappear at survey completion, since the observational strategy
foresees an eight-pass coverage with two mask designs at each pointing.
The expected final sampling rate is around ![]() %.
%.
The redshift distribution of the observed galaxies covers the
range ![]() and peaks at redshift
and peaks at redshift ![]() .
The error in the redshift measurement, as determined from repeated
observations, is around 100 km s-1,
an accuracy well suited to the original survey scientific goals of the
investigation of large scale structure and the detection
of groups.
.
The error in the redshift measurement, as determined from repeated
observations, is around 100 km s-1,
an accuracy well suited to the original survey scientific goals of the
investigation of large scale structure and the detection
of groups.
For each measured redshift, we adopted a ranking scheme reflecting our confidence in its correctness. It is based on six broad confidence classes (0-1-2-3-4-9) reflecting the quality of the redshift measurement as obtained from the spectra. This scheme is similar to that originally adopted in the CFRS (Le Fevre et al. 1995) and VVDS (Le Fèvre et al. 2005), but with some further refinements taking advantage of the wealth of photometric information available for each targeted object.
The large, exquisite quality, ancillary photometric database
provided by the COSMOS survey (from HST data, to Spitzer, Galex,
Chandra, CFHTLS, and Subaru data, see Scoville
et al. 2007) has enabled us to derive reliable
photometric redshifts for all objects in the zCOSMOS-bright parent
photometric catalogue, with an uncertainty as low as
![]()
![]() (1+z) (Ilbert
et al. 2009).
(1+z) (Ilbert
et al. 2009).
The photometric redshift information was used to incorporate
in our analysis objects whose spectroscopic redshift, although less
secure, was consistent with its photometric value and therefore deemed
reliable (![]() smaller that 0.08
smaller that 0.08 ![]() (1+z), see Lilly
et al. 2009, for more details). In this way one can
use
(1+z), see Lilly
et al. 2009, for more details). In this way one can
use ![]() %
of the observed sample, totalling
%
of the observed sample, totalling
![]() galaxies
up to z=2.0 (
galaxies
up to z=2.0 (
![]() including stars and with no
high redshift cut-off), with a nominal
spectroscopic confirmation rate of
including stars and with no
high redshift cut-off), with a nominal
spectroscopic confirmation rate of
![]() % as found
by duplicate observations. This sample represents roughly half of the
final zCOSMOS sample and when we talk of the 10K-sample we always refer
to this subset of objects, the same used to perform group searches
(Knobel et al. 2009).
% as found
by duplicate observations. This sample represents roughly half of the
final zCOSMOS sample and when we talk of the 10K-sample we always refer
to this subset of objects, the same used to perform group searches
(Knobel et al. 2009).
For the 10K-samplegalaxies, absolute rest-frame magnitudes and stellar masses were obtained using standard multicolor spectral energy distribution (SED) fitting analysis. Rest-frame absolute magnitudes were obtained using the ZEBRA code, for which a detailed description is provided in Feldmann et al. (2006) and Oesch et al. (in prep.). We note here that the templates used by ZEBRA are the standard CWW templates (Coleman et al. 1980) and starburst templates from Kinney et al. (1996), and the best fit template is normalized to each galaxy photometry and spectroscopic redshift.
Stellar masses in units of solar masses were obtained by fitting stellar population synthesis models to the multicolor spectral SED of the observed magnitudes using the Hyperzmass code (Pozzetti et al. 2009; Bolzonella et al. 2009). In the subsequent analysis, we use stellar masses calculated adopting the Bruzual & Charlot (2003) libraries, and assuming a Chabrier initial mass function (Chabrier 2003). More details about the Hyperzmass code can be found in Bolzonella et al. (2009).
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12558F2.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg64.png)
|
Figure 2:
Panel a) shows the distribution along the
line of sight of
the 6204 galaxies used in our analysis, the subset of the
10K-samplegalaxies sample located within the central, high sampling
rate, region of the survey and in the redshift range
|
| Open with DEXTER | |
Panel (a) of Fig. 2 shows the
distribution along the line of sight of the galaxies within the
boundaries defined by
![]() ,
,
![]() and
and
![]() .
These boundaries (see Sect. 3.1) are
those adopted in our analysis to avoid being affected by the
inhomogeneous coverage of the 10K-sample. The number of galaxies
surviving within these
.
These boundaries (see Sect. 3.1) are
those adopted in our analysis to avoid being affected by the
inhomogeneous coverage of the 10K-sample. The number of galaxies
surviving within these ![]() boundaries
equals 6204, of which 1966 are in groups, while 1146
define the so-called isolated galaxy sample
(see Sect. 2.3).
boundaries
equals 6204, of which 1966 are in groups, while 1146
define the so-called isolated galaxy sample
(see Sect. 2.3).
The transverse dimension of this restricted sample
along ![]() is
is ![]() h-170 Mpc
at z=0.1, and
h-170 Mpc
at z=0.1, and ![]() h-170 Mpc
at z=1.0. In the same redshift interval the total
contiguous comoving volume sampled is
h-170 Mpc
at z=1.0. In the same redshift interval the total
contiguous comoving volume sampled is ![]()
![]() 106
h-170 Mpc3.
106
h-170 Mpc3.
2.2 The 10 K group catalogue
In our analysis, we use the catalogue of groups presented in Knobel et al. (2009)
and refer the reader to that paper for a detailed presentation of both
the group finding algorithm and the group
catalogue. Here we summarize the main points and advantages of the
adopted group finding algorithm and briefly discuss the resulting group
catalogue. Knobel et al.
(2009) introduced a novel method,
defined as a ``multi-pass procedure'', to achieve an impressive quality
in group reconstruction as tested using realistic mock catalogues. This
method, when combined with the standard fried-of-friends (FOF)
algorithm, yields values of completeness and purity for the group
catalogue obtained that are extremely stable with both redshift and
number of members observed in the reconstructed groups. Typical values
of these two quantities for groups reconstructed with more than five
observed members are around ![]() % at all redshifts and do not
decrease substantially for groups with lower number of members.
Correspondingly the interloper fraction always remains below
% at all redshifts and do not
decrease substantially for groups with lower number of members.
Correspondingly the interloper fraction always remains below ![]() % at all
redshifts for groups reconstructed with more than five observed
members, with only a slight increase for groups with lower number of
members (Knobel et al. 2009).
% at all
redshifts for groups reconstructed with more than five observed
members, with only a slight increase for groups with lower number of
members (Knobel et al. 2009).
These results provide reassurance that the group catalogue
that we use in our subsequent analysis is highly homogeneous up to ![]() ,
a fundamental prerequisite, since the aim of this paper is to
explore redshift trends in group galaxy colors. If our results are to
be reliable, we need to be confident that the group catalogue we use is
almost entirely free from redshift dependent biases. The presence of a
significantly higher interloper fraction with increasing redshift could
surreptitiously increase the fraction of blue (field) galaxies observed
in our group catalogue and be mistakenly interpreted as evidence of
evolution. The extensive tests performed in Knobel
et al. (2009) place on solid basis the analysis that
we perform in the following sections.
,
a fundamental prerequisite, since the aim of this paper is to
explore redshift trends in group galaxy colors. If our results are to
be reliable, we need to be confident that the group catalogue we use is
almost entirely free from redshift dependent biases. The presence of a
significantly higher interloper fraction with increasing redshift could
surreptitiously increase the fraction of blue (field) galaxies observed
in our group catalogue and be mistakenly interpreted as evidence of
evolution. The extensive tests performed in Knobel
et al. (2009) place on solid basis the analysis that
we perform in the following sections.
Panel (b) of Fig. 2 shows the
distribution along the line of sight of the group galaxy population
(1966 galaxies in total) within the boundaries defined by
![]() ,
,
![]() and
and
![]() .
The presence of large structures is clearly delineated by the group
galaxy sample. In fact there are quite a few conspicuous
structures visible in this plot, e.g., those around redshifts
.
The presence of large structures is clearly delineated by the group
galaxy sample. In fact there are quite a few conspicuous
structures visible in this plot, e.g., those around redshifts
![]() and
and ![]() ,
while
there are, on the other hand, regions devoid of large structures, e.g.,
in the redshift range
,
while
there are, on the other hand, regions devoid of large structures, e.g.,
in the redshift range ![]() (see Kovac et al. 2009a,
for a detailed description of the density field structures in the
10K-sample
field).
(see Kovac et al. 2009a,
for a detailed description of the density field structures in the
10K-sample
field).
We also note that our survey does not contain any single rich cluster, for example comparable to Coma cluster in the local Universe. This is not unexpected: because the size of the volume of the Universe explored by zCOSMOS-bright the probability of one such cluster being observed is negligible (see also Finoguenov et al. 2007).
2.3 The isolated galaxy sample
We complemented the analysis performed on the sample of group galaxies with a parallel one on a sample of isolated galaxies, i.e., a sample of galaxies located in low density regions. This comparative analysis should highlight the differences - if any - in properties (rest frame colors in our analysis) from the group galaxy sample and therefore allow us to quantify the environmental dependencies of the properties explored more reliably.
To define the isolated galaxy sample, we use the Voronoi Tessellation method (Voronoi 1908). Voronoi Tessellation divides the space occupied by the survey into a set of unique polyhedral sub-volumes, each containing exactly one galaxy and all points in space that are closer to that galaxy than to any other. As a consequence, while galaxies with many neighbors (e.g., those in groups and high density environments) have small Voronoi volumes, relatively isolated galaxies have larger Voronoi volumes. Voronoi Tessellation has been used in the literature as a basis for group-finding algorithms (Knobel et al. 2009; Gerke et al. 2005; Marinoni et al. 2002; Cucciati et al. 2009b). It is quite straightforward to use Voronoi volumes to select a sample of isolated galaxies, defined as galaxies occupying the largest Voronoi volumes. This strategy has the advantage of being non-parametric, i.e., it avoids any arbitrarily chosen smoothing/window profile in defining low density regions.
However, proper attention must be taken to exclude galaxies that are close to survey borders and correct for the progressive increase in the typical size of Voronoi volumes between low and high redshifts in our flux-limited galaxy sample.
To avoid the first problem, i.e., of galaxies near the survey
boundaries entering the isolated galaxy sample because of their
apparently large Voronoi volumes, we decided to restrict the volume of
the search for isolated galaxies within the boundaries defined by
![]() ,
,
![]() and
and
![]() ,
which is slightly more restrictive than the limits adopted for the
group analysis indicated by the red lines in Fig. 1.
Furthermore, in all the subsequent analysis we decided to reject all
isolated galaxies located in areas of lower sampling, that is galaxies
with mean correction factor
,
which is slightly more restrictive than the limits adopted for the
group analysis indicated by the red lines in Fig. 1.
Furthermore, in all the subsequent analysis we decided to reject all
isolated galaxies located in areas of lower sampling, that is galaxies
with mean correction factor
![]() (see Sect. 3.1). For
these galaxies, a large measured Voronoi volume could be the result of
the low spectroscopic sampling rate in the surrounding area.
(see Sect. 3.1). For
these galaxies, a large measured Voronoi volume could be the result of
the low spectroscopic sampling rate in the surrounding area.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12558F3.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg76.png)
|
Figure 3: Top panel: distribution of logarithm of normalized Voronoi volumes as a function of redshift. The stripes extending towards lower Voronoi volumes values are due to the presence of groups. Points marked with a cyan cross correspond to galaxies removed from the isolated galaxy sample because their Voronoi volume exceeded by a factor of 100 that of the median at the corresponding redshift. Bottom panel: histogram of the total distribution of normalized Voronoi volumes. The shaded blue area corresponds to the last quartile of the distribution, chosen to select our isolated galaxies sample, while the long tail in cyan extending to higher values - and indicated also by the vertical line - is the one clipped from the sample. |
| Open with DEXTER | |
To avoid the second possible problem, of being biased in the
definition of isolated galaxies by the progressive decrease in the
galaxy density in our flux-limited sample, we computed the median
value of the logarithm of Voronoi volumes sizes as a function of
redshift using running bins of size
![]() in
redshift steps of 0.05. A simple linear fit to
this quantity (as deemed
reasonable by visual inspection) was then used to normalize all
measured Voronoi volumes, correcting for the progressive increase with
redshift in the mean inter-galaxy separation. We then selected the
highest quartile of the normalized volumes distribution obtained in
this way, after taking the simple precaution of further rejecting
galaxies (148 in total, 80 at
in
redshift steps of 0.05. A simple linear fit to
this quantity (as deemed
reasonable by visual inspection) was then used to normalize all
measured Voronoi volumes, correcting for the progressive increase with
redshift in the mean inter-galaxy separation. We then selected the
highest quartile of the normalized volumes distribution obtained in
this way, after taking the simple precaution of further rejecting
galaxies (148 in total, 80 at
![]() )
whose normalized Voronoi volume was more than 100 times larger
than the median one: mostly galaxies located too close to the survey
borders, as suggested by the large predominance of low redshift objects
and by their general distribution on the sky. Figure 3
illustrates the method adopted to select isolated galaxies. The final
number of isolated galaxies obtained this way is 1146, after
the removal of galaxies (206, out of which 128
located in pairs) listed in our group catalogue.
)
whose normalized Voronoi volume was more than 100 times larger
than the median one: mostly galaxies located too close to the survey
borders, as suggested by the large predominance of low redshift objects
and by their general distribution on the sky. Figure 3
illustrates the method adopted to select isolated galaxies. The final
number of isolated galaxies obtained this way is 1146, after
the removal of galaxies (206, out of which 128
located in pairs) listed in our group catalogue.
We checked the reliability of our approach by selecting
isolated galaxies in simulations. We used the 24 COSMOS mock
light-cones kindly provided by Kitzbichler, (Kitzbichler & White 2007),
based on the Millennium DM N-body simulations (Springel 2005). We applied
the same observational strategy to these cones used to select the
10K-sample: we chose the same pointings observed in
10K-sample, used SPOC to select observed targets
and included the same redshift success rate as the real data. Out of
the sample of isolated galaxies obtained from the mocks using the
procedure described above, ![]() % are truly isolated galaxies,
with a variance of a few percent from cone to cone, i.e., galaxies that
in mock light-cones are inside a halo that contains only one galaxy
down to the R=26 mag limit. However, when
considering the 10 K mock samples - limited to
IAB
= 22.5 and with our sampling rate applied - this number
increases to
% are truly isolated galaxies,
with a variance of a few percent from cone to cone, i.e., galaxies that
in mock light-cones are inside a halo that contains only one galaxy
down to the R=26 mag limit. However, when
considering the 10 K mock samples - limited to
IAB
= 22.5 and with our sampling rate applied - this number
increases to ![]() %.
In other words, only
%.
In other words, only ![]() % of the galaxies in the
isolated sample selected using our strategy are located in groups with
at least two members in the 10 K mock samples. We should get
rid of most of this contamination by the last step of our procedure:
the final trimming of galaxies listed in our real group catalogue.
% of the galaxies in the
isolated sample selected using our strategy are located in groups with
at least two members in the 10 K mock samples. We should get
rid of most of this contamination by the last step of our procedure:
the final trimming of galaxies listed in our real group catalogue.
Panel (c) of Fig. 2 shows the distribution along the line of sight of the isolated galaxy sample, whose uniformity is evident.
3 Measuring F
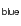
We use in this paper the diagnostic tool introduced in the
literature in the seminal work by Butcher
& Oemler (1978). These authors were the first to note
that the fraction of blue galaxies (
![]() from now onwards) in clusters
seems to increase with redshift. Their
work started a long-lasting wave of observational and theoretical
papers, which is still far from being completed (see the short
literature review presented in the introduction).
from now onwards) in clusters
seems to increase with redshift. Their
work started a long-lasting wave of observational and theoretical
papers, which is still far from being completed (see the short
literature review presented in the introduction).
After thirty years, the value of
![]() is
still a valuable and effective empirical tool in studying of the
dependence of galaxy evolution from the environment in which they
reside.
is
still a valuable and effective empirical tool in studying of the
dependence of galaxy evolution from the environment in which they
reside.
Galaxy color is the easiest parameter to measure among those that exhibit a distinctive bi-modality: spectral class, morphology, star formation rates and metallicities (see Mignoli et al. 2009; Strateva et al. 2001). Therefore it is the simplest to adopt in parametrizing the differences between evolution of groups and field or isolated galaxies. As far as its physical meaning is concerned, the rest-frame (U-B) color adopted in our analysis, bracketing the 4000 Å break, can be used to study the average star formation histories over longer time-scales than emission lines indicators such as, e.g., [OII]. This choice could therefore provide clearer insights into mechanisms that operate on longer time scales, such as possibly those in action in dense environments as groups, where member galaxies have resided for a significant fraction of their lifetime.
Despite the apparent simplicity of this parameter, the origin
of the physical mechanisms responsible for the variations in
![]() in
the group/cluster population still remains to be fully explained.
In particular we are still unable to determine the relative
influences of processes related to the environment and those that are
intrinsic to the galaxy itself, and therefore the dichotomy between
ab-initio/internal and external mechanisms responsible for the
variation of
in
the group/cluster population still remains to be fully explained.
In particular we are still unable to determine the relative
influences of processes related to the environment and those that are
intrinsic to the galaxy itself, and therefore the dichotomy between
ab-initio/internal and external mechanisms responsible for the
variation of ![]() is still an open one. The fraction of galaxies on either sides of the
bimodality in (U-B) colors
has been shown to depend strongly on galaxy luminosity and stellar mass
(see,
e.g., Baldry
et al. 2006,2004). Therefore, in studying
the dependence of
is still an open one. The fraction of galaxies on either sides of the
bimodality in (U-B) colors
has been shown to depend strongly on galaxy luminosity and stellar mass
(see,
e.g., Baldry
et al. 2006,2004). Therefore, in studying
the dependence of ![]() on group environment, we define and adopt both luminosity
volume-limited and mass volume limited samples.
on group environment, we define and adopt both luminosity
volume-limited and mass volume limited samples.
In this section, we discuss the strategy adopted to correct
for the 10K-sampleincompleteness when measuring
![]() ,
the cut-off adopted in defining
,
the cut-off adopted in defining
![]() ,
and how we estimate errors on this quantity.
,
and how we estimate errors on this quantity.
3.1 Correcting for survey incompleteness
The left panel of Fig. 1 shows
that the coverage in
![]() of the 10K-sampleremains very
uneven. While the mean sampling rate of
the 10K-sampleis around
of the 10K-sampleremains very
uneven. While the mean sampling rate of
the 10K-sampleis around ![]() %, this number varies
significantly as a function of position: in the central
regions the sampling rate is as high as
%, this number varies
significantly as a function of position: in the central
regions the sampling rate is as high as ![]() %, while it is as low
as
%, while it is as low
as ![]() %
in the regions near the borders. This unevenness can create problems
when defining groups of homogeneous numerosity/richness
irrespective of their position in the sky (see Sect. 6.1).
%
in the regions near the borders. This unevenness can create problems
when defining groups of homogeneous numerosity/richness
irrespective of their position in the sky (see Sect. 6.1).
To correct for this problem we adopted for each galaxy a
weighting scheme consisting of two factors: ![]() and
and
![]() .
The first factor
.
The first factor ![]() is similar to one adopted for the luminosity and mass function
estimates (see Zucca et al.
2009, for more details). It is obtained by a
parabolic fit to the product W of the
inverse of the target sampling rate (
is similar to one adopted for the luminosity and mass function
estimates (see Zucca et al.
2009, for more details). It is obtained by a
parabolic fit to the product W of the
inverse of the target sampling rate (![]() )
and
the inverse of the spectroscopic sampling rate (
)
and
the inverse of the spectroscopic sampling rate (![]() ):
):
| (1) |
The second factor
![]() corrects for the variation,
as a function of
corrects for the variation,
as a function of ![]() ,
of the mean correction factor expressed by
,
of the mean correction factor expressed by ![]() .
We estimated
.
We estimated ![]() in two passes. In a grid of steps equal to
in two passes. In a grid of steps equal to
![]() in
right ascension and declination and in squares of
in
right ascension and declination and in squares of
![]()
![]()
![]() ,
we computed the ratio of the number of observed objects whose redshift
was reliably measured to the total number of potential targets, as
defined as above,
within the same area. We then obtained
,
we computed the ratio of the number of observed objects whose redshift
was reliably measured to the total number of potential targets, as
defined as above,
within the same area. We then obtained
![]() by normalizing to unity the
mean value of this ratio over the full
by normalizing to unity the
mean value of this ratio over the full
![]() coverage
of the 10K-samplesurvey. The right panel of Fig. 1 shows
in color-scale the resulting function
coverage
of the 10K-samplesurvey. The right panel of Fig. 1 shows
in color-scale the resulting function
![]() before normalization. The
parameters chosen in calculating this
function allow us to reproduce well the inhomogeneities in the survey,
even the vertical banding, visible in left panel of Fig. 1.
To each galaxy we therefore assigned a weight:
before normalization. The
parameters chosen in calculating this
function allow us to reproduce well the inhomogeneities in the survey,
even the vertical banding, visible in left panel of Fig. 1.
To each galaxy we therefore assigned a weight:
![]()
![]()
![]() which
is the galaxy weighting scheme used in
the following analysis.
which
is the galaxy weighting scheme used in
the following analysis.
At the borders of the survey sampling is lower than average
resulting both in higher galaxy weights and higher incompleteness in
group detection. To alleviate this problem, we decided to
restrict the
analysis to the central area of the survey, where the inhomogeneity in
sampling rate is significantly lower. This region is indicated by red
lines in Fig. 1
and corresponds to galaxies within the following boundaries:
![]() ,
,
![]() .
.
We note that our results are relatively insensitive to changes
in the strategy used to define the weights, for example larger
smoothing boxes in defining
![]() .
Even when no weights at all are used, our results are almost unchanged.
A weighting scheme is needed when estimating in a homogeneous
way group richness (for example when exploring trends of
.
Even when no weights at all are used, our results are almost unchanged.
A weighting scheme is needed when estimating in a homogeneous
way group richness (for example when exploring trends of
![]() as
a function of groups richness). When dealing with the galaxy group
population as a whole, the impact of the use of weights
is minimal.
as
a function of groups richness). When dealing with the galaxy group
population as a whole, the impact of the use of weights
is minimal.
3.2 Computing the blue fraction
We divided galaxies into red and blue sub-samples taking
advantage of the observed bimodality in galaxy (U-B) rest-frame
colors, visible in Fig. 4
(see also Cucciati et al. 2009). Accordingly, we defined blue
galaxies as those with rest-frame colors
![]() .
This value agrees with both the value chosen by Gerke
et al. (2007) in their analysis of
.
This value agrees with both the value chosen by Gerke
et al. (2007) in their analysis of
![]() in
the DEEP2 groups sample and with the value adopted in a
parallel analysis to our own by Cucciati
et al. (2009b). We did not allow this value to vary
with galaxy luminosity, as suggested for example by van Dokkum et al. (2000)
and Blanton et al. (2006).
Given the relatively small variation in MB
of the bulk of our galaxy sample (of roughly 3 mag), the
color-magnitude relationship quoted by these authors would imply a
corresponding variation in the cut-off color value
in
the DEEP2 groups sample and with the value adopted in a
parallel analysis to our own by Cucciati
et al. (2009b). We did not allow this value to vary
with galaxy luminosity, as suggested for example by van Dokkum et al. (2000)
and Blanton et al. (2006).
Given the relatively small variation in MB
of the bulk of our galaxy sample (of roughly 3 mag), the
color-magnitude relationship quoted by these authors would imply a
corresponding variation in the cut-off color value ![]() mag,
which we deemed to be negligible.
mag,
which we deemed to be negligible.
From our data, there is no obvious evidence of evolution to
redshift ![]() in the adopted cut-off value, and in our analysis we therefore decided
to keep its value fixed with redshift.
in the adopted cut-off value, and in our analysis we therefore decided
to keep its value fixed with redshift.
After defining the cut-off value between red and blue galaxies
we obtained a set of
![]() blue galaxies from the total
sample of
blue galaxies from the total
sample of ![]() galaxies, each with a weight wi.
The corrected blue fraction was then given by:
galaxies, each with a weight wi.
The corrected blue fraction was then given by:
| (2) |
where the number of blue galaxies
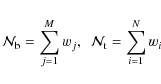
|
(3) |
where the index j corresponds to all the blue galaxies, while the index i corresponds to the full galaxy sample.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12558F4.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg103.png)
|
Figure 4:
Rest-frame (U-B) colors plotted
vs. B-band rest-frame magnitudes. In each
panel redshift bins of width
|
| Open with DEXTER | |
3.3 Estimating errors in F
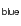
To estimate errors in the values computed for
![]() ,
we adopted a bootstrap re-sampling strategy. We randomly sampled by
replacement the entire data set under consideration, e.g., all isolated
galaxies in a given volume-limited sample. The error in
,
we adopted a bootstrap re-sampling strategy. We randomly sampled by
replacement the entire data set under consideration, e.g., all isolated
galaxies in a given volume-limited sample. The error in
![]() was
then estimated to be the standard deviation in
was
then estimated to be the standard deviation in
![]() distribution
for 1000 such Montecarlo samples.
distribution
for 1000 such Montecarlo samples.
We used also the approximate analytical formulas provided by Gehrels (1986) to estimate the
error in ![]() but the differences in value with respect to the bootstrapping
technique are
minimal. In our plots we always show bootstrap errors.
but the differences in value with respect to the bootstrapping
technique are
minimal. In our plots we always show bootstrap errors.
Another source of errors and noise in our plots is cosmic
variance. At lower redshifts, the volume sampled by
zCOSMOS survey is not large enough to be considered a fair
representation of the universal matter distribution. It is
therefore possible that the presence of large scale structures
introduces large fluctuations in the trends of
![]() as
a function of redshift, lowering significantly
as
a function of redshift, lowering significantly
![]() at
the redshift where these structures are located. Our survey shows
quite a few of these prominent structures, for example those located at
at
the redshift where these structures are located. Our survey shows
quite a few of these prominent structures, for example those located at
![]() and
and
![]() ,
readily visible in the top two panels of Fig. 2 (see also Kovac et al. 2009b).
To alleviate this problem in our analysis we tried to adopt
redshift bins
large enough to smooth out as much as possible this effect.
,
readily visible in the top two panels of Fig. 2 (see also Kovac et al. 2009b).
To alleviate this problem in our analysis we tried to adopt
redshift bins
large enough to smooth out as much as possible this effect.
4 Defining luminosity volume-limited samples
The zCOSMOS survey provides a unique data-set for measuring
the evolution of the blue fraction up to ![]() .
The excellent quality of the observed spectra prevent any possible bias
against red,
absorption lines only spectra (Lilly
et al. 2009), while the simple
.
The excellent quality of the observed spectra prevent any possible bias
against red,
absorption lines only spectra (Lilly
et al. 2009), while the simple
![]() mag
limit used to select survey targets translates into a selection in the
rest-frame B-band at
mag
limit used to select survey targets translates into a selection in the
rest-frame B-band at
![]() .
Therefore the zCOSMOS galaxy sample when rest-frame B-band
selection is adopted is free from significant color-dependent
incompleteness in (U-B) rest-frame
colors to the highest redshift
bin explored.
.
Therefore the zCOSMOS galaxy sample when rest-frame B-band
selection is adopted is free from significant color-dependent
incompleteness in (U-B) rest-frame
colors to the highest redshift
bin explored.
However the reader should be warned that completeness in B-band rest frame selection does not imply completeness in, e.g., mass selection, as we will discuss at lenght in Sect. 7 and following. As a consequence any trend observed in rest-frame B-band selected samples needs to be re-examined when the selection criterion of the sample changes (see also, e.g., De Propris et al. 2004).
The absence of (U-B) color incompleteness in zCOSMOS B-band volume limited samples can be visually appreciated in Fig. 4, where we plot for different redshift bins (as indicated in each panel) the rest-frame (U-B) color versus rest-frame B-band absolute magnitude MB.
Table 1:
Summary of the four volume-limited data samples;
![]() .
.
In each panel distinctive red and blue populations of galaxies are visible, with loci that are separated approximately at (U-B) = 1 at all redshifts. The cut-off in the galaxy population distribution visible on the left hand side of each panel is a consequence of zCOSMOS purely I-band flux-limited target-selection strategy and moves towards brighter magnitudes as the redshift increases. However, this progressively brighter cut-off does not introduce obvious biases against red galaxies as indicated by the cut-off line being nearly vertical in all panels with the possible exception of the last redshift bin, where the observed I-band begins moving blue-ward of the rest-frame B-band and a slight slanting of the cut-off in the galaxy population distribution starts becoming appreciable. Therefore, in this last redshift bin we need to be more conservative in the definition of the cut-off in absolute B-band rest-frame magnitude to avoid biases against red galaxies, even if this choice will result in smaller number of objects for our analysis.
Another factor to consider in our definition of volume-limited samples is that the typical galaxy luminosity evolves with redshift. We need to include an evolutionary term in our definition of cut-off magnitudes for the volume-limited samples because we aim to select a population of galaxies that is similar with respect to M*B at all redshifts.
As suggested by the results obtained for the global luminosity
function evolution of our sample (see Zucca
et al. 2009, for more details), the evolution in M*B
can be parametrized linearly by
the equation
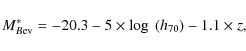
|
(4) |
which includes an evolution with redshift of roughly 1 mag between
The galaxy luminosities quoted from now on are always evolutionary-corrected present-day luminosities to ensure that galaxies of similar luminosity are being compared in different redshifts bins.
We defined four different luminosity volume-limited samples,
from sample I to sample IV, each covering
progressively higher ranges of redshift, and defined by evolving the
cut-off magnitudes
![]() ,
as illustrated in Fig. 5.
,
as illustrated in Fig. 5.
Table 1
summarizes the properties of these four different volume-limited
samples: the different redshift ranges covered and the total
numbers of galaxies and isolated/group galaxies
contained within the ![]() limits
described in Sect. 3.1.
limits
described in Sect. 3.1.
From now onwards when we will talk of the field population we always mean the total galaxy sample, i.e., the full galaxy population including group/isolated galaxies.
We note that while the full group catalogue was obtained using
the entire 10K-samplegalaxy catalogue, for each of the volume-limited
samples defined above we selected a corresponding uniform sample of
groups possessing at least two member galaxies brighter than the B-band
rest-frame
![]() considered (Group
galaxies I). This strategy avoids the
redshift inhomogeneity introduced in our group catalogue by the
progressive brightening of the rest-frame B-band
magnitudes sampled by the survey as redshift increases.
A given group will have a different number of members in each
volume-limited sample, but within each volume-limited sample
group's numerosity/richness will be
measured consistently at all redshifts. Unless explicitly mentioned
when we talk of group galaxies, we refer to Group galaxies I.
considered (Group
galaxies I). This strategy avoids the
redshift inhomogeneity introduced in our group catalogue by the
progressive brightening of the rest-frame B-band
magnitudes sampled by the survey as redshift increases.
A given group will have a different number of members in each
volume-limited sample, but within each volume-limited sample
group's numerosity/richness will be
measured consistently at all redshifts. Unless explicitly mentioned
when we talk of group galaxies, we refer to Group galaxies I.
We also introduced a further set of galaxy groups:
those that possess at least two members in sample IV
(Group galaxies II). By studying the variation in
![]() for
galaxies of different luminosities that are members of this group
sample one can hope to disentangle the effect of
galaxy luminosity on
for
galaxies of different luminosities that are members of this group
sample one can hope to disentangle the effect of
galaxy luminosity on ![]() from that of group richness: this is because the groups in
this sample should be homogeneous in terms of richness as a function of
redshift, irrespective of the magnitude of the member galaxies
considered in the analysis (see Sect. 5). For
the sake of robustness, the value of the group observed line-of-sight
velocity dispersion
from that of group richness: this is because the groups in
this sample should be homogeneous in terms of richness as a function of
redshift, irrespective of the magnitude of the member galaxies
considered in the analysis (see Sect. 5). For
the sake of robustness, the value of the group observed line-of-sight
velocity dispersion ![]() ,
whenever used in our analysis, is always estimated using all observed
group members, irrespective of their absolute magnitude.
,
whenever used in our analysis, is always estimated using all observed
group members, irrespective of their absolute magnitude.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12558F5.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg121.png)
|
Figure 5:
Redshift distribution of the 10K-samplezCOSMOS galaxies. Red points
represent galaxies located in groups. The lines drawn correspond to the
four different volume-limited samples discussed in the text. We assumed
|
| Open with DEXTER | |
After defining galaxy weights, volume-limited samples and the
corresponding group/isolated subsets, we proceeded to estimate
![]() ,
the fraction of blue galaxies, for each galaxy sample
and its dependence on group properties, galaxy luminosity,
and redshift.
,
the fraction of blue galaxies, for each galaxy sample
and its dependence on group properties, galaxy luminosity,
and redshift.
![\begin{figure}
\par\includegraphics[angle=270,width=12cm,clip,origin=rb]{12558F6.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg122.png)
|
Figure 6:
The four panels show |
| Open with DEXTER | |
5 Blue fraction as a function of galaxy luminosity and environment up
to z  1
1
In the local Universe, the correlation between galaxy luminosities and colors is a well-known observational result: more luminous galaxies have typically redder colors than less luminous galaxies (see Baldry et al. 2004, and references therein). A similar color segregation has been observed between local groups and field samples: redder galaxies are preferentially located in galaxy groups and clusters (see De Propris et al. 2004, and references therein). It is therefore interesting to use our sample to check whether these trends survive at higher redshifts and if they show weakening or even any visible reversal.
A similar analysis was performed using DEEP2 data for the
redshift range ![]() by Gerke et al. (2007),
and using VVDS data for the range
by Gerke et al. (2007),
and using VVDS data for the range
![]() by
Cucciati et al.
(2009b). The VVDS and DEEP2 surveys were the first
to use in their investigation a
homogeneous dataset from the lowest to the highest redshift bins
explored, and a group sample spanning a wide range of richnesses, down
to poorest systems, in contrast to previous work that mainly considered
higher richness, and more easily detectable, systems. With respect to
these two pioneering large high-redshift surveys, zCOSMOS presents some
non-negligible advantages. We have a larger volume coverage enabling us
to complete more robust statistical analyses than VVDS, and smaller
errors in galaxy redshift measurements - around
275 km s-1 for VVDS,
(see Le Fèvre et al. 2005),
which allows us to compile a group catalogue that is less prone to
contamination and incompleteness, especially for low richness and low
velocity dispersion systems. We are also less plagued by the color
incompleteness (and, more importantly for the subsequent analysis, mass
incompleteness) that affects DEEP2 data in the redshift range
covered by their analysis, and have the ability to cover the complete
redshift range
by
Cucciati et al.
(2009b). The VVDS and DEEP2 surveys were the first
to use in their investigation a
homogeneous dataset from the lowest to the highest redshift bins
explored, and a group sample spanning a wide range of richnesses, down
to poorest systems, in contrast to previous work that mainly considered
higher richness, and more easily detectable, systems. With respect to
these two pioneering large high-redshift surveys, zCOSMOS presents some
non-negligible advantages. We have a larger volume coverage enabling us
to complete more robust statistical analyses than VVDS, and smaller
errors in galaxy redshift measurements - around
275 km s-1 for VVDS,
(see Le Fèvre et al. 2005),
which allows us to compile a group catalogue that is less prone to
contamination and incompleteness, especially for low richness and low
velocity dispersion systems. We are also less plagued by the color
incompleteness (and, more importantly for the subsequent analysis, mass
incompleteness) that affects DEEP2 data in the redshift range
covered by their analysis, and have the ability to cover the complete
redshift range ![]() ,
monitoring the redshift evolution in
,
monitoring the redshift evolution in
![]() in
a continuous way.
in
a continuous way.
As a first step, we explored how
![]() varies
with galaxy luminosity. We defined four independent redshift
bins as shown in Fig. 6:
[0.25:0.45], [0.45:0.6], [0.6:0.8],
[0.8:1.0]. Within each of these redshift intervals and using the
volume-limited samples defined in Table 1, we
defined sub-samples of galaxies in independent bins of galaxy
luminosities. The binning in galaxy luminosity was chosen in such a way
to ensure a sizeable number of galaxies in each environment and
redshift bin considered.
varies
with galaxy luminosity. We defined four independent redshift
bins as shown in Fig. 6:
[0.25:0.45], [0.45:0.6], [0.6:0.8],
[0.8:1.0]. Within each of these redshift intervals and using the
volume-limited samples defined in Table 1, we
defined sub-samples of galaxies in independent bins of galaxy
luminosities. The binning in galaxy luminosity was chosen in such a way
to ensure a sizeable number of galaxies in each environment and
redshift bin considered. ![]() and its error bar were estimated using the procedures described in
Sect. 3,
while the error bars drawn along the luminosity axis link the upper and
lower quartiles of the luminosity distribution of galaxies within
each bin.
and its error bar were estimated using the procedures described in
Sect. 3,
while the error bars drawn along the luminosity axis link the upper and
lower quartiles of the luminosity distribution of galaxies within
each bin.
Figure 6 shows the results obtained for the different galaxy samples: red circles for group galaxies, blue triangles for isolated galaxies, and black squares for the total galaxy population. In each redshift bin all the different galaxy populations display a decrease in the fraction of blue galaxies for increasing rest-frame galaxy luminosities, while at a fixed luminosity bin, blue galaxies are always less common in the group environment than in the field and most common among the isolated galaxy population. Figure 6 therefore suggests that at all redshifts explored the color of galaxies at a given luminosity becomes redder earlier in groups than in the field or in lower density regions.
Furthermore, the differences between the galaxy population of the three different environments seem to increase at higher luminosities in each of the four panels of Fig. 6 and this result echoes a similar one in Cucciati et al. (2006).
Towards redshift ![]() the differences among the three environments progressively decrease.
However up to the highest redshift bin explored we do not see any hint
of a possible reversal of
the trend of
the differences among the three environments progressively decrease.
However up to the highest redshift bin explored we do not see any hint
of a possible reversal of
the trend of ![]() as a function of luminosity, a robust result as our sample is free from
significant color-dependent incompleteness up to
as a function of luminosity, a robust result as our sample is free from
significant color-dependent incompleteness up to ![]() (see Sect. 4).
Such possible trend reversal was tentatively detected by Gerke et al. (2007),
albeit with
large error bars, for the redshift bin
(see Sect. 4).
Such possible trend reversal was tentatively detected by Gerke et al. (2007),
albeit with
large error bars, for the redshift bin
![]() and
for magnitudes brighter than
and
for magnitudes brighter than
![]() .
.
We used the four volume-limited samples and the three galaxy
samples defined in Table 1 to explore
in better detail the redshift trends implied by Fig. 6. For each of
these samples, we plotted ![]() as a function of redshift in
Fig. 7,
to help determine directly whether the rate of variation in
as a function of redshift in
Fig. 7,
to help determine directly whether the rate of variation in
![]() differs
significantly in groups compared to the field/isolated galaxy
population. Each panel refers to a
volume-limited sample defined by the labels at its bottom, where red
circles indicate
differs
significantly in groups compared to the field/isolated galaxy
population. Each panel refers to a
volume-limited sample defined by the labels at its bottom, where red
circles indicate ![]() for group galaxies, while black squares and blue triangles show the
same quantity for field and isolated galaxies, respectively.
for group galaxies, while black squares and blue triangles show the
same quantity for field and isolated galaxies, respectively.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12558F7.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg129.png)
|
Figure 7:
The four panels show |
| Open with DEXTER | |
Table 2:
Summary of fits results for
![]() as
a function of redshift in the volume-limited samples defined in
Table 1;
as
a function of redshift in the volume-limited samples defined in
Table 1;
![]() .
.
The first piece of information conveyed by Fig. 7 is that color
segregation appears to be already in place at ![]() :
panel (d) shows that even in the highest redshift bin explored
there is a small, but significant, difference in
:
panel (d) shows that even in the highest redshift bin explored
there is a small, but significant, difference in
![]() among
the different galaxy samples, mirroring the information provided
by panel (d) of Fig. 6. Furthermore
for each of the luminosity bins explored color segregation increases
with cosmic time, as the differences of
among
the different galaxy samples, mirroring the information provided
by panel (d) of Fig. 6. Furthermore
for each of the luminosity bins explored color segregation increases
with cosmic time, as the differences of
![]() in
the group, field and isolated galaxy populations increase
significantly moving from high to low redshifts.
in
the group, field and isolated galaxy populations increase
significantly moving from high to low redshifts.
These results are in good agreement with those from the
VVDS survey presented by Cucciati
et al. (2009b). However we seem to detect evolution
in ![]() across the range
across the range ![]() ,
in contrast with the results of Gerke
et al. (2007) using DEEP2 data-set. We note
that comparing directly our panel (d) of Fig. 7 with the first
panel of their Fig. 7,
where the magnitude ranges explored are quite similar and the sample
analyzed is purely volume-limited as in our analysis, the disagreement
is not so evident.
,
in contrast with the results of Gerke
et al. (2007) using DEEP2 data-set. We note
that comparing directly our panel (d) of Fig. 7 with the first
panel of their Fig. 7,
where the magnitude ranges explored are quite similar and the sample
analyzed is purely volume-limited as in our analysis, the disagreement
is not so evident.
We chose to parametrize the evolution in
![]() with
redshift with a law of the form
with
redshift with a law of the form
![]()
![]()
![]() .
The results of the best fit solutions obtained with this
parametrization are given in Table 2 and shown
as dashed lines in Fig. 7.
These lines tend to diverge between high and low z.
Toward higher redshift, one can consider whether, irrespective of the
environment considered, most galaxies in the luminosity ranges explored
resided in the blue cloud, while the red sequence remained more or less
empty. As cosmic time increases, the blue cloud may then
become progressively depleted and the rate at which this depletion
occurs seems to be higher in higher density environments, implying
that the star-formation rate is declining more rapidly in groups
and clusters.
.
The results of the best fit solutions obtained with this
parametrization are given in Table 2 and shown
as dashed lines in Fig. 7.
These lines tend to diverge between high and low z.
Toward higher redshift, one can consider whether, irrespective of the
environment considered, most galaxies in the luminosity ranges explored
resided in the blue cloud, while the red sequence remained more or less
empty. As cosmic time increases, the blue cloud may then
become progressively depleted and the rate at which this depletion
occurs seems to be higher in higher density environments, implying
that the star-formation rate is declining more rapidly in groups
and clusters.
While the extrapolated values of
![]() at
at
![]() vary as
a function both of environment and the luminosity
cut-off considered, the values of
vary as
a function both of environment and the luminosity
cut-off considered, the values of ![]() do not exhibit any appreciable differences
between the different environments as a function of the chosen
luminosity cut-off. On the other hand, there is a noticeable increase
in the value of
do not exhibit any appreciable differences
between the different environments as a function of the chosen
luminosity cut-off. On the other hand, there is a noticeable increase
in the value of ![]() moving from isolated to group galaxies,
although the error bars are quite large.
moving from isolated to group galaxies,
although the error bars are quite large.
Since ![]() implies that there is a fractional decrease in
implies that there is a fractional decrease in
![]() with
cosmic time (or, alternatively, a fractional increase of
the percentage of red galaxies with cosmic time) this result suggests
that we detect the signature of an environmental dependence of the
variations in
with
cosmic time (or, alternatively, a fractional increase of
the percentage of red galaxies with cosmic time) this result suggests
that we detect the signature of an environmental dependence of the
variations in ![]() with cosmic time. However the mechanisms responsible for the
environmental trends that we witness cannot be accurately constrained.
with cosmic time. However the mechanisms responsible for the
environmental trends that we witness cannot be accurately constrained.
Our results could be the consequence of physical mechanisms operating in the denser group environment or simply the result of an ab initio bias relating galaxy luminosity/mass and its environment. In other words, we could be witnessing the more rapid quenching of star formation - and, as a consequence, the faster build-up of the red sequence - in denser environments, or the delayed and more efficient replenishing of the blue cloud in lower density environments. We will return to this point in the following sections.
The group points in Fig. 7 do not correspond
to a group population that is homogeneous across each of the four
different panels but to the samples indicated as Group
galaxies I in Table 1, i.e.,
galaxies in groups of more than two members observed within the
volume-limited sample plotted in each panel. Moving from
panel (a) to panel (d) in Fig. 7, we consider
groups that are intrinsically more rich, since they possess
two or more members at progressively brighter cut-off magnitudes.
Accordingly the observed decrease in
![]() for
the group galaxy population between the first and the last panel of
Fig. 7
is the result of two different effects: the brightening of the galaxy
population, an effect easily visible also for the isolated and
the field samples, and the increasing richness of groups observed in
the brighter volume-limited samples.
for
the group galaxy population between the first and the last panel of
Fig. 7
is the result of two different effects: the brightening of the galaxy
population, an effect easily visible also for the isolated and
the field samples, and the increasing richness of groups observed in
the brighter volume-limited samples.
It is therefore interesting to remove the richness-dependent
effect from this plot and to compare galaxies residing in groups of
homogeneous richness across the different volume-limited samples,
using the sample of groups with two or more members brighter than
![]() ,
i.e., the brightest absolute magnitude cut-off in our sample.
This way, we select for each panel, except panel (d) whose
group sample remains unchanged by definition, a set of groups
richer than those considered before. Obviously, once a group survives
in the catalogue defined by the more stringent luminosity cut-off, we
then plot in the appropriate panel all its members observed within the
volume-limited sample under study. The result of this exercise is shown
by the brown stars in Fig. 7
and by the last row of Table 2, labeled
Group galaxies II. In this case, the groups considered are
homogeneous in richness up to
,
i.e., the brightest absolute magnitude cut-off in our sample.
This way, we select for each panel, except panel (d) whose
group sample remains unchanged by definition, a set of groups
richer than those considered before. Obviously, once a group survives
in the catalogue defined by the more stringent luminosity cut-off, we
then plot in the appropriate panel all its members observed within the
volume-limited sample under study. The result of this exercise is shown
by the brown stars in Fig. 7
and by the last row of Table 2, labeled
Group galaxies II. In this case, the groups considered are
homogeneous in richness up to ![]() .
The difference compared to the field population (and the
isolated galaxies) increases significantly for these richer groups. In
contrast the dependence of
.
The difference compared to the field population (and the
isolated galaxies) increases significantly for these richer groups. In
contrast the dependence of ![]() on the rest-frame B magnitude of the group
population is reduced significantly. Table 2 shows that
the slopes of the fits to the Group galaxies II points are
virtually indistinguishable among themselves, irrespective of the
luminosity limits adopted in each of the four different panels.
on the rest-frame B magnitude of the group
population is reduced significantly. Table 2 shows that
the slopes of the fits to the Group galaxies II points are
virtually indistinguishable among themselves, irrespective of the
luminosity limits adopted in each of the four different panels.
6 Blue fraction as a function of group properties to z
 1
1
The results obtained in the previous section using Group
galaxies II samples suggest that group richness is an
important ingredient in setting the value of
![]() ,
possibly more influential than the galaxy rest-frame B magnitude.
,
possibly more influential than the galaxy rest-frame B magnitude.
Group richness can be considered, albeit with a large scatter, a proxy for the mass of the halo where the group resides (see Knobel et al. 2009). Therefore, the results just obtained echo at higher redshifts findings in the local Universe by Weinmann et al. (2000). Using both galaxy colors and specific star formation rate indicators to define samples of early/late type galaxies, these authors showed that at fixed halo mass the dependence of the galaxy type fraction on luminosity is quite weak.
Concerning the dependence of
![]() on
group richness and/or velocity dispersion - another
possible proxy of halo mass - many conflicting observational
results, however, exist in the
literature. Some authors have claimed the presence of a relationship
between group and galaxy properties (see, e.g., Zabludoff & Mulchaey
1998; Martínez
et al. 2002; Margoniner et al. 2001;
Gerke
et al. 2007; Biviano et al. 1997; De Lucia
et al. 2007; Goto et al. 2003; Tanaka
et al. 2004; Koyama et al. 2007; Poggianti
et al. 2006, to quote a few), while other
authors have claimed that such relationships are not present (see,
e.g., Goto
2005; Popesso
et al. 2007; Ellingson et al. 2001;
Wilman
et al. 2005b; Fairley et al. 2002; Smail
et al. 1998; De Propris et al. 2004).
on
group richness and/or velocity dispersion - another
possible proxy of halo mass - many conflicting observational
results, however, exist in the
literature. Some authors have claimed the presence of a relationship
between group and galaxy properties (see, e.g., Zabludoff & Mulchaey
1998; Martínez
et al. 2002; Margoniner et al. 2001;
Gerke
et al. 2007; Biviano et al. 1997; De Lucia
et al. 2007; Goto et al. 2003; Tanaka
et al. 2004; Koyama et al. 2007; Poggianti
et al. 2006, to quote a few), while other
authors have claimed that such relationships are not present (see,
e.g., Goto
2005; Popesso
et al. 2007; Ellingson et al. 2001;
Wilman
et al. 2005b; Fairley et al. 2002; Smail
et al. 1998; De Propris et al. 2004).
In the following, we explore with our sample the dependence
of
![]() on group richness and velocity
dispersion.
on group richness and velocity
dispersion.
6.1 Blue fraction as a function of group richness
The use of the term ``richness'' for galaxy clusters dates back to Abell, who introduced a broad classification of clusters in three richness classes based on counting galaxies between m3 and m3 + 2 mag, where m3 is the magnitude of the third-brightest galaxy (see Abell 1958). In this paper, we use the term richness for each group to simply indicate the number of members observed in each of the different volume-limited samples. As such, the richness of a group is not an absolute number, but varies depending on the absolute magnitude cut-off chosen to define the sample of groups. A possible better name for this quantity could be group numerosity. In estimating group richness/numerosity, however, even within this more limited definition, one has to consider corrections to the number of galaxy members observed, to properly account for the large-scale variations in the mean sampling rate of the 10K-sample.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12558F8.ps}\vspace*{-1.5mm}
\vspace*{-1.5mm}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg140.png)
|
Figure 8:
Dependence of the blue fraction
|
| Open with DEXTER | |
While the mean sampling rate of the 10K-sampleis about ![]() % and
increases up to
% and
increases up to ![]() %
in the restricted central area adopted for our analysis, there are
large spatial variations in this number (see Fig. 1).
%
in the restricted central area adopted for our analysis, there are
large spatial variations in this number (see Fig. 1).
To correct for this problem, we estimated richness using the
weighting scheme discussed in Sect. 3.1. For
each volume limited sample we simply added galaxy weights to count the
group members, by writing richness as
![]() ,
where M is the number of members observed
in each volume-limited sample.
,
where M is the number of members observed
in each volume-limited sample.
Figure 8
shows the dependence of the value of
![]() on group richness. In each
panel, we consider different redshift
ranges, corresponding to the four volume-limited samples
defined in Table 1,
and divide the corresponding group sample according to richness. In all
panels, the red dashed line indicates the fit to the global galaxy
population obtained in Sect. 5. In
the first three panels, the yellow points correspond to groups of
observed richness
on group richness. In each
panel, we consider different redshift
ranges, corresponding to the four volume-limited samples
defined in Table 1,
and divide the corresponding group sample according to richness. In all
panels, the red dashed line indicates the fit to the global galaxy
population obtained in Sect. 5. In
the first three panels, the yellow points correspond to groups of
observed richness
![]() ,
the orange points to groups of observed richness
,
the orange points to groups of observed richness
![]() and
the brown points to groups of observed richness
and
the brown points to groups of observed richness
![]() .
In panel (d), yellow points correspond to groups of observed
richness
.
In panel (d), yellow points correspond to groups of observed
richness ![]() and brown points to groups of observed richness
and brown points to groups of observed richness
![]() .
The limits chosen to divide the groups into bins of richness
are arbitrary but ensure that each richness bin contains a sizeable
number of group member galaxies (always above
.
The limits chosen to divide the groups into bins of richness
are arbitrary but ensure that each richness bin contains a sizeable
number of group member galaxies (always above ![]() ).
).
The main result presented in Fig. 8 is that for
all redshifts explored and volume limited samples,
![]() decreases
monotonically between higher and lower redshifts and richer groups have
a lower value of
decreases
monotonically between higher and lower redshifts and richer groups have
a lower value of
![]() .
This result is in agreement with similar trends observed in the local
Universe (see Margoniner
et al. 2001; Goto et al. 2003).
.
This result is in agreement with similar trends observed in the local
Universe (see Margoniner
et al. 2001; Goto et al. 2003).
We noted in Sect. 2.2 that in our sample we do not have any more massive relaxed clusters, especially at low redshift, but instead we probe mainly the poorer clusters and group environment. For our lower richness groups, the results obtained - especially in the lowest redshift bin, where we are dealing with the poorest groups of the sample in absolute terms - blend with those observed for the global field population. We may be concerned that these results are just the by-product of a higher interloper fraction for these (poorer) groups. However, as discussed in detail in Knobel et al. (2009), the interloper fraction of our group catalogue shows a minimal increase when the number of detected members decreases. Furthermore in the local Universe extremely poor groups are known to be dominated by spiral galaxies (Zabludoff & Mulchaey 1998), and so what we are witnessing is most probably a real physical trend.
6.2 Blue fraction as a function of group velocity dispersion
We binned our group sample using also the observed
line-of-sight velocity dispersion ![]() ,
another possible proxy for group mass. The estimate of
,
another possible proxy for group mass. The estimate of ![]() is difficult, especially when one is dealing, as in our case,
with groups of only a few members with measured redshifts (see Beers et al. 1990).
However, restricting the analysis to groups with observed numbers of
members equal or greater than 5 allows us to observe a
reasonable correlation between
is difficult, especially when one is dealing, as in our case,
with groups of only a few members with measured redshifts (see Beers et al. 1990).
However, restricting the analysis to groups with observed numbers of
members equal or greater than 5 allows us to observe a
reasonable correlation between ![]() and
halo group mass (Knobel
et al. 2009). We therefore used only groups with at
least 5 members with measured redshifts in the 10K-sampleto
explore how
and
halo group mass (Knobel
et al. 2009). We therefore used only groups with at
least 5 members with measured redshifts in the 10K-sampleto
explore how ![]() depends on the measured
depends on the measured ![]() in different redshift bins and for different volume-limited samples.
in different redshift bins and for different volume-limited samples.
Our results are shown in Fig. 9. In
panel (a), the yellow point indicates
![]() for
groups with
for
groups with ![]() km s-1,
the orange point for groups with
km s-1,
the orange point for groups with
![]() km s-1,
and the brown point for groups with
km s-1,
and the brown point for groups with
![]() km s-1.
In the three remaining panels, the yellow points show
km s-1.
In the three remaining panels, the yellow points show
![]() for
groups with
for
groups with ![]() km s-1,
the orange points for groups with
km s-1,
the orange points for groups with
![]() km s-1,
and the brown points for groups with
km s-1,
and the brown points for groups with
![]() km s-1.
In all panels, the red dashed line corresponds to the fits obtained for
the entire galaxy groups population in the volume-limited sample,
as in Fig. 8,
while the red points are those corresponding to the sample of groups
detected with at least 5 members in the flux-limited sample
irrespective of their velocity dispersion. Figure 9 shows that
there is a consistent trend in all panels: groups with higher velocity
dispersion tend to have a lower fraction of blue galaxies.
km s-1.
In all panels, the red dashed line corresponds to the fits obtained for
the entire galaxy groups population in the volume-limited sample,
as in Fig. 8,
while the red points are those corresponding to the sample of groups
detected with at least 5 members in the flux-limited sample
irrespective of their velocity dispersion. Figure 9 shows that
there is a consistent trend in all panels: groups with higher velocity
dispersion tend to have a lower fraction of blue galaxies.
Limiting the sample in the analysis only to groups of at least
5 observed members, produces the systematic offset towards
lower
![]() observed in each of the panels
when comparing the red points to the
dashed red lines: with the requirement of
observed in each of the panels
when comparing the red points to the
dashed red lines: with the requirement of ![]() we remove from the sample the poorer groups in each volume-limited
sample.
we remove from the sample the poorer groups in each volume-limited
sample.
We conclude this section with a word of caution. One would be
tempted to compare points as a function of redshift across the
last three different panels, since the ![]() cut-off chosen is
equal for each of them, and after showing in Sect. 8.2 that
galaxy luminosity is of much less importance in determining
cut-off chosen is
equal for each of them, and after showing in Sect. 8.2 that
galaxy luminosity is of much less importance in determining
![]() than group richness. This
comparison would apparently result in a
statement of non-evolution of
than group richness. This
comparison would apparently result in a
statement of non-evolution of
![]() as
a function of
redshift for groups of similar velocity dispersion.
as
a function of
redshift for groups of similar velocity dispersion.
However one needs to be extremely careful when comparing
results obtained at different redshifts. As cosmic time
increases a system will experience an increase in its velocity
dispersion, as its halo mass becomes higher due to structure
growth (see, e.g., the prescriptions obtained by using semi-analytic
models by Wechsler
et al. 2002 and Poggianti
et al. 2006, for an application).
Furthermore, one should keep in mind that the imposed cut-off on the
number of members observed in the flux-limited sample is expected to
introduce a strong bias favoring richer groups moving from
panel (a) to panel (d), as the absolute luminosity of
the observed galaxies becomes brighter. What appears as an absence in
evolution of
![]() as a function of redshift at a
fixed velocity dispersion is thus at
least partly caused by the progressive bias against lower richness
groups moving from panel (a) to panel (d).
as a function of redshift at a
fixed velocity dispersion is thus at
least partly caused by the progressive bias against lower richness
groups moving from panel (a) to panel (d).
Estimates of group richness and group velocity dispersion
often have large error bars, due to the paucity of member-galaxy
samples available, and group richness/group velocity dispersion are
properties that have a large scatter in their relationship to more
fundamental quantities - as the mass of the halo
where the group resides. As a consequence, it is
unsurprising to observe a large scatter in the trends that relate group
richness and group velocity dispersion with
the value of
![]() .
.
To avoid producing biased results on evolution proper care has to be taken to compare properties of group samples that are truly homogeneous in the different redshift bins explored.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{12558F9.ps}\vspace{-1.5mm}\vspace{-2mm}\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg148.png)
|
Figure 9:
Dependence of the blue fraction
|
| Open with DEXTER | |
7 Moving from luminosity to stellar mass: redefining the Butcher-Oemler effect
The results obtained in the previous section can all be interpreted in the framework of the classical Butcher-Oemler effect (Butcher & Oemler 1978), in its wider context extended to group population (see Allington-Smith et al. 1993).
Taking advantage of the wide redshift and galaxy/group
population coverage of the 10K-samplegalaxy/groups catalogue, we have
been able to show that the blueing of the galaxy population in
groups/clusters when moving to higher redshift, originally observed by
these authors thirty years ago, is a real effect, which
differs from that observed for the global galaxy population. It also
exhibits specific trends as a function of both galaxy B-band
rest-frame luminosity and group properties. These trends are present as
a function of environment in all luminosity and redshift bins explored
and seem to become progressively more conspicuous moving from ![]() to lower redshifts and from lower to higher luminosities.
to lower redshifts and from lower to higher luminosities.
However almost galaxy properties depend strongly on galaxy stellar mass, and this is true particularly for galaxy colors. Galaxy stellar mass in turn is known to correlate with environment and can be a key player in determining galaxy properties and in linking them to the environment in which they reside.
It is therefore important to check whether the strong effects evident in luminosity-selected samples are still present when the analysis is repeated using stellar-mass-selected samples. In this way, we probe the possibility of these effects being the distorted/amplified reflection - related to the biased view imposed by the luminosity selection - of more fundamental relationships either between masses and environment, or between masses and galaxy colors.
In the following sections, we re-examine the original
Butcher-Oemler results using mass-limited samples instead of
volume-limited samples. What becomes of the observed strong trends in
![]() as
a function of environment and redshift, shown in, e.g.,
Fig. 7,
when one utilizes samples complete in mass? Are we able to
confirm the existence of a higher proportion of blue galaxies in higher
redshift groups with respect to their lower redshift counterparts, when
using
mass-limited samples? Can we still see an excess of red
galaxies in groups with respect to the field/isolated galaxy population
even when analyzing mass bins?
as
a function of environment and redshift, shown in, e.g.,
Fig. 7,
when one utilizes samples complete in mass? Are we able to
confirm the existence of a higher proportion of blue galaxies in higher
redshift groups with respect to their lower redshift counterparts, when
using
mass-limited samples? Can we still see an excess of red
galaxies in groups with respect to the field/isolated galaxy population
even when analyzing mass bins?
Obviously analyzing volume-limited stellar-mass selected samples involves a significant reduction in the galaxy sample size available to our study, as the selection of mass-complete samples implies the rejection of a large number of low-mass galaxies for which our IAB selected redshift survey is incomplete. However this is an unavoidable step in clarifying the key mechanisms determining the relationships observed for luminosity-selected samples.
Galaxy stellar mass has the further advantage of being more stable
than its luminosity. The B-band galaxy rest-frame
luminosity may indeed change dramatically during a galaxy lifetime
because of bursts of star-formation. Even in the absence of these
bursts, the rest-frame B-band luminosity evolves
with redshift, possibly in different ways for different galaxy
populations, and one needs to introduce - as we
have - an average evolution correction term to sample
homogeneous galaxy populations in the different redshift bins explored.
On the other hand, stellar mass varies to a far lesser extent during a
galaxy's life; it also increases due to star formation and mergers, but
by a smaller percentage, as confirmed both by observational evidence,
showing that up to ![]() the mass function evolves only mildly (see Pozzetti
et al. 2007, and references therein), and by
numerical simulations, (De Lucia
et al. 2006). As a consequence,
the selection of mass-limited samples eases the task of tracing the
same population of galaxies in the different redshift bins
explored. In the subsequent Sections, we will investigate the impact of
the use of mass-selected samples on our analysis.
the mass function evolves only mildly (see Pozzetti
et al. 2007, and references therein), and by
numerical simulations, (De Lucia
et al. 2006). As a consequence,
the selection of mass-limited samples eases the task of tracing the
same population of galaxies in the different redshift bins
explored. In the subsequent Sections, we will investigate the impact of
the use of mass-selected samples on our analysis.
8 Defining stellar-mass, volume-limited samples
To construct volume-limited, stellar-mass selected samples, we followed a simple approach. For each of the four redshift bins adopted in the previous analysis, we estimated the limiting mass at which even the oldest/reddest galaxies (i.e., those with the maximum possible stellar mass-to-light ratio) would be observable given the magnitude limit of our survey.
To estimate this limiting mass, we first proceeded by
calculating the limiting stellar mass of each galaxy, i.e., the stellar
mass it would have, at its spectroscopic redshift, if its
apparent magnitude were equal to the limiting magnitude of our survey (
IAB
= 22.5). We then used these estimated limiting masses to define, in
bins of (U-B) rest-frame
colors for each redshift bin, the mass
![]() below
which 85% of galaxies of that color lie. The value
of
below
which 85% of galaxies of that color lie. The value
of
![]() for
the reddest galaxies in each redshift bin is the one that we use as
limiting mass.
for
the reddest galaxies in each redshift bin is the one that we use as
limiting mass.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12558F10.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg150.png)
|
Figure 10: Rest-frame (U-B) colors plotted versus galaxy stellar mass in solar mass units for the samples defined in Table 1. On top of each panel, we write the redshift bins considered. For each panel, only galaxies contained in the corresponding volume-limited sample have been plotted (sample I to sample IV). The points in red show galaxies located in groups, while those in black correspond to the total population of galaxies. The blue dashed line in each panel indicates the color-dependent 85% completeness mass-limit (see text for more details on how it is computed). The shaded area indicates the mass bins that we used in our analysis, and its lower boundary in mass equals the limiting mass above which all galaxies, irrespective of their color, are observed in our flux-limited survey. |
| Open with DEXTER | |
Table 3:
Summary of the four mass volume-limited data samples; Mass
is in units of
![]() .
.
![\begin{figure}
\par\includegraphics[angle=270,width=12cm,clip,origin=rb]{12558F11.ps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg157.png)
|
Figure 11: Top panels: normalized histograms of galaxy mass for different galaxy populations. Isolated galaxies are in blue, group galaxies are in red and black galaxies are the full sample. Labels on top indicate the redshift bin considered and the cut-off mass adopted. Bottom panels: histogram of normalized differences with respect to the full galaxy sample of the group population (shaded in red) and the isolated galaxy population (shaded in blue). With respect to the whole galaxy population there is a visible and statistically significant excess of low/high mass galaxies in the isolated/group galaxy sample. |
| Open with DEXTER | |
Figure 10 shows the distribution of (U-B) colors versus stellar masses for each of the volume-limited samples defined in Table 1. The points in red show galaxies located in groups, while those in black correspond to the total population of galaxies. The blue, dashed line in each panel indicates the fit to the values of the color-dependent 85% completeness mass-limit, estimated as described above. The lower boundary to the shaded rectangular area in each panel indicates the limiting mass above which all galaxies, even those redder in colors, are observed in our magnitude-limited survey. Figure 10 confirms that adopting mass volume-limited samples rejects a large number of lower-mass, bright, blue galaxies, which were included in B-band luminosity, volume-limited samples.
For each of the mass volume-limited samples Table 3 summarizes its lower mass limit and the number of galaxies contained in both the full galaxy sample and isolated/group galaxy samples.
Comparing the numbers in Table 3 with
those in Table 1,
it is clear that the samples that become more depleted moving
from a luminosity to a mass selection are those of isolated galaxies.
On average, these samples experience a decrease in number by a factor
of ![]() .
The group samples, instead, are at most just halved. The blue low-mass
galaxies that are excluded when moving from luminosity to mass limited
samples are a larger fractions of galaxies residing in low-density
environments. It is natural to conclude that at least part of
the strong trends of
.
The group samples, instead, are at most just halved. The blue low-mass
galaxies that are excluded when moving from luminosity to mass limited
samples are a larger fractions of galaxies residing in low-density
environments. It is natural to conclude that at least part of
the strong trends of ![]() as a function of environment observed in our volume-limited samples are
driven by the large population of lower mass, bright blue galaxies for
which we miss the redder, equally low mass, counterparts (see De Propris et al. 2003,
for a similar suggestion). In other words, the trends that we witness
in Fig. 7
are at least partly due to the bias in B-band
magnitudes volume-limited samples against red, low-mass galaxies, which
are too faint to be included by the adopted luminosity cut-off.
as a function of environment observed in our volume-limited samples are
driven by the large population of lower mass, bright blue galaxies for
which we miss the redder, equally low mass, counterparts (see De Propris et al. 2003,
for a similar suggestion). In other words, the trends that we witness
in Fig. 7
are at least partly due to the bias in B-band
magnitudes volume-limited samples against red, low-mass galaxies, which
are too faint to be included by the adopted luminosity cut-off.
It remains to be seen whether these trends are still observed
when adopting mass volume-limited samples for the analysis, or whether
mass is all that is needed for predicting galaxy colors, irrespective
of environment, a possibility still compatible with our results until
now. Such a possibility is the one expected in simple, pure nature,
galaxy formation models, where the characteristics of a galaxy
(e.g., colors, spin) are primarily determined by the mass of
the dark matter halo in which it resides, which is in turn closely
related to the galaxy stellar mass on one side, and to the density
field on a
![]() scale on the other
side (see, e.g., Cooray
& Sheth 2002). In this framework, the color
segregation just mirrors the change in the distribution of galaxy
stellar masses as a function of environment.
scale on the other
side (see, e.g., Cooray
& Sheth 2002). In this framework, the color
segregation just mirrors the change in the distribution of galaxy
stellar masses as a function of environment.
8.1 Mass
segregation in groups up to z  1
1
The variation in the galaxy stellar mass function between different environments has been observed in the local Universe (see, e.g., Baldry et al. 2006), and, at higher redshifts, in DEEP2 data (Bundy et al. 2006), in VVDS data (Scodeggio et al. 2009), in COSMOS data (Scoville et al. 2007), and in zCOSMOS 10K-sample data (Bolzonella et al. 2009). In this section, we check whether mass segregation is detectable using our group, field, and isolated galaxy samples.
Table 4:
Summary of the four mass volume-limited data samples; Mass
is in units of
![]() .
.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12558F12.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg164.png)
|
Figure 12:
The four panels show |
| Open with DEXTER | |
Figure 11
shows in its top panels the normalized histograms of the mass
distribution for the first three mass volume-limited samples of
Table 3,
plotted in red, blue and black for the group, isolated, and
all galaxy samples, respectively. The bottom panels show, shaded in
red, the difference between the group and all-galaxy normalized
histograms, and shaded in blue the difference between the isolated and
all-galaxy normalized histograms. There is a visible excess of both
low-mass galaxies in the isolated galaxy sample and high-mass galaxies
in the group galaxy sample, and the significance of this trend,
estimated using a K-S test, is always at
least ![]() or more for all mass/redshift ranges considered. For sample M-IV of
Table 3,
there is no significant difference between the mass distributions of
isolated and group galaxies, a result possibly caused by both
the lower number statistic and the narrower mass range considered. We
therefore have not plotted the corresponding histograms.
or more for all mass/redshift ranges considered. For sample M-IV of
Table 3,
there is no significant difference between the mass distributions of
isolated and group galaxies, a result possibly caused by both
the lower number statistic and the narrower mass range considered. We
therefore have not plotted the corresponding histograms.
Given these differences in the mass distribution in different environments, we need to define mass bins that are narrow enough for mass segregation to become negligible before we can disentangle the mass/environment influence in determining galaxy colors. Only in this way shall we be able to check if environment has truly some influence on galaxy colors other than being the by-product of mass segregation. This is the approach we adopt in the following section, using as mass bins those indicated by the gray shaded areas in Fig. 10. A K-S test applied to the mass distribution within these bins confirms that there is no residual significant difference in mass among galaxies located in different environments.
Table 5:
Summary of fits results for mass bins of Table 4
Mass is in units of
![]() .
.
![\begin{figure}
\par\includegraphics[angle=270,width=12cm,clip,origin=rb]{12558F13.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg166.png)
|
Figure 13:
The three panels show, in the redshift bin indicated by the top labels,
|
| Open with DEXTER | |
8.2 Blue fraction as a function of galaxy mass and environment up to z
 1
1
We explore how ![]() changes as a function of environment in bins of mass volume-limited
samples. For our analysis, we use the logarithmic mass bins shown by
the shaded rectangles in
Fig. 10,
whose number of galaxies are listed in Table 4. Because
of the large reduction in our sample when adopting mass volume-limited
samples, we used bins
partially overlapping in mass, a choice dictated by the desire to have
a sufficient number of galaxies in each bin such that our findings
could be deemed statistically significant.
As a consequence, the results shown for the various
mass bins are not completely independent. Needless to say, the
completion of zCOSMOS bright will enable a much more detailed analysis.
changes as a function of environment in bins of mass volume-limited
samples. For our analysis, we use the logarithmic mass bins shown by
the shaded rectangles in
Fig. 10,
whose number of galaxies are listed in Table 4. Because
of the large reduction in our sample when adopting mass volume-limited
samples, we used bins
partially overlapping in mass, a choice dictated by the desire to have
a sufficient number of galaxies in each bin such that our findings
could be deemed statistically significant.
As a consequence, the results shown for the various
mass bins are not completely independent. Needless to say, the
completion of zCOSMOS bright will enable a much more detailed analysis.
Figure 12
shows the fraction of blue galaxies as a function of redshift in the
four samples and in the three galaxy samples listed in Table 4. In each
of the four
panels, the red circles show
![]() for
group galaxies, while the black squares and the blue triangles show
the same quantity for field and isolated galaxies, respectively. The
labels in each panel indicate the mass range under inspection.
for
group galaxies, while the black squares and the blue triangles show
the same quantity for field and isolated galaxies, respectively. The
labels in each panel indicate the mass range under inspection.
The first information that this plot conveys is that color
segregation is still present in the lowest mass bin explored, the one
shown in panel (a), while in the intermediate-mass bins, i.e.,
in panels (b) and (c), is barely detectable and only
at the highest limits of the redshift ranges explored. For the highest
mass bin, in panel (d), there is no hint of a color
segregation up to ![]() and no evolution with redshift is detectable.
and no evolution with redshift is detectable.
We parametrized the evolution in
![]() with
a fit of the form
with
a fit of the form ![]()
![]()
![]() ,
and the results are indicated by the dashed lines in Fig. 12. When
dealing with samples defined by bins in mass, however, at odds with
what we discussed in Sect. 8.2, the
dashed lines obtained from the fit to the data points seem,
if anything, to indicate that the relative differences of
,
and the results are indicated by the dashed lines in Fig. 12. When
dealing with samples defined by bins in mass, however, at odds with
what we discussed in Sect. 8.2, the
dashed lines obtained from the fit to the data points seem,
if anything, to indicate that the relative differences of
![]() between
group, field, and isolated galaxy samples progressively
disappear moving from high to low redshift.
between
group, field, and isolated galaxy samples progressively
disappear moving from high to low redshift.
One can imagine a time when, irrespective of the environment
considered, most galaxies in each of the mass bin ranges explored,
reside on the red sequence, having exhausted their fuel for star
formation, while the blue cloud becomes more or less empty. This seems
to be already the case for the highest mass bin in our plot.
Panel (d) indicates that the majority of red-sequence galaxies
in the mass range
![]() ,
were already in place, irrespective of the environment, at the
highest redshift bin we can explore (
,
were already in place, irrespective of the environment, at the
highest redshift bin we can explore (
![]() ).
).
In contrast, for the lower mass bins explored, our data
display a significant decrease in
![]() between
high and low redshifts. Extrapolating the observed trends
further back in time up
to
between
high and low redshifts. Extrapolating the observed trends
further back in time up
to ![]() ,
one can speculate that there must have been a time when most galaxies
resided in the blue cloud, irrespective of their environment.
Panel (a) of Fig. 12 clearly
suggests that the time when blue galaxies were in the majority has
ended earlier for galaxies in groups than for those in field or
isolated galaxies, and a similar trend is present, albeit at a far
lower significance, also for galaxies in panels (b)
and (c).
,
one can speculate that there must have been a time when most galaxies
resided in the blue cloud, irrespective of their environment.
Panel (a) of Fig. 12 clearly
suggests that the time when blue galaxies were in the majority has
ended earlier for galaxies in groups than for those in field or
isolated galaxies, and a similar trend is present, albeit at a far
lower significance, also for galaxies in panels (b)
and (c).
Unfortunately, as shown by Table 5, the
error bars in the slopes of the fit are quite large and it is difficult
to draw definitive conclusions on the fractional rate of change
in
![]() for the different environments
of each mass bin considered. In each
redshift bin, all the values obtained for
for the different environments
of each mass bin considered. In each
redshift bin, all the values obtained for ![]() are compatible with each other for the three environments considered,
given their large error bars.
are compatible with each other for the three environments considered,
given their large error bars.
In parallel with the analysis completed in Sect. 5 for
the mass volume-limited samples we proceeded to plot in Fig. 12 results for
galaxies residing in groups homogeneous in richness across the
different panels. We again used the sample of groups with two or more
members in the brighter absolute magnitude cut-off sample, and then
repeated our
measurements of
![]() for the group members
satisfying the mass-bins limits. The numbers of
the galaxy group samples defined in this way are those indicated by the
entry Group galaxies II in Table 4.
for the group members
satisfying the mass-bins limits. The numbers of
the galaxy group samples defined in this way are those indicated by the
entry Group galaxies II in Table 4.
With the possible exception of panel (a), moving to
richer groups does not seem to affect significantly the value
of
![]() .
This result is consistent with the previous one: only for galaxies of
lower stellar masses do we still see color segregation as a function of
environment and therefore only for these masses can we expect to see a
significant dependence of
.
This result is consistent with the previous one: only for galaxies of
lower stellar masses do we still see color segregation as a function of
environment and therefore only for these masses can we expect to see a
significant dependence of ![]() on group richness.
on group richness.
An interesting trend suggested by Fig. 12 is that for
more massive galaxies the predominance of the redder-color galaxy
population started earlier in cosmic time than for lower mass galaxies.
We decided to investigate this trend directly by plotting at fixed
redshift
![]() as a function
of mass.
as a function
of mass.
The results are shown in Fig. 13. The label on each of the three panels shows the redshift ranges adopted, while the color code is, as usual, blue, red, and black for isolated, group and field galaxies, respectively.
We adopted the following three redshift bins where to perform
this analysis [0.25:0.45], [0.45:0.60]
and [0.60:0.80]. For these bins, we had already defined
complete mass limited samples as listed in
Table 3.
However, to increase the range of masses probed in each
redshift bin we decided to extend the analysis down to masses where,
according to the procedure described in
Sect. 8,
we had in the redshift bin considered a completeness lower than ![]() for the reddest galaxies of our sample. Obviously such a strategy can
be adopted only if one is sure
that a representative (in color) sample of the lower mass
galaxies under scrutiny is observed in a large fraction of the volume
under consideration, so that it can be statistically reconstructed,
e.g., applying a correction using the
for the reddest galaxies of our sample. Obviously such a strategy can
be adopted only if one is sure
that a representative (in color) sample of the lower mass
galaxies under scrutiny is observed in a large fraction of the volume
under consideration, so that it can be statistically reconstructed,
e.g., applying a correction using the
![]() technique.
We therefore lowered our mass limit to masses such that the
completeness even for the reddest galaxies was always around
technique.
We therefore lowered our mass limit to masses such that the
completeness even for the reddest galaxies was always around ![]() at the lowest limit of the redshift bin considered. We then weighted
each observed galaxy with its corresponding volume correction,
estimated as the ratio of the volume contained within the [
at the lowest limit of the redshift bin considered. We then weighted
each observed galaxy with its corresponding volume correction,
estimated as the ratio of the volume contained within the [
![]() :
:
![]() ] bin and the actual
volume up to which the galaxy can be observed within the survey
] bin and the actual
volume up to which the galaxy can be observed within the survey
![]() selection.
selection.
Filled points in Fig. 13 are those
referring to bins in masses where we are complete, while empty points
refer to the lower masses bins where the
![]() corrections
discussed above have been applied.
corrections
discussed above have been applied.
In the x-axis we plot the median mass
value for each mass bin, while in the y-axis is the
value of ![]() for the same bin. The error-bars along the y-axis
are those obtained with bootstrap analysis, and the ones along the x-axis
indicate the inter-quartiles ranges of the mass distribution within the
mass bin considered. The choice of the mass bins is somewhat arbitrary,
as for the isolated galaxies sample we were forced to split
the sample in fewer bins for
statistical reasons.
for the same bin. The error-bars along the y-axis
are those obtained with bootstrap analysis, and the ones along the x-axis
indicate the inter-quartiles ranges of the mass distribution within the
mass bin considered. The choice of the mass bins is somewhat arbitrary,
as for the isolated galaxies sample we were forced to split
the sample in fewer bins for
statistical reasons.
The trends displayed in the lowest redshift bin well agree
qualitatively with similar trends detected at z ![]() 0
(e.g., Kauffmann
et al. 2004; Baldry et al. 2006),
showing a clear dependence
of
0
(e.g., Kauffmann
et al. 2004; Baldry et al. 2006),
showing a clear dependence
of
![]() both on mass and on
environment. However, there are some new
interesting points, obserbed thanks to the unprecedented wide
redshift/mass ranges covered by our dataset.
both on mass and on
environment. However, there are some new
interesting points, obserbed thanks to the unprecedented wide
redshift/mass ranges covered by our dataset.
On one hand, at all redshift bins more massive galaxies always
display a lower
![]() ,
near to zero values, irrespective of the environment they live
in, while for lower mass galaxies the value of
,
near to zero values, irrespective of the environment they live
in, while for lower mass galaxies the value of
![]() raises towards unity, again
irrespective of the environment they
live in. Therefore, in each redshift range, and more clearly
in the first two ones plotted, where the mass coverage is wider, we
witness the presence of a progressive saturation of
raises towards unity, again
irrespective of the environment they
live in. Therefore, in each redshift range, and more clearly
in the first two ones plotted, where the mass coverage is wider, we
witness the presence of a progressive saturation of
![]() towards
high/low values at the extremes of the mass ranges studied. However,
there is a restricted range of masses for which the color of galaxies
show a visible dependence on environment. This mass range is the one
where both sides of the bimodal distribution of galaxy colors are well
populated and we can detect a considerable environment dependent
variation of
towards
high/low values at the extremes of the mass ranges studied. However,
there is a restricted range of masses for which the color of galaxies
show a visible dependence on environment. This mass range is the one
where both sides of the bimodal distribution of galaxy colors are well
populated and we can detect a considerable environment dependent
variation of
![]() .
This result echoes a similar one obtained by Kauffmann et al. (2004)
in the local Universe.
.
This result echoes a similar one obtained by Kauffmann et al. (2004)
in the local Universe.
On the other hand, moving from lower to higher redshifts we
witness a progressive increase of
![]() for
each mass bin, with the possible exception of the highest masses,
as already observed in the previous section. Such decrease of
for
each mass bin, with the possible exception of the highest masses,
as already observed in the previous section. Such decrease of
![]() as
cosmic time goes by seem to be
accompanied by a progressive opening along the x-axis
of the difference between the different environments, most prominent in
the mass ranges for which
as
cosmic time goes by seem to be
accompanied by a progressive opening along the x-axis
of the difference between the different environments, most prominent in
the mass ranges for which ![]()
![]() 0.5.
0.5.
8.3 Detection of the possible signature of environmental effects
It is interesting to quantify the trend discussed at the end
of the previous section using a simple parameter: the value,
for each mass bin and environment, of the redshift when
![]() =
0.5. We can call this quantity t50-50
to indicate that it corresponds to the time when the galaxies in the
environment and mass bin considered were equally partitioned between
blue and red colors.
Although obtained through a slightly different type of analysis, this
quantity is equivalent to the transitional mass
=
0.5. We can call this quantity t50-50
to indicate that it corresponds to the time when the galaxies in the
environment and mass bin considered were equally partitioned between
blue and red colors.
Although obtained through a slightly different type of analysis, this
quantity is equivalent to the transitional mass
![]() identified by various authors,
both in the low redshift regime by Baldry
et al. (2004)
and Kauffmann et al.
(2004) and at higher redshifts by Bundy
et al. (2006)
and for the 10K-sampleby Bolzonella
et al. (2009).
identified by various authors,
both in the low redshift regime by Baldry
et al. (2004)
and Kauffmann et al.
(2004) and at higher redshifts by Bundy
et al. (2006)
and for the 10K-sampleby Bolzonella
et al. (2009).
Figure 14
shows the value of t50-50,
expressed in units of time on the left-hand scale and redshift on the
right-hand scale, for different galaxy stellar masses. The triangles,
circles, and squares refer to the sample of isolated, group and field
galaxies, respectively. Filled points are estimated from Fig. 12 using the
fits to the points plotted in each mass bin as shown in Table 5. The
values obtained in this way for t50-50
do not need any incompleteness correction, since they are observed
directly in our 10K-sample in a mass range where we are complete, but
they cover only a limited range of mass and environments. Empty points
are obtained using a
![]() correction and
Fig. 13.
These values for t50-50
are therefore more uncertain, since they are based on incompleteness
corrections.
correction and
Fig. 13.
These values for t50-50
are therefore more uncertain, since they are based on incompleteness
corrections.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{12558F14.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg174.png)
|
Figure 14:
The time t50-50, at which
|
| Open with DEXTER | |
For filled points, the error bars along the x-axis link the upper and lower quartiles of the mass distribution in the mass bin considered, while the error bars along the y-axis are obtained by the rms of the value of t50-50 as obtained by bootstrapping the sample of galaxies that enters in the corresponding panels of Fig. 12. For empty points, the error bars along the y-axis indicate the redshift bin where the value of t50-50 was estimated, while the error bars along the x-axis show the upper and lower interval for the masses as obtained from the error bars in Fig. 13.
For the sake of comparison, we have added boxes indicating
masses for which t50-50 ![]() 0.05, as obtained from the relationship between mass, galaxy
colors, and environment in the local Universe determined in Baldry et al. (2006).
These values are only indicative and extracted from their Fig. 11,
panel b, where curves of the fraction of red
galaxies versus stellar mass are shown in
12 different bins of galaxy density. We choose to use as
representative of the global population the two central curves of their
plot, corresponding to
0.05, as obtained from the relationship between mass, galaxy
colors, and environment in the local Universe determined in Baldry et al. (2006).
These values are only indicative and extracted from their Fig. 11,
panel b, where curves of the fraction of red
galaxies versus stellar mass are shown in
12 different bins of galaxy density. We choose to use as
representative of the global population the two central curves of their
plot, corresponding to
![]() ,
while for isolated/group galaxies in the local Universe we used the
curves covering densities
,
while for isolated/group galaxies in the local Universe we used the
curves covering densities
![]() and
and
![]() .
This last choice was made considering that our total span in densities
is not as wide as theirs: the bulk of the galaxy
population in our groups/isolated galaxies is located in regions that
are roughly a factor of 3 above/below median densities (see
Fig. 15, panel a in Kovac
et al. 2009b, and a similar plot for our isolated
galaxy population).
.
This last choice was made considering that our total span in densities
is not as wide as theirs: the bulk of the galaxy
population in our groups/isolated galaxies is located in regions that
are roughly a factor of 3 above/below median densities (see
Fig. 15, panel a in Kovac
et al. 2009b, and a similar plot for our isolated
galaxy population).
The vertical size of the boxes plotted in Fig. 14 corresponds to the redshift range of the sample used in Baldry et al. (2006), while the mass range corresponding to the horizontal box size corresponds to the range of galaxy stellar mass values where the fraction of galaxies in the red sequence equals 0.5 for the three different environments defined by the curves mentioned above. It should be noticed that the masses in Baldry et al. (2006) were estimated using a Kroupa (2001) initial mass function and recurrent bursts of star formation superimposed to continuous models of star formation. As a consequence the Baldry et al. (2006) masses have a systematically offset towards higher values with respect to our masses by a factor that can be as high as 0.15 dex, possibly explaining the slight offset of local points with respect to the trends displayed by our high-z points.
Figure 14 highlights the main result of our paper. The first visible trend is that as cosmic time goes by the typical mass at which the galaxy population is equally partitioned between red and blue galaxies moves progressively to lower values. This is another way of expressing the well-known downsizing pattern observed in galaxy population evolution. In our plot the decrease in galaxy K-band luminosity with decreasing redshift of galaxies dominated by star formation, as originally reported by Cowie et al. (1996), translates into a progressive increase of t50-50 when considering galaxies of lower masses.
But this global behavior displays differences depending on the subset of the galaxy population we are considering. A consistent trend emerges, despite the large error bars: for each mass considered t50-50 is progressively delayed moving from groups to the field and to the isolated galaxy population. In other words the downsizing for the galaxy population is further modulated by the environment: galaxies located in more massive halos (groups) become red earlier in cosmic time, a trend that shows again a downsizing behavior on the larger scales now considered. The trends displayed by our data well match those observed in the local Universe by Baldry et al. (2006).
Last but not least, another interesting trend suggested by Fig. 14 is the convergence, visible at higher masses, of the value of t50-50, irrespective of the environment considered. We are aware that this interpretation is plagued by uncertainties, as for these high masses the redshifts are correspondingly higher and those most affected by various incompleteness/contamination effects. Two possible biases can be at play at higher redshifts: the progressive degradation in the efficiency of the group/isolated galaxies algorithms and the progressive incompleteness towards the red galaxy population. Both biases act in the direction of reducing the differences between the color properties of the galactic populations we are studying. However we expect that these two biases are minimal, as discussed at length in the previous sections.
One should also consider that for galaxies residing in more
extreme density regimes, as those represented by rich cluster
cores and not observed in our sample, there could be a residual
difference even at redshift ![]() from the general galaxy population (see, e.g., Tanaka
et al. 2008). As already suggested in the
introduction, however, the physical mechanisms responsible for these
differences are presumably not the same as those at play in the group
environment. Our results parallel those obtained, although by
a different kind of analysis, by Bolzonella
et al. (2009), and those shown for galaxies
morphologies by Kovac
et al. (2009b).
from the general galaxy population (see, e.g., Tanaka
et al. 2008). As already suggested in the
introduction, however, the physical mechanisms responsible for these
differences are presumably not the same as those at play in the group
environment. Our results parallel those obtained, although by
a different kind of analysis, by Bolzonella
et al. (2009), and those shown for galaxies
morphologies by Kovac
et al. (2009b).
We note that the evidence we presented, i.e., the faster shutdown of star formation in group environment - as the color transition from blue to red galaxy can broadly be interpreted - cannot be interpreted utilizing only ab initio/internal mechanisms, and was obtained thanks to the unprecedented wide redshift, mass and environment ranges covered by our survey.
The different value of t50-50 for galaxies of different stellar masses, irrespective of environment, can be explained by resorting to internally driven mechanisms shutting-down star formation. The presence of an active galactic nucleus (AGN) feedback and shock-heating physics can be enough to explain the anti-hierarchical nature of the relation between stellar mass and stellar age of galaxies, because these mechanisms can be more efficient in more massive galaxies (see Cattaneo et al. 2008; Bundy et al. 2006; Birnboim & Dekel 2003; Bower et al. 2006; Croton et al. 2006).
In a similar way, the detection of an offset in the value of t50-50 between samples of group/isolated galaxies at fixed stellar mass does not necessarily imply that nurture mechanisms are at work. It could be explained by a different time of assembly of galaxies in haloes of different masses, a nature mechanism that results in a more evolved galaxy population in groups and clusters, at fixed stellar mass, in a given redshift bin (see Balogh et al. 2007; Gao et al. 2005).
In contrast, the trend suggested by Fig. 14 indicates that the migration of galaxies from the blue cloud to the red sequence is a process more efficient/faster in groups than in isolated/field galaxies, and is therefore the signature of environmental processes at play in groups in shaping galaxy evolution.
Interestingly, such mechanisms seem to become progressively
more relevant moving to lower galaxy stellar masses, while they seem to
be irrelevant to galaxies of higher stellar masses, at least in the
redshift range we explored (see also Bolzonella
et al. 2009). We can therefore distinguish between
two different channels for the production of red galaxies,
corresponding respectively, to use a common nomenclature, to nature
red galaxies and nurture red galaxies. Our results
suggest that galaxies of masses
![]() solar
in logarithmic scale are already in place by
solar
in logarithmic scale are already in place by ![]() and their origin could be due primarily to so-called nature/internal
mechanisms, as no strong environmental dependency is visible up to
and their origin could be due primarily to so-called nature/internal
mechanisms, as no strong environmental dependency is visible up to ![]() .
In contrast, for masses below this value and at redshifts lower than
.
In contrast, for masses below this value and at redshifts lower than ![]() ,
we witness the emergence in
groups of an additional contribution of red galaxies. This is what we
can call nurture red galaxies: galaxies that
deviate slightly from the trend of the downsizing scenario as displayed
by the global galaxy population. This nurture population is the one
responsible for the earlier value of t50-50
in groups, and its importance grows as cosmic time goes by, causing the
steady growth in the difference of t50-50
moving to lower galaxy masses.
,
we witness the emergence in
groups of an additional contribution of red galaxies. This is what we
can call nurture red galaxies: galaxies that
deviate slightly from the trend of the downsizing scenario as displayed
by the global galaxy population. This nurture population is the one
responsible for the earlier value of t50-50
in groups, and its importance grows as cosmic time goes by, causing the
steady growth in the difference of t50-50
moving to lower galaxy masses.
There are various mechanisms that occur in groups and that are
more efficient for less massive galaxies, including the gradual
cessation of star formation induced by gentle gas stripping and
starvation by a diffuse intragroup medium, or by slow group-scale
harassment (see, e.g., Roediger & Hensler 2005;
Gnedin 2003;
Larson
et al. 1980; Kawata & Mulchaey 2008;
Moore
et al. 1999). These mechanisms could be natural
candidates for explaining the trends we observe. Their increasing
importance after ![]() most probably mirrors the progressive emergence of structures, as
predicted by hierarchical clustering growth scenario, where such
mechanisms can effectively take place.
most probably mirrors the progressive emergence of structures, as
predicted by hierarchical clustering growth scenario, where such
mechanisms can effectively take place.
9 Summary and conclusions
Taking advantage of the large coverage both of redshift and galaxy/group properties in the 10 K galaxy/groups catalogue, we revisited of the blueing of the galaxy population in groups toward higher redshift, originally observed by Butcher & Oemler (1978), gaining some interesting new insights, that can be summarized as follows.
- 1.
- We have showed that using rest-frame B-band
volume-limited samples, the group galaxy population becomes bluer as
redshift increases, but maintains a systematic difference with
respect to the global galaxy population, and an even larger difference
with respect to the isolated
galaxy population. Superimposed on this global effect, we detected
additional trends as a function of both galaxy B-band
rest-frame luminosity and group properties. More luminous galaxies
exhibit
stronger variations in
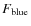 among group, field, and isolated environments and groups richer or with
higher
among group, field, and isolated environments and groups richer or with
higher 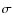 show a lower
show a lower
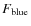 .
.
- 2.
- The difference between the three different environments
increases between high and low redshift. At the highest
redshift bin explored (
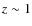 ),
there is a small but still significant
difference in
),
there is a small but still significant
difference in
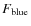 among group,field, and
isolated samples. This gradual increase in the
among group,field, and
isolated samples. This gradual increase in the
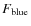 difference
with cosmic time is a clear signature of an environmental
dependence, but not necessarily of the existence of environmental
effects at work. It could be the result of an
ab initio bias that favors later formation of lower-mass
galaxies in lower density environments, causing the delayed and more
efficient replenishing of the blue cloud in lower density environments.
difference
with cosmic time is a clear signature of an environmental
dependence, but not necessarily of the existence of environmental
effects at work. It could be the result of an
ab initio bias that favors later formation of lower-mass
galaxies in lower density environments, causing the delayed and more
efficient replenishing of the blue cloud in lower density environments.
- 3.
- Moving to mass-selected samples, a necessary step in clarifying the key mechanisms in determining the relationship observed using luminosity-selected samples, allows us to realize almost immediately that at least part of the strong trends observed when using rest-frame evolving B-band volume-limited samples are caused by the large population of lower mass, bright blue galaxies for which we miss the redder, equally low mass, counterparts. In other words, the biased view imposed by the B-band luminosity selection amplifies the findings obtained using B-band volume-limited samples.
- 4.
- Another effect has to be taken into consideration if one wants to disentangle the mass and environment influence on galaxy colors. The existence of different mass functions in different environments (see Bolzonella et al. 2009) forces us to work in mass bins narrow enough so that any color segregation cannot be attributed simply to the different mass distribution.
- 5.
- The first outcome of this careful analysis is that there is
still a significant residual difference in color as a function of
environment only for the lowest mass bin explored (
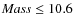 ,
solar masses in logarithmic scale), while this difference progressively
disappears moving to higher masses.
,
solar masses in logarithmic scale), while this difference progressively
disappears moving to higher masses.
- 6.
- By using a
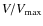 correction, we can extend our analysis to lower masses, witnessing, in
all the redshift range we explore, the presence of progressive
saturation of
correction, we can extend our analysis to lower masses, witnessing, in
all the redshift range we explore, the presence of progressive
saturation of 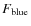 towards high/low values at the extremes of the mass ranges studied.
At each redshift, there is a restricted range of
masses for which the color of galaxies show a visible dependence on
environment, and as cosmic time increases the typical mass at
which the galaxy population is equally partitioned
between red and blue galaxies moves progressively to lower values. This
pattern, consistent with the well known downsizing pattern observed in
galaxy population evolution, is further modulated by
environment: galaxies located in more massive halos (groups) become red
earlier in cosmic time.
towards high/low values at the extremes of the mass ranges studied.
At each redshift, there is a restricted range of
masses for which the color of galaxies show a visible dependence on
environment, and as cosmic time increases the typical mass at
which the galaxy population is equally partitioned
between red and blue galaxies moves progressively to lower values. This
pattern, consistent with the well known downsizing pattern observed in
galaxy population evolution, is further modulated by
environment: galaxies located in more massive halos (groups) become red
earlier in cosmic time.
- 7.
- Finally our most interesting finding is that there is evidence that the color transition from blue to red galaxies seems to be faster in groups as cosmic time increases. In other words, we seem to witness the slow emergence of an environmental/nurture effect on galaxy evolution, which causes the faster migration of galaxies from the blue cloud to the red sequence in groups (with respect to isolated/field galaxies) and effect that becomes more relevant moving from higher to lower galaxy stellar masses (see also Kovac et al. 2009b, for a parallel analysis using galaxy morphologies).
- 8.
- Our results suggest that galaxies of
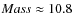 solar
masses in logarithmic scale are already in place by
solar
masses in logarithmic scale are already in place by 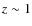 and their origin could be due primarily to so-called nature/internal
mechanisms, since no strong environmental dependency is detectable up
to
and their origin could be due primarily to so-called nature/internal
mechanisms, since no strong environmental dependency is detectable up
to 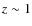 .
.
- 9.
- In contrast, for masses below this value and at redshifts
lower than
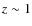 we witness the emergence of what we call nurture
red galaxies: galaxies that slightly deviate from the trend of the
downsizing scenario displayed by the global galaxy population and do
more so as cosmic time progresses.
we witness the emergence of what we call nurture
red galaxies: galaxies that slightly deviate from the trend of the
downsizing scenario displayed by the global galaxy population and do
more so as cosmic time progresses.
The completion of zCOSMOS bright, and subsequent availability
of 20K-sample, will enable us to place on a more robust basis this
result, which indicates that environment starts playing an active role
in shaping galaxy evolution after ![]() .
.
We acknowledge support from an INAF contract PRIN-2007/1.06.10.08 and an ASI grant ASI/COFIS/WP3110 I/026/07/0.
References
- Abell, G. O. 1958, ApJS, 3, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Allington-Smith, J. R., Ellis, R., Zirbel, E. L., & Oemler, A. J. 1993, ApJ, 404, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S., & Ettori, S. 1999, ApJ, 516, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S., Lobo, C., & Iovino, A. 2004, MNRAS, 349, 889 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S., Quintana, H., Tajer, M., Galaz, G., & Surdej, J. 2006, MNRAS, 365, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Baldry, I. K., Glazebrook, K., Brinkmann, J., et al. 2004, ApJ, 600, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Baldry, I. K., Balogh, M. L., Bower, R. G., et al. 2006, MNRAS, 373, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Balogh, M., Eke, V., Miller, C., et al. 2004a, MNRAS, 348, 1355 [Google Scholar]
- Balogh, M. L., Baldry, I. K., Nichol, R., et al. 2004b, ApJ, 615, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Balogh, M. L., Wilman, D., Henderson, R. D. E., et al. 2007, MNRAS, 374, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T., Flynn, K., & Gebhardt, K. 1990, ApJ, 100, 32 [Google Scholar]
- Berlind, A. A., Frieman, J., Weinberg, D. H., et al. 2006, ApJS, 167, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Birnboim, Y., & Dekel, A. 2003, MNRAS, 345, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Biviano, A., Katgert, P., Mazure, A., et al. 1997, A&A, 321, 84 [Google Scholar]
- Blanton, M. R., & Berlind, A. A. 2007, ApJ, 664, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., Eisenstein, D., Hogg, D. W., & Zehavi, I. 2006, ApJ, 645, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Bolzonella, M., Kovac, K., Pozzetti, L., et al. 2009, A&A, submitted [arXiv:0907.0013] [Google Scholar]
- Bottini, D., Garilli, B., Maccagni, D., et al. 2005, PASP, 117, 996 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Brüggen, M., & De Lucia, G. 2008, MNRAS, 383, 1336 [NASA ADS] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Ellis, R. S., Conselice, C. J., et al. 2006, ApJ, 651, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Butcher, H., & Oemler, Jr., A. 1978, ApJ, 219, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Butcher, H., & Oemler, Jr., A. 1984, ApJ, 285, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, A., Dekel, A., Faber, S. M., & Guiderdoni, B. 2008, MNRAS, 389, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, ApJ, 586, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Coleman, G. D., Wu, C.-C., & Weedman, D. W. 1980, ApJS, 43, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, M. C., Newman, J. A., Croton, D. J., et al. 2006, MNRAS, 370, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, M. C., Newman, J. A., Coil, A. L., et al. 2007, MNRAS, 376, 1445 [NASA ADS] [CrossRef] [Google Scholar]
- Cooray, A., & Sheth, R. 2002, Phys. Rep., 372, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., Songaila, A., Hu, E. M., & Cohen, J. G. 1996, AJ, 112, 839 [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Cucciati, O., Iovino, A., Marinoni, C., et al. 2006, A&A, 458, 39 [Google Scholar]
- Cucciati, O., Iovino, A., Kovac, K., et al. 2009a, A&A, submitted [Google Scholar]
- Cucciati, O., Marinoni, M., Iovino, A., et al. 2009b, A&A, submitted [Google Scholar]
- De Lucia, G., Springel, V., White, S. D. M., Croton, D., & Kauffmann, G. 2006, MNRAS, 366, 499 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Poggianti, B. M., Aragón-Salamanca, A., et al. 2007, MNRAS, 374, 809 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Stanford, S. A., Eisenhardt, P. R., & Dickinson, M. 2003, ApJ, 598, 20 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Colless, M., Peacock, J. A., et al. 2004, MNRAS, 351, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., & Gunn, J. E. 1982, ApJ, 263, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., & Gunn, J. E. 1992, ApJS, 78, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Eke, V. R., Baugh, C. M., Cole, S., et al. 2004, MNRAS, 348, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Ellingson, E., Lin, H., Yee, H. K. C., & Carlberg, R. G. 2001, ApJ, 547, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Fabricant, D. G., McClintock, J. E., & Bautz, M. W. 1991, ApJ, 381, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Fairley, B. W., Jones, L. R., Wake, D. A., et al. 2002, MNRAS, 330, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Feldmann, R., Carollo, C. M., Porciani, C., et al. 2006, MNRAS, 372, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Finoguenov, A., Guzzo, L., Hasinger, G., et al. 2007, ApJS, 172, 182 [Google Scholar]
- Gao, L., Springel, V., & White, S. D. M. 2005, MNRAS, 363, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, G., Pierini, D., & Boselli, A. 1996, A&A, 312, 397 [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Gerke, B. F., Newman, J. A., Davis, M., et al. 2005, ApJ, 625, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Gerke, B. F., Newman, J. A., Faber, S. M., et al. 2007, MNRAS, 376, 1425 [NASA ADS] [CrossRef] [Google Scholar]
- Gnedin, O. Y. 2003, ApJ, 589, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, T. 2005, MNRAS, 356, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, T., Okamura, S., Yagi, M., et al. 2003, PASJ, 55, 739 [NASA ADS] [Google Scholar]
- Hopkins, A. M. 2004, ApJ, 615, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Huchra, J. P., & Geller, M. J. 1982, ApJ, 257, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., White, S. D. M., Heckman, T. M., et al. 2004, MNRAS, 353, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Kawata, D., & Mulchaey, J. S. 2008, ApJ, 672, L103 [Google Scholar]
- Kenney, J. D. P., van Gorkom, J. H., & Vollmer, B. 2004, AJ, 127, 3361 [NASA ADS] [CrossRef] [Google Scholar]
- Kinney, A. L., Calzetti, D., Bohlin, R. C., et al. 1996, ApJ, 467, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Kitzbichler, M. G., & White, S. D. M. 2007, MNRAS, 376, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Knobel, C., Lilly, S. J., Iovino, A., et al. 2009, ApJ, 697, 1842 [NASA ADS] [CrossRef] [Google Scholar]
- Kodama, T., & Bower, R. G. 2001, MNRAS, 321, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Aussel, H., Calzetti, D., et al. 2007, ApJS, 172, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Kovac, K., Lilly, S. J., Cucciati, O., et al. 2009a, ApJ, submitted [arXiv:0903.3409] [Google Scholar]
- Kovac, K., Lilly, S. J., Knobel, C., et al. 2009b, ApJ, submitted [arXiv:0909.2032] [Google Scholar]
- Koyama, Y., Kodama, T., Tanaka, M., Shimasaku, K., & Okamura, S. 2007, MNRAS, 382, 1719 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B., Tinsley, B. M., & Caldwell, C. N. 1980, ApJ, 237, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Lavery, R. J., & Henry, J. P. 1986, ApJ, 304, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Lavery, R. J., & Henry, J. P. 1988, ApJ, 330, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fevre, O., Crampton, D., Lilly, S. J., Hammer, F., & Tresse, L. 1995, ApJ, 455, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Vettolani, G., Garilli, B., et al. 2005, A&A, 439, 845 [Google Scholar]
- Lilly, S. J., Le Fevre, O., Hammer, F., & Crampton, D. 1996, ApJ, 460, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., LeBrun, V., Maier, C., et al. 2009, ApJS, 184, 218 [Google Scholar]
- Madau, P., Pozzetti, L., & Dickinson, M. 1998, ApJ, 498, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Margoniner, V. E., & de Carvalho, R. R. 2000, AJ, 119, 1562 [NASA ADS] [CrossRef] [Google Scholar]
- Margoniner, V. E., de Carvalho, R. R., Gal, R. R., & Djorgovski, S. G. 2001, ApJ, 548, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Marinoni, C., Davis, M., Newman, J. A., & Coil, A. L. 2002, ApJ, 580, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez, H. J., Zandivarez, A., Domínguez, M., Merchán, M. E., & Lambas, D. G. 2002, MNRAS, 333, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Mignoli, M., Zamorani, G., Scodeggio, M., et al. 2009, A&A, 493, 39 [Google Scholar]
- Moore, B., Lake, G., Quinn, T., & Stadel, J. 1999, MNRAS, 304, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., Smail, I., Dressler, A., et al. 1999, ApJ, 518, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., von der Linden, A., De Lucia, G., et al. 2006, ApJ, 642, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Popesso, P., Biviano, A., Romaniello, M., & Böhringer, H. 2007, A&A, 461, 411 [Google Scholar]
- Pozzetti, L., Bolzonella, M., Lamareille, F., et al. 2007, A&A, 474, 443 [Google Scholar]
- Pozzetti, L., Bolzonella, M., Zucca, E., et al. 2009, A&A, submitted [arXiv:0907.5416] [Google Scholar]
- Rakos, K. D., & Schombert, J. M. 1995, ApJ, 439, 47 [Google Scholar]
- Roediger, E., & Hensler, G. 2005, A&A, 433, 875 [Google Scholar]
- Schiminovich, D., Ilbert, O., Arnouts, S., et al. 2005, ApJ, 619, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Silverman, J. D., Kovac, K., Knobel, C., et al. 2009, ApJ, 695, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Smail, I., Edge, A. C., Ellis, R. S., & Blandford, R. D. 1998, MNRAS, 293, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Strateva, I., Ivezic, Z., Knapp, G. R., et al. 2001, AJ, 122, 1861 [Google Scholar]
- Tanaka, M., Goto, T., Okamura, S., Shimasaku, K., & Brinkmann, J. 2004, AJ, 128, 2677 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, M., Finoguenov, A., Kodama, T., et al. 2008, A&A, 489, 571 [Google Scholar]
- Tasca, L. A. M., Kneib, J.-P., Iovino, A., et al. 2009, A&A, 503, 379 [Google Scholar]
- van Dokkum, P. G., Franx, M., Fabricant, D., Illingworth, G. D., & Kelson, D. D. 2000, ApJ, 541, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Vergani, D., Zamorani, G., Lilly, S. J., et al. 2010, A&A, 509, A42 [Google Scholar]
- Vollmer, B., Beck, R., Kenney, J. D. P., & van Gorkom, J. H. 2004, AJ, 127, 3375 [NASA ADS] [CrossRef] [Google Scholar]
- Voronoi, G. 1908, J. Reine Angew. Math., 134, 198 [CrossRef] [Google Scholar]
- Wechsler, R. H., Bullock, J. S., Primack, J. R., Kravtsov, A. V., & Dekel, A. 2002, ApJ, 568, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Weinmann, P. G., PP, M., GG, D., Illingworth, G. D., & Kelson, D. D. 2000, ApJ, 541, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Wilman, D. J., Balogh, M. L., Bower, R. G., et al. 2005a, MNRAS, 358, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Wilman, D. J., Balogh, M. L., Bower, R. G., et al. 2005b, MNRAS, 358, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Zabludoff, A. I., & Mulchaey, J. S. 1998, ApJ, 496, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Zucca, E., Bardelli, S., Bolzonella, M., et al. 2009, A&A, 508, 1217 [Google Scholar]
Footnotes
- ... trends
![[*]](/icons/foot_motif.png)
- based on data obtained with the European Southern Observatory Very Large Telescope, Paranal, Chile, program 175.A-0839, PI: S. Lilly.
All Tables
Table 1:
Summary of the four volume-limited data samples;
![]() .
.
Table 2:
Summary of fits results for
![]() as
a function of redshift in the volume-limited samples defined in
Table 1;
as
a function of redshift in the volume-limited samples defined in
Table 1;
![]() .
.
Table 3:
Summary of the four mass volume-limited data samples; Mass
is in units of
![]() .
.
Table 4:
Summary of the four mass volume-limited data samples; Mass
is in units of
![]() .
.
Table 5:
Summary of fits results for mass bins of Table 4
Mass is in units of
![]() .
.
All Figures
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12558F1.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg52.png)
|
Figure 1:
The left panel shows the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12558F2.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg64.png)
|
Figure 2:
Panel a) shows the distribution along the
line of sight of
the 6204 galaxies used in our analysis, the subset of the
10K-samplegalaxies sample located within the central, high sampling
rate, region of the survey and in the redshift range
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12558F3.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg76.png)
|
Figure 3: Top panel: distribution of logarithm of normalized Voronoi volumes as a function of redshift. The stripes extending towards lower Voronoi volumes values are due to the presence of groups. Points marked with a cyan cross correspond to galaxies removed from the isolated galaxy sample because their Voronoi volume exceeded by a factor of 100 that of the median at the corresponding redshift. Bottom panel: histogram of the total distribution of normalized Voronoi volumes. The shaded blue area corresponds to the last quartile of the distribution, chosen to select our isolated galaxies sample, while the long tail in cyan extending to higher values - and indicated also by the vertical line - is the one clipped from the sample. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12558F4.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg103.png)
|
Figure 4:
Rest-frame (U-B) colors plotted
vs. B-band rest-frame magnitudes. In each
panel redshift bins of width
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12558F5.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg121.png)
|
Figure 5:
Redshift distribution of the 10K-samplezCOSMOS galaxies. Red points
represent galaxies located in groups. The lines drawn correspond to the
four different volume-limited samples discussed in the text. We assumed
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=12cm,clip,origin=rb]{12558F6.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg122.png)
|
Figure 6:
The four panels show |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12558F7.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg129.png)
|
Figure 7:
The four panels show |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12558F8.ps}\vspace*{-1.5mm}
\vspace*{-1.5mm}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg140.png)
|
Figure 8:
Dependence of the blue fraction
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{12558F9.ps}\vspace{-1.5mm}\vspace{-2mm}\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg148.png)
|
Figure 9:
Dependence of the blue fraction
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12558F10.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg150.png)
|
Figure 10: Rest-frame (U-B) colors plotted versus galaxy stellar mass in solar mass units for the samples defined in Table 1. On top of each panel, we write the redshift bins considered. For each panel, only galaxies contained in the corresponding volume-limited sample have been plotted (sample I to sample IV). The points in red show galaxies located in groups, while those in black correspond to the total population of galaxies. The blue dashed line in each panel indicates the color-dependent 85% completeness mass-limit (see text for more details on how it is computed). The shaded area indicates the mass bins that we used in our analysis, and its lower boundary in mass equals the limiting mass above which all galaxies, irrespective of their color, are observed in our flux-limited survey. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=12cm,clip,origin=rb]{12558F11.ps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg157.png)
|
Figure 11: Top panels: normalized histograms of galaxy mass for different galaxy populations. Isolated galaxies are in blue, group galaxies are in red and black galaxies are the full sample. Labels on top indicate the redshift bin considered and the cut-off mass adopted. Bottom panels: histogram of normalized differences with respect to the full galaxy sample of the group population (shaded in red) and the isolated galaxy population (shaded in blue). With respect to the whole galaxy population there is a visible and statistically significant excess of low/high mass galaxies in the isolated/group galaxy sample. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12558F12.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg164.png)
|
Figure 12:
The four panels show |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=12cm,clip,origin=rb]{12558F13.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg166.png)
|
Figure 13:
The three panels show, in the redshift bin indicated by the top labels,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{12558F14.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12558-09/Timg174.png)
|
Figure 14:
The time t50-50, at which
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


