EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 509 (January 2010) A&A, 509 (2010) A101 Full HTML
Free Access
Issue
A&A
Volume 509, January 2010
Article Number A101
Number of page(s) 9
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/200912434
Published online 26 January 2010
A&A 509, A101 (2010)

The outer atmospheric layers of the early M dwarf Gliese 1

E. Lexen1 - R. Wehrse1,2 - J. Liebert3 - M. S. Bessell4

1 - Institut für Theoretische Astrophysik, Zentrum für Astronomie der Universität Heidelberg, Albert-Ueberle-Str. 2, 69120 Heidelberg, Germany
2 - Interdisziplinäres Zentrum für Wissenschaftliches Rechnen (IWR), Im Neuenheimer Feld 368, 69120 Heidelberg, Germany
3 - Steward Observatory, Univ. of Arizona, Tucson, AZ 85721, USA
4 - RSAA, College of Science, The Australian National University, Cotter Road , Weston Creek ACT 2611, Australia

Received 6 May 2009 / Accepted 5 October 2009

Abstract
Using infrared and high-resolution optical observations of the M dwarf Gliese 1, we investigated the temperatures in the upper atmospheric layers of this star with low atmospheric activity. To fit the H${\alpha }$ and metal line profiles, the normal radiative equilibrium temperature decrease must be truncated at about log $~\tau_{1.2\mu}\approx-1.9$ above which a steep chromospheric ( $T\approx4900$ K) rise must be imposed. Unfortunately, the position of the onset of the chromosphere depends to some extent on the temperature distribution in the inner parts of the photosphere. The chromosphere is just not sufficiently optically thick to be seen in the infrared up to $\approx$30 ${\mu }$m. The persistent strength of the TiO bands leads us to check for indications of surface inhomogeneities with negative results.

Key words: stars: atmospheres - stars: chromospheres - stars: late-type - stars: low-mass - stars: fundamental parameters

1 Introduction

M dwarfs are the most numerous stars (70%) in the Milky Way. Even though they contribute about 40% to the total mass of the stellar contents, their atmospheres are still poorly understood due to the myriads of atomic and molecular lines, efficient convection that reaches very shallow layers, and strong chromospheres and coronae. Although model atmospheres have been used with increasing success to model the spectra of M dwarfs in recent years (Gustafsson et al. 2003; Brett & Plez 1993; Hauschildt et al. 1999; Allard 1990; Gustafsson et al. 2008; Mould 1976,1975), uncertainties, particularly in the opacity data and in the modeling of nonradiative fluxes have up to now inhibited an accurate theoretical determination of the temperature distribution in the outer layers. Generally, the model atmosphere/synthetic spectra fits have emphasized the overall energy distributions and the molecular bands, with little attention paid to the profiles of atomic lines that are very sensitive to the outer layers. It is clear that a temperature inversion takes place at the top of the normal atmosphere in M dwarfs that show evidence of chromospheric activity, that is, emission lines of H${\alpha }$ and/or Ca II. However, many M dwarfs, especially those with kinematics that suggest they are very old, show little or no evidence of overt chromospheric activity.

Golimowski et al. (2004) present M band photometry for many dwarfs; however, only a few of the brightest M dwarfs have been observed spectroscopically in the M and N bands. In this paper, we report (in Sect. 2) observations of the M dwarf Gliese 1 (Gl 1) with the ISOPHOT spectrophotometer (Lemke et al. 1996) of the Infrared Space Observatory (ISO) in the wavelength range 2.5-12.5 ${\mu }$m and the InfraRed Spectrograph (IRS) on the Spitzer Space Telescope (Houck et al. 2004) in the wavelength range 5.3-38 ${\mu }$m. These ISO and Spitzer observations are discussed in Sect. 3. In Sect. 2, medium and high-dispersion optical spectrophotometry of Gl 1 are also reported, while in Sect. 4 we attempt empirical determinations of the vertical temperature distribution of Gl 1 and show that the observed spectra do show evidence of chromospheric reversals. The summary discussion is given in Sect. 5.

2 Observations

2.1 Parameters of the observed star

The star targeted for ISO and Spitzer observations provides ideal tests of the hypothesis that even inactive M dwarfs may retain chromospheric temperature reversals. Table 1 includes some relevant parameters and data for the target. It is noteworthy that Gl 1 is a dM star known to lack H${\alpha }$ emission, one sign of an active chromosphere. It shows old disk or halo kinematics. Eggen (1979) classified Gl 1 as old disk whereas Leggett (1992) and Leggett & Hawkins (1988) classified Gl 1 as a halo star noting that it is subluminous in an MI I-K color magnitude diagram, the signature of a metal-poor, Pop II M subdwarf. Gl 1 has an age of many Gyr, whether it is from the old disk or halo population. It has a slight metal deficiency in accordance with its space motion and it is probably massive enough to possess a small radiative core. Thus, it should be an example of a star in which a normal magnetic dynamo has had time to spin down the star. To our knowledge, direct measurements of the rotation ( $v_{\sin_i}$) are not available, since the star is generally too far south for the survey of Gliese stars by Stauffer & Hartmann (1986). In the literature, the spectral type of Gl 1 ranges from M1.5V (Hawley et al. 1996; Cincunegui & Mauas 2004) to M4V (Gliese 1969; Evans 1961). The spectral type would be close to M2V from R-I and V-I whereas B-V is slightly bluer than an M2V star and implies M1V (Bessell 1991; Reid & Hawley 2000). It is more physically realistic to use the red R-I or V-I color rather than the blue B-V color (Bessell 1990). Using the TiO5 bandstrengths as suggested in Hawley et al. (1996) indicates it is close to M1.5V.

2.2 ISOPHOT and IRS

Table 1:   Relevant parameters of Gl 1.

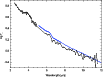
\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f01.eps}} \end{figure} Figure 1:

ISOPHOT S (solid line) and IRS (dotted line) flux distributions for Gl 1.

Open with DEXTER
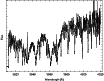
\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f02.eps}} \end{figure} Figure 2:

The spectrum of Gl 1 in the range of 3910-4020 Å around the Ca II H and K lines with a resolution of 100 mÅ. Note the strong but very narrow emission in the cores of Ca II K (3933.7 Å) and Ca II H (3968.5 Å).

Open with DEXTER
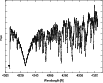
\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f03.eps}} \end{figure} Figure 3:

The spectrum of Gl 1 in the range of 4206-4324 Å around the Ca I line with a resolution of 100 mÅ.

Open with DEXTER
Observational data in the infrared were obtained from the Infrared Space Observatory (ISO) ISOPHOT (spectrophotometer) and the Infrared Spectrograph (IRS) on board the Spitzer Space Telescope in the wavelength range 5.3-38 ${\mu }$m in December 2003. Details of the Spitzer science archive, pipeline upgrades and analysis tools are given in the IRS data handbook. The ISOPHOT (PHT40) spectrophotometry presented in this paper were obtained simultaneously in the two bands 2.5-5 ${\mu }$m and 6-12 ${\mu }$m on December 1996. The data were reduced using the ISOPHOT interactive analysis (PIA) package (Gabriel et al. 1997), a joint development by the ESA Astrophysics Division and the ISOPHOT Consortium. The data reduction procedure is fully described in the ISO Handbook (Laureijs et al. 2003). Figure 1 shows the good agreement between the observed ISOPHOT S and IRS fluxes in the overlapping wavelength region.

2.3 Mt. Stromlo and Siding Spring spectrophotometry

In order to investigate further the properties of this ISO and Spitzer target - in particular, to determine from line profiles whether they show any evidence of chromospheric activity or non-LTE effects - spectra were obtained in June 2007 with the Boller & Chivens grating cross dispersed echelle spectrograph on the Nasmyth B focus on the 2.3 m reflector at Siding Spring Observatories. A 79 g/mm echelle grating with dispersion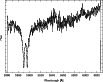 $\lambda/1000$ Å/mm and a 2kx2k Site CCD was used. The spectra have been divided by a smooth spectrum star to remove the telluric lines and the shape of the orders. The four wavelength regions contain the lines Ca II H and K (Fig. 2), Ca I (Fig. 3), Na I D1 and D2 (Fig. 4) and H${\alpha }$ (Fig. 5). In addition, high resolution spectra were obtained with the coude echelle spectrograph on the 1.9 m reflector at Mount Stromlo Observatory prior to its loss in the 2003 fires. A 31.6 g/mm echelle grating with the 81 cm camera and 2kx4k Site CCD was used providing a resolution of 30 mÅ. Different cross-disperser settings were required for blue and red wavelengths. These spectra have similarly been divided through by a smooth spectrum star to remove the telluric lines and to roughly flatten the spectrum. The spectra in each order was then flattened by hand so that the continuum was normalized to 1.0.

\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f04.eps}} \end{figure} Figure 4:

The spectrum of Gl 1 in the range of 5860-6027 Å around the Na I D2 and D1 lines with a resolution of 200 mÅ.

Open with DEXTER
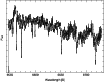
\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f05.eps}} \end{figure} Figure 5:

The spectrum of Gl 1 in the range of 6546-6730 Å around the H${\alpha }$ line with a resolution of 200 mÅ.

Open with DEXTER
\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f06.eps}} \end{figure} Figure 6:

The spectra of the stars Gl 1 (M1.5), Arcturus (K1.5) and the Sun (G2) from top to bottom in the range of 3910-4020 Å around the Ca II H and K lines.

Open with DEXTER
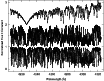
\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f07.eps}} \end{figure} Figure 7:

The spectra of the stars Gl 1 (M1.5), Arcturus (K1.5) and the Sun (G2) from top to bottom in the range of 4206-4324 Å around the Ca I line.

Open with DEXTER
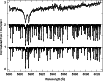
\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f08.eps}} \end{figure} Figure 8:

The spectra of the stars Gl 1 (M1.5), Arcturus (K1.5) and the Sun (G2) from top to bottom in the range of 5860-6027 Å around the Na I D lines.

Open with DEXTER
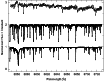
\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f09.eps}} \vspace{-3mm}\end{figure} Figure 9:

The spectra of the stars Gl 1 (M1.5), Arcturus (K1.5) and the Sun (G2) from top to bottom in the range of 6546-6730 Å around the H${\alpha }$ line.

Open with DEXTER
\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f10.eps}} \end{figure} Figure 10:

Flux distributions for Gl 1 as shown in Fig. 1 in the range 3.5-35 ${\mu }$m - and of synthetic spectra of models with (top gray line) and without (lower gray line) an additional cool chromosphere. A black body distribution of the same effective temperature is indicated by the solid line (center).

Open with DEXTER
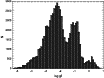
\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f11.eps}} \end{figure} Figure 11:

Distribution of the numbers of titanium oxide lines (Plez 1998) used in the modeling of the spectrum in the wavelength range 6550-6580 Å as a function of the gf-values of the lines. It is seen that there are essentially three peaks but the distributions are essentially continuous.

Open with DEXTER
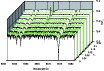
\begin{figure} \resizebox{9cm}{!}{\includegraphics{12434f12.eps}} \end{figure} Figure 12:

Model series with gray temperature stratification for $T_{\rm eff}=3600$ K and log g=5 and chromospheric temperature rises for $\delta =0.01$, $\tau _{0}=0.1$ and $\Delta t_{\rm c} = 0.02$ $t_{\rm c} \in \lbrack 0.0{-}0.24 \rbrack $ in ascending order. For the definitions of parameters see text. The chemical composition in the models is assumed to be solar except for Ca and Fe reduced by 1 dex and Ti reduced by 0.3 dex.

Open with DEXTER

\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f13.eps}} \end{figure} Figure 13:

Temperature as a function of the optical depth at $1.2\mu $ with one data point per 0.1 in log $~\tau_{1.2\mu}$. Stratifications for the fluxes plotted in Fig. 12 with $\delta =0.01$ and $\tau _{0}=0.1$ (dotted lines) and $\tau _{0}=0.09$ (dashed lines). The temperature rise starts at log $~\tau_{1.2\mu}=-0.9$ and $T \approx 3160$ K. Temperature stratifications with $t_{\rm c}=0.18$, $\tau _{0}=0.1$ and $t_{\rm c}=0.175$, $\tau _{0}=0.09$ (full lines) for the best model of this series are plotted in Figs. 14 and 15. For the meaning of the parameters modeling the chromospheric temperature rise see text.

Open with DEXTER
\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f14.eps}} \end{figure} Figure 14:

Comparison of high resolution observations of Gl 1 (full line) and synthetic spectra calculated with an additional cool chromosphere with parameters $t_{\rm c}=0.175$, $\tau _{0}=0.09$ as shown in Fig. 13 (dashed line).

Open with DEXTER
\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f15.eps}} \end{figure} Figure 15:

Same as Fig. 14 but for parameters $t_{\rm c}=0.18$ and $\tau _{0}=0.1$.

Open with DEXTER

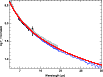
3 Infrared flux distribution

In Fig. 10 is shown the observed ISOPHOT S (solid line) and IRS fluxes (dotted line) (shifted by an additional constant) compared with the distribution of a black body of $T_{\rm eff}=3600$ K and two calculated models with and without an additional cool chromosphere. The temperature stratification for the model with an additional component is shown in Fig. 18 (full line).

4 Interpretation of the line profiles

The obtained optical spectra of the M 1.5V dwarf Gl 1 (Figs. 2-5) was compared with the spectra of the red giant Arcturus (${\alpha }$ Boo) (K1.5 III) and the Sun (G2V) (Figs. 6-9). The resolution of the spectra of Gl 1 are inferior to the others. The spectra of Arcturus (Hinkle et al. 2000) and the Sun (Kurucz 2005) are freely available on the web. For our purpose the spectrum of Arcturus has been corrected for negative values that were introduced by the observer for regions with poorly corrected telluric absorption features and for regions that were suspected to be affected by detector blemishes. Note that the very different appearances of the Ca II H and K lines of these objects reflect to a large extent the very different line blanketing. Furthermore, the emission components in the H and K lines (Fig. 6) reflect differences in the chromospheres. It is seen that in the dwarf Gl 1 very few lines and weak band heads can be identified and other lines form a quasi-continuum in the spectral range 6546-6730 Å (Fig. 9). A close look at the spectra of Gl 1 shows that several profiles of strong lines in the high dispersion optical and far-red spectra indicate deviations from the radiative equilibrium temperature distribution and from LTE level occupations in the top layers of the atmosphere: Fig. 2 shows evidence for reversals of the Ca II resonance line cores. The emission cores for the early objects require a reversal in the temperature in the top layers for at least some part of the photospheric disk.

A spectrum covering the H${\alpha }$ line is shown for Gl 1 in Fig. 5. Also seen in the spectral region of Fig. 5 is the strong Ca I line at 6572.795 Å, lines of Ti I 6554.298 and 6556.077 Å, and numerous weak TiO absorption features across the spectra. H${\alpha }$ is seen strongly in absorption in Gl 1. With an equivalent width of -0.39 Å and R-I = 1.15 (Robinson et al. 1990), Gl 1 falls near the bottom of the envelope of M dwarfs of similar color in Fig. 3 of Stauffer & Hartmann (1986), Fig. 6 of Gizis et al. (2002) and Fig. 7 of Robinson et al. (1990).

The n = 2 lower level of hydrogen has an excitation potential of 10.2 eV. For a simple atmosphere in radiative equilibrium at the indicated temperature near 3600 K, the corresponding Boltzmann factor would be smaller than 10-17 and no H${\alpha }$ absorption should appear. Instead, it is necessary to assume that the line is actually formed in hotter, outer layers and is subject to strong NLTE effects that reduce the source function. These findings are in accordance with the calculations of Cram & Mullan (1979), Houdebine et al. (1995) and Short & Doyle (1997) and others; these show that the first effect of a weak chromospheric reversal in the outer atmospheric layers is to produce a pure absorption line. As the reversal becomes stronger, the line gets weaker, then finally goes into emission. Empirical evidence in favor of this interpretation is discussed by Stauffer & Hartmann (1986). The strength of the absorption actually indicates a weak chromosphere compared with stars of similar colors (Fig. 14) in the Stauffer & Hartmann (1986) sample, because the absorptions are stronger than the average. Cram & Mullan (1979) calculated for an atmospheric $T_{\rm eff}$ of 3500 K that the maximum absorption equivalent width would be -0.69 Å, of which only -0.08 Å is caused by the normal photosphere. Gl 1 has an equivalent width of -0.39 Å (Panagi & Mathioudakis 1993; Robinson et al. 1990). The neighboring Ca I resonance line (6572 Å) is deeper than expected from a radiative equilibrium atmosphere. We suspect therefore that it is also formed in ``scattering mode''. It is very narrow, implying that the microturbulence plus rotational velocity is quite low. The spectra certainly require a full NLTE analysis. Unfortunately, a corresponding program is presently not available to us.

\begin{figure} \par\includegraphics[width=17cm]{12434f16.eps} \end{figure} Figure 16:

Synthetic spectra calculated with an additional cool chromosphere including convection with $T_{\rm eff}=3600$ K and log g=5. Chromospheric temperature rise is shown for parameters $\delta =0.0001$, $\tau _{0}=0.001$ with temperature stratification $t_{\rm c} =$ [0.10; 0.15; 0.20; 0.23; 0.25; 0.28; 0.30; 0.32; 0.35; 0.40] (from front to back). The chemical composition in the models is assumed to be solar except for Ca and Fe reduced by 1 dex. Note the lack of H${\alpha }$ absorption in the series of spectra.

Open with DEXTER
However, in order to see qualitatively the consequences of a chromospheric temperature rise on the spectrum in the H${\alpha }$ region, we used the program of Wehrse (1981) that can treat 2-level atoms, i.e. we split the extinction coefficient into an absorption and a scattering fraction and describe the ratio of absorption to extinction coefficient by the parameter $\epsilon$ (cf. Mihalas 1978; Jefferies 1968). We include the TiO line list of Plez (1998) and the atomic lines Ti I (6554.238 and 6556.077 Å), Ca I (6572.795 Å) and Fe I (6574.254 Å) and assume for all lines $\epsilon$ =10-4, i.e. nearly complete scattering mode. A statistical evaluation of the transition probability $\times$ statistical weight plane for the used TiO lines is shown in Fig. 11. Due to the uncertainties we choose $T_{\rm eff}=3600$ K, however from V-I a more reasonable value would be closer to 3500 K. First we calculated classical models with gray temperature stratification (Fig. 12), hereafter we included convection by using the extrapolated temperature stratification from MARCS. In order to model a chromospheric temperature inversion we add to the temperature distribution $~t_{\rm c} ~ \left(1-\tanh \left( \frac{\tau_{1.2\mu} - \tau_{0}}{\delta} \right) \right)$. By varying the parameters $t_{\rm c}$, $\tau_{0}$ and $\delta$ we can now modify the height, the abruptness and the inflection point of the chromospheric temperature rise. Assumed gray temperature stratification with various chromospheric distributions are shown in Fig. 13. The best model fits are compared with the observations in Figs. 14 and 15.

\begin{figure} \par\includegraphics[width=17cm]{12434f17.eps} \end{figure} Figure 17:

Same as Fig. 16 but for parameters $\delta =0.001$ and $\tau _{0}=0.01$. The temperature stratification for this model series is shown in Fig. 18. Note that weak H${\alpha }$ absorption is evident in some spectra but with a strong emission core.

Open with DEXTER

From these comparisons we see that:

(i)
without an outer temperature rise the molecular lines are reasonably well reproduced. A large fraction of the discrepancies most probably result from uncertainties in the TiO line data as comparisons with Kurucz's and Joergensen's list have shown, but the atomic lines do not fit at all; in particular, H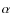${\alpha }$ absorption is completely absent, as expected from the cited earlier papers;

(ii)
with an increasing temperature rise, the atomic lines fit reasonably well but now the molecular features are too weak;

(iii)
the predicted H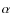${\alpha }$ line is completely absent without an outer temperature rise. With a temperature rise, H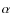${\alpha }$ starts with an increasing absorption component, finally superimposed with a very narrow emission core that is not observed. We therefore modified the temperature distribution in various ways to avoid the emission core without losing the absorption part.

In order to include convection, we use an extrapolated temperature stratification from MARCS. The chemical composition for the calculated models is assumed to be solar except for Ca and Fe which were reduced by 1 dex. In these models it can be shown that synthetic spectra in agreement with observations can only be reached by starting the chromospheric temperature rise at the specific optical depth that was empirically determined. Calculated fluxes are shown for parameters $\delta =0.0001$ and $\tau _{0}=0.001$ that indicate the chromospheric temperature rise at an optical depth log $~\tau_{1.2\mu}\approx -2.5$ for different temperature stratifications (Fig. 16). In these series the H${\alpha }$ absorption is completely absent. Varying the parameters $\delta =0.001$ and $\tau _{0}=0.01$ for starting the beginning of the chromospheric temperature rise at an optical depth log $~\tau_{1.2\mu}\approx-1.9$ leads to the models shown in Fig. 17. The temperature stratification for this model series is shown in Fig. 18. The best model fit of this series is compared with high resolution observations of Gl 1 (Fig. 19). In the last series, we use the parameters $\delta =0.01$ and $\tau _{0}=0.07$ so the beginning of the chromospheric temperature rise starts at an optical depth log $~\tau_{1.2\mu}\approx 1.9$ log $~\tau_{1.2\mu}\approx -1$ (Fig. 20). As expected, the molecular features are too weak and the H${\alpha }$ line can't be modeled in absorption without an emission core in this series. It seems impossible to get a comparable fit for a model in which only the abundances of ${\alpha }$ elements relative to iron are enhanced.

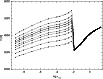
\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f18.eps}} \end{figure} Figure 18:

Temperature as a function of the optical depth at $1.2\mu $ for the fluxes plotted in Fig. 17. The temperature rise starts at log $~\tau_{1.2\mu}=-1.9$ and T = 3140 K the temperature stratification with $t_{\rm c}=0.3$ (full line) for the best model of this series is plotted in Fig. 19.
Open with DEXTER
\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f19.eps}} \end{figure} Figure 19:

Comparison of high resolution observations of Gl 1 (full line) and best model fit from Fig. 17. It is calculated with an additional cool chromosphere including convection with parameters $t_{\rm c}=0.3$ (temperature stratification as shown in Fig. 18), $\tau _{0}=0.01$ and $\delta =0.001$ (dashed line).

Open with DEXTER

5 Discussion

It had been the original plan (Wehrse et al. 1997) to detect - as a consequence of the strong increase of the H- absorption coefficient with wavelength - the chromosphere of M dwarfs in the IR range accessible to the ISO and Spitzer space crafts, and to use these observations to model empirically the temperature distributions in the very outer layers of these stars. This would allow the study of the outer radiative boundary condition needed in the construction of chromospheric and interior models.

Unfortunately, a flux excess increasing to longer wavelengths is not seen for Gl 1 up to about 35 ${\mu }$m. The reason for this can be seen from Fig. 21. In spite of a strong increase with wavelength, $\tau_{\lambda}$( $\tau_{\rm std}=10^{-1.9}$) does yet not reach increase unity, i.e. we see essentially only the layers around the temperature minimum! This is most probably the reason for the flux decrease that is steeper than that of a black body (Fig. 10). With increasing wavelengths, layers of lower and lower temperature are seen. Since we have not modelled the flux of Gl 1 consistently from the UV to the IR (e.g. with respect to the inclusion of all relevant lines), we cannot give accurate total acoustic plus magnetic fluxes that are dissipated in the chromosphere but our models indicate an appreciable fraction (up to about 25%) of the total flux entering the atmosphere must be of non-radiative nature. If this is confirmed, these fluxes will have severe consequences for the temperature stratification for layers below the chromosphere also and must consistently be taken into account in future modeling. This would imply that the effective temperature, the gravity, and the chemical composition are not sufficient to determine the atmospheres of M dwarf stars uniquely.

\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f20.eps}} \end{figure} Figure 20:

Same as Fig. 16 but for parameters $\delta =0.01$ and $\tau _{0}=0.07$. Note the strong H${\alpha }$ absorption accompanied by an emission core in many of the spectra while the molecular lines are always too weak.
Open with DEXTER
\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f21.eps}} \end{figure} Figure 21:

Essential run of the optical depth of the layer $\tau _{1.2\mu }=1$ with wavelength for the same parameters as the model plotted in Fig. 15. Note that continuous and water absorption coefficients at wavelengths indicated by the dots are involved.
Open with DEXTER
The combination of the strong H${\alpha }$and Ca I absorption, the Ca II emission reversals, and the persistent strength of the TiO bands lead us to check for indications of surface inhomogeneities. We assume that the atmosphere is divided into two components (e.g. Giampapa 1985). Some fraction of the surface is spotted with chromospheric activity, but the majority of the surface probably lacks activity. Just like Houdebine et al. (1995) we try to merge our calculated atmospheres. This method did not provide any significant indications of surface inhomogeneities.

The element abundances given in Sect. 4 have been determined iteratively starting from solar values and seemed to give the best fits to our spectra. In view of the complicated dependencies of the line strengths and profiles on the details of the temperature stratification and of the chemical composition (cf. Allard & Hauschildt 1995; see also Wehrse 1985, for an analogue discussion for M giants), we cannot, however, exclude that a fit to the full spectrum may result in a somewhat different composition, e.g. in an enhanced abundance ratio of the ${\alpha }$ elements to iron. A thorough quantitative error analysis on the basis of well calibrated high dispersion spectra extending from the visible to the infrared range is certainly an urgent need for cool dwarf stars such as Gl 1.

In summary, we have analyzed high resolution optical and low resolution infra-red spectra of the early M dwarf Gliese 1 in order to study the temperature structure of the upper photospheric layers. From the H${\alpha }$ and adjacent metal line profiles it is found that there should be a temperature reversal at about $\tau_{1.2\mu} \approx 0.01$ and an outer temperature of $\sim$4900 K. There are no indications of horizontal inhomogeneities or of chromospheric flux enhancements in the IR up to $\lambda \approx 30 ~ \mu {\rm m}.$ It was beyond the scope of this paper to perform a full and consistent abundance analysis, the modeling of the metal lines requiered decreased abundances for Ca, Fe and Ti.

References

  1. Allard, F. 1990, Ph.D. Thesis, Ruprecht Karls Univ Heidelberg [Google Scholar]
  2. Allard, F., & Hauschildt, P. H. 1995, ApJ, 445, 433 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bessell, M. S. 1990, A&AS., 83, 357 [Google Scholar]
  4. Bessell, M. S. 1991, AJ, 101, 662 [NASA ADS] [CrossRef] [Google Scholar]
  5. Brett, J. M., & Plez, B. 1993, Proc. Astron. Soc. Australia, 10, 250 [Google Scholar]
  6. Cincunegui, C., & Mauas, P. J. D. 2004, A&A, 414, 699 [Google Scholar]
  7. Cram, L. E., & Mullan, D. J. 1979, ApJ, 234, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Eggen, O. J. 1979, ApJ, 230, 786 [NASA ADS] [CrossRef] [Google Scholar]
  9. Evans, D. S. 1961, Royal Greenwich Observatory Bulletin, 48, 389 [NASA ADS] [Google Scholar]
  10. Gabriel, C., Acosta-Pulido, J., Heinrichsen, I., Morris, H., & Tai, W.-M. 1997, in Astronomical Data Analysis Software and Systems VI, ed. G. Hunt, & H. Payne, ASP, 125, 108 [Google Scholar]
  11. Giampapa, M. S. 1985, ApJ, 299, 781 [NASA ADS] [CrossRef] [Google Scholar]
  12. Gizis, J. E., Reid, I. N., & Hawley, S. L. 2002, AJ, 123, 3356 [NASA ADS] [CrossRef] [Google Scholar]
  13. Gliese, W. 1969, Veröffentlichungen des Astronomischen Rechen-Instituts Heidelberg, 22, 1 [Google Scholar]
  14. Golimowski, D. A., Leggett, S. K., Marley, M. S., et al. 2004, AJ, 127, 3516 [NASA ADS] [CrossRef] [Google Scholar]
  15. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2003, in Stellar Atmosphere Modeling, ed. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 331 [Google Scholar]
  16. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [Google Scholar]
  17. Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
  18. Hawley, S. L., Gizis, J. E., & Reid, I. N. 1996, AJ, 112, 2799 [NASA ADS] [CrossRef] [Google Scholar]
  19. Hinkle, K., Wallace, L., Valenti, J., & Harmer, D. 2000, Visible and Near Infrared Atlas of the Arcturus Spectrum 3727-9300 Å, ed. K. Hinkle, L. Wallace, J. Valenti, D. Harmer [Google Scholar]
  20. Houck, J. R., Roellig, T. L., van Cleve, J., et al. 2004, ApJ, 154, 18 [Google Scholar]
  21. Houdebine, E. R., Doyle, J. G., & Koscielecki, M. 1995, A&A, 294, 773 [Google Scholar]
  22. Jefferies, J. T. 1968, Spectral line formation, ed. J. T. Jefferies [Google Scholar]
  23. Kurucz, R. L. 2005, Mem. Soc. Astron. Ital. Supp., 8, 189 [Google Scholar]
  24. Laureijs, R. J., Klaas, U., Richards, P. J., Schulz, B., & Abraham, P. 2003, The ISO Handbook, Vol. IV - PHT - The Imaging Photo-Polarimeter, ed. T.G. Mueller, J.A.D.L. Blommaert, & P. Garcia-Lario., ESA SP-1262 [Google Scholar]
  25. Leggett, S. K. 1992, ApJ, 82, 351 [Google Scholar]
  26. Leggett, S. K., & Hawkins, M. R. S. 1988, MNRAS, 234, 1065 [NASA ADS] [CrossRef] [Google Scholar]
  27. Lemke, D., Klaas, U., Abolins, J., et al. 1996, A&A, 315, L64 [Google Scholar]
  28. Mihalas, D. 1978, Stellar atmospheres, 2nd edition, ed. J. Hevelius [Google Scholar]
  29. Mould, J. R. 1975, A&A, 38, 283 [Google Scholar]
  30. Mould, J. R. 1976, A&A, 48, 443 [Google Scholar]
  31. Panagi, P. M., & Mathioudakis, M. 1993, A&AS, 100, 343 [Google Scholar]
  32. Plez, B. 1998, A&A, 337, 495 [Google Scholar]
  33. Reid, N., & Hawley, S. L., 2000, New light on dark stars: red dwarfs, low mass stars, brown dwarfs [Google Scholar]
  34. Robinson, R. D., Cram, L. E., & Giampapa, M. S. 1990, ApJS, 74, 891 [NASA ADS] [CrossRef] [Google Scholar]
  35. Short, C. I., & Doyle, J. G. 1997, A&A, 326, 287 [Google Scholar]
  36. Stauffer, J. R., & Hartmann, L. W. 1986, ApJS, 61, 531 [NASA ADS] [CrossRef] [Google Scholar]
  37. Wehrse, R. 1981, MNRAS, 195, 553 [NASA ADS] [Google Scholar]
  38. Wehrse, R. 1985, in Cool Stars with Excesses of Heavy Elements, Proceedings of the Strasbourg Observatory Colloquium, Universite de Strasbourg I, France, July 3-6, 1984 (Dordrecht: D. Reidel Publishing Co.) ed. M. Jaschek, & P. C. Keenan, Astrophysics and Space Science Library, 114, 293 [Google Scholar]
  39. Wehrse, R., Rosenau, P., Suvernev, A., Liebert, J., & Leinert, C. 1997, in The first ISO workshop on Analytical Spectroscopy, ed. A. M. Heras, K. Leech, N. R. Trams, & M. Perry, ESA SP, 419, 309 [Google Scholar]

All Tables

Table 1:   Relevant parameters of Gl 1.

All Figures

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f01.eps}} \end{figure} Figure 1:

ISOPHOT S (solid line) and IRS (dotted line) flux distributions for Gl 1.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f02.eps}} \end{figure} Figure 2:

The spectrum of Gl 1 in the range of 3910-4020 Å around the Ca II H and K lines with a resolution of 100 mÅ. Note the strong but very narrow emission in the cores of Ca II K (3933.7 Å) and Ca II H (3968.5 Å).

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f03.eps}} \end{figure} Figure 3:

The spectrum of Gl 1 in the range of 4206-4324 Å around the Ca I line with a resolution of 100 mÅ.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f04.eps}} \end{figure} Figure 4:

The spectrum of Gl 1 in the range of 5860-6027 Å around the Na I D2 and D1 lines with a resolution of 200 mÅ.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f05.eps}} \end{figure} Figure 5:

The spectrum of Gl 1 in the range of 6546-6730 Å around the H${\alpha }$ line with a resolution of 200 mÅ.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f06.eps}} \end{figure} Figure 6:

The spectra of the stars Gl 1 (M1.5), Arcturus (K1.5) and the Sun (G2) from top to bottom in the range of 3910-4020 Å around the Ca II H and K lines.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f07.eps}} \end{figure} Figure 7:

The spectra of the stars Gl 1 (M1.5), Arcturus (K1.5) and the Sun (G2) from top to bottom in the range of 4206-4324 Å around the Ca I line.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f08.eps}} \end{figure} Figure 8:

The spectra of the stars Gl 1 (M1.5), Arcturus (K1.5) and the Sun (G2) from top to bottom in the range of 5860-6027 Å around the Na I D lines.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f09.eps}} \vspace{-3mm}\end{figure} Figure 9:

The spectra of the stars Gl 1 (M1.5), Arcturus (K1.5) and the Sun (G2) from top to bottom in the range of 6546-6730 Å around the H${\alpha }$ line.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f10.eps}} \end{figure} Figure 10:

Flux distributions for Gl 1 as shown in Fig. 1 in the range 3.5-35 ${\mu }$m - and of synthetic spectra of models with (top gray line) and without (lower gray line) an additional cool chromosphere. A black body distribution of the same effective temperature is indicated by the solid line (center).

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f11.eps}} \end{figure} Figure 11:

Distribution of the numbers of titanium oxide lines (Plez 1998) used in the modeling of the spectrum in the wavelength range 6550-6580 Å as a function of the gf-values of the lines. It is seen that there are essentially three peaks but the distributions are essentially continuous.

Open with DEXTER
In the text

  \begin{figure} \resizebox{9cm}{!}{\includegraphics{12434f12.eps}} \end{figure} Figure 12:

Model series with gray temperature stratification for $T_{\rm eff}=3600$ K and log g=5 and chromospheric temperature rises for $\delta =0.01$, $\tau _{0}=0.1$ and $\Delta t_{\rm c} = 0.02$ $t_{\rm c} \in \lbrack 0.0{-}0.24 \rbrack $ in ascending order. For the definitions of parameters see text. The chemical composition in the models is assumed to be solar except for Ca and Fe reduced by 1 dex and Ti reduced by 0.3 dex.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f13.eps}} \end{figure} Figure 13:

Temperature as a function of the optical depth at $1.2\mu $ with one data point per 0.1 in log $~\tau_{1.2\mu}$. Stratifications for the fluxes plotted in Fig. 12 with $\delta =0.01$ and $\tau _{0}=0.1$ (dotted lines) and $\tau _{0}=0.09$ (dashed lines). The temperature rise starts at log $~\tau_{1.2\mu}=-0.9$ and $T \approx 3160$ K. Temperature stratifications with $t_{\rm c}=0.18$, $\tau _{0}=0.1$ and $t_{\rm c}=0.175$, $\tau _{0}=0.09$ (full lines) for the best model of this series are plotted in Figs. 14 and 15. For the meaning of the parameters modeling the chromospheric temperature rise see text.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f14.eps}} \end{figure} Figure 14:

Comparison of high resolution observations of Gl 1 (full line) and synthetic spectra calculated with an additional cool chromosphere with parameters $t_{\rm c}=0.175$, $\tau _{0}=0.09$ as shown in Fig. 13 (dashed line).

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f15.eps}} \end{figure} Figure 15:

Same as Fig. 14 but for parameters $t_{\rm c}=0.18$ and $\tau _{0}=0.1$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm]{12434f16.eps} \end{figure} Figure 16:

Synthetic spectra calculated with an additional cool chromosphere including convection with $T_{\rm eff}=3600$ K and log g=5. Chromospheric temperature rise is shown for parameters $\delta =0.0001$, $\tau _{0}=0.001$ with temperature stratification $t_{\rm c} =$ [0.10; 0.15; 0.20; 0.23; 0.25; 0.28; 0.30; 0.32; 0.35; 0.40] (from front to back). The chemical composition in the models is assumed to be solar except for Ca and Fe reduced by 1 dex. Note the lack of H${\alpha }$ absorption in the series of spectra.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm]{12434f17.eps} \end{figure} Figure 17:

Same as Fig. 16 but for parameters $\delta =0.001$ and $\tau _{0}=0.01$. The temperature stratification for this model series is shown in Fig. 18. Note that weak H${\alpha }$ absorption is evident in some spectra but with a strong emission core.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f18.eps}} \end{figure} Figure 18:

Temperature as a function of the optical depth at $1.2\mu $ for the fluxes plotted in Fig. 17. The temperature rise starts at log $~\tau_{1.2\mu}=-1.9$ and T = 3140 K the temperature stratification with $t_{\rm c}=0.3$ (full line) for the best model of this series is plotted in Fig. 19.
Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f19.eps}} \end{figure} Figure 19:

Comparison of high resolution observations of Gl 1 (full line) and best model fit from Fig. 17. It is calculated with an additional cool chromosphere including convection with parameters $t_{\rm c}=0.3$ (temperature stratification as shown in Fig. 18), $\tau _{0}=0.01$ and $\delta =0.001$ (dashed line).

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f20.eps}} \end{figure} Figure 20:

Same as Fig. 16 but for parameters $\delta =0.01$ and $\tau _{0}=0.07$. Note the strong H${\alpha }$ absorption accompanied by an emission core in many of the spectra while the molecular lines are always too weak.
Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12434f21.eps}} \end{figure} Figure 21:

Essential run of the optical depth of the layer $\tau _{1.2\mu }=1$ with wavelength for the same parameters as the model plotted in Fig. 15. Note that continuous and water absorption coefficients at wavelengths indicated by the dots are involved.
Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.