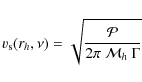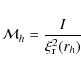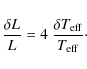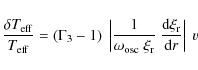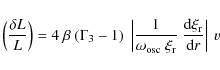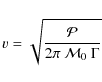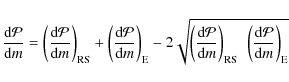EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 509 (January 2010) A&A, 509 (2010) A16 Full HTML
Free Access
Issue
A&A
Volume 509, January 2010
Article Number A16
Number of page(s) 7
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/200911868
Published online 12 January 2010
A&A 509, A16 (2010)

The CoRoT target HD 49933[*]

II. Comparison of theoretical mode amplitudes with observations

R. Samadi1 - H.-G. Ludwig2 - K. Belkacem1,3 - M. J. Goupil1 - O. Benomar4 - B. Mosser1 - M.-A. Dupret1,3 - F. Baudin4 - T. Appourchaux4 - E. Michel1

1 - Observatoire de Paris, LESIA, CNRS UMR 8109, Université Pierre et Marie Curie, Université Denis Diderot, 5 Pl. J. Janssen, 92195 Meudon, France
2 - Observatoire de Paris, GEPI, CNRS UMR 8111, 5 Pl. J. Janssen, 92195 Meudon, France
3 - Institut d'Astrophysique et de Géophysique de l'Université de Liège, Allé du 6 Août 17, 4000 Liège, Belgium
4 - Institut d'Astrophysique Spatiale, CNRS UMR 8617, Université Paris XI, 91405 Orsay, France

Received 17 February 2009 / Accepted 27 October 2009

Abstract
Context. The seismic data obtained by CoRoT for the star HD 49933 enable us for the first time to measure directly the amplitudes and linewidths of solar-like oscillations for a star other than the Sun. From those measurements it is possible, as was done for the Sun, to constrain models of the excitation of acoustic modes by turbulent convection.
Aims. We compare a stochastic excitation model described in Paper I with the asteroseismology data for HD 49933, a star that is rather metal poor and significantly hotter than the Sun.
Methods. Using the seismic determinations of the mode linewidths detected by CoRoT for HD 49933 and the theoretical mode excitation rates computed in Paper I for the specific case of HD 49933, we derive the expected surface velocity amplitudes of the acoustic modes detected in HD 49933. Using a calibrated quasi-adiabatic approximation relating the mode amplitudes in intensity to those in velocity, we derive the expected values of the mode amplitude in intensity.
Results. Except at rather high frequency, our amplitude calculations are within 1-$\sigma $ error bars of the mode surface velocity spectrum derived with the HARPS spectrograph. The same is found with respect to the mode amplitudes in intensity derived for HD 49933 from the CoRoT data. On the other hand, at high frequency ( $\nu \ga 1.9$ mHz), our calculations depart significantly from the CoRoT and HARPS measurements. We show that assuming a solar metal abundance rather than the actual metal abundance of the star would result in a larger discrepancy with the seismic data. Furthermore, we present calculations which assume the ``new'' solar chemical mixture to be in better agreement with the seismic data than those that assumed the ``old'' solar chemical mixture.
Conclusions. These results validate in the case of a star significantly hotter than the Sun and $\alpha$ Cen A the main assumptions in the model of stochastic excitation. However, the discrepancies seen at high frequency highlight some deficiencies of the modelling, whose origin remains to be understood. We also show that it is important to take the surface metal abundance of the solar-like pulsators into account.

Key words: convection - turbulence - stars: oscillations - Sun: helioseismology - stars: individual: HD 49933

1 Introduction

The amplitudes of solar-like oscillations result from a balance between excitation and damping. The mode linewidths are directly related to the mode damping rates. Once we can measure the mode linewidths, we can derive the theoretical value of the mode amplitudes from theoretical calculations of the mode excitation rates, which in turn can be compared to the available seismic constraints. This comparison allows us to test the model of stochastic mode excitation investigated in a companion paper (Samadi et al. 2010, hereafter Paper I).

As shown in Paper I, a moderate deficit of the surface metal abundance results in a significant decrease of the mode driving by turbulent convection. Indeed, by taking into account the measured iron-to-hydrogen abundance ([Fe/H]) of HD 49993 ([Fe/H] = -0.37), we have derived the theoretical values of the mode excitation rates ${\cal P}$ expected for this star. The resulting value of ${\cal P}$ is found to be about two times smaller than for a model with the same gravity and effective temperature, but with a solar metal abundance (i.e. [Fe/H] = 0).

The star HD 49933 was first observed in Doppler velocity by Mosser et al. (2005) with the HARPS spectrograph. More recently, this star has been observed twice by CoRoT. A first time this was done continuously during about 61 days (initial run, IR) and a second time continuously during about 137 days (first long run in the center direction, LRc01). The combined seismic analysis of these data (Benomar et al. 2009) has provided the mode linewidths as well as the amplitudes of the modes in intensity. Then, using mode linewidths obtained for HD 49933 with the CoRoT data and the theoretical mode excitation rates (obtained in Paper I), we derive the expected values of the mode surface velocity amplitudes. We next compare these values with the mode velocity spectrum derived following Kjeldsen et al. (2005) with seismic data from the HARPS spectrograph (Mosser et al. 2005).

Mode amplitudes in terms of luminosity fluctuations have also been derived from the CoRoT data for 17 radial orders. These data provide us with not only a constraint on the maximum of the mode amplitude but also with the frequency dependence. The relative luminosity amplitudes  $\delta L/L$ are linearly related to the velocity amplitudes. This ratio is determined by the solution of the non-adiabatic pulsation equations and is independent of the stochastic excitation model (see Houdek et al. 1999). Such a non-adiabatic calculation requires us to take into account, not only the radiative damping, but also the coupling between the pulsation and the turbulent convection. However, there are currently very significant uncertainties concerning the modeling of this coupling (for a recent review see Houdek 2008). We relate further for the sake of simplicity the mode luminosity amplitudes to computed mode velocity amplitudes by assuming adiabatic oscillations as Kjeldsen & Bedding (1995). Such a relation is calibrated in order to reproduce the helioseismic data.

The comparison between theoretical values of the mode amplitudes (both in terms of surface velocity and intensity) constitutes a test of the stochastic excitation model with a star significantly different from the Sun and $\alpha$ Cen A. In addition it is also possible to test the validity of the calibrated quasi-adiabatic relation, since both mode amplitudes, in terms of surface velocity and intensity, are available for this star.

This paper is organized as follows: we describe in Sect. 2 the way mode amplitudes in terms of surface velocity $v_{\rm s}$ are derived from the theoretical values of ${\cal P}$ and from the measured mode linewidths ($\Gamma$). Then, we compare the theoretical values of the mode surface velocity with the seismic constraint obtained from HARPS observations. We describe in Sect. 3 the way mode amplitudes in terms of intensity fluctuations  $\delta L/L$ are derived from theoretical values of $v_{\rm s}$ and compare  $\delta L/L$ with the seismic constraints obtained from the CoRoT observations. Finally, Sects. 4 and 5 are dedicated to a discussion and conclusion respectively.

2 Surface velocity mode amplitude

2.1 Derivation of the surface velocity mode amplitude

The intrinsic rms mode surface velocity $v_{\rm s}$ is related to the mode exitation rate  $\mathcal P(\nu) $ and the mode linewidth  $\Gamma(\nu)$ according to (see, e.g., Baudin et al. 2005):

\begin{displaymath}% v_{\rm s}(r_{h},\nu) = \sqrt{\mathcal P \over{ 2 \pi ~ {\cal M}_{h} ~ \Gamma } } \end{displaymath} (1)

where ${\cal P}$ is the mode excitation rate derived as described in Paper I, $\Gamma$ is the mode full width at half maximum (in $\nu $), $\nu = \omega_{\rm osc} / 2 \pi$ the mode frequency and  ${\mathcal M}_{h}$ is the mode mass defined as:

\begin{displaymath}% {\cal M}_{h}= { I \over { \xi_{\rm r}^2(r_{h}) } } \end{displaymath} (2)

where I is the mode inertia (see Eq. (2) of Paper I), $\xi_{\rm r}$ the radial mode eigendisplacement, $r_h \equiv R + h$ the layer in the atmosphere where the mode is measured in radial velocity, R the radius at the photosphere (i.e. at $T=T_{\rm eff}$) and h the height above the photosphere.

In Sect. 2.2 we will compare estimated values of $v_{\rm s}$ with the seismic constraint obtained by Mosser et al. (2005) with the HARPS spectrograph. We therefore need to estimate $v_{\rm s}$ at the layer h where the HARPS spectrograph is the most sensitive to the mode displacement. As discussed by Samadi et al. (2008a), the seismic measurements obtained with HARPS spectrograph are likely to arise from the optical depth $\tau_{\rm ~500~nm} \simeq 0.013$, which corresponds to the depth where the potassium (K) spectral line is formed. We then compute the mode mass at the layer h associated with the optical depth  $\tau_{\rm 500~nm}$ (Christensen-Dalsgaard & Gough 1982). For the model with [Fe/H] = 0 (resp. [Fe/H] = -1) this optical depth corresponds to h $\simeq$ 390 km (resp. h $\simeq$ 350 km).

For the mode linewidth $\Gamma$ we use the seismic measurement obtained from the seismic analysis of the CoRoT data performed by Benomar et al. (2009). This seismic analysis combined the two CoRoT runs available for HD 49933. Two different approaches were considered in this analysis: one based on the maximum likelihood estimator and the second one using the Bayesian approach coupled with a Markov Chains Monte Carlo algorithm. The Bayesian approach remains in general more reliable even in low signal-to-noise conditions. Nevertheless, in terms of mode amplitudes, mode heights and mode linewidths, both methods agree within 1-$\sigma $. We will consider here the seismic parameters and associated error bars obtained on the basis of the Bayesian approach.

\begin{figure} \par\hspace*{2mm}\includegraphics[width=8.2cm,clip]{11868fig1.eps}\vspace*{3mm} \includegraphics[width=8.5cm,clip]{11868fig2.eps} \end{figure} Figure 1:

Top: intrinsic mode surface velocity as a function of the mode frequency ($\nu $). The filled circles connected by the thick solid line correspond to the mode surface velocity ($v_{\rm s}$) derived for HD 49933 according to Eq. (1), where the mode excitation rates ${\cal P}$ are derived as explained in Paper I and the mode linewidths and their associated error bars are derived by Benomar et al. (2009) from the CoRoT data. The thick dashed line corresponds to the mode velocity associated with the model with [Fe/H] = 0. The thick and red solid line corresponds to the amplitude spectrum derived from the seismic observations obtained with the HARPS spectrograph (see text). The dotted line corresponds to the 1-$\sigma $ domain associated with this measurement. Bottom: differences between $v_{\rm s}$ and  $v_{\rm HARPS}$. The 1-$\sigma $ error bars correspond to $\sigma _v \equiv \sqrt { \Delta v_{\rm s}^2 + \Delta v_{\rm HARPS}^2}$ (see text).

Open with DEXTER

2.2 Comparison with the HARPS measurements

The seismic analysis in velocity has been performed by Mosser et al. (2005) using data from the HARPS spectrograph. The quality of these data is too poor to perform a direct comparison between the observed spectrum and the calculated amplitude spectrum ($v_{\rm s}$, Eq. (1)). Indeed, the observed spectrum is highly affected by the day aliases. Furthermore, the quality of the data does not allow to isolate individual modes, in particular modes of a different angular degree ($\ell$). A consequence is that energies of modes which are close in frequency are mixed.

In order to measure the oscillation amplitude in a way that is independent of these effects, we have followed the method introduced by Kjeldsen et al. (2005, see also Kjeldsen et al. 2008). This method consists in deriving the oscillation amplitudes from the oscillation power density spectrum smoothed over typically four times the large separation (i.e. four radial orders). Next, we multiply this smoothed spectrum by a coefficient in order to convert the apparent amplitudes into intrinsic amplitudes. This coefficient takes into account the spatial response function of the angular degrees $\ell$ = 0-3 (see Kjeldsen et al. 2008). We have checked that the sensitivity of the visibility factor with the limb-darkening law is significantly smaller in comparison with the error associated with the Mosser et al. (2005) seismic measurements. The amplitude spectrum  $v_{\rm HARPS}$ derived following Kjeldsen et al. (2005) is shown in Fig. 1. The 1-$\sigma $ error bar associated with each values of  $v_{\rm HARPS}$ is constant and equal to $\Delta V_{\rm HARPS} = 7$ cm/s.

The maximum of $v_{\rm HARPS}$ reaches $V_{\rm max}= 50.2$ $\pm$ 7 cm/s. By comparison, Mosser et al. (2005) found a maximum of 40 $\pm$ 10 cm/s, which once converted into intrinsic amplitude represents a maximum of 42 $\pm$ 10 cm/s. The difference between the two values is within the 1-$\sigma $ error bars. The different value found by Mosser et al. (2005) can be explained by the way the maximum of the mode amplitude was derived. Indeed, Mosser et al. (2005) have constructed synthetic time series based on a theoretical low degree p-modes eigenfrequency pattern and theoretical mode lines widths (Houdek et al. 1999). The maximum amplitudes were assumed to follow a Gaussian distribution in frequency. Using a Monte-Carlo approach, the maximum amplitude was then determined in order to obtain comparable energy per frequency bin in the synthetic and observed spectra. On the other hand, except for the mode response function, the method by Kjeldsen et al. (2005) does not impose a priori constraints concerning the modes. This method can then be considered to be more reliable than the method by Mosser et al. (2005).

We compare in Fig. 1 $v_{\rm HARPS}$ with the calculated mode surface velocity $v_{\rm s}$ (Eq. (1)). However, in order to have a consistent comparison, we have smoothed $v_{\rm s}$ quadratically over four radial orders. We note $\Delta v_{\rm s}$ the 1-$\sigma $ error bars associated with $v_{\rm s}$. They are derived from  $\Delta \Gamma$, the 1-$\sigma $ error bars associated with $\Gamma$. As pointed out in Paper I, the uncertainty related to our knowledge of the metal abundance Z for HD 49933 results in an uncertainty about the determination of ${\cal P}$. However, in terms of amplitude, this uncertainty is of the order of 5%; this is negligible compared to the uncertainty that arises from  $\Delta \Gamma$ (ranging between 25% to 50% in terms of amplitude).

The difference between computed values and observations is shown in the bottom panel of Fig. 1. This difference must be compared with $\sigma_v$, the 1-$\sigma $ interval resulting from the errors associated with $v_{\rm s}$ and this in turn associated with  $v_{\rm HARPS}$, that is $\sigma _v \equiv \sqrt { \Delta v_{\rm s}^2 + \Delta v_{\rm HARPS}^2}$. As seen in Fig. 1, except at high frequency ( $\nu \ga 1.9$ mHz), the theoretical $v_{\rm s}$ lie well in the 1-$\sigma_v$ domain. However, there is a clear disagreement at high frequencies where the computed mode surface velocities overestimate the observations. This disagreement is attributed to the assumptions in the theoretical model of stochastic excitation (see Sect. 4.5).

Assuming the 3D model with the solar abundance results in significantly larger $v_{\rm s}$. In that case the differences between computed $v_{\rm s}$ and the seismic constraint are in general larger than 2-$\sigma_v$. This shows that ignoring the metal abundance of HD 49933 would result in a larger discrepancy between $v_{\rm s}$ and  $v_{\rm HARPS}$.

3 Amplitudes of mode in intensity

3.1 Derivation of mode amplitudes in intensity

Fluctuations of the luminosity L due to variations of the stellar radius can be neglected since we are looking at high n order modes; accordingly the bolometric mode intensity fluctuations $\delta L$ are mainly due to variations of the effective temperature, that is:

\begin{displaymath}% { {\delta L} \over L } = 4 ~ {\delta T_{\rm eff} \over T_{\rm eff}}\cdot \end{displaymath} (3)

As in Kjeldsen & Bedding (1995), we now assume that $\delta T_{\rm eff}$ is proportional to the variation of the temperature induced by the modes at the photosphere (i.e. at $T=T_{\rm eff}$). This assumption is discussed in Sect. 4.3. Assuming further low degree $\ell$ and adiabatic oscillations, one can derive a relation between  $\delta T_{\rm eff}/{T_{\rm eff}}$ and the radial mode velocity v that is:

\begin{displaymath}% {\delta T_{\rm eff} \over T_{\rm eff}} = ( \Gamma_3 -1) ~ ... ... { {{\rm d}\xi_{\rm r}} \over {{\rm d} r} } }\right \vert ~ v \end{displaymath} (4)

where $\Gamma_3= \nabla_{\rm ad}~ \Gamma_1 + 1$, $\nabla_{\rm ad}$is the adiabatic temperature gradient, $\Gamma_1 = \left (\frac {\partial \ln P_g } {\partial \ln\rho} \right )_{\rm s}$, $\xi_{\rm r}$ the radial mode eigendisplacement, and v the mode velocity at the photosphere. Finally, according to Eqs. (3) and (4), one has:

\begin{displaymath}% \left ( { {\delta L} \over L } \right ) = 4 ~ \beta ~ (\Gam... ...{ {{\rm d} \xi_{\rm r}} \over {{\rm d} r} } }\right \vert ~ v \end{displaymath} (5)

where v is computed using Eq. (1) with h = 0 (the photosphere), that is:

\begin{displaymath}% v = \sqrt{\mathcal P \over{ 2 \pi ~ {\cal M}_0 ~ \Gamma } } \end{displaymath} (6)

where ${\cal M}_0$ is the mode mass evaluated at the photosphere (h = 0).

In Eq. (5), $\beta$is a free parameter introduced so that Eq. (5) gives, in the case of the solar p modes, the correct maximum in  $\delta L/L$. Indeed, Eq. (5) applied to the case of the solar p modes, overestimates by ${\sim}10$ times the mode amplitudes in intensity. This important discrepancy is mainly a consequence of the adiabatic approximation.

From the SOHO/GOLF seismic data (Baudin et al. 2005), we derive the maximum of the solar mode (intrinsic) surface velocity, that is 32.6 $\pm$ 2.6 cm/s. Then, using $\xi_{\rm r}$, we infer the maximum of mode velocity at the photosphere, that is 18.5 $\pm$ 1.5 cm/s. According to Michel et al. (2009), the maximum of the solar mode (bolometric) amplitude in intensity is equal to 2.53 $\pm$ 0.11 ppm. Then, by applying Eq. (5) in the case of the Sun, we derive the scaling factor $\beta=0.103$ $\pm$ 10%. We have checked that this calibration depends very little on the choice of the chemical mixture (see also Sect. 4.3). We then adopt this value for the case of HD 49933.

3.2 The mode intensity fluctuations measured by CoRoT

The seismic analysis by Benomar et al. (2009) provides the apparent amplitude $A_\ell$ of the $\ell$ = 0-2 modes and the associated error bars. However, the CoRoT measurements $A_\ell$ correspond to relative intensity fluctuations in the CoRoT passband. Furthermore, the observed (apparent) mode amplitudes depend on the degree $\ell$. Therefore, to transform them into bolometric and intrinsic intensity fluctuations normalised to the radial modes, we divide them by the CoRoT response function, $R_{\ell}$, derived here for $\ell$ = 0-2, following Michel et al. (2009). The adopted values for $R_{\ell}$ are: R0=0.90, R1=1.10, and R2=0.66. We finally derive the bolometric intensity fluctuations normalised to the radial modes according to:

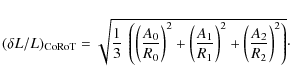
\begin{displaymath}% (\delta L/L)_{\rm CoRoT} = \sqrt{ {1 \over 3} ~ \left ( \l... ...\right )^2 + \left ( A_2 \over R_2 \right )^2 \right ) }\cdot \end{displaymath} (7)

We shall stress that the differences between the amplitudes derived by Benomar et al. (2009) and by Appourchaux et al. (2008) are smaller than the 1-$\sigma $ error bars. Furthermore, these amplitudes are in agreement with those found by Michel et al. (2008), using a different technique.

3.3 Comparison with the CoRoT measurements

We compute the mode amplitudes in terms of bolometric intensity fluctuations, $\delta L/L$, according to Eqs. (5) and (6) (see Sect. 3.1). As for $v_{\rm s}$, the uncertainty associated with the measured mode linewidths, $\Gamma$, put uncertainties on the theoretical values of  $\delta L/L$. Furthermore, the uncertainty associated with the calibrated factor $\beta$ (see Sect. 3.1) also puts an additional uncertainty on  $\delta L/L$. From here on, $\Delta (\delta L/L)$ will refer to the 1-$\sigma $ uncertainties associated with $\delta L/L$. Accordingly, we have $\Delta (\delta L/L) = (\delta L/L) ~ \sqrt { \left ( {1 \over 2} ~ \Delta \Gamma/\Gamma \right )^2 + \left ( \Delta \beta/\beta \right )^2}$, where  $\Delta \Gamma$ (reps.  $\Delta \beta$) is the 1-$\sigma $ uncertainty associated with $\Gamma$ (resp. $\beta$).

Figure 2 compares, as a function of the mode frequency, $\delta L/L$ to the CoRoT measurements: $(\delta L/L)_{\rm CoRoT}$. The difference between our calculations and the observations is shown in the bottom panel. As for the velocity, this difference must be compared with $\sigma_L$, the 1-$\sigma $ interval resulting from the association of the 1-$\sigma $ error bars $\Delta (\delta L/L)$ and the 1-$\sigma $ error, $\Delta(\delta L/L)_{\rm CoRoT}$, associated with the CoRoT measurements. Accordingly, we have $\sigma_L \equiv \sqrt{ a ^2 + b ^2}$ where $a \equiv \Delta (\delta L/L)$ and $b \equiv \Delta (\delta L/L)_{\rm CoRoT}$.

As seen in Fig. 2, below $\nu \la 1.9$ mHz, values of  $\delta L/L$ are within approximately 1-$\sigma_L$ in agreement with $(\delta L/L)_{\rm CoRoT}$. However, above $\nu \sim 1.9$ mHz, the differences between  $\delta L/L$ and  $(\delta L/L)_{\rm CoRoT}$ exceed 2-$\sigma_L$.

Assuming a solar abundance ([Fe/H] = 0) results in a clear overestimation of $\Delta(\delta L/L)_{\rm CoRoT}$. Furthermore, calculations which assume the Grevesse & Noels (1993) chemical mixture result in mode amplitudes larger by $\sim$15%.

Both in terms of intensity and velocity, differences between the calculated mode amplitudes and those derived from the observations (CoRoT and HARPS) are approximately within the 1-$\sigma $ domain below $\nu $ $\sim$ 1.9 mHz. This then validates the intensity-velocity relation given by Eq. (5) at the level of the current seismic precision.

The maximum $(\delta L/L)$ peaks at $\nu_{\rm max} \simeq 1.9$ mHz and the maximum of $v_{\rm s}$ at $\nu_{\rm max} \simeq 1.8$ mHz. By comparison, $(\delta L/L)_{\rm CoRoT}$ peaks at $\nu_{\rm max} \simeq 1.8$ mHz and $v_{\rm HARPS}$ peaks at $\nu_{\rm max} \simeq 1.7$ mHz. The difference in  $\nu_{\rm max}$ between the observations (CoRoT and HARPS) and the model can be partially a consequence of the clear tendency at high frequency toward over-estimated amplitudes compared to the observations.

\begin{figure} \par\hspace*{2.5mm}\includegraphics[width=8.3cm,clip]{11868fig3.eps}\vspace*{3mm} \includegraphics[width=8.5cm,clip]{11868fig4.eps} \end{figure} Figure 2:

Top: mode bolometric amplitude in intensity as a function of the mode frequency ($\nu $). The filled circles connected by the thick solid line correspond to the mode amplitudes in intensity, $\delta L/L$, derived for HD 49933 according to Eqs. (5) and (1) where the mode surface velocity v is evaluated at the photosphere. The thick dashed solid line corresponds to the mode amplitude in intensity associated with the model with [Fe/H] = 0. The red triangles and associated error bars correspond to the mode amplitudes in intensity, $(\delta L/L)_{\rm CoRoT}$, obtained from the CoRoT data (Benomar et al. 2009). These measurements have been translated into bolometric amplitudes following Michel et al. (2009). Bottom: same as top for the difference between  $\delta L/L$ and  $(\delta L/L)_{\rm CoRoT}$. The 1-$\sigma $ error bars correspond here to $\sqrt {a ^2 + b ^2}$ where $a \equiv \Delta (\delta L/L)$ and $b \equiv \Delta (\delta L/L)_{\rm CoRoT}$ (see text).

Open with DEXTER

4 Discussion

4.1 Uncertainties in the knowledge of the fundamental parameters of HD 49933

Uncertainties in the knowledge of $T_{\rm eff}$ and $\log~g$ place uncertainties on the theoretical values of ${\cal P}$ and hence on the mode amplitudes ($v_{\rm s}$ and  $\delta L/L$). However, estimating these uncertainties would require the consideration of 3D models with a  $T_{\rm eff}$ and a $\log g$ that depart more than 1-$\sigma $ from the values adopted in our modeling, i.e.  $T_{\rm eff} = 6750$ K and $\log~g = 4.25$. This is beyond the scope of our efforts since such 3D models are not yet available.

4.2 Influence of the mode mass

As discussed in details in Samadi et al. (2008a), the computed mode surface velocities $v_{\rm s}$ significantly depend on the choice of the height h in the atmosphere where the mode masses are evaluated. According to Samadi et al. (2008a), seismic measurements performed with the HARPS spectrograph reflect conditions slightly below the formation depth of the K line. Accordingly, we have evaluated by default the mode masses at the optical depth where the K line is expected to be formed (i.e.  $\tau_{\rm 500~nm} \simeq 0.013$), which corresponds, for our 3D models, to a height of about 350 km above the photosphere. We can evaluate how sensitive we are to the choice of h. Indeed, evaluating the mode mass at the photosphere results in values of $v_{\rm s}$which are about 15% lower and hence would reduce the discrepancy with the HARPS observations. On the other hand, evaluating the mode mass one pressure scale height ($\sim$300 km at the photosphere) above h = 350 km results in an increase of $v_{\rm s}$ of about 10%. A more rigorous approach to derive the different heights in the atmosphere where the measurements are sensitive would require a dedicated modeling (see a discussion in Samadi et al. 2008a).

4.3 The intensity-velocity relation

Sensitivity to the location:

the derivation of Eq. (4) (or equivalently Eq. (5)) is based on the assumption that $\delta T_{\rm eff} \propto \left . \delta T \right \vert _{T=T_{\rm eff}}$ (see Sect. 3.1). This is quite a arbitrary simplification. In order to check how sensitive our results are to this assumption, we have computed Eqs. (5) and (6) for two different positions in the atmosphere. The first position, h = h1, is chosen one pressure scale height ( ${\simeq}300$ km) above the photosphere, which corresponds to an optical depth of $\tau \sim 0.02$. The second position, h = h2, is chosen one pressure scale height beneath the photosphere, that is around $\tau \sim 200$. For both positions, the mode amplitudes with frequencies below ${\sim}1.9$ mHz are almost unchanged. Concerning the amplitudes of modes with frequencies above ${\sim}1.9$ mHz, they are increased by up to $\sim$20% when h=h1 and are in turn almost unchanged when h=h2. Since the fluctuations of L induced by the oscillations are mostly due to temperature changes that occur around an optical depth of the order of the unit, we can conclude that our calculations are almost insensitive to the choice of the layer in the visible atmosphere where $\delta T$ is evaluated.

Non-adiabatic effects:

the modes are measured at the surface of the star where non-adiabatic interactions between the modes and convection as well as radiative losses of the modes are important. Assuming Eq. (4) is then a crude approximation. In fact, it is clearly non-valid in the case of the Sun since it results in a severe over-estimation of the solar mode amplitudes in intensity (see Sect. 3.1). Avoiding this approximation requires non-adiabatic eigenfunctions computed with a time-dependent convection model. However, such models (e.g. Balmforth 1992; Grigahcène et al. 2005) are subject to large uncertainties, and there is currently no consensus about the non-adiabatic mechanisms that play a significant role (see e.g. the recent review by Houdek 2008). For instance, parameters are usually introduced in the theories so that they cannot be used in a predictive way.

In the present study, we adopt by default the adiabatic approximation and introduce in Eq. (5) the parameter $\beta$ calibrated with helioseismic data. We show here that despite the deficiency of the quasi-adiabatic approximation, it nevertheless provides the correct scaling, at least at low frequency and at the level of the present seismic precisions.

As an alternative approach, comparing the spectrum obtained from the 3D models in intensity with that obtained in velocity can provide valuable information concerning the intensity-velocity relation, in particular concerning the departure from the adiabatic approximation and the sensitivity to the surface metal abundance. We have started to carry out such a study. For the velocity, the (few) acoustic modes trapped in the simulated boxes can be extracted and their properties measured. But this was impossible to do for the intensity with the simulations at our disposal because the computed spectrum for the intensity is dominated by the granulation background. As a consequence it is not possible to extract the mode amplitudes in intensity with sufficient accuracy. A comparison between the spectra obtained from the 3D models requires a much longer time series (work in progress).

Sensitivity to the metal abundance:

we have shown in this study how the mode amplitudes in the velocity are sensitive to the surface metal abundance. An open question is how sensitive is the intensity-velocity relation in general to the metal abundance? A theoretical answer to this question would require a realistic and validated non-adiabatic treatment. The pure numerical approach mentionned above can also in principle provide some answers to this question. However, as discussed above, this approach is not applicable with the time series at our disposal. Concerning the quasi-adiabatic relation of Eq. (5): a change of the metal abundance has a direct effect on $\Gamma_3$ and an indirect effect on the properties of the (radial) eigen-displacement  $\xi_{\rm r}$. However, the comparison between the metal-poor 3D model (S1) and the 3D model with the solar abundances (S0) shows that - at a fixed frequency  $\omega_{\rm osc}$ - the ratio  $(\delta L/L) / v$, which is equal to $4 ~ \beta ~ (\Gamma_3-1) ~ ({\rm d} \xi_{\rm r}/ {\rm d} r)/ (\xi_{\rm r} ~ \omega_{\rm osc})$, is almost unchanged between S0 and S1 (the differences are less than $\sim$1%). In conclusion, the quasi-adiabatic relation of Eq. (5) depends very weakly on the surface metal abundance. Accordingly, the choice of the solar chemical mixture has a negligible impact on the value of the calibration factor $\beta$.

4.4 The solar case

As seen in this study, the surface metal abundance has a pronounced effect on the mode excitation rates. One may then wonder about the previous validation of the theoretical model of stochastic excitation in the case of the Sun (Belkacem et al. 2006; Samadi et al. 2008b). Indeed, this validation was carried out with the use of a solar 3D model based on an ``old'' solar chemical mixture (namely those proposed by Anders & Grevesse 1989) while the ``new'' chemical mixture by Asplund et al. (2005) is characterized by a significantly lower metal abundance.

In order to adress this issue, we have first considered two global 1D solar models. One model has an ``old'' solar abundance (Grevesse & Noels 1993, model  $M_{\rm old}$ hereafter) while the second one has the ``new'' abundances (Asplund et al. 2005, model  $M_{\rm new}$ hereafter). At the surface where the excitation occurs, the density of the solar model  $M_{\rm new}$ is only $\sim$5% lower compared to the model  $M_{\rm old}$. According to the arguments developed in Paper I, this difference in the density must imply a difference in the convective velocities ($\tilde u$) of the order of ${\sim}(\rho_{\rm old}/\rho_{\rm new})^{1/3}$, where  $\rho_{\rm old}$ (resp.  $\rho_{\rm new}$) is the surface density associated with  $M_{\rm old}$ (resp.  $M_{\rm new}$). Accordingly, $\tilde u$ is expected to be $\sim$1.7% higher for  $M_{\rm new}$ compared to  $M_{\rm old}$.

The next question is what is the change in the solar mode excitation rates induced by the above difference in $\tilde u$? We have computed the solar mode excitation rates exactly in the same manner as for HD 49333 by using a solar 3D simulations based on the ``old'' abundances. We obtained a rather good agreement with the different helioseismic data (see the result in Samadi et al. 2008b). To derive the solar mode excitations expected with the ``new'' solar abudance, we have proceeded in a similar way as the one done in Paper I: we have increased the convective velocity $\tilde u$ derived from the solar 3D model by 2% while keeping the kinetic flux constant (see details in Paper I). This increase of $\sim$2% of $\tilde u$ results in an increase of $\sim$10% of the mode excitation rates. This increase is significantly lower than the current uncertainties associated with the different helioseismic data (Baudin et al. 2005; Samadi et al. 2008b).

4.5 Discrepancy at high frequency

The discrepancy betwen theoretical calculations and observations is particularly pronounced at high frequency. This discrepancy may be attributed to a canceling between the entropy and the Reynolds stress contributions (see Sect. 4.5.1) or the ``scale length separation'' assumption (see Sect. 4.5.2).

4.5.1 Canceling between the entropy and the Reynolds stress contributions

The relative contribution of the entropy fluctuations to the excitation is found to be about 30% of the total excitation. This is two times larger than in the case of the Sun ($\sim$15%). This can be explained by the fact HD 49933 is significantly hotter than the Sun and, as pointed-out by Samadi et al. (2007), the larger $(L/M) \propto T_{\rm eff}^4/g$, the more important the relative contribution of the entropy. Although more important than in the Sun, the contribution of the entropy fluctuations remains relatively smaller than the uncertainties associated with the current seismic data. This is illustrated in Fig. 3: the difference between theoretical mode amplitudes which take into account only the Reynolds stress contribution ( $C_{\rm R}^2$, see Eq. (3) of Paper I) and those that include both contributions (entropy and Reynolds stress) is lower than $\sigma_v$. In terms of amplitudes, the entropy fluctuations contribute only $\sim$15% of the global amplitude. This is significantly smaller than the uncertainties associated with the current seismic measurements. Seismic data of a better quality are then needed to constrain the entropy contribution and its possible canceling with the Reynolds stress.

Numerical simulations show some cancellation between the entropy source term and the one due to the Reynolds stress (Stein et al. 2004). However, in the present theoretical model of stochastic excitation, the cross terms between the entropy fluctuations and the Reynolds stresses vanish (see Samadi & Goupil 2001). This is a consequence of the different assumptions concerning the entropy fluctuations (see Samadi & Goupil 2001; see also the recent discussion in Samadi et al. 2008b). Accordingly, the entropy source term is included as a source independent from the Reynolds stress contribution. As suggested by Houdek (2006), a partial canceling between the entropy fluctuations and the Reynolds stress can decrease the mode amplitudes of F-type stars and reduce the discrepancy between the theoretical calculations and the observations.

\begin{figure} \par\hspace*{-1mm}\includegraphics[width=8.5cm,clip]{11868fig5.eps}\vspace*{3mm} \includegraphics[width=8.4cm,clip]{11868fig6.eps} \end{figure} Figure 3:

Top: same as Fig. 1. The thin dashed line corresponds to a calculation that takes only the contribution of the Reynolds stress into account. The dot-dashed line corresponds to a calculation in which we have assumed that the contribution of the Reynolds stress interferes totally with that of the entropy fluctuations (see text). The thick solid line has the same meaning as in Fig. 1. Bottom: same as top for  $\delta L/L$. The triangles and associated error bars have the same meaning as in Fig. 2.

Open with DEXTER

There is currently no theoretical description of these interferences. In order to have an upper limit of the interferences, we assume that both contributions locally and fully interfer. This assumption leads to the computation of the excitation rates per unit mass as:

\begin{displaymath}% { {{\rm d} {\cal P}}\over {{\rm d} m}} = \left ( { {{\rm d}... ...t ( { {{\rm d} {\cal P}}\over {{\rm d} m}} \right )_{\rm E} } \end{displaymath} (8)

where $\left ( { {{\rm d} {\cal P}} / {{\rm d} m}} \right)_{\rm RS}$ and $\left ( { {{\rm d} {\cal P}} / {{\rm d} m}} \right )_{\rm E} $ are the contributions per unit mass of the Reynolds stress and entropy respectively. The result is presented in Fig. 3 in terms of velocity (top pannel) and in terms of intensity (bottom pannel). The mode amplitudes are decreased by up to ${\sim}55$%. In that case, $(\delta L/L)_{\rm CoRoT}$ is systematically under-estimated. Obviously, a partial canceling between the entropy contribution and the Reynolds stress would result in a smaller decrease.

We have assumed here that the cancellation between the two terms is independent of the mode frequency (see Eq. (8)). However, according to Stein et al. (2004), the level of the cancellation depends on the frequency (see their Fig. 8). In particular, for F-type stars, the cancellation is expected to be more important around and above the peak frequency.

As a conclusion, the existence of a partial canceling between the entropy fluctuations and the Reynolds stress can decrease the mode amplitude and could improve the agreement with the seismic observations at high frequency. However, there is currently no theoretical modeling of the interference between theses two terms. Further theoretical developements are required.

4.5.2 The ``scale length separation'' assumption

The ``scale length separation'' assumption (see the review by Samadi et al. 2008b) consists of the assumption that the eddies contributing effectively to the driving have a characteristic length scale smaller than the mode wavelength. This assumption is justified for a low Mach number ($M_{\rm t}$). However, this approximation is less valid in the super-adiabatic region where $M_{\rm t}$ reaches a maximum (for the Sun $M_{\rm t}$ is up to 0.3) and accordingly affects the high-frequency modes more. This approximation is then expected to be even more questionable for stars hotter than the Sun, since $M_{\rm t}$ increases with  $T_{\rm eff}$. This spatial separation can be avoided, however if the kinetic energy spectrum associated with the turbulent elements (E(k)) is properly coupled with the spatial dependence of the modes (work in progress). In that case, we expect a more rapid decrease of the driving efficiency with increasing frequency than in the present formalism where the spatial dependence of the modes is totally decoupled from E(k) (i.e. ``scale length separation'').

5 Conclusion

From the mode linewidths measured by CoRoT and theoretical mode excitation rates derived for HD 49933, we have derived the expected mode surface velocities $v_{\rm s}$ which we have compared with  $v_{\rm HARPS}$, the mode velocity spectrum derived from the seismic observations obtained with the HARPS spectrograph (Mosser et al. 2005). Except at high frequency ($\nu $ $\ga$ 1.9 mHz), the agreement between computed $v_{\rm s}$ and  $v_{\rm HARPS}$ is within the 1-$\sigma $ domain associated with the seismic data from the HARPS spectrograph. However, there is a clear tendency to overestimate  $v_{\rm HARPS}$ above $\nu $ $\sim$ 1.9 mHz.

Using a calibrated quasi-adiabatic approximation to relate the mode velocity to the mode amplitude in intensity (Eq. (5)), we have derived for the case of HD 49933 the expected mode amplitudes in intensity. Computed mode intensity fluctuations, $\delta L/L$, are within 1-$\sigma $ in agreement with the seismic constraints derived from the CoRoT data (Benomar et al. 2009). However, as for the velocity, there is a clear tendency at high frequency ($\nu $ $\ga$ 1.9 mHz) towards over-estimated $\delta L/L$ compared to the CoRoT observations.

Calculations that assume a solar surface metal abundance result, both in velocity and in intensity, in amplitudes larger by $\sim$35% around the peak frequency ( $\nu_{\rm max}$ $\simeq$ 1.8 mHz) and by up to a factor of two at lower frequency. It follows that, ignoring the current surface metal abundance of the star results in a more severe over-estimation of the computed amplitudes compared with observations. This illustrates the importance of taking the surface metal abundance of the solar-like pulsators into account when modeling the mode driving. In addition, we point out that the Grevesse & Noels (1993) solar chemical mixture results in mode amplitudes larger by about 15% with respect to calculations that assume the ``new'' solar abundance by Asplund et al. (2005). However, this increase remains significantly smaller than the uncertainties associated with current seismic measurements.

Since both mode amplitudes in terms of surface velocity and intensity are available for this star, it was possible to test the validity of the calibrated quasi-adiabatic relation (Eq. (5)). Our comparison shows that this relation provides the correct scaling, at least at the level of the present seismic precisions.

Both in terms of surface velocity and of intensity, the differences between predicted and observed mode amplitudes are within the 1-$\sigma $ uncertainty domain, except at high frequency. This result then validates for low frequency modes the basic underlying physical assumptions included in the theoretical model of stochastic excitation for a star significantly different in effective temperature, surface gravity, turbulent Mach number ($M_{\rm t}$) and metallicity compared to the Sun or $\alpha$ Cen A.

As discussed in Sect. 4, the clear discrepancy between predicted and observed mode amplitudes seen at high frequency may have two possible origins: first, a canceling between the entropy contribution and the Reynolds stress is expected to occur and to be important around and above the frequency of the maximum of the mode excitation rates (see Sect. 4.5.1). Second, the assumption called the ``scale length separation'' (Samadi et al. 2008b) may also result in an over-estimation of the mode amplitudes at high frequency (see Sect. 4.5.2). These issues will be investigated in a forthcoming paper.

Acknowledgements
The CoRoT space mission, launched on December 27 2006, has been developed and is operated by CNES, with the contribution of Austria, Belgium, Brasil, ESA, Germany and Spain. We are grateful to the referee for his pertinent comments. We are indebted to J. Leibacher for his careful reading of the manuscript. K.B. acknowledged financial support from Liège University through the Subside Fédéral pour la Recherche 2009.

References

  1. Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
  2. Appourchaux, T., Michel, E., Auvergne, M., et al. 2008, A&A, 488, 705 [Google Scholar]
  3. Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ed. T. G. Barnes, III, & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]
  4. Balmforth, N. J. 1992, MNRAS, 255, 603 [NASA ADS] [CrossRef] [Google Scholar]
  5. Baudin, F., Samadi, R., Goupil, M.-J., et al. 2005, A&A, 433, 349 [Google Scholar]
  6. Belkacem, K., Samadi, R., Goupil, M. J., Kupka, F., & Baudin, F. 2006, A&A, 460, 183 [Google Scholar]
  7. Benomar, O., Baudin, F., Campante, T., et al. 2009, A&A, 507, L13 [Google Scholar]
  8. Christensen-Dalsgaard, J., & Gough, D. O. 1982, MNRAS, 198, 141 [NASA ADS] [CrossRef] [Google Scholar]
  9. Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements, ed. N. Prantzos, E. Vangioni-Flam, & M. Cassé (Cambridge University Press), 15 [Google Scholar]
  10. Grigahcène, A., Dupret, M.-A., Gabriel, M., Garrido, R., & Scuflaire, R. 2005, A&A, 434, 1055 [Google Scholar]
  11. Houdek, G. 2006, in Proceedings of SOHO 18/GONG 2006/HELAS I, Beyond the spherical Sun, Published on CDROM, ESA SP, 624, 28.1 [Google Scholar]
  12. Houdek, G. 2008, Commun. Asteroseismol., 157, 137 [NASA ADS] [Google Scholar]
  13. Houdek, G., Balmforth, N. J., Christensen-Dalsgaard, J., & Gough, D. O. 1999, A&A, 351, 582 [Google Scholar]
  14. Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [Google Scholar]
  15. Kjeldsen, H., Bedding, T. R., Butler, R. P., et al. 2005, ApJ, 635, 1281 [NASA ADS] [CrossRef] [Google Scholar]
  16. Kjeldsen, H., Bedding, T. R., Arentoft, T., et al. 2008, ApJ, 682, 1370 [NASA ADS] [CrossRef] [Google Scholar]
  17. Michel, E., Baglin, A., Auvergne, M., et al. 2008, Science, 322, 558 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  18. Michel, E., Samadi, R., Baudin, F., et al. 2009, A&A, 495, 979 [Google Scholar]
  19. Mosser, B., Bouchy, F., Catala, C., et al. 2005, A&A, 431, L13 [Google Scholar]
  20. Samadi, R., & Goupil, M. . 2001, A&A, 370, 136 [Google Scholar]
  21. Samadi, R., Georgobiani, D., Trampedach, R., et al. 2007, A&A, 463, 297 [Google Scholar]
  22. Samadi, R., Belkacem, K., Goupil, M. J., Dupret, M.-A., & Kupka, F. 2008a, A&A, 489, 291 [Google Scholar]
  23. Samadi, R., Belkacem, K., Goupil, M.-J., Ludwig, H.-G., & Dupret, M.-A. 2008b, Commun. Asteroseismol., 157, 130 [NASA ADS] [Google Scholar]
  24. Samadi, R., Ludwig, H.-G., Belkacem, K., Goupil, M., & Dupret, M.-A. 2010, A&A, 509, A15 (Paper I) [Google Scholar]
  25. Stein, R., Georgobiani, D., Trampedach, R., Ludwig, H.-G., & Nordlund, Å. 2004, Sol. Phys., 220, 229 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... HD 49933[*]
The CoRoT space mission, launched on December 27 2006, has been developped and is operated by CNES, with the contribution of Austria, Belgium, Brasil, ESA, Germany and Spain.

All Figures

  \begin{figure} \par\hspace*{2mm}\includegraphics[width=8.2cm,clip]{11868fig1.eps}\vspace*{3mm} \includegraphics[width=8.5cm,clip]{11868fig2.eps} \end{figure} Figure 1:

Top: intrinsic mode surface velocity as a function of the mode frequency ($\nu $). The filled circles connected by the thick solid line correspond to the mode surface velocity ($v_{\rm s}$) derived for HD 49933 according to Eq. (1), where the mode excitation rates ${\cal P}$ are derived as explained in Paper I and the mode linewidths and their associated error bars are derived by Benomar et al. (2009) from the CoRoT data. The thick dashed line corresponds to the mode velocity associated with the model with [Fe/H] = 0. The thick and red solid line corresponds to the amplitude spectrum derived from the seismic observations obtained with the HARPS spectrograph (see text). The dotted line corresponds to the 1-$\sigma $ domain associated with this measurement. Bottom: differences between $v_{\rm s}$ and  $v_{\rm HARPS}$. The 1-$\sigma $ error bars correspond to $\sigma _v \equiv \sqrt { \Delta v_{\rm s}^2 + \Delta v_{\rm HARPS}^2}$ (see text).

Open with DEXTER
In the text

  \begin{figure} \par\hspace*{2.5mm}\includegraphics[width=8.3cm,clip]{11868fig3.eps}\vspace*{3mm} \includegraphics[width=8.5cm,clip]{11868fig4.eps} \end{figure} Figure 2:

Top: mode bolometric amplitude in intensity as a function of the mode frequency ($\nu $). The filled circles connected by the thick solid line correspond to the mode amplitudes in intensity, $\delta L/L$, derived for HD 49933 according to Eqs. (5) and (1) where the mode surface velocity v is evaluated at the photosphere. The thick dashed solid line corresponds to the mode amplitude in intensity associated with the model with [Fe/H] = 0. The red triangles and associated error bars correspond to the mode amplitudes in intensity, $(\delta L/L)_{\rm CoRoT}$, obtained from the CoRoT data (Benomar et al. 2009). These measurements have been translated into bolometric amplitudes following Michel et al. (2009). Bottom: same as top for the difference between  $\delta L/L$ and  $(\delta L/L)_{\rm CoRoT}$. The 1-$\sigma $ error bars correspond here to $\sqrt {a ^2 + b ^2}$ where $a \equiv \Delta (\delta L/L)$ and $b \equiv \Delta (\delta L/L)_{\rm CoRoT}$ (see text).

Open with DEXTER
In the text

  \begin{figure} \par\hspace*{-1mm}\includegraphics[width=8.5cm,clip]{11868fig5.eps}\vspace*{3mm} \includegraphics[width=8.4cm,clip]{11868fig6.eps} \end{figure} Figure 3:

Top: same as Fig. 1. The thin dashed line corresponds to a calculation that takes only the contribution of the Reynolds stress into account. The dot-dashed line corresponds to a calculation in which we have assumed that the contribution of the Reynolds stress interferes totally with that of the entropy fluctuations (see text). The thick solid line has the same meaning as in Fig. 1. Bottom: same as top for  $\delta L/L$. The triangles and associated error bars have the same meaning as in Fig. 2.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.