EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 509 (January 2010) A&A, 509 (2010) A18 Full HTML
Free Access
Issue
A&A
Volume 509, January 2010
Article Number A18
Number of page(s) 14
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/200911671
Published online 12 January 2010
A&A 509, A18 (2010)

Relativistic apsidal motion in eccentric eclipsing binaries[*]

M. Wolf1 - A. Claret2 - L. Kotková3 - H. Kucáková4 - R. Kocián4 - L. Brát5 - P. Svoboda6 - L. Smelcer7

1 - Astronomical Institute, Faculty of Mathematics and Physics, Charles University Prague, 18000 Praha 8, V Holesovickách 2, Czech Republic
2 - Instituto de Astrofísica de Andalucía, CSIC, Apartado 3004, 18080 Granada, Spain
3 - Astronomical Institute, Academy of Sciences, Fricova 298, 25165 Ondrejov, Czech Republic
4 - Johann Palisa Observatory and Planetarium, Technical University Ostrava, 70833 Ostrava, Czech Republic
5 - Private Observatory, Velká Úpa 193, 54221 Pec pod Snezkou, Czech Republic
6 - Private Observatory, Výpustky 5, 61400 Brno, Czech Republic
7 - Observatory Valasské Mezirící, Vsetínská 78, 75701 Valasské Mezirící, Czech Republic

Received 16 January 2009 / Accepted 3 October 2009

Abstract
Context. The study of apsidal motion in detached eclipsing binary systems is known to be an important source of information about stellar internal structure as well as the possibility of verifying of General Relativity outside the Solar System.
Aims. As part of the long-term Ondrejov and Ostrava observational projects, we aim to measure precise times of minima for eccentric eclipsing binaries, needed for the accurate determination of apsidal motion, providing a suitable test of the effects of General Relativity.
Methods. About seventy new times of minimum light recorded with photoelectric or CCD photometers were obtained for ten eccentric-orbit eclipsing binaries with significant relativistic apsidal motion. Their O-C diagrams were analysed using all reliable timings found in the literature, and new or improved elements of apsidal motion were obtained.
Results. We confirm very long periods of apsidal motion for all systems. For BF Dra and V1094 Tau, we present the first apsidal-motion solution. The relativistic effects are dominant, representing up to 100% of the total observable apsidal-motion rate in several systems. The theoretical and observed values of the internal structure constant k2 were compared for systems with lower relativistic contribution. Using the light-time effect solution, we predict a faint third component for V1094 Tau orbiting with a short period of about 8 years.

Key words: binaries: eclipsing - stars: general - stars: fundamental parameters - relativity

1 Introduction

The apsidal motion in eccentric eclipsing binaries (hereafter EEB) is not only caused by the combined effect of the tidal distortion and rotational flattening of components. There is a subgroup amongst EEB, in which apsidal advance period is dominantly affected by the relativistic contribution. It is well known that these systems can provide additional confirmation of General Relativity outside the Solar System. A good review of apsidal-motion tests in close binaries was presented by Giménez (2007).

All EEB analysed here have properties that make them important relativistic laboratories for verifying General Relativity. In particular, ten northern hemisphere objects are relatively bright, eclipsing binaries with orbital periods in the range 4-15 days. Most systems are also included in the list of EEB suitable for studies of the relativistic apsidal motion (Giménez 1985, 1994) as well as in the latest catalogue of EEB (Bulut & Demircan 2007). This study is part of a series of papers on apsidal motion, where we present the results of our long-term photometric monitoring of EEB eclipses (Wolf et al. 2001, 2004, 2005). Similar studies of relativistic apsidal motion in individualbinary systems were published by Giménez & Margrave (1985), Giménez et al. (1987), and Claret (1997, 1998). Regularly updated ephemeris, based on all compiled times of minima, can be found in the database of the O-C diagrams (Kreiner 2004)[*].

2 Observations of minimum light

Over the past 15 years, we have accumulated over 5000 photometric observations at selected phases during primary and secondary eclipses and derived over 70 precise times of minimum light for specific eccentric systems. This observational programme utilizes only moderately sized or small telescopes equipped with a photoelectric photometer or a CCD camera. Moreover, a large amount of observing time is needed, which is unavailable presently at large telescopes but is more practical for small amateur telescopes equipped with modern detectors.

New photoelectric or CCD photometry was obtained at several different observatories:

$\bullet$Ondrejov Observatory, Czech Republic: the 0.65-m reflecting telescope with the CCD camera SBIG ST-8 or Apogee AP7 and Johnson VR filters.

$\bullet$ Hvar Observatory, Croatia: the 0.65-m Cassegrain telescope with the single-channel photoelectric photometer housing an EMI 9789 QB photomultiplier and Johnson's UBV filters.

$\bullet$ Johann Pallisa Observatory and Planetarium Ostrava, Czech Republic: 0.2-m or 0.3-m telescopes with the CCD camera SBIG ST-8XME and VRI filters.

$\bullet$ Observatory Valasské Mezirící, Czech Republic: the 0.3-m Celestron Ultima telescope with the CCD camera SBIG ST-7 and RI filters.

$\bullet$ Private observatory of LB at Pec pod Snezkou, Czech Republic: 0.2-m Cassegrain telescope with the CCD cameras SBIG ST-8 or G2-402 and VRI filters.

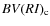$\bullet$ Private observatory of PS at Brno, Czech Republic: 0.2-m Cassegrain telescope with the CCD camera ST-7XME and Johnson-Cousins $BV(RI)_{\rm c}$ filters.
CCD measurements at most observatories were flat-fielded using sky exposures taken at either dusk or dawn. Several comparison stars were chosen in the same frame as the variables. No variations in the brightness of these stars exceeding the expected error of measurements were detected (typically $\sigma \simeq 0.007$ mag in Ondrejov). The C-Munipack[*] (Motl 2007), a user-friendly software package, was used to reduce most of our CCD images. No correction for differential extinction was applied, because of the proximity of the comparison stars to the variable and the resulting negligible differences in air mass.

Table 1:   Apsidal-motion elements for ten selected eclipsing systems.

The new times of primary and secondary minima and their errors were generally determined by the classical Kwee-van Woerden (1956) algorithm. In some cases (Hipparcos data, scattered points), the light-curve fitting by polynomials of the third or fourth order and the least squares method were used. All new times are given in Table A.1. In general, only the bottom parts of the eclipses were used. All epochs in Table A.1 are calculated from the light elements given in Table 1, and the other columns are self-explanatory.

3 Apsidal motion analysis

The motion of the apsis of a binary star is a direct consequence of the finite size of its components. This effect has been known for a long time (Cowling 1938; Sterne 1939). The rate of motion of the apsis is dependent on the internal structure of each component. Determination of the characteristics of a binary thus provides an observational test of the theory of stellar structure and evolution. Moreover, there is a relativistic contribution to the periastron advance in a way similar to what occurs in the orbit of the planet Mercury.

The apsidal motion in all systems was studied by means of an O-C diagram analysis. The method described by Giménez & García-Pelayo (1983), which is a weighted least squares iterative procedure, including terms in eccentricity up to the fifth order, was slightly modified. There are in principle five independent variables $(T_0, P_{\rm s}, e, \dot{\omega}, \omega_0)$ determined in this procedure. The values of eccentricity e and the length of periastron $\omega_0$ were fixed if known by the previous light curve or radial velocity curve solution. The periastron position $\omega$ at epoch E is defined by the linear equation

\begin{displaymath}\omega = \omega_0 + \dot{\omega}\ E, \end{displaymath}

where $\dot{\omega}$ is the rate of periastron advance, and the position of periastron for the zero epoch T0 is denoted by $\omega_0$. The relation between the sidereal and the anomalistic period, $P_{\rm s}$ and $P_{\rm a}$, is given by

\begin{displaymath}P_{\rm s} = P_{\rm a} ~(1 - \dot{\omega}/360^\circ), \end{displaymath}

and the period of apsidal motion by

\begin{displaymath}U = 360^\circ P_{\rm s}/\dot{\omega}. \end{displaymath}

We collected all CCD and photoelectric times of minimum light available in the literature. Their weights are given directly by the inverse of the sigma squared. The earlier visual and photographic times (especially the times of the mid-exposure of a photographic plate) were not used in our calculations because of the large scatter in these data.

3.1 IT Cas

The detached and double-lined eclipsing binary IT Cassiopeiae (also GSC 3650.0959, FL 3517, $V_{\max} = 11$ $^{\rm m}\!\!.$2, Sp. F5V+F5V) is a relatively well-known and frequently observed eclipsing binary with an eccentric orbit (e = 0.08) and orbital period of about 4 days. It was first discovered to be a spectroscopic binary by Fadeeva (Parenago 1939). Busch (1975a) obtained a photographic light curve, which was later measured photoelectricaly by Khaliullin & Kozyreva (1989). Holmgren & Wolf (1996) analysed the O-C diagram and found a relatively short period of apsidal motion $U = 404 \pm 63$ years. See also history summarized in that paper. Accurate masses and radii was determined spectroscopically by Lacy et al. (1997), who detected components of similar mass and size (see Table 3). They also excluded the previous reports of $\delta$ Scuti variations. Kozyreva & Zakharov (2001) obtained WBVR photoelectric measurements and determined the longer apsidal-motion period of $U = 3300 \pm 750$ years.

Apart from the minima given in Table A.1, we add numerous times of minimum obtained by several observers: Lacy et al. (1997, their Table 4, 1998, 2001), Agerer & Hübscher (2003), Diethelm (2003), Nakajima (2003)[*], Hübscher (2005), Hübscher et al. (2005), Smith & Caton (2007), and Hübscher & Walter (2007). A total of 95 times of minimum are now available, of which 51 correspond to primary eclipses and 44 to secondary eclipses (Table A.2). The computed apsidal-motion elements and their internal errors in the least squares fit (in brackets) are given in Table 1. In this table, $P_{\rm s}$ denotes the sidereal period, e represents the eccentricity, and $\dot{\omega}$ is the rate of periastron advance (in degrees per cycle). The zero epoch is given by T0, and the corresponding position of the periastron is represented by $\omega_0$.

The O-C residuals for all times of minimum with respect to the linear part of the apsidal-motion equation (O-C diagram, ephemeris curve) are shown in Fig. 1. The non-linear predictions, corresponding to the fitted parameters, are plotted as continuous and dashed curves for primary and secondary eclipses, respectively.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{1671fig1.eps} \vspace*{3.5mm} \end{figure} Figure 1:

The O-C diagram for the times of minimum of IT Cas. The continuous and dashed lines represent predictions for the primary and secondary eclipses, respectively. The individual primary and secondary minima are denoted by circles and triangles, respectively. Larger symbols correspond to the photoelectric or CCD measurements, which were given higher weights in the calculations.

Open with DEXTER

3.2 V459 Cas

The double-lined and detached eclipsing binary V459 Cassiopeiae (also BV 5, CSV 5894, FL 83, $V_{\rm max} = 10$ $^{\rm m}\!\!.$33, Sp. A1V+A1V) is a known close binary system with a slightly eccentric orbit (e=0.024) and a longer orbital period of about 8.5 days. It was discovered to be variable by Strohmeier (1955). The first light elements were measured by Meinunger & Wenzel (1967), who also recognized that the orbit is eccentric. Moments of photographic minima were then determined by Busch (1976ba). Precise absolute dimensions of the components of V459 Cas were derived spectroscopically by Lacy et al. (2004), who detected components of similar mass and size (see Table 3) and a period of apsidal motion U = 6100 yr. The apsidal motion in V459 Cas was later studied by Dariush et al. (2006), who confirmed the slow rate $\dot{\omega} = 19\hbox{$.\!\!^\circ$ }8$ per century and found a discrepancy with the theory of stellar structure.

Since the above-mentioned papers were published, a substantial number of new times of minima have been obtained, which have allowed us to reduce the observational uncertainties. Using the Hipparcos photometry (ESA 1997), we were able to derive three additional times of minimum light using the light-curve profile fitting method. Besides those minima given in Table A.1, we have added numerous times of minimum obtained by Lacy et al. (2004, their Table 1), Lacy (2004), Hübscher (2005), Hübscher & Walter (2007), Sobotka (2007), and Brát et al. (2007). A total of 91 times of minimum light were found with 37 secondary eclipses among them (Table A.3). The orbital inclination was adopted to be $i = 89\hbox{$.\!\!^\circ$ }47$, based on the photometric analysis (Lacy et al. 2004). The computed apsidal-motion parameters and their internal errors in the least squares fitting are given in Table 1, and the corresponding O-C diagram is shown in Fig. 2.

3.3 V541 Cyg

The detached eclipsing binary V541 Cygni (also SVS 1034, BD$+30^\circ$3704, and FL 2814; $V_{\max} = 10$ $^{\rm m}\!\!.$35, Sp. B9.5V+B9.5V) is also a relatively well-known eclipsing binary with a highly eccentric orbit (e = 0.48) and a long orbital period of about 15.34 days. It was discovered to be a variable star by Kulikowski (1948), photographic observations later being obtained by Karpowicz (1961) and Wachmann (1961). The very slow apsidal motion in V541 Cyg and its important relativistic contribution was studied by Wolf (1995) and Guinan et al. (1996). A review of studies of this binary can be found in Lacy (1998), where precise absolute parameters are given (see Table 3). Volkov & Khaliullin (1999) later confirmed the slow apsidal motion $\dot{\omega} = 0.86 \pm 0.05 \hbox{$^\circ$ }$/100 years, obtaining good agreement with their theoretical results.

We include all times of minimum light collected in Lacy (1998, his Table 3), Volkov & Khaliullin (1999, their Table 1), and Smith & Caton (2007) as well as our new timings given in Table A.1. The orbital inclination was assumed to be $i = 89\hbox{$.\!\!^\circ$ }88$, based on the last photometric analysis of Lacy (1998). In total, 56 minimum light times were collected in our analysis, with 30 primary eclipses among them (Table A.4). The resulting apsidal-motion parameters are given in Table 1, and the O-C diagram is shown in Fig. 3.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{1671fig2.eps} % \end{figure} Figure 2:

O-C diagram of V459 Cas. See legend to Fig. 1.

Open with DEXTER

3.4 V1143 Cyg

The detached and double-lined eclipsing binary V1143 Cygni (also HD 185912, BD$+54^\circ$2193, HR 7484, HIP 96620, and FL 2597; $V_{\rm max} = 5$ $^{\rm m}\!\!.$86, Sp. F5V+F5V) is a bright and well-known binary system of high orbital eccentricity (0.54) and a rather long orbital period of 7.6 days. It was discovered to be an eclipsing binary by Snowden (1966), although it was already known to be a double-line spectroscopic binary (Harper 1919, 1935). The analysis of the radial velocity curve and UBV photometry was performed by Snowden & Koch (1969). The relativistic apsidal motion in V1143 Cyg was studied by Giménez & Margrave (1985) with good agreement with theoretical results. The physical properties of the system were later carefully derived by Andersen et al. (1987). The next apsidal-motion study was presented by Burns et al. (1996), who obtained the apsidal-motion rate of $\dot{\omega} = 3\hbox{$.\!\!^\circ$ }52$/100 yr. Finally, a light-curve analysis and apsidal-motion study was published by Dariush et al. (2005) with good agreement with results of previous investigators. The reader is also referred to the history of work on this binary described in the paper of Giménez & Margrave (1985).

New primary minimum was measured photoelectrically at Hvar Observatory, Croatia, in October 2008. The nearby comparison star HD 185978 = BD$+53^\circ$2282 (Sp.F8, V = 7 $^{\rm m}\!\!.$88, $B\!-\!V$ = 0 $^{\rm m}\!\!.$49, $U\!-\!B$ = 0 $^{\rm m}\!\!.$07) - used also in the previous photometric study of Burns et al. (1996) - was used during these UBV observations, which consisted of 10-s integrations in each filter. They were carefully reduced to the standard $U\!B{}V$ system and corrected for differential extinction using the reduction program HEC 22 rel. 16.1[*]. The standard errors of these measurements were about 0.011, 0.008, and 0.006 mag in the U, B, and V filters, respectively.

Using the Hipparcos photometry (ESA 1997), we were able to derive one additional time of minimum light, and two revised precise CCD times of minima obtained at Pec in September 2005 are given in Table A.1. All photoelectric times of minimum light given in Giménez & Margrave (1985, their Table 1), Guinan et al. (1987), Caton & Burns (1993), Lacy & Fox (1994), Burns et al. (1996), Hegedüs et al. (1996), Dariush et al. (2001, 2003, 2005, their Tables 2 and 3) were included in this dataset. The orbital inclination $i = 87\hbox{$.\!\!^\circ$ }3$ was taken from Dariush et al. (2004). A total of 35 times of minimum light were collected in our analysis, 10 secondary eclipses being among them (Table A.5). The computed apsidal-motion parameters are given in Table 1, and the O-C graph is shown in Fig. 4.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{1671fig3.eps}\vspace*{3.5mm} \end{figure} Figure 3:

O-C diagram of V541 Cyg. See legend for Fig. 1.

Open with DEXTER

3.5 V1147 Cyg

The detached eclipsing binary V1147 Cygni (also HBV 423, $V_{\max} = 12$ $^{\rm m}\!\!.$0, Sp. A) is a faint, poorly studied binary system with a moderate orbital eccentricity ( $e \simeq 0.28$) and a long orbital period of 15.25 days. It was discovered as variable by Wachmann (1961), Chinarova (1997) later publishing a photographic light curve based on Odessa Sky Patrol photographic plates. The CCD photometry was obtained by Bloomer et al. (1998), who found the correct period. Wetterer et al. (2006) presented the photometric study and derived the slow apsidal motion of about $0\hbox{$.\!\!^\circ$ }80$ per century.

We used all times of minima published in Wachmann (1966), Chinarova (1997), Bloomer et al. (1998), and Wetterer et al. (2006, their Table 2) as well as our new times obtained at Ondrejov and Pec observatories in our analysis. The orbital inclination was adopted to be $i = 89\hbox{$.\!\!^\circ$ }7$, based on the photometric study of Wetterer et al. (2006). Altogether, 49 times of minimum light were collected, including 20 secondary eclipses (Table A.6). The calculated apsidal-motion parameters are given in Table 1, and the O-C diagram is shown in Fig. 5.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{1671fig4.eps}\vspace*{3.5mm} \end{figure} Figure 4:

O-C graph for V1143 Cyg. See legend to Fig. 1.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{1671fig5.eps} % \end{figure} Figure 5:

O-C diagram for the times of minimum of V1147 Cyg. See legend to Fig. 1.

Open with DEXTER

3.6 BF Dra

The detached and double-lined eclipsing binary BF Draconis (also BD$+69^\circ$1006, HIP 92489, BV 379, $V_{\max}$ = 9 $^{\rm m}\!\!.$83, Sp. F8) is a poorly studied eccentric binary system with a high eccentricity ( $e \simeq 0.4$) and a longer orbital period of about 11.2 days. It was discovered to be a variable star by Strohmeier et al. (1962). Döpner (1962) measured the light elements using an incorrect orbital period of 5.6 days. In his spectroscopic analysis, Imbert (1985) obtained the precise physical properties of both components and derived the correct period. Diethelm et al. (1993) obtained a photoelectric light curve and confirmed the existence of an eccentric orbit.

Using the Hipparcos photometry (ESA 1997), we were able to derive one additional time of secondary minimum using the light-curve profile fitting method, in addition to precise CCD times obtained at Ondrejov, Ostrava and Brno observatories. Numerous precise times of minima presented in Agerer & Hübscher (1998), Caton & Smith (2005), Lacy (2006), Brát et al. (2007), Lacy (2007), as well as Smith & Caton (2007) were used in our analysis. Additional CCD photometry of BF Dra was obtained by Mr. Kamil Hornoch on Dec. 9, 2002 and Jan. 17, 2003. The observations were carried out with the 35-cm reflecting telescope and the SBIG ST-8 CCD camera at Lelekovice, Czech Republic. The star GCS 4435.426, observed also in previous photometric measurements of Diethelm et al. (1993), was targeted. Altogether 65 times of minimum light were collected in our dataset, 36 primary and 29 secondary eclipses being among them (Table A.7). The orbital inclination was assumed to be $i \simeq 90\hbox{$^\circ$ }$, because lack of a precise light curve analysis. It is known that the apsidal-motion solution is practically insensitive to relatively large changes in inclination, but strongly depends on the orbital eccentricity. The resulting apsidal-motion parameters are given in Table 1, and the O-C graph is shown in Fig. 6.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{1671fig6.eps}\vspace*{3.5mm} \end{figure} Figure 6:

O-C graph for BF Dra. See legend to Fig. 1.

Open with DEXTER

3.7 V345 Lac

The detached eclipsing binary V345 Lacertae (also GSC 3986.2900, FL 3354, $V_{\rm max}$ = 11 $^{\rm m}\!\!.$3, Sp. B8) is a relatively little know early-type eccentric binary with a high orbital eccentricity $e \simeq 0.45$ and a longer orbital period of about 7.5 days. It was discovered to be a variable star photographically by Miller & Wachmann (1973). The photographic light curve and new times of minimum light were later derived by Busch (1978) from the plates of Sonnenberg and Hartha Observatories. Wolf et al. (2004) presented an O-C diagram analyses and found the slow apsidal motion with a period of $U = 7000 \pm 700$ years with the substantial relativistic contribution.

Our previous times of minima given in Wolf et al. (2004, Table A.1) as well as new timings published in Caton & Smith (2005), Smith & Caton (2007), and Hübscher et al. (2008) were included. Two new additional CCD times of minimum light obtained at Ostrava observatory are given in Table A.1. A total of 72 times of minimum light were collected in our analysis, with 33 secondary eclipses among them (Table A.8). The orbital inclination was assumed to be $i = 90\hbox{$^\circ$ }$, bacause of the absence of a photometric analysis of this system to date. The computed apsidal-motion parameters are given in Table 1, and the O-C graph is shown in Fig. 7.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{1671fig7.eps} % \end{figure} Figure 7:

O-C graph for V345 Lac. See legend to Fig. 1.

Open with DEXTER
\begin{figure} \par\includegraphics[width=8.5cm,clip]{1671fig8.eps}\vspace*{3.5mm} \end{figure} Figure 8:

O-C diagram for EW Ori. See legend to Fig. 1.

Open with DEXTER

3.8 EW Ori

The detached and double-lined eclipsing binary EW Orionis (also HD 287727, BD$+01^\circ$0976, HBV 421, $V_{\rm max} = 9$ $^{\rm m}\!\!.$9, Sp. G0+G5) is another relatively neglected binary system with a modest eccentric orbit (e = 0.08) and a longer orbital period of about 7 days. It was discovered to be a variable star by Hoffmeister (1930), and later visual observations were provided by Lause (1937), Gaposchkin (1953), and Kordylewski (1962). The first photoelectric observations were obtained by Pierce (1951), and photographic moments of minima were later determined by Busch (1976b). Radial velocities and two-colour V,R photometry of EW Ori were analysed by Popper et al. (1986). The relativistic apsidal motion was studied by Wolf et al. (1997), who found a very slow apsidal motion of period $U = 160~000 \pm 40~000$ years.

All precise times of minima given in Wolf et al. (1997), Agerer & Hübscher (2003), and Smith & Caton (2007) as well as our new times obtained at Ondrejov and Ostrava observatories were included. A total of 65 times of minimum light were collected in our database, with 45 primary and 20 secondary eclipses among them (Table A.9). The orbital inclination was assumed to be $i = 89\hbox{$.\!\!^\circ$ }8$, based on the photometric analysis of Popper et al. (1986). The computed apsidal-motion parameters are given in Table 1, and the O-C graph is shown in Fig. 8.

3.9 GG Ori

The detached and double-lined eclipsing binary GG Orionis (also HD 290842, $V_{\rm max}$ = 10 $^{\rm m}\!\!.$37, Sp. B9.5V+B9.5V) is poorly studied binary with an orbit of moderate eccentricity ( $e \simeq 0.22 $), as a probable member of the Orion OB1 association. It was discovered to be a variable star by Hoffmeister (1934) at Sonneberg Observatory. The correct orbital period of P = 6.631 days was first determined by Kordylewski (1951). Numerous moments of photographic minima were determined by Busch (1975a), but the first photoelectric light curve in UBVR was presented later by Zakirov (1997). The absolute dimensions were derived spectroscopically in Torres et al. (2000), who obtained the precise masses given in Table 3 as well as an apsidal period of $U = 10~470 \pm 4500$ yr (see also bibliography on GG Ori published in that paper). Additional WBVR photoelectric photometry was obtained by Volkov & Khaliullin (2002), who also confirmed a slow apsidal motion $0\hbox{$.\!\!^\circ$ }046 \pm 0\hbox{$.\!\!^\circ$ }005$ per year with a dominant relativistic contribution.

All new precise times of minima published in Zakirov (1997), Torres et al. (2000, their Table 3), Volkov & Khaliullin (2002, their Table 7), Caton & Smith (2005), Hübscher et al. (2006), Nakajima (2006)[*], Mossakovskaya (2006), as well as Hübscher & Walter (2007) were included in our analysis. In total 85 times of minimum light were collected in this dataset (Table A.10), 43 secondary eclipses being among them. The orbital inclination was assumed to be $i = 89\hbox{$.\!\!^\circ$ }3$, based on the comprehensive study of Torres et al. (2000). The apsidal-motion parameters are given in Table 1, and the O-C graph is shown in Fig. 9.

3.10 V1094 Tau

\begin{figure} \par\includegraphics[width=8.5cm,clip]{1671fig9.eps}\vspace*{3.5mm} \end{figure} Figure 9:

O-C graph for GG Ori. See legend to Fig. 1.

Open with DEXTER

The detached eclipsing binary V1094 Tauri (also HDE 284195, BD$+21^\circ$605, DHK 41, $V_{\rm max} = 8$ $^{\rm m}\!\!.$96, Sp. G0+G3) is a newly discovered binary (Kaiser 1994) with a longer orbital period ( $P \simeq 9.0$ day), which is a possible member of the Hyades star cluster. With its long period of almost precisely an integer number of days, V1094 Tau is a difficult object to study with light curve photometry. Its absolute dimensions were derived spectroscopically by Griffin & Boffin (2003), where the precise value of eccentricity e = 0.2697(18) and the length of periastron $\omega = 333\hbox{$.\!\!^\circ$ }2(3)$ are in accordance with our own results.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{1671figa.eps}\vspace*{3.5mm} \end{figure} Figure 10:

O-C diagram for V1094 Tau. See legend to Fig. 1.

Open with DEXTER

All times of minima presented in Kaiser et al. (1995, their Table 1), Kaiser & Frey (1998, their Table 1), Lacy (2002, 2003), Hübscher (2005), and Hübscher et al. (2005) as well as our new times obtained at Ondrejov were included in the final data set (Table A.11). Only 18 times of minimum light were collected in our analysis, with 9 secondary eclipses among them. The orbital inclination was assumed to be $i = 90\hbox{$^\circ$ }$, because of absence to date of a photometric analysis of this system. The calculated apsidal-motion parameters are given in Table 1, and the O-C graph is shown in Fig. 10.

By subtracting the slow apsidal motion in the previous O-C diagram, we also tried to ascertain the light-time effect (LITE) and the possible presence of a third body in this system. A preliminary solution of the LITE in V1094 Tau is given in Table 2, where P3 is the orbital period of the third body, A is a semi-amplitude, and e3 is an orbital eccentricity. Assuming a coplanar orbit ( $i_3 = 90 \hbox{$^\circ$ }$) and the total mass of the eclipsing pair M1 + M2 = 2.11 $M_{\odot}$ (Griffin & Boffin 2003), we obtain a lower limit to the mass of the third component $M_{3,{\rm min}}$.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{1671figb.eps}\vspace*{3.5mm} \end{figure} Figure 11:

O-C2 residuals for the times of minimum of V1094 Tau after subtraction of apsidal motion. The sinusoidal curve represents a light-time effect for the possible third-body circular orbit with a short period of about 8 yr and an amplitude of about 4 min.

Open with DEXTER

Table 2:   Third-body orbit in V1094 Tau.

The deviations of the O-C residuals from the apsidal motion for V1094 Tau are plotted in Fig. 11. The third component may be a red dwarf of a spectral type M 7-M 8 with a bolometric magnitude of about +11.2 mag (Harmanec 1988), hardly detectable in the G0+G3 binary system.

Table 3:   Adopted masses of the selected EEB and their classical and relativistic apsidal motion.

4 Discussion

The observable apsidal motion in close binaries is not only due to the combined effect of tidal distortion and rotational flattening of components. An independent contribution is represented by general relativistic equations of motion. The total observable rate of apsidal motion is equal to

\begin{displaymath}\dot{\omega}_{\rm obs} = \dot{\omega}_{\rm cl} + \dot{\omega}_{\rm rel}, \end{displaymath} (1)

where $\dot{\omega}_{\rm cl}$ denotes the classical or Newtonian contribution and $\dot{\omega}_{\rm rel}$ is the relativistic term. The relativistic contribution was first derived by Levi-Civita (1937), and later presented in Giménez (1985). The classical or Newtonian contribution is given by

\begin{displaymath}\dot{\omega}_{\rm cl} = 360 (c_{21} k_{21} + c_{22} k_{22}), \end{displaymath} (2)

where k2i are the second-order internal structure constants of each component, which can be evaluated from theoretical models by numerical integration of the Radau differential equation. The c2i coefficients are a known function of the mass ratio, the orbital eccentricity, and the relative radii (Kopal 1978). The values of $\dot{\omega}_{\rm cl}$, $\dot{\omega}_{\rm rel}$, and their percentage of the total apsidal rate for systems under study and several known EEB are given in Table 3. The values of $\dot{\omega}_{\rm obs}$ and $\dot{\omega}_{\rm rel}$ are compared in Fig. 12.

\begin{figure} \par\includegraphics[width=7.5cm,clip]{1671figc.eps} \vspace*{3.5mm} \end{figure} Figure 12:

A comparison between total observed and computed relativistic apsidal motion.

Open with DEXTER

Before comparing the theoretical and observed k2, we carried out a careful comparison of the theoretical and observed absolute dimensions of each system. The comparison with the absolute dimensions of some systems can be found in Claret & Willems (2002) and in Claret (1997). The absolute dimensions of the remaining systems were compared with theoretical values and we found good agreement between values for a given isochrone, as required.

The stellar models were computed for the precise observed masses. The apsidal-motion test will only be reliable if the adopted stellar models are capable of reproducing the absolute dimensions. The grids of stellar models used here are based on the code described in detail in Claret (2004). The convective core overshooting is introduced by means of an excess distance beyond the classical convective border (see also Claret 2007). This distance is defined as $d_{\rm over} = \alpha_{\rm ov} H_{\rm p}$, where $H_{\rm p}$ is the pressure scale height taken at the edge of the convective core given by Schwarzschild's criterion and $\alpha_{\rm ov} = 0.20$ is a free parameter. The tables of opacities are those taken from Iglesias & Rogers (1996), completed by the calculations by Alexander & Ferguson (1994) for lower temperatures.

The observed k2 of the systems IT Cas, V459 Cas, V541 Cyg, RW Lac, and EW Ori show large discrepancies (and large relativistic contributions) compared with their theoretical counterparts, and the remaining systems are displayed in Fig. 13. The agreement can be considered to be good and perfectly within the error bars, except in the case of BW Aqr. This confirms the results obtained by Claret (1997) for systems with moderate relativistic contributions and accurate absolute dimensions. However, for the 5 systems mentioned above the situation is different: the discrepancies are large, in the sense that the true stars seems to be more mass-concentrated than theoretically predicted. For V541 Cyg, when we consider only the hypothetical case of no distortional contribution, it is possible to fit the observed k2.

Table 4:   Observed and theoretical internal structure constants of selected EEB.

\begin{figure} \par\includegraphics[width=7.5cm,clip]{1671figd.eps}\vspace*{3.5mm} \end{figure} Figure 13:

A comparison between theoretical and observed internal structure constants.

Open with DEXTER

When the relativistic contribution is large, the error in $\log k_{\rm 2,obs}$ is also large and no significant interpretation can be derived from the comparison with the predictions of the theoretical models. Even so, some information can be extracted, such as for example, that the observed k2 are systematically smaller than their theoretical counterparts (see Table 4). This trend that real stars seem to be more mass-concentrated than predicted by the stellar models, is well known (see for example, Claret & Giménez 1993). However, the systems investigated in that paper did not have high relativistic contributions. For systems with the high relativistic contributions, several hypotheses were proposed to explain this type of discrepancy, particularly inthe case of DI Her (Claret 1998 and references): the inclination of the axes of rotation, rapid circularization of the orbit, the presence of a circumstellar cloud in the system, a third star, and the use of an alternative theory of gravitation. Concerning the alternative theory of gravitation, there are several problems in its formalism, as pointed out by Claret (1998).

An additional explanation of the large discrepancies may be related to observational aspects of the apsidal-motion rates. Indeed, the time dedicated to observe the apsidal-motion of the problematic systems is small compared to the period U. This could lead to poor results. In addition, different techniques and instruments (with different detectors and different levels of confidence) were used. The position of the longitude of periastron can also influence the measurement of the apsidal-motion rates. We refer the interested reader to the paper by Claret (1998) for a more detailed discussion of the subject. More accurate determination of the apsidal-motion rates is necessary to elucidate the reasons for these discrepancies.

5 Conclusions

The apsidal motion in eccentric eclipsing binaries has been used for decades to test evolutionary stellar models. This study provides accurate information about the relativistic apsidal motion of twenty main-sequence eclipsing binary systems (Table 3). We confirmed the long apsidal-motion periods for all systems under study reaching 50 000 years. For the systems BF Dra and V1094 Tau, the new periods of the apsidal motion have been derived. Compared to similar studies by previous authors, the database has been enlarged in time by at least 500 orbital cycles.

All of the analysed binaries contain an important relativistic contribution of up to 100% of the total apsidal-motion rate, but there is no case of an anomalously slow rate (Fig. 12). Some systems with a very high relativistic contribution (IT Cas, V459 Cas, V541 Cyg, RW Lac, and RW Ori) show large discrepancies with theoretical predictions. Moreover, our results indicate that the system V1094 Tau is probably a member of an interesting group of triple or multiple EEB (e.g., RU Mon, U Oph, YY Sgr, and DR Vul) illustrating various phenomena of celestial mechanics and meriting a regular photometric and spectroscopic monitoring. Because of the insufficient coverage of the ephemeris curve, the results for V1147 Cyg and V1094 Tau must be considered preliminary. More than 20 years has elapsed since the last similar studies of several of these binaries by Giménez & Margrave (1985) and Giménez et al. (1987). Additional observations will be needed to increase the data coverage of the apsidal motion periods as well as to derive accurate absolute dimensions and orbital parameters.

Acknowledgements
This investigation was supported by the Grant Agency of the Czech Republic, grants Nos. 205/04/2063 and 205/06/0217. The research of MW was also supported by the Research Program MSM0021620860 of the Ministry of Education of the Czech Republic. The authors would like to thank Mr. Jirí Kohoutek, Tomás Hynek and Tomás Kalisch, Ostrava Observatory, Mr. Kamil Hornoch, Ondrejov Observatory, and Dr. Miloslav Zejda, Masaryk University Brno, for their important help with photometric observations.

The following internet-based resources were used in research for this paper: the SIMBAD database and the VizieR service operated at CDS, Strasbourg, France; the NASA's Astrophysics Data System Bibliographic Services; the O-C Gateway of the Czech Astronomical Society (http://var.astro.cz/ocgate/); the BAV and BBSAG Bulletins. We gratefully acknowledge very useful suggestions by the referee, Prof. Álvaro Giménez.

Appendix A: Tables of minima

Table A.1:   New times of minimum light.

Table A.2:   The list of minima timings of IT Cas.

Table A.3:   The list of minima timings of V459 Cas.

Table A.4:   The list of minima timings of V541 Cyg.

Table A.5:   The list of minima timings of V1143 Cyg.

Table A.6:   The list of minima timings of V1147 Cyg.

Table A.11:   The list of minima timings of V1094 Tau.

References

  1. Agerer, F., & Hübscher, J. 1998, IBVS, 4562 [Google Scholar]
  2. Agerer, F., & Hübscher, J. 2003, IBVS, 5484 [Google Scholar]
  3. Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] [Google Scholar]
  4. Andersen, J., Clausen, J. V., & Nordström, B. 1984, A&A, 134, 147 [Google Scholar]
  5. Andersen, J., García, J. M., Giménez, A., et al. 1987, A&A, 174, 107 [Google Scholar]
  6. Bakis, V., Zejda, M., Bulut, I., et al. 2008, MNRAS, 390, 399 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bloomer, R., Wetterer, C., Mumpower, A., et al. 1998, IBVS, 4568 [Google Scholar]
  8. Brát, L., Zejda, M., & Svoboda, P. 2007, OEJV, 74, 1 [NASA ADS] [Google Scholar]
  9. Bulut, I., & Demircan, O. 2007, MNRAS, 378, 179 [NASA ADS] [CrossRef] [Google Scholar]
  10. Burns, J. F., Guinan, E. F., & Marshall, J. J. 1996, IBVS, 4363 [Google Scholar]
  11. Busch, H. 1975a, Mitt. Bruno-H.-Bürgel-Sternwarte Hartha, 9, 2 [Google Scholar]
  12. Busch, H. 1975b, Mitt. Bruno-H.-Bürgel-Sternwarte Hartha, 9, 18 [Google Scholar]
  13. Busch, H. 1976a, Mitt. Bruno-H.-Bürgel-Sternwarte Hartha, 10, 1 [Google Scholar]
  14. Busch, H. 1976b, Mitt. Bruno-H.-Bürgel-Sternwarte Hartha, 10, 11 [Google Scholar]
  15. Busch, H. 1978, Mitt. Bruno-H.-Bürgel-Sternwarte Hartha, 13, 20 [Google Scholar]
  16. Caton, D. B., & Burns, W. C. 1993, IBVS, 3900 [Google Scholar]
  17. Caton, D. B., & Smith, A. B. 2005, IBVS, 5595 [Google Scholar]
  18. Chinarova, L. 1997, IBVS, 4455 [Google Scholar]
  19. Claret, A. 1997, A&A, 327, 11 [Google Scholar]
  20. Claret, A. 1998, A&A, 330, 533 [Google Scholar]
  21. Claret, A. 2004, A&A, 424, 919 [Google Scholar]
  22. Claret, A. 2007, A&A, 475, 1019 [Google Scholar]
  23. Claret, A., & Giménez, A. 1993, A&A, 277, 487 [Google Scholar]
  24. Claret, A., & Willems, B. 2002, A&A, 388, 518 [Google Scholar]
  25. Clausen, J. V. 1991, A&A, 246, 397 [Google Scholar]
  26. Clausen, J. V., Vaz, L. P. R., García, J. M., et al. 2008, A&A, 487, 1081 [Google Scholar]
  27. Cowling, T. G. 1938, MNRAS, 98, 734 [NASA ADS] [Google Scholar]
  28. Dariush, A., Afroozeh, A., & Riazi, N. 2001, IBVS, 5136 [Google Scholar]
  29. Dariush, A., Mosleh, M., & Dariush, D. 2006, Ap&SS, 305, 85 [Google Scholar]
  30. Dariush, A., Riazi, N., & Afroozeh, A. 2005, Ap&SS, 296, 141 [Google Scholar]
  31. Dariush, A., Zabihinpoor, S. M., Bagheri, M. R., et al. 2003, IBVS, 5456 [Google Scholar]
  32. Diethelm, R. 2003, IBVS, 5438 [Google Scholar]
  33. Diethelm, R., Wolf, M., & Agerer, F. 1993, IBVS, 3867 [Google Scholar]
  34. Döppner, M. 1962, Mitt. Veränderliche Sterne No. 699 [Google Scholar]
  35. ESA 1997, The Hipparcos and Tycho Catalogues, ESA SP-1200 [Google Scholar]
  36. Gaposchkin, S. 1953, Ann. Harvard Coll. Obs., 113, 2 [Google Scholar]
  37. Giménez, A. 1985, ApJ, 297, 405 [NASA ADS] [CrossRef] [Google Scholar]
  38. Giménez, A. 1994, Exp. Astron., 5, 91 [Google Scholar]
  39. Giménez, A. 2007, in Binary Stars as Critical Tools & Tests, ed. W. Hartkopf, E. Guinan, & P. Harmanec, Proc. IAU Symp. 240, 290 [Google Scholar]
  40. Giménez, A., & García-Pelayo, J. M. 1983, Ap&SS, 92, 203 [Google Scholar]
  41. Giménez, A., & Margrave, T. E. 1985, AJ, 90, 358 [NASA ADS] [CrossRef] [Google Scholar]
  42. Giménez, A., Kim, C.-H., & Nha, I.-S. 1987, MNRAS, 224, 543 [NASA ADS] [CrossRef] [Google Scholar]
  43. Griffin, R. F., & Boffin, H. M. J. 2003, Observatory, 123, 203 [Google Scholar]
  44. Guinan, E. F., Boyd, P. T., Najafi, S. I., et al. 1987, IBVS, 3070 [Google Scholar]
  45. Guinan, E. F., Maley, J. A., Marshall, J. J. 1996, IBVS, 4362 [Google Scholar]
  46. Harmanec, P. 1988, Bull. Astr. Inst. Czech. 39, 329 [Google Scholar]
  47. Harper, W. E. 1919, Publ. Dom. Astrophys. Obs. Victoria, 1, 157 [NASA ADS] [Google Scholar]
  48. Harper, W. E. 1935, Publ. Dom. Astrophys. Obs. Victoria, 6, 207 [Google Scholar]
  49. Hegedüs, T., Biró, I. B., Borkovits, T., et al. 1996, IBVS, 4340 [Google Scholar]
  50. Hoffmeister, C. 1930, Astron. Nachr., 238, 190 [NASA ADS] [Google Scholar]
  51. Hoffmeister, C. 1934, Astron. Nachr., 253, 195 [NASA ADS] [CrossRef] [Google Scholar]
  52. Holmgren, D., & Wolf, M. 1996, Observatory, 116, 307 [NASA ADS] [Google Scholar]
  53. Hübscher, J. 2005, IBVS, 5643 [Google Scholar]
  54. Hübscher, J. & Walter, F. 2007, IBVS, 5761 [Google Scholar]
  55. Hübscher, J., Paschke, A., & Walter, F. 2005, IBVS, 5657 [Google Scholar]
  56. Hübscher, J., Paschke, A., & Walter, F. 2006, IBVS, 5731 [Google Scholar]
  57. Hübscher, J., Steinbach, H.-M., & Walter, F. 2008, IBVS, 5830 [Google Scholar]
  58. Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
  59. Imbert, M. 1985, A&AS, 59, 357 [Google Scholar]
  60. Kaiser, D. H. 1994, IBVS, 4119 [Google Scholar]
  61. Kaiser, D. H., & Frey, G. 1998, IBVS, 4544 [Google Scholar]
  62. Kaiser, D. H., Terrell, D., Baldwin, M. E. et al. 1995, IBVS, 4168 [Google Scholar]
  63. Karpowicz, M. 1961, Acta Astron., 11, 51 [NASA ADS] [Google Scholar]
  64. Khaliullin, Kh. F., & Khaliullina, A. I. 2002, Astron. Rep., 46, 137 [CrossRef] [Google Scholar]
  65. Khaliullin, Kh. F., & Kozyreva, V. S. 1989, Ap&SS, 155, 53 [Google Scholar]
  66. Kopal, Z. 1978, Dynamics of Close Binary Systems (Holland, Dordrecht: Reidel) [Google Scholar]
  67. Kordylewski, K. 1951, Acta Astron. Ser. C, 4, 134 [Google Scholar]
  68. Kordylewski, K. 1962, Acta Astron. Suppl., 5, 610 [Google Scholar]
  69. Kozyreva, V. S., & Zakharov, A. I. 2001, Astron. Lett., 27, 712 [NASA ADS] [CrossRef] [Google Scholar]
  70. Kreiner, J. M. 2004, Acta Astron., 54, 207 [NASA ADS] [Google Scholar]
  71. Kulikowski, P. G. 1948, Perem. Zvezdy, 6, 101 [Google Scholar]
  72. Kwee, K. K., & van Woerden, H. 1956, Bull. Astron. Inst. Netherlands, 12, 327 [Google Scholar]
  73. Lacy, C. H. S. 1998, AJ, 115, 801 [Google Scholar]
  74. Lacy, C. H. S. 2002, IBVS, 5357 [Google Scholar]
  75. Lacy, C. H. S. 2003, IBVS, 5487 [Google Scholar]
  76. Lacy, C. H. S. 2004, IBVS, 5577 [Google Scholar]
  77. Lacy, C. H. S. 2006, IBVS, 5670 [Google Scholar]
  78. Lacy, C. H. S. 2007, IBVS, 5764 [Google Scholar]
  79. Lacy, C. H. S., & Fox, G. W. 1994, IBVS, 4009 [Google Scholar]
  80. Lacy, C. H. S., Torres, G., Latham, D. W., et al. 1997, AJ, 114, 1206 [Google Scholar]
  81. Lacy, C. H. S., Clem, J. L., Zakirov, M., et al. 1998, IBVS, 4597 [Google Scholar]
  82. Lacy, C. H. S., Hood, B., & Straughn, A. 2001, IBVS, 5067 [Google Scholar]
  83. Lacy, C. H. S., Claret, A., & Sabby, J. A. 2004, AJ, 128, 1340 [NASA ADS] [CrossRef] [Google Scholar]
  84. Lacy, C. H. S., Torres, G., & Claret, A., et al. 2005, AJ, 130, 2838 [NASA ADS] [CrossRef] [Google Scholar]
  85. Lause, F. 1937, Astron. Nachr., 263, 115 [NASA ADS] [CrossRef] [Google Scholar]
  86. Levi-Civita, T. 1937, Amer. J. Math., 59, 225 [CrossRef] [Google Scholar]
  87. Meinunger, L., & Wenzel, W. 1967, Mitt. Veränderliche Sterne, 4, 141 [Google Scholar]
  88. Miller, W. J., & Wachmann, A. A. 1973, Ric. Astr. Specola Vaticana 8, 18 [Google Scholar]
  89. Mossakovskaja, L. V. 2006, IBVS, 5675 [Google Scholar]
  90. Motl, D. 2007, C-M UNIPACK, http://c-munipack.sourceforge.net/ [Google Scholar]
  91. Parenago, P. P. 1939, Perem. Zvezdy, 5, 161 [Google Scholar]
  92. Pierce, N. L. 1951, Princeton Contr., 25, 93 [Google Scholar]
  93. Popper, D. M. 1987, AJ, 93, 672 [NASA ADS] [CrossRef] [Google Scholar]
  94. Popper, D. M., Lacy, C. H., Frueh, M. L., et al. 1986, AJ, 91, 383 [NASA ADS] [CrossRef] [Google Scholar]
  95. Smith, A. B., & Caton, D. B. 2007, IBVS, 5745 [Google Scholar]
  96. Snowden, M. S. 1966, IBVS, 217 [Google Scholar]
  97. Snowden, M. S., & Koch, R. H. 1969, ApJ, 156, 667 [NASA ADS] [CrossRef] [Google Scholar]
  98. Sobotka, P. 2007, IBVS, 5809 [Google Scholar]
  99. Sterne, T. E. 1939, MNRAS, 99, 662 [NASA ADS] [Google Scholar]
  100. Strohmeier, W. 1955, Kleine Veröff. Remeis-Sternw. Bamberg, No. 9 [Google Scholar]
  101. Strohmeier, W., Knige, R., & Ott, H. 1962, Bamberg Veröffent. V, No. 14 [Google Scholar]
  102. Torres, G., Lacy, C. H. S., Claret, A., et al. 2000, AJ, 120, 3226 [NASA ADS] [CrossRef] [Google Scholar]
  103. Volkov, I. M., & Khaliullin, Kh. F. 1999, IBVS, 4680 [Google Scholar]
  104. Volkov, I. M., & Khaliullin, Kh. F. 2002, Astron. Rep., 46, 747 [NASA ADS] [CrossRef] [Google Scholar]
  105. Wachmann, A. A. 1961, Astron. Abh. Hamburger Sternw., 6, 78 [Google Scholar]
  106. Wachmann, A. A. 1966, Astron. Abh. Hamburger Sternw., 6, 281 [NASA ADS] [Google Scholar]
  107. Wetterer, Ch. J., Bloomer, R. H., & Caton, D. B. 2006, PASP, 118, 436 [NASA ADS] [CrossRef] [Google Scholar]
  108. Wolf, M. 1995, IBVS, 4217 [Google Scholar]
  109. Wolf, M., Sarounová, L., Kozyreva, V. S., et al. 1997, IBVS, 4542 [Google Scholar]
  110. Wolf, M., Diethelm, R., & Hornoch, K. 2001, A&A, 374, 243 [Google Scholar]
  111. Wolf, M., Harmanec, P., Sarounová, L., et al. 2004, A&A, 420, 619 [Google Scholar]
  112. Wolf, M., Diethelm, R., & Zejda, M. 2005, Ap&SS, 296, 109 [Google Scholar]
  113. Zakirov, M. M. 1997, Pisma Astrophys. Zh., 23, 626 [NASA ADS] [Google Scholar]

Footnotes

... binaries[*]
Partly based on photoelectric observations secured at the Hvar Observatory, Faculty of Geodesy, Zagreb, Croatia, in October 2008.
...2004)[*]
http://www.as.wsp.krakow.pl/o-c/index.php3
... C-Munipack[*]
http://c-munipack.sourceforge.net/
... (2003)[*]
http://www.ztv.ne.jp/web/K.Nakajima/light_curve.htm
... rel. 16.1[*]
http://astro.troja.mff.cuni.cz/ftp/hec/HEC22/
... (2006)[*]
http://www.ztv.ne.jp/web/K.Nakajima/light_curve.htm

All Tables

Table 1:   Apsidal-motion elements for ten selected eclipsing systems.

Table 2:   Third-body orbit in V1094 Tau.

Table 3:   Adopted masses of the selected EEB and their classical and relativistic apsidal motion.

Table 4:   Observed and theoretical internal structure constants of selected EEB.

Table A.1:   New times of minimum light.

Table A.2:   The list of minima timings of IT Cas.

Table A.3:   The list of minima timings of V459 Cas.

Table A.4:   The list of minima timings of V541 Cyg.

Table A.5:   The list of minima timings of V1143 Cyg.

Table A.6:   The list of minima timings of V1147 Cyg.

Table A.11:   The list of minima timings of V1094 Tau.

All Figures

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1671fig1.eps} \vspace*{3.5mm} \end{figure} Figure 1:

The O-C diagram for the times of minimum of IT Cas. The continuous and dashed lines represent predictions for the primary and secondary eclipses, respectively. The individual primary and secondary minima are denoted by circles and triangles, respectively. Larger symbols correspond to the photoelectric or CCD measurements, which were given higher weights in the calculations.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1671fig2.eps} % \end{figure} Figure 2:

O-C diagram of V459 Cas. See legend to Fig. 1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1671fig3.eps}\vspace*{3.5mm} \end{figure} Figure 3:

O-C diagram of V541 Cyg. See legend for Fig. 1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1671fig4.eps}\vspace*{3.5mm} \end{figure} Figure 4:

O-C graph for V1143 Cyg. See legend to Fig. 1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1671fig5.eps} % \end{figure} Figure 5:

O-C diagram for the times of minimum of V1147 Cyg. See legend to Fig. 1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1671fig6.eps}\vspace*{3.5mm} \end{figure} Figure 6:

O-C graph for BF Dra. See legend to Fig. 1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1671fig7.eps} % \end{figure} Figure 7:

O-C graph for V345 Lac. See legend to Fig. 1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1671fig8.eps}\vspace*{3.5mm} \end{figure} Figure 8:

O-C diagram for EW Ori. See legend to Fig. 1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1671fig9.eps}\vspace*{3.5mm} \end{figure} Figure 9:

O-C graph for GG Ori. See legend to Fig. 1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1671figa.eps}\vspace*{3.5mm} \end{figure} Figure 10:

O-C diagram for V1094 Tau. See legend to Fig. 1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1671figb.eps}\vspace*{3.5mm} \end{figure} Figure 11:

O-C2 residuals for the times of minimum of V1094 Tau after subtraction of apsidal motion. The sinusoidal curve represents a light-time effect for the possible third-body circular orbit with a short period of about 8 yr and an amplitude of about 4 min.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{1671figc.eps} \vspace*{3.5mm} \end{figure} Figure 12:

A comparison between total observed and computed relativistic apsidal motion.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{1671figd.eps}\vspace*{3.5mm} \end{figure} Figure 13:

A comparison between theoretical and observed internal structure constants.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.