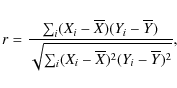EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 509 (January 2010) A&A, 509 (2010) A85 Full HTML
Free Access
Issue
A&A
Volume 509, January 2010
Article Number A85
Number of page(s) 7
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/200911649
Published online 22 January 2010
A&A 509, A85 (2010)

Hydrodynamic simulations of correlation and scatter in galaxy cluster maps

A. Finoguenov1,2 - A. J. R. Sanderson3 - J. J. Mohr4,1 - J. J. Bialek5 - A. Evrard5

1 - Max-Planck-Institut für extraterrestrische Physik, Giessenbachstraße, 85740 Garching, Germany
2 - University of Maryland Baltimore County, 1000 Hilltop circle, Baltimore, MD 21250, USA
3 - School of Physics and Astronomy, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK
4 - Department of Physics, Ludwig-Maximilians-Universitaet, Scheiner Strasse 1, 81679 Munich, Germany
5 - Physics Department, University of Michigan, Ann Arbor, MI 48109; Astronomy Department, University of Michigan, Ann Arbor, MI 48109; Michigan Centre for Theoretical Physics, Ann Arbor, MI 48109, USA

Received 12 January 2009 / Accepted 24 November 2009

Abstract
Aims. The two dimensional structure of hot gas in galaxy clusters contains information about the hydrodynamical state of the cluster, which can be used to understand the origin of scatter in the thermodynamical properties of the gas, and to improve the use of clusters to probe cosmology.
Methods. Using a set of hydrodynamical simulations, we provide a comparison between various maps currently employed in the X-ray analysis of merging clusters and those cluster maps anticipated from forthcoming observations of the thermal Sunyaev-Zel'dovich effect.
Results. We show the following: 1) an X-ray pseudo-pressure, defined as square root of the soft band X-ray image times the temperature map is a good proxy for the SZ map; 2) we find that clumpiness is the main reason for deviation between X-ray pseudo-pressure and SZ maps; 3) the level of clumpiness can be well characterized by X-ray pseudo-entropy maps; 4) we describe the frequency of deviation in various maps of clusters as a function of the amplitude of the deviation. This enables both a comparison to observations and a comparison to effects of introduction of complex physical processes into simulation.

Key words: galaxies: clusters: general - cosmology: theory - cosmology: observations - X-rays: galaxies: clusters

1 Introduction

The X-ray emission from clusters of galaxies has been conventionally characterized in terms of an X-ray surface brightness image and a temperature map. Historically, due to the success of the Einstein (Gursky et al. 1972) and ROSAT (Boehringer et al. 2000, 2001) missions, X-ray imaging data are available for a wide range of clusters, both in mass and redshift, while cluster searches based on the level of X-ray emission have become one of the primary cosmological tools (for a review see Borgani & Guzzo 2001).

The availability of cluster temperatures, on the other hand, has long been limited to single emission-weighted values, as provided by Ginga, Einstein and EXOSAT (David et al. 1993; Edge et al. 1992), and although the first temperature maps were made with ROSAT (Briel & Henry 1994) and ASCA (Markevitch 1996, 1999) data, they were limited in either spectral range (ROSAT) or spatial resolution (ASCA). With the advent of Chandra and XMM-Newton, temperature maps have become widely available, revealing an unprecedented amount of detail (Vikhlinin et al. 2001; Mazzotta et al. 2002; Briel et al. 2004; Finoguenov et al. 2004; Henry et al. 2004). However, neither temperature maps nor X-ray images are the primary characteristics of the gas, and are instead results of underlying pressure and entropy distribution, that trace the dark matter potential, reflect the thermodynamical history of the gas and the on-going magneto-hydrodynamical processes. However, projection effects complicate this study and in practice X-ray pseudo pressure and entropy maps have been introduced (Markevitch et al. 1996; Finoguenov et al. 2004, 2005, 2006a,b, 2007; Briel et al. 2004; Henry et al. 2004), addressing an immediate goal of discriminating between the various origins of fluctuations, e.g. to differentiate between shocks and gas displacement, also known as cold fronts (Vikhlinin et al. 2001). The way these maps work is that at the position of the cold front the contrast in the entropy map is increased, while the contrast in the pressure map is removed, compared to either images or temperature maps, while on the positions of the weak shocks, the contrast in the entropy maps is suppressed, while the contrast on the pressure map is enhanced. Some astonishing discoveries using these maps were made using very deep XMM observations of M 87, recovering the details of AGN feedback (Simionescu et al. 2007) and the underlying triaxiality of the dark matter distribution.

These pressure and entropy distributions are called pseudo maps to reflect the fact that both pressure and entropy are local quantities, while the projected emission weighted temperature and X-ray surface brightness are averaged along the line of sight. The effect of projection in reducing the fluctuation has been found to be a function of the spatial scale of fluctuation (Schuecker et al. 2004), with small-scale fluctuations being more strongly suppressed. Since all cluster maps suffer from projection effects, it is important to understand the link between various methods of studying clusters, such as thermal SZ, weak lensing and X-ray.

In order to improve our understanding of cluster physics, we employ a set of hydrodynamical simulations to study how well various cluster maps compare. We paid a particular attention on possible use of cluster maps for diagnostics not readily available to the observer. In Sect. 2, we describe the simulation sample. In Sect. 3 we look for correlation among the maps, discuss the general trends and look for correlations of deviations from the general trends. We also present the statistical expectation for deviations to occur as a function of their strength. We summarize our findings in Sect. 4.

2 Mock observations

We use a catalog of 68 galaxy clusters evolved with the P3MSPH code (Evrard 1988, 1990), incorporating preheating of the ICM to mimic the effects of galaxy feedback. The level of entropy introduced into the initial conditions is tuned to 106 keV cm2 in order to match the observed scalings of luminosity and ICM mass with temperature (Bialek et al. 2001). No additional AGN feedback and radiative cooling has been included into the simulations.

\begin{figure} \par\includegraphics[height=17.1cm]{11649_fig1.ps} \end{figure} Figure 1:

Example of the cluster maps in one of the simulation runs. From the top left to the bottom right we show the dark matter column density, gas column density, X-ray images in the 0.5-2 keV band, X-ray temperature map, pseudo entropy map, pseudo pressure map, Compton Y map, clumpiness map, ratio of Compton Y to X-ray image. The grey scale is set to depict the central structure in black in all the maps.

Open with DEXTER
\begin{figure} \par\mbox{\includegraphics[width=8cm]{11649_fig2a.ps}\hfill \includegraphics[width=8cm]{11649_fig2b.ps} } \end{figure} Figure 2:

The distribution of correlation coefficients between various simulated maps for each of the 68 simulated clusters, calculated using Eq. (1). Left panel represents correlations between dark matter column density and each of the pressure (solid), Compton Y (dashed) and square root of the X-ray surface brightness $I_{\rm X}^{0.5}$(dotted). Right panel represents correlations between Compton Y and each of the pressure (solid) and $I_{\rm X}^{0.5}$ (dotted). The dashed line shows a correlation between the ratio of Compton Y and X-ray surface brightness with pseudo entropy. All comparisons are carried out within 1/4 of r200.

Open with DEXTER

The simulations were produced using a multi-step procedure outlined in Bialek et al. (2001). A single cluster from this dataset was found to exhibit a post-merger cold front/features driven by sub-halo sloshing, as presented in Bialek et al. (2002) and further detailed in Pawl et al. (2005). The simulations evolve isolated cut-outs of a larger N-body realization, with regions chosen such that final halo masses are sampled with roughly equal likelihood across the mass range $M_{200} = 0.2{-}2 \times 10^{15}~M_\odot$. The runs are of moderate resolution, with gravitational softenings between 50 and 150 kpc, and dark matter particle masses of $0.4{-}4 \times 10^{10}~M_\odot$. While Lewis et al. (2000) caution that large softening can affect the overall cluster potential, the comparison study of Frenk et al. (1999) demonstrates that moderate resolution runs offer good convergence in dark matter and gas properties on scales larger than roughly twice the hydrodynamic smoothing scale.

A typical halo is resolved by $\sim$50 000 particles. With preheating of 106 keV cm-2, this is sufficient to resolve low-order measures of ICM properties, such as temperature and luminosity, and morphological features driven by mergers with mass ratios of order 0.1 and larger. The underlying cosmology is a flat, concordance model with $\Omega_{\rm m} = 0.3$, $\Omega_{\Lambda} = 0.7$, $\Omega_{b} = 0.03$, $\sigma_8 = 1.0$, and h = 0.7, where the Hubble constant is defined as 100 h km s-1 Mpc-1and $\sigma_8$ is the power spectrum normalization on 8 h-1 Mpc scales. Details of the full ensemble are presented on the project web-page[*].

In this paper we only used the final (z=0) configuration of 68 model clusters and employ 3 orthogonal projections of each model as independent data, giving a total of 204 separate datasets. Every map has 256 pixels on a side, spanning a region twice the virial radius of the system. By construction the maps are designed to study the appearance of individual clusters and not the projected effects in cluster surveys (e.g. White 2003). From an initial set of X-ray surface brightness (I) and temperature maps (T), we have constructed the X-ray pseudo pressure and entropy maps (hereafter P and S, respectively) as P=I1/2*T and S=T/I1/3 and compared those to the column density of the both ionized gas (G) and dark matter (DM), as well as the predicted Compton Y parameter of the thermal Sunyaev-Zel'dovich (SZ; Sunyaev & Zel'dovich 1980) effect (Y). We define the clumpiness as $C = G / \sqrt{I}$, which differs from its exact definition by the square root of the projection length. In Fig. 1 we show the simulated cluster maps obtained for the g1 run, 1st projection.

The dark matter maps in simulations appear much clumpier compared to the gas. This is likely due to erosion of small-scale structure in the gas by setting the entropy floor. A careful comparison between dark matter subhalos and the hot gas has been made in Powell et al. (2009). Using the case of one halo simulated with and without cooling, they show that occupation of small subhalos by hot gas is efficiently suppressed under both treatments. Dark matter maps of cluster are thus likely to appear clumpier than the X-ray gas irrespective of the detailed gas physics assumptions. Near equilibrium, the gas will trace the equipotential surfaces, which tend to be smoother and rounder than the density isosurfaces. In order to remove the small-scale power in the comparison, we have convolved the dark matter maps with the Gaussian. The members of the simulated sample range in spectral temperature from 1.5 keV to about 8 keV, with cluster masses M200ranging from (0.015-2.4)  $\times 10^{15}~M_{\odot}$. The derived images, along with associated parameters describing the simulations are publicly available as part of VCE, the Virtual Cluster Exploratory[*].

3 Results

For each simulated cluster we can quantify the correlation between the different maps within a fixed fraction of the virial radius. We use the following expression for the correlation coefficient between images X and Y for a given cluster

\begin{displaymath} r = {\sum_i ( X_i-\overline{X}) ( Y_i- \overline{Y}) \over \sqrt{\sum_i ( X_i- \overline{X})^2 ( Y_i- \overline{Y})^2 }} , \end{displaymath} (1)

where i sums over all the pixels in the image. We search for correlations between all primary maps. The distribution of correlation coefficients across the ensemble of simulated clusters is shown in Fig. 2. The strongest correlation occurs between P and Y. The dark matter is equally well correlated with either Y or P, and somewhat less well with I.

We have found strong correlations between X-ray pseudo-entropy and the ratio of Y to I; which we attribute to the fact that the entropy can also be defined as Y / I5/6. This can useful in case where only X-ray imaging is available as well as good SZ-data, but no temperature map, as should be the case for high-z clusters. Historically, the ratio of Y-to-I was proposed for measurement of the Hubble constant (see e.g. Bonamente et al. 2007). Our results provide an insight on the origin of scatter in this measurement, and our proposal to reduce the scatter in this comparison consists of the use of pseudo pressure maps instead of X-ray images and also estimating the expected deviation based on the amplitude of the scatter seen in the pseudo entropy maps.

3.1 Estimated influence of the general trend

In this section we estimate analytically the effect of projection on the derived correlation coefficient, accounting therefore for differences in the radial trends between the maps and compare these predictions to the observed correlation coefficients.

Consider the scaling with radius of different properties.

$\displaystyle n \propto (1+(r/r_{\rm c})^2)^{-3 \beta /2 }$     (2)
$\displaystyle \beta=2/3$     (3)
$\displaystyle S \propto (1+(r/r_{\rm c})^2)^{0.55}$     (4)
$\displaystyle \longrightarrow T \propto n^{0.12}$     (5)
$\displaystyle \longrightarrow I \propto (1+(r/r_{\rm c})^2)^{-3\beta + 0.5 } \propto (1+(r/r_{\rm c})^2)^{-1.5}$     (6)
$\displaystyle \longrightarrow I^{0.5} \propto (1+(r/r_{\rm c})^2)^{-0.75}$     (7)
$\displaystyle \longrightarrow P = I^{0.5}T \propto (1+(r/r_{\rm c})^2)^{-0.87}$     (8)
$\displaystyle \longrightarrow Y \propto (1+(r/r_{\rm c})^2)^{-3\beta /2 \times 1.12 + 0.5 } \propto (1+(r/r_{\rm c})^2)^{-0.62}$     (9)
$\displaystyle DM \propto (1+(r/r_{\rm c})^2)^{-1.3+0.5} \propto (1+(r/r_{\rm c})^2)^{-0.8}$     (10)

where n is the gas density, $\beta$ is the radial slope for which we assumed a typical cluster value. The entropy profile is assumed, based on the results of observations (e.g. Finoguenov et al. 2005). The DM is the projected column density of dark matter, for which the distribution was taken to resemble closely the NFW profile (Navarro et al. 1997). Other parameters can be derived based on these assumptions. Addition of the constant 0.5 is a result of the Abell integral.

In order to illustrate the effect of differences in the radial slope on the observed correlation, in Fig. 3 we calculated an expected reduction in the correlation coefficient, assuming $(1+(r/r_{\rm c})^2)^{-(0.62+\Delta \beta )}$, varying $\Delta \beta$ to cover the range of all the observed clusters. The main conclusion of this test is that while the typical correlation coefficients between Compton Y vs. pseudo pressure are reproduced, the observed correlations between simulated X-ray image and Compton Y as well as all the correlation of Compton Y with dark matter column density are much weaker. This implies both that the gas is only an approximate tracer of the dark matter and that hydrodynamical processes involving gas displacements (cold fronts) are playing a dominant role in defining the soft X-ray band images of the cluster, in accordance with recent Chandra and XMM results (Vikhlinin et al. 2001, Mazzotta et al. 2002; Briel et al. 2004) and other numerical simulations (Powell et al. 2009).

\begin{figure} \par\includegraphics[width=8cm]{11649_fig3.ps} \end{figure} Figure 3:

Variation in the correlation coefficient as a function of change in the radial slope. The changes are calculated in respect to the Compton Y two-dimensional distribution with the profile of $(1+(r/r_{\rm c})^2)^{-(0.62+\Delta \beta )}$. The points show the actually measured correlation strength and the range enclosing 68% of the data. The dotted, dashed and solid lines represent a correlation between Compton Y and each of the pseudo pressure, the dark matter column density and the square root of X-ray surface brightness ( $I_{\rm X}^{0.5}$), respectively. While the pseudo pressure and Compton Y parameter exhibit a correlation consistent with the predicted trend, the correlation with both dark matter and the X-ray image is lower than the expectation based merely on differences in the profiles.

Open with DEXTER

\begin{figure} \par\mbox{\includegraphics[width=6.02cm]{11649_fig4a.ps}\hfill \i... ...fill \includegraphics[width=6.02cm]{11649_fig4c.ps} } \vspace*{3mm} \end{figure} Figure 4:

The distribution of the pixel-by-pixel correlation coefficient (Eq. (1)) between the maps, after correcting for the mean trend in each map. Left panel represents correlations between dark matter column density and each of the pressure (solid), Compton Y (dashed) and square root of the X-ray surface brightness $I_{\rm X}^{0.5}$ (dotted). Middle panel represents correlations between Compton Y and pressure (solid) and $I_{\rm X}^{0.5}$ (dotted). Right panel represents correlations between the entropy and the clumpiness (solid line) and correlations between the ratio of Compton Y and X-ray surface brightness with entropy (dashed). All comparisons are carried out within 1/2 of r200. Changing the radii of the comparison to 1/4 r200 does not change these results.

Open with DEXTER

\begin{figure} \par\mbox{ \includegraphics[width=4.6cm]{11649_fig5a.ps}\includeg... ...9_fig5c.ps}\hfill \includegraphics[width=4.6cm]{11649_fig5d.ps} } \end{figure} Figure 5:

Correlations between the rms values of various maps with respect to the mean trend. Each point corresponds to a single dataset from our ensemble of $68\times 3$ simulated clusters (see Sect. 2). All calculations have been carried out within 0.5 r200. The dotted lines on all the plots show 1:1 correspondence in rms level.

Open with DEXTER

3.2 Definition of substructure as deviation from the mean trend

In order to see the correlation in the substructure on the images, we have corrected for the radial variation in all maps. We perform this correction by calculating an average map for each quantity, across the ensemble of simulated clusters, which captures the broad systematic trend. This average map is then used to normalize each individual cluster map, to reveal the deviations about the global trend caused by interesting cluster physics. The correlation between these corrected maps then more cleanly probes the relation between these deviations.

To eliminate bias from anomalous clusters, we identify and exclude outliers from the calculation of the average map using the following iterative scheme. Firstly, we take the logarithm of all the pixel values in the map for every cluster and calculate the mean of these logged images. We then compute the correlation coefficient between this mean logged image and the individual logged map for each cluster. Any clusters with a correlation below 0.85 are identified as outliers and the mean logged image is recalculated with them excluded; the process is repeated until no further clusters are excluded. This process is found to change the resultant map by only $\sim$5%. The distribution of correlation coefficients for the corrected maps is plotted in Fig. 4 and a comparison with Fig. 2 shows the much broader spread of values obtained when the mean trend is removed. Intuitively, the level of correlation between the gas-related maps and dark matter maps should be quite sensitive to the physics introduced in simulations, such as cooling, conduction and viscosity. Thus a comparison of predictions of various simulations to the observational data shall be rewarding. The correlation between the gas-tracing maps has also decreased. For example a correlation between the pseudo-pressure to Compton Y maps dropped from 0.98 to 0.95. In order to understand the origin of this decline we move to our next test - a direct comparison of the levels of fluctuations of each cluster.

3.3 Scatter

In addition to the similarity of the maps as traced by the correlation estimators, we can quantify the link between the maps by examining the degree of deviations in the map ratios. It is also advantageous to compare the deviations seen in the maps to deviations from the average trend, as well as their typical amplitudes. Our primary results are outlined in Fig. 5.

When comparing the rms level for pseudo pressure and Compton Y, one sees that although the two scale very well, the pseudo pressure depicts the large deviations more strongly. This explains why there is a reduction in the correlation strength between taking the full map or only comparing the deviations from the mean trend. A comparison between the pressure and entropy deviations shows that although the pressure deviations are typically larger, if all the deviations would be due to the shocks, the expected level of entropy deviations would be limited to 0.05. The observed entropy fluctuations are typically 10 times larger and therefore require different explanation, such as survival of low-entropy gas during the cluster assembly. A similar range of the fluctuations is reported for the REFLEX-DXL cluster sample (Finoguenov et al. 2005); in Poole et al. (2007, 2008) the amplitude of fluctuations in the maps is further linked to the merger state of the cluster, which has also been suggested observationally by Zhang et al. (2009).

\begin{figure} \par\mbox{\includegraphics[width=8cm]{11649_fig6a.ps}\hspace*{2.2cm} \includegraphics[width=8cm]{11649_fig6b.ps} } \end{figure} Figure 6:

Fraction of the sample with rms of studied parameter greater than the x-axis value. Left panel: shows pressure (grey line), square root of X-ray image (solid line), Compton Y (dotted line), dark matter (dashed line). Right panel: shows P2Y (grey), temperature (solid), clumpiness (dotted), $C_{\rm p}$ (short-dashed), Y2I (long-dashed line), entropy (dot-dashed line).

Open with DEXTER
Figure 5 reveals a good correlation between the dispersion in the entropy and clumpiness. The very presence of such a correlation implies that the clumpiness of the gas is dominated by the large-scale gas displacements, which are traced by the entropy map. Previously, we have shown that the entropy deviations are nearly cospatial with deviations in clumpiness, as shown by their reasonable correlation shown in Fig. 4. It implies that to reduce the effect of clumpiness (which for example introduce a scatter in the measurement of Hubble constant based on the X-ray and SZE comparison), one should excise the zones most deviating in the entropy maps.

This suggestion can be further strengthened when considering the rms of the P-to-Y ratio. First, we note that the rms in the individual pressure maps are much higher than the rms of the P-to-Y ratio. The latter has a scatter lower by a factor of 5, typically at the 10% level. To prove that clumpiness is the reason for these residual fluctuations, we first note that a ratio between P and Y could be written as ${T \times \sqrt{I} \over Y} = {T \times G \over Y \times C}$, where C is clumpiness. So we construct the additional map, $C_{\rm p} = {T \times G \over Y}$ to examine the fluctuations associated with averaging in Compton Y maps. The scatter in P/Y is a factor of two larger than in $C_{\rm p}$, which proves that the clumpiness is the dominant effect in producing deviations between pressure inferred from X-ray observations and SZ signal.

To estimate the importance of certain level of deviations, we next perform the analysis of the frequency of their occurrence. Fig. 6 displays the histogram of the rms distribution for the major parameters of this study. Already in Finoguenov et al. (2005, 2007) we have compared the observations to these predictions, revealing deviations in pressure fluctuations observed on the mass scale of galaxy groups. The first distribution of dark matter substructure has been presented in Smith et al. (2005), manifesting that comparison with various datasets will not be limited to X-ray observations. As evident from Fig. 6, the Compton Y has the smallest deviations compared to either dark matter, X-ray pressure or the square root of the X-ray image. The latter three exhibit similar deviations, with the exception that for the dark matter, deviations at the 25% level are seen much more frequently. As already mentioned above, the deviations in P/Y are intermediate between the temperature and $C_{\rm p}$. Fluctuations in the clumpiness itself are much larger and the frequency of their appearance is similar to that of entropy.

4 Conclusions

We have used a set of hydrodynamical galaxy cluster simulations to investigate the two-dimensional comparison between maps of different quantities which are increasingly becoming available to the observer. We test the idea of using these maps for hydrodynamical analysis and for achieving better accuracy in using clusters for cosmological studies. We conclude that the X-ray pseudo pressure map is a very good proxy for the Compton Y image obtained from SZ observations. It could be used to simulate the observational appearance of the clusters on the SZ sky, their scatter from the averaged trend and, most importantly, provide the lowest scatter comparison between spatially resolved SZ and X-rays measurements.

We have also shown that the pseudo entropy maps can be used as a proxy of clumpiness of the gas, which cannot otherwise be observed directly. We demonstrate that the scatter in the ratio of the X-ray pressure estimate to the Compton Y is driven by clumpiness and not by shocks, so elimination of clumpy zones, e.g. marked as deviant on the entropy maps, is the most critical step towards achieving a consistent picture of clusters with various methods. With the prescriptions discussed in this work, we anticipate a reduction of scatter in the SZE-to-X-ray comparisons from 30% to 5%, through the use of X-ray pressure restoration and excising strongly deviant zones in the entropy maps.

We have shown that the structure in dark matter maps are poorly correlated with the structure in any gas-based maps. Therefore the power of using the gas-maps to trace the dark matter substructure is quite limited. A degree to which this correlation will be observed in the real data is sensitive to the detailed physics of gas disruption and as such should allow to constrain the role of cooling, conduction and viscosity through matching the observations to sets of hydrodynamical simulations, as advocated in Dolag et al. (2004). We have also introduced a different test, which describes the frequency of the observed rms in the maps. The has already enabled a comparison to observations (Finoguenov et al. 2005, 2007), revealing that while the scatter in both entropy and pressure maps in clusters agree well with the prediction of these simulations, the amount of scatter seen in the pressure maps of galaxy groups is much larger, indicating a larger role of internal feedback processes there.



Acknowledgements
A.F. acknowledges support from BMBF/DLR under grant 50 OR 0207 and MPG. A.F. thanks the UIUC for the hospitality during his visits. This work has been partially supported by a SAO grant GO8-9126B to UMBC. A.E.E. acknowledges support from NASA TM4-5008X and NSF AST-0708150. The authors thank the anonymous referee for insightful comments on the manuscript. A.F. thanks Yu-Ying Zhang and James Taylor for their comments on the manuscript.

References

  1. Bialek, J. J., Evrard, A. E., & Mohr, J. J. 2001, ApJ, 555, 597 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bialek, J. J., Evrard, A. E., & Mohr, J. J. 2002, ApJ, 587, L9 [NASA ADS] [CrossRef] [Google Scholar]
  3. Böhringer, H., Schuecker, P., Guzzo, L., et al. 2001, A&A, 369, 826 [Google Scholar]
  4. Böhringer, H., Voges, W., Huchra, J. P., et al. 2000, ApJS, 129, 435 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bonamente, M., Joy, M. K., LaRoque, S. J., et al. 2006, ApJ, 647, 25 [NASA ADS] [CrossRef] [Google Scholar]
  6. Borgani, S., & Guzzo, L. 2001, Nature, 409, 39 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  7. Briel, U. G., Finoguenov, A., & Henry, J. P. 2004, A&A, 426, 1 [Google Scholar]
  8. David, L. P., Slyz, A., Jones, C., et al. 1993, ApJ, 412, 479 [NASA ADS] [CrossRef] [Google Scholar]
  9. Dolag, K., Jubelgas, M., Springel, V., Borgani, S., & Rasia, E. 2004, ApJ, 606, L97 [NASA ADS] [CrossRef] [Google Scholar]
  10. Edge, A. C., Stewart, G. C., & Fabian, A. C. 1992, MNRAS, 258, 177 [NASA ADS] [CrossRef] [Google Scholar]
  11. Evrard, A. E. 1988, MNRAS, 235, 911 [NASA ADS] [CrossRef] [Google Scholar]
  12. Evrard, A. E. 1990, ApJ, 363, 349 [NASA ADS] [CrossRef] [Google Scholar]
  13. Finoguenov, A., Henriksen, M. J., Briel, U. G., de Plaa, J., & Kaastra, J. S. 2004, ApJ, 611, 811 [NASA ADS] [CrossRef] [Google Scholar]
  14. Finoguenov, A., Böhringer, H., & Zhang, Y.-Y. 2005, A&A, 442, 827 [Google Scholar]
  15. Finoguenov, A., Davis, D. S., Zimer, M., & Mulchaey, J. S. 2006a, ApJ, 646, 143 [NASA ADS] [CrossRef] [Google Scholar]
  16. Finoguenov, A., Henriksen, M. J., Miniati, F., Briel, U. G., & Jones, C. 2006b, ApJ, 643, 790 [NASA ADS] [CrossRef] [Google Scholar]
  17. Finoguenov, A., Ponman, T. J., Osmond, J. P. F., & Zimer, M. 2007, MNRAS, 374, 737 [NASA ADS] [CrossRef] [Google Scholar]
  18. Gursky, H., Solinger, A., Kellogg, E. M., et al. 1972, ApJ, 173, L99 [NASA ADS] [CrossRef] [Google Scholar]
  19. Henry, J. P., Finoguenov, A., & Briel, U. G. 2004, ApJ, 615, 181 [NASA ADS] [CrossRef] [Google Scholar]
  20. Markevitch, M. 1996, ApJ, 465, L1 [NASA ADS] [CrossRef] [Google Scholar]
  21. Markevitch, M. L., Sarazin, C. L., & Irwin, J. A. 1996, ApJ, 472, L17 [NASA ADS] [CrossRef] [Google Scholar]
  22. Markevitch, M., Sarazin, C. L., & Vikhlinin, A. 1999, ApJ, 521, 526 [Google Scholar]
  23. Mazzotta, P., Kaastra, J. S., Paerels, F. B., et al. 2002, ApJ, 567, L37 [NASA ADS] [CrossRef] [Google Scholar]
  24. Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
  25. Pawl, A., Evrard, A. E., & Dupke, R. A. 2005, ApJ, 631, 773 [NASA ADS] [CrossRef] [Google Scholar]
  26. Powell, L. C., Kay, S. T., & Babul, A. 2009, MNRAS, 400, 705 [NASA ADS] [CrossRef] [Google Scholar]
  27. Poole, G. B., Fardal, M. A., Babul, A., et al. 2006, MNRAS, 373, 881 [NASA ADS] [CrossRef] [Google Scholar]
  28. Poole, G. B., Babul, A., McCarthy, I. G., et al. 2007, MNRAS, 380, 437 [NASA ADS] [CrossRef] [Google Scholar]
  29. Schuecker, P., Finoguenov, A., Miniati, F., Böhringer, H., & Briel, U. G. 2004, A&A, 426, 387 [Google Scholar]
  30. Simionescu, A., Böhringer, H., Brüggen, M., & Finoguenov, A. 2007, A&A, 465, 749 [Google Scholar]
  31. Smith, G. P., Kneib, J.-P., Smail, I., et al. 2005, MNRAS, 359, 417 [NASA ADS] [CrossRef] [Google Scholar]
  32. Sunyaev, R. A., & Zeldovich, I. B. 1980, ARA&A, 18, 537 [Google Scholar]
  33. Vikhlinin, A., Markevitch, M., & Murray, S. S. 2001, ApJ, 551, 160 [NASA ADS] [CrossRef] [Google Scholar]
  34. Zhang, Y.-Y., Reiprich, T. H., Finoguenov, A., Hudson, D. S., & Sarazin, C. L. 2009, ApJ, 699, 1178 [NASA ADS] [CrossRef] [Google Scholar]
  35. White, M. 2003, ApJ, 597, 650 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

...[*]
http://vce.physics.lsa.umich.edu

All Figures

  \begin{figure} \par\includegraphics[height=17.1cm]{11649_fig1.ps} \end{figure} Figure 1:

Example of the cluster maps in one of the simulation runs. From the top left to the bottom right we show the dark matter column density, gas column density, X-ray images in the 0.5-2 keV band, X-ray temperature map, pseudo entropy map, pseudo pressure map, Compton Y map, clumpiness map, ratio of Compton Y to X-ray image. The grey scale is set to depict the central structure in black in all the maps.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=8cm]{11649_fig2a.ps}\hfill \includegraphics[width=8cm]{11649_fig2b.ps} } \end{figure} Figure 2:

The distribution of correlation coefficients between various simulated maps for each of the 68 simulated clusters, calculated using Eq. (1). Left panel represents correlations between dark matter column density and each of the pressure (solid), Compton Y (dashed) and square root of the X-ray surface brightness $I_{\rm X}^{0.5}$(dotted). Right panel represents correlations between Compton Y and each of the pressure (solid) and $I_{\rm X}^{0.5}$ (dotted). The dashed line shows a correlation between the ratio of Compton Y and X-ray surface brightness with pseudo entropy. All comparisons are carried out within 1/4 of r200.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm]{11649_fig3.ps} \end{figure} Figure 3:

Variation in the correlation coefficient as a function of change in the radial slope. The changes are calculated in respect to the Compton Y two-dimensional distribution with the profile of $(1+(r/r_{\rm c})^2)^{-(0.62+\Delta \beta )}$. The points show the actually measured correlation strength and the range enclosing 68% of the data. The dotted, dashed and solid lines represent a correlation between Compton Y and each of the pseudo pressure, the dark matter column density and the square root of X-ray surface brightness ( $I_{\rm X}^{0.5}$), respectively. While the pseudo pressure and Compton Y parameter exhibit a correlation consistent with the predicted trend, the correlation with both dark matter and the X-ray image is lower than the expectation based merely on differences in the profiles.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=6.02cm]{11649_fig4a.ps}\hfill \i... ...fill \includegraphics[width=6.02cm]{11649_fig4c.ps} } \vspace*{3mm} \end{figure} Figure 4:

The distribution of the pixel-by-pixel correlation coefficient (Eq. (1)) between the maps, after correcting for the mean trend in each map. Left panel represents correlations between dark matter column density and each of the pressure (solid), Compton Y (dashed) and square root of the X-ray surface brightness $I_{\rm X}^{0.5}$ (dotted). Middle panel represents correlations between Compton Y and pressure (solid) and $I_{\rm X}^{0.5}$ (dotted). Right panel represents correlations between the entropy and the clumpiness (solid line) and correlations between the ratio of Compton Y and X-ray surface brightness with entropy (dashed). All comparisons are carried out within 1/2 of r200. Changing the radii of the comparison to 1/4 r200 does not change these results.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{ \includegraphics[width=4.6cm]{11649_fig5a.ps}\includeg... ...9_fig5c.ps}\hfill \includegraphics[width=4.6cm]{11649_fig5d.ps} } \end{figure} Figure 5:

Correlations between the rms values of various maps with respect to the mean trend. Each point corresponds to a single dataset from our ensemble of $68\times 3$ simulated clusters (see Sect. 2). All calculations have been carried out within 0.5 r200. The dotted lines on all the plots show 1:1 correspondence in rms level.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=8cm]{11649_fig6a.ps}\hspace*{2.2cm} \includegraphics[width=8cm]{11649_fig6b.ps} } \end{figure} Figure 6:

Fraction of the sample with rms of studied parameter greater than the x-axis value. Left panel: shows pressure (grey line), square root of X-ray image (solid line), Compton Y (dotted line), dark matter (dashed line). Right panel: shows P2Y (grey), temperature (solid), clumpiness (dotted), $C_{\rm p}$ (short-dashed), Y2I (long-dashed line), entropy (dot-dashed line).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.