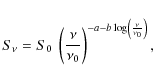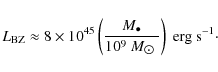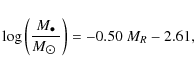Power for dry BL Lacertae objects

A. Paggi; A. Cavaliere; V. Vittorini; M. Tavani

doi:10.1051/0004-6361/200913566

Home

All issues

Volume 508 / No 3 (December IV 2009)

A&A, 508 3 (2009) L31-L34

Full HTML

Free Access

Issue		A&A Volume 508, Number 3, December IV 2009


Page(s)		L31 - L34
Section		Letters
DOI		https://doi.org/10.1051/0004-6361/200913566
Published online		04 December 2009

A&A 508, L31-L34 (2009)

LETTER TO THE EDITOR

Power for dry BL Lacertae objects

A. Paggi¹ - A. Cavaliere¹ - V. Vittorini² - M. Tavani^1,2

1 - Dipartimento di Fisica, Università di Roma ``Tor Vergata'', and INFN Roma Tor Vergata via della Ricerca Scientifica 1, 00133 Roma, Italy
2 - INAF/IASF-Roma, via Fosso del Cavaliere 1, 00100 Roma, Italy

Received 28 October 2009 / Accepted 16 November 2009

Abstract
Is it significant that the intrinsic outputs of several BL Lacs are observed to level off at values of about 10⁴⁶ erg s^-1? In searching for an answer, we compare $\gamma$ -ray observations by the AGILE satellite of the BL Lac S5 0716+714 with those of Mrk 421 and Mrk 501; the former are particularly marked by intense flares up to fluxes of $2 \times {10}^{-6}$ photons cm^-2 s^-1 in the 0.1-10 GeV energy range. These ``dry'' BL Lacs show evidence of neither thermal disk emissions nor emission lines signaling any accreting or surrounding gas; the spectral distributions of their pure non-thermal radiations are effectively represented by the synchrotron self-Compton process. With source parameters correspondingly derived and tuned with simultaneous multiwavelength observations, we find for S5 0716+714 a total jet power of about $3 \times {10}^{45}$ erg s^-1, which makes it one of the brightest dry BL Lacs so far detected in $\gamma$ rays. We evaluate the mass of the associated Kerr hole to be around $5 \times 10^8~M_{\hbox{$\odot$ }}$ , implying that the source is significantly gauged in terms of the maximal power around $4 \times {10}^{45}$ erg s^-1 extractable via the Blandford-Znajek electrodynamical mechanism; other dry BL Lacs observed in $\gamma$ rays remain well below that threshold. These findings and those forthcoming from Fermi-LAT will provide a powerful test of electrodynamics in the surroundings of the hole, that are dominated by GR effects.

Key words: BL Lacertae objects: general - radiation mechanisms: non-thermal - black hole physics - accretion, accretion disks

1 Introduction

Blazars rank among the brightest active galactic nuclei on the basis of their inferred isotropic luminosities that may attain some $L_{\rm iso}\sim {10}^{48}$ erg s^-1. Actually, these sources radiate from a narrow relativistic jet closely aligned with the observer's line of sight. The jet emits highly beamed non-thermal radiations, with observed fluxes enhanced by aberration and Doppler effects of Special Relativity (Begelman et al. 1984; Königl 1986; Urry & Padovani 1995). So the luminosities $L_{\rm iso}$ greatly exceed the intrinsic outputs of the jets that easily level off at ${10}^{-2}{-}{10}^{-3}~L_{\rm iso}$ .

The BL Lac objects (henceforth BL Lacs) in particular are blazars that show no or just weak and intermittent emission lines. Their spectra are represented well as a continuous spectral energy distribution (SED) $S_\nu = \nu F_\nu$ featuring two peaks: one at a lower frequency due to synchrotron emission by highly relativistic electrons; and a higher frequency counterpart due to inverse Compton upscattering by the same electron population of seed photons provided by the synchrotron emission itself (synchrotron self-Compton, SSC; see Jones et al. 1974; Marscher & Gear 1985; Maraschi et al. 1992), with possible additions from sources external to the beam (external Compton, EC; see Dermer & Schlickeiser 1993; Sikora et al. 1994).

The BL Lacs also exhibit strong variability on timescales of days to minutes with substantial flux variations (flares) particularly at high energies as realized early on (see Setti & Woltjer 1994, and references therein).

Here we focus on ``dry'' BL Lacs, that is, sources with no evidence of surrounding gas, such as emission lines or a big blue bump (see Peterson 1997; Kembhavi & Narlikar 1999) related to current accretion. They provide an appropriate testing ground for comparing their intrinsic outputs with maximal powers extractable from rotating supermassive black holes and from the dragged accretion disks by means of large-scale electromagnetic fields, via the intriguing, variously debated Blandford-Znajek electrodynamics (BZ et al. 1977; see also Ghosh & Abramowicz 1997; Krolik 1999; Livio et al. 1999; Cavaliere & D'Elia 2002; McKinney 2005; Nemmen et al. 2007; Tchekhovskoy, et al. 2009). The bare hole contribution can yield up to $L_K \sim 2 \times 10^{45} \left( M_{\bullet}/10^9~M_{\hbox{$\odot$ }}\right)$ erg s^-1, given the hole mass $M_{\bullet}$ in units of ${10}^9~M_{\hbox{$\odot$ }}$ and a magnetic field $B \sim 10^4$ G threading its horizon.

In the following, we adopt the standard, flat cosmology with H₀ = 72 km s^-1 Mpc^-1 and $\Omega_\Lambda = 0.74$ (Dunkley et al. 2009).

2 The radiation process

The SEDs of the dry BL Lacs are widely understood in terms of the simple, homogeneous SSC process. This is based on radiations produced in a region containing a magnetic field and relativistic electrons accelerated to high random energies $\gamma m c^2$ (with $\gamma$ up to 10⁶-10⁸) that move toward the observer with bulk Lorentz factors $\Gamma \sim 10{-}20$ (see Ghisellini et al. 1993).

To begin with, we assume the sources to have an isotropic geometry with a radius R as a single size parameter, and to contain the relativistic electrons and non-relativistic protons with the same $\Gamma$ , at a common density n. Observed (primed) frequencies and fluxes are related to the rest frame (unprimed) quantities by means of $\nu' = \nu~\delta$ and $F'= F~ \delta^4$ (Begelman et al. 1984), where $\delta = \left[{\Gamma\left({1-\beta\cos{\theta}}\right)}\right]^{-1}$ is the beaming factor related to the angle $\theta$ between the jet and the line of sight. Small viewing angles $\theta \sim 1/\Gamma$ yield $\delta \approx 2 \Gamma$ . Correspondingly, the intrinsic variability and crossing times R/c will be longer than the observed ones $R/\delta c$ .

On empirical and theoretical grounds, we adopt log-parabolic shapes for the electron energy distributions. These are obtained from a Fokker-Planck equation in the presence of systematic and stochastic acceleration processes as first shown by Kardashev (1962) and computed in detail by Paggi et al. (2009); the acceleration times scale as $t_{\rm a} \propto \gamma / E$ , in terms of the effective electric field E (Cavaliere & D'Elia 2002). We therefore write the electron distribution in the form

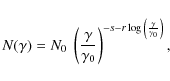
$\begin{displaymath}N(\gamma)=N_0~ \left({\frac{\gamma}{\gamma_0}}\right)^{-s-r \log{\left(\frac{\gamma}{\gamma_0} \right)}}, \end{displaymath}$

(1)

where s is the constant contribution to the slope, r is the ``curvature'', and $\gamma_0$ is the injection energy. The energetic content of such an electron population can be expressed in terms of the rms adimensional energy $\gamma_{\rm p} = \left( \int \gamma^2 N \left( \gamma \right)~ {\rm d} \gamma/\!\int N \left( \gamma \right)~ {\rm d} \gamma \right)^{1/2}$ , to yield an energy density close to $n~\gamma_{\rm p}~m c^2$ .

The emitted synchrotron SED is correspondingly given by (Massaro et al. 2004; Tramacere et al. 2007, and references therein)

$\begin{displaymath} S_\nu = S_0 ~ \left(\frac{\nu}{\nu_0} \right)^{-a-b \log \left(\frac{\nu}{\nu_0}\right)}, \end{displaymath}$

(2)

with a constant contribution a=(s-3)/2 to the spectral index, a spectral curvature $b \approx r/5$ , and a peak frequency $\nu_S \propto B \gamma_{\rm p}^2$ . For the IC, an analogous SED applies, where in the Thomson regime one has a=(s-3)/2, $b \approx r/10$ and a peak frequency $\nu_C \propto B \gamma_{\rm p}^4$ , whilst in the Klein-Nishina regime a=s, $b \approx r$ , and $\nu_C \propto \gamma_{\rm p}$ hold.

In these SEDs and distributions, the peaks where most of the energy resides are not materially affected by radiative cooling active on timescales $t_{\rm c} \propto 1/ \gamma_{\rm p}$ longer than the crossing time R/c; cooling will rather erode the high energy tails. As an added bonus, the synchrotron and IC radiations from a log-parabolic electron population irreversibly broaden under the action of the stochastic acceleration component, following $b \propto 1/t$ (Paggi et al. 2009); thus, a sudden increase in the spectral curvature will mark the emergence of a new electron population. Last but not least, Eq. (2) closely fits (as we illustrate in Fig. 1) the spectra of the sources that we focus on in view of extended spectral coverage provided by their multiwavelength, simultaneous observations.

$\begin{figure} \includegraphics[width=9cm,clip]{13566fg1.eps} \vspace*{4mm} \end{figure}$	Figure 1: SEDs of the BL Lacs considered in the text: S5 0716+174 ( upper-left frame), Mrk 501 ( upper-right frame) and Mrk 421 ( lower-left and lower-right frames), each in a low (blue line) and a high (red line) state. In terms of intrinsic luminosity S5 0716+714 is the strongest source (data referenced in Sect. 2).
Open with DEXTER

This is the case for S5 0716+714, which has the following data available: a low state provided by historical AIT and EGRET data (Lin et al. 1995); a high state in September 2007, in the $\gamma$ -ray range covered by AGILE-GRID where the IC peaks for this ``intermediate'' BL Lac (Padovani & Giommi 1995); optical and radio data taken with GASP-WEBT on September 7-12 (Villata et al. 2008; Vittorini et al. 2009). The multiwavelength variations observed by Giommi et al. (2008) and the increased spectral curvature (see Fig. 1) in 2007 are indicative of the injection of a second component.

The source may be compared with Mrk 501, for which we consider two states with simultaneous BeppoSAX and CAT observations on April 7 and 16, 1997 (Massaro et al. 2006); and with Mrk 421, for which we have low and high states in 2000 from BeppoSAX and HEGRA data (Konopelko et al. 2003), and multiwavelength observations performed with GASP-WEBT, RXTE/ASM, Swift, SuperAGILE, AGILE-GRID, ARGO-YBJ, and VERITAS in June 2008 (Donnarumma et al. 2009; Di Sciascio et al. 2009).

3 The source power

We are interested in the intrinsic outputs referred to the jet frame, rather than in the luminosities $L_{\rm iso} = 4 \pi~ D_L^2~ F$ inferred from insisting on an isotropic distribution of the observed flux F, at the luminosity distance D_L. We assume one ``cold'' proton per electron satisfying $\left \langle \gamma \right\rangle \la m_{\rm p} / m_{\rm e}$ (with the average $\left \langle \gamma \right \rangle = \gamma_{\rm p} \times {10}^{-1/4r}$ bounded in terms of the electron $m_{\rm e}$ and the proton $m_{\rm p}$ masses), and follow Celotti & Ghisellini (2008) in writing for the intrinsic radiative luminosity $L_{\rm r}$ contributed by both the synchrotron and IC radiations and for the related powers carried by the jet, the expressions

$\displaystyle L_{\rm r}$	=	$\displaystyle L_{\rm iso}~{\Gamma^2}/{\delta^4} \approx L_{\rm iso}/16~\Gamma^2,$	(3)
$\displaystyle L_{\rm e}$	=	$\displaystyle \frac{4}{3} \pi ~R^2 ~ c ~ n ~ m_{\rm e} ~ c^2 \left \langle{\gamma}\right\rangle \Gamma^2,$	(4)
$\displaystyle L_{\rm p}$	$\textstyle \quad \sim$	$\displaystyle L_{\rm e}~ {m_{\rm p}}/{m_{\rm e}\left\langle{\gamma}\right\rangle}, \qquad L_B \ll L_{\rm r,~e,~p}.$	(5)

The total jet power is therefore given by $L_{T} = L_{\rm r} + L_{\rm e}+ L_{\rm p}+L_B$ ; this is dominated by $L_{\rm r}$ and by $L_{\rm e}$ , with $L_B < L_{\rm p} \la L_{\rm e}$ for the fields $B \sim 0.1{-}1$ G implied by the spectral fits.

The simultaneous, multiwavelength observations enable extended spectral fits to determine the five key observables (beside the spectral curvature b) from the SSC model, namely: the synchrotron peak frequency and flux, the IC peak frequency and flux, and the variation time (see Paggi et al. 2009). These lead to robust evaluations of the five source parameters n, R, B, $\left\langle{\gamma}\right\rangle$ , and $\delta$ (or $\Gamma$ ) entering Eqs. (3)-(5); the main parameters are collected in Table 1.

Table 1: Parameters for the BL Lac sources discussed in the text.

4 The BZ benchmark

As anticipated in Sect. 1, a natural benchmark for these powers is provided by the BZ mechanism for electrodynamical energy extraction from a Kerr hole spun up to maximal rotation by past accretion episodes. A minimal, vestigial disk is required to hold the poloidal magnetic field threading the horizon; the disk is kept active by low accretion rates $\dot{m} \la {10}^{-2}$ in Eddington units, loses angular momentum mainly via the large-scale field, and contributes some 3 L_K to the total power (Blandford & Znajek 1977; Livio et al. 1999). The two contributions add to yield

$\begin{displaymath} L_{\rm BZ} \approx 8 \times 10^{45} \left( \frac{M_{\bullet}... ...9~M_{\hbox{$\odot$ }}} \right) ~\mbox{erg}~\mbox{s}^{-1} \cdot \end{displaymath}$

(6)

We note that the balance $B^2 /4\pi \sim p$ between the magnetic stress and the kinetic or radiation pressure p in the disk yields $B \sim 10^4$ G; for a radiation-pressure dominated disk, we have at the inner rim $B^2 \propto 1/M_{\bullet}$ , so B has dropped out of Eq. ( In the text 6).

The hole mass is then the key parameter, that we evaluate from its correlation with the absolute red magnitude M_R of the host galactic bulge (Ferrarese et al. 2000; Gebhardt et al. 2000; Falomo et al. 2003); for our cosmology this reads

$\begin{displaymath} \log \left( \frac{M_{\bullet}}{M_{\hbox{$\odot$ }}} \right) = -0.50~M_R - 2.61, \end{displaymath}$

(7)

with scatter ${\pm}0.4$ dex (Bettoni et al. 2003). For the host galaxy of S5 0716+714, observations of the magnitude $R = 18.3 \pm 0.5$ reported by Nilsson et al. (2008), besides indicating the redshift $z = 0.31 \pm 0.08$ , yield a mass $M_{\bullet} \simeq {5.5 ^{+8.0}_{-3.3}} \times {10}^8~M_{\hbox{$\odot$ }}$ ; the central value is consistent with estimates from microvariability of the optical flux (Sasada et al. 2008), which yield $M_{\bullet} \sim {10}^8~M_{\hbox{$\odot$ }}$ . For Mrk 501 and Mrk 421, one obtains $M_{\bullet} \simeq {1.0^{+2.4}_{-0.7}} \times {10}^9~M_{\hbox{$\odot$ }}$ and $M_{\bullet} \simeq {4.1^{+7.8}_{-2.7}} \times {10}^8~M_{\hbox{$\odot$ }}$ , respectively.

Our results normalized to the respective $L_{\rm BZ}$ from Eq. (6) are represented in Fig. 2. During flares, the electron rms energies (and the peak frequencies) are boosted in all sources, and so are the luminosities; this indicates that rising flares are directly related to increased acceleration of the emitting electrons.

We emphasize that the powerful source S5 0716+714 is apparently constrained to move sideways, as if to skirt the BZ limit; Mrk 421 in the 2008 states exhibits a similar behaviour, although with lower significance. On the other hand, the weaker source Mrk 421 in 2000 and the yet weaker Mrk 501 remain considerably below the BZ limit and so are expected to be free to move more vertically, as they do.

$\begin{figure} \par\includegraphics[width=9cm,clip]{13566fg2.eps} \vspace*{4mm} \end{figure}$	Figure 2: For the named sources the total jet luminosities normalized to their BZ power are plotted against the electron rms energy. Bars represent the hole mass uncertainties reflecting those (at the $1-\sigma$ level) in host bulge luminosities, and including the scatter in Eq. (7).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm,clip]{13566fg3.eps} \vspace*{5.5mm} \end{figure}$

Figure 3:

Bright BL Lacs in their context, adapted from Celotti & Ghisellini (2008) with historical data in terms of L_T and the energy $\gamma _{\rm peak}$ related to the synchrotron peak $\gamma _{\rm peak} = \gamma _{\rm p} \times {10}^{1/2r}$ . Blue circles indicate dry, while violet circles indicate wet BL Lacs. The lower-left region of the diagram corresponds to the source condition $t_{\rm c} > R/c$ , and the upper-right to $t_{\rm c} \gtrsim t_{\rm a}$ . Bright FSRQs lie at lower $\gamma _{\rm peak}$ and higher powers, with increasing signs of current $\dot{m} \rightarrow 1$ ; selection effects depopulate weaker sources in the lower region (see Padovani 2007). The dashed oval highlights sources in the transition region from dry to wet BL Lacs, interesting to compare with $L_{\rm BZ}$ from Eq. (6) particularly when at $z \gtrsim 0.3$ .

Open with DEXTER

5 Discussion and conclusions

For dry BL Lacs with accretion rates $\dot{m} < 10^{-2}$ , the SSC radiation process provides a robust evaluation of the jet luminosities. Whence we conclude that $L_{\rm BZ}$ provides a significant benchmark for the output of the BL Lacs discussed here, and indeed an upper limit to both their quiescent states and flares. In fact, during a recent flare S5 0716+714 was observed to be constrained by $L_{\rm BZ} \lesssim {10}^{46}$ erg s^-1, and a similar behavior was observed in 2008 for Mrk 421. Non-thermal, beamed powers in the range $L_K - L_{\rm BZ}$ also provide evidence of an accretion disk that is active mainly in launching and channeling the jets by means of large-scale fields.

Referring to Fig. 3 and its caption, we note that during flares the sources move in the L_T - $\gamma _{\rm peak}$ plane away from the envelope that is outlined by bright BL Lacs with increasing rates $\dot{m}$ ; the envelope ends up in the locus of the yet brighter flat spectrum radio quasars (FSRQs) with $\dot{m} \sim 1$ . The flares then move into a region of faster radiative cooling (Celotti & Ghisellini 2008, and references therein). This implies short-lived flares on timescales ${\la}1$ day, or requires shorter acceleration times $t_{\rm a} \sim \gamma /E$ with higher E, as an alternative to structured sources such as decelerating (Georganopoulos & Kazanas 2003) or spine-sheath jets with inner scale R₁ < R (Tavecchio & Ghiselllini 2008). Faster acceleration and deviations from the envelope are consistent with flares caused by electron boost rather than episodes of increased accretion onto the disk.

In this context, we recall (see Blandford 1990; Padovani et al. 2007) that sources lying along the envelope in Fig. 3 at higher L and lower $\gamma _{\rm peak}$ often exhibit stronger evidence of current accretion up to $\dot{m} \sim 1$ , such as thermal emissions and surrounding gas (big blue bump and broad emission lines), with a larger contribution from EC. In fact, the progression from dry BL Lacs to FSRQs is likely to involve an enhanced and extended disk contribution as described by Blandford & Payne (1982), starting with ``wet'' BL Lacs with $\dot{m} \sim {10}^{-1}$ ; these feature larger EC contributions (Dermer et al. 2008) and looming evidence of gas, including some thermal disk emission and weak or intermittent lines (Celotti et al. 2007). The last step in this progression is constituted by the powerful FSRQs with extant broad lines, a big blue bump from disks accreting at full rates $\dot{m} \sim 1$ , and a dominant or towering EC (Maraschi & Tavecchio 2001).

We add that the outputs of even misaligned BL Lacs may be calorimetrically gauged from their feedback actions on the intra-cluster plasma surrounding their host galaxy when located in a cluster or a group of galaxies, as discussed by McNamara et al. (2009). These authors evaluate average powers around 10⁴⁶ erg s^-1 injected into the cluster MS0735.6+7421, and possibly also in the cluster A2029 and the group AWM 4.

The whole of the above evidence provides observational support to the relevance of the electrodynamical BZ mechanism, and invites extended sampling of other interesting sources (see Fig. 3).

If in dry BL Lacs with $M_{\bullet} < {10}^9~M_{\hbox{$\odot$ }}$ the $L_{\rm BZ}$ limit were found to be substantially exceeded by outputs L_T > 10⁴⁶ erg s^-1, this would require B > 10⁴ G at the Kerr horizon. These fields imply large dynamical stresses bounded only by $B^2/4 \pi \leq \rho c^2$ , associated with particle orbits plunging from the disk toward the hole horizon (Meier 2002) into a region fully controlled by strong gravity effects.

Thus, all such sources will provide powerful tests for the coupling of electrodynamics with General Relativity in full swing, and constitute an exciting arena for AGILE and Fermi-LAT data.

Acknowledgements

We are grateful to R. Falomo for useful discussions concerning $M_{\bullet}$ evaluations for BL Lacs, and specifically in S5 0716+714. We acknowledge our referee for useful comments and helpful suggestions.

References

Begelman, M. C., Blandford, R. D., & Rees, M. J. 1984, RvMP, 56, 255 [NASA ADS] [CrossRef]
Bettoni, D., Falomo, R., Fasano, G., et al. 2003, A&A, 399, 869 [NASA ADS] [EDP Sciences] [CrossRef]
Blandford, R. D. 1990, in Saas-Fee Advanced Course 20, Active Galactic Nuclei, ed. R. D. Blandford, H. Netzer, & L. Woltjer (Springer), 161
Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS]
Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS]
Cavaliere, A., & D'Elia, V. 2002, ApJ, 571, 226 [NASA ADS] [CrossRef]
Celotti, A., & Ghisellini, G. 2008, MNRAS, 385, 283 [NASA ADS] [CrossRef]
Celotti, A., Ghisellini, G., & Fabian, A. C. 2007, MNRAS, 375, 417 [NASA ADS] [CrossRef]
Dermer, C. D., & Schlickeiser, R. 1993, ApJ, 416, 458 [NASA ADS] [CrossRef]
Dermer, C. D., Finke, J. D., & Menon, G. 2008, in Workshop on Blazar Variability across the Electromagnetic Spectrum, Proceedings of Science [arXiv:0810.1055]
Di Sciascio, G. and the ARGO-YBJ Collaboration 2009, Mem. S. A. It., 75, 282
Donnarumma, I., Vittorini, V., Vercellone, S., et al. 2009, ApJ, 691, L13 [NASA ADS] [CrossRef]
Dunkley, J., Komatsu, E., Nolta, M. R., et al. 2009, ApJS, 180, 306 [NASA ADS] [CrossRef]
Falomo, R., Kotilainen, J. K., & Carangelo, N., et al. 2003, ApJ, 595, 624 [NASA ADS] [CrossRef]
Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [NASA ADS] [CrossRef]
Gebhardt, K., Bender, R., Bower, G., et al. 2000, ApJ, 539, L13 [NASA ADS] [CrossRef]
Georganopoulos, M., & Kazanas, D. 2003, ApJ, 594, 27 [NASA ADS] [CrossRef]
Ghisellini, G., Padovani, P., Celotti, A., et al. 1993, ApJ, 407, 65 [NASA ADS] [CrossRef]
Ghosh, P., & Abramowicz, M. 1997, MNRAS, 292, 887 [NASA ADS]
Giommi, P., Colafrancesco, S., Cutini, S., et al. 2008, A&A, 487, L49 [NASA ADS] [EDP Sciences] [CrossRef]
Jones, T. W., O'Dell, S. L., & Stein, W. A. 1974, ApJ, 188, 353 [NASA ADS] [CrossRef]
Kardashev, N. S. 1962, SvA, 6, 317 [NASA ADS]
Kembhavi, A. K., & Narlikar, J. V. 1999, Quasars and Active Galactic Nuclei (Cambridge: Cambridge University Press)
Königl, A. 1986, NYASA, 470, 88 [NASA ADS] [CrossRef]
Krolik, J. H. 1999, ApJ, 515, 73 [NASA ADS] [CrossRef]
Konopelko, A., Mastichiadis, A., Kirk, J., et al. 2003, ApJ, 597, 851 [NASA ADS] [CrossRef]
Lin, Y. C., Bertsch, D. L., Dingus, B. L., et al. 1995, ApJ, 442, 96 [NASA ADS] [CrossRef]
Livio, M., Ogilvie, G., & Pringle, J. 1999, ApJ, 512, 100 [NASA ADS] [CrossRef]
McNamara, B. R., Kazemzadeh, F., Rafferty, D. A., et al. 2007, ApJ, 698, 594 [NASA ADS] [CrossRef]
Maraschi, L., & Tavecchio, F. 2001, ASPC, 227, 40 [NASA ADS]
Maraschi, L., Ghisellini, G., & Celotti, A. 1992, ApJ, 397, L5 [NASA ADS] [CrossRef]
Marscher, A. P., & Gear, W. K. 1985, ApJ, 298, 114 [NASA ADS] [CrossRef]
Massaro, E., Perri, M., Giommi, P., et al. 2004, A&A, 413, 489 [NASA ADS] [EDP Sciences] [CrossRef]
Massaro, E., Tramacere, A., Perri, M., et al. 2006, A&A, 448, 861 [NASA ADS] [EDP Sciences] [CrossRef]
McKinney, J. C. 2005, ApJ, 630, 5 [NASA ADS] [CrossRef]
McKinney, J. C., & Gammie, C. F. 2004, ApJ, 611, 977 [NASA ADS] [CrossRef]
Meier, D. L. 1999, ApJ, 522, 753 [NASA ADS] [CrossRef]
Meier, D. L. 2002, NewAR, 46, 247 [NASA ADS] [CrossRef]
Nemmen, R. S., Bower, R. G., Babul, A., et al. 2007, MNRAS, 377, 1652 [NASA ADS] [CrossRef]
Nilsson, K., Pursimo, T., Sillanpää, A., et al. 2008, A&A, 487, L29 [NASA ADS] [EDP Sciences] [CrossRef]
Paggi, A., Massaro, F., Vittorini, V., et al. 2009, A&A, 504, 821 [EDP Sciences] [CrossRef]
Padovani, P. 2007, Ap&SS, 309, 63 [NASA ADS] [CrossRef]
Padovani, P., & Giommi, P. 1995, ApJ, 444, 567 [NASA ADS] [CrossRef]
Padovani, P., Giommi, P., Landt, H., et al. 2007, ApJ, 662, 182 [NASA ADS] [CrossRef]
Peterson, B. M. 1997, An Introduction to Active Galactic Nuclei (Cambridge: Cambridge University Press)
Sasada, M., Uemura, M., Arai, A., et al. 2008, PASJ, 60, 37 [NASA ADS]
Sikora, M., Begelman, M. C., & Rees, M. J. 1994, ApJ, 421, 123 [NASA ADS] [CrossRef]
Setti, G., & Woltjer, L. 1994, ApJS, 92, 629 [NASA ADS] [CrossRef]
Tavecchio, F., & Ghisellini, G. 2008, MNRAS, 385, 98 [NASA ADS]
Tchekhovskoy, A., McKinney, J. C., & Narayan, R. 2009, ApJ, 699, 1789 [NASA ADS] [CrossRef]
Tramacere, A., Massaro, F., & Cavaliere, A. 2007, A&A, 466, 521 [NASA ADS] [EDP Sciences] [CrossRef]
Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef]
Villata, M., Raiteri, C. M., Larionov, V. M., et al. 2008, A&A, 481, 79 [NASA ADS] [EDP Sciences] [CrossRef]
Vittorini, V., Tavani, M., Paggi, A., et al. 2009, ApJ, 706, 1433 [CrossRef]

All Tables

Table 1: Parameters for the BL Lac sources discussed in the text.

All Figures

$\begin{figure} \includegraphics[width=9cm,clip]{13566fg1.eps} \vspace*{4mm} \end{figure}$	Figure 1: SEDs of the BL Lacs considered in the text: S5 0716+174 ( upper-left frame), Mrk 501 ( upper-right frame) and Mrk 421 ( lower-left and lower-right frames), each in a low (blue line) and a high (red line) state. In terms of intrinsic luminosity S5 0716+714 is the strongest source (data referenced in Sect. 2).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{13566fg2.eps} \vspace*{4mm} \end{figure}$	Figure 2: For the named sources the total jet luminosities normalized to their BZ power are plotted against the electron rms energy. Bars represent the hole mass uncertainties reflecting those (at the $1-\sigma$ level) in host bulge luminosities, and including the scatter in Eq. (7).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{13566fg3.eps} \vspace*{5.5mm} \end{figure}$	Figure 3: Bright BL Lacs in their context, adapted from Celotti & Ghisellini (2008) with historical data in terms of L_T and the energy $\gamma _{\rm peak}$ related to the synchrotron peak $\gamma _{\rm peak} = \gamma _{\rm p} \times {10}^{1/2r}$ . Blue circles indicate dry, while violet circles indicate wet BL Lacs. The lower-left region of the diagram corresponds to the source condition $t_{\rm c} > R/c$ , and the upper-right to $t_{\rm c} \gtrsim t_{\rm a}$ . Bright FSRQs lie at lower $\gamma _{\rm peak}$ and higher powers, with increasing signs of current $\dot{m} \rightarrow 1$ ; selection effects depopulate weaker sources in the lower region (see Padovani 2007). The dashed oval highlights sources in the transition region from dry to wet BL Lacs, interesting to compare with $L_{\rm BZ}$ from Eq. (6) particularly when at $z \gtrsim 0.3$ .
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.