EDP Sciences
Home All issues Volume 508 / No 3 (December IV 2009) A&A, 508 3 (2009) 1217-1234 Full HTML
Free Access
Issue
A&A
Volume 508, Number 3, December IV 2009
Page(s) 1217 - 1234
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/200912665
Published online 01 October 2009

A&A 508, 1217-1234 (2009)

The zCOSMOS survey: the role of the environment in the evolution of the luminosity function of different galaxy types[*]

E. Zucca1 - S. Bardelli1 - M. Bolzonella1 - G. Zamorani1 - O. Ilbert2 - L. Pozzetti1 - M. Mignoli1 - K. Kovac3 - S. Lilly3 - L. Tresse2 - L. Tasca4 - P. Cassata5 - C. Halliday6 - D. Vergani1 - K. Caputi3 - C. M. Carollo3 - T. Contini7 - J.-P. Kneib2 - O.Le Fèvre2 - V. Mainieri8 - A. Renzini9 - M. Scodeggio4 - A. Bongiorno10 - G. Coppa1,14 - O. Cucciati2 - S. de la Torre11,4 - L. de Ravel2 - P. Franzetti4 - B. Garilli4 - A. Iovino11 - P. Kampczyk3 - C. Knobel3 - F. Lamareille7 - J.-F.Le Borgne7 - V. Le Brun2 - C. Maier3 - R. Pellò7 - Y. Peng3 - E. Perez-Montero7,26 - E. Ricciardelli12 - J. D. Silverman3 - M. Tanaka8 - U. Abbas13 - D. Bottini4 - A. Cappi1 - A. Cimatti14 - L. Guzzo11 - A. M. Koekemoer15 - A. Leauthaud16 - D. Maccagni4 - C. Marinoni17 - H. J. McCracken18 - P. Memeo4 - B. Meneux10,27 - M. Moresco14 - P. Oesch3 - C. Porciani3,28 - R.Scaramella19 - S. Arnouts20 - H. Aussel21 - P. Capak22 - J. Kartaltepe23 - M. Salvato22 - D. Sanders23 - N. Scoville22 - Y. Taniguchi24 - D. Thompson25

1 - INAF - Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
2 - Laboratoire d'Astrophysique de Marseille, Université d'Aix-Marseille, CNRS, 38 rue Frederic Joliot-Curie, 13388 Marseille Cedex 13, France
3 - Institute of Astronomy, Swiss Federal Institute of Technology (ETH Hönggerberg), 8093 Zürich, Switzerland
4 - INAF - IASF Milano, via Bassini 15, 20133 Milano, Italy
5 - Department of Astronomy, University of Massachusetts, 710 North Pleasant Street, Amherst, MA 01003, USA
6 - INAF - Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze, Italy
7 - Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de Toulouse, CNRS, 14 avenue Edouard Belin, 31400 Toulouse, France
8 - European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching, Germany
9 - INAF - Osservatorio Astronomico di Padova, vicolo Osservatorio 5, 35122 Padova, Italy
10 - Max-Planck-Institut für extraterrestrische Physik, 84571 Garching, Germany
11 - INAF - Osservatorio Astronomico di Brera, via Brera 28, 20121 Milano, Italy
12 - Dipartimento di Astronomia, Università di Padova, vicolo Osservatorio 3, 35122 Padova, Italy
13 - INAF - Osservatorio Astronomico di Torino, strada Osservatorio 20, 10025 Pino Torinese, Italy
14 - Dipartimento di Astronomia, Università di Bologna, via Ranzani 1, 40127 Bologna, Italy
15 - Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MS 21218, USA
16 - LBNL & BCCP, University of California, Berkeley, CA 94720, USA
17 - Centre de Physique Theorique, Marseille, France
18 - Institut d'Astrophysique de Paris, UMR 7095 CNRS, Université Pierre et Marie Curie, 98 bis Boulevard Arago, 75014 Paris, France
19 - INAF, Osservatorio Astronomico di Roma, via di Frascati 33, 00040 Monteporzio Catone, Italy
20 - Canada-France-Hawaii Telescope Corporation, 65-1238 Mamalahoa Hwy, Kamuela, HI 96743, USA
21 - AIM Unité Mixte de Recherche CEA CNRS, Université Paris VII UMR 158, Paris, France
22 - California Institute of Technology, MC 105-24, 1200 East California Boulevard, Pasadena, CA 91125, USA
23 - Institute for Astronomy, University of Hawaii, 2680 Woodlawn Drive, Honolulu, HI, 96822, USA
24 - Research Center for Space and Cosmic Evolution, Ehime University, Bunkyo-cho, Matsuyama 790-8577, Japan
25 - Large Binocular Telescope Observatory, University of Arizona, 933 N. Cherry Ave., Tucson, AZ 85721-0065, USA
26 - Instituto de Astrofisica de Andalucia, CSIC, Apdo. 3004, 18080 Granada, Spain
27 - Universitäts-Sternwarte, Scheinerstrasse 1, 81679 Munich, Germany
28 - Argelander-Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn, Germany

Received 9 June 2009 / Accepted 17 September 2009

Abstract
Aims. An unbiased and detailed characterization of the galaxy luminosity function (LF) is a basic requirement in many astrophysical issues: it is of particular interest in assessing the role of the environment in the evolution of the LF of different galaxy types.
Methods. We studied the evolution in the B band LF to redshift $z\sim 1$ in the zCOSMOS 10k sample, for which both accurate galaxy classifications (spectrophotometric and morphological) and a detailed description of the local density field are available.
Results. The global B band LF exhibits a brightening of $\sim$0.7 mag in M* from $z\sim 0.2 $ to $z\sim 0.9$. At low redshifts (z<0.35), spectrophotometric late types dominate at faint magnitudes ( MBAB > -20), while the bright end is populated mainly by spectrophotometric early types. At higher redshift, spectrophotometric late-type galaxies evolve significantly and, at redshift $z\sim 1$,the contribution from the various types to the bright end of the LF is comparable. The evolution for spectrophotometric early-type galaxies is in both luminosity and normalization: M* brightens by $\sim$0.6 mag but $\phi^*$ decreases by a factor $\sim$1.7 between the first and the last redshift bin. A similar behaviour is exhibited by spectrophotometric late-type galaxies, but with an opposite trend for the normalization: a brightening of $\sim$0.5 mag is present in M*, while $\phi^*$ increases by a factor $\sim$1.8.
Studying the role of the environment, we find that the global LF of galaxies in overdense regions has always a brighter M* and a flatter slope. In low density environments, the main contribution to the LF is from blue galaxies, while for high density environments there is an important contribution from red galaxies to the bright end.
The differences between the global LF in the two environments are not due to only a difference in the relative numbers of red and blue galaxies, but also to their relative luminosity distributions: the value of M* for both types in underdense regions is always fainter than in overdense environments. These results indicate that galaxies of the same type in different environments have different properties.
We also detect a differential evolution in blue galaxies in different environments: the evolution in their LF is similar in underdense and overdense regions between $z\sim 0.25$ and $z\sim 0.55$, and is mainly in luminosity. In contrast, between $z\sim 0.55$ and $z\sim 0.85$ there is little luminosity evolution but there is significant evolution in $\phi^*$, that is, however, different between the two environments: in overdense regions $\phi^*$ increases by a factor $\sim$1.6, while in underdense regions this increase reaches a factor $\sim$2.8. Analyzing the blue galaxy population in more detail, we find that this evolution is driven mainly by the bluest types.
Conclusions. The ``specular'' evolution of late- and early-type galaxies is consistent with a scenario where a part of blue galaxies is transformed in red galaxies with increasing cosmic time, without significant changes in the fraction of intermediate-type galaxies. The bulk of this tranformation in overdense regions probably happened before $z\sim 1$, while it is still ongoing at lower redshifts in underdense environments.

Key words: galaxies: evolution - galaxies: luminosity function, mass function - galaxies: statistics - Surveys

1 Introduction

The COSMOS project (Scoville et al. 2007) aims to identify the physical processes that drive the evolution of galaxies. For example, dynamical processes are likely to play a major role in determining the galaxy morphology, whereas dissipative phenomena affect the gas content and therefore the star formation, altering the galaxy spectral energy distribution. The interplay between these two types of processes is not yet completely understood, as well as the role of the environment in the evolution of galaxy properties.

From the observational point of view, the investigation of these topics requires: a) high quality images, for deriving accurate morphological classifications; b) complete multiwavelength coverage, for determining spectral energy distributions; c) galaxy spectra, for obtaining spectroscopic redshifts (necessary for a precise environment description) and measuring spectral features (to be used as diagnostics of the gas and stellar physics).

The COSMOS multiwavelength imaging project provides data for points a) and b), while the zCOSMOS survey (Lilly et al. 2007) was developed to fullfill point c). The combination of these data allows us to study with unprecedented completeness the properties and evolutionary histories of galaxies as a function of their type and environment at the same time. The luminosity function is the first and most direct estimator in quantifying this evolution.

Several works have already demonstrated that the global luminosity function evolves. The Canadian network for observational cosmology field galaxy redshift survey (CNOC-2, Lin et al. 1999) and the ESO sculptor survey (ESS, deLapparent et al. 2003) derived the luminosity function up to $z\sim 0.5$ using $\sim$2000 and $\sim$600redshifts, respectively. At higher redshift, the Canada France redshift survey (CFRS, Lilly et al. 1995) allowed to study the luminosity function up to $z\sim 1.1$ with a sample of $\sim$600 redshifts.

A major improvement in this field was obtained with the VIMOS VLT Deep Survey (VVDS, Le Fèvre et al. 2005), which detected a significant brightening of the M* parameter, amounting to $\sim$2 mag in the B band from $z\sim 0$ to $z\sim 2$ (Ilbert et al. 2005), using a sample of $\sim$11 000 spectra. With the same sample, Zucca et al. (2006) studied the evolution in the luminosity function for different spectrophotometric types, finding a strong type-dependent evolution and identifying the latest types as being responsible for most of the evolution in the global luminosity function.

Establishing the role of the environment is more difficult, because accurate redshifts and surveys with high sampling rates are necessary for reliable density estimates. These constraints are satisfied by large local surveys, such as the two-degree Field Galaxy Redshift Survey (2dFGRS, Colless et al. 2001) and the Sloan Digital Sky Survey (SDSS, York et al. 2000). From the 2dFGRS, Croton et al. (2005) measured the dependence of the luminosity function on the density contrast (defined in spheres of radius 8 h-1 Mpc) and galaxy types, finding that the void regions are dominated by faint late-type galaxies and that the cluster regions exhibit an excess of very bright early-type galaxies. The parameter M* brightens in overdense regions for all galaxy types, while the slope $\alpha $ steepens with increasing density for late-type galaxies and remains constant for early-type galaxies.

At high redshift, the situation becomes more complicated: many surveys are based on photometric redshifts, which do not allow an accurate reconstruction of the density field, and/or lack galaxy classifications (morphological and/or spectrophotometric).

Deep surveys based on spectroscopic redshifts, such as the VIMOS-VVDS (Le Fèvre et al. 2005) and the DEEP2 Galaxy Redshift Survey (Davis et al. 2003), are able to study galaxy properties as a function of the environment to $z \sim 1.5$. Cucciati et al. (2006), using VVDS data, and Cooper et al. (2006, 2007), using DEEP2 data, claimed that the color-density relation significantly evolves with redshift, and Cucciati et al. (2006) found that this relation is established at higher redshift for brighter galaxies. To understand these results, it is necessary to study the evolution in the luminosity function of different galaxy types in different environments. Until now, the data required to complete this study as a function of galaxy type, environment, and redshift, has been unavailable.

In this paper, we study the effect of the environment on the evolution in the luminosity function of different galaxy types for the zCOSMOS 10k bright sample. Parallel studies discuss the evolution of the luminosity density (Tresse et al. 2009, in prep.), the mass function for different types (Pozzetti et al. 2009) and in various environments (Bolzonella et al. 2009), the spectrophotometric properties as a function of the environment (Cucciati et al. 2009; Iovino et al. 2009) and the morphology-density relation (Tasca et al. 2009; Kovac et al. 2009b).

The paper is organized as follows: in Sect. 2, we present the data on which this work is based and in Sect. 3 we describe the method used to estimate luminosity functions. The results concerning the luminosity function evolution are described in Sect. 4 and the contribution of the different galaxy types is presented in Sect. 5, paying particular attention to early-type galaxies in Sect. 6. The role of the environment is discussed in Sect. 7, and the results are summarized in Sect. 8.

Throughout this paper we adopt a flat $\Omega_{\rm m} = 0.25$ and $\Omega_\Lambda = 0.75$ cosmology, with H0 = 70 km s-1 Mpc-1. Magnitudes are given in the AB system.

2 Data

The zCOSMOS project is a large redshift survey (Lilly et al. 2007) that was undertaken to study the COSMOS field using 600 hours of observations with the ESO VLT. COSMOS is an HST Treasury Project (Scoville et al. 2007) survey of a 2 square degree equatorial field with the advanced camera for surveys (ACS). It is the largest survey ever completed by HST, utilizing 10% (640 orbits) of its observing time over two years (HST Cycles 12 and 13), as described further in Koekemoer et al. (2007). The primary goal of COSMOS is to understand how galaxies and AGN evolve over cosmic time in terms of their environment, on all scales from groups up to the large scale structure of filaments and voids. The COSMOS field is accessible to almost all astronomical facilities, which has enabled the compilation of complete multiwavelength datasets (X-ray, UV, optical/IR, FIR/submillimeter to radio) to be used in combination with the high resolution HST images.

2.1 Photometric data

Photometric data in the COSMOS field are available for a wide range of wavelengths. In the following, we make use of the magnitudes measured in the filters CFHT u* and $K_{\rm s}$, Subaru BJ, VJ, g+, r+, i+ and z+, and of the Spitzer IRAC magnitudes at 3.6 $\mu$m and 4.5 $\mu$m. Details about Subaru observations are given in Taniguchi et al. (2007), while $K_{\rm s}$ data are described in McCracken et al. (2010). Spitzer IRAC data are presented in Sanders et al. (2007).

Capak et al. (2007) provided a full description of the completed data reduction and characteristics of the optical observations. We recall that photometry can be optimized by applying offsets to the observed magnitudes to reduce the differences between observed and reference magnitudes computed from a set of template spectral energy distributions (SEDs), as demonstrated by Capak et al. (2007, see their Table 13). We adopted the same approach, but we derived our own offsets by using the set of SEDs that we used to compute absolute magnitudes (see Sect. 3.1). In all cases, the offsets that we derived are similar to those of Capak et al. (2007).

2.2 Morphologies from ACS images

Morphological parameters for the galaxies are obtained from the HST ACS imaging (Koekemoer et al. 2007). The COSMOS I band ACS images have sufficient depth and resolution to allow classical bulge-disk decomposition of L* galaxies at $z\le 2$. The size of the COSMOS sample suggests the use of an automatic and objective morphological classification technique. The method adopted for the morphological classification is described in detail in Cassata et al. (2007, 2009, in prep.) and Tasca et al. (2009), and here we summarize the main steps of the procedure.

Using a training set of $\sim$500 galaxies for which eye-ball morphological classification is available, the parameters describing the galaxy morphology were determined. The classification scheme was based on three non-parametric diagnostics of galaxy structures (Abraham et al. 2003; Lotz et al. 2004), the concentration index C, the asymmetry parameter A and the Gini coefficient G, and the galaxy magnitude in the I band (F814W HST/ACS band). These parameters were then converted into morphological classes: this is done computing in the multi-dimensional parameter space the distance of each galaxy from objects in the training set. The morphological class was then assigned on the basis of the most frequent class of the 11 nearest neighbours. Given the fact that the classification is based on the observed F814W band, in the redshift range considered in this work (z<1) the effects of morphological K-correction are small (Cassata et al. 2007; Tasca et al. 2009).

In the following, we use this morphological classification, dividing galaxies into early-types (including ellipticals and lenticulars), spirals, and irregulars.

2.3 Spectroscopic data

Spectroscopic redshifts in the zCOSMOS survey are obtained with the VIMOS spectrograph (Le Fèvre et al. 2003) at the ESO Very Large Telescope. The zCOSMOS survey consists of two parts. The first part (zCOSMOS-bright) is a pure magnitude-limited survey with $15\le I \le 22.5$ (the I magnitude having been measured in the F814W HST/ACS band) and covers the entire 1.7 deg2 COSMOS field. This magnitude limit will yield a sample of $\sim$20 000 galaxies in the redshift range $0.05 \la z \la 1.2$. The second part (zCOSMOS-deep) aims to observe $\sim$10 000 galaxies in the redshift range $1.5 \la z \la 3.0$, selected by clearly defined color criteria, and is restricted to the central 1 deg2 of the COSMOS field.

Spectroscopic data were reduced with the VIMOS interactive pipeline graphical interface (VIPGI, Scodeggio et al. 2005) and redshift measurements were derived using the EZ package (Garilli et al. 2009, in prep.) and then visually checked. Each redshift measurement was assigned a quality flag, between ``0'' (impossible to determine a redshift) and ``4'' (for which the measurement is 100% certain); flag ``9'' indicates spectra with a single emission line, for which multiple solutions are possible. Specific flags are used to denote broad line AGNs. A decimal digit indicates how closely the redshift agrees with its photometric redshift (Feldmann et al. 2006) computed from optical and near IR photometry, using the code ZEBRA (Feldmann et al. 2008). Further details of the reduction procedure, redshift determination, and quality flags are given in Lilly et al. (2007, 2009).

2.4 Environment

One of the main scientific objectives of the zCOSMOS survey is to study the role of the environment on galaxy evolution to high redshift. For the zCOSMOS-bright survey, spectroscopic observations were performed with the medium resolution ($R\sim 600$) red grism, which provides a velocity accuracy of $\sim$100 km s-1. Repeated observations of $\sim$100 galaxies enabled us to estimate the rms velocity uncertainty in each measurement to be of the order of 110 km s-1 (Lilly et al. 2009). The measurement of redshifts to such precision allows us to define environments of galaxies from the scale of galaxy groups to the larger scales of the cosmic web.

The density field of the COSMOS survey and the local environment of zCOSMOS galaxies have been derived in Kovac et al. (2009a), where various estimators based on counts in fixed comoving apertures (cylindrical, spherical and Gaussian) and the distance to the nearest neighbours are presented, using different tracers (flux-limited or volume-limited subsamples).

In the following, we use overdensities derived by the 5th nearest neighbour estimator and computed using volume-limited tracers. This choice is a good compromise between the smallest accessible scales, the robustness of the estimator, and the covered redshift range. Bolzonella et al. (2009) discuss in detail the effects of different choices, in terms of estimators and tracers, on the estimate of the galaxy stellar mass function.

2.5 The zCOSMOS 10k bright sample

The zCOSMOS survey is currently ongoing: the data used in the present paper are the so-called ``10k bright sample'' (Lilly et al. 2009), which consists of the first $10\ 644$ observed objects, over an area of 1.402 deg2 with 1 or 2 passes per VIMOS pointing and a mean sampling rate of $\sim$33%.

For the present analysis we excluded Broad Line AGNs, stars, and objects that had not been included in the statistical sample defined in the magnitude range $15\le I \le 22.5$. We used only galaxies with reliable redshifts, i.e. starting from flags 1.5 (see Lilly et al. 2007, and 2009, for details about the flag definition): such a sample has an overall reliability of $\sim$$99\%$. These objects comprise $88\%$ of the overall sample and $95\%$ of the objects in the redshift range 0.5 < z < 0.8.

To obtain a reliable SED fitting when deriving absolute magnitudes and spectrophotometric types (see Sect. 3.1), we considered only objects with apparent magnitudes measured in more than 3 photometric bands.

The final sample used in this paper consists of 8478 galaxies satisfying the criteria described above.

3 Luminosity function estimate

3.1 Absolute magnitudes and spectrophotometric types

Absolute magnitudes were computed following the method described in the Appendix of Ilbert et al. (2005). The K-correction was computed using a set of templates and all available photometric information. However, to reduce the template dependency, the rest-frame absolute magnitude in each band was derived using the apparent magnitude from the closest observed band, shifted to the redshift of the galaxy. With this method, the applied K-correction was as small as possible.

The spectrophotometric types are defined by matching the rest-frame magnitudes to the set of templates described in Ilbert et al. (2006a): the four locally observed CWW spectra (Coleman et al. 1980) and two starburst SEDs from Kinney et al. (1996), extrapolated toward UV and mid-IR wavelengths, interpolated to obtain 62 SEDs, and optimized by using the VVDS spectroscopic data. The SED fitting was performed by minimizing a $\chi^2$ variable on these templates at the spectroscopic redshift of each galaxy, providing as output the best-fit spectrum template. Galaxies were then classified into four types, corresponding to colors of E/S0 (type 1), early spirals (type 2), late spirals (type 3), and irregular and starburst galaxies (type 4).

3.2 The ALF tool

Luminosity functions were computed using the ``algorithm for luminosity function'' (ALF), a dedicated tool that implements several estimators: the non-parametric $1/V_{\max}$ (Schmidt 1968), C+(Lynden Bell 1971, in its modified version described by Zucca et al. 1997), SWML (Efstathiou et al. 1988), and the parametric STY (Sandage et al. 1979), for which we assumed a Schechter function (Schechter 1976). The tool and these estimators were described in detail by Ilbert et al. (2005).

Ilbert et al. (2004) demonstrated that the estimate of the global luminosity function can be biased, mainly at the faint end, when the measurement band differs in wavelength considerably from the rest-frame band in which galaxies are selected. This is caused by the fact that, because of the K-corrections, different galaxy types are visible in different absolute magnitude ranges at a given redshift and fixed apparent magnitude limit. When computing the luminosity functions we avoided this bias by using in each redshift range (for the C+, SWML, and STY estimates) only galaxies within the absolute magnitude range for which the entire wavelength range of their SEDs is potentially observable. We used the complete magnitude range for only the $1/V_{\max}$ estimate. Since this estimator underestimates the luminosity function for absolute magnitudes fainter than the bias limit (Ilbert et al. 2004), it provides a lower limit of the faint-end slope.

\begin{figure} \par\includegraphics[width=12cm,clip]{12665f1.ps} \end{figure} Figure 1:

Evolution of the global luminosity function in the B rest-frame band. Each panel refers to a different redshift bin, which is indicated in the label, with also the number of galaxies. The vertical dashed and dotted lines represent the faint absolute limit considered in the STY estimate for the zCOSMOS and VVDS sample, respectively. The luminosity functions are estimated with different methods (see text for details) but for clarity we plot only the results from C+ (squares) and STY (solid line). The dotted line represents the luminosity function estimated in the redshift range [0.2-0.4] and it is reported in each panel as a reference. The STY estimates from the VVDS sample are plotted with dashed lines. In the redshift bins [0.8-1.0] and [1.0-1.3] for the zCOSMOS sample we fixed $\alpha $ to the VVDS value.

Open with DEXTER

Even if this bias is less important when estimating the luminosity function of galaxies divided by type, because the K-corrections are more similar to each other, we have, however, taken it into account. The absolute magnitude limits for the STY estimate are indicated by vertical dashed lines in the figures, and in the tables where the best-fit parameters are reported, we provide both the total number of objects and the number of galaxies within this magnitude limit.

\begin{figure} \par\mbox{\includegraphics[width=8.8cm]{12665f2a.ps}\includegraphics[width=8.8cm]{12665f2b.ps} } \end{figure} Figure 2:

Observed fraction of bright galaxies ( MB < -20.77) of different types as a function of redshift. Error bars are $1\sigma $Poisson errors. Left panel: spectrophotometric type 1 (short dashed red line), type 2 (solid orange line), type 3 (dotted green line) and type 4 (long dashed blue line) galaxies. Right panel: morphological early-type (ellipticals and lenticulars) (short dashed red line), spiral (solid green line) and irregular (dotted blue) galaxies; in gray (long dashed line) unclassified galaxies.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.8cm]{NEW_12665f3a-cmjn.eps}\includeg... ...5f3c-cmjn.eps}\includegraphics[width=8.8cm]{NEW_12665f3d-cmjn.eps} \end{figure} Figure 3:

Luminosity functions of the different spectrophotometric types in redshift bins (indicated in each panel): type 1 in red, type 2 in orange, type 3+4 in blue, total sample in black. The squares represent the results from the C+ and the solid lines are the results from the STY method. The vertical dashed line represents the faint absolute limit considered in the STY estimate. The shaded regions represent the $68\%$ uncertainties on the parameters $\alpha $ and M*.

Open with DEXTER

\begin{figure} \par\mbox{\includegraphics[width=6cm]{12665f4a.ps}\includegraphics[width=6cm]{12665f4b.ps}\includegraphics[width=6cm]{12665f4c.ps} } \end{figure} Figure 4:

Evolution of the luminosity functions for different galaxy types: type 1 ( left panel), type 2 ( middle panel) and type 3+4( right panel) galaxies. The colors refer to different redshift ranges: [0.10-0.35]in black, [0.35-0.55] in cyan, [0.55-0.75] in magenta and [0.75-1.00] in green. The STY estimates are derived with $\alpha $ fixed. The meaning of lines is the same as in Fig. 3: points from the C+ estimates are not reported for clarity.

Open with DEXTER

Table 1:   STY parameters (with $1\sigma $ errors) in different redshift bins for total sample and different galaxy type subsamples.

3.3 The weighting scheme

To take account of unknown redshifts (for unobserved objects and poor quality spectra), it is necessary to apply a weight to each galaxy (Zucca et al. 1994; Ilbert et al. 2005). This weight is a combination of two different contributions: the target sampling rate (TSR) and the spectroscopic success rate (SSR).

For each galaxy i, we computed the weight wi, defined to be the product of two factors:

a)
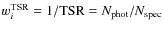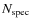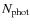$w_i^{\rm TSR}=1/{\rm TSR}=N_{\rm phot}/N_{\rm spec}$, where $N_{\rm spec}$ is the number of observed sources in the spectroscopic survey and $N_{\rm phot}$ is the number of sources contained in the parent catalogue used to select the targets; the TSR thus describes the fraction of sources observed in the spectroscopic survey;

b)
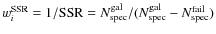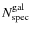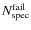$w_i^{\rm SSR}=1/{\rm SSR}=N_{\rm spec}^{\rm gal}/(N_{\rm spec}^{\rm gal}-N_{\rm spec}^{\rm fail})$, where $N_{\rm spec}^{\rm gal}$ is the number of galaxies observed spectroscopically (i.e., excluding spectroscopically confirmed stars and broad line AGNs) and $N_{\rm spec}^{\rm fail}$ is the number of objects without a reliable measure of redshift, i.e., ``failures''.
Since the galaxies observed spectroscopically were randomly selected from the parent sample, the TSR is independent of both the apparent magnitude and other observed quantities, with an approximately constant value of $\sim$$33\%$.

In contrast, the SSR is a function of the selection magnitude, which is linked to the signal-to-noise ratio of the spectrum and ranges between 97.5% at bright magnitudes and 82% at the faintest ones for our subsample of galaxies. Moreover, from the photometric redshift distribution is evident that low-confidence redshift flags or complete failures correspond to objects at high redshift or in redshift ranges where most of the prominent lines fall outside the observed wavelength range (Lilly et al. 2009). For this reason, we used the Ilbert et al. (2009) release of $z_{\rm phot}$ and computed the SSR in $\Delta z=0.2$ redshift bins. Finally, the characteristic emission or absorption lines are different for different galaxy types, as shown in Lilly et al. (2009). We further split the computation of SSR in each redshift bin separating red and blue galaxies, selected on the basis of their rest-frame U-V color. We computed the final weights $w_i=w_i^{\rm TSR}\times w_i^{\rm SSR}$ considering all the described dependencies.

This scheme was applied to each observed galaxy, a part from two groups of special objects. The spectroscopic catalogue contains not only randomly targeted objects, because a small fraction of sources (mainly X-ray sources) were flagged as ``compulsory'' when preparing the masks; the TSR of these sources is much higher than the global one and was computed separately. In some cases, a slit also contained objects in addition to the primary target. For these ``secondary targets'', the SSR was found to be far lower than the global relation, because most of these sources had not been centered well in the slit, resulting in faint spectra. For these objects, the SSR was computed separately. The contribution of these two classes of objects to the total sample was only $\sim$$2\%$ and $\sim$$3\%$, respectively.

4 The global luminosity function

The global luminosity function was computed as a function of redshift to z=1.3, adopting the same redshift bins used in the analysis of the VVDS deep field (Ilbert et al. 2005), to allow a direct comparison to be made. In the following, we show the results for the Johnson B rest-frame band.

Figure 1 shows the global luminosity function in redshift bins, obtained with the C+ and STY methods. The luminosity functions derived with the other two methods ( $1/V_{\max}$ and SWML) are consistent with those shown in the figures, but are not drawn for clarity. The dotted line represents the luminosity function estimated in the redshift range [0.2-0.4] and is shown in each panel for reference. The STY estimates from the VVDS sample are plotted with dashed lines. Vertical lines represent the bias limit described in Sect. 3.2.

The global luminosity function agrees well with the VVDS estimates: there are small differences in the normalization in some redshift bins, due to the presence of underdense and overdense regions in both samples, which is particularly strong in the zCOSMOS sample (see Lilly et al. 2009). In particular, the high zCOSMOS LF normalization in the redshift bin [0.8-1.0] is due to a prominent structure, discussed in detail in Kovac et al. (2009a). We note also that the VVDS luminosity functions were derived with slightly different cosmological parameters ( $\Omega_{\rm m} = 0.3$ and $\Omega_\Lambda = 0.7$).

Because of the larger area, the zCOSMOS sample is more suitable for constraining the bright part of the luminosity function with respect to the VVDS deep sample. With the zCOSMOS data, it is also possible to derive some constraints on the M* value in the first redshift bin, where for the VVDS sample it was necessary to fix M* to the local SDSS value. On the other hand, the VVDS fainter magnitude limit allowed us to estimate the slope $\alpha $ more reliably at high redshift, where the estimate from the zCOSMOS sample is almost unconstrained. For this reason, we fixed $\alpha $ to the VVDS value in the redshift bins [0.8-1.0] and [1.0-1.3].

Having shown full consistency between the zCOSMOS and VVDS luminosity functions, we then derived the luminosity function in the redshift bins [0.10-0.35], [0.35-0.55], [0.55-0.75] and [0.75-1.00], following the choice of Pozzetti et al. (2009) for their study of the zCOSMOS mass function, and in Table 1 we report the STY parameters for each bin.

The errors reported in this table represent a $1\sigma $ confidence level for a 1-parameter estimate ( $\Delta\chi^2 = 1.0$). These errors underestimate the true errors. In particular, they are smaller than the projection onto the parameter axes of the 2-parameter $68\%$ confidence ellipses, which, on the other hand, are always an overestimate of the true errors, especially when the errors on the two parameters are highly correlated.

The luminosity function evolves by $\sim$0.7 mag in M* from the first ( [0.10-0.35]) to the last ( [0.75-1.00]) redshift bins. This result agrees with the VVDS results for the same redshift range. For the evolution in slope, we find that $\alpha $ is almost constant in the first three redshift bins, and then steepens in the last bin.

To understand how the different galaxy populations contribute to this evolution in the global luminosity function, we now quantify the contribution of the different galaxy types, by deriving their luminosity functions separately.

5 The contribution of the different galaxy types

5.1 Spectrophotometric types

Galaxies were divided into four spectrophotometric classes (see Sect. 3.1 above). In the left panel of Fig. 2, we plot the observed fraction of bright galaxies for each type as a function of redshift. We identified and selected objects with MB < -20.77 to be galaxies visible for the entire redshift range [0-1.0]. The same cut was adopted for the VVDS, but in that case it was possible to sample the range [0-1.5] because of the fainter magnitude limit of the survey. From this figure, it is clear that the bright late-type population becomes increasingly dominant at higher redshifts, while, correspondingly, the fraction of bright early-type galaxies decreases. These trends in the fraction of the bright galaxy population with redshift are similar to those found in the VVDS (in the common redshift range), although with some differences in the normalizations. The decrease of early-type galaxies in the zCOSMOS sample appears less significant than in the VVDS sample: starting from similar values at $z\sim 0.3$, the zCOSMOS curve remains significantly (at $\sim$$2\sigma$ level) higher by $\sim$$20\%$than the VVDS one. This fraction decreases by a factor $\sim$2 at $z\sim 0.9$ in zCOSMOS, while it decreases by a factor of $\sim$2.3 at the same redshift in the VVDS. In the same redshift range, the fraction of bright type 3 galaxies increases by a factor $\sim$6; the strong increase in type 4 galaxies detected in the VVDS is not visible here, due to the lower redshift range.

Luminosity functions were derived for each type in different redshift bins. For each type, we derived the luminosity function also by fixing $\alpha $ to the value obtained in the redshift range [0.30-0.80]. This choice allowed us to better constrain the evolution of M* with redshift and is acceptable because most of the $\alpha $ values estimated in the various redshift bins are consistent with the [0.30-0.80] value. This consistency is marginal for the highest redshift bin of type 1 galaxies, but in this bin the STY estimate is poorly constrained because the faint end of the luminosity function is inadequately sampled, due to the magnitude limit of the survey.

For type 1, 2 and 3 galaxies, this value of $\alpha $ agrees with the VVDS estimate. For type 4 galaxies, the parameter $\alpha $ is unconstrained for z>0.3: for this reason, we fixed $\alpha $ to be the value derived from the first redshift bin, which is consistent with the VVDS value for type 4 galaxies.

The evolution of M* and $\phi^*$ with redshift for the different types are consistent with the VVDS results in the common redshift range.

Given the uncertainties in the luminosity function estimate of type 4 galaxies, we repeated the analysis by grouping together type 3 and 4 galaxies: the results are shown in Fig. 3 and the STY parameters for each bin are reported in Table 1, for both $\alpha $free and $\alpha $ fixed. Parameters for the reference bin [0.30-0.80] are also reported in the table. In Fig. 3 the squares represent the results from the C+ and the solid lines are the results from the STY method: type 1 galaxies are shown in red, type 2 galaxies in orange, type 3+4 galaxies in blue. The total sample is shown in black. The shaded regions represent the $68\%$ uncertainties in the parameters $\alpha $ and M*. From this figure, it is clear that at low redshifts (z<0.35) late-type galaxies dominate for faint magnitudes ( MB > -20), while the bright end is populated mainly by type 1 galaxies. At higher redshift, late-type galaxies evolve strongly and at redshift z > 0.55 the contributions of the various types to the bright end of the luminosity function are comparable. The faint end remains dominated by late-type galaxies over the entire redshift range.

To visualize the evolution with redshift, in Fig. 4 we plot the luminosity functions in different redshift bins for each galaxy type: type 1 galaxies in the left panel, type 2 galaxies in the middle panel, and type 3+4 galaxies in the right panel. The different colors represent different redshift bins: [0.10-0.35] in black, [0.35-0.55] in cyan, [0.55-0.75] in magenta, and [0.75-1.00] in green. To follow the evolution in M* and $\phi^*$, we show the STY estimates obtained with $\alpha $ fixed. For type 1 galaxies, evolution occurs in both luminosity and normalization: M* brightens by $\sim$0.6 mag and $\phi^*$ decreases by a factor $\sim$1.7 between the first and the last redshift bin. Type 3+4 galaxies also evolve both in luminosity and normalization, but with an opposite trend for the normalization: a brightening with redshift of $\sim$0.5 mag is evident in M*, while $\phi^*$ increases by a factor $\sim$1.8. Type 2 galaxies exhibit a milder evolution, involving a brightening of $\sim$0.25 mag in M* and no significant evolution in $\phi^*$.

The galaxy stellar mass functions of the various types (Pozzetti et al. 2009) show differences in the massive part stronger that the differences we find in the bright part of the luminosity functions. This is due to the fact that the mass-to-light ratio of early-type galaxies is on average higher than that of late-type galaxies: in fact, the contribution to the bright end of our B band luminosity functions comes from both massive red galaxies and blue galaxies with strong star formation. This fact also implies that the bimodality observed in the global galaxy stellar mass function by Pozzetti et al. (2009) is not detected in the global luminosity function.

5.2 Morphological types

A major advantage of the zCOSMOS survey is the availability of galaxy morphologies obtained from the HST ACS images (Koekemoer et al. 2007). Galaxies were divided into early types (including ellipticals and lenticulars), spirals, and irregulars following the classification described in Sect. 2.2 above. In the right panel of Fig. 2, we plot the observed fraction of bright galaxies of each morphological type as a function of redshift. Unclassified galaxies are a very small fraction of the sample ($\sim$$3\%$) and are uniformly distributed with redshift.

As observed for spectrophotometric types, late-type galaxies steadily increase their fraction with increasing redshift, while the fraction of early types decreases. However, at low redshift the fraction of morphologically classified early types is higher than that of type 1 galaxies, as is evident by comparing the left and right panels in Fig. 2.

The luminosity functions of the different types are shown in Fig. 5 (early types in red, spirals in green, irregulars in blue) and the STY parameters for each bin are reported in Table 1, where we show results for both $\alpha $ free and $\alpha $ fixed to the value determined in the redshift range [0.30-0.80].

At low redshift (z<0.35), early-type galaxies dominate the bright end of the luminosity function, while spiral galaxies dominate the faint end. Irregular galaxies increase their contribution at the lowest luminosities. At intermediate redshift ( [0.35-0.75]), spiral galaxies increase their luminosities and their contribution to the bright end of the luminosity function is similar to that of the early types. At high redshift (z>0.75), irregular galaxies evolve strongly and the three morphological types contribute almost equally to the total luminosity function. Irregular galaxies show an evolution of a factor $\sim$3.3 in $\phi^*$from low to high redshift. This evolution occurs mainly in the last redshift bin, while for z<0.75, the contribution of these galaxies to the global luminosity function is significantly lower than that of spirals and early types.

Scarlata et al. (2007) derived luminosity functions for COSMOS galaxies, using photometric redshifts and the ZEST morphological classification. The shape parameters we find for early types and spirals are consistent with those found by Scarlata et al. (2007) for their early-type and disk galaxies, but are significantly different for irregular galaxies, which have a much flatter slope in Scarlata et al. (2007). These differences are likely due to the different morphological classification applied.

Although the general trend in the luminosity functions of the different morphological types is similar to the results obtained in the previous section for spectrophotometric types, some differences are present. In particular, there are more morphological early-type than type 1 galaxies at the faint end of the luminosity function ( $M_{B} \ga -19.5$in the first redshift bin). In the following, we discuss the relationship between spectrophotometric and morphological types, paying particular attention to early-type galaxies.

\begin{figure} \par\mbox{\includegraphics[width=8.8cm]{12665f5a.ps}\includegraph... ...th=8.8cm]{12665f5c.ps}\includegraphics[width=8.8cm]{12665f5d.ps} }\end{figure} Figure 5:

Luminosity functions of the different morphological types in redshift bins: early types (ellipticals and lenticulars) in red, spirals in green, irregulars in blue. The meaning of symbols and lines is the same as in Fig. 3.

Open with DEXTER

\begin{figure} \par\mbox{\includegraphics[width=8.8cm]{12665f6a.ps}\includegraphics[width=8.8cm]{12665f6b.ps} }\end{figure} Figure 6:

Composite spectra of morphologically classified early types brighter ( left panel) and fainter ( right panel) than MB = -20.77. Morphological early types are divided on the basis of their spectrophotometric type (see the text for details): ``blue'' early types in blue (lower spectra), ``red'' early types in magenta (middle spectra), ``very red'' early types in red (upper spectra). The flux on the Y-axis is in arbitrary units and the spectra have been vertically shifted for clarity.

Open with DEXTER

\begin{figure} \par\mbox{\includegraphics[width=8.8cm]{12665f7a.ps}\includegraph... ...th=8.8cm]{12665f7c.ps}\includegraphics[width=8.8cm]{12665f7d.ps} }\end{figure} Figure 7:

Luminosity functions of early-type galaxies: bona-fide ET (black), type 1 (red) and morphological early-type (in green) galaxies. The meaning of symbols and lines is the same as in Fig. 3.

Open with DEXTER

6 Spectrophotometric versus morphological types

Although there is a broad agreement between our results for spectrophotometric and morphological types, it is reasonable that there should also be some differences. Spectrophotometric types are based on the galaxy SEDs and therefore depend on the star formation history, while morphological types reflect mainly the dynamical history of the galaxy. These classifications can also be affected by different observational and methodological biases.

We compared the spectrophotometric and morphological results for each galaxy. Considering early-type galaxies, we have 2387 morphological early types, 1504 of which ($63\%$) are classified as type 1 galaxies. In contrast, $71\%$ of the 2105 type 1 galaxies are classified as morphological early types. If we consider only galaxies whose SED is most accurately reproduced by the most extreme (i.e. reddest) type 1 template, the fraction increases to $80\%$. The remaining fraction of type 1 galaxies that are not classified as morphological early types is in part due to objects being without morphological classification ($\sim$$3\%$) and in part due to a population of ``red" spirals, many of which on visual inspection appear to be edge-on spiral galaxies, often dominated by a strong dust lane (see Tasca et al. 2009, for a detailed discussion). The red SED for these galaxies is probably caused by a significant amount of dust extinction.

We then considered in more detail the $\sim$$37\%$ of morphological early-type galaxies that were not classified as spectrophotometric type 1. We termed ``blue'' early types those with spectrophotometric type 2, 3 or 4; among the morphological early types with spectrophotometric type 1, we termed ``very red'' those best fitted by the reddest type 1 template and ``red'' those best fitted by the other type 1 templates. These ``blue'' early types were visually inspected (see details in Tasca et al. 2009) revealing a class of face-on late-type galaxies with morphological parameters typical of an early-type population.

To explore the properties of these classes of morphological early types, composite spectra were generated for these objects (following Mignoli et al. 2009) by averaging their spectra and dividing them into bins brighter and fainter than MB = -20.77.

These spectra are shown in Fig. 6, where the Y-axis is rescaled arbitrary for clarity, for the bright sample on the left and for the faint sample on the right. Blue, magenta, and red spectra correspond, respectively, to ``blue'', ``red'', and ``very red'' early types. From this figure, clear differences are visible in the spectra, in particular prominent emission lines are present in ``blue'' early types. By comparing the bright and the faint ``blue'' early types, we find that the H$\alpha $ line equivalent width increases for fainter galaxies and that the ratio between [NII] and H$\alpha $lines is stronger for brighter galaxies. The [NII] / H$\alpha $ and [OIII] / H$\beta$ ratios of the bright ``blue'' early types are consistent with those of liners. Bright ``blue'' early types are $\sim$$30\%$ of the total number of bright early types; by considering the faint early types, the fraction of ``blue'' early types increases to $\sim$$44\%$.

Similar spectra for ``blue'' early types at low (log ${\cal M}/{{\cal M}_{\odot}}\ $<9) and high (log ${\cal M}/{{\cal M}_{\odot}}\ $>10.5) masses are shown by Pozzetti et al. (2009), who find a more evident separation between the properties of objects in these two subclasses.

As a final check we also considered a sample of bona-fide early-type (ET) galaxies (Moresco et al. 2009, in prep.) selected in a more conservative way by combining information on morphologies, spectrophotometric types, colors, and emission line equivalent widths (see Pozzetti et al. 2009, for the exact criteria adopted). This conservative selection reduces the number of objects in the early-type sample to 981: therefore, we use bona-fide ET galaxies mainly as a comparison sample.

We now explore the luminosity function of early-type galaxies.

6.1 The luminosity function of early-type galaxies


In Fig. 7 we show the luminosity function of early-type galaxies from different samples: bona-fide ET (in black), type 1 (in red), and morphological early-type (in green) galaxies.

Table 2:   STY parameters (with $1\sigma $ errors) for different galaxy samples in different environments: total sample quartiles.

The most apparent feature in this figure is the excess of faint ( $M_{B} \ga -19.5$) morphological early-type galaxies at z<0.55. This effect is not evident at higher redshift because this faint population is cut by the magnitude limit of the survey. This excess is due to the population of ``blue'' early types discussed in the previous section. A similar effect was already noticed by Ilbert et al. (2006b), who found that the main contribution to the faint end of the luminosity function of bulge-dominated galaxies comes from blue objects.

\begin{figure} \par\mbox{\includegraphics[width=6cm]{NEW_12665f8a-cmjn.eps}\incl... ...-cmjn.eps}\includegraphics[width=6cm]{NEW_12665f8i-cmjn.eps} }\\ \end{figure} Figure 8:

Left column: luminosity functions in the lowest (blue) and highest (red) quartile of the density distribution in redshift bins for the total sample. Overdensities are derived from the 5 nearest neighbours. Middle and right columns: luminosity functions in the lowest ( middle column) and highest ( right column) quartile of the density distribution in redshift bins. In each panel the global luminosity function is shown in black, while the luminosity function of type 1 and type 3+4 galaxies are drawn in red and blue, respectively. The meaning of symbols and lines is the same as in Fig. 3. The shaded regions represent the $68\%$ uncertainties on the parameters $\alpha $ and M*. For type 1 and type 3+4 samples the STY estimates with $\alpha $ fixed are shown and therefore the shaded area is not drawn.

Open with DEXTER

Moreover, it is interesting that the bright ends of the luminosity functions of type 1 and morphological early-type galaxies are almost indistinguishable at all redshifts.

We also note that type 1 and bona-fide ET galaxies luminosity functions have similar shapes, but different normalizations. The slopes are consistent to within the errors, as well as the M* values; the difference in $\phi^*$ is about a factor of 2, due to the selection criteria adopted in constructing the bona-fide ET sample. The similarity between these luminosity functions implies that, even if the type 1 galaxy sample is contaminated by a fraction of ``red" spirals, the contribution of this population is approximately constant with both luminosity and redshift.

7 The role of the environment

To understand the effect of the environment, we derived the luminosity functions for galaxies in underdense and overdense regions, using the density estimates described in Sect. 2.2. We repeated the analysis using various density estimators, finding that the general trends are similar in all cases. In the following, we show the results obtained for overdensities derived with the 5th nearest neighbour estimator.

Table 3:   STY parameters (with $1\sigma $ errors) as a function of the environment (from the 5 nearest neighbours) in different redshift bins, for different galaxy types. In each sample the appropriate quartiles are used.

\begin{figure} \par\mbox{\includegraphics[width=6cm]{NEW_12665f9a-cmjn.eps}\incl... ...5f9c-cmjn.eps}\includegraphics[width=6cm]{NEW_12665f9d-cmjn.eps} }\end{figure} Figure 9:

Evolution of the luminosity functions for different galaxy types in different environments (low density on the left, high density on the right): type 1 ( upper panels) and type 3+4 ( lower panels) galaxy samples. The color refer to different redshift ranges: [0.10-0.40]in black, [0.40-0.70] in blue and [0.70-1.00] in green. The STY estimates are derived with $\alpha $ fixed. The meaning of lines is the same as in Fig. 3: points from the C+ estimates are not reported for clarity.

Open with DEXTER
To emphasize the differences between the underdense and overdense environments, we consider only the two extreme tails of the overdensity distribution. We also ensure that we had roughly the same number of objects in each subsample, to avoid spurious normalization effects. For this reason, we divided the galaxy density distribution into quartiles, within each redshift bin, and derived the luminosity functions for each subsample. In the following, we compare the results for the lowest and highest quartiles of the overdensity distributions. The use of both quartiles and subsamples reduces the number of usable objects, and we therefore decided to use only three redshift bins, [0.1-0.4], [0.4-0.7], and [0.7-1.0].

The most appropriate choice of quartile values depends on the topic being investigated. To measure the contribution of different galaxy types to the global luminosity function in different environments, it is necessary to derive the quartile values for the total sample and use the same density cuts for all the subsamples. However, if the aim is to compare the behaviour of the luminosity function of specific subsamples of galaxies in underdense and overdense environments, we must carefully select for each subsample the appropriate quartiles (i.e., as derived for that particular subsample).

The use of quartiles makes difficult to derive a number density from the $\phi^*$parameter of the luminosity function, because this kind of selection does not conserve information about the volume occupied by the overdensity associated to each galaxy. Therefore, when analysing luminosity functions in different environments, only a shape comparison is allowed. However, the comparison of $\phi^*$ values is correct when luminosity functions for galaxies in the same quartile are compared.

In the following, we show results both for the total sample and for early- and late-type galaxies, using the type 1 and type 3+4 subsamples. For the early-type galaxies we decided to use the type 1 instead of the bona-fide ET sample for three reasons: 1. the more reliable statistical analysis possible for a higher number of objects; 2. the homogeneity in the classification compared to the late-type galaxy sample; 3. the similarity between the type 1 and bona-fide ET galaxy luminosity functions (see previous section). However, we checked that the results obtained with the bona-fide ET sample (although with larger uncertainties) are consistent with those derived in the following for the type 1 sample.

In the first column of Fig. 8, we show the luminosity function for the total sample in the lowest (blue lines and points) and highest (red lines and points) quartiles of the density distribution in redshift bins. The luminosity function of galaxies in overdense regions is consistently of brighter M*: the slope in underdense regions is steeper in the first and second redshift bins, while the $\alpha $ values in the highest redshift bin, in both environments, are consistent with each other, in the significant margins of large error. Increasing the redshift, the contribution from the luminosity function of galaxies in underdense environments increases and the crossing point between the two LFs progressively moves towards brighter magnitudes. To explore whether this behaviour is due to the different morphological mixes in the two environments, in the second and third column of Fig. 8 we show the luminosity function in underdense and overdense environments: the total luminosity function is shown in black, while the contribution from type 1 and type 3+4 galaxies are drawn in red and blue, respectively. In this case, the quartile values are those derived for the total sample. The parameters of the STY estimates are reported in Table 2. The STY parameters for type 1 and type 3+4 galaxies samples, although formally constrained, are poorly determined. We therefore repeated the STY estimate by fixing $\alpha $ for each type to the global value derived in Sect. 5.1, after verifying that this choice is acceptable. In low density environments, the main contribution to the luminosity function is from type 3+4 galaxies, while for high density environments an important contribution is that of type 1 galaxies at the bright end. The differences between the global luminosity function in the two environments are due not only to the different relative numbers of type 1 and type 3+4 galaxies, but also to their relative luminosity distributions. The value of M* in underdense regions is always fainter than in overdense environments, by $\sim$0.50 mag and $\sim$0.65 mag for type 1 and type 3+4 galaxies, respectively. For $\phi^*$, between underdense and overdense environments there is a decrease of a factor $\sim$2 for type 3+4 galaxies and an increase of $\sim$2 for type 1 galaxies (except in the last redshift bin, where the STY estimate is poorly determined). These results indicate that galaxies of the same type in different environments have different properties.

We now investigate if there is also a differential evolution for different environments within each class of objects. To achieve this, we need to use, for each subsample, the appropriate quartiles (i.e., those derived for that particular subsample). The parameters of the STY estimates obtained with this choice are reported in Table 3.

To visualize the evolutionary effects more clearly, in Fig. 9 we plot in the same panel the luminosity functions in different redshift bins for each galaxy type in the two environments, showing for clarity only the STY estimates. For type 3+4 galaxies, the evolution in the luminosity function within underdense and overdense regions is similar for the first and the second redshift bin, and occurs mainly in luminosity: there is a brightening of $\sim$0.5 mag in M* for all cases, and a slight variation in $\phi^*$. In contrast, between the second and the third redshift bins there is little luminosity evolution, but a significant evolution in $\phi^*$, which differs in the two environments: in overdense regions $\phi^*$increases by a factor $\sim$1.6, while in underdense regions this increase reaches a factor $\sim$2.8.

By analyzing the type 3+4 galaxy population in more detail, we find that the evolution in the relative ratio of type 3 to type 4 galaxies differs between the two environments: in particular, moving from the second to the third redshift bin, the ratio $N_{\rm type~4}/N_{\rm type~3}$for bright ( MB < -20.25) galaxies changes from $33\%$ to $46\%$ in low density environments, but remains almost constant ($\sim$35%) in high density environments. Therefore, the strong evolution observed for type 3+4 galaxies from $z\sim 0.5$ to $z\sim 0.9$ is mainly due to type 4 galaxies. The adopted limit in absolute magnitude corresponds to the bias limit (see Sect. 3.2) in the highest redshift bin and allows a direct comparison of galaxy numbers at different redshifts.

For type 1 galaxies, the situation is more unclear, because the lower number of objects introduces larger uncertainties in the luminosity function estimates. Between the first and the second redshift bin, there is a similar evolution in both environments, while passing from the second to the third redshift bins there are indications of a more significant evolution in underdense regions.

To check if the choice of different quartiles for each redshift bin can affect these results, we repeated the analysis using in each redshift bin the value of the quartiles derived for the whole redshift range [0.1-1], finding that the trends do not change.

These results agree with those found studying the galaxy stellar mass function in different environments (Bolzonella et al. 2009). In particular, in high density environments there is a strong contribution of early-type galaxies, which are dominant at high masses in the galaxy stellar mass function and at bright magnitudes in the luminosity function: however, this dominance is clear at all redshifts in the galaxy stellar mass function, but decreases with increasing redshifts in the luminosity function. This is due to the fact that at high redshift blue galaxies brighten because they increase their star formation activity. Finally, Bolzonella et al. (2009) find that the contribution of early-type galaxies to the total galaxy stellar mass function increases more rapidly in high density environments: consistently, we find that the relative contribution of type 1 and type 3+4 galaxies to the bright end of the luminosity function is similar at high redshift in both environments, but at low redshift type 1 galaxies dominate mainly at high density.

\begin{figure} \par\includegraphics[width=7.334cm,clip]{12665f10a.ps}\\ \includ... ...12665f10b.ps}\\ \includegraphics[width=7.334cm,clip]{12665f10c.ps} \end{figure} Figure 10:

Evolution of the $M^* - \phi ^*$ parameters (derived with $\alpha $ fixed) for different samples: the label near each point indicates the mean redshift of the considered bin. Upper panel: type 1 (red circles), type 2 (orange triangles) and type 3+4 (blue squares) galaxies in the total sample. Middle panel: type 1 galaxies in overdense (red circles) and underdense (magenta triangles) environments. Lower panel: type 3+4 galaxies in overdense (blue circles) and underdense (cyan triangles) environments.

Open with DEXTER

8 Summary and conclusions

An unbiased and detailed characterization of the luminosity function is the basic requirement in many astrophysical issues and it is of particular interest to assess the role of environment on the evolution in the luminosity function of different galaxy types. With this aim, we have studied the evolution in the luminosity function to redshift $z\sim 1$ for the zCOSMOS 10k sample, for which both accurate galaxy classifications and a detailed description of the density field are available.

The main results of this analysis are the following:

-
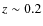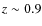Global luminosity function: the global luminosity function shows a brightening of $\sim$0.7 mag in M* from $z\sim 0.2 $ to $z\sim 0.9$, in agreement with the VVDS results in similar redshift ranges.
-
Luminosity functions by spectrophotometric types: to quantify the contribution of the different spectrophotometric types, we have considered three classes of objects: type 1 galaxies, corresponding to early-type SEDs, type 3+4 galaxies, corresponding to late-type SEDs, and the intermediate class of type 2 galaxies. At low redshift (z<0.35), type 3+4 galaxies dominate the luminosity function at faint magnitudes ( MB > -20), while the bright end is populated mainly by type 1 galaxies. 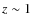At higher redshift, type 3+4 galaxies evolve strongly and therefore, at redshift $z\sim 1$, the contribution to the bright end of the luminosity function of the various types is comparable. The faint end remains dominated by type 3+4 galaxies over the entire redshift range. 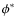For type 1 galaxies, the evolution occurs in both luminosity and normalization: not only does M* brighten by $\sim$0.6 mag but $\phi^*$ also decreases by a factor $\sim$1.7 between the first and the last redshift bin. 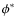Type 3+4 galaxies also evolve in both luminosity and normalization, but with an opposite trend for the normalization: a brightening with redshift by $\sim$0.5 mag is present in M*, while $\phi^*$ increases by a factor $\sim$1.8. Type 2 galaxies show a milder evolution, of a brightening of $\sim$0.25 mag in M* and no significant evolution in $\phi^*$.

-
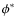Luminosity functions by morphological types: at low redshift (z<0.35), morphological early-type galaxies dominate the bright end of the luminosity function, while spiral galaxies dominate the faint end. Irregular galaxies increase their contribution at the lowest luminosities. At intermediate redshift ( [0.35-0.75]), spiral galaxies increase their luminosities and their contribution to the bright end of the luminosity function is similar to that of the morphological early-type one. At high redshift (z>0.75), irregular galaxies evolve strongly and therefore the three morphological types contribute almost equally to the total luminosity function. 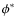Irregular galaxies exhibit an evolution of a factor $\sim$3.3 in $\phi^*$from low to high redshift: this evolution occurs mainly in the last redshift bin, while, for z<0.75, the contribution of these galaxies to the global luminosity function is significantly lower than that of spirals and early types.

-
The role of the environment: for the total sample, the luminosity function of galaxies in overdense regions always has a brighter M* and a flatter slope. Increasing the redshift, the contribution to the luminosity function of galaxies in underdense environments increases, and the crossing point between the two LFs moves progressively towards brighter magnitudes. In low density environments, the main contribution to the luminosity function originates in type 3+4 galaxies, while for high density environments there is an important contribution from type 1 galaxies to the bright end.
The differences between the global luminosity functions in the two environments are due not only to a difference in relative numbers of type 1 and type 3+4 galaxies, but also to their relative luminosity distributions. The value of M* in underdense regions is always fainter than in overdense environments, by $\sim$0.50 mag and $\sim$0.65 mag for type 1 and type 3+4 galaxies, respectively. For $\phi^*$, between underdense and overdense environments, there is a decrease of a factor $\sim$2 for type 3+4 galaxies and an increase of $\sim$2 for type 1 galaxies. These results indicate that galaxies of the same type in different environments have different properties.

We have also detected differential evolution for type 3+4 galaxies in different environments. We found that the evolution in their luminosity function in underdense and overdense regions is similar between $z\sim 0.25$ and $z\sim 0.55$, and is mainly in luminosity: there is a brightening of $\sim$0.5 mag in M* in all cases, but only a slight variation in $\phi^*$. In contrast, between $z\sim 0.55$ and $z\sim 0.85$ there is little luminosity evolution but a strong evolution in $\phi^*$, which differs in the two environments: in overdense regions, $\phi^*$ increases by a factor $\sim$1.6, while in underdense regions there is an increase of a factor $\sim$2.8.

Analyzing the type 3+4 galaxy population in more detail, we find that the evolution in the relative ratio of type 3 to type 4 galaxies differs between the two environments: in particular, between $z\sim 0.55$ and $z\sim 0.85$, the ratio $N_{\rm type~4}/N_{\rm type~3}$ for bright ( MB < -20.25) galaxies changes from $33\%$ to $46\%$ in low density environments, but remains almost constant ($\sim$$35\%$) in high density environments. Therefore, the strong evolution observed for type 3+4 galaxies between $z\sim 0.55$ and $z\sim 0.85$ is mainly due to type 4 galaxies.

For type 1 galaxies, the situation is unclear, because the lower number of objects introduce larger uncertainties in the luminosity function estimates. Between the first and the second redshift bins, there is a similar evolution in both environments, while passing from the second to the third redshift bins, there are indications of a more significant evolution in underdense regions.

All these results are summarized in Fig. 10, where the evolution of the parameters M* and $\phi^*$, obtained with $\alpha $ fixed, is shown for different samples; the label near each point indicates the mean redshift of the considered bin. The upper panel of Fig. 10 refers to galaxies of different spectrophotometric types in the total sample: type 1 galaxies in red (circles), type 2 galaxies in orange (triangles) and type 3+4 galaxies in blue (squares). From this figure it is immediately evident the symmetric behaviour of type 1 and type 3+4 galaxies, as well as the almost negligible evolution of type 2 galaxies. While we find that the M* evolution for type 1 and type 3+4 galaxies is consistent with passive evolution, it is more interesting the density evolution. Given the fact that $\phi^*$ is proportional to the density of M* galaxies, this figure is consistent with a scenario where a part of type 3+4 galaxies is transformed in type 1 galaxies with increasing cosmic time, without significant changes in the fraction of intermediate-type galaxies.

The middle and lower panels of Fig. 10 show the evolution of the parameters M* and $\phi^*$ for galaxies of different types in different environments: type 1 galaxies in underdense (magenta triangles) and overdense (red circles) environments in the middle panel, type 3+4 galaxies in underdense (cyan triangles) and overdense (blue circles) environments in the lower panel. The behaviour of type 1 and type 3+4 galaxies in overdense environments is consistent with the transformation scenario described above for the total sample. In underdense environments, a similar scenario is acceptable, with the exception of the highest redshift bin, where type 1 galaxies show a strong increase of $\phi^*$ with respect to the previous bin.

The lower panel of Fig. 10 clearly shows the different evolution which type 3+4 galaxies are undergoing in the different environments, with a much stronger density evolution in underdense regions.

This indicates that the bulk of the tranformation described above from blue to red galaxies in overdense regions probably happened before $z\sim 1$, while it is still ongoing at lower redshifts in underdense environments.

Acknowledgements
We acknowledge support from an INAF contract PRIN-2007/1.06.10.08 and an ASI grant ASI/COFIS/WP3110 I/026/07/0.

References

  • Abraham, R. G., van den Bergh, S., & Nair, P. 2003, ApJ, 588, 218 [NASA ADS] [CrossRef]
  • Bolzonella, M., Kovac, K., Pozzetti, L., et al. 2009, A&A, submitted [arXiv:0907.0013]
  • Capak, P., Aussel, H., Ajiki, M., et al. 2007, ApJS, 172, 99 [NASA ADS] [CrossRef]
  • Cassata, P., Guzzo, L., Franceschini, A., et al. 2007, ApJS, 172, 270 [NASA ADS] [CrossRef]
  • Coleman, G. D., Wu, C. C., & Weedman, D. W. 1980, ApJS, 43, 393 [NASA ADS] [CrossRef]
  • Colless, M., Dalton, G., Maddox, S., et al. 2001, MNRAS, 328, 1039 [NASA ADS] [CrossRef]
  • Cooper, M. J., Newman, J. A., Croton, D. J., et al. 2006, MNRAS, 370, 198 [NASA ADS]
  • Cooper, M. J., Newman, J. A., Coil, A., et al. 2007, MNRAS, 376, 1445 [NASA ADS] [CrossRef]
  • Croton, D. J., Farrar, G. R., Norberg, P., et al. 2005, MNRAS, 356, 1155 [NASA ADS] [CrossRef]
  • Cucciati, O., Iovino, A., Marinoni, C., et al. 2006, A&A, 458, 39 [NASA ADS] [EDP Sciences] [CrossRef]
  • Cucciati, O., Iovino, A., Kovac, K., et al. 2009, A&A, submitted
  • Davis, M., Faber, S. M., Newman, J., et al. 2003, SPIE, 4834, 161 [NASA ADS]
  • deLapparent, V., Galaz, G., Bardelli, S., & Arnouts, S. 2003, A&A, 404, 831 [NASA ADS] [EDP Sciences] [CrossRef]
  • Efstathiou, G., Ellis, R. S., & Peterson, B. A. 1988, MNRAS, 232, 431 [NASA ADS]
  • Feldmann, R., Carollo, C. M., Porciani, C., et al. 2006, MNRAS, 372, 565 [NASA ADS] [CrossRef]
  • Feldmann, R., Carollo, C. M., Porciani, C., Lilly, S. J., & Oesch, P. 2008, [arXiv:0801.3275]
  • Ilbert, O., Tresse, L., Arnouts, S., et al. 2004, MNRAS, 351, 541 [NASA ADS] [CrossRef]
  • Ilbert, O, Tresse, L., Zucca, E., et al. 2005, A&A , 439, 863 [NASA ADS] [CrossRef]
  • Ilbert, O, Arnouts, S., McCracken, H. J., et al. 2006a, A&A , 457, 841 [NASA ADS] [CrossRef]
  • Ilbert, O, Lauger, S., Tresse, L., et al. 2006b, A&A , 453, 809 [NASA ADS] [CrossRef]
  • Ilbert, O, Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef]
  • Iovino, A., Cucciati, O., Scodeggio, M., et al. 2009, A&A, in press [arXiv:0909.1951]
  • Kinney, A. L., Calzetti, D., Bohlin, R. C., et al. 1996, ApJ, 467, 38 [NASA ADS] [CrossRef]
  • Koekemoer, A. M., Aussel, H., Calzetti, D., et al. 2007, ApJS, 172, 196 [NASA ADS] [CrossRef]
  • Kovac, K., Lilly, S. J., Cucciati, O., et al. 2009a, ApJ, in press [arXiv:0903.3409]
  • Kovac, K., Lilly, S. J., Knobel, C., et al. 2009b, ApJ, submitted [arXiv:0909.2032]
  • Le Fèvre, O., Vettolani, G., Maccagni, D., et al. 2003, SPIE, 4841, 1670 [NASA ADS]
  • Le Fèvre, O., Vettolani, G., Garilli, B., et al. 2005, A&A, 439, 845 [NASA ADS] [EDP Sciences] [CrossRef]
  • Lilly, S. J., Tresse, L., Hammer, F., Crampton, D., & Le Fèvre, O. 1995, ApJ, 455, 108 [NASA ADS] [CrossRef]
  • Lilly, S. J., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef]
  • Lilly, S. J., Le Brun, V., Maier, C., et al. 2009, ApJS, 184, 218 [CrossRef]
  • Lin, H., Yee, H. K. C., Carlberg, R. G., et al. 1999, ApJ, 518, 533 [NASA ADS] [CrossRef]
  • Lotz, J. M., Primack, J., & Madau, P. 2004, AJ, 128, 163 [NASA ADS] [CrossRef]
  • Lynden Bell, D. 1971, MNRAS, 155, 95 [NASA ADS]
  • McCracken, H. J., Capak, P., Salvato, M., et al. 2010, ApJ, 708, 202 [CrossRef]
  • Mignoli, M., Zamorani, G., Scodeggio, M., et al. 2009, A&A, 493, 39 [NASA ADS] [EDP Sciences] [CrossRef]
  • Pozzetti, L., Bolzonella, M., Zucca, E., et al. 2009, A&A, submitted [arXiv:0907.5416]
  • Sandage, A., Tammann, G. A., & Yahil, A. 1979, ApJ, 232, 352 [NASA ADS] [CrossRef]
  • Sanders, D. B., Salvato, M., Aussel, H., et al. 2007, ApJS, 172, 86 [NASA ADS] [CrossRef]
  • Scarlata, C., Carollo, C. M., Lilly, S. J., et al. 2007, ApJS, 172, 406 [NASA ADS] [CrossRef]
  • Schechter, P. 1976, ApJ, 203, 297 [NASA ADS] [CrossRef]
  • Schmidt, M. 1968, ApJ, 151, 393 [NASA ADS] [CrossRef]
  • Scodeggio, M., Franzetti, P., Garilli, B., et al. 2005, PASP, 117, 1284 [NASA ADS] [CrossRef]
  • Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef]
  • Taniguchi, Y., Scoville, N., Murayama, T., et al. 2007, ApJS, 172, 9 [NASA ADS] [CrossRef]
  • Tasca, L., Kneib, J. P., Iovino, A., et al. 2009, A&A, 503, 379 [NASA ADS] [EDP Sciences] [CrossRef]
  • York, D. G., Adelman, J., Anderson, J. E., et al. 2000, AJ, 120, 1579 [NASA ADS] [CrossRef]
  • Zucca, E., Pozzetti, L., & Zamorani, G. 1994, MNRAS, 269, 953 [NASA ADS]
  • Zucca, E., Zamorani, G., Vettolani, G., et al. 1997, A&A, 326, 477 [NASA ADS]
  • Zucca, E., Ilbert, O, Bardelli, S., et al. 2006, A&A , 455, 879 [NASA ADS] [CrossRef]

Footnotes

... types[*]
Based on data obtained with the European Southern Observatory Very Large Telescope, Paranal, Chile, program 175.A-0839.

All Tables

Table 1:   STY parameters (with $1\sigma $ errors) in different redshift bins for total sample and different galaxy type subsamples.

Table 2:   STY parameters (with $1\sigma $ errors) for different galaxy samples in different environments: total sample quartiles.

Table 3:   STY parameters (with $1\sigma $ errors) as a function of the environment (from the 5 nearest neighbours) in different redshift bins, for different galaxy types. In each sample the appropriate quartiles are used.

All Figures

  \begin{figure} \par\includegraphics[width=12cm,clip]{12665f1.ps} \end{figure} Figure 1:

Evolution of the global luminosity function in the B rest-frame band. Each panel refers to a different redshift bin, which is indicated in the label, with also the number of galaxies. The vertical dashed and dotted lines represent the faint absolute limit considered in the STY estimate for the zCOSMOS and VVDS sample, respectively. The luminosity functions are estimated with different methods (see text for details) but for clarity we plot only the results from C+ (squares) and STY (solid line). The dotted line represents the luminosity function estimated in the redshift range [0.2-0.4] and it is reported in each panel as a reference. The STY estimates from the VVDS sample are plotted with dashed lines. In the redshift bins [0.8-1.0] and [1.0-1.3] for the zCOSMOS sample we fixed $\alpha $ to the VVDS value.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=8.8cm]{12665f2a.ps}\includegraphics[width=8.8cm]{12665f2b.ps} } \end{figure} Figure 2:

Observed fraction of bright galaxies ( MB < -20.77) of different types as a function of redshift. Error bars are $1\sigma $Poisson errors. Left panel: spectrophotometric type 1 (short dashed red line), type 2 (solid orange line), type 3 (dotted green line) and type 4 (long dashed blue line) galaxies. Right panel: morphological early-type (ellipticals and lenticulars) (short dashed red line), spiral (solid green line) and irregular (dotted blue) galaxies; in gray (long dashed line) unclassified galaxies.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm]{NEW_12665f3a-cmjn.eps}\includeg... ...5f3c-cmjn.eps}\includegraphics[width=8.8cm]{NEW_12665f3d-cmjn.eps} \end{figure} Figure 3:

Luminosity functions of the different spectrophotometric types in redshift bins (indicated in each panel): type 1 in red, type 2 in orange, type 3+4 in blue, total sample in black. The squares represent the results from the C+ and the solid lines are the results from the STY method. The vertical dashed line represents the faint absolute limit considered in the STY estimate. The shaded regions represent the $68\%$ uncertainties on the parameters $\alpha $ and M*.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=6cm]{12665f4a.ps}\includegraphics[width=6cm]{12665f4b.ps}\includegraphics[width=6cm]{12665f4c.ps} } \end{figure} Figure 4:

Evolution of the luminosity functions for different galaxy types: type 1 ( left panel), type 2 ( middle panel) and type 3+4( right panel) galaxies. The colors refer to different redshift ranges: [0.10-0.35]in black, [0.35-0.55] in cyan, [0.55-0.75] in magenta and [0.75-1.00] in green. The STY estimates are derived with $\alpha $ fixed. The meaning of lines is the same as in Fig. 3: points from the C+ estimates are not reported for clarity.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=8.8cm]{12665f5a.ps}\includegraph... ...th=8.8cm]{12665f5c.ps}\includegraphics[width=8.8cm]{12665f5d.ps} }\end{figure} Figure 5:

Luminosity functions of the different morphological types in redshift bins: early types (ellipticals and lenticulars) in red, spirals in green, irregulars in blue. The meaning of symbols and lines is the same as in Fig. 3.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=8.8cm]{12665f6a.ps}\includegraphics[width=8.8cm]{12665f6b.ps} }\end{figure} Figure 6:

Composite spectra of morphologically classified early types brighter ( left panel) and fainter ( right panel) than MB = -20.77. Morphological early types are divided on the basis of their spectrophotometric type (see the text for details): ``blue'' early types in blue (lower spectra), ``red'' early types in magenta (middle spectra), ``very red'' early types in red (upper spectra). The flux on the Y-axis is in arbitrary units and the spectra have been vertically shifted for clarity.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=8.8cm]{12665f7a.ps}\includegraph... ...th=8.8cm]{12665f7c.ps}\includegraphics[width=8.8cm]{12665f7d.ps} }\end{figure} Figure 7:

Luminosity functions of early-type galaxies: bona-fide ET (black), type 1 (red) and morphological early-type (in green) galaxies. The meaning of symbols and lines is the same as in Fig. 3.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=6cm]{NEW_12665f8a-cmjn.eps}\incl... ...-cmjn.eps}\includegraphics[width=6cm]{NEW_12665f8i-cmjn.eps} }\\ \end{figure} Figure 8:

Left column: luminosity functions in the lowest (blue) and highest (red) quartile of the density distribution in redshift bins for the total sample. Overdensities are derived from the 5 nearest neighbours. Middle and right columns: luminosity functions in the lowest ( middle column) and highest ( right column) quartile of the density distribution in redshift bins. In each panel the global luminosity function is shown in black, while the luminosity function of type 1 and type 3+4 galaxies are drawn in red and blue, respectively. The meaning of symbols and lines is the same as in Fig. 3. The shaded regions represent the $68\%$ uncertainties on the parameters $\alpha $ and M*. For type 1 and type 3+4 samples the STY estimates with $\alpha $ fixed are shown and therefore the shaded area is not drawn.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=6cm]{NEW_12665f9a-cmjn.eps}\incl... ...5f9c-cmjn.eps}\includegraphics[width=6cm]{NEW_12665f9d-cmjn.eps} }\end{figure} Figure 9:

Evolution of the luminosity functions for different galaxy types in different environments (low density on the left, high density on the right): type 1 ( upper panels) and type 3+4 ( lower panels) galaxy samples. The color refer to different redshift ranges: [0.10-0.40]in black, [0.40-0.70] in blue and [0.70-1.00] in green. The STY estimates are derived with $\alpha $ fixed. The meaning of lines is the same as in Fig. 3: points from the C+ estimates are not reported for clarity.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.334cm,clip]{12665f10a.ps}\\ \includ... ...12665f10b.ps}\\ \includegraphics[width=7.334cm,clip]{12665f10c.ps} \end{figure} Figure 10:

Evolution of the $M^* - \phi ^*$ parameters (derived with $\alpha $ fixed) for different samples: the label near each point indicates the mean redshift of the considered bin. Upper panel: type 1 (red circles), type 2 (orange triangles) and type 3+4 (blue squares) galaxies in the total sample. Middle panel: type 1 galaxies in overdense (red circles) and underdense (magenta triangles) environments. Lower panel: type 3+4 galaxies in overdense (blue circles) and underdense (cyan triangles) environments.

Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.