| Issue |
A&A
Volume 508, Number 3, December IV 2009
|
|
|---|---|---|
| Page(s) | 1517 - 1526 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/200911729 | |
| Published online | 27 October 2009 | |
A&A 508, 1517-1526 (2009)
Benchmarking atomic data for astrophysics: Fe XVII EUV lines
G. Del Zanna1 - Y. Ishikawa2
1 - DAMTP, Centre for Mathematical Sciences, Wilberforce road,
Cambridge, CB3 0WA, UK
2 - Department of Chemistry, University of Puerto Rico, PO Box 23346,
San Juan, PR 00931-3346, USA
Received 26 January 2009 / Accepted 1 October 2009
Abstract
In the light of accurate structure and scattering calculations for Fe XVII,
we review the status of identifications in the EUV spectrum of this ion
using various experimental data, from the X-rays to the UV.
Most previous identifications are confirmed, although a critical
revision leads to changes in many wavelength values, in particular for
the 2p5 3s-2p5 3p
and 2p5 3p-2p5 3d
transitions,
which we observed with the Hinode EUV Imaging Spectrometer (EIS).
Several lines are identified here for the first time. We find good
agreement between expected and measured line intensities,
with a few notable exceptions. In particular, the strong line in the
EIS spectra, observed at 254.88 Å,
has a consistently low observed intensity.
We present two Hinode/EIS observations and discuss which lines are
clearly blended in these datasets, and which are reliable for
diagnostic purposes.
Key words: atomic data - line: identification
1 Introduction
This paper is one of a series in which atomic data and line identifications are benchmarked against experimental data (Del Zanna et al. 2004). It is now timely for us to review the Fe XVII EUV spectrum for the following reasons. First, the R-matrix scattering calculations of Loch et al. (2006) predict Fe XVII line intensities that largely differ (factors of 2-3) from previous estimates. Hence, previous identifications need to be reassessed in light of these new data. Second, new accurate ab-initio theoretical calculations of level energies for Ne-like ions are now available (Ishikawa et al. 2009). These theoretical energies are of great help in the line identification process. Third, accurate wavelengths and intensities of some EUV lines are now measurable by the Hinode EUV Imaging Spectrometer (EIS, see Culhane et al. 2007). Fourth, the Fe XVII EUV lines observed by EIS are of particular importance because they are among the very few lines formed at temperatures (4-10 MK) that provide useful information about the nature of the heating in the solar corona.
In this paper we focus on the EUV lines, principally the 2p5
3s-2p5 3p
and 2p5 3p-2p5 3d
transitions that occur at EUV wavelengths (200-500 Å) and for
which we can provide accurate EUV wavelengths based on EIS
observations (a preliminary assessment of the most prominent Fe XVII lines
was published in Del Zanna
2008).
The weaker ![]() and
and ![]() transitions,
which occur in the 30-150 Å range are also considered, as well
as wavelength measurements in the X-rays.
transitions,
which occur in the 30-150 Å range are also considered, as well
as wavelength measurements in the X-rays.
Section 2 describes the experimental data we have selected, with particular emphasis on the analysis of Hinode EIS data. Section 3 briefly describes the benchmark method used. Section 4 discusses the lines observed in the 30-150 Å range, while Sect. 5 discusses those observed in the 171-630 Å range. In Sect. 6, we draw our conclusions.
2 Experimental data
2.1 X-ray observations
The identification of Fe XVII lines started with the excellent work of Tyrén (1938) on the soft-X-ray transitions to the L shell, providing identifications and at the time excellent wavelengths. We reviewed the measurements of X-ray wavelengths found in the literature, and found that Hutcheon et al. (1976a) and Hutcheon et al. (1976b) provide very accurate values. There is excellent agreement, within 1 m Å, between the Hutcheon et al. measurements and the most accurate measurements in the X-rays, from laboratory spectra (Boiko et al. 1978) to solar SMM/FCS ones (Phillips et al. 1982).
The set of observed wavelengths ![]() that we consider most accurate are provided in Table 1. We used them,
as described in the Appendix, in conjunction with the EUV wavelengths
to obtain a consistent set of experimental energies for this ion.
that we consider most accurate are provided in Table 1. We used them,
as described in the Appendix, in conjunction with the EUV wavelengths
to obtain a consistent set of experimental energies for this ion.
2.2 EUV observations in the 30-150 Å range
The 30-150 Å range is rich in (weaker) Fe XVII
![]() and
and ![]() transitions. Fawcett
et al. (1979) provided many wavelength measurements
and identifications using laboratory spectra.
We adopted their wavelengths as shown in Table 2.
Finkenthal et al.
(1985) provided a few additional measurements
and identifications
again based on laboratory spectra, which we also considered.
The highest quality solar flare spectrum at these wavelengths is
probably that obtained during a rocket flight by Acton et al. (1985).
Wavelengths were not accurate, but the spectrum was radiometrically
calibrated, so we could use their line intensities for the benchmark.
transitions. Fawcett
et al. (1979) provided many wavelength measurements
and identifications using laboratory spectra.
We adopted their wavelengths as shown in Table 2.
Finkenthal et al.
(1985) provided a few additional measurements
and identifications
again based on laboratory spectra, which we also considered.
The highest quality solar flare spectrum at these wavelengths is
probably that obtained during a rocket flight by Acton et al. (1985).
Wavelengths were not accurate, but the spectrum was radiometrically
calibrated, so we could use their line intensities for the benchmark.
Table 1: List of wavelengths and identifications for the X-ray lines.
2.3 EUV observations in the 171-630 Å range
The Skylab NRL slitless spectrograph produced spectra of solar flares in the 171-630 Å range. For this benchmark, we considered the calibrated intensities of a solar flare reported by Doschek et al. (1991). We also adopted some of the wavelengths measured by Dere (1978), listed in Table 2. We replaced the Skylab wavelengths with the more accurate SERTS and Hinode/EIS values, whenever available. The intensities of a few lines recorded during the 1989 SERTS rocket flight (Thomas & Neupert 1994) were also used for the benchmark. Thomas & Neupert (1994) provided very accurate wavelengths which were adopted, as shown in Table 2.
Table 2: List of wavelengths and identifications for the EUV lines.
2.4 Hinode/EIS observations
![\begin{figure}
{\includegraphics[width=14.cm]{H11729_f1a.eps} }
{\includegraphics[width=14.cm]{H11729_f1b.eps} }\end{figure}](/articles/aa/full_html/2009/48/aa11729-09/Timg8.png)
|
Figure 1: Monochromatic images (negative) of a selection of EIS lines from the 2007 May 21 observation. Ion and wavelength in Å are indicated, as well as the logarithm of the temperature (K) of line formation in collisional ionisation equilibrium. We note that all the identified Fe XVII lines have the same morphology. |
| Open with DEXTER | |
The EIS instrument covers two wavelength bands
(SW: 165-211 Å; LW: 245-291 Å,
approximately).
We analysed many Hinode/EIS observations containing Fe XVII lines,
although only the results from two observations are
presented here. The first observation is a full spectrum recorded on
2007 June 2. A preliminary analysis of this observation was
presented in Del Zanna
(2008).
Here, the same observation is reanalysed in various respects.
First, by including a treatment of ``warm'', ``hot'', and ``dust''
pixels (in the sense that these pixels are excluded from the analysis).
Second, by applying a geometrical correction to the spectra.
It has been known that there are offsets in both N-S (18
![]() )
and E-W (2
)
and E-W (2
![]() )
directions between the two EIS channels.
The offset in the E-W direction means that observations
in the two channels are neither simultaneous nor cospatial. A further
significant effect found during the course of this work is a slant in
the spectra relative to the axes of the CCD. The intensities
of lines emitted by the same ion within each channel
were cross-correlated to measure the slant.
We found the presence of a linear slant in both channels, equivalent to
a displacement in the N-S direction of about 3.66(
)
directions between the two EIS channels.
The offset in the E-W direction means that observations
in the two channels are neither simultaneous nor cospatial. A further
significant effect found during the course of this work is a slant in
the spectra relative to the axes of the CCD. The intensities
of lines emitted by the same ion within each channel
were cross-correlated to measure the slant.
We found the presence of a linear slant in both channels, equivalent to
a displacement in the N-S direction of about 3.66(![]() 0.2) pixels
end-to-end
(each pixel along the slit corresponding to 1
0.2) pixels
end-to-end
(each pixel along the slit corresponding to 1
![]() ). The slant has a significant
impact on the data analysis, and was corrected by rotating the spectra.
We note that a similar slant in the SW channel was independently
reported by Young
et al. (2009).
). The slant has a significant
impact on the data analysis, and was corrected by rotating the spectra.
We note that a similar slant in the SW channel was independently
reported by Young
et al. (2009).
The location of the brightest Fe XVII emission considered in Del Zanna (2008) is an area where lines are broadened and very strong emission of cooler features is present. For this study, an average spectrum was obtained from three consecutive exposures in two locations where the Fe XVII emission was less affected by blending.
The EIS instrument is affected by a strong
(75 km s-1) orbital variation
in the wavelength scale. This was removed, and a wavelength calibration
obtained by using the bottom 50
![]() of the field of view as the reference. The locations chosen to obtain
an averaged spectrum are places where Dopplershifts in coronal lines
are smaller than
of the field of view as the reference. The locations chosen to obtain
an averaged spectrum are places where Dopplershifts in coronal lines
are smaller than ![]() 5 km s-1.
The averaged spectrum was calibrated in wavelength, using a set of
about 30 coronal lines (formed around 1 MK) in each
channel and a quadratic wavelength calibration. The adopted rest-frame
wavelengths originated in various laboratory and solar observations,
and can be found e.g., in the CHIANTI atomic package
(Landi
et al. 2006; Dere et al. 1997).
Very good agreement (to within 5 mÅ) between observed and
rest-frame wavelengths was found across both EIS spectral ranges. A
conservative uncertainty of 10 mÅ is adopted.
We found no measurable Dopplershifts in the strongest Fe XVII
lines,
and therefore believe that the Fe XVII
wavelengths that we measured are to be considered as being at rest.
5 km s-1.
The averaged spectrum was calibrated in wavelength, using a set of
about 30 coronal lines (formed around 1 MK) in each
channel and a quadratic wavelength calibration. The adopted rest-frame
wavelengths originated in various laboratory and solar observations,
and can be found e.g., in the CHIANTI atomic package
(Landi
et al. 2006; Dere et al. 1997).
Very good agreement (to within 5 mÅ) between observed and
rest-frame wavelengths was found across both EIS spectral ranges. A
conservative uncertainty of 10 mÅ is adopted.
We found no measurable Dopplershifts in the strongest Fe XVII
lines,
and therefore believe that the Fe XVII
wavelengths that we measured are to be considered as being at rest.
The second EIS observation is a full spectrum recorded on 2007
May 21 with the 2
![]() slit and a long exposure of 40 s.
The long exposure allowed the measurement of the line intensities for
each 2
slit and a long exposure of 40 s.
The long exposure allowed the measurement of the line intensities for
each 2
![]()
![]() 2
2
![]() area in the field of view. The observation was processed in the same
way as the previous one. Figure 1 shows the
resulting monochromatic images for a selection of lines formed over a
range of temperatures.
We note that the bulk of the Fe XVII
emission is concentrated within a loop structure, which only becomes
visible in Fe XVI.
We also note that the Fe XXIII
263.765 Å line
is dominated by two unidentified coronal lines (at 263.70 Å)
that have a
formation temperature similar to Fe XII.
Figure 1
is important because it clearly shows that all the Fe XVII lines
identified in this paper have the same morphology, although many of
them are blended.
area in the field of view. The observation was processed in the same
way as the previous one. Figure 1 shows the
resulting monochromatic images for a selection of lines formed over a
range of temperatures.
We note that the bulk of the Fe XVII
emission is concentrated within a loop structure, which only becomes
visible in Fe XVI.
We also note that the Fe XXIII
263.765 Å line
is dominated by two unidentified coronal lines (at 263.70 Å)
that have a
formation temperature similar to Fe XII.
Figure 1
is important because it clearly shows that all the Fe XVII lines
identified in this paper have the same morphology, although many of
them are blended.
We selected two averaged spectra, one from the lower part of the flare loop, where blending should be at a minimum, and one from a transition-region brightening located at the bottom left of the field of view. The averaged spectra were wavelength-calibrated to an accuracy of 5 mÅ. With this calibration, we found the same Fe XVII wavelengths (to within a few mÅ) as in the 2007 June 2 observation. No Dopplershifts in Fe XVII lines were observed. Portions of the spectra where Fe XVII lines are present are shown in Fig. 2. For comparison, the spectra of the transition-region brightening are also shown on the same Fig. 2. It is quite clear which Fe XVII lines can be blended with lines formed at transition-region temperatures (when sufficient plasma at those temperatures is present along the line of sight). The most notable case is the 204.66 Å line, which is blended, on its red wing, by a strong (unidentified) transition-region line, located at 204.72 Å. This line has the same morphology as Fe VIII (or Si VII) and becomes much stronger than the Fe XVII line at all locations where Fe VIII is bright. Another notable feature is that the 283.93 Å line still clearly shows some residual blending with the far blue wing of the very bright Fe XV 284.15 Å resonance line. We note, however, that in the flare loop region, Fe XVII lines are strong and not severely blended.
|
Figure 2: Hinode EIS spectra (ordinates are averaged counts per pixel, while abscissae are wavelengths in Å) over an area where Fe XVII emission was more clearly isolated (black line) and over a transition-region brightening (red thick line). |
| Open with DEXTER | |
3 The benchmark method
As described in Del
Zanna et al. (2004), the benchmark process starts
with an assessment of the observed wavelengths ![]() .
For Fe XVII, we reviewed all previous
measurements from the X-rays to the UV, as briefly described in the
previous section. These observed wavelengths
.
For Fe XVII, we reviewed all previous
measurements from the X-rays to the UV, as briefly described in the
previous section. These observed wavelengths
![]() are provided in Tables 1
and 2.
are provided in Tables 1
and 2.
From the observed wavelengths ![]() a set of experimental level energies
a set of experimental level energies ![]() is obtained
(see the Appendix and Tables A.1
and A.2).
is obtained
(see the Appendix and Tables A.1
and A.2).
From the level energies ![]() ,
experimental wavelengths
,
experimental wavelengths
![]() are derived. We note that there can be cases when lines with
experimental wavelengths
are derived. We note that there can be cases when lines with
experimental wavelengths ![]() have not been observed yet, and cases when
have not been observed yet, and cases when
![]() and
and
![]() are not exactly the same.
are not exactly the same.
As an aid to the identification process, relativistic
multi-reference many-body perturbation theory calculations were
performed along the Ne-like sequence (see Ishikawa et al. 2009).
In these, state-averaged multiconfiguration
Dirac-Fock-Breit self-consistent field (MCDFB SCF)
and multi-reference configuration interaction (MR-CI) calculations
are followed by a state-specific multi-reference Møller-
Plesset perturbation treatment.
This procedure (hereafter referred to as MR-MP)
yields highly accurate level energies,
the average deviation between experimental and theoretical values
being 0.01%.
For details of the procedure, we refer to Ishikawa & Vilkas (2008).
Wavelengths obtained from the energies of the MR-MP calculations are
also shown in Table 4,
together with those from the
NIST database![]() . The NIST wavelengths were
obtained from the published list of energies.
Table 4
clearly shows excellent agreement between the MR-MP wavelengths and the
experimental ones,
with deviations of only about 0.1 Å (the only notable
exception being the two decays from the 3p 1S0 level).
We note that typical deviations of other ab-initio calculations are of
the order of 5-10 Å, as shown, e.g., by the theoretical
wavelengths
. The NIST wavelengths were
obtained from the published list of energies.
Table 4
clearly shows excellent agreement between the MR-MP wavelengths and the
experimental ones,
with deviations of only about 0.1 Å (the only notable
exception being the two decays from the 3p 1S0 level).
We note that typical deviations of other ab-initio calculations are of
the order of 5-10 Å, as shown, e.g., by the theoretical
wavelengths ![]() obtained from the scattering target energies
and also shown in Table 4.
The MR-MP wavelengths were used to identify additional weaker lines.
obtained from the scattering target energies
and also shown in Table 4.
The MR-MP wavelengths were used to identify additional weaker lines.
Line intensities were calculated with the rates and transition
probabilities provided by Loch
et al. (2006), at the temperature of peak ion
abundance for Fe XVII in ionisation
equilibrium (
![]() ).
Table 4
shows the relative line intensities calculated
at an electron density of 1011 cm-3,
which is typical of solar flares but still in the low-density regime
for this ion.
The lines are ordered by their intensities. It is reassuring to see
that all the lines expected to be brightest have now been observed.
Line intensities, whenever available, were compared to confirm
identifications and assess the possible presence of blending.
This was achieved using the ``emissivity ratio'' technique,
whereby the observed intensity of a line is divided by its emissivity
(in this paper, as a function of density). In one single plot, this
allows us to compare at once for a group of lines observed and
theoretical intensities
(see Del Zanna
et al. 2004, for details),
and assess which of the respective emissivities have a different
sensitivity to electron density.
).
Table 4
shows the relative line intensities calculated
at an electron density of 1011 cm-3,
which is typical of solar flares but still in the low-density regime
for this ion.
The lines are ordered by their intensities. It is reassuring to see
that all the lines expected to be brightest have now been observed.
Line intensities, whenever available, were compared to confirm
identifications and assess the possible presence of blending.
This was achieved using the ``emissivity ratio'' technique,
whereby the observed intensity of a line is divided by its emissivity
(in this paper, as a function of density). In one single plot, this
allows us to compare at once for a group of lines observed and
theoretical intensities
(see Del Zanna
et al. 2004, for details),
and assess which of the respective emissivities have a different
sensitivity to electron density.
Table 3: List of strongest Fe XVII lines in the 30-150 Å range.
Table 4: List of the Fe XVII strongest lines in the 200-450 Å range.
4 Benchmark in the 30-150 Å range
![\begin{figure}
\includegraphics[angle=90,width=8.8cm,clip]{H11729_f3.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa11729-09/Timg80.png)
|
Figure 3:
The emissivity ratio curves of a few lines observed during a flare by a
rocket (Acton et al. 1985).
|
| Open with DEXTER | |
Fawcett et al. (1979) performed an excellent analysis to identify the transitions that become strong at high densities, as Table 3 shows (see the intensities calculated at 1019 cm-3). We confirm all their identifications, but note that in various other literature and databases (e.g., NIST, CHIANTI) some incorrect identifications are present.
As mentioned in Ishikawa et al. (2009), there are large discrepancies between the reported (e.g., NIST) and calculated MR-MP energies for a number of 2s 2p6 3s, p, d levels along the whole sequence, so doubt should be cast upon the reliability of previous identifications. We studied the Fe XVII 2s 2p6 3s, p, d levels closely and propose that all previous identifications, in particular those of Finkenthal et al. (1985), are incorrect. Finkenthal et al. (1985) studied the 2s2 2p5 3s - 2s 2p6 3s transitions in Cr XV, Fe XVII, and Ni XIX along the sequence and identified a number of transitions.
The strongest Fe XVII 2p5 3s-2p6 3s transitions are the branching ratios 1P1-1S0 (3-29) and 3P1-1S0 (5-29). The strongest of them is the 3-29, and Finkenthal et al. (1985) assigns this transition to a line observed in their laboratory spectra at 87.30 Å. There are two problems with this identification. First, our MR-MP calculations predict a wavelength of 89.79 Å. Second, this line, in solar flare conditions, ought to be bright enough to be observed.
In the rocket flight spectrum of Acton et al. (1985), no line is reported around 87.30 Å. On the other hand, Acton et al. (1985) reports an unidentified line at 89.76 Å, in excellent agreement with our predicted wavelength. Its intensity is within an excellent 30% agreement with theory, together with various other transitions that we believe to have identified for the first time in the same spectrum, as shown in Fig. 3 and Tables 2, 3.
A second assignment given by Finkenthal et al. (1985) is the level 2p6 3s 3S1 (28). They identify the decays from this level to those of 2p5 3s 1P1 (3) and 2p5 3s 3P0 (4) with lines observed at 90.77 and 98.38 Å. There are three problems with this identification. First, the wavelength difference between those two lines does not match the energy difference between the 1P1 and 3P0. Indeed, those two wavelengths provide an energy for 2p6 3s 3S1 of 6 966 446 and 6 967 945 cm-1, respectively (i.e., with a large difference of 1500 cm-1). Second, our predicted intensities indicate that these two transitions should be weak, and the decay to 2p5 3s 3P2 is much stronger and should have been observed. Third, the energy is very different from our MR-MP calculated one.
It is therefore likely that all the decays from 2p6 3s 1S0, 3S1 in Cr XV and Ni XIX were also incorrectly identified in Finkenthal et al. (1985). In support of our 2p6 3s identifications, we note that the energies of two of the observed 2p6 3p levels (obtained from X-ray lines) are in excellent agreement with those from our MR-MP calculations. Concerning the 2p6 3d levels, the only level that produces observable lines is the 1D2 (level 37). NIST does not report any observed value. The first identification is given by Landi & Phillips (2005), who identified the decay to the ground state with a blend observed in an SMM/FCS spectrum at 13.142 Å. There are two problems with this identification. First, this would mean that the 2p6 3p 1P1-2p6 3d 1D2 (33-37) transition should correspond to 266.22 Å, where no flare line is observed by Hinode/EIS. Second, the 1D2 energy would be quite different from the MR-MP predicted one. Instead, it is quite obvious that the 2p6 3p 1P1 - 2p6 3d 1D2 (33-37) transition is the previously unidentified flare line that we observed at 273.347 Å. The 2p6 3p 1P1 level energy is known from the decay to the ground state observed at 13.825 Å, which provides an energy for the 2p6 3d 1D2 level of 7 599 108 cm-1. This energy is in excellent agreement with the MR-MP predicted one, and provides a decay to the ground state at 13.159 Å, where a previously unidentified line is present (13.161 Å by Landi & Phillips 2005, 13.159 Å by Bromage et al. 1977).
5 Benchmark in the 171-630 Å range
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{H11729_f4a.ps}\includegraphics[angle=90,width=8.8cm,clip]{H11729_f4b.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa11729-09/Timg81.png)
|
Figure 4: The emissivity ratio curves (at log T[K] = 6.6) relative to the transitions observed by the Skylab NRL spectrometer during a flare (Doschek et al. 1991) ( left) and the 1989 SERTS rocket flight (Thomas & Neupert 1994) ( right). |
| Open with DEXTER | |
5.1 Previous identifications
The Skylab NRL slitless spectrograph produced spectra of solar flares in the 171-630 Å range, which allowed a number of identifications to be made (cf. Sandlin et al. 1976; and Dere 1978). It was, however, a spectral analysis along the Ne isoelectronic sequence that allowed Jupén (1984) to suggest a more complete list of identifications in the Skylab spectra. Readers should note that Jupén (1984) labelled levels based on the LS coupling of ions in the lower part of the sequence. This LS labelling differs from the correct labelling, which takes into account the dominant percentage contribution for mixed levels, and changes along the isoelectronic sequence.
The key to the interpretation of the Jupén (1984) identifications is given in the energies listed in Jupén & Litzén (1984). Soon after, Feldman et al. (1985) analysed Skylab spectra in the 290-410 Å wavelength range and revised a number of identifications proposed by Jupén (1984). The labelling of levels in Feldman et al. (1985) follows the conventions used in Jupén & Litzén (1984), but the identifications are based on the distorted-wave structure calculations presented by Bhatia et al. (1985), calculations that have since been improved by adding more configurations. Feldman et al. (1985) used the morphology of the observed lines as an analysis tool, and used estimated intensities from the calculations as an aid in the identification process. However, these line intensities (listed within Table 4) are very different from those obtained on the basis of the calculations by Loch et al. (2006), by factors of 2-3 for the strongest lines, up to a factor of 10 for the weaker ones.
At about the same time, Buchet et al. (1985) published a list of line identifications from laboratory spectra obtained by foil excitation of fast ion beams. The beam-foil wavelength determinations were much less accurate than the corresponding solar observations, and the line intensities are rather different, because the beam-foil light source relies on excitation at high electron density.
5.2 Line intensities and wavelengths
The first check was done on the EUV lines in the longer wavelength range observed by Skylab. Figure 4 (left) shows the emissivity ratio curves based on the measurements of Doschek et al. (1991). The agreement between observed and predicted intensities for the two strongest lines (observed at 204.65, 254.87 Å) is excellent (within 10%), although large departures are present for some of the weaker lines. The observed intensities of the 254.53, 269.88, 266.42, and 275.55 Å lines can be explained with the presence of blends. However, the 351.55, 358.24, and 409.69 Å lines are too weak by a factor of about 2, which could be due to a problem with either the measurements or the calculation.
The second check (see Fig. 4 right) was completed with the intensities observed during the SERTS-89 rocket flight (Thomas & Neupert 1994). Intensities are weak overall since the instrument observed a non-flaring active region, and possible blending with lower-temperature lines becomes more likely. The 254.88 and 389.11 Å lines appear to be significantly blended in this observation. The 389.11 Å line has a known blend with Ar XVI, but the intensity of the former line is puzzling.
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{H11729_f5a.ps}\includegraphics[angle=90,width=8.8cm,clip]{H11729_f5b.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa11729-09/Timg82.png)
|
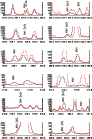
Figure 5: The emissivity ratio curves (at log T[K] = 6.6) relative to the transitions observed by Hinode/EIS. Left: 2007 June 2 observation; right: 2007 May 21. |
| Open with DEXTER | |
In what follows, we discuss identifications based on Hinode EIS data. We used three key new features to identify a number of new lines and revise many wavelengths, as listed in Tables 2 and 4. First, we used the morphology of the lines to assess which line could be due to Fe XVII (cf. Fig. 1). Second, we used the accurate EIS wavelengths that we measured (see Table 2). Third, we used the measured intensities. We note that in many cases our wavelengths differ significantly from those from the NIST database. The high spectral resolution of the Hinode EIS spectra, combined with most lines being either blended or having other lines very close-by, means that many lines would be misidentified in the EIS spectra, if the NIST wavelengths are used. Some specific examples are given below.
Figure 5 shows the emissivity ratio curves obtained from the Hinode EIS spectra of 2007 June 2 and May 21. The results from the two observations are similar. For most lines, agreement to within 20% is found. The strongest transitions are the decays of 2p5 3p 1S0 to the 3s 3,1P1 levels (5-15 and 3-15, see Table 4). We provide new accurate wavelengths for these decays at 254.885 Å and 204.668 Å. We note that the NIST wavelengths are very different. The 204.668 Å line has a strong transition-region line in its red wing, as Fig. 2 shows, and accurate wavelength calibration and deblending are required to obtain a reliable measurement of this line. The 254.885 Å line has also to be carefully measured, since it has other transitions nearby, as Fig. 2 shows. The NIST wavelength for this line is incorrect. The new wavelengths for the decays from 2p5 3p 1S0 provide an energy splitting for the 3s 3,1P1 levels of 96 262 cm-1, in excellent agreement with the energy difference of 96 495 cm-1 obtained from the X-ray wavelengths of 17.051 and 16.775 Å. One problem with these lines, as already mentioned in Del Zanna (2008), is that the observed intensity of the 254.885 Å line is almost 50% weaker than it should be. This is consistently true for both observations. The two lines form a branching ratio, so their relative intensity should be accurate to within 10% or so.
During the assessment, we studied the possibility that the 204.668 Å and 254.885 Å lines are not due to Fe XVII. The morphology of the 204.66 Å and 254.88 Å lines clearly indicates that these two strong lines must be due either to Fe XVII or an ion formed at the same temperature. There are no other strong lines within a few Å of the same morphology. For example, there are no strong flare lines within a few Å of the 254.885 Å line. In theory, the decay of the 2p5 3p 1S0 to the 3P1 level could be blended with the group of lines around 256.3-256.4 Å, although this would require the decay to 1P1 to be placed around 205.6 Å, where no flare lines are present.
We note that Träbert & Jupén (1987) identified the decays of the 2p5 3p 1S0 in Ti XIII and discussed the identifications along the Neon-like sequence. As shown in Ishikawa et al. (2009), the MR-MP energies are offset along the entire Neon-like sequence by similarly small amounts. For Fe, it is 0.04%, one to two orders of magnitude less than typical inaccuracies in most calculations found in previous literature.
All the above arguments support the identification of the 254.885 and 204.668 Å lines. The nearby 254.54 Å line is also weaker by the same amount. This suggests that an instrumental problem is present around these wavelengths in Hinode EIS.
The next strongest transition is the 8-19, which we identify with a line that we observe at 283.945 Å, and not with the line reported by NIST at 284.010 Å. The 283.945 Å line has the appropriate morphology (cf. Fig. 1) and intensity. The marginal agreement with its intensity is caused by its intensity being very difficult to measure, the line lying close to an Al IX line and also in the wings of the strong Fe XV 284.1 Å line, as Fig. 2 shows. The next strongest transition is the 7-20 269.420 Å. This line is relative free from blending. We note that NIST provides an incorrect wavelength (269.295 Å). The 280.16 Å line is a self-blend identified in Del Zanna (2008). The 13-25 281.12 Å line is a relatively strong line free of blends and for which a 20% agreement in its intensity is found. The 12-24 266.417 Å line also appears free from blending and shows good agreement in its intensity. The 9-21 275.550 Å is a weak transition for which we provide a new correct wavelength. We note that NIST and CHIANTI provide incorrect wavelengths (275.596 and 275.673 Å), which would locate this transition where another nearby strong line from Si VII is. We also identify here for the first time various weaker transitions, at 259.71, 262.70, 273.35, and 279.24 Å, although many of them appear to be significantly blended.
6 Conclusions
We have shown that a combination of MR-MP and R-matrix scattering calculations is a powerful tool to assessing line identifications and blending. The wavelengths based on the MR-MP calculations are in excellent agreement with the observed ones, to a few hundredths of an Å in the 30-150 Å range and to a few tenths of an Å in the 200-450 Å range. This gives us confidence in using them to assess the line identifications along the isoelectronic sequence.
We have confirmed most previous Fe XVII identifications, but revised a significant number of wavelengths, mostly in the Hinode/EIS spectral range. This is a particularly important result, considering the high spectral resolution of EIS, and that many Fe XVII lines are either blended or have other nearby lines. We have obtained level energies that do not differ much from the NIST compilation (see Tables A.1, A.2), although in several cases NIST wavelengths are incorrect and would lead to a wrong identification in the EIS spectra, as shown in Table 4.
We have also identified several lines for the first time, some of which are visible in the Hinode/EIS spectra. We find excellent agreement overall between the observed and theoretical line intensities, the latter being calculated with the atomic data of Loch et al. (2006). However, we have noted a large number of cases in which line blending occurs.
We note that most Hinode/EIS ``studies'' of active regions do not include Fe XVII lines. Of those that do, the majority include only the two brightest Fe XVII transitions. However, both of these lines are problematic. The 204.66 Å line is a close blend with a strong cool line, and careful deblending is needed. The 254.88 Å line does not appear to be blended but consistently appears to be underestimated in Hinode/EIS data. The brightest unblended transition is the 3p 3D2-3d 3F3 269.42 Å, and we recommend that future EIS ``studies'' include this line.
AcknowledgementsSupport from STFC (Advanced Fellowship and APAP network) is acknowledged by G.D.Z. We thank E. Träbert (Bochum and Livermore) for helpful comments on the manuscript. Y.I. acknowledges partial support from LLNL subcontract No. B568401. Hinode is a Japanese mission developed and launched by ISAS/JAXA, with NAOJ as domestic partner and NASA and STFC (UK) as international partners. It is operated by these agencies in co-operation with ESA and NSC (Norway). We thank the anonymous referee for careful reading and detailed comments, which helped to improve the manuscript. We warmly thank C. Ballance for providing the atomic data in electronic form.
Appendix A: Details about the energies of the n = 3 levels
The energy of level 2 is obtained from the 1-2 17.096 Å line and by taking into account the wavelengths of the 2-10, 3-10 and 2-7, 3-7 transitions. The energy of level 3 is obtained from the 1-3 17.051 Å line. The energy of level 4 relates to the 3-4 1153.16 Å line. The energy of level 5 is obtained from the energy of level 3 and the measured splitting of the 3-15 and 5-15 transitions. The resulting wavelength of the 1-5 transition is 16.776 Å, only 1 mÅ different from the measured 16.775 Å value, and well within the uncertainties. The energy of level 6 is obtained from the 2-6 409.705 Å line. The energy of level 7 is from the 367.287 Å line. The 3-7 line was observed at 389.11 Å, and the 1-7 is predicted to be blended at 16.335 Å. The energy of level 8 is from the 2-8 350.477 Å line. The energy of level 9 is from the 3-9 358.247 Å line. The energy of level 10 is from the 2-10 and 3-10 transitions, observed at 323.57, 340.40 Å. The energy of level 11 is from the stronger 3-11 295.98 Å,line. The energy of level 12 is from the 5-12 387.23 Å line. The 4-12 is then predicted to be at 373.43 Å, close to the line observed by F85 at 373.41 Å. The energy of level 13 is from the stronger decay, the 4-13 340.12 Å line. The weaker 5-13 line is then predicted to be at 351.53 Å, in slight disagreement with the observed 351.55, 351.58 Å measurements found in the literature.
Table A.1: List of energies for the n=3 levels.
Table A.2: List of energies for a selection of n=4,5 levels.
The energy of level 14 is from the 5-14 347.814 Å line. The energy of level 15 is from the 3-15 and 5-15 204.668, 254.885 Å lines. The energy of level 16 is from the 6-16 269.886 Å line. The energy of level 17 is from the 1-17 15.453 Å line. The energy of level 18 is from the 6-18 254.536 Å line. This predicts that the 10-18 line is at 304.971 Å, in slight disagreement with the B85 measurement; we notehowever that this latter line is blended. The energy of level 19 is from the strongest decay, the 8-19 283.945 Å line. The energy of level 20 is from the strong 7-20 269.420 Å line, in agreement with the 8-20 line at 279.24 Å. The energy of level 21 is from the 9-21 275.55 Å line, which provides a wavelength of 259.705 Å for the weaker and blended 7-21 line, observed at 259.722 Å. The energy of level 22 is from the 8-22 and 10-22 transitions, observed at 262.699, 280.16 Å. The energy of level 23 is from the 1-23 15.262 Å line. The energy of level 24 is from the 12-24 266.417 Å line. The energy of level 25 is from the 13-25 281.12 Å line, a new measurement close to the J84 one (281.09). The energy of level 26 is from the 14-26 280.16 Å line, which is a self-blend. The energy of level 27 is from the 1-27 15.013 Å line. The energy of level 28 is uncertain, considering that Finkenthal et al. (1985) only proposed a value, and that the energy of level 29 suggested by the same authors is incorrect (see main text). The energy of level 31 is from the 1-31 13.890 Å line. The energy of level 33 is from the 1-33 13.825 Å line. The energy of level 37 is from the new measurement of the 33-37 273.347 Å line (see main text).
References
- Acton, L. W., Bruner, M. E., Brown, W. A., et al. 1985, ApJ, 291, 865 [NASA ADS] [CrossRef]
- Bhatia, A. K., Feldman, U., & Seely, J. F. 1985, Atomic Data and Nuclear Data Tables, 32, 435 [NASA ADS] [CrossRef]
- Boiko, V. A., Faenov, A. I., & Pikuz, S. A. 1978, J. Quant. Spec. Radiat. Transf., 19, 11 [NASA ADS] [CrossRef]
- Bromage, G. E., Cowan, R. D., Fawcett, B. C., et al. 1977, RAL report, 170
- Brown, G. V., Beiersdorfer, P., Liedahl, D. A., Widmann, K., & Kahn, S. M. 1998, ApJ, 502, 1015 [NASA ADS] [CrossRef]
- Buchet, J.-P., Buchet-Poulizac, M.-C., Denis, A., et al. 1985, Phys. Scr., 31, 364 [NASA ADS] [CrossRef]
- Culhane, J. L., Harra, L. K., James, A. M., et al. 2007, Sol. Phys., 60
- Del Zanna, G. 2008, A&A, 481, L69 [NASA ADS] [EDP Sciences] [CrossRef]
- Del Zanna, G., Berrington, K. A., & Mason, H. E. 2004, A&A, 422, 731 [NASA ADS] [EDP Sciences] [CrossRef]
- Dere, K. P. 1978, ApJ, 221, 1062 [NASA ADS] [CrossRef]
- Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&AS, 125, 149 [NASA ADS] [EDP Sciences] [CrossRef]
- Doschek, G. A., Feldman, U., & Bhatia, A. K. 1991, Phys. Rev. A, 43, 2565 [NASA ADS] [CrossRef]
- Fawcett, B. C., Bromage, G. E., & Hayes, R. W. 1979, MNRAS, 186, 113 [NASA ADS]
- Feldman, U., Doschek, G. A., & Seely, J. F. 1985, MNRAS, 212, 41P [NASA ADS]
- Feldman, U., Curdt, W., Doschek, G. A., et al. 1998, ApJ, 503, 467 [NASA ADS] [CrossRef]
- Finkenthal, M., Mandelbaum, P., Bar-Shalom, A., et al. 1985, J. Phys. B Atom. Mol. Phys., 18, L331 [NASA ADS] [CrossRef]
- Hutcheon, R. J., Pye, J. P., & Evans, K. D. 1976a, MNRAS, 175, 489 [NASA ADS]
- Hutcheon, R. J., Pye, J. P., & Evans, K. D. 1976b, A&A, 51, 451 [NASA ADS]
- Ishikawa, Y., & Vilkas, M. J. 2008, Phys. Rev. A, 78, 042501 [NASA ADS] [CrossRef]
- Ishikawa, Y., López-Encarnación, J. M., & Träbert, E. 2009, Phys. Scr., 79, 025301 [NASA ADS] [CrossRef]
- Jupén, C. 1984, MNRAS, 208, 1P [NASA ADS]
- Jupén, C., & Litzén, U. 1984, Phys. Scr., 30, 112 [NASA ADS] [CrossRef]
- Landi, E., & Phillips, K. J. H. 2005, ApJS, 160, 286 [NASA ADS] [CrossRef]
- Landi, E., Del Zanna, G., Young, P. R., et al. 2006, ApJS, 162, 261 [NASA ADS] [CrossRef]
- Loch, S. D., Pindzola, M. S., Ballance, C. P., & Griffin, D. C. 2006, J. Phys. B Atom. Mol. Phys., 39, 85 [NASA ADS] [CrossRef]
- Parkinson, J. H. 1973, A&A, 24, 215 [NASA ADS]
- Phillips, K. J. H., Fawcett, B. C., Kent, B. J., et al. 1982, ApJ, 256, 774 [NASA ADS] [CrossRef]
- Sandlin, G. D., Brueckner, G. E., Scherrer, V. E., & Tousey, R. 1976, ApJ, 205, L47 [NASA ADS] [CrossRef]
- Swartz, M., Kastner, S., Rothe, E., & Neupert, W. 1971, J. Phys. B Atom. Mol. Phys., 4, 1747 [NASA ADS] [CrossRef]
- Thomas, R. J., & Neupert, W. M. 1994, ApJS, 91, 461 [NASA ADS] [CrossRef]
- Träbert, E., & Jupén, C. 1987, Phys. Scr., 36, 586 [NASA ADS] [CrossRef]
- Tyrén, F. 1938, ZAp, 111, 314
- Young, P. R., Watanabe, T., Hara, H., & Mariska, J. T. 2009, A&A, 495, 587 [NASA ADS] [EDP Sciences] [CrossRef]
Footnotes
- ... database
![[*]](/icons/foot_motif.png)
- http://physics.nist.gov/PhysRefData/ASD/index.html
All Tables
Table 1: List of wavelengths and identifications for the X-ray lines.
Table 2: List of wavelengths and identifications for the EUV lines.
Table 3: List of strongest Fe XVII lines in the 30-150 Å range.
Table 4: List of the Fe XVII strongest lines in the 200-450 Å range.
Table A.1: List of energies for the n=3 levels.
Table A.2: List of energies for a selection of n=4,5 levels.
All Figures
![\begin{figure}
{\includegraphics[width=14.cm]{H11729_f1a.eps} }
{\includegraphics[width=14.cm]{H11729_f1b.eps} }\end{figure}](/articles/aa/full_html/2009/48/aa11729-09/Timg8.png)
|
Figure 1: Monochromatic images (negative) of a selection of EIS lines from the 2007 May 21 observation. Ion and wavelength in Å are indicated, as well as the logarithm of the temperature (K) of line formation in collisional ionisation equilibrium. We note that all the identified Fe XVII lines have the same morphology. |
| Open with DEXTER | |
| In the text | |

|
Figure 2: Hinode EIS spectra (ordinates are averaged counts per pixel, while abscissae are wavelengths in Å) over an area where Fe XVII emission was more clearly isolated (black line) and over a transition-region brightening (red thick line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[angle=90,width=8.8cm,clip]{H11729_f3.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa11729-09/Timg80.png)
|
Figure 3:
The emissivity ratio curves of a few lines observed during a flare by a
rocket (Acton et al. 1985).
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{H11729_f4a.ps}\includegraphics[angle=90,width=8.8cm,clip]{H11729_f4b.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa11729-09/Timg81.png)
|
Figure 4: The emissivity ratio curves (at log T[K] = 6.6) relative to the transitions observed by the Skylab NRL spectrometer during a flare (Doschek et al. 1991) ( left) and the 1989 SERTS rocket flight (Thomas & Neupert 1994) ( right). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{H11729_f5a.ps}\includegraphics[angle=90,width=8.8cm,clip]{H11729_f5b.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa11729-09/Timg82.png)
|
Figure 5: The emissivity ratio curves (at log T[K] = 6.6) relative to the transitions observed by Hinode/EIS. Left: 2007 June 2 observation; right: 2007 May 21. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


