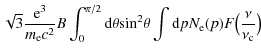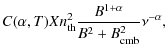| Issue |
A&A
Volume 508, Number 2, December III 2009
|
|
|---|---|---|
| Page(s) | 599 - 602 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200913177 | |
| Published online | 15 October 2009 | |
A&A 508, 599-602 (2009)
Constraining relativistic protons and magnetic fields in galaxy clusters through radio and 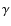 -ray observations: the case of A2256
-ray observations: the case of A2256
(Research Note)
G. Brunetti
INAF - Istituto di Radioastronomia, via P. Gobetti 101, 40129 Bologna, Italy
Received 25 August 2009 / Accepted 18 September 2009
Abstract
Giant radio halos are the most relevant examples of diffuse
synchrotron emission from galaxy clusters. A number of these
sources have very steep spectra, of spectral index
![]() (
(
![]() ),
and are ideal targets for testing current models of the origin of the
relativistic particles. A2256 hosts the nearest radio halo with a very
steep spectrum, of
),
and are ideal targets for testing current models of the origin of the
relativistic particles. A2256 hosts the nearest radio halo with a very
steep spectrum, of
![]() ,
and a very large population of relativistic protons in the cluster
would be necessary if the halo were produced by synchrotron emission
from secondary particles. In this case, the 0.1-1 GeV
,
and a very large population of relativistic protons in the cluster
would be necessary if the halo were produced by synchrotron emission
from secondary particles. In this case, the 0.1-1 GeV ![]() -ray
luminosity is expected to be 10-20 times higher than that of
clusters hosting radio halos of similar radio power at
GHz frequencies but with spectra more typical of the presently
observed halo population,
-ray
luminosity is expected to be 10-20 times higher than that of
clusters hosting radio halos of similar radio power at
GHz frequencies but with spectra more typical of the presently
observed halo population,
![]() .
Based on these assumptions, future FERMI/GLAST observations are
expected to detect A2256, provided that the magnetic field in the
central cluster region is
.
Based on these assumptions, future FERMI/GLAST observations are
expected to detect A2256, provided that the magnetic field in the
central cluster region is ![]() 10-15
10-15 ![]() G.
We show that this will provide a prompt test of hadronic models for the
origin of radio halos, and complementary constraints on both the
cluster magnetic field and the physics of particle acceleration
mechanisms.
G.
We show that this will provide a prompt test of hadronic models for the
origin of radio halos, and complementary constraints on both the
cluster magnetic field and the physics of particle acceleration
mechanisms.
Key words: radiation mechanisms: non-thermal - galaxies: clusters: general - radio continuum: general - gamma rays: theory
1 Introduction
Galaxy clusters are the largest gravitationally bound objects in the Universe. During cluster mergers, energy may be channelled into both the amplification of the magnetic fields (Dolag et al. 2005; Ryu et al. 2008) and the acceleration of relativistic primary electrons (CRe) and protons (CRp) via shocks and turbulence (e.g., Ensslin et al. 1998; Sarazin 1999; Blasi 2001; Ryu et al. 2003; Gabici & Blasi 2003; Pfrommer et al. 2006; Brunetti & Lazarian 2007). CRp have long lifetimes and remain confined within clusters for a Hubble time (Völk et al. 1996; Berezinsky et al. 1997; Ensslin et al. 1997). They are expected to be the dominant non-thermal particle component in the ICM and should produce secondary particles due to collisions with thermal protons (e.g., Blasi et al. 2007, for a review).
Direct evidence of magnetic fields and relativistic particles, mixed
with the thermal intracluster medium (ICM) comes from radio
observations that detect Mpc-sized diffuse radio sources, radio halos
and relics, in a fraction of X-ray luminous galaxy clusters in merging
phase (e.g., Ferrari et al. 2008,
for a review). Extended and fairly regular diffuse synchrotron
emission, in the
form of giant radio halos, may be produced by secondary electrons
injected during proton-proton collisions (hadronic models, e.g.,
Dennison 1980; Blasi & Colafrancesco 1999; Pfrommer & Ensslin 2004),
or by assuming that relativistic electrons are re-accelerated in-situ
by MHD turbulence generated in the ICM during cluster-cluster
mergers (re-acceleration models, e.g.,
Brunetti et al. 2001, 2004; Petrosian 2001; Fujita et al. 2003; Cassano & Brunetti 2005).
Unavoidable ![]() -ray
emission, due to the decay of the neutral pions generated by
proton-proton collisions, is expected in the context of hadronic models
(e.g., Blasi & Colafrancesco 1999; Miniati 2003; Pfrommer & Ensslin 2004). Some
-ray
emission, due to the decay of the neutral pions generated by
proton-proton collisions, is expected in the context of hadronic models
(e.g., Blasi & Colafrancesco 1999; Miniati 2003; Pfrommer & Ensslin 2004). Some ![]() -ray emission is also expected by re-acceleration models that account for the general situation where relativistic protons
and electrons (including secondaries) interact with MHD turbulence (Brunetti & Blasi 2005; Brunetti 2009). Those halos with very steep spectrum are suitable targets for
constraining models and their properties are most consistent with a turbulent re-acceleration
scenario (e.g., Brunetti et al. 2008).
Indeed clusters hosting radio halos with very steep spectrum should
contain a very large population of CRp according to the hadronic
scenario; this also implies an unavoidably large amount of
-ray emission is also expected by re-acceleration models that account for the general situation where relativistic protons
and electrons (including secondaries) interact with MHD turbulence (Brunetti & Blasi 2005; Brunetti 2009). Those halos with very steep spectrum are suitable targets for
constraining models and their properties are most consistent with a turbulent re-acceleration
scenario (e.g., Brunetti et al. 2008).
Indeed clusters hosting radio halos with very steep spectrum should
contain a very large population of CRp according to the hadronic
scenario; this also implies an unavoidably large amount of ![]() -ray emission from these clusters.
-ray emission from these clusters.
Only upper limits to the ![]() -ray emission from clusters have been so far obtained (Reimer et al. 2003; Aharonian et al. 2009b),
providing in some cases a fairly stringent constraint on the energy
density of CRp, <10% of that of the thermal ICM (Aharonian
et al. 2009a). The FERMI/GLAST telescope will soon provide tighter constraints on both the
-ray emission from clusters have been so far obtained (Reimer et al. 2003; Aharonian et al. 2009b),
providing in some cases a fairly stringent constraint on the energy
density of CRp, <10% of that of the thermal ICM (Aharonian
et al. 2009a). The FERMI/GLAST telescope will soon provide tighter constraints on both the ![]() -ray properties of clusters and the energy density of CRp.
-ray properties of clusters and the energy density of CRp.
The radio halo in A2256 is our most nearby steep-spectrum halo, and we
show that the incoming FERMI/GLAST data will provide a prompt test of
the hadronic scenario and allow us to constrain the cluster-magnetic
field. We assume a ![]() CDM cosmology (
CDM cosmology (
![]() ,
,
![]() ,
,
![]() )
throughout the paper.
)
throughout the paper.
2 The cluster Abell 2256
Abell 2256 is a massive galaxy cluster at z=0.058, with a 0.1-2.4 keV X-ray luminosity
![]() erg/s (e.g., Ebeling et al. 1996).
The dynamical state of A2256 is complex and is thought to consist of at
least three merging systems based on optical velocity dispersion
(Berrington et al. 2002; Miller et al. 2003).
A complex dynamical status of A2256 is also suggested by X-ray
observations that detect two separate peaks in the X-ray surface
brightness distribution corresponding to the primary cluster and the
secondary subcluster, which is infalling onto the primary from the
northeast (Briel et al. 1991; Sun et al. 2002).
erg/s (e.g., Ebeling et al. 1996).
The dynamical state of A2256 is complex and is thought to consist of at
least three merging systems based on optical velocity dispersion
(Berrington et al. 2002; Miller et al. 2003).
A complex dynamical status of A2256 is also suggested by X-ray
observations that detect two separate peaks in the X-ray surface
brightness distribution corresponding to the primary cluster and the
secondary subcluster, which is infalling onto the primary from the
northeast (Briel et al. 1991; Sun et al. 2002).
Radio observations have detected complex diffuse emission on large scales (Bridle et al. 1979; Rottgering et al. 1994; Clarke & Ensslin 2006; Brentjens 2008)
consisting of a bright relic, northwest of the cluster center and a
fainter steep-spectrum Mpc-scale radio halo in the cluster central
region. Deep observations at 1400 and 300 MHz detect diffuse
radio-halo emission out to a distance from the cluster center
![]() kpc (Clarke & Ensslin 2006;
Brentjens 2008). A detailed spectral analysis of the halo emission derived an integrated spectral index between 0.3-1.4 GHz of
kpc (Clarke & Ensslin 2006;
Brentjens 2008). A detailed spectral analysis of the halo emission derived an integrated spectral index between 0.3-1.4 GHz of
![]() (
(
![]() ), once the
contribution from embedded discrete radio sources had been subtracted (Brentjens 2008).
), once the
contribution from embedded discrete radio sources had been subtracted (Brentjens 2008).
3 Hadronic models: formalism
The decay chain that we consider for the injection
of secondary particles in the ICM due to p-pcollisions is (Blasi & Colafrancesco 1999)
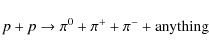
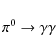
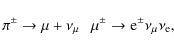
which is a threshold reaction that requires protons with kinetic energies higher than
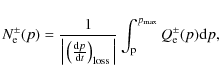
The injection rate of pions is
where
The spectrum of ![]() -rays produced by the decay of the secondary
-rays produced by the decay of the secondary
![]() is (e.g., Dermer 1986a,b; Blasi & Colafrancesco 1999)
is (e.g., Dermer 1986a,b; Blasi & Colafrancesco 1999)
where
Charged pions decay into muons and secondary pairs (electrons and positrons).
Based on the assumption that secondaries are not accelerated by other
mechanisms, their spectrum approaches a stationary distribution because of
the competition between injection and energy losses
(e.g., Dolag & Ensslin 2000)
where
Assuming a power law distribution of CRp,
where C is a constant,
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13177f1.ps}
\end{figure}](/articles/aa/full_html/2009/47/aa13177-09/Timg53.png)
|
Figure 1:
Ratio of relativistic CRp to thermal energy densities (for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13177f2a.ps}\hspace*{3mm}
\includegraphics[width=6.85cm,clip]{13177f2b.ps}
\end{figure}](/articles/aa/full_html/2009/47/aa13177-09/Timg54.png)
|
Figure 2:
Radio ( left) and ( |
| Open with DEXTER | |
4 Results
We show that the steep spectrum of the halo in A2256 (Sect. 2) allows a prompt test of hadronic models and a constraint of the magnetic field in the ICM.
We assume that the radio halo is produced by synchrotron emission
from secondary electrons, where the observed synchrotron spectral index,
![]() ,
implies that
s=3.4-3.5.
The parameters for the thermal ICM distribution in A2256,
,
implies that
s=3.4-3.5.
The parameters for the thermal ICM distribution in A2256,
![]() ,
T,
,
T, ![]() ,
and
,
and ![]() ,
were taken from Henry
et al. (1993) and Myers et al. (1997).
,
were taken from Henry
et al. (1993) and Myers et al. (1997).
We first adopt a steep model that assumes a constant ratio of
the energy density of CRp to thermal protons,
![]() ,
and model the halo region with a
homogeneus sphere of radius
,
and model the halo region with a
homogeneus sphere of radius
![]() and a volume-averaged field (weighted for synchrotron emissivity)
and a volume-averaged field (weighted for synchrotron emissivity)
![]() .
For relativistic CRp only, the value of X required to reproduce the observed synchrotron spectrum is shown in Fig. 1 as a function of
.
For relativistic CRp only, the value of X required to reproduce the observed synchrotron spectrum is shown in Fig. 1 as a function of
![]() .
We find that
.
We find that
![]() G can be excluded since the CRp
energy density becomes higher than the cluster thermal budget.
For stronger magnetic fields,
G can be excluded since the CRp
energy density becomes higher than the cluster thermal budget.
For stronger magnetic fields,
![]() G,
G,
![]() and the non-thermal
component is dominated by the magnetic field.
The non-thermal energy content reaches a minimum,
and the non-thermal
component is dominated by the magnetic field.
The non-thermal energy content reaches a minimum,
![]() 0.16
0.16
![]() ,
for
,
for
![]() G, which represents
the minimum energy condition for hadronic models (Pfrommer & Ensslin 2004).
If we do not restrict ourselves to relativistic CRp
and also include subrelativistic CRp, because of the very steep spectrum,
the required energy budget of CRp is much greater than that in Fig. 1,
G, which represents
the minimum energy condition for hadronic models (Pfrommer & Ensslin 2004).
If we do not restrict ourselves to relativistic CRp
and also include subrelativistic CRp, because of the very steep spectrum,
the required energy budget of CRp is much greater than that in Fig. 1,
![]() .
.
We assume a spatial profile of
the magnetic field
![]() (e.g., Govoni & Feretti 2004)
and find that the steep model produces a radio-halo brightness
profile that decreases by a factor 25-40 at
(e.g., Govoni & Feretti 2004)
and find that the steep model produces a radio-halo brightness
profile that decreases by a factor 25-40 at
![]() ,
by
adopting b=0.5-1 and
,
by
adopting b=0.5-1 and
![]() G.
This is inconsistent with the observed profile that drops, at the same
distance, by only a factor 5-8 (Clarke & Ensslin 2006; Brentjens 2008).
Thus, we consider a flat hadronic model, with
G.
This is inconsistent with the observed profile that drops, at the same
distance, by only a factor 5-8 (Clarke & Ensslin 2006; Brentjens 2008).
Thus, we consider a flat hadronic model, with
![]() = constant
to
= constant
to
![]() and X = constant for larger r,
that produces a decrease of the brightness by a factor 8-12 at
and X = constant for larger r,
that produces a decrease of the brightness by a factor 8-12 at
![]() for the range
of (b,
for the range
of (b, ![]() )
given above; this is our reference model.
The energy request of the flat hadronic model is also reported
in Fig. 1 by considering the conservative case of relativistic
CRp only.
The large energy budget of the non-thermal components
is a problem for a hadronic origin of the radio halo in A2256.
)
given above; this is our reference model.
The energy request of the flat hadronic model is also reported
in Fig. 1 by considering the conservative case of relativistic
CRp only.
The large energy budget of the non-thermal components
is a problem for a hadronic origin of the radio halo in A2256.
This large budget and the steep spectrum of CRp unavoidably imply
that there is an efficient production of ![]() -rays at 0.1-1 GeV due to
-rays at 0.1-1 GeV due to ![]() decay.
Consequently, FERMI/GLAST observations provide an
efficient and complementary way to test a hadronic origin of the halo.
decay.
Consequently, FERMI/GLAST observations provide an
efficient and complementary way to test a hadronic origin of the halo.
In Fig. 2, we show the expected radio (left) and
![]() -ray (right) spectra of A2256
for different values of
-ray (right) spectra of A2256
for different values of ![]() (see caption) (models anchored to the observed
1.4 GHz emission); we also report results for the case of
a hadronic model with s=2.4.
(see caption) (models anchored to the observed
1.4 GHz emission); we also report results for the case of
a hadronic model with s=2.4.
We find that by assuming a hadronic origin of the radio halo and
adopting the appropriate spectrum of CRp,
the ![]() -ray upper limit obtained with EGRET observations
(Reimer et al. 2003) already constrains
-ray upper limit obtained with EGRET observations
(Reimer et al. 2003) already constrains
![]() G.
Most importantly, FERMI/GLAST should be able to detect Abell 2256 in the
next few years, provided that
G.
Most importantly, FERMI/GLAST should be able to detect Abell 2256 in the
next few years, provided that
![]() G.
This is highlighted in Fig. 3, where we show the expected photon number
with
G.
This is highlighted in Fig. 3, where we show the expected photon number
with
![]() MeV as a function of
MeV as a function of ![]() in the case of both
steep and flat hadronic models.
in the case of both
steep and flat hadronic models.
5 Discussion and conclusions
Radio halos have typical synchrotron spectral indices
![]() (e.g., Ferrari et al. 2008), yet halos with steeper spectra
might be more common in the Universe (e.g., Cassano et al. 2006) and
present observations at GHz frequencies may preferentially
select those halos with flatter spectra. The discovery of a few radio halos with spectral index
(e.g., Ferrari et al. 2008), yet halos with steeper spectra
might be more common in the Universe (e.g., Cassano et al. 2006) and
present observations at GHz frequencies may preferentially
select those halos with flatter spectra. The discovery of a few radio halos with spectral index
![]() suggests that the emitting electrons are accelerated by rather
inefficient mechanisms, e.g., turbulent acceleration, and constrains
models, such as the hadronic one, that would require a very large
energy budget to be
supplied to explain the properties of these sources (e.g., Brunetti
et al. 2008).
suggests that the emitting electrons are accelerated by rather
inefficient mechanisms, e.g., turbulent acceleration, and constrains
models, such as the hadronic one, that would require a very large
energy budget to be
supplied to explain the properties of these sources (e.g., Brunetti
et al. 2008).
A2256 hosts the closest radio halo with
a steep spectrum, of
![]() ,
that would require a spectral
slope of CRp
s=3.4-3.5 adopting the hadronic scenario; in this case, only a
small fraction of the total energy-budget of supra-thermal CRp is
expected to be associated with relativistic CRp.
We exploit two approaches based on hadronic models: a steep
model that assumes a constant fraction
,
that would require a spectral
slope of CRp
s=3.4-3.5 adopting the hadronic scenario; in this case, only a
small fraction of the total energy-budget of supra-thermal CRp is
expected to be associated with relativistic CRp.
We exploit two approaches based on hadronic models: a steep
model that assumes a constant fraction
![]() and a flat model that assumes
and a flat model that assumes
![]() =constant in the halo
volume and X = constant outside. The last one is our reference model
since the observed halo-brightness profile of A2256 implies a rather
flat spatial distribution of CRp.
=constant in the halo
volume and X = constant outside. The last one is our reference model
since the observed halo-brightness profile of A2256 implies a rather
flat spatial distribution of CRp.
Even by considering only relativistic CRp, the hadronic model requires
a large CRp-energy budget to explain the halo
in A2256 for central fields
![]() G. This is a drawback
of the hadronic scenario and also implies that
the expected
G. This is a drawback
of the hadronic scenario and also implies that
the expected ![]() -ray luminosity of A2256 should be a factor of
10-20 higher than
that of similar clusters hosting halos of the same radio
luminosity but with
-ray luminosity of A2256 should be a factor of
10-20 higher than
that of similar clusters hosting halos of the same radio
luminosity but with
![]() .
In these conditions, we show that FERMI/GLAST should be able to detect A2256.
.
In these conditions, we show that FERMI/GLAST should be able to detect A2256.
Non-detection would either imply that the halo is not of hadronic origin,
or that the magnetic field in the central cluster region is
![]() G. In the latter case, however we would
concede to the ad hoc possibility that A2256 is a cluster with an unusually
strong magnetic field since strong fields are presently
observed only in cool-core clusters (e.g., Carilli & Taylor 2002; Govoni &
Feretti 2004); future observations of Faraday rotation will provide
complementary information about the cluster magnetic field.
G. In the latter case, however we would
concede to the ad hoc possibility that A2256 is a cluster with an unusually
strong magnetic field since strong fields are presently
observed only in cool-core clusters (e.g., Carilli & Taylor 2002; Govoni &
Feretti 2004); future observations of Faraday rotation will provide
complementary information about the cluster magnetic field.
On the other hand, detection of steep-spectrum ![]() -ray
emission from A2256 would imply a hadronic origin of the halo,
providing us
also with an unprecedented measure of the magnetic field strength in
the cluster. This will also suggest that very unusual acceleration
mechanisms operate in the ICM, channeling a large fraction of the
cluster energy into a population of
CRp with very steep spectrum.
-ray
emission from A2256 would imply a hadronic origin of the halo,
providing us
also with an unprecedented measure of the magnetic field strength in
the cluster. This will also suggest that very unusual acceleration
mechanisms operate in the ICM, channeling a large fraction of the
cluster energy into a population of
CRp with very steep spectrum.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13177f3.ps}\vspace{3mm}
\end{figure}](/articles/aa/full_html/2009/47/aa13177-09/Timg78.png)
|
Figure 3:
Photon fluxes for >100 MeV are shown as a function of
|
| Open with DEXTER | |
If the halo is generated by turbulent re-acceleration, the maximum ![]() -ray
luminosity expected from A2256 can be estimated by requiring that the
emission from secondaries matches the radio flux at the highest
frequencies and is much lower than that at lower frequencies (assumed
to be dominated by re-accelerated electrons) (Reimer et al. 2004; Donnert et al. 2009). This implies a
-ray
luminosity expected from A2256 can be estimated by requiring that the
emission from secondaries matches the radio flux at the highest
frequencies and is much lower than that at lower frequencies (assumed
to be dominated by re-accelerated electrons) (Reimer et al. 2004; Donnert et al. 2009). This implies a ![]() -ray luminosity similar to that of the model with s=2.4 in Fig. 2 implying that detection would be possible only for weakfields,
-ray luminosity similar to that of the model with s=2.4 in Fig. 2 implying that detection would be possible only for weakfields,
![]() G. In this case the
G. In this case the ![]() -ray spectrum is
much flatter than that in the case of a hadronic origin of the halo.
-ray spectrum is
much flatter than that in the case of a hadronic origin of the halo.
This work is partially supported by grants PRIN-INAF2007 and 2008, and ASI-INAF I/088/06/0.
References
- Aharonian, F. A., Akhperjanian, A. G., Anton, G., et al. 2009a, A&A, 495, 27 [NASA ADS] [EDP Sciences] [CrossRef]
- Aharonian, F. A., Akhperjanian, A. G., Anton, G., et al. 2009b, A&A, 502, 437 [NASA ADS] [EDP Sciences] [CrossRef]
- Berezinsky, V. S., Blasi, P., & Ptuskin, V. S. 1997, ApJ, 487, 529 [NASA ADS] [CrossRef]
- Berrington, R. C., Lugger, P. M., & Cohn, H. N. 2002, AJ, 123, 2261 [NASA ADS] [CrossRef]
- Blasi, P. 2001, APh, 15, 223 [NASA ADS]
- Blasi, P., & Colafrancesco, S. 1999, APh, 12, 169 [NASA ADS]
- Blasi, P., Gabici, S., & Brunetti, G. 2007, Int. J. Mod. Phys. A, 22, 681 [NASA ADS] [CrossRef]
- Brentjens, M. A. 2008, A&A, 489, 69 [NASA ADS] [EDP Sciences] [CrossRef]
- Bridle, A. H., Fomalont, E. B., Miley, G. K., & Valentijn, E. A. 1979, A&A, 80, 201 [NASA ADS]
- Briel, U. G., Henry, J. P., Schwarz, R. A., et al. 1991, A&A, 246, L10 [NASA ADS]
- Brunetti, G. 2009, RMxAC, 36, 201
- Brunetti, G., & Blasi, P. 2005, MNRAS, 363, 1173 [NASA ADS] [CrossRef]
- Brunetti, G., & Lazarian, A. 2007, MNRAS, 378, 245 [NASA ADS] [CrossRef]
- Brunetti, G., Setti, G., Feretti, L., & Giovannini, G. 2001, MNRAS, 320, 365 [NASA ADS] [CrossRef]
- Brunetti, G., Blasi, P., Cassano, R., & Gabici, S. 2004, MNRAS, 350, 1174 [NASA ADS] [CrossRef]
- Brunetti, G., Giacintucci, S., Cassano, R., et al. 2008, Nature, 455, 944 [NASA ADS] [CrossRef]
- Carilli, C. L., & Taylor, G. B. 2002, ARA&A, 40, 319 [NASA ADS] [CrossRef]
- Cassano, R., & Brunetti, G. 2005, MNRAS, 357, 1313 [NASA ADS] [CrossRef]
- Cassano, R., Brunetti, G., & Setti, G. 2006, MNRAS, 369, 1577 [NASA ADS] [CrossRef]
- Clarke, T. E., & Ensslin, T. A. 2006, ApJ, 131, 2900 [NASA ADS]
- Dennison, B. 1980, ApJ, 239, L93 [NASA ADS] [CrossRef]
- Dermer, C. D. 1986a, A&A, 157, 223 [NASA ADS]
- Dermer, C. D. 1986b, ApJ, 307, 47 [NASA ADS] [CrossRef]
- Dolag, K., & Ensslin, T. A. 2000, A&A, 362, 151 [NASA ADS]
- Dolag, K., Grasso, D., Springel, V., & Tkachev, I. 2005, JCAP, 1, 9 [NASA ADS]
- Donnert, J., Dolag, K., Brunetti, G., Cassano, R., & Bonafede, A. 2009, MNRAS, in press [arXiv:0905.2418]
- Ebeling, H., Voges, W., Böhringer, H., et al. 1996, MNRAS, 281, 799 [NASA ADS]
- Ensslin, T. A., Biermann, P. L., Kronberg, P. P., & Wu, X.-P. 1997, ApJ, 477, 560 [NASA ADS] [CrossRef]
- Ensslin, T. A., Biermann, P. L., Klein, U., & Kohle, S. 1998, A&A, 332, 395 [NASA ADS]
- Ferrari, F., Govoni, F., Schindler, S., et al. 2008, SSRv, 134, 93 [NASA ADS]
- Fujita, Y., Takizawa, M., & Sarazin, C. L. 2003, ApJ, 584, 190 [NASA ADS] [CrossRef]
- Gabici, S., & Blasi, P. 2003, ApJ, 583, 695 [NASA ADS] [CrossRef]
- Govoni, F., & Feretti, L. 2004, Int. J. Mod. Phys. D, 13, 1549 [NASA ADS] [CrossRef]
- Henry, J. P., Briel, U. G., & Nulsen, P. E. J. 1993, A&A, 271, 413 [NASA ADS]
- Miller, N. A., Owen, F. N., & Hill, J. M. 2003, AJ, 125, 2393 [NASA ADS] [CrossRef]
- Miniati, F. 2003, MNRAS, 342, 1009 [NASA ADS] [CrossRef]
- Moskalenko, I. V., & Strong, A. W. 1998, ApJ, 493, 694 [NASA ADS] [CrossRef]
- Myers, S. T., Baker, J. E., Readhead, A. C. S., & Leitch, E. M. 1997, ApJ, 485, 1 [NASA ADS] [CrossRef]
- Petrosian, V. 2001, ApJ, 557, 560 [NASA ADS] [CrossRef]
- Pfrommer, C., & Enßlin, T. A. 2004, A&A, 413, 17 [NASA ADS] [EDP Sciences] [CrossRef]
- Pfrommer, C., Springel, V., Enßlin, T. A., & Jubelgas, M. 2006, MNRAS, 367, 113 [NASA ADS] [CrossRef]
- Reimer, O., Pohl, M., Sreekumar, P., & Mattox, J. R. 2003, ApJ, 588, 155 [NASA ADS] [CrossRef]
- Reimer, A., Reimer, O., Schlickeiser, R., & Iyudin, A. 2004, A&A, 424, 773 [NASA ADS] [EDP Sciences] [CrossRef]
- Rybicky, G. B., & Lightmann, A. P. 1979, Radiative Processes in Astrophysics (New York: Wiley-Interscience)
- Röttgering, H., Snellen, I., Miley, G., et al. 1994, ApJ, 436, 654 [NASA ADS] [CrossRef]
- Ryu, D., Kang, H., Hallman, E., & Jones, T. W. 2003, ApJ, 593, 599 [NASA ADS] [CrossRef]
- Ryu, D., Kang, H., Cho, J., & Das, S. 2008, Science, 320, 909 [NASA ADS] [CrossRef]
- Sun, M., Murray, S. S., Markevitch, M., & Vikhlinin, A. 2002, ApJ, 565, 867 [NASA ADS] [CrossRef]
- Völk, H. J., Aharonian, F. A., & reitschwerdt, D. 1996, SSRv, 75, 279 [NASA ADS]
All Figures
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13177f1.ps}
\end{figure}](/articles/aa/full_html/2009/47/aa13177-09/Timg53.png)
|
Figure 1:
Ratio of relativistic CRp to thermal energy densities (for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13177f2a.ps}\hspace*{3mm}
\includegraphics[width=6.85cm,clip]{13177f2b.ps}
\end{figure}](/articles/aa/full_html/2009/47/aa13177-09/Timg54.png)
|
Figure 2:
Radio ( left) and ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13177f3.ps}\vspace{3mm}
\end{figure}](/articles/aa/full_html/2009/47/aa13177-09/Timg78.png)
|
Figure 3:
Photon fluxes for >100 MeV are shown as a function of
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



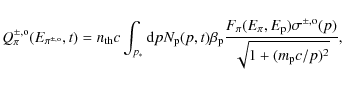
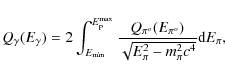
![\begin{displaymath}\Big\vert \left( {{ {\rm d} p }\over{{\rm d} t}}\right)_{\rm ...
...t( {{ B_{\mu\rm G} }\over{
3.2}} \right)^2 + (1+z)^4 \right] .
\end{displaymath}](/articles/aa/full_html/2009/47/aa13177-09/img38.png)