EDP Sciences
Home All issues Volume 508 / No 2 (December III 2009) A&A, 508 2 (2009) 1073-1083 Full HTML
Free Access
Issue
A&A
Volume 508, Number 2, December III 2009
Page(s) 1073 - 1083
Section Astronomical instrumentation
DOI https://doi.org/10.1051/0004-6361/200913016
Published online 04 November 2009

A&A 508, 1073-1083 (2009)

VEGA: Visible spEctroGraph and polArimeter for the CHARA array: principle and performance

D. Mourard1 - J. M. Clausse1 - A. Marcotto1 - K. Perraut2 - I. Tallon-Bosc3 - Ph. Bério1 - A. Blazit1 - D. Bonneau1 - S. Bosio1 - Y. Bresson1 - O. Chesneau1 - O. Delaa1 - F. Hénault1 - Y. Hughes1 - S. Lagarde1 - G. Merlin1 - A. Roussel1 - A. Spang1 - Ph. Stee1 - M. Tallon3 - P. Antonelli1 - R. Foy3 - P. Kervella4 - R. Petrov1 - E. Thiebaut3 - F. Vakili1 - H. McAlister5,6 - T. ten Brummelaar6 - J. Sturmann6 - L. Sturmann6 - N. Turner6 - C. Farrington6 - P. J. Goldfinger6

1 - Laboratoire Fizeau, OCA/UNS/CNRS UMR6525, Parc Valrose, 06108 Nice Cedex 2, France
2 - Laboratoire d'Astrophysique de Grenoble (LAOG), Université Joseph-Fourier, UMR 5571 CNRS, BP 53, 38041 Grenoble Cedex 09, France
3 - Université de Lyon, 69003 Lyon, France; Université Lyon 1, Observatoire de Lyon, 9 avenue Charles André, 69230 Saint Genis Laval, France; CNRS, UMR 5574, Centre de Recherche Astrophysique de Lyon; École Normale Supérieure, 69007 Lyon, France
4 - LESIA, Observatoire de Paris, CNRS UMR 8109, UPMC, Université Paris Diderot, 5 place Jules Janssen, 92195 Meudon, France
5 - Georgia State University, PO Box 3969, Atlanta GA 30302-3969, USA
6 - CHARA Array, Mount Wilson Observatory, 91023 Mount Wilson CA, USA

Received 30 July 2009 / Accepted 1 October 2009

Abstract
Context. Among optical stellar interferometers, the CHARA Array located at Mt Wilson in California offers the potential of very long baselines (up to 330 m) and the prospect of coupling multiple beam combiners. This paper presents the principle and the measured performance of VEGA, Visible spEctroGraph and polArimeter installed in September 2007 at the coherent focus of the array.
Aims. With 0.3 ms of arc of spatial resolution and up to 30 000 of spectral resolution, VEGA intends to measure fundamental parameters of stars, to study stellar activities and to image and analyze circumstellar environments. We describe the observing modes that have been implemented for this spectro-polarimeter and show actual performances measured on the sky during the first observing runs.
Methods. The astrophysical programs are described in relation to the observing modes of the instrument, the presentation of the spectrograph and of the interface table is shown and finally the data is presented. We discuss the perspectives of further development in the framework of the CHARA Array.
Results. We show that VEGA/CHARA is fully operational. The current limiting magnitude is nearly 7 but the results depend on the observing conditions (seeing, spectral resolution, etc.). We have validated the stability of the instrumental visibility at the level of 1 to 2% over half an hour and of the instrumental polarization for various declinations. Some examples of squared visibility and differential visibility are presented.
Conclusions. The spectro-polarimeter VEGA has been installed and successfully tested on CHARA. It will permit stellar physics studies at unprecedented spectral and spatial resolutions.

Key words: instrumentation: high angular resolution - instrumentation: interferometers

1 Introduction

The Center for High Angular Resolution Astronomy (CHARA) of the Georgia State University operates an optical interferometric array located at Mount Wilson Observatory (ten Brummelaar et al. 2005). It is formed by six telescopes placed in pairs on the arms of a Y-shaped configuration. It yields 15 baselines ranging from 34 to 331 m. The distribution of length and orientation of these baselines, as given in Table 1 of ten Brummelaar et al. (2005), allows a good coverage of the spatial frequency plane and permits the instrument to reach very high angular resolution. Operated in the near-infrared with CLASSIC (ten Brummelaar et al. 2005), FLUOR (Coudé du Foresto et al. 2003) or MIRC (Monnier et al. 2008) and in the visible with PAVO (Ireland et al. 2008) and VEGA, the CHARA array allows a maximum angular resolution ($\lambda/B$) of 1.3 and 0.3 ms of arc in the K and V bands respectively. The 1 m diameter alt-azimuth telescopes collect the stellar light and supply a compressed Coudé beam after 7 reflections. The light is transported into vacuum pipes to the central building housing 6 delay lines, beam management systems and the beam combination laboratory (BCL).

The VEGA instrument works in the visible domain [0.45 $\mu$m; 0.85 $\mu$m] and benefits from three spectral resolutions.

The medium (6000) and high (30 000) spectral resolutions are well suited to perform kinematic analysis of the interferometric signal, providing resolution of 60 and 10 km s-1 respectively. These spectral resolutions are best dedicated to the extraction of differential spectral information. Radiative winds and fast rotating photospheres of hot stars can be probed efficiently with the medium spectral resolution.

The low (1700) and medium resolutions are well suited to absolute visibility studies and are also well adapted for the study of binaries or multiple systems.

Another interesting possibility is the presence of a polarimeter that could be inserted into the beam. This gives new insight into many physical processes. Many science sources are linearly polarized, in particular at a small angular scale, and the interferometric polarized signal is a powerful probe of circumstellar scattering environments that contain ionized gas or dust (see for examples: Ireland et al. 2005; Chesneau et al. 2003; Elias et al. 2008) and of magnetic properties (Rousselet-Perraut et al. 2000,2004).

This paper presents the principle of VEGA and its performance. Section 2 presents the main astrophysical programs of VEGA. Section 3 presents the instrument: the spectrograph, the interface table and the general principles of the control of the instrument. In Sect. 4 we present the performances measured during the first observing runs and for the various observing modes. In Sect. 5, we discuss the perspectives of VEGA including its use with an external fringe tracking system and its performance in the context of the future implementation of adaptive optics on the CHARA telescopes.

2 Science rationale

The most promising science drivers of VEGA are within the fields of fundamental stellar parameters, stellar activity (rotation, surface structures, polarization, pulsation) and circumstellar environment studies.

2.1 Fundamental stellar parameters

Physical processes working in the stellar interiors as well as the evolution of stars are based on some fundamental measurements (mass, radius, luminosity or abundances). The effective temperature, the surface gravity and the mean density are useful parameters defined from these fundamental values. Some other physical parameters like mass loss rate, pulsation period, rotation period or magnetic fields are interesting for the study of peculiar evolutionary stages. A classical way to test stellar interior models is to compare the predicted and observed location of a star on theoretical evolutionary tracks in an H-R diagram. This can be done only for stars for which the mass, radius, luminosity and abundances are well known. To obtain significant results, an accuracy of 1%-2% for the mass and the radius and an error in the effective temperature better than 50 K is necessary. Then a precision of about 5%-10% luminosity is sufficient.

The combination of the visibility accuracy (Sect. 4.1), sensitivity (Sect. 4.4) and angular resolution of VEGA/CHARA gives access to a broad range of stellar properties. Based on the Hipparcos catalogue V band photometry, K band magnitudes from 2MASS, and (V,V-K) surface brightness color relations from Kervella et al. (2004), we computed the limb-darkened angular diameter of all stars brighter than mV=6.5. We then estimated the accuracy we can obtain on the measurement of their angular diameter with VEGA/CHARA, and selected only the stars for which the accuracy is better than 2%. Such an accuracy in the radius is sufficient to provide a strong constraint of their evolutionary state and internal structure, as shown e.g. by Creevey et al. (2007) and Kervella et al. (2008). The resulting sample shown in Fig. 1 contains more than 4000 stars, with spectral types ranging from B to late-M. On the main sequence, the faintness of the late-type dwarfs in the visible limits the observability to the mid-K spectral type. Giants can be observed down to late M type. The large sample available towards early spectral types opens a new window currently poorly covered by existing interferometric facilities that usually observe in the near-infrared domain.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{figures/13016fg1.eps} \end{figure} Figure 1:

Sample of stars brighter than mV=6.5 and for which VEGA can determine the angular diameter with a precision better than 2%.

Open with DEXTER

Long-baseline interferometers currently provide a new quasi-geometrical way to calibrate the Cepheid period-luminosity relation; indeed it is now possible to determine the distance of galactic Cepheids up to 1 kpc using the Interferometric Baade-Wesselink method (Davis et al. 2009; Kervella et al. 2004; Sasselov & Karovska 1994). Interferometric measurements lead to angular diameter estimations over the whole pulsation period, while the stellar radius variations can be obtained from the integration of the pulsation velocity curve deduced from line profiles by the so-called projection factor p.

According to the survey of Cepheid angular diameters by Moskalik & Gorynya (2005), thirty Cepheids are bright and large enough so that the variation of their angular diameter can be resolved with VEGA. Compared to interferometric observations in the infrared, the application of the interferometric Baade-Wesselink method will be more efficient using visible angular diameters from VEGA, as the complementary spectroscopic velocimetry is also obtained in the visible. The high spectral resolution will also make it possible to study the atmosphere dynamics in metallic lines (Nardetto et al. 2007), as well as the signatures of their envelopes in hydrogen lines (Kervella et al. 2009; Nardetto et al. 2008).

Although binaries and more generally multiple systems are complex objects both from observational and modeling points of view, their study can provide fundamental data to refine the theory of single-star formation and constrain possible scenarios of double star formation. The angular diameters can be combined with the distance to obtain the stellar radii. On the other hand, combining interferometric and spectroscopic orbits leads to direct determination of distances. Finally, combining all these data using classical methods allows the masses to be determined. Moreover, if the flux ratio can be determined as a function of the wavelength, the observed spectro-photometric flux distribution of individual stars can be combined with the angular diameter to derive the effective temperatures and luminosity of the components. The geometrical structure of more evolved and interacting binaries involves not only the stellar disks but also various components of circumstellar matter: the accretion disk, the scattering envelope and jet-like structures outside the orbital plane and also the gaseous stream between the components.

2.2 Stellar activity


Interferometry can contribute to the study of stellar activity by detecting and mapping star spots. A limited number of stars have features large enough to allow interferometric imaging. The gain in resolution by the use of visible light will substantially increase the number of targets. Sunspots are relatively small (1% of the solar radius), they are usually formed in the equatorial region, and tend to move to the largest latitude. It seems that no solar spots have been observed close to the poles. Doppler imaging has a number of drawbacks so the uniqueness and the accuracy of many images may be questionable. Combining interferometric data with the spectroscopic eliminates the north-south ambiguity in equator-on stars and allows the separation of spatial and spectral features (Lagarde 1994; Petrov et al. 1986).

VEGA is able to image $\delta$ Scuti and B stars and possibly red giants. It will also be possible to study photospheric lines and resolve the stellar diameter of stellar spots. For the observation of stellar spots and for asteroseismology there are significantly more spectral features below 0.6 $\mu$m than between 0.6 and 0.8 $\mu$m. This requires access to measurements with the blue camera on VEGA, i.e. at wavelengths close to H$\beta$.

2.3 Circumstellar environments


The envelopes of Be stars are a popular topic for visible interferometric observation. However, the mechanisms causing the mass loss and shaping the resulting circumstellar envelopes remain unclear, as well as the mechanisms of the formation and the disappearance of the circumstellar disk as a function of time. One important parameter is the typical size of the envelope for a given wavelength. One can try to understand the morphology and the kinematics of the envelope. Modeling by Stee & Bittar (2001) shows that images in narrow wavelength bins can allow extremely strong constraints on the envelope structure. However, such images have not been observed so far, because interferometers have not combined an imaging capability with adequate spectroscopic resolution. The size of the envelope, the ratio between rotation and expansion velocity and the velocity law (solid, Keplerian, ...) are typically the kind of data one can extract from differential visibility measurement on this class of star.

The closest Wolf-Rayet stars are typically found at 1 kpc and their ``pseudo-photosphere'' radii range from 3 to about 25 solar radii. Determining the extension of the lines formed in the wind of these stars would provide a direct constraint on the physical conditions in the wind. In the visible, the brightest and most extended lines are the carbon lines for WC stars and mostly helium lines for WN stars. Baselines ranging from 100 m to 300 m are mandatory to provide a detectable effect that could be measured accurately for the closest WR stars. SUSI (Davis et al. 2007) and the VLTI (Glindemann et al. 2004) have already carried out pioneering works in this field (Millour et al. 2007; North et al. 2007).

3 Principle of the VEGA instrument

3.1 The spectrograph

\begin{figure} \par\begin{tabular}{cc} \includegraphics[width=12cm]{figures/130... ...ncludegraphics[width=2cm]{figures/13016fg2b.eps}\\ \end{tabular} \end{figure} Figure 2:

Optical layout of the VEGA spectrograph from its entrance ( upper-centre) to the two outputs represented by the photon-counting detectors. In the right corner, we show a representation of the common coherent focus with speckles and fringes and the entrance slit.

Open with DEXTER

The spectrograph is designed to sample the visible band from 0.45 to 0.85 $\mu$m. It is equipped with two photon counting detectors looking at two different spectral bands. The main characteristics are summarized in Table 1. The simultaneous operation of the two detectors is only possible in high and medium spectral resolution. The optical design allows simultaneous recording of data, in medium spectral resolution, of the spectral region around H$\alpha $ with the red detector and around H$\beta$ with the blue detector. Observing in the blue requires good seeing conditions but increases by 30% the limit of spatial resolution of the instrument with respect to its operation around 700 nm.

Table 1:   Spectral resolution (R) and bandwidth ( $\Delta \lambda $) of the VEGA spectrograph, as well as the spectral separation between the two detectors.

The spectrograph, represented by the schematic layout of Fig. 2, has been described by Mourard et al. (2006). It is fed by four CHARA parallel beams vertically aligned so that fringes appear as horizontal lines at the coherent focus. The beams are 5 mm in diameter and two adjacent beams are separated by 10 mm (center to center). The first optics is an off-axis parabola (Par) forming the common coherent focus on the entrance slit (not represented). The width of the slit has been defined so that almost two speckles are selected in the horizontal direction. Vertically, the slit covers a field of 4 s of arc on the sky. Various slit widths are available, depending on the central wavelength and various heights are also available to allow a field reduction to 2 s of arc for the observations in polarized light (see below). After the slit, a set of two cylindrical mirrors (Cyl1, Cyl2) performs a vertical anamorphosis of a factor 12, in order to correctly sample the horizontal fringes without over sampling the width of the slit and hence the spectral resolution on the detector. Then, the VEGA spectrograph is very similar to a classical spectrograph with a collimator (Col), a grating (Gr) and a camera for reimaging the spectrum on the detector. The collimator is set so that the grating is lit by parallel beams and the pupil images are located on its surface. Due to the high magnification needed for the correct sampling of the fringes, the camera is made up of a set of two mirrors (primary R1 and B1 and secondary R2 and B2) as well as a tertiary flat mirror (R3 and B3) to feed the detector entrance plane. The optical layout at the output of the grating provides two separate spectral domains, as previously explained. The grating turret rotates to adjust the central wavelength of the bands. The three different gratings are interchangeable through a motorized device.

A polarimeter (Pol) can be placed just before the spectrograph grating as described by Rousselet-Perraut et al. (2006). It is composed of a Wollaston prism to separate two orthogonal polarization states and a movable quarter wave plate. A fixed quarter wave plate is placed after the Wollaston prism to transform the two linearly polarized output beams into two circularly polarized beams. This helps avoid unbalanced transmission by the grating. After being spectrally dispersed, the two beams carrying both the interference pattern and the polarization information are focused on the photon-counting detectors that contain two (x, $\lambda $) images, one per polarization state referred to as High and Low with respect to their position on the detector.

The main improvement in VEGA for CHARA has been the renovation of the two photon counting detectors, now equipped with a new generation of image intensifiers and with CMOS detectors allowing us to reach a quantum efficiency of between 20 and 30%, depending on the wavelength and on the detector. More details can be found in Blazit et al. (2008).

3.2 The interface table

The interface between the CHARA visible beams and the VEGA spectrograph is through different optical subsystems installed on the VEGA Interface Optical Table (IOT) (Fig. 3a).

The CHARA collimated beams are sent to the IOT through a periscopic device. The beams are then compressed by a factor of 4 in the beam compressors (BCP, Fig. 3b) and geometrically rearranged as needed for the spectrograph configuration. This optical configuration allows a correct conjugation of the four CHARA and VEGA beams, both in orientation and position, during the initial setting. During night operation, fine adjustments are possible to optimize the entrance flux on the spectrograph slit. For this purpose we use the M10 mirrors of the telescope Coudé train for the pupil and the tip/tilt set points for the image.

The differential position of the BCP allows an accurate equalization of the internal optical paths. Thanks to the CHARA reference source, we have been able to reduce the difference of optical path between VEGA and CHARA to less than 100 $\mu$m. The beam compressors also include the function of reimaging the CHARA pupils at their correct locations (Fig. 3c) to minimize the visibility losses introduced by Fresnel diffraction (Mekarnia & Gay 1989). In the VEGA configuration, an error of $\pm$150 mm on the pupil position for a visibility loss of 1% is acceptable. The output pupil of the CHARA Coudé train is formed behind the beam reducing telescope and its position depends on the location of the moving cart on the delay line rails. This position could vary between 15 and 26 m. The minimization of this bias is made through a correct choice of the fixed delays, of the position of the reference cart and of the distribution of the telescope's beams on VEGA pupils. A model of this pupil imaging has been developed and is presented in Appendix A.

The IOT includes various artificial sources (laser, spectral lamp, extended or point-like white light source, see Fig. 3d) that can be projected towards the spectrograph and simultaneously to CHARA for alignment and calibration purposes. Prior to arrival at the spectrograph, the four beams can be directed toward a reference device that records an image of the four image and pupil planes at the same time. This is used for alignment control as well as data processing.

The last important effect we have to consider is the correction of the differential longitudinal atmospheric dispersion. With the lowest spectral resolution and a maximum of about 88 m of differential air paths due to the operation of the delay line in the air, the chromatic optical path difference (OPD) inside a single spectral channel is less than 0.5 $\mu$m and thus the effect could be neglected. However, VEGA is operated with two detectors spectrally separated by 170 nm in the worst case. This could introduce up to 220 $\mu$m of chromatic OPD between the two detectors. Moreover, VEGA could be operated simultaneously with an infrared combiner and the chromatic OPD could reach a value of 0.5 mm. As a consequence, the use of the CHARA longitudinal dispersion compensators (Berger 2003) is necessary when observing simultaneously with an infrared instrument. These devices are installed on the optical beams, just after the beam reducing telescopes.

\begin{figure} \par\includegraphics[width=15.5cm,clip]{figures/13016fg3.eps} \end{figure} Figure 3:

General position of VEGA in the CHARA optical laboratory and details of the VEGA interface optical table  a). This table supports the beam compressors b) that help guide the exit pupils to their correct location  c). The calibration and alignment sources are located in the d) position.

Open with DEXTER

3.3 Control of the instrument

The VEGA control system conforms to the CHARA control system and can now observe via remote operation. A detailed description of this control system is presented in Clausse (2008).

The first step of the process is the software to prepare the observations. It aims at generating ASCII files containing the parameters of observing blocks. These blocks contain all the necessary information regarding the configuration of CHARA and VEGA. They serve as input for the observation control software.

The second step is the observation itself. After selecting a target, the operator checks the steps of the automatic sequence: initialization, control of pupil and image alignment, flux optimization, fringe tracking, data recording and calibration recording. Contextual information such as configuration, dark file, pupil and image file, operator comments, etc... are collected with the raw data. This entire operation can be made remotely from France with a limited network bandwidth.

While the observing software is based on a preferred setup (baseline, spectrograph capability, etc.), the data reduction pipeline is based on predefined sequences: V2 mode, $V{\rm e}^{{\rm i}\phi}$ differential visibility mode or SPIN mode for spectro-polarimetric interferometry. During the data reduction process, intermediate or final results are stored in files and linked to entries in the VEGA database.

3.4 Data reduction

3.4.1 V2 measurements

For the V2 measurements, we use the C1 estimator defined by Roddier & Lena (1984). The ratio of the high frequency energy by the low frequency energy of the averaged spectral density gives an estimation of V2. Indeed, in the VEGA configuration, the ratio D/r0 is smaller than in the GI2T measurements and thus our preferred estimator (Mourard et al. 1994) is now difficult to implement. This last estimator used a part of the low frequency peak, called the speckle peak, instead of using the whole low frequency peak. The main advantage of this estimator is that it is nearly independent of the atmospheric coherence time. So, rapid changes between target and calibrators are now mandatory to ensure stable seeing conditions and a reliable calibration of the instrumental visibility. Initial results are presented in Sect. 4.1.

3.4.2 Cross-spectrum method

This method aims at measuring differential interferometric quantities between two different spectral channels and consists of calculating W12, the averaged cross-spectrum between two bands of the interferogram:

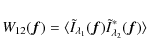
\begin{displaymath}W_{12}(\vec f)=\langle \tilde{I}_{\lambda_1}(\vec f)\tilde{I}_{\lambda_2}^{*}(\vec f)\rangle \end{displaymath} (1)

where $\tilde{I}_{\lambda_i}$ is the Fourier transform of the interferogram in the spectral band centered at $\lambda_i$. The complex differential visibility $V_{\rm diff}$ is the product of the complex visibility of each spectral band:

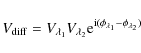
\begin{displaymath}V_{\rm diff}=V_{\lambda_1}V_{\lambda_2}{\rm e}^{{\rm i}(\phi_{\lambda_1}-\phi_{\lambda_2})} \end{displaymath} (2)

where $V_{\lambda_i}$ and $\phi_{\lambda_i}$ are the absolute visibility and the phase of the fringes in the spectral band centered at $\lambda_i$. The argument of  $V_{\rm diff}$ is the differential phase $\Delta\phi_{12}$. This phase is estimated by calculating the energy of the high frequency peaks in the real and imaginary parts of $W_{12}(\vec f)$. The absolute differential visibility is estimated, as in the power spectrum method, by calibrating the high frequency energy with the low frequency energy of $W_{12}(\vec f)$. This method has been extensively described in Berio et al. (1999) and Tatulli et al. (2007).

One advantage of this method is to correctly permit measurements at the spectral resolution of VEGA. Indeed, in the cross-spectrum method, the signal to noise ratio (SNR) is proportional to $\sqrt{N_1 N_2}$ where Ni is the number of photons in the spectral band centered at $\lambda_i$. So, choosing a large spectral band (called the reference channel) and a narrow spectral band (within the reference channel) allows an estimation of the absolute visibility of the narrow spectral band and the differential phase with a sufficient SNR. During the process, the estimation of $V_{\lambda_1}$ (for the reference channel) is obtained with the power spectrum method.

\begin{figure} \par\includegraphics[width=7.8cm,height=7.8cm,clip]{figures/13016fg4.eps} \end{figure} Figure 4:

$\left \vert V_{\rm diff}\right \vert$ vs. wavelength (in nm) for the observations of HD 172167 ( bottom) and the reference star HD 166014 ( top). Each data point corresponds to a spectral channel of 0.5 nm. For each visibility curve, we plot (dotted line) the fit of the corresponding model of the visibility curve (Eq. (3)). The plot in the middle of the figure represents the calibrated modulus of the differential visibility of HD 172167.

Open with DEXTER

As usual, this processing is applied for the science and reference stars in order to remove instrumental signatures. Figure 4 shows the results (in terms of absolute visibility) of this processing applied to the observations of HD 172167 and a reference star (HD 166014). We note that the $V_{\lambda_2}$ plots present a specific shape: the visibility is maximal (resp. minimal) when $\lambda_2$ is at the center (resp. edge) of the reference channel. This shape, that is mainly due to residual atmospheric piston, could be calibrated by observing a reference star in the same turbulent conditions. It is also possible to apply a simple model by adjusting the following function:

\begin{displaymath}V_{\lambda_2}\propto \exp{\left[-2\pi^2 \sigma_{\rm p}^2 \left(\frac{1}{\lambda_1}-\frac{1}{\lambda_2}\right)^2\right]} \end{displaymath} (3)

where $\sigma_{\rm p}^2$ is the variance of the atmospheric piston during the observation time. The quality of this model is illustrated in Fig. 4. We found $\sigma_{\rm p}=12.2\pm0.9~\mu$m and $\sigma_{\rm p}=12.0\pm0.1~\mu$m for HD 166014 and HD 172167 respectively. This modeling is useful when the turbulent conditions change between the observations of the science and reference stars. We note that the calibrated visibility modulus shows no systematic variation with wavelength.

4 Measured performance

4.1 Instrumental visibility

During the night of July 28th 2008, we observed two calibrators and the bright stars Vega and Deneb with the S1S2 baseline to validate the calibrated V2 measurements with the instrument. The calibrators were selected with the SearchCal (Bonneau et al. 2006) software provided by the JMMC. We used the medium spectral resolution and recorded data on both detectors. The red (resp. blue) channel is centered on 700 nm (resp. 555) and the spectral bandwidth is 20 nm wide. The log of observations is presented in Table 2.

Table 2:   Observation log for the night of July 28th 2008.

\begin{figure} \par\includegraphics[angle=-90,width=7.5cm,clip]{figures/13016fg5.ps} \end{figure} Figure 5:

Instrumental squared visibility measured with VEGA in the red channel ( upper panel) and blue channel ( lower panel). The log of observations is presented in Table 2. The filled circles (starting at UT 06h47 and 08h18) represent the measurements of HD 166014 and the triangles (starting at UT 08h07 and 08h32) represent the points of HD 176437. Each data point represents a measurement averaged over 75 s.

Open with DEXTER

We used the two calibrators HD 166014 and HD 176437 to estimate the visibility and stability of the instrument during the observation. Their UD angular diameters have been estimated at 600 nm by converting the existing limb darkened diameters (van Belle et al. 2008) for HD 166014 and (Zorec et al. 2009) for HD 176437. The results are presented in Fig. 5. Each data point represents the instrumental squared visibility averaged over 75 s.

While we can identify a small change over about two hours, one can see that over a short period of time (30 mn), the instrument's visibility is stable at about 2% around a mean value of $\langle V^2_{\rm inst}\rangle=0.54\pm0.02$ for the red channel (700 nm) and at 1.5% around a mean value of $\langle V^2_{\rm inst}\rangle=0.40\pm0.02$ for the blue channel (555 nm). This first result validates the stability of the VEGA measurements and allows us to accurately measure angular diameters. It is important to point out that the value of the instrumental visibility depends on parameters such as the seeing, the central wavelength and the bandwidth (see for example Berio et al. 1997).

The next step was to check the reliability of our measurements. We used the raw V2 measurements on Vega and Deneb and the previous estimation of the instrumental visibility to determine their angular diameters.

For Vega (HD 172167) we found $\theta_{\rm UD-700~nm}=2.90\pm0.03$ mas and $\theta_{\rm UD-555~nm}=3.08\pm0.03$ mas, which matches well with the results determined by Mark III (Mozurkewich et al. 2003): $\theta_{\rm UD-800~nm}=3.149\pm0.31$ and $\theta_{\rm UD-500~nm}=2.996\pm0.047$.

For Deneb (HD 197345) we found $\theta_{\rm UD-700~nm}=2.41\pm0.03$. The value determined by Aufdenberg et al. (2002) is $2.363\pm0.002$, which shows again that our measurements agree with previous determinations, taking into account the difference of observing configurations.

4.2 Instrumental polarization

Several theoretical studies have been conducted to describe the effects of instrumental polarization on the interferometric observables (Tinbergen 2003; Rousselet-Perraut et al. 1996; Le Bouquin et al. 2008; Elias et al. 2008). These works clearly show that instrumental polarization can dramatically reduce the interferometric performance since the various reflections on the mirrors of the Coudé trains shift the different interferometric patterns with respect to each other. The more symmetric the array (regarding incidence and coatings), the smaller this degradation due to polarization.

Table 3:  Raw squared visibility in natural light (Col. 4) and in polarized light (Cols. 5 and 6) computed on a 6.6 nm-wide spectral channel centered on $\lambda $ (Col. 3).

In the CHARA array the Coudé trains have been designed to be symmetric. However, having in mind to study the polarization of astrophysical objects with VEGA, we decided to accurately calibrate the instrumental polarization for each baseline. We characterized the instrumental polarization on the baseline S1S2 by observing three calibrators of different declinations during a whole night in July 2008: HD 166014, HD 184006 and HD 195725. We alternated between measurements in the two polarizations and natural light. For each calibrator, we recorded more than 15 files spread along 5 h around the transit. We computed the squared visibility for each file at two different wavelengths to look for differences between the two polarized measurements, and between polarized and natural measurements. The absolute value of these measurements is not significant since we are just interested in relative behaviors. We discovered later that HD 195725 is known to be a spectroscopic binary, which may explain the difference of raw measurements on this star. No significant trend appears at this shortest baseline (Table 3), which is in agreement with the symmetrical design of the Coudé trains of the CHARA array.

4.3 Differential visibility

Differential visibility means the variation of the modulus and phase of the visibility as a function of wavelength. It is a very powerful tool to study, inside spectral lines, the kinematics of the stellar environment around hot stars. Spectrally filtering a source inside a line allows us to isolate iso-velocity regions thanks to the Doppler effect. A spectral bandwidth of 0.2 nm isolates velocity regions within $\pm$46 km s-1 at 0.65 $\mu$m. For each spectral channel, one can determine the size of the corresponding iso-velocity region by measuring the modulus of the visibility. Moreover, the phase of the visibility across a line gives information related to the position of the photocenter of the iso-velocity region. Fringe displacement measured as a phase signal $\phi$ corresponds to a fraction ($\phi/2\pi$) of the fringe spacing ($\lambda/B$, with B the projected baseline) and can be translated into a spatial displacement on the sky along the direction of the projected baseline.

To illustrate the differential visibility mode of VEGA, we present some results obtained, in medium spectral resolution, for the Be star $\psi $ Per (HD 22192) during the night of October 7 2008, using the S1S2 baseline. The observation log is presented in Table 4 and the results are presented Fig. 6.

Table 4:   Observation log for the Be star $\psi $ Per (HD 22192) and its calibrator (Col. 1). Apart from the baseline information (Cols. 3 and 4).

Each measurement is made over a narrow spectral channel of 0.2 nm. $\psi $ Per exhibits a strong variation of the visibility in the H$\alpha $ line as well as a clear differential phase signal of the differential phase indicating the presence of a rotating disk (Stee 1996). The residual noise in the phase measurements ($3^\circ$) corresponds to an astrometric accuracy of $\frac{3^\circ}{360^\circ}\frac{\lambda}{B}$ i.e. 35 microseconds of arc for this observation. In the continuum the standard deviation of the visibility is 0.05. This observation is part of a program studying the kinematics of a set of Be stars and will be presented in a future paper (Delaa et al. in preparation).

\begin{figure} \par\includegraphics[width=9cm,height=4cm,clip]{figures/13016fg6a... ...\includegraphics[width=9cm,height=4cm,clip]{figures/13016fg6b.eps} \end{figure} Figure 6:

Calibrated visibility (above) and differential phase in degree (below) of $\psi $ Per around the H$\alpha $ line as obtained with the S1S2 baseline. Each data point corresponds to a spectral channel of 0.2 nm.

Open with DEXTER

4.4 Limiting magnitudes

When considering interferometry in the speckle regime, we usually consider two domains for the signal to noise ratio, depending on the number of photons per speckle and per single exposure. If this number is larger than 1, then the signal to noise ratio increases as the square root of the number of photons, whereas if it is smaller than 1, the signal to noise ratio increases with the number of photons (Roddier 1988). As a consequence, we define the limiting magnitude as the magnitude giving a signal to noise ratio of 10 for an unresolved source (V2=1). It is clear however that the signal to noise ratio could reach high values at this limit, since one can integrate a large number of single exposures containing a large number of speckles. This high signal to noise ratio is usually used in our case for measurements in narrow spectral channels. In the differential regime, it has been shown in Petrov et al. (1986) that the signal to noise ratio is the geometrical mean of the signal to noise ratio in the two channels.

\begin{figure} \par\includegraphics[width=7.5cm,clip]{figures/13016fg7.ps} \end{figure} Figure 7:

VEGA limiting magnitude for a 10 s integration time. The dotted line is for the high spectral resolution mode ( $\Delta \lambda =6$ nm), the dash-dotted one for the medium resolution mode ( $\Delta\lambda=40~$nm) and the solid line for the low resolution mode limited to a band of $\Delta \lambda =50$ nm to correctly take into account the limited spectral coherence of the atmosphere. The central wavelength used for the simulation is 650 nm.

Open with DEXTER

In this paper we have adapted the parameters of the simulation to correctly reproduce the observations during the VEGA observing run in 2008. The results of the simulation are shown in Fig. 7. For the low resolution mode, we limit the spectral bandwidth to the typical value of the spectral coherence of the atmosphere. In order to correctly reproduce the signal to noise ratio measurement in the various conditions of spectral resolution, magnitude, seeing and visibility, we adjust the global transmission in our numerical simulation. If we assume an instrumental squared visibility of 0.55, as previously measured (for a spectral band of 20 nm around 700 nm and a r0 value of 10 cm), the simulation agrees with the measurements if one assumes a raw global transmission of 0.3%. This estimation has to be corrected for the effective operating cycle of the detectors, i.e. 40 frames per second, each frame being exposed during 15 ms. Thus, the global transmission is estimated to be 0.5% distributed roughly with 5% for CHARA, 30% for VEGA and 30% for the quantum efficiency of the detector. We indicate in Table 5 the typical limiting magnitudes as well as the best performances obtained in the different observing modes.

Table 5:   Estimation of typical limiting magnitude as a function of the different spectral resolution modes.

For VEGA observations carried out in the visible with baselines as long as 330 m, high visibility (typically V2 > 0.80) can only be obtained for calibrators that have an angular diameter of less than 0.15 mas. Taking into account the limiting magnitude reached with VEGA ( $V_{\rm mag} \leq 7$), such small diameters can only be obtained for early type stars (spectral type A or B) fainter than the magV = 5. The majority of the observations are then carried out using partially resolved calibrators for which the estimation of a precise value of the angular diameter is crucial to reach the ultimate precision in the absolute calibration process. In this case, the statistic value of the angular diameter usually computed using a visual brightness method based on calibrated magnitude-color index relations is not sufficient. It is more suitable to use a value of the intrinsic angular diameter given by a more sophisticated method using spectro-photometric data available for the object (Zorec et al. 2009; Cohen et al. 1999).

5 Conclusions and perspectives

\begin{figure} \par\includegraphics[width=17cm,clip]{figures/13016fg8.eps} \end{figure} Figure 8:

Left. S2W2W1 telescope triplet for the preliminary tests of the VEGA 3-telescopes mode. Middle. Spectral density containing the three high-frequency peaks of the fringes recorded with the three baselines (S2W2, W2W1, S2W1). Right. Preliminary data processing: the instrumental visibility is a free parameter adjusted during the processing as well as the angular diameter of the source.

Open with DEXTER

5.1 Summary of results

We have shown in this paper that VEGA is ready for scientific operation. The various instrumental modes have been shown to be successful.

For the V2 measurements we have shown that a stable instrumental visibility can be obtained and that the bias on the visibility measurements is correctly controlled so that angular diameters can be measured reliably. It is clear however that the observing strategy for accurate angular diameter determination relies on rapid changes between the target and calibrator. With the long baselines of CHARA, it is difficult to find unresolved and bright calibrators and to avoid calibration errors, it is thus necessary to observe as many calibrators as possible. As a consequence, for an observation with two calibrators and a target, we use the sequence: C1-C2-Tar-C2-C1-Tar-C1-C2. Each block being almost 5 min, a calibrated measurement typically requires 40 min of observation.

The differential visibility mode has been commissioned and tested and differential phase measurements are possible at the level of a few degrees. This will provide useful information on kinematics in circumstellar environment as presented in Sect. 2.

The instrumental polarization of CHARA and VEGA has been quantified on three different stars of declination ranging from $29^\circ$ to $63^\circ$ on the S1S2 baseline. Measurements of Stokes visibility on stellar sources will be presented in a subsequent paper.

5.2 The 3T/4T mode

In October 2008, we successfully commissioned the three-telescope configuration on two different triplets of telescopes (S2W2W1 and S1S2W2, see Table 6). We servo-controlled the fringe positions on the two smaller internal baselines (for instance W2W1 and W2S2 in Fig. 8, middle) with the VEGA delay tracker. The third fringe system (3) on S2W1 appears at higher frequency due to the larger output pupil distance. We recorded preliminary observations on calibrator HD 3360 and were able to compute the raw squared visibility on each baseline (Fig. 8-right). These measurements are consistent with the angular diameter of HD 3360 estimated as 0.31 mas. Dedicated observing runs are foreseen in 2009 to fully validate this three-telescope configuration by obtaining calibrated visibilities and phase closures on well-known stars. An attempt to use four telescopes is planned for the future.

Table 6:   Length and orientation of the different baselines of the triplets S2W2W1 and S1S2W2 on HD 3360.

Operating VEGA on CHARA in the three- or four-telescope mode will automatically lead to observations with baselines from 200 to 330 m. According to the current limiting magnitude of VEGA and with respect to the high spatial resolution introduced by these long baselines, scientific programs have to be checked carefully so that good calibrators can be found and that the (u, v) coverage is well adapted to the science goals.

5.3 Perspectives

Infrared and visible measurements are complementary for correct and complete radiative transfer modeling. On one hand, many of the astrophysical processes involved in stellar physics and investigated by interferometry have stronger signatures at visible wavelengths. On the other hand, new physical processes will be investigated, broadening the field of astrophysical domains. CHARA is well adapted to coordinate programs between VEGA and infrared combiners. This can be done either by sharing the same telescopes on both combiners or by obtaining simultaneous data on both combiners and on different baselines. Specific observational strategies will be developed in the future to achieve this goal.

\begin{figure} \par\includegraphics[width=8cm,clip]{figures/13016fg9.eps} \end{figure} Figure 9:

Estimation of signal to noise ratio with VEGA for an integration time of 1000 s, the use of an external group delay tracking and with telescopes equipped with adaptive optics systems as described in the text. The dotted line is for the high spectral resolution mode ( $\Delta \lambda =6$ nm), the dash-dotted one for the medium resolution mode ( $\Delta \lambda =40$ nm) and the solid line for the low resolution mode limited to a band of $\Delta \lambda =50$ nm to correctly take into account the limited spectral coherence of the atmosphere. The central wavelength used for the simulation is 650 nm.

Open with DEXTER

Apart from the scientific compatibility of visible and infrared, it should also be noted that an infrared combiner or an infrared fringe tracker like CHAMP (Berger et al. 2008) that is able to correct for the group delay variation will greatly aid the operation of VEGA. Indeed, it will no longer be necessary for VEGA to perform its own group delay tracking and we can calculate limiting magnitude for longer integration times. Considering a maximum integration time of 1000 s, in order to avoid the spatial frequency smearing, one can conclude that this observing mode will provide an increase of 2.5 mag on the simulation presented in Fig. 7 and in Table 5.

Finally, it is foreseen that CHARA will equip all telescopes with an adaptive optics system. We present in Fig. 9 an estimation of limiting magnitude with AO systems providing a Strehl ratio of 0.4 at 650 nm for magnitude less than 6 and decreasing linearly to 0 for V=10. We also assume that 50% of the visible light will be used for the wavefront sensing. We consider the use of an external fringe tracking system permitting an integration of 1000 s. Depending on the spectral resolution, this will lead to a limiting magnitude between 8 and 9.5 for a signal to noise ratio of 10.

All these future developments on CHARA will allow various improvements for the VEGA scientific programs. This will help in finding good calibrators and so permit a better accuracy and precision of the V2 measurements. This will also allow better access to the longest baselines of CHARA and so, as described in Sect. 5.2, to a better use of the 3T/4T capabilities of VEGA. Finally the other observing modes of VEGA (differential and polarimetric analysis) will be possible for a larger number of objects and will give access to new classes of stars.

Acknowledgements
VEGA is a collaboration between CHARA and Laboratoire Fizeau (OCA/UNS/CNRS-Nice), LAOG in Grenoble, CRAL in Lyon and LESIA in Paris-Meudon. It has been supported by French programs for stellar physics and high angular resolution PNPS and ASHRA, by INSU-CNRS and by the Région PACA. The project has benefited from the strong support of the OCA and CHARA technical teams. The CHARA Array is operated with support from the National Science Foundation and Georgia State University. This research has made use of the SearchCal service of the Jean-Marie Mariotti Center[*], and of CDS Astronomical Databases SIMBAD and VIZIER. We want also to warmly thank Steve Ridgway for his continuous support in the VEGA development and Sallie Cruise for her careful reading of the manuscript.

Appendix A: CHARA pupils transfer to the VEGA spectrograph

In order to minimize the visibility losses introduced by Fresnel diffraction (Mekarnia & Gay 1989), the CHARA output pupils have to be reimaged near the location of the VEGA input pupil. The minimization of this bias is made through a correct choice of fixed delays (POP), position of the reference cart and distribution of the telescope's beams on VEGA pupils. We present below the main characteristics of this optimization.

\begin{figure} \par\includegraphics[width=15.5cm,clip]{figures/13016fgA1.eps} \end{figure} Figure A.1:

Definition of the successive pupil planes in the CHARA Coudé trains. P is the primary mirror, P' is the image of P formed by the secondary mirror of the telescope, P'' is the image of P' formed by the cat's eye of the delay line and P''' is the image of P'' formed by the beam reducing telescope (BRT). Y defines the position of pupil P''' after the BRT. Depending on the telescope, the fixed delay (POP) and the position X of the cart. Y (see Table A.1) is given with respect to the vertex of the BRT secondary mirror.

Open with DEXTER

Table A.1:   Position of the CHARA output pupil.

Table A.2:   Optical paths in meters introduced by the beam selector on the Chara output pupil image.

The entrance pupil plane P is defined by the primary mirror of the telescope. P' is the image of P formed by the secondary mirror of the telescope, P'' is the image of P' formed by the cat's eye of the delay line and P''' is the image of P'' formed by the beam reducing telescope (BRT). Y defines the pupil position of P''' after the BRT. This depends on the telescope, the POP and the position X of the cart. Y (see Table A.1) is given with respect to the vertex of the BRT secondary mirror.

After the BRT, the telescope beam has to be affected by one of the 6 beams that feed the instrument. This is achieved through the configuration of the beam selector. This choice introduces additional optical paths that modify the distance of the output pupil. The values for the different telescopes and the different beams are given in Table A.2.

The CHARA output pupil P''' is then reimaged by the VEGA beam compressor (BCP). This is done through the three reflections on the three mirrors of the BCP and the output pupil is then formed near the position of the entrance pupil of the VEGA spectrograph. The correct choice of POP, beam and position of the reference cart are critical for correct pupil transfer. This is important to minimize the visibility losses but also to avoid vignetting effects.

As an illustration, the following configuration is used: S1-POP1 on beam 1 and S2-POP1 on beam 2, with the delay line cart located around 20 m. Pupil S1 is then formed at a distance of 261 mm from the correct location, whereas pupil S2 is formed at a distance of 200 mm. With S1-POP4 on beam 2 and S2-POP5 on beam 1, then pupil S1 is at 17 mm and pupil S2 is at 51 mm. This second configuration is the correct setting to minimize the visibility losses.

The VEGA observation preparation software includes the correct calculation of the pupil reimaging so that the configuration can be optimized. In the two telescope configuration of VEGA, the optimization of the pupil position is always possible and compatible with the constraint on the sky coverage introduced by the POP choices. Nevertheless, this pupil optimization becomes more constrained as soon as 3 or 4 telescopes are used simultaneously and the observability of some sources can become reduced.

References

  • Aufdenberg, J. P., Hauschildt, P. H., Baron, E., et al. 2002, ApJ, 570, 344 [NASA ADS] [CrossRef]
  • Berger, D. H. 2003, Ph.D. Thesis, AA (Georgia State University)
  • Berger, D. H., Monnier, J. D., Millan-Gabet, R., et al. 2008, in SPIE Conf. Ser., 7013
  • Berio, P., Mourard, D., Bonneau, D., et al. 1999, J. Opt. Soc. Am. A, 16, 872 [NASA ADS] [CrossRef]
  • Berio, P., Mourard, D., Vakili, F., Borgnino, J., & Ziad, A. 1997, J. Opt. Soc. Am. A, 14, 114 [NASA ADS] [CrossRef]
  • Blazit, A., Rondeau, X., Thiébaut, E., et al. 2008, Appl. Opt., 47, 1141 [NASA ADS] [CrossRef]
  • Bonneau, D., Clausse, J.-M., Delfosse, X., et al. 2006, A&A, 456, 789 [NASA ADS] [EDP Sciences] [CrossRef]
  • Chesneau, O., Wolf, S., & Domiciano de Souza, A. 2003, A&A, 410, 375 [NASA ADS] [EDP Sciences] [CrossRef]
  • Clausse, J.-M. 2008, in SPIE Conf. Ser., 7019
  • Cohen, M., Walker, R. G., Carter, B., et al. 1999, AJ, 117, 1864 [NASA ADS] [CrossRef]
  • Coudé du Foresto, V., Borde, P. J., Merand, A., et al. 2003, in SPIE Conf. Ser. 4838, ed. W. A. Traub, 280
  • Creevey, O. L., Monteiro, M. J. P. F. G., Metcalfe, T. S., et al. 2007, ApJ, 659, 616 [NASA ADS] [CrossRef]
  • Davis, J., Ireland, M. J., Chow, J., et al. 2007, PASA, 24, 138 [NASA ADS]
  • Davis, J., Jacob, A. P., Robertson, J. G., et al. 2009, MNRAS, 394, 1620 [NASA ADS] [CrossRef]
  • Elias, II, N. M., Jones, C. E., Schmitt, H. R., et al. 2008, ArXiv e-prints
  • Glindemann, A., Albertsen, M., Andolfato, L., et al. 2004, in SPIE Conf. Ser. 5491, ed. W. A. Traub, 447
  • Ireland, M. J., Mérand, A., ten Brummelaar, T. A., et al. 2008, in SPIE Conf. Ser., 7013
  • Ireland, M. J., Tuthill, P. G., Davis, J., & Tango, W. 2005, MNRAS, 361, 337 [NASA ADS] [CrossRef]
  • Kervella, P., Mérand, A., & Gallenne, A. 2009, A&A, 498, 425 [NASA ADS] [EDP Sciences] [CrossRef]
  • Kervella, P., Mérand, A., Pichon, B., et al. 2008, A&A, 488, 667 [NASA ADS] [EDP Sciences] [CrossRef]
  • Kervella, P., Thévenin, F., Di Folco, E., & Ségransan, D. 2004, A&A, 426, 297 [NASA ADS] [EDP Sciences] [CrossRef]
  • Lagarde, S. 1994, Ph.D. Thesis, University of Nice-Sophia Antipolis
  • Le Bouquin, J.-B., Rousselet-Perraut, K., Berger, J.-P., et al. 2008, in SPIE Conf. Ser., 7013
  • Mekarnia, D., & Gay, J. 1989, J. Opt., 20, 131 [NASA ADS] [CrossRef]
  • Millour, F., Petrov, R. G., Chesneau, O., et al. 2007, A&A, 464, 107 [NASA ADS] [EDP Sciences] [CrossRef]
  • Monnier, J. D., Zhao, M., Pedretti, E., et al. 2008, in SPIE Conf. Ser., 7013
  • Moskalik, P., & Gorynya, N. A. 2005, Acta Astron., 55, 247 [NASA ADS]
  • Mourard, D., Blazit, A., Bonneau, D., et al. 2006, in SPIE Conf. Ser., 6268
  • Mourard, D., Tallon-Bosc, I., Rigal, F., et al. 1994, A&A, 288, 675 [NASA ADS]
  • Mozurkewich, D., Armstrong, J. T., Hindsley, R. B., et al. 2003, AJ, 126, 2502 [NASA ADS] [CrossRef]
  • Nardetto, N., Groh, J. H., Kraus, S., Millour, F., & Gillet, D. 2008, A&A, 489, 1263 [NASA ADS] [EDP Sciences] [CrossRef]
  • Nardetto, N., Mourard, D., Mathias, P., Fokin, A., & Gillet, D. 2007, A&A, 471, 661 [NASA ADS] [EDP Sciences] [CrossRef]
  • North, J. R., Tuthill, P. G., Tango, W. J., & Davis, J. 2007, MNRAS, 377, 415 [NASA ADS] [CrossRef]
  • Petrov, R., Roddier, F., & Aime, C. 1986, J. Opt. Soc. Am. A, 3, 634 [NASA ADS] [CrossRef]
  • Roddier, F. 1988, Phys. Rep., 170, 97 [NASA ADS] [CrossRef]
  • Roddier, F., & Lena, P. 1984, J. Opt., 15, 171 [NASA ADS] [CrossRef]
  • Rousselet-Perraut, K., Chesneau, O., Berio, P., & Vakili, F. 2000, A&A, 354, 595 [NASA ADS]
  • Rousselet-Perraut, K., Le Bouquin, J. B., Mourard, D., et al. 2006, A&A, 451, 1133 [NASA ADS] [EDP Sciences] [CrossRef]
  • Rousselet-Perraut, K., Stehlé, C., Lanz, T., et al. 2004, A&A, 422, 193 [NASA ADS] [EDP Sciences] [CrossRef]
  • Rousselet-Perraut, K., Vakili, F., & Mourard, D. 1996, Opt. Engineering, 35, 2943 [NASA ADS] [CrossRef]
  • Sasselov, D., & Karovska, M. 1994, ApJ, 432, 367 [NASA ADS] [CrossRef]
  • Stee, P. 1996, A&A, 311, 945 [NASA ADS]
  • Stee, P., & Bittar, J. 2001, A&A, 367, 532 [NASA ADS] [EDP Sciences] [CrossRef]
  • Tatulli, E., Millour, F., Chelli, A., et al. 2007, A&A, 464, 29 [NASA ADS] [EDP Sciences] [CrossRef]
  • ten Brummelaar, T. A., McAlister, H. A., Ridgway, S. T., et al. 2005, ApJ, 628, 453 [NASA ADS] [CrossRef]
  • Tinbergen, J. 2003, in SPIE Conf. Ser. 4843, ed. S. Fineschi, 122
  • van Belle, G. T., van Belle, G., Creech-Eakman, M. J., et al. 2008, ApJS, 176, 276 [NASA ADS] [CrossRef]
  • Zorec, J., Cidale, L., Arias, M. L., et al. 2009, ArXiv e-prints

Footnotes

... Center[*]
Available at http://www.jmmc.fr/searchcal.

All Tables

Table 1:   Spectral resolution (R) and bandwidth ( $\Delta \lambda $) of the VEGA spectrograph, as well as the spectral separation between the two detectors.

Table 2:   Observation log for the night of July 28th 2008.

Table 3:   Raw squared visibility in natural light (Col. 4) and in polarized light (Cols. 5 and 6) computed on a 6.6 nm-wide spectral channel centered on $\lambda $ (Col. 3).

Table 4:   Observation log for the Be star $\psi $ Per (HD 22192) and its calibrator (Col. 1). Apart from the baseline information (Cols. 3 and 4).

Table 5:   Estimation of typical limiting magnitude as a function of the different spectral resolution modes.

Table 6:   Length and orientation of the different baselines of the triplets S2W2W1 and S1S2W2 on HD 3360.

Table A.1:   Position of the CHARA output pupil.

Table A.2:   Optical paths in meters introduced by the beam selector on the Chara output pupil image.

All Figures

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{figures/13016fg1.eps} \end{figure} Figure 1:

Sample of stars brighter than mV=6.5 and for which VEGA can determine the angular diameter with a precision better than 2%.

Open with DEXTER
In the text

  \begin{figure} \par\begin{tabular}{cc} \includegraphics[width=12cm]{figures/130... ...ncludegraphics[width=2cm]{figures/13016fg2b.eps}\\ \end{tabular} \end{figure} Figure 2:

Optical layout of the VEGA spectrograph from its entrance ( upper-centre) to the two outputs represented by the photon-counting detectors. In the right corner, we show a representation of the common coherent focus with speckles and fringes and the entrance slit.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15.5cm,clip]{figures/13016fg3.eps} \end{figure} Figure 3:

General position of VEGA in the CHARA optical laboratory and details of the VEGA interface optical table  a). This table supports the beam compressors b) that help guide the exit pupils to their correct location  c). The calibration and alignment sources are located in the d) position.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm,height=7.8cm,clip]{figures/13016fg4.eps} \end{figure} Figure 4:

$\left \vert V_{\rm diff}\right \vert$ vs. wavelength (in nm) for the observations of HD 172167 ( bottom) and the reference star HD 166014 ( top). Each data point corresponds to a spectral channel of 0.5 nm. For each visibility curve, we plot (dotted line) the fit of the corresponding model of the visibility curve (Eq. (3)). The plot in the middle of the figure represents the calibrated modulus of the differential visibility of HD 172167.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=7.5cm,clip]{figures/13016fg5.ps} \end{figure} Figure 5:

Instrumental squared visibility measured with VEGA in the red channel ( upper panel) and blue channel ( lower panel). The log of observations is presented in Table 2. The filled circles (starting at UT 06h47 and 08h18) represent the measurements of HD 166014 and the triangles (starting at UT 08h07 and 08h32) represent the points of HD 176437. Each data point represents a measurement averaged over 75 s.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,height=4cm,clip]{figures/13016fg6a... ...\includegraphics[width=9cm,height=4cm,clip]{figures/13016fg6b.eps} \end{figure} Figure 6:

Calibrated visibility (above) and differential phase in degree (below) of $\psi $ Per around the H$\alpha $ line as obtained with the S1S2 baseline. Each data point corresponds to a spectral channel of 0.2 nm.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{figures/13016fg7.ps} \end{figure} Figure 7:

VEGA limiting magnitude for a 10 s integration time. The dotted line is for the high spectral resolution mode ( $\Delta \lambda =6$ nm), the dash-dotted one for the medium resolution mode ( $\Delta\lambda=40~$nm) and the solid line for the low resolution mode limited to a band of $\Delta \lambda =50$ nm to correctly take into account the limited spectral coherence of the atmosphere. The central wavelength used for the simulation is 650 nm.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm,clip]{figures/13016fg8.eps} \end{figure} Figure 8:

Left. S2W2W1 telescope triplet for the preliminary tests of the VEGA 3-telescopes mode. Middle. Spectral density containing the three high-frequency peaks of the fringes recorded with the three baselines (S2W2, W2W1, S2W1). Right. Preliminary data processing: the instrumental visibility is a free parameter adjusted during the processing as well as the angular diameter of the source.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{figures/13016fg9.eps} \end{figure} Figure 9:

Estimation of signal to noise ratio with VEGA for an integration time of 1000 s, the use of an external group delay tracking and with telescopes equipped with adaptive optics systems as described in the text. The dotted line is for the high spectral resolution mode ( $\Delta \lambda =6$ nm), the dash-dotted one for the medium resolution mode ( $\Delta \lambda =40$ nm) and the solid line for the low resolution mode limited to a band of $\Delta \lambda =50$ nm to correctly take into account the limited spectral coherence of the atmosphere. The central wavelength used for the simulation is 650 nm.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15.5cm,clip]{figures/13016fgA1.eps} \end{figure} Figure A.1:

Definition of the successive pupil planes in the CHARA Coudé trains. P is the primary mirror, P' is the image of P formed by the secondary mirror of the telescope, P'' is the image of P' formed by the cat's eye of the delay line and P''' is the image of P'' formed by the beam reducing telescope (BRT). Y defines the position of pupil P''' after the BRT. Depending on the telescope, the fixed delay (POP) and the position X of the cart. Y (see Table A.1) is given with respect to the vertex of the BRT secondary mirror.

Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.