| Issue |
A&A
Volume 508, Number 2, December III 2009
|
|
|---|---|---|
| Page(s) | 695 - 706 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200913003 | |
| Published online | 27 October 2009 | |
A&A 508, 695-706 (2009)
Intrinsic iron spread and a new
metallicity scale for globular
clusters![[*]](/icons/foot_motif.png)
E. Carretta1 - A. Bragaglia1 - R. Gratton2 - V. D'Orazi2 - S. Lucatello2,3
1 - INAF-Osservatorio Astronomico di Bologna, via Ranzani 1, 40127
Bologna, Italy
2 - INAF-Osservatorio Astronomico di Padova, Vicolo dell'Osservatorio
5, 35122 Padova, Italy
3 - Excellence Cluster Universe, Technische Universität München,
Boltzmannstr. 2, 85748 Garching, Germany
Received 28 July 2009 / Accepted 1 October 2009
Abstract
We have collected spectra of about 2000 red giant branch (RGB) stars in
19 Galactic globular clusters (GC) using FLAMES@VLT (about 100 stars
with GIRAFFE and about 10 with UVES, respectively, in each GC). These
observations provide an unprecedented, precise, and homogeneous
data-set of Fe abundances in GCs. We use it to study the cosmic scatter
of iron and find that, as far as Fe is concerned, most GCs can still be
considered mono-metallic, since the upper limit to the scatter of iron
is less than 0.05 dex, meaning that the degree of homogeneity
is better than 12%. The scatter in Fe we find seems to have a
dependence on luminosity, possibly due to the well-known inadequacies
of stellar atmospheres for upper-RGB stars and/or to intrinsic
variability. It also seems to be correlated with cluster properties,
like the mass, indicating a larger scatter in more massive GCs which is
likely a (small) true intrinsic scatter. The 19 GCs, covering the
metallicity range of the bulk of Galactic GCs, define an accurate and
updated metallicity scale. We provide transformation equations for a
few existing scales. We also provide new values of [Fe/H], on our
scale, for all GCs in the Harris catalogue.
Key words: stars: abundances - stars: atmospheres - stars: population II - globular clusters: general
1 Introduction
The chemical composition of globular cluster (GC) stars cannot be regarded anymore as strictly homogeneous, as implied from the classical paradigm that these old stellar aggregates were the best approximation in nature of simple stellar populations (see Gratton et al. 2004, for an extensive review and references). Recent investigations using large samples of stars observed with multi-object spectrographs at large telescopes highlight that every GC studied so far harbours at least two different stellar generations, distinct in chemical composition and age (Carretta et al. 2009a,b).These different populations are found to differ in abundances of light elements (C, N, O, Na, Mg, Al, Si, F; Smith & Martell 2003; Smith et al. 2005; Carretta et al. 2009a,b; Yong et al. 2008a,b; Melendez & Cohen 2009, to quote a few studies; see also Gratton et al. 2004, and references therein) involved in proton-capture reactions of H-burning at high temperature (Denisenkov & Denisenkova 1989; Langer et al. 1993). Star to star abundance variations in these elements are expected to also come with differences in the main outcome of the H burning, the He content (Gratton et al. 2009; Bragaglia et al. in preparation; Prantzos & Charbonnel 2006; Ventura et al. 2001). Apart from a few alterations presently well understood in term of an extra-mixing episode after the red giant branch (RGB) bump (Charbonnel 1994, 1995; Charbonnel & Zahn 2007; Eggleton et al. 2007) the abundance variations are inherited by currently observed, long lived GC stars from a previous stellar component/generation: both spectroscopic (Gratton et al. 2001; Ramirez & Cohen 2002; Carretta et al. 2004; Piotto et al. 2005) and photometric (e.g. Bedin et al. 2004) observations convincingly showed that the observed pattern of chemical composition is present also among unevolved stars on the subgiant branch and the main sequence.
On the other hand, apart from a few notable exceptions![]() GCs
are still found to be mono-metallic objects, as far as abundances of
heavier elements
are concerned (see Gratton et al. 2004, for a
recent review on this subject).
Their heavy (Z>13) element metallicity,
usually represented by the ratio [Fe/H]
GCs
are still found to be mono-metallic objects, as far as abundances of
heavier elements
are concerned (see Gratton et al. 2004, for a
recent review on this subject).
Their heavy (Z>13) element metallicity,
usually represented by the ratio [Fe/H]![]() ,
is found to be extremely homogeneous from star to star in each cluster.
,
is found to be extremely homogeneous from star to star in each cluster.
The sites of production of heavy elements (in particular ![]() -capture
elements, Fe-group
elements) are stars with large and intermediate initial masses,
exploding as core-collapse or thermonuclear supernovae (see Wheeler
et al. 1989).
By studying the level and the dispersion of their yields
inherited by stars in GCs we have the possibility of investigating the
past history of
the precursors from whom the present-day globular clusters formed (see
Carretta et al. 2009c).
-capture
elements, Fe-group
elements) are stars with large and intermediate initial masses,
exploding as core-collapse or thermonuclear supernovae (see Wheeler
et al. 1989).
By studying the level and the dispersion of their yields
inherited by stars in GCs we have the possibility of investigating the
past history of
the precursors from whom the present-day globular clusters formed (see
Carretta et al. 2009c).
The recently completed analysis of high resolution spectra of almost 2000 RGB stars in 19 Galactic GCs (Carretta et al. 2009a,b and references therein) provides an unprecedented sample of stars analysed in a fully homogeneous way. By exploiting these data we can examine in detail the issue of the cosmic scatter in the metallicity (hereafter the abundance of Fe-peak elements) of GCs and hopefully provide clues to the early evolution of their progenitors.
Moreover, abundances of iron from high resolution spectra are traditionally the calibrating points for metallicity scales based on photometric and/or low-resolution spectroscopic indices that are sensitive to metal abundances (see the excellent discussion and historical review on this issue by Kraft & Ivans 2003). Thus, our sample is perfectly suited to provide robust (for statistics) and homogeneous (for technique of analysis) ``pillars'' onto which anchor several existing metallicity scales.
The paper is organized as follows.
We give in Sect. 2 a brief description of the data set and of
the analysis.
We discuss the intrinsic (cosmic) spread of iron in Sect. 3,
where we also
present some correlations of the spread with GC properties, like the
absolute
total luminosity or the ![]() -elements
abundance. We discuss the dependence
of this spread on the stars luminosity in Sect. 4 and present
a recalibration
of four metallicity scales to our new one in Sect. 5. A
summary is given in
Sect. 6 and we give metallicity values on our new scale for
all GCs in the
Harris (1996)
catalogue in the Appendix.
-elements
abundance. We discuss the dependence
of this spread on the stars luminosity in Sect. 4 and present
a recalibration
of four metallicity scales to our new one in Sect. 5. A
summary is given in
Sect. 6 and we give metallicity values on our new scale for
all GCs in the
Harris (1996)
catalogue in the Appendix.
2 The dataset and analysis
Briefly, in our survey we collected GIRAFFE spectra of intermediate
resolution
(
![]() )
for about 100 stars and UVES spectra (
)
for about 100 stars and UVES spectra (
![]() )
for
about 10 stars, on average, in each of our 19 programme GCs. The
GIRAFFE
gratings were chosen to include the Na I
lines at 568.2-568.8 nm (grating
HR11) and the forbidden [O I] lines at
630.0-636.3 nm (HR13). The number
of clean Fe I lines typically falling in
the corresponding spectral
ranges, and used in our analysis, varied from about 10 to a maximum of
about 40,
depending on the S/N, the
metallicity and whether the stars were observed with
HR11 only, HR13 only, or both. The UVES spectra covered the
480-680 nm region and
plenty of Fe lines were measured even in the most metal-poor clusters.
)
for
about 10 stars, on average, in each of our 19 programme GCs. The
GIRAFFE
gratings were chosen to include the Na I
lines at 568.2-568.8 nm (grating
HR11) and the forbidden [O I] lines at
630.0-636.3 nm (HR13). The number
of clean Fe I lines typically falling in
the corresponding spectral
ranges, and used in our analysis, varied from about 10 to a maximum of
about 40,
depending on the S/N, the
metallicity and whether the stars were observed with
HR11 only, HR13 only, or both. The UVES spectra covered the
480-680 nm region and
plenty of Fe lines were measured even in the most metal-poor clusters.
The data analysis has already been described in detail
elsewhere (Carretta et al. 2006,
2007a-c;
Gratton et al. 2006,
2007;
Carretta et al. 2009a,b)
and will not be repeated here. Only a few procedures will be briefly
summarised here.
Atmospheric parameters were homogeneously derived for all stars using
visual
and near-IR photometry and the relations given by Alonso
et al. (1999,
2001).
Equivalent widths (EWs) were measured by an updated
semi-automatic routine,
in the
package ROSA (Gratton 1988),
using an homogeneous method for the continuum
positioning (described in Bragaglia et al. 2001). The
line list is
adopted from Gratton et al. (2003), where
the atomic parameters and solar
reference abundances are fully discussed. This list was used for all
stars in
our program clusters, and we believe that this represents a remarkable
strength
of this project, resulting in a huge database of stellar abundances
derived in
the most homogeneous way for a significant part (![]()
![]() of the Galactic GC population, spanning the range in [Fe/H] from -2.5
to -0.4 dex.
of the Galactic GC population, spanning the range in [Fe/H] from -2.5
to -0.4 dex.
As discussed in the papers quoted above, all EWs measured on the GIRAFFE spectra were shifted to a system defined by those derived from high resolution UVES spectra, using stars and lines observed with both instruments.
Table 1: Average abundances of [Fe/H] I and observed rms scatters in our sample.
Taking into account the stars in common between UVES and
GIRAFFE observations,
we have values of [Fe/H] for 1958 individual RGB stars in 19 GCs.
Average abundances of iron derived from both UVES and GIRAFFE
spectra are summarised in Table 1. Only abundances
derived from
neutral Fe lines are reported (and will be used in the following)
because we
already showed in Papers VII and VIII that the
differences in iron abundances as
obtained from neutral and singly ionised species are negligible in our
analysis![]() .
Thus, we will adopt the [Fe/H] I ratio as
representative of the
metallicity of each star, because it is based on a much larger number
of lines, thus
providing a more robust estimate.
.
Thus, we will adopt the [Fe/H] I ratio as
representative of the
metallicity of each star, because it is based on a much larger number
of lines, thus
providing a more robust estimate.
Once EWs measured from GIRAFFE spectra are
corrected to the system defined by
UVES spectra, the abundance analysis provides very similar results for
the
average metallicity in each cluster: the mean difference (in the sense
UVES
minus GIRAFFE) is ![]() dex
with an rms scatter of 0.037 dex
from 19 GCs. The largest difference
(0.098 dex) is found for NGC 6441, for which
the observations in service mode could not be completed as requested,
so that
the available spectra have low S/N,
due both to the large
distance modulus and incomplete observations.
Figure 1,
reproduced from Paper VIII, shows the quite good agreement
between abundances of iron as obtained from both instruments; thus,
although we
will use [Fe/H] I values from the high
resolution UVES spectra, we are
confident that the new metallicity scale presented in the present paper
rests ultimately on very accurate and homogeneous abundances
for a sample of almost 2000 cluster stars.
dex
with an rms scatter of 0.037 dex
from 19 GCs. The largest difference
(0.098 dex) is found for NGC 6441, for which
the observations in service mode could not be completed as requested,
so that
the available spectra have low S/N,
due both to the large
distance modulus and incomplete observations.
Figure 1,
reproduced from Paper VIII, shows the quite good agreement
between abundances of iron as obtained from both instruments; thus,
although we
will use [Fe/H] I values from the high
resolution UVES spectra, we are
confident that the new metallicity scale presented in the present paper
rests ultimately on very accurate and homogeneous abundances
for a sample of almost 2000 cluster stars.
3 Intrinsic spread of iron in globular clusters
We compare in Fig. 2 the bona fide observed intrinsic spreads in Fe (defined as the rms scatter of all stars in each cluster), as given by GIRAFFE and UVES spectra (Cols. 5 and 8 in Table 1). The error bars show the maximum and minimum spread allowed for each cluster taking into account the statistical errors.
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{13003f01.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg50.png)
|
Figure 1:
Comparison for [Fe/H] I ratios (
upper panel) and for
[Fe/H] II ratios
( lower panel) obtained from GIRAFFE and UVES
spectra in the 19 programme
clusters in our sample. Metal abundances from GIRAFFE are from
Papers I, II, IV, V,
and VII. Metallicities from UVES are from
Paper III, VI, and VIII.
Error bars are 1 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{13003f02.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg51.png)
|
Figure 2: Comparison of the intrinsic spreads in [Fe/H] for the 19 GCs in our sample, as derived from UVES and GIRAFFE spectra. Error bars show the maximum and minimum spread allowed for each cluster by the statistical errors. The line indicating equality is also shown. |
| Open with DEXTER | |
Looking at this figure, two features are immediately evident: first, on average, the rms scatter obtained from UVES spectra is larger than the one we derived from the analysis of GIRAFFE spectra. At first sight, this result is just the opposite one would expect, given the higher resolution and spectral coverage of the UVES spectra. Possible explanations for this effect will be examined in the next section.
Second, intrinsic scatters from GIRAFFE spectra show quite
small associated
error bars, owing to the much larger statistics; if we focus on these
values, the
first conclusion is that the cosmic scatter in Fe in globular
clusters is very small. On average, we found a value of
0.048 dex (with ![]() dex)
from 19 GCs; i.e. the iron abundance in each
cluster is homogeneous within 12%.
dex)
from 19 GCs; i.e. the iron abundance in each
cluster is homogeneous within 12%.
Furthermore, we note that these are strictly upper limits to the actual dispersion of [Fe/H] values in GCs. The true intrinsic values should be estimated by subtracting (in quadrature) the scatter expected from errors in the analysis, namely in the derivation of the atmospheric parameters and in the measurement of EWs. These quantities were estimated with a thorough procedure amply described in previous papers and are reported in the Appendix of Paper VII and in Papers I to VI. Unfortunately, for the GIRAFFE spectra these estimates often exceed the observed scatter, probably because of the overestimate of the effect of some error sources, making difficult to derive the intrinsic scatter by deconvolving for this uncertainty. For 8 out 19 GCs this deconvolution was possible and from this, as well as from the analysis of UVES spectra, we found that a reasonable estimate is that the observed values of the rms scatter must be further reduced by 1-2%, to account for the analysis uncertainties.
To obtain a larger statistical sample we considered the observed scatters, noting however that they are upper limits. Therefore, our first conclusion is that, as far as iron is concerned, at first approximation the GCs can still be considered mono-metallic aggregates, apart from the few exceptions mentioned in the Introduction.
Table 2: Pearson's correlation coefficients, degrees of freedom and significance for relations with iron spread in our GC sample.
However, the high degree of homogeneity in our analysis, coupled with our very large sample, allow us to highlight subtle features that might be lost in the noise when collecting data from separate sources. In particular, we found several statistically significant relations between the intrinsic iron spread and global cluster parameters. In Table 2 we summarise the Pearson's linear correlation coefficients, the degrees of freedom and the statistical significance for a number of these relations.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{13003f03.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg62.png)
|
Figure 3: Observed intrinsic dispersion in iron from GIRAFFE spectra as a function of the visual total absolute magnitude of the clusters ( upper panel), of the median S/N for HR13 spectra ( middle panel),and of the maximum temperature along the horizontal branch ( lower panel). In each panel of this and the next figures we list the Spearman and Pearson correlation coefficients. |
| Open with DEXTER | |
Our main finding is that the observed dispersion in iron is correlated
with the
cluster absolute magnitude MV
(upper panel in Fig. 3),
a proxy for
the cluster present-day mass. More massive clusters show a larger
spread in
[Fe/H]. Note that this correlation would extend to brighter cluster
absolute
magnitudes if we include very massive clusters like M 54 and ![]() Cen.
Cen.
The rms seems preferentially larger in farther GCs, which could possibly indicate that the trend may be driven by the data quality. However, this is unlikely to be an observational artifact; as shown in the middle panel of Fig. 3, where we plot the median S/N ratio for the HR13 spectra, there is not a significant correlation between the quality of spectra and the rms scatter. Most clusters have a typical S/N around 120, yet show very different observed scatters. Moreover, our sample includes disk and inner halo GCs, and in general more massive clusters are preferentially found at larger distances (i.e. among the inner halo component) also in the global population of galactic GCs (Harris 1996).
Several theoretical models (Larson 1987; Suntzeff
& Kraft 1996;
D'Ercole et al. 2008;
Decressin et al. 2009)
suggest that currently observed GCs are only
a small fraction in mass of the original parent structures where they
formed.
In Carretta et al. (2009c)
we proposed a formation scenario for GCs
where a so-called precursor raises the metallicity
to a level which
corresponds to the primordial abundances currently observed in a
cluster. In other words, in present-day GCs we are not seeing the
contribution of massive SNe: the
level of iron and ![]() -elements
is already homogeneously established in the gas by the explosion of
core-collapse SNe in the precursor/proto-cluster.
Of course the idea of pre-enrichment in large fragments seeding the
present galactic
GC population is not new (see Searle & Zinn 1978). In our
scenario, the second effect of SNe in the precursor is to trigger a
burst of
star formation leading to the build up of the primordial population, a
fraction
of which we can still observe in GCs, making up about 1/3 of the total
cluster stars (see Carretta et al. 2009a).
However, the correlation we see between iron spread and cluster mass
tells us
that clusters originating in more massive precursors are probably more
capable to
retain inhomogeneities in the metallicity plateau established in the
previous
phase of rapid enrichment.
-elements
is already homogeneously established in the gas by the explosion of
core-collapse SNe in the precursor/proto-cluster.
Of course the idea of pre-enrichment in large fragments seeding the
present galactic
GC population is not new (see Searle & Zinn 1978). In our
scenario, the second effect of SNe in the precursor is to trigger a
burst of
star formation leading to the build up of the primordial population, a
fraction
of which we can still observe in GCs, making up about 1/3 of the total
cluster stars (see Carretta et al. 2009a).
However, the correlation we see between iron spread and cluster mass
tells us
that clusters originating in more massive precursors are probably more
capable to
retain inhomogeneities in the metallicity plateau established in the
previous
phase of rapid enrichment.
This is just what is observed for the rms scatter in [Fe/H] as a function of MV and of other cluster parameters strictly related to the cluster mass: the maximum temperature reached along the cluster HB (lower panel of Fig. 3; see Recio Blanco et al. 2006; Carretta et al. 2009c), the slope of the cluster global mass function (see Djorgovski et al. 2003), the velocity dispersion at half-mass radius (Gnedin et al. 2002).
We note that a (small) part of the higher values for the spread in more massive clusters may also be due to variations in He content, which are expected to be larger in GCs of larger masses (Gratton et al. 2009). In this case, of course, the effect is due not only to the higher capability to retain ejecta but also to the enhanced He in some stars formed by gas heavily polluted in H-processed material, which lowers the denominator in the [Fe/H] ratio (see also Bragaglia et al. in prep.). We can check the relevance of this effect by computing the iron spread using only stars in the primordial component P (see Carretta et al. 2009a), which are not expected to be formed from matter polluted with additional He.
We found that the difference in the rms of [Fe/H] (in the
sense all stars
minus P stars) is on average ![]() (with
(with ![]() for 19 GCs). For the two most massive clusters in the
sample (NGC 6388 and NGC 6441) this difference goes
in opposite directions and
the largest differences are found for the three GCs with
lower quality spectra (NGC 6388 and NGC 6441 again,
plus NGC 6752). We conclude
that the contribution to the spread in iron caused by variations in the
He
content is probably very small.
for 19 GCs). For the two most massive clusters in the
sample (NGC 6388 and NGC 6441) this difference goes
in opposite directions and
the largest differences are found for the three GCs with
lower quality spectra (NGC 6388 and NGC 6441 again,
plus NGC 6752). We conclude
that the contribution to the spread in iron caused by variations in the
He
content is probably very small.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{13003f04.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg65.png)
|
Figure 4: Observed spread of [Fe/H] in our programme clusters as a function of their peri-galactic distance ( upper left panel), age ( upper right panel), total sum of Mg+Al+Si nuclei ( lower left panel) and [Ca/Fe] ratio. |
| Open with DEXTER | |
A support for the proposed scenario comes from a second set of
(anti)correlations involving the observed spread of iron and the
position
of GCs in the Galaxy (or related quantities; see
Table 2
and Fig. 4).
The dispersion
in [Fe/H] is larger in GCs spending, on average, more time at larger
distances
from the Galactic centre (upper left panel). At the same time, the
spread decreases for older clusters and for increasing abundances of
the
![]() -element
-element![]() .
.
In Carretta et al. (2009c) we
emphasised that inner halo clusters
preferentially include
more massive clusters with respect to disc clusters; moreover,
the first are also younger, on average, and with a slightly smaller
level of
![]() -elements
than that found in disc/bulge GCs. All these features concur
to explain the good correlation and the anti-correlations displayed in
Fig. 4.
-elements
than that found in disc/bulge GCs. All these features concur
to explain the good correlation and the anti-correlations displayed in
Fig. 4.
| Figure 5: Fraction of stars in the P ( upper panel), I ( middle panel), and E component ( lower panel) of our programme clusters as a function of the observed rms scatter in [Fe/H]. |
|
| Open with DEXTER | |
Finally, in Fig. 5 we show the run of the rms scatter in Fe as a function of the fraction of first generation stars P, as well as the second generation components of intermediate modified (I), and extreme modified (E) composition (see Carretta et al. 2009a for detailed definitions of these stellar populations). The dispersion in Fe increases along with the fraction of P stars still observed in GCs, again pointing toward a deeper potential well in more massive clusters, more able to retain both SN ejecta and low mass P stars. On the other hand, we know that the fraction of E stars is larger in more massive clusters, and this explains also the correlation between the spread and the E component. The complementarity between I and E fractions (Carretta et al. 2009c) well accounts for the anti-correlation shown in the middle panel of Fig. 5.
4 Fe scatter as a function of the luminosity
Coming back to the comparison of the rms scatters in Table 1, we now look at the rather surprising fact that the rms we derive for Fe abundances is higher from the high-resolution UVES spectra than from the intermediate-resolution GIRAFFE ones. This effect is particularly clear for clusters with metallicity -1.4<[Fe/H]<-0.7 dex in our programme sample, which have data of higher quality. More metal-rich clusters (e.g. NGC 6388 and NGC 6441) are quite distant, bulge clusters, severely affected by field contamination and required a series of long exposures which were not always completed in the ESO observing service queue (in particular for NGC 6441). Analysis of more metal-poor clusters is somewhat hampered by the weakness of lines, increasing the difficulty of EW measurements.
To explain the abovementioned effect, a possibility is that stars observed with UVES have intrinsically a larger scatter than those observed with GIRAFFE. This would happen if the intrinsic scatter is partly a function of the stellar luminosity, because we preferentially chose brighter stars as UVES targets (although the majority of the objects - about 170 out of 214 stars - are in common between the two data sets).
Table 3: Average residuals with respect to the mean [Fe/H] for clusters with metallicities -1.4<[Fe/H]<-0.7 dex.
To better understand this point we need to improve the estimate of the intrinsic scatter and in order to clarify the issue we proceeded as follows. For each star observed with GIRAFFE or UVES (separately) we evaluated the difference between the [Fe/H] value for the individual stars and the average value [Fe/H] of the cluster. These residuals were then plotted as a function of the absolute K magnitude MK0 corrected for the apparent distance modulus and reddening in each cluster. We chose the K band because (i) all near-IR magnitudes are from the 2MASS catalogue and they represent a very homogeneous dataset and (ii) this filter is much less sensitive to errors in the reddening estimate.
Finally, all stars were binned in luminosity intervals and the average residual and rms scatter from the mean was computed for each bin. These averages are listed in Table 3 and plotted in Fig. 6. We restricted this exercise to the metallicity range [Fe/H] from -1.4 to -0.7 dex, where we have better quality data.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{13003f06.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg85.png)
|
Figure 6: Average differences between individual stars and the mean [Fe/H] value in each cluster in the metallicity range -1.4<[Fe/H]<-0.7, as a function of the near IR de-reddened absolute magnitude MK0. Filled circles: stars observed with GIRAFFE; empty squares: stars observed with UVES. The open star symbols are the weighted average of residuals from UVES and GIRAFFE in the corresponding luminosity bin. |
| Open with DEXTER | |
We can see that the brighter stars (for which the S/N
ratio is higher) show a
larger scatter in the abundances of iron than the fainter stars. The
difference
is quite significant, considering the errors associated to the estimate
of the
scatter: in the bin
-2< MK0
<-1, with 271 stars, we
obtain an rms scatter of ![]() from the GIRAFFE
observations, whereas for the brighter bin
-4< MK0
<-3 (81 stars) we have
from the GIRAFFE
observations, whereas for the brighter bin
-4< MK0
<-3 (81 stars) we have ![]() .
This difference is
statistically significant, at a level of more than 4
.
This difference is
statistically significant, at a level of more than 4![]() .
The results from the UVES spectra are essentially consistent with those
derived
from GIRAFFE (although with larger statistical errors owing to the much
smaller
number of stars available) and reveal a clear trend of the rms as a
function
of the luminosity.
.
The results from the UVES spectra are essentially consistent with those
derived
from GIRAFFE (although with larger statistical errors owing to the much
smaller
number of stars available) and reveal a clear trend of the rms as a
function
of the luminosity.
This trend can be explained with the reasonable assumption
that the atmosphere
of each star (among
the more luminous objects) has a distinct peculiarity or intrinsic time
variability. Ita et al. (2002)
found that very bright RGB stars in the LMC are
indeed variables (likely pulsating). However, the stars considered here
are
considerably fainter, so that we are more inclined to attribute this
variability
to the large sizes (and small numbers) of convective
cells with respect, e.g., to solar analogues![]() .
As a consequence, there is an
uncertainty (of the order of about 0.04-0.05 dex) in the Fe
abundances derived
from an instantaneous observation, since the convective elements of a
red giant
are so large that only a small number of them occupy the surface of the
star at
any time (Schwarzschild 1975;
Gray et al. 2008).
To account for this uncertainty we would need to assume that the
temperature in
the line formation region differs from star to stars, with an rms
scatter of
about 50 K.
.
As a consequence, there is an
uncertainty (of the order of about 0.04-0.05 dex) in the Fe
abundances derived
from an instantaneous observation, since the convective elements of a
red giant
are so large that only a small number of them occupy the surface of the
star at
any time (Schwarzschild 1975;
Gray et al. 2008).
To account for this uncertainty we would need to assume that the
temperature in
the line formation region differs from star to stars, with an rms
scatter of
about 50 K.
While Schwarzschild (1975) estimated as about 400 the number of convective cells in the atmosphere of a red giant, our sample is mostly formed by warmer stars. We then assume that the number of convective cells is larger, in our case, say about 1000. Of those, only half are obviously visible and not all of them with the same weight, because of the limb darkening. Thus, we would get random fluctuations of about a factor 20 smaller than those expected at the star surface between the hotter regions (the top of the ascending columns) and the cooler regions (descending columns), having temperature differences by about 1000 K. Hence, we could expect that random fluctuations of the temperature in the region of line formation in a giant are effectively of the order of 50 K, even at similar effective temperatures. Following the same line of thought, one could expect that the luminosity is not perfectly constant, but should show fluctuations up to 0.01 mag (over timescales of a few tens of days); the same would show up in fluctuations of radial velocity (over similar timescales and amplitude of about 200-300 m/s). These expectations seem to agree with observations of stars similar to those in our sample (the threshold being -2<MV<-1.4, Cummings 1999; Carney et al. 2008).
In summary, since the spread measured from brighter stars could include the intrinsic noise due to the convection and pulsation (both in radial and non-radial mode), the implication is that it is better to use fainter stars in order to obtain the star-to-star scatter. From these stars (practically restricted to those with GIRAFFE spectra) the typical rms in a cluster should be about 0.033 dex (see Table 3), or less, since this scatter value includes also the measurement errors.
Finally, we remark that the scatter seems to be larger for more metal-poor clusters. We speculate that this is in part due to possibly larger observational errors, but in part it could be due to an increased transparency of the atmosphere, hence pointing to a larger relevance of the 3D-structure.
4.1 Alternative scenario: contamination from AGB
An alternative explanation of the larger scatter observed at higher luminosities (in particular in the magnitude bin -4< MK <-3) could be contamination from asymptotic giant branch (AGB) stars. Were this the case, we would expect that the sequences are sufficiently well separated (and the contamination negligible) at fainter magnitudes. On the other hand, the temperature difference between RGB and AGB is small, in the more luminous bin. However, the error would be larger where the two sequences are so close that cannot be distinguished, but separated enough to give a wrong temperature when the luminosity is used, as in the procedure adopted in our analysis (see Carretta et al. 2009a for further details).
In this scenario, we would expect a distribution essentially Gaussian in form at lower luminosities, where the contamination is negligible. At higher magnitudes, the distribution should become asymmetric, with a tail toward lower abundances given by the possible interlopers AGB stars for which the effective temperature (hence the abundance) would be underestimated. This asymmetry should be more pronounced in the bin -4< MK <-3.
We checked this possible effect by computing the residuals in Fe abundances derived from GIRAFFE spectra in different bins of magnitudes, again restricting to the clusters in the metallicity range -1.4<[Fe/H]<-0.7 dex. The histogram of the residuals in various magnitude bins are plotted in Fig. 7
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13003f07.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg88.png)
|
Figure 7: Histograms of the residuals in Fe abundances in several magnitude bins for clusters in our sample with metallicity -1.4<[Fe/H]<-0.7. |
| Open with DEXTER | |
There seems to be no particular asymmetry in the range -4< MK <-3, where the distribution appears only slightly larger. In conclusion, this test seems to support the idea that the larger spread is due to the stellar atmospheres and to the variability provoked by the photospheric convection and stellar pulsation.
5 A new homogeneous metallicity scale
Having at hand an unprecedented large sample of GC red giants with homogeneously measured metal abundances, a logic step is to re-address the issue of an accurate metallicity scale for GCs. This is an indispensable tool in several issues, like age derivation (both absolute and relative to other clusters) of individual GCs as well as the study of age-metallicity relation for cluster populations.
In the following we provide the relations to transform previous metallicity scales against the one that can be defined on the basis of our UVES sample of stars.
Recalibration of the Carretta & Gratton (1997; CG97) scale -
since its appearance, this metallicity scale has been widely used due to the effort made to use the most homogeneous approach. Briefly, the CG97 scale was derived from the re-analysis of a large sample (![\begin{figure}
\par\includegraphics[width=8cm,clip]{13003f08.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg93.png)
|
Figure 8: Calibration of the CG97 metallicity scale vs average metal abundances derived by us from UVES spectra for 13 clusters in common. The dotted line is the equality line, the solid line is the linear regression obtained by least-squares fit to the points. Error bars are rms scatters of the mean. |
| Open with DEXTER | |
We used 13 clusters in common between CG97 and the present analysis to
provide a new calibration of the metallicity scale. The regression line
is
obtained by least-squares fit, by averaging
values derived exchanging the independent and dependent variables, and
is
with
Our new [Fe/H] values are systematically lower (by
0.19 dex on average, with
![]() dex) than those by
CG97, and the difference increases with
decreasing [Fe/H]. We must note, however, that the average values for
the three
most metal-poor clusters (NGC 4590, NGC 7078, and
NGC 7099) are based in CG97
only on a few stars (from 2 to 4) in each cluster, compared to more
than 10 stars per cluster in our new analysis. The above
relation shows that there is
almost only a multiplicative constant between the two scales and
provides the
transformation required to bring the CG97 scale onto the new system.
dex) than those by
CG97, and the difference increases with
decreasing [Fe/H]. We must note, however, that the average values for
the three
most metal-poor clusters (NGC 4590, NGC 7078, and
NGC 7099) are based in CG97
only on a few stars (from 2 to 4) in each cluster, compared to more
than 10 stars per cluster in our new analysis. The above
relation shows that there is
almost only a multiplicative constant between the two scales and
provides the
transformation required to bring the CG97 scale onto the new system.
Part of the difference is certainly due to the adopted temperature scale. Since we observed different stars (farther away from the RGB tip in the present study) and different colours (2MASS rather than on the CIT system, Frogel et al. 1983) a very precise comparison is not possible. Anyway, the Alonso et al. scale is cooler: we found differences between 57 and 97 K, for the same V-K colours and different metallicities, with the larger difference found for more metal-poor GCs. Using the new Alonso et al. scale we would have had lower abundances also on the CG97 scale, by about 0.09-0.10 dex for the more metal-poor GCs and by only 0.02-0.03 dex for the more metal-rich GCs, which accounts for most of the difference we found between the two scales. The metallicity found here for M 30 can be explained by the different temperatures: a star of magnitude similar to the two examined in CG97 has a temperature lower by about 140 K in our new analysis. This difference, larger than the average one for metal-poor GCs (about 100 K), justifies the observed offset.
However, even including this correction we would still have an
offset of about
0.08-0.12 dex. Part of this residual difference is due to the gf
values: those
currently adopted by us (see Gratton et al. 2003) are
larger on average by
![]() dex. The remaining
difference of 0.05-0.09 dex are probably
due to the EWs, measured on higher quality and
higher resolution spectra and in a more homogeneous way in the present
project.
dex. The remaining
difference of 0.05-0.09 dex are probably
due to the EWs, measured on higher quality and
higher resolution spectra and in a more homogeneous way in the present
project.
Finally, we note that most of the scatter around the best fit is given (with opposite sign) by two clusters, NGC 6121 (M 4) and NGC 7099 (M 30). For the first case, the difference is essentially due to the anomalous value of the ratio AV/E(B-V), which was taken into account for this cluster in the present programme. The difference between the classical value 3.1 (CG97) and 4.0 (used in this work) implies a difference of 0.28 mag in the correction of V-K, which in turn translates in a difference of about 200 K in the effective temperatures, just enough to shift M 4 on the best fit regression given by the other GCs.
Concerning NGC 7099 (M 30), the original data adopted by CG97 were from Minniti et al. (1993) who derived the effective temperatures from the spectra; these temperature were adopted also in CG97, due to the lack of V-K colours for the two stars analysed.
Recalibration of the Zinn & West (1984; ZW) scale -
the other most used metallicity scale for globular clusters is the one defined by Zinn & West (1984), based on a variety of integrated-light photometric and spectroscopic indices calibrated from the few echelle photographic spectra existing at the time. Its popularity was due to the ranking this scale provided for the first time for a large number of clusters; in fact, all 19 GCs of our project have a corresponding [Fe/H] entry in the ZW scale.![\begin{figure}
\par\includegraphics[width=8cm,clip]{13003f09.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg98.png)
|
Figure 9: Comparison of the ZW metallicity scale vs average [Fe/H] values obtained by us from UVES spectra for all 19 clusters in our programme sample. The dotted line is the line of equality, the solid (red) line is the linear regression obtained by least-squares fit to the points and the dashed (blue) line is a second-order polynomial relation to the data. Error bars are rms scatters of the mean. |
| Open with DEXTER | |
The comparison between our average metallicities from UVES spectra and
the ZW average [Fe/H] values is shown in Fig. 9. A least-squares
linear fit
(again obtained by exchanging the independent and dependent variables
and averaging the
results) gives the following relation to transform ZW values to our new
scale:
with
On average, the two scales formally differ by only
0.01 dex over the sampled
metallicity range, but the scatter of the points is now clearly larger
than in
the case of the CG97 scale. By looking at Fig. 9 a better
transformation is obtained when a second-order polynomial is used:
|
|
= | ||
with
We note however that metallicities on the ZW scale are obtained by averaging the results from a heterogeneous series of indices, calibrated on the best metal abundances from high dispersion spectroscopy available at the time (Cohen 1983; Frogel et al. 1983). A better approach is to directly calibrate the original and homogeneous Q39 index by Zinn & West (1984), available for a large sample of GCs, on the new metallicities presented here and use it in addition to other homogeneous estimate of [Fe/H] to obtain an accurate ranking in metal abundance for Galactic GCs. This is done in the Appendix.
Recalibration of the Kraft & Ivans (2003; KI03) scale -
in Fig. 10 we show the comparison of our [Fe/H] values from UVES with those of the metallicity scale by Kraft & Ivans (2003), not much used in spite of being based on the homogeneous re-analysis of EWs of Fe II lines from high resolution spectra. We adopted their values from the Kurucz model with convective overshooting turned on (their Table 4, Col. 6) for consistency with the models used in the present work.![\begin{figure}
\par\includegraphics[width=8cm,clip]{13003f10.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg105.png)
|
Figure 10: Comparison of the Kraft & Ivans (2003) metallicity scale based on Fe II abundances vs average [Fe/H] values obtained by us from Fe I lines measured on UVES spectra for 10 clusters in common. The dotted line is the identity line, the solid (red) line is the linear regression obtained by least-squares fit to the points. Error bars are rms scatters of the mean. |
| Open with DEXTER | |
The relation to transform the KI03 values on our new scale is:
with a scatter of only
This finding is rather strange because the basic reason for which Kraft and Ivans used Fe II is that it is generally assumed that currently available one-dimensional LTE model atmospheres give a correct representation of abundances from singly ionized Fe lines, but not of the abundances from Fe I lines, more affected by departures from the LTE assumption. Hence, they concluded that the safest approach was to rely on Fe II lines alone. However, Fig. 10 seems to question these conclusion for two related reasons. First, because of the good agreement we found on average, being our abundances derived from a neutral specie and theirs from a singly ionized specie; second, because departures from LTE are expected to be larger where the stellar atmospheres become more transparent and less line-blanketed, i.e. the effects increase toward lower metallicities, whereas just the opposite is shown by the comparison. At the moment, we have no clear explanation for this occurrence; we only note that our samples are composed by stars not so close to the RGB tip, where NLTE effects might be more relevant.
Recalibration of the near-infrared Ca II scale (Rutledege et al 1997; R97) -
finally, we provide here a new calibration of the metallicity scale based on the strength of the near-infrared Ca II triplet, used in particular to estimate the metallicity of stars in distant systems, such as the nearby dwarf spheroidals, because the triplet is measurable even at large distances.![\begin{figure}
\par\includegraphics[width=8cm,clip]{13003f11.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg108.png)
|
Figure 11: Comparison of our [Fe/H] average values with the reduced strength of the near-infrared Ca II triplet W' from Rutledge et al. (1997) for 17 clusters in common. The superimposed solid (red) line is the linear regression obtained by least-squares fit to the points. Error bars are rms scatters of the mean. |
| Open with DEXTER | |
In Fig. 11
we show the comparison between our UVES
metallicities and the values of the reduced
strength W'(Ca II)
of the near-infrared Ca triplet taken from Rutledge et al.
(1997;
R97). The two variables are linearly correlated over the whole range
defined by the clusters analysed in the present paper (![]() Fe/H
Fe/H
![]() ;
unfortunately, values of W' are not given for
NGC 6388 or NGC 6441). The transformation of the
reduced
strength W' to the UVES metallicities
;
unfortunately, values of W' are not given for
NGC 6388 or NGC 6441). The transformation of the
reduced
strength W' to the UVES metallicities
![\begin{displaymath}{\rm [Fe/H]_{UVES}} = 0.513(\pm 0.022) W'_{R97} -3.189\end{displaymath}](/articles/aa/full_html/2009/47/aa13003-09/img111.png)
(with a correlation coefficient r=0.99 and a rms scatter of only
6 Summary
Within our survey of 19 Galactic GCs with FLAMES (UVES and GIRAFFE), we have measured the iron abundance of about 2000 RGB stars in a accurate and homogeneous way (determination of atmospheric parameters, measure of EWs, spectroscopic analysis, etc). In the present paper we exploit this huge, homogeneous data set, covering (almost) the entire range of GC metallicity in our Galaxy and a summary of our findings follows:- i)
- We obtain a measure of the intrinsic spread of iron in GCs from the rms scatter of our metallicities. We confirm that the cosmic scatter in Fe of most GCs is very small: the upper limit to this scatter is less than 0.05 dex, i.e., the iron abundance is homogeneous within 12% in each GC, on average.
- ii)
- The rms scatter we find for the UVES sample within each GC is larger than the one derived for the GIRAFFE sample. This can be ascribed to the different magnitude ranges observed. The UVES stars are usually brighter, nearer the RGB tip, and may suffer from larger inadequacies in the treatment of atmospheres and intrinsic stellar variability.
- iii)
- This is confirmed by a increase in scatter for brighter stars also in the GIRAFFE samples, that is not explained by AGB contamination, and that is larger for metal-poor GCs.
- iv)
- There are interesting correlations between the rms scatter
in Fe
and several GC parameters, like MV,
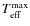 (HB),
(HB),
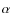 -element
abundance, that seem to indicate a better capability of more massive
clusters
to self-enrich.
-element
abundance, that seem to indicate a better capability of more massive
clusters
to self-enrich.
- v)
- We recalibrate several metallicity scales of GCs using our 19 precise, homogeneous values; we have done it for the GC97, ZW, KI03, and R97 ones, giving transformation equations.
- vi)
- Finally, in the Appendix we give [Fe/H] on our new scale for all clusters in the Harris (1996) compilation.
We wish to thank the ESO Service Mode personnel for their efforts. We also thank the referee for his/her useful comments. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This work was partially funded by the Italian MIUR under PRIN 2003029437. We also acknowledge partial support from the grant INAF 2005 ``Experimental nucleosynthesis in clean environments''. S.L. is grateful to the DFG cluster of excellence ``Origin and Structure of the Universe'' for support.
Appendix A: Cluster metallicities on a new homogeneous UVES scale
In this Section, we provide an updated compilation of cluster metallicity for all the Galactic GCs included in the Harris (1996) catalogue referred to modern measurements of stellar abundances from high dispersion spectroscopy. We use as reference ``pillars'' the accurate and homogeneous [Fe/H] values derived in our project from high resolution UVES spectra for 214 giants stars in 19 GCs. The very good agreement between these abundances and those obtained for stars observed also with GIRAFFE means that our scale is supported by the observed metallicities of almost 2000 red giants, all analysed in the same way.In our approach we selected two sets of data to be included in our new calibration:
- (i)
- recent and homogeneous metallicities from high resolution spectroscopy of stars in a limited number of GCs (CG97, 24 clusters; Kraft & Ivans 2003, 16 clusters)
- (ii)
- metallicity dependent indices homogeneously derived for large; samples of GCs (Q39 from Zinn & West 1984, 60 clusters; W' from Rutledge et al. 1997, 69 clusters).
To alleviate this problem, we add to our 19 GCs two very
metal-rich clusters,
whose metal abundances were newly analysed (or revised) in Carretta
et al.
(2001):
NGC 6528 ([Fe/H]=+0.07 dex, ![]() dex)
and NGC 6553
([Fe/H]=-0.06 dex,
dex)
and NGC 6553
([Fe/H]=-0.06 dex, ![]() dex).
For these two clusters the
analysis is of course not strictly homogeneous with the
other 19 GCs, however the gf scale
is very similar and their addition to the sample is unavoidable to
obtain a
reasonable calibration of the metal rich end of the GC scale,
as
we will see below.
dex).
For these two clusters the
analysis is of course not strictly homogeneous with the
other 19 GCs, however the gf scale
is very similar and their addition to the sample is unavoidable to
obtain a
reasonable calibration of the metal rich end of the GC scale,
as
we will see below.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{13003f12.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg118.png)
|
Figure A.1: Calibration of the Q39 index from Zinn & West (1984) using our [Fe/H] values from high resolution spectroscopy. Filled red circles are our clusters with UVES spectra; blue filled squares are the two metal-rich bulge clusters whose metallicities were analysed (or revised) in Carretta et al. (2001), based on Keck HIRES spectra. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{13003f13.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg119.png)
|
Figure A.2: Calibration of the reduced strength W' of the calcium triplet from Rutledge et al. (1997) after adding the metal-rich bulge cluster NGC 6553 (NGC 6528 does not have W' measured by Rutledge et al.) from Carretta et al. (2001; blue filled square). The blue dotted line is the linear regression of Fig. 11 and the red solid line the cubic spline fit to the data. |
| Open with DEXTER | |
Table A.1: Compilation of cluster metallicities on the present scale.
In Fig. A.1
we show the calibration of the Q39
index from Zinn & West (1984)
using
the 12 GCs with UVES metallicities in common with that work and the two
added clusters NGC 6528
and NGC 6553. From this figure it is clearly evident that the
run of Q39 as a function of
metal
abundance is not linear in the high metallicity regime.
The fitting second-order polynomial is
|
|
= | ||
with
Although anchored to only one cluster, NGC 6553, in
the near solar metallicity region, the new
calibration of the calcium triplet reduced strength, of the form
|
|
= | ||
(with
Moreover, from Figs. A.1 and A.2 we note that simple linear extrapolations would result in [Fe/H] values for clusters with [Fe/H]>-0.5 that would be overestimated from the Q39 index and underestimated when using the W' index. This fact underlines the risks of a too crude extrapolation procedure, and we believe that this justifies the inclusion of NGC 6553 and NGC 6528 among our calibrating clusters.
We used these transformations to derive [Fe/H] values on our scale and the previous relations of Sect. 5 to transform metallicities from Carretta & Gratton (1997) and from Kraft & Ivans (2003) to the present scale. Finally, we computed the weighted average of the metallicity for each cluster, assuming as weights the rms scatters of the fitting relations in each case. For our UVES based metal abundances we adopted internal errors (see Carretta et al. 2009b) as weighting factor.
The resulting metallicities are listed in Table A.1 for 95
GCs in the Harris (1996)
catalogue for which this average was possible. Associated errors are 1![]() rms
of the
weighted average and they represent the errors associated with the
metallicity with respect to the
metallicity scale/ranking defined in this paper.
rms
of the
weighted average and they represent the errors associated with the
metallicity with respect to the
metallicity scale/ranking defined in this paper.
The other 38 entries in the Harris catalogue have no
determinations of [Fe/H] from homogeneous
high resolution spectroscopy or compilation of metallicity-dependent
indices. In general, these
are distant clusters, not included in any of the previous main studies.
Their metal abundance in
the Harris catalogue is based on a variety of metallicity indicators.
For these objects we proceeded as
follows. The comparison of our weighted average [Fe/H] values with
metallicity entries in the
Harris catalogue for 94 clusters in common![]() provides a slope equal to unity (when metallicity
from Harris is used as independent variable) with an offset
of 0.025 dex. Hence, for the 38
remaining clusters we simply added this offset to the [Fe/H] values
listed in the Harris
catalogue (flag 2 in Table A.1). In this
case, the associated error is simply the rms scatter from the
comparison of the 94 clusters, i.e. 0.09 dex.
provides a slope equal to unity (when metallicity
from Harris is used as independent variable) with an offset
of 0.025 dex. Hence, for the 38
remaining clusters we simply added this offset to the [Fe/H] values
listed in the Harris
catalogue (flag 2 in Table A.1). In this
case, the associated error is simply the rms scatter from the
comparison of the 94 clusters, i.e. 0.09 dex.
References
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1999, A&AS, 140, 261 [NASA ADS] [EDP Sciences] [CrossRef]
- Alonso, A., Arribas, S., & Martinez-Roger, C. 2001, A&A, 376, 1039 [NASA ADS] [EDP Sciences] [CrossRef]
- Bedin, L., Piotto, G., Anderson, J., et al. 2004, ApJ, 605, L125 [NASA ADS] [CrossRef]
- Bellazzini, M., Ibata, R. A., Chapman, S. C., et al. 2008, AJ, 136, 1147 [NASA ADS] [CrossRef]
- Bragaglia, A., Carretta, E., Gratton, R. G., et al. 2001, AJ, 121, 327 [NASA ADS] [CrossRef]
- Carney, B. W., Latham, D. W., Stefanik, R. P., & Laird, J. B. 2008, AJ, 135, 196 [NASA ADS] [CrossRef]
- Carretta, E., & Gratton, R. G. 1997, A&AS, 121, 95 [NASA ADS] [EDP Sciences] [CrossRef]
- Carretta, E., Cohen, J. G., Gratton, R. G., & Behr, B. B. 2001, AJ, 122, 1469 [NASA ADS] [CrossRef]
- Carretta, E., Gratton, R. G., Bragaglia, A., Bonifacio, P., & Pasquini, L. 2004, A&A, 416, 925 [NASA ADS] [EDP Sciences] [CrossRef]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2006, A&A, 450, 523 [NASA ADS] [EDP Sciences] [CrossRef] (Paper I)
- Carretta, E., Bragaglia, A., Gratton, R. G., Lucatello, S., & Momany, Y. 2007a, A&A, 464, 927 [NASA ADS] [EDP Sciences] [CrossRef] (Paper II)
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2007b, A&A, 464, 939 [NASA ADS] [EDP Sciences] [CrossRef] (Paper IV)
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2007c, A&A, 464, 967 [NASA ADS] [EDP Sciences] [CrossRef] (Paper VI)
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009a, A&A, 505, 117 [EDP Sciences] [CrossRef] (Paper VII)
- Carretta, E., Bragaglia, A., Gratton, R. G., & Lucatello, S. 2009b, A&A, 505, 139 [EDP Sciences] [CrossRef] (Paper VIII)
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009c, A&A, submitted
- Casetti-Dinescu, D. I., Girard, T. M., Herrera, D., et al. 2007, AJ, 134, 195 [NASA ADS] [CrossRef]
- Charbonnel, C. 1994, A&A, 282, 811 [NASA ADS]
- Charbonnel, C. 1995, ApJ, 453, L41 [NASA ADS] [CrossRef]
- Charbonnel, C., & Zahn, J.-P. 2007, A&A, 467, L15 [NASA ADS] [EDP Sciences] [CrossRef]
- Cohen, J. G. 1983, ApJ, 270, 654 [NASA ADS] [CrossRef]
- Cohen, J. G., Frogel, J. A., & Persson, S. E. 1978, ApJ, 222, 165 [NASA ADS] [CrossRef]
- Cummings, I. N. 1999, J Astron. Data, 5, 2
- De Angeli, F., et al. 2005, AJ, 122, 3171
- Decressin, T., Baumgardt, H., Kroupa, P., Meynet, G., & Charbonnel, C. 2009, IAU Symp. 258, ed. D. Soderblom et al., 265
- D'Ercole, A., Vesperini, E., D'Antona, F., McMillan, S. L. W., & Recchi, S. 2008, MNRAS, 391, 825 [NASA ADS] [CrossRef]
- Denisenkov, P. A., & Denisenkova, S. N. 1989, A.Tsir., 1538, 11 [NASA ADS]
- Dinescu, D. I., Girard, T. M., & van Altena, W. F. 1999, AJ, 117, 1792 [NASA ADS] [CrossRef]
- Djorgovski, S., Piotto, G., & Capaccioli, M. 1993, AJ, 105, 2148 [NASA ADS] [CrossRef]
- Eggleton, P. P., Dearborn, D. S. P., & Lattanzio, J. C. 2007, IAUS, 239, 286 [NASA ADS]
- Frogel, J. A., Cohen, J. G., & Persson, S. E. 1983, ApJ, 275, 773 [NASA ADS] [CrossRef]
- Gnedin, O. Y., Zhao, H. S., Pringle, J. E., et al. 2002, ApJ, 568, L23 [NASA ADS] [CrossRef]
- Gratton, R. G. 1988, Rome Obs. Preprint Ser., 29
- Gratton, R. G., Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [NASA ADS] [EDP Sciences] [CrossRef]
- Gratton, R. G., Carretta, E., Claudi, R., Lucatello, S., & Barbieri, M. 2003, A&A, 404, 187 [NASA ADS] [EDP Sciences] [CrossRef]
- Gratton, R. G., Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 [NASA ADS] [CrossRef]
- Gratton, R. G., Lucatello, S., Bragaglia, A., et al. 2006, A&A, 455, 271 [NASA ADS] [EDP Sciences] [CrossRef] (Paper III)
- Gratton, R. G., Lucatello, S., Bragaglia, A., et al. 2007, A&A, 464, 953 [NASA ADS] [EDP Sciences] [CrossRef] (Paper V)
- Gratton, R. G., Carretta, E., Bragaglia, A., Lucatello, S., & D'Orazi, V. 2009, A&A, submitted
- Gray, D. F., Carney, B. W., & Yong, D. 2008, AJ, 135, 2033 [NASA ADS] [CrossRef]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef]
- Ita, Y., Tanabé, T., Matsunaga, N., et al. 2002, MNRAS, 337, L31 [NASA ADS] [CrossRef]
- Kraft, R. P., & Ivans, I. I. 2003, PASP, 115, 143 [NASA ADS] [CrossRef]
- Kurucz, R. L. 1993, CD-ROM 13, Smithsonian Astrophysical Observatory, Cambridge
- Langer, G. E., Hoffman, R., & Sneden, C. 1993, PASP, 105, 301 [NASA ADS] [CrossRef]
- Larson, R. B. 1987, in Nearby normal galaxies, ed. S. Faber (NY: Springer), 26
- Marino, A. F., Milone, A., Piotto, G., et al. 2009, A&A, 505, 1099 [EDP Sciences] [CrossRef]
- Melendez, J., & Cohen, J. G. 2009, ApJ, 699, 2017 [NASA ADS] [CrossRef]
- Minniti, D., Geisler, D., Peterson, R. C., & Claria, J. J. 1993, ApJ, 413, 548 [NASA ADS] [CrossRef]
- Piotto, G., Villanova, S., Bedin, L. R., et al. 2005, ApJ, 621, 777 [NASA ADS] [CrossRef]
- Prantzos, N., & Charbonnel, C. 2006, A&A, 458, 135 [NASA ADS] [EDP Sciences] [CrossRef]
- Ramirez, S. V., & Cohen, J. G. 2002, AJ, 123, 3277 [NASA ADS] [CrossRef]
- Recio Blanco, A., Aparicio, A., Piotto, G., De Angeli, F., & Djorgovski, S. G. 2006, A&A, 452, 875 [NASA ADS] [EDP Sciences] [CrossRef]
- Rosenberg, A., Saviane, I., Piotto, G., & Aparicio, A. 1999, AJ, 118, 2306 [NASA ADS] [CrossRef]
- Rutledge, G. A., Hesser, J. E., & Stetson, P. B. 1997, PASP, 109, 907 [NASA ADS] [CrossRef]
- Schwarzschild, M. 1975, ApJ, 195, 137 [NASA ADS] [CrossRef]
- Searle, L., & Zinn, R. 1978, ApJ, 225, 357 [NASA ADS] [CrossRef]
- Smith, G. H., & Martell, S. 2003, PASP, 115, 1211 [NASA ADS] [CrossRef]
- Smith, V. V., Cunha, K., Ivans, I. I., et al. 2005, ApJ, 633, 392 [NASA ADS] [CrossRef]
- Soszynski, I., Udalski, A., Kubiak, M., et al. 2004, Acta Astron., 54, 129 [NASA ADS]
- Suntzeff, N. B., & Kraft, R. P. 1996, AJ, 111, 1913 [NASA ADS] [CrossRef]
- Ventura, P., D'Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550, L65 [NASA ADS] [CrossRef]
- Wheeler, J. C., Sneden, C., & Truran, J. W. Jr. 1989, ARA&A, 27, 279 [NASA ADS] [CrossRef]
- Yong, D., Grundahl, F., Johnson, J. A., & Asplund, M. 2008a, ApJ, 684, 1159 [NASA ADS] [CrossRef]
- Yong, D., Melendez, J., Cunha, K., et al. 2008b, ApJ, 689, 1020 [NASA ADS] [CrossRef]
- Zinn, R., & West, M. J. 1984, ApJS, 55 45
Footnotes
- ...
clusters
![[*]](/icons/foot_motif.png)
- Based on observations collected at ESO telescopes under programmes 072.D-507 and 073.D-0211.
- ... exceptions
![[*]](/icons/foot_motif.png)
- The GC
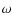 Cen (widely considered to be the remnant of a dwarf galaxy) shows evidence of
several bursts of star formation, with corresponding peaks in the metal
abundance (see Gratton et al. 2004 for a comprehensive discussion) and a spread
in metallicity seems to be confirmed in M 22 (Marino et al. 2009) as well as
in M 54 (Bellazzini et al. 2008; Carretta et al., in preparation).
Cen (widely considered to be the remnant of a dwarf galaxy) shows evidence of
several bursts of star formation, with corresponding peaks in the metal
abundance (see Gratton et al. 2004 for a comprehensive discussion) and a spread
in metallicity seems to be confirmed in M 22 (Marino et al. 2009) as well as
in M 54 (Bellazzini et al. 2008; Carretta et al., in preparation).
- ...
[Fe/H]
![[*]](/icons/foot_motif.png)
- We adopt the usual spectroscopic notation, i.e.
![$[X]= \log(X)_{\rm star} - \log(X)_\odot$](/articles/aa/full_html/2009/47/aa13003-09/img3.png) for any abundance quantity X, and
for any abundance quantity X, and
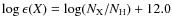 for absolute number
density abundances.
for absolute number
density abundances.
- ...
analysis
![[*]](/icons/foot_motif.png)
- Note that we usually avoided observations of stars close to the RGB tip, that may be more problematic.
- ...
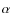 -element
-element![[*]](/icons/foot_motif.png)
- The [(Mg+Al+Si)/Fe] ratio represents the primordial
abundances of
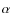 -elements in a cluster, mostly Mg and Si, as modified
by the following conversion of Mg into Al and, slightly, into Si in H-burning at
high temperature (see Carretta et al. 2009b).
-elements in a cluster, mostly Mg and Si, as modified
by the following conversion of Mg into Al and, slightly, into Si in H-burning at
high temperature (see Carretta et al. 2009b).
- ... analogues
![[*]](/icons/foot_motif.png)
- Note, however, that this cannot be the full explanation. Studies of small amplitude variable red giants in LMC and SMC from the huge OGLE-II database (Soszynski et al. 2004) reveal that multi-periodic variability affects the majority of stars, with indications of non-radial oscillations for a sizable fraction of objects.
- ... common
![[*]](/icons/foot_motif.png)
- Ter 7 is the most discrepant cluster in this comparison and is omitted from the fit.
All Tables
Table 1: Average abundances of [Fe/H] I and observed rms scatters in our sample.
Table 2: Pearson's correlation coefficients, degrees of freedom and significance for relations with iron spread in our GC sample.
Table 3: Average residuals with respect to the mean [Fe/H] for clusters with metallicities -1.4<[Fe/H]<-0.7 dex.
Table A.1: Compilation of cluster metallicities on the present scale.
All Figures
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{13003f01.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg50.png)
|
Figure 1:
Comparison for [Fe/H] I ratios (
upper panel) and for
[Fe/H] II ratios
( lower panel) obtained from GIRAFFE and UVES
spectra in the 19 programme
clusters in our sample. Metal abundances from GIRAFFE are from
Papers I, II, IV, V,
and VII. Metallicities from UVES are from
Paper III, VI, and VIII.
Error bars are 1 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{13003f02.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg51.png)
|
Figure 2: Comparison of the intrinsic spreads in [Fe/H] for the 19 GCs in our sample, as derived from UVES and GIRAFFE spectra. Error bars show the maximum and minimum spread allowed for each cluster by the statistical errors. The line indicating equality is also shown. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{13003f03.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg62.png)
|
Figure 3: Observed intrinsic dispersion in iron from GIRAFFE spectra as a function of the visual total absolute magnitude of the clusters ( upper panel), of the median S/N for HR13 spectra ( middle panel),and of the maximum temperature along the horizontal branch ( lower panel). In each panel of this and the next figures we list the Spearman and Pearson correlation coefficients. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{13003f04.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg65.png)
|
Figure 4: Observed spread of [Fe/H] in our programme clusters as a function of their peri-galactic distance ( upper left panel), age ( upper right panel), total sum of Mg+Al+Si nuclei ( lower left panel) and [Ca/Fe] ratio. |
| Open with DEXTER | |
| In the text | |
| |
Figure 5: Fraction of stars in the P ( upper panel), I ( middle panel), and E component ( lower panel) of our programme clusters as a function of the observed rms scatter in [Fe/H]. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{13003f06.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg85.png)
|
Figure 6: Average differences between individual stars and the mean [Fe/H] value in each cluster in the metallicity range -1.4<[Fe/H]<-0.7, as a function of the near IR de-reddened absolute magnitude MK0. Filled circles: stars observed with GIRAFFE; empty squares: stars observed with UVES. The open star symbols are the weighted average of residuals from UVES and GIRAFFE in the corresponding luminosity bin. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13003f07.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg88.png)
|
Figure 7: Histograms of the residuals in Fe abundances in several magnitude bins for clusters in our sample with metallicity -1.4<[Fe/H]<-0.7. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13003f08.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg93.png)
|
Figure 8: Calibration of the CG97 metallicity scale vs average metal abundances derived by us from UVES spectra for 13 clusters in common. The dotted line is the equality line, the solid line is the linear regression obtained by least-squares fit to the points. Error bars are rms scatters of the mean. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13003f09.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg98.png)
|
Figure 9: Comparison of the ZW metallicity scale vs average [Fe/H] values obtained by us from UVES spectra for all 19 clusters in our programme sample. The dotted line is the line of equality, the solid (red) line is the linear regression obtained by least-squares fit to the points and the dashed (blue) line is a second-order polynomial relation to the data. Error bars are rms scatters of the mean. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13003f10.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg105.png)
|
Figure 10: Comparison of the Kraft & Ivans (2003) metallicity scale based on Fe II abundances vs average [Fe/H] values obtained by us from Fe I lines measured on UVES spectra for 10 clusters in common. The dotted line is the identity line, the solid (red) line is the linear regression obtained by least-squares fit to the points. Error bars are rms scatters of the mean. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13003f11.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg108.png)
|
Figure 11: Comparison of our [Fe/H] average values with the reduced strength of the near-infrared Ca II triplet W' from Rutledge et al. (1997) for 17 clusters in common. The superimposed solid (red) line is the linear regression obtained by least-squares fit to the points. Error bars are rms scatters of the mean. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{13003f12.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg118.png)
|
Figure A.1: Calibration of the Q39 index from Zinn & West (1984) using our [Fe/H] values from high resolution spectroscopy. Filled red circles are our clusters with UVES spectra; blue filled squares are the two metal-rich bulge clusters whose metallicities were analysed (or revised) in Carretta et al. (2001), based on Keck HIRES spectra. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{13003f13.eps}
\end{figure}](/articles/aa/full_html/2009/47/aa13003-09/Timg119.png)
|
Figure A.2: Calibration of the reduced strength W' of the calcium triplet from Rutledge et al. (1997) after adding the metal-rich bulge cluster NGC 6553 (NGC 6528 does not have W' measured by Rutledge et al.) from Carretta et al. (2001; blue filled square). The blue dotted line is the linear regression of Fig. 11 and the red solid line the cubic spline fit to the data. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


