Asteroseismic study of helium and heavy element diffusion in solar-type stars

N. Gai; S. L. Bi; Y. K. Tang; L. H. Li

doi:10.1051/0004-6361/200912417

Home

All issues

Volume 508 / No 2 (December III 2009)

A&A, 508 2 (2009) 849-854

Full HTML

Free Access

Issue		A&A Volume 508, Number 2, December III 2009


Page(s)		849 - 854
Section		Stellar structure and evolution
DOI		https://doi.org/10.1051/0004-6361/200912417
Published online		21 October 2009

A&A 508, 849-854 (2009)

Asteroseismic study of helium and heavy element diffusion in solar-type stars

N. Gai¹ - S. L. Bi¹ - Y. K. Tang² - L. H. Li³

1 - Department of Astronomy, Beijing Normal University, Beijing 100875, PR China
2 - Department of Physics, Dezhou University, Dezhou 253023, PR China
3 - Department of Astronomy, Yale University, New Haven, CT06520, USA

Received 3 May 2009 / Accepted 18 September 2009

Abstract
Aims. Element diffusion is a basic physical element transport mechanism which induces the redistribution of chemical elements. Using the asteroseismic method, we study the effects of helium and heavy element diffusion on the internal structure and stellar evolution of solar-type stars. We also provide asteroseismic parameters for a grid of models which would be useful for direct comparison with the Kepler mission observations.
Methods. We construct a grid of solar-type stellar models with various masses (from 0.8 $M_{\odot }$ to 1.2 $M_{\odot }$ ) and metallicities (Z_i = 0.03, 0.025, 0.02, 0.015, 0.01, 0.005) with and without helium and heavy element diffusion. We compute ``second differences'' and ``small separations'' of the solar-metallicity models (Z_i = 0.02) to analyze the effects of diffusion on the convection zone, helium abundance and the evolutionary sequence of the star. In order to study the asteroseismic property of models with and without diffusion, we compute the p-mode oscillation frequencies of low-degree modes for a grid of models and construct the ( $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ ) asteroseismic diagram.
Results. We find that the element diffusion could speed up the evolution of the star, especially in the main sequence. The results show that it could enlarge the convective core and change the base of the convection envelope. In addition, the helium and heavy element diffusion make the models evolve to lower large and small separations in the asteroseismic diagram. This effect is more efficient at lower metallicity.

Key words: stars: evolution - stars: interiors - stars: oscillations

1 Introduction

Element diffusion is a basic physical transport mechanism that results in a microscopic redistribution of stellar matter. Helium and metal elements settle to the core and deplete their abundances in the outer layers, while the hydrogen abundance is enriched at the surface. The main diffusion mechanism includes pressure diffusion, thermal diffusion and concentrational diffusion. Radiative acceleration is also another very important mechanism predicted to be important for solar-metallicity stars with masses greater than approximately 1.2 $M_{\odot }$ (Chaboyer et al. 2001) or for main sequence stars with $T_{\rm eff}> 6000~{\rm K}$ (Michaud et al. 1976). In the present work, we do not consider the effect of radiative acceleration.

Helioseismic inferences have demonstrated the importance of including element diffusion in solar models (Christensen-Dalsgaard et al. 1993). Following the success of helioseismology, asteroseismology can help us to know the stellar internal structure and understand stellar evolution. Due to oscillation frequencies depending on density, temperature, and other properties of the stellar interior, it can give information about regions where the sound speed change rapidly. In the stellar outer regions, the partial reflection of acoustic waves occurs at the bottom of the outer convective zone, because there is a helium element gradient which is induced by diffusion (Vauclair & Théado 2004; Théado et al. 2005; Castro & Vauclair 2006; Mazumdar 2005). In the second helium ionization zone, the depression of $\Gamma_{1}$ can also cause an oscillatory signal in the frequencies, which can be used to determine the helium abundance in the envelope (Basu & Antia 1995; Basu et al. 2004). These are generally studied with the help of the ``second differences'', defined as $\delta_{2}\nu_{n,l}$ = $\nu_{n+1,l}$ + $\nu_{n-1,l}$ - 2 $\nu_{n,l}$ (Gough 1990).

In the stellar internal regions, small separations have been successfully applied to extract information about the stellar interior. They are determined predominantly by the sound-speed gradient in the core. Using the asymptotic theory of p-modes, the small separation is given by d_ll+2 = $\nu_{n,l}$ - $\nu_{n-1, l+2}$ (see, e.g., Basu et al. 2007). It could be used to derive the size of the convective core (Roxburgh & Vorontsov 2001; Mazumdar et al. 2006), and give evidence for the presence or absence of overshooting (Bi et al. 2008). In addition, it is sensitive to the helium core, and gives hints as to its evolutionary state. For stars at the end of the main sequence, or at the beginning of the sub-giant branch, the small separations d_ll+2 computed between l = 0 and l = 2 modes may become negative. The reason is that the helium accumulates in the convective core, which leads to a slightly steeper variation of the sound speed than in the case of convection alone (Vauclair 2007; Soriano et al. 2007; Soriano & Vauclair 2008).

Asteroseismology is a powerful method for testing both the stellar internal structure and evolution through the asteroseismic observational data directly. Many ground telescopes and the space missions, like the CoRoT mission (Baglin et al. 2006), are providing extensive data of very high quality on oscillations in a broad range of stars. NASA's Kepler mission was launched in 2009. The Kepler mission will soon yield precise high-cadence time-series photometry of hundreds of pulsating stars every few months for at least 3.5 years (Christensen-Dalsgaard et al. 2007; Metcalfe 2009). Except for the Sun, seismic observations of distant stars is likely to permit the detection of only low degree modes of oscillations (l = 0-3). The most traditional asteroseismic diagram, which was proposed by Christensen-Dalsgaard (1984, 1988, 1993), is a very useful technique combining useful features of the frequency spectrum of stars to extract information about physical processes, for example helium and heavy element diffusion, in the stellar interior, that affect the frequencies. This well-known asteroseismic diagram exploits the fact that the average large separation of radial modes $\langle \Delta\nu_{0} \rangle$ reflects the gross properties of a star, like its mass and radius, and the average small separation $\langle d_{02} \rangle$ is more sensitive to the innermost layers of the star, and therefore to its evolutionary state (Mazumdar 2005; Tang et al. 2008).

In our work, firstly we compute evolutionary tracks with various masses and metallicities, with and without helium and heavy element diffusion. Using the ``second differences'' and ``small separations'', we choose the solar-metallicity models to study the effects of helium and heavy element diffusion on the internal structure and stellar evolution. Secondly, in order to study the asteroseismic property of models with and without diffusion and test the effect of diffusion by using real seismic data, we construct the ( $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ ) asteroseismic diagram. In the online material, we provide the asteroseismic parameters $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ , $\langle d_{13} \rangle$ for all the models with various masses and metallicities to compare them directly with frequency separations from the Kepler mission observations.

$\begin{figure} \par\includegraphics[width=14cm,clip]{12417fg1.eps} \end{figure}$

Figure 1:

Evolutionary tracks computed for solar metallicity Z = 0.02 with masses of 0.8 $M_{\odot }$ , 0.9 $M_{\odot }$ , 1.0 $M_{\odot }$ , 1.1 $M_{\odot }$ and 1.2 $M_{\odot }$ . Solid lines: standard homogeneous models without diffusion. Dash dot lines: models with helium and heavy element diffusion. Several groups of models are selected. Their ages are labeled in the figure in units of Gye. Model A (3.80 Gyr) and model B (3.28 Gyr) have similar positions in the H-R diagram.

Open with DEXTER

In Sect. 2, we give details of the evolutionary models and the computational method. The effects of diffusion on the stellar internal structure, evolution and its asteroseismic property also are analyzed in this section. We summarize our conclusions in Sect. 3.

2 Computation and analysis

2.1 Computation

Using the Yale stellar evolution code (YREC; Guenther et al. 1992; Demarque et al. 2008), we compute evolutionary sequences for models with masses 0.8 $M_{\odot }$ , 0.9 $M_{\odot }$ , 1.0 $M_{\odot }$ , 1.1 $M_{\odot }$ , 1.2 $M_{\odot }$ , the initial metallicities Z_i = 0.03, 0.025, 0.02, 0.015, 0.01, 0.005, fixed helium abundance Y_i = 0.28 and mixing-length parameter $\alpha$ = 1.75. The initial zero-age main sequence (ZAMS) models are derived from pre-main-sequence evolution models. The input physics are described as follows:

Diffusion: diffusion of both the helium and heavy element abundances (by weight Y and Z respectively) is considered in the stellar model computations, using the diffusion coefficients of Thoul et al. (1994). The diffusion of all metal elements are assumed to diffuse at the same rate as fully ionized iron. The differences in the diffusion velocities among the metal elements are small for the low mass stars (M $\leq$ 1.3 $M_{\odot }$ solar-metallicity stars). The 1.1 $M_{\odot }$ model especially behaves much like a solar model and all elements are affected by gravitational settling at a similar pace (Turcotte et al. 1998a).

Radiative acceleration: we note that the Thoul et al. (1994) diffusion coefficients include the effects of pressure diffusion (i.e., gravitational settling), thermal diffusion and concentrational diffusion, but exclude the effect of radiative acceleration. Turcotte and collaborators have researched the effects of radiative acceleration in detail in the Sun, solar metallicity F-stars, AmFm stars, metal-poor stars and so on (Richer et al. 1998; Turcotte et al. 1998a,b; Richer et al. 2000; Richard et al. 2002a,b). Radiative acceleration is another important chemical transport mechanism. It is predicted to be important for main sequence stars with $T_{\rm eff}$ > 6000 K (Michaud et al. 1976). The above mentioned studies have shown further that radiative acceleration is predicted to be important for solar metallicity stars with masses greater than approximately 1.2 $M_{\odot }$ (Chaboyer et al. 2001; Turcotte et al. 1998a). The metallicity dependence of the effects of atomic diffusion was studied by Richard et al. (2002b). They calculated evolutionary models for population II stars of 0.5-1.2 $M_{\odot }$ and [Fe/H] = -4.31 $\sim$ -0.71 to determine the effect of metallicity on the size of abundance anomalies to be expected from gravitational settling, thermal diffusion and radiative acceleration. From their discussion, especially Fig. 3 of Richard et al. (2002b), we found that radiative acceleration could only counteract about 10% of the gravitational diffusion even for their metal-richest models Z_i = 0.0067 ( $[\rm Fe/H]$ $\approx$ -1.22). Since radiative acceleration is reduced for higher metallicity, it is unlikely that radiative acceleration is very important in the stars that we will model in this paper and we concentrate on the effect of pressure diffusion, thermal diffusion and concentrational diffusion.

Opacity: we use the OPAL GN93 opacities (Iglesias & Rogers 1996) along with low temperature opacities (Ferguson et al. 2005). The low temperature opacities are used for $\log T$ < 4.4 and the OPAL opacities are used for $\log T$ > 4.5. In the transition region for 4.4 $\leq$ $\log T$ $\leq$ 4.5, the low temperature opacities tables and the OPAL opacities are used.

Both the OPAL opacities and low temperature opacities will automatically interpolate to the required Z. The opacity routines, with YREC, perform a four-point Lagrangian interpolation scheme over a 4-dimensional grid of Z, X, T and $\rho$ . The temperature range of OPAL GN93 is 3.75 < $\log T$ < 8.7 and of low temperature opacity is 2.7 < $\log T$ < 4.5, the radius range is -8.0 < $\log R$ < 1.0. According to the formula $\rho$ = R(T/10^-6)³, the opacity tables span nearly all of the temperature and density space at all metallicities needed for the model grid and the extremes of evolution state that we considered.

Equation-of-state: the OPAL equation-of-state tables EOS2003 (Rogers & Nayfonov 2002) are used in the computation. In the outer regions ( $\log T$ < 5.8), the equation-of-state (i.e., EOS) routines determine particle densities by solving the Saha equation for the single ionization state of H and metals, and the single and double ionization states of He. In the inner regions ( $\log T$ > 6.3), the gas is assumed to be fully ionized and the Saha equation is not used in the EOS calculation. In the transition region between these two regions (5.8 $\leq$ $\log T$ $\leq$ 6.3), the EOS interpolates between the partially and fully ionized solutions with a ramp function and is averaged to obtain a smooth transition.

Boundary condition: the two inner boundary conditions set the values of the radius and luminosity variables to zero at the innermost mass shell which is not at the very center, but in a shell chosen close to the center.

The surface boundary condition use a triangulation method as described in Kippenhahn et al. (1967). In order to specify the surface boundary condition, three inward envelope integrations are constructed. For all the stellar models the Eddington $T - \tau$ relation are used. The inward integration starts from an optical depth near $\tau$ = 10^-10 to $\tau$ = 2/3 at which the temperature reaches $T_{\rm eff}$ (Demarque et al. 2008).

Model zoning and time step: as we computed the evolution of stars of various masses, the main sequence model has about 1500 mass shells in the interior, approximately 600 shells in the envelope and 600 shells in the atmosphere. We have YREC automatically determine the optimum time step during the evolution.

In order to investigate the influence of diffusion on the internal structure and evolution of the models, we also computed two series of models with and without helium and heavy element diffusion for a given stellar mass and metallicity. The subsequent pulsation analysis of low degree p-modes (l= 0-3) for models in each given mass is implemented using the Guenther & Demarque pulsation code under the adiabatic approximation (Guenther et al. 1992).

2.2 Solar-metallicity stars

Figure 1 displays the computed evolutionary tracks with Z_i = 0.02. For each evolutionary track, we plot several groups of models. In each group, the dot sign represents the model without diffusion, and the asterisk represents the model with helium and heavy element diffusion. Furthermore, at the same group, the models of 1.2 $M_{\odot }$ and some other groups of subgiant models have similar positions in the H-R diagram, i.e. the similar luminosities and effective temperatures, but they have different ages, which can be seen in Fig. 1. In the case of 0.8 $M_{\odot }$ , 0.9 $M_{\odot }$ , 1.0 $M_{\odot }$ and 1.1 $M_{\odot }$ , each group of main sequence models has the same age. But the increase of the opacity in the envelope due to the settling of helium and metal elements provides evolutionary tracks cooler than those without diffusion. From Fig. 1 we found that element diffusion could speed up the evolution of the star, especially in the main sequence. However, when stars evolve past the turn off point, the surface convection zone rapidly deepens, and the diffusion is suppressed.

In order to study the effect of helium and heavy element diffusion on the internal structure (not only outer layers but also the internal core), we selected the relatively high mass star 1.2 $M_{\odot }$ . Model A and model B for 1.2 $M_{\odot }$ are also shown in Fig. 1. They are at the similar positions in the H-R diagram, i.e. $\log(L/L_{\odot})_{A}$ = 0.44, $\log(L/L_{\odot})_{B}$ = 0.42 and $\log(T_{\rm eff})_{A}$ = 3.79, $\log(T_{\rm eff})_{B}$ = 3.79, but their ages are different. The age of model A is 3.80 Gyr (without diffusion) and model B is 3.28 Gyr (with diffusion). Then, we use the Guenther & Demarque pulsation code (Guenther 1992) to compute the low degree p-mode oscillation frequencies (l= 0-3) for the above two models, and show their oscillation characteristics in Figs. 2 and 3, respectively.

$\begin{figure} \par\hspace{-1.5mm}\includegraphics[width=6.8cm,clip]{12417fg2.eps}\vspace{1mm} \includegraphics[width=7cm,clip]{12417fg3.eps} \end{figure}$	Figure 2: Upper panel: the second differences of the oscillation frequencies. The errorbars are obtained using the error propagation formula and assuming errors of 1 part in 10⁴ in frequencies. Lower panel: the Fourier transform of the second differences as a function of the acoustic depth for model A and model B. Solid lines describe model A and dash dot lines describe model B.
Open with DEXTER

$\begin{figure} \par\hspace{-5.1mm}\includegraphics[width=7.25cm,clip]{12417fg4.... ...g5.eps}\vspace{1mm} \includegraphics[width=7cm,clip]{12417fg6.eps} \end{figure}$	Figure 3: Upper panel: buoyancy frequency, middle panel: sound speed gradient profiles, lower panel: small separations for model A and model B. The black line describes model A and the red line describes model B.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12417fg7.eps} \end{figure}$

Figure 4:

( $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ ) asteroseismic diagram for models with Z_i = 0.03, 0.025, 0.02, 0.015, 0.01, 0.005. For a given metallicity, a model without diffusion (solid lines) and another with helium and heavy element diffusion (dot-dashed lines) is shown to illustrate the shift in the tracks. For a given mass, there are the same numbers of circles and asterisks on the no-diffusion and diffusion tracks respectively which indicates the age of models from 0.05 Gyr in steps of 0.05 Gyr increases in the main sequence stage. The asteroseismic parameters of these models are listed in Tables 1-6.

Open with DEXTER

In the framework of Tassoul's asymptotic theory (Tassoul 1980), Gough (1990) mentioned the ``second differences'' which give interesting information on the stellar outer layers. Stellar acoustic p-modes with low l values propagate deep inside the stars. But the rapid change in the derivatives of the sound speed, which may be due to the boundary of the convective zone, to the helium ionization region or to element gradients, produces a periodic variation in the phase shift $\alpha (\nu, l)$ of acoustic waves as a function of frequency with a period 2 $t_{\rm s}$ , where $t_{\rm s}$ is the time needed for the acoustic waves to travel between the surface and the considered region (acoustic depth), i.e.:

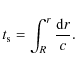
$\begin{displaymath}% t_{\rm s}=\int^{r}_{R}\frac{{\rm d}r}{c}. \end{displaymath}$

(1)

These effects on the frequencies can be clearly seen in the second differences and their sinusoidal modulation appears as a peak in the Fourier spectrum (Fig. 2), for a timescale t = 2 $t_{\rm s}$ .

We estimate the errors in $\delta_{2}\nu$ through the error propagation formula and assuming errors of 1 part in 10⁴ in frequencies. Such an error margin in the frequencies is consistent with the expectations from the asteroseismic space missions MOST (Walker et al. 2003) and CoRoT (Baglin 2003) and ground-based seismic observations (e.g., Bedding & Kjeldsen 2003; Bouchy & Carrier 2002) (Mazumdar 2005). We also use the exact frequencies of model A, B and frequencies for which $\sigma_{\nu}$ = $\pm10^{-4}\nu$ is added to the exact frequencies to fit the Fourier transform of $\delta_{2}\nu$ .

From the lower panel of Fig. 2, i.e. the Fourier transform of the second differences, we can see the difference between model A and B. The peaks around t $\approx$ 2000 s are caused by HeII ionisation zones which lead to depression in the thermodynamical coefficient $\Gamma_{1}$ . For model B with diffusion, the feature due to the helium ionisation zone is smaller; helium depletion occurs in the HeII zone by diffusion. The boundary of the convection envelope also leads to characteristic features at t $\approx$ 6400 s (A) and t $\approx$ 5800 s (B). The peak due to the bottom of the convective zone of model B is much higher than A. That is because the helium and heavy elements are accumulated and formed a gradient at the base of the convective zone by diffusion. Diffusion can change the convective depth and the helium and heavy element gradient also affects the sound velocity.

Figure 3 presents the buoyancy (or Brunt-Väisälä) frequency (upper panel), the sound speed gradient (W(r) = $(1/g)({\rm d}c^{2}/{\rm d}r)$ ) profiles (middle panel) and the small separations (lower panel) for model A and B. The differences between the models with and without diffusion are clearly visible.

Firstly, we compute the square of the buoyancy frequency N². This parameter is very sensitive to the convection zone. In this region N² < 0, hence the frequency N is imaginary (Guenther 2002). For plotting purposes, we set the buoyancy frequency N to zero in the convection zone. From the upper panel of Fig. 3, we can see that there are bumps at the boundary of the convective core for both model A and B. The surface convection zone is also revealed in the propagation diagram. The frequency N again drops quickly to zero (actually becomes imaginary) at the base of the convection envelope.

Secondly, in the middle panel of Fig. 3, there is a discontinuity in the sound speed gradient profile at the boundary of the convective core of the star which is about $R_{\rm cc}/R$ = 0.042 (model A) and 0.053 (models B). For a solar-metallicity model with diffusion, the size of the convective core is greater than the case without diffusion by about 26 $\%$ . The sound speed gradient of model A is steeper than that of B.

Thirdly, as shown in the lower panel of Fig. 3, the values of the small separations of model A are smaller than those of B. As the age of the star increases, the values of the small separations decrease. Model B is younger than A.

In addition, the small separations of model A for the degrees l=0 - l=2 become negative at a frequency of about 3.6 mHz. Soriano & Vauclair (2008) showed that the small separations may become negative at the end of the main sequence for the d₀₂ separations. This effect is directly related to the presence of a helium core; it was also induced by convection in the central stellar regions. At the end of the main sequence, the chemical gradient induces a much larger sound velocity gradient than convection alone, and leads to negative small separations. So we can see that model B is at the main sequence, while model A is at the end of the main sequence.

2.3 Asteroseismic diagram

In order to study the asteroseismic property of models with and without diffusion, we compute the p-mode oscillation frequencies of low-degree modes for a grid of models under the adiabatic approximation. These models include the initial metallicity Z_i = 0.03, 0.025, 0.02, 0.015, 0.01, 0.005 and the masses range from 0.8 $M_{\odot }$ to 1.2 $M_{\odot }$ in steps of 0.1 $M_{\odot }$ . Then we construct the ( $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ ) asteroseismic diagram in Fig. 4. For a given metallicity and mass, we have shown two sets of models with and without helium and heavy element diffusion. The solid lines and circles represent the no-diffusion models; the dot-dashed lines and asterisks represent the diffusion models.

The diagram shows that helium and heavy element diffusion make the models evolve to lower large and small separations. For a given metallicity, as the evolutionary ages become shorter for larger masses and because of the very long diffusion time scale, the effect of diffusion reduces with larger mass. For the models with the same mass, since the outer convective envelope grows thinner for lower metallicity models, the effect of diffusion becomes more efficient for models with Z_i = 0.01 and 0.005. But models with mass greater than 1.0 $M_{\odot }$ with Z_i = 0.005 and much poorer-metallicity models (for example, Z_i = 0.001) have a much thinner surface convective envelope ( $\log (M_{\rm envp}/M)$ < -7). These models are hard to analyze with asteroseismology since they do not obey the asymptotic frequency relation (Tassoul 1980; Karoff et al. 2009).

In Fig. 4, for a given metallicity and mass, we also labeled the same number of circles and asterisks on the no-diffusion and diffusion tracks, which indicates the age of models from 0.05 Gyr and in steps of 0.05 Gyr in the main sequence stage. The asteroseismic parameters, i.e. the average large and small separations $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ , $\langle d_{13} \rangle$ of these models are calculated averaging over n = 10, 11, 12, ..., 30 and listed in Tables 1-6. For each group of models with the same ages, the large and small separations of diffusion model are smaller than ones of the no-diffusion model. From the formulas (Ulrich 1986)

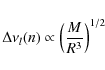
$\begin{displaymath}% \Delta\nu_{l}(n)\propto \left(\frac{M}{R^{3}}\right)^{1/2} \end{displaymath}$

(2)

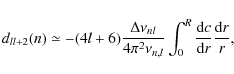
$\begin{displaymath}% d_{ll+2}(n)\simeq -(4l+6)\frac{\Delta\nu_{nl}}{4\pi^{2}\nu_{n,l}}\int^{R}_{0}\frac{{\rm d}c}{{\rm d}r}\frac{{\rm d}r}{r}, \end{displaymath}$

(3)

we find that the diffusion could enlarge the radius. The small separation is very sensitive to the variation in the sound speed in the center part of the star, and may provide information about the composition of the star in its nuclear region. The smaller d₀₂ indicats that the diffusion could speed the evolution of stars.

Thus, the helium and heavy element diffusion has very important effects on the internal structure and evolution of a star. Many ground telescopes and asteroseismic space missions, like MOST, CoRoT, and especially Kepler, will soon provide accurate seismic data on solar-type stars. On the one hand, we expect to have enough accurate seismic data to test the effect of diffusion. On the other hand, the ( $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ ) asteroseismic diagram and asteroseismic parameters in our Tables 1-6 can compare results to frequency separations from the Kepler mission observations directly. They also can help in estimating physical parameters of targeted stars efficiently. In addition, they may be useful in deducing the common age and composition of a cluster of stars.

3 Conclusion

Element diffusion is a basic physical element transport mechanism which is driven by pressure diffusion, thermal diffusion and concentrational diffusion. In our paper, we study the effects of helium and heavy element diffusion on solar-type stars with metallicity Z_i = 0.03, 0.025, 0.02, 0.015, 0.01, 0.005 and masses from 0.8 $M_{\odot }$ to 1.2 $M_{\odot }$ .

We computed ``second differences'' and ``small separations'' of the solar-metallicity models to analyze the effects of diffusion on the convection zone, helium abundance and the evolutionary sequence of the star.

We also constructed a ( $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ ) asteroseismic diagram to study the asteroseismic property of models with and without diffusion.

We find that:

(1): The helium and heavy element diffusion could speed up the evolution of the star, especially in the main sequence; diffusion could enlarge the convective core by about 26 $\%$ for solar-metallicity stars and change the base of the convection envelope.
(2): Helium and heavy element diffusion made the models evolve to lower large and small separations in the asteroseismic diagram. This effect is more efficient at lower metallicity. We expect that the effect of diffusion will be tested by accurate seismic data from ground telescopes and space missions.

In the online material, we provide the asteroseismic parameters $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ , $\langle d_{13} \rangle$ in Tables 1-6 for all the models with various masses and metallicities. NASA's Kepler mission is going to provide much stellar pulsation data. Metcalfe et al. (2009) are researching a stellar model-fitting pipeline for asteroseismic data from the Kepler mission. We hope that our models will be useful for model grid comparisons planned as part of the Kepler Asteroseismic Consortium by Metcalfe and collaborators. We also hope that the provided asteroseismic parameters will be useful for comparison with the Kepler mission observations.

Acknowledgements

We thank the anonymous referee for constructive comments that lead to significant improvements of this paper. We wish to thanks Sarbani Basu for her comments and help with the software. This work was supported by The Ministry of Science and Technology of the People's Republic of China through grant 2007CB815406, and by NSFC grants 10773003, 10778601 and 10933002. Y. K. Tang acknowledge the support of Shandong Nature Science Foundation and Dezhou University Foundation(08RC11).

References

Baglin, A. 2003, AdSpR, 31, 345 [NASA ADS]
Baglin, A., Michel, E., Auvergne, M., & the CoRoT team 2006, in Proc. SOHO 18/GONG 2006/HELAS I Conf., Beyond the Spherical Sun, ed. K. Fletcher, & M. Thompson (Noordwijk: ESA), ESA SP-624, 34
Basu, S., & Antia, H. M. 1995, MNRAS, 276, 1402 [NASA ADS]
Basu, S., Mazumdar, A., Antia, H. M., & Demarque, P. 2004, MNRAS, 350, 277 [NASA ADS] [CrossRef]
Basu, S., Chaplin, W. J., Elsworth, Y., et al. 2007, ApJ, 655, 660 [NASA ADS] [CrossRef]
Bedding, T. R., & Kjeldsen, H. 2003, PASA, 20, 203 [NASA ADS]
Bi, S. L., Basu, S., & Li, L. H. 2008, ApJ, 673, 1093 [NASA ADS] [CrossRef]
Bouchy, F., & Carrier, F. 2002, A&A, 390, 205 [NASA ADS] [EDP Sciences] [CrossRef]
Castro, M., & Vauclair, S. 2006, A&A, 456, 611 [NASA ADS] [EDP Sciences] [CrossRef]
Chaboyer, B., Fenton, W. H., Nelan, J. E., Patnaude, D. J., & Simon, F. E. 2001, ApJ, 562, 521 [NASA ADS] [CrossRef]
Christensen-Dalsgaard, J. 1984, in Space Research Prospects in Stellar Activity and Variability, ed. F. Praderie (Paris Observatory Press), 11
Christensen-Dalsgaard, J. 1988, in Advances in helio- and asteroseismology, ed. J. Christensen-Dalsgaard, & S. Frandsen (Dordrecht: Reidel), Proc. IAU Symp., 123, 295
Christensen-Dalsgaard, J. 1993, in Seismic Investigation of the Sun and Stars, ed. T. M. Bron, ASP Conf. Ser., 42, 347
Christensen-Dalsgaard, J., Proffitt, C. R., & Thompson, M. J. 1993, ApJ, 403, L75 [NASA ADS] [CrossRef]
Christensen-Dalsgaard, J., Arentoft, T., Brown, T. M., et al. 2007, Commun. Asteroseismol., 150, 350 [CrossRef]
Demarque, P., Guenther, D. B., Li, L. H., et al. 2008, Ap&SS, 316, 31 [NASA ADS] [CrossRef]
Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef]
Gough, D. O. 1990, in progress of Seismology of the Sun and Stars, Proc. Oji International Seminar Hakone (Japan: Springer Verlag), Lect. Notes Phys., 367, 283
Guenther, D. B. 2002, ApJ, 569, 911 [NASA ADS] [CrossRef]
Guenther, D. B., Demarque, P., Kim, Y.-C., et al. 1992, ApJ, 387, 372 [NASA ADS] [CrossRef]
Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef]
Karoff, C., Metcalfe, T. S., & Chaplin, W. J. 2009, MNRAS, accepted [arXiv:0906.5441v1]
Kippenhahn, R., Weigert, A., & Hofmeister, E. 1967, Methods Comput. Phys., 7, 129
Mazumdar, A. 2005, A&A, 441, 1079 [NASA ADS] [EDP Sciences] [CrossRef]
Mazumdar, A., Basu, S., Collier, B. L., et al. 2006, MNRAS, 372, 949 [NASA ADS] [CrossRef]
Metcalfe, T. S., Creevey, O. L., & Christensen-Dalsgaard, J. 2009, ApJ, 699, 373 [NASA ADS] [CrossRef]
Michaud, G., Charland, Y., Vauclair, S., & Vauclair, G. 1976, ApJ, 210, 447 [NASA ADS] [CrossRef]
Richard, O., Michaud, G., Richer, J., et al. 2002a, ApJ, 568, 979 [NASA ADS] [CrossRef]
Richard, O., Michaud, G., & Richer, J. 2002b, ApJ, 580, 1100 [NASA ADS] [CrossRef]
Richer, J., Michaud, G., Rogers, F., et al. 1998, ApJ, 492, 833 [NASA ADS] [CrossRef]
Richer, J., Michaud, G., & Turcotte, S. 2000, ApJ, 529, 338 [NASA ADS] [CrossRef]
Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [NASA ADS] [CrossRef]
Roxburgh, I. W., & Vorontsov, S. V. 2001, MNRAS, 322, 85 [NASA ADS] [CrossRef]
Soriano, M., & Vauclair, S. 2008, A&A, 488, 975 [NASA ADS] [EDP Sciences] [CrossRef]
Soriano, M., Vauclair, S., Vauclair, G., & Laymand, M. 2007, A&A, 471, 885 [NASA ADS] [EDP Sciences] [CrossRef]
Tang, Y. K., Bi, S. L., & Gai, N. 2008, A&A, 492, L49 [NASA ADS] [EDP Sciences] [CrossRef]
Tassoul, M. 1980, ApJS, 43, 469 [NASA ADS] [CrossRef]
Théado, S., Vauclair, S., Castro, M., et al. 2005, A&A, 437, 553 [NASA ADS] [EDP Sciences] [CrossRef]
Thoul, A. A., Bahcall, J. N., & Loeb, A. 1994, ApJ, 421, 828 [NASA ADS] [CrossRef]
Turcotte, S., Richer, J., & Michaud, G. 1998a, ApJ, 504, 559 [NASA ADS] [CrossRef]
Turcotte, S., Richer, J., Michaud, G., et al. 1998b, ApJ, 504, 539 [NASA ADS] [CrossRef]
Ulrich, R. K. 1986, ApJ, 306, 37 [NASA ADS] [CrossRef]
Vauclair, S. 2007, AIPC, 948, 3 [NASA ADS]
Vauclair, S., & Théado, S. 2004, A&A, 425, 179 [NASA ADS] [EDP Sciences] [CrossRef]
Walker, G., Matthews, J., Kuschnig, R., et al. 2003, PASP, 115, 1023 [NASA ADS] [CrossRef]

Online Material

Table 1: The average large and small separations $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ , $\langle d_{13} \rangle$ for models with Z_i = 0.03.

Table 2: The average large and small separations $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ , $\langle d_{13} \rangle$ for models with Z_i = 0.025.

Table 3: The average large and small separations $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ , $\langle d_{13} \rangle$ for models with Z_i = 0.02.

Table 4: The average large and small separations $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ , $\langle d_{13} \rangle$ for models with Z_i = 0.015.

Table 5: The average large and small separations $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ , $\langle d_{13} \rangle$ for models with Z_i = 0.01.

Table 6: The average large and small separations $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ , $\langle d_{13} \rangle$ for models with Z_i = 0.005.

Footnotes

... stars: Tables 1-6 are only available in electronic form at http://www.aanda.org

All Tables

Table 1: The average large and small separations $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ , $\langle d_{13} \rangle$ for models with Z_i = 0.03.

Table 2: The average large and small separations $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ , $\langle d_{13} \rangle$ for models with Z_i = 0.025.

Table 3: The average large and small separations $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ , $\langle d_{13} \rangle$ for models with Z_i = 0.02.

Table 4: The average large and small separations $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ , $\langle d_{13} \rangle$ for models with Z_i = 0.015.

Table 5: The average large and small separations $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ , $\langle d_{13} \rangle$ for models with Z_i = 0.01.

Table 6: The average large and small separations $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ , $\langle d_{13} \rangle$ for models with Z_i = 0.005.

All Figures

$\begin{figure} \par\includegraphics[width=14cm,clip]{12417fg1.eps} \end{figure}$	Figure 1: Evolutionary tracks computed for solar metallicity Z = 0.02 with masses of 0.8 $M_{\odot }$ , 0.9 $M_{\odot }$ , 1.0 $M_{\odot }$ , 1.1 $M_{\odot }$ and 1.2 $M_{\odot }$ . Solid lines: standard homogeneous models without diffusion. Dash dot lines: models with helium and heavy element diffusion. Several groups of models are selected. Their ages are labeled in the figure in units of Gye. Model A (3.80 Gyr) and model B (3.28 Gyr) have similar positions in the H-R diagram.
Open with DEXTER
In the text

$\begin{figure} \par\hspace{-1.5mm}\includegraphics[width=6.8cm,clip]{12417fg2.eps}\vspace{1mm} \includegraphics[width=7cm,clip]{12417fg3.eps} \end{figure}$	Figure 2: Upper panel: the second differences of the oscillation frequencies. The errorbars are obtained using the error propagation formula and assuming errors of 1 part in 10⁴ in frequencies. Lower panel: the Fourier transform of the second differences as a function of the acoustic depth for model A and model B. Solid lines describe model A and dash dot lines describe model B.
Open with DEXTER
In the text

$\begin{figure} \par\hspace{-5.1mm}\includegraphics[width=7.25cm,clip]{12417fg4.... ...g5.eps}\vspace{1mm} \includegraphics[width=7cm,clip]{12417fg6.eps} \end{figure}$	Figure 3: Upper panel: buoyancy frequency, middle panel: sound speed gradient profiles, lower panel: small separations for model A and model B. The black line describes model A and the red line describes model B.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12417fg7.eps} \end{figure}$	Figure 4: ( $\langle \Delta\nu_{0} \rangle$ , $\langle d_{02} \rangle$ ) asteroseismic diagram for models with Z_i = 0.03, 0.025, 0.02, 0.015, 0.01, 0.005. For a given metallicity, a model without diffusion (solid lines) and another with helium and heavy element diffusion (dot-dashed lines) is shown to illustrate the shift in the tracks. For a given mass, there are the same numbers of circles and asterisks on the no-diffusion and diffusion tracks respectively which indicates the age of models from 0.05 Gyr in steps of 0.05 Gyr increases in the main sequence stage. The asteroseismic parameters of these models are listed in Tables 1-6.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.